A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays
Abstract
:1. Introduction
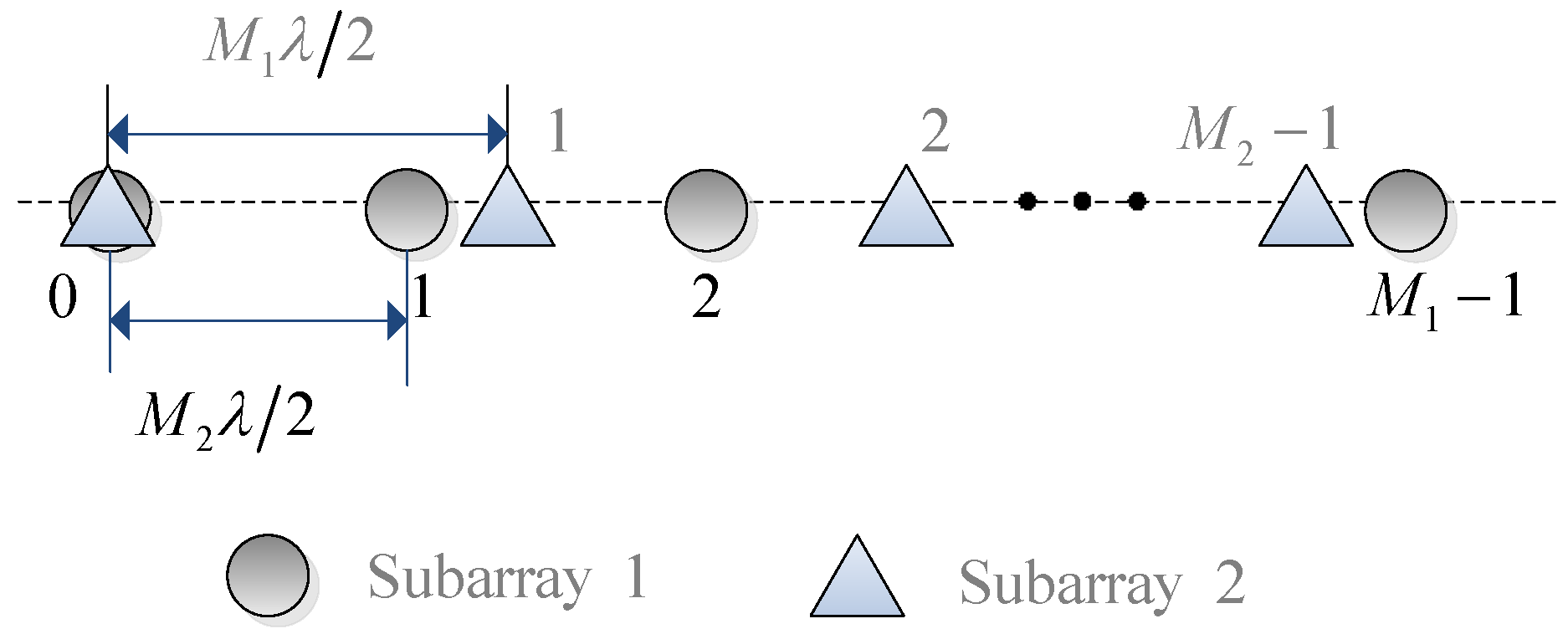
2. System Model
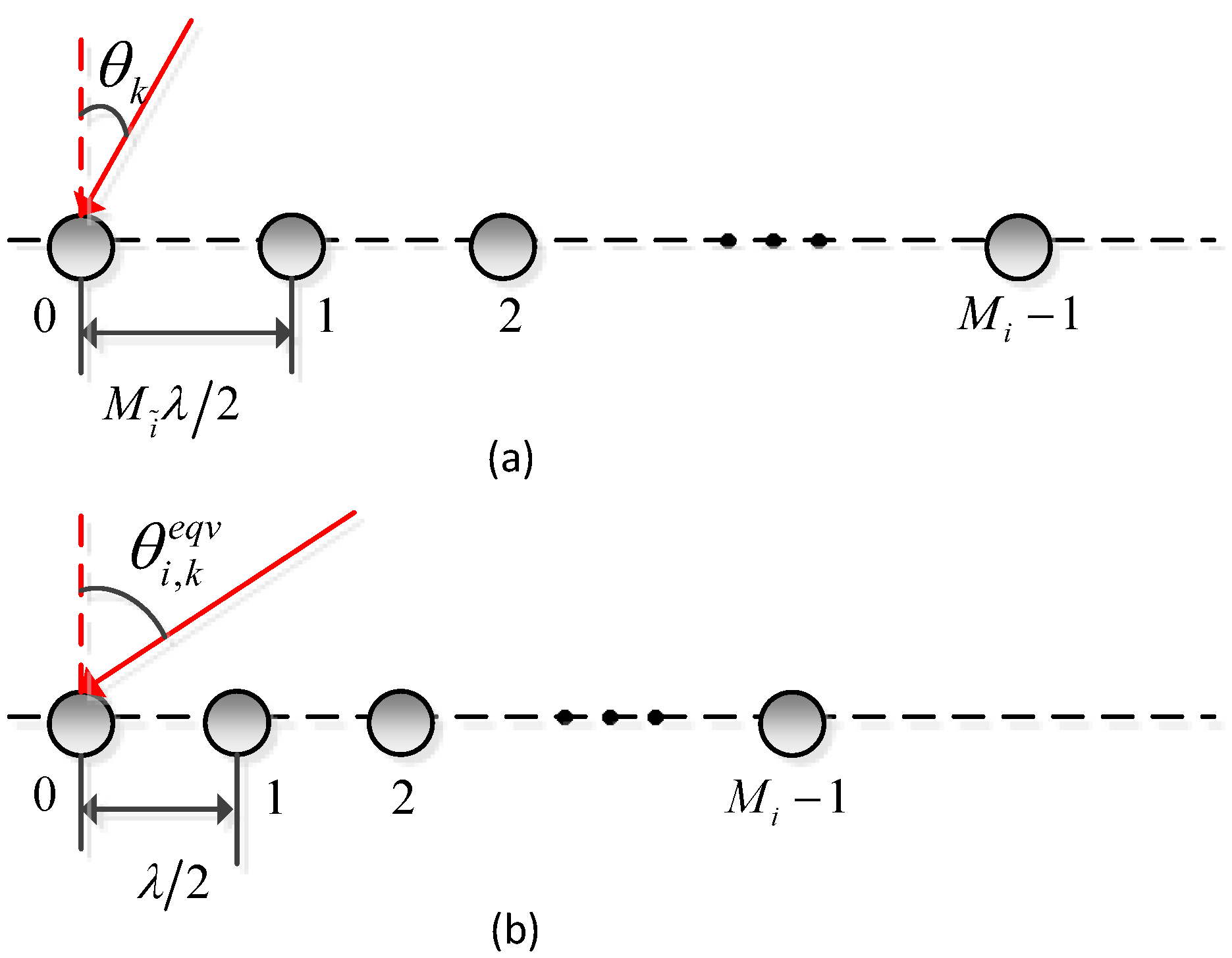
3. Proposed DOA Estimation Method
3.1. Proposed Method
3.2. Complexity Analysis
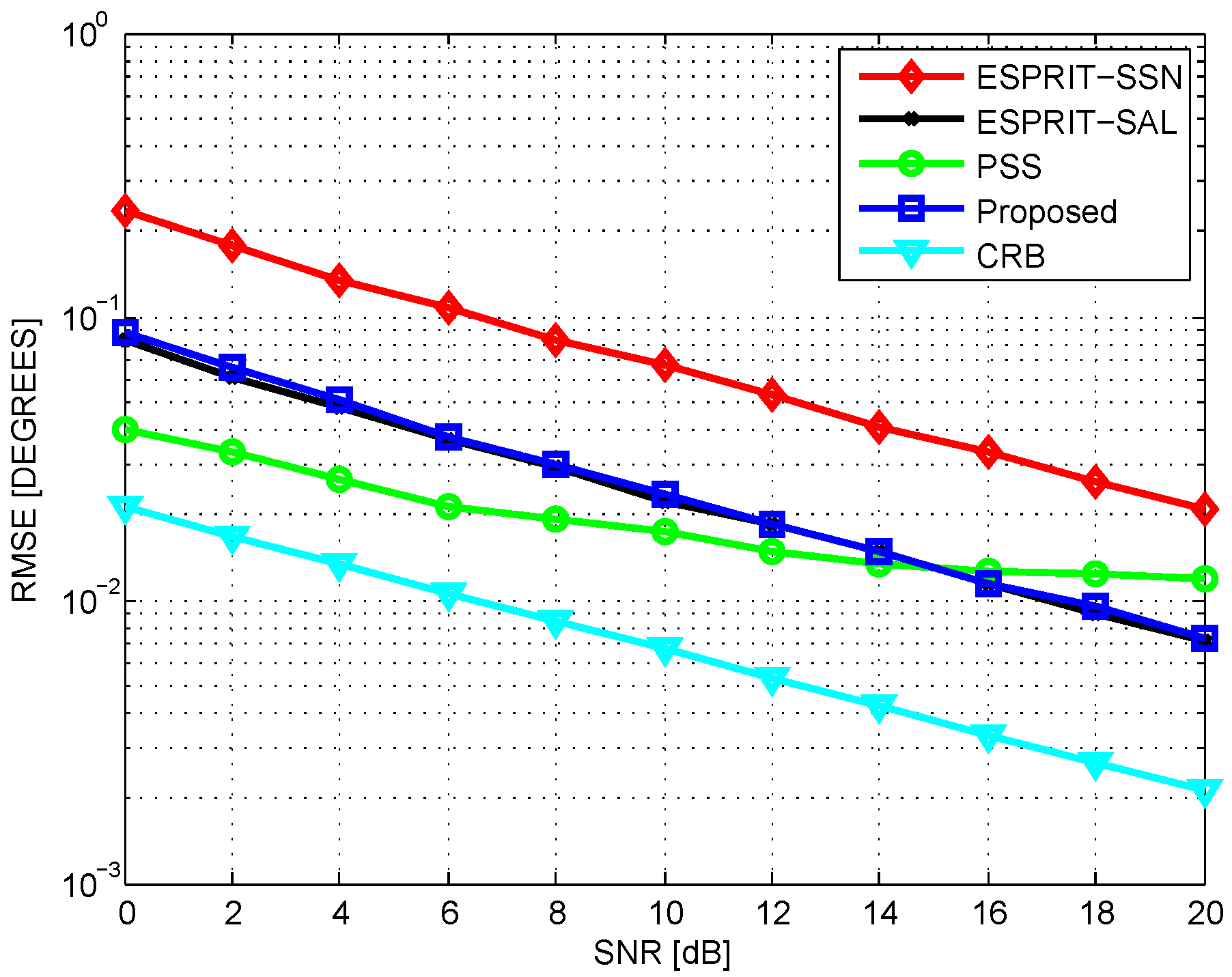
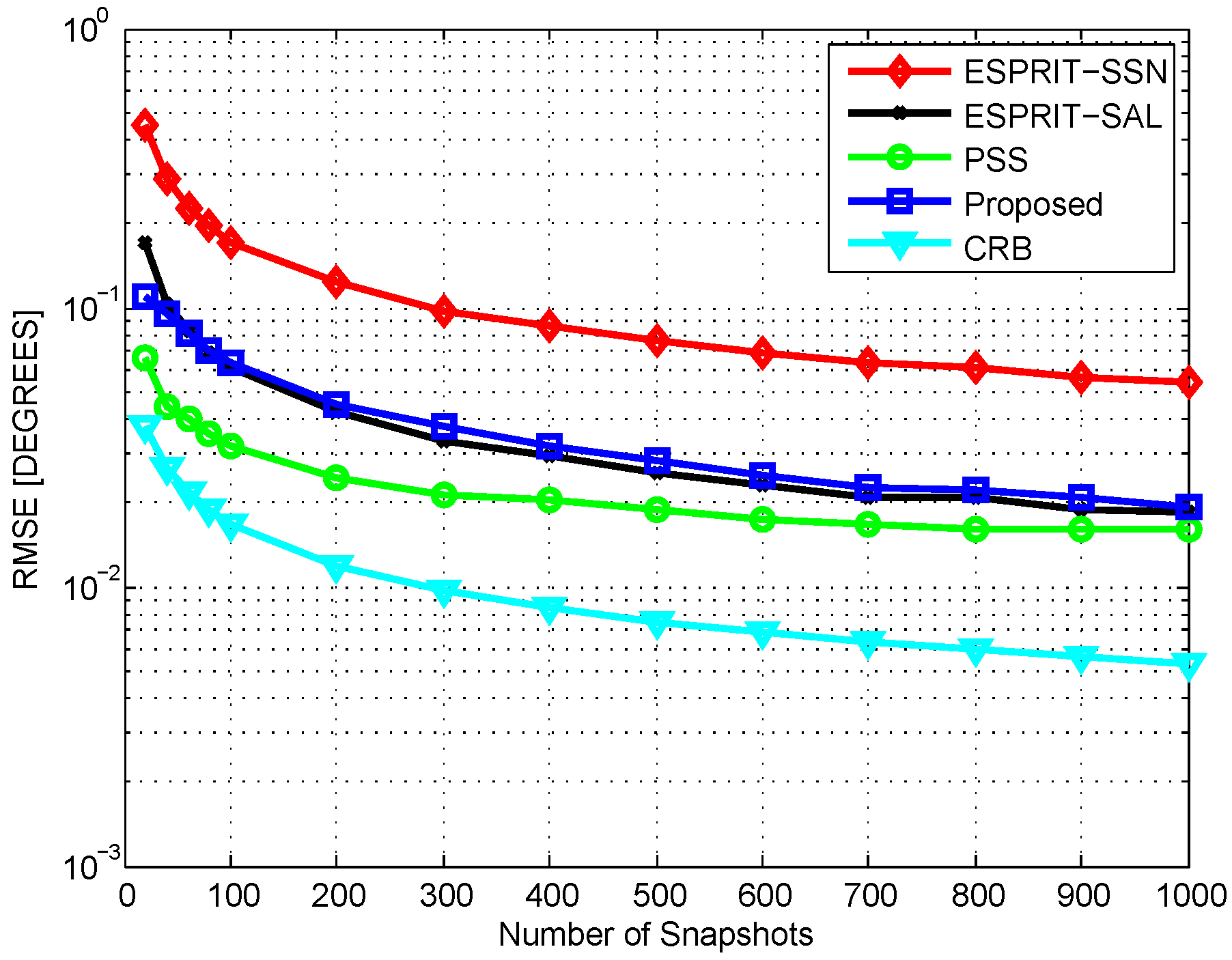
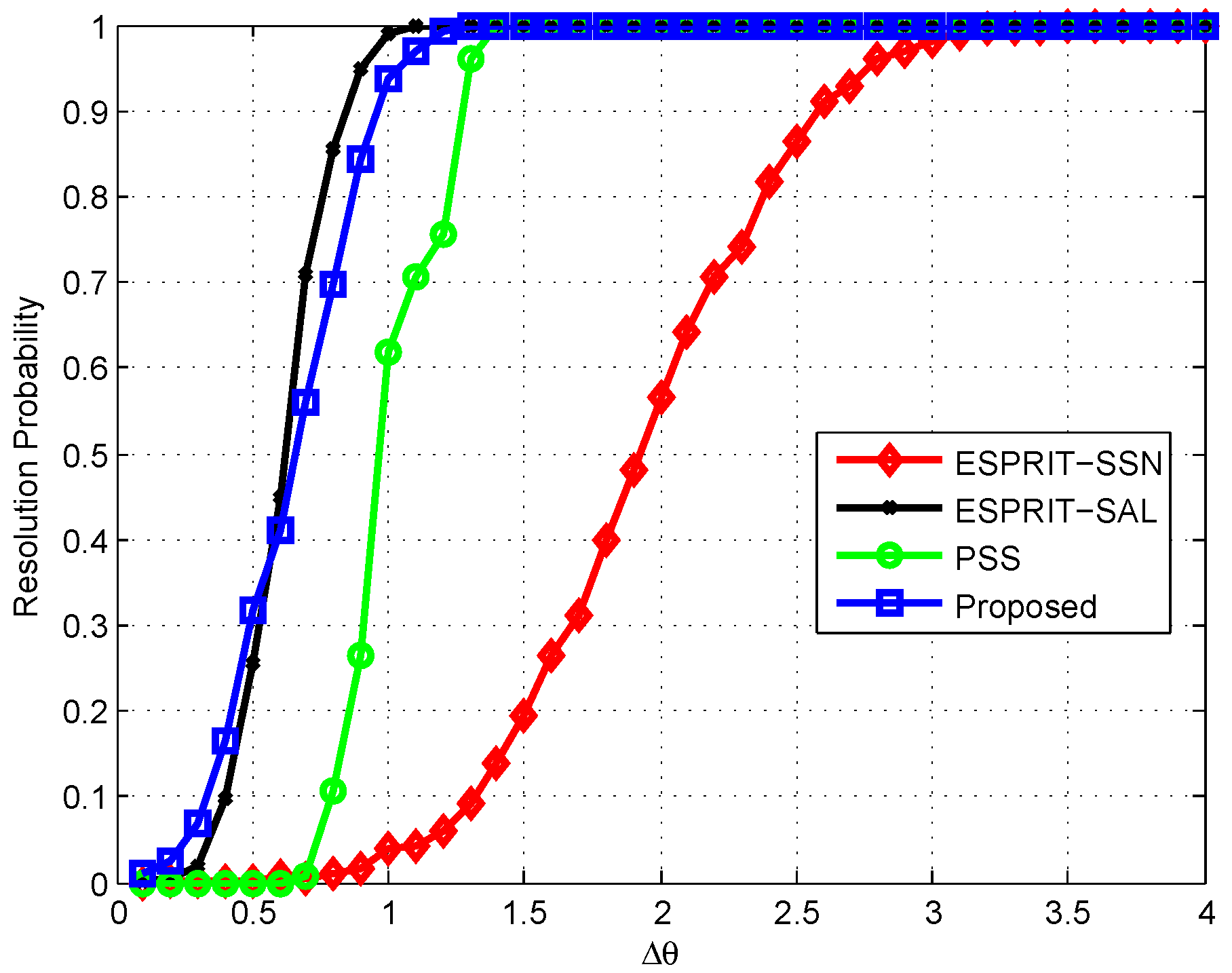
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DOA | Direction of arrival |
| ULA | Uniform linear array |
| ESPRIT | Estimation of signal parameters via rotational invariance technique |
| MUSIC | Multiple signal classification |
| TSS | Total spectral search |
| PSS | Partial spectral search |
| CBF | Classical beamforming |
| MVDR | Minimum variance distortionless response |
| ESPRIT-SSN | ESPRIT with the same sensor number |
| ESPRIT-SAL | ESPRIT with the same aperture length |
| CRB | Crame-Rao bound |
| RMSE | Root mean square error |
| SNR | Signal-to-noise ratio |
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT—Estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Chen, T.; Wu, H.; Zhao, Z. The real-valued sparse direction of arrival (DOA) estimation based on the Khatri-Rao product. Sensors 2016, 16, 693. [Google Scholar] [CrossRef] [PubMed]
- Inghelbrecht, V.; Verhaevert, J.; van Hecke, T.; Rogier, H. The influence of random element displacement on DOA estimates obtained with (Khatri-Rao-) root-MUSIC. Sensors 2014, 14, 21258–21280. [Google Scholar] [CrossRef] [PubMed]
- Ye, Z.; Xu, X. DOA estimation by exploiting the symmetric configuration of uniform linear array. IEEE Trans. Antennas Propag. 2007, 55, 3716–3720. [Google Scholar] [CrossRef]
- Zoltowski, M.; Wong, K. Closed-form eigenstructure-based direction finding using arbitrary but identical subarrays on a sparse uniform Cartesian array grid. IEEE Trans. Signal Process. 2000, 48, 2205–2210. [Google Scholar] [CrossRef]
- Wong, K.; Zoltowski, M. Direction-finding with sparse rectangular dual-size spatial invariance array. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1320–1336. [Google Scholar] [CrossRef]
- Miron, S.; Song, Y.; Brie, D.; Wong, K. Multilinear direction finding for sensor-array with multiple scales of invariance. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2057–2070. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Vaidyanathan, P.; Pal, P. Sparse sensing with co-prime samplers and arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Shen, Q.; Zhang, Y.; Amin, M.G. Generalized coprime array configurations for direction-of-arrival estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the MUSIC algorithm. In Proceedings of the Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 289–294.
- Weng, Z.; Djuric, P. A search-free DOA estimation algorithm for coprime arrays. Digit. Signal Process. 2014, 24, 27–33. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, Z.; Gu, Y.; Shen, X. DECOM: DOA estimation with combined MUSIC for coprime array. In Proceedings of the International Conference on Wireless Communications & Signal Processing (WCSP), Hangzhou, China, 24–26 October 2013; pp. 1–5.
- Sun, F.; Lan, P.; Gao, B. Partial spectral search-based DOA estimation method for co-prime linear arrays. Electron. Lett. 2015, 51, 2053–2055. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, F.; Lan, P.; Ding, G.; Zhang, X. Two-dimensional direction-of-arrival estimation for co-prime planar arrays: A partial spectral search approach. IEEE Sens. J. 2016, 16, 5660–5670. [Google Scholar] [CrossRef]
- Godara, L.C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations. Proc. IEEE 1997, 85, 1195–1245. [Google Scholar] [CrossRef]
- Capon, J. High resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. A generalized MVDR spectrum. IEEE Signal Process. Lett. 2005, 12, 827–830. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. Performance study of conditional and unconditional direction-of-arrival estimation. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1783–1795. [Google Scholar] [CrossRef]
- Stoica, P.; Gershman, A.B. Maximum-likelihood DOA estimation by data-supported grid search. IEEE Signal Process. Lett. 1999, 6, 273–275. [Google Scholar] [CrossRef]
| Subarray 1 with | −58.0, −34.2, −16.1, 0.51, 17.1, 35.5, 60.0 | |
| Subarray 2 with | −47.2, −19.5, 3.8, 27.8, 60.0 | |
| Subarray 1 with | −74.4, −42.6, −23.1, −6.1, 10.4, 27.8, 48.7 | |
| Subarray 2 with | −58.0, −26.7, −2.8, 20.6, 48.7 |
| ESPRIT | |
| PSS [16] | |
| Proposed |
| θ | ||||
| | | 0.6122|0.0931 | 0.5974|0.0926 | 1.3082|0.9561 | 1.2529|0.9454 |
| True or false | false|false | false|false | true|true | true|true |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, F.; Gao, B.; Chen, L.; Lan, P. A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays. Sensors 2016, 16, 1367. https://doi.org/10.3390/s16091367
Sun F, Gao B, Chen L, Lan P. A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays. Sensors. 2016; 16(9):1367. https://doi.org/10.3390/s16091367
Chicago/Turabian StyleSun, Fenggang, Bin Gao, Lizhen Chen, and Peng Lan. 2016. "A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays" Sensors 16, no. 9: 1367. https://doi.org/10.3390/s16091367
APA StyleSun, F., Gao, B., Chen, L., & Lan, P. (2016). A Low-Complexity ESPRIT-Based DOA Estimation Method for Co-Prime Linear Arrays. Sensors, 16(9), 1367. https://doi.org/10.3390/s16091367






