Towards a Graphene-Based Low Intensity Photon Counting Photodetector
Abstract
:1. Introduction
2. Existing Technologies
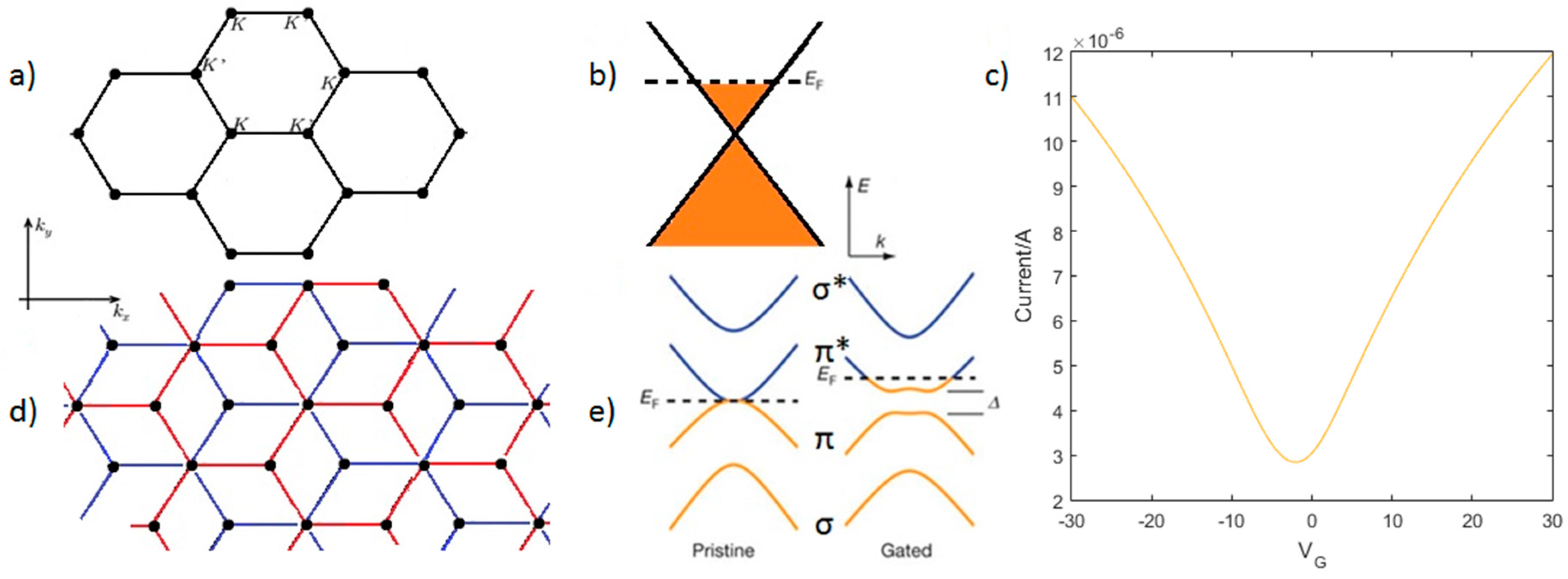
3. Properties of Single and Bilayer Graphene
4. Bilayer Graphene Single Photon Counting Photodetector—Simulations and Design
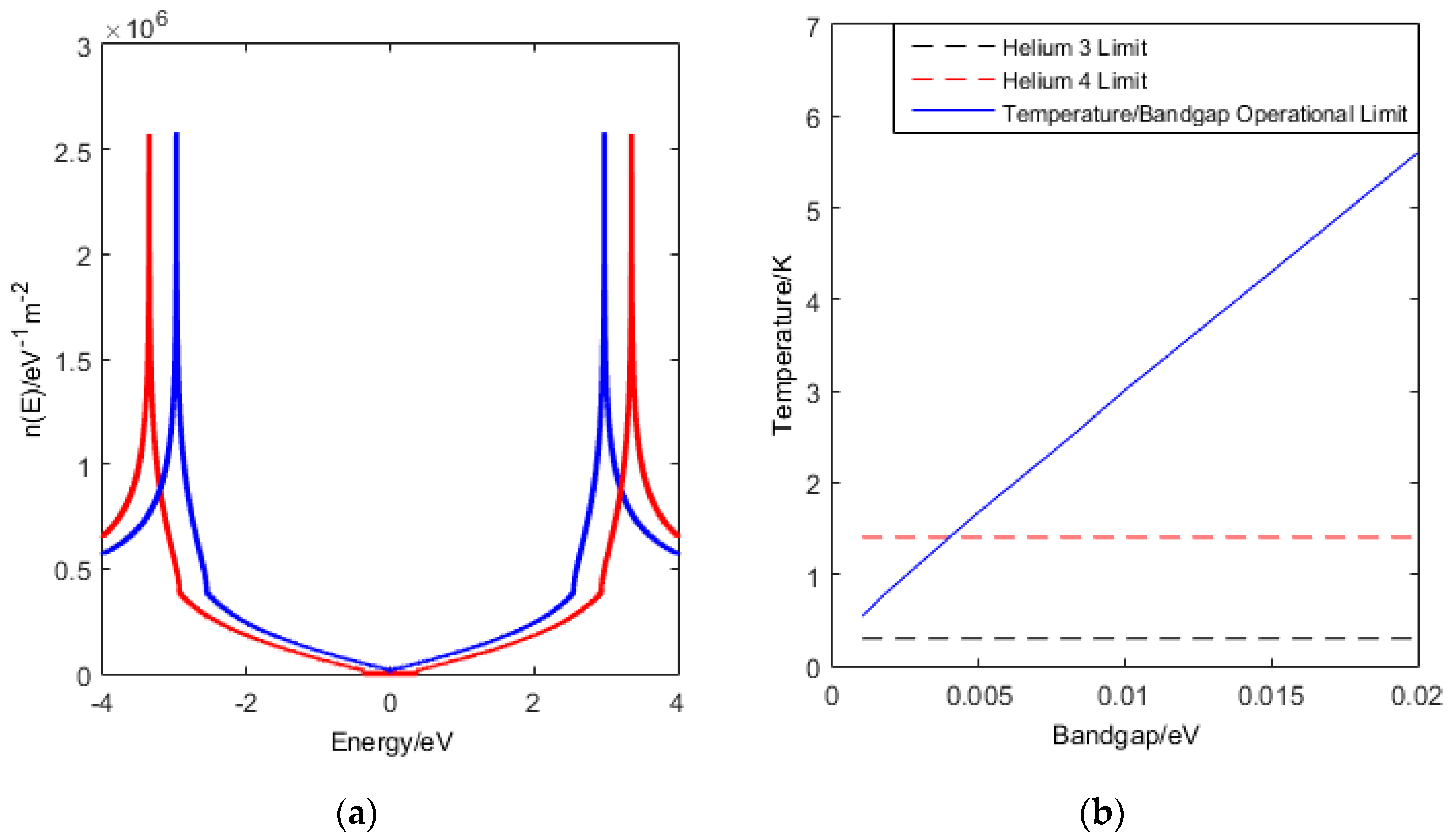
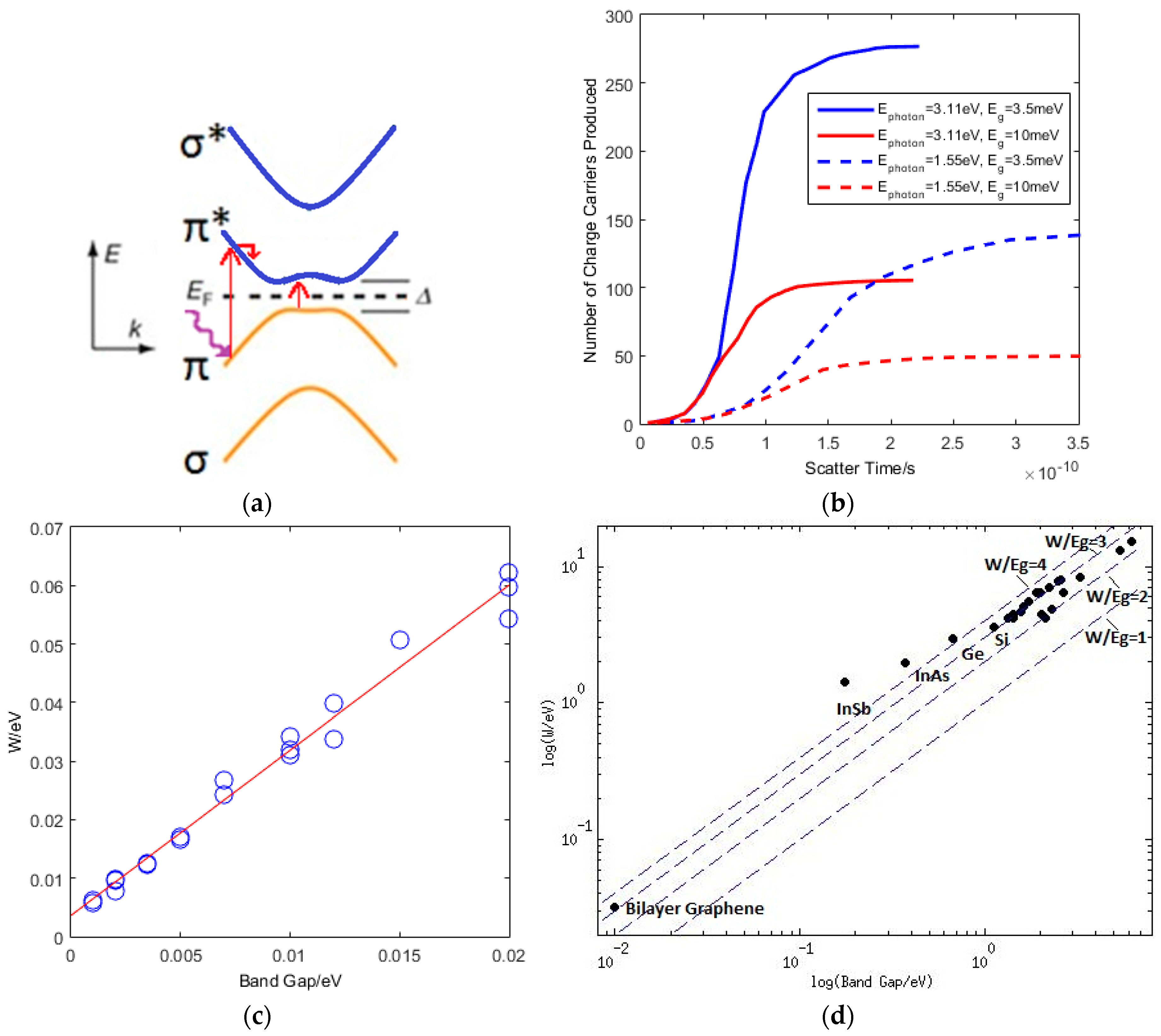
4.1. Density of States and Optimum Operational Window
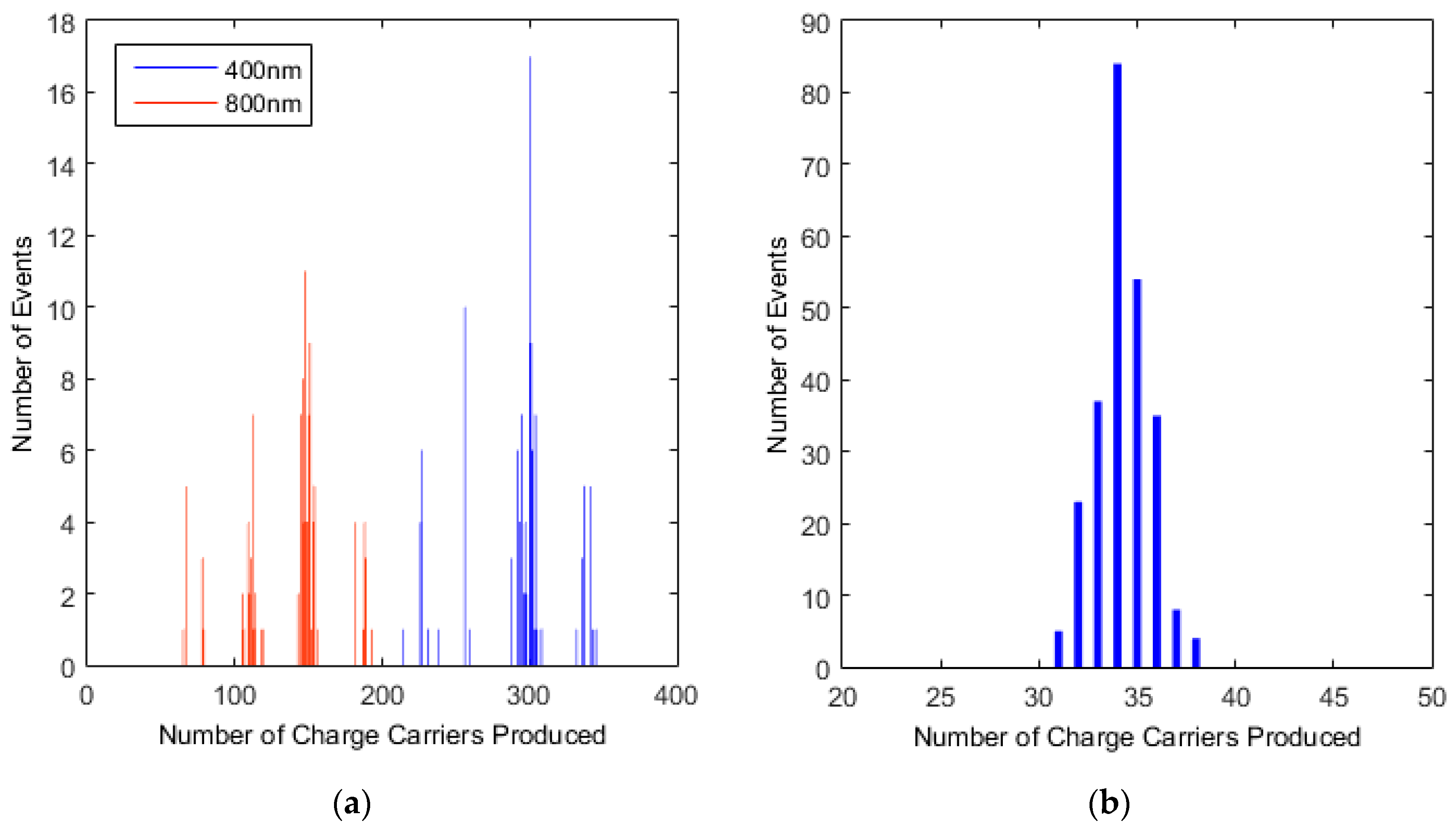
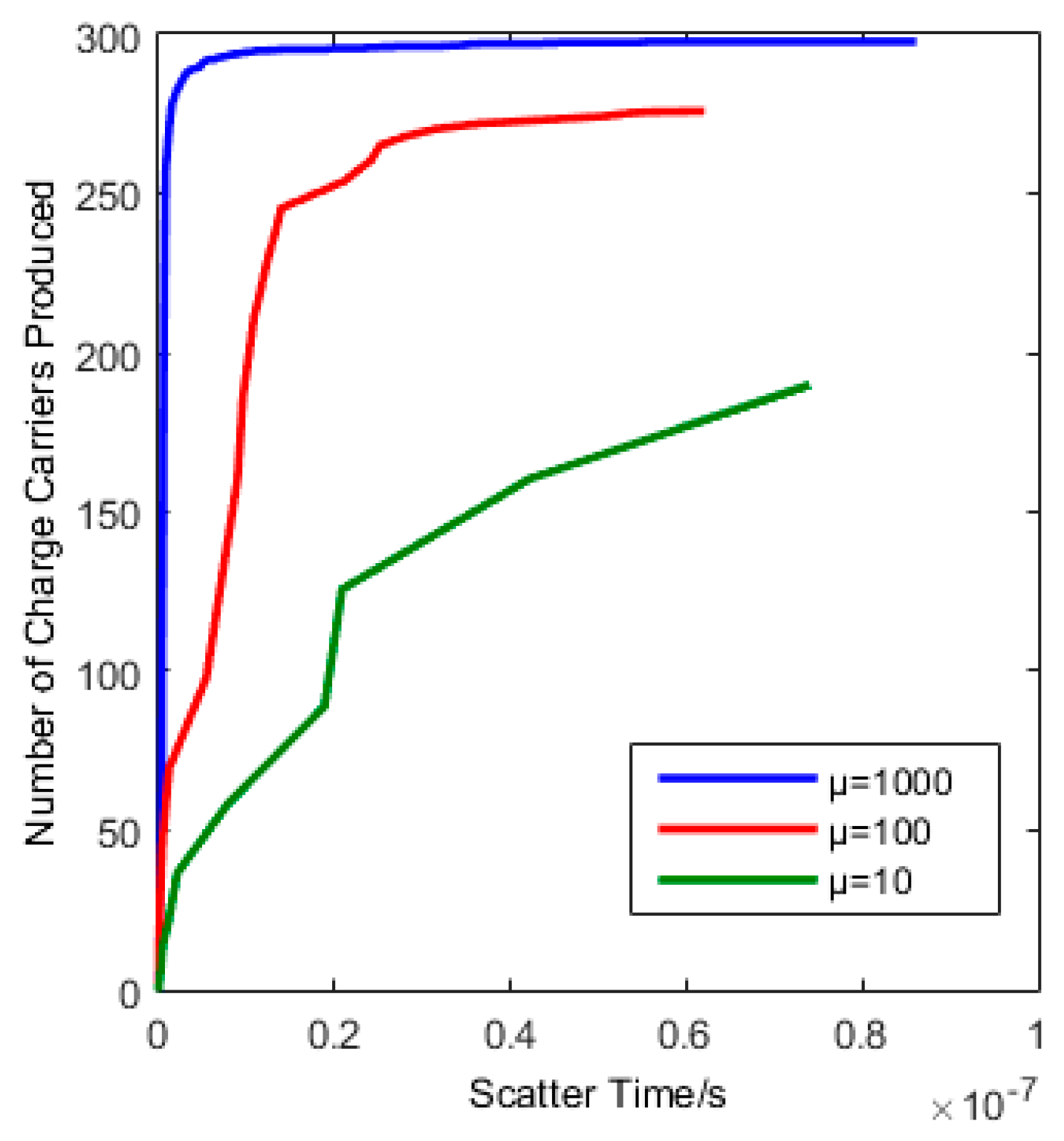
4.2. Monte Carlo Simulations
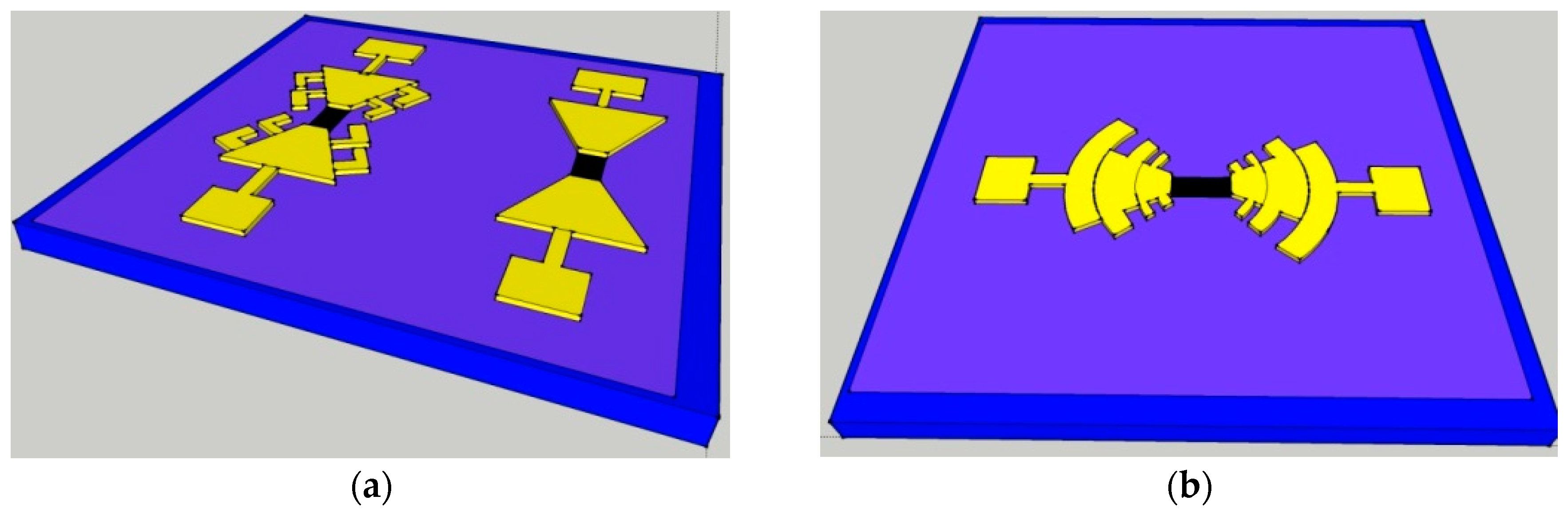
5. Dyakonov-Shur GFET Optimised for 1.2 THz—Simulations and Design
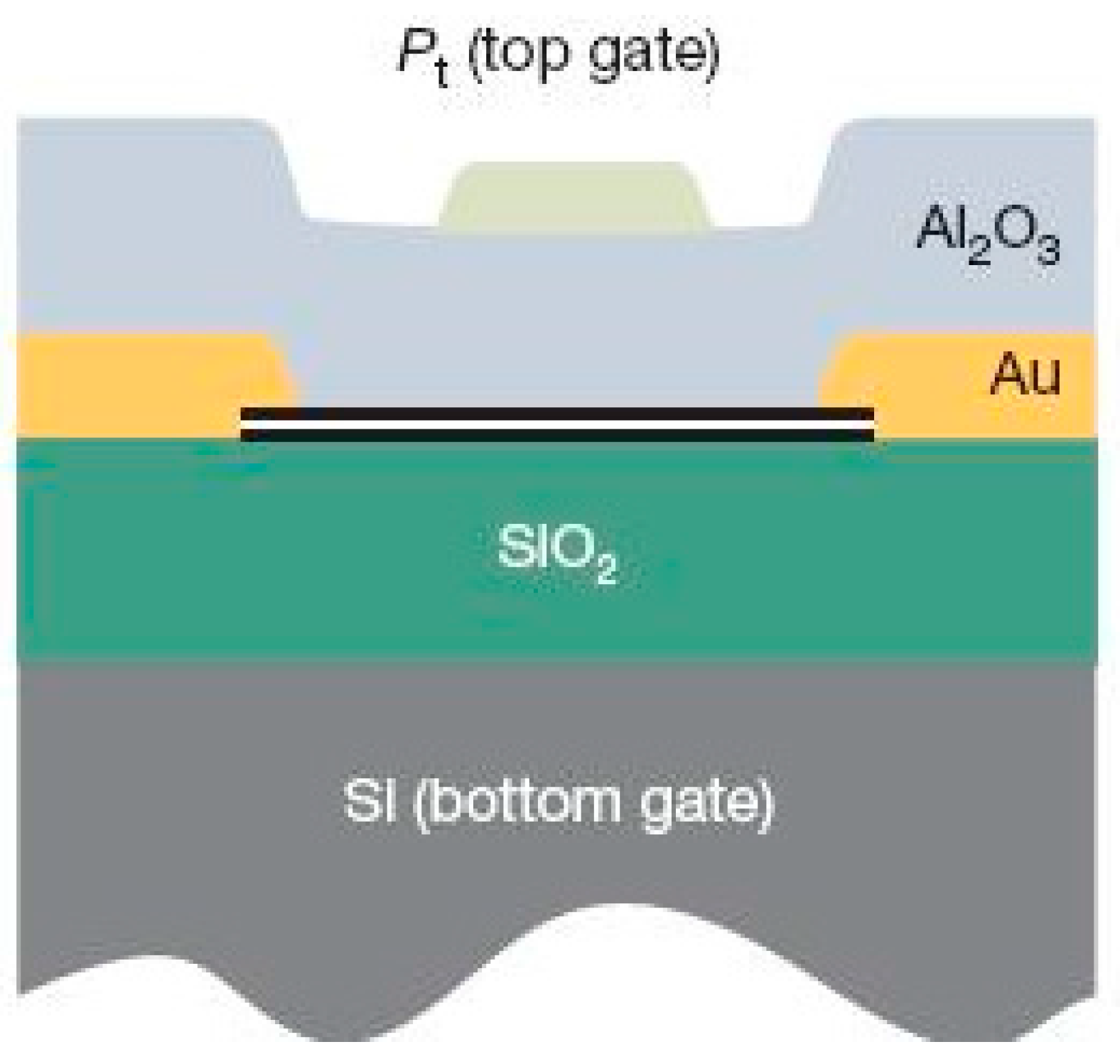
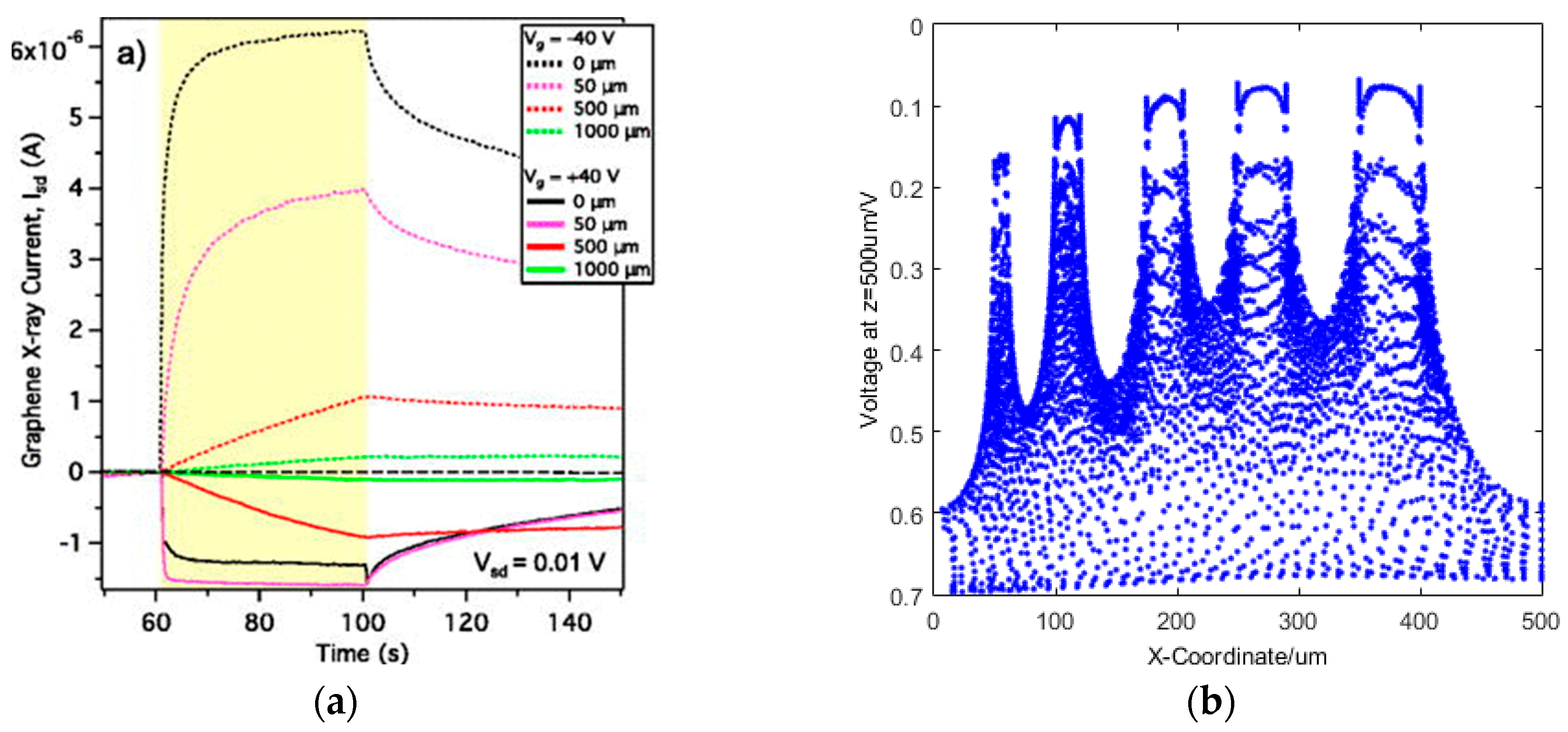
6. X-ray Graphene Field Effect Transistor
7. Device Fabrication, Challenges and Progress
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Santavicca, D.F.; Carter, F.W.; Prober, D.E. Proposal for a GHz Count Rate Near-IR Single-Photon Detector Based on a Nanoscale Superconducting Transition Edge Sensor. Available online: http://arxiv.org/ftp/arxiv/papers/1202/1202.4722.pdf (accessed on 17 August 2016).
- Rajteri, M.; Taralli, E.; Portesi, C.; Monticone, E. Single Photon Light Detection with Transition Edge Sensors. Nuovo Cimento C 2009, 31, 549–555. [Google Scholar]
- Dierickx, B.; Yao, Q.; Witrouwen, N.; Uwaerts, D.; Vandewiele, S.; Gao, P. X-ray Photon Counting and Two-Colour X-ray Imaging Using Indirect Detection. Sensors 2016, 16, 764. [Google Scholar] [CrossRef] [PubMed]
- Fraser, G.W.; Heslop-Harrison, J.S.; Schwarzacher, T.; Holland, A.D.; Verhoeve, P.; Peacock, A. Detection of multiple fluorescent labels using superconducting tunnel junctions. Rev. Sci. Instrum. 2003, 74. [Google Scholar] [CrossRef]
- Comandar, L.C.; Frohlich, B.; Lucamarini, M.; Patel, K.A.; Sharpe, A.W.; Dynes, J.F.; Yuan, Z.L.; Penty, R.V.; Shields, A.J. Room temperature single-photon detectors for high bit rate quantum key distribution. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82. [Google Scholar] [CrossRef] [PubMed]
- Korneev, A.; Vachtomin, Y.; Minaeva, O.D.; Smirnov, K.; Okunev, O.; Gol’tsman, G.; Zinoni, C.; Chauvin, N.; Balet, L.; Marsili, F.; et al. Single-photon detection system for quantum optics applications. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 944–951. [Google Scholar] [CrossRef]
- Hadfield, R.H. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar] [CrossRef]
- Varnava, M.; Browne, D.E.; Rudolph, T. How good must single photon sources and detectors be for efficient linear optical quantum computation? Phys. Rev. Lett. 2008, 100, 060502. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z.; Klima, M.; Fudenberg, G.; Hone, J.; Kim, P.; Stormer, H.L. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Hwang, E.H.; Adam, S.; Das Sarma, S. Carrier Transport in Two-Dimensional Graphene Layers. Phys. Rev. Lett. 2007, 98, 186806. [Google Scholar] [CrossRef] [PubMed]
- Nair, R.R.; Blake, P.; Grigorenko, A.N.; Novoselov, K.S.; Booth, T.J.; Stauber, T.; Peres, N.M.R.; Geim, A.K. Fine Structure Constant Defines Visual Transparency of Graphene. Science 2008, 320, 1308. [Google Scholar] [CrossRef] [PubMed]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- McKitterick, C.B.; Prober, D.E.; Karasik, B.S. Performance of Graphene Thermal Photon Detectors. J. Appl. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Tielrooij, K.J.; Piatkowski, L.; Massicotte, M.; Woessner, A.; Ma, Q.; Lee, Y.; Myrho, K.S.; Lau, C.N.; Jarillo-Herrero, P.; van Hulst, N.F.; et al. Generation of photovoltage in graphene on a femotosecond timescale through efficient carrier heating. Nat. Nanotechnol. 2015. [Google Scholar] [CrossRef] [PubMed]
- Monfardini, A.; Benoit, A.; Bideaud, A.; Swenson, L.; Cruciani, A.; Camus, P.; Hoffmann, C.; Deser, F.X.; Doyle, S.; Ade, P.; et al. A Dual-Band Millimeter-Wave Kinetic Inductance Camerca for the IRAM 30 m Telescope. Astrophys. J. Suppl. Ser. 2011, 194. [Google Scholar] [CrossRef]
- Van Rantwijk, J.; Grim, M.; van Loon, D.; Yates, S.; Baryshev, A.; Baselmans, J. Multiplexed readout for 1000-pixel arrays of microwave kinetic inductance detectors. IEEE Trans. Microw. Theory Tech. 2016, 64, 1876–1883. [Google Scholar] [CrossRef]
- Day, P.K.; LeDuc, H.G.; Mazin, B.A.; Vayonakis, A.; Zmuidzinas, J. A broadband superconducting detector suitable for use in large arrays. Nature 2003, 425, 817–821. [Google Scholar] [CrossRef] [PubMed]
- Princeton. Josephson Junctions. Available online: http://www.princeton.edu/~romalis/PHYS210/stj.htm (accessed on 17 August 2016).
- Martin, D.D.; Verhoeve, P. Superconducting Tunnel Junctions. ISSI SR 2010, 9, 441–457. [Google Scholar]
- Czakon, N.G.; Vaykonakis, A.; Schlaerth, J.; Hollister, M.I.; Golwala, S.; Day, P.K.; Gao, J.S.; Glenn, J.; LeDuc, H.; Maloney, P.R.; et al. Microwave Kinetic Inductance Detector (MKID) Camera Testing for Submillimeter Astronomy. Available online: http://web.physics.ucsb.edu/~bmazin/Papers/preprint/czakon_LTD13.pdf (accessed on 17 August 2016).
- Mazin, B.A. Microwave Kinetic Inductance Detectors: The First Decade. In Proceedings of the AIP Thirteenth International Workshop on Low Temperature Detectors, Stanford, CA, USA, 20–24 July 2009.
- Xia, F. Electrons en masse. Nat. Nanotechnol. 2014, 9, 575–576. [Google Scholar] [CrossRef] [PubMed]
- Yoon, H.; Forsythe, C.; Wang, L.; Tombros, N.; Watanabe, K.; Taniguchi, T.; Hone, J.; Kim, P.; Ham, D. Measurement of Collective Dynamical Mass of Dirac Fermions in Graphene. Nat. Nanotechnol. 2014, 9, 594–599. [Google Scholar] [CrossRef] [PubMed]
- Karasik, B.S.; Sergeev, A.V.; Prober, D.E. Nanobolometers for THz Photon Detection. Available online: https://arxiv.org/ftp/arxiv/papers/1208/1208.5803.pdf (accessed on 17 August 2016).
- Matsuo, H. Photon Statistics for Space Terahertz Astronomy. 2014. Available online: http://www.nrao.edu/meetings/isstt/papers/2014/2014067000.pdf (accessed on 17 August 2016).
- Matsuo, H. Photon Counting Terahertz Interferometry (PCTI). Available online: http://fisica.iaps.inaf.it/2014-02-15-Fisica-Presentations/pres_FISICA-Matsuo.pdf (accessed on 17 August 2016).
- Matsuo, H. Requirements on Photon Counting Detectors for Terahertz Interferometry. J. Low Temp. Phys. 2012, 167, 840–845. [Google Scholar] [CrossRef]
- Hajime, E.; Go, F.; Hiroshi, M.; Shigetomo, S.; Masahiro, U. SIS Detectors for Terahertz Photon Counting System. In Proceedings of the 16th International Workshop on Low Temperature Detectors, Grenoble, France, 20–24 July 2015.
- Bulter, A. Single-Photon Counting Detectors for the Visible Range Between 300 and 1000 nm. In Advanced Photon Counting; Springer International Publishing: Cham, Switzerland, 2014; pp. 23–42. [Google Scholar]
- Wahl, M. Time Correlated Single Photon Counting. Available online: https://www.picoquant.com/images/uploads/page/files/7253/technote_tcspc.pdf (accessed on 17 August 2016).
- STJ X-ray Spectrometers. Available online: http://starcryo.com/stj-x-ray-spectrometers/ (accessed on 17 August 2016).
- Doyle, S. Lumped Element Kinetic Inductance Detectors. Available online: http://www.astro.cardiff.ac.uk/~spxsmd/Lumped_Element_Kinetic_Inductance_Detectors.pdf (accessed on 17 August 2016).
- White, S.; Chiu, M.; Diwan, M.; Atoyan, G.; Issakov, V. Design of a 10 picosecond Time of Flight Detector using Avalanche Photodiodes. 2009; arXiv:0901.2530. [Google Scholar]
- Tan, C.H.; Gomes, R.B.; David, J.P.; Barnett, A.M.; Bassford, D.J.; Lees, J.E.; Shien, J. Avalanche Gain and Energy Resolution of Semiconductor X-Ray Detectors. IEEE Trans. Electron Dev. 2011, 58, 1696–1701. [Google Scholar]
- Excelitas. Avalanche Photodiode—A User Guide. Available online: http://www.excelitas.com/downloads/app_apd_a_user_guide.pdf (accessed on 17 August 2016).
- Oshima, T.; Yamakawa, Y.; Kurabayashi, H.; Hoshnino, A.; Ishisaki, Y.; Ohashi, T.; Mitsuda, K.; Tanaka, K. A High Energy Resolution Gamma-Ray TES Microcalorimeter with Fast Response Time. J. Low Temp. Phys. 2008, 151, 430–435. [Google Scholar] [CrossRef]
- Figueroa Group, MIT. Transition Edge Sensors (TES). Available online: http://web.mit.edu/figueroagroup/ucal/ucal_tes/ (accessed on 17 August 2016).
- Lee, S.-F.; Gildemeister, J.M.; Holmes, W.; Lee, A.T.; Richards, P.L. Voltage-viased superconducting transition-edge bolometer with strong electrothermal feedback operated at 370 mK. Appl. Opt. 1998, 37, 3391–3397. [Google Scholar] [CrossRef] [PubMed]
- Foxe, M.; Lopez, G.; Childres, I.; Patil, A.; Roecker, C.; Boguski, J.; Jovanovic, I.; Chen, Y.P. Graphene Field-Effect Transistors on Undoped Semiconductor Substrates for Radiation Detectors. IEEE Trans. Nanotechnol. 2012, 11, 581–587. [Google Scholar] [CrossRef]
- Jovanovic, I.; Cazalas, E.; Childres, I.; Patil, A.; Koybasi, O.; Chen, Y.P. Graphene field effect transistor-based detectors for detection of ionising radiation. In Proceedings of the 2013 3rd International Conference on Advancements in Nuclear Instrumentation, Measurement Methods and Their Applications, Marseille, France, 23–27 June 2013.
- Koybasi, O.; Cazalas, E.; Childres, I.; Jovanovic, I.; Chen, Y.P. Detection of light, X-rays and gamma rays using graphene field effect transistors fabricated on SiC, CdTe and AlGaAs/GaAs substrates. In Proceedings of the IEEE Nuclear Science Symposium Conference Record, Seoul, Korea, 27 October–2 November 2013.
- Koybasi, O.; Childres, I.; Jovanovic, I.; Chen, Y.P. Graphene field effect transistor as a radiation and photo detector. Proc. SPIE 2012, 8373. [Google Scholar] [CrossRef]
- Koybasi, O.; Childres, I.; Jovanovic, I.; Chen, Y. Design and Simulation of a Graphene DEPFET Detector. In Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference Record, Anaheim, CA, USA, 27 October–3 November 2012; pp. 4249–4254.
- Patil, A.; Koybasi, O.; Lopez, G.; Foxe, M.; Childres, I.; Roecker, C.; Boguski, J.; Gu, J.; Bolen, M.L.; Capano, M.A.; et al. Graphene Field Effect Transistor as Radiation Sensor. In Proceedings of the 2011 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Valencia, Spain, 23–29 October 2011.
- Cazalas, E.; Sarker, B.K.; Moore, M.E.; Childres, I.; Chen, Y.P.; Jovanovic, I. Position sensitivity of graphene field effect transistors to X-rays. Appl. Phys. Lett. 2015, 106, 223503. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Lin, Y.-M.; Valdes-Garcia, A.; Avouris, P. Ultrafast Graphene Photodetector. Nature 2009, 4, 839–843. [Google Scholar] [CrossRef] [PubMed]
- Tomadin, A.; Tredicucci, A.; Pellegrini, V.; Vitiello, M.S.; Polini, M. Photocurrent-Based detection of Terahertz radiation in graphene. Appl. Phys. Lett. 2013, 103, 211120. [Google Scholar] [CrossRef]
- Vicarelli, L.; Vitiello, M.S.; Coquillat, D.; Lombardo, A.; Ferrari, A.C.; Knap, W.; Polini, M.; Pellegrini, V.; Tredicucci, A. Graphene field effect transistors as room-temperature Terahertz detectors. Nat. Mater. 2012, 11, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Hetsch, F.; Zhao, N.; Kershaw, S.V.; Rogach, A.L. Quantum Dot Field Effect Transistors. Mater. Today 2013, 16, 312–325. [Google Scholar] [CrossRef]
- Jeon, P.J.; Lee, Y.T.; Lim, J.Y.; Kim, J.S.; Hwang, D.K.; Im, S. Black Phosphorus-Zinc Oxide Nanomaterial Heterojunction for p-n Diode and Junction Field Effect Transistor. Nano Lett. 2016, 16, 1293–1298. [Google Scholar] [CrossRef] [PubMed]
- Bucsema, M.; Groenendijk, D.J.; Blanter, S.L.; Steele, G.A.; van den Zant, H.S.; Castellanos-Gomez, A. Fast and Broadband Photoresponse of Few-Layer Black Phosphorus Field Effect Transistors. Nano Lett. 2014, 14, 3347–3352. [Google Scholar]
- Song, J.C.W.; Rudner, M.S.; Marcus, C.M.; Levitov, L.S. Hot Carrier Transport and Photocurrent Response in Graphene. Nano Lett. 2011, 11, 4688–4692. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Kim, M.H.; Elle, J.A.; Sushkov, A.B.; Jenkins, G.S.; Milchberg, H.M.; Fuhrer, M.S.; Drew, H.D. Dual-gated bilayer graphene hot-electron bolometer. Nat. Nanotechnol. 2012, 7, 472–478. [Google Scholar] [CrossRef] [PubMed]
- Jessop, D.S.; Kindness, S.J.; Xiao, L.; Braeuninger-Weimer, P.; Lin, H.; Ren, Y.; Ren, C.X.; Hofmann, S.; Zeitler, J.A.; Beere, H.E.; et al. Graphene based plasmonic terahertz amplitude modulator operating above 100 MHz. Appl. Phys. Lett. 2016, 108, 171101. [Google Scholar] [CrossRef]
- Schedin, F.; Geim, A.K.; Morozov, S.V.; Hill, E.W.; Blake, P.; Katsnelson, M.I.; Novoselov, K.S. Detection of individual gas molecules absorbed on graphene. Nat. Mater. 2007, 6, 652–655. [Google Scholar] [CrossRef] [PubMed]
- Deacon, R.S.; Chuang, K.C.; Nicholas, R.J.; Novoselov, K.S.; Geim, A.K. Cyclotron resonance study of the electron and hole velocity in graphene monolayers. Phys. Rev. B 2007, 76, 081406(R). [Google Scholar] [CrossRef]
- Sagade, A.A.; Neumaier, D.; Schall, D.; Otto, M.; Pesquera, A.; Centeno, A.; Zurutuza Elorza, A.; Kurz, H. Highly air stable passivation of graphene based field effect devices. Nanoscale 2015, 7, 3558–3564. [Google Scholar] [CrossRef] [PubMed]
- Koppens, F.H.L.; Mueller, T.; Avouris, P.; Ferrari, A.C.; Vitiello, M.S.; Polini, M. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 2014, 9, 780–793. [Google Scholar] [CrossRef] [PubMed]
- Kretinin, A.V.; Cao, Y.; Tu, J.S.; Yu, G.L.; Jalil, R.; Novoselov, K.S.; Haigh, S.J.; Gholinia, A.; Mishchenko, A.; Lozada, M.; et al. Electronic Properties of Graphene Encapsulated with Different Two-Dimensional Atomic Crystals. Nano Lett. 2014, 14, 3270–3276. [Google Scholar] [CrossRef] [PubMed]
- Sanders, S.; Cabrero-Vilatela, A.; Kidambi, P.R.; Alexander-Webber, J.A.; Weijtens, C.; Braeuninger-Weimer, P.; Aria, A.I.; Qasim, M.M.; Wilkinson, T.D.; Robertson, J.; et al. Engineering high charge transfer n-doping of graphene electrodes and its application to organic electronics. Nanoscale 2015, 7, 13135–13142. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.; Kidambi, P.R.; Bayer, B.C.; Weijtens, C.; Kuhn, A.; Centeno, A.; Pesquera, A.; Zurutuza, A.; Robertson, J.; Hofmann, S. Metal Oxide Induced Charge Transfer Doping and Band Alignment of Graphene Electrodes for Efficient Organic Light Emitting Diodes. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Zhan, B.; Li, C.; Yang, J.; Jenkins, G.; Huang, W.; Dong, X. Graphene field-effect transistor and its application for electronic sensing. Small 2014, 10, 4042–4065. [Google Scholar] [CrossRef] [PubMed]
- Foxe, M.; Cazalas, E.; Lamm, H.; Majcher, A.; Piotrowski, C.; Childres, I.; Patil, A.; Chen, Y.P.; Jovanovic, I. Graphene-Based Neutron Detectors. In Proceedings of the 2011 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Valencia, Spain, 23–29 October 2011; pp. 352–355.
- Foxe, M.; Lopez, G.; Childres, I.; Jalilian, R.; Roecker, C.; Boguski, J.; Jovanovic, I.; Chen, Y.P. Detection of Ionizing Radiation Using Graphene Field Effect Transistors. In Proceedings of 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, USA, 25–31 October 2009; pp. 90–95.
- Zou, K.; Hong, X.; Zhu, J. Effective mass of electrons and holes in bilayer graphene: Electron-Hole asymmetry and electron-electron interaction. Phys. Rev. B 2011, 84, 085408. [Google Scholar] [CrossRef]
- Xia, F.; Mueller, T.; Golizadeh-Mojarad, R.; Freitag, M.; Lin, Y.-M.; Tsang, J.; Perebeinos, V.; Avouris, P. Photocurrent Imaging and Efficient Photon Detection in a Graphene Transistor. Nano Lett. 2009, 9, 1039–1044. [Google Scholar] [CrossRef] [PubMed]
- Mueller, T.; Xia, F.; Avouris, P. Graphene photodetectors for high-speed optical communications. Nat. Photonics 2010, 4, 297–301. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, R.; Liao, L.; Zhou, H.; Bai, J.; Liu, G.; Liu, L.; Huang, Y.; Duan, X. Plasmon resonance enhance multicolour photodetection by graphene. Nat. Commun. 2011, 2. [Google Scholar] [CrossRef] [PubMed]
- Van Veldhoven, Z.A.; Alexander-Webber, J.A.; Sagade, A.A.; Braeuninger-Weimer, P.; Hofmann, S. Electronic properties of CVD graphene: The role of grain boundaries, atmospheric doping and encapsulation by ALD. Phys. Stat. Sol. B 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, T.-T.; Girit, C.; Hao, Z.; Martin, M.C.; Zettl, A.; Crommie, M.F.; Shen, Y.R.; Wang, F. Direct Observation of a Widely Tunable Bandgap in Bilayer Graphene. Nature 2009, 459, 820–823. [Google Scholar] [CrossRef] [PubMed]
- De Fazio, D.; Goykhman, I.; Bruna, M.; Eiden, A.; Milana, S.; Yoon, D.; Sassi, U.; Barbone, M.; Dumcenco, D.; Marinov, K.; et al. High Responsivity, Large-Area Graphene/MoS2 Flexible Photodetectors. Available online: http://arxiv.org/pdf/1512.08312v1.pdf (accessed on 17 August 2016).
- McCann, E.; Koshino, M. The electronic properties of bilayer graphene. Rep. Prog. Phys. 2013, 76. [Google Scholar] [CrossRef] [PubMed]
- Yavari, F.; Kritzinger, C.; Gaire, C.; Song, L.; Gullapalli, H.; Borca-Tasciuc, T.; Ajayan, P.M.; Koratkar, N. Tunable Bandgap in Graphene by the Controlled Adsorption of Water Molecules. Small 2010, 6, 2535–2538. [Google Scholar] [CrossRef] [PubMed]
- Balog, R.; Jorgensen, B.; Nilsson, L.; Andersen, M.; Rienks, E.; Bianchi, M.; Fanetti, M.; Laegsgaard, E.; Baraldi, A.; Lizzit, S.; et al. Bandgap Opening in Graphene Induced by Patterned Hydrogen Adsorption. Nat. Mater. 2010, 9, 315–319. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-K.; Yamazaki, S.; Yun, H.; Park, J.; Kennedy, G.P.; Kim, G.-T.; Pietzsch, O.; Wiesendanger, R.; Lee, S.; Hong, S.; et al. Modification of Electrical Properties of Graphene by Substrate-Induced Nanomodulation. Nano 2013, 13, 3494–3500. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Lin, C.-T.; Liu, K.-K.; Tite, T.; Su, C.-Y.; Chang, C.-H.; Lee, Y.-H.; Chu, C.-W.; Wei, K.-H.; Kuo, J.-L.; et al. Opening an Electrical Band Gap of Bilayer Graphene with Molecular Doping. Nano 2011, 5, 7517–7524. [Google Scholar]
- Williams, J.O.D.; Lapington, J.S.; Roy, M.; Hutchinson, I.B. Graphene as a Novel Single Photon Counting Optical and IR Photodetector. IET 2015. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact Stochastic Simulation of Coupled Chemical Reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Pop, E.; Varshney, V.; Roy, A.K. Thermal Properties of Graphene: Fundamentals and Applications. MRS Bull. 2012, 37, 1273–1280. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Meng, B.; Li, X.; Liang, G.; Hu, X.; Wang, Q.J. Broadband High Photoresponse from Pure Monolayer Graphene Photodetector. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef] [PubMed]
- Winzer, T.; Knorr, A.; Malic, E. Carrier Multiplication in Graphene. Nano Lett. 2010, 10, 4839–4843. [Google Scholar] [CrossRef] [PubMed]
- Winzer, T.; Malic, E. Impact of Auger Processes on Carrier Dynamics in Graphene. Phys. Rev. B 2012, 85, 241404. [Google Scholar] [CrossRef]
- Borysenko, K.M.; Mullen, J.T.; Li, X.; Semenov, Y.G.; Zavada, J.M.; Nardelli, M.B.; Kim, K.W. Electron-Phonon interactions in bilayer graphene. Phys. Rev. B 2011, 83, 161402. [Google Scholar] [CrossRef]
- European Space Agency. Future Missions Preparations Office. Available online: http://sci.esa.int/science-e/www/object/index.cfm?fobjectid=41034 (accessed on 17 August 2016).
- Chen, Z.; Li, W.; Li, R.; Zhang, Y.; Xu, G.; Cheng, H. Fabrication of Highly Transparent and Conductive Indium-Tin Oxide Thin Films with a High Figure of Merit via Solution Processing. Am. Chem. Soc. 2013, 29, 13836–13842. [Google Scholar] [CrossRef] [PubMed]
- Knap, W.; Rumyantsev, S.; Vitiello, M.S.; Coquillat, D.; Blin, S.; Dyakanova, N.; Shur, M.; Teppe, F.; Tredicucci, A.; Nagatsuma, T. Nanometer size field effect transistors for terahertz detectors. Nanotechnology 2013, 24. [Google Scholar] [CrossRef] [PubMed]
- Knap, W.; Dyakonov, M.I.; Coquillat, D.; Teppe, F.; Dyakanova, N.; Lusakowski, J.; Karpierz, K.; Sakowicz, M.; Valusis, G.; Seluita, D.; et al. Field Effect Transistors for Terahertz Detection: Physics and First Imaging Applications. J. Infrared Millim. Terahertz Waves 2009, 30. [Google Scholar] [CrossRef]
- Tuan Trinh, M.; Sfeir, M.Y.; Choi, J.J.; Owen, J.S.; Zhu, X. A Hot Electron-Hole Pair Breaks the Symmetry of a Semiconductor Quantum Dot. Nanoletters 2013, 13, 6091–6097. [Google Scholar] [CrossRef] [PubMed]
- Trinh, M.T.; Wu, X.; Niesner, D.; Zhu, X.-Y. Many-Body interactiosn in photoexcited lead iodide perovskite. J. Mater. Chem. A 2015, 3, 9285–9290. [Google Scholar] [CrossRef]
- Schroder, D.K. Carrier Lifetimes in Silicon. IEEE Trans. Electron Dev. 1997, 44, 160–170. [Google Scholar] [CrossRef]
- Hofmann, S.; Braeuninger-Weimer, P.; Weatherup, R.S. CVD-Enabled Graphene Manufacture and Technology. J. Phys. Chem. Lett. 2015, 6, 2714–2721. [Google Scholar] [CrossRef] [PubMed]
- Nature Nanotechnology. Ten years in two dimensions. Nat. Nanotechnol. 2014, 9, 725. [Google Scholar]
- Ruan, M.; Hu, Y.; Guo, Z.; Dong, R.; Palmer, J.; Hankinson, J.; Berger, C.; de Heer, W.A. Epitaxial graphene on silicon carbide: Introduction to structured graphene. MRS Bull. 2012, 37, 1138–1147. [Google Scholar] [CrossRef]
- Melios, C.; Panchal, V.; Giusca, C.E.; Strupinski, W.; Silva, S.R.P.; Kazakova, O. Carrier type inversion in quasi-free standing graphene: Studies of local electronic and structural properties. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Alexander-Webber, J.A.; Janssen, T.J.B.M.; Tzakenchuk, A.; Yager, T.; Lara-Avils, S.; Kubatkin, S.; Myers-Ward, R.L.; Wheeler, V.D.; Gaskill, D.K. Hot carrier relaxation of Dirac fermions in bilayer epitaxial graphene. J. Phys. Condensed Matter 2015, 27, 164202. [Google Scholar] [CrossRef] [PubMed]
- Cabrero-Vilatela, A.; Weatherup, R.S.; Braeuninger-Weimer, P.; Caneva, S.; Hofmann, S. Towards a general growth model for graphene CVD on transition metal catalysts. Nanoscale 2016, 8, 2149–2158. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-H.; Lee, E.K.; Joo, W.-J.; Jang, Y.; Kim, B.-S.; Lim, J.Y.; Choi, S.-H.; Ahn, S.J.; Ahn, J.R.; Park, M.-H.; et al. Wafer-Scale Growth of Single-Crystal Monolayer Graphene on Reusable Hydrogen-Terminated Germanium. Science 2014, 344, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Babenko, V.; Murdock, A.T.; Koos, A.A.; Britton, J.; Crossley, A.; Holdway, P.; Moffat, J.; Huang, J.; Alexander-Webber, J.A.; Nicholas, R.J.; et al. Rapid epitaxy-free graphene synthesis on silicidated polycrystalline platinum. Nat. Commun. 2015, 6, 7536. [Google Scholar] [CrossRef] [PubMed]
- Degl’Innocenti, R.; Jessop, D.S.; Sol, C.W.; Xiao, L.; Kindness, S.J.; Lin, H.; Zeitler, J.A.; Braeuninger-Weimer, P.; Hofmann, S.; Ren, Y.; et al. Fast Modulation of Terahertz Quantum Cascade Lasers Using Graphene Loaded Plasmonic Antennas. ACS Photonics 2016, 3, 464–470. [Google Scholar] [CrossRef]
- Batzill, M. The surface science of graphene: Metal interfaces, CVD synthesis, nanoribbons, chemical modifications and defects. Surf. Sci. Rep. 2012, 67, 83–115. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, X.; Yuan, Q.; Xue, J.; Lu, G.; Liu, Z.; Wang, H.; Wang, H.; Ding, F.; Yu, Q.; et al. Fast growth of inch-sized single crystalline graphene from a controlled single nucleus on Cu-Ni alloys. Nat. Mater. 2015, 15, 43–47. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Wang, L.; Liu, Y.; Chen, H.; Wang, X.; Tan, C.; Nie, S.; Suk, J.W.; Jiang, T.; Liang, T.; Xiao, J.; Ye, W.; Dean, C.R.; et al. Oxygen-activated growth and bandgap tunability of large single-crystal bilayer graphene. Nat. Nanotechnol. 2016, 11, 426–431. [Google Scholar] [CrossRef] [PubMed]
- Caneva, S.; Weatherup, R.S.; Bayer, B.C.; Brennan, B.; Spencer, S.J.; Mingard, K.; Cabrero-Vilatela, A.; Baehtz, C.; Pollard, A.J.; Hofmann, S. Nucleation Control for Large, Single Crystalline Domains of Monolayer Hexagonal Boron Nitride via Si-Doped Fe Catalysts. Nanoletters 2015, 15, 1867–1875. [Google Scholar] [CrossRef] [PubMed]
- Caneva, S.; Weatherup, R.S.; Bayer, B.C.; Blume, R.; Cabrero-Vilatela, A.; Braeuninger-Weimer, P.; Martin, M.-B.; Wang, R.; Baehtz, C.; Schloegl, R.; et al. Controlling Catalyst Bulk Reservoir Effects for Monolayer Hexagonal Boron Nitride CVD. Nano Lett. 2016, 16, 1250–1261. [Google Scholar] [CrossRef] [PubMed]
- Piquemal-Banci, M.; Galceran, R.; Caneva, S.; Martin, M.-B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; Petroff, F.; et al. Magnetic tunnel junctions with monolayer hexagonal boron nitride tunnel barriers. Appl. Phys. Lett. 2016, 108, 102404. [Google Scholar] [CrossRef]
- Kang, K.; Xie, S.; Huang, L.; Han, Y.; Huang, P.Y.; Mak, K.F.; Kim, C.-J.; Muller, D.; Park, J. High-mobility three-atom-thick semiconducting films with wafer-scale homogeneity. Nature 2015, 520, 656–660. [Google Scholar] [CrossRef] [PubMed]
- Bhimanapati, G.R.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.S.; Cooper, V.R.; et al. Recent Advances in Two-Dimensional Materials Beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef] [PubMed]
- Kidambi, P.R.; Blume, R.; Kling, J.; Wagner, J.B.; Baehtz, C.; Weatherup, R.S.; Schloegl, R.; Bayer, B.C.; Hofmann, S. In Situ Observations during Chemical Vapour Deposition of Hexagonal Boron Nitride on Polycrystalline Copper. Chem. Mater. 2014, 26, 6380–6392. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Sun, Y.; Wu, N.; Mendes, R.G.; Chen, L.; Xu, Z.; Zhang, T.; Rummeli, M.H.; Rellinghaus, B.; Pohl, D.; et al. Direct Growth of MoS2/h-BN Heterostructures via a Sulfide-Resistance Alloy. ACS Nano 2016, 10, 2063–2070. [Google Scholar] [CrossRef] [PubMed]
- Jain, N.; Durcan, C.A.; Jacobs-Gedrim, R.; Xu, Y.; Yu, B. Graphene interconnects fully encapsulated in layered insulator hexagonal boron nitride. Nanotechnology 2013, 24, 355202. [Google Scholar] [CrossRef] [PubMed]
- Barnard, H.R.; Zossimova, E.; Mahlmeister, N.H.; Lawton, L.M.; Luxmoore, I.J.; Nash, G.R. Boron nitride encapsulated graphene infrared emitters. Appl. Phys. Lett. 2016, 108, 131110. [Google Scholar] [CrossRef]
- Petrone, N.; Chari, T.; Meric, I.; Wang, L.; Shepard, K.L.; Hone, J. Flexible Graphene Field-Effect Transistors Encapsulated in Hexagonal Boron Nitride. ACS Nano 2015, 9, 8953–8959. [Google Scholar] [CrossRef] [PubMed]

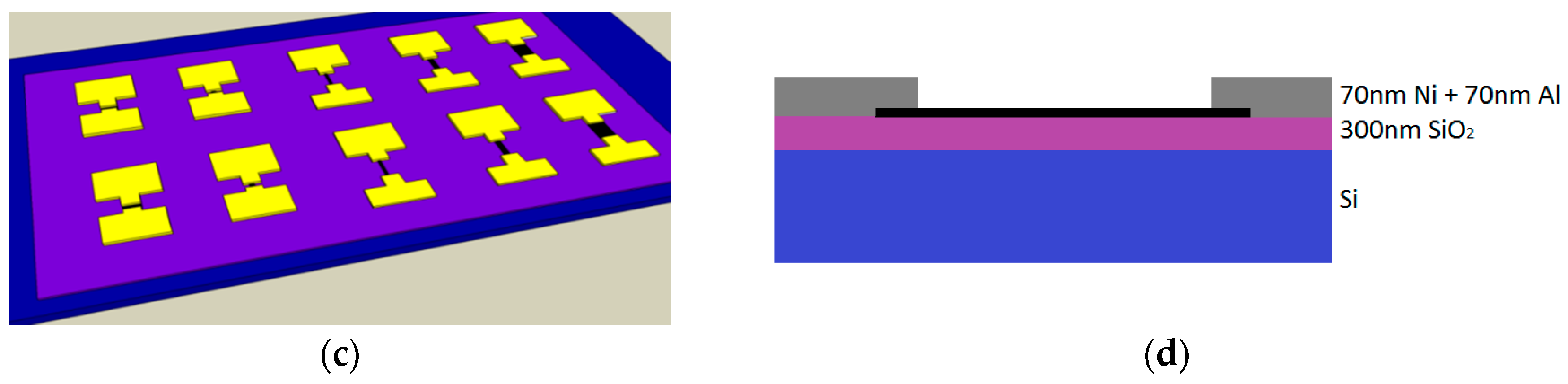

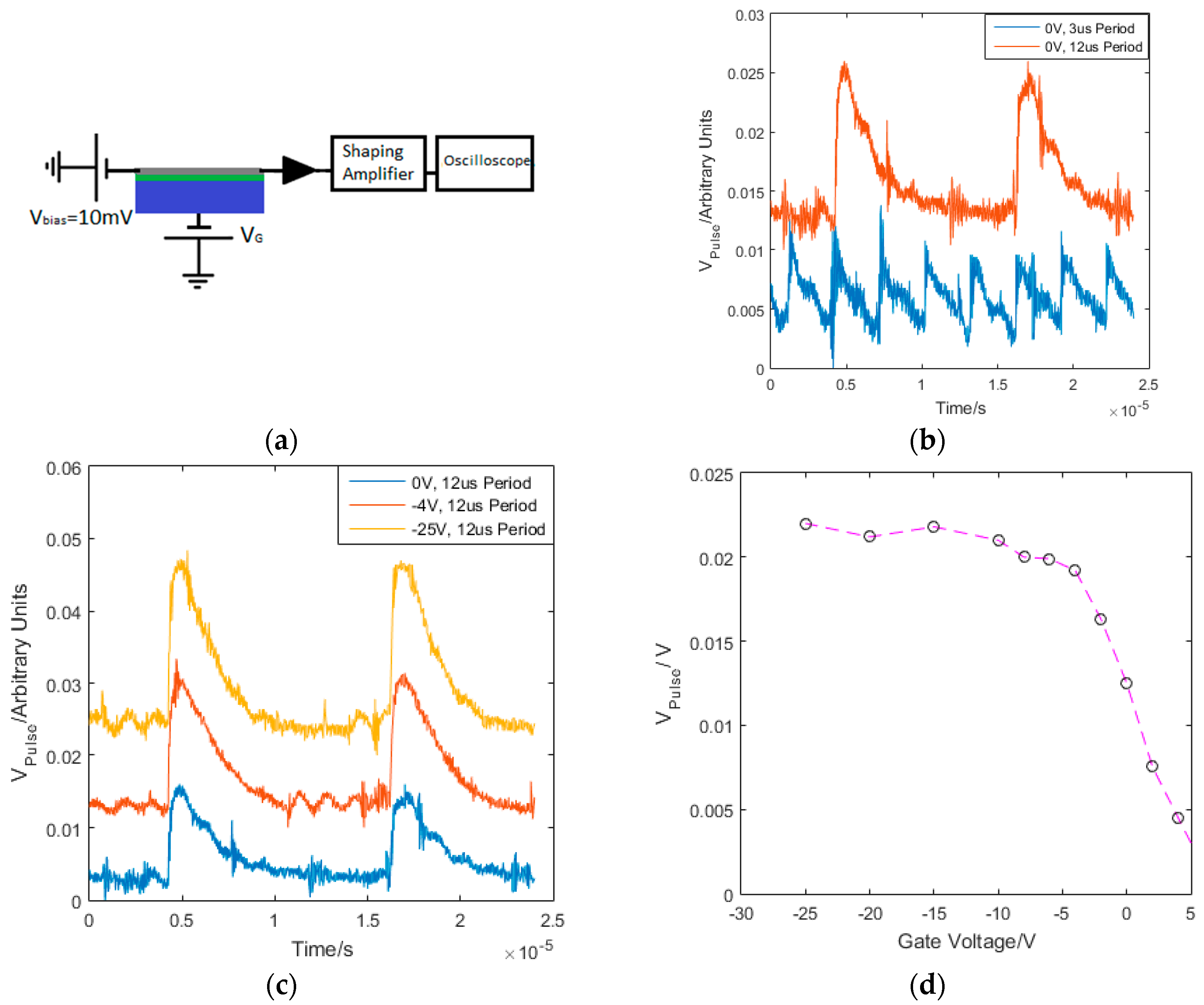

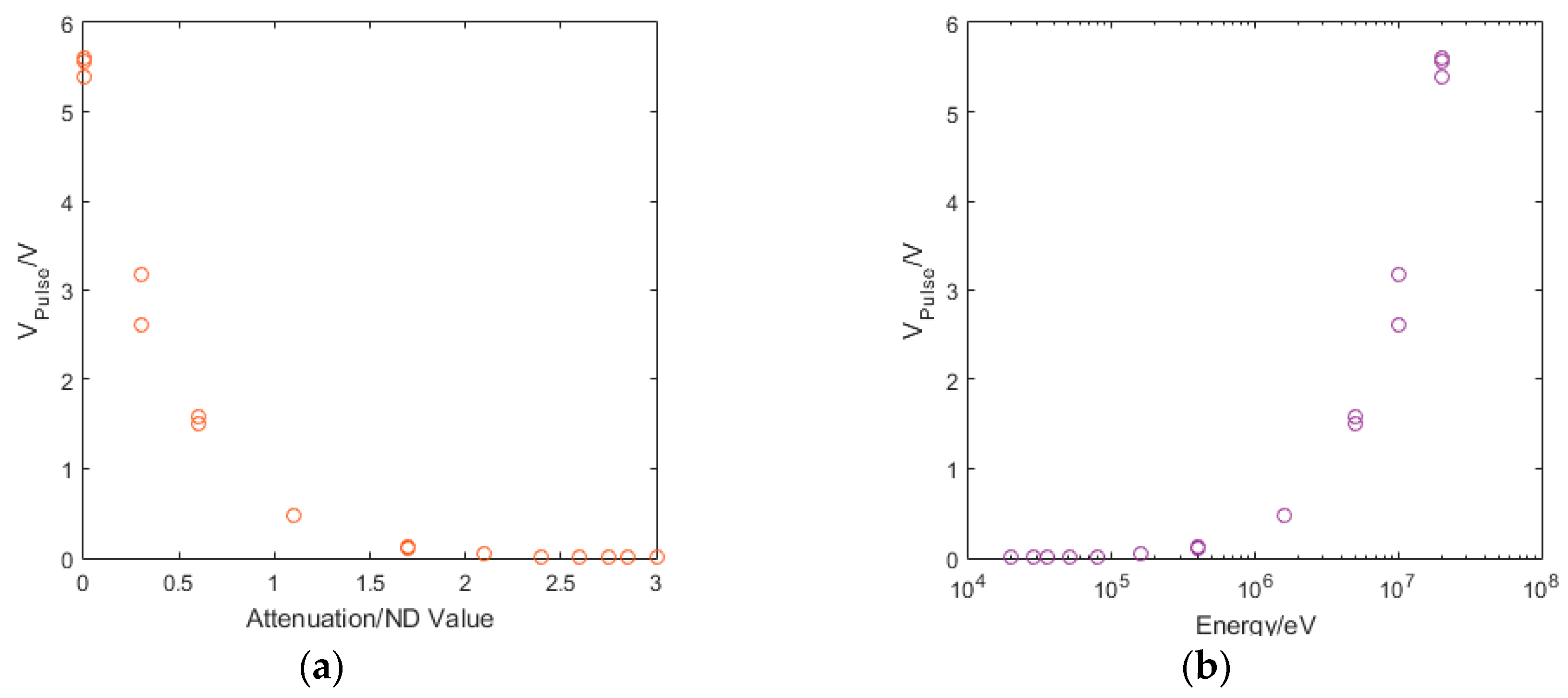
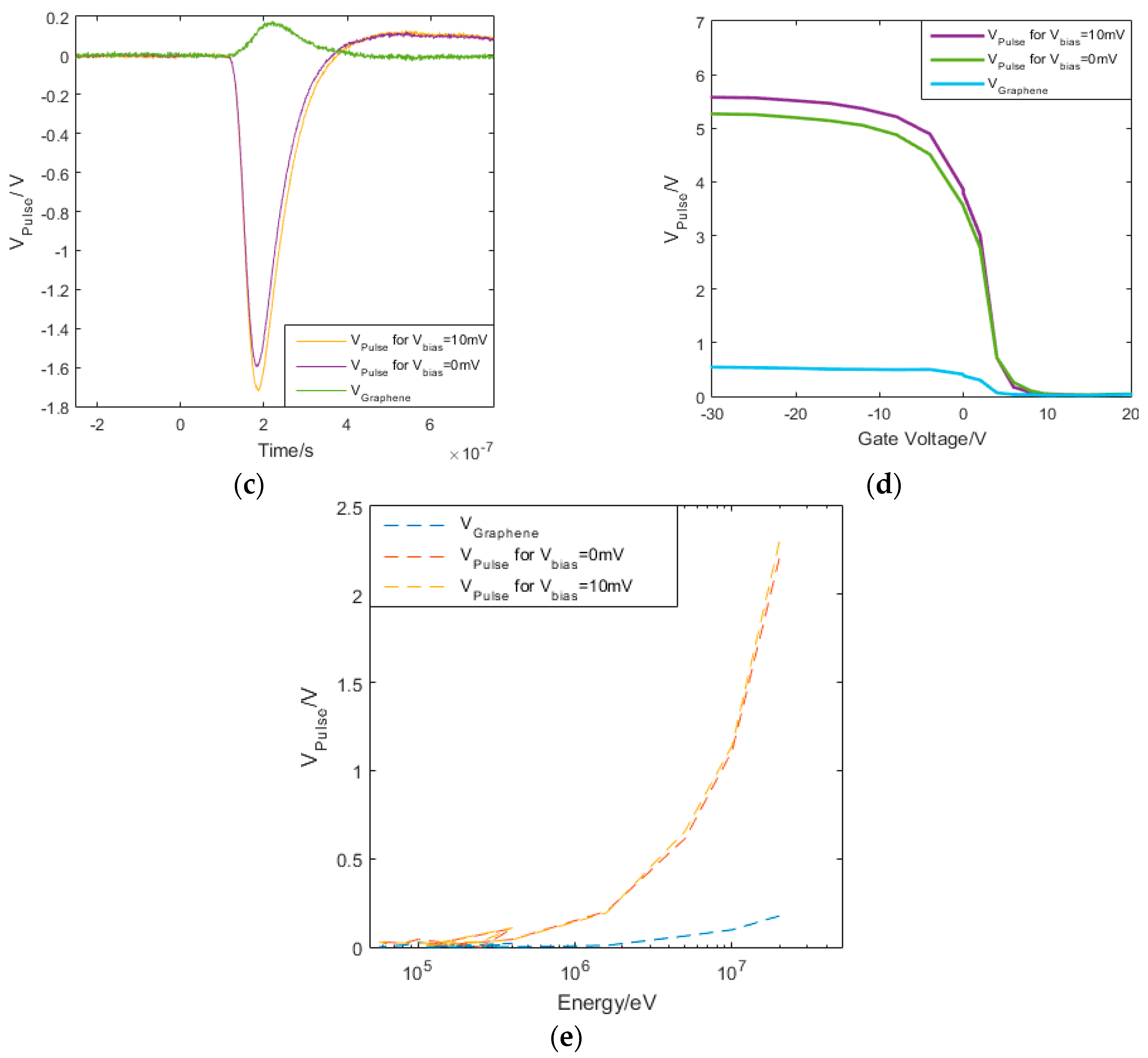
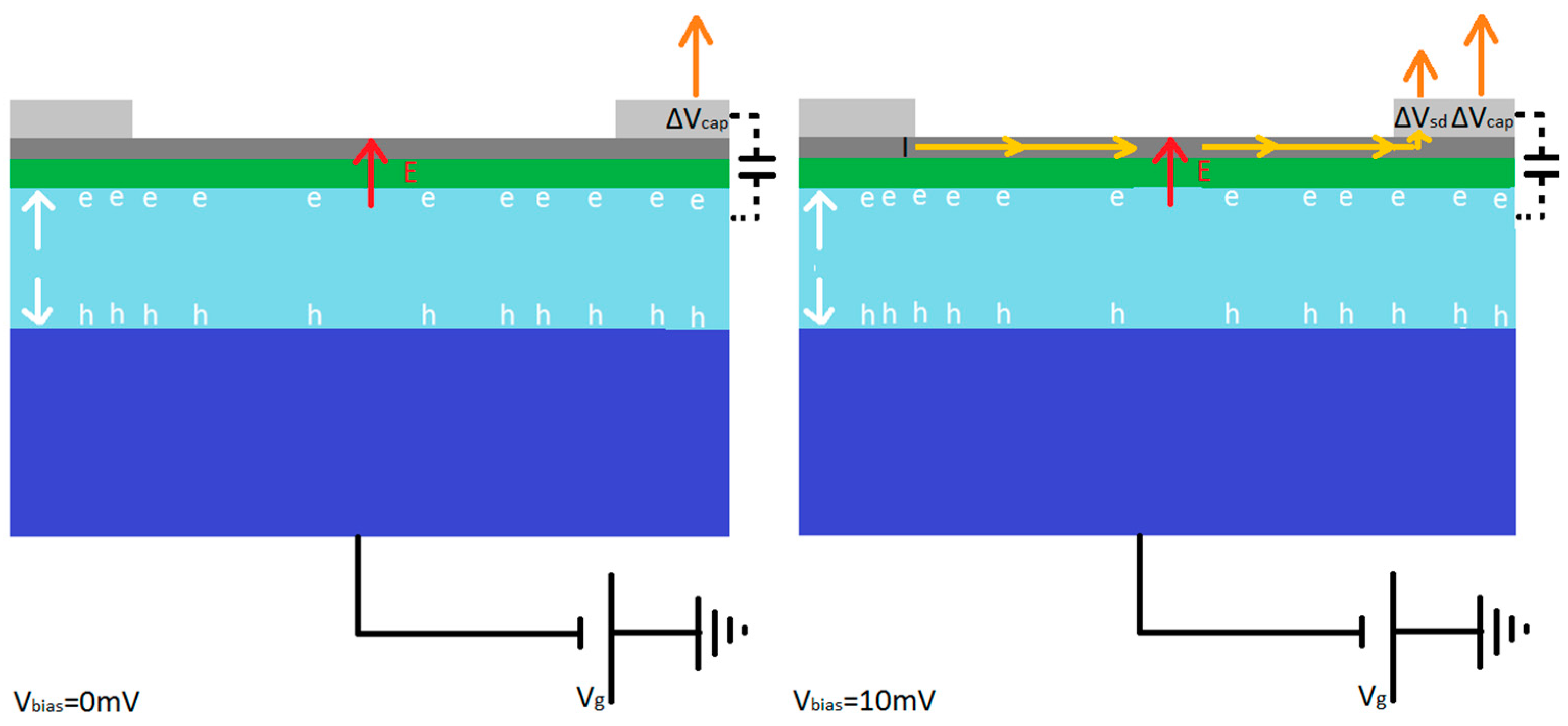

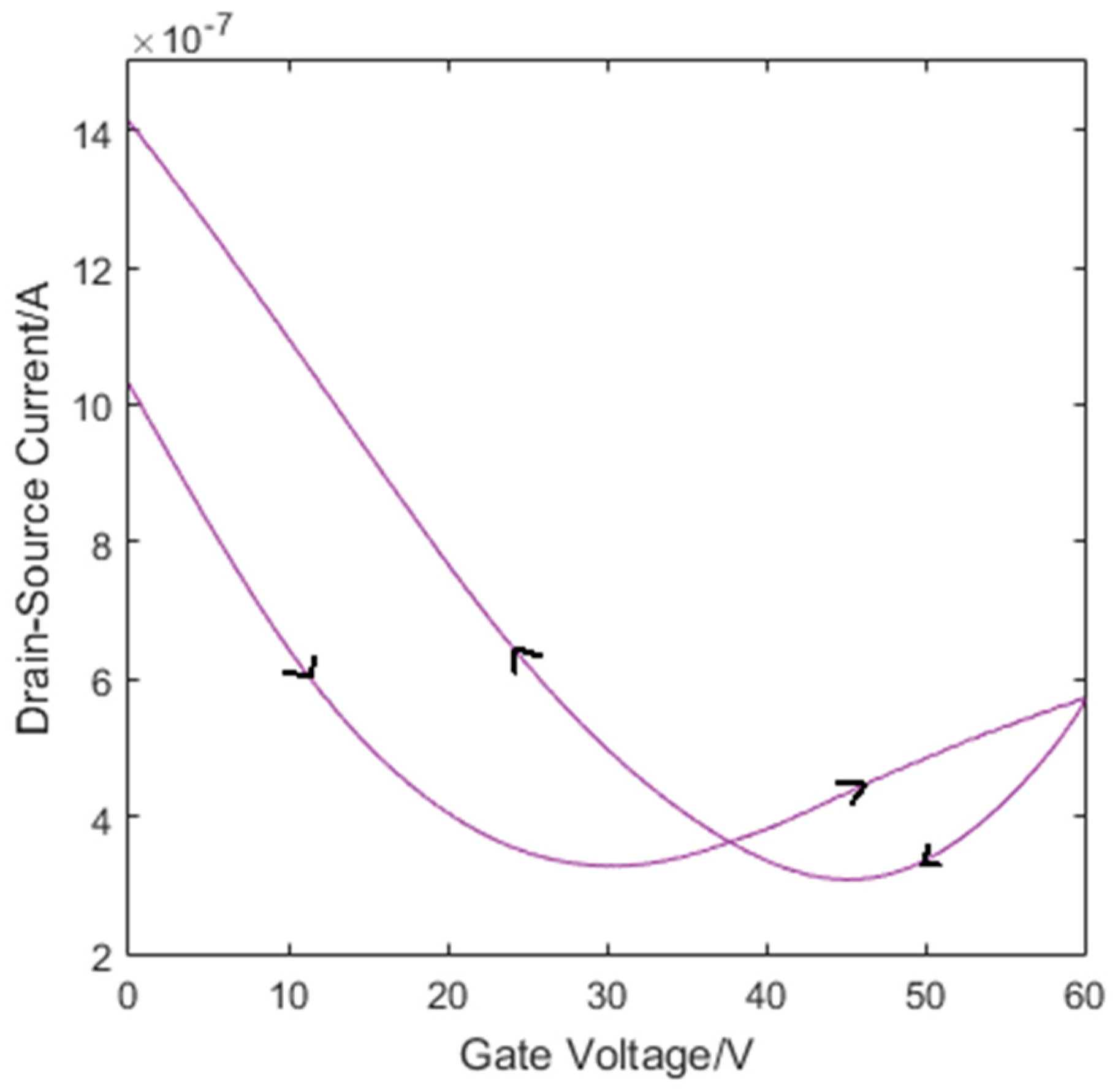
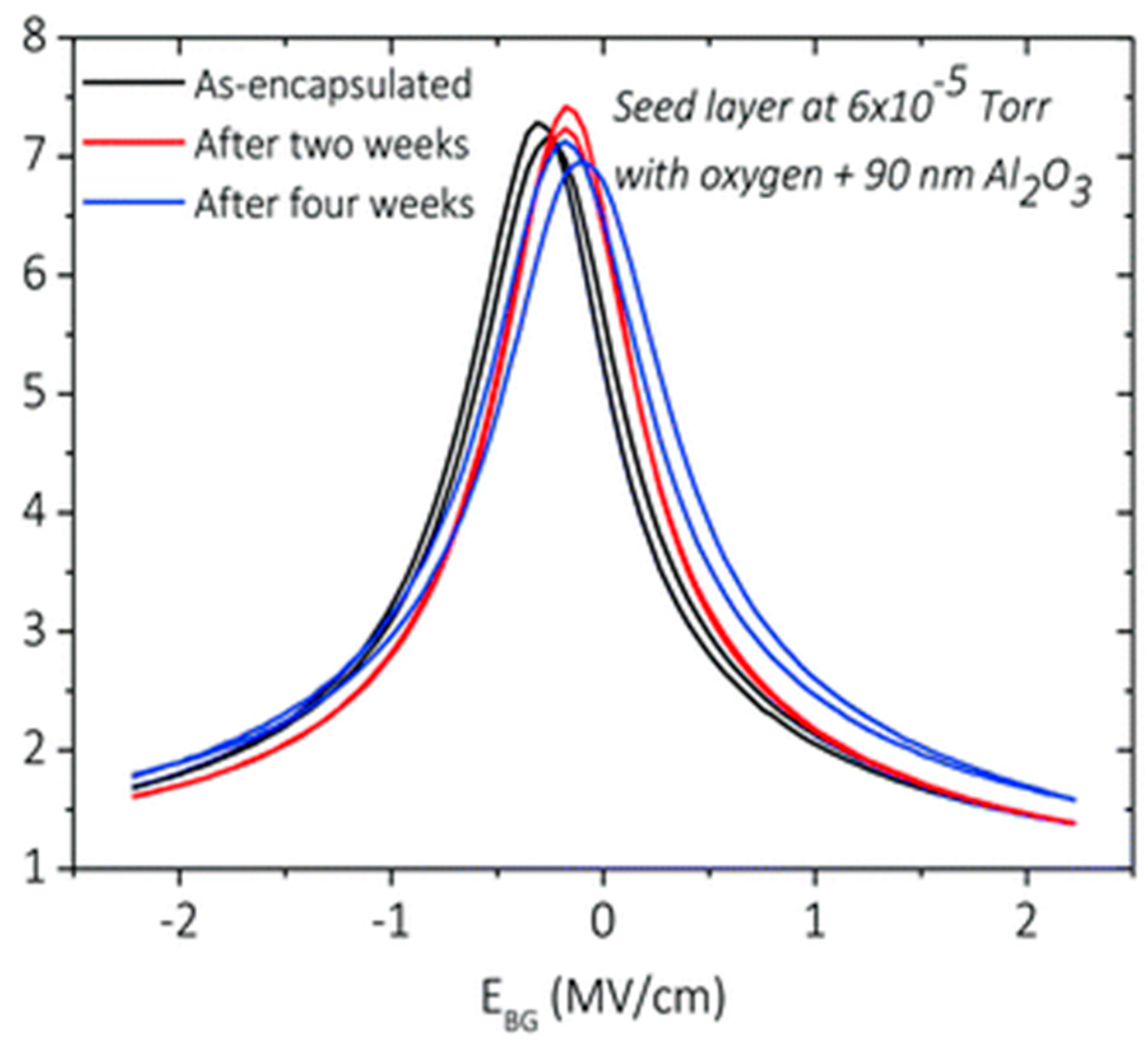
| Detector Type [34] | Operating Temperature | Operational Wavelength | Timing Resolution | Energy Resolution | Responsivity | Size of Active Area | Photon Intensity |
|---|---|---|---|---|---|---|---|
| Superconducting Tunnelling Junction [23,35] | <1 K | 1 nm–100 µm | 1 µs | <20 (for E = 1.8 eV) | >~100 AW−1 | ~1 mm2 | Single photon |
| <6 (for E = 3.1 eV) | |||||||
| ~200 (for E = 0.4 keV) | |||||||
| ~500 (for E = 5.9 keV) | |||||||
| Microwave Kinetic Inductance Detector [22,23,24,25,36] | 0.1 K–1 K | Sub-mm and mm | ~1 µs | >20 | 10−7 rad per quasi-particle | >1000 pixel array. | Single photon |
| Avalanche Photodiodes [37,38,39] | −20 °C | ~<1 µm | 40 ps+ | ~16 (for E = 5.9 keV) | ~50 AW−1 | <~25 mm2 | Single photon |
| −90 °C | ~45 (for E = 5.9 keV) | ||||||
| Transition Edge Sensors [40,41,42] | 0.1 K | ~1 nm | 0.5 ms | ~70 (for E = 0.1 keV) | ~100,000 AW−1 on transition region | ~5 cm2 | Single photon |
| ~7000 (for E = 10 keV) | |||||||
| Microchannel plate photomultiplier tube [33] | 300 K | X-ray to IR | 25 + ps | None across most of the spectrum, very poor at soft X-ray. | 5–1000 mAW−1 | >1000 mm2 | Single photon |
| Ultrafast Graphene-based Photodetector. Photothermoelectric effect [18] | 40–300 K | 500–1500 nm | ~50 fs | Photovoltage greater for lower temperatures. | ~100 µAW−1 | ~10 µm | 50 µW |
| X-ray GFET on SiC substrate. Field effect. [43,44,45,46,47,48,49] | 300 K | ~0.01–0.03 nm | - | 10,000 (for E = 15 keV) | 0.1 AW−1 | 20 µm × 4 µm | 15 kV, 15 µA → 40 kV, 80 µA |
| X-ray GFET on Si substrate. Field effect. [43,44,45,46,47,48] | 4.3 K | ~0.01–0.03 nm | - | - | - | ~10 µm | |
| Ultrafast GFET [50]. Photovoltaic effect. | 300 K | 1.55 µm | ~25 ps (2 ps theory) | - | 0.5 mAW−1 | 1 µm × 2.5 µm | 3 mW |
| THz GFET. Dyakanov-Shur effect [51,52] | 300 K | 100 µm | ~1 s | - | 100 mVW−1 | 10 µm | - |
| Quantum Dot (Field Effect Transistor) [8,53] | 4 K | 805 nm | 1 µs–1 ms | - | 650 AW−1 | 15 µm | ~3.5 mW |
| Black Phosphorus FET [54,55] | 323–383 K | <940 nm | ~1 ms | - | 4.8 mAW−1 | ~10 µm | ~500 µW |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, J.O.D.; Alexander-Webber, J.A.; Lapington, J.S.; Roy, M.; Hutchinson, I.B.; Sagade, A.A.; Martin, M.-B.; Braeuninger-Weimer, P.; Cabrero-Vilatela, A.; Wang, R.; et al. Towards a Graphene-Based Low Intensity Photon Counting Photodetector. Sensors 2016, 16, 1351. https://doi.org/10.3390/s16091351
Williams JOD, Alexander-Webber JA, Lapington JS, Roy M, Hutchinson IB, Sagade AA, Martin M-B, Braeuninger-Weimer P, Cabrero-Vilatela A, Wang R, et al. Towards a Graphene-Based Low Intensity Photon Counting Photodetector. Sensors. 2016; 16(9):1351. https://doi.org/10.3390/s16091351
Chicago/Turabian StyleWilliams, Jamie O. D., Jack A. Alexander-Webber, Jon S. Lapington, Mervyn Roy, Ian B. Hutchinson, Abhay A. Sagade, Marie-Blandine Martin, Philipp Braeuninger-Weimer, Andrea Cabrero-Vilatela, Ruizhi Wang, and et al. 2016. "Towards a Graphene-Based Low Intensity Photon Counting Photodetector" Sensors 16, no. 9: 1351. https://doi.org/10.3390/s16091351
APA StyleWilliams, J. O. D., Alexander-Webber, J. A., Lapington, J. S., Roy, M., Hutchinson, I. B., Sagade, A. A., Martin, M.-B., Braeuninger-Weimer, P., Cabrero-Vilatela, A., Wang, R., De Luca, A., Udrea, F., & Hofmann, S. (2016). Towards a Graphene-Based Low Intensity Photon Counting Photodetector. Sensors, 16(9), 1351. https://doi.org/10.3390/s16091351







