Spatiotemporal Interpolation for Environmental Modelling
Abstract
:1. Introduction
1.1. Objective
- Computationally effective: The sensor network is assumed to collect hundreds (or even thousands) of data items every second, and thus, a fast algorithm is critical for effective processing.
- The ability to obtain close-to-reality measurements (i.e., low statistical error and visually not-abrupt: To ensure environmental managers can make confident interpretations at a later stage.
2. Materials and Methods
2.1. Experimental Data
2.2. Interpolation Techniques
2.2.1. Ordinary Kriging
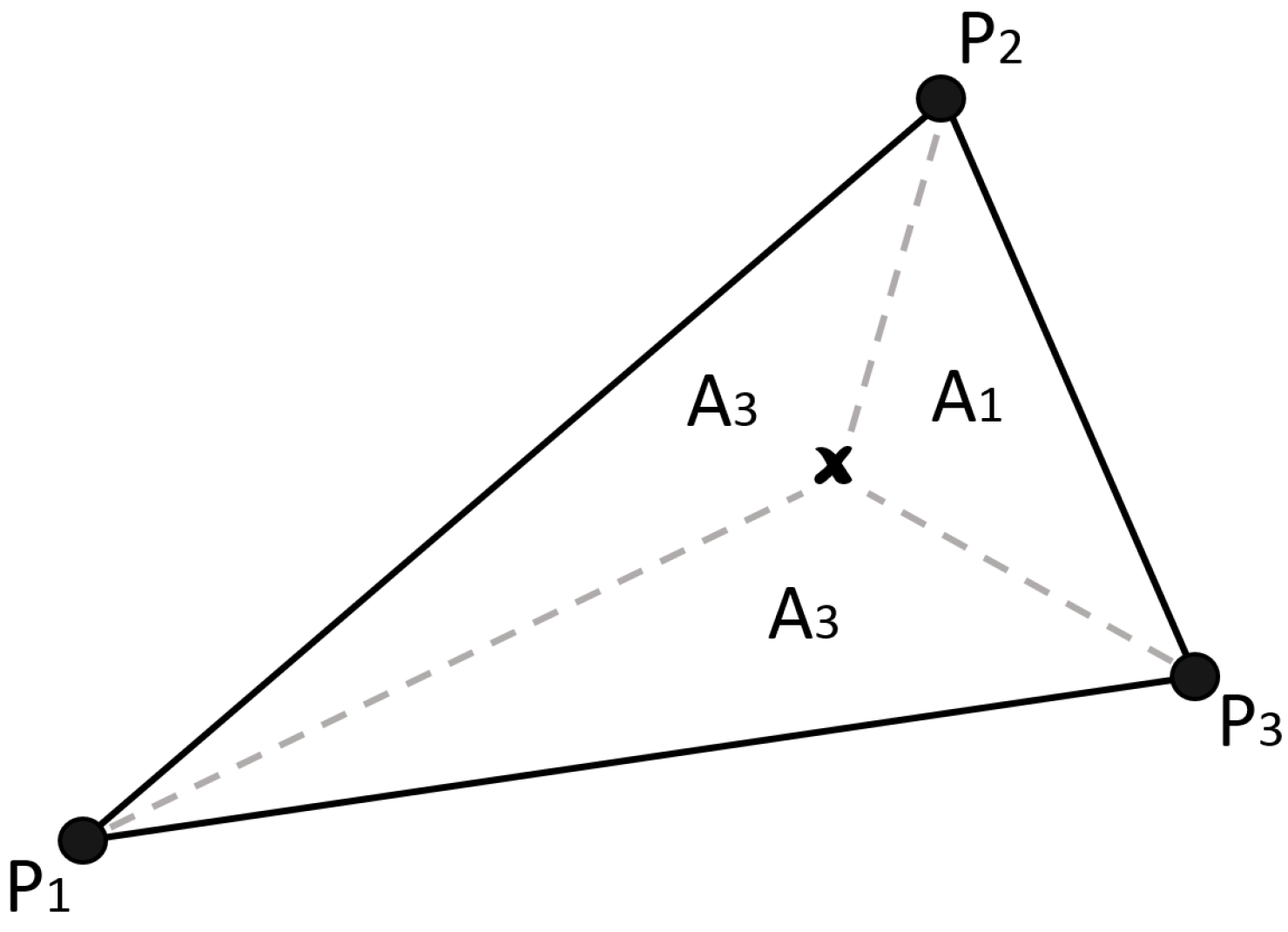
2.2.2. Shape Function: Triangular Irregular Network
2.2.3. Classic Inverse Distance Weighting
2.2.4. Improved Inverse Distance Weighting
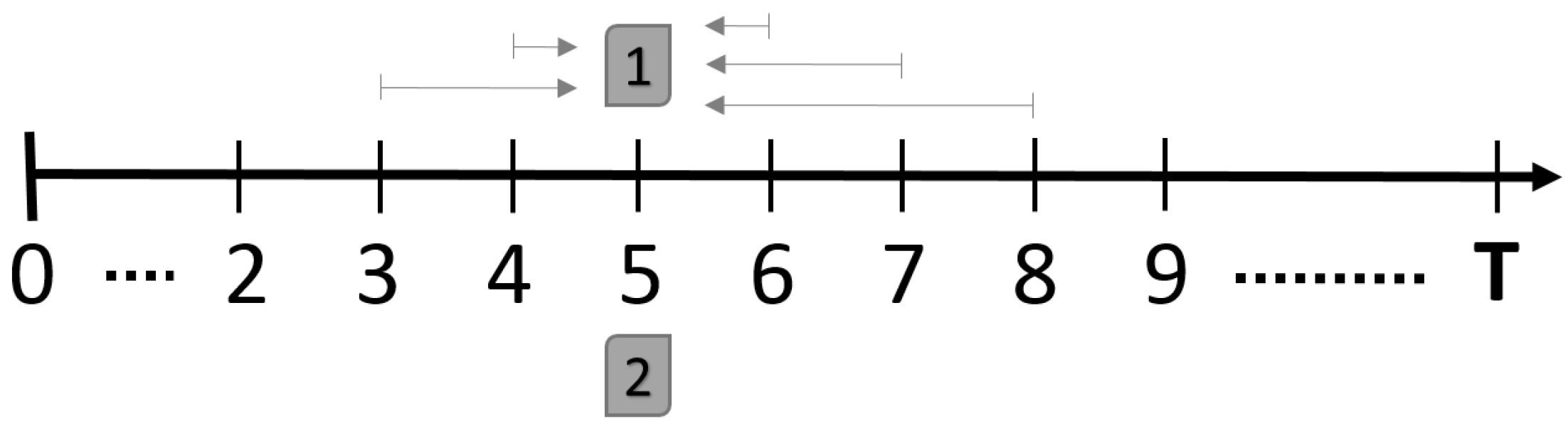
2.2.5. STI Technique : Extension Approach
2.3. Proposed Methodology
2.3.1. STI Technique: Reduction Approach
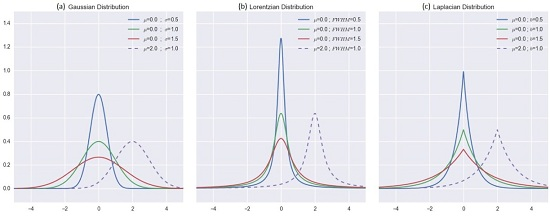
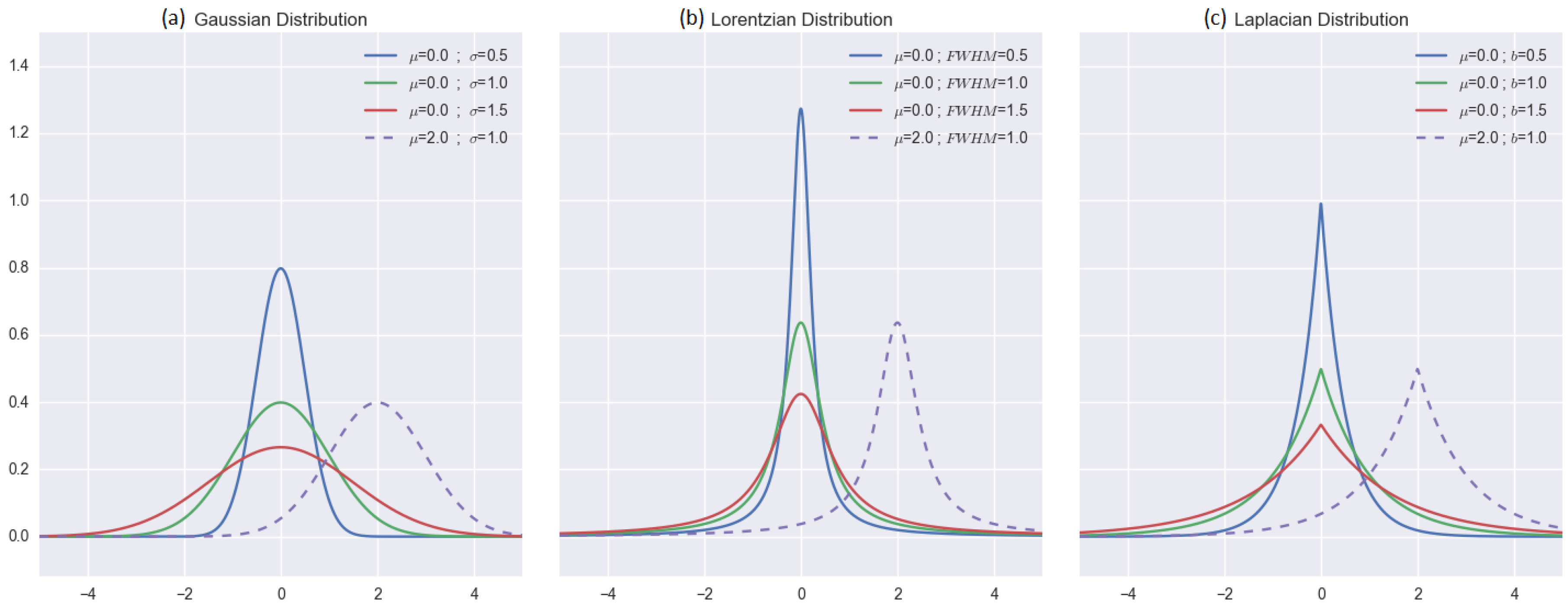
2.3.2. Distribution-Based Distance Weighting
3. Simulation Procedure and Performance Assessment
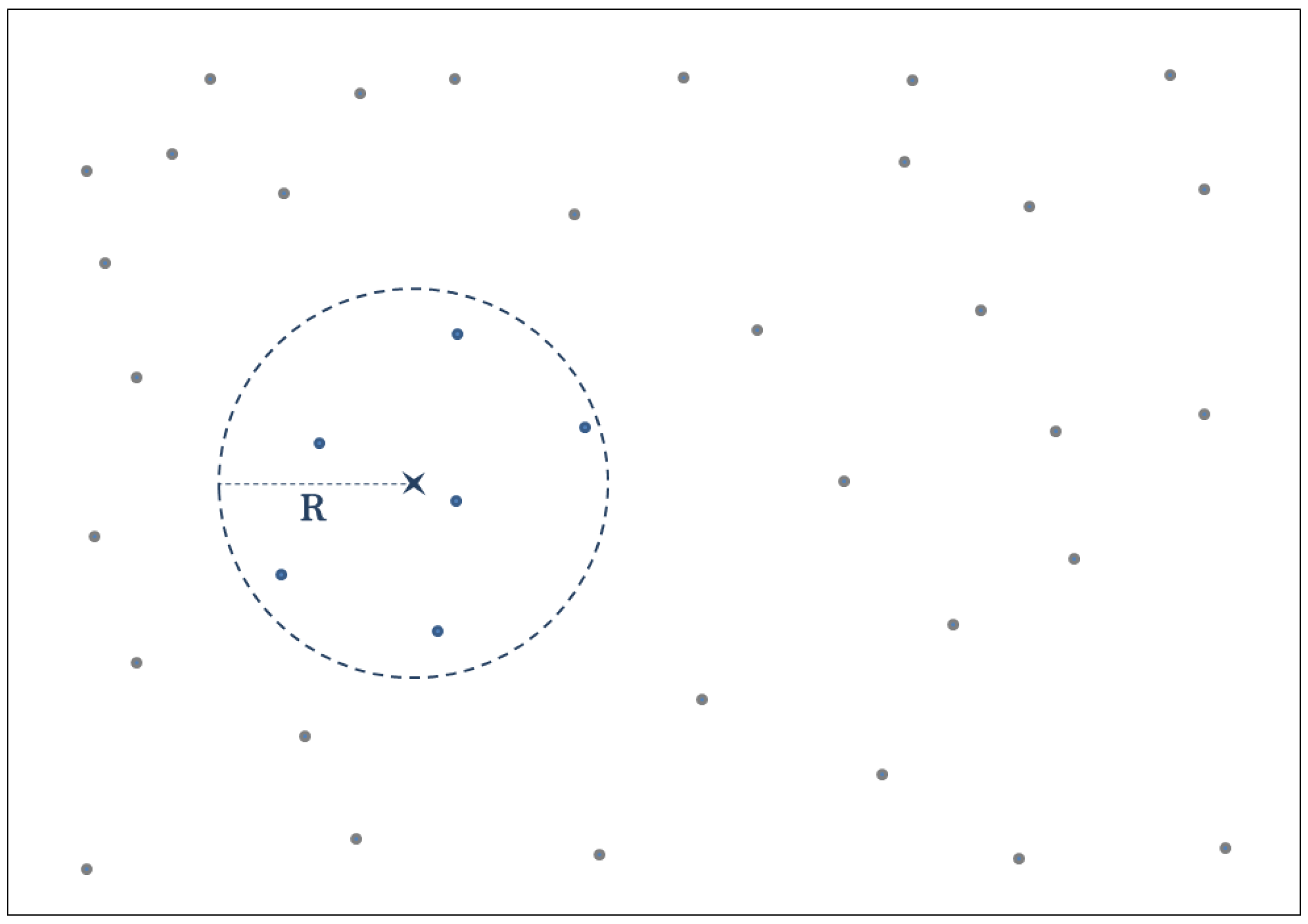
3.1. Sensor Networks Spatial Samplings
3.2. Choosing a “Balanced” 2D Spatial Interpolation Method
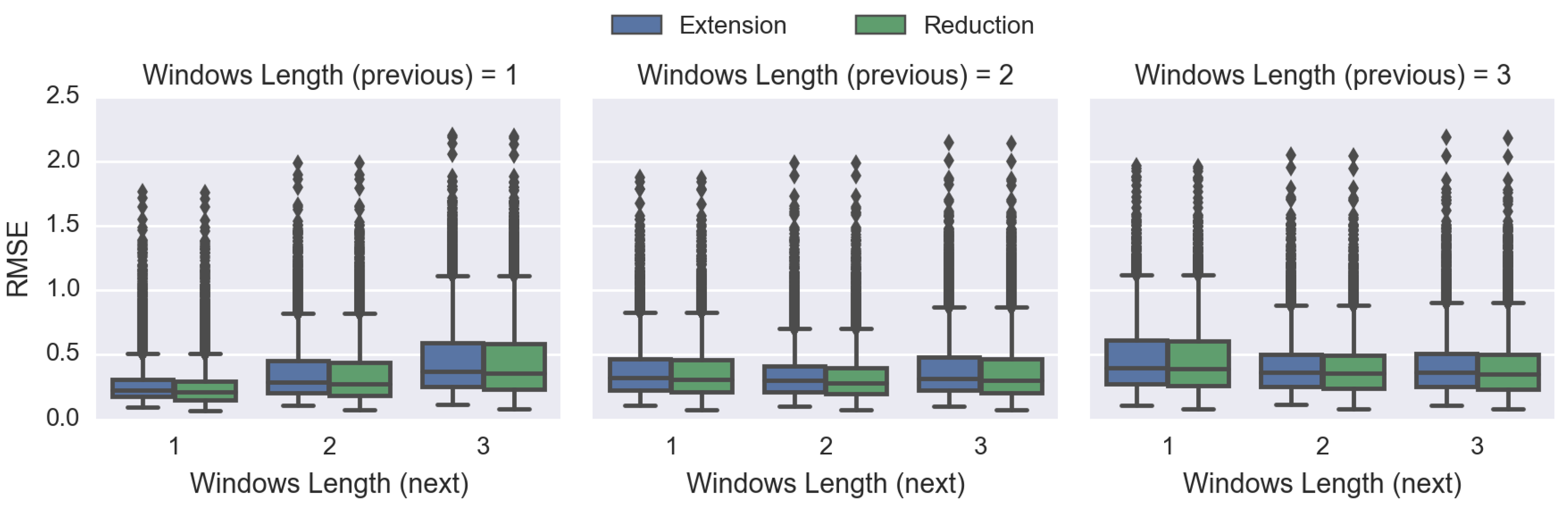
3.3. Comparing Spatiotemporal Approaches and Evaluating the DDW
4. Results
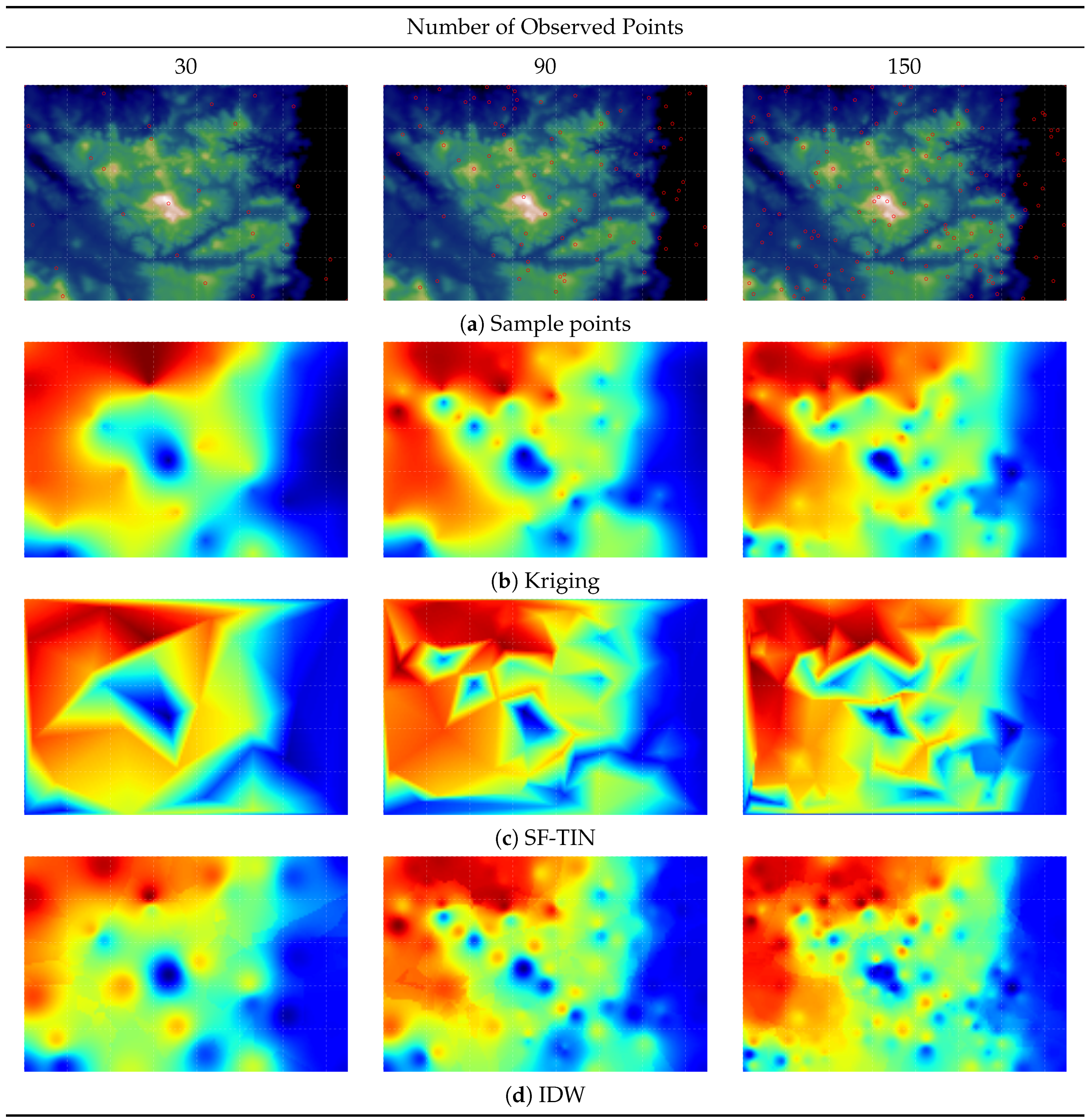
4.1. Original Data Visualisation
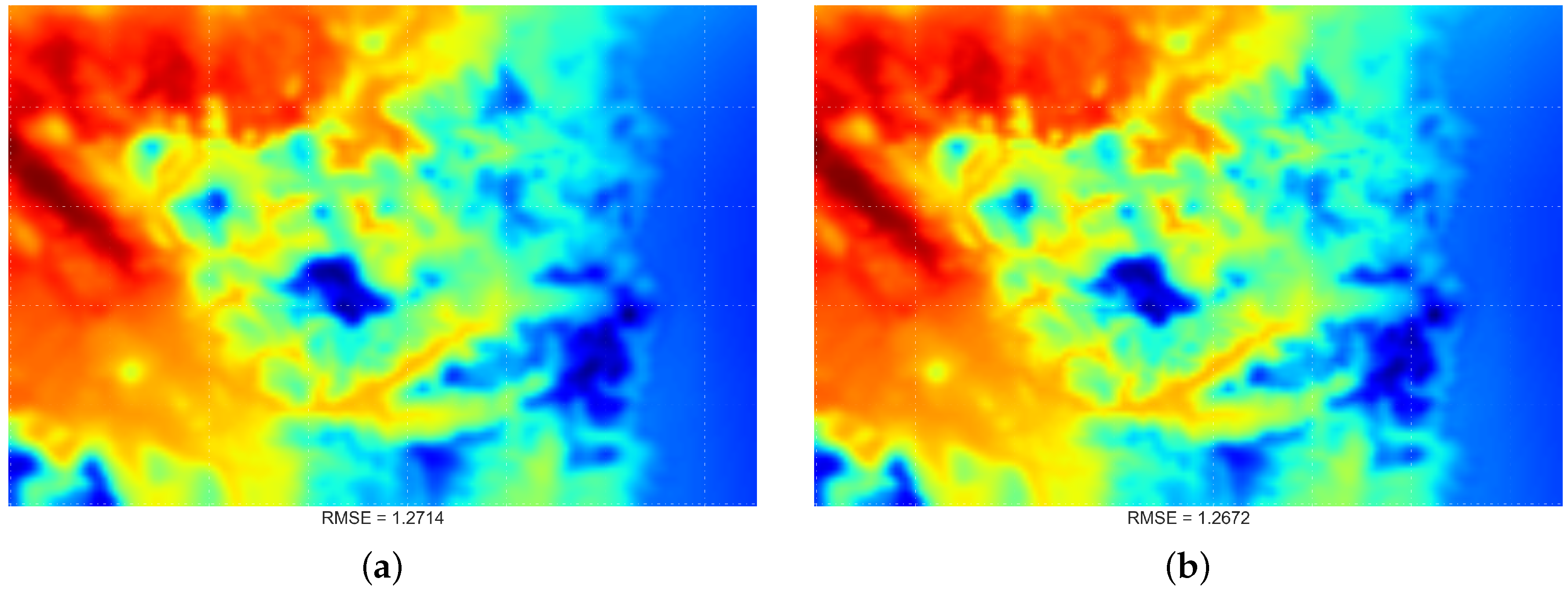
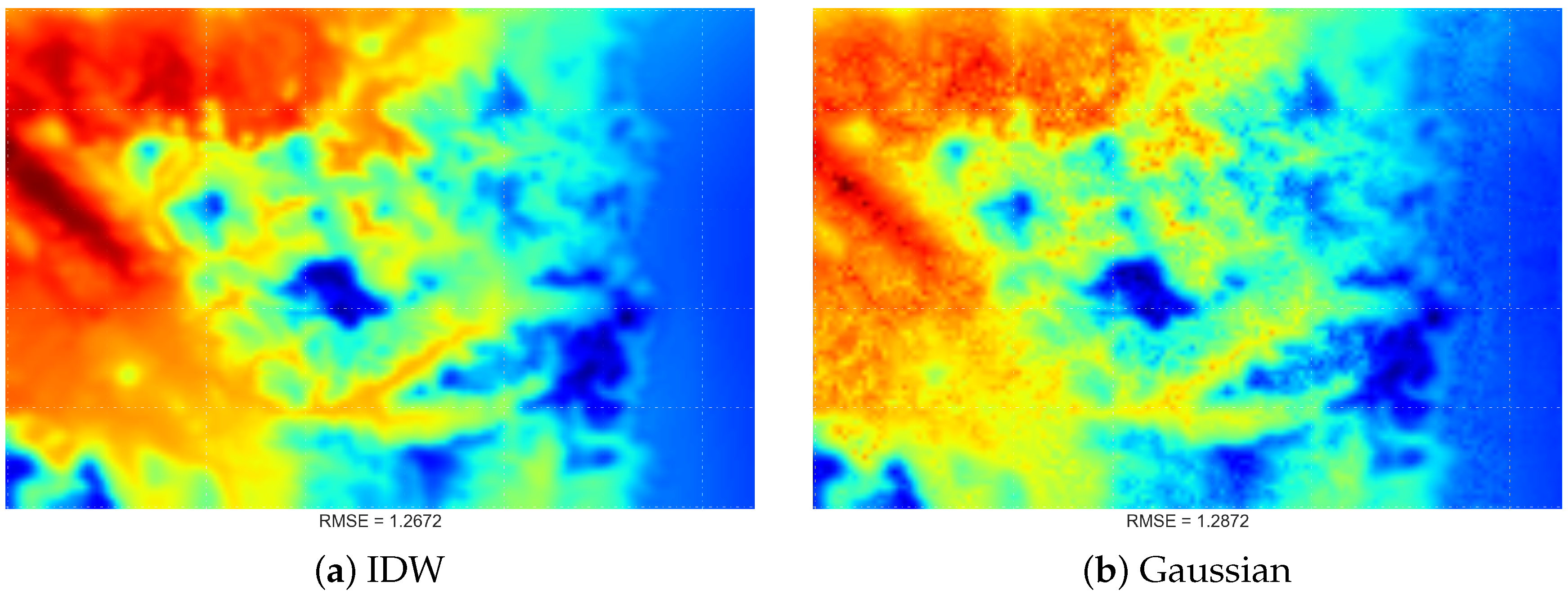
4.2. Comparing Spatial Interpolation Methods
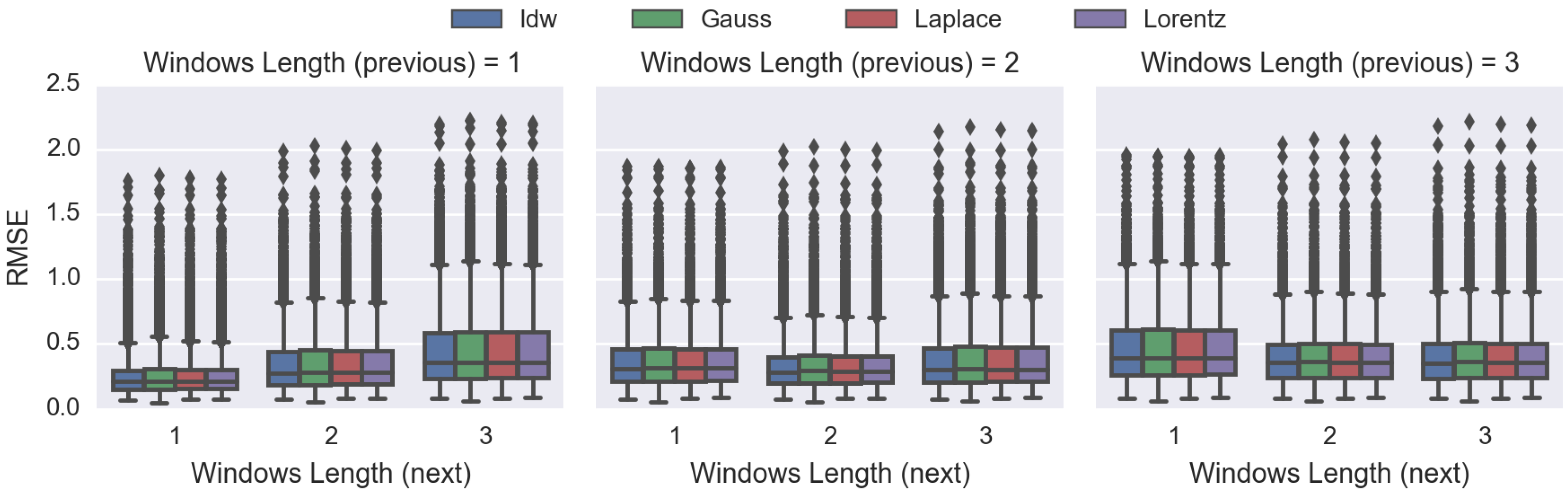
4.3. Comparing Spatiotemporal Approaches
4.4. Comparing the Proposed DDW Methods
5. Discussion
6. Conclusions and Future Work
- Computational time does not increase as the number of sample points grows significantly;
- The objective results are comparable with other techniques;
- The technique does not create abrupt visual results.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ROI | Region of interest |
| STI | Spatio temporal interpolation |
| DDW | Distribution-based distance weighting |
| IDW | Inverse distance weighting |
| AIDW | Angular IDW |
| GIDW | Gradient IDW |
| SK | Simple kriging |
| OK | Ordinary kriging |
| BK | Bayesian kriging |
| UK | Universal kriging |
| CAR | Clustering assisted regression |
| TPS | Thin plate splines |
| RBF | Radial basis function |
| RF | Random forest |
| RFIDW | RF + IDW |
| RFOK | RF + OK |
| TS | Trend surface |
| TP | Thiessen polygon |
| RMSE | Root mean squared error |
| MAE | Mean absolute error |
| SE | Standard error |
References
- Sanabria, L.A.; Qin, X.; Li, J.; Cechet, R.P.; Lucas, C. Spatial interpolation of McArthur’s Forest Fire Danger Index across Australia: Observational study. Environ. Model. Softw. 2013, 50, 37–50. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. Spatial interpolation methods applied in the environmental sciences: A review. Environ. Model. Softw. 2014, 53, 173–189. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
- Chen, F.; Liu, C. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Tang, L.; Su, X.; Shao, G.; Zhang, H.; Zhao, J. A Clustering-Assisted Regression (CAR) approach for developing spatial climate data sets in China. Environ. Model. Softw. 2012, 38, 122–128. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Joseph, V.R.; Kang, L. Regression-Based Inverse Distance Weighting with Applications to Computer Experiments. Technometrics 2011, 53, 254–265. [Google Scholar] [CrossRef]
- Anderson, S. An Evaluation of Spatial Interpolation Methods on Air Temperature in Phoenix. Available online: http://www.cobblestoneconcepts.com/ucgis2summer/anderson/anderson.htm (accessed on 5 August 2016).
- Plouffe, C.C.F.; Robertson, C.; Chandrapala, L. Comparing interpolation techniques for monthly rainfall mapping using multiple evaluation criteria and auxiliary data sources: A case study of Sri Lanka. Environ. Model. Softw. 2015, 67, 57–71. [Google Scholar] [CrossRef]
- Sun, Y.; Kang, S.; Li, F.; Zhang, L. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China. Environ. Model. Softw. 2009, 24, 1163–1170. [Google Scholar] [CrossRef]
- Naoum, S.; Tsanis, I. Ranking spatial interpolation techniques using a GIS-based DSS. Glob. Nest 2004, 6, 1–20. [Google Scholar]
- Li, J. A Review of Spatial Interpolation Methods for Environmental Scientists/Jin Li and Andrew D. Heap; Geoscience Australia: Canberra, Australia, 2008.
- Burrough, P.A.; McDonnell, R.A. Principles of Geographical Information Systems; Oxford University Press: New York, NY, USA, 1998. [Google Scholar]
- Li, L. Spatiotemporal Interpolation Methods in GIS. Ph.D. Thesis, The University of Nebraska, Lincoln, NE, USA, 2003. [Google Scholar]
- Li, L.; Zhang, X.; Holt, J.B.; Tian, J.; Piltner, R. Spatiotemporal Interpolation Methods for Air Pollution Exposure. In Proceedings of the Ninth Symposium on Abstraction, Reformulation and Approximation (AAAI), Catalonia, Spain, 17–18 July 2011.
- Li, L.; Losser, T.; Yorke, C.; Piltner, R. Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation: A Web-Based Application of Interpolating Daily Fine Particulate Matter PM2.5 in the Contiguous U.S. Using Parallel Programming and k-d Tree. Int. J. Environ. Res. Public Health 2014, 11, 9101–9141. [Google Scholar] [CrossRef] [PubMed]
- Kilibarda, M.; Hengl, T.; Heuvelink, G.B.M.; Gräler, B.; Pebesma, E.; Perčec Tadić, M.; Bajat, B. Spatio-temporal interpolation of daily temperatures for global land areas at 1 km resolution. J. Geophys. Res. Atmos. 2014, 119, 2294–2313. [Google Scholar] [CrossRef]
- Katzfey, J.; Thatcher, M. Ensemble One-Kilometre Forecasts for the South Esk Hydrological Sensor Web. In Proceedings of the 19th International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; pp. 3511–3517.
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In ACM ’68 Proceedings of the 1968 23rd ACM National Conference; ACM: New York, NY, USA, 1968. [Google Scholar]
- De Mesnard, L. Pollution models and inverse distance weighting: Some critical remarks. Comput. Geosci. 2013, 52, 459–469. [Google Scholar] [CrossRef]
- Scipy Community. Scipy V0.15.1 Reference Guide—Differential Evolution. Available online: http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html (accessed on 8 August 2015).
- Susanto, F.; Budi, S.; Souza, P.D.; Engelke, U.; He, J. Design of Environmental Sensor Networks Using Evolutionary Algorithms. IEEE Geosci. Remote Sens. Lett. 2016, 13, 575–579. [Google Scholar] [CrossRef]
- Montero, J.; Fernandez-Aviles, G.; Mateu, J. Spatial and Spatio-Temporal Geostatistical Modeling and Kriging; Wiley: West Sussex, UK, 2015. [Google Scholar]



| Process | Techniques | Findings | Ref. |
|---|---|---|---|
| Spatial rainfall mapping using IDW in the middle of Taiwan. | IDW | - IDW can be improved by the adjustment of the distance-decay parameter and the search radius. | [4] |
| - Does not have significant interpolating ability for extreme values. | |||
| Compared to the developed CAR method with IDW for climate datasets in China. | IDW, CAR | - High-elevation data are an important factor for meteorological studies. | [5] |
| - CAR performs slightly better than GIDW in terms of objective comparisons, especially in estimating local neighbouring patterns. | |||
| Comparing different techniques for precipitation and elevation. | IDW, AIDW, Kriging | - Varying the distance-decay parameter of IDW based on the spatial pattern can improve overall performance (AIDW). | [6] |
| - AIDW can perform better than kriging in some cases. | |||
| Proposing regression-based IDW and comparing it with IDW and kriging. | IDW, RIDW, Kriging | - Integrating linear regression in IDW provides comparable objective evaluation to kriging and is computationally less demanding. | [7] |
| - The confidence interval (CI) of RIDW also surpasses kriging CI. | |||
| Evaluating different interpolation techniques for air temperature data. | Spline, IDW, Kriging | - Kriging performs better overall, followed by IDW and spline. | [8] |
| Comparing different techniques for rainfall mapping in Sri Lanka. | IDW, TPS, OK, BK | - Interpolation results are very much dependent on the settings. | [9] |
| - Different methods with different settings must be tested to define the suitable technique. | |||
| - Bayesian kriging and splines performed best overall. | |||
| Assessing different interpolation methods to define the most suitable technique for the McArthur Forest Fire Danger Index (FFDI). | IDW, OK, RF, RFOK, RFIDW | - Combination of methods: RFOK and RFIDW shows the most promising results (least error). | [1] |
| - Fire danger index is highly related to the behaviour of climate change, and should be considered carefully. | |||
| Investigated several techniques for depth to underground water in northwest China. | IDW, RBF, OK, SK, UK | - Simple kriging is the optimal method in terms of result consistency and the smallest prediction interval of 95%. | [10] |
| - Depth of underground water increases significantly over the year because of excessive exploitation. | |||
| Ranking spatial interpolation techniques using GIS-based DSS. | Spline, IDW, Kriging, TP, TS | - No optimal technique that can accurately predict the rainfall. | [11] |
| - Performance of each technique depends on the scale of the input data. | |||
| - Kriging is the recommended technique, as it produces the most consistent results. | |||
| Using an interpolation method to construct a comprehensive archive of Australian climate data. | TPS, OK | - Different climate variables can be more accurately interpolated using different techniques due to the characteristic variability. | [3] |
| Title | Abbreviations |
|---|---|
| IDW | Inverse Distance Weighting |
| AIDW | Angular IDW |
| GIDW | Gradient IDW |
| SK | Simple Kriging |
| OK | Ordinary Kriging |
| BK | Bayesian Kriging |
| UK | Universal Kriging |
| CAR | Clustering Assisted Regression |
| TPS | Thin Plate Splines |
| RBF | Radial Basis Function |
| RF | Random Forest |
| RFIDW | RF + IDW |
| RFOK | RF + OK |
| TS | Trend Surface |
| TP | Thiessen Polygon |
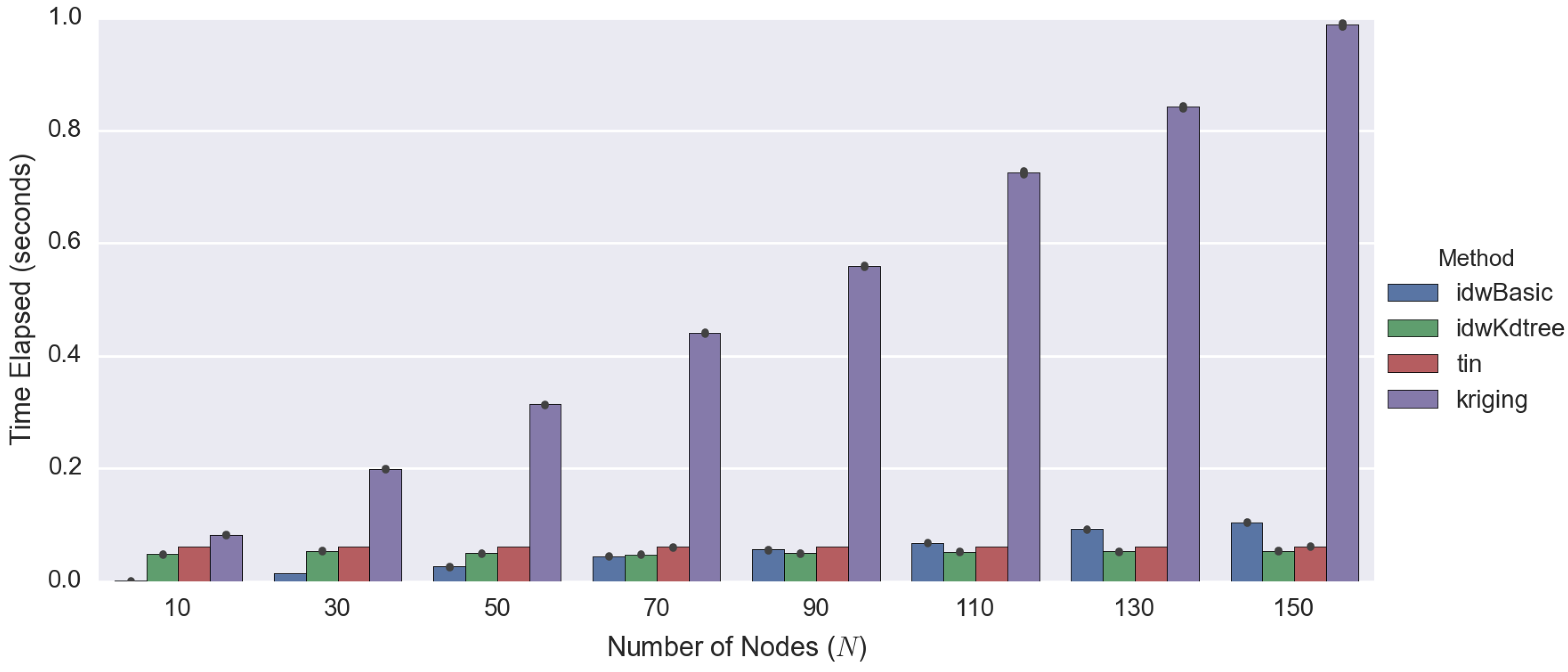
| Number of Observed Points | Total Time Elapsed | |||
|---|---|---|---|---|
| Basic IDW | Improved IDW | TIN | Kriging | |
| 10 | 0.0024 | 0.0252 | 0.0289 | 0.3034 |
| 30 | 0.0096 | 0.0278 | 0.0281 | 0.3852 |
| 50 | 0.0214 | 0.0268 | 0.0291 | 0.4706 |
| 70 | 0.0355 | 0.0253 | 0.0291 | 0.6582 |
| 90 | 0.0447 | 0.0040 | 0.0286 | 0.7808 |
| 110 | 0.0545 | 0.0283 | 0.0288 | 0.8633 |
| 130 | 0.0596 | 0.0322 | 0.0283 | 0.9720 |
| 150 | 0.0596 | 0.0322 | 0.0283 | 0.9720 |
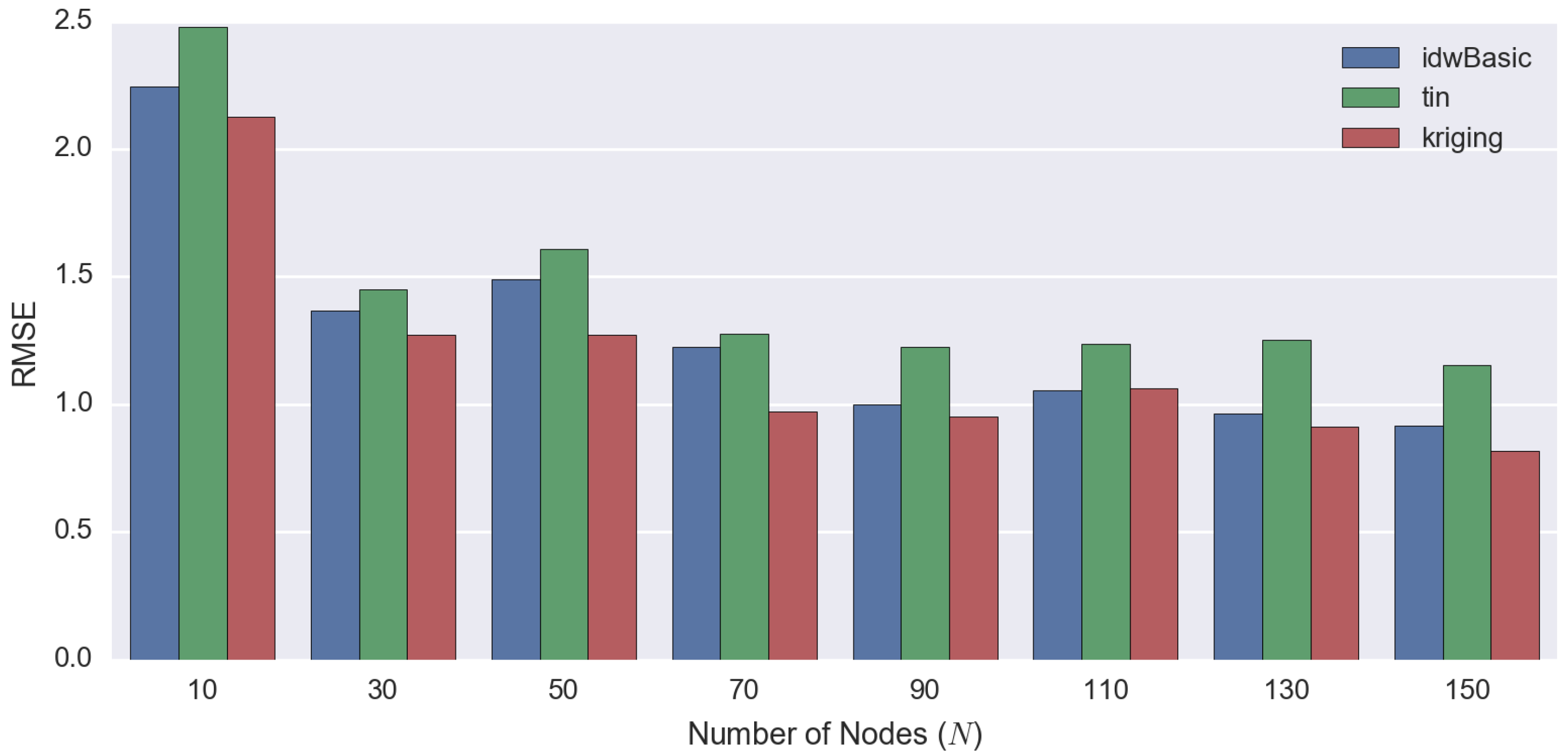
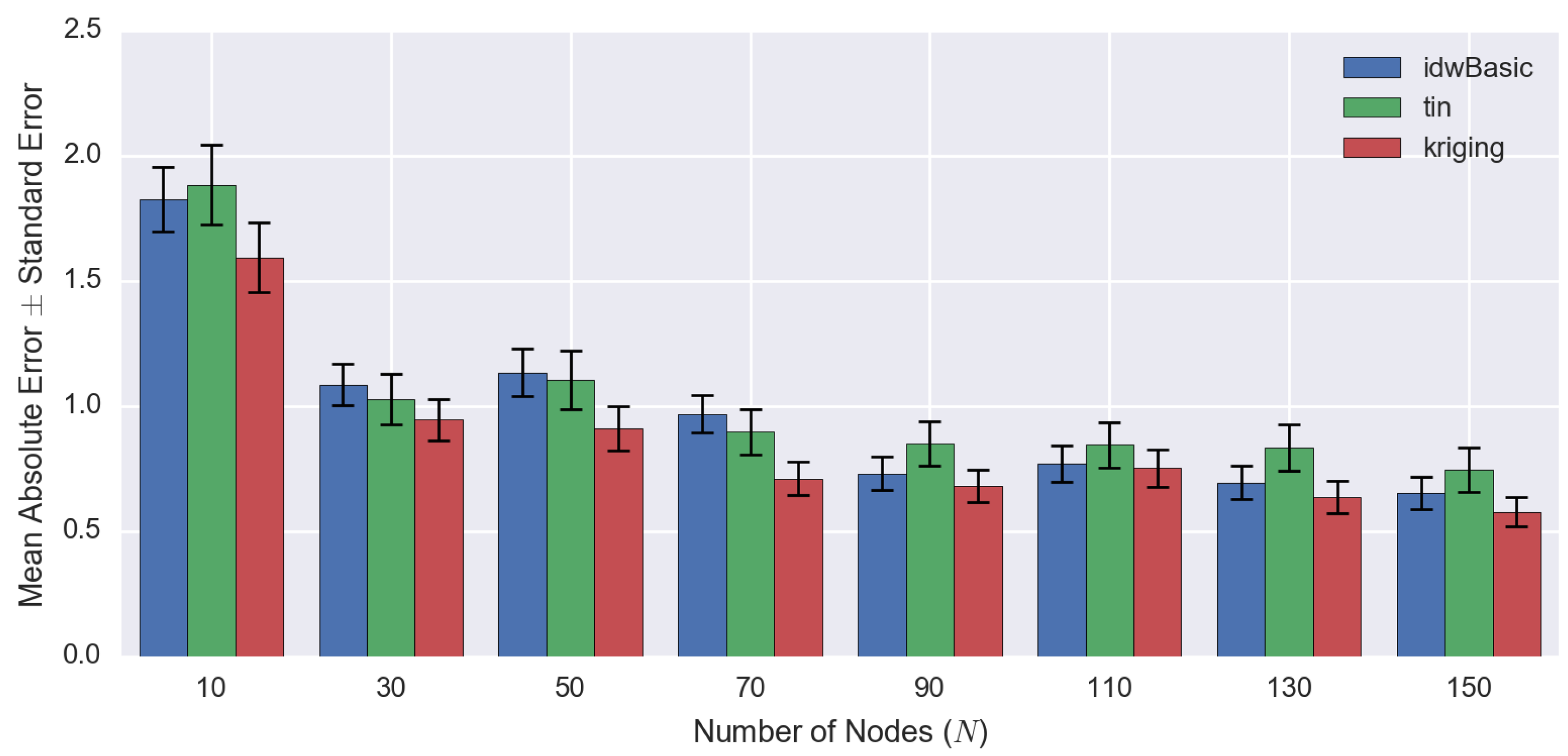
| Number of Observed Points | RMSE | MAE ± SE | ||||
|---|---|---|---|---|---|---|
| IDW | TIN | Kriging | IDW | TIN | Kriging | |
| 10 | 2.2461 | 2.4767 | 2.1257 | 1.83 ± 0.13 | 1.89 ± 0.16 | 1.60 ± 0.14 |
| 30 | 1.3667 | 1.4503 | 1.2720 | 1.09 ± 0.08 | 1.03 ± 0.10 | 0.95 ± 0.08 |
| 50 | 1.4897 | 1.6080 | 1.2718 | 1.14 ± 0.10 | 1.11 ± 0.12 | 0.91 ± 0.09 |
| 70 | 1.2259 | 1.2755 | 0.9727 | 0.97 ± 0.07 | 0.90 ± 0.09 | 0.71 ± 0.07 |
| 90 | 0.9985 | 1.2243 | 0.9517 | 0.73 ± 0.07 | 0.85 ± 0.09 | 0.68 ± 0.07 |
| 110 | 1.0565 | 1.2378 | 1.0640 | 0.77 ± 0.07 | 0.85 ± 0.09 | 0.75 ± 0.07 |
| 130 | 0.9645 | 1.2533 | 0.9136 | 0.70 ± 0.07 | 0.84 ± 0.09 | 0.64 ± 0.07 |
| 150 | 0.9146 | 1.1537 | 0.8168 | 0.65 ± 0.06 | 0.75 ± 0.09 | 0.58 ± 0.06 |
| Advantages | Disadvantages | |
|---|---|---|
| OK |
|
|
| IDW |
|
|
| TIN |
|
|
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Susanto, F.; De Souza, P., Jr.; He, J. Spatiotemporal Interpolation for Environmental Modelling. Sensors 2016, 16, 1245. https://doi.org/10.3390/s16081245
Susanto F, De Souza P Jr., He J. Spatiotemporal Interpolation for Environmental Modelling. Sensors. 2016; 16(8):1245. https://doi.org/10.3390/s16081245
Chicago/Turabian StyleSusanto, Ferry, Paulo De Souza, Jr., and Jing He. 2016. "Spatiotemporal Interpolation for Environmental Modelling" Sensors 16, no. 8: 1245. https://doi.org/10.3390/s16081245
APA StyleSusanto, F., De Souza, P., Jr., & He, J. (2016). Spatiotemporal Interpolation for Environmental Modelling. Sensors, 16(8), 1245. https://doi.org/10.3390/s16081245