Short-Range Noncontact Sensors for Healthcare and Other Emerging Applications: A Review
Abstract
:1. Introduction
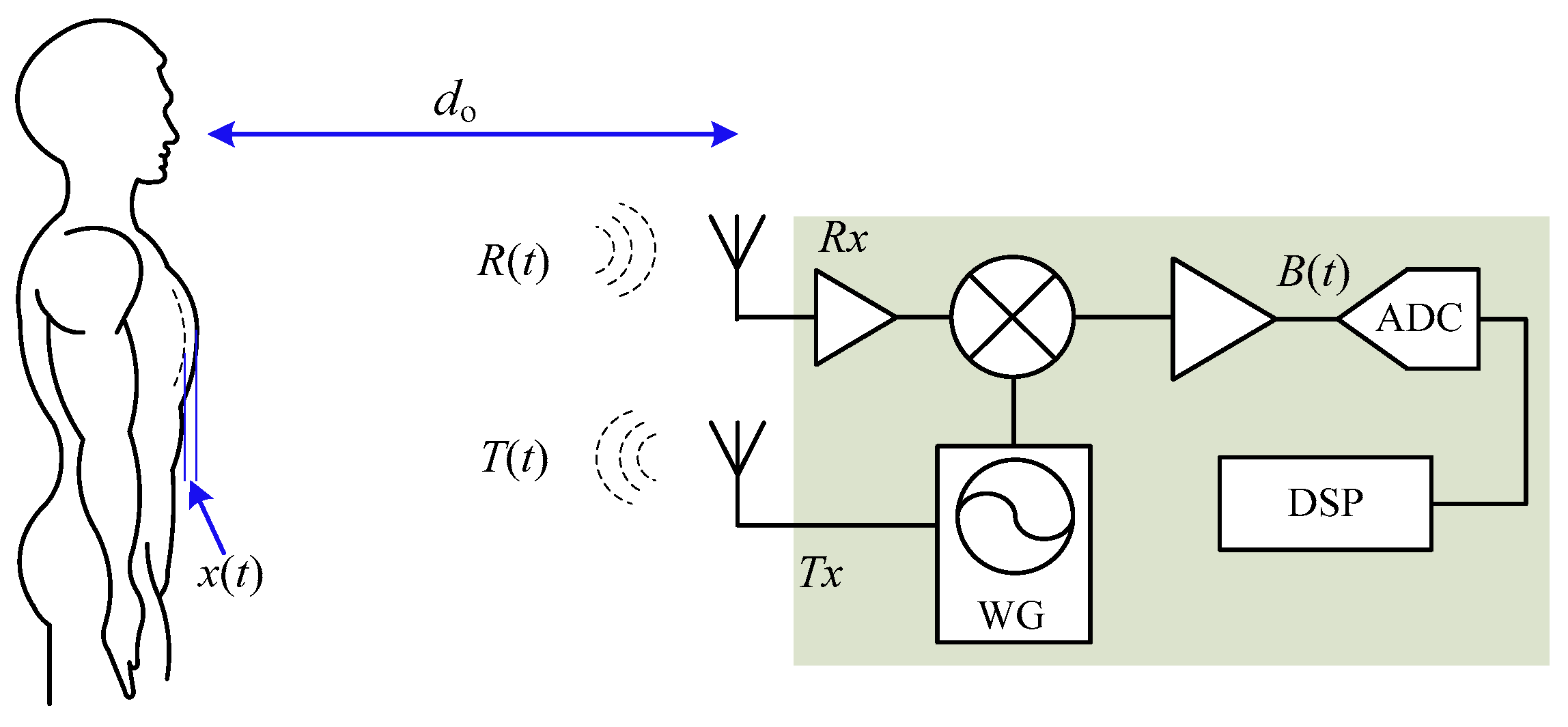
2. Working Principle of CW Doppler Radar
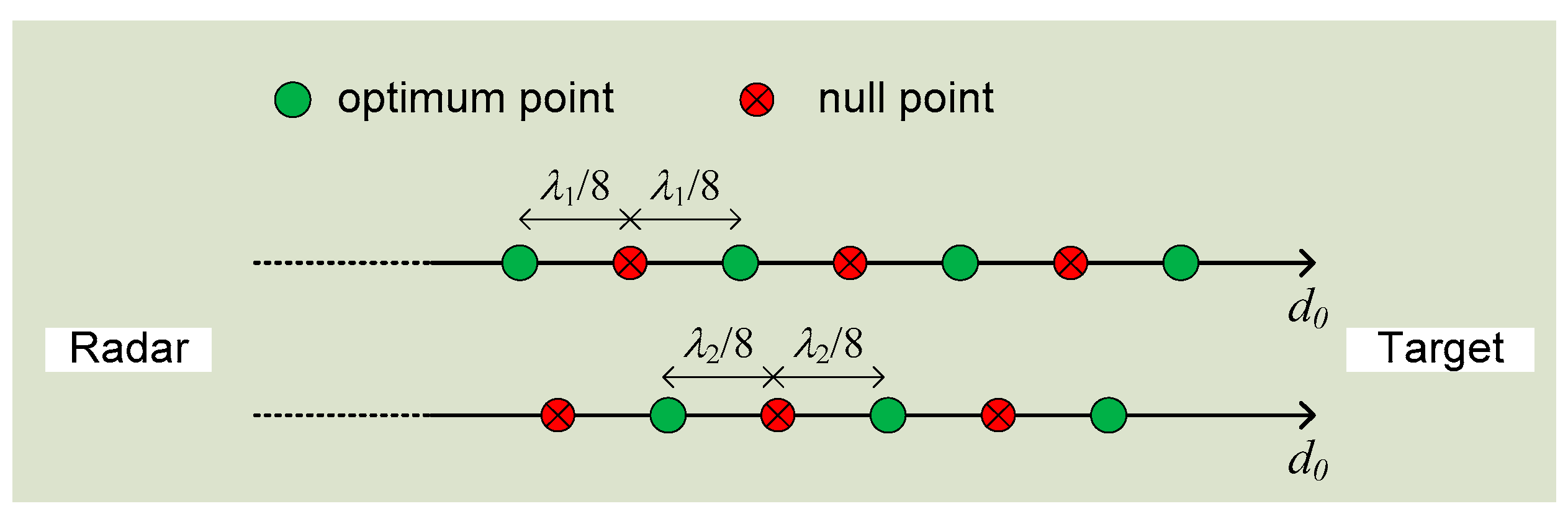
2.1. Theory
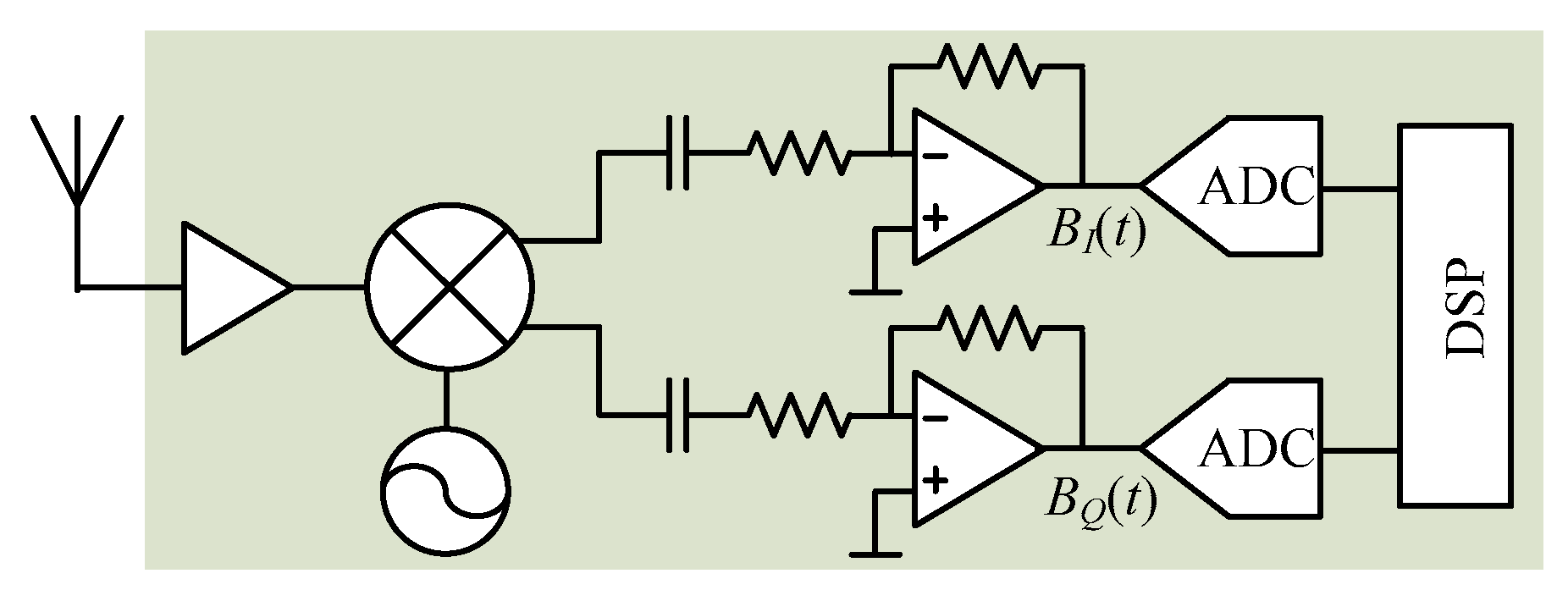
2.2. Demodulation Techniques
- Small Angle Approximation
- Arctangent demodulation
3. Recent Technical Advancements
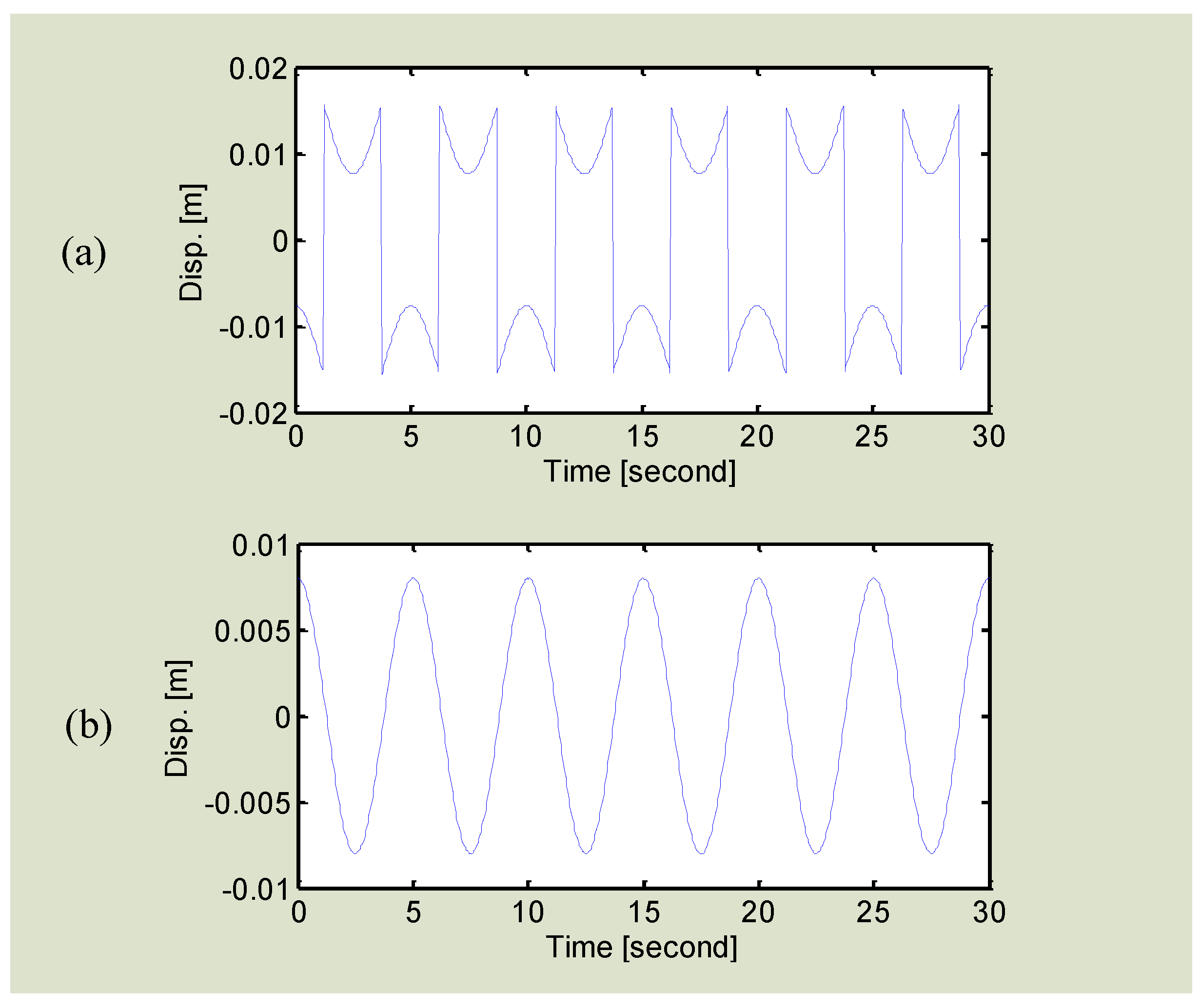
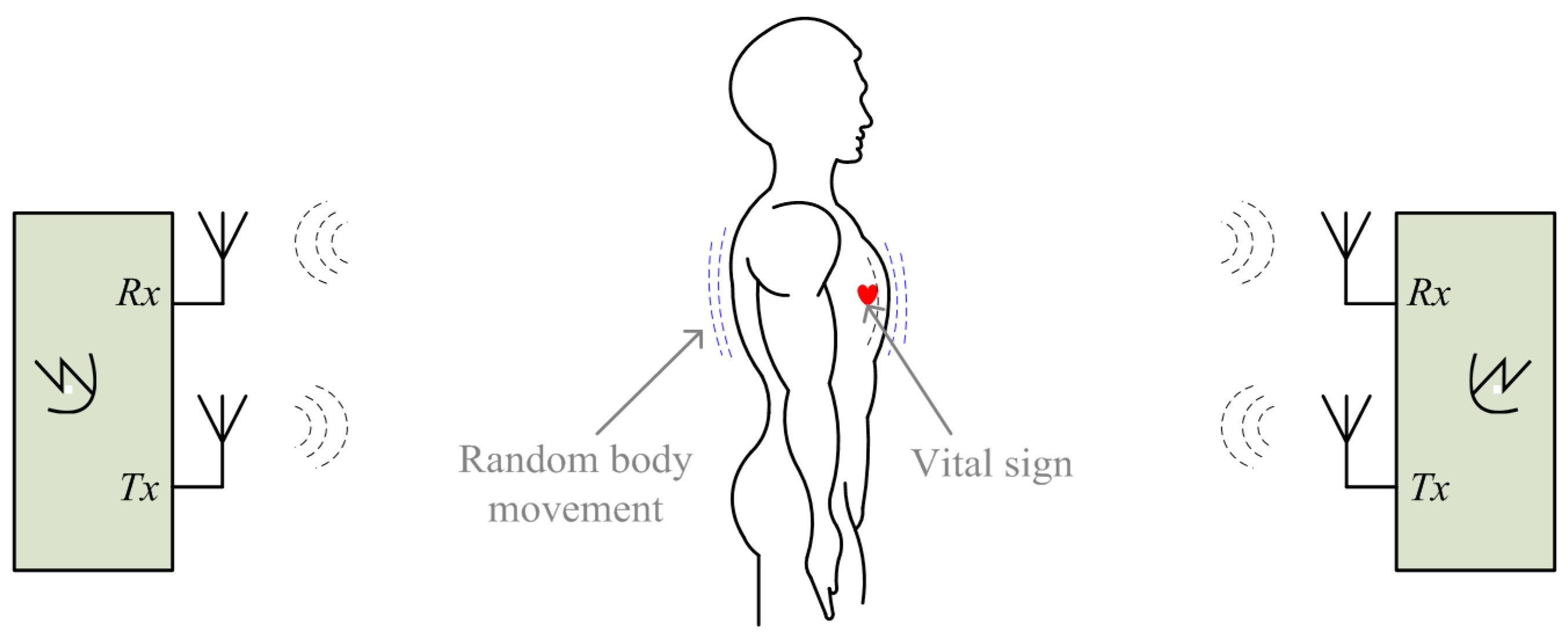
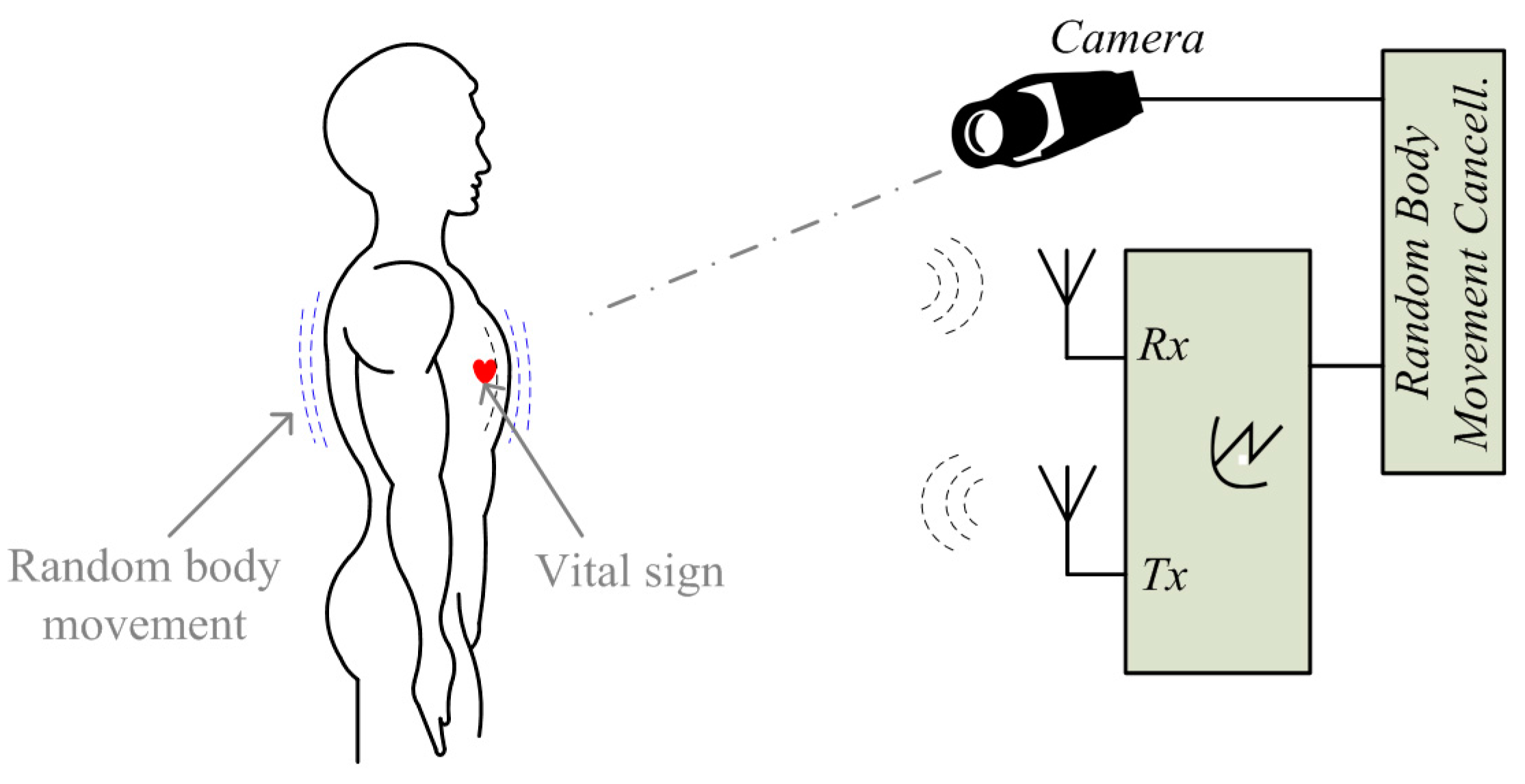
3.1. Random Movement Cancellation
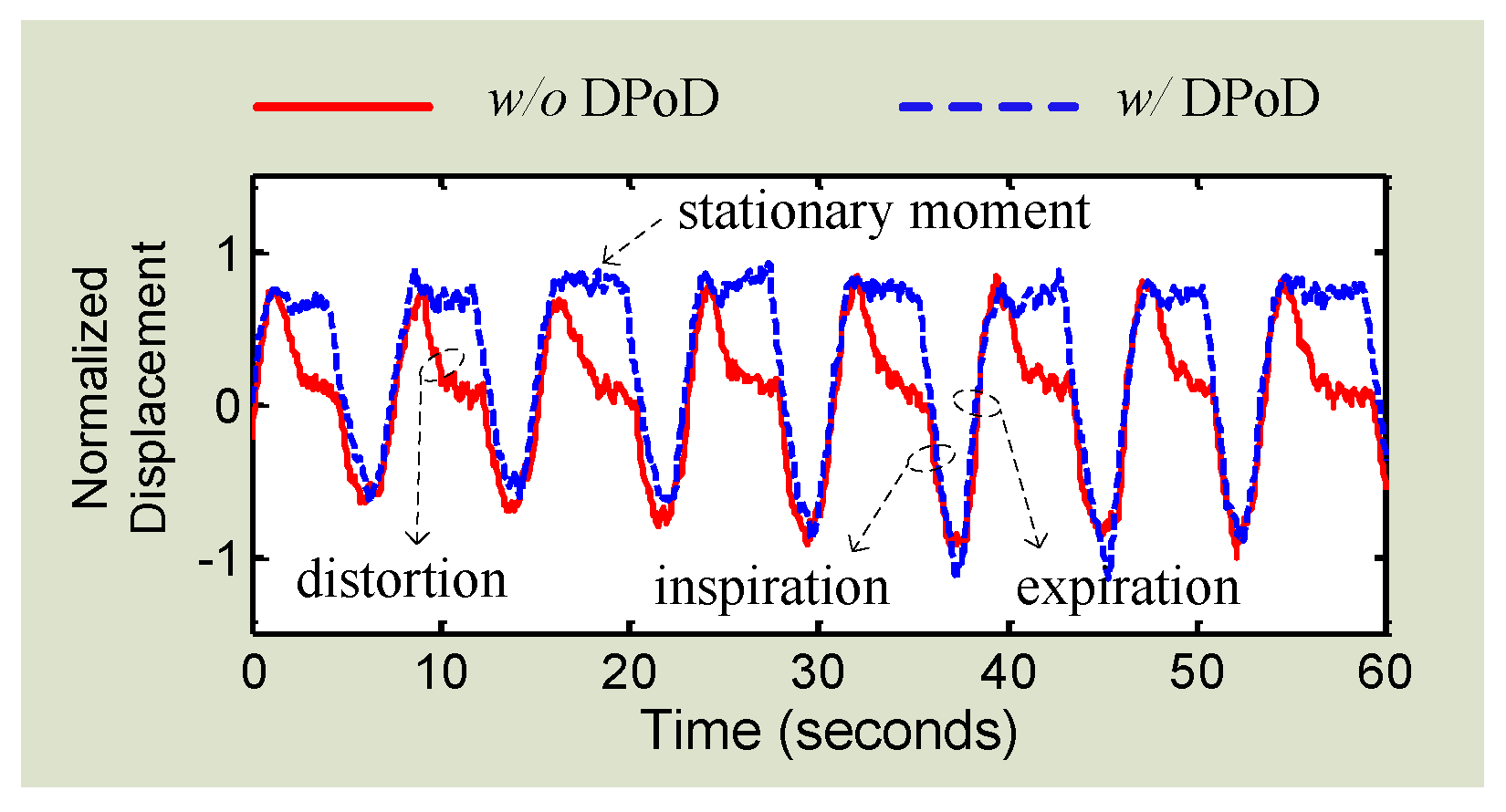
3.2. Signal Distortion Analysis and Compensation
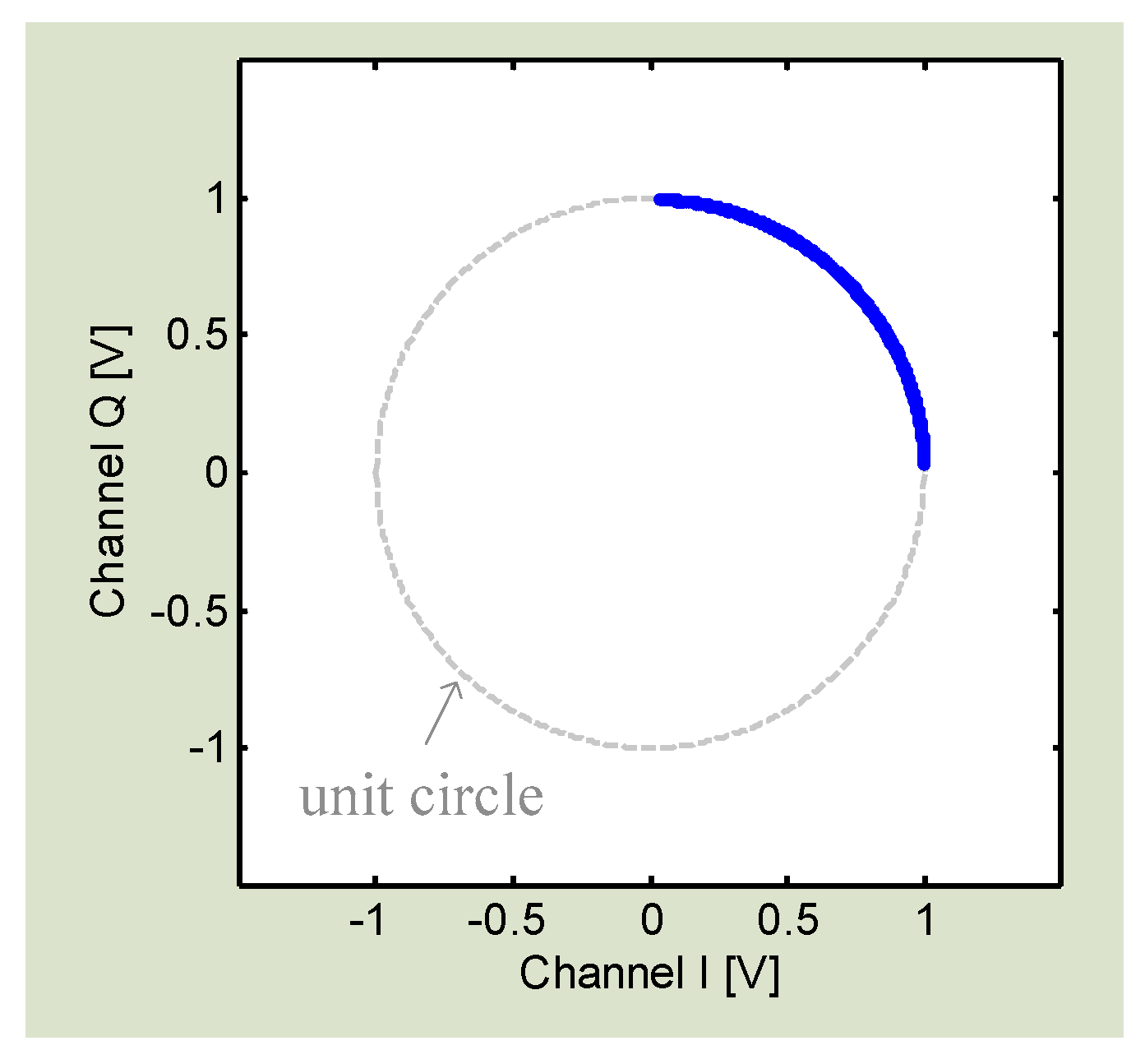
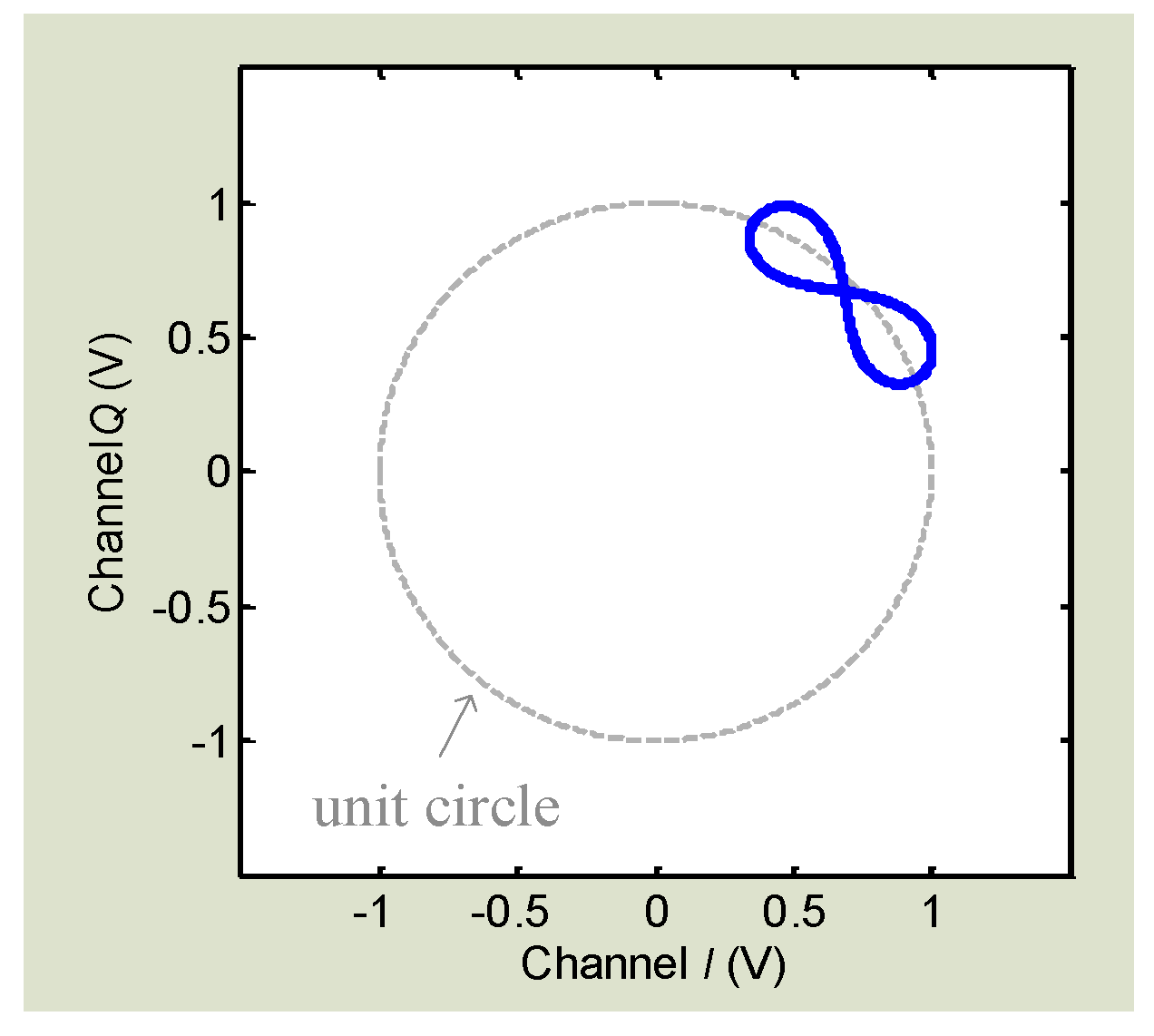
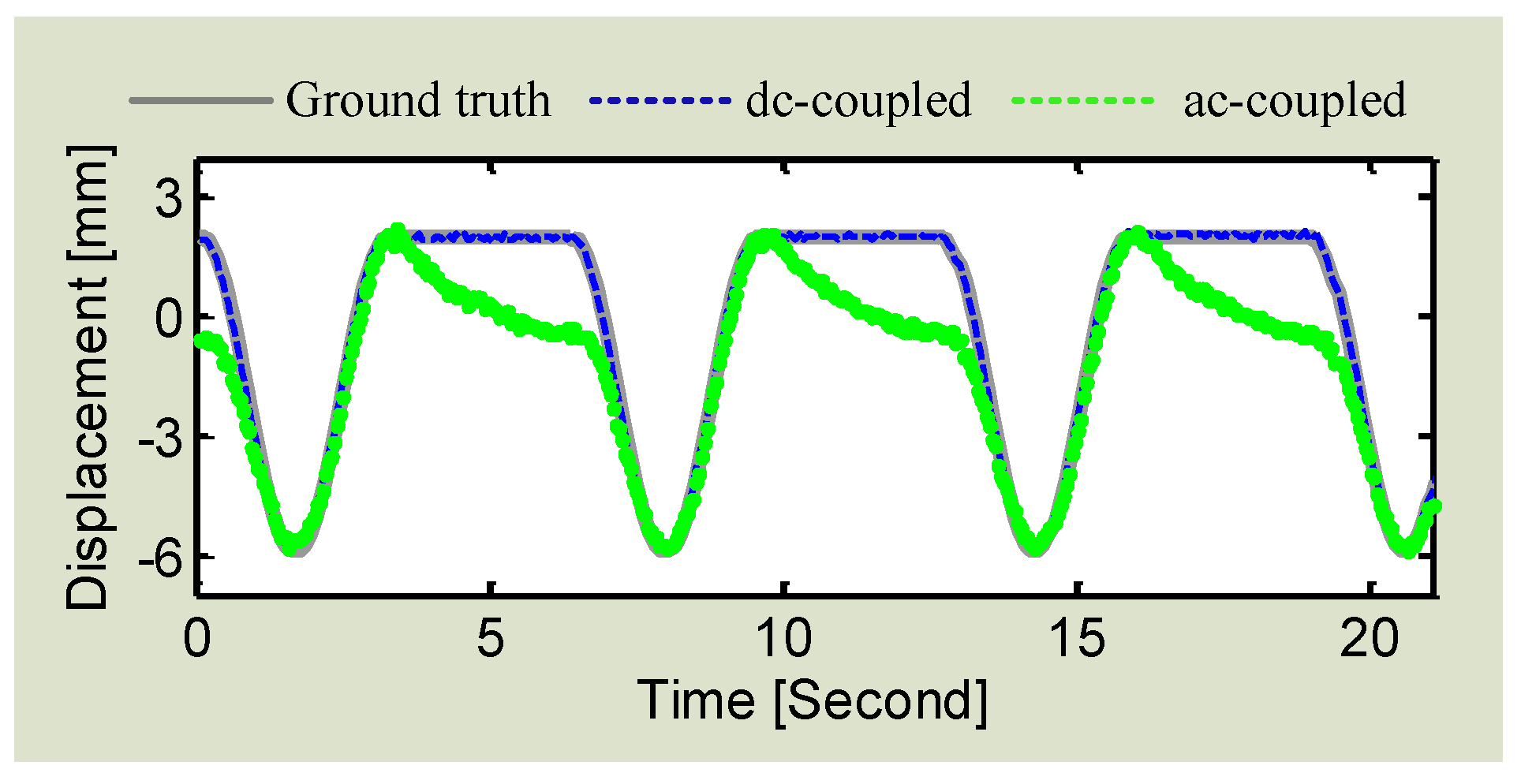
3.3. I/Q Mismatch Mitigation
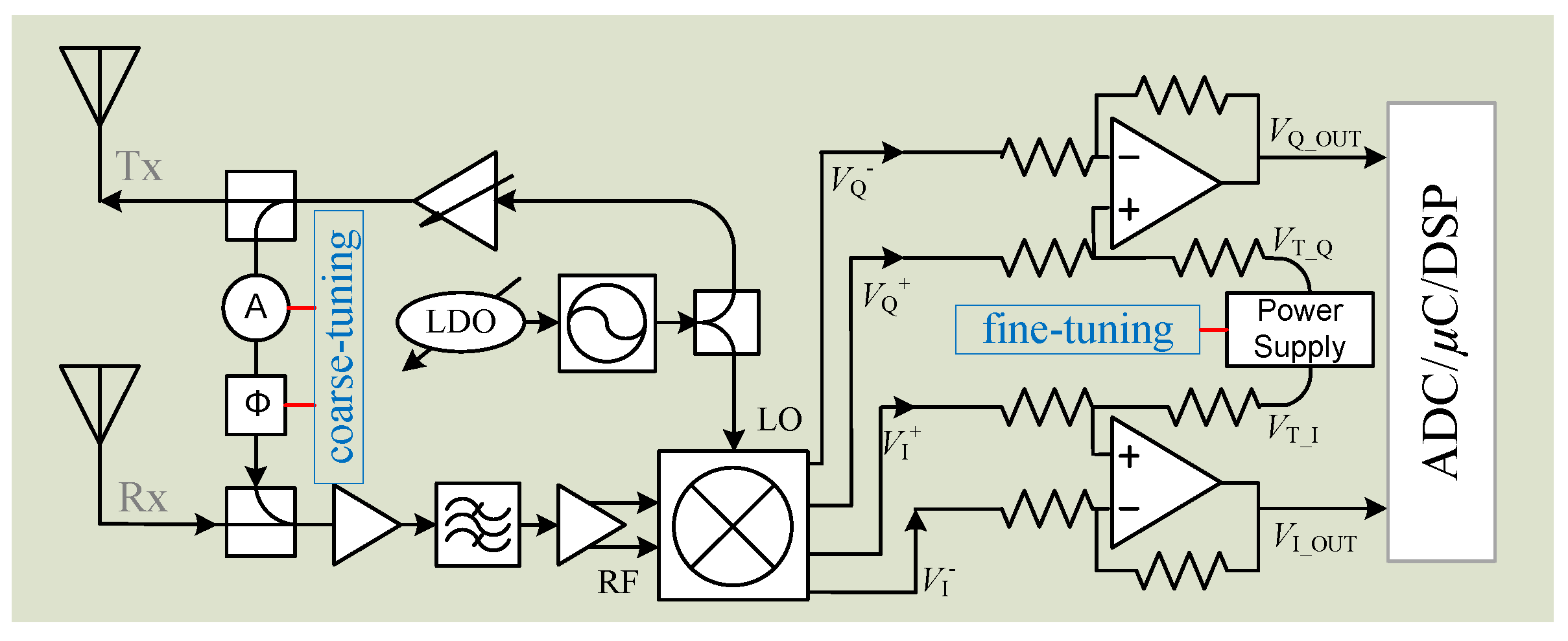
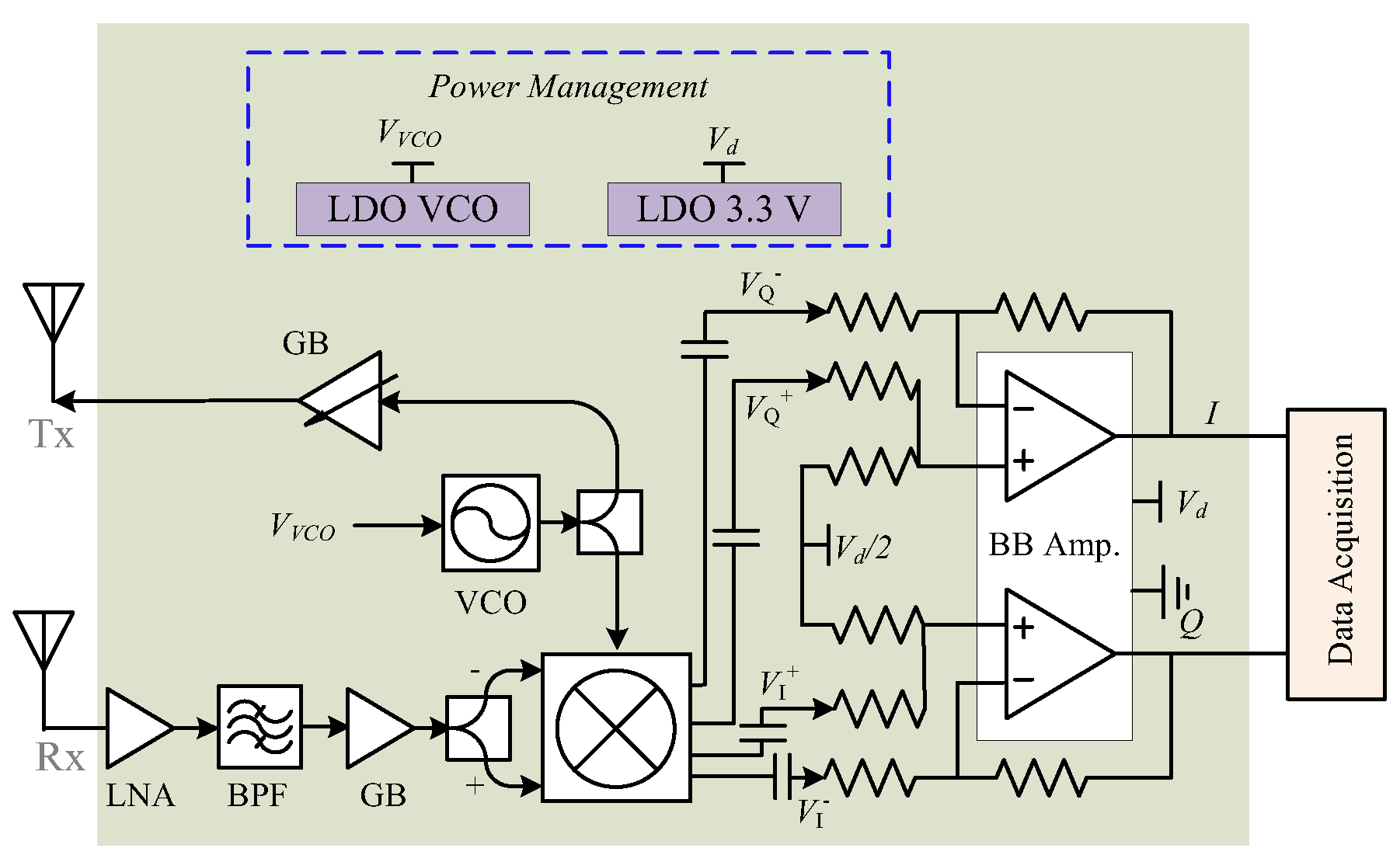
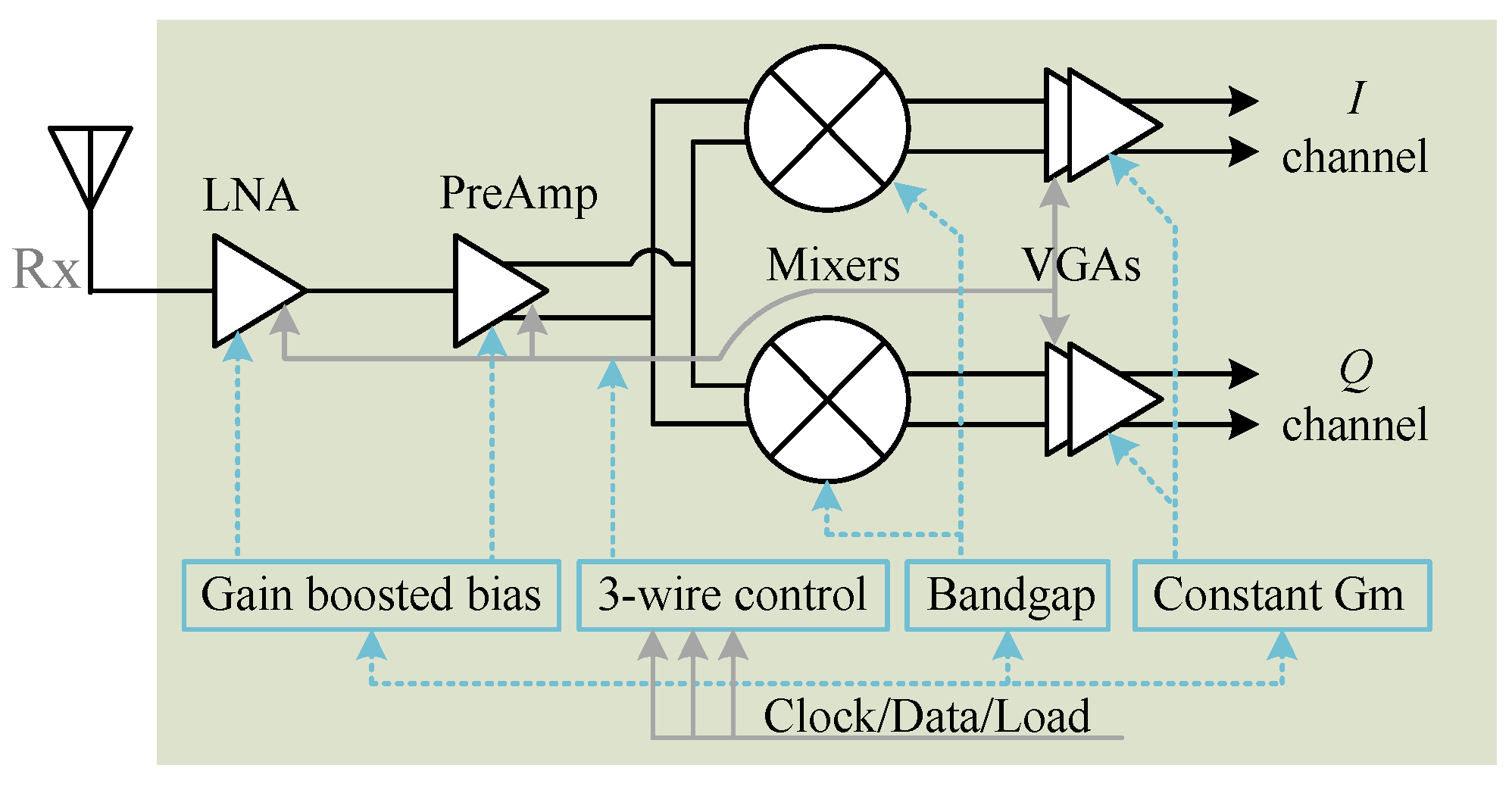
3.4. Hardware System Integration
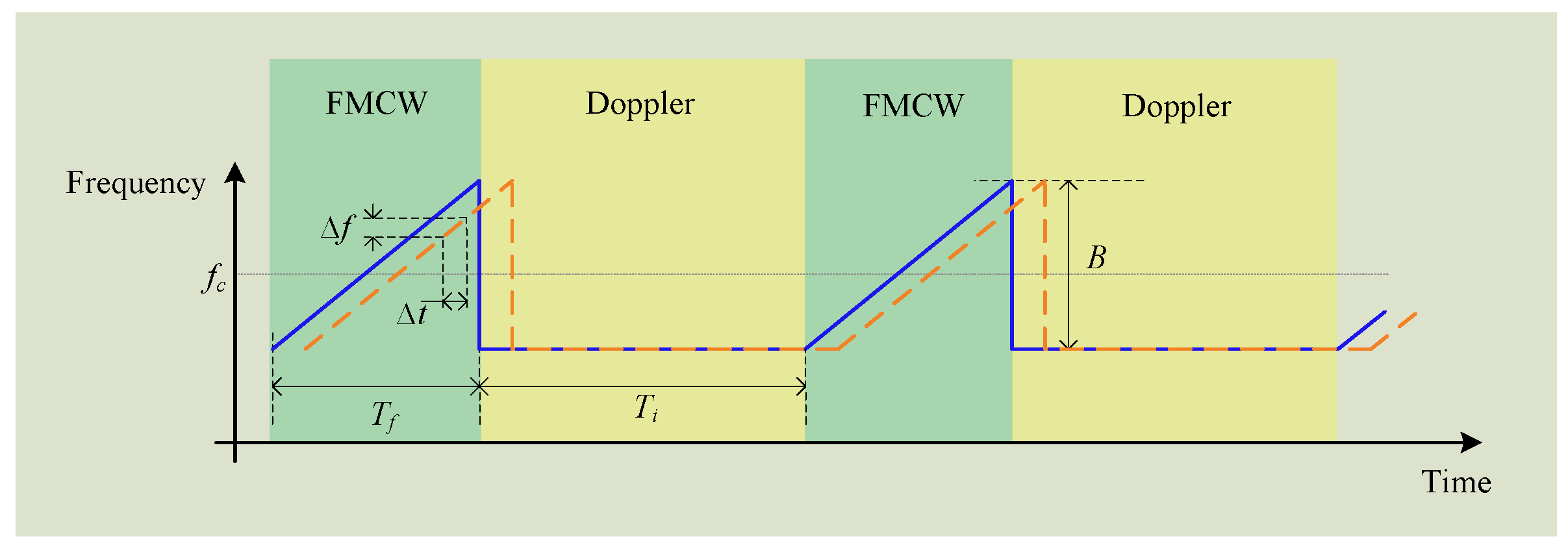
3.5. Hybrid FMCW-Interferometry Radar
3.6. Concurrent Detection of Range and Displacement
4. Emerging Applications
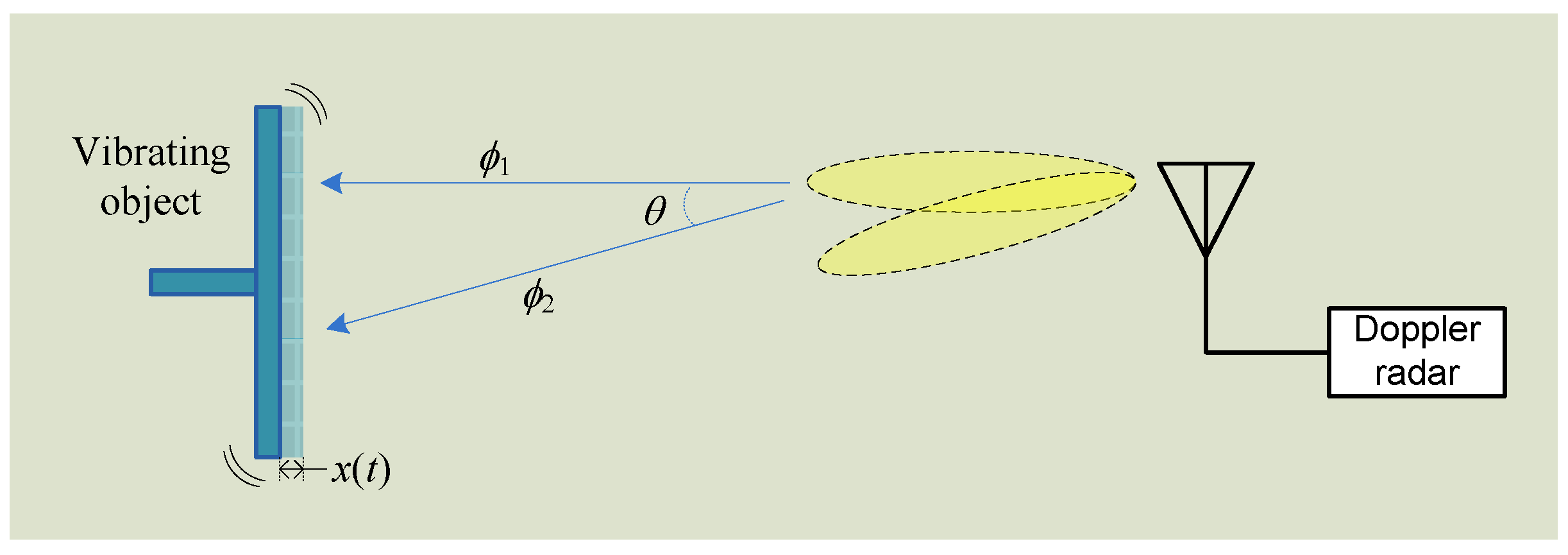
4.1. Guesture Sensing
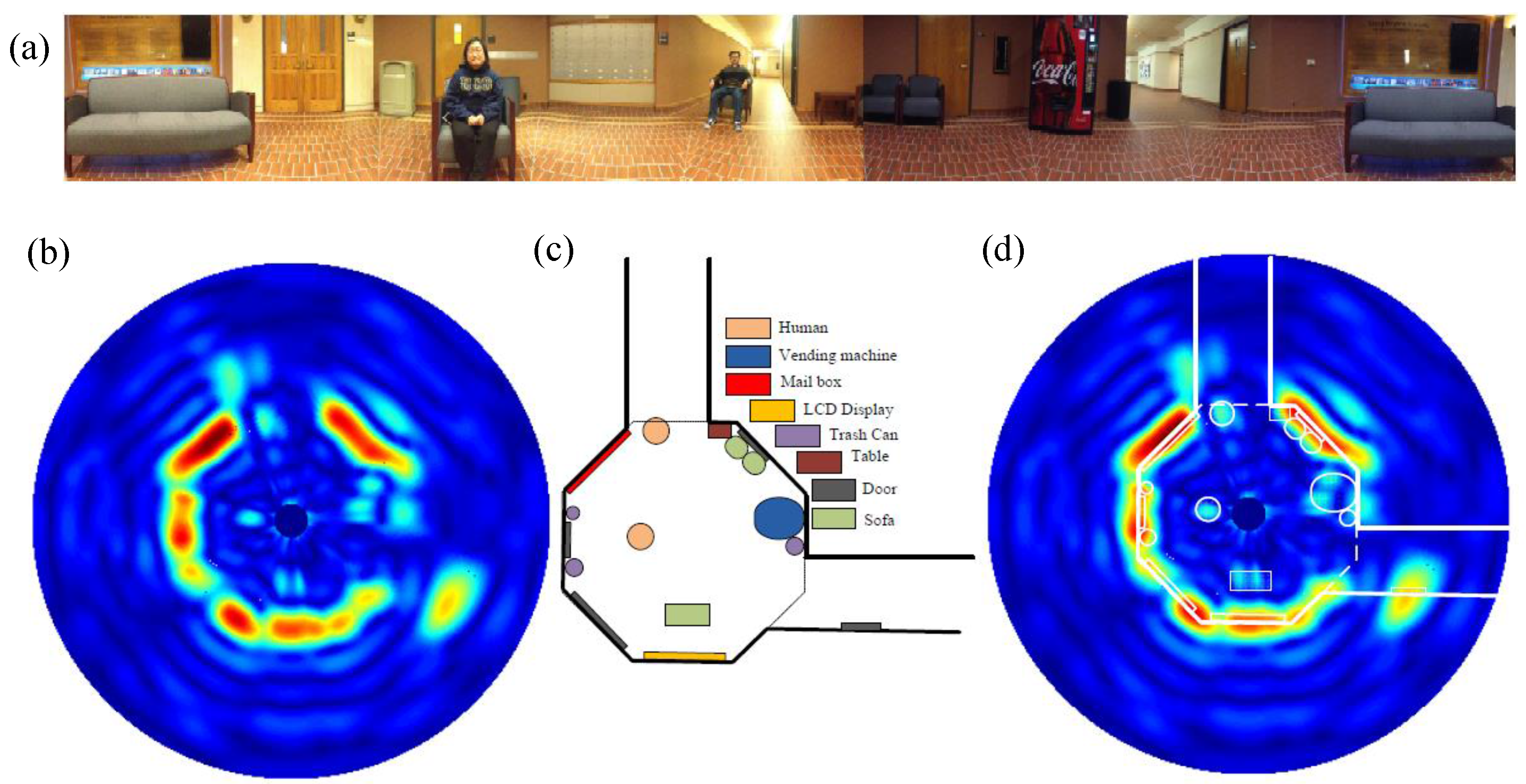
4.2. Occupancy Sensing
5. Future Trends
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Watson-Watt, R. Radar in War and in Peace. Nature 1945, 155, 319–324. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to radar. In Radar Handbook 2; McGraw-Hill Company: New York, NY, USA, 1962; pp. 1–18. [Google Scholar]
- Lin, J.C. Non-invasive microwave measurement of respiration. IEEE Proc. 1975, 63, 1530. [Google Scholar] [CrossRef]
- Gu, C.; Li, C. Assessment of Human Respiration Patterns via Noncontact Sensing Using Doppler Multi-Radar System. Sensors 2015, 15, 6383–6398. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Chen, F.; Jin, J.; Lv, H.; Li, S.; Lu, G.; Wang, J. A Method for Remotely Sensing Vital Signs of Human Subjects Outdoors. Sensors 2015, 15, 14830–14844. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.-M.; Misra, D.; Wang, H.; Chuang, H.-R.; Postow, E. An X-band microwave life-detection system. IEEE Trans. Biomed. Eng. 1986, 7, 697–701. [Google Scholar] [CrossRef] [PubMed]
- Massagram, W.; Lubecke, V.; Høst-Madsen, A.; Boric-Lubecke, O. Assessment of Heart Rate Variability and Respiratory Sinus Arrhythmia via Doppler Radar. IEEE Trans. Microw. Theory Tech. 2009, 57, 2542–2549. [Google Scholar] [CrossRef]
- Droitcour, A.D.; Boric-Lubecke, O.; Lubecke, V.M.; Lin, J.; Kovac, G.T. Range correlation and I/Q performance benefits in single-chip silicon Doppler radars for noncontact cardiopulmonary monitoring. IEEE Trans. Microw. Theory Tech. 2004, 52, 838–848. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Y.; Lin, J. Experiment and spectral analysis of a low-power -band heartbeat detector measuring from four sides of a human body. IEEE Trans. Microw. Theory Tech. 2006, 54, 4464–4471. [Google Scholar] [CrossRef]
- Wang, F.-K.; Horng, T.-S.; Peng, K.-C.; Jau, J.-K.; Li, J.-Y.; Chen, C.-C. Single-antenna Doppler radars using self and mutual injection locking for vital sign detection with random body movement cancellation. IEEE Trans. Microw. Theory Tech. 2011, 59, 3577–3587. [Google Scholar] [CrossRef]
- Li, C.; Lin, J.; Xiao, Y. Robust overnight monitoring of human vital signs by a non-contact respiration and heartbeat detector. In Engineering in Medicine and Biology Society, Proceedings of the 28th Annual International Conference of the IEEE, New York, NY, USA, 31 August–3 September 2006; pp. 2235–2238.
- Lin, J.C. Microwave sensing of physiological movement and volume change: A review. Bioelectromagnetics 1992, 13, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.-M.; Huang, Y.; Zhang, J.; Norman, A. Microwave life-detection systems for searching human subjects under earthquake rubble or behind barrier. IEEE Trans. Biomed. Eng. 2000, 27, 105–114. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, T.; Foster, R.; Hao, Y. Detecting Vital Signs with Wearable Wireless Sensors. Sensors 2010, 10, 10837–10862. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Nguyen, C. A displacement measurement technique using millimeter-wave interferometry. IEEE Trans. Microw. Theory Tech. 2003, 51, 1724–1728. [Google Scholar]
- Wang, T.; Zheng, N.; Xin, J.; Ma, Z. Integrating Millimeter Wave Radar with a Monocular Vision Sensor for On-Road Obstacle Detection Applications. Sensors 2011, 11, 8992–9008. [Google Scholar] [CrossRef] [PubMed]
- Guan, S.; Rice, J.; Li, C.; Gu, C. Advanced DC Offset Calibration Strategy for Structural Health Monitoring Based on Portable CW Radar Sensor. IEEE Trans. Instrum. Meas. 2014, 63, 3111–3118. [Google Scholar] [CrossRef]
- Yavari, E.; Jou, H.; Lubecke, V.; Boric-Lubecke, O. Doppler radar sensor for occupancy monitoring. In Biomedical Wireless Technologies, Networks, and Sensing Systems (BioWireleSS), Proceedings of the 2013 IEEE Topical Conference, Austin, TX, USA, 20–23 January 2013; pp. 139–141.
- Yavari, E.; Song, C.; Lubecke, V.; Boric-Lubecke, O. Is There Anybody in There?: Intelligent Radar Occupancy Sensors. IEEE Microw. Mag. 2014, 15, 57–64. [Google Scholar] [CrossRef]
- Wang, F.-K.; Tang, M.-C.; Chiu, Y.-C.; Horng, T.-S. Gesture Sensing Using Retransmitted Wireless Communication Signals Based on Doppler Radar Technology. IEEE Trans. Microw. Theory Tech. 2015, 63, 4592–4602. [Google Scholar] [CrossRef]
- Liu, C.; Gu, C.; Li, C. Non-contact Hand Interaction with Smart Phones Using the Wireless Power Transfer Features. In Proceedings of the IEEE Radio and Wireless Symposium (RWS), San Diego, CA, USA, 25–28 January 2015; pp. 20–22.
- Kim, S.; Nguyen, C. On the development of a multifunction millimeter-wave sensor for displacement sensing and low-velocity measurement. IEEE Trans. Microw. Theory Tech. 2004, 52, 2503–2512. [Google Scholar] [CrossRef]
- Droitcour, A.; Lubecke, V.; Lin, J.; Boric-Lubecke, O. A microwave radio for Doppler radar sensing of vital signs. In Microwave Symposium Digest, Proceedings of the 2001 IEEE MTT-S International, Phoenix, AZ, USA, 20–25 May 2001; pp. 175–178.
- Gu, C.; Li, C.; Lin, J.; Long, J.; Huangfu, J.; Ran, L. Instrument-based noncontact Doppler radar vital sign detection system using heterodyne digital quadrature demodulation architecture. IEEE Trans. Instrum. Meas. 2010, 59, 1580–1588. [Google Scholar]
- Vivet, D.; Checchin, P.; Chapuis, R. Localization and Mapping Using Only a Rotating FMCW Radar Sensor. Sensors 2013, 13, 4527–4552. [Google Scholar] [CrossRef] [PubMed]
- Tessmann, A.; Kudszus, S.; Feltgen, T.; Riessle, M.; Sklarczyk, C.; Haydl, W.-H. Compact single-chip W-band FMCW radar modules for commercial high-resolution sensor applications. IEEE Trans. Microw. Theory Tech. 2002, 50, 2995–3001. [Google Scholar] [CrossRef]
- Li, Y.-A.; Hung, M.-H.; Huang, S.-J.; Lee, J. A fully integrated 77 GHz FMCW radar system in 65nm CMOS. In Proceedings of the 2010 IEEE International Solid-State Circuits Conference—(ISSCC), San Francisco, CA, USA, 7–11 February 2010; pp. 216–217.
- Li, Z.; Wu, K. 24-GHz frequency-modulation continuous-wave radar front-end system-on-substrate. IEEE Trans. Microw. Theory Tech. 2008, 56, 278–285. [Google Scholar] [CrossRef]
- Zhang, C.; Kuhn, M.-J.; Merkl, B.-C.; Fathy, A.-E.; Mahfouz, M.-R. Real-time noncoherent UWB positioning radar with millimeter range accuracy: Theory and experiment. IEEE Trans. Microw. Theory Tech. 2010, 58, 9–20. [Google Scholar] [CrossRef]
- Zhang, X.; Xi, X.; Li, M.; Wu, D. Comparison of Impulse Radar and Spread-Spectrum Radar in Through-Wall Imaging. IEEE Trans. Microw. Theo. Tech. 2016, 64, 699–706. [Google Scholar] [CrossRef]
- Chudobiak, W.J.; Gray, R.; Wight, J.S. A nanosecond impulse X-band radar. IEEE Proc. 1978, 66, 523–524. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Fathy, A.E. Reconfigurable ultra-wide band see-through-wall imaging radar system. In Proceedings of the 2009 IEEE Antennas and Propagation Society International Symposium, North Charleston, SC, USA, 1–5 June 2009; pp. 1–4.
- Gu, C.; Li, C. From Tumor Targeting to Speech Monitoring: Accurate Respiratory Monitoring Using Medical Continuous-Wave Radar Sensors. IEEE Microw. Mag. 2014, 15, 66–76. [Google Scholar]
- Li, C.; Lubecke, V.; Boric-Lubecke, O.; Lin, J. A Review on Recent Advances in Doppler Radar Sensors for Noncontact Healthcare Monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2046–2060. [Google Scholar] [CrossRef]
- Li, C.; Xiao, Y.; Lin, J. A 5 GHz double-sideband radar sensor chip in 0.18 m CMOS for non-contact vital sign detection. IEEE Microw. Wire. Compon. Lett. 2008, 18, 494–496. [Google Scholar]
- Yan, Y.; Li, C.; Rice, J.A.; Lin, J. Wavelength division sensing RF vibrometer. In Microwave Symposium Digest (MTT), Proceedings of the 2011 IEEE/MTT-S International Microwave Symposium, Baltimore, MD, USA, 5–10 June 2011; pp. 1–4.
- Anghel, A.; Vasile, G.; Cacoveanu, R.; Ioana, C.; Ciochina, S. Short-Range Wideband FMCW Radar for Millimetric Displacement Measurements. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5633–5642. [Google Scholar] [CrossRef]
- Li, Y.; O’Young, S. Method of doubling range resolution without increasing bandwidth in FMCW radar. Electron. Lett. 2015, 51, 933–935. [Google Scholar] [CrossRef]
- Lu, L.; Li, C.; Rice, J.A. A software-defined multifunctional radar sensor for linear and reciprocal displacement measurement. In Wireless Sensors and Sensor Networks (WiSNet), Proceedings of the 2011 IEEE Topical Conference, Phoenix, AZ, USA, 16–19 January 2011; pp. 17–20.
- Gu, C.; Li, R.; Li, C.; Jiang, S.-B. Doppler radar respiration measurement for gated lung cancer radiotherapy. In Biomedical Wireless Technologies, Networks, and Sensing Systems (BioWireleSS), Proceedings of the 2011 IEEE Topical Conference, Phoenix, AZ, USA, 16–19 January 2011; pp. 91–94.
- Huang, M.-C.; Liu, J.; Xu, W.; Gu, C.; Li, C.; Sarrafzadeh, M. A Self-Calibrating Radar Sensor System Design for Measuring Vital Signs. IEEE Trans. Biomed. Circuits Syst. 2016, 10, 352–363. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Cattafesta, L.; Li, C.; Lin, J. Analysis of Detection Methods and Realization of a Real-time Monitoring RF Vibrometer. IEEE Trans. Microw. Theory Tech. 2011, 59, 3556–3566. [Google Scholar] [CrossRef]
- Gu, C.; Wang, G.; Rice, J.A.; Li, C. Interferometric Radar Sensor with Active Transponders for Signal Boosting and Clutter Rejection in Structural Health Monitoring. In Microwave Symposium Digest (MTT), Proceedings of the 2012 IEEE/MTT-S International Microwave Symposium, Montreal, QC, Canada, 17–22 June 2012; pp. 1–3.
- Wang, G.; Gu, C.; Inoue, T.; Li, C. Hybrid FMCW-interferometry radar system in the 5.8 GHz ISM band for indoor precise position and motion detection. In Microwave Symposium Digest (IMS), Proceedings of the 2013 IEEE MTT-S International Microwave Symposium, Seattle, WA, USA, 2 June 2013; pp. 1–4.
- Wang, G.; Gu, C.; Inoue, T.; Li, C. A Hybrid FMCW-Interferometry Radar for Indoor Precise Positioning and Versatile Life Activity Monitoring. IEEE Trans. Microw. Theory Tech. 2014, 62, 2812–2822. [Google Scholar] [CrossRef]
- Nasr, I.; Karagozler, E.; Poupyrev, I.; Trotta, S. A Highly Integrated 60-GHz 6-Channel Transceiver Chip in 0.35 μm SiGe Technology for Smart Sensing and Short-Range Communications. In Proceedings of the 2015 IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), New Orleans, LA, USA, 11–14 October 2015; pp. 1–4.
- Google’s Project Soli. Available online: https://atap.google.com/soli/ (accessed on 17 July 2016).
- Droitcour, A.-D.; Boric-Lubecke, O.; Lubecke, V.-M.; Lin, J. 0.25/spl mu/m CMOS and BiCMOS single-chip direct-conversion Doppler radar for remote sensing of vital signs. In Solid-State Circuits Conference, 2002. Digest of Technical Papers. ISSCC. In Proceedings of the 2002 IEEE International, San Francisco, CA, USA, 7 February 2002; pp. 278–505.
- Yavari, E.; Boric-Lubecke, O. Low IF demodulation for physiological pulse Doppler radar. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium, Tampa, FL, USA, 1 June 2014; pp. 1–3.
- Wang, F.-K.; Chou, Y.-R.; Chiu, Y.-C.; Horng, T.-S. Chest-Worn Health Monitor Based on a Bistatic Self-Injection-Locked Radar. IEEE Trans. Microwave Theory Tech. 2015, 62, 2931–2940. [Google Scholar]
- Horng, T.-S. Self-injection-locked radar: An advance in continuous-wave technology for emerging radar systems. In Proceedings of the 2013 Asia-Pacific Microwave Conference Proceedings, Seoul, South Korea, 5–8 November 2013; pp. 566–569.
- Gabor, V.; Lindner, S.; Barbon, F.; Mann, S.; Hofmann, M.; Duda, A.; Weigel, R.; Koelpin, A. Six-port radar sensor for remote respiration rate and heartbeat vital-sign monitoring. IEEE Trans. Microwa. Theory Tech. 2013, 61, 2093–2100. [Google Scholar]
- Kao, T.; Yan, Y.; Shen, T.; Chen, A.; Lin, J. Design and Analysis of a 60-GHz CMOS Doppler Micro-Radar System-in-Package for Vital-Sign and Vibration Detection. IEEE Trans. Microw. Theory Tech. 2013, 61, 1649–1659. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Complex signal demodulation and random body movement cancellation techniques for non-contact vital sign detection. In Microwave Symposium Digest, Proceedings of the 2008 IEEE MTT-S International Microwave Symposium, Atlanta, GA, USA, 15–18 June 2008; pp. 567–570.
- Park, B.K.; Boric-Lubecke, O.; Lubecke, V.M. Arctangent demodulation with DC offset compensation in quadrature Doppler radar receiver systems. IEEE Trans. Microw. Theory Tech. 2007, 55, 1073–1079. [Google Scholar] [CrossRef]
- Xu, W.; Gu, C.; Li, C.; Sarrafzadeh, M. Robust Doppler radar demodulation via compressed sensing. IET Electron. Lett. 2012, 48, 1428–1430. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Random body movement cancellation in Doppler radar vital sign detection. IEEE Trans. Microw. Theory Tech. 2008, 56, 3143–3152. [Google Scholar]
- Gu, C.; Peng, Z.; Li, C. High-Precision Motion Detection Using Low-Complexity Doppler Radar with Digital Post-Distortion Technique. IEEE Trans. Microw. Theory Tech. 2016, 64, 961–971. [Google Scholar] [CrossRef]
- Singh, A.; Gao, X.; Yavari, E.; Zakrzewski, M.; Cao, X.H.; Lubecke, V.; Boric-Lubecke, O. Data-based quadrature imbalance compensationfor a CW Doppler radar system. IEEE Trans. Microw. Theory Tech. 2013, 61, 1718–1724. [Google Scholar] [CrossRef]
- Zakrzewski, M.; Singh, A.; Yavari, E.; Gao, X.; Boric-Lubecke, O.; Vanhala, J.; Palovuori, K. Quadrature Imbalance Compensation With Ellipse-Fitting Methods for Microwave Radar Physiological Sensing. IEEE Trans. Microw. Theory Tech. 2013, 62, 1400–1408. [Google Scholar] [CrossRef]
- Gu, C.; Li, R.; Zhang, H.; Fung, A.; Torres, C.; Jiang, S.; Li, C. Accurate respiration measurement using DC-coupled continuous-wave radar sensor for motion-adaptive cancer radiotherapy. IEEE Trans. Biomed. Eng. 2012, 59, 3117–3123. [Google Scholar] [PubMed]
- Gu, C.; Inoue, T.; Li, C. Analysis and Experiment on the Modulation Sensitivity of Doppler Radar Vibration Measurement. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 566–568. [Google Scholar] [CrossRef]
- Bakhtiari, S.; Elmer, T.W.; Cox, N.M.; Gopalsami, N.; Raptis, A.C.; Liao, S.; Mikhelson, I.; Sahakian, A.V. Compact millimeter-wave sensor for remote monitoring of vital signs. IEEE Trans. Instrum. Meas. 2012, 61, 830–841. [Google Scholar] [CrossRef]
- Gatesman, A.J.; Danylov, A.; Goyette, T.M.; Dickinson, J.C.; Giles, R.H.; Goodhue, W.; Waldman, J.; Nixon, W.E.; Hoen, W. Terahertz behavior of optical components and common materials—Art. no. 62120E. Terahertz Military Security Appl. IV 2006, 6212. [Google Scholar] [CrossRef]
- Xiao, Y.; Lin, J.; Boric-Lubecke, O.; Lubecke, M. Frequency-tuning technique for remote detection of heartbeat and respiration using low-power double-sideband transmission in the Ka-band. IEEE Trans. Microw. Theory Tech. 2006, 54, 2023–2032. [Google Scholar] [CrossRef]
- Gu, C.; Li, C. DC coupled CW radar sensor using fine-tuning adaptive feedback loop. IET Electron. Lett. 2012, 48, 344–345. [Google Scholar] [CrossRef]
- Gu, C.; Li, C. Frequency-Selective Distortion in Continuous-Wave Radar Displacement Sensor. IET Electron. Lett. 2012, 48, 1495–1497. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Chen, L.; Huangfu, J.; Li, C.; Ran, L. Non-contact Distance and Amplitude Independent Vibration Measurement Based on an Extended DACM Algorithm. IEEE Trans. Instrum. Meas. 2014, 63, 145–153. [Google Scholar] [CrossRef]
- Gu, C.; Wang, G.; Inoue, T.; Li, C. Doppler radar vital sign detection with random body movement cancellation based on adaptive phase compensation. In Microwave Symposium Digest (IMS), Proceedings of the 2013 IEEE MTT-S International Microwave Symposium, Seattle, WA, USA, 2–7 June 2013.
- Gu, C.; Wang, G.; Inoue, T.; Li, C. A Hybrid Radar-Camera Sensing System with Phase Compensation for Random Body Movement Cancellation in Doppler Vital Sign Detection. IEEE Trans. Microw. Theory Tech. 2013, 61, 4678–4688. [Google Scholar] [CrossRef]
- Rahman, A.; Yavari, E.; Singh, A.; Lubecke, V.-M.; Lubecke, O.-B. A Low-IF Tag-Based Motion Compensation Technique for Mobile Doppler Radar Life Signs Monitoring. IEEE Trans. Microw. Theory Tech. 2015, 63, 3034–3041. [Google Scholar] [CrossRef]
- Gao, X.; Boric-Lubecke, O. AC Coupled Quadrature Doppler Radar Displacement Estimation. In Microwave Symposium Digest (IMS), Proceedings of the 2015 IEEE MTT-S International Microwave Symposium, Phoenix, AZ, USA, 17–22 May 2015.
- Gao, X.; Singh, A.; Yavari, E.; Lubecke, V.; Boric-Lubecke, O. Non-contact Displacement Estimation Using Doppler Radar. In Proceedings of the 2012 34th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 Septembre 2012; pp. 1602–1605.
- Yan, Y.; Li, C.; Lin, J. Effects of I/Q mismatch on measurement of periodic movement using a Doppler radar sensor. In Proceedings of the 2010 IEEE Radio and Wireless Symposium (RWS), New Orleans, LA, USA, 10–14 January 2010; pp. 196–199.
- Li, C.; Yu, X.; Lee, C.-M.; Li, D.; Ran, L.; Lin, J. High-sensitivity software-configurable 5.8-GHz radar sensor receiver chip in 0.13-m CMOS for noncontact vital sign detection. IEEE Trans. Microw. Theory Tech. 2010, 58, 1410–1419. [Google Scholar]
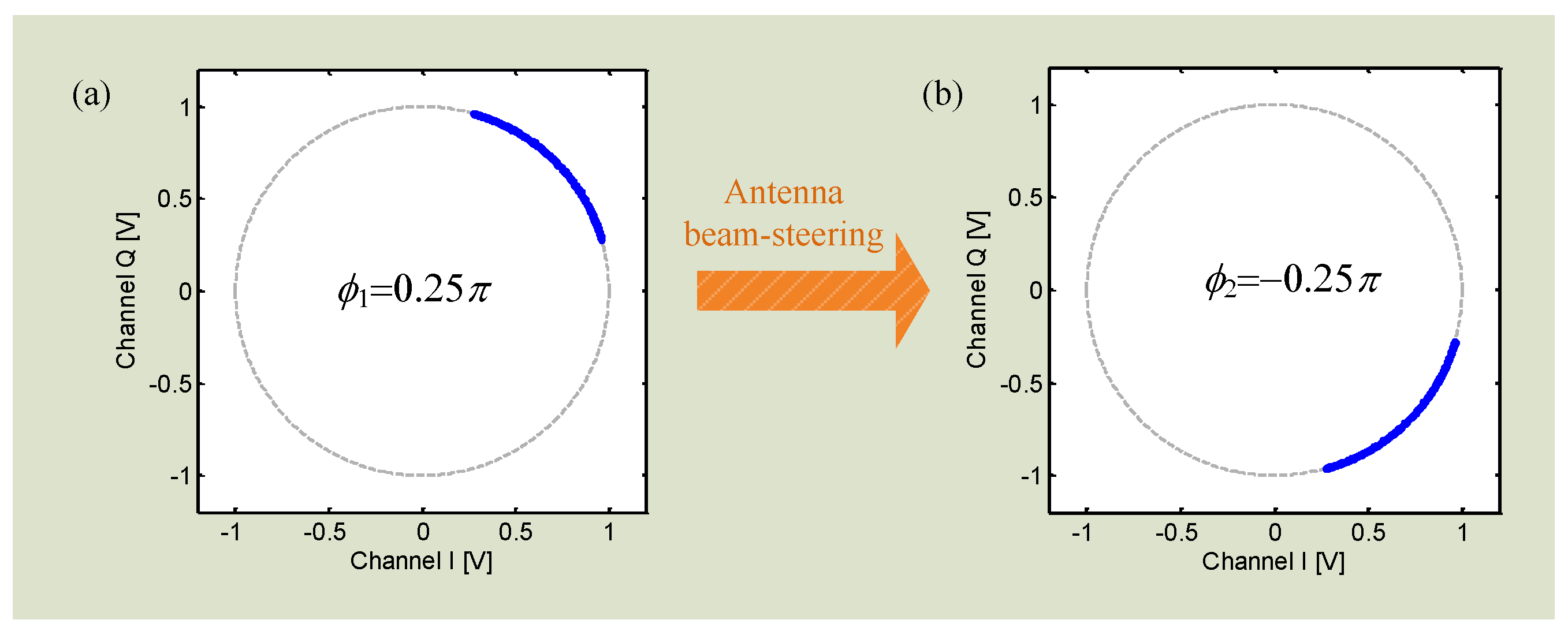
- Nieh, C.-M.; Wei, C.; Lin, J. Concurrent Detection of Vibration and Distance Using Unmodulated CW Doppler Vibration Radar with an Adaptive Beam-Steering Antenna. IEEE Trans. Microw. Theory Tech. 2015, 63, 2069–2078. [Google Scholar] [CrossRef]
- Gu, C.; Xu, W.; Wang, G.; Inoue, T.; Rice, J.; Ran, L.; Li, C. Noncontact Large-Scale Displacement Tracking: Doppler Radar for Water Level Gauging. IEEE Microw. Wire. Componen. Lett. 2014, 24, 899–901. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Microwave Noncontact Motion Sensing and Analysis, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Boric-Lubecke, O.; Lubecke, V.M.; Droitcour, A.D.; Park, B.K.; Singh, A. Doppler Radar Physiological Sensing, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Lien, J.; Gillian, N.; Karagozler, M.E.; Amihood, P.; Schwesig, C.; Olson, E.; Raja, H.; Poupyrev, I. Soli: Ubiquitous Gesture Sensing with Millimeter Wave Radar. ACM Trans. Graph. 2016, 35, 142. [Google Scholar] [CrossRef]


© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, C. Short-Range Noncontact Sensors for Healthcare and Other Emerging Applications: A Review. Sensors 2016, 16, 1169. https://doi.org/10.3390/s16081169
Gu C. Short-Range Noncontact Sensors for Healthcare and Other Emerging Applications: A Review. Sensors. 2016; 16(8):1169. https://doi.org/10.3390/s16081169
Chicago/Turabian StyleGu, Changzhan. 2016. "Short-Range Noncontact Sensors for Healthcare and Other Emerging Applications: A Review" Sensors 16, no. 8: 1169. https://doi.org/10.3390/s16081169
APA StyleGu, C. (2016). Short-Range Noncontact Sensors for Healthcare and Other Emerging Applications: A Review. Sensors, 16(8), 1169. https://doi.org/10.3390/s16081169




