Abstract
The conventional channel estimation methods based on a preamble for filter bank multicarrier with offset quadrature amplitude modulation (FBMC/OQAM) systems in mobile-to-mobile sensor networks are inefficient. By utilizing the intrinsicsparsity of wireless channels, channel estimation is researched as a compressive sensing (CS) problem to improve the estimation performance. In this paper, an AdaptiveRegularized Compressive Sampling Matching Pursuit (ARCoSaMP) algorithm is proposed. Unlike anterior greedy algorithms, the new algorithm can achieve the accuracy of reconstruction by choosing the support set adaptively, and exploiting the regularization process, which realizes the second selecting of atoms in the support set although the sparsity of the channel is unknown. Simulation results show that CS-based methods obtain significant channel estimation performance improvement compared to that of conventional preamble-based methods. The proposed ARCoSaMP algorithm outperforms the conventional sparse adaptive matching pursuit (SAMP) algorithm. ARCoSaMP provides even more interesting results than the mostadvanced greedy compressive sampling matching pursuit (CoSaMP) algorithm without a prior sparse knowledge of the channel.
1. Introduction
Filter bank multicarrier(FBMC) techniques have drawn increasing attention from many researchers [1,2,3]. In recent years,it has become a competitive alternative to the most famous and accepted Orthogonal Frequency Division Multiplexing (OFDM) schemes, particularly in wireless communication systems. As a potential candidate multicarrier modulation scheme for next generation wireless communication networks [4,5,6,7,8], filter bank multicarrier with offset quadrature amplitude modulation (FBMC/OQAM) is a particular type of FBMC. It utilizes time frequency localization (TFL) well and it employs a property pulse shaping based filter [9] bank, which has a theoretically higher spectral efficiency [10,11]. FBMC/OQAM also demonstrates robustness to frequency offset and Doppler spread. Besides, CP is not needed in FBMC/OQAM systems, which can provide higher data rates than conventional OFDM [12]. FBMC/OQAM system has its root in the pioneering works of Chang [13] and Saltzberg [14] who introduced multicarrier techniques over two decades ago. However, with the conventional OFDM transmission complex-valued symbols in a given symbol rate, FBMC/OQAM transmits real-valued symbols at the symbol rate of two times. The subcarrier functions are only orthogonal in the real field, therefore, an inherent imaginary interference among neighboring subcarriers and symbols is always existed.
The intrinsic inter-carrier/inter-symbol interference will complicate channel estimation processing. Hence, the existing OFDM channel estimation methods cannot be directly applied in FBMC/OQAM systems. Many training schemes and related estimation methods have been recently researched in literature [15,16,17,18]. The two classical preamble-based methods are interference approximation method (IAM) [15,16] and interference cancellation method (ICM) [17,18]. They can be summed up as aiming at avoiding the intrinsic interference or constructively utilizing it to improve the estimation performance. However, it has been proved that the performance of estimator utilizing preamble-based method is inefficient since it is difficult to fully avoid intrinsic interference.
A number of efforts have been devoted to improving the performance of channel estimation. A coded auxiliary pilot channel estimation method for FBMC/OQAM has been proposed [19]. The method is using coded auxiliary pilot symbols to eliminate the imaginary interference on each scatted pilot. Semi-blind and blind symbol timing estimation methods for FBMC/OQAM system have also been studied [20,21]. However, these schemes have a higher computational complexity, and the phase ambiguity may occur and need longer observation data, which, to some extent, limits the availability. A more attractive approach to obtain well channel estimation performance is the recently researched compressive sensing (CS) method [22,23,24,25,26,27], where the wireless channels in practice tend to exhibit a sparse multipath structure. Some channel estimation based on CS methods for OFDM systems have been studied in the past few years [28,29,30,31]. However, there are only few literatures about CS-based channel estimation for FBMC/OQAM systems. An improved IAM that reconstructs channel impulse response by utilizing the orthogonal matching pursuit (OMP) algorithm based on channel estimation for FBMC/OQAM has been proposed in [32]. It is proved that the OMP [33] based method can get remarkable performance improvement compared with the conventional preamble based method. For the most greedy CS algorithms, such as OMP and compressive sampling matching pursuit (CoSaMP) [34], the sparsitylevel of the channel is given as a priori information. However, the sparsity of the channel is usually unknown in most practical application scenarios.
In this paper, a novel channel estimation method named sparse adaptive regularized compressive sampling matching pursuit (ARCoSaMP) is proposed for FBMC/QOAM transmission networks. To the best of our knowledge, sparse adaptive CS-based channel estimation approach has not yet been studied for FBMC/OQAM systems. The advantage of the proposed ARCoSaMP method is that it does not need priori channel sparse information. Furthermore, the proposed algorithm is based on the idea of regularization and the backtracking mechanism that attaches to CoSaMP algorithm, which removes the unreliable support and refines the current approximation iteratively. Simulations verify the proposed channel estimation scheme performs better than the conventional SAMP algorithm and the proposed algorithm can obtain an approximate performance compared with the CoSaMP algorithm.
The purpose of this paper is to propose an efficient sparse adaptive channel estimation method. We would like to convince the reader with the potential of the proposed method as a high performance channel estimator.
The remainder of this paper is organized as follows. The FBMC/OQAM transmission system model is described in Section 2. Section 3 reviews some conventional channel estimation methods (including preamble-based methods and conventional CS recovery algorithms) and presents the proposed scheme. In Section 4, the performances of the proposed scheme associated with the conventional preamble-based and CS-based schemes are compared and simulation results are shown. Finally, Section 5 gives the concluding remarks.
2. System Model
In FBMC/OQAM systems, the transmitted signal is given in the following form [15]:
where are real valued OQAM symbols, and denotes the synthesis basis, which can be obtained by the prototype function in the following way:
where is an even number of sub-carriers, the sub-carrier spacing of , and an additional phase term. denotes OFDM symbol duration, and denotes the time offset between the real and imaginary parts of the OQAM symbols. is the sub-carrier index and is the OQAM symbol time index.
The design of pulse enables the associated sub-carrier functions to be orthogonal in the real field,
where denotes Kronecker delta, if and if . We can find that, even in the distortion-free channel and with perfect time and frequency synchronization, some purely imaginary inter-carrier interference at the output still be existed, thus, we set interference weights
where denotes a purely imaginary term for .
Through the channel, with an additive noise, the received signal can be expressed as
with
where denotes the channel impulse response, and denotes a complex response of the channel at instant . Figure 1 shows an implementation diagram of the FBMC/OQAM system.
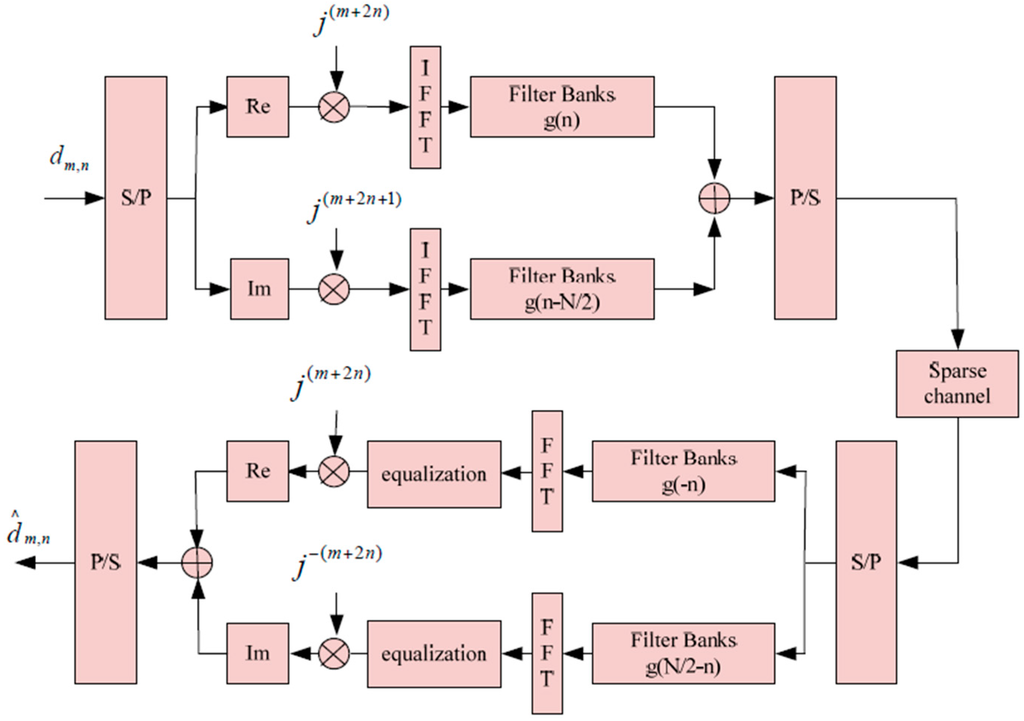
Figure 1.
Implementation diagram of the FBMC/OQAM system [35].
3. Compressive Sensing Based Preamble Channel Estimation
In this section, we present a novel sparse adaptive channel estimation method based on CS for FBMC/OQAM systems. We first review the two classical preamble structures and CS theory for channel estimation. We briefly introduce the conventional CS signal recovery algorithms, OMP, CoSaMP and SAMP [36]. Then, we propose the new CS algorithm. Along with the algorithm process, we present numerical evidence showing that our proposed algorithm provides attractive results.
3.1. Preamble Structures
In FBMC/OQAM, the preamble pilots exist in all sub-carriers, the preamble sequence is superimposed on the data. Figure 2a,b show the IAM and ICM preamble structures. Assuming that a pilot symbol is transmitted at a prior known position to the receiver, the LS estimation is
where is imaginary interference.
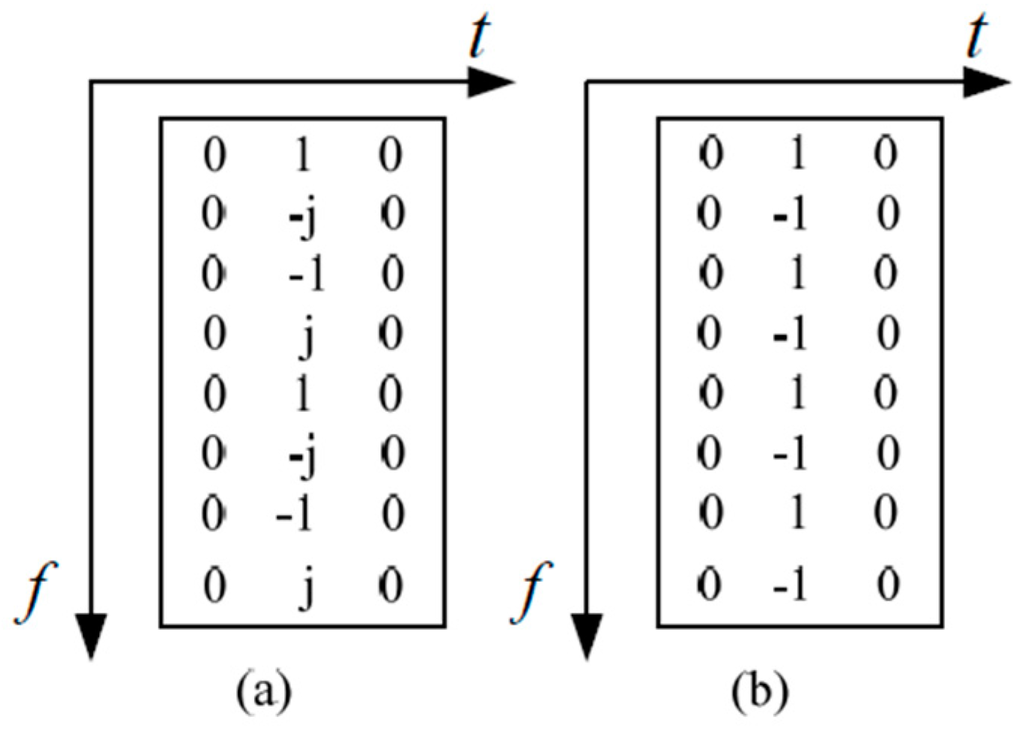
Figure 2.
Preamble structures: (a) Interference approximation method (IAM); (b) Interference cancellation method (ICM).
3.2. CS Theory for Channel Estimation
CS theories [37,38,39] state that a sparse signal can be recovered steadily from linear measurement
where is the measurement matrix, and denotes the matrix with ; here, , and denotes the noise, by minimizing the -norm of . The prerequisite is that satisfies the Restricted Isometry Property (RIP), that is, for all -sparse signal ,
where is the RIP parameter, .
The signal in Equation (5) can be given in matrix form as [31]
where , , and denotes the multipath channel frequency response sampling value, . denotes a row discrete Fourier Transform matrix, is the channel length; and denotes the noise matrix, with zero mean and variance of , and the matrix with .
We set for the number of pilots, denotes a pilot selection matrix with , and is utilized to seeking the pilots position from the whole sub-carriers. indicate the pilot’s position. Rewrite Equation (10) as
where is received pilot signal; in this paper, is the LS estimation channel values, , with column vectors. , and denotes a diagonal matrix, where the diagonal elements are pilot values.
Let us assume that , rewrite Equation (11) as
where denotes sparse multipath channel response, and we can obtain and in the transmission process. Then, we can use the CS recovery algorithm to recover sparse signal .
3.3. Adaptive Regularized Compressive Sampling Matching Pursuit Algorithm
3.3.1. CS Algorithms Overview
A number of CS recovery algorithms have been proposed. One of the popular kinds of recovery algorithms is based on the iterative greedy pursuit. OMP, CoSaMP and SAMP belong to this class. According to whether the sparse K is known prior or not, this class of algorithms also can be divided into two types.
OMP and CoSaMP are the first type of algorithms with the sparsity K is known prior. For the OMP algorithm, in each iteration, the atom maximizes its inner product with the residual signal. However, the results of each iteration may be suboptimal. CoSaMP is proven to be the most advanced greedy algorithm. CoSaMP introduces the idea of backtracking that reduces the chance of error accumulation, selects coordinates and utilizes an iterative checking to refine them, and overcomes the defects of OMP, so that the atoms could not be changed once deposited in the candidate set.
In practical applications, the second type of algorithms has better prospects than the first. SAMP is the second type of algorithm. The sparsity of signal is not required in SAMP as an a priori condition, and SAMP attempts to evaluate the sparsity of source signal by iteration.
3.3.2. Proposed Algorithm
CoSaMP algorithm can reconstruct source signals with high efficiency. However, the algorithm requires the prior knowledge of sparsity. SAMP algorithm provides a way for blind sparse reconstruction. Motivated by the advantages in the two greedy algorithms and associated with a regularized process, we propose a new greedy algorithm, named sparse adaptive regularized compressive sampling matching pursuit (ARCoSaMP).
The proposed algorithm can automatically adjust the selected atoms to reconstruct the unknown sparsity signal in the iterative process. A similar backtracking theory of CoSaMP is utilized to reconstruct partial information of the target signal in the iterative process. An iterative process is divided into multiple stages, the proposed algorithm adaptively estimates the sparsity with steps through stage by stage and set it to the length of the initial support, then gets the accurate target signal by regularization screening of atoms in every stage. The algorithm basic steps are shown below:
- Input: measurement matrix , the measurement vector , the initial step size
- Output: a -sparse approximation of the channel
- (1)
- Initialization: residual , iterative , initial step , , index value set .
- (2)
- Set a threshold value , if the reconstruction satisfies , and stop the iteration; otherwise, continue to Step 3. The deviation norm 2 is chosen as the basis of the iterative termination. In the simulation, .
- (3)
- Calculate the correlation coefficient by the Equation (13), which calculates the absolute value of inner product between residual and each atom of measurement matrix , and deposit the index values corresponding the maximum values from to :
- (4)
- Regularization: using Equation (14) to regularizechoose with the maximal energy , add the set to the index set , and update the support set .
- (5)
- Use Equation (15) to get , according to the backtracking mechanism, take atoms corresponded to the largest elements of to , update the support set :
- (6)
- Update the residual
- (7)
- Make a comparison between the update residual and the last iteration residual; if , , return to Step 3; otherwise, and return to Step 2.
The selection of the initial step is very important, and if the step size is too large, there may an overestimating problem. In the proposed algorithm, the initial step size is 1, which is less than the reality of the sparsity until the final stage. Iteration loop follows the CoSaMP and regularization to identify support sets in the target signal. When , it is necessary to take an effective mechanism for stage switching. In the proposed algorithm, we trigger the stage switching between two consecutive iterations when the relevant residual improvement begins to disappear.
4. Simulation Results
In this section, simulation results are presented to compare the performance between convention LS, OMP, CoSaMP, SAMP and the proposed algorithm. The evaluations are mainly based on bit error rate (BER) and mean square error (MSE). The MSE is plotted with respect to the signal to noise ratio (SNR). The estimation of multipath delay profile and percentage recovered of the algorithms are also given. We take modulation as 4OQAM, the number of subcarriers in FBMC/OQAM systems is . The square root raise cosine filter is employed in FBMC/OQAM, the roll off factor of the filter is one, and length of the filter is We adopt the IEEE 802.22 channel with sampling frequency 6.86 MHz as a simulation channel. The channel profile is shown in Table 1. The channel sparse K is 6. The channel coding adopts convolutional code ( with and code rate = 1/2).

Table 1.
IEEE 802.22 channel profile.
Figure 3 is a snapshot of the original and estimated delay profiles of IEEE 802.22 channel. It shows that the proposed ARCoSaMP for FBMC/OQAM successfully detect the channel with sixmultipaths and SNR = 8 dB. The proposed scheme not only precisely estimates the multipath delay values but also exactly estimates the relative power of the multipath.
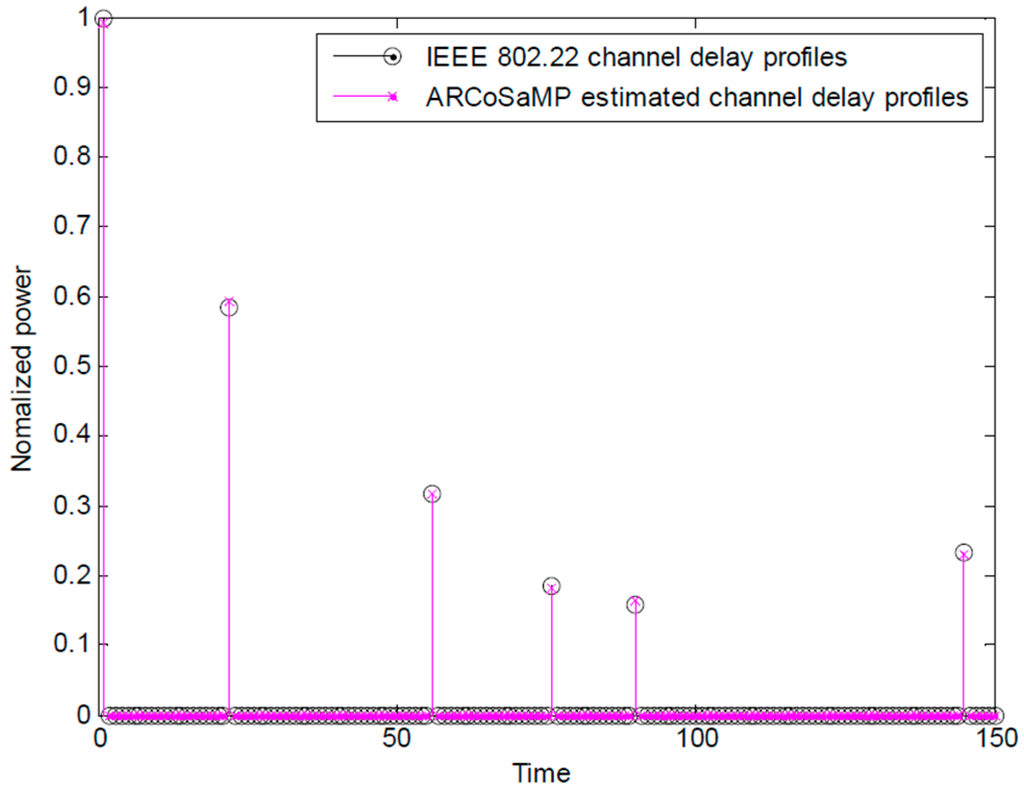
Figure 3.
IEEE 802.22 channel delay profile and estimated channel delay profile.
We also investigate the probability of recovery for a fixed signal sparsity among the above-mentioned algorithms. Figure 4 depicts the probability curves of Gaussian sparse signal. It can be seen that ARCoSaMP outperforms the other three algorithms in the range of to . ARCoSaMP also requires the least measurements for exact recovery. When the measurements , CoSaMP provides better recovery probability than SAMP. With the measurement increasing, ARCoSaMP provides recovery probability approximate to that in CoSaMP without prior knowledge of sparsity.
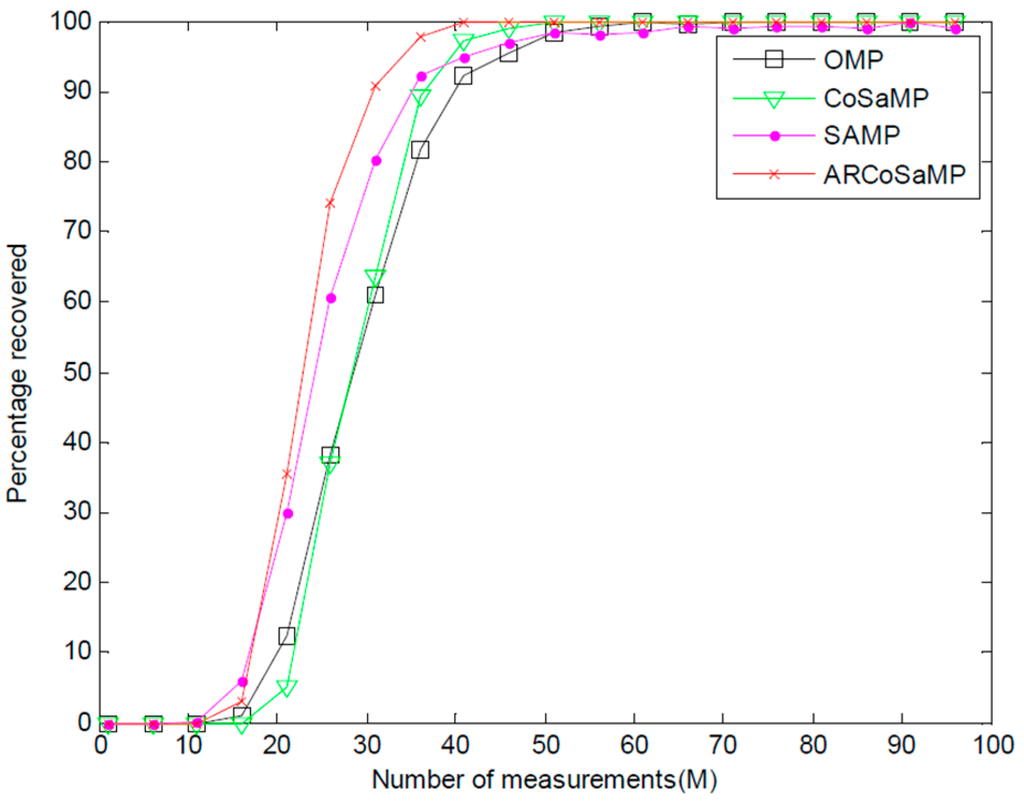
Figure 4.
Probability of exact recovery versus the number of measurements.
Figure 5a,b shows the BER and MSE performance comparisons when IAM preamble structure is adopted in FBMC/QOAM systems. In Figure 5a, it is obvious that CS based channel estimation methods can obtain significantly BER improvement compared with conventional least squares (LS) method. Careful observation shows that CoSaMP outperforms other algorithms in the whole SNR range considered. CoSaMP can obtain about 4.2 dB gain compared with LS when BER of is considered. ARCoSaMP performs slightly better than OMP, and has a gain of 0.3 dB compared with SAMP, when the BER of about is considered. Figure 5b plots the MSE performance comparisons. We can see that CoSaMP still performs the best MSE performance in the five schemes. It enjoys a significant SNR gain compared to those of LS, when at the same MSE level. ARCoSaMP is slightly worse performing than CoSaMP, but well performing than OMP and SAMP. It should be noted that ARCoSaMP provides BER performance comparable to CoSaMP algorithm without the prior known of sparsity and exceeds the conventional SAMP algorithm. In addition, we compare simulation time of SAMP and ARCoSaMP, where both of the two algorithms do not need to know the prior knowledge of sparisity. The result shows that ARCoSaMP needs less simulation time than SAMP, with ARCoSaMP simulation time is 30.1824 s and SAMP simulation time is 32.8995 s.
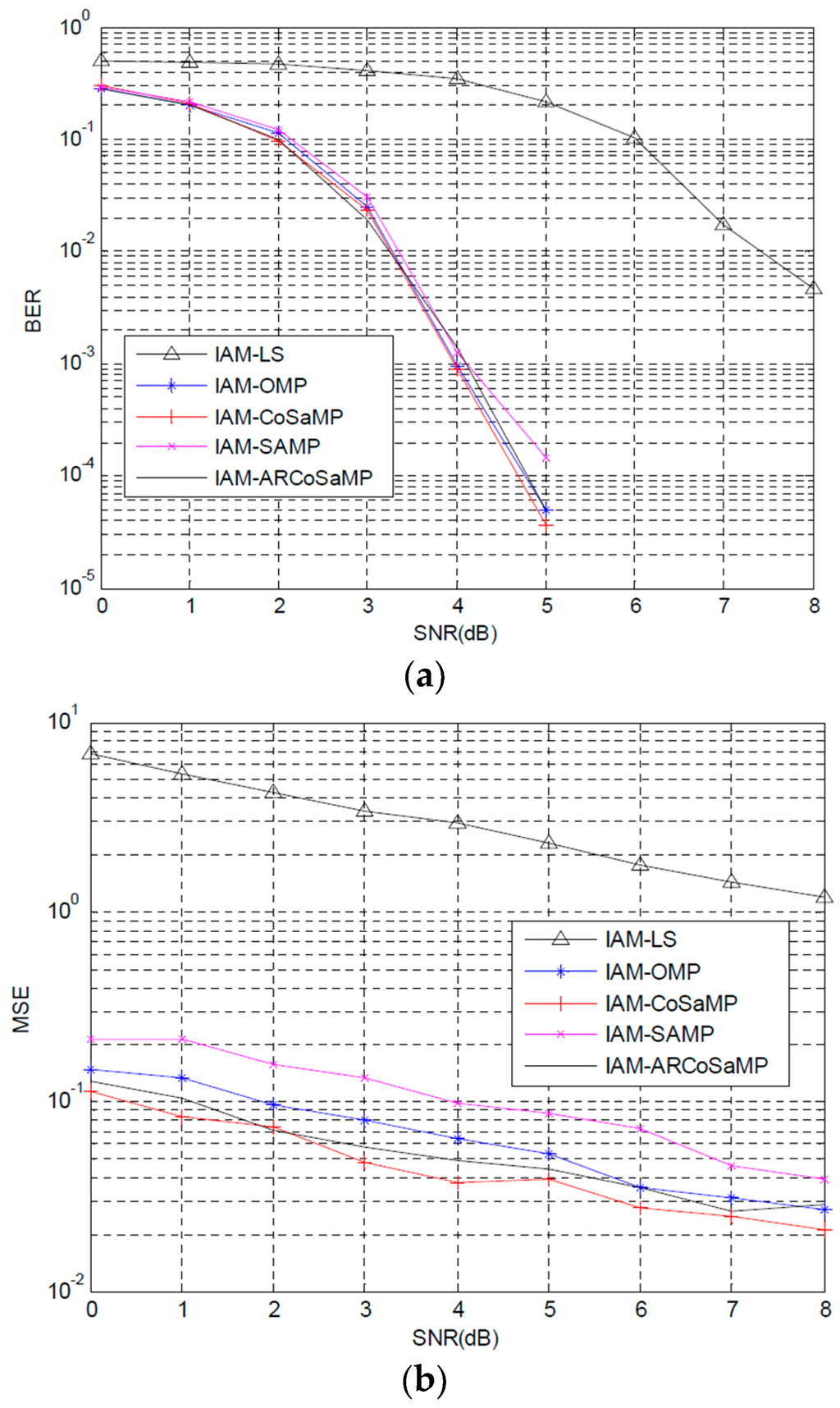
Figure 5.
Bit error rate (BER) and mean square error (MSE) performance comparisons based IAM preamble structure: (a) BER and (b) MSE.
Figure 6a,b depict the BER and MSE performance comparisons when ICM preamble structure is adopted in FBMC/QOAM systems. We can find that the trends of both BER and MSE curves are the same as that in Figure 5. Preamble structure ICM based channel estimation outperforms the IAM scheme. ICM-LS provides significant BER improvement compared with IAM-LS. ICM-CS has slight BER improvement compared with IAM-CS but obvious improvement in MSE performance. CoSaMP algorithm obtains the best BER and MSE performances. In Figure 6a, ARCoSaMP gives performance that are about 0.2 dB better than SAMP method, when BER = . CoSaMP can obtain about 1.2 dB gain compared with LS when BER of is considered. In Figure 6b, the OMP, CoSaMP and ARCoSaMP, the three curves, are very close. ARCoSaMP and OMP provide similar MSE performance, and CoSaMP is less well performing than ARCoSaMP. The simulation times of ICM-SAMP and ICM-ARCoSaMP are less than IAM-SAMP and IAM-ARCoSaMP. ICM-ARCoSaMPstill needs less time than ICM-SAMP.
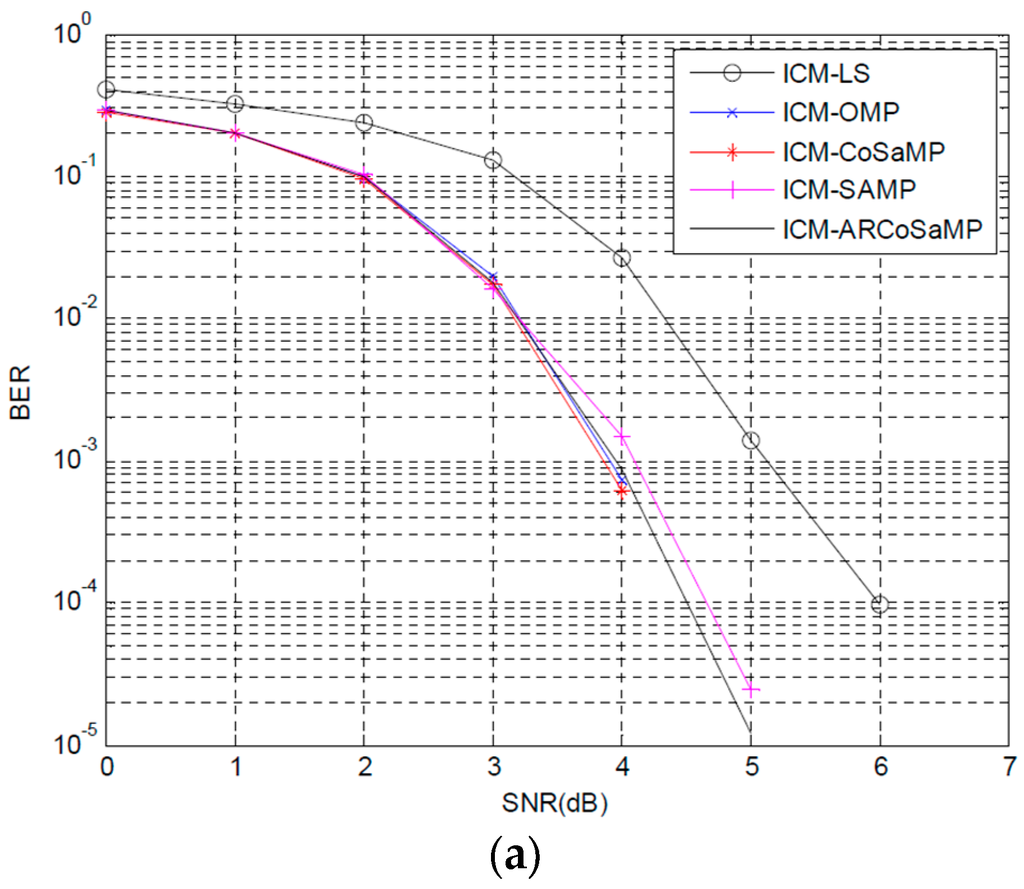
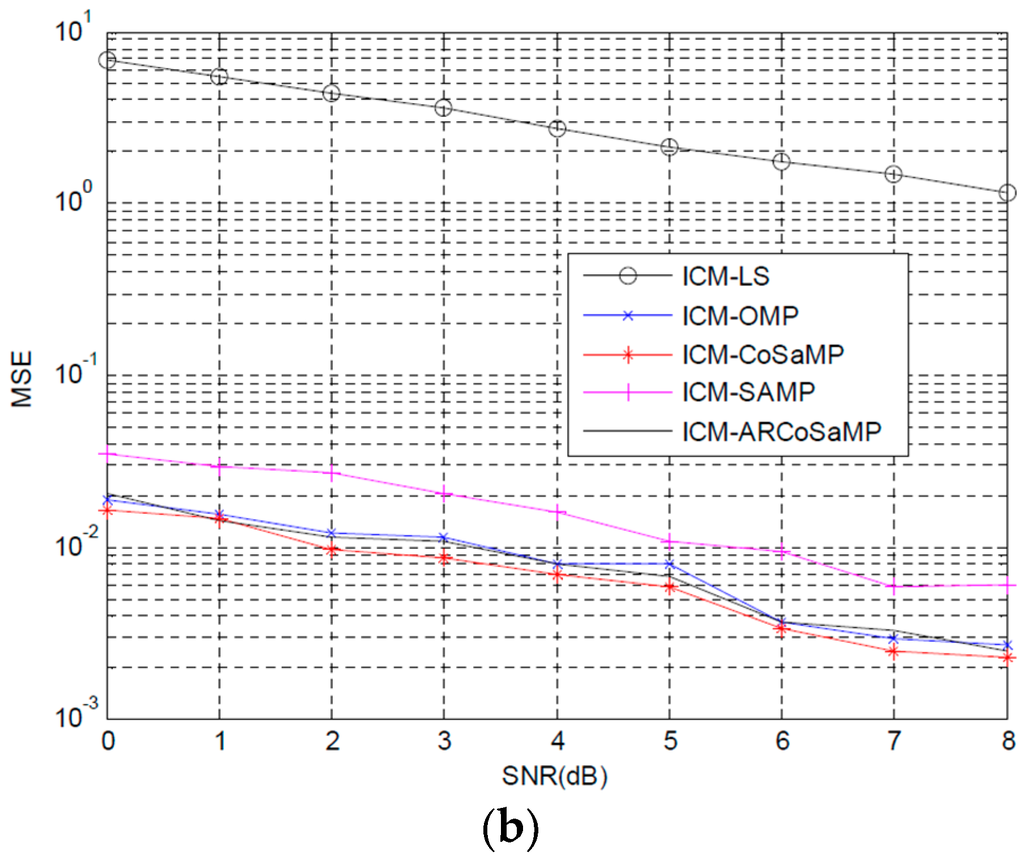
Figure 6.
BER and MSE performance comparison based ICM preamble structure: (a) BER and (b) MSE.
As shown in the simulation results, it can be verified that the CS-based channel estimation approach can provide more effective performance than conventional LS methods in FBMC/OQAM systems. The proposed ARCoSaMP based channel estimation method can achieve similar performance than CoSaMP without a prior sparse knowledge of the channel and has better channel estimation performance than SAMP with lesser time complexity.
5. Conclusions
In this paper, we have studied the preamble channel estimation based on compressive sensing for FMBC/OQAM systems under an IEEE 802.22 sparse multipath channel. A new sparse adaptive regularized compressive sampling matching pursuit algorithm for channel estimation is proposed, which is associated with adaptive, regularized and CoSaMP. The proposed algorithm can accurately estimate the multipath components. Simulation results demonstrate that a CS based preamble approach can achieve significantly better BER and MSE performance than conventional LS methods. The proposed scheme outperforms SAMP for channel estimation with lesser time complexity and can provide approximate results than the state-of–the-art CoSaMP algorithm without a prior sparse knowledge of the channel. It has been verified that the ARCoSaMP scheme is an efficient method for sparse adaptive channel estimation in FBMC/OQAM transmission networks.
Acknowledgments
This work is supported by the Hainan University Excellent Paper Cultivation Plan, and the National Natural Science Foundation of China, Grant No.61561017, No.61561018. The authors would like to thank the editor and the anonymous reviewers for their valuable comments.
Author Contributions
Han Wang proposed the sparse adaptive regularized compressive sampling matching pursuit algorithm; Wencai Du conceived and designed the simulations and provided some comments on the paper organization; Lingwei Xu contributed towards the performance results and analytic evaluations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FP7-ICT PHYDYAS Project. Prototype Filter and Structure Optimization, Project Deliverable D5.1, (Section 5.2.3). Available online: http://www.ict-phydyas.org/delivrables (accessed on 20 June 2016).
- Shao, K.; Alhava, J.; Kaakinen, J.Y.; Renfors, M. Fast-convolution implementation of filter bank multicarrier waveform processing. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems, Lisbon, Portugal, 24–27 May 2015; pp. 978–981.
- Nadal, J.; Nour, C.A.; Baghdadi, A. Low-complexity pipelined architecture for FBMC/OQAM transmitter. IEEE Trans. Circuits Syst. II Express Briefs 2016, 63, 19–23. [Google Scholar] [CrossRef]
- Schellmann, M.; Zhao, Z.; Lin, H.; Siohan, P.; Rajatheva, N. FBMC-based air interface for 5G Mobile: Challenges and proposed solutions. In Proceedings of the 9th International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Oulu, Finland, 2–4 June 2014; pp. 102–107.
- Nadal, J.; Nour, C.A.; Baghdadi, A.; Lin, H. Hardware prototyping of FBMC/OQAM baseband for 5G mobile communication. In Proceedings of the 2014 25th IEEE International Symposium on Rapid System Prototyping, New Delhi, India, 16–17 October 2014; pp. 72–77.
- David, L.-P.; Chu, X.L.; Athanasios, V.V.; Holger, C. On Distributed and Coordinated Resource Allocation for Interference Mitigation in Self-Organizing LTE Networks. IEEE/ACM Trans. Netw. 2012, 21, 1145–1158. [Google Scholar]
- Zhang, Z.S.; Chai, X.M.; Long, K.P.; Vasilakos, A.V. Full deplex techniques for 5G networks: Self-interference cancellation, protocol design, and relay selection. IEEE Commun. Mag. 2015, 53, 128–137. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Wang, X.Y.; Long, K.P.; Vasilakos, A.V. Large-scale MIMO-based wireless backhaul in 5G networks. IEEE Wirel. Commun. 2015, 22, 58–66. [Google Scholar] [CrossRef]
- Rodger, J.A. Toward reducing failure risk in an integrated vehicle health maintenance system: A fuzzy multi-sensor data fusion Kalman filter approach for IVHMS. Expert Syst. Appl. 2012, 39, 9821–9836. [Google Scholar] [CrossRef]
- Chen, X.W.; Zhao, M.J.; Xu, C.L. Preamble-Based Channel Estimation Methods with High Spectral Efficiency for Pulse Shaping OFDM/OQAM Systems. In Proceedings of the 6th International Conference on Wireless Communications and Signal Processing, Hefei, China, 23–25 October 2014; pp. 1–6.
- Razavi, R.; Xiao, P.; Tafazolli, R. Information Theoretic Analysis of OFDM/OQAM with Utilized Intrinsic Interference. IEEE Signal Process. Lett. 2015, 22, 618–622. [Google Scholar] [CrossRef]
- Siohan, P.; Siclet, C.; Lacaille, N. Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Trans. Signal Process. 2002, 50, 1170–1183. [Google Scholar] [CrossRef]
- Chang, R. High-speed multichannel data transmission with band limited orthogonal signals. Bell Syst. Tech. 1996, 45, 1775–1796. [Google Scholar] [CrossRef]
- Saltzberg, B. Performance of an efficient parallel data transmission system. IEEE Trans. Commun. Technol. 1967, 15, 805–811. [Google Scholar] [CrossRef]
- Lele, C.; Javaudin, J.P.; Legouable, R.; Skrzypczak, A.; Siohan, P. Channel estimation methods for preamble-based OFDM/OQAM modulations. Eur. Trans. Telecommun. 2008, 19, 741–750. [Google Scholar] [CrossRef]
- Du, J.F.; Signell, S. Novel Preamble-Based Channel Estimation for OFDM/OQAM Systems. In Proceedings of the IEEE International Conference on Communications, Dresden, Germany, 14–18 June 2009; pp. 1–6.
- Deng, F.; He, X.; Cheng, G.B.; Li, S.Q. An effective Preamble-based Channel Estimation Structure for OFDM/OQAM Systems. In Proceedings of the 6th International Conference on Wireless Communications Networking and Mobile Computing, Chengdu, China, 23–25 September 2010; pp. 1–4.
- Hu, S.; Wu, G.; Li, T.; Xiao, Y.; Li, Q.S. Preamble design with ICI cancellation for channel estimation in OFDM/OQAM system. IEICE Trans. Commun. 2010, E93-B, 211–214. [Google Scholar] [CrossRef]
- Cui, W.; Qu, D.; Jiang, T.; Boroujeny, B.F. Coded Auxiliary Pilots for Channel Estimation in FBMC-OQAM Systems. IEEE Trans. Veh. Technol. 2015, 64, 1–11. [Google Scholar] [CrossRef]
- Fusco, T.; Izzo, L.; Petrella, A.; Tanda, M. Blind Symbol Timing Estimation for OFDM/QOAM Systems. IEEE Trans. Signal Process. 2009, 57, 4952–4958. [Google Scholar] [CrossRef]
- Hou, W.K.; Champagne, B. Semiblind Channel Estimation for OFDM/OQAM Systems. IEEE Signal Process. Lett. 2015, 22, 400–403. [Google Scholar] [CrossRef]
- Berger, C.R.; Wang, Z.; Huang, J.; Zhou, S. Application of compressive sensing to sparse channel estimation. IEEE Commun. Mag. 2010, 48, 164–174. [Google Scholar] [CrossRef]
- Bajwa, W.U.; Haupt, J.; Sayeed, A.M.; Nowak, R. Compressed Channel Sensing: A New Approach to Estimating Sparse Multipath Channels. IEEE Proc. 2010, 98, 1058–1076. [Google Scholar] [CrossRef]
- Xiang, L.; Luo, J.; Vasilakos, A. Compressed data aggregation for energy efficient wireless sensor networks. In Proceedings of 2011 8th IEEE Communications Society Conference on Sensor, Mesh and ad hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011; pp. 46–54.
- Jiang, D.; Xu, Z.; Chen, Z.; Han, Y.; Xu, H. Joint time-frequency sparse estimation of large-scale network traffic. Comput. Netw. 2011, 55, 3533–3547. [Google Scholar] [CrossRef]
- Gui, G.; Peng, W.; Adachi, F. Improved adaptive sparse channel estimation based on the least mean square algorithm. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference, Shanghai, China, 7–10 April 2013; pp. 3105–3109.
- Jiang, D.; Wang, Y.; Yao, C.; Han, Y. An effective dynamic spectrum access algorithm for multi-hop cognitive wireless networks. Comput. Netw. 2015, 84, 1–16. [Google Scholar] [CrossRef]
- Meng, J.; Yin, W.T.; Li, Y.Y.; Nguyen, N.T.; Han, Z. Compressive Sensing Based High-Resolution Channel Estimation for OFDM System. IEEE J. Sel. Top. Signal Process. 2012, 6, 15–25. [Google Scholar] [CrossRef]
- Hu, D.; Wang, X.D.; He, L.H. A New Sparse Channel Estimation and Tracking Method for Time-Varying OFDM Systems. IEEE Trans. Veh. Technol. 2013, 62, 4648–4653. [Google Scholar]
- Pan, H.; Xue, Y.; Mei, L.; Gao, F. An improved CoSaMP sparse channel estimation algorithm in OFDM system. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing, Ningbo, China, 19–22 September 2015; pp. 1–4.
- Wang, H.; Du, W.C.; Bai, Y. Compressed Sensing Based Channel Estimation for OFDM Transmission under 3GPP Channels. Int. J. Future Gener. Commun. Netw. 2016, 9, 85–94. [Google Scholar] [CrossRef]
- Liu, X.M.; Cai, Z.W.; .Jia, A.L.; Wang, P.; Ou, J.L. A Novel Channel Estimation Method Based on Compressive Sensing for OFDM/OQAM Systems. J. Comput. Inf. Syst. 2013, 9, 5955–5963. [Google Scholar]
- Tropp, J.; Gilbert, A. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Commun. ACM 2010, 53, 93–100. [Google Scholar] [CrossRef]
- Du, J.F.; Signell, S. Time Frequency Localization of Pulse Shaping Filters in OFDM/OQAM Systems. In Proceedings of the 6th International Conference of Information, Communications and Signal Processing, Singapore, 10–13 December 2007; pp. 1–5.
- Do, T.T.; Gan, L.; Nguyen, N.; Tran, D.T. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 518–587.
- Candes, E.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal recovery from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Baraniuk, R.G. Compressive Sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).