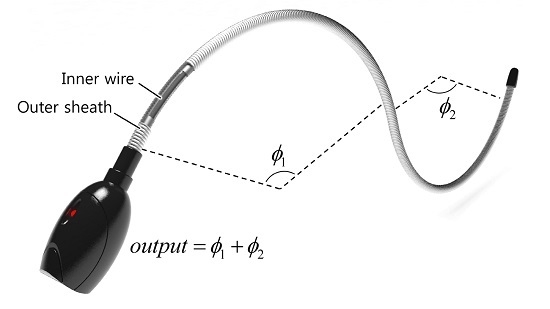
A Novel Low-Cost, Large Curvature Bend Sensor Based on a Bowden-Cable
Abstract
:1. Introduction
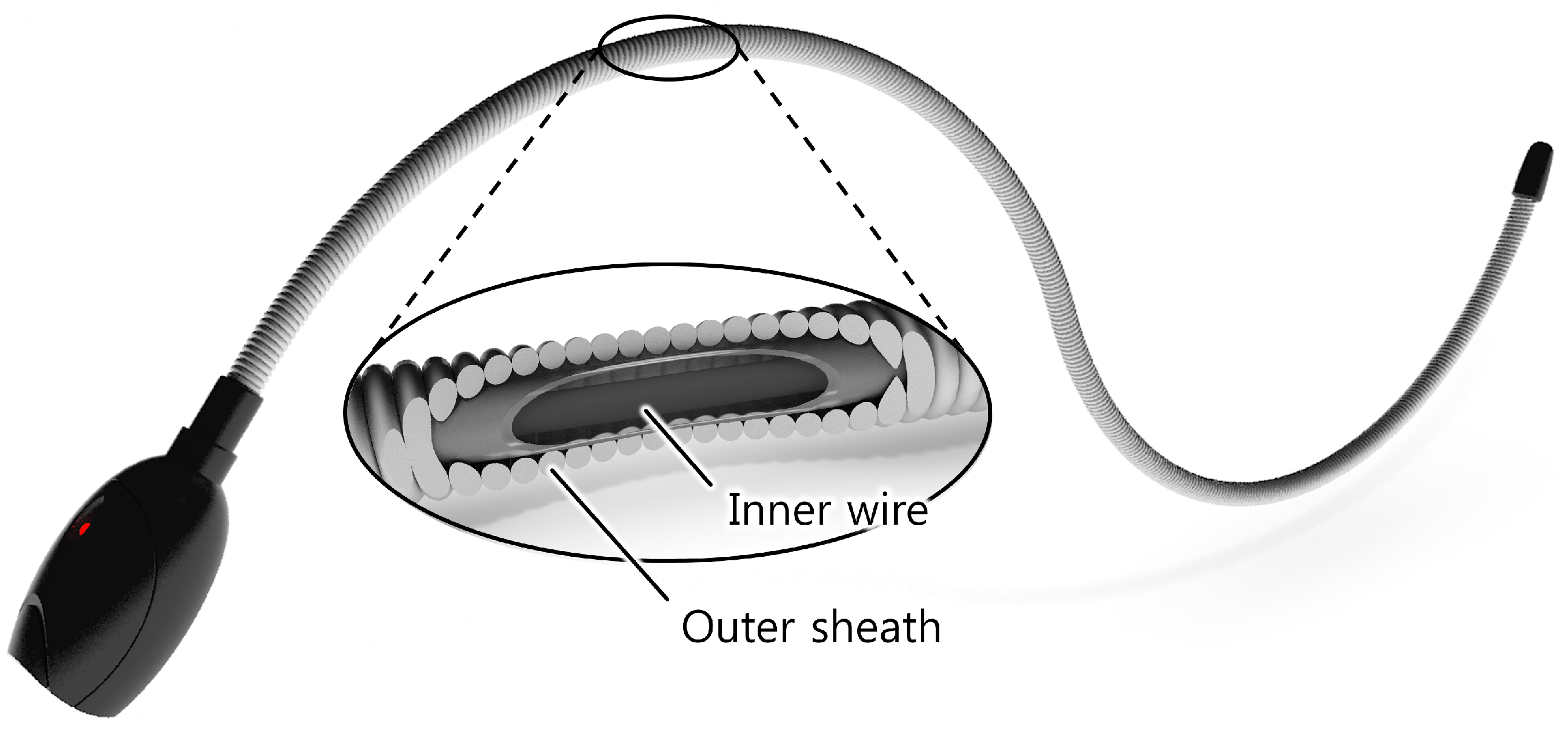
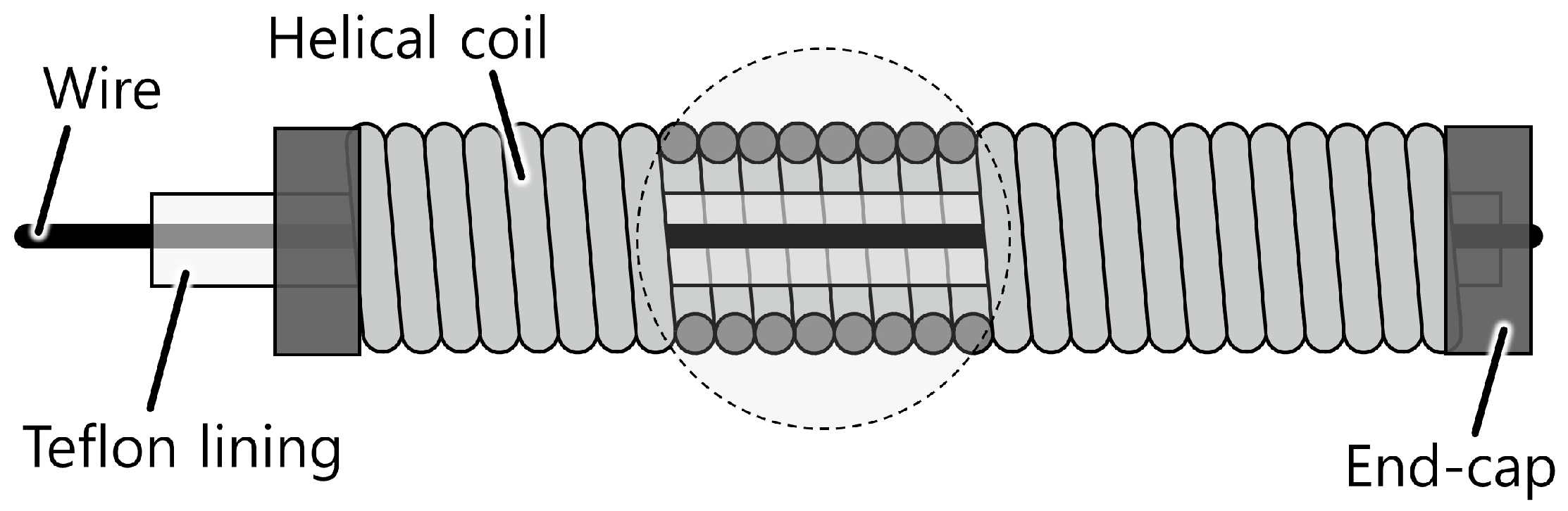
2. Concept and Design
2.1. Principle
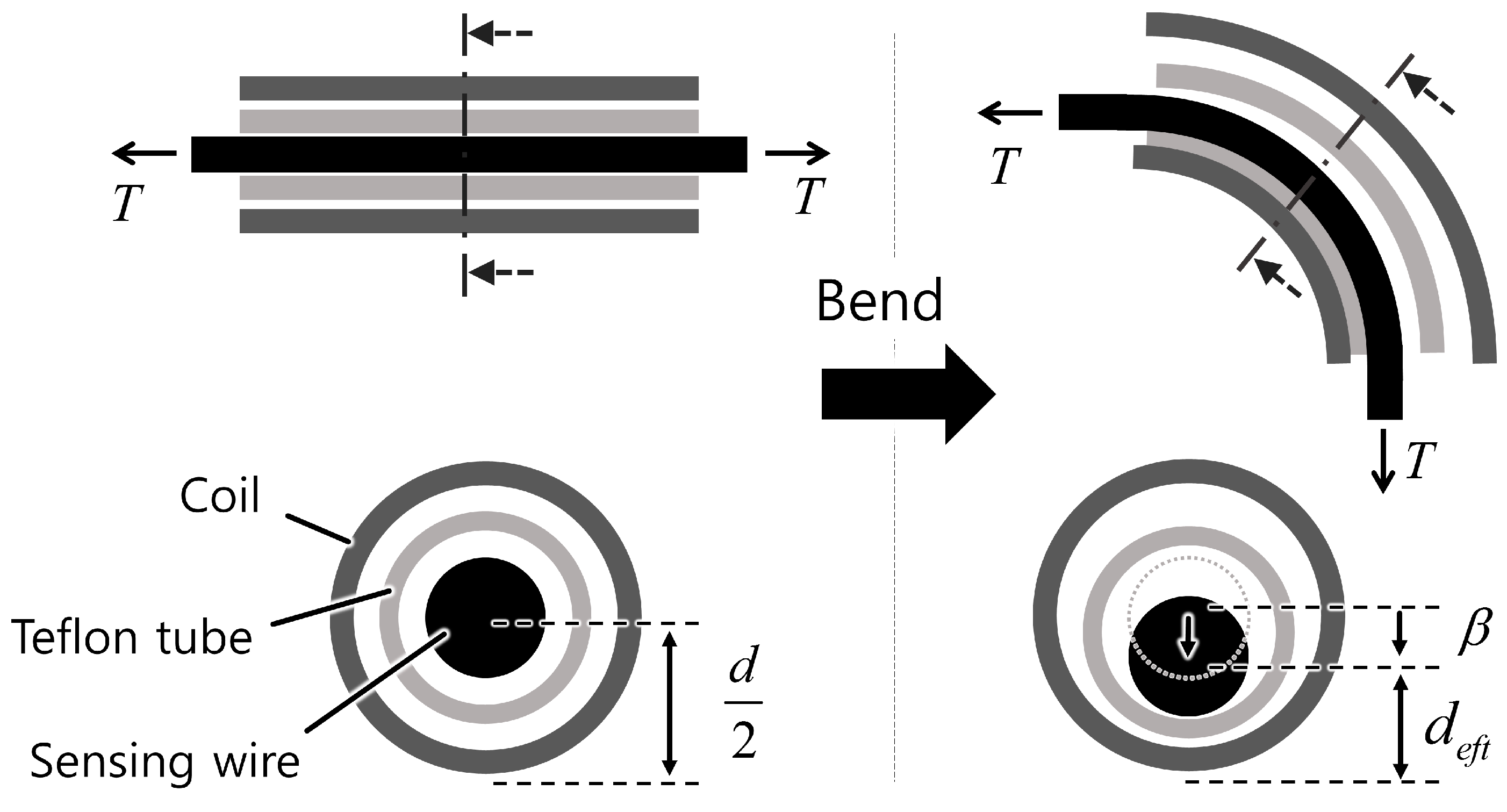
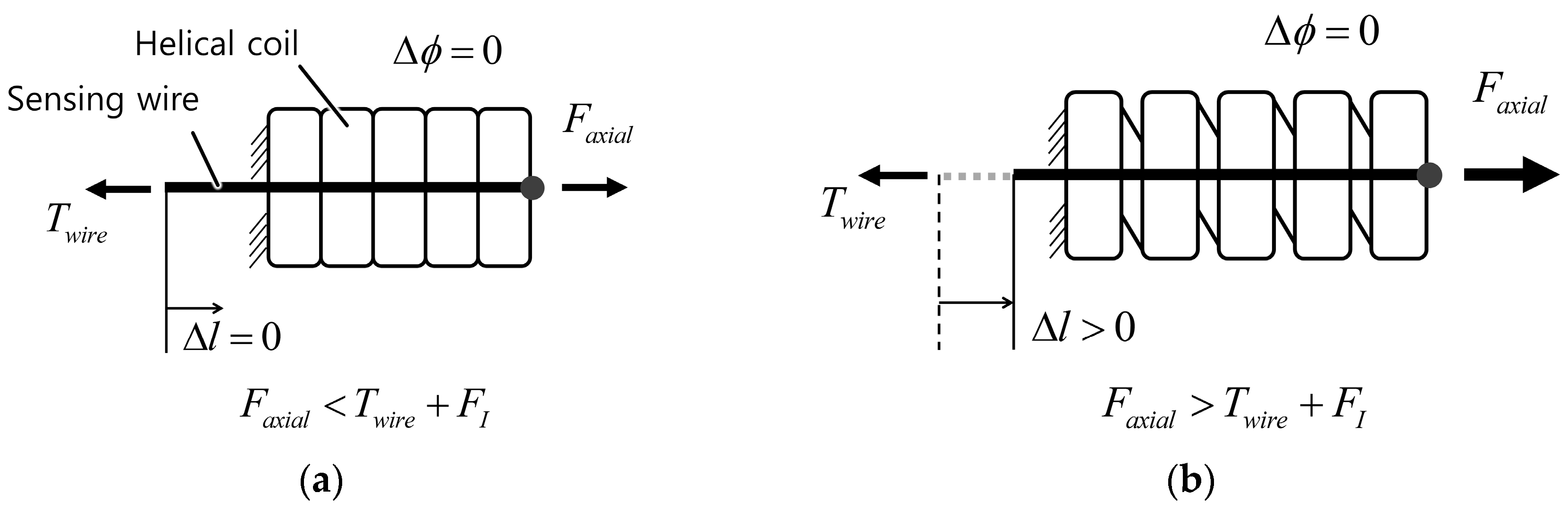
2.2. Maintaining Internal Tension
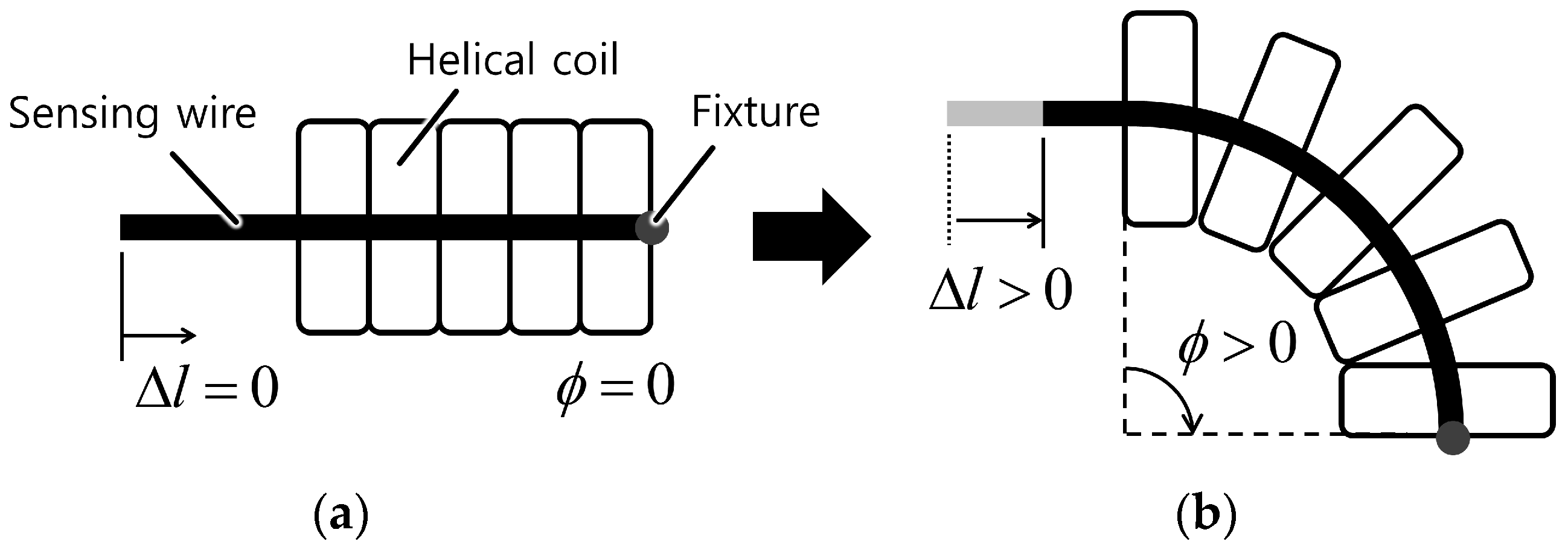
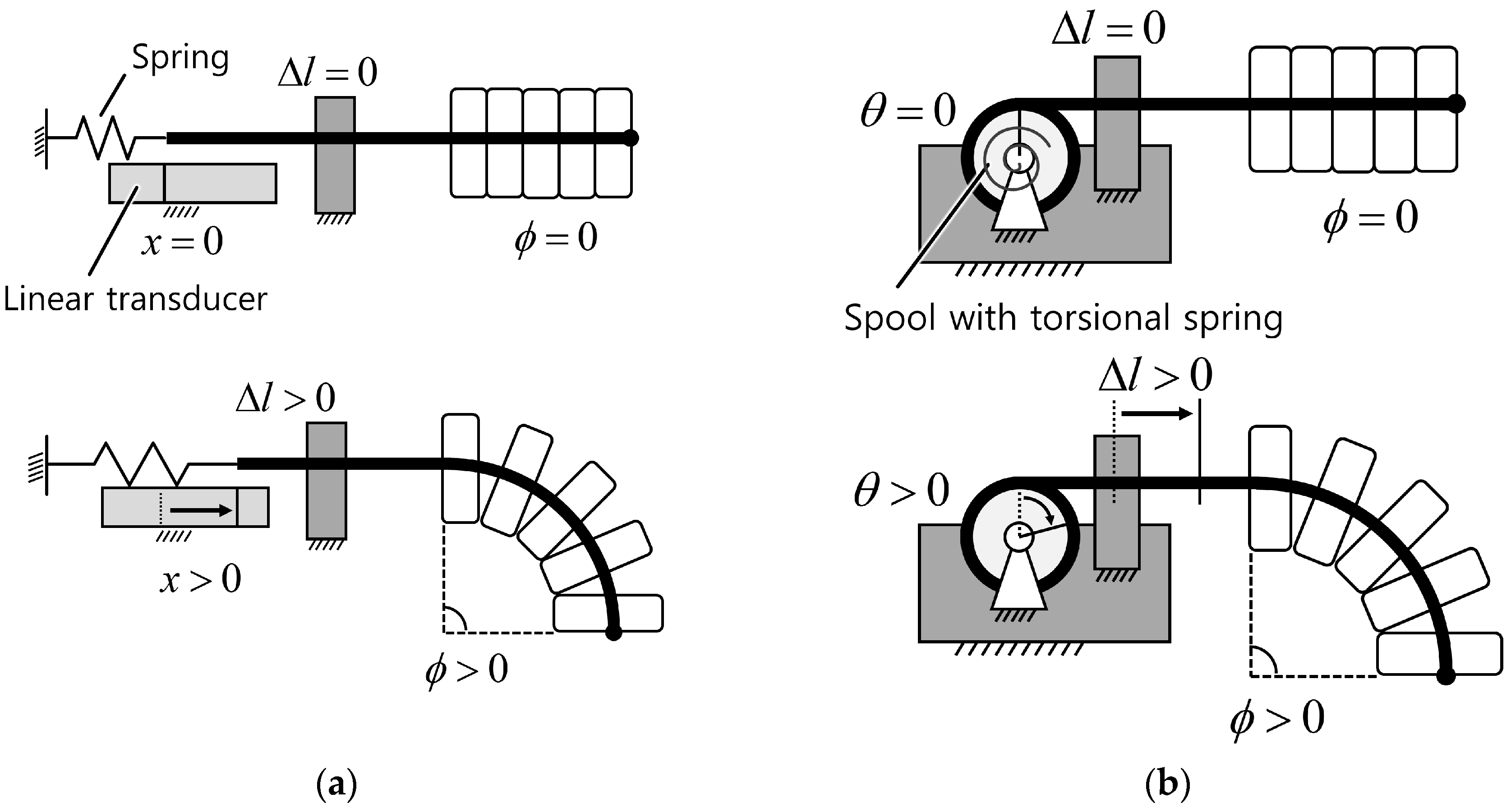
2.3. Displacement Change Measurement
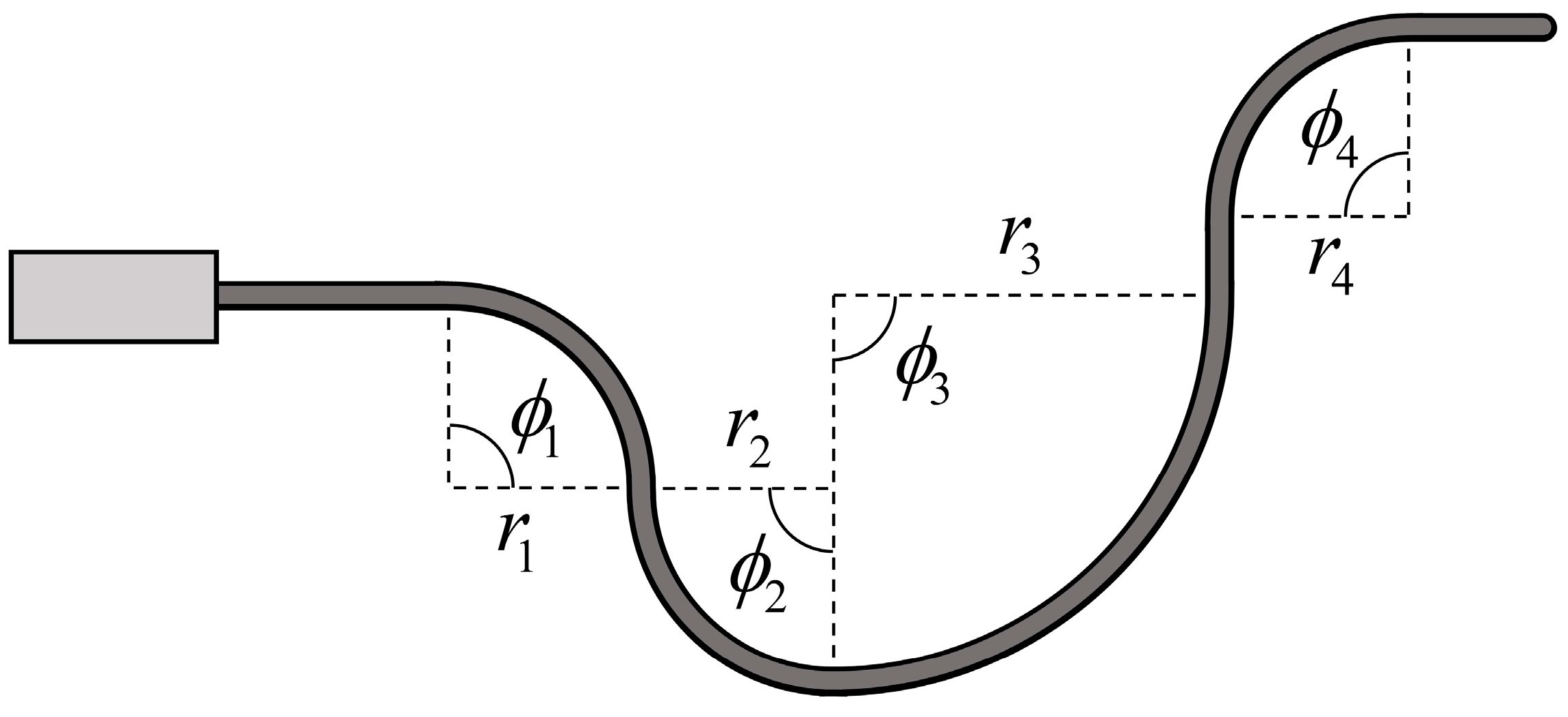
3. Modeling
3.1. Basic Model
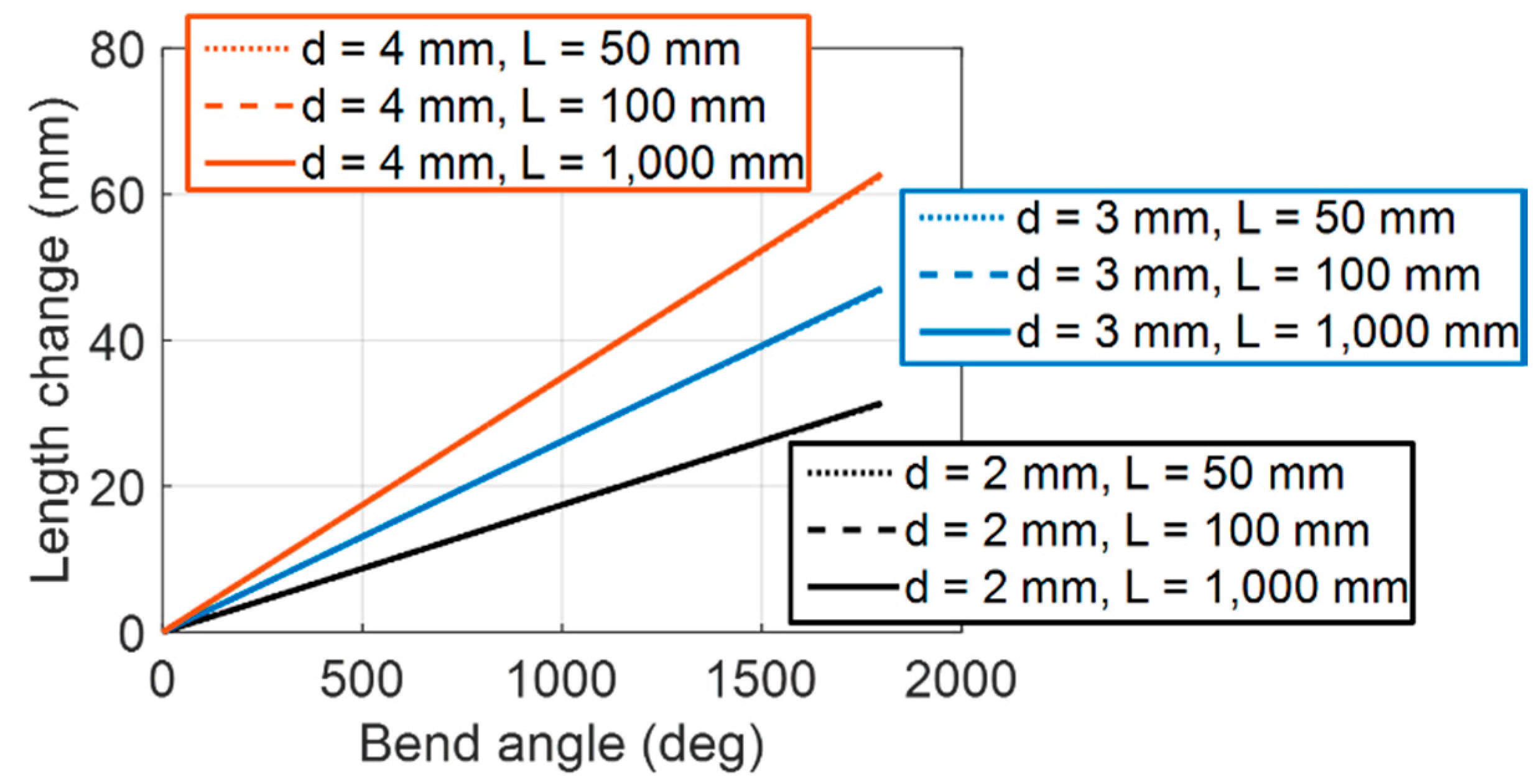
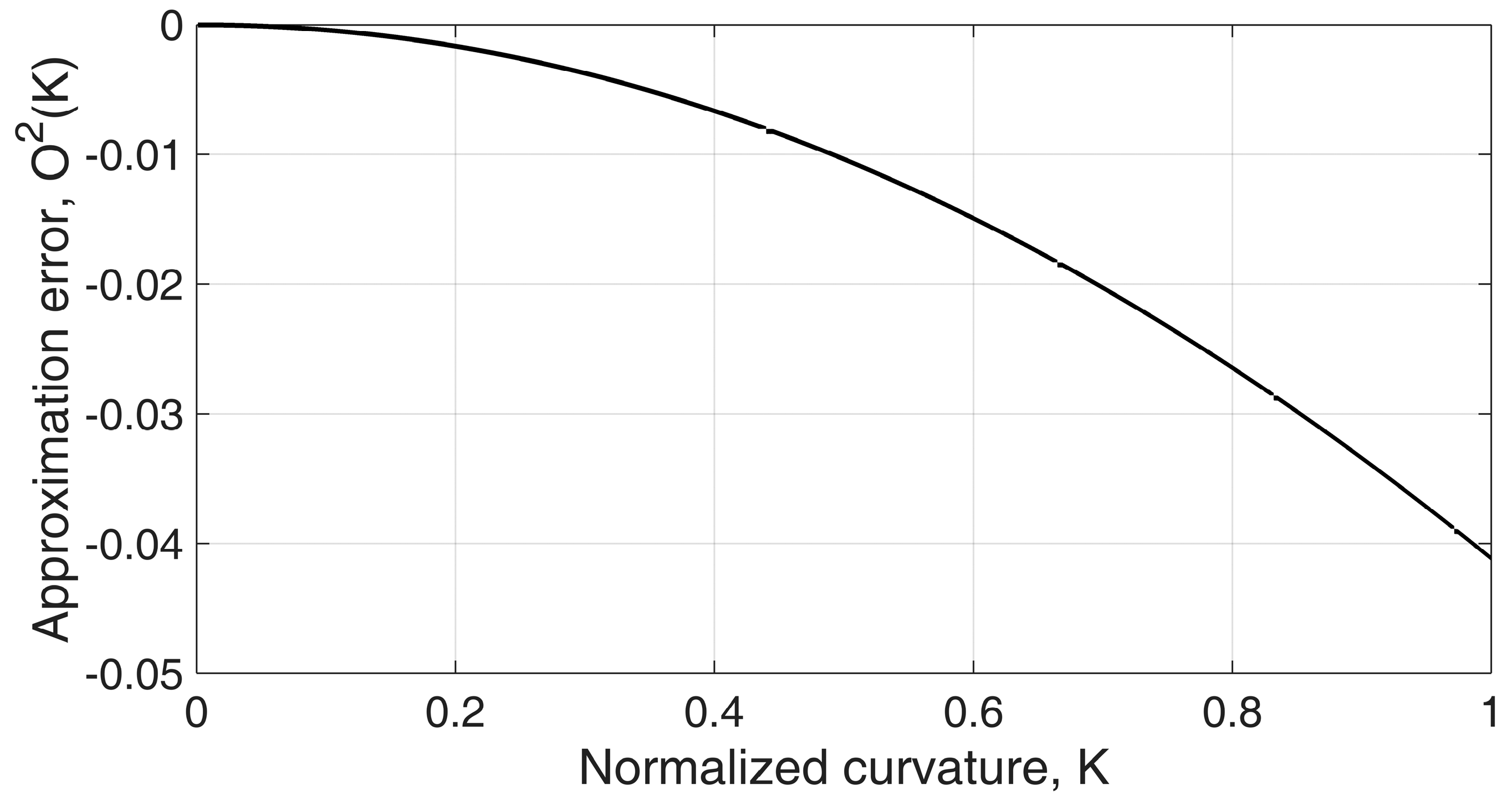
3.2. Linearity
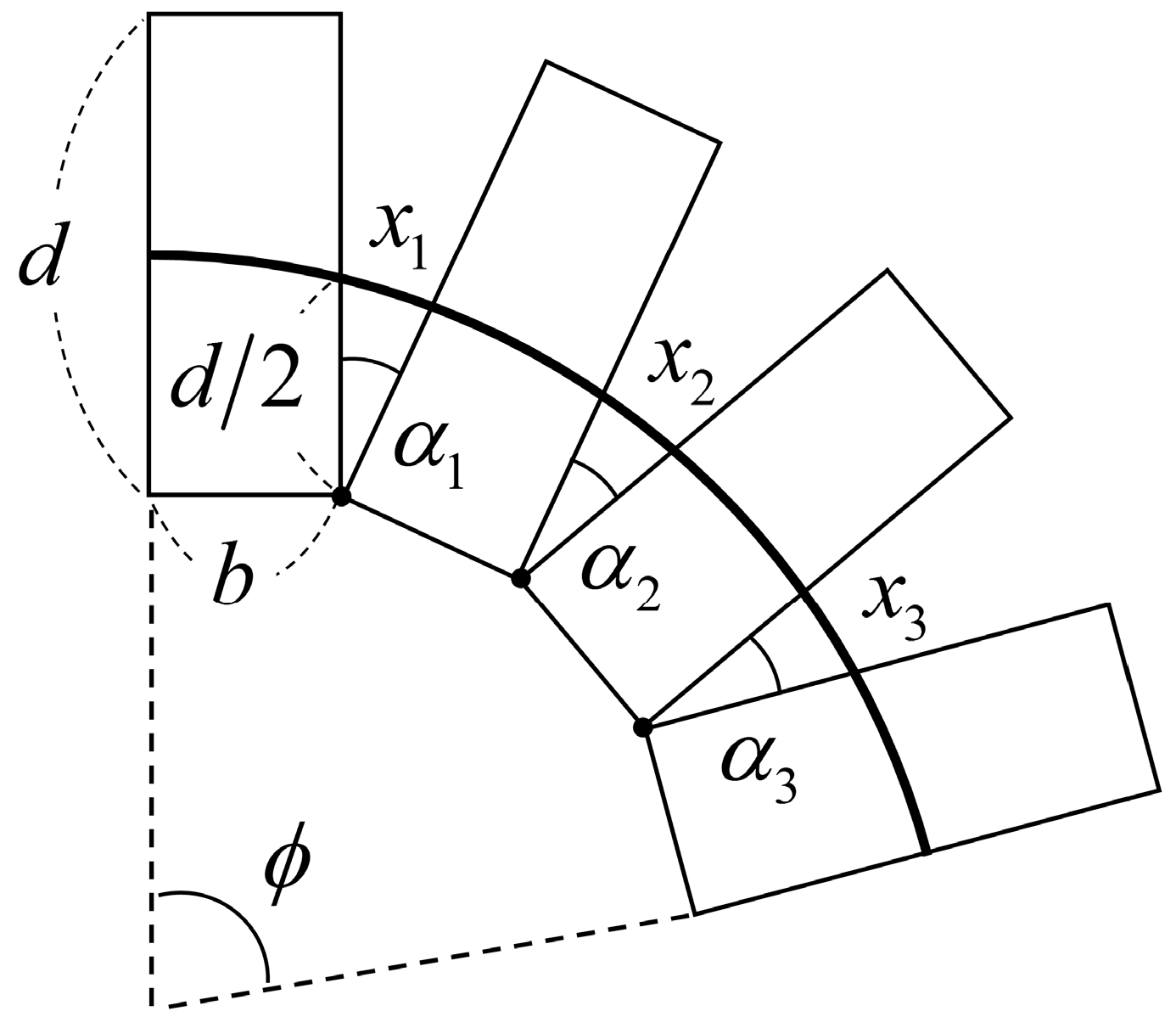
3.3. Advanced Model
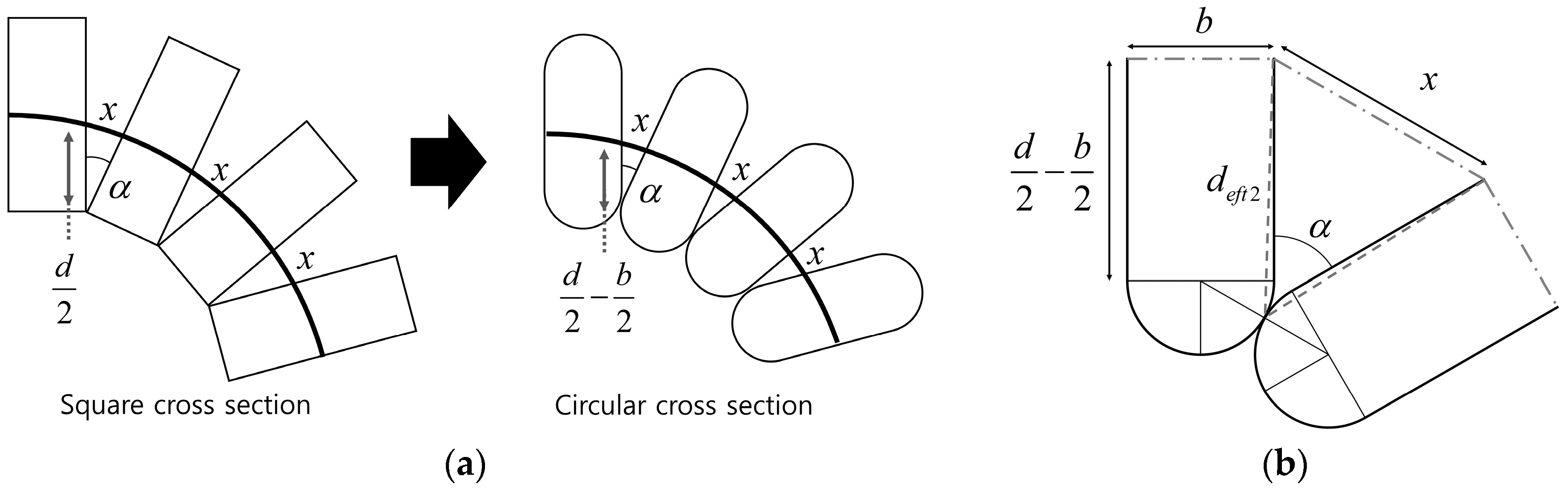
3.3.1. Gap between Parts
3.3.2. Shape of the Cross Section
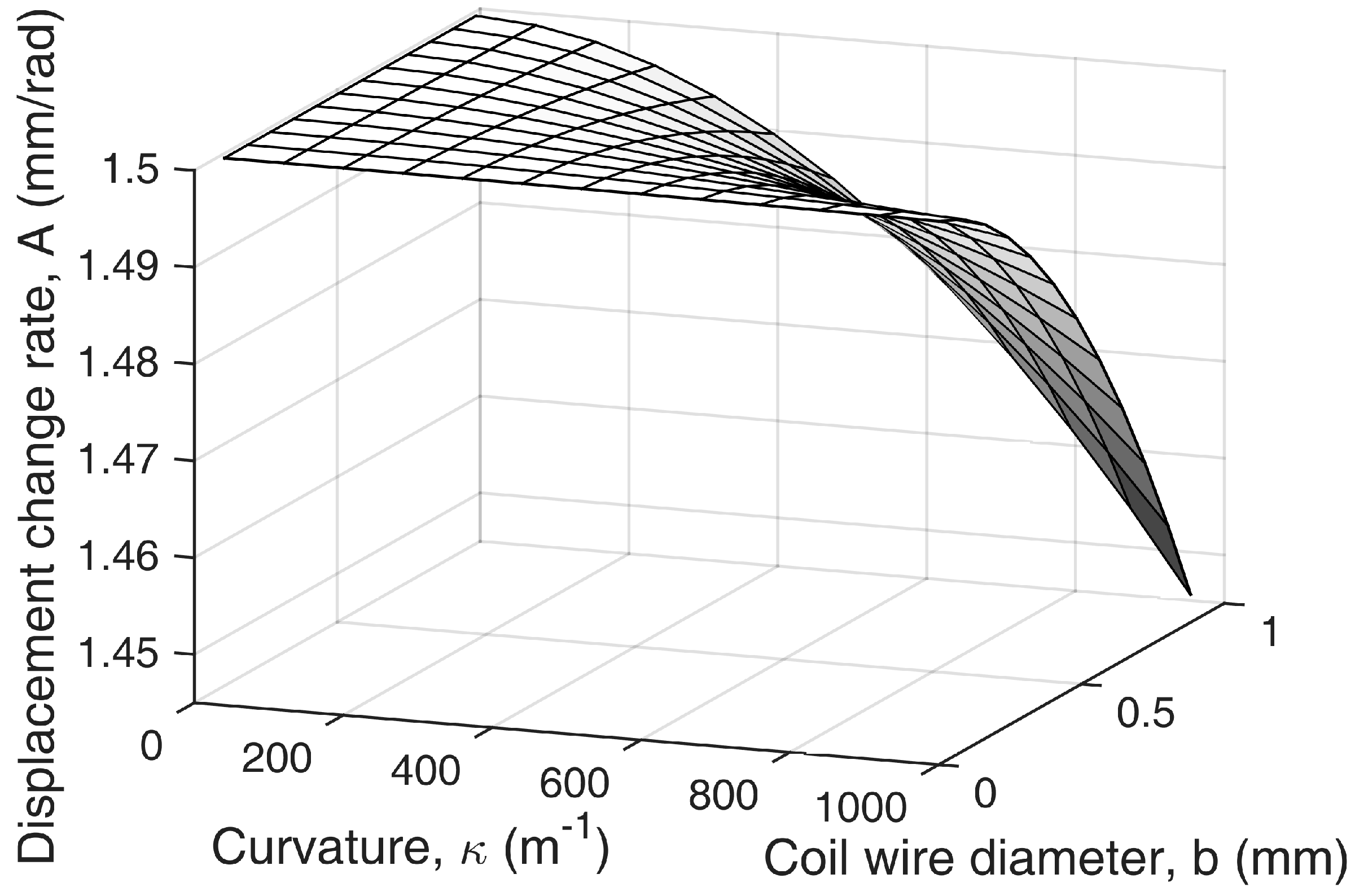
3.4. Sensor Gain
3.5. Axial Force Robustness
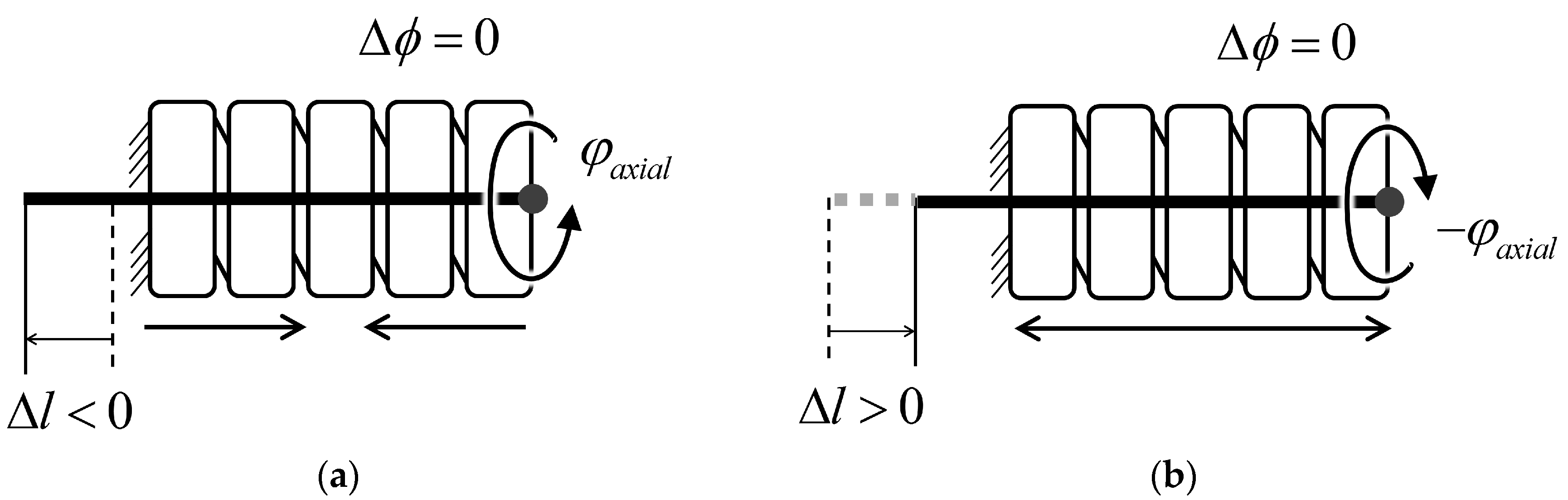
3.6. Axial Rotation Robustness
4. Characteristics of the Proposed Bend Sensor
- Low costThe proposed sensor is made of low-cost materials and can be manufactured easily without specialized fabrication techniques. The sensor can be assembled with off-the-shelf parts within 15 min.
- High degrees of freedom for the sensor’s dimensionsThe dimensions of the sensor are determined by the diameter and length of the helical coil. Thus the size of the sensor can be easily and finely adjusted because there is a wide range of choices for the diameter of the extension spring, and the spring can be cut to the desired size.
- Intuitive and easy to useThe principle of the proposed sensor is the mechanical conversion of information about bending to information about displacement of the sensing wire. Thus the measurand of the proposed sensor is the displacement of the sensing wire. Because there are various options for the displacement transducer, the user can select one based on their preferences. No complex signal processing or specialized data acquisition device is required because the measurement from the displacement transducer is proportional to the bend angle of the sensor.
- No directionalityThis sensor can detect bending in any direction because the helical coil’s shape and properties are symmetrical along the axial line. And because the sensing wire is placed in the center of the helical coil, the axial displacement of the sensing wire changes with bending in any direction along the helical coil.
- Measures the accumulated bend angleThis sensor cannot detect the direction of bending or the specific location where bending occurs because it only measures one-degree-of-freedom information, that is, central displacement changes of the coil. However, it can detect the accumulated bend angle along the sensor, as depicted in Figure 4, because any local bending along the helical coil causes a central displacement change along the sheath.
- Large sensing rangeThe sensor’s physical sensing range is restricted only by the maximum bend curvature of the helical coil that does not cause permanent strain on the sheath. Widely used extension springs made of spring steel or stainless steel have high elasticity and can enable large curvature of the sensor.
- Theoretical performanceThe theoretical performance of the sensor depends on the design parameters and performance of the sensor that is used to measure the displacement change of the sensing wire. The Hall-effect sensor provides high performance for both a linear and a rotary configuration. An incremental Hall-effect encoder with 8192 counts per resolution can provide 0.2° resolution for a bend sensor consisting of a 3-mm outer diameter helical coil and a 6-mm diameter spool. A potentiometer is an economical option that provides sufficient performance.
- Bend stiffnessThe bend stiffness of the sensor is determined by the stiffness of the helical coil and the tension of the sensing wire. A large spring constant and a large-diameter coil lead to high bend stiffness of the sensor because energy is required to elongate the spring coil, as shown in Figure 6. Also, greater tension in the sensing wire and a larger helical coil diameter contribute to the restoring force from the sensing wire, which increases the bend stiffness. Bend stiffness increases as the sensor bends if a spring is used to provide tension on the sensing wire. Because bend stiffness can be modeled as a function of design parameters, a bend stiffness profile can be adjusted by changing the radius of the spool and the constant of the linear spring. An actuator can be used as a tensioning device to provide more degrees of freedom for the stiffness profile or to allow variable sensor stiffness.
- Environmental robustnessThe absence of electronic components on the bending part ensures good robustness to environmental conditions. Stainless steel, Teflon, and aramid, which are used in the helical coil, liner, and sensing wires, respectively, have high chemical resistance and thermal resistance (the melting point of Teflon and aramid is 327 °C and 500 °C, respectively). Because the sensor is mechanically operated, it is immune to electromagnetic interference and moisture, allowing it to be used even when submerged in boiling water or high-temperature oil.
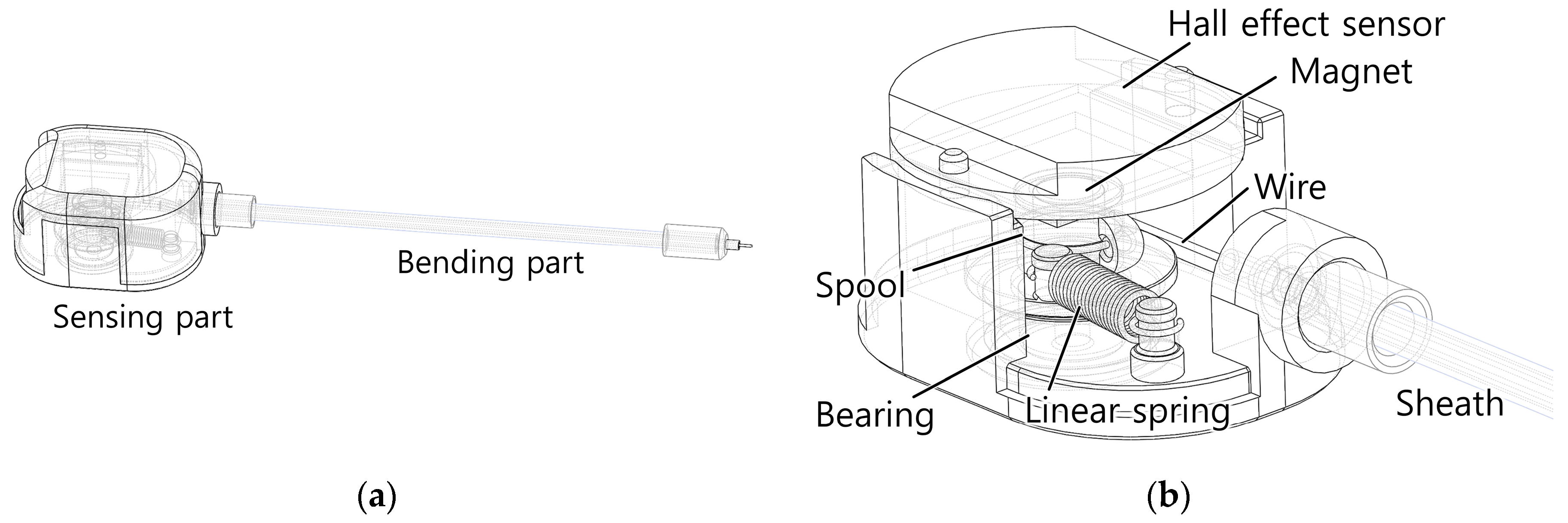
5. Prototype Development
6. Experiments
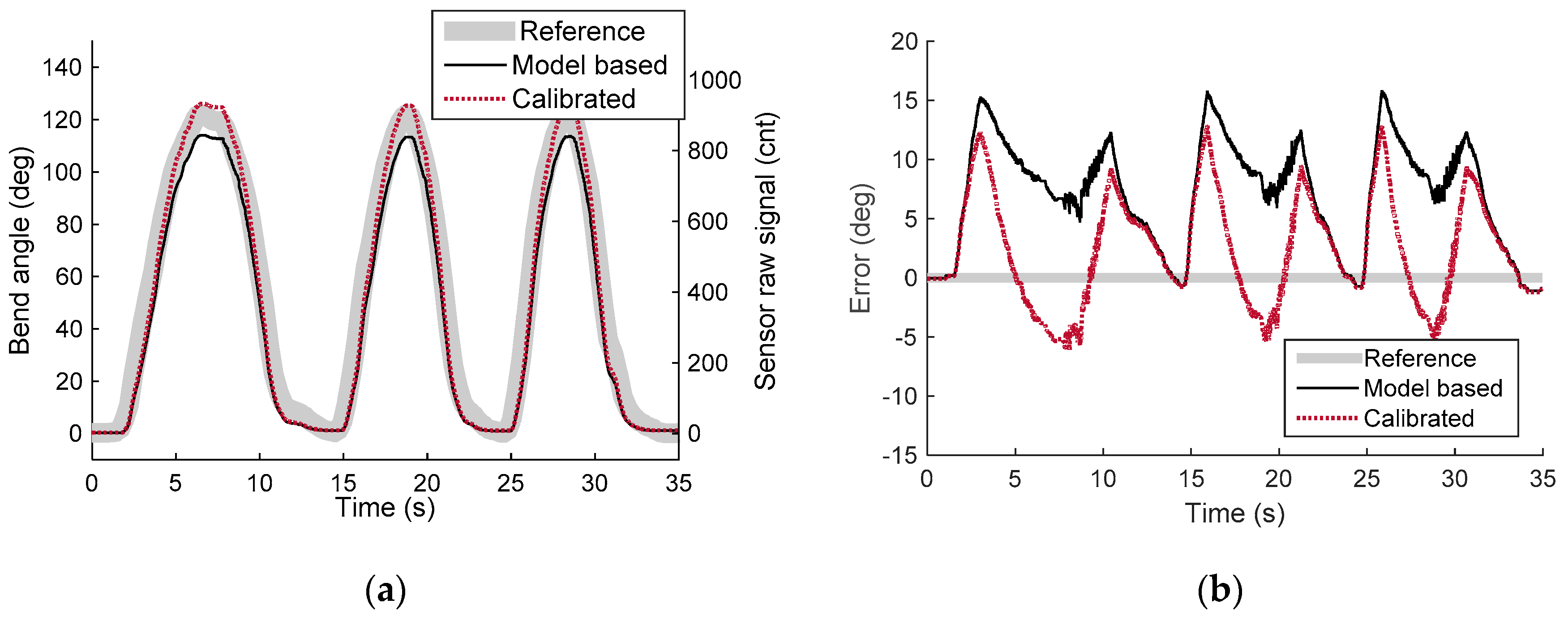
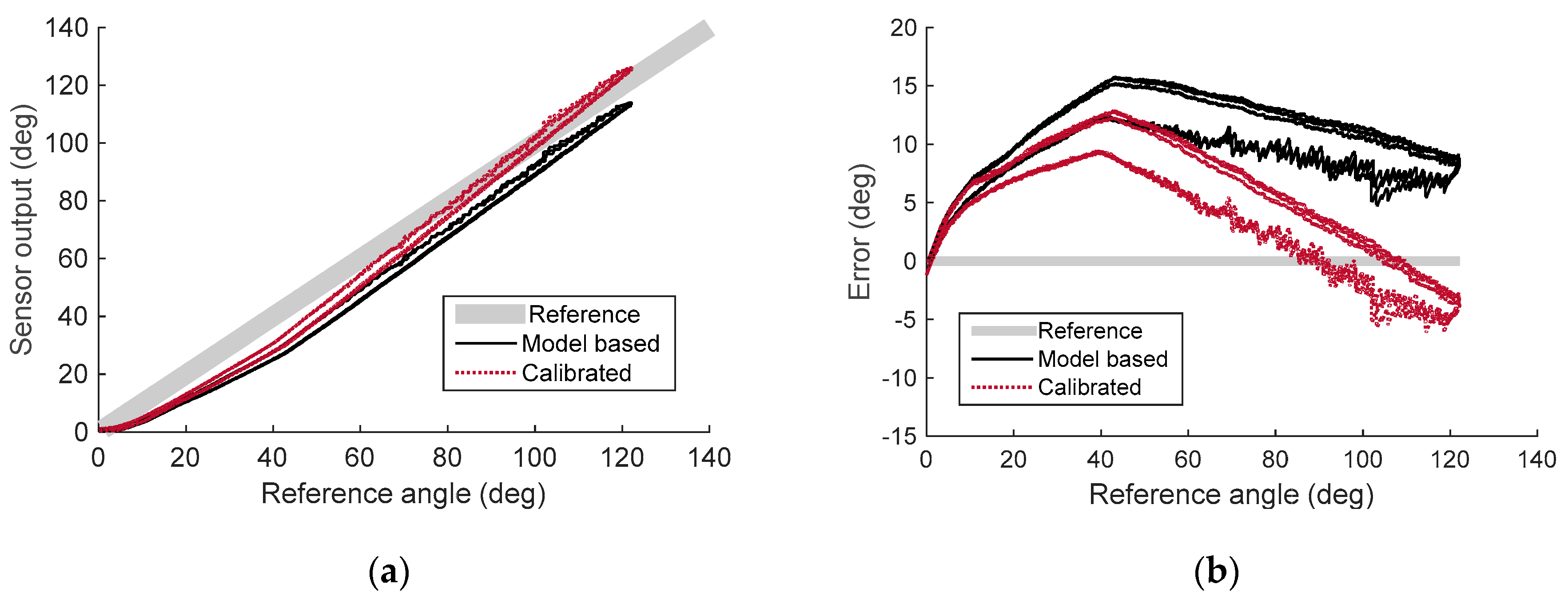
6.1. Quasi-Static Experiment
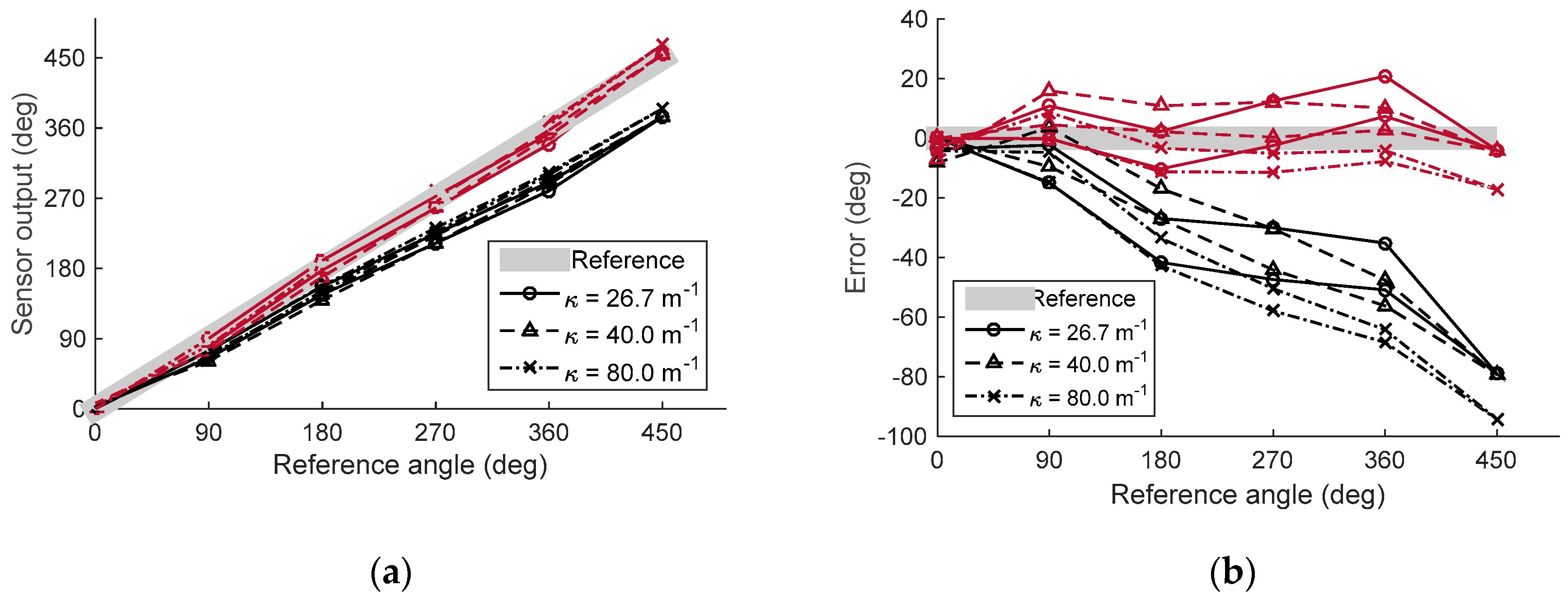
6.2. Static Large Deflection Experiment
7. Discussion
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Jurgens, J.; Patterson, P.E. Development and evaluation of an inexpensive sensor system for use in measuring relative finger positions. Med. Eng. Phys. 1997, 19, 1–6. [Google Scholar] [CrossRef]
- Mulder, A. How to build an instrumented glove based on the Powerglove flex sensors. PCVR Mag. 1994, 16, 10–14. [Google Scholar]
- Simone, L.K.; Kamper, D.G. Design considerations for a wearable monitor to measure finger posture. J. NeuroEng. Rehabil. 2005, 2. [Google Scholar] [CrossRef] [PubMed]
- Dunne, L.E.; Smyth, B.; Caulfield, B. A Comparative Evaluation of Bend Sensors for Wearable Applications. In Proceedings of the 11th IEEE International Symposium on Wearable Computers, Boston, MA, USA, 11–13 October 2007.
- Gentner, R.; Classen, J. Development and evaluation of a low-cost sensor glove for assessment of human finger movements in neurophysiological settings. J. Neurosci. Methods 2009, 178, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Sturman, D.J.; Zeltzer, D. A survey of glove-based input. IEEE Comput. Graph. Appl. 1994, 14, 30–39. [Google Scholar] [CrossRef]
- Zimmerman, T.G. Optical Flex Sensor. U.S. Patent 4 542 291, 17 September 1985. [Google Scholar]
- Harvill, Y.L.; Zimmerman, T.G.; Grimaud, J.J.G. Motion Sensor which Produces an Asymmetrical Signal in Response to Symmetrical Movement. U.S. Patent 5 097 252, 17 March 1992. [Google Scholar]
- Tognetti, A.; Lorussi, F.; Carbonaro, N.; de Rossi, D. Wearable Goniometer and Accelerometer Sensory Fusion for Knee Joint Angle Measurement in Daily Life. Sensors 2015, 15, 28435–28455. [Google Scholar] [CrossRef] [PubMed]
- Stoppa, M.; Chiolerio, A. Wearable Electronics and Smart Textiles: A Critical Review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.T.; Shen, C.L.; Tang, C.F.; Chang, S.H. A wearable yarn-based piezo-resistive sensor. Sens. Actuators A Phys. 2008, 141, 396–403. [Google Scholar] [CrossRef]
- Ponticelli, R.; Gonzalez de Santos, P. Full perimeter obstacle contact sensor based on flex sensors. Sens. Actuators A Phys. 2008, 147, 441–448. [Google Scholar] [CrossRef]
- Peng, W.; Tianhuai, D.; Feng, X. A novel flexible sensor for compression stress relaxation. In Proceedings of IEEE Sensors, Toronto, ON, Canada, 22–24 October 2003.
- Starck, J.R.; Murray, G.; Lawford, P.V.; Hose, D.R. An inexpensive sensor for measuring surface geometry. Med. Eng. Phys. 1999, 21, 725–729. [Google Scholar] [CrossRef]
- Gentile, C.T.; Wallace, M.; Avalon, T.D.; Goodman, S.; Fuller, R.; Hall, T. Angular displacement sensors. U.S. Patent 5 086 785, 11 Feburay 1992. [Google Scholar]
- Flex Sensor Manufacturers | Spectra Symbol. Available online: http://www.spectrasymbol.com/flex-sensor (accessed on 12 April 2016).
- Flexpoint Sensor Systems. Available online: http://www.flexpoint.com/ (accessed on 12 April 2016).
- Kure, K.; Kanda, T.; Suzumori, K.; Wakimoto, S. Flexible displacement sensor using injected conductive paste. Sens. Actuators A Phys. 2008, 143, 272–278. [Google Scholar] [CrossRef]
- Saggio, G. Electrical Resistance Profiling of Bend Sensors Adopted to Measure Spatial Arrangement of the Human Body. In Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies, Barcelona, Spain, 26–29 October 2011.
- Saggio, G. Mechanical model of flex sensors used to sense finger movements. Sens. Actuators A Phys. 2012, 185, 53–58. [Google Scholar] [CrossRef]
- Qi, Y.; Ma, L.; Sun, J.; Kang, Z.; Bai, Y.; Jian, S. Highly sensitive bending sensor based on multimode-multimode-coreoffset fiber structure. Opt. Laser Technol. 2015, 75, 52–56. [Google Scholar] [CrossRef]
- Kuang, K.S.C.; Cantwell, W.J.; Scully, P.J. An evaluation of a novel plastic optical fibre sensor for axial strain and bend measurements. Meas. Sci. Technol. 2002, 13, 1523–1534. [Google Scholar] [CrossRef]
- Liu, Y.; Williams, J.A.R.; Bennion, I. Optical bend sensor based on measurement of resonance mode splitting of long-period fiber grating. IEEE Photonics Technol. Lett. 2000, 12, 531–533. [Google Scholar] [CrossRef]
- Chen, S.; Tong, Z.; Zhao, Q.; Liu, Z.; Dong, X. A smart bending sensor with a novel temperature- and strain-insensitive long-period grating. Sens. Actuators A Phys. 2004, 116, 103–106. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, Y.; Shen, C.; Chu, J.; Zou, X.; Zhong, C.; Dong, X. Novel bending sensor based on a meniscus shaped beam with LPG. Opt. Int. J. Light Electron. Opt. 2013, 124, 6737–6739. [Google Scholar] [CrossRef]
- Taghipour, A.; Rostami, A.; Bahrami, M.; Baghban, H.; Dolatyari, M. Comparative study between LPFG- and FBG-based bending sensors. Opt. Commun. 2014, 312, 99–105. [Google Scholar] [CrossRef]
- Miao, Y.; Zhang, K.; Liu, B.; Lin, W.; Yao, J. Characteristics of bend sensor based on two-notch Mach-Zehnder fiber interferometer. Opt. Fiber Technol. 2012, 18, 509–512. [Google Scholar] [CrossRef]
- In, H.; Kang, B.B.; Sin, M.; Cho, K.J. Exo-Glove: A Wearable Robot for the Hand with a Soft Tendon Routing System. IEEE Robot. Autom. Mag. 2015, 22, 97–105. [Google Scholar] [CrossRef]
- Jeong, U.; In, H.-K.; Cho, K.-J. Implementation of various control algorithms for hand rehabilitation exercise using wearable robotic hand. Intell. Serv. Robot. 2013, 6, 181–189. [Google Scholar] [CrossRef]
- Veneman, J.F.; Kruidhof, R.; Hekman, E.E.G.; Ekkelenkamp, R.; Asseldonk, E.H.F.V.; Van Der Kooij, H. Design and Evaluation of the LOPES Exoskeleton Robot for Interactive Gait Rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Galiana, I.; Asbeck, A.; Quinlivan, B.; De Rossi, S.M.M.; Walsh, C. Multi-joint actuation platform for lower extremity soft exosuits. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hongkong, China, 31 May–7 June 2014.
- Phee, S.J.; Low, S.C.; Dario, P.; Menciassi, A. Tendon sheath analysis for estimation of distal end force and elongation for sensorless distal end. Robotica 2010, 28, 1073–1082. [Google Scholar] [CrossRef]
- Bardou, B.; Nageotte, F.; Zanne, P.; Mathelin, M. Improvements in the control of a flexible endoscopic system. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 3725–3732.
- Do, T.N.; Tjahjowidodo, T.; Lau, M.W.S.; Phee, S.J. Adaptive control of position compensation for Cable-Conduit Mechanisms used in flexible surgical robots. In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Vienna, Austria, 1–3 September 2014; pp. 110–117.
- Kesner, S.B.; Howe, R.D. Robotic catheter cardiac ablation combining ultrasound guidance and force control. Int. J. Robot. Res. 2014, 33, 631–644. [Google Scholar] [CrossRef]
- Jeong, U.; Cho, K.J. Feedforward friction compensation of Bowden-cable transmission via loop routing. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5948–5953.
- Dyneema Comprehensive Factsheet. Available online: http://www.pelicanrope.com/pdfs/Dyneema-Comprehensive-factsheet-UHMWPE.pdf (accessed on 9 June 2016).
- Carlson, L.E.; Veatch, B.D.; Frey, D.D. Efficiency of Prosthetic Cable and Housing. J. Prosthet. Orthot. 1995, 7, 96–99. [Google Scholar]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Kim, W.B.; Choi, W.Y.; Cho, K.J. Development of a Modularized Design Concept for Soft Robotics: Introducing SoBL, a Soft Robotic Block. IEEE Robot. Autom. Mag. 2016, 23. in press. [Google Scholar]
- Knuth, D.E. Two notes on notation. Am. Math. Mon. 1992, 99, 403–422. [Google Scholar] [CrossRef]
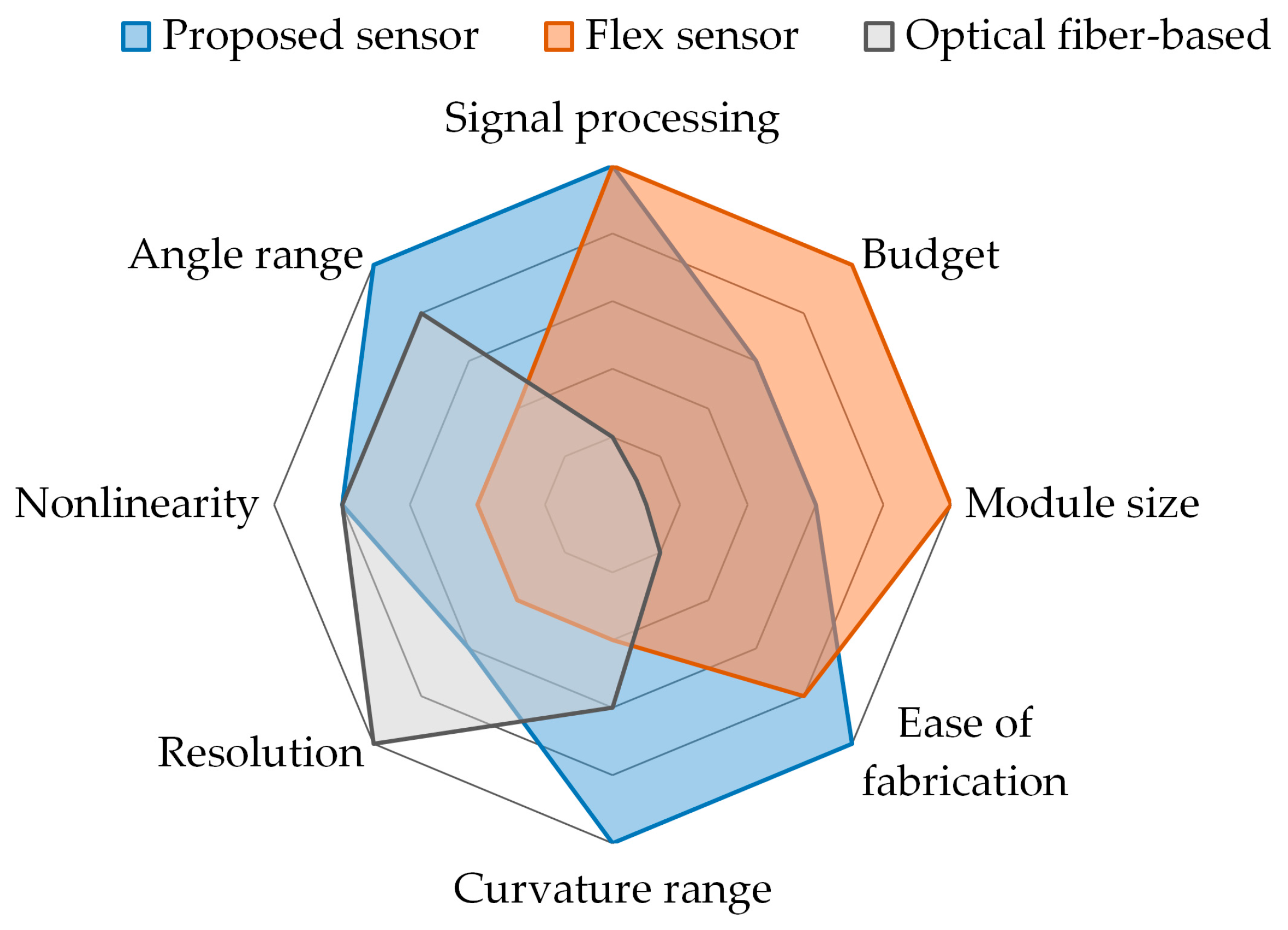



| Property | Proposed Sensor | Flex Sensor | Optical Fiber-Based Sensor |
|---|---|---|---|
| Size | Thin | Wide | Very thin |
| Length | Unlimited 1 | Fixed | Unlimited 1 |
| Measurand | Position | Electrical resistance | Light 2 |
| Module size 3 | Medium | Compact | Large |
| Signal processing | Simple | Simple | Complicated |
| Fabrication | Simple | Off the shelf | Complicated |
| Cost 4 | Cheap | Cheap | Expensive |
| Directionality | Any-direction | Uni-/bi-direction | Any-direction |
| Curvature range | Wide | Narrow | Restricted |
| Stiffness 5 | Adjustable | Fixed | Depends on fiber |
| Nonlinearity | Low | High | High |
| Resolution 6 | High | Low | High |
| Component | Specification | Price |
|---|---|---|
| Helical coil | Extension spring: Φ3.0 mm × Φ2.0 mm × 500 mm | $1 |
| Lining | Outer Teflon tube: Φ1.38 mm × Φ1.88 mm; Inner Teflon tube: Φ1.40 mm × Φ0.90 mm | $0.2 |
| Wire | Braided Dyneema wire: Φ0.45 mm | $0.1 |
| Structure | 3D printed with VeroWhitePlus™ (Objet Connex; Stratasys Ltd., Eden Prairie, MN, USA) | $1 |
| Spring | Miniature extension spring | $0.3 |
| Displacement sensor | Hall-effect sensor: RMB20IC13BC10 (RLS; 8192 pulses per turn, ±0.5° accuracy, 0.18° hysteresis, onboard RC filter with 720 Hz cut-off frequency for sine and cosine signal of magnetic flux); Magnet: Φ4 mm × 4 mm | $50 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, U.; Cho, K.-J. A Novel Low-Cost, Large Curvature Bend Sensor Based on a Bowden-Cable. Sensors 2016, 16, 961. https://doi.org/10.3390/s16070961
Jeong U, Cho K-J. A Novel Low-Cost, Large Curvature Bend Sensor Based on a Bowden-Cable. Sensors. 2016; 16(7):961. https://doi.org/10.3390/s16070961
Chicago/Turabian StyleJeong, Useok, and Kyu-Jin Cho. 2016. "A Novel Low-Cost, Large Curvature Bend Sensor Based on a Bowden-Cable" Sensors 16, no. 7: 961. https://doi.org/10.3390/s16070961
APA StyleJeong, U., & Cho, K.-J. (2016). A Novel Low-Cost, Large Curvature Bend Sensor Based on a Bowden-Cable. Sensors, 16(7), 961. https://doi.org/10.3390/s16070961