Vibration Sensitivity Reduction of Micromachined Tuning Fork Gyroscopes through Stiffness Match Method with Negative Electrostatic Spring Effect
Abstract
:1. Introduction
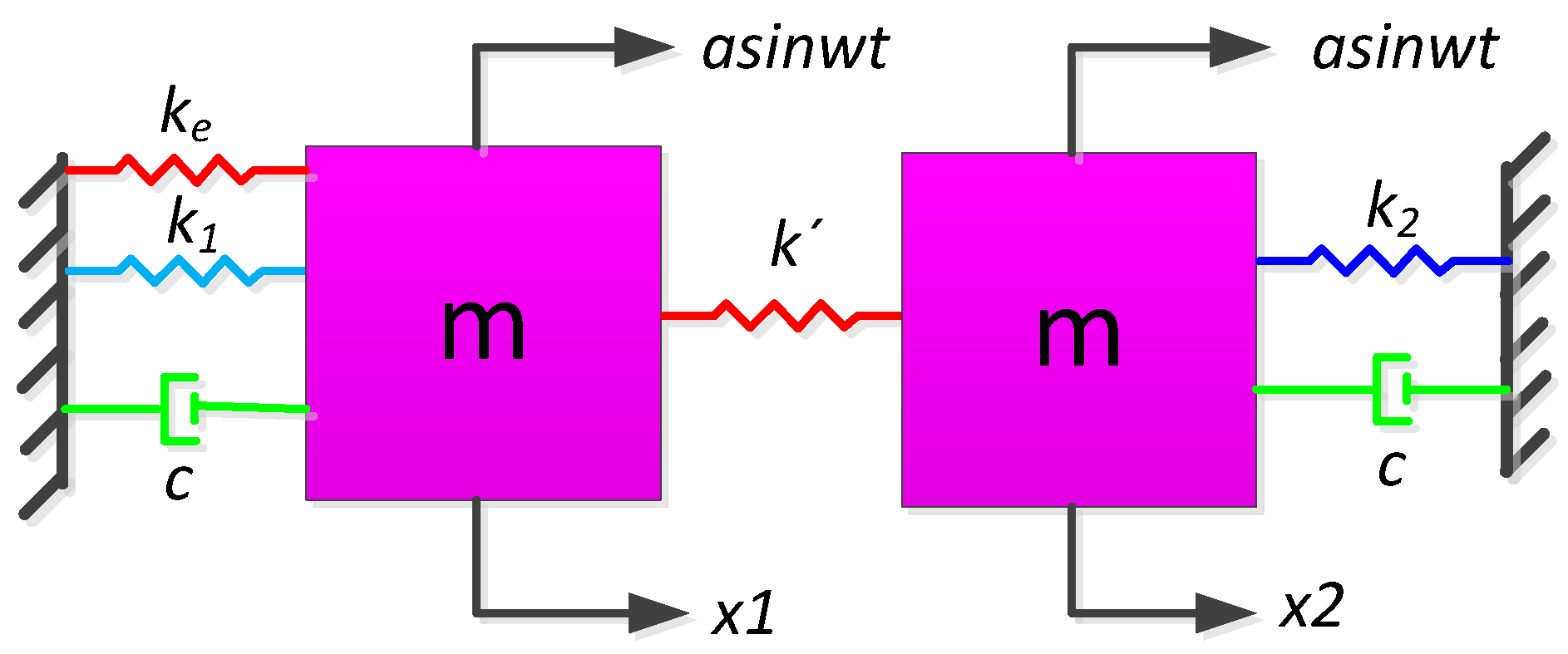
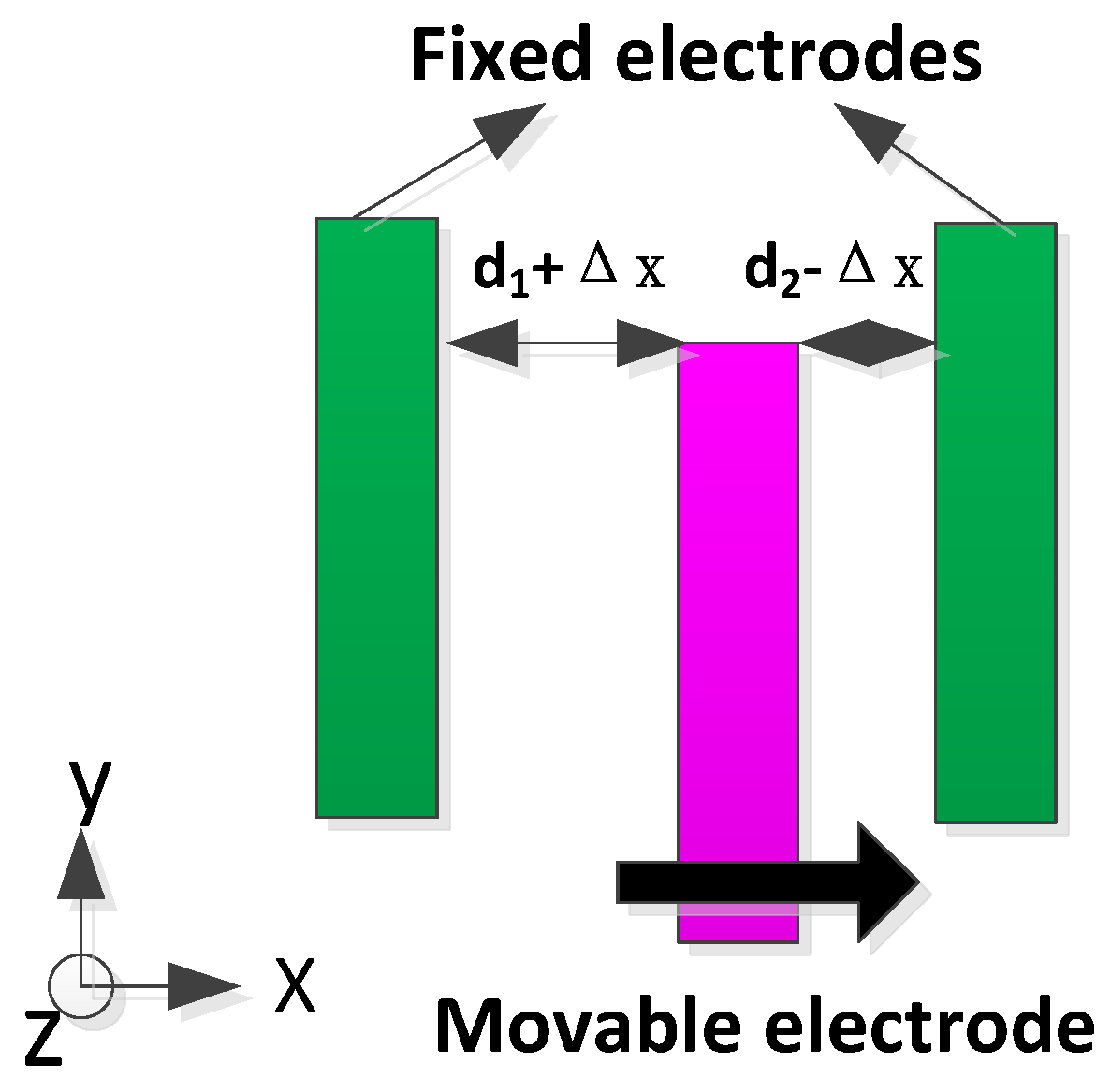
2. Theoretical Analysis of Stiffness Match Method
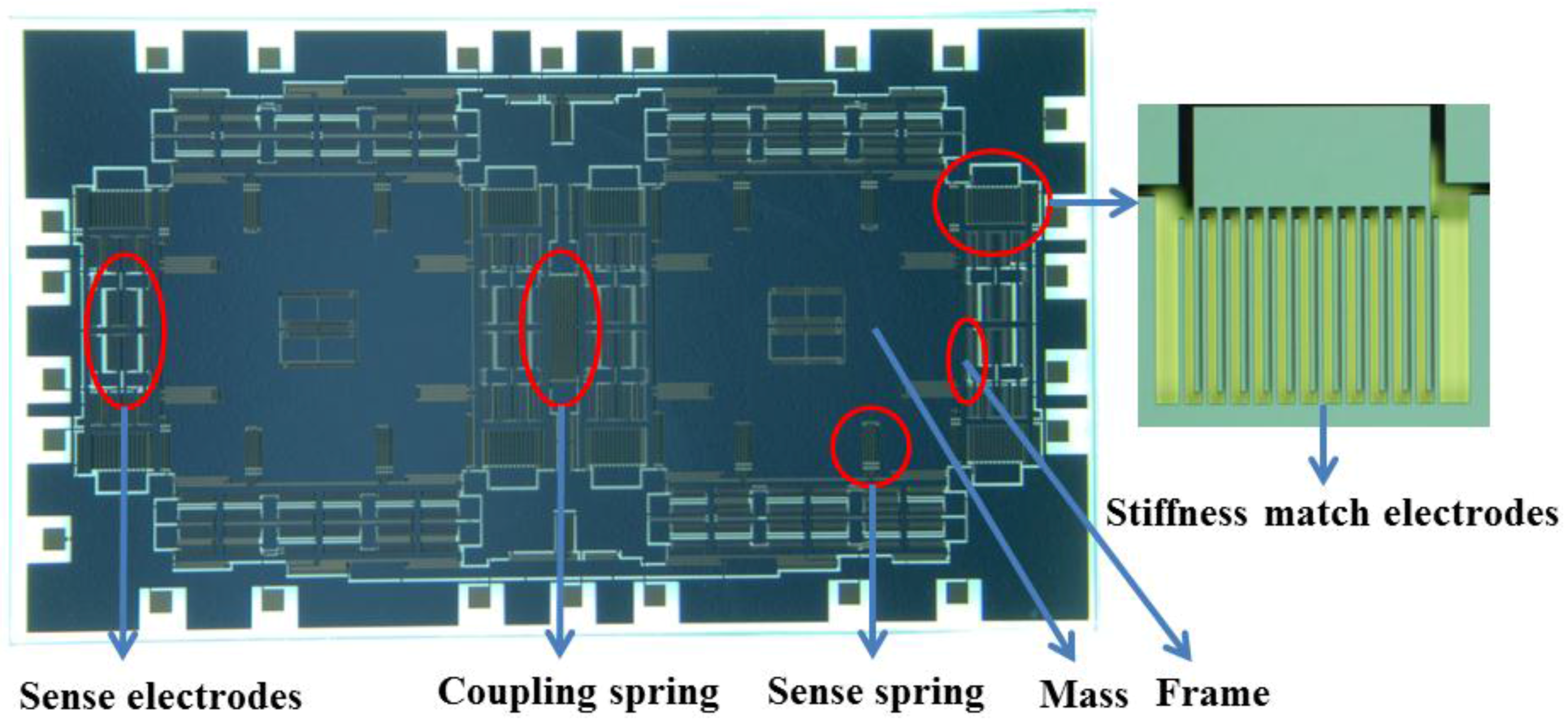
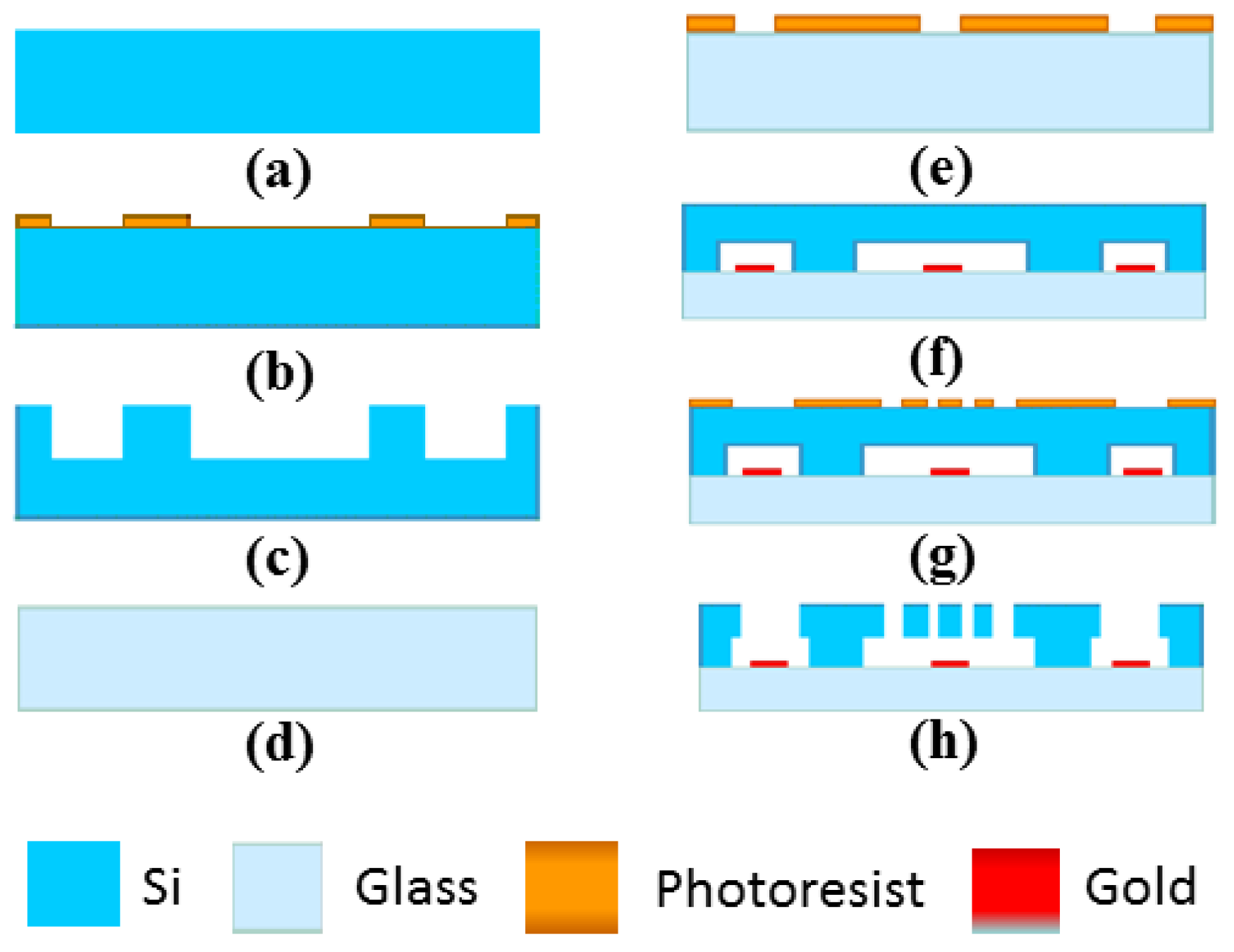
3. Design and Fabrication
4. Experimental Study and Comparison with Theoretical Model
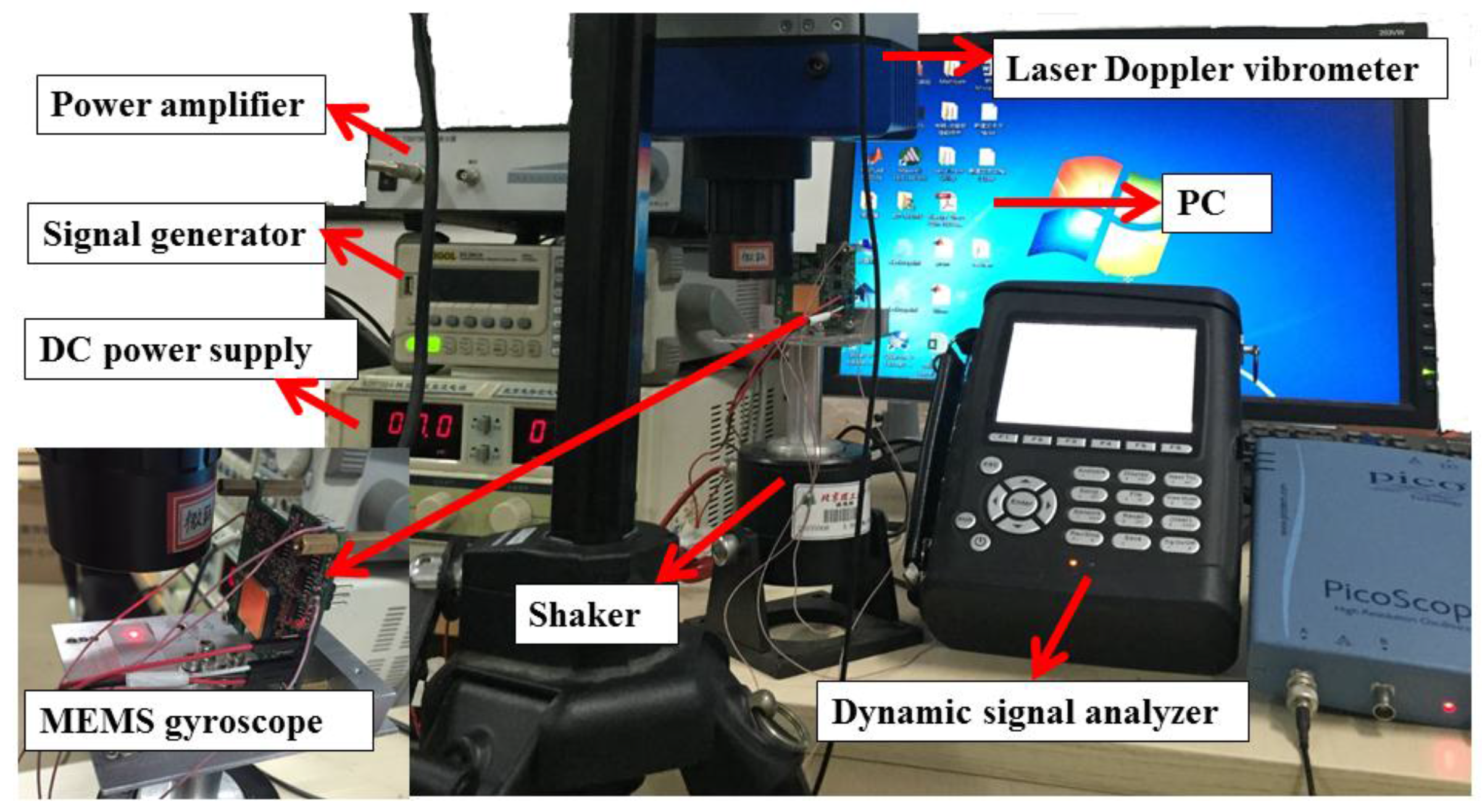
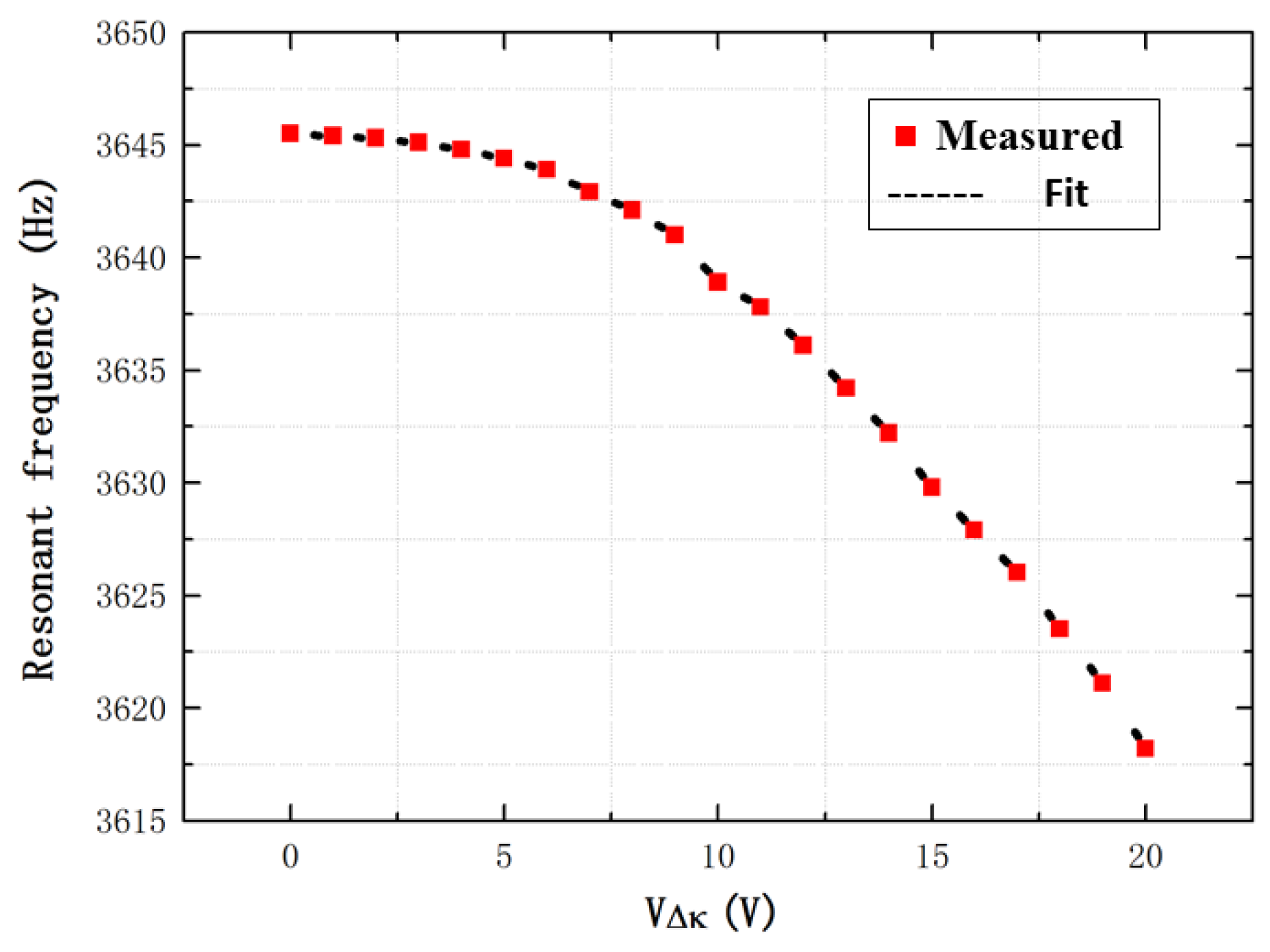
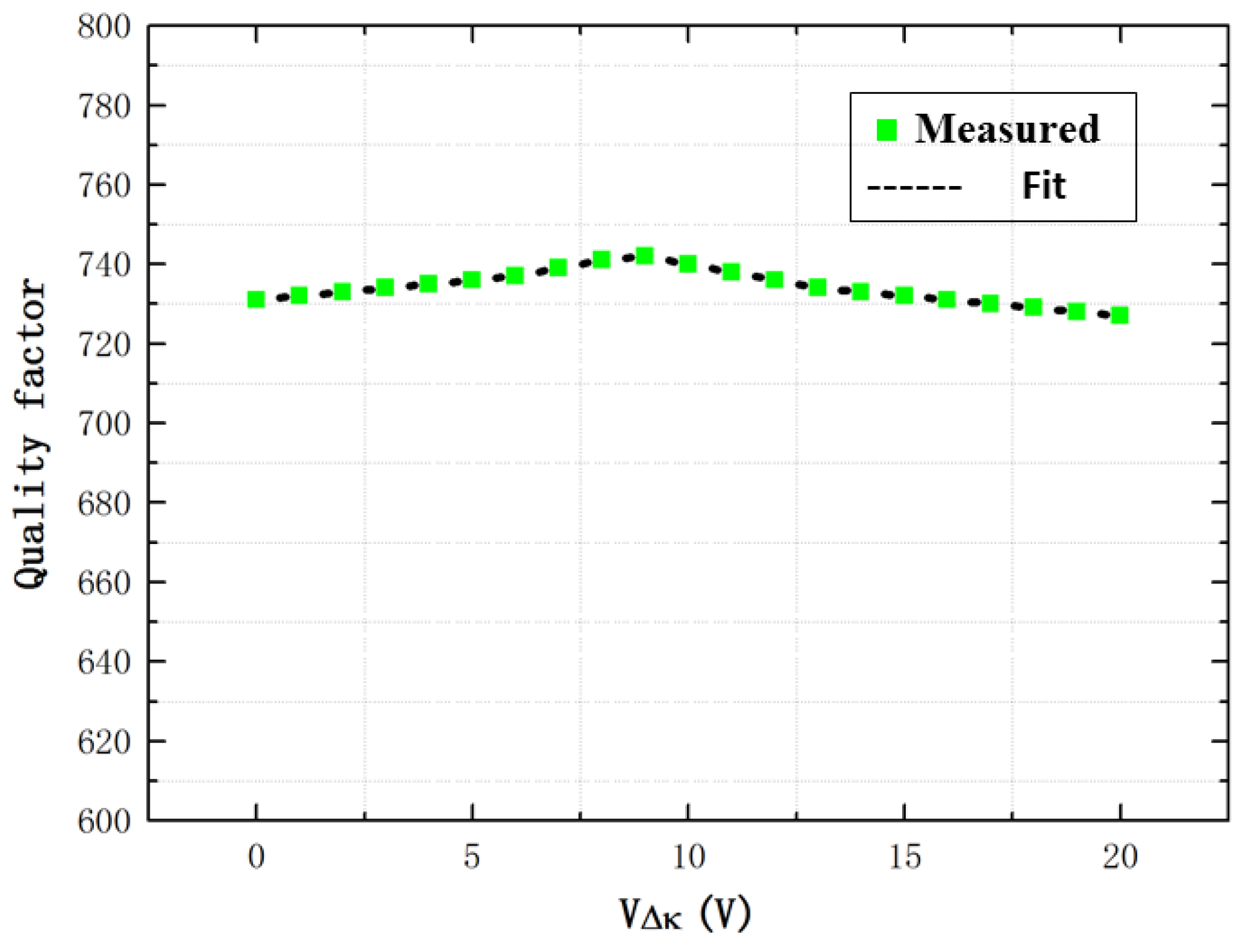
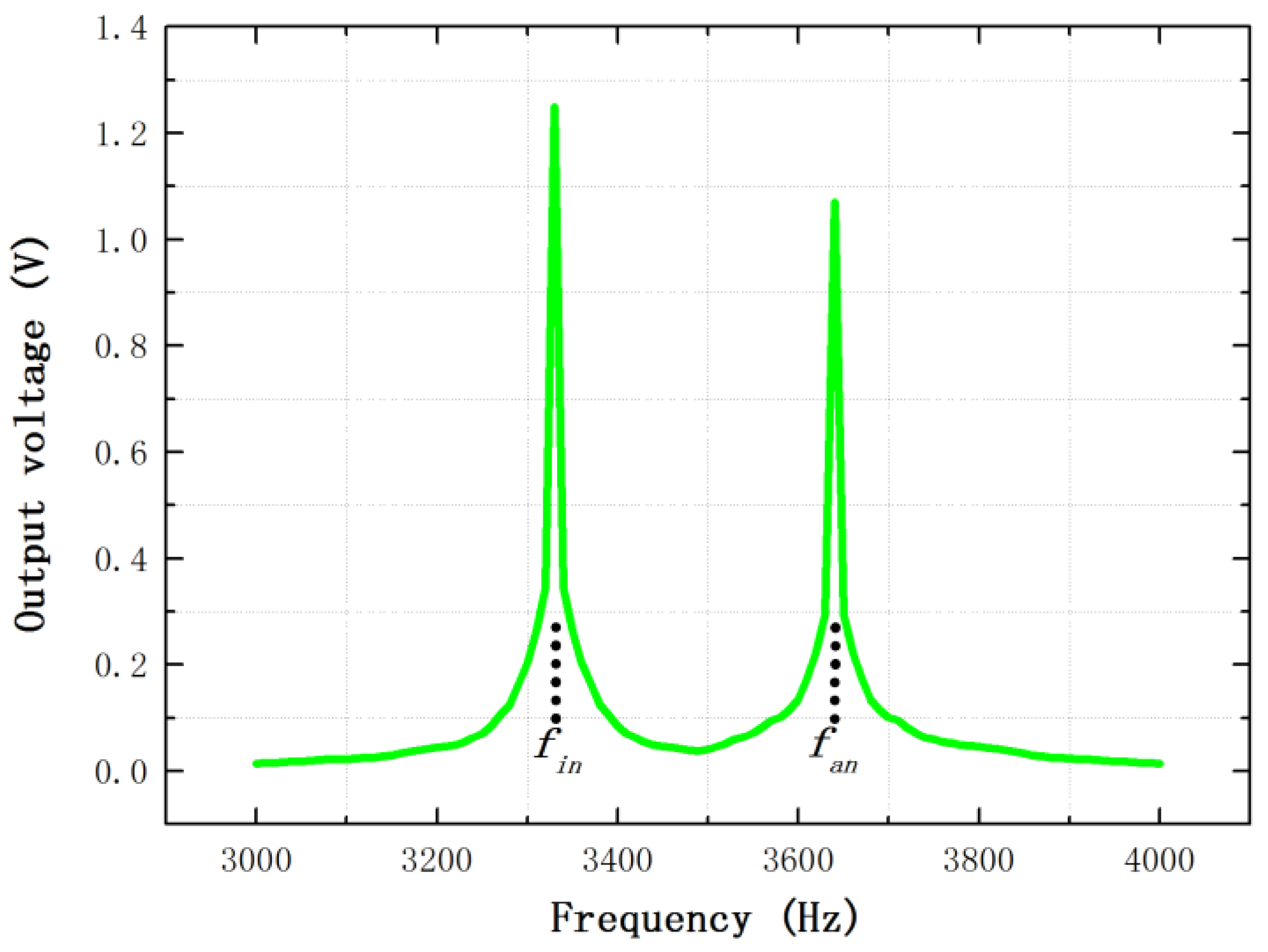
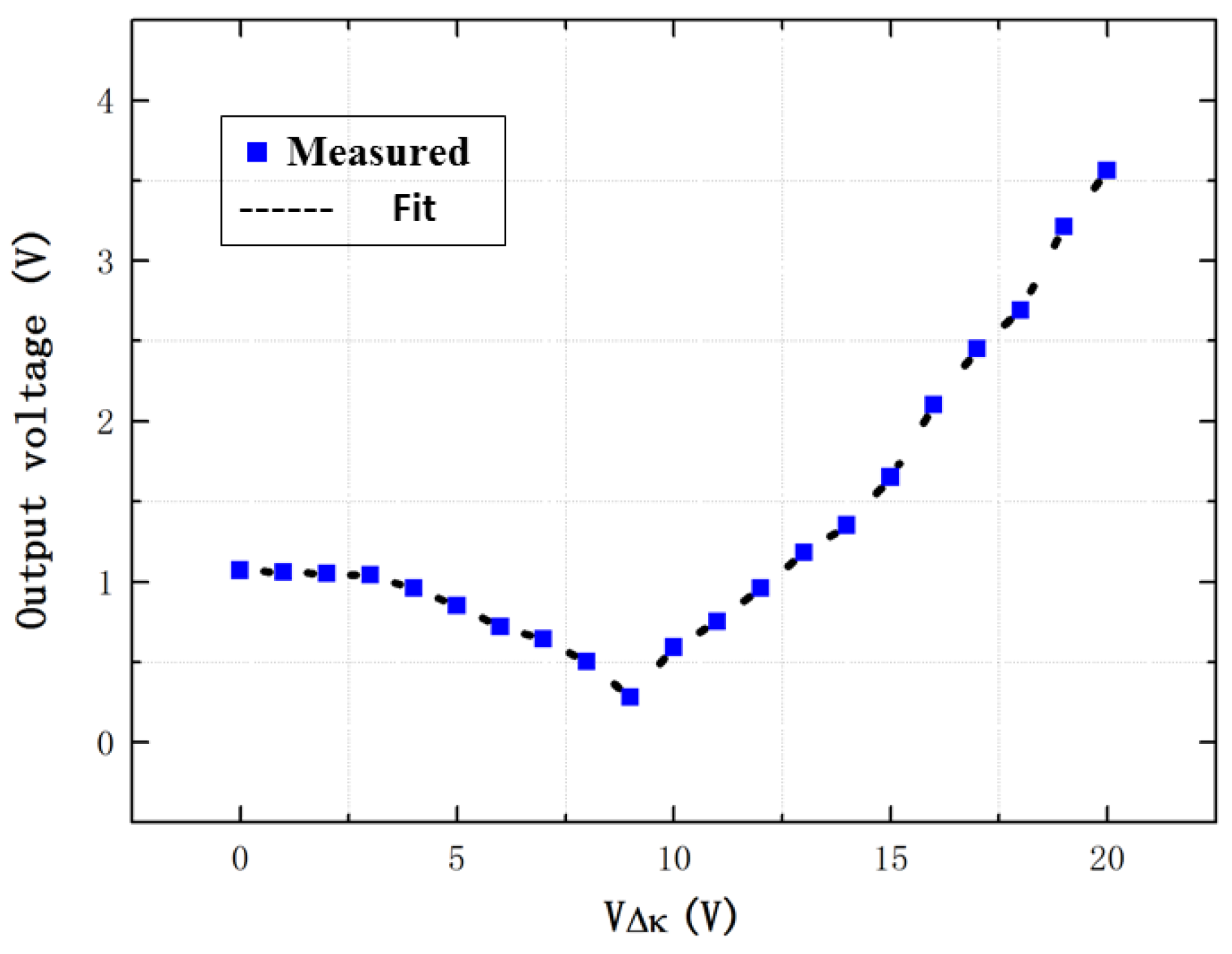
4.1. Experimental Study
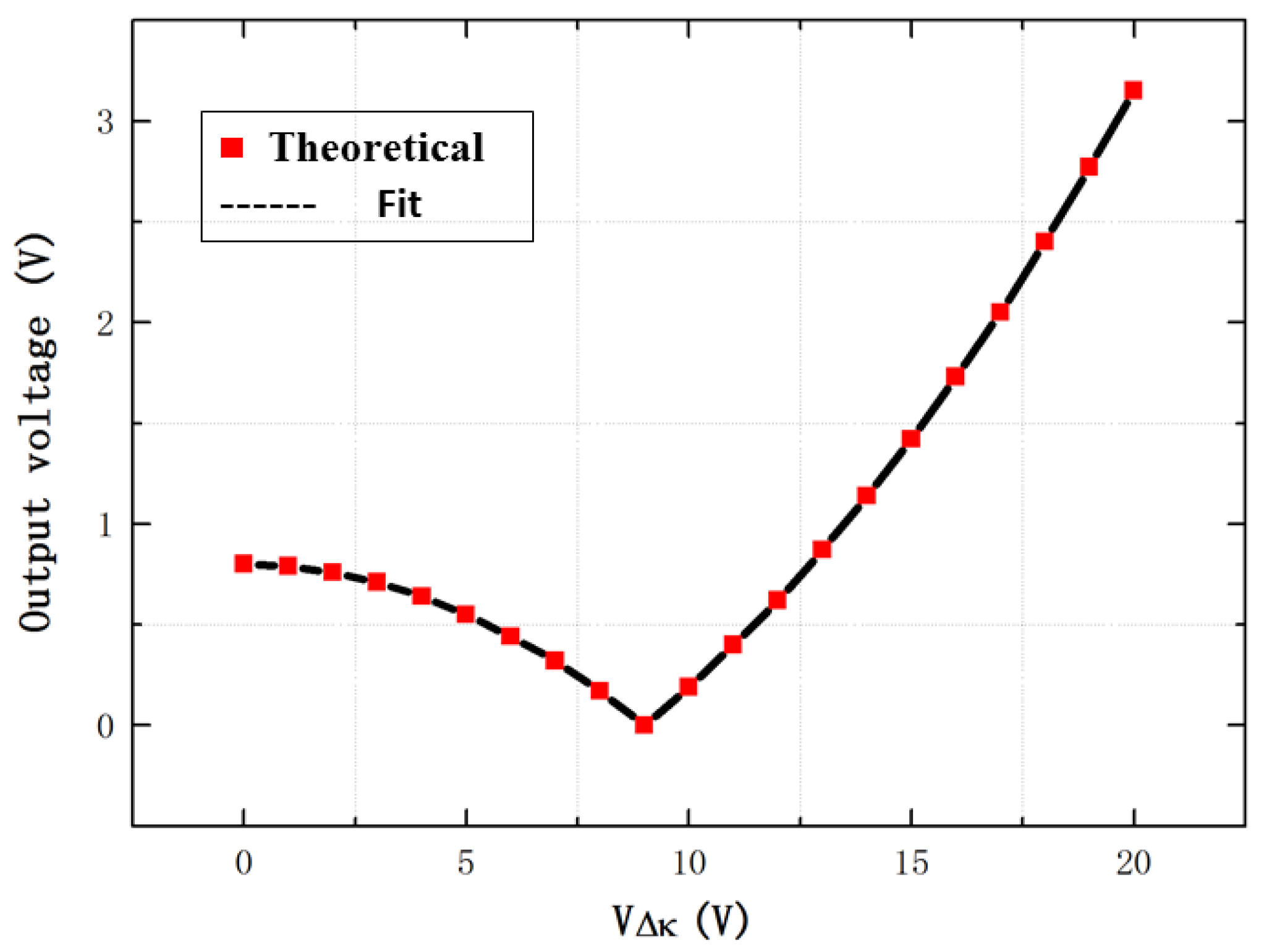
4.2. Theoretical Calculation
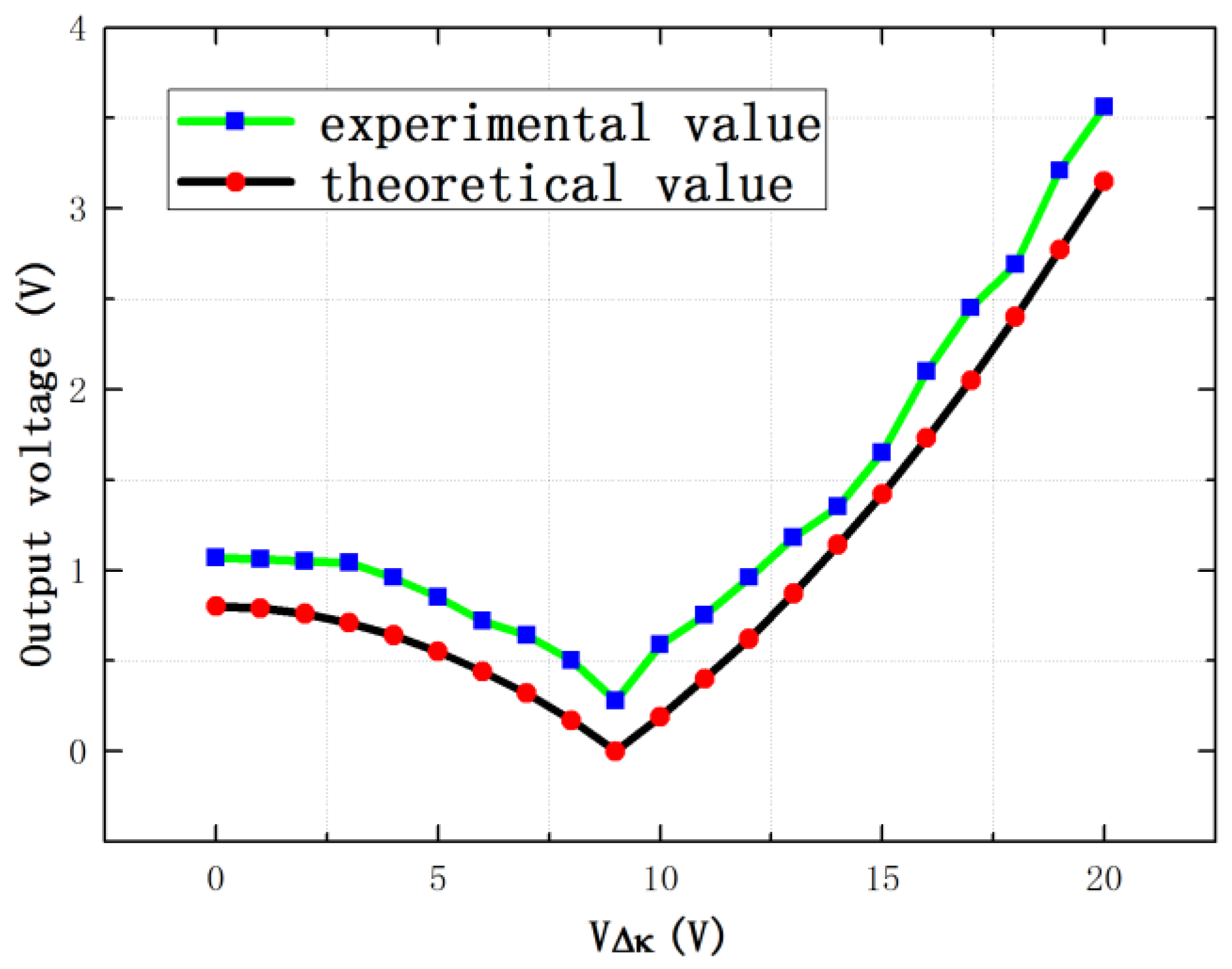
4.3. Experimental and Theoretical Comparisons
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shkel, A.M. Type I and type II micromachined vibratory gyroscopes. In Proceedings of the IEEE PLANS, Position Location and Navigation Symposium, San Diego, CA, USA, 25–27 April 2006; pp. 586–593.
- Sharma, A.; Zaman, M.F.; Ayazi, F. A sub-0.2 °/h bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching. IEEE J. Solid State Circuits 2009, 44, 1593–1608. [Google Scholar] [CrossRef]
- Zotov, S.A.; Trusov, A.A.; Shkel, A.M. High-range angular rate sensor based on mechanical frequency modulation. J. Microelectromech. Syst. 2012, 21, 398–405. [Google Scholar] [CrossRef]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration-induced errors in MEMS tuning fork gyroscopes. Sens. Actuator A Phys. 2012, 180, 32–44. [Google Scholar] [CrossRef]
- Wang, W.; Lv, X.Y.; Sun, F. Design of a novel MEMS gyroscope array. Sensors 2013, 13, 1651–1663. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.Z.; Yu, C.; Kong, L. The development of micromachiend gyroscope structure and circuitry technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed]
- Zaman, M.F.; Sharma, A.; Hao, Z.L.; Ayazi, F.A. A mode-matched silicon-yaw tuning-fork gyroscope with subdegree-per-hour Allan deviation bias instability. J. Microelectromech. Syst. 2008, 17, 1526–1536. [Google Scholar] [CrossRef]
- Yoon, S.W.; Lee, S.; Najafi, K. Vibration sensitivity analysis of MEMS vibratory ring gyroscopes. Sens. Actuator A Phys. 2012, 171, 163–177. [Google Scholar] [CrossRef]
- Senkal, D.; Askari, S.; Ahamed, M.J.; Ng, E.J.; Hong, V.; Yang, Y.; Ahn, C.H.; Kenny, T.W.; Shkel, A.M. 100k Q-factor toroidal ring gyroscope implemented in wafer-level epitaxial silicon encapsulation process. In Proceedings of the IEEE MEMS, San Francisco, CA, USA, 26–30 January 2014; pp. 24–27.
- Xie, H.K.; Fedder, G.K. Fabrication, characterization, and analysis of a DRIE CMOS-MEMS gyroscope. IEEE Sens. J. 2003, 3, 622–631. [Google Scholar]
- Zaman, M.F.; Sharma, A.; Amini, B.; Ayazi, F.A. Towards inertial grade vibratory microgyros: A high-Q in-plane silicon-on-insulator tuning fork device. In Proceedings of the Solid-State Sensor, Actuator and Microsystems Workshop, Hilton Head Island, SC, USA, 6–10 June 2004; pp. 384–385.
- Azgin, K.; Temiz, Y.; Akin, T. An SOI-MEMS tuning fork gyroscope with linearly coupled drive mechanism. In Proceedings of the IEEE 20th International Conference on Micro Electro Mechanical Systems, Kobe, Japan, 21–25 January 2007; pp. 607–610.
- Ding, X.K.; Li, H.S.; Ni, Y.F.; Sang, P.C. Analysis of frequency response and scale-factor of tuning fork micro-gyroscope operating at atmospheric pressure. Sensors 2015, 15, 2453–2472. [Google Scholar] [CrossRef] [PubMed]
- Trusov, A.A.; Schofield, A.R.; Shkel, A.M. Micromachined rate gyroscope architecture with ultra-high quality factor and improved mode ordering. Sens. Actuators A Phys. 2011, 165, 26–34. [Google Scholar] [CrossRef]
- Singh, T.P.; Sugano, K.; Tsuchiya, T.; Tabata, O. Experimental verification of frequency decoupling effect on acceleration sensitivity in tuning fork gyroscopes using in-plane coupled resonators. Microsyst. Technol. 2013, 20, 403–411. [Google Scholar]
- Guan, Y.W.; Gao, S.Q.; Liu, H.P.; Niu, S.H. Acceleration sensitivity of tuning fork gyroscopes: Theoretical model, simulation and experimental verification. Microsyst. Technol. 2015, 21, 1313–1323. [Google Scholar] [CrossRef]
- Simon, B.R.; Trusov, A.A.; Shkel, A.M. Anti-phase mode isolation in tuning-fork MEMS using a lever coupling design. In Proceedings of the 2012 IEEE Sensors, Taipei, Taiwan, 28–31 October 2012; pp. 42–45.
- Guan, Y.W.; Gao, S.Q.; Jin, L.; Cao, L.M. Design and vibration sensitivity of a MEMS tuning fork gyroscope with anchored coupling mechanism. Microsyst. Technol. 2016, 22, 247–254. [Google Scholar] [CrossRef]
- Guan, Y.W.; Gao, S.Q.; Liu, H.P.; Jin, L.; Niu, S.H. Design and Vibration Sensitivity Analysis of a MEMS Tuning Fork Gyroscope with an Anchored Diamond Coupling Mechanism. Sensors 2016, 16, 468. [Google Scholar] [CrossRef] [PubMed]
- Trusov, A.A.; Zotov, S.A.; Shkel, A.M. Electrostatic regulation of quality factor in non-ideal tuning fork MEMS. In Proceedings of the 2011 IEEE Sensors, Limerick, Ireland, 28–31 October 2011; pp. 20–23.

| Parameters | Value | Parameters | Value |
|---|---|---|---|
| Sense-mode mass | 1.3951 × 10−6 kg | Structural thickness | 80 µm |
| Mismatch stiffness | 8.1 N/m | Sense-mode Q | 740 |
| Springs stiffness k2 | 607 N/m | Common acceleration | 9.8 m/s2 |
| Stiffness mismatch | 1.33% | Coupling stiffness | 60 N/m |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, Y.; Gao, S.; Liu, H.; Jin, L.; Zhang, Y. Vibration Sensitivity Reduction of Micromachined Tuning Fork Gyroscopes through Stiffness Match Method with Negative Electrostatic Spring Effect. Sensors 2016, 16, 1146. https://doi.org/10.3390/s16071146
Guan Y, Gao S, Liu H, Jin L, Zhang Y. Vibration Sensitivity Reduction of Micromachined Tuning Fork Gyroscopes through Stiffness Match Method with Negative Electrostatic Spring Effect. Sensors. 2016; 16(7):1146. https://doi.org/10.3390/s16071146
Chicago/Turabian StyleGuan, Yanwei, Shiqiao Gao, Haipeng Liu, Lei Jin, and Yaping Zhang. 2016. "Vibration Sensitivity Reduction of Micromachined Tuning Fork Gyroscopes through Stiffness Match Method with Negative Electrostatic Spring Effect" Sensors 16, no. 7: 1146. https://doi.org/10.3390/s16071146
APA StyleGuan, Y., Gao, S., Liu, H., Jin, L., & Zhang, Y. (2016). Vibration Sensitivity Reduction of Micromachined Tuning Fork Gyroscopes through Stiffness Match Method with Negative Electrostatic Spring Effect. Sensors, 16(7), 1146. https://doi.org/10.3390/s16071146







