Beamforming Based Full-Duplex for Millimeter-Wave Communication
Abstract
:1. Introduction
| Expectation operation. | |
| Absolute value of scalar variable x. | |
| 2-norm of vector . | |
| Inner product, equals to . | |
| Optimal value of variable . |
2. System Model and Problem Formulation
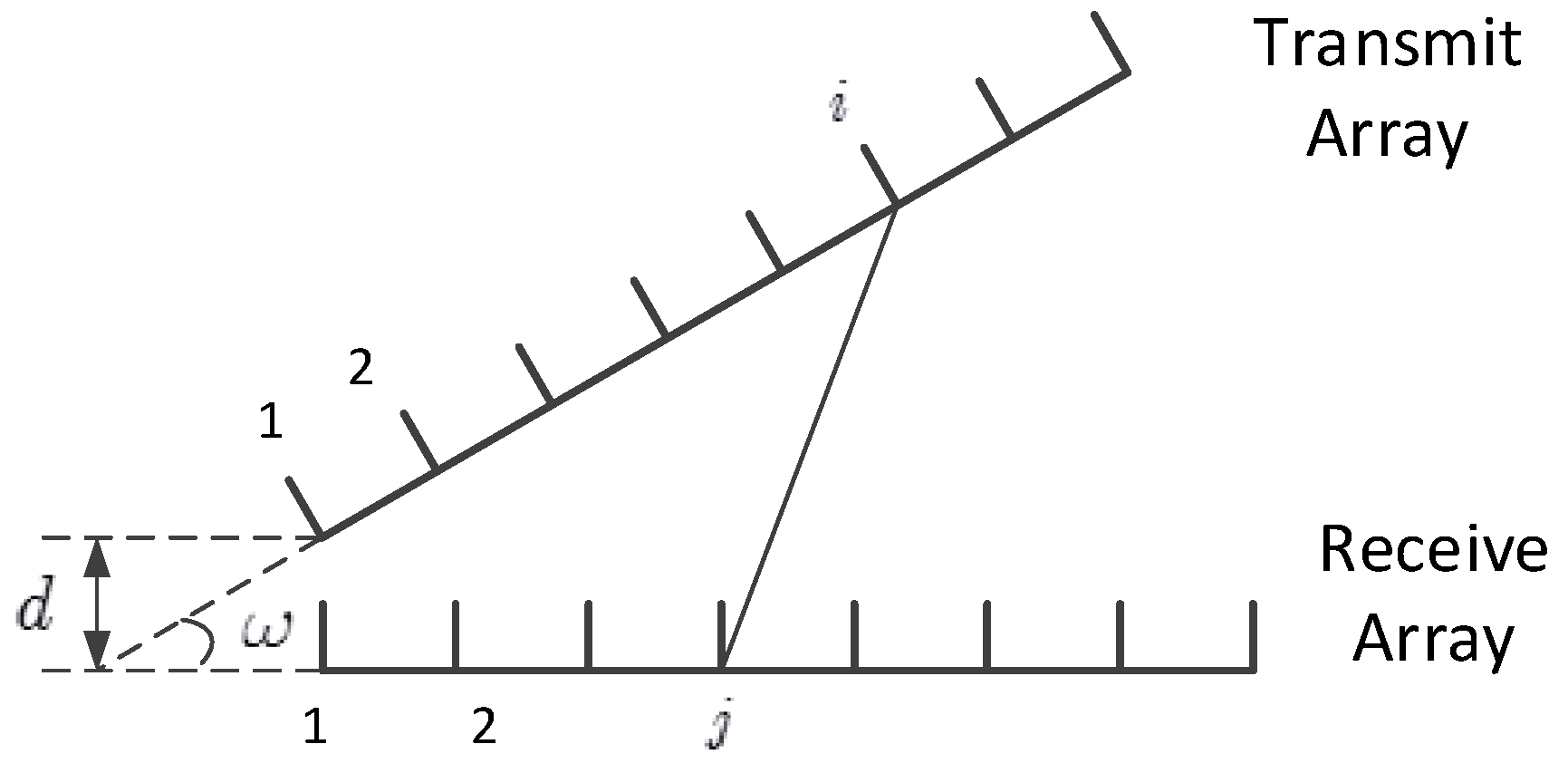
2.1. System Model
2.2. Channel Model
2.2.1. Communication Channel
2.2.2. SI Channel
2.3. Problem Formulation
3. The ZF-Max-Power Approach
3.1. Upper Bound of the JAR
3.2. The ZF-Max-Power Approach
| Algorithm 1 The ZF-Max-Power Scheme. |
|
3.3. Convergence Analysis and Complexity Comparison
4. Closed-Form Solutions
4.1. LB-MMSE
4.2. SI-ZF-MRT
4.3. Steering Beamforming
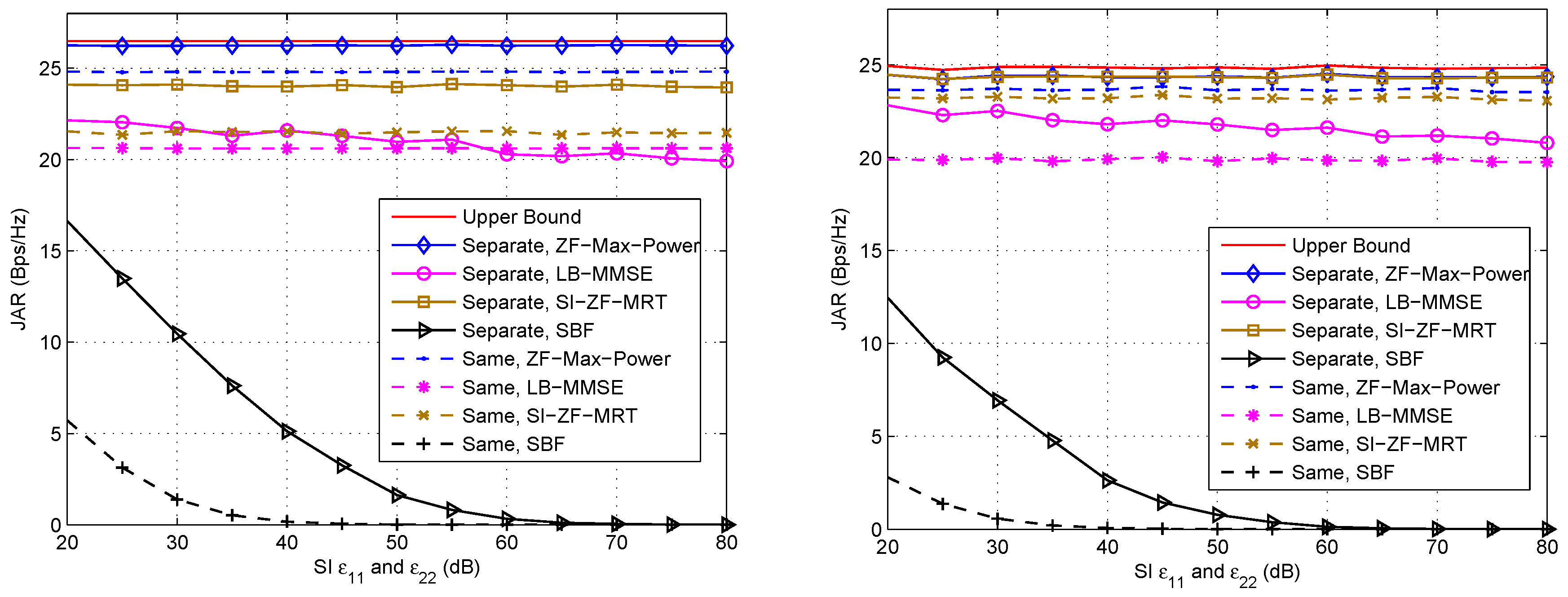
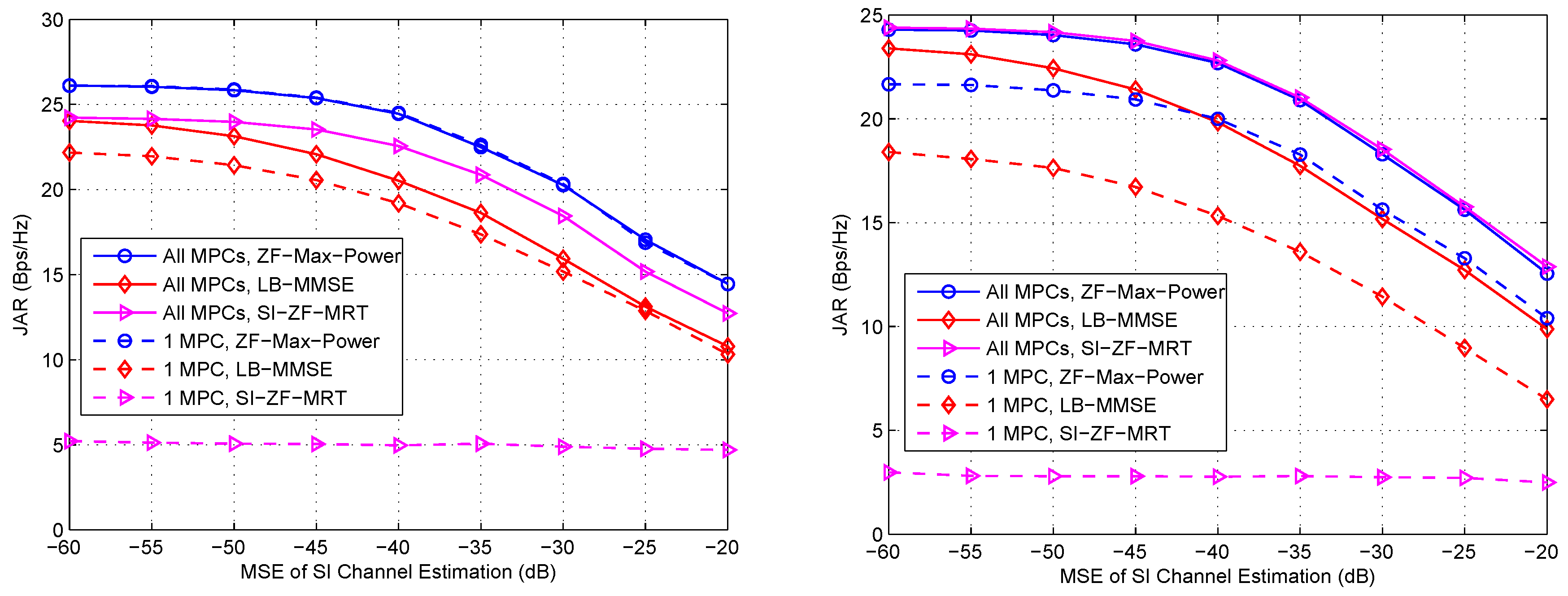
5. Simulation Results
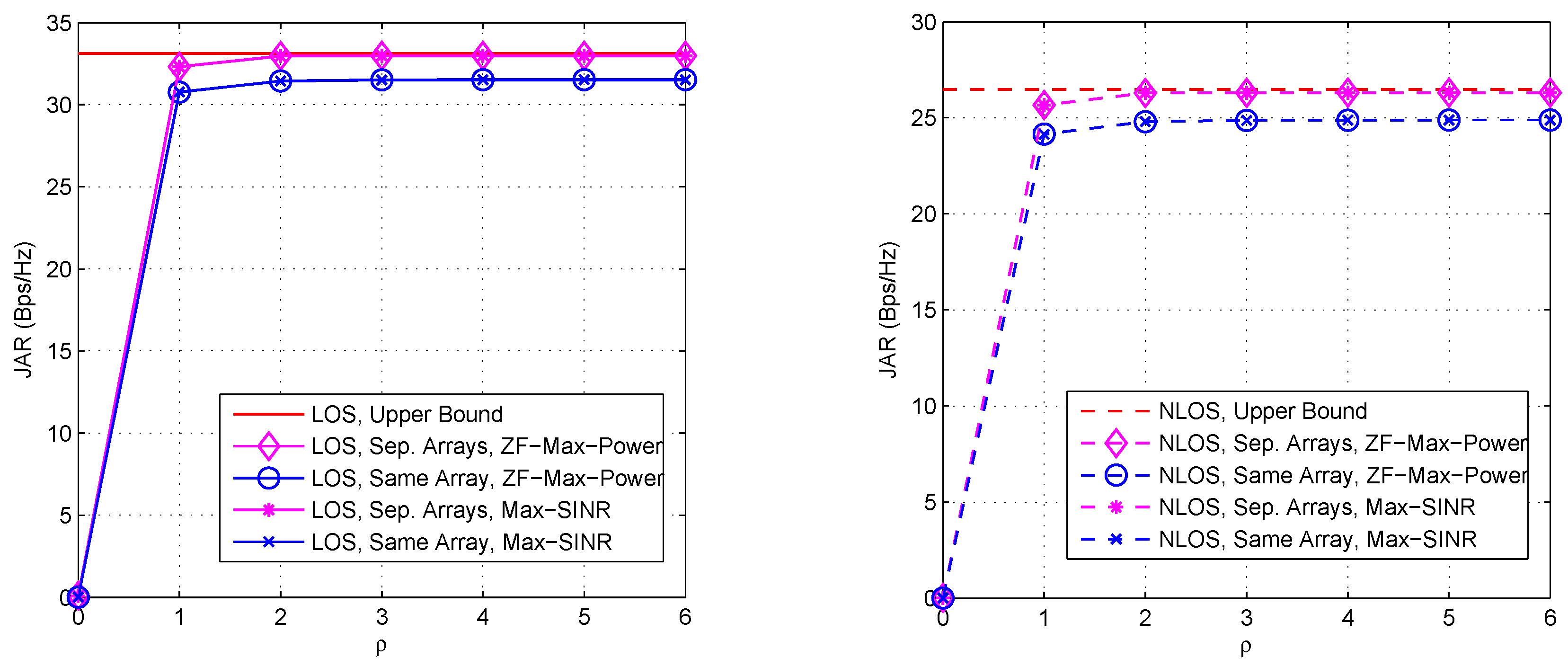
- (i)
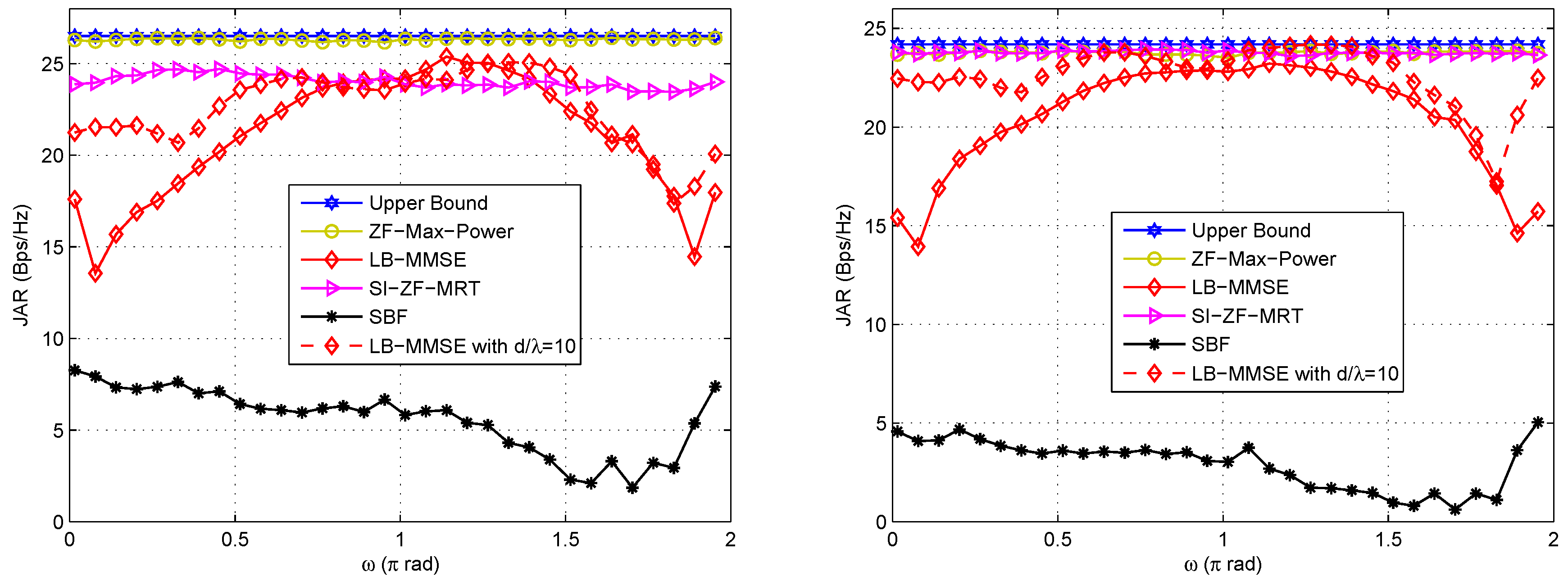
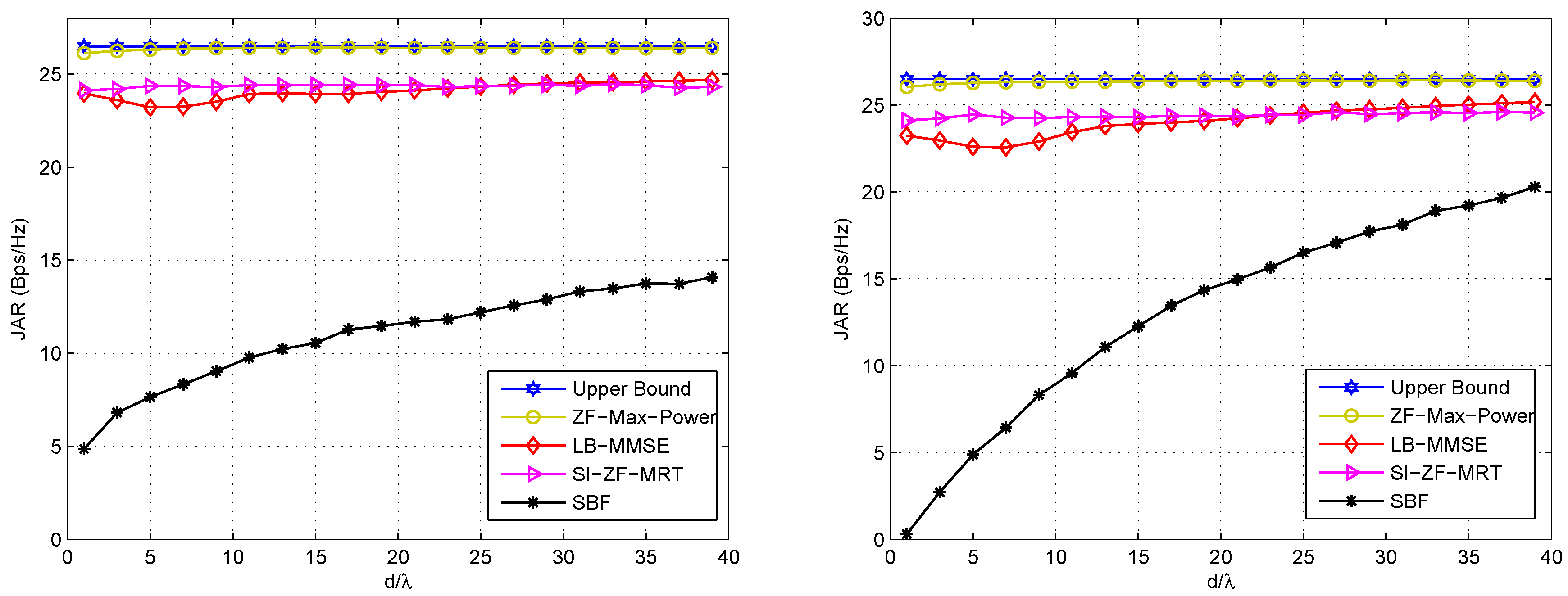
- ZF-Max-Power is robust against ω, d and SI, and approaches the upper bound in all these cases. This is because ZF-Max-Power not only forces SI to zero, but also iteratively maximizes signal power. Thus, it achieves compelling performance that is insensitive to the geometry of the Tx/Rx arrays and SI.
- (ii)
- SI-ZF-MRT is also robust against ω, d and SI, thanks to its zero-forcing filtering to SI. In addition, it also achieves an acceptable performance, which is close to the upper bound. It is noted that the JAR gap between SI-ZF-MRT and the upper bound is greater under LOS channel than that under NLOS channel. This phenomenon can be explained by referring to Equation (34), where is in fact set within an -dimension subspace, due to the two zero forcing equations shown in Equation (31). Clearly if in Equation (34), which represents the dimension with the largest power of the channel, has less energy projected on the -dimension subspace, the JAR performance will be poorer. Under LOS channel, the majority of the channel energy concentrates on a single path, or a single dimension. Once this dimension has a small projection on the subspace, the performance will be poor. In contrast, under NLOS channel the channel energy evenly disperses on multiple paths. Only when all of these paths have a small projection on the subspace, the performance will be poor. In other words, the probability of a poor performance is lower under NLOS channel than that under LOS channel. Hence, on average the JAR gap between SI-ZF-MRT and the upper bound is greater under LOS channel than that under NLOS channel.
- (iii)
- LB-MMSE is sensitive to ω and d. From Figure 4 we observe that the performance of LB-MMSE fluctuates as ω changes, and the fluctuation is different for different d. From Figure 5 we observe that the performance of LB-MMSE has a ∪-shape as d increases, but behaves stable when d is large. To understand these, we need to go back to Equations (28) and (29). From these two equations we can see that the transmit AWVs are decided to maximize the SINR rather than minimize SI based on the local information. Taking Equation (28) for illustration, since usually is big, when has a low rank, the eigenvector of has a high probability to locate within the null space of . In such a case, a high signal power can be achieved while little SI locates within the signal subspace; thus good performance is achieved. Note that this statement is just for illustration. In practice, is generally with full rank except when or π. However, when most energy of locates at a low-dimensional subspace, the situation will be similar to the statement that has a low rank. In comparison, when has a high or even full rank, SI will almost unavoidably locate within the signal subspace and affects the received SINR, and thus the performance will be poor. When d is small, the energy dispersion of is sensitive to ω and d according to the SI channel model, and thus the JAR performance is also sensitive to ω and d. However, when d is large, the SI channel almost reduces to a directional channel with rank 1, and thus SI has a low probability to locate within the signal subspace. In such a case, LB-MMSE can stably achieve a near-optimal performance.
- (iv)
- SBF is also sensitive to ω, d and SI. This is because SBF does not even consider SI in the beamforming design. Meanwhile, from Figure 5 it is found that SBF becomes improved as d increases. In the right hand side of Figure 5 the improving speed of SBF is faster than that in Figure 5, because SI is reduced as d increases. This phenomenon suggests that when the near-field SI channel gradually reduces to a directional channel, the conventional beamforming schemes that to simply steer towards each other may also achieve good performance, because usually the communication channel and SI channel have difference steering angles. However, in practical FD mmWave communication where d is generally small, the SI channel does not have the feature of directivity; thus SBF is much poorer than the other candidates, and the performance of SBF does not show monotonicity with ω, as shown in Figure 4. Thus, SBF may not be a good choice for FD mmWave communication, where SI must be taken into account.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemma 1
Appendix B. Proof of Theorem 1
Appendix C. Lemmas 2, 3, 4
References
- Sabharwal, A.; Schniter, P.; Guo, D.; Bliss, D.; Rangarajan, S.; Wichman, R. In-band full-duplex wireless: Challenges and opportunities. IEEE J. Sel. Areas Commun. 2014, 32, 1637–1652. [Google Scholar] [CrossRef]
- Ahmed, E.; Eltawil, A.; Sabharwal, A. Simultaneous transmit and sense for cognitive radios using full-duplex: A first study. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (APSURSI), Chicago, IL, USA, 8–14 July 2012; IEEE: Chicago, IL, USA, 2012; pp. 1–2. [Google Scholar]
- Duarte, M.; Dick, C.; Sabharwal, A. Experiment-driven characterization of full-duplex wireless systems. IEEE Trans. Wirel. Commun. 2011, 11, 4296–4307. [Google Scholar] [CrossRef]
- Duarte, M.; Sabharwal, A.; Aggarwal, V.; Jana, R.; Ramakrishnan, K.; Rice, C.; Shankaranarayanan, N. Design and characterization of a full-duplex multiantenna system for WiFi networks. IEEE Trans. Veh. Technol. 2014, 63, 1160–1177. [Google Scholar] [CrossRef]
- Jain, M.; Choi, J.I.; Kim, T.; Bharadia, D.; Seth, S.; Srinivasan, K.; Levis, P.; Katti, S.; Sinha, P. Practical, real-time, full duplex wireless. In Proceedings of the 17th Annual International Conference on Mobile Computing and Networking, Las Vegas, NV, USA, 19–23 September 2011; ACM: New York, NY, USA, 2011; pp. 301–312. [Google Scholar]
- Li, N.; Zhu, W.; Han, H. Digital interference cancellation in single channel, full duplex wireless communication. In Proceedings of the 8th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Shanghai, China, 21–23 September 2012; IEEE: Shanghai, China, 2012; pp. 1–4. [Google Scholar]
- Li, S.; Murch, R.D. Full-duplex wireless communication using transmitter output based echo cancellation. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM 2011), Houston, TX, USA, 5–9 December 2011; IEEE: Houston, TX, USA, 2011; pp. 1–5. [Google Scholar]
- Choi, J.I.; Jain, M.; Srinivasan, K.; Levis, P.; Katti, S. Achieving single channel, full duplex wireless communication. In Proceedings of the 16th Annual International Conference on Mobile Computing and Networking (MobiCom 2010), Chicago, IL, USA, 20–24 September 2010; IEEE: Chicago, IL, USA, 2010; pp. 301–312. [Google Scholar]
- Khojastepour, M.A.; Sundaresan, K.; Rangarajan, S.; Zhang, X.; Barghi, S. The case for antenna cancellation for scalable full-duplex wireless communications. In Proceedings of the 10th ACM Workshop on Hot Topics in Networks, Cambridge, MA, USA, 14–15 November 2011; ACM: New York, NY, USA, 2011; pp. 1–6. [Google Scholar]
- Bharadia, D.; McMilin, E.; Katti, S. Full duplex radios. In Proceedings of the Special Interest Group on Data Communication (SIGCOMM), Hong Kong, China, 12–16 August 2013; ACM: Hong Kong, China, 2013. [Google Scholar]
- Daniels, R.C.; Murdock, J.N.; Rappaport, T.S.; Heath, R.W. 60 GHz wireless: Up close and personal. IEEE Microw. Mag. 2010, 11, 44–50. [Google Scholar] [CrossRef]
- Perahia, E.; Cordeiro, C.; Park, M.; Yang, L.L. IEEE 802.11 ad: Defining the next generation multi-Gbps Wi-Fi. In Proceedings of the IEEE Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 9–12 January 2010; IEEE: Las Vegas, NV, USA, 2010; pp. 1–5. [Google Scholar]
- Yong, S.K.; Xia, P.; Valdes-Garcia, A. 60GHz Technology for Gbps WLAN and WPAN: From Theory to Practice; Wiley: West Sussex, UK, 2011. [Google Scholar]
- Wang, P.; Li, Y.; Yuan, X.; Song, L.; Vucetic, B. Tens of gigabits wireless communications over E-band LoS MIMO channels with uniform linear antenna arrays. IEEE Trans. Wirel. Commun. 2014, 13, 3791–3805. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Song, L.; Vucetic, B. Multi-gigabit millimeter wave wireless communications for 5G: From fixed access to cellular networks. IEEE Commun. Mag. 2015, 53, 168–178. [Google Scholar] [CrossRef]
- Gao, X.; Dai, L.; Han, S.; Chih-Lin, I.; Heath, R.W. Energy-efficient hybrid analog and digital precoding for mmWave MIMO systems with large antenna arrays. IEEE J. Sel. Areas Commun. 2016, 34, 998–1009. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Wang, Z.; Chen, S. Spatially common sparsity based adaptive channel estimation and feedback for FDD massive MIMO. IEEE Trans. Signal Process. 2015, 63, 6169–6183. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Lu, Z.; Yuen, C.; Wang, Z. Super-resolution sparse MIMO-OFDM channel estimation based on spatial and temporal correlations. IEEE Commun. Lett. 2014, 18, 1266–1269. [Google Scholar] [CrossRef]
- Niu, Y.; Li, Y.; Jin, D.; Su, L.; Vasilakos, A.V. A survey of millimeter wave communications (mmWave) for 5G: Opportunities and challenges. Wirel. Netw. 2015, 21, 2657–2676. [Google Scholar] [CrossRef]
- Tang, Y.; Vucetic, B.; Li, Y. An iterative singular vectors estimation scheme for beamforming transmission and detection in MIMO systems. IEEE Commun. Lett. 2005, 9, 505–507. [Google Scholar] [CrossRef]
- Xiao, Z. Suboptimal Spatial Diversity Scheme for 60 GHz Millimeter-Wave WLAN. IEEE Commun. Lett. 2013, 17, 1790–1793. [Google Scholar] [CrossRef]
- Xiao, Z.; Bai, L.; Choi, J. Iterative Joint Beamforming Training with Constant-Amplitude Phased Arrays in Millimeter-Wave Communications. IEEE Commun. Lett. 2014, 18, 829–832. [Google Scholar] [CrossRef]
- Park, M.; Pan, H. A Spatial Diversity Technique for IEEE 802.11 ad WLAN in 60 GHz Band. IEEE Commun. Lett. 2012, 16, 1260–1262. [Google Scholar] [CrossRef]
- Nsenga, J.; Van Thillo, W.; Horlin, F.; Ramon, V.; Bourdoux, A.; Lauwereins, R. Joint transmit and receive analog beamforming in 60 GHz MIMO multipath channels. In Proceedings of the 2009 IEEE International Conference on Communications (ICC), Dresden, Germany, 14–18 June 2009; IEEE: Dresden, Germany, 2009; pp. 1–5. [Google Scholar]
- Li, B.; Zhou, Z.; Zhang, H.; Nallanathan, A. Efficient beamforming training for 60-GHz millimeter-wave communications: A novel numerical optimization framework. IEEE Trans. Veh. Technol. 2014, 63, 703–717. [Google Scholar] [CrossRef]
- Li, B.; Zhou, Z.; Zou, W.; Sun, X.; Du, G. On the Efficient Beam-Forming Training for 60GHz Wireless Personal Area Networks. IEEE Trans. Wirel. Commun. 2013, 12, 504–515. [Google Scholar] [CrossRef]
- Chun, B.; Lee, Y.H. A spatial self-interference nullification method for full duplex amplify-and-forward MIMO relays. In Proceedings of the 2010 IEEE Wireless Communications and Networking Conference (WCNC), Sydney, Australia, 18–21 April 2010; IEEE: Sydney, Australia, 2010; pp. 1–6. [Google Scholar]
- Riihonen, T.; Werner, S.; Wichman, R. Mitigation of loopback self-interference in full-duplex MIMO relays. IEEE Trans. Signal Process. 2011, 59, 5983–5993. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, X.G.; Zhang, H. Distributed space-time coding for full-duplex asynchronous cooperative communications. IEEE Trans. Wirel. Commun. 2012, 11, 2680–2688. [Google Scholar] [CrossRef]
- Liu, Y.; Xia, X.G.; Zhang, H. Distributed linear convolutional space-time coding for two-relay full-duplex asynchronous cooperative networks. IEEE Trans. Wirel. Commun. 2013, 12, 6406–6417. [Google Scholar] [CrossRef]
- Snow, T.; Fulton, C.; Chappell, W.J. Transmit–receive duplexing using digital beamforming system to cancel self-interference. IEEE Trans. Microw. Theory Tech. 2011, 59, 3494–3503. [Google Scholar] [CrossRef]
- Gomadam, K.; Cadambe, V.R.; Jafar, S.A. A distributed numerical approach to interference alignment and applications to wireless interference networks. IEEE Trans. Inf. Theory 2011, 57, 3309–3322. [Google Scholar] [CrossRef]
- Santamaria, I.; Gonzalez, O.; Heath, R.; Peters, S.W. Maximum sum-rate interference alignment algorithms for MIMO channels. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM 2010), Miami, FL, USA, 6–10 December 2010; IEEE: Miami, FL, USA, 2010; pp. 1–6. [Google Scholar]
- Peters, S.W.; Heath, R.W. Cooperative algorithms for MIMO interference channels. IEEE Trans. Veh. Technol. 2011, 60, 206–218. [Google Scholar] [CrossRef]
- Schmidt, D.A.; Shi, C.; Berry, R.A.; Honig, M.L.; Utschick, W. Comparison of distributed beamforming algorithms for MIMO interference networks. IEEE Trans. Signal Process. 2013, 61, 3476–3489. [Google Scholar] [CrossRef]
- Wang, J.; Lan, Z.; Pyo, C.; Baykas, T.; Sum, C.; Rahman, M.; Gao, J.; Funada, R.; Kojima, F.; Harada, H. Beam codebook based beamforming protocol for multi-Gbps millimeter-wave WPAN systems. IEEE J. Sel. Areas Commun. 2009, 27, 1390–1399. [Google Scholar] [CrossRef]
- Maltsev, A.; Maslennikov, R.; Sevastyanov, A.; Lomayev, A.; Khoryaev, A.; Davydov, A.; Ssorin, V. Characteristics of indoor millimeter-wave channel at 60 GHz in application to perspective WLAN system. In Proceedings of the Fourth European Conference on Antennas and Propagation (EuCAP), Barcelona, Spain, 12–16 April 2010; IEEE: Barcelona, Spain, 2010; pp. 1–5. [Google Scholar]
- Alkhateeb, A.; Mo, J.; González-Prelcic, N.; Heath, R. MIMO precoding and combining solutions for millimeter-wave systems. IEEE Commun. Mag. 2014, 52, 122–131. [Google Scholar] [CrossRef]
- Hur, S.; Kim, T.; Love, D.J.; Krogmeier, J.V.; Thomas, T.A.; Ghosh, A. Millimeter wave beamforming for wireless backhaul and access in small cell networks. IEEE Trans. Commun. 2013, 61, 4391–4403. [Google Scholar] [CrossRef]
- Xiao, Z.; Xia, P.; Xia, X.G. Enabling UAV cellular with millimeter-wave communication: Potentials and approaches. IEEE Commun. Mag. 2016, 54, 66–73. [Google Scholar] [CrossRef]
- Rangan, S.; Rappaport, T.S.; Erkip, E. Millimeter-wave cellular wireless networks: Potentials and challenges. Proc. IEEE 2014, 102, 366–385. [Google Scholar] [CrossRef]
- El Ayach, O.; Rajagopal, S.; Abu-Surra, S.; Pi, Z.; Heath, R. Spatially Sparse Precoding in Millimeter Wave MIMO Systems. IEEE Trans. Wirel. Commun. 2014, 13, 1499–1513. [Google Scholar] [CrossRef]
- Fenn, A.J. Evaluation of adaptive phased array antenna, far-field nulling performance in the near-field region. IEEE Trans. Antennas Propag. 1990, 38, 173–185. [Google Scholar] [CrossRef]
- Yaghjian, A.D. An overview of near-field antenna measurements. IEEE Trans. Antennas Propag. 1986, 34, 30–45. [Google Scholar] [CrossRef]
- Sayers, A.; Dorsey, W.; O’Haver, K.; Valenzi, J. Planar near-field measurement of digital phased arrays using near-field scan plane reconstruction. IEEE Trans. Antennas Propag. 2012, 60, 2711–2718. [Google Scholar] [CrossRef]
- Liao, Y.P.; Han, H.; Guo, Q. Design of robust near-field multi-beam forming based on improved LCMV algorithm. J. Inf. Hiding Multimed. Signal Process. 2015, 6, 783–791. [Google Scholar]
- Lin, J.R.; Peng, Q.C.; Shao, H.Z. Near-field robust adaptive beamforming based on worst-case performance optimization. Int. J. Electr. Comput. Eng. 2006, 1, 712–718. [Google Scholar]
- Lee, M.S.; Park, J.Y.; Katkovnik, V.; Itoh, T.; Kim, Y.H. Adaptive robust DOA estimation for a 60-GHz antenna-array system. IEEE Trans. Veh. Technol. 2007, 56, 3231–3237. [Google Scholar] [CrossRef]
- Tsang, Y.M.; Poon, A.S.; Addepalli, S. Coding the beams: Improving beamforming training in mmwave communication system. In Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM 2011), Houston, TX, USA, 5–9 December 2011; IEEE: Houston, TX, USA, 2011; pp. 1–6. [Google Scholar]
- Xiao, Z.; Xia, X.G.; Jin, D.; Ge, N. Iterative Eigenvalue Decomposition and Multipath-Grouping Tx/Rx Joint Beamformings for Millimeter-Wave Communications. IEEE Trans. Wirel. Commun. 2015, 14, 1595–1607. [Google Scholar] [CrossRef]
- Alkhateeb, A.; El Ayach, O.; Leus, G.; Heath, R. Channel estimation and hybrid precoding for millimeter wave cellular systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 831–846. [Google Scholar] [CrossRef]
- Peng, Y.; Li, Y.; Wang, P. An Enhanced Channel Estimation Method for Millimeter Wave Systems with Massive Antenna Arrays. IEEE Commun. Lett. 2015, 19, 1592–1595. [Google Scholar] [CrossRef]
- Vía, J.; Santamaría, I.; Elvira, V.; Eickhoff, R. A general criterion for analog Tx-Rx beamforming under OFDM transmissions. IEEE Trans. Signal Process. 2010, 58, 2155–2167. [Google Scholar] [CrossRef]
- Kokshoorn, M.; Wang, P.; Li, Y.; Vucetic, B. Fast channel estimation for millimetre wave wireless systems using overlapped beam patterns. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; IEEE: London, UK, 2015; pp. 1304–1309. [Google Scholar]
- Kang, D.W.; Kim, J.G.; Min, B.W.; Rebeiz, G.M. Single and four-element-Ka-band transmit/receive phased-array silicon RFICs with 5-bit amplitude and phase control. IEEE Trans. Microw. Theory Tech. 2009, 57, 3534–3543. [Google Scholar] [CrossRef]
- Li, Q.; Hong, M.; Wai, H.T.; Liu, Y.F.; Ma, W.K.; Luo, Z.Q. Transmit Solutions for MIMO Wiretap Channels using Alternating Optimization. IEEE J. Sel. Areas Commun. 2013, 31, 1714–1727. [Google Scholar] [CrossRef]
- Li, W.; Lilleberg, J.; Rikkinen, K. On rate region analysis of half-and full-duplex OFDM communication links. IEEE J. Sel. Areas Commun. 2014, 32, 1688–1698. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Xiao, Z.; Bai, L.; Choi, J.; Xia, P.; Xia, X.-G. Beamforming Based Full-Duplex for Millimeter-Wave Communication. Sensors 2016, 16, 1130. https://doi.org/10.3390/s16071130
Liu X, Xiao Z, Bai L, Choi J, Xia P, Xia X-G. Beamforming Based Full-Duplex for Millimeter-Wave Communication. Sensors. 2016; 16(7):1130. https://doi.org/10.3390/s16071130
Chicago/Turabian StyleLiu, Xiao, Zhenyu Xiao, Lin Bai, Jinho Choi, Pengfei Xia, and Xiang-Gen Xia. 2016. "Beamforming Based Full-Duplex for Millimeter-Wave Communication" Sensors 16, no. 7: 1130. https://doi.org/10.3390/s16071130
APA StyleLiu, X., Xiao, Z., Bai, L., Choi, J., Xia, P., & Xia, X.-G. (2016). Beamforming Based Full-Duplex for Millimeter-Wave Communication. Sensors, 16(7), 1130. https://doi.org/10.3390/s16071130





