Generalized Theory and Decoupled Evaluation Criteria for Unmatched Despreading of Modernized GNSS Signals
Abstract
:1. Introduction
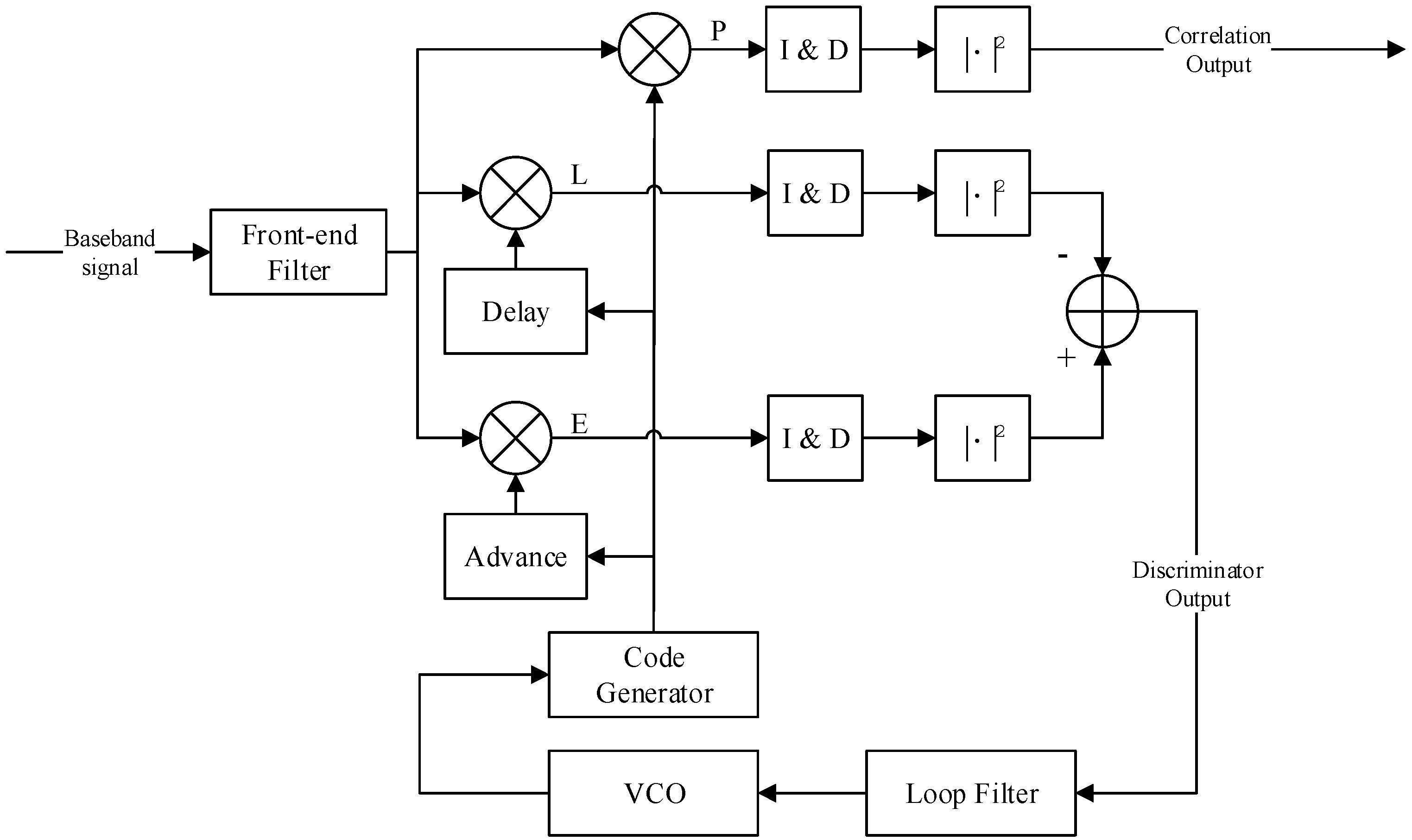
2. Basic Principles of Code Tracking
3. Code Chip Waveform Mismatch
4. Signal Evaluation Approach under the Local Despreading Waveform Mismatch
4.1. Formulation and Statistical Properties of Correlator Output
4.2. Formulation and Statistical Properties of Discriminator Output
4.3. Multipath Effects under Unmatched Receiving
5. Decoupled Criteria for GNSS Code Tracking Evaluation
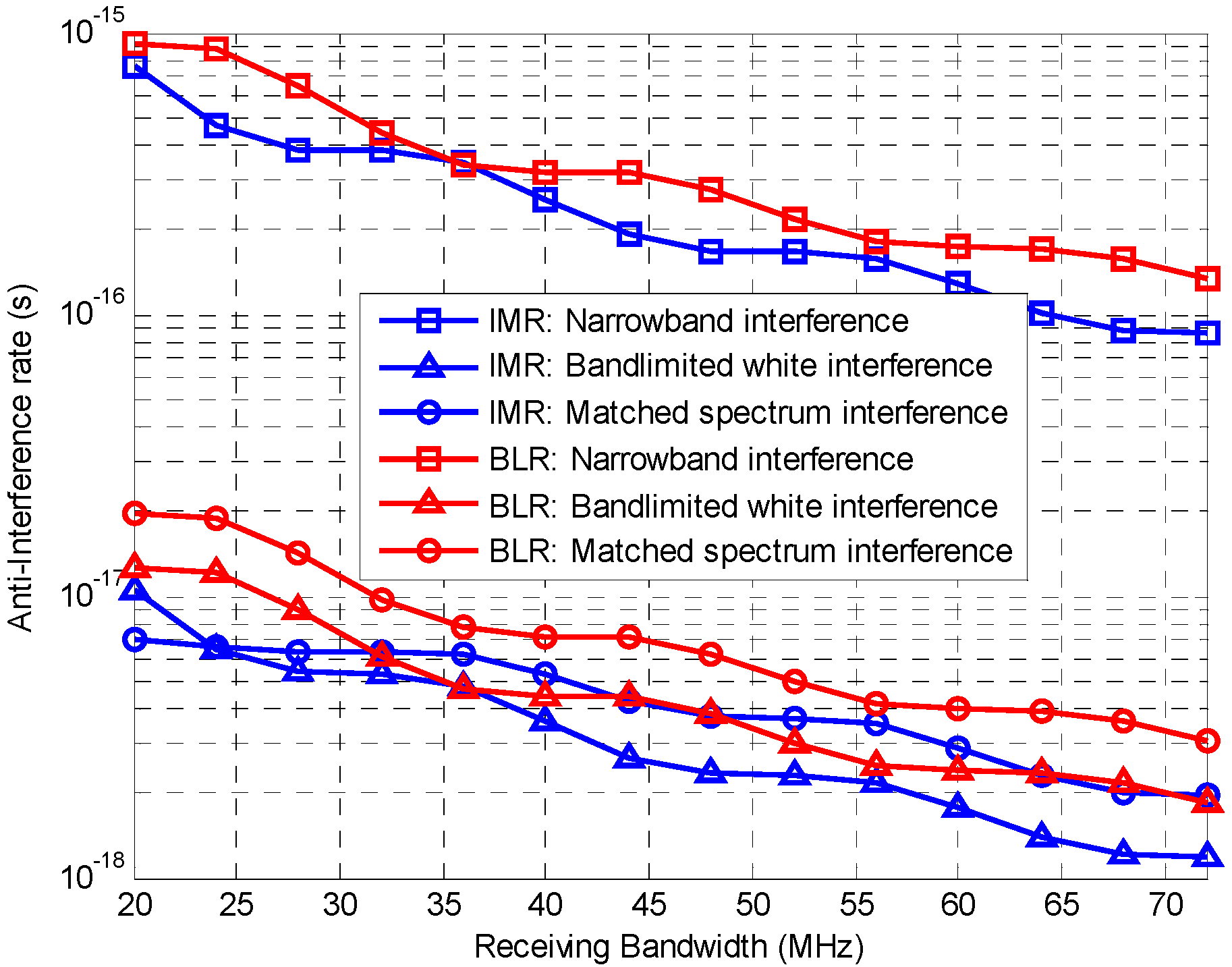
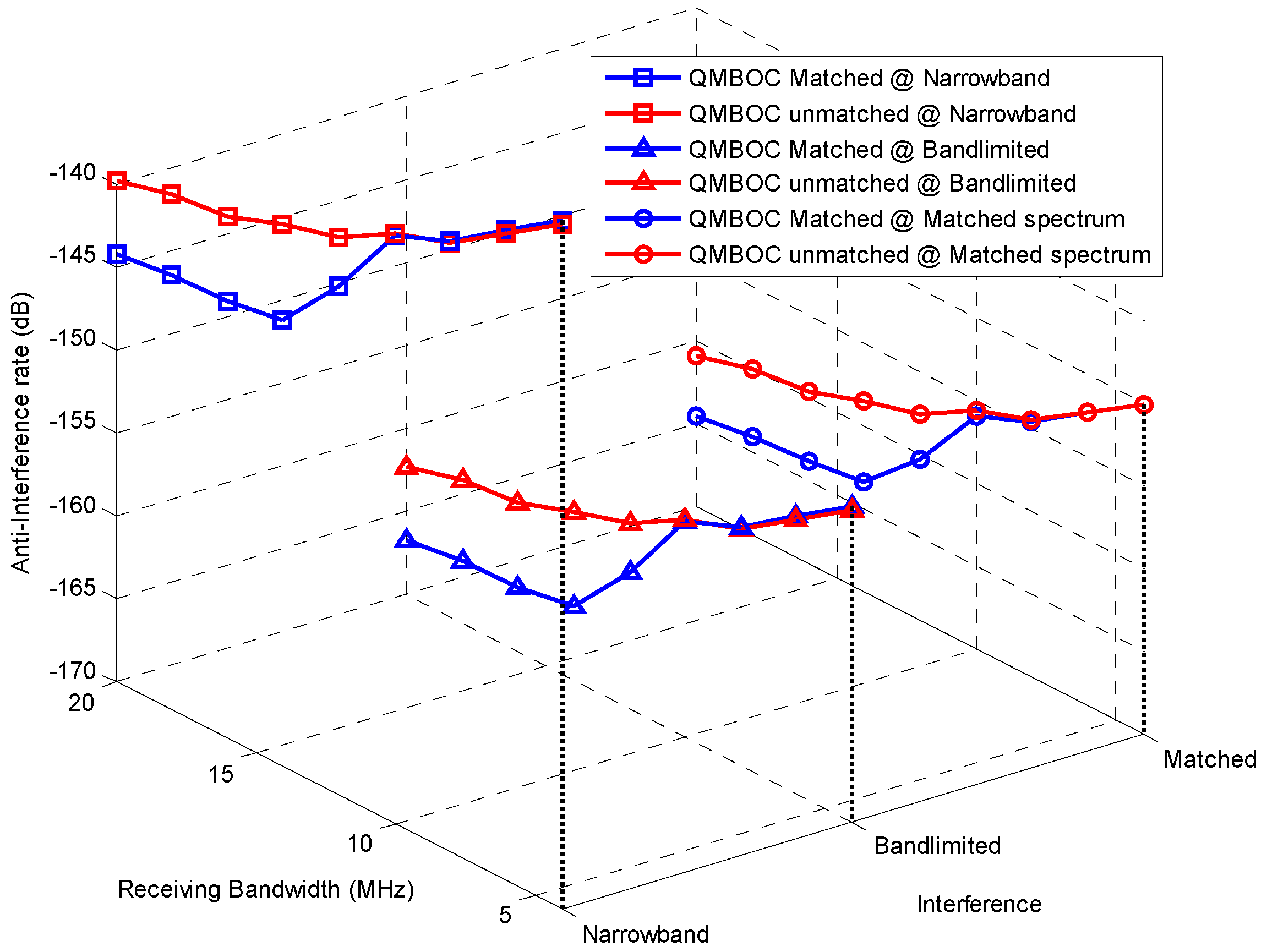
5.1. Anti-Interference Rate
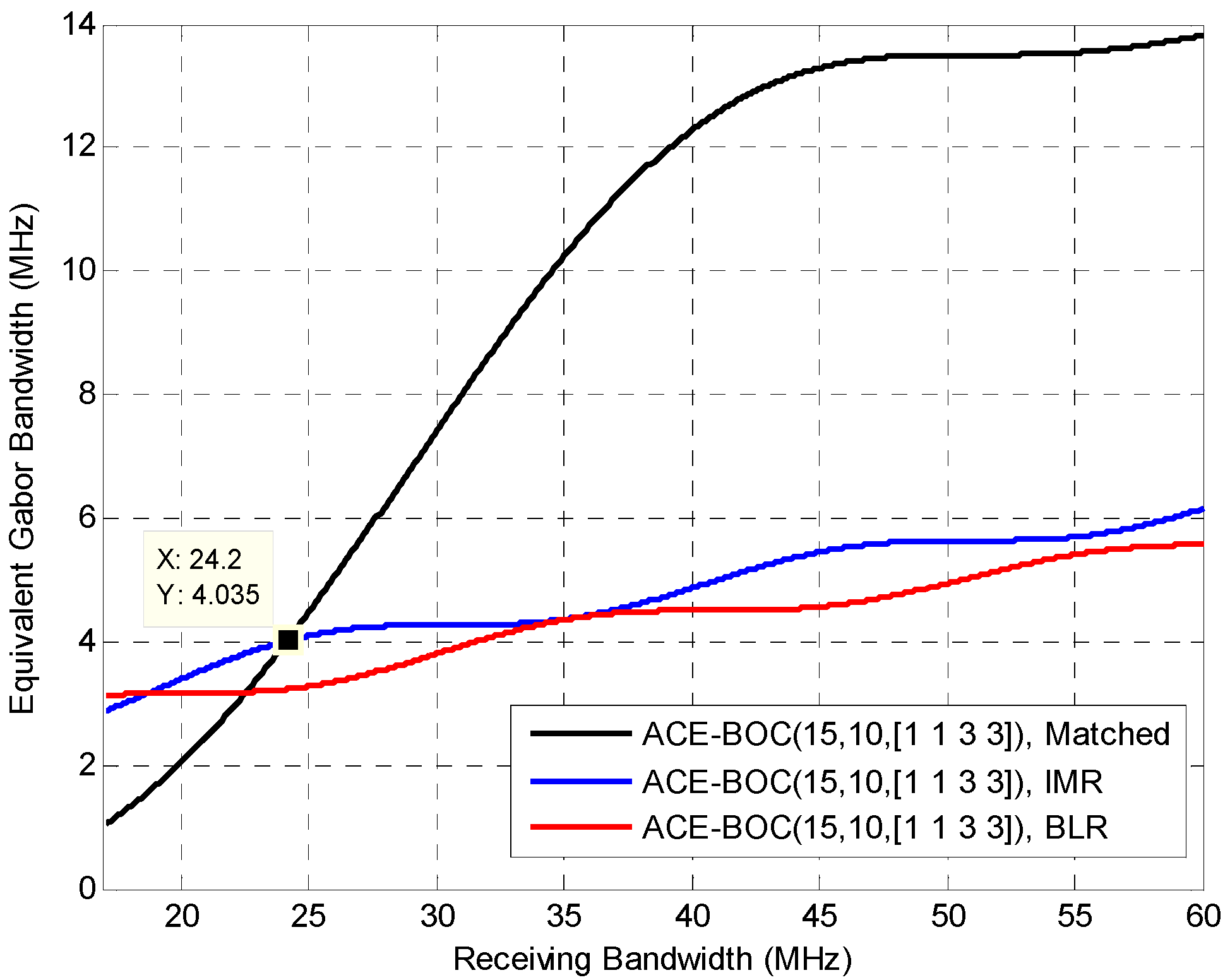
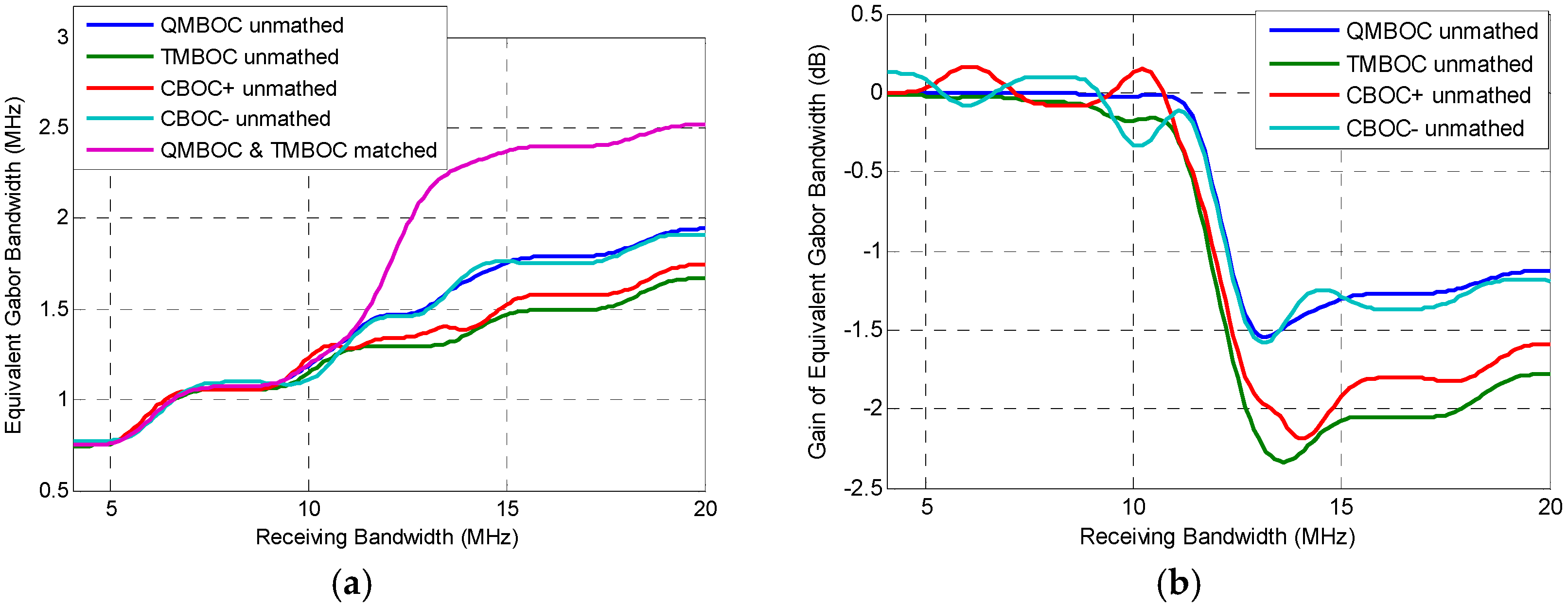
5.2. Equivalent Gabor Bandwidth
6. The Evaluation of Unmatched Receiving of ACE-BOC
6.1. ACE-BOC Overview and Receiving Strategies
- Matched Receiving
- Independent Matched Receiving (IMR)
- BPSK-like Receiving (BLR)
6.2. Performance Evaluation
6.2.1. Acquisition Performance Evaluation
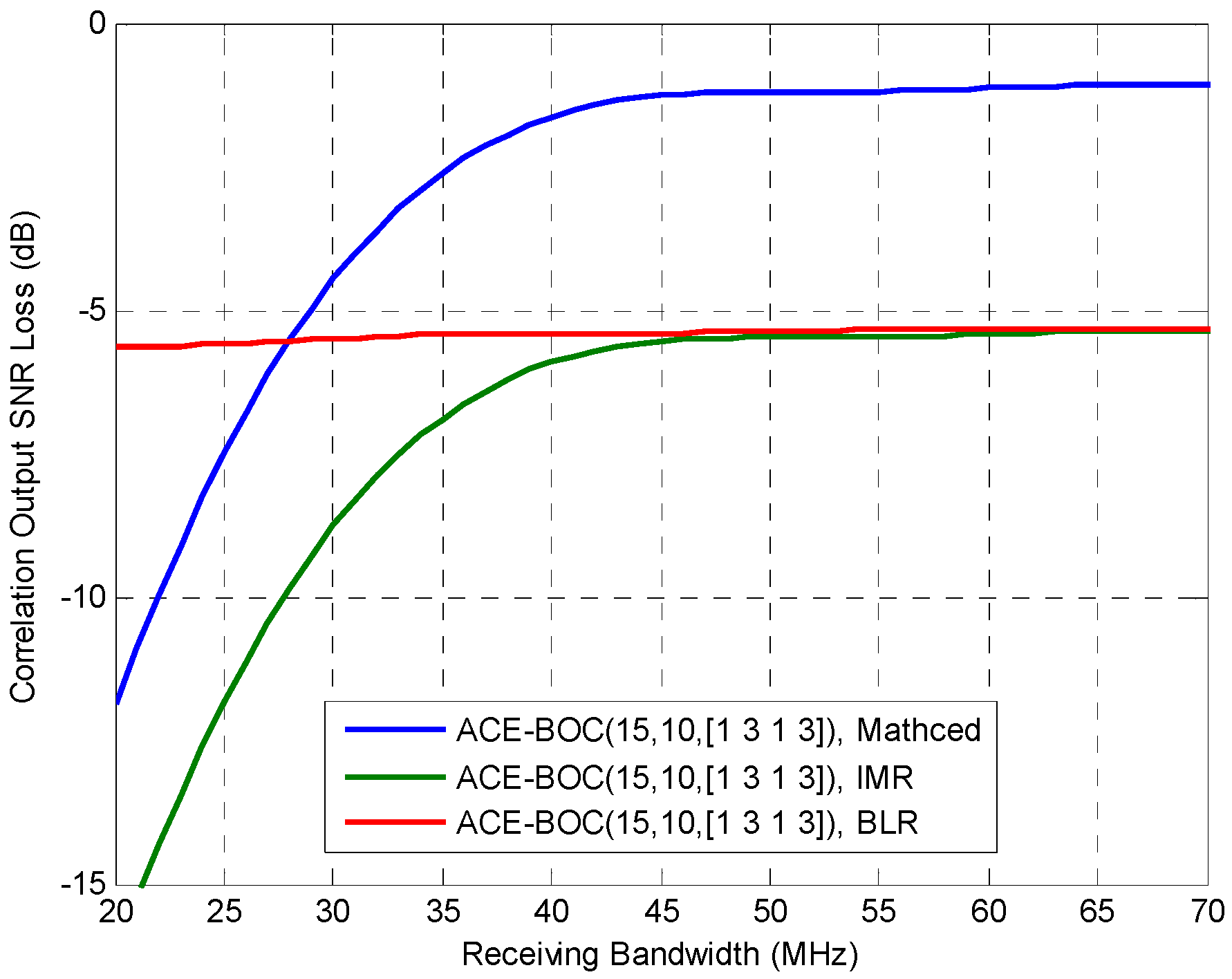
6.2.2. Tracking Performance under WGN
6.2.3. Tracking Performance under Interference
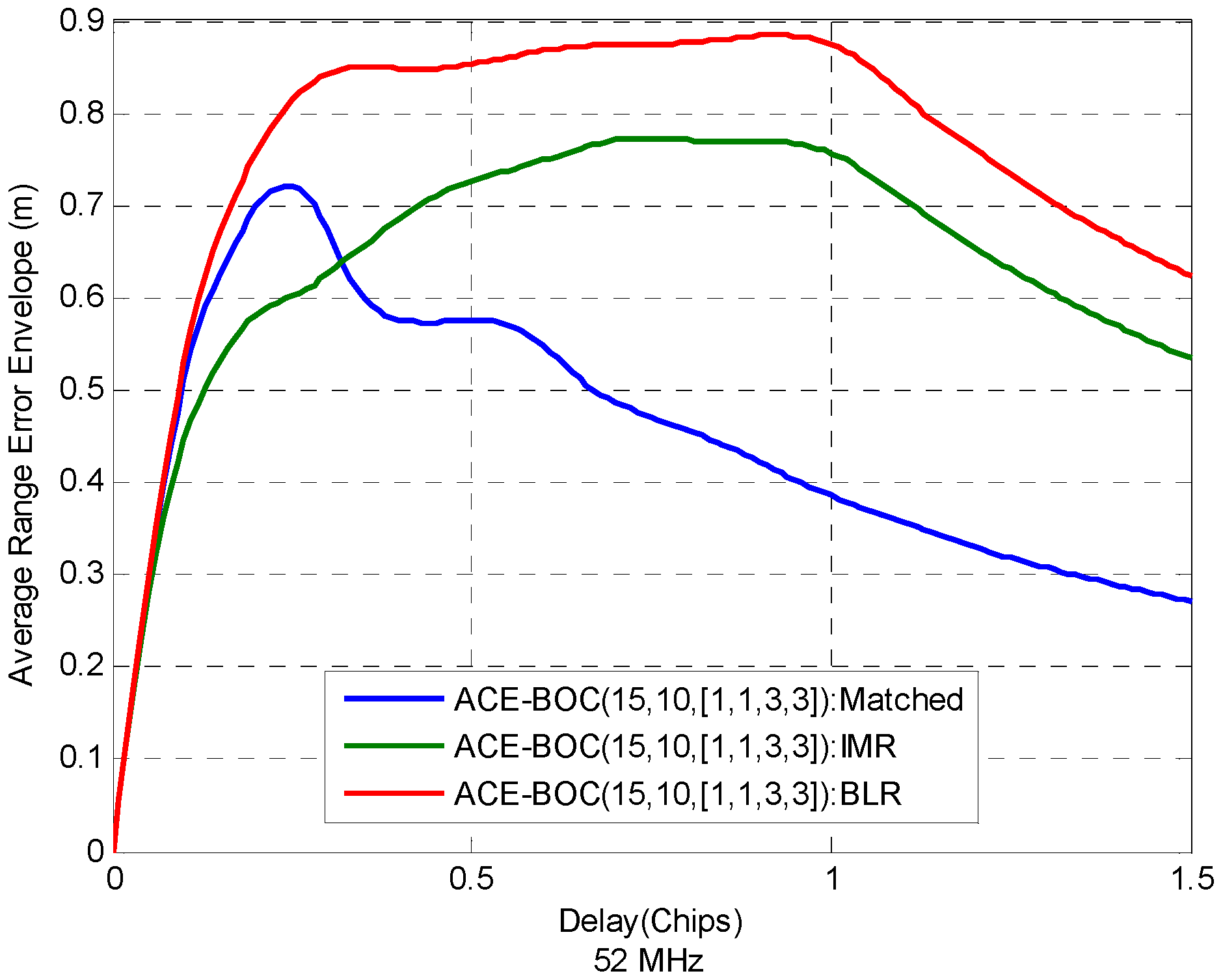
6.2.4. Multipath Resisting Performance
7. The Evaluation of BOC-Like Receiving of MBOC
7.1. MBOC Overview and Receiving Strategies
7.2. Performance Evaluation
7.2.1. Acquisition Performance
7.2.2. Tracking Performance under WGN
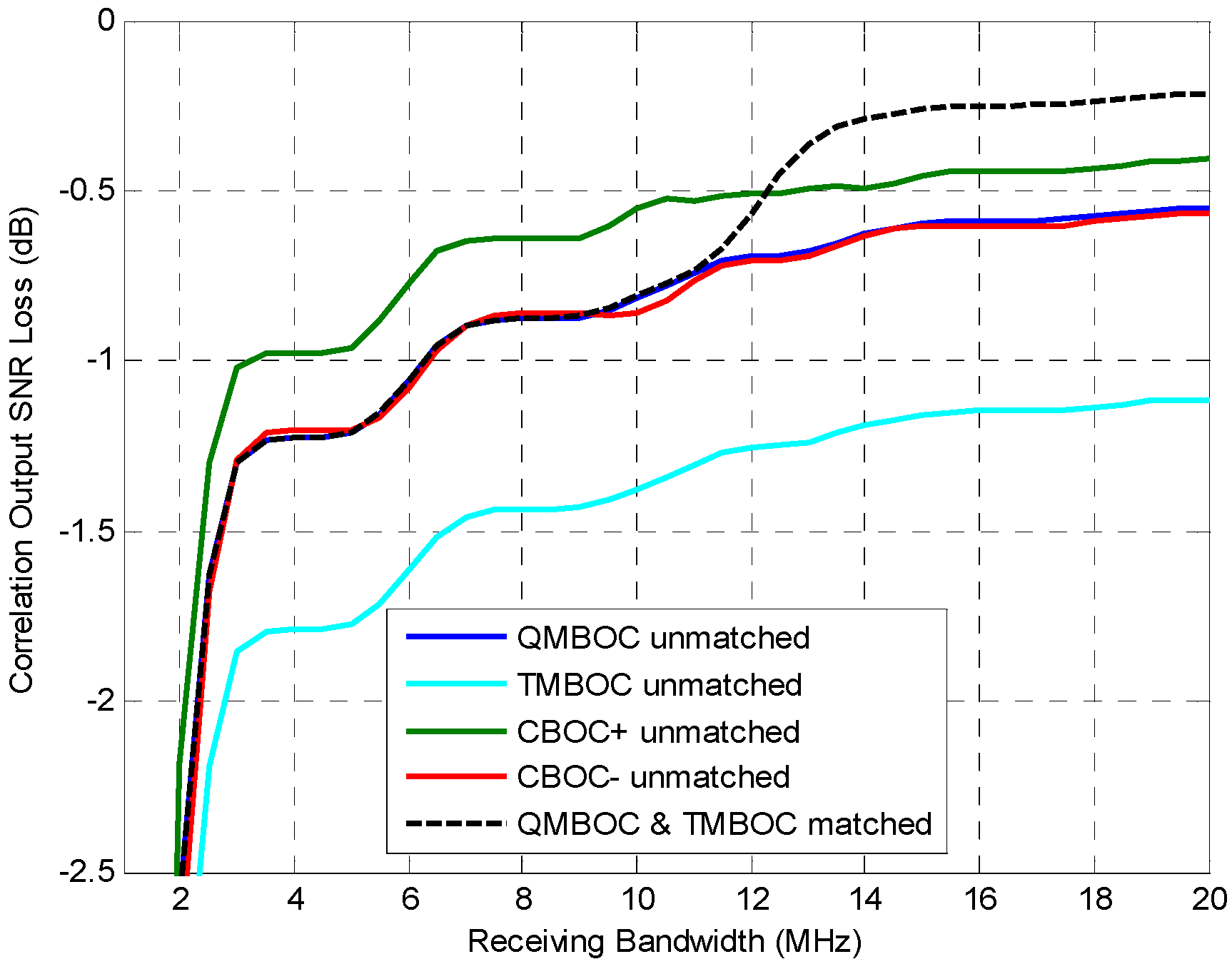
7.2.3. Anti-Interference Performance
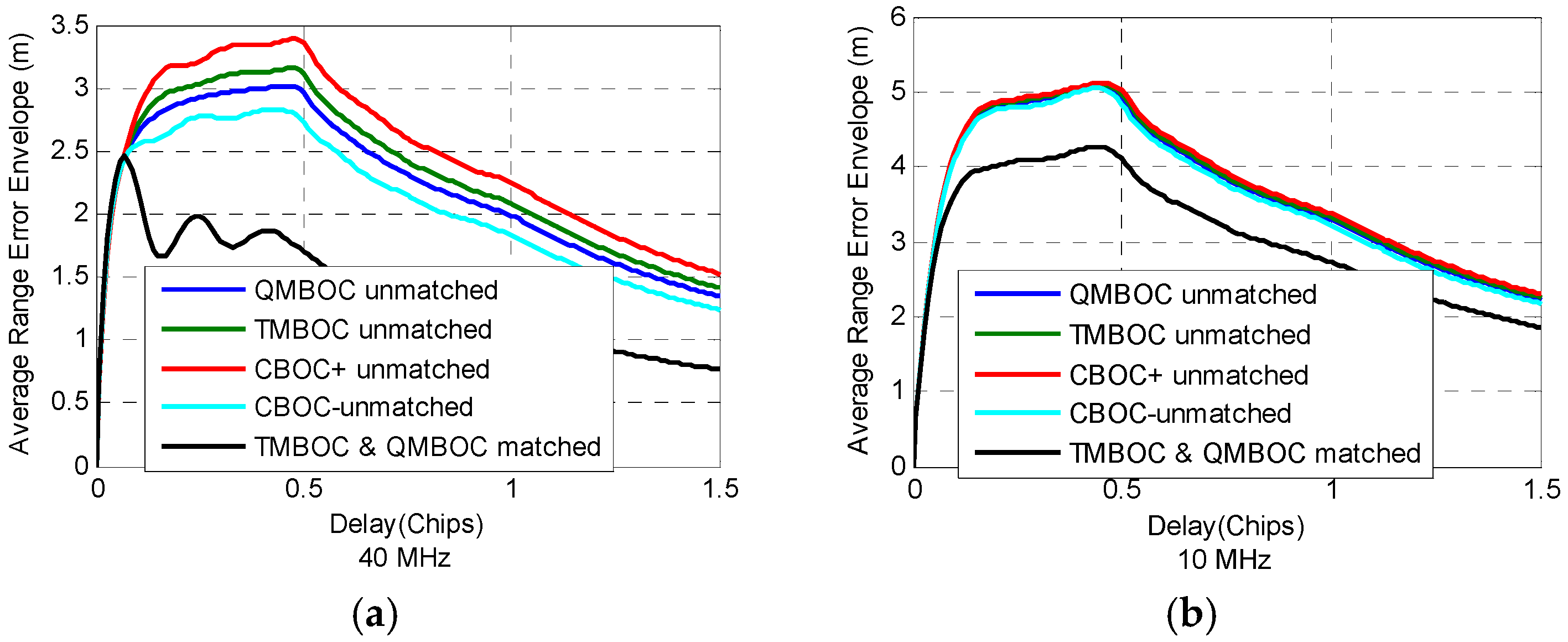
7.2.4. Multipath Resisting Performance
8. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Gabor bandwidth. | |
| Equivalent Gabor bandwidth. | |
| DSSS waveform from the received signal. | |
| DSSS waveform from the local despreading signal. | |
| Subcarrier frequency. | |
| PRN chip rate, . | |
| Pulse width of . | |
| True value of TOA. | |
| Fixed delay of correlators, stands for the branches of early, prompt and late. | |
| White Gaussian Noise (WGN). | |
| Double-sided spectral density of WGN. | |
| Non-white Gaussian interference. | |
| Gaussian noise and interference. | |
| Normalized PSD of interference, satisfying . | |
| Normalized PSD of signal , satisfying. | |
| Average carrier power, defined on the infinite bandwidth. | |
| Carrier to noise ratio. | |
| Cross-spectrum between the received signal and the local signal. | |
| Correlation loss under unmatched receiving, used to characterize the performance of acquisition and demodulation. | |
| Code tracking spectral separation coefficient (CT-SSC). | |
| Low bound of code tracking error, considering the unmatched despreading. | |
| Anti-interference rate. | |
| Average range error envelope caused by multipath. |
References
- Yang, C.; Miller, M.; Nguyen, T.; Akos, D. Generalized frequency-domain correlator for software GPS receiver: Preliminary test results and analysis. In Proceedings of the 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, 26–29 September 2006; pp. 2346–2630.
- Nunes, F.D.; Sousa, F.M.; Leitao, J.M. Gating functions for multipath mitigation in GNSS BOC signals. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 951–964. [Google Scholar] [CrossRef]
- Fishman, P.M.; Betz, J.W. Predicting performance of direct acquisition for the M-code signal. In Proceedings of the 2000 National Technical Meeting of the Institute of Navigation, Anaheim, CA, USA, 26–28 January 2000; pp. 574–582.
- Martin, N.; Leblond, V.; Guillotel, G.; Heiries, V. BOC (x, y) signal acquisition techniques and performances. In Proceedings of the 16th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003; pp. 188–198.
- Hodgart, M.S.; Blunt, P.D. Dual estimate receiver of binary offset carrier modulated signals for global navigation satellite systems. Electron. Lett. 2007, 43, 877–878. [Google Scholar] [CrossRef]
- Simon, M.K.; Omura, J.K.; Scholtz, R.A.; Levitt, B.K. Spread Spectrum Communications; Vols. 1–3; Computer Science Press, Inc.: New York, NY, USA, 1985. [Google Scholar]
- Holmes, J.K. Code tracking loop performance including the effects of channel filtering and Gaussian interference. In Proceedings of the IAIN World Congress and the 56th Annual Meeting of the Institute of Navigation, San Diego, CA, USA, 26–28 June 2000; pp. 382–398.
- Betz, J.W.; Shnidman, N.R. Receiver processing losses with bandlimiting and one-bit sampling. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 1244–1256.
- Hegarty, C.J.; Cerruti, A.P. Results from an analytical model for GNSS receiver implementation losses. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 2820–2834.
- Betz, J.W.; Kolodziejski, K.R. Generalized theory of code tracking with an early-late discriminator part I: Lower bound and coherent processing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1538–1556. [Google Scholar] [CrossRef]
- Betz, J.W.; Kolodziejski, K.R. Generalized theory of code tracking with an early-late discriminator part II: Noncoherent processing and numerical results. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1557–1564. [Google Scholar] [CrossRef]
- Lohan, E.S. Analytical performance of CBOC-modulated Galileo E1 signal using sine BOC(1,1) receiver for mass-market applications. In Proceedings of the Position Location and Navigation Symposium (PLANS), 2010 IEEE/ION, Indian Wells, CA, USA, 4–6 May 2010; pp. 245–253.
- Anantharamu, P.B.; Borio, O.; Lachapelle, G. Space-Time Equalization Techniques for New GNSS Signals. Ph.D Thesis, University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Yao, Z.; Lu, M. Lower bound on spreading code tracking error under unmatched de-spreading mode. Electron. Lett. 2011, 47, 878–879. [Google Scholar] [CrossRef]
- Proakis, J.; Salehi, M. Digital Communications, 5th ed.; McGraw-Hill Science/Engineering/Math: Boston, MA, USA, 2007. [Google Scholar]
- Thayaparan, S.; Ng, T.-S.; Wang, J. Half-sine and triangular despreading chip waveforms for coherent delay-locked tracking in DS/SS systems. IEEE Trans. Commun. 2000, 48, 1384–1391. [Google Scholar] [CrossRef]
- Wu, X.; Ling, C.; Xiang, H. Despreading chip waveform design for coherent delay-locked tracking in DS/SS systems. In Proceedings of the IEEE International Conference on Communications, 2002, ICC 2002, New York, NY, USA, 28 April–2 May 2002; Volume 1, pp. 631–635.
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications, 2nd ed.; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- James, J.S., Jr.; Penina, A.; Parkinson, B.W. Per Enge “Multipath Effect”, Global Positioning System: Theory and Applications, Volume I; Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Washington, DC, USA, 1996. [Google Scholar]
- Yao, Z.; Lu, M. Constant Envelope Combination for Components on Different Carrier Frequencies with Unequal Power Allocation. In Proceedings of the ION ITM 2013, San Diego, CA, USA, 27–29 January 2013; pp. 629–637.
- Yao, Z.; Lu, M. Design, Implementation, and Performance Analysis of ACE-BOC Modulation. In Proceedings of the ION GNSS+ 2013, Nashville, TN, USA, 16–20 September 2013; pp. 361–368.
- Yao, Z.; Zhang, J.; Lu, M. ACE-BOC: Dual-frequency Constant Envelope Multiplexing for Satellite Navigation. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 466–485. [Google Scholar] [CrossRef]
- Shivaramaiah, N.C.; Dempster, A.G.; Rizos, C. Hybrid tracking loop architectures for the Galileo E5 signal. In Proceedings of the European Navigation Conference on Global Navigation Satellite Systems ENC GNSS, Citeseer, Braunschweig, Germany, 19–21 October 2009.
- Hein, G.W.; Avila-Rodriguez, J.-A.; Wallner, S.; Pratt, A.R.; Owen, J.; Issler, J.-L.; Betz, J.W.; Hegarty, C.J.; Lenahan, L.S.; Rushanan, J.J.; et al. MBOC: The new optimized spreading modulation recommended for GALILEO L1 OS and GPS L1C. Proc. IEEEION PLANS 2006, 2006, 884–892. [Google Scholar]
- Rodríguez, J.Á.Á.; Hein, G.W.; Wallner, S.; Issler, J.-L.; Ries, L.; Lestarquit, L.; Latour, A.; de Godet, J.; Bastide, F.; Pratt, T.; et al. The MBOC modulation: The final touch to the Galileo frequency and signal plan. Navigation 2008, 55, 15–28. [Google Scholar]
- Yao, Z.; Lu, M.; Feng, Z.M. Quadrature multiplexed BOC modulation for interoperable GNSS signals. Electron. Lett. 2010, 46, 1234–1236. [Google Scholar] [CrossRef]
- Yao, Z.; Lu, M. Optimized modulation for Compass B1-C signal with multiple processing modes. In Proceedings of the ION GNSS 24th International Technical Meeting of the Satellite Division, Portland, MA, USA, 19–23 September 2011; pp. 1234–1242.
| Receiving Central Frequency(fr) | Receiving Components | |
|---|---|---|
| BLR | f0 − fsc | sLQ |
| IMR | f0 | sLQ |
| FMR | f0 | Integral signal |
| Central Frequency of Narrowband Interference | Bandwidth of Narrowband Interference | Bandwidth of Bandlimited Interference |
|---|---|---|
| fr ± 1 MHz 1 | 10 kHz | 5 MHz |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Yao, Z.; Lu, M. Generalized Theory and Decoupled Evaluation Criteria for Unmatched Despreading of Modernized GNSS Signals. Sensors 2016, 16, 1128. https://doi.org/10.3390/s16071128
Zhang J, Yao Z, Lu M. Generalized Theory and Decoupled Evaluation Criteria for Unmatched Despreading of Modernized GNSS Signals. Sensors. 2016; 16(7):1128. https://doi.org/10.3390/s16071128
Chicago/Turabian StyleZhang, Jiayi, Zheng Yao, and Mingquan Lu. 2016. "Generalized Theory and Decoupled Evaluation Criteria for Unmatched Despreading of Modernized GNSS Signals" Sensors 16, no. 7: 1128. https://doi.org/10.3390/s16071128
APA StyleZhang, J., Yao, Z., & Lu, M. (2016). Generalized Theory and Decoupled Evaluation Criteria for Unmatched Despreading of Modernized GNSS Signals. Sensors, 16(7), 1128. https://doi.org/10.3390/s16071128





