The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation
Abstract
:1. Introduction
2. Related Work
3. Method
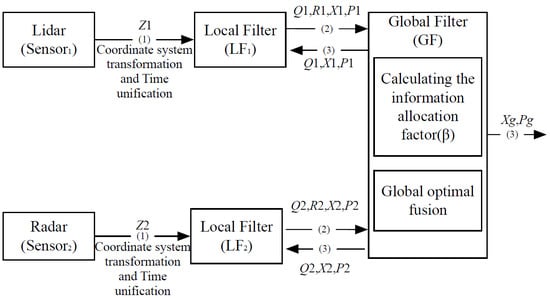
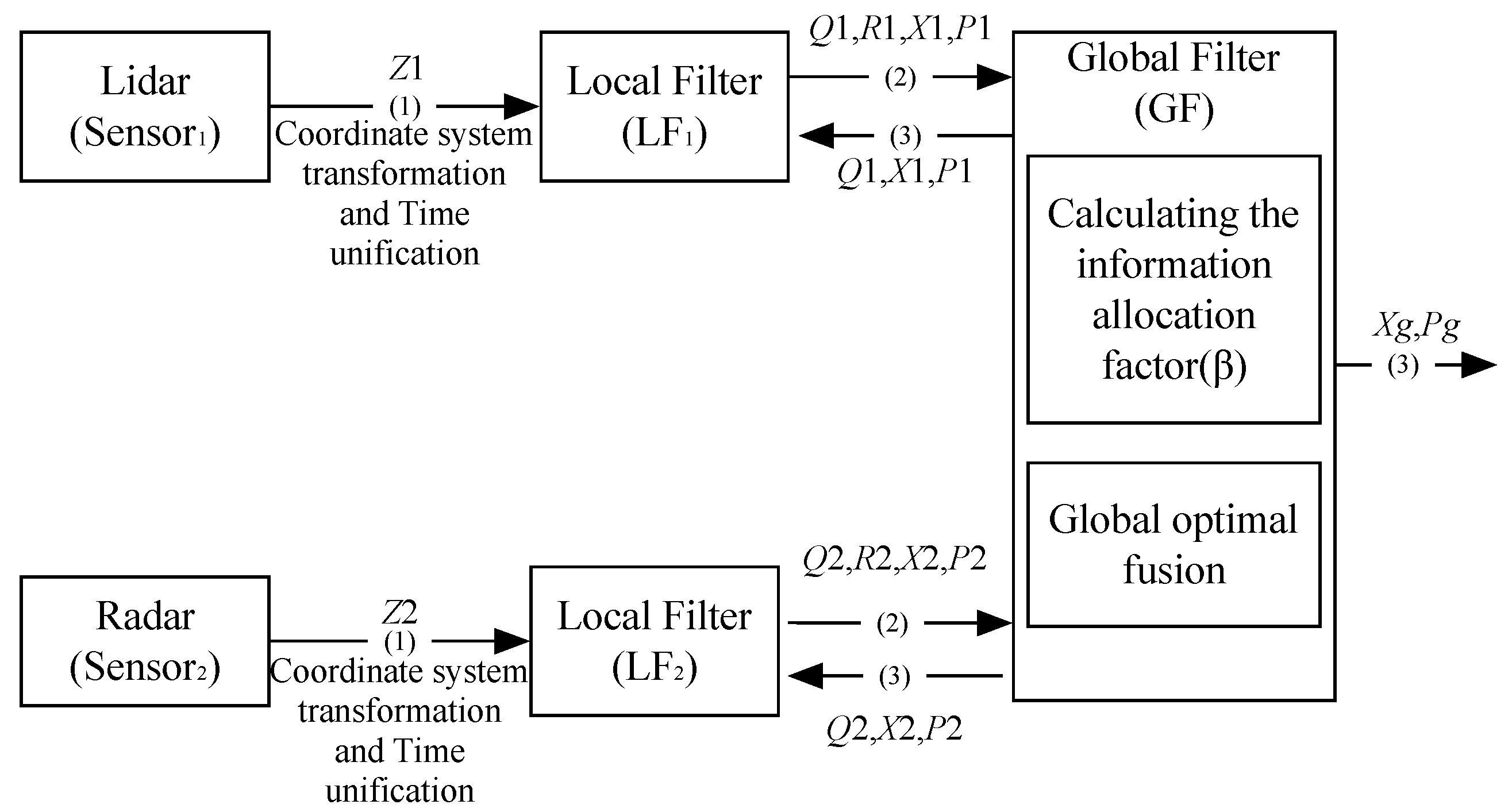
3.1. The Structure of JAKF
3.2. Local Kalman Filter
3.3. Global Kalman Filter
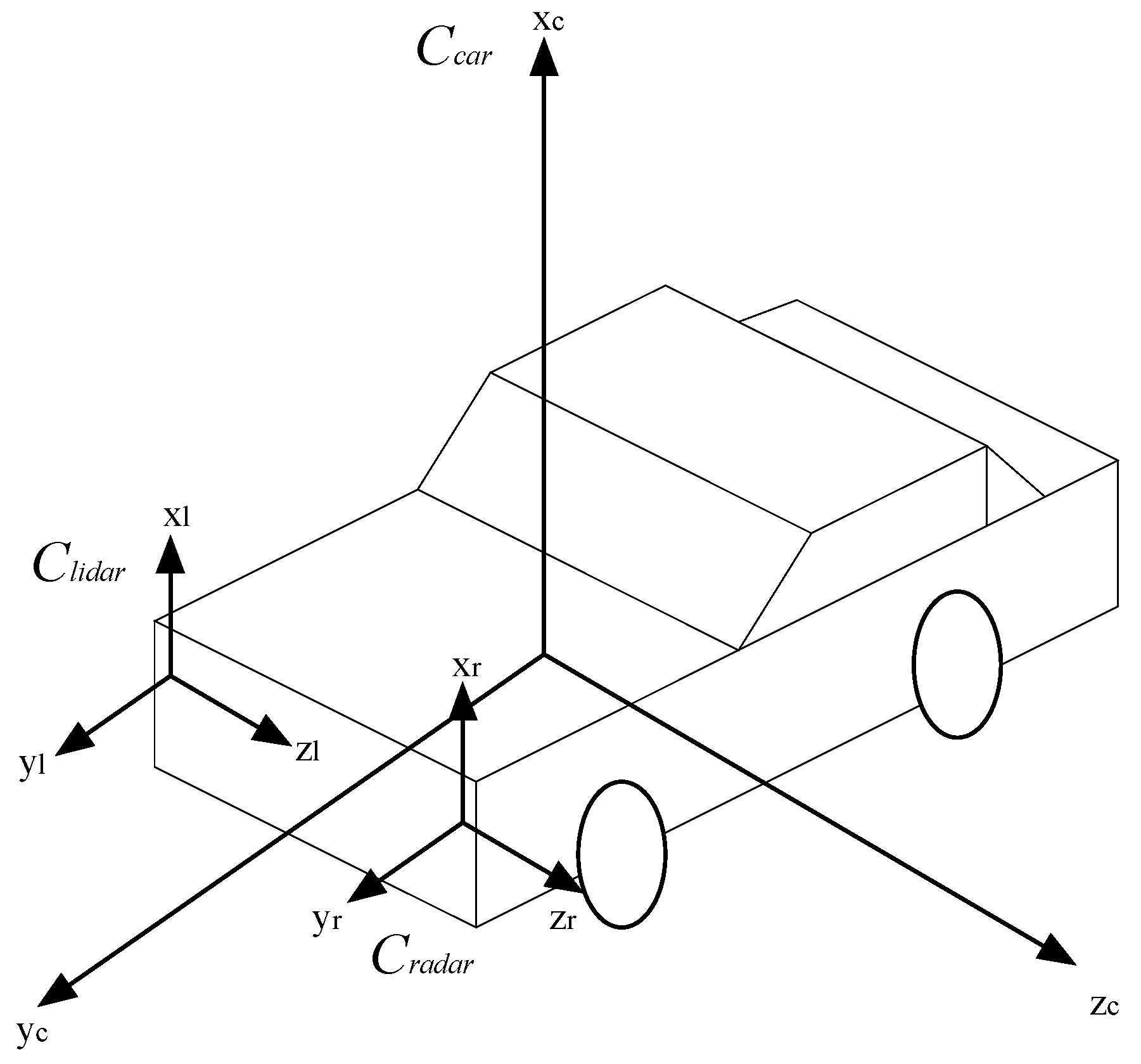
3.4. Coordinate Transformation
3.5. Time Synchronization
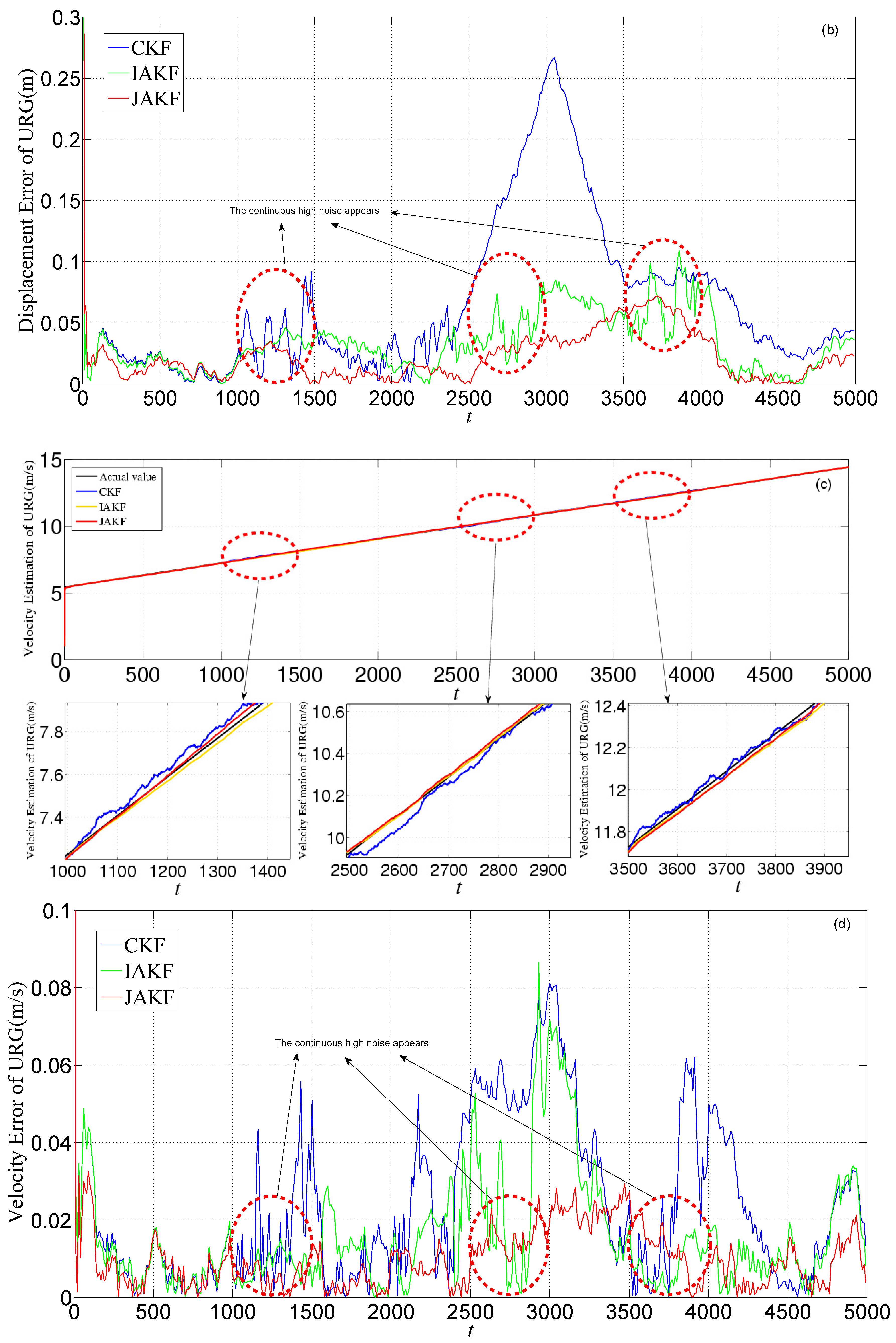
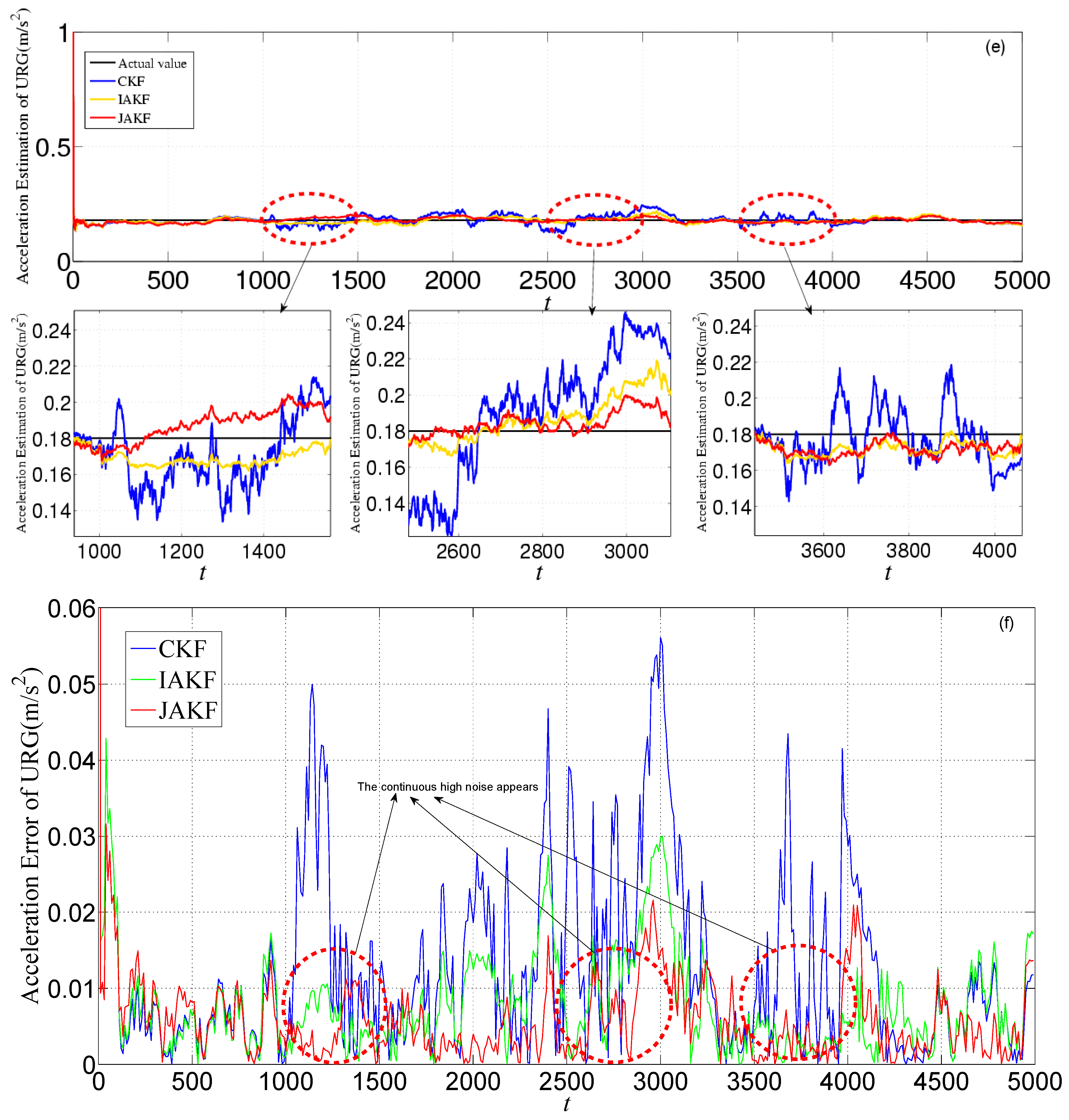
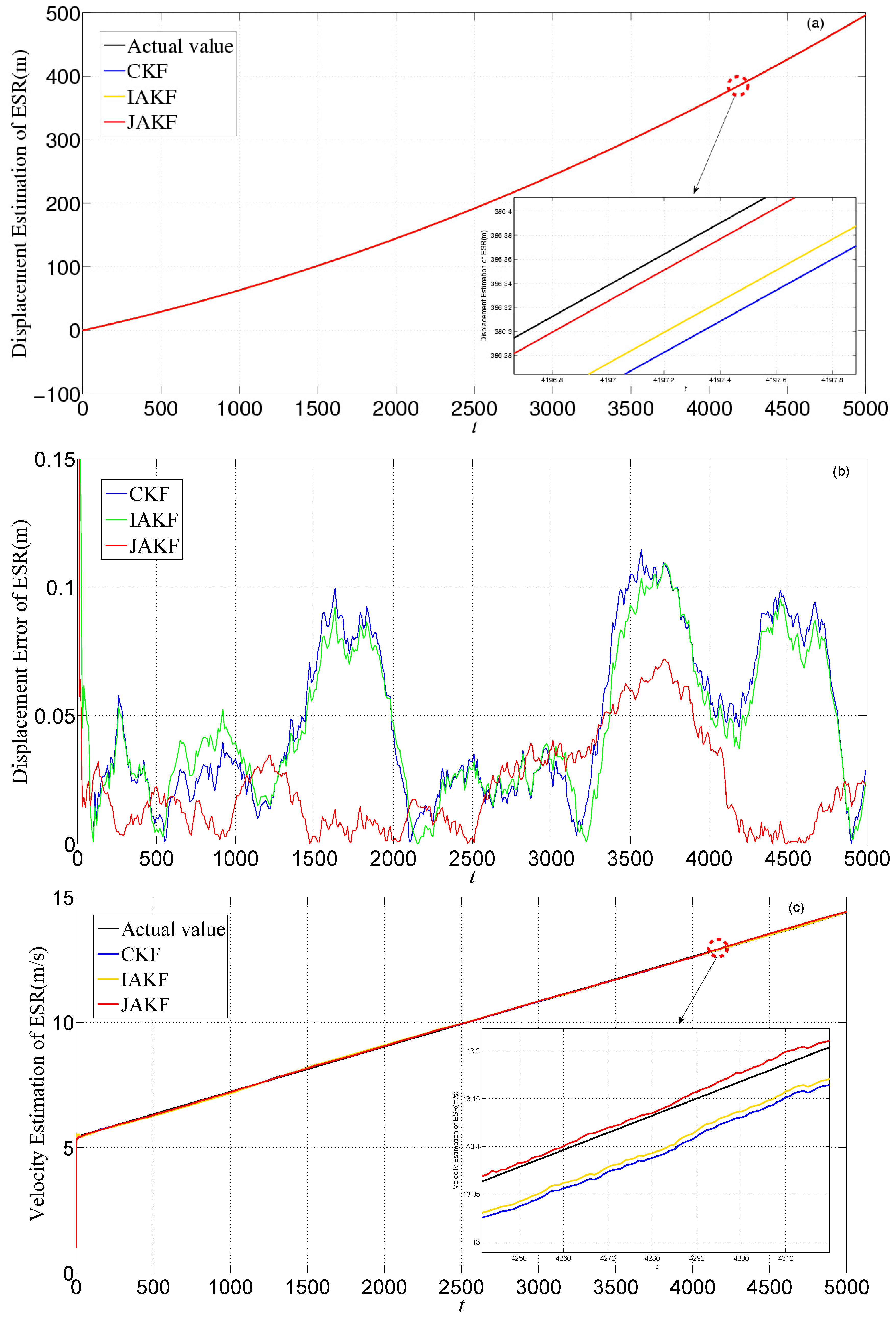
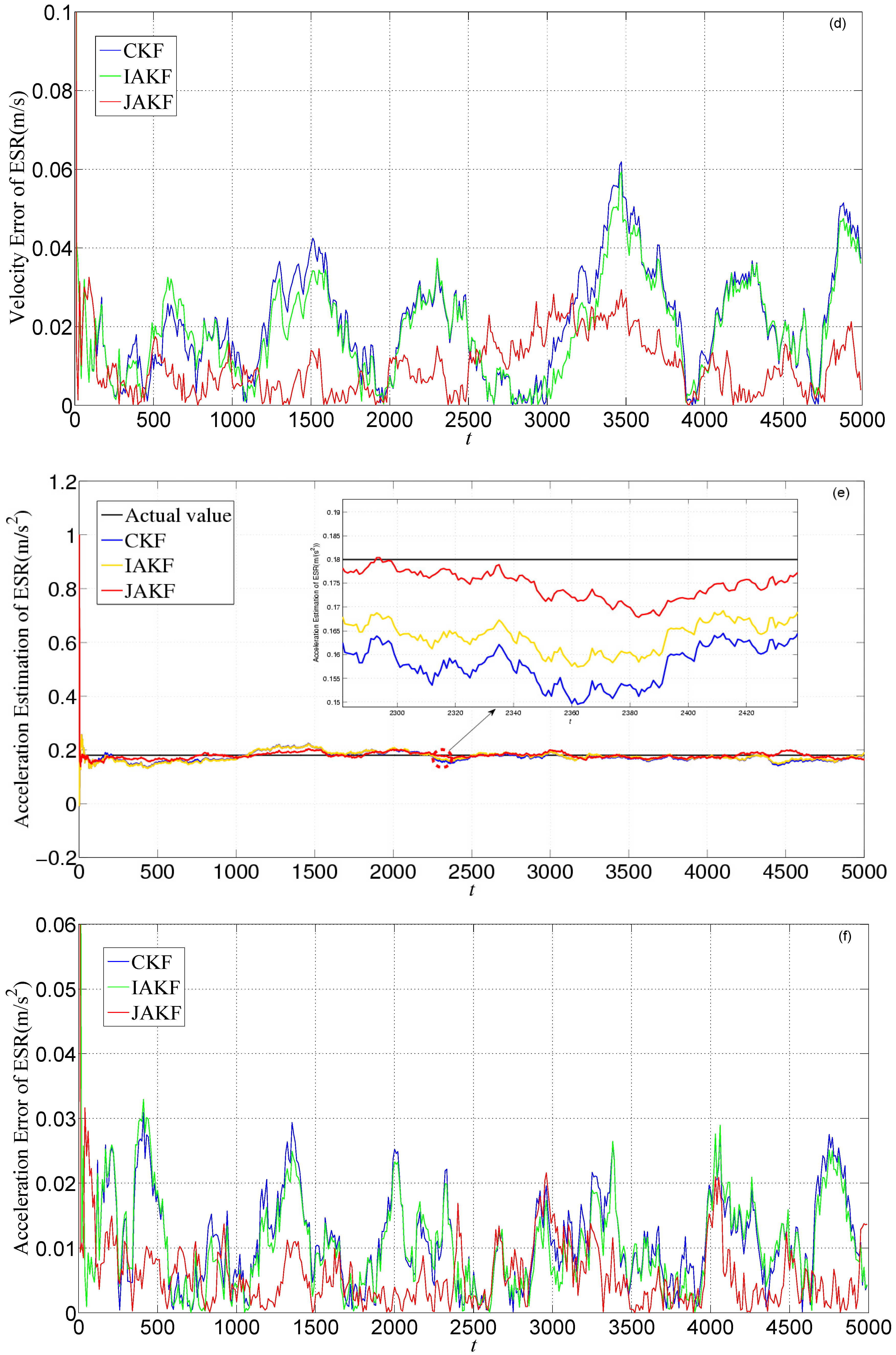
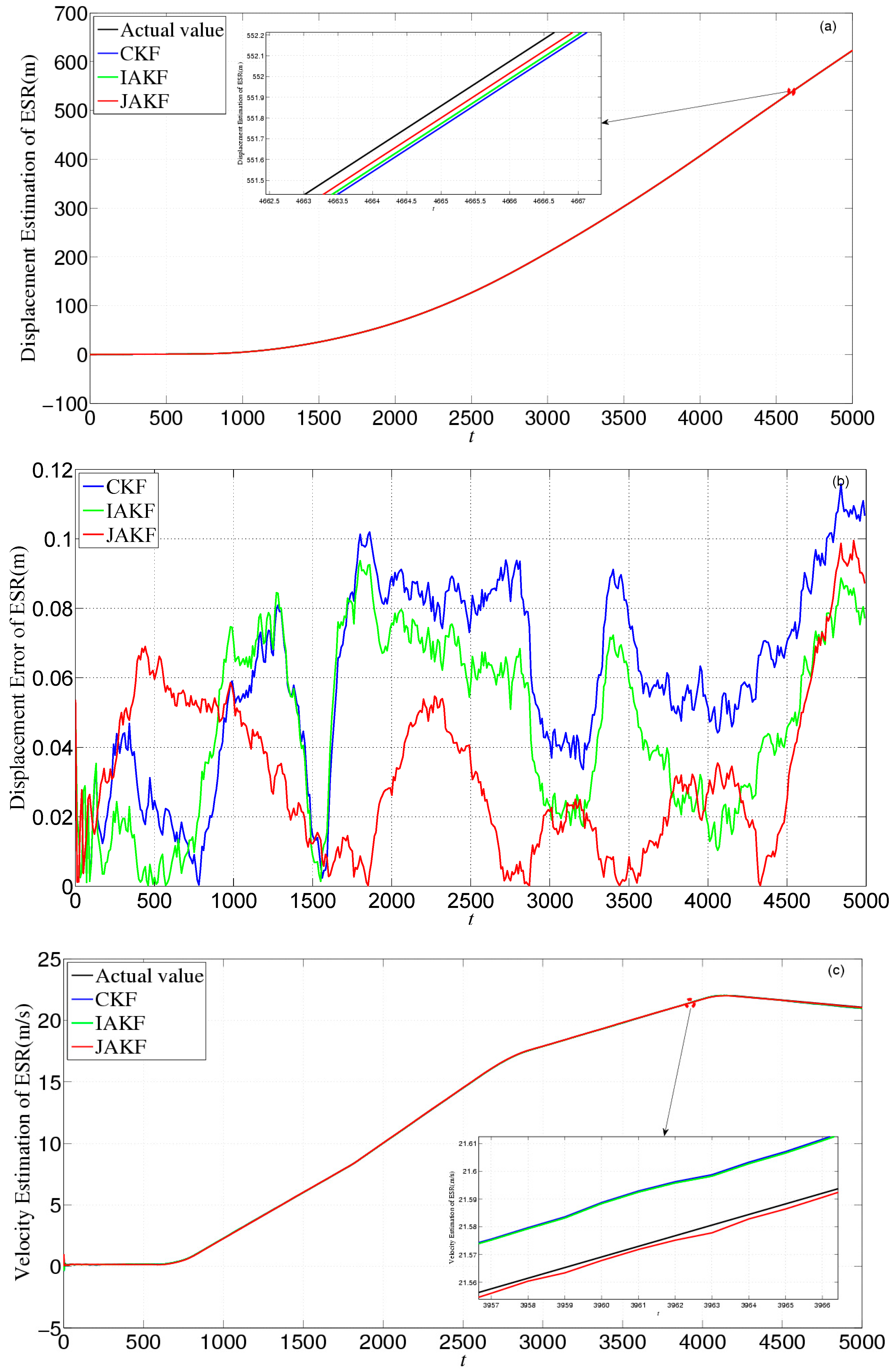
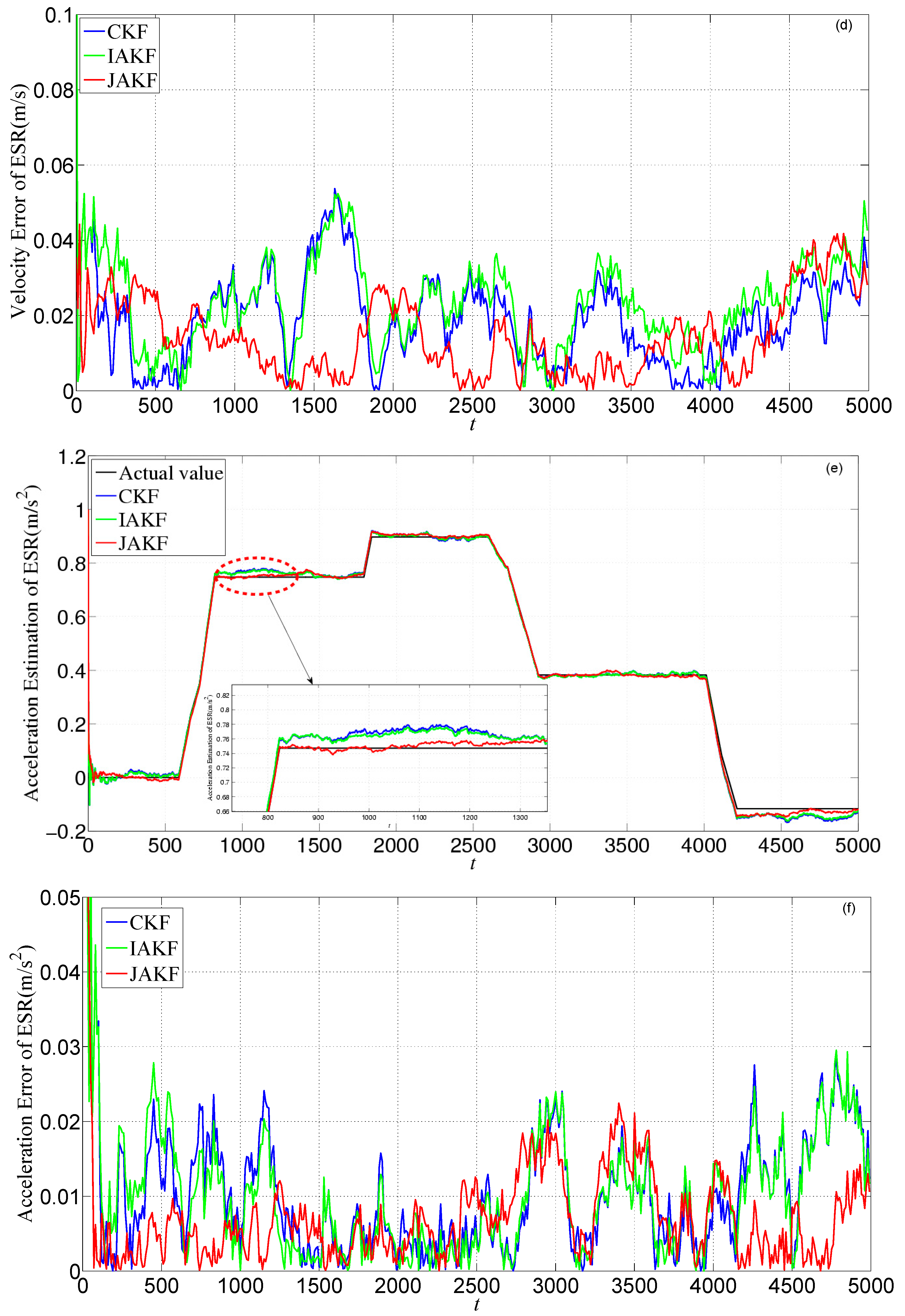
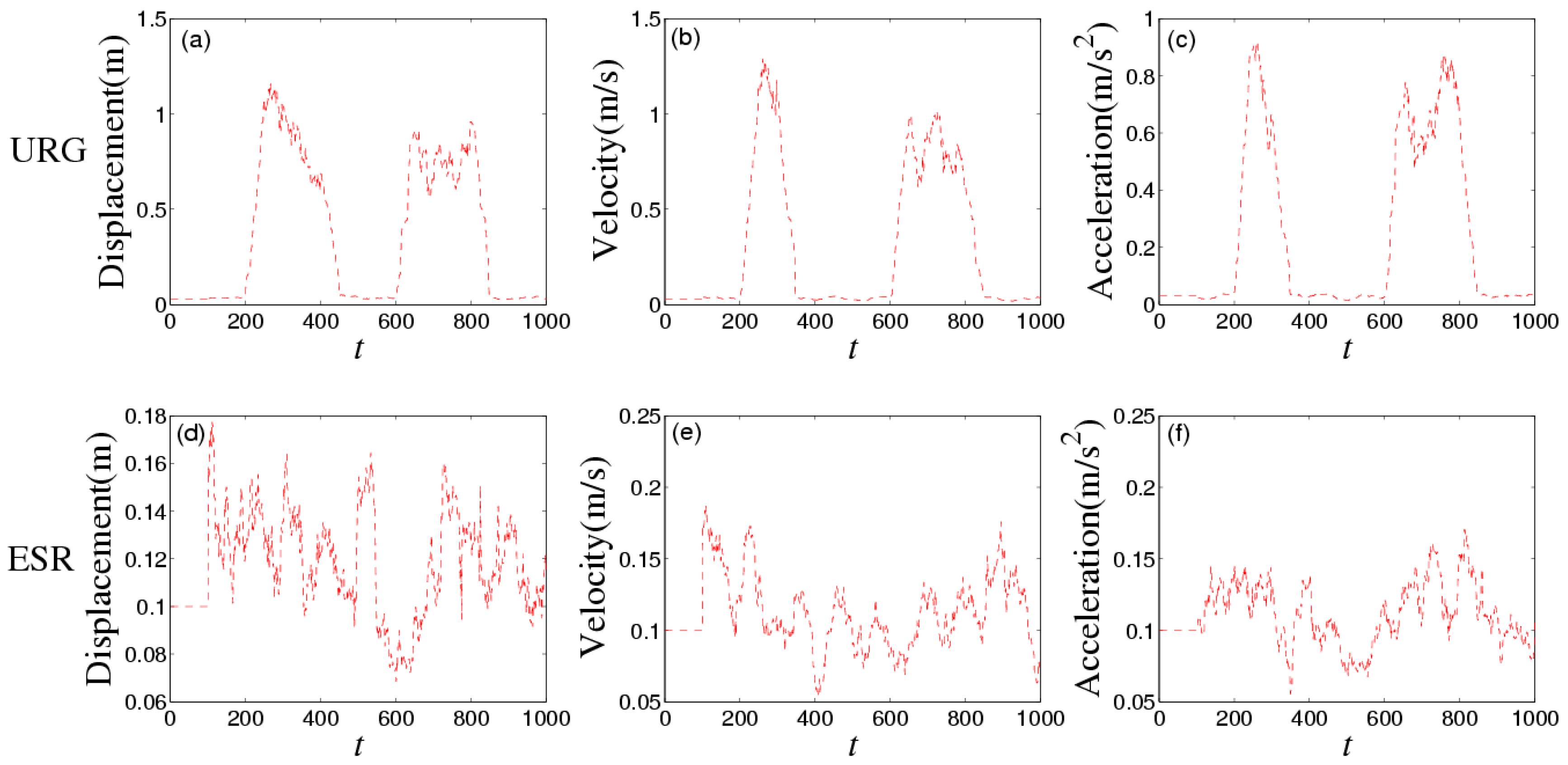
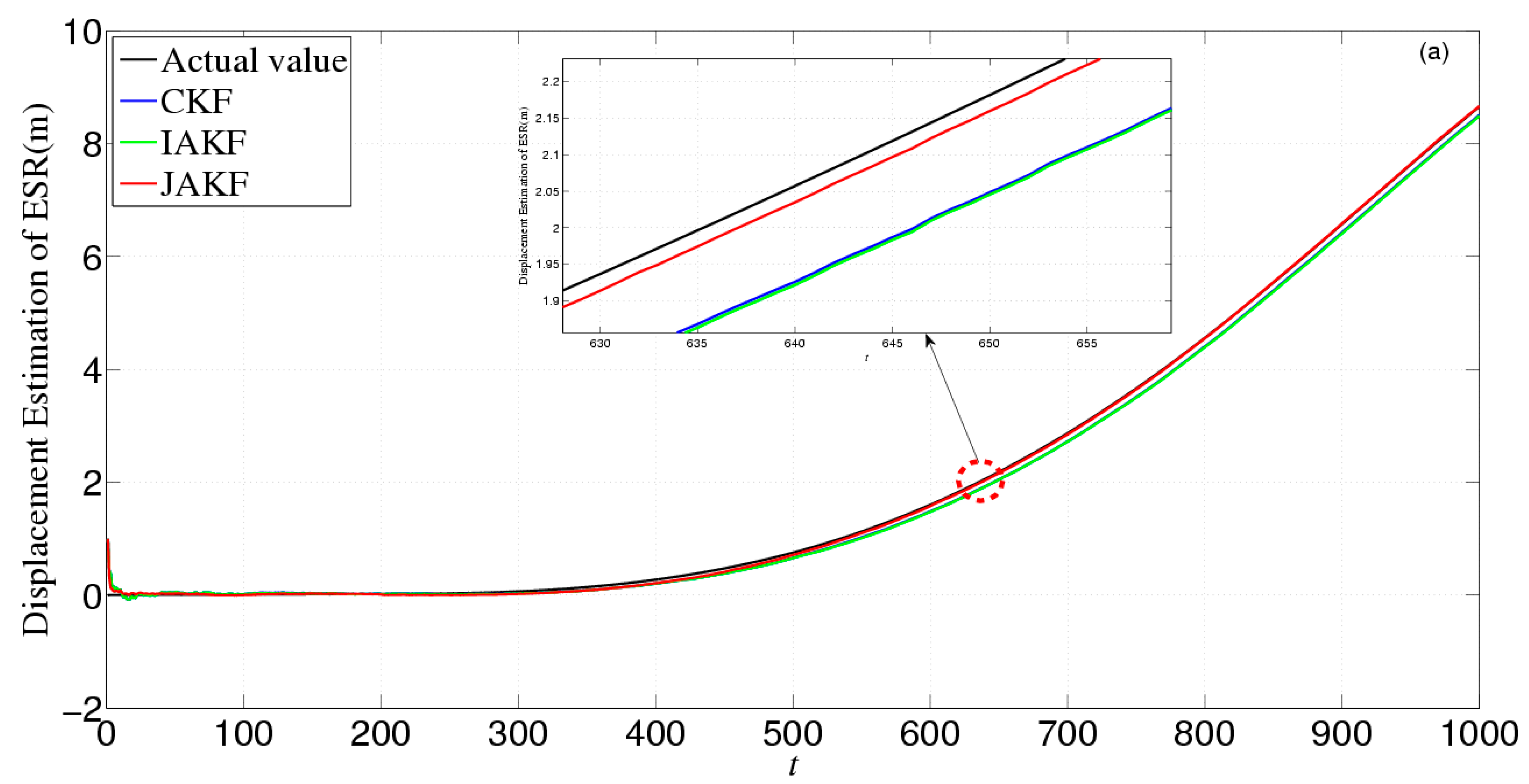
4. Results
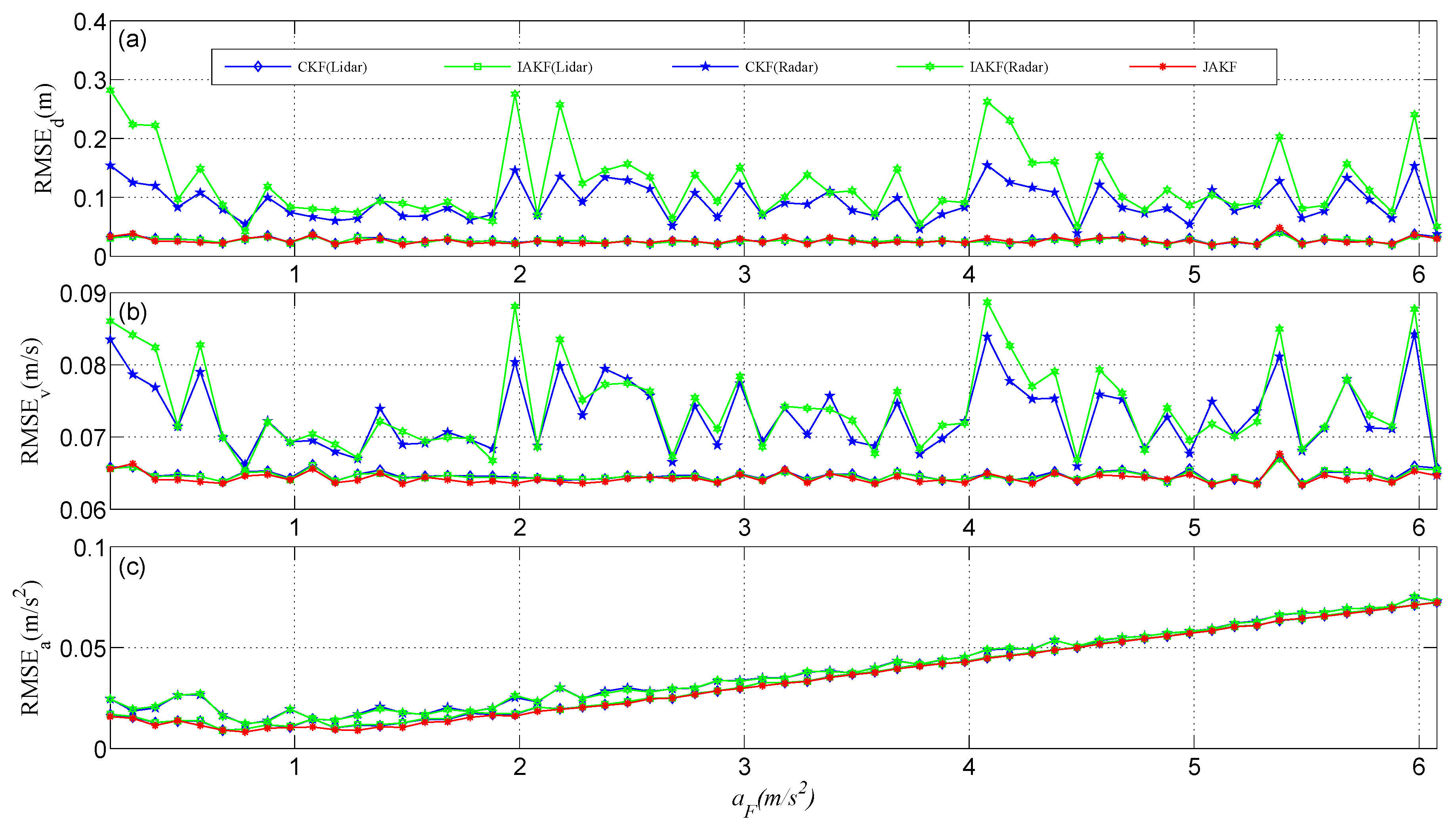
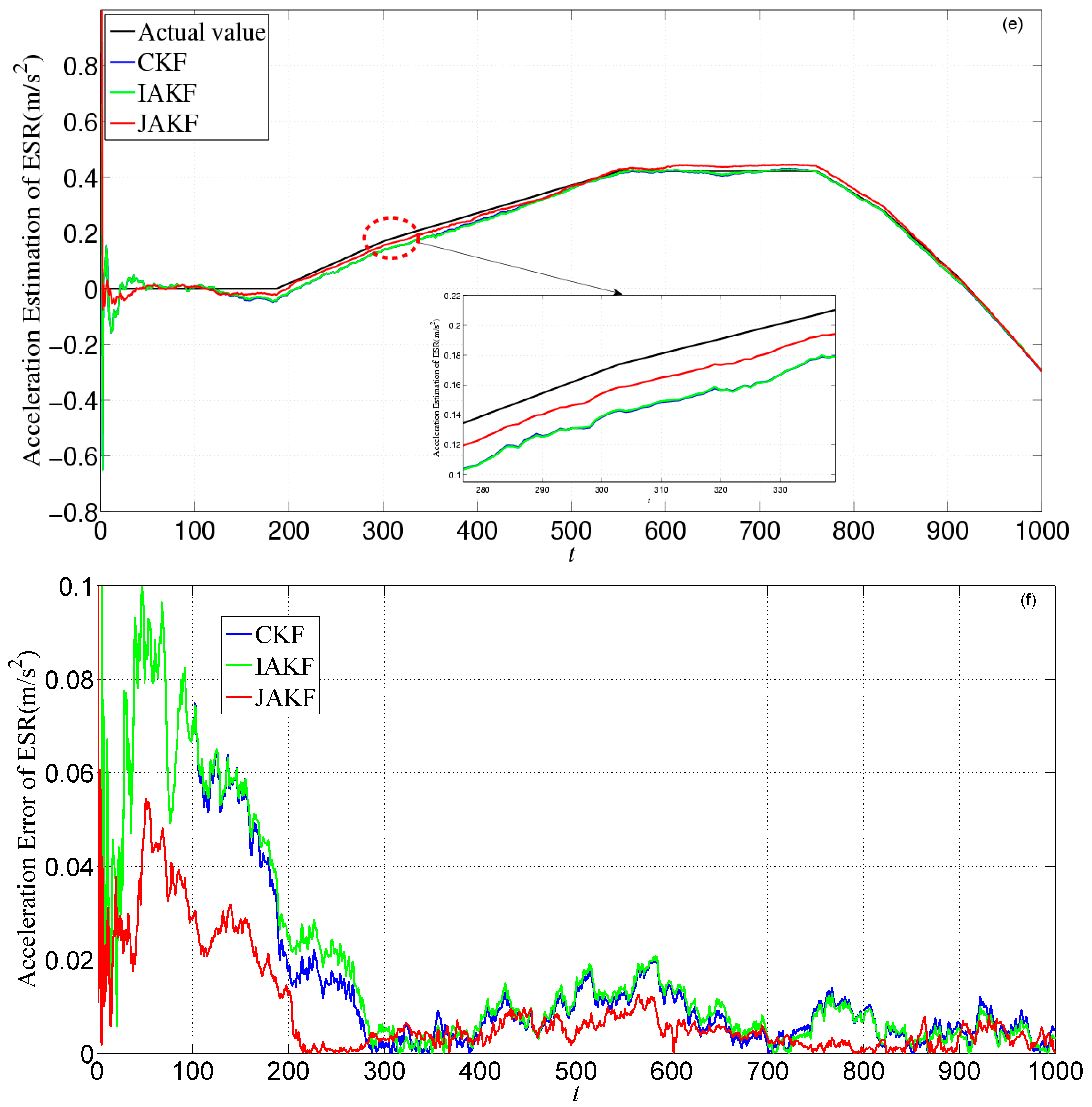
4.1. Simulation
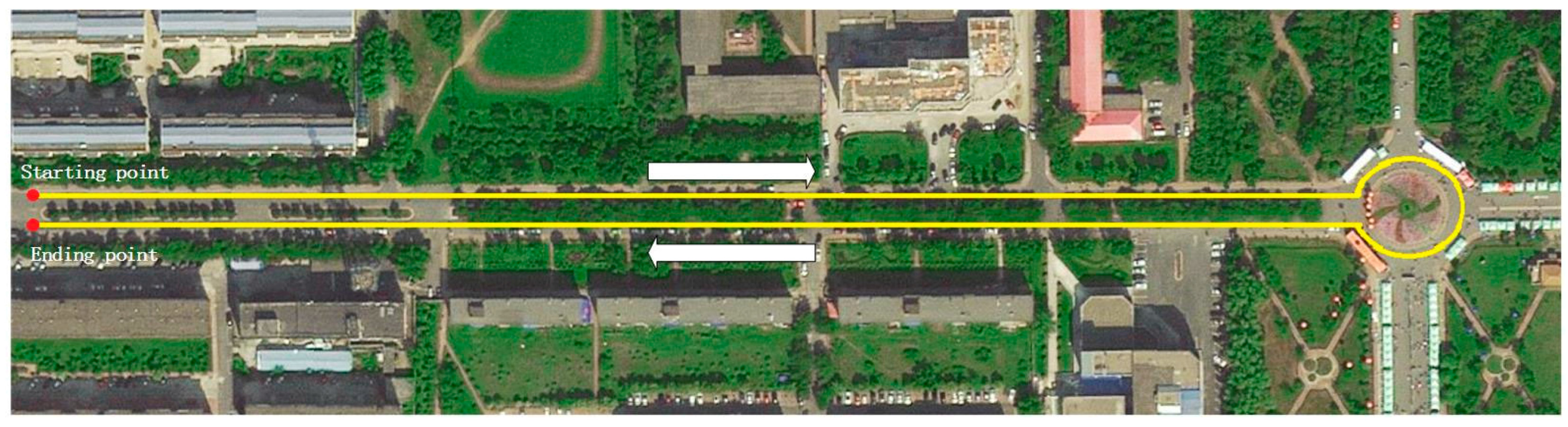
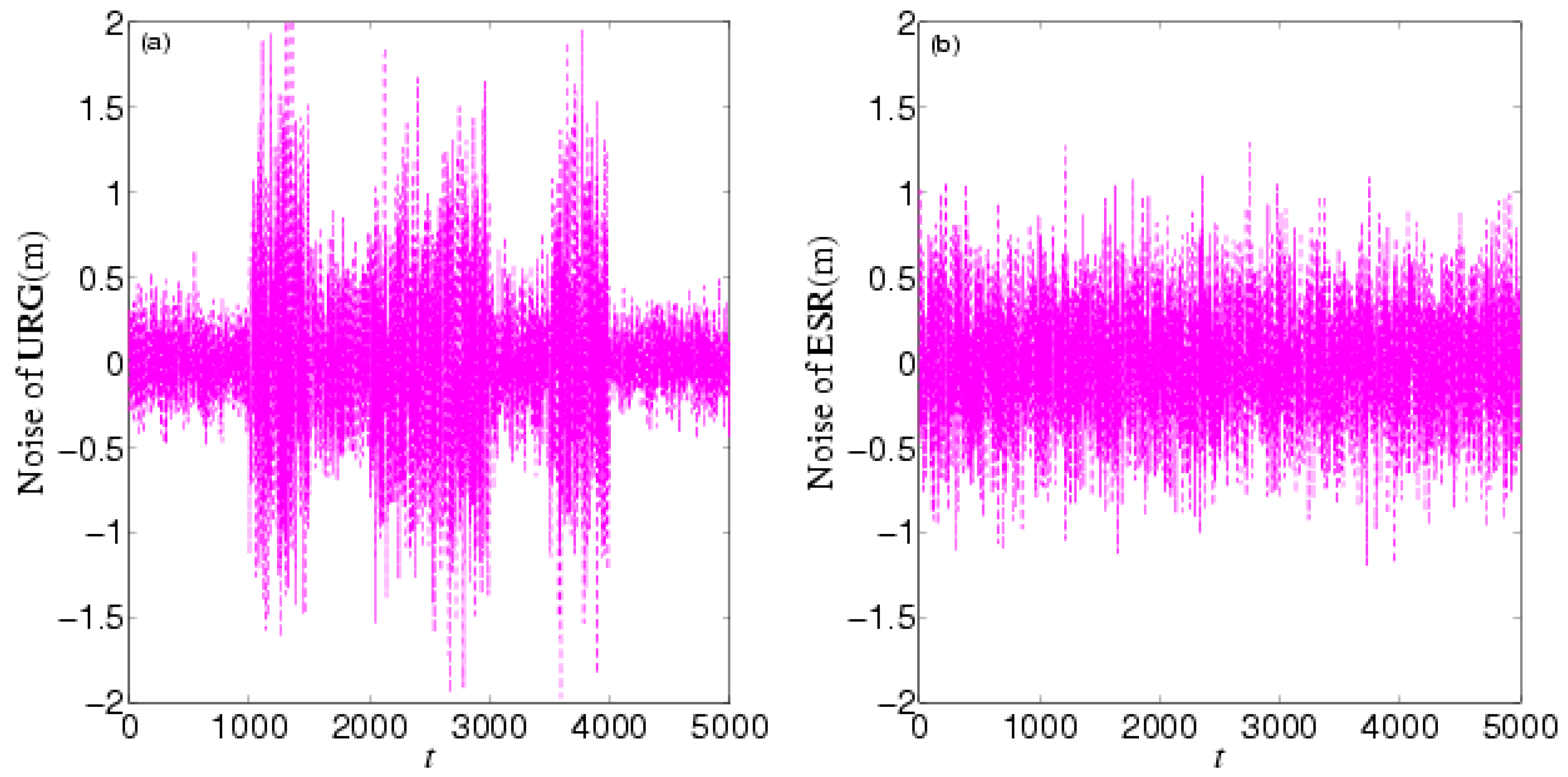
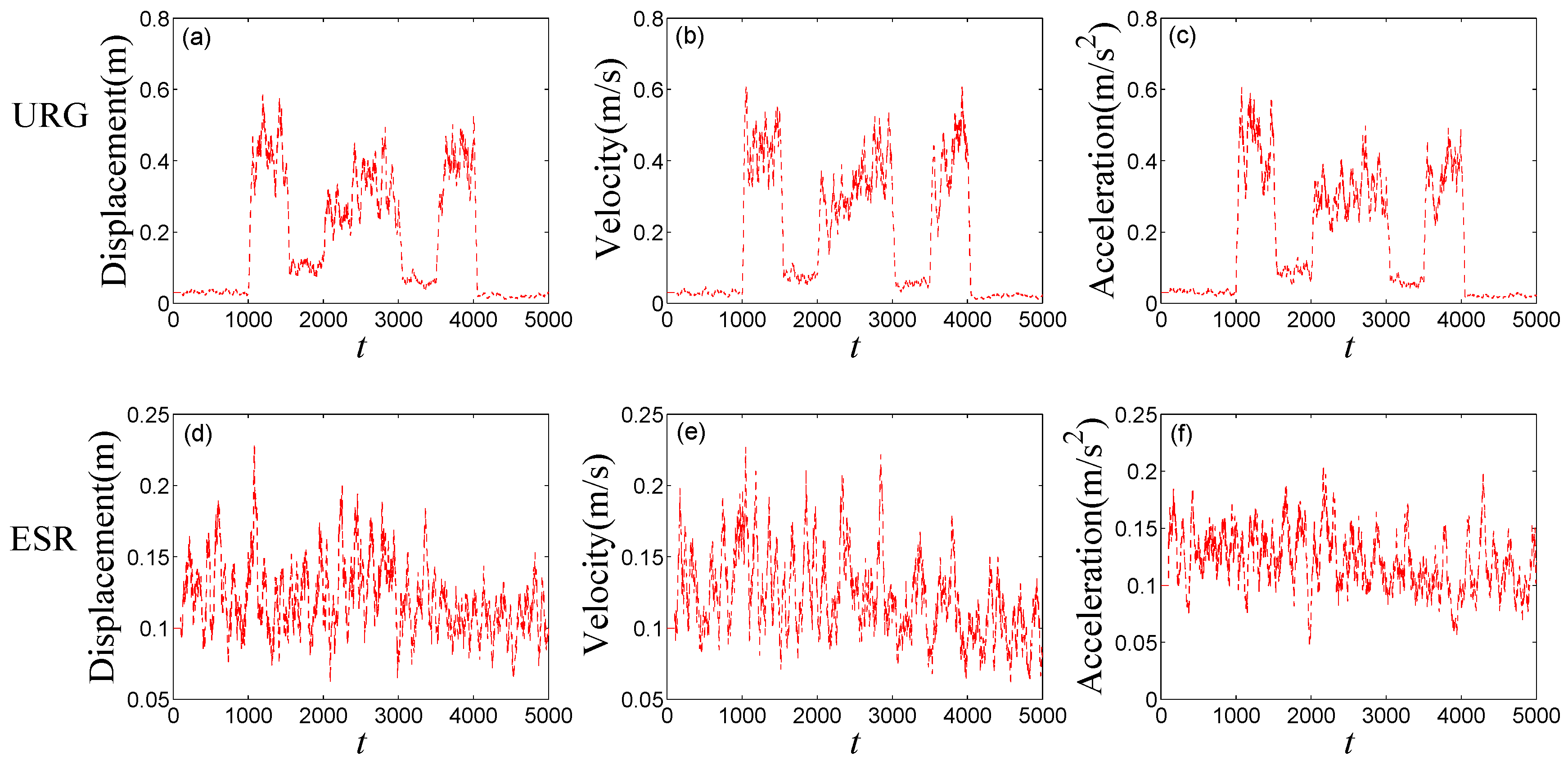
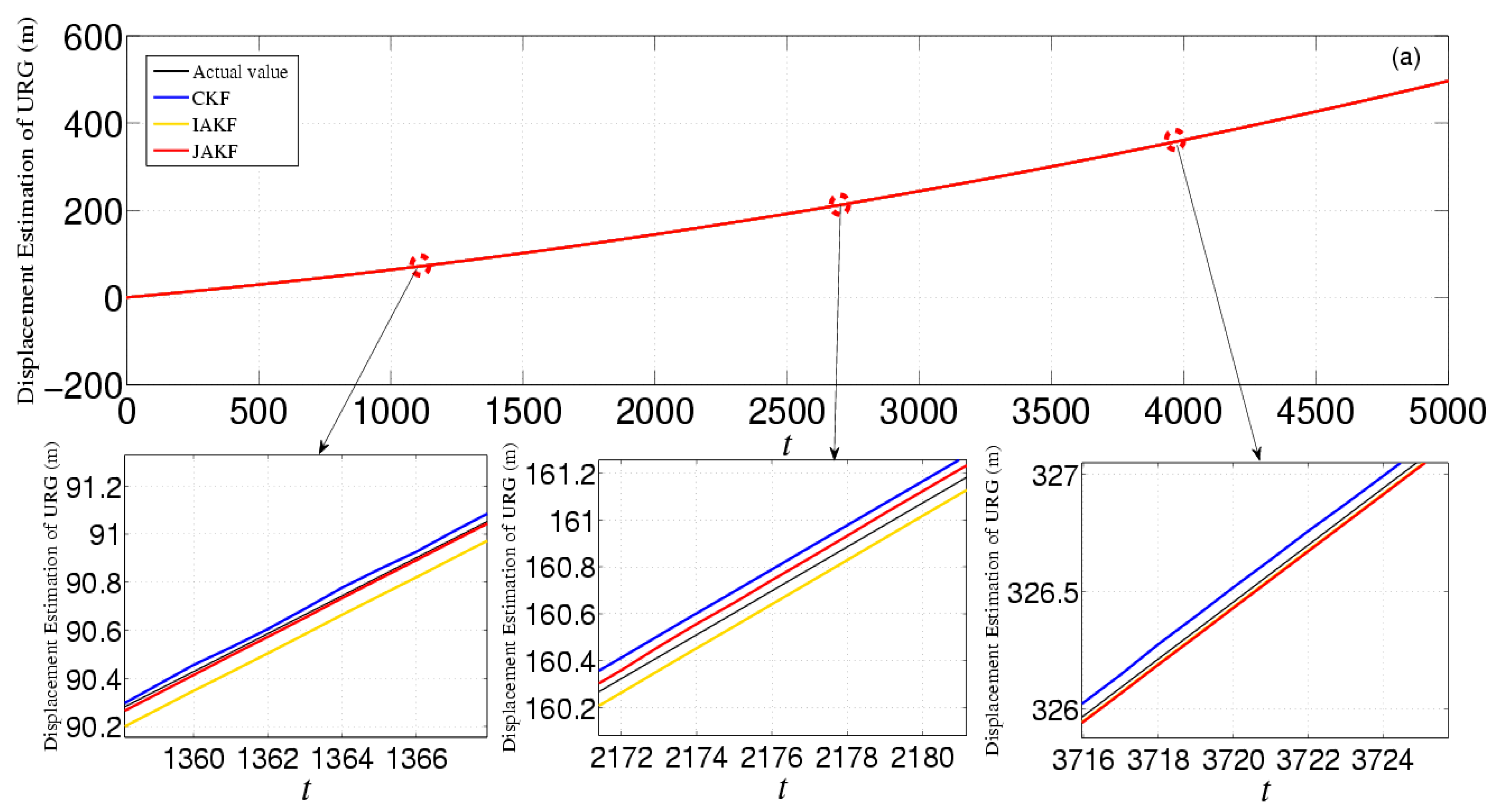
4.2. Experiment
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Darms, M.S.; Rybski, P.E.; Baker, C.; Urmson, C. Obstacle detection and tracking for the urban challenge. IEEE Trans. Intell. Transp. Syst. 2009, 10, 475–485. [Google Scholar] [CrossRef]
- Leonard, J.; How, J.; Teller, S.; Berger, M.; Campbell, S.; Fiore, G.; Fletcher, L.; Frazzoli, E.; Huang, A.; Karaman, S.; et al. A perception-driven autonomous urban vehicle. J. Field Robot. 2008, 25, 727–774. [Google Scholar] [CrossRef]
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnkeand, B.; et al. Junior: The stanford entry in the urban challenge. J. Field Robot. 2008, 25, 569–597. [Google Scholar]
- Fiorino, S.T.; Bartell, R.J.; Cusumano, S.J. Worldwide uncertainty assessments of ladar and radar signal-to-noise ratio performance for diverse low altitude atmospheric environments. J. Appl. Remote Sens. 2010, 4, 1312–1323. [Google Scholar] [CrossRef]
- Vostretsov, N.A.; Zhukov, A.F. About temporary autocorrelation function of fluctuations of the scattered radiation of the focused laser beam (0.63 mm) in the surface atmosphere in rain, drizzle and fog. Int. Symp. Atmos. Ocean Opt. Atmo. Phys. 2015. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, H.; Zhang, X.J. Propagating characteristics of pulsed laser in rain. Int. J. Antennas Propag. 2015, 4, 1–7. [Google Scholar] [CrossRef]
- Hollinger, J.; Kutscher, B.; Close, R. Fusion of lidar and radar for detection of partially obscured objects. SPIE Def. Secur. Int. Soc. Opt. Photonics 2015, 1–9. [Google Scholar] [CrossRef]
- Simon, D.; Chia, T.L. Kalman filtering with state equality constraints. IEEE Trans. Aerosp. Electr. Syst. 2002, 38, 128–136. [Google Scholar] [CrossRef]
- Carlson, N.A.; Berarducci, M.P. Federated Kalman filter simulation results. Navigation 1994, 41, 297–322. [Google Scholar] [CrossRef]
- Mohamed, A.H.; Schwarz, K.P. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aerosp. Electr. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Lee, Y.L.; Chen, Y.W. IMM estimator based on fuzzy weighted input estimation for tracking a maneuvering target. Appl. Math. Model. 2015, 39, 5791–5802. [Google Scholar] [CrossRef]
- Close, R. Ground vehicle based LADAR for standoff detection of road-side hazards. SPIE Def. Secur. Int. Soc. Opt. Photonics 2015. [Google Scholar] [CrossRef]
- Hong, S.; Lee, M.H.; Kwon, S.H.; Chun, H.H. A car test for the estimation of GPS/INS alignment errors. IEEE Trans. Intell. Transp. Syst. 2004, 5, 208–218. [Google Scholar] [CrossRef]
- Xian, Z.W.; Hu, X.P.; Lian, J.X. Robust innovation-based adaptive Kalman filter for INS/GPS land navigation. Chin. Autom. Congr. 2013. [Google Scholar] [CrossRef]
- Han, B.; Xin, G.; Xin, J.; Fan, L. A study on maneuvering obstacle motion state estimation for intelligent vehicle using adaptive Kalman filter based on current statistical model. Math. Probl. Eng. 2015, 4, 1–14. [Google Scholar] [CrossRef]
- Mirzaei, F.M.; Roumeliotis, S.I. A Kalman filter-based algorithm for IMU-Camera calibration: Observability analysis and performance evaluation. IEEE Trans. Robot. 2008, 24, 1143–1156. [Google Scholar] [CrossRef]
- Sarunic, P.; Evans, R. Hierarchical model predictive control of UAVs performing multitarget-multisensor tracking. IEEE Trans. Aerosp. Electr. Syst. 2014, 50, 2253–2268. [Google Scholar] [CrossRef]
- Hostettler, R.; Birk, W.; Nordenvaad, M.L. Joint vehicle trajectory and model parameter estimation using road side sensors. IEEE Sens. J. 2015, 15, 5075–5086. [Google Scholar] [CrossRef]
- Naets, F.; Croes, J.; Desmet, W. An online coupled state/input/parameter estimation approach for structural dynamics. Comput. Methods Appl. Mech. Eng. 2015, 283, 1167–1188. [Google Scholar] [CrossRef]
- Chatzi, E.N.; Smyth, A.W. The unscented Kalman filter and particle filter methods for nonlinear structural system identification with non-collocated heterogeneous sensing. Control Health Monit. 2009, 16, 99–123. [Google Scholar] [CrossRef]
- Chatzi, E.N.; Fuggini, C. Online correction of drift in structural identification using artificial white noise observations and an unscented Kalman filter. Smart Struct. Syst. 2015, 16, 295–328. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. Trans. 2015, 82, 35–45. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]



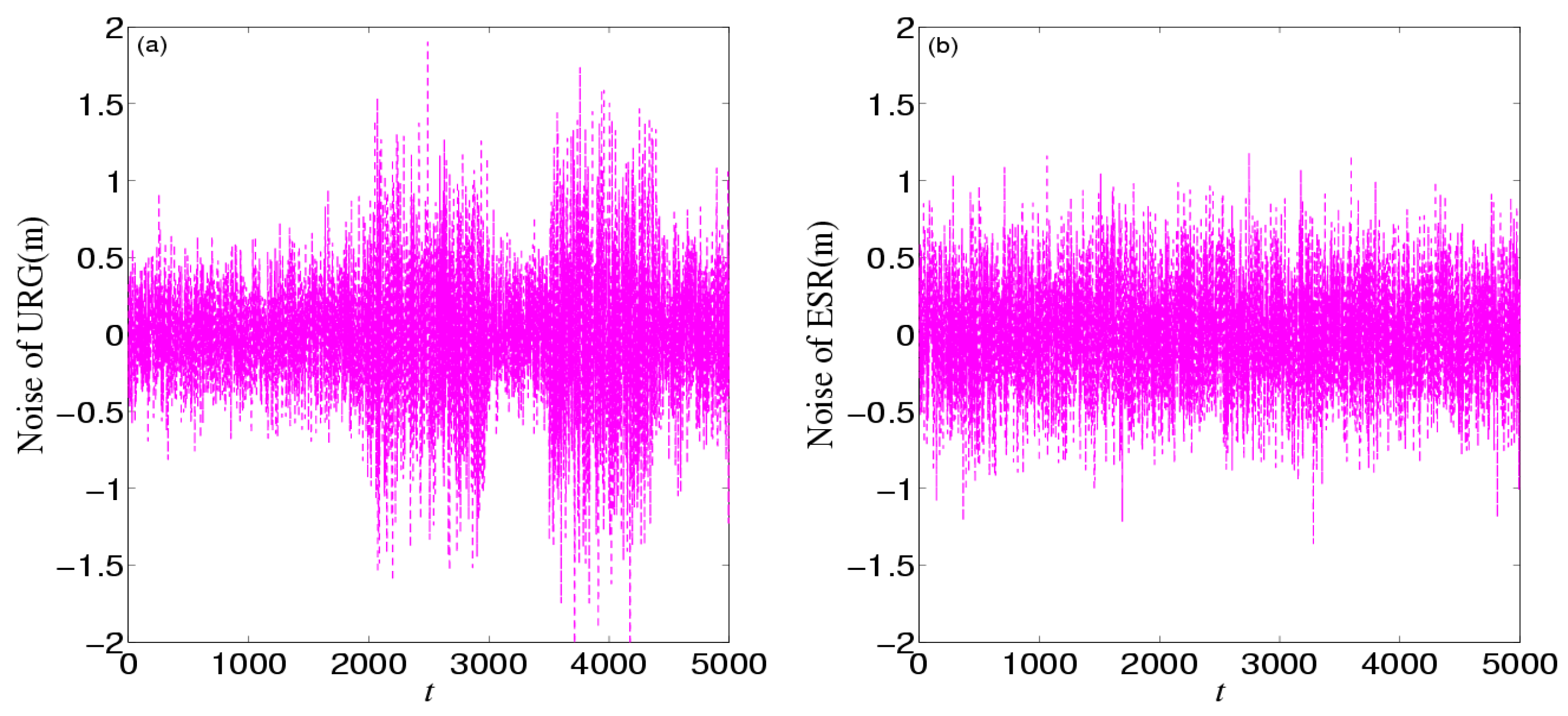
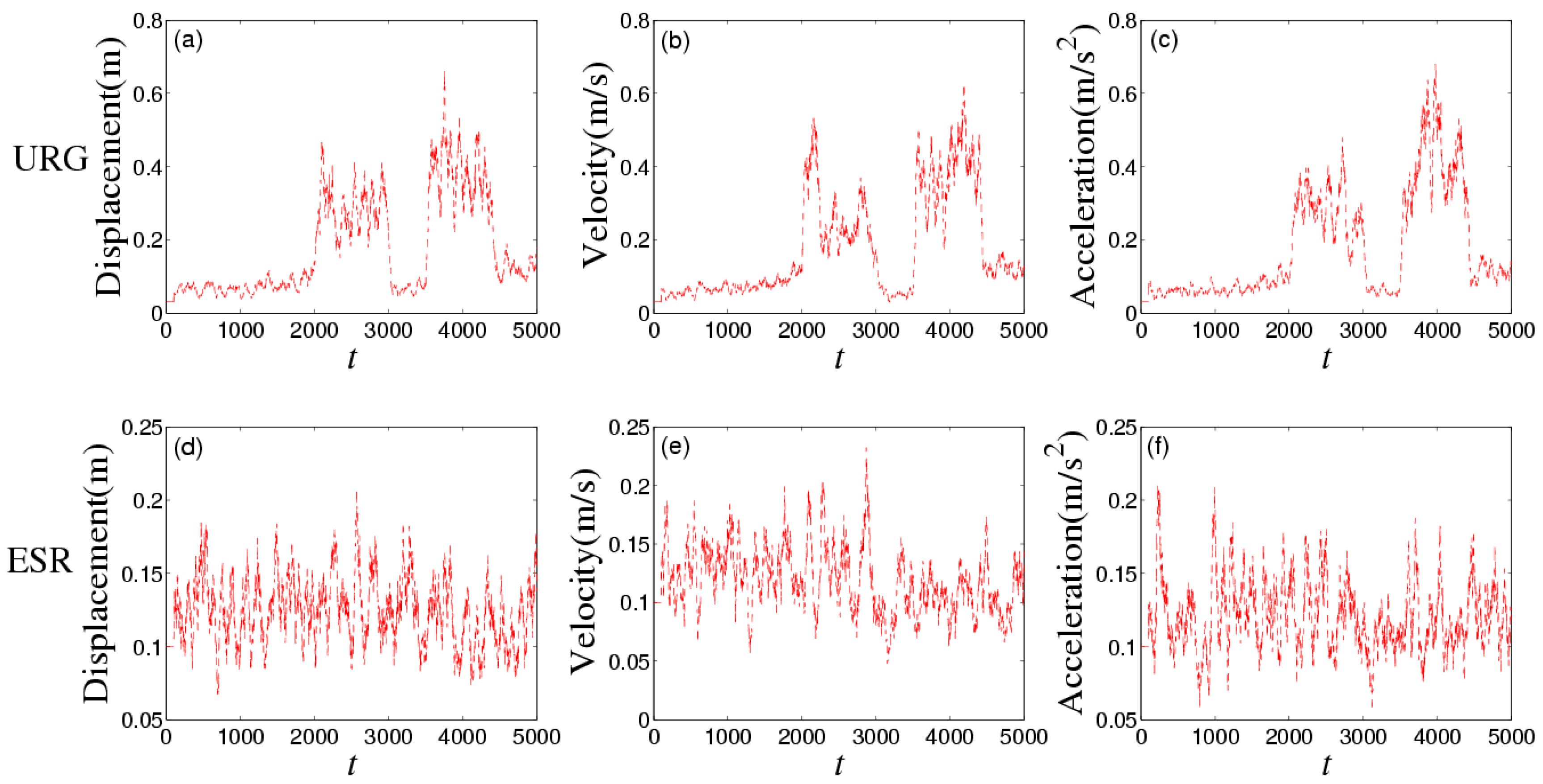
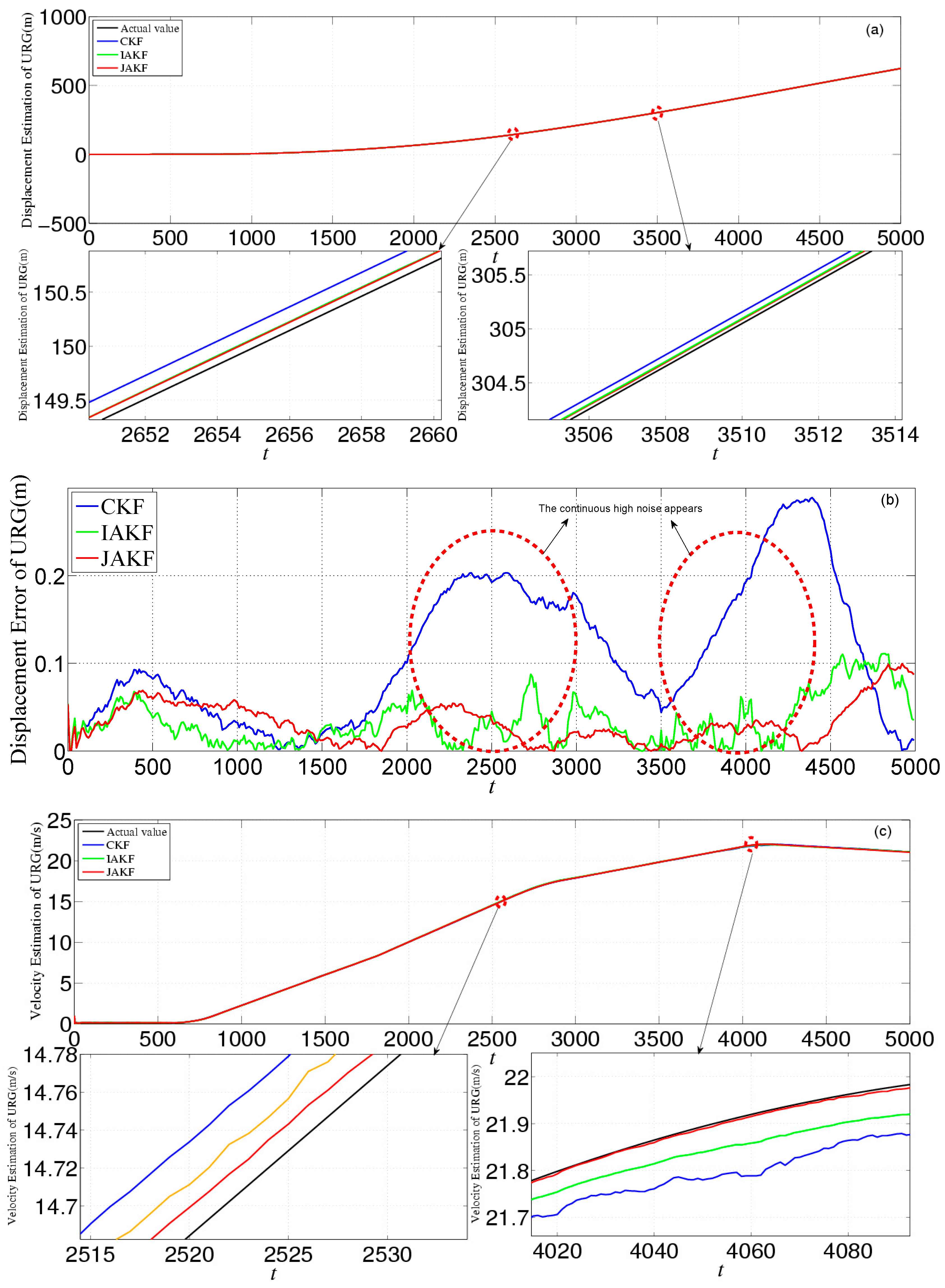
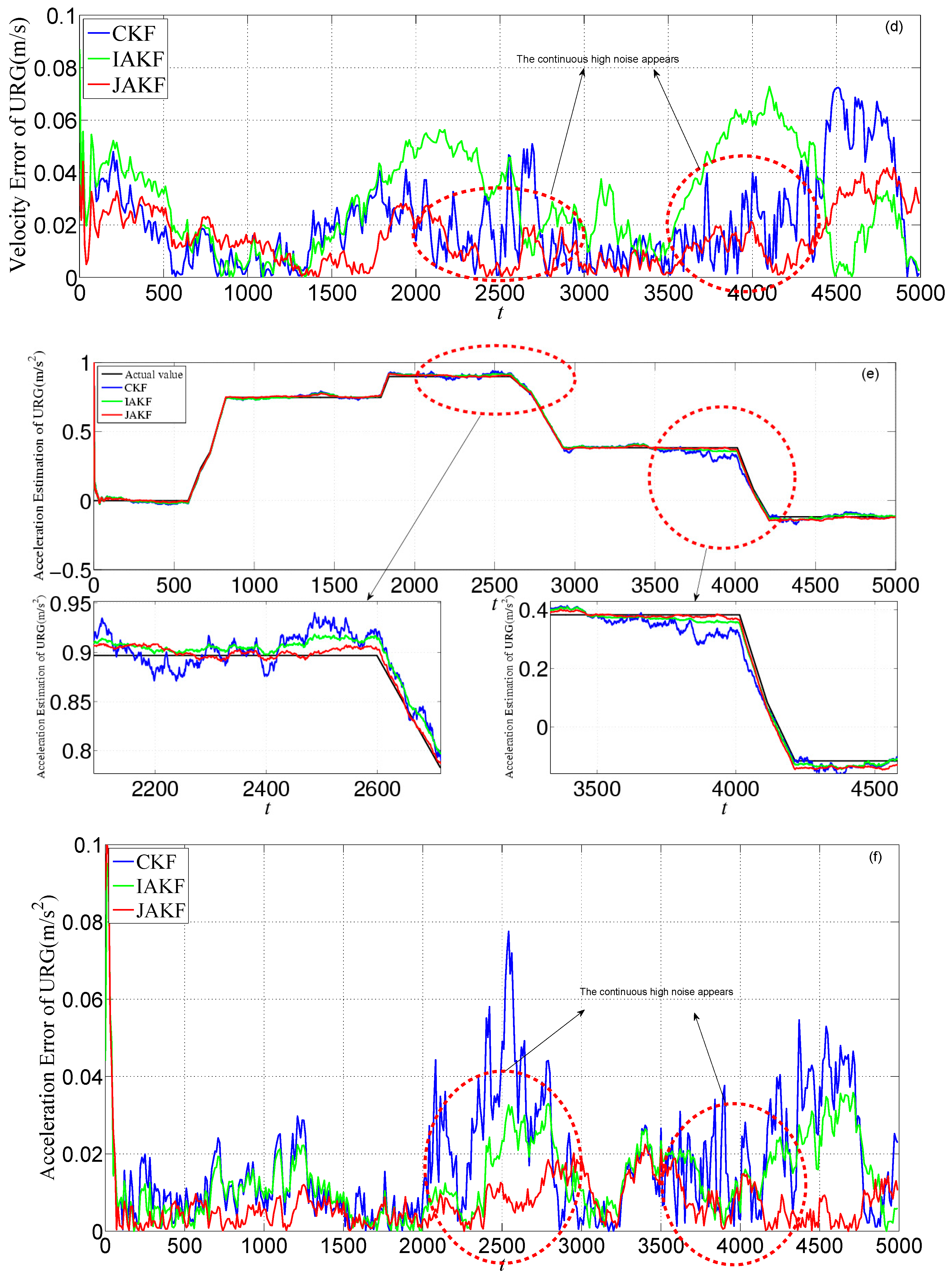





| SNR (dB) | 80 | 81 | 82 | 83 | 84 | 85 | 86 | 87 |
|---|---|---|---|---|---|---|---|---|
| R | 0.0021 | 0.0016 | 0.0013 | 0.0010 | 0.0008 | 0.0006 | 0.0005 | 0.0004 |
| Accuracy (m) | 0.0362 | 0.0318 | 0.0284 | 0.0254 | 0.0226 | 0.0201 | 0.0180 | 0.0164 |
| URG | ESR | |
|---|---|---|
| Measuring distance | 0.1 m~30 m | 0.5 m~60 m |
| Distance accuracy | ±0.03 m | ±0.25 m |
| Scanning angle | ±120° | ±45° |
| Angular resolution | 0.36° | ±1° |
| Scanning time | 25 ms/scan | 50 ms/scan |
| CKFURG | IAKFURG | CKFESR | IAKFESR | JAKF | |
|---|---|---|---|---|---|
| RMS Distance Error (m) | 0.0880 | 0.0479 | 0.0595 | 0.0565 | 0.0320 |
| Distance Variance | 2.0833 × 104 | 2.0831 × 104 | 2.0833 × 104 | 2.0832 × 104 | 2.0831 × 104 |
| RMS Velocity Error (m/s) | 0.0702 | 0.0665 | 0.0676 | 0.0669 | 0.0640 |
| Velocity Variance | 6.7979 | 6.7852 | 6.7722 | 6.7699 | 6.7737 |
| RMS Acceleration Error (m/s2) | 0.0175 | 0.0155 | 0.0184 | 0.0179 | 0.0140 |
| Acceleration Variance | 4.2133 × 10−4 | 2.2840 × 10−4 | 3.1428 × 10−4 | 3.0290 × 10−4 | 1.8763 × 10−4 |
| CKFURG | IAKFURG | CKFESR | IAKFESR | JAKF | |
|---|---|---|---|---|---|
| RMS Distance Error (m) | 0.0912 | 0.0883 | 0.1754 | 0.1296 | 0.0685 |
| Distance Variance | 2.8775 × 104 | 2.8744 × 104 | 2.8771 × 104 | 2.8774 × 104 | 2.8773 × 104 |
| RMS Velocity Error (m/s) | 0.0367 | 0.0338 | 0.0527 | 0.0551 | 0.0269 |
| Velocity Variance | 6.8020 | 6.7737 | 6.7849 | 6.7872 | 6.7794 |
| RMS Acceleration Error (m/s2) | 0.0190 | 0.0133 | 0.0205 | 0.0203 | 0.0135 |
| Acceleration Variance | 0.1355 | 0.1364 | 0.1351 | 0.1348 | 0.1356 |
| CKFURG | IAKFURG | CKFESR | IAKFESR | JAKF | |
|---|---|---|---|---|---|
| RMS Distance Error (m) | 0.0779 | 0.0636 | 0.0681 | 0.0636 | 0.0549 |
| Distance Variance | 2.8638 × 104 | 2.8635 × 104 | 2.8642 × 104 | 2.8641 × 104 | 2.8633 × 104 |
| RMS Velocity Error (m/s) | 0.0437 | 0.0431 | 0.0431 | 0.0414 | 0.0385 |
| Velocity Variance | 0.6702 | 0.6688 | 0.6711 | 0.6772 | 0.6619 |
| RMS Acceleration Error (m/s2) | 0.0415 | 0.0380 | 0.0442 | 0.0443 | 0.0368 |
| Acceleration Variance | 0.0414 | 0.0410 | 0.0420 | 0.0424 | 0.0409 |
| JAKF Compare | Displacement | Velocity | Acceleration | |
|---|---|---|---|---|
| The first experiment | CKF | 54.93% | 27.08% | 21.96% |
| IAKF | 28.28% | 19.05% | 15.74% | |
| The second experiment | CKF | 42.91% | 37.85% | 36.43% |
| IAKF | 35.03% | 35.79% | 16% | |
| The third experiment | CKF | 25.14% | 13.29% | 14.02% |
| IAKF | 13.68% | 9.84% | 10.04% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, S.; Liu, Y.; Wang, J.; Deng, W.; Oh, H. The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation. Sensors 2016, 16, 1103. https://doi.org/10.3390/s16071103
Gao S, Liu Y, Wang J, Deng W, Oh H. The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation. Sensors. 2016; 16(7):1103. https://doi.org/10.3390/s16071103
Chicago/Turabian StyleGao, Siwei, Yanheng Liu, Jian Wang, Weiwen Deng, and Heekuck Oh. 2016. "The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation" Sensors 16, no. 7: 1103. https://doi.org/10.3390/s16071103
APA StyleGao, S., Liu, Y., Wang, J., Deng, W., & Oh, H. (2016). The Joint Adaptive Kalman Filter (JAKF) for Vehicle Motion State Estimation. Sensors, 16(7), 1103. https://doi.org/10.3390/s16071103