1. Introduction
The indoor location sensing technology has emerged as an inherent part of the “smart buildings” as it provides great potential for building operation improvement and energy saving. For instance, an on-demand ventilation or lighting control policy must know the usage of the building spaces, which may involve when building occupants enter or exit the building, where they inhabit, what time they occupy the spaces, the duration of occupancy, etc. Such applications require the location sensing systems to provide real-time estimate of occupants’ locations, which is also termed “indoor tracking”, in order to realize fine-grained, responsive building operations.
Most indoor tracking systems necessitate each occupant to carry or wear a powered device such as an infrared [
1], ultrasonic [
2,
3,
4], or Radio Frequency transceiver [
5,
6,
7]. Even if the transceiver is miniaturized into a convenient form, occupants are not willing or likely to carry it at all times. Another subset of tracking systems alleviate the need for carrying specialized devices by using the inertial sensors on smartphones to perform dead reckoning [
8,
9,
10]. However, specialized programs are required to be installed on smartphones to continuously collect inertial sensing data, and thereby the associated energy issues or occupants’ engagement become the main impediment.
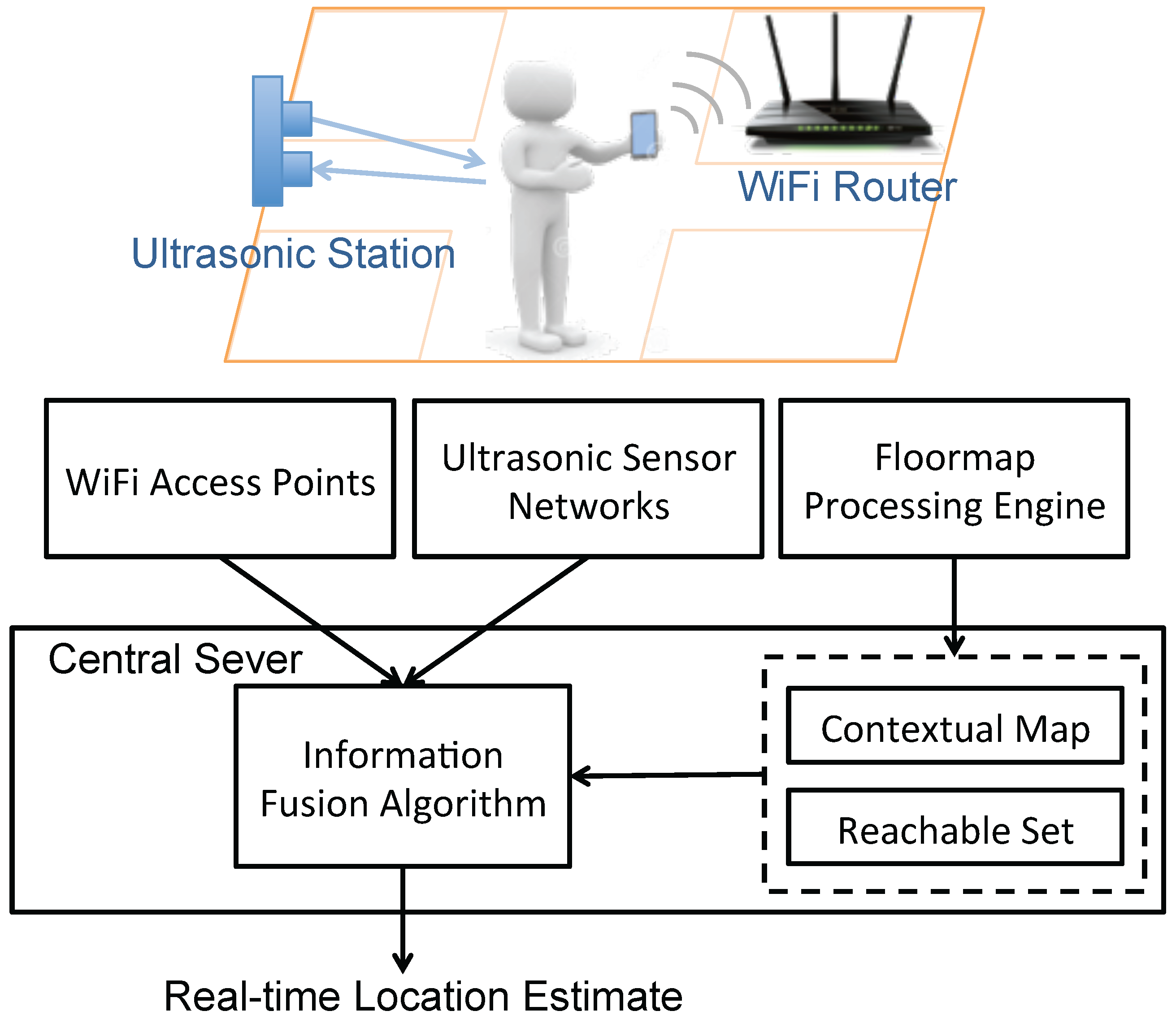
On the contrary, we enable non-intrusive indoor tracking by developing an information fusion system that takes advantage of noisy measurements from various sensors, namely, WiFi access points and ultrasonic sensors. WiFi access points are beneficial for wide spatial coverage while WiFi signals transmitted in the indoor environments suffer from large variations [
11]; ultrasonic sensors are able to accurately locate the occupants in their detection zones which are nevertheless limited spatially. Our vision is of occupants carrying some device with WiFi module, which can be smartphones, tablets, wearable devices,
etc., in the indoor space where ultrasonic sensors can provide opportunistic calibration of the location estimation. The location sensing system is operating in a passive way,
i.e., there is no need for specialized devices or programs for location inference.
In addition to the sensor measurements, another key input for our system is the floormap of the indoor space of interest. Floormap information has been used to refine walking trajectory estimates by eliminating wall-crossings or unfeasible locations [
12,
13,
14]. There has also been efforts to use the floormap to reduce the complexity of the tracking task by properly quantizing the indoor space [
15,
16,
17,
18]. In effect, we can also acquire some prior knowledge of occupants’ dynamic motion from the floormap. The indoor space comprises several typical components, such as cubicles, offices, corridors, open areas,
etc., where occupants’ motion exhibit distinctive patterns. For example, when located at his/her office or cubicle, the occupant is very likely to keep static; the occupant walking on a particular corridor tends to continue the motion constrained along the corridor, while an occupant in an open space is free to move in any direction. Such information of space use is useful to track occupants’ movement, notwithstanding it is less considered in previous work. Gusenbauer
et al. [
19] exploited different types of movements to improve the tracking model. This was done by introducing an activity recognition algorithm based on accelerometer data to model pedestrians’ steps more reliably. Park [
20] proposed incorporating the floormap information by “path compatibility”, where occupants’ motion sequences and motion-related information (e.g., duration and speed) are first estimated based on mobile sensing data, and then localization is achieved via matching occupants’ motion sequences and the hypothetical trajectories provided by the floormap. Kaiser
et al. [
21] proposed a motion model based on the floormap, which weights the possible headings of the pedestrian as a function of the local environment. Our work differs from [
19] and [
20] in that our work does not rely on the inertial measurements to recognize the motion. Instead, the motion information is extracted from the floormap. We exploit the prior knowledge that the floormap endows us about the occupants’ typical movement and activity, not merely the possible headings at each point of the floormap as in [
21]. It is, therefore, the objective of this paper to propose MapSentinel, a non-intrusive location sensing system via information fusion, which combines the various sensor measurements with the floormap information, not only as a sanity check of estimating trajectories but as an input for occupants’ kinematic models.
Our main contributions are as follows:
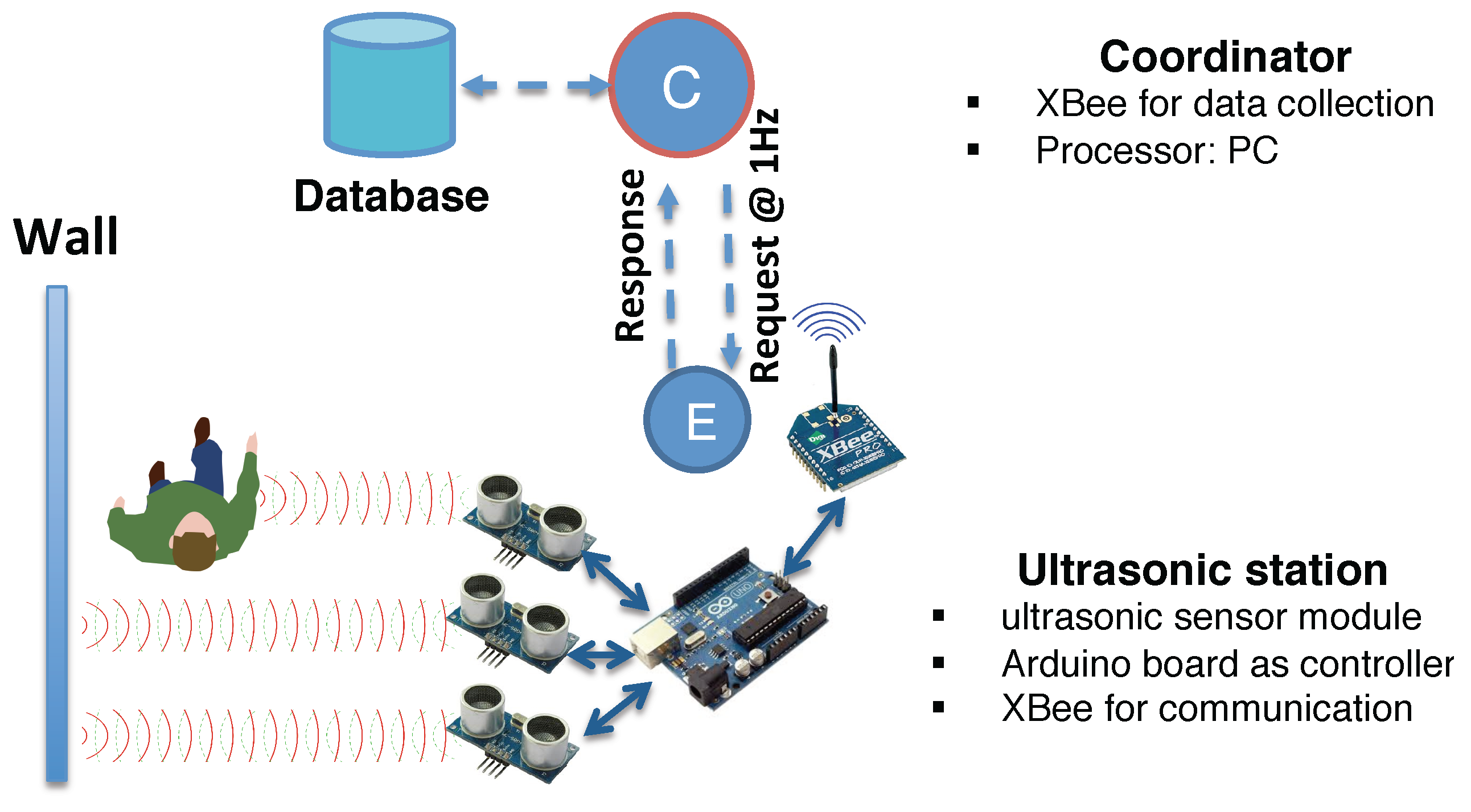
We build a non-intrusive location sensing network consisting of modified WiFi access points and ultrasonic calibration stations, which does not require the occupants to install any specialized programs on their smartphones and prevents the energy and occupant engagement issues.
We propose an information fusion framework for indoor tracking, which theoretically formalizes the fusion of the floormap information and the noisy sensor data using Factor Graph. The Context-Augmented Particle Filtering algorithm is developed to efficiently solve the walking trajectories in real time. The fusion framework can flexibly graft floormap information onto other types of tracking systems, not limited to the WiFi tracking schemes that we will demonstrate in this paper.
We evaluate our system in a large typical office environment, and our tracking system can achieve significant tracking accuracy improvement over the purely WiFi-based tracking systems.
The rest of this paper expands on each of these contributions. We conclude the paper and discuss the future work in
Section 6.
3. Information Fusion Framework
In this section, we propose an information fusion framework that manages the heterogeneous sensor measurements as well as the floormap and occupants’ context-related motion characteristics to provide an online estimate of occupants’ location. There are two key components in the fusion framework: Context-Dependent Kinematic Models (CDKM) and Probabilistic Sensor Measurement Models (PSMM). CDKM is based on the observation that occupants’ movements exhibit distinctive features in different parts of buildings as described in
Section 2.3, and it captures this context-dependency by defining different kinematic models for distinctive contexts. PSMM models each sensor measurement as a probability distribution and multiple sensor data are combined via Bayes’ rule to support the location inference.
3.1. Problem Formulation
Consider that the indoor space of interest is composed of M contexts, in each of which occupants exhibit a particular sort of kinematic patterns. Denote the context at time k as where . The subscript of represents the index of the certain direction of constrained space and R is the total number of different directions. Let the state consist of the position and velocity components of the occupant in the Cartesian coordinates , as well as the context . If the position is known, the context can be uniquely determined by the contextual floormap. We characterize this correspondence via a function which assigns a specific context for . The tracking problem can be viewed as a statistical filtering problem where is to be estimated based on a set of noisy measurements up to time k. Specifically, is the measurements available at time k, and, in our case, it includes measurements from multiple sensors, where is total number of sensors deployed in the space of interest. We model the uncertainty about the observations and the states by treating them as random variables and assigning certain probability distribution to each random variable. In this setting, we want to compute the posterior distribution of the state given the measurements up to time k, i.e., .
The impact of introducing context as an auxiliary state variable is manifold. Firstly, the transition of contexts
to
determines the type of motion executed during the time interval
. For instance, if the context remains the same, then the occupant should follow the motion type defined by the two identical contexts; on the contrary, if the context varies during
, then the occupant would execute the motion that is defined by neither of the contexts. For simplicity, we will assume a free motion. That is, the position/velocity state at time
k,
, depends on not only the past state
and
, but also the current context
stochastically. Moreover, there is a deterministic mapping between
and
as is specified by the contextual map. In order to facilitate visualization and analysis of the complex dependencies among the variables, we use a factor graph to represent the states, observations and the functions bridging these variables, as illustrated in
Figure 4.
A factor graph has two types of nodes,
variable node for each variable and
function node for each local function, which are indicated by circles and squares, respectively. The edges in the graph represents the “is an argument of” relation between variables and local functions. For example, the function
has four arguments,
,
,
and
. Three types of local functions are involved in our model:
: transition model, or the prior information on the state evolution over time. Inspired by Variable Structure Multiple Model Estimator in [
23], we propose CDKM to capture the context-dependent characteristics of occupants’ motion in the indoor space.
: observation model, or how the unknown states and sensor observations relate. We will introduce PSMM where the relationship between locations and sensor observations is characterized by certain conditional probabilities and multiple sensor observations are combined via Bayes’ theorem.
: characteristic function that checks the validity of the correspondence between and using the contextual floormap.
Note that the prior knowledge abstracted from the floormap is inherently accommodated to this problem by defining characteristic function and parameterizing the transition model as will be elaborated in the following section.
3.2. Context-Dependent Kinematic Model
We assume that given
,
and
, the current position/velocity
follows a Gaussian distribution, of which the mean and covariance matrix are specified as
The equivalent state space model of Equation (2) is given by
where
determines the mean of the distribution of the next state. Let
a denote the acceleration, we have the following kinematic equations,
where
T is the sampling period. We will assume constant velocity in this paper, and model
a as a Gaussian noise term. If we manipulate Equations (4) and (5) into matrix forms, then it can be identified that
has two possible values corresponding to moving or remaining static,
imposes the velocity component of the state to be zero and when the context remains to be static space, i.e., ; otherwise, .
stands for the process noise and, as the notation indicates, it is also a function of the context transition from
to
k. We will adopt the concept of directional noise to handle the constraints imposed by the contextual map. To see this, note that occupants in the free space (
) can move in any direction with equal probability, therefore using equal process noise variance in both
x and
y direction,
i.e.,
For occupants moving on the constrained space (
) such as corridors, more uncertainty exists along than orthogonal to the corridor. Denote the variances along and orthogonal to the corridor by
and
(
), respectively, and the canonical direction of the constrained space
is specified by the angle
(measured clockwise from y-axis). Then the process noise covariance matrix corresponding to the motion in the constrained space is given by
The preceding model specification incorporates the scenarios where the context remains the same during the time interval
and the occupant will keep the motion type defined by the two identical contexts. On the contrary, if the context switches during the time interval
, we will assume a free motion pattern,
i.e.,
,
.
Table 2 summarizes our model given all possible context transitions.
3.3. Probabilistic Sensor Measurement Model
We construct probabilistic models for each sensor and multisensor fusion can be performed via Bayes’ rule. Assuming that
different sensors function independently, then the observation model
can be factored as
This actually forms a convenient and unified interface to combine distinctive sensor data by projecting the heterogeneous measurements () to the probability space via likelihood function, . If one more sensor is added into the system, then the observation model can be simply updated by multiplying the corresponding likelihood. Different likelihood functions requires being trained for different types of sensors.
WiFi Measurement. In the free space, the WiFi signal strength is a log linear function of the distance between the transmitter and receiver. However, due to the multipath effect caused by obstacles and moving objects in the indoor environments, the log linear relationship no longer holds. Previous work has proposed to adding a Gaussian noise term to account for the variations arising from the multipath effect; however, the simple model-based method can hardly guarantee a reasonable performance in practice. Another popular way is to construct a WiFi database comprising WiFi measurements at known locations to fingerprint the space of interest, but it requires onerous calibration to ensure the accuracy. We propose a novel WiFi modeling method based on a relatively small WiFi training set to accommodate for the complex variations of WiFi signals in the indoor space. The key insight is to use Gaussian process (GP) to model the WiFi signal where the simple model-based method provides a prior over the function space of GP.
We collect WiFi signal strength data at
reference points over the space and let
denote the training dataset, where
is a vector containing the distances of
jth reference point to each of the WiFi APs deployed in the field and
is the observed WiFi signal strengths. Assume the WiFi observations are drawn from the GP,
where the mean function
is imposed to be a linear model with the parameters adapted to the training samples. The covariance function
takes the squared exponential form,
where
stands for the variance of the additive Gaussian noise term in the observation process, and
and
r are the hyperparameters of the GP. These parameters can be tweaked according to the training data, and we set
,
,
in our experiments. At an arbitrary point
in the space of interest, the posterior mean and variance of the WiFi signal
are
where
and
are the vectors concatenated by
and
, respectively.
denotes the
matrix of the covariances evaluated at all pairs of training and testing points, and similarly for the other entries
and
. In previous work using GP to model the WiFi signal strength [
24], the WiFi signal is assumed to follow the Gaussian distribution with the mean and variance given by Equations (13) and (14), respectively. However, the posterior variance derived from GP is a indicator of estimation confidence. It depends largely on the density of training samples in the vicinity of the evaluated position. That is, if the evaluated point
happens to fall into the area that is densely calibrated, then the posterior variance will be relatively small. The posterior variance derived from GP cannot truly reflect the variations of WiFi signals over time. Therefore, instead of using the posterior Variance (14) in classical predictive equations, we model the likelihood as
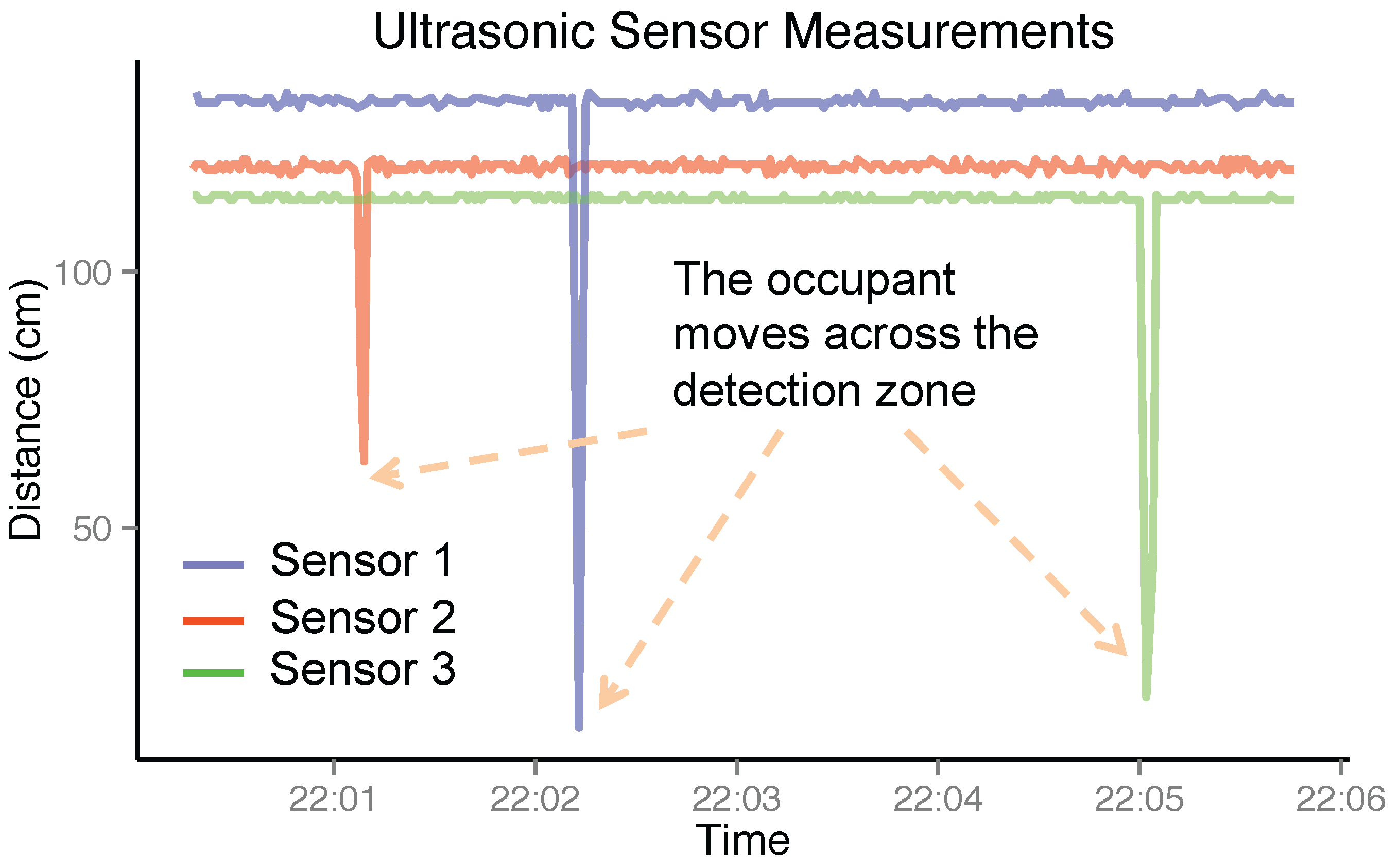
Ultrasonic Measurement. Essentially, each of the ultrasonic sensors in the ultrasonic station can output the distance to the occupant passing in front of it. However, due to the missing data and measurement noise, the distance measurement is not always steady. Here, we will consider the ultrasonic station to be a binary sensor to indicate the occupancy in its detection zone. To be specific, the likelihood function is modeled as
where
η is the threshold for ultrasonic measurements.
3.4. Characteristic Function
The characteristic function imposes constraints on the correspondence between the position and the context, and embodies the prior knowledge available from the floormap. In the preceding section, we have defined a function
that sets up the relationship between the context and the position/velocity,
i.e.,
, and
can be readily read out from the contextual map. We thereby define the characteristic function to be
where
is an indicator function. In other words, the characteristic function enforces the local correspondence defined by
.
4. Context-Augmented Particle Filter
In this section, we will discuss how to perform inference on the underlying factor graph of the tracking problem we formulated previously. The particle filter is a technique for implementing a recursive Bayesian filter by Monte-Carlo simulations [
25]. The key idea of particle filter is to represent the required posterior density function by a set of random samples or “particles” associated with discrete probability mass, and compute the state estimate based on these “particles”. The original particle filter proposed by Gordon
et al. [
26] was designed for a simple hidden Markov chain, which is also a cycle-free factor graph, using the Sampling Importance Resampling (SIR) algorithm to propagate and update the particles. However, the factor graph in our problem, as illustrated in
Section 4, does have cycles due to the introduction of the context variable, and only approximate inference algorithms exist. We present a recursive approximate inference method for the cyclic factor graph by extending the particle filter and the resulting algorithm is termed
Context-Augmented Particle Filter (CAPF).
To see the operation of the CAPF, consider a set of particles
that represents the posterior distribution
of the state. Note that
can be uniquely determined by
via the characteristic function. At time
k, we have some new measurement
. It is required to construct a new set of particles
which characterizes the posterior distribution
. Now, suppose we have an “
oracle" that is capable of providing the context value
of the corresponding
even before we generate
’s, then our task is equivalent to draw samples from the distribution
This can be carried out in two steps: First, the historical density
is propagated via the transition model
to produce the prediction density
where
since
is completely determined conditioning on
. Second, our interested density
can be updated from the prediction density using Bayes’ theorem,
where
γ is a normalization constant. Thus, Equation (
19) and Equation (
20) form a recursive solution to Equation (18). In particle filter framework, the aforementioned prediction and update steps are performed by propagating and weighting the random samples.
Prediction Step. In the prediction phase, we generate the predicted particles by
where
is a set of particles representing the estimates of
produced by the “oracle”. Given the different possible values of
and
,
will be sampled from different models, detailed in
Table 2. We will then perform sanity check on newly generated particles, where the particles
absent from the reachable set of
will be eliminated.
Update Step. To update, each predicted particle
is assigned with a weight proportional to its likelihood.
The weight is then normalized by
We resample
N times with replacement from the set
using weights
to obtain a new set of samples
such that
. Correspondingly, the contexts
’s are obtained through the characteristic function,
i.e.,
“Oracle” Design. The oracle is supposed to be able to answer the query about the next possible contexts
, based upon which the position/velocity component of the state can be properly propagated according to different transition models. For computational efficiency, we adopt a simple discriminative model to produce
’s. Given a small database of WiFi fingerprints, we apply the K-Nearest Neighbors (K-NN) algorithm and a modified distance weighted rule to generate an empirical distribution of the context. To be specific, let the WiFi database be denoted by
, and
is the number of WiFi fingerprints. When the new WiFi observation
is querying the possible contexts, the
K nearest neighbors of
are found among the given training set. Let these
K nearest neighbors of
, with their associated context, be given by
. In addition, let the corresponding distances of these neighbors from
be given by
,
. The weight attributed to the
th nearest neighbor is then defined as
We then normalize the weights,
, and sample the context according to the following discrete probability distribution,
where
α is a context resilience factor and
. We incorporate
α to accommodate for the prior knowledge that the context will not change too often and to make the “oracle” more robust to the observation noise. Moreover, for the particles on the boundary of distinctive contexts,
is equally probable to be these contexts. The pseudo-code of the CAPF algorithm is provided in Algorithm 1.
| Algorithm 1 Context-Augmented Particle Filter |
| function CAPF() |
| Initialization: |
| Uniformly generate N samples |
| Set , , |
| for do |
| for do |
| Context Estimate: |
| if on the boundary of then |
| Uniformly sample from |
| else |
| Sample from Equation (27) |
| end if |
| Prediction Step: |
| |
| Discard particles |
| Update Step: |
| Compute weight |
| end for |
| Normalize weights: |
| Resampling: |
| Select N particle indices according to weights |
| Set and |
| Set |
| Estimate: |
| |
| end for |
| return |
| end function |
5. Performance Evaluation
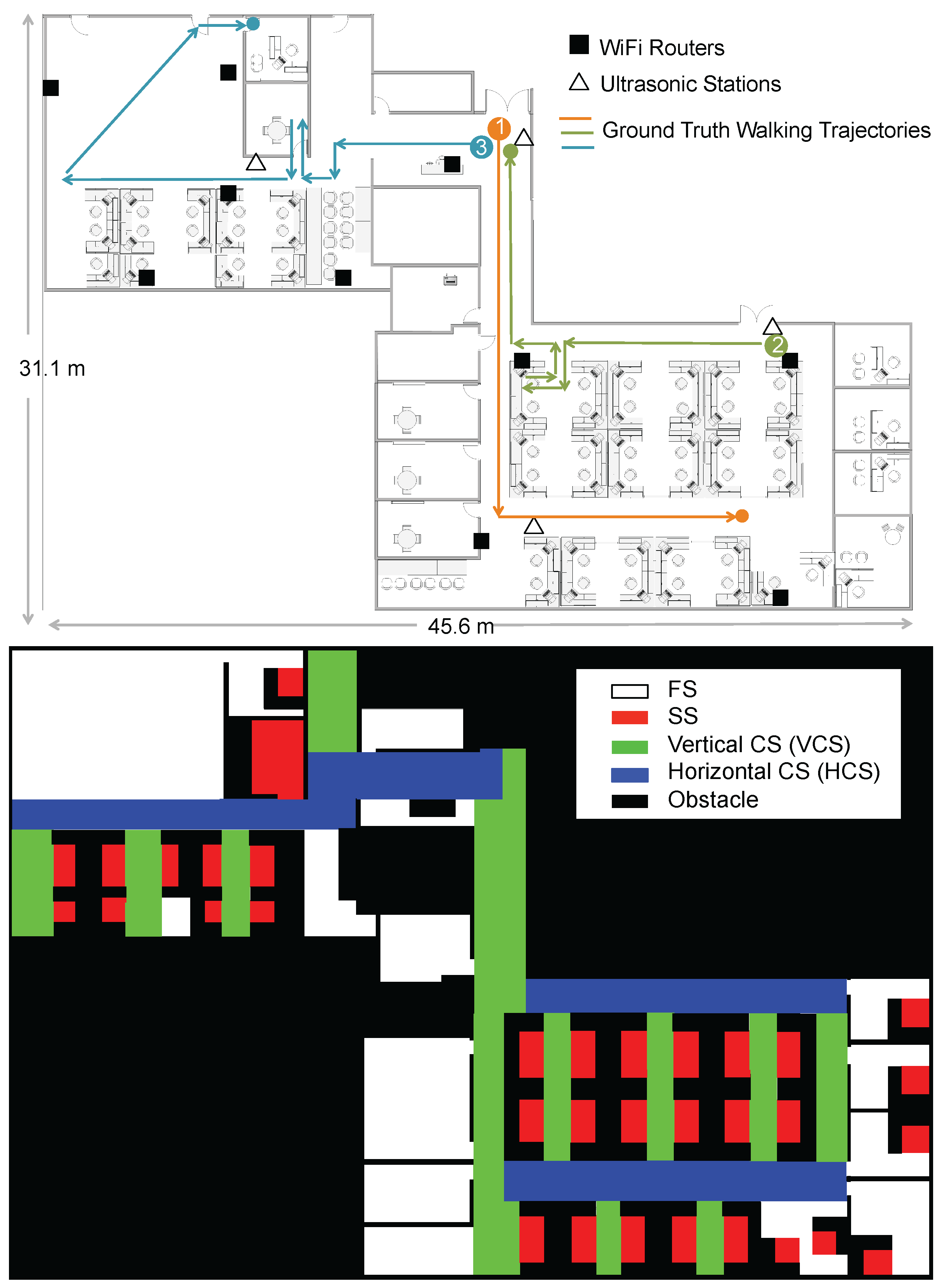
Our experiment was carried out in the Singapore–Berkeley Building Efficiency and Sustainability in the Tropics (SinBerBEST) located in CREATE Tower at the National University of Singapore campus, which is a typical office environment consisting of cubicles, individual offices, corridors and obstacles like walls, desks,
etc. The total area of the testbed is around 1000 m
. There are 10 WiFi routers and four ultrasonic stations deployed in the testbed in total. We utilize TP-LINK TL-WDR4300 Wireless N750 Dual Band Routers (manufactured in Shenzhen, China) as WiFi APs and HC-SR04 Ultrasonic Sensors (manufactured in Shenzhen, China) as the components of ultrasonic stations. The floormap and the corresponding contextual map are shown in
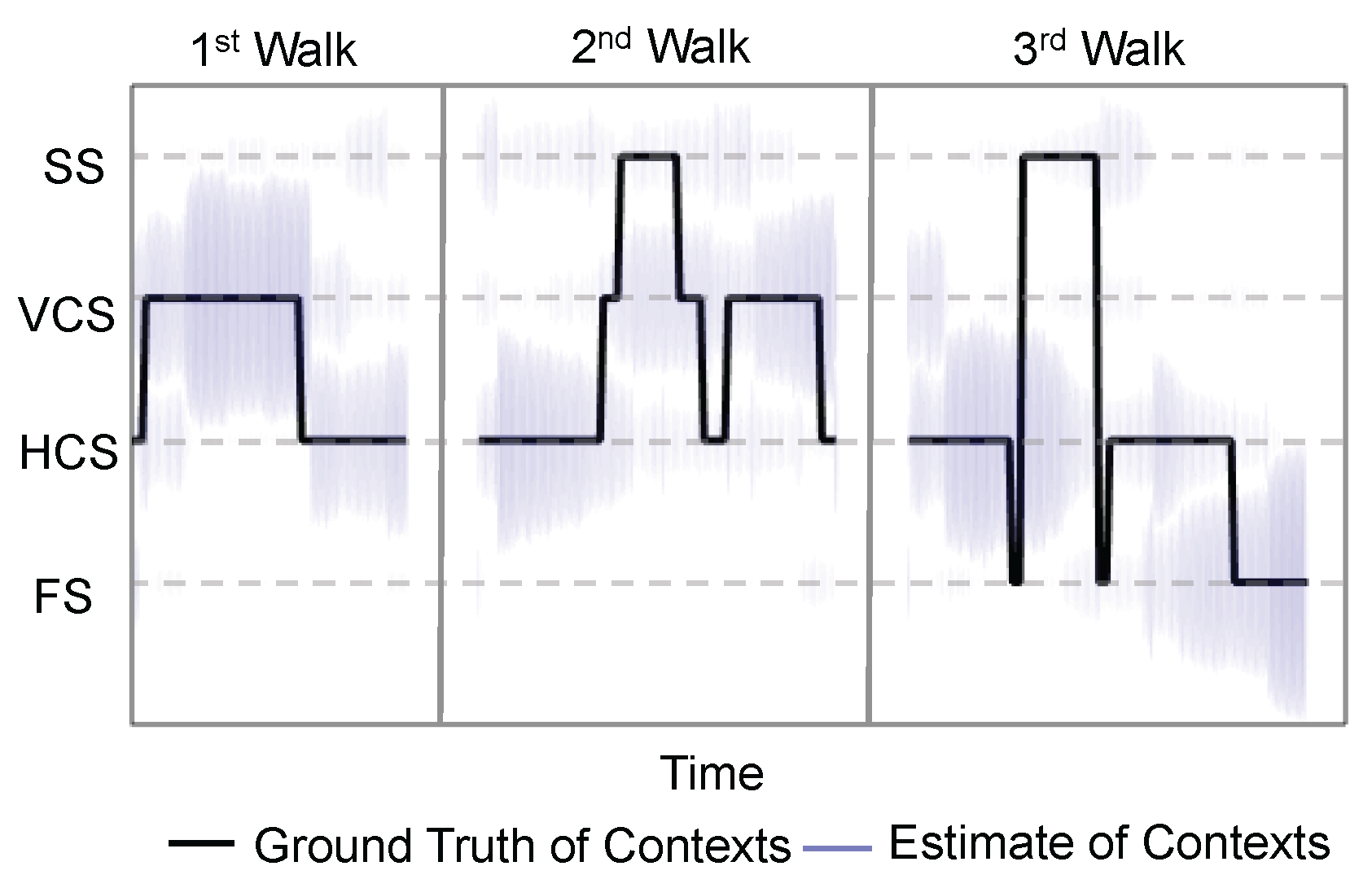
Figure 5. Different contexts are colored differently in the contextual map. The static space contains the seating areas in the cubicles and offices, where occupants hardly move. The corridors of horizontal and vertical directions are considered to be two types of constrained spaces (HCS and VCS, respectively). The free space includes the open areas where occupants can freely move. We seek to answer the questions including how well MapSentinel is able to track the occupant, and whether the map information exploited by way of MapSentinel can bring additional benefits to the tracking performance.
Experimental methodology. In a real-world setting, we expect the occupant to carry the smartphone as they walk through various sections of an indoor space. Moreover, occupants are unlikely to walk continuously; they would walk between locations of special interest and dwell at certain locations for a significant length of time. Our experiment aims at emulating these practical scenarios in an office environment and incorporating all the contexts defined in our model. Therefore, the following routes were designed as the ground truth for evaluation: (1) A enters the office from the front gate and walks through the corridors to find her colleague (different CSs are included); (2) B enters the office from the side door, walks to her own seat, stays there for a while and exits the office from the front gate (CSs, SS are included); (3) C enters the office from the front gate, walks through corridors, takes some time at her office and goes to the open area (CSs, SS, FS are included). We asked the experimenter to behave as usual when walking in the space. At the same time, the WiFi APs and ultrasonic stations constantly collect the measurements and send them to the central server. To obtain the ground truth at the sampling time of the tracking system, we mark the ground with a 1 m grid on the pre-specified route and ask the experimenter to create lap times with a stopwatch when happening to be on the grid. By recording the starting time of the experiment, we can obtain the time stamp of each grid and then interpolate the ground truth at the sampling time.
Does the “oracle” work? The current context estimation done by the “oracle” is critical to the CAPF algorithm, as the tuple of the current and previous context jointly steer the states in our model. Here, we would like to evaluate the context prediction performance of the “oracle” we constructed in light of several design rules presented in the
Section 4.
Figure 6 illustrates the result of the context estimation for different walks. Since the context estimates are represented by a set of particles in the algorithm, we visualize the context estimate by the purple lines centered at the possible contexts, and the lengths of the purple lines are scaled by the proportions of the particles of different contexts. Ideally, the purple cloud should scatter around the ground truth context.
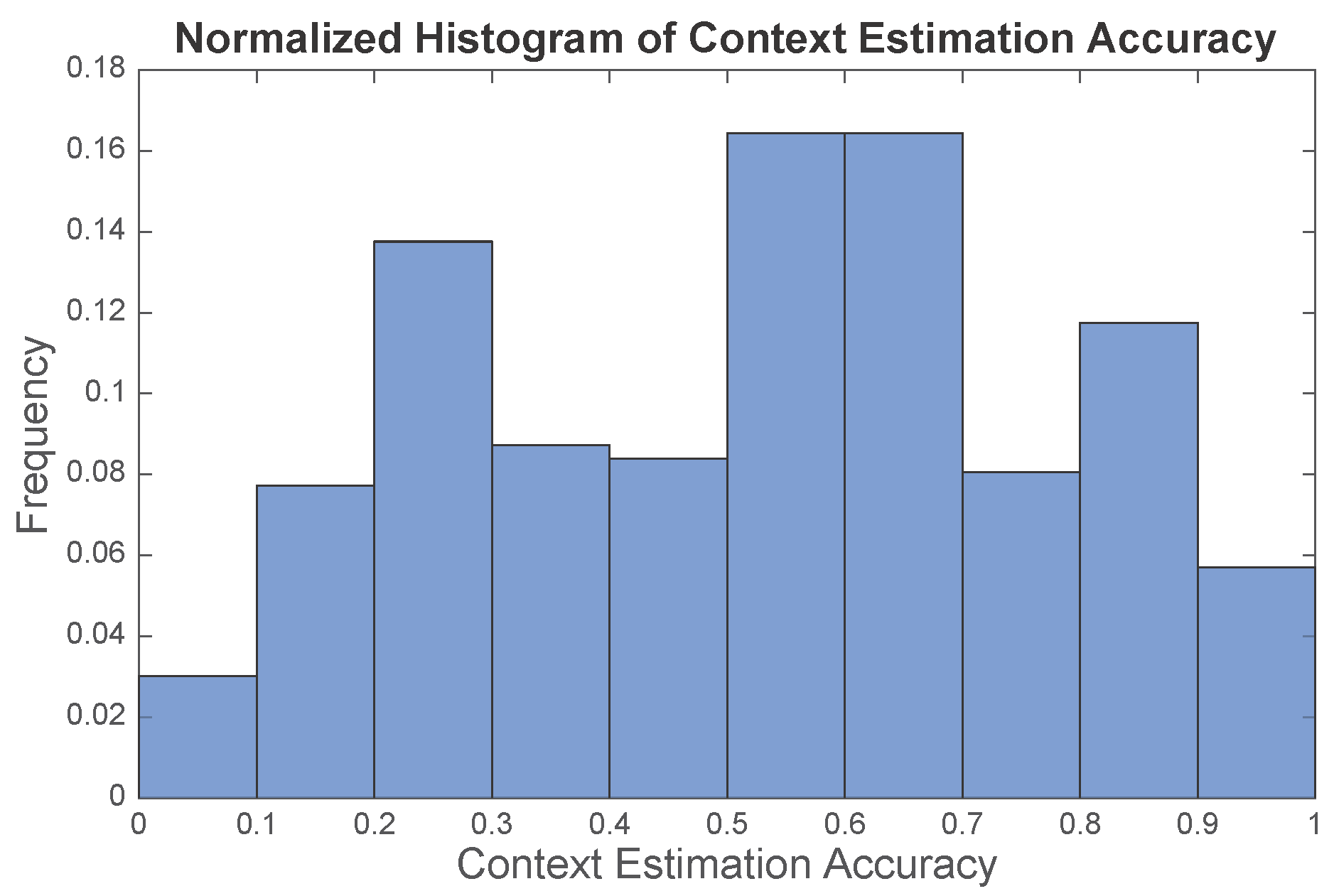
Figure 6 suggests that the estimates given by the “oracle” can generally capture the ground truth. Evidently, the context estimate is not perfect, especially for the static space (SS). However, these approximate “ground truths” essentially present other possibilities of the current context and avoids particles trapping in the static space. We define the context estimation accuracy to be the ratio of the number of particles with correct context estimate to the total number of particles. The context estimation accuracy is calculated for each time step of the experiments, and the empirical distribution of the context estimation accuracy is illustrated in
Figure 7, where the mean accuracy is
. With this noisy “oracle”, the system can achieve median tracking error of
m, while the tracking error would be
m if a perfect “oracle” was utilized. Therefore, our work has the potential to be further improved with a more advanced “oracle” design.
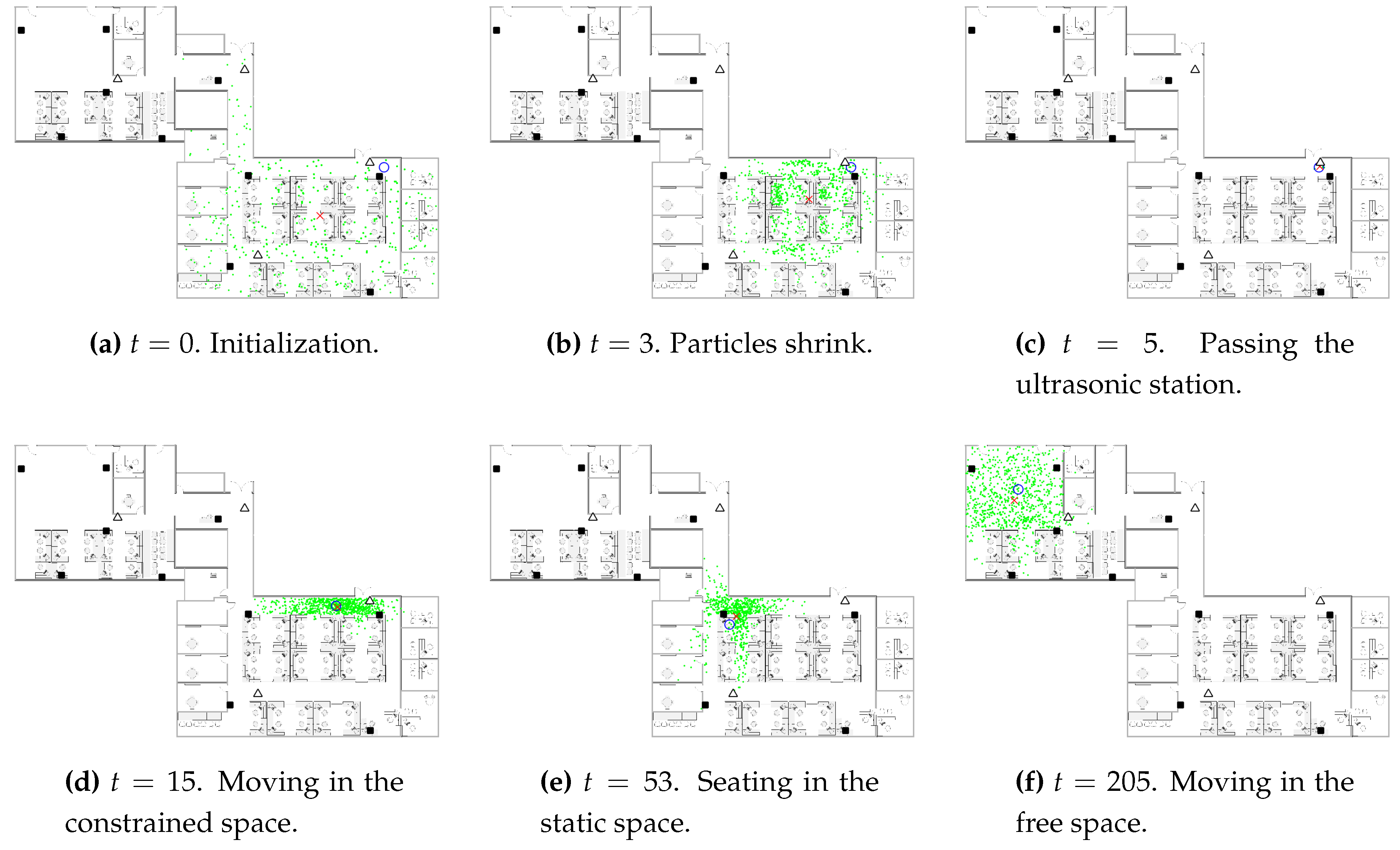
Figure 8 demonstrates some snapshots of the CAPF algorithm in progress. At the beginning, the particles are initialized to be uniformly distributed in the space. In addition, the spread of the particles shrinks as the new WiFi observations come. When the ultrasonic station reports a detection, the particles are concentrated in the corresponding detection zone. As the occupant exits the detection zone, the particles spread out along the direction of the corridor. When the occupant sits in the cubicle, the particles distribute over the seating area as well as some possible routes through which the occupant might leave the seating area. The particles distribute evenly along different directions when the occupant is moving in the free space, in which case our model is identical to the traditional constant velocity dynamic model for the particle filter.
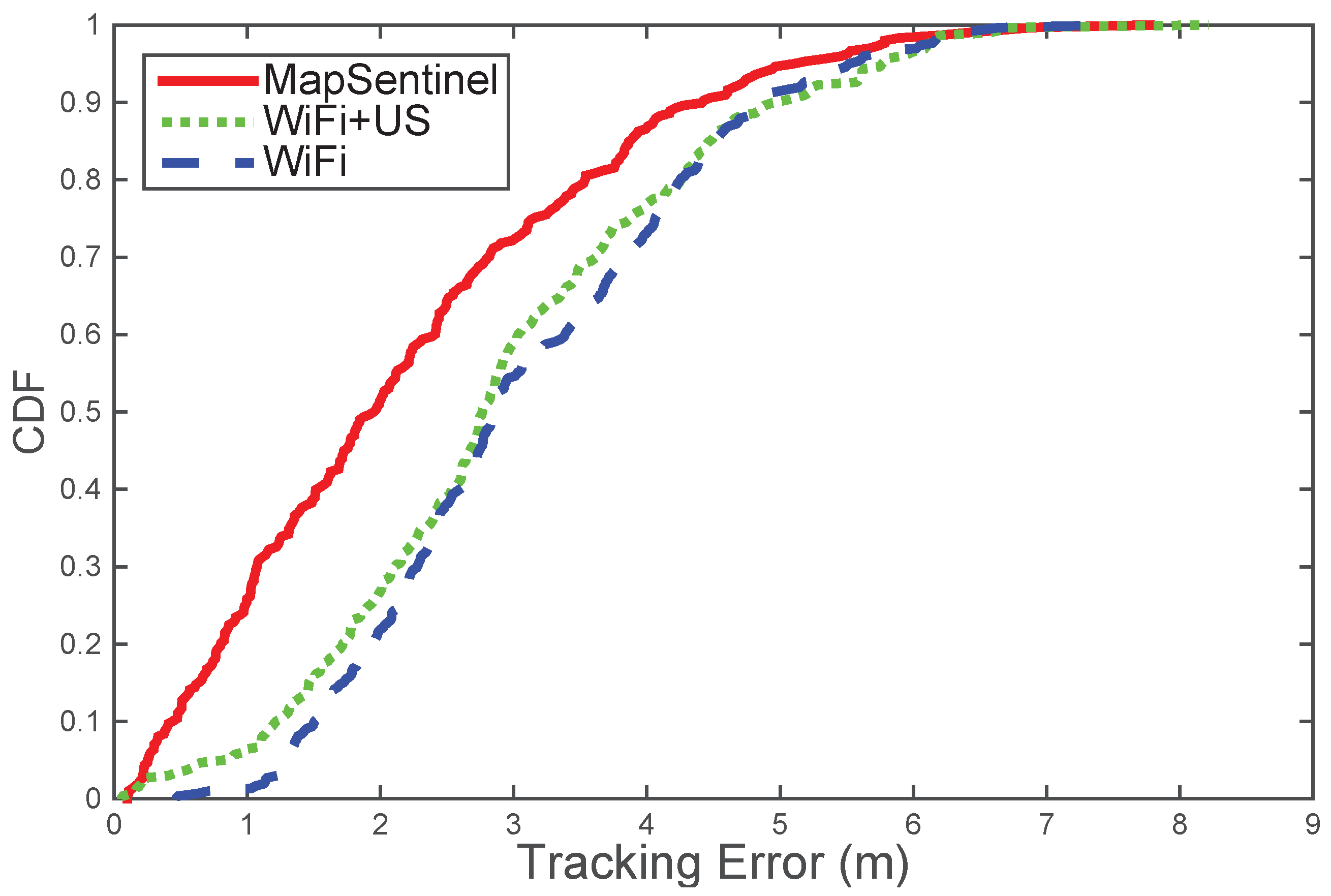
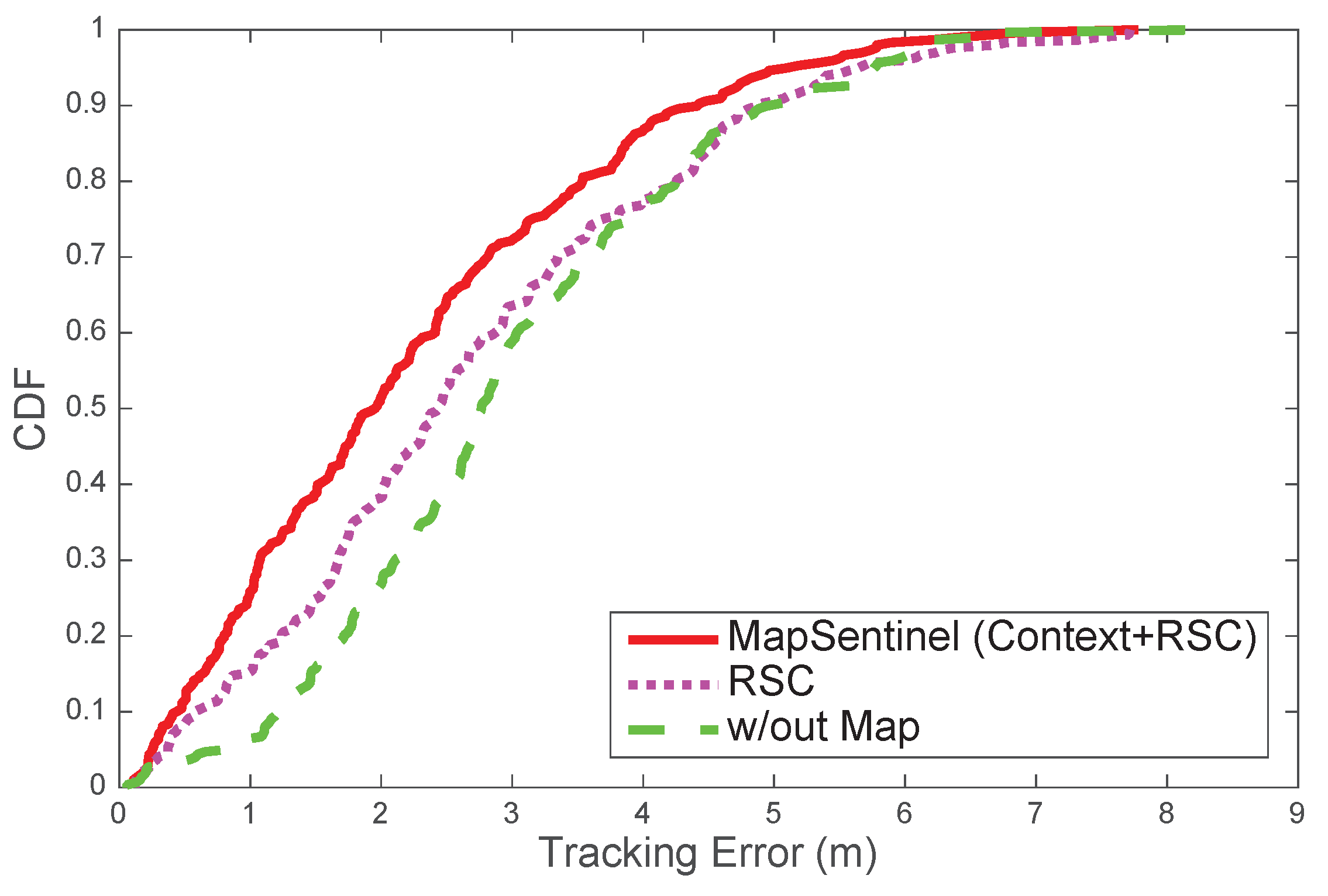
MapSentinel’s tracking performance. We aggregate the data from different walks and compare the performance of MapSentinel against the fusion system of WiFi and ultrasonic station without leveraging the floormap information, as well as the purely WiFi-based tracking system. The tracking error distributions are depicted in
Figure 9. As can be seen, the MapSentinel achieves an essential performance improvement,
over the WiFi tracking system and
over the fusion scheme. Note that adding the ultrasonic calibration into the WiFi system is able to realize a small amount of accuracy increment. Due to the high degree of uncertainty of WiFi signals, the effect of ultrasonic calibration will not last for long. The map information elongates the effect of the ultrasonic calibration via imposing additional constraints to the motion, and that is why MapSentinel greatly enhances the tracking performance compared with the purely WiFi-based system. We also evaluate the tracking performance in different contexts, and the result is shown by boxplots in
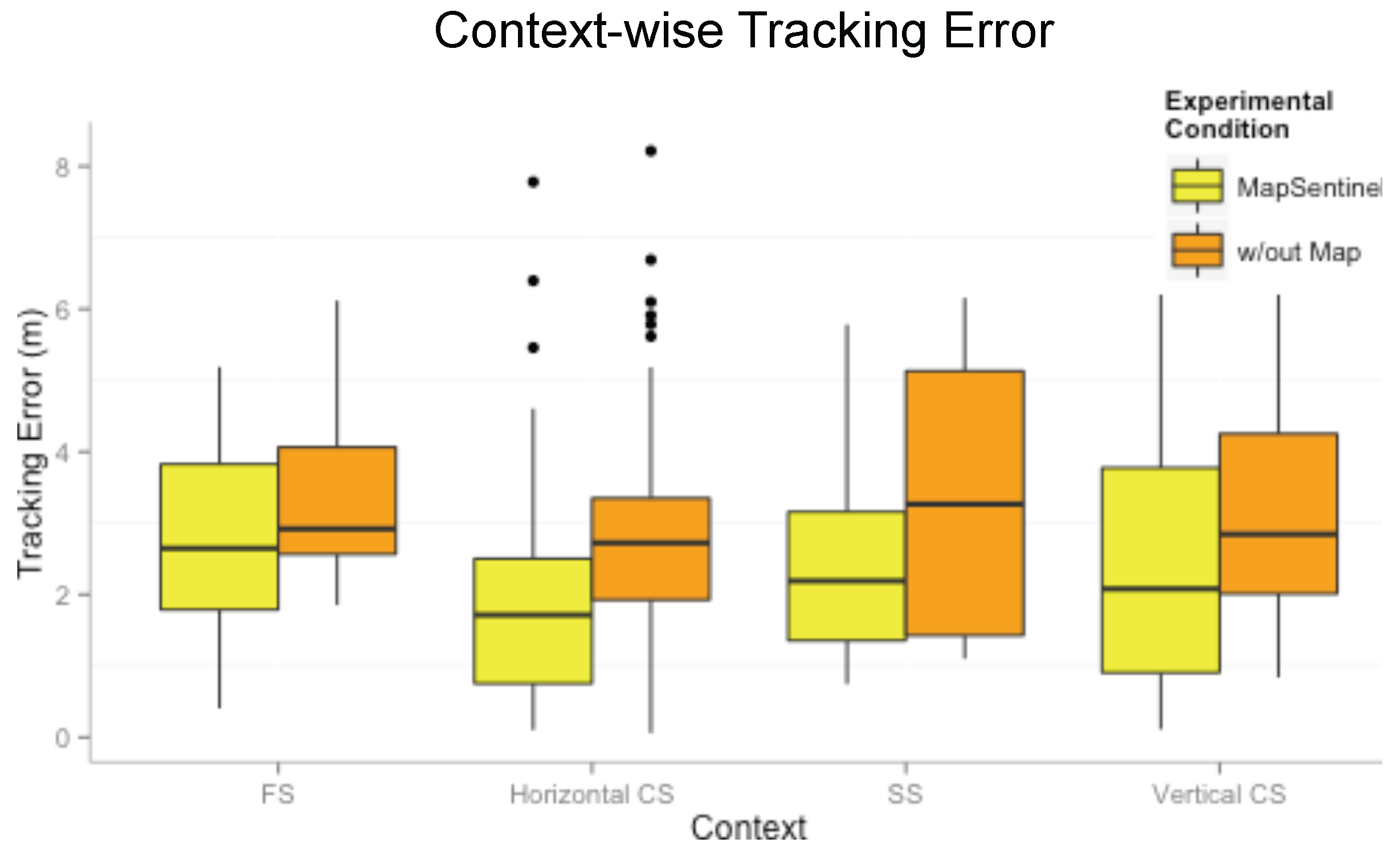
Figure 10. Here, “without map” means using the WiFi and ultrasonic sensing systems without taking into account the reachable set as well as the context-dependent kinematic model. A unified dynamical model, the free space model, is applied in this case, and a traditional particle filter is implemented to estimate the location. As can be readily read from the figure, the MapSentinel performs better in all contexts. More significant increase is achieved in constrained spaces and static spaces, as expected.
Figure 11 compares the performance of tracking systems with distinctive floormap usage. MapSentinel exploits the floormap information in two folds: first, MapSentinel integrates the context information into the kinematic model, and the movement patterns of people on different locations of the map are better captured. Secondly, MapSentinel takes into account the speed restrictions as well as physical obstacles in the indoor space by checking if the particles fall inside the reachable set at each time step. The second fold of the floormap information has been widely utilized in the previous work, while the context information is less explored. We therefore compare the tracking error of our system with the one that merely uses the reachable conditions.
Figure 11 shows that incorporating information about physical constraints, as the previous work did, is surely beneficial to the tracking system. Particularly, the performance can be further improved by
by introducing the context information into the tracking system.
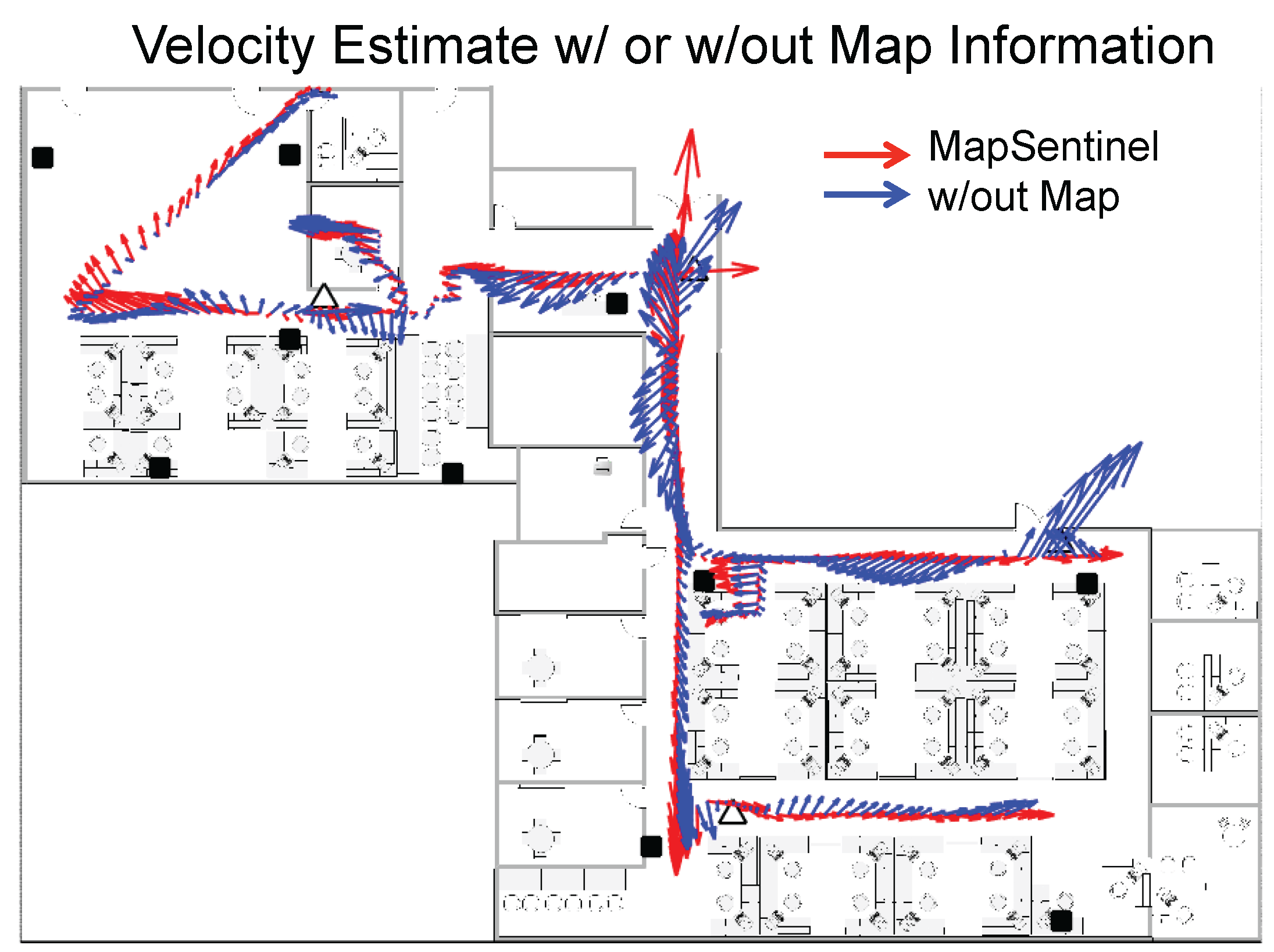
To better understand how the map helps improve the location estimation, we demonstrate the velocity estimation of different tracking schemes in
Figure 12. Typically, the occupants will not perform complex motions in the indoor space due to the constraints of the wall and other barricades. The more the velocity estimate deviates from the canonical directions defined by the indoor environment, the worse the tracking performance can be. Using the fusion schemes of WiFi and ultrasonic calibration, only the location is the observable state. The velocity estimates depend largely on the location estimate and it has little effect in smoothing out the location estimate. Hence, extensive research has been focusing on using inertial measurements to perform dead reckoning, which makes the velocity observable. Analogously, the MapSentinel creates a
virtual inertial sensor for the occupant, which mimics the actual inertial sensor to provide the possible walking speed and directions. As is shown in
Figure 12, the velocity estimation without map information tends to point to any direction while the MapSentinel constrains the velocity via the context-dependent kinematic model.