Potential of IMU Sensors in Performance Analysis of Professional Alpine Skiers
Abstract
:1. Introduction
- What is the best location on the body to attach an IMU sensor to capture the key characteristic of the turns in alpine skiing?
- From the selected location, how should data be analyzed to evaluate the skier’s performance, particularly the lateral-asymmetric test and the adaptation effect of training?
2. Literature
2.1. Motion Analysis Using Different Experimental Devices
2.2. Performance Analysis Using Different Experimental Devices
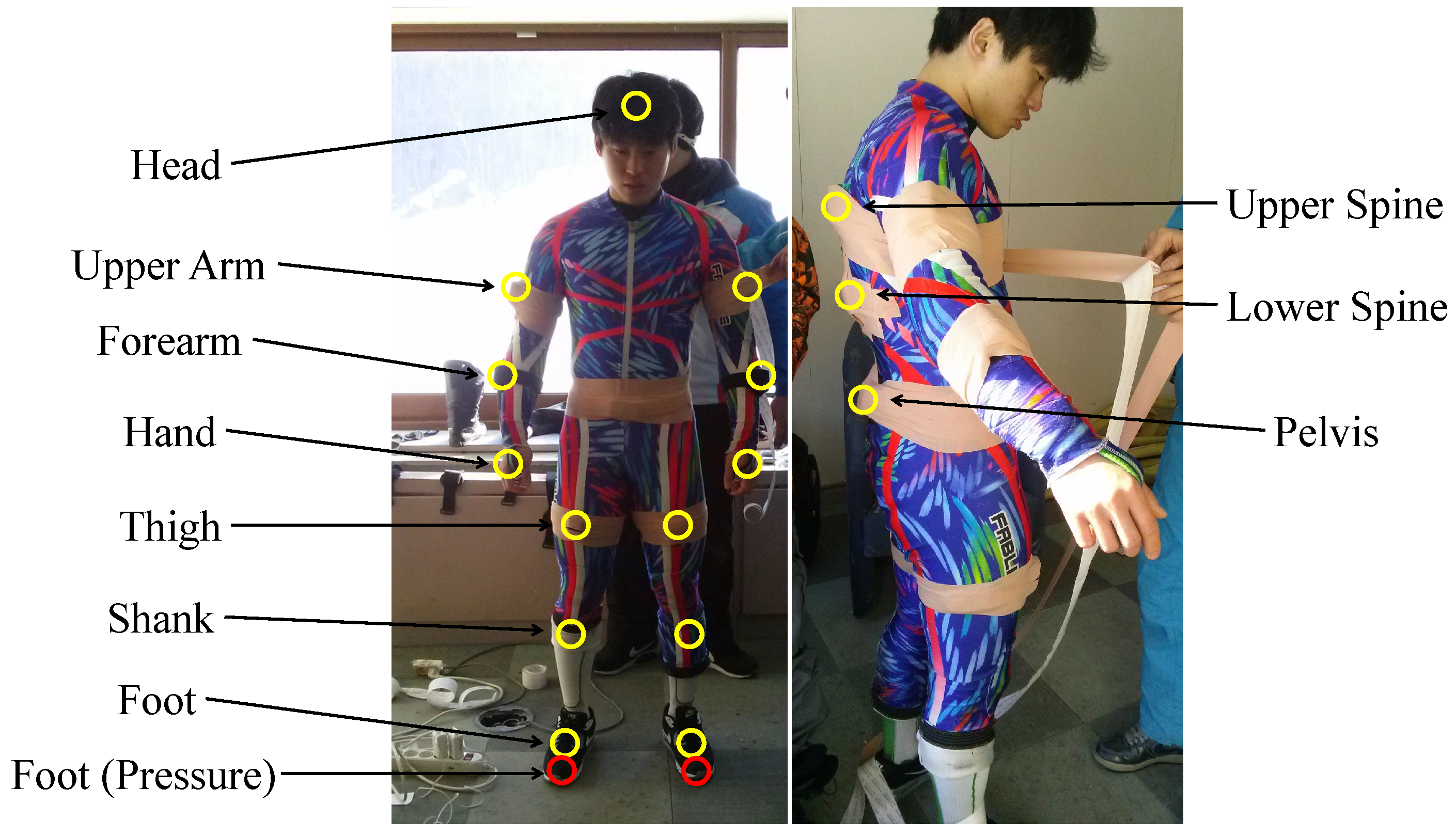
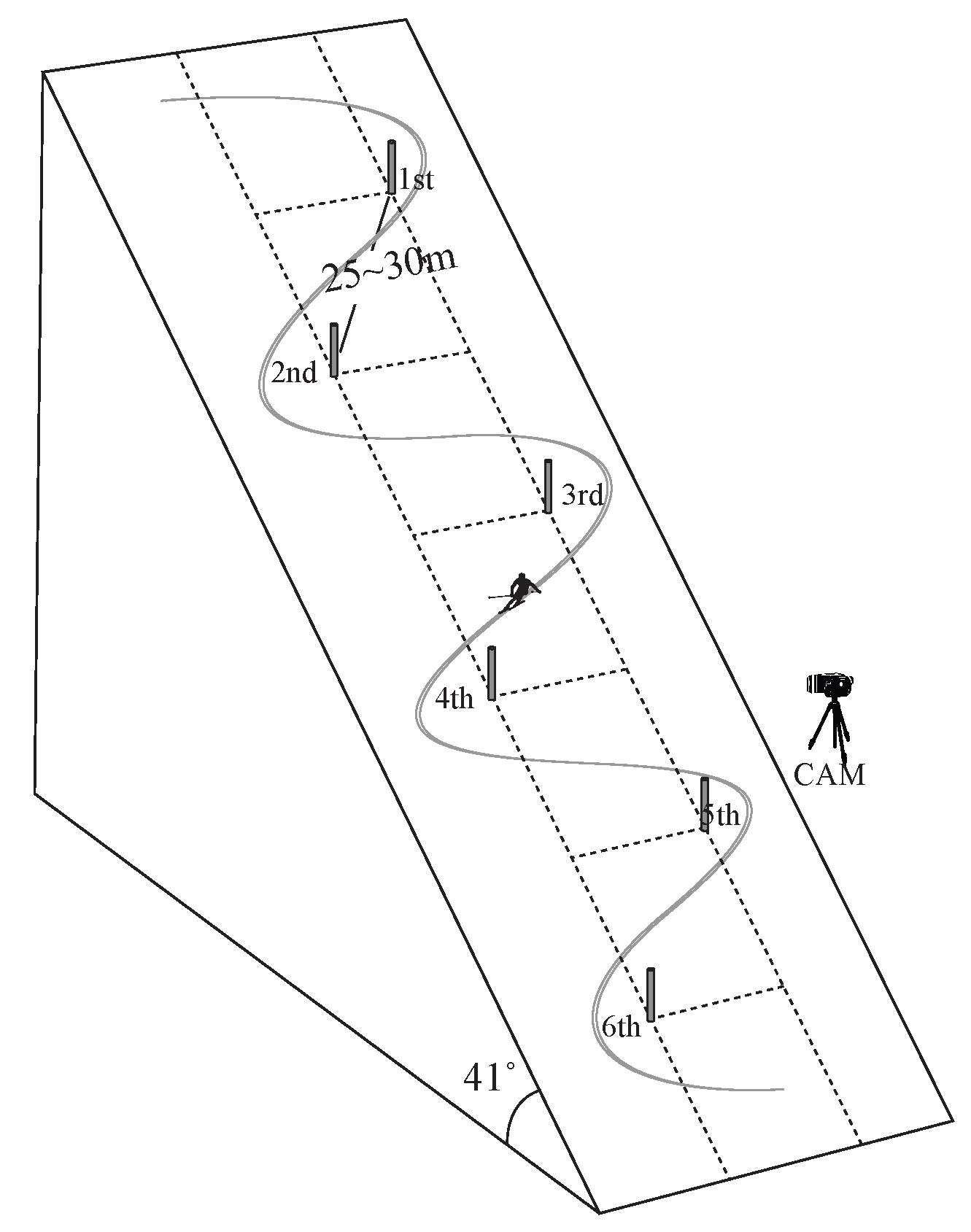
3. Description of the Experiment
4. IMU Location Analysis
- Pattern correlation analysis;
- Clustering analysis;
- Turn detection analysis.
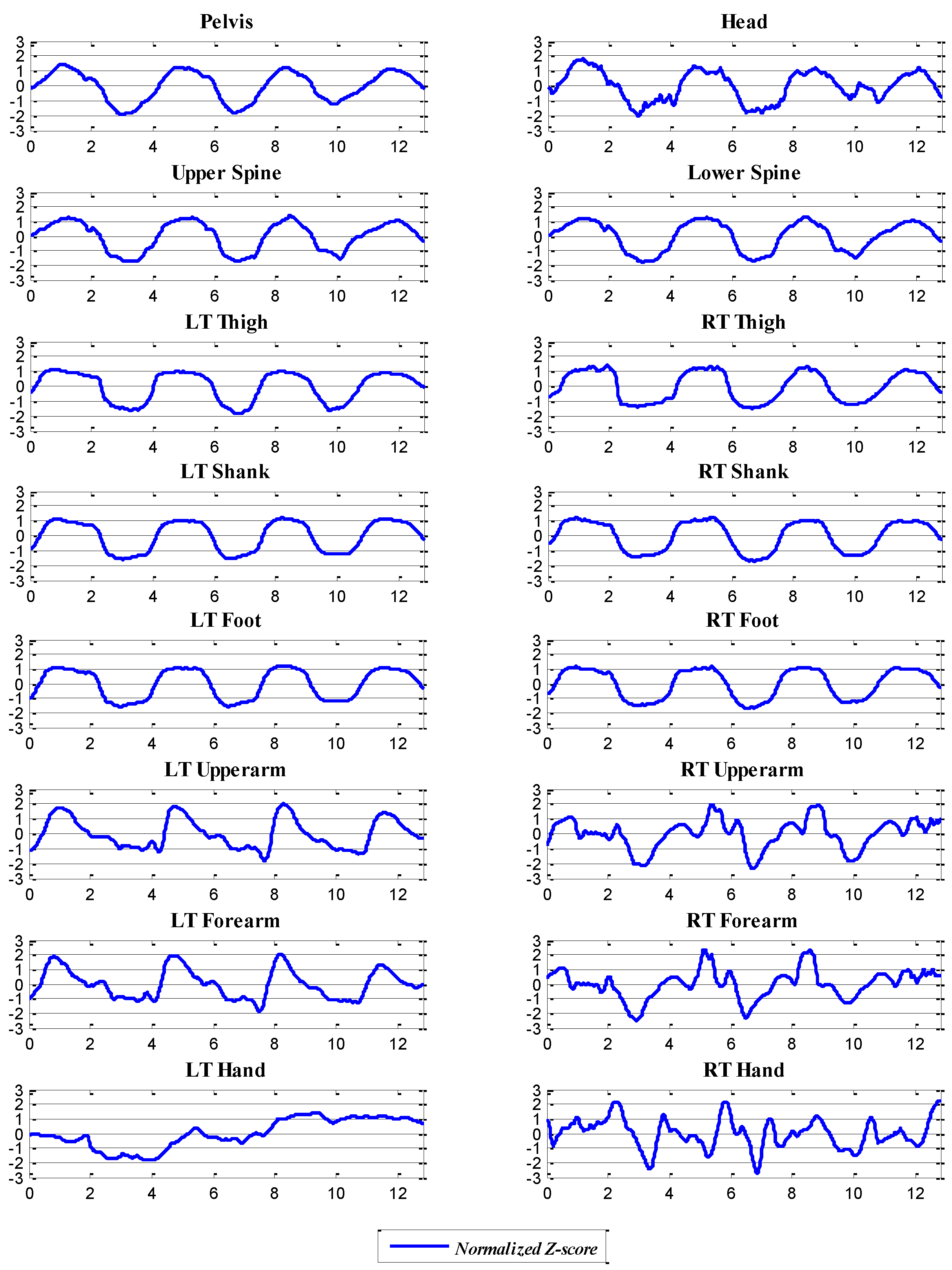
4.1. Pattern Correlation Analysis
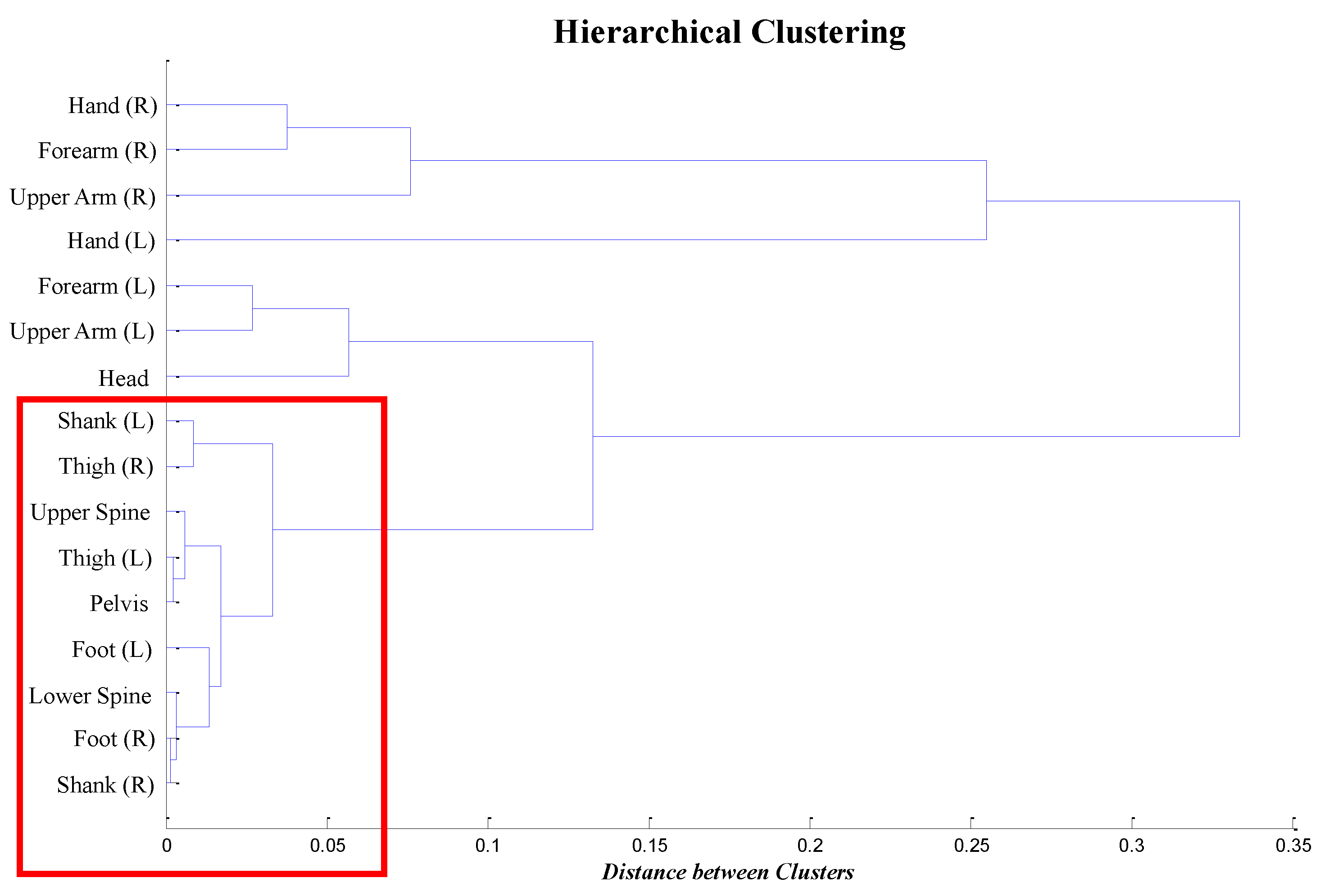
4.2. Clustering Analysis
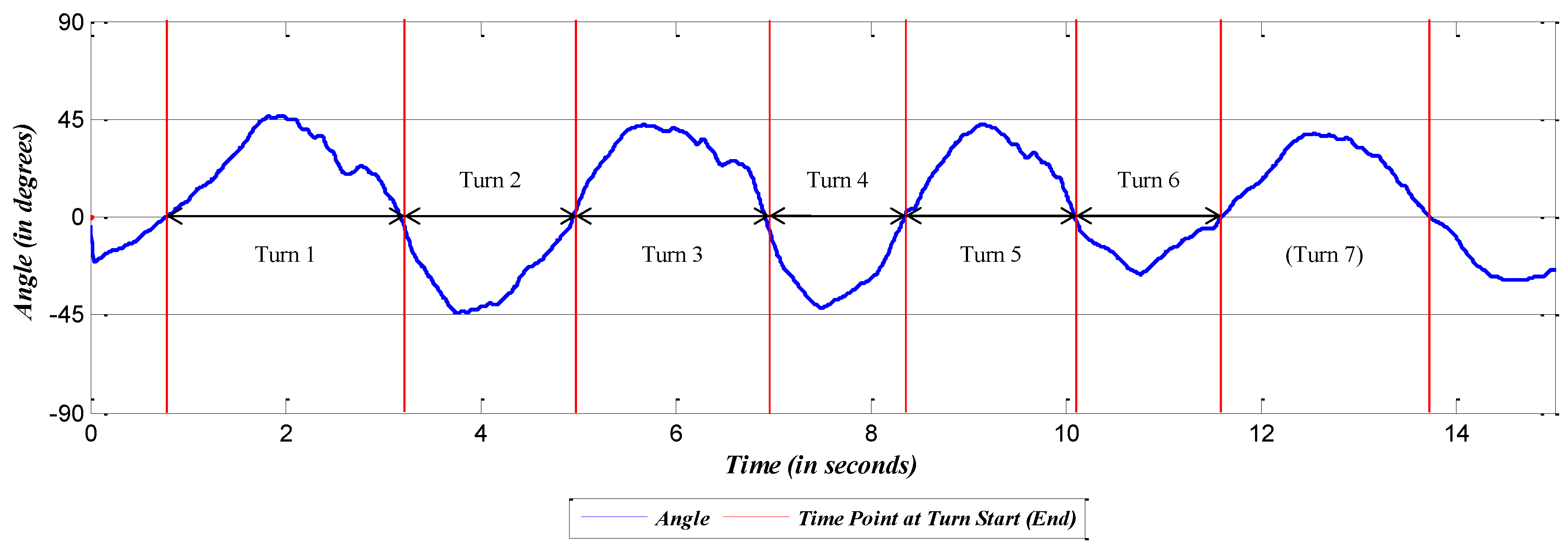
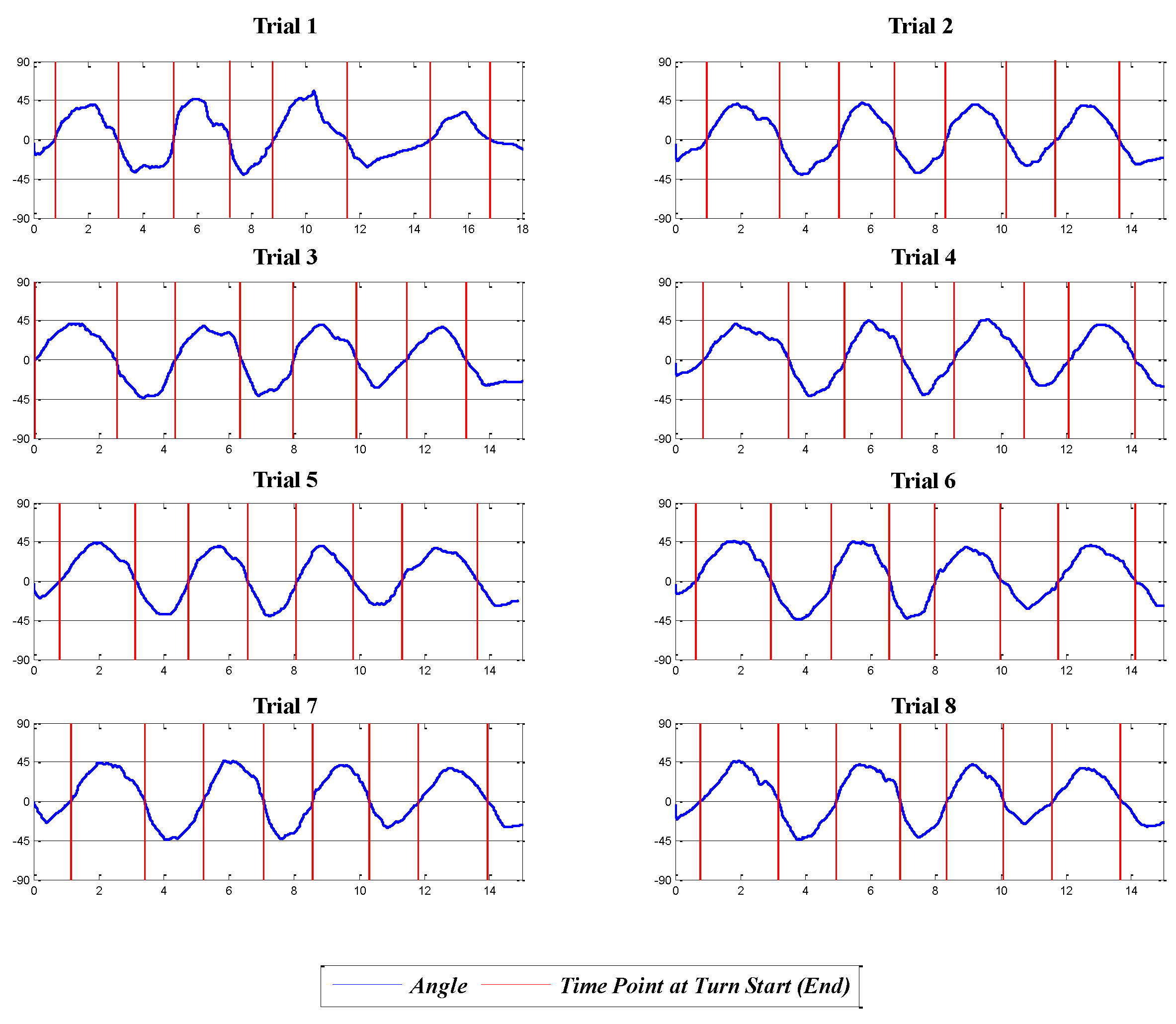
4.3. Turn Detection Analysis
5. Skiing Performance Analysis and Validation
- Lateral-asymmetric performance test;
- Test for the adaptation effect of training.
5.1. Lateral-Asymmetric Performance Test
- Hypothesis test for the time duration:In the hypothesis test from Equation (6), the null hypothesis, , is that there is no significant difference in the time duration between left and right turns . The alternative, , is that there is a significant difference in the time duration between left and right turns . Because the population variances of the time duration data for left and right turns are equal, the test statistic, , is defined as the following Equation (8). In this equation, and indicate the sample means of the time duration in left and right turns, whereas and indicate the sample variances of the time duration in left and right turns. and are the number of samples for each dataset.Finally, the calculated test statistic is 4.27, and its absolute value, , is larger than , such that it falls into the rejection region. Thus, the null hypothesis that there is a significant difference in the time duration between left and right turns is rejected.
- Hypothesis test for the maximum foot pressure ratio:Following the hypothesis test of Equation (7), the null hypothesis, , is that there is no significant difference in the maximum foot pressure ratio between left and right turns . The alternative, , is that there is a significant difference in the maximum foot pressure ratio between left and right turns . Because the population variances of the maximum foot pressure ratio data for left and right turns are not equal, the test statistic, , is defined as Equation (9). In this equation, and indicate the sample means of the maximum foot pressure ratio in left and right turns, whereas and indicate the sample variances of the maximum foot pressure ratio in left and right turns. and are the number of samples for each dataset.Finally, the calculated test statistic is 2.62, and its absolute value, , is larger than , such that it falls into the rejection region. Thus, the null hypothesis that there is a significant difference in the maximum foot pressure ratio or the balance in weight shifts between left and right turns is rejected.
5.2. Test for the Adaptation Effect of Training
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IMU | Inertial measurement unit |
| FIS | FÉDÉRATION INTERNATIONALE DE SKI |
| 3-D | 3-dimensional |
| IoT | Internet of Things |
| KNSU | Korea National Sports University |
| K-S test | Kolmogorov–Smirnov test |
| CV | Critical value |
Appendix A: Hypothesis Tests for Lateral-Asymmetry Analysis
A.1. K-S Test
| K-S Test | K-S Statistics | CV (α = 0.05) |
|---|---|---|
| Time duration (R) | 0.146 | 0.269 |
| Time duration (L) | 0.231 | 0.269 |
| Foot pressure ratio (R) | 0.106 | 0.269 |
| Foot pressure ratio (L) | 0.186 | 0.269 |
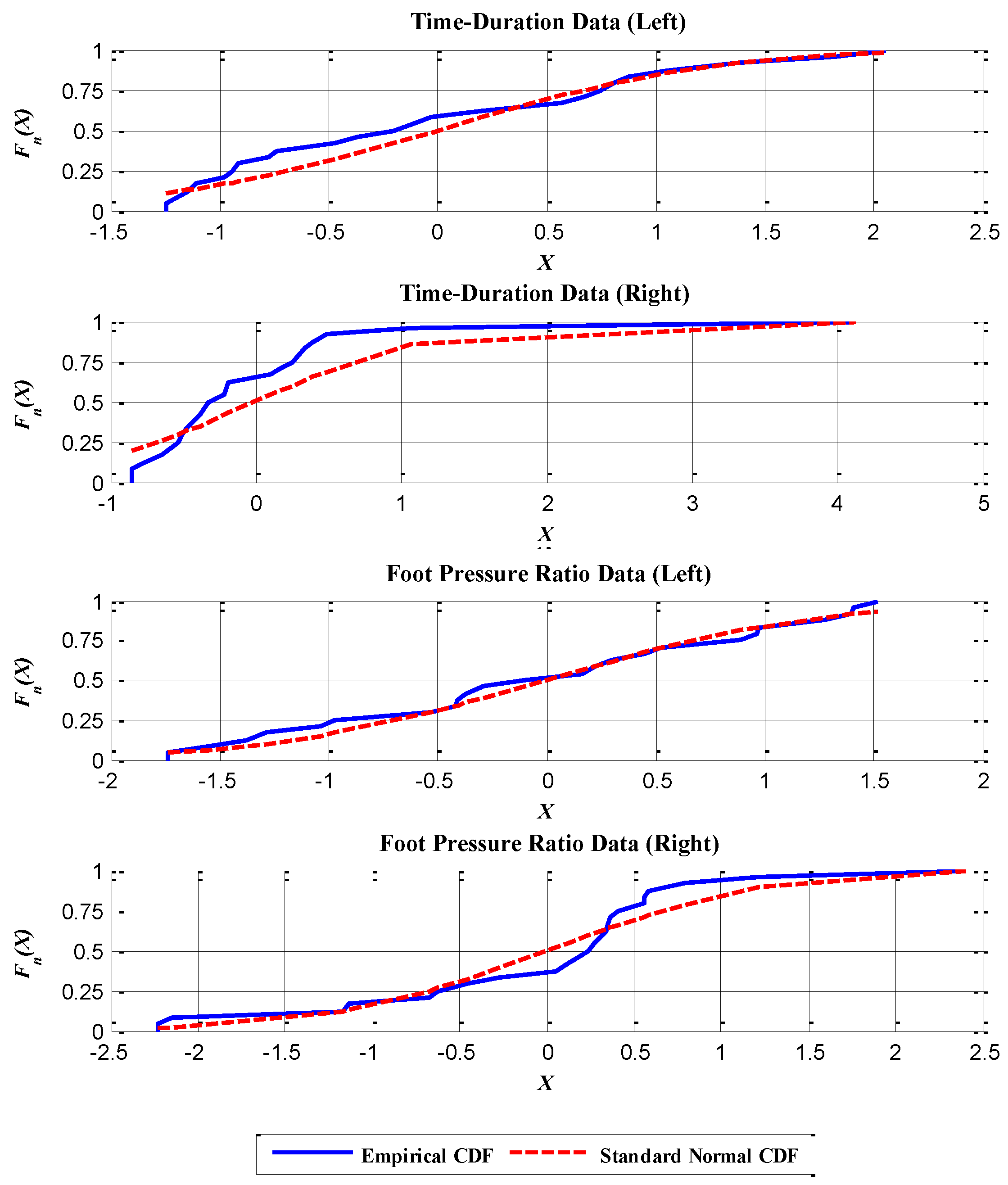
A.2. Checking the Variance of Population Data
- Hypothesis test for the variances of the time duration data:Following Equation (A2), the null hypothesis, , is that there is no significant difference in the population variances of the time durations between left and right turns . The alternative, , is that there is a significant difference in the population variances of the time durations between left and right turns . Finally, the calculated test statistic, , is 0.743, that the null hypothesis cannot be rejected because .Thus, there is no significant difference in the population variances of the time duration between left and right turns.
- Hypothesis test for the variances of the maximum foot pressure ratio:Following Equation (A2), the null hypothesis, , is that there is no significant difference in the population variance of the maximum foot pressure ratio between left and right turns . The alternative, , is that there is a significant difference in the population variance of the maximum foot pressure ratio between left and right turns (). Finally, the calculated test statistic, , is 3.40 that the null hypothesis is rejected because .Thus, there is a significant difference in the population variances of the maximum foot pressure ratio between left and right turns.
Appendix B: Adaptation Effect of Training
- Hypothesis test for the number of trials vs. time duration:In the hypothesis test from Equation (B1), the null hypothesis, , is that there is no significant correlation between the number of trials and the time duration. The alternative, , is that there is a significant correlation between the number of trials and the time duration.Finally, the calculated t-statistics is with and the degree of freedom ; with a significance level (α) of 0.10, . Because , the null hypothesis is rejected. By this analysis, the causal relationship between the number of trials and the time duration is confirmed.
Appendix C: Summary of the Survey
| Question 1: Are there any personal characteristics that might affect the performance? |
| • It is quite demanding to maintain against the forces acting on the left foot or leg, because of the aftereffects of inveteratedisc surgery on the left lumbar. |
| • For the best performance, some period of adaptation to the experimental equipment and the course would be required. |
| • Thorough inspection of the snow surface is mandatory for the best performance (i.e., distribution and quality of snow on the surface). |
| • Because I could not thoroughly inspect the experimental course, I expected that this would have a negative effect on performance. |
| Question 2: Are there any comments for the experiments? |
| • Because the experimental course was short and enough time was given for rest after each trial, there was less effect of fatigue when performing the turns during the whole experiment. Rather, I felt that my performances improved as I gradually adapted to the experimental devices and factors, such as snow quality and snow distribution. |
| • I believe that the performance was greatly affected by the quality of the snow among many other factors that might affect performance. |
| • In my point of view, there was more snow on the surface than ice, which is not a favorable environment to perform carving turns. |
| • The pressure sensors in the boots did not influence significantly the performance during the experiments. However, I do not want to use them for daily training. |
| • The IMU sensors attached to the feet distracted from the control of skis while performing the turns. |
| Question 3: Evaluate yourself in a range from one to 10 (10 for the best) for each trial. |
| • Please refer to Table 6 in Section 5 |
References
- Kwak, D.H.; Kim, Y.K.; Hirt, E.R. Exploring the role of emotions on sport consumers’ behavioral and cognitive responses to marketing stimuli. Eur. Sport Manag. Q. 2011, 11, 225–250. [Google Scholar] [CrossRef]
- Ko, M.; Yeo, J.; Lee, J.; Lee, U.; Jang, Y. What Makes Sports Fans Interactive? Identifying Factors Affecting Chat Interactions in Online Sports Viewing. PloS ONE 2016, 11, e0148377. [Google Scholar] [CrossRef] [PubMed]
- “Sport Technology” by Chris Hume Dr Ralph Richards. Available online: https://www.clearinghouseforsport.gov.au/knowledge_base/organised_sport/sports_and_sports_organisations/sport_technology (accessed on 26 March 2016).
- CNN-Smart sports equipment turns phones into coaches. Available online: http://edition.cnn.com/2014/11/28/tech/innovation/smart-sports-equipment/ (accessed on 26 March 2016).
- Müller, E.; Schwameder, H. Biomechanical aspects of new techniques in alpine skiing and ski-jumping. J. Sports Sci. 2003, 21, 679–692. [Google Scholar] [CrossRef] [PubMed]
- Klous, M.; Müller, E.; Schwameder, H. Three-dimensional knee joint loading in alpine skiing: A comparison between a carved and a skidded turn. J. Appl. Biomech. 2012, 28, 655–664. [Google Scholar] [PubMed]
- Big-Data Analytics in World Cup. Available online: https://www.informationweek.com/big-data/big-data-analytics/world-cup-assist-goes-to-big-data/a/d-id/1278822 (accessed on 11 January 2016).
- Lee, M.R.; Bojanova, I.; Suder, T. The New Wearable Computing Frontier. IT Prof. 2015, 17, 16–19. [Google Scholar] [CrossRef]
- Nakazato, K.; Scheiber, P.; Müller, E. A comparison of ground reaction forces determined by portable force-plate and pressure-insole systems in alpine skiing. J. Sports Sci. Med. 2011, 10, 754–762. [Google Scholar] [PubMed]
- Vaverka, F.; Vodickova, S. Laterality of the lower limbs and carving turns. Biol. Sport 2010, 27, 129–134. [Google Scholar] [CrossRef]
- Maxwell, S.M.; Hull, M.L. Measurement of strength and loading variables on the knee during alpine skiing. J. Biomech. 1989, 22, 609–624. [Google Scholar] [CrossRef]
- Schaff, P.; Hauser, W. 3-D video motion analysis on the slope-A practical way to analyze motion patterns in Alpine skiing. In Skiing Trauma and Safety: Ninth International Symposium; ASTM International: West Conshohocken, PA, USA, 1993; Volume 1182, p. 169. [Google Scholar]
- Muller, E.; Bartlett, R.; Raschner, C.; Schwameder, H.; Benko-Bernwick, U.; Lindinger, S. Comparisons of the ski turn techniques of experienced and intermediate skiers. J. Sports Sci. 1998, 16, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, T.; Kagawa, H.; Okamoto, A.; Sawada, M. Joint motion and reacting forces in the carving ski turn compared with the conventional ski turn. Sports Eng. 2000, 3, 161–176. [Google Scholar] [CrossRef]
- Scott, N.; Yoneyama, T.; Kagawa, H.; Osada, K. Measurement of ski snow-pressure profiles. Sports Eng. 2007, 10, 145–156. [Google Scholar] [CrossRef]
- Park, S.K.; Yoon, S.; Ryu, J.; Kim, J.; Kim, J.N.; Yoo, S.H.; Jeon, H.M.; Ha, S.; Cho, H.J.; Park, H.R.; et al. Lower extremity kinematics of ski motion on hills. ISBS-Conf. Proc. Arch. 2013, 1, 1–4. [Google Scholar]
- Brodie, M.; Walmsley, A.; Page, W. Fusion motion capture: A prototype system using inertial measurement units and GPS for the biomechanical analysis of ski racing. Sports Technol. 2008, 1, 17–28. [Google Scholar] [CrossRef]
- Krüger, A.; Edelmann-Nusser, J. Application of a full body inertial measurement system in alpine skiing: A comparison with an optical video based system. J. Appl. Biomech. 2010, 26, 516–521. [Google Scholar] [PubMed]
- Kondo, A.; Doki, H.; Hirose, K. Motion Analysis and Joint Angle Measurement of Skier Gliding on the Actual Snow Field Using Inertial Sensors. Procedia. Eng. 2013, 60, 307–312. [Google Scholar] [CrossRef]
- Marsland, F.; Lyons, K.; Anson, J.; Waddington, G.; Macintosh, C.; Chapman, D. Identification of cross-country skiing movement patterns using micro-sensors. Sensors 2012, 12, 5047–5066. [Google Scholar] [CrossRef] [PubMed]
- Nemec, B.; Petrič, T.; Babič, J.; Supej, M. Estimation of Alpine Skier Posture Using Machine Learning Techniques. Sensors 2014, 14, 18898–18914. [Google Scholar] [CrossRef] [PubMed]
- Michahelles, F.; Schiele, B. Sensing and monitoring professional skiers. Pervasive Comput. IEEE 2005, 4, 40–45. [Google Scholar] [CrossRef]
- Kirby, R. Development of a real-time performance measurement and feedback system for alpine skiers. Sports Technol. 2009, 2, 43–52. [Google Scholar] [CrossRef]
- Supej, M. 3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. J. Sports Sci. 2010, 28, 759–769. [Google Scholar] [CrossRef] [PubMed]
- Federolf, P.A. Quantifying instantaneous performance in alpine ski racing. J. Sports Sci. 2012, 30, 1063–1068. [Google Scholar] [CrossRef] [PubMed]
- Debski, R. High-performance simulation-based algorithms for an alpine ski racer’s trajectory optimization in heterogeneous computer systems. Int. J. Appl. Math. Comput. Sci. 2014, 24, 551–566. [Google Scholar] [CrossRef]
- Athlete Biography: Seung-pyo LEE. Available online: https://www.fis-ski.com/dynamic/athlete-biography.html?sector=AL&competitorid=165690&type=result (accessed on 26 October 2015).
- MyoMotion Articles. Available online: http://www.noraxon.com/myomotion-articles/ (accessed on 10 March 2016).
- MyoMotion (3D Inertial Sensor System). Available online: http://www.noraxon.com/homepageslider/PDFs/IntromyoMOTION.pdf (accessed on 11 March 2016).
- MyoMotion: 3D Wireless Inertial Motion Measurement System. Available online: http://www.velamed.com/files/myomotion-white-paper.pdf (accessed on 11 March 2016).
- Aleshin, V.; Klimenko, S.; Astakhov, J.; Bobkov, A.; Borodina, M.; Volegov, D.; Kazansky, I.; Novgorodtsev, D.; Frolov, P. 3D scenes simulation, animation, and synchronization in training systems with force back-coupling. In Proceedings of the 19 International Conference GraphiCon-2009, Moscow, Russia, 19–24 October 2009; pp. 166–170.
- Song, G.H.; Park, W.H.; Lim, E.J.; Jeong, G.C.; Kim, S.Y. An Immersive Ski Game Based on a Simulator. In IT Convergence and Security 2012; Springer: Berlin, Germany, 2013; pp. 777–785. [Google Scholar]
- Hall, B.L.; Schaff, P.S.; Nelson, R.C. Dynamic displacement and pressure distribution in alpine ski boots. In Skiing Trauma and Safety: Eighth International Symposium; ASTM International: West Conshohocken, PA, USA, 1991; Volume 1104, p. 186. [Google Scholar]
- Keränen, T.; Vallela, R.; Lindén, P. Ground Reaction Force and Centre of Pressure in Alpine Skiing Carved Turn; ICSS: Bangkok, Thailand, 2007. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Estevan, I.; Falco, C.; Álvarez, O.; Molina-García, J. Effect of Olympic weight category on performance in the roundhouse kick to the head in taekwondo. J. Hum. Kinet. 2012, 31, 37–43. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, T.M.; Morais, J.E.; Costa, M.J.; Goncalves, J.; Marinho, D.A.; Silva, A.J. Young swimmers’ classification based on kinematics, hydrodynamics, and anthropometrics. J. Appl. Biomech. 2014, 30, 310–315. [Google Scholar] [CrossRef] [PubMed]
- Rubin, A. Statistics for Evidence-Based Practice and Evaluation; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Kozak, M. What is strong correlation? Teach. Stat. 2009, 31, 85–86. [Google Scholar] [CrossRef]
- Reyes-Ortiz, J.L.; Oneto, L.; Samà, A.; Parra, X.; Anguita, D. Transition-aware human activity recognition using smartphones. Neurocomputing 2016, 171, 754–767. [Google Scholar] [CrossRef]
- Miller, L.H. Table of percentage points of Kolmogorov statistics. J. Am. Stat. Assoc. 1956, 51, 111–121. [Google Scholar] [CrossRef]
- K-S Test in Matlab. Available online: http://www.mathworks.com/help/stats/kstest.html?stid=gnlocdrop (accessed on 11 March 2016).



| Specification (IMU) | |
| Channel | Up to 18 sensors |
| Static accuracy | |
| Dynamic accuracy | |
| Sampling frequency | 100 Hz |
| Data output | Joint angles, acceleration, quaternions |
| Specification (Foot Pressure) | |
| Channel | 13 sensors per insole |
| Sensitivity | 0.25 N/cm |
| Coverage | Up to 50% |
| Range | 0.0∼40.0 N/cm |
| Sampling frequency | 50 Hz |
| Principle | Capacitive |
| Category | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | Trial 6 | Trial 7 | Trial 8 | Mean | Median |
|---|---|---|---|---|---|---|---|---|---|---|
| Head | 0.76 | 0.85 | 0.79 | 0.75 | 0.78 | 0.76 | 0.84 | 0.75 | 0.78 | 0.77 |
| Upper Spine | 0.71 | 0.89 | 0.88 | 0.88 | 0.88 | 0.88 | 0.93 | 0.85 | 0.86 | 0.88 |
| Lower Spine | 0.72 | 0.43 | 0.88 | 0.88 | 0.88 | 0.32 | 0.93 | 0.85 | 0.74 | 0.87 |
| Pelvis | 0.74 | 0.91 | 0.88 | 0.88 | 0.89 | 0.89 | 0.92 | 0.85 | 0.87 | 0.88 |
| Upper Arm (L) | 0.70 | 0.71 | 0.68 | 0.69 | 0.72 | 0.70 | 0.74 | 0.70 | 0.71 | 0.70 |
| Upper Arm (R) | 0.48 | 0.69 | 0.73 | 0.43 | 0.60 | 0.44 | 0.79 | 0.63 | 0.60 | 0.61 |
| Forearm (L) | 0.72 | 0.74 | 0.72 | 0.74 | 0.55 | 0.73 | 0.75 | 0.69 | 0.70 | 0.73 |
| Forearm (R) | 0.50 | 0.66 | 0.70 | 0.43 | 0.53 | 0.42 | 0.78 | 0.58 | 0.58 | 0.56 |
| Hand (L) | 0.40 | -0.13 | 0.51 | 0.61 | 0.52 | 0.21 | 0.14 | 0.16 | 0.30 | 0.31 |
| Hand (R) | 0.49 | 0.64 | 0.53 | 0.50 | 0.61 | 0.67 | 0.48 | 0.48 | 0.55 | 0.52 |
| Thigh (L) | 0.69 | 0.91 | 0.88 | 0.88 | 0.90 | 0.89 | 0.92 | 0.87 | 0.87 | 0.89 |
| Thigh (R) | 0.74 | 0.84 | 0.84 | 0.80 | 0.83 | 0.79 | 0.89 | 0.85 | 0.82 | 0.84 |
| Shank (L) | 0.78 | 0.89 | 0.84 | 0.82 | 0.84 | 0.87 | 0.89 | 0.85 | 0.85 | 0.84 |
| Shank (R) | 0.71 | 0.89 | 0.87 | 0.87 | 0.86 | 0.88 | 0.89 | 0.85 | 0.85 | 0.87 |
| Foot (L) | 0.73 | 0.87 | 0.86 | 0.82 | 0.85 | 0.86 | 0.88 | 0.84 | 0.84 | 0.86 |
| Foot (R) | 0.73 | 0.90 | 0.88 | 0.84 | 0.86 | 0.89 | 0.90 | 0.85 | 0.86 | 0.87 |
| Average | 0.66 | 0.72 | 0.78 | 0.74 | 0.75 | 0.70 | 0.79 | 0.72 | 0.73 | 0.75 |
| Location | Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | Trial 6 | Trial 7 | Trial 8 | Total (Avg.) |
|---|---|---|---|---|---|---|---|---|---|
| Upper Spine | 100% | 100% | 100% | 129% | 100% | 100% | 100% | 100% | 104% |
| Lower Spine | 100% | 0% | 100% | 100% | 100% | 0% | 100% | 100% | 75% |
| Pelvis | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Thigh (L) | 129% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 104% |
| Thigh (R) | 200% | 129% | 114% | 100% | 171% | 114% | 286% | 171% | 161% |
| Shank (L) | 86% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 98% |
| Shank (R) | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Foot (L) | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Foot (R) | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% | 100% |
| Turns | Turn 1 (R) | Turn 3 (R) | Turn 5 (R) | |||
| Attributes | Time Duration (s) | Max Pressure Ratio | Time Duration (s) | Max Pressure Ratio | Time Duration (s) | Max Pressure Ratio |
| Trial 1 | 2.32 | 0.89 | 2.07 | 0.85 | 2.69 | 0.85 |
| Trial 2 | 2.25 | 0.94 | 1.71 | 0.88 | 1.86 | 0.78 |
| Trial 3 | 2.49 | 0.80 | 2.02 | 0.72 | 1.94 | 0.72 |
| Trial 4 | 2.62 | 0.93 | 1.79 | 0.78 | 2.14 | 0.77 |
| Trial 5 | 2.34 | 0.93 | 1.81 | 0.77 | 1.74 | 0.76 |
| Trial 6 | 2.30 | 0.92 | 1.80 | 0.83 | 2.05 | 0.70 |
| Trial 7 | 2.28 | 0.83 | 1.85 | 0.82 | 1.74 | 0.67 |
| Trial 8 | 2.39 | 0.89 | 1.97 | 0.69 | 1.75 | 0.66 |
| Turns | Turn 2 (L) | Turn 4 (L) | Turn 6 (L) | |||
| Attributes | Time Duration (s) | Max Pressure Ratio | Time Duration (s) | Max Pressure Ratio | Time Duration (s) | Max Pressure Ratio |
| Trial 1 | 2.05 | 0.81 | 1.62 | 0.92 | 3.10 | 0.97 |
| Trial 2 | 1.82 | 0.88 | 1.57 | 0.83 | 1.50 | 0.89 |
| Trial 3 | 1.80 | 0.88 | 1.62 | 0.83 | 1.55 | 0.87 |
| Trial 4 | 1.72 | 0.87 | 1.57 | 0.87 | 1.39 | 0.89 |
| Trial 5 | 1.61 | 0.81 | 1.52 | 0.76 | 1.46 | 0.87 |
| Trial 6 | 1.85 | 0.76 | 1.39 | 0.85 | 1.74 | 0.84 |
| Trial 7 | 1.80 | 0.87 | 1.51 | 0.88 | 1.53 | 0.88 |
| Trial 8 | 1.77 | 0.86 | 1.42 | 0.89 | 1.50 | 0.90 |
| IMU Sensor | Foot Pressure Sensors | ||
|---|---|---|---|
| Null () | Null () | ||
| Alternative () | Alternative () | ||
| Critical points () | 2.01 | Critical points () | 2.03 |
| t-statistics | 4.27 | t-statistics | 2.62 |
| Results | rejected | Results | rejected |
| Trial | Trial 1 | * | Trial 2 | Trial 3 | Trial 4 | Trial 5 | Trial 6 | Trial 7 | Trial 8 |
|---|---|---|---|---|---|---|---|---|---|
| Self-assessment (out of 10) | 2.5 | 3.5 | 3.5 | 4.5 | 5 | 5 | 5 | 5 | 6 |
| Time duration | 13.85 | N/A | 10.71 | 11.42 | 11.23 | 10.48 | 11.13 | 10.71 | 10.80 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, G.; Jang, Y.J.; Kim, J.; Kim, J.H.; Kim, H.Y.; Kim, K.; Panday, S.B. Potential of IMU Sensors in Performance Analysis of Professional Alpine Skiers. Sensors 2016, 16, 463. https://doi.org/10.3390/s16040463
Yu G, Jang YJ, Kim J, Kim JH, Kim HY, Kim K, Panday SB. Potential of IMU Sensors in Performance Analysis of Professional Alpine Skiers. Sensors. 2016; 16(4):463. https://doi.org/10.3390/s16040463
Chicago/Turabian StyleYu, Gwangjae, Young Jae Jang, Jinhyeok Kim, Jin Hae Kim, Hye Young Kim, Kitae Kim, and Siddhartha Bikram Panday. 2016. "Potential of IMU Sensors in Performance Analysis of Professional Alpine Skiers" Sensors 16, no. 4: 463. https://doi.org/10.3390/s16040463
APA StyleYu, G., Jang, Y. J., Kim, J., Kim, J. H., Kim, H. Y., Kim, K., & Panday, S. B. (2016). Potential of IMU Sensors in Performance Analysis of Professional Alpine Skiers. Sensors, 16(4), 463. https://doi.org/10.3390/s16040463








