Self-Tuning Fully-Connected PID Neural Network System for Distributed Temperature Sensing and Control of Instrument with Multi-Modules
Abstract
:1. Introduction
2. Problem Model and Design of Self-Tuning FCPIDNN Temperature Sensing and Control System
2.1. Temperature Control Problem Formulation
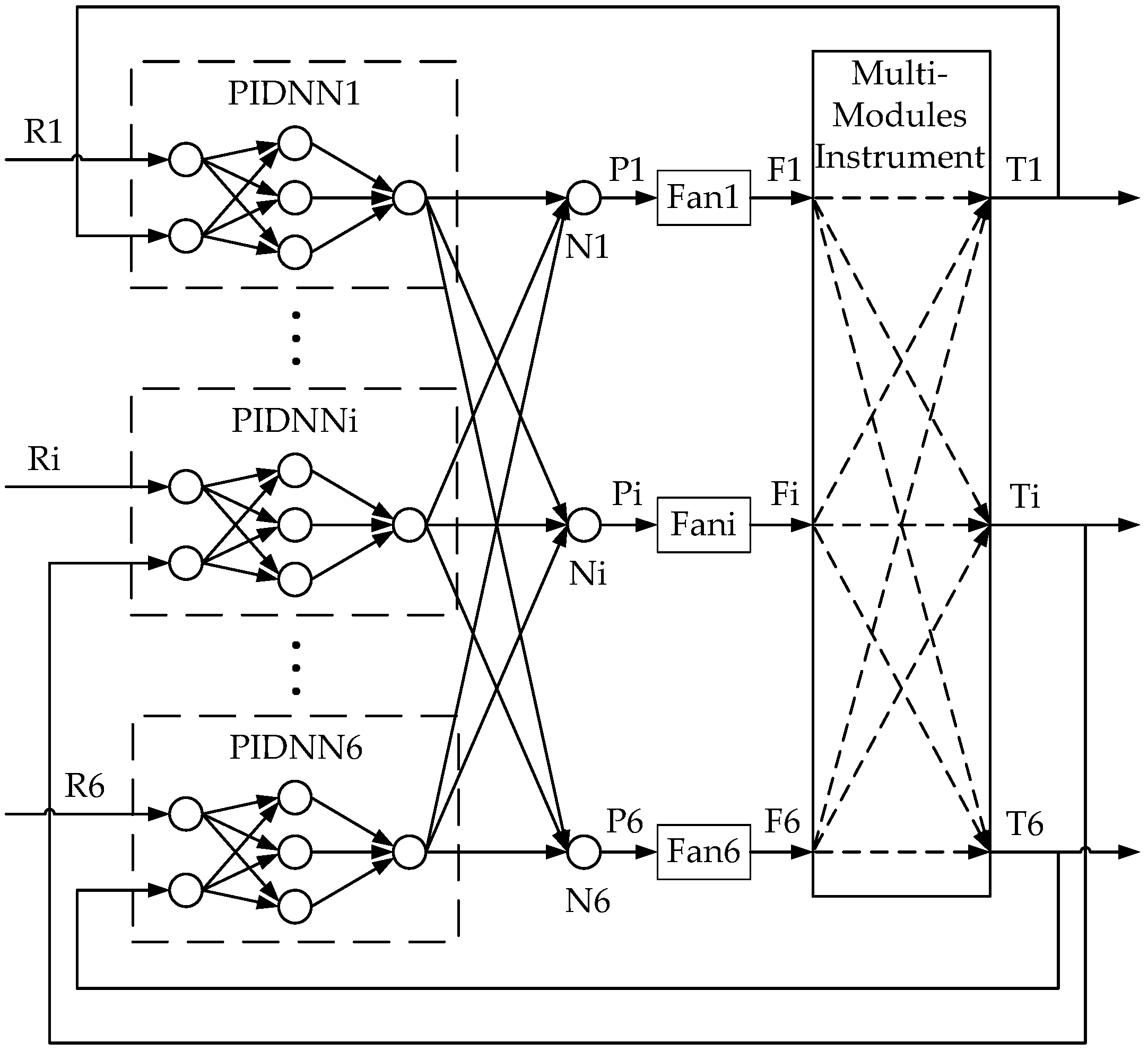
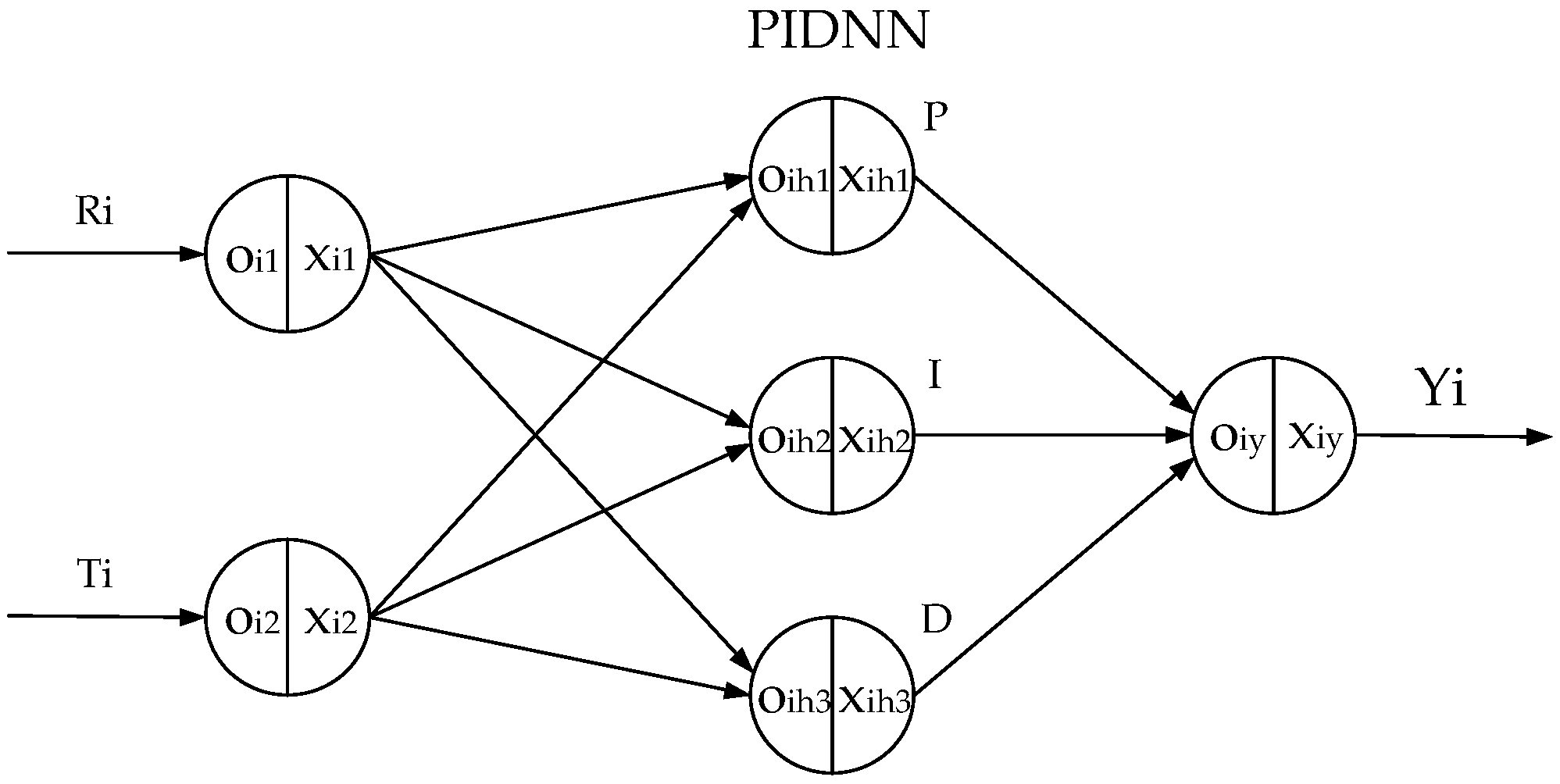
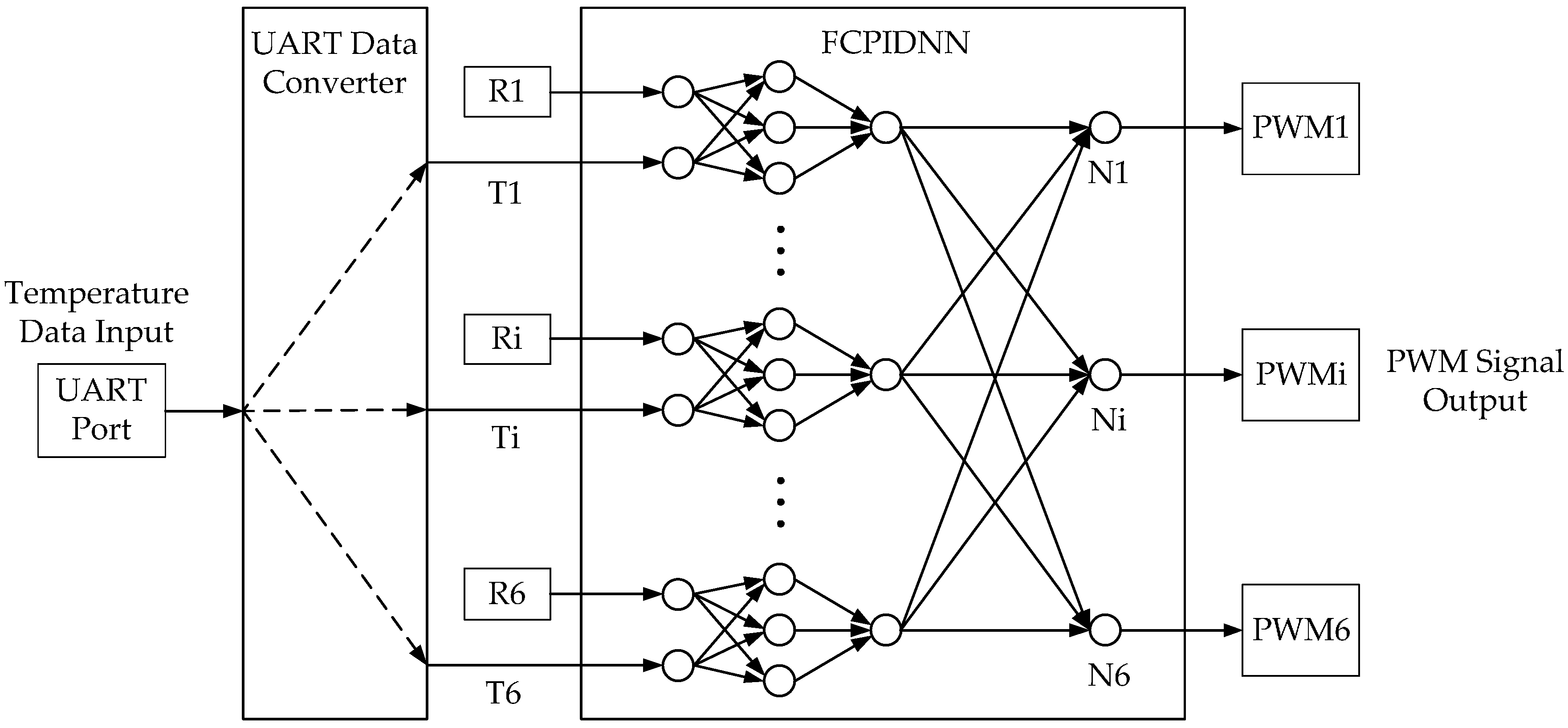
2.2. MIMO Temperature Sensing and Control System
2.3. Convergence Analysis
3. Experiments and Discussion
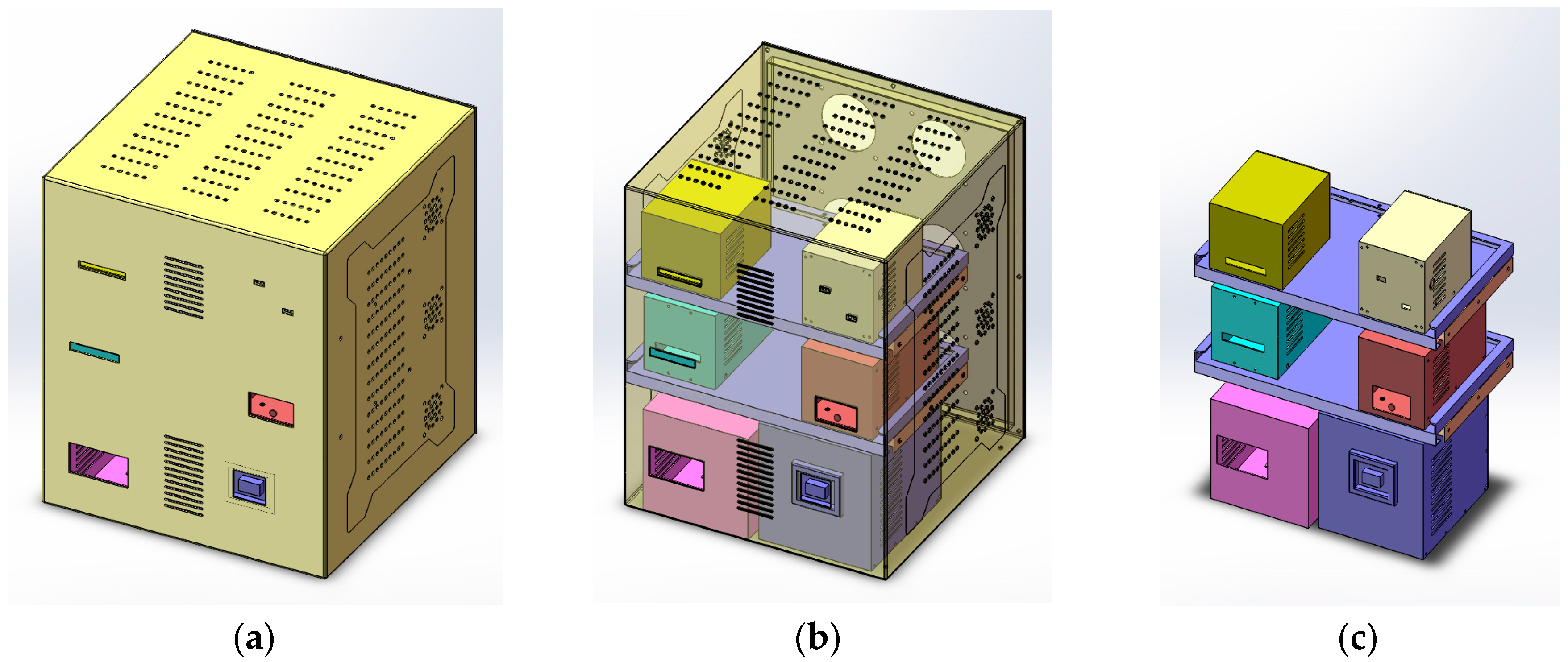
3.1. Instrument Mockup
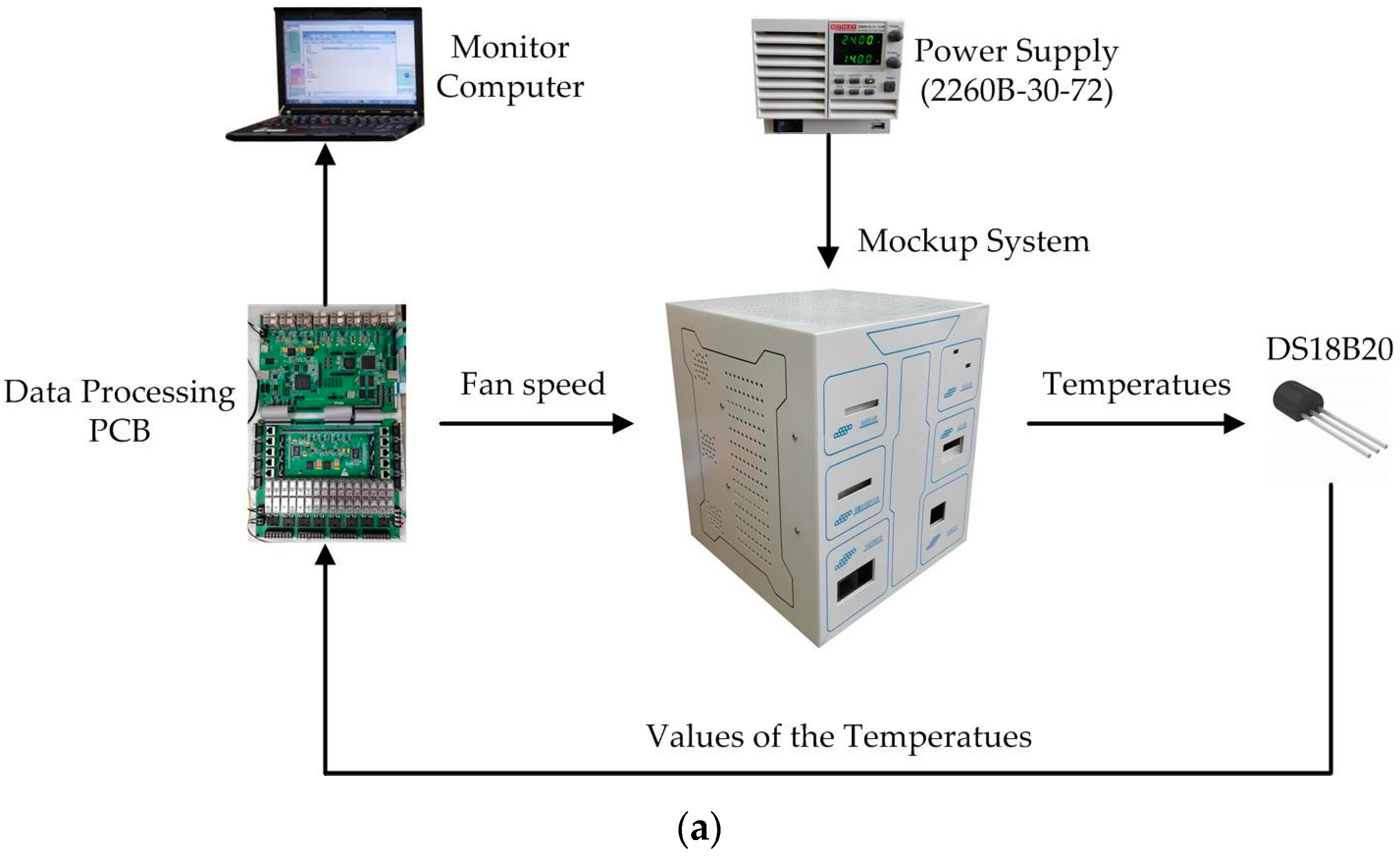
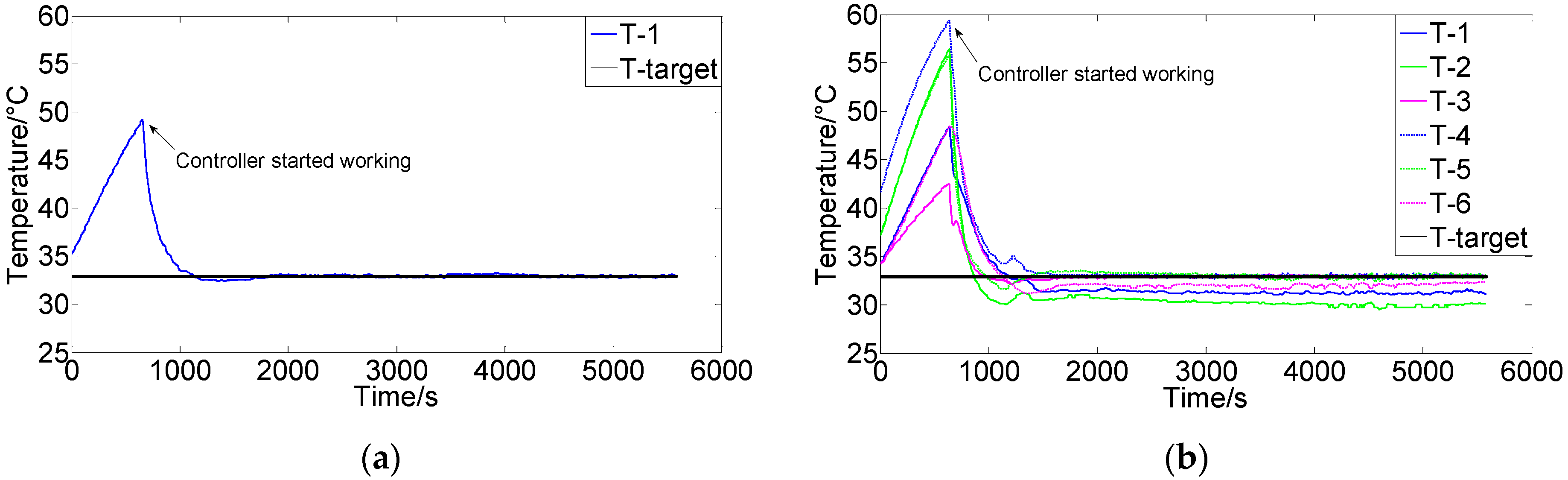
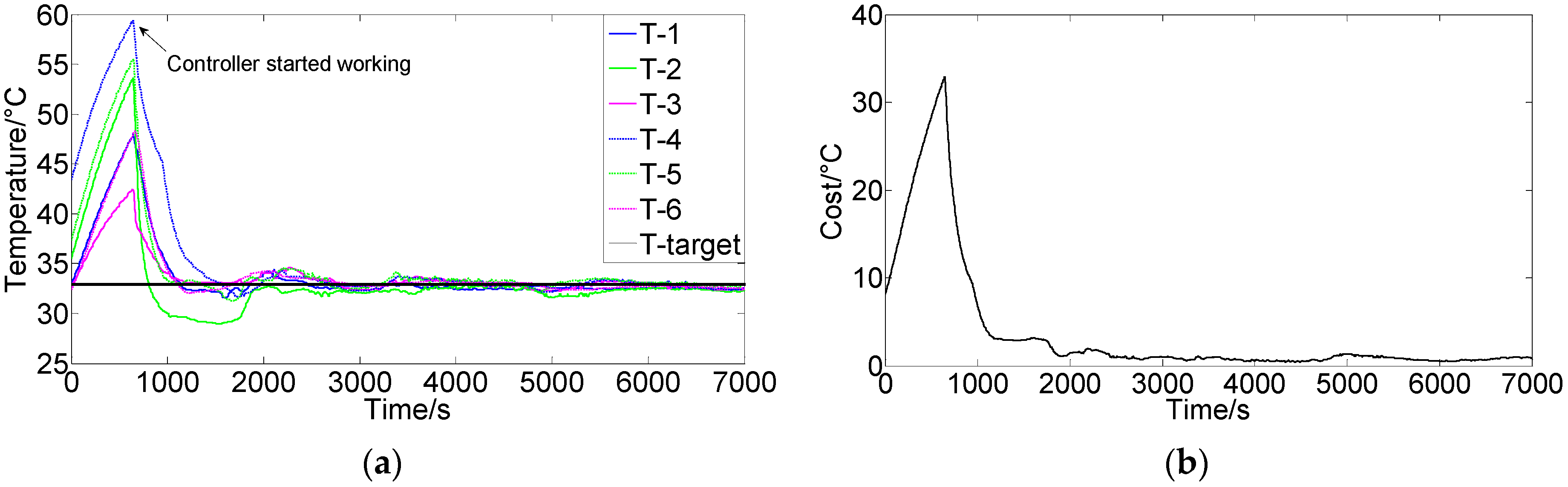
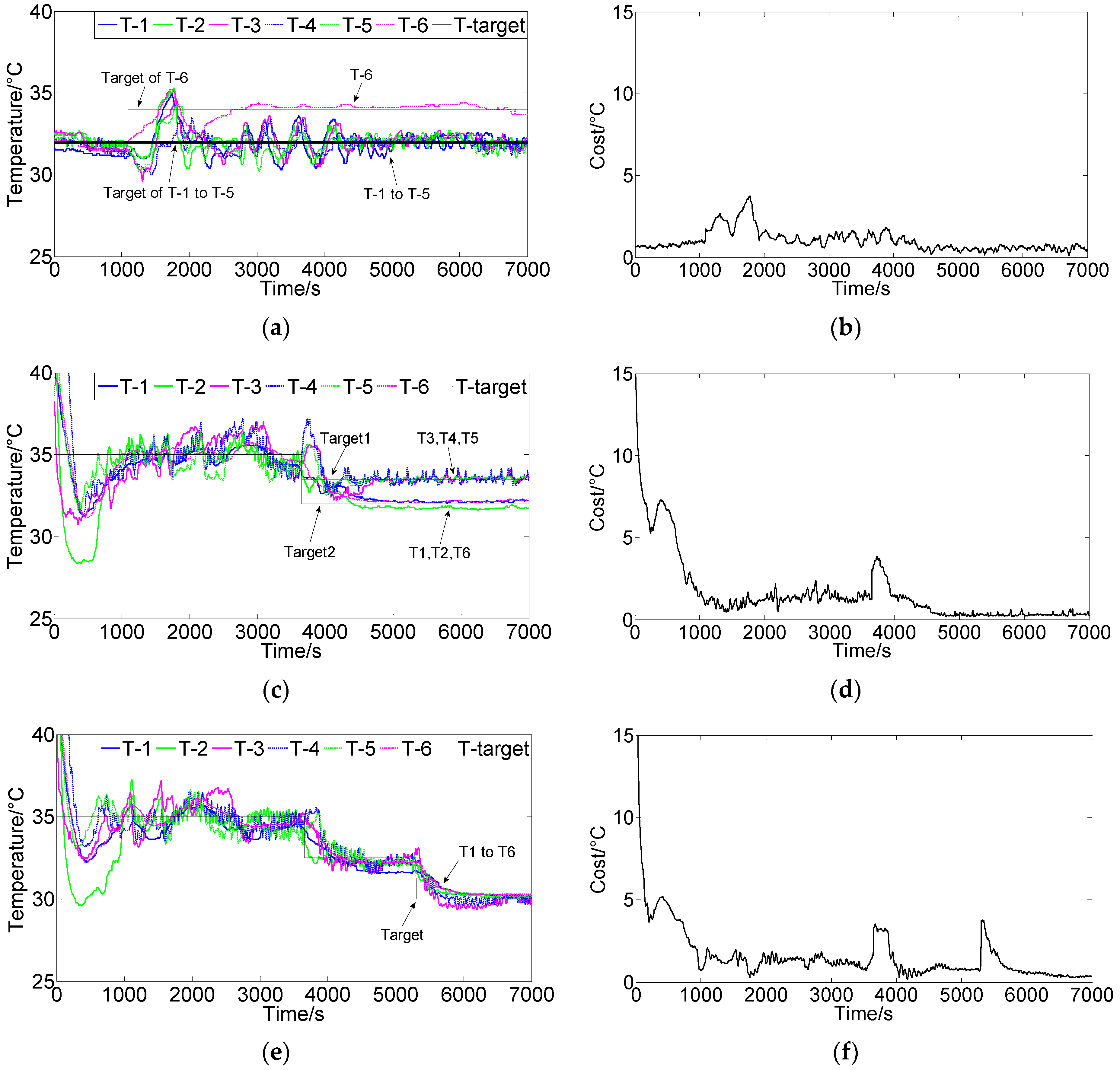
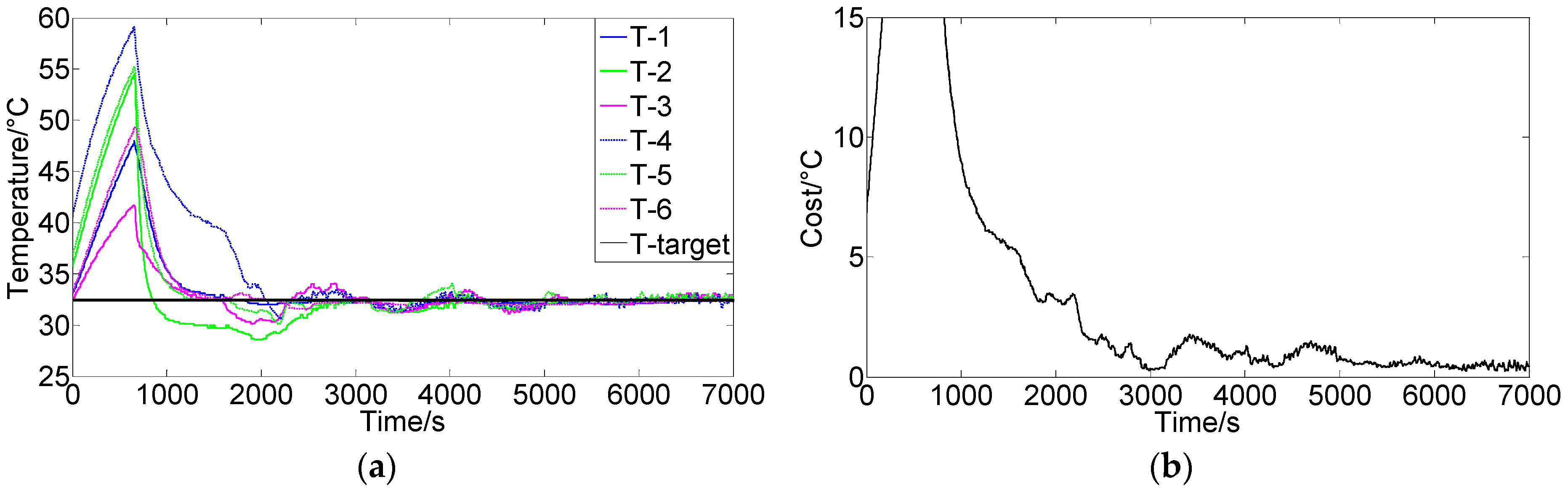
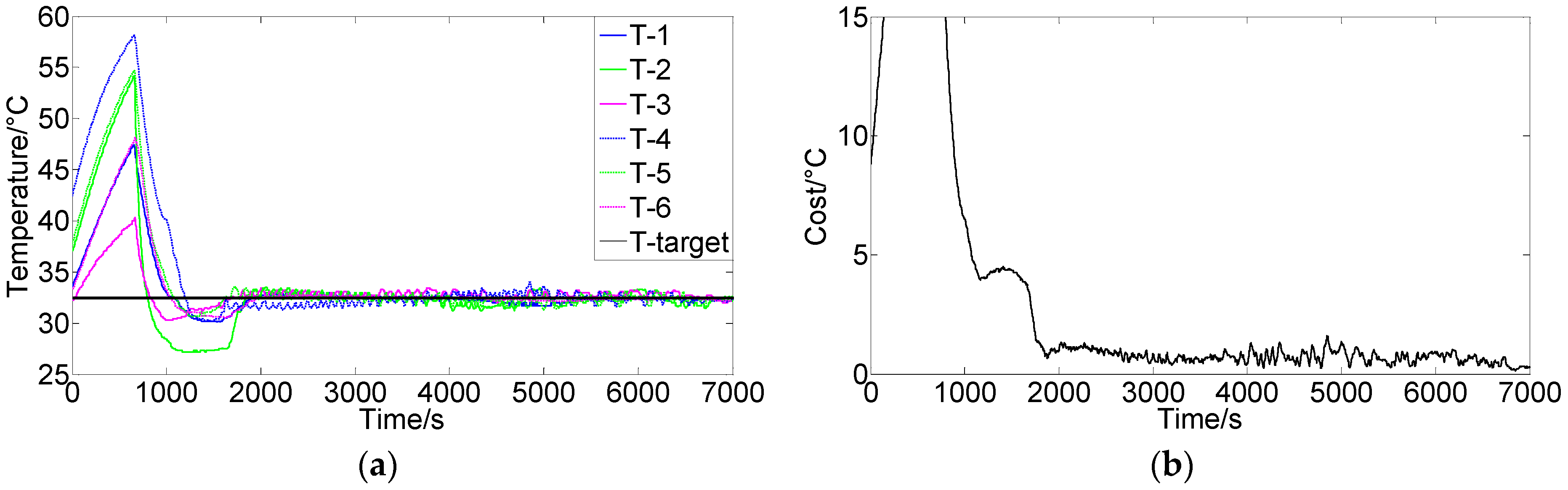
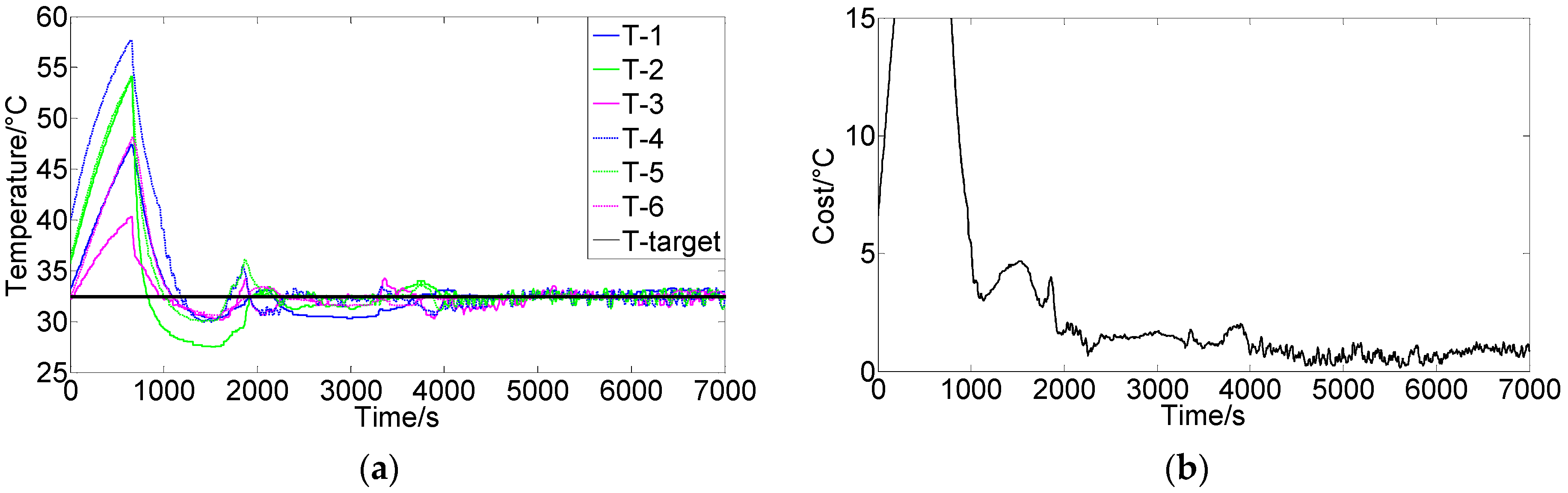
3.2. Experimental System and Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, C.S.; Xu, J.L.; Ma, W.L.; Zheng, W.L. PCR microfluidic devices for DNA amplification. Biotechnol. Adv. 2006, 3, 243–284. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, Z.; Jia, H.; Yan, J. One-step ultrasensitive detection of microRNAs with loop-mediated isothermal amplification (LAMP). Chem. Commun. 2011, 9, 2595–2597. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Hsiung, S.; Hung, Y.; Chang, C.; Liao, T.; Lee, G. A cell counting/sorting system incorporated with a microfabricated flow cytometer chip. Meas. Sci. Technol. 2006, 7, 2001–2009. [Google Scholar] [CrossRef]
- Pires, N.M.M.; Dong, T.; Hanke, U.; Hoivik, N. Recent Developments in Optical Detection Technologies in Lab-on-a-Chip Devices for Biosensing Applications. Sensors 2014, 8, 15458–15479. [Google Scholar] [CrossRef] [PubMed]
- Ahrberg, C.D.; Ilic, B.R.; Manz, A.; Neuzil, P. Handheld real-time PCR device. Lab Chip 2016, 3, 586–592. [Google Scholar] [CrossRef] [PubMed]
- Joo, S.; Kim, K.H.; Kim, H.C.; Chung, T.D. A portable microfluidic flow cytometer based on simultaneous detection of impedance and fluorescence. Biosens. Bioelectron. 2010, 6, 1509–1515. [Google Scholar] [CrossRef] [PubMed]
- Roda, A.; Mirasoli, M.; Dolci, L.S.; Buragina, A.; Bonvicini, F.; Simoni, P.; Guardigli, M. Portable Device Based on Chemiluminescence Lensless Imaging for Personalized Diagnostics through Multiplex Bioanalysis. Anal. Chem. 2011, 8, 3178–3185. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Murray, B.T.; Sammakia, B. Airflow and temperature distribution optimization in data centers using artificial neural networks. Int. J. Heat Mass Transf. 2013, 64, 80–90. [Google Scholar] [CrossRef]
- Shen, Y.; Cai, W.; Li, S. Normalized decoupling control for high-dimensional MIMO processes for application in room temperature control HVAC systems. Control Eng. Pract. 2010, 6, 652–664. [Google Scholar] [CrossRef]
- Pohjoranta, A.; Halinen, M.; Pennanen, J.; Kiviaho, J. Model predictive control of the solid oxide fuel cell stack temperature with models based on experimental data. J. Power Sources 2015, 277, 239–250. [Google Scholar] [CrossRef]
- Moon, U.; Kim, W. Temperature Control of Ultrasupercritical Once-through Boiler-turbine System Using Multi-input Multi-output Dynamic Matrix Control. J. Electr. Eng. Technol. 2011, 3, 423–430. [Google Scholar] [CrossRef]
- Li, J.; Meng, X. Temperature decoupling control of double-level air flow field dynamic vacuum system based on neural network and prediction principle. Eng. Appl. Artif. Intell. 2013, 4, 1237–1245. [Google Scholar]
- Gil, P.; Henriques, J.; Cardoso, A.; Carvalho, P.; Dourado, A. Affine Neural Network-Based Predictive Control Applied to a Distributed Solar Collector Field. IEEE Trans. Control Syst. Technol. 2014, 2, 585–596. [Google Scholar] [CrossRef]
- Shen, L.; He, J.; Yang, C.; Gui, W.; Xu, H. Temperature Uniformity Control of Large-Scale Vertical Quench Furnaces for Aluminum Alloy Thermal Treatment. IEEE Trans. Control Syst. Technol. 2016, 1, 24–39. [Google Scholar] [CrossRef]
- Lee, C.; Chen, R. Optimal Self-Tuning PID Controller Based on Low Power Consumption for a Server Fan Cooling System. Sensors 2015, 5, 11685–11700. [Google Scholar] [CrossRef] [PubMed]
- Rossomando, F.G.; Soria, C.M. Identification and control of nonlinear dynamics of a mobile robot in discrete time using an adaptive technique based on neural PID. Neural Comput. Appl. 2015, 5, 1179–1191. [Google Scholar] [CrossRef]
- Maraba, V.A.; Kuzucuoglu, A.E. PID Neural Network Based Speed Control of Asynchronous Motor Using Programmable Logic Controller. Adv. Electr. Comput. Eng. 2011, 4, 23–28. [Google Scholar] [CrossRef]
- Stafford, J.; Walsh, E.; Egan, V.; Grimes, R. Flat plate heat transfer with impinging axial fan flows. Int. J. Heat Mass Transf. 2010, 53, 5629–5638. [Google Scholar] [CrossRef]
- Grimes, R.; Davies, M. Air flow and heat transfer in fan cooled electronic systems. J. Electron. Packag. 2004, 1, 124–134. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Ma, C.; Zhu, R. Self-Tuning Fully-Connected PID Neural Network System for Distributed Temperature Sensing and Control of Instrument with Multi-Modules. Sensors 2016, 16, 1709. https://doi.org/10.3390/s16101709
Zhang Z, Ma C, Zhu R. Self-Tuning Fully-Connected PID Neural Network System for Distributed Temperature Sensing and Control of Instrument with Multi-Modules. Sensors. 2016; 16(10):1709. https://doi.org/10.3390/s16101709
Chicago/Turabian StyleZhang, Zhen, Cheng Ma, and Rong Zhu. 2016. "Self-Tuning Fully-Connected PID Neural Network System for Distributed Temperature Sensing and Control of Instrument with Multi-Modules" Sensors 16, no. 10: 1709. https://doi.org/10.3390/s16101709
APA StyleZhang, Z., Ma, C., & Zhu, R. (2016). Self-Tuning Fully-Connected PID Neural Network System for Distributed Temperature Sensing and Control of Instrument with Multi-Modules. Sensors, 16(10), 1709. https://doi.org/10.3390/s16101709





