A Temperature Compensation Method for Piezo-Resistive Pressure Sensor Utilizing Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM
Abstract
:1. Introduction
2. Temperature Effect on Piezoresistive Pressure Sensor
3. Hybrid Kernel LSSVM
3.1. LSSVM
3.2. Hybrid Kernel Function
4. Chaotic Ions Motion Algorithm
4.1. Ions Motion Algorithm
| Algorithm 1 |
| if (CbestFit ≥ CworstFit/2 and AbestFit ≥ AworstFit/2) |
| if rand() > 0.5 |
| Ai = Ai + Φ1 * (Cbest − 1) |
| else |
| Ai = Ai + Φ1 * Cbest |
| end |
| if rand() > 0.5 |
| Ci = Ci + Φ2 * (Abest − 1) |
| else |
| Ci = Ci + Φ2 * Abest |
| end |
| if rand() < 0.05 |
| Re - initialized Ai and Ci |
| end |
| end |
4.2. Chaotic Initialization and Searching
- (1)
- Chaotic initializationThe initialization of the ions group is one of the key points regarding whether the convergence speed is acceptable and the final solution quality is pleased. Even though the initial position of each ions is random in original ions motion algorithm, ions might be located far away from the optimal ion. Chaotic initialization is for the purpose of increasing the diversity among the population and accelerating the convergence speed.
- (2)
- Chaotic searchingRestart with the last ion position in the latest generation and replace all other ion positions by generating a new chaotic sequence. Continuing to generate new ion positions by chaotic sequence rather than by probability distributions could avoid stagnation and speed the convergence in the optimization searching process.
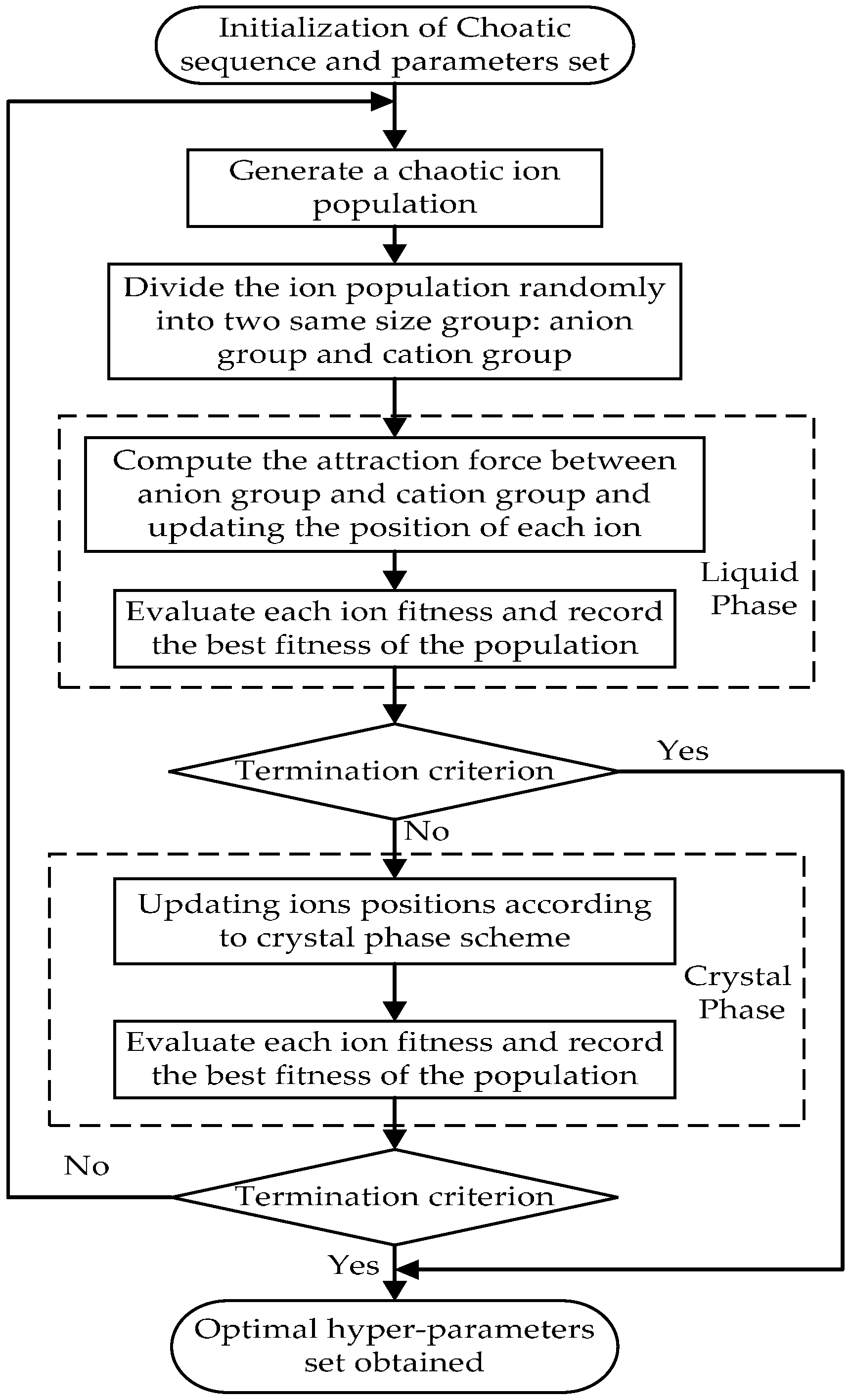
4.3. Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM (CIMA-Hybrid-LSSVM)
- (1)
- Chaotic initialization
- Chaotically distribute the seeds according to the dimension number of an ion by logistic map within the range of (0, 1).
- Calculate the chaotic sequence with chaotic seeds until the chaotic sequence length reaches the ions population size.
- Transform the chaotic sequence members into every parameter’s range, and take the transforming of as an example:where i is the index of the chaotic sequence, is the lower limitation of C, and is the upper limitation of .
- (2)
- Generate the initial ion population by Equation (23) and divide it randomly into an anion group and a cation group at the same size.
- (3)
- Evaluate each ion in liquid phase and rank them in terms of fitness. Record the best fitness and position of anion group, cation group and the ion population. If the best fitness of the ion population can neither satisfy the predetermined estimation precision nor reach the maximum searching generation number, then go to Step 4.
- (4)
- Take the last seed of the chaotic sequence generated by Step 1 and repeat the procedure as in Step 1 to obtain a new chaotic sequence. Compute each ion fitness according to the rules stated in crystal phase with the new chaotic sequence. The computation comes to an end as the best fitness satisfies the predetermined estimation precision or reaches the maximum searching generation number. If the stop criterion can not be met, then take the last ion position as the chaotic seed and go back to Step 1.
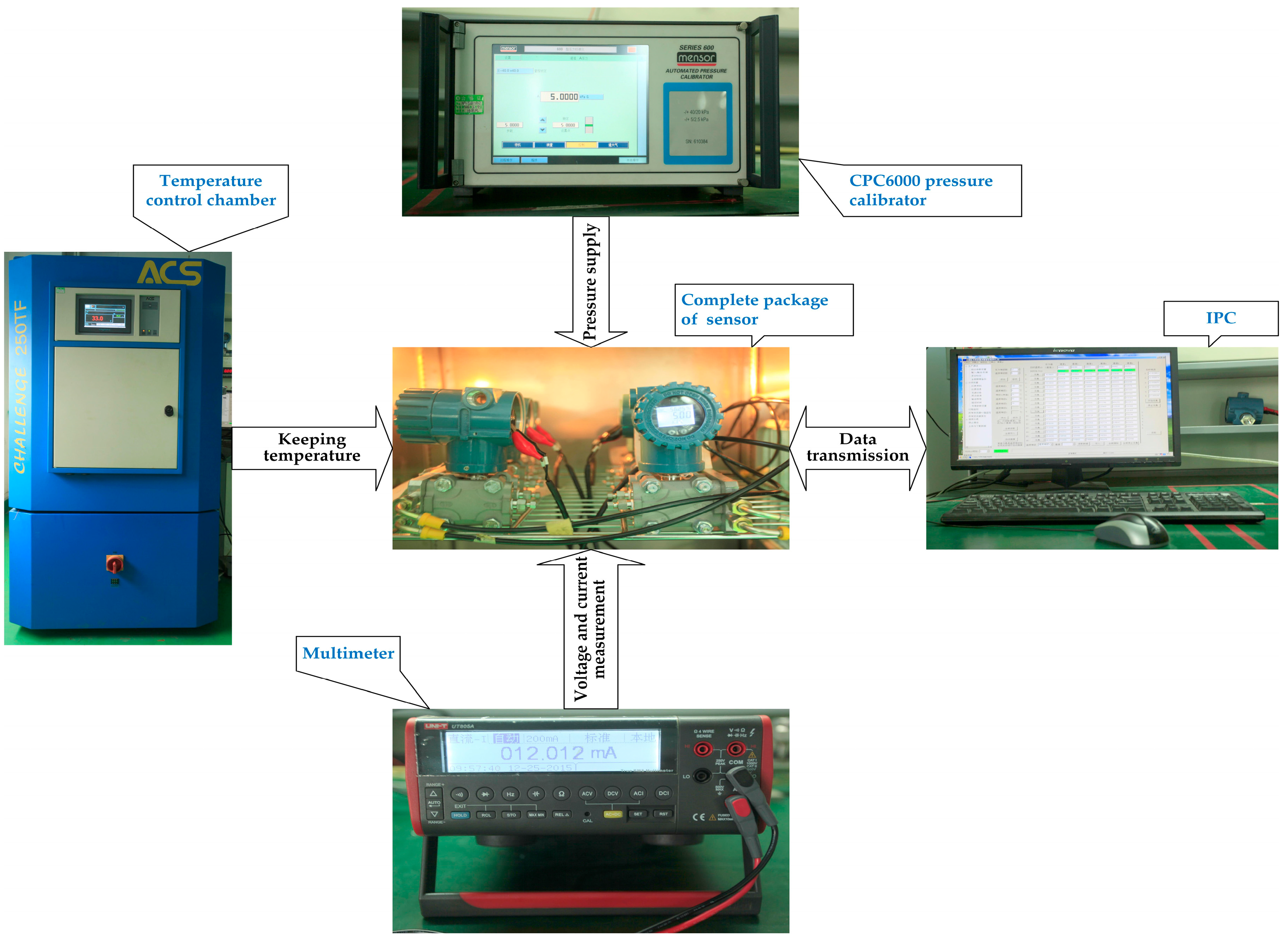
5. Data Calibration Experiment and Result Analysis
5.1. Data Calibration
5.2. Data Preprocessing
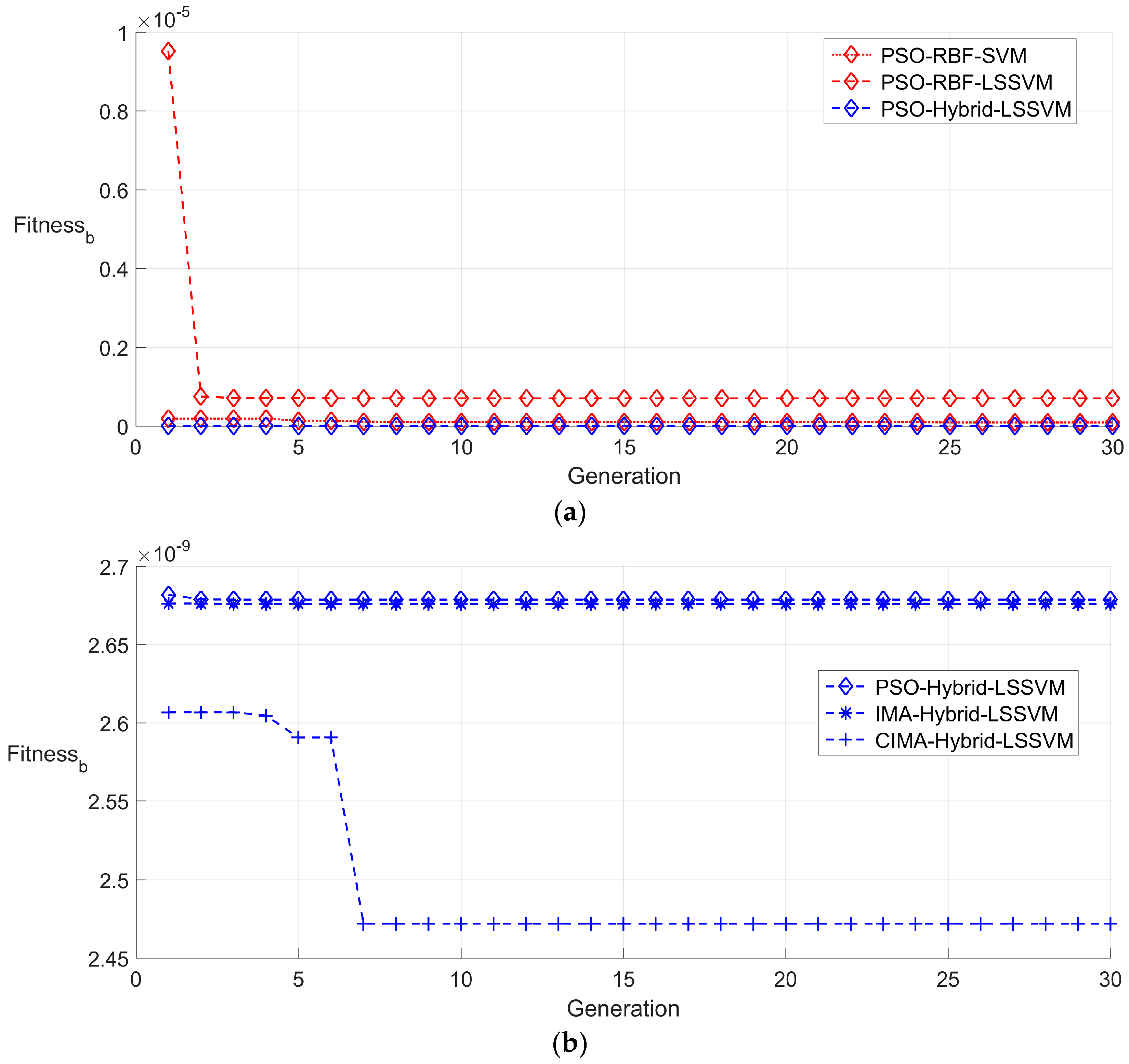
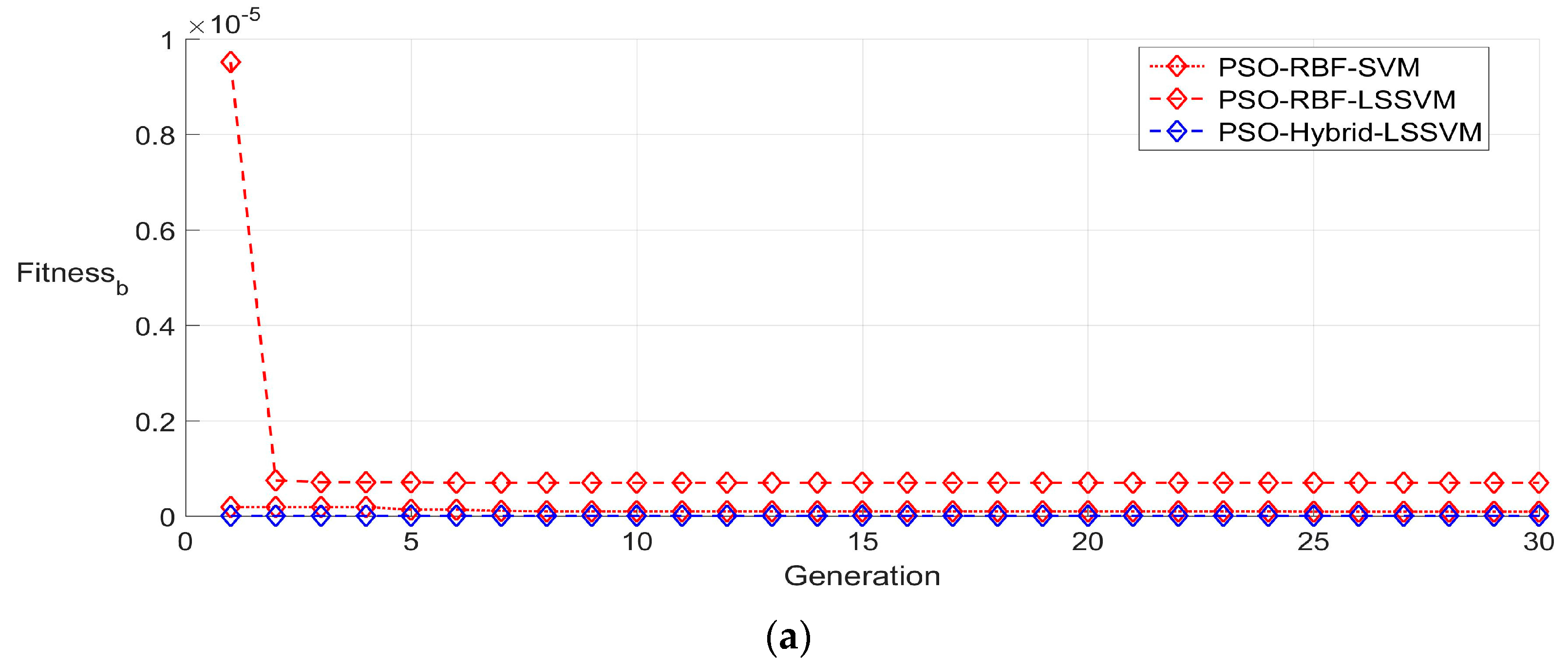
5.3. Modeling Temperature Compensation and Result Analysis
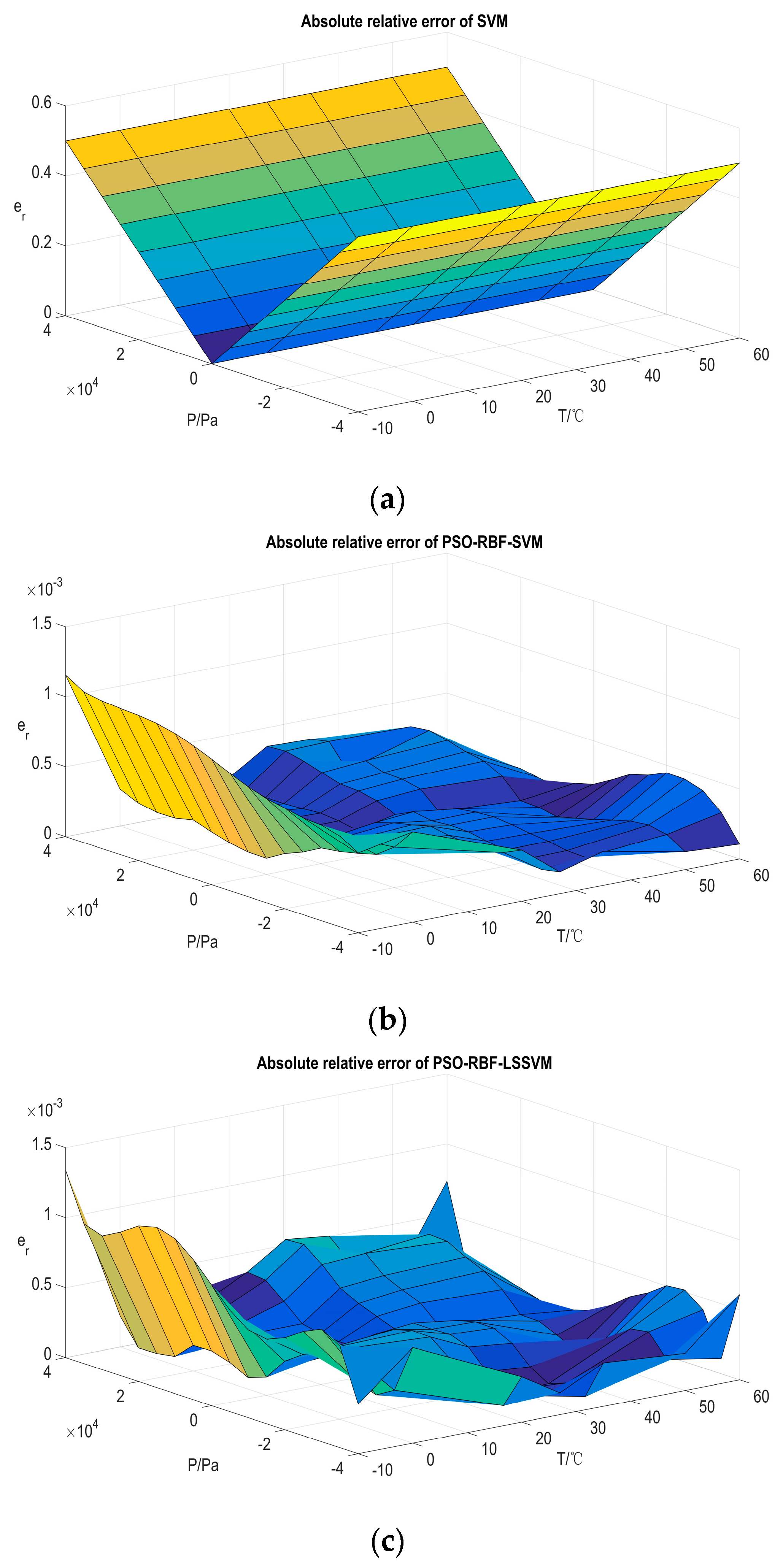
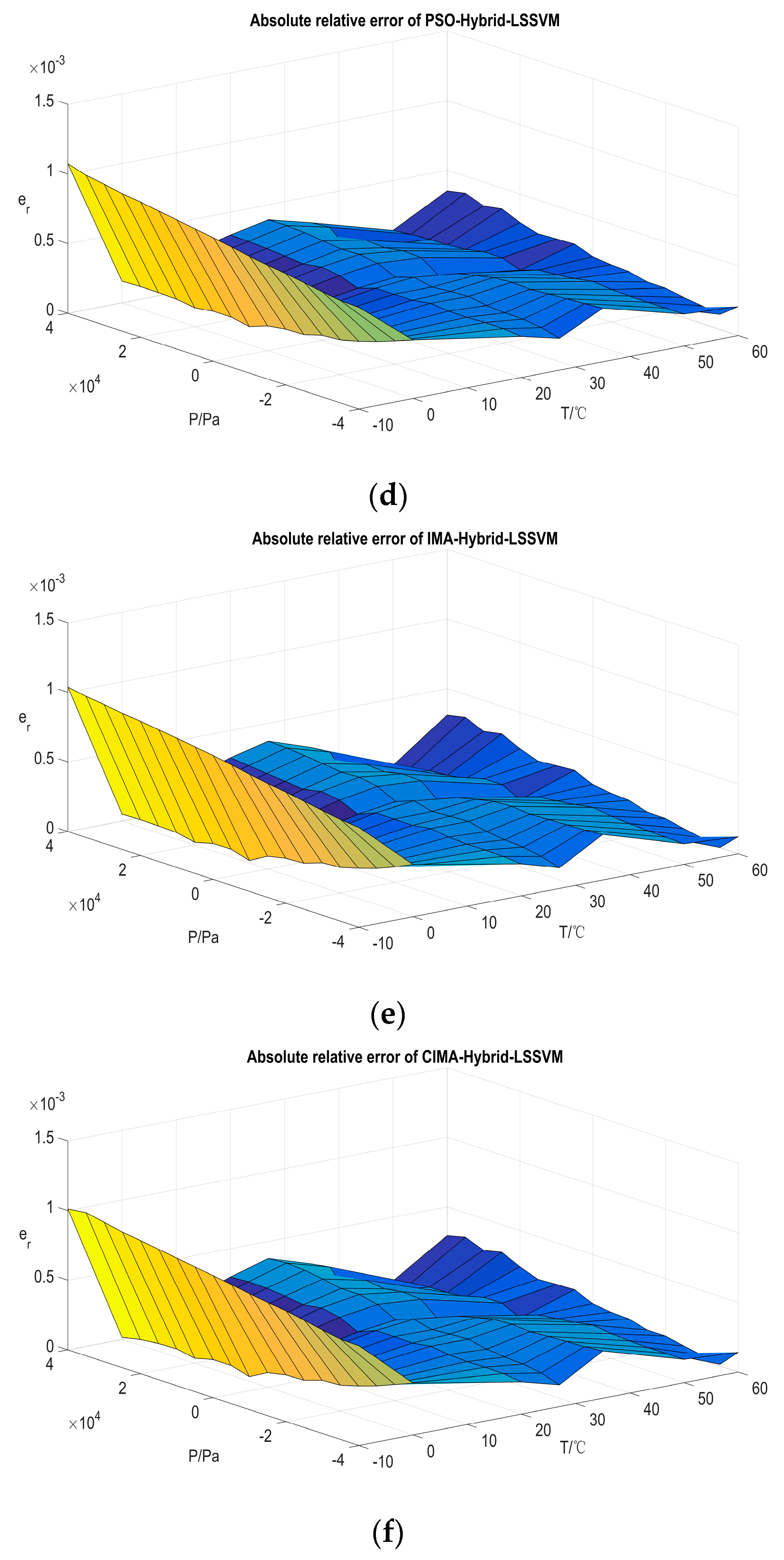
5.3.1. Random Partition of the Sample
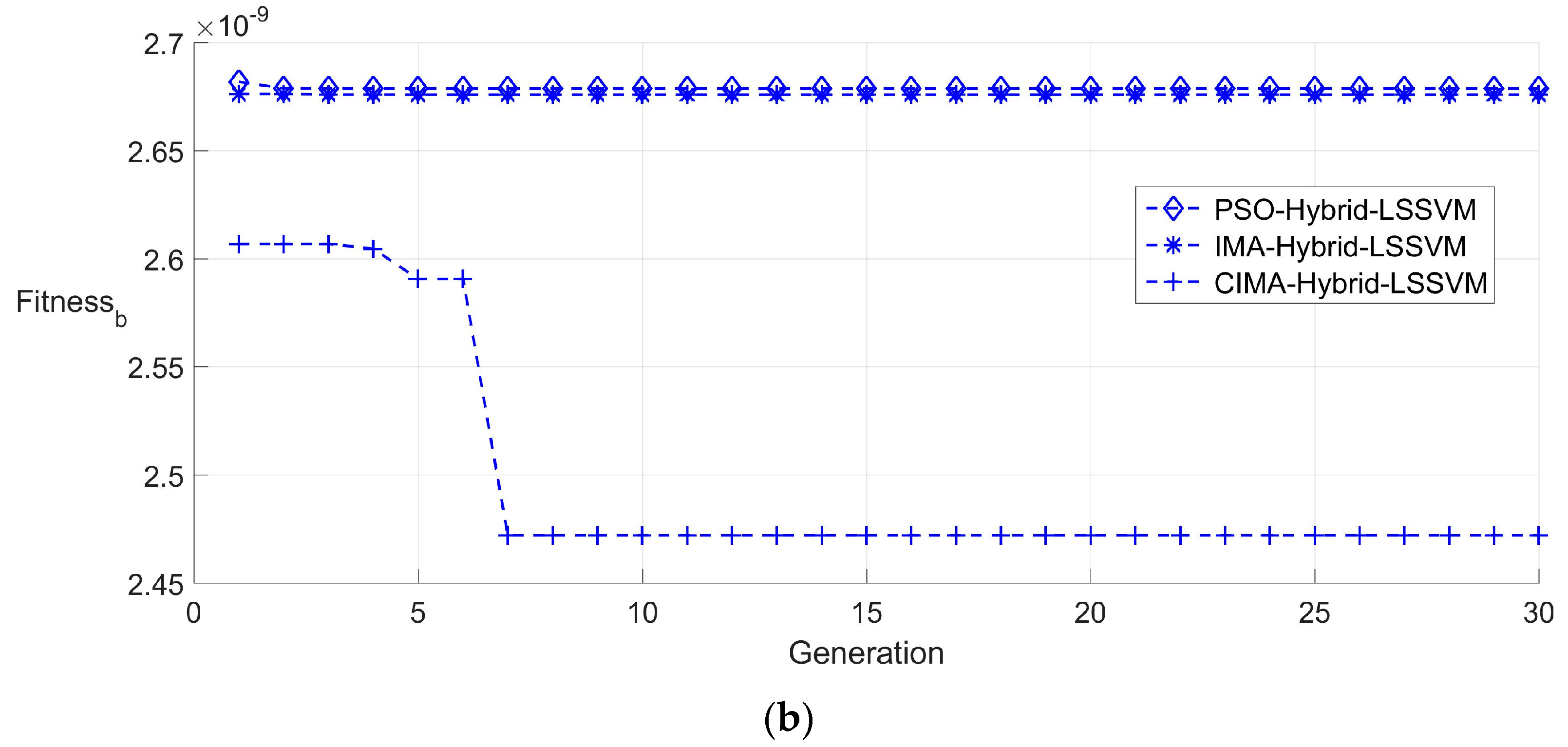
5.3.2. Fixed Partition of the Sample
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, G.; Zhao, Y.; Guo, F.; Xu, W. A smart high accuracy silicon piezoresistive pressure sensor temperature compensation system. Sensors 2014, 14, 12174–12190. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, J.; Hu, R.; Sun, G.Q. Transistor Compensation Technology of Pressure Sensor Sensitivity Temperature Coefficient. Adv. Mechatron. Technol. 2011, 43, 371–375. [Google Scholar] [CrossRef]
- Yoo, S.K.; Shin, K.Y.; Lee, T.B.; Jin, S.O.; Kim, J.U. Development of a Radial Pulse Tonometric (RPT) Sensor with a Temperature Compensation Mechanism. Sensors 2013, 13, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Aryafar, M.; Hamedi, M.; Ganjeh, M.M. A novel temperature compensated piezoresistive pressure sensor. Measurement 2015, 63, 25–29. [Google Scholar] [CrossRef]
- Mozek, M.; Vrtacnik, D.; Resnik, D.; Pecar, B.; Amon, S. Compensation and Signal Conditioning of Capacitive Pressure Sensors. Inf. Midem 2011, 41, 272–278. [Google Scholar]
- Luo, Y.; Yang, K.; Shi, Y.B.; Shang, C.X. Research of radiosonde humidity sensor with temperature compensation function and experimental verification. Sens. Actuators A Phys. 2014, 218, 49–59. [Google Scholar] [CrossRef]
- Chae, C.S.; Kwon, J.H.; Kim, Y.H. A Study of Compensation for Temporal and Spatial Physical Temperature Variation in Total Power Radiometers. IEEE Sens. J. 2012, 12, 2306–2312. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Q.; Qin, J. Temperature compensation of pressure sensor based on the interpolation of splines. J. Beijing Univ. Aeronaut. Astronaut. 2006, 32, 684–686. [Google Scholar]
- Wang, H.R.; Zhang, W.; You, L.D.; Yuan, G.Y.; Zhao, Y.L.; Jiang, Z.D. Back propagation neural network model for temperature and humidity compensation of a non dispersive infrared methane sensor. Instrum. Sci. Technol. 2013, 41, 608–618. [Google Scholar] [CrossRef]
- Ding, J.C.; Zhang, J.; Huang, W.Q.; Chen, S. Laser Gyro Temperature Compensation Using Modified RBFNN. Sensors 2014, 14, 18711–18727. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Qi, B.; Chen, D.; Landry, R.,Jr. Modification of an RBF ANN-Based Temperature Compensation Model of Interferometric Fiber Optical Gyroscopes. Sensors 2015, 15, 11189–11207. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.M.; Liu, S.D.; Miao, F.J.; Tao, B.R. Research on Pressure Sensor Temperature Compensation by WNN Based on FA. New Trends Mechatron. Mater. Eng. 2012, 151, 213–217. [Google Scholar] [CrossRef]
- Xing, H.; Wu, X.; Lv, W.; Xu, W. Environmental temperature compensation for the temperature channel of data-acquisition unit in automatic weather station. Chin. J. Sci. Instrum. 2012, 33, 1868–1875. [Google Scholar]
- Xu, Z.; Liu, Y.-F.; Dong, J.-X. Thermal drift prognosis and compensation model of MEMS accelerometer. J. Chin. Inert. Technol. 2012, 5, 21. [Google Scholar]
- Qiu, H.-M.; Chen, D.; Li, G.-Y.; Huang, Y.; Chen, Z.-C.; Liang, J.-T. Temperature compensation of light addressable potentiometric sensor based on support vector machine. J. Optoelectron. Laser 2015, 26, 2272–2277. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Wiley & Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Suykens, J.A.K.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhao, L.B.; Jiang, Z.D. A novel high temperature pressure sensor on the basis SOI layers. Sens. Actuator A Phys. 2003, 108, 108–111. [Google Scholar]
- Xia, D.Z.; Chen, S.L.; Wang, S.R.; Li, H.S. Microgyroscope Temperature Effects and Compensation-Control Methods. Sensors 2009, 9, 8349–8376. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-T.; Seo, H.-D.; Kawamura, A.; Yamada, T.; Matsumoto, Y.; Ishida, M.; Nakamura, T. Compensation method of offset and its temperature drift in silicon piezoresistive pressure sensor using double wheatstone-bridge configuration. In Proceedings of the 1995 8th International Conference on Solid-State Sensors and Actuators and Eurosensors IX, Stockholm, Sweden, 25–29 June 1995; pp. 570–573.
- Hu, J.; Wang, J.; Ma, K. A hybrid technique for short-term wind speed prediction. Energy 2015, 81, 563–574. [Google Scholar] [CrossRef]
- Yu, L.; Chen, H.; Wang, S.; Lai, K.K. Evolving Least Squares Support Vector Machines for Stock Market Trend Mining. IEEE Trans. Evolut. Comp. 2009, 13, 87–102. [Google Scholar]
- Javidy, B.; Hatamlou, A.; Mirjalili, S. Ions motion algorithm for solving optimization problems. Appl. Soft Comp. 2015, 32, 72–79. [Google Scholar] [CrossRef]
- Guo, Z.L.; Wang, S.; Zhuang, J. A novel immune evolutionary algorithm incorporating chaos optimization. Pattern Recognit. Lett. 2006, 27, 2–8. [Google Scholar]
- Chahkandi, V.; Yaghoobi, M.; Veisi, G. CABC-CSA: A new chaotic hybrid algorithm for solving optimization problems. Nonlinear Dyn. 2013, 73, 475–484. [Google Scholar] [CrossRef]
- Coelho, L.D.S.; Mariani, V.C. Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization. Expert Syst. Appl. 2008, 34, 1905–1913. [Google Scholar] [CrossRef]
- Pressure/Differential-Pressure Transmitter for Use in Industrial-Process Measure and Control Systems—Part 1: General Specification. Available online: http://dbpub.cnki.net/grid2008/dbpub/detail.aspx?QueryID=31&CurRec=6&dbcode=SCHF&dbname=SCSF&filename=SCSF00038855&urlid=&yx=&uid=WEEvREcwSlJHSldRa1FhdkJkdjFtWWtTRkFDSFVtVnR6NTdKV1M5eE5IVT0=$9A4hF_YAuvQ5obgVAqNKPCYcEjKensW4ggI8Fm4gTkoUKaID8j8gFw (accessed on 14 September 2016).
- Zhang, Y.-S.; Yang, T. Modeling and compensation of MEMS gyroscope output data based on support vector machine. Measurement 2012, 45, 922–926. [Google Scholar] [CrossRef]
- Cheng, J.; Fang, J.; Wu, W.; Li, J. Temperature drift modeling and compensation of RLG based on PSO tuning SVM. Measurement 2014, 55, 246–254. [Google Scholar] [CrossRef]
- Sun, Y.J.; Liu, Y.W.; Liu, H. Temperature Compensation for a Six-Axis Force/Torque Sensor Based on the Particle Swarm Optimization Least Square Support Vector Machine for Space Manipulator. IEEE Sens. J. 2016, 16, 798–805. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- LS-SVMlab, version 1.8; Available online: http://www.esat.kuleuven.be/sista/lssvmlab/ (accessed on 14 September 2016).
- Prechelt, L. Automatic early stopping using cross validation: Quantifying the criteria. Neural Netw. 1998, 11, 761–767. [Google Scholar] [CrossRef]




| P (Pa) | T (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 | −10 | 0 | 10 | 20 | 27 | 35 | 40 | 50 | 60 | 70 | |
| TAD | |||||||||||
| 46113 | 45715 | 45268 | 44875 | 44445 | 44066 | 43834 | 43559 | 43255 | 42833 | 42449 | |
| UAD | |||||||||||
| −40000 | 225163 | 229882 | 235926 | 240350 | 245293 | 249365 | 251904 | 254585 | 257738 | 261883 | 265502 |
| −35000 | 258948 | 263075 | 268467 | 272361 | 276787 | 280403 | 282638 | 285002 | 287807 | 291422 | 294694 |
| −30000 | 292891 | 296416 | 301166 | 304587 | 308434 | 311591 | 313534 | 315581 | 318035 | 321166 | 324036 |
| −25000 | 326975 | 329900 | 334016 | 336931 | 340227 | 342921 | 344579 | 346307 | 348415 | 351061 | 353526 |
| −20000 | 361190 | 363517 | 367004 | 369421 | 372163 | 374394 | 375763 | 377152 | 378937 | 381095 | 383158 |
| −15000 | 395535 | 397260 | 400131 | 402004 | 404232 | 406003 | 407086 | 408178 | 409595 | 411274 | 412937 |
| −10000 | 429974 | 431111 | 433352 | 434705 | 436398 | 437712 | 438518 | 439281 | 440352 | 441555 | 442817 |
| −5000 | 464508 | 465059 | 466694 | 467572 | 468680 | 469525 | 470046 | 470503 | 471221 | 471962 | 472818 |
| 0 | 499132 | 499093 | 500112 | 500490 | 501053 | 501453 | 501666 | 501827 | 502188 | 502462 | 502916 |
| 5000 | 533794 | 533200 | 533579 | 533466 | 533475 | 533419 | 533347 | 533205 | 533214 | 533028 | 533077 |
| 10000 | 568569 | 567362 | 567163 | 566524 | 566019 | 565509 | 565185 | 564690 | 564373 | 563699 | 563370 |
| 15000 | 603351 | 601564 | 600769 | 599619 | 598591 | 597628 | 597024 | 596217 | 595555 | 594429 | 593697 |
| 20000 | 638130 | 635788 | 634383 | 632731 | 631170 | 629766 | 628882 | 627762 | 626757 | 625174 | 624052 |
| 25000 | 672932 | 670020 | 668039 | 665862 | 663787 | 661936 | 660781 | 659345 | 657996 | 655939 | 654454 |
| 30000 | 707712 | 704235 | 701674 | 699016 | 696402 | 694107 | 692600 | 690934 | 689248 | 686760 | 684868 |
| 35000 | 742451 | 738421 | 735281 | 732121 | 728999 | 726261 | 724565 | 722513 | 720489 | 717537 | 715282 |
| 40000 | 777129 | 772552 | 768840 | 765221 | 761560 | 758380 | 756415 | 754060 | 751701 | 748336 | 745668 |
| Parameters | PSO [29] | PSO [30] | IMA |
|---|---|---|---|
| swarm size | 50 | 50 | 50 |
| maximum iteration number | 30 | 30 | 30 |
| fitness | MSE | MSE | MSE |
| maximum weight | 0.9 | 0.9 | |
| minimum weight | 0.4 | 0.4 | |
| social factor | [1, 3] | 2 | |
| cognitive factor | [1, 3] | 2 |
| Temperature Compensation Methods | eir (min) | eir (max) | eir (mean) | eir (variance) | MTT (s) |
|---|---|---|---|---|---|
| SVM | 4.814 × 10−3 | 5.026 × 10−3 | 4.973 × 10−3 | 2.237 × 10−9 | 1.499 × 10−2 |
| PSO-RBF-SVM | 5.550 × 10−4 | 1.334 × 10−3 | 9.673 × 10−4 | 3.385 × 10−9 | 2.107 × 102 |
| PSO-RBF-LSSVM | 2.199 × 10−4 | 3.556 × 10−4 | 2.703 × 10−4 | 1.080 × 10−9 | 1.200 × 10−2 |
| PSO-Hybrid-LSSVM | 2.586 × 10−4 | 3.588 × 10−4 | 3.126 × 10−4 | 4.996 × 10−10 | 1.478 × 10−2 |
| IMA-Hybrid-LSSVM | 1.593 × 10−4 | 2.401 × 10−4 | 1.933 × 10−4 | 3.776 × 10−10 | 1.418 × 10−2 |
| CIMA-Hybrid-LSSVM | 1.353 × 10−5 | 4.413 × 10−5 | 2.497 × 10−5 | 5.258 × 10−11 | 1.392 × 10−2 |
| Temperature Compensation Methods | eir (min) | eir (max) | eir (mean) | eir (variance) |
|---|---|---|---|---|
| SVM | 2.106 × 10−1 | 3.197 × 10−1 | 2.648 × 10−1 | 5.562 × 10−4 |
| PSO-RBF-SVM | 5.924 × 10−4 | 2.187 × 10−3 | 1.235 × 10−3 | 1.085 × 10−7 |
| PSO-RBF-LSSVM | 2.422 × 10−4 | 6.706 × 10−4 | 4.011 × 10−4 | 6.286 × 10−9 |
| PSO-Hybrid-LSSVM | 2.733 × 10−4 | 5.165 × 10−4 | 3.687 × 10−4 | 1.494 × 10−9 |
| IMA-Hybrid-LSSVM | 1.841 × 10−4 | 3.424 × 10−4 | 2.517 × 10−4 | 9.659 × 10−10 |
| CIMA-Hybrid-LSSVM | 1.155 × 10−4 | 2.559 × 10−4 | 1.770 × 10−4 | 1.104 × 10−9 |
| Temperature Compensation Methods | eir (min) | eir (max) | eir (mean) | eir (variance) | MTT (s) |
|---|---|---|---|---|---|
| SVM | 3.272 × 10−4 | 5.220 × 10−3 | 4.722 × 10−3 | 1.227 × 10−6 | 1.507 × 10−2 |
| PSO-RBF-SVM | 4.343 × 10−5 | 3.248 × 10−4 | 1.850 × 10−4 | 5.467 × 10−9 | 10.71 × 101 |
| PSO-RBF-LSSVM | 8.946 × 10−6 | 1.111 × 10−3 | 1.927 × 10−4 | 3.692 × 10−8 | 2.448 × 10−2 |
| PSO-Hybrid-LSSVM | 1.085 × 10−4 | 1.564 × 10−4 | 1.251 × 10−4 | 1.159 × 10−10 | 2.549 × 10−2 |
| IMA-Hybrid-LSSVM | 4.095 × 10−7 | 6.063 × 10−5 | 1.444 × 10−5 | 1.844 × 10−10 | 2.641 × 10−2 |
| CIMA-Hybrid-LSSVM | 9.921 × 10−6 | 6.401 × 10−5 | 2.029 × 10−5 | 1.210 × 10−10 | 2.568 × 10−2 |
| Temperature Compensation Methods | eir (min) | eir (max) | eir (mean) | eir (variance) |
|---|---|---|---|---|
| SVM | 3.414 × 10−4 | 5.003 × 10−1 | 2.647 × 10−1 | 2.387 × 10−2 |
| PSO-RBF-SVM | 7.647 × 10−5 | 1.154 × 10−3 | 3.290 × 10−4 | 6.368 × 10−8 |
| PSO-RBF-LSSVM | 1.953 × 10−5 | 1.338 × 10−3 | 3.549 × 10−4 | 7.548 × 10−8 |
| PSO-Hybrid-LSSVM | 1.082 × 10−4 | 1.074 × 10−3 | 3.555 × 10−4 | 5.374 × 10−8 |
| IMA-Hybrid-LSSVM | 1.831 × 10−6 | 1.038 × 10−3 | 3.007 × 10−4 | 6.565 × 10−8 |
| CIMA-Hybrid-LSSVM | 1.224 × 10−5 | 1.066 × 10−3 | 3.056 × 10−4 | 6.427 × 10−8 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Hu, G.; Zhou, Y.; Zou, C.; Peng, W.; Alam SM, J. A Temperature Compensation Method for Piezo-Resistive Pressure Sensor Utilizing Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM. Sensors 2016, 16, 1707. https://doi.org/10.3390/s16101707
Li J, Hu G, Zhou Y, Zou C, Peng W, Alam SM J. A Temperature Compensation Method for Piezo-Resistive Pressure Sensor Utilizing Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM. Sensors. 2016; 16(10):1707. https://doi.org/10.3390/s16101707
Chicago/Turabian StyleLi, Ji, Guoqing Hu, Yonghong Zhou, Chong Zou, Wei Peng, and Jahangir Alam SM. 2016. "A Temperature Compensation Method for Piezo-Resistive Pressure Sensor Utilizing Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM" Sensors 16, no. 10: 1707. https://doi.org/10.3390/s16101707
APA StyleLi, J., Hu, G., Zhou, Y., Zou, C., Peng, W., & Alam SM, J. (2016). A Temperature Compensation Method for Piezo-Resistive Pressure Sensor Utilizing Chaotic Ions Motion Algorithm Optimized Hybrid Kernel LSSVM. Sensors, 16(10), 1707. https://doi.org/10.3390/s16101707






