An Enhanced Error Model for EKF-Based Tightly-Coupled Integration of GPS and Land Vehicle’s Motion Sensors
Abstract
:1. Introduction
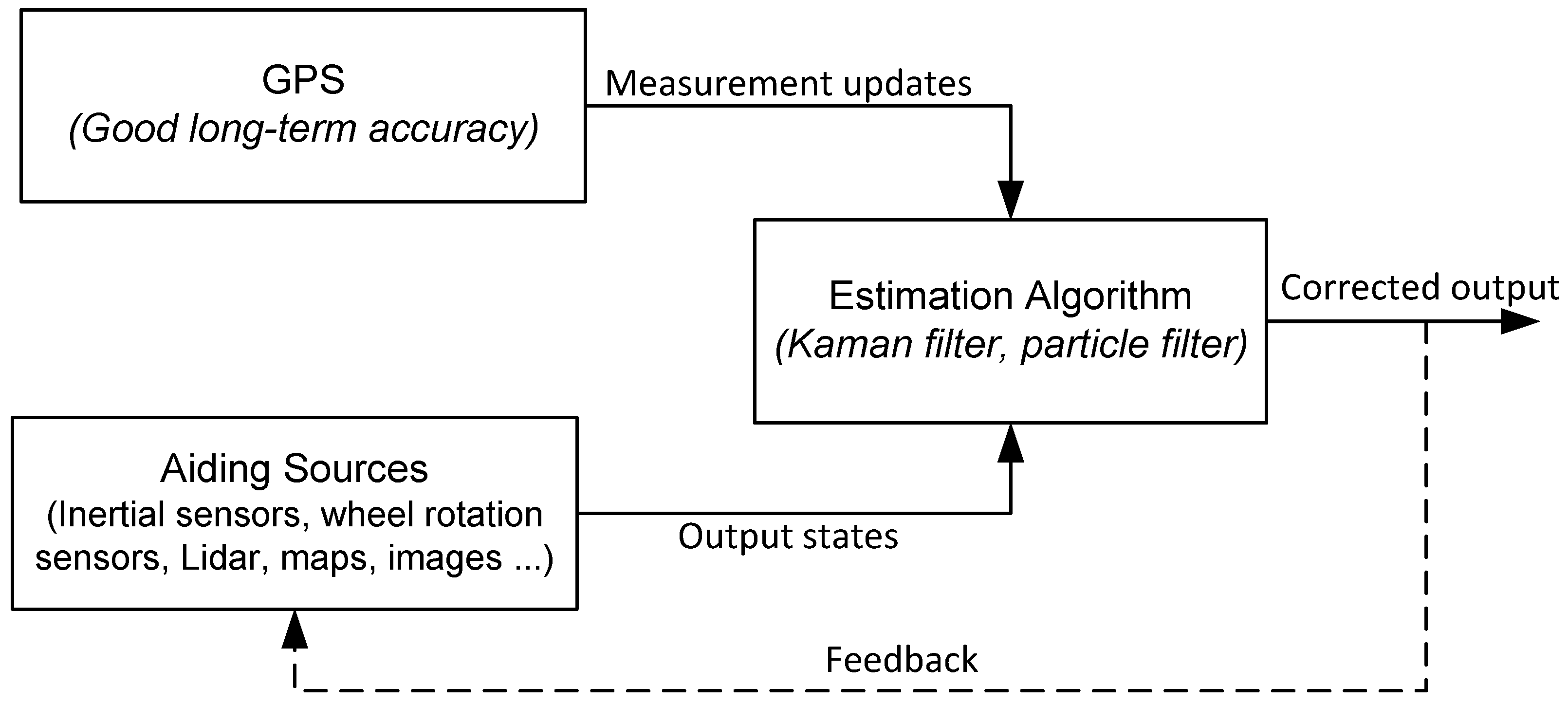
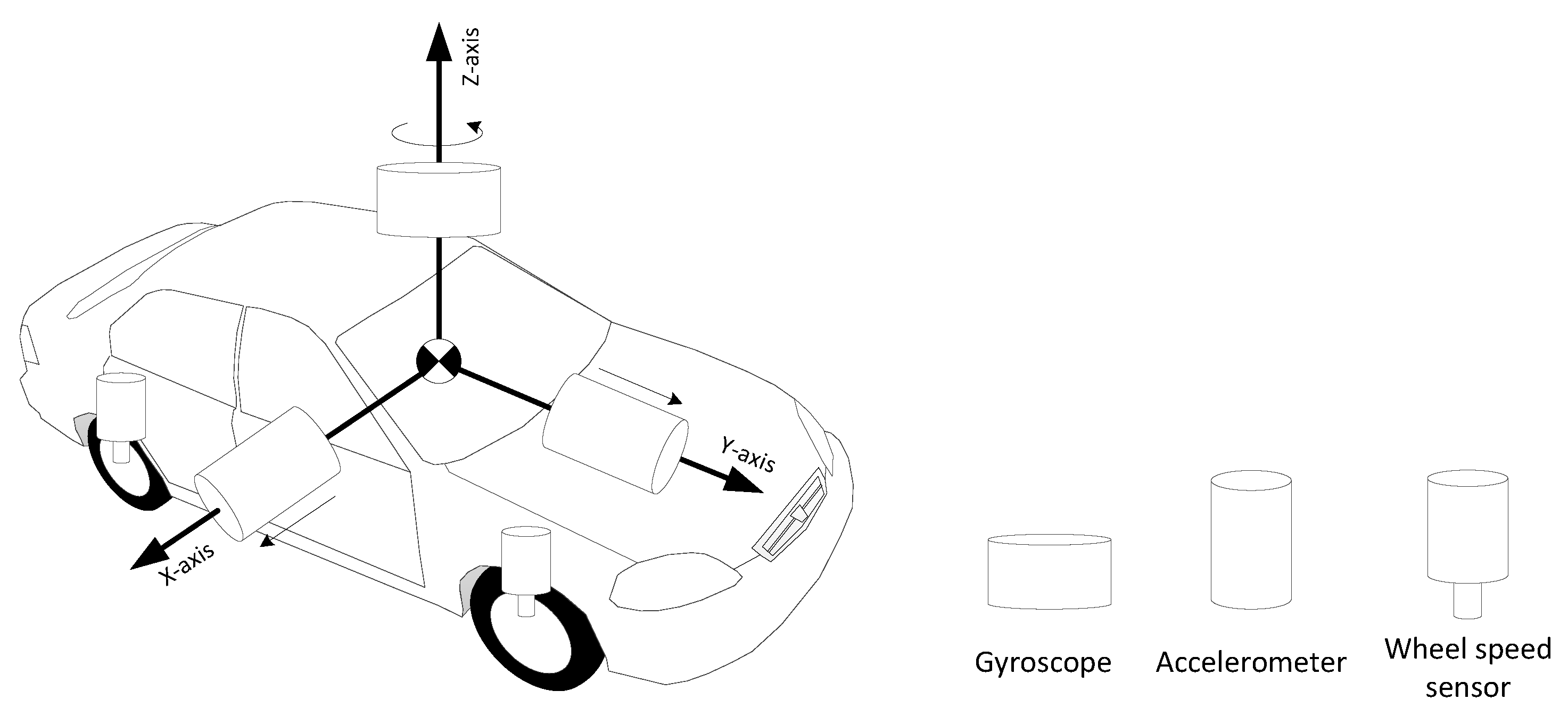
2. The 3D Reduced Inertial Sensor System
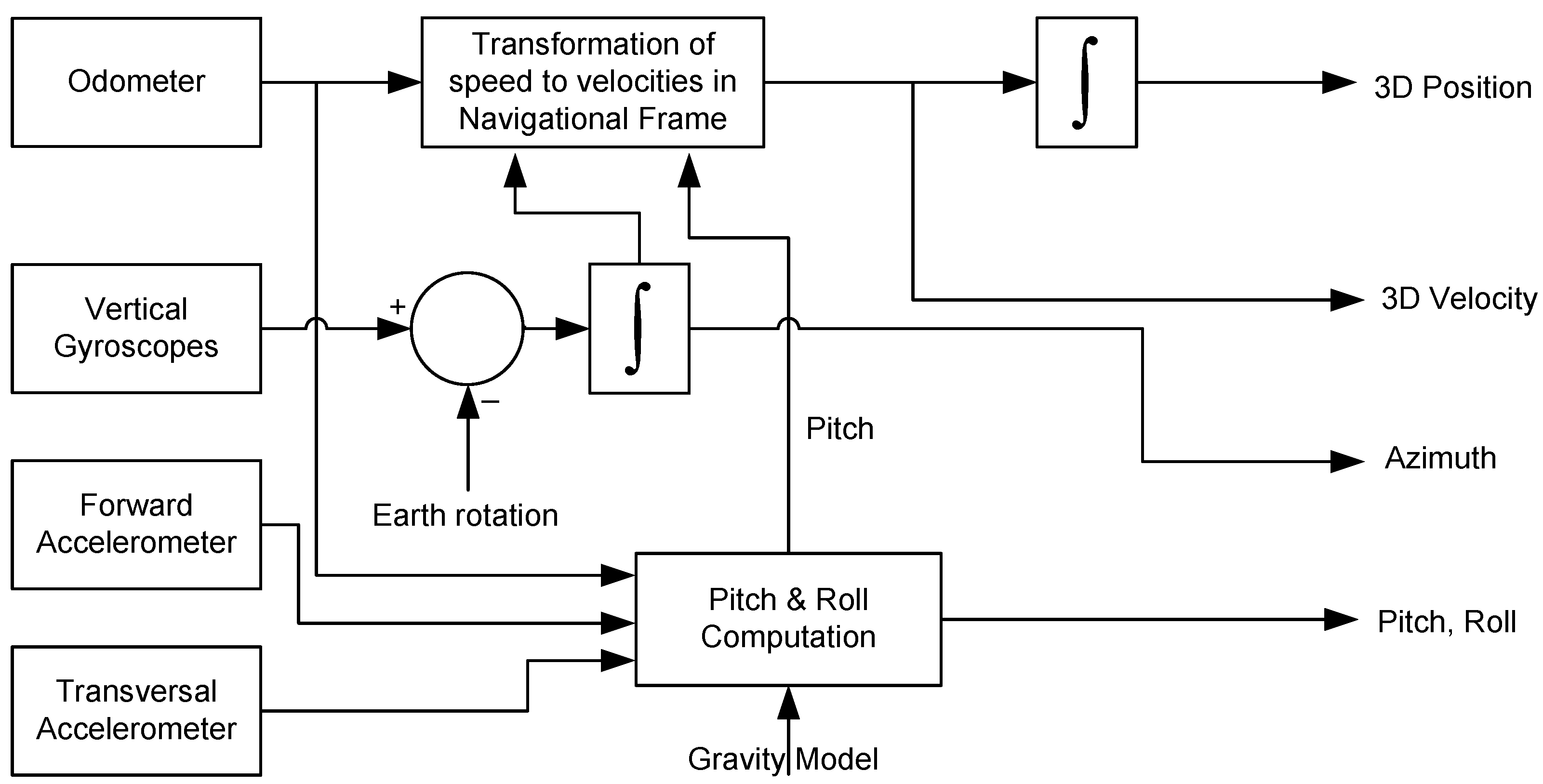
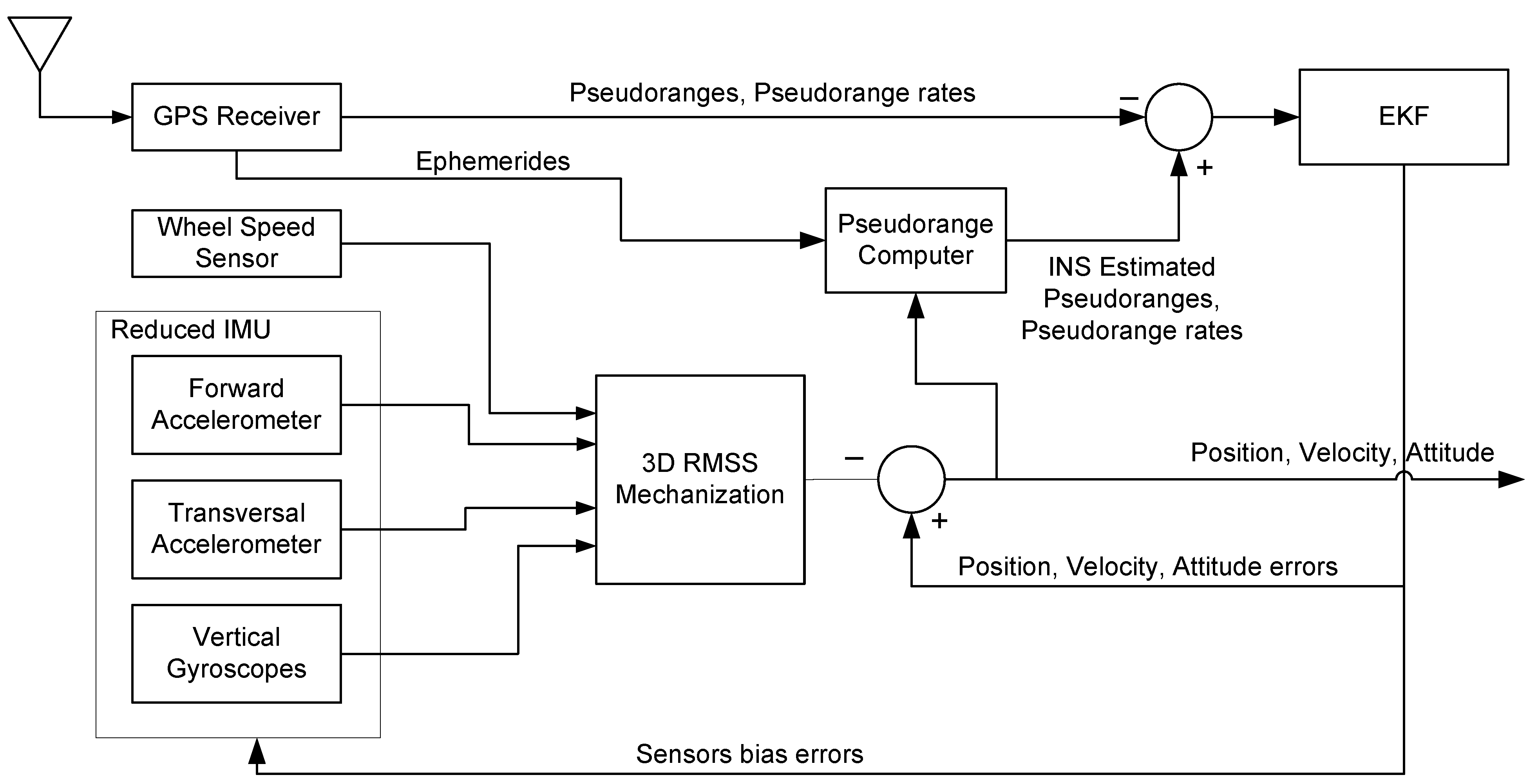
3. Proposed EKF-Based 3D RISS/GPS Integration Algorithm
3.1. System Model
3.1.1. Latitude
3.1.2. Longitude
3.1.3. Altitude
3.1.4. Attitude
3.1.5. East Velocity
3.1.6. North Velocity
3.1.7. Up Velocity
3.1.8. Forward Velocity
3.1.9. Modelling of Horizontal Channel Errors
3.1.10. Modelling of the Wheel Rotation Sensor and Gyroscope
3.2. The GPS System Model for Tightly-Coupled RISS/GPS Integration
3.3. Measurements Model for Tightly-Coupled RISS/GPS Integration
3.3.1. GPS Measurement Updates
3.3.2. Horizontal Channel Measurement Updates
4. Experimental Work and Results
4.1. Equipment Setup

| Crossbow IMU300CC | HG1700 | |
|---|---|---|
| Size | 7.62 × 9.53 × 8.13 cm | 16 × 16 × 10 cm |
| Weight | 0.59 kg | 3.4 kg |
| Max data rate | 200 Hz | 100 Hz |
| Start-up time | <1 s | <0.8 s |
| Accelerometer | ||
| Range | ±2 g | ±50 g |
| Bias | 30 mg | 1 mg |
| Scale factor | <1 % | 300 ppm |
| Random walk | <0.15 m/s/ | <0.198 m/s/ |
| Gyroscope | ||
| Range | /s | /s |
| Bias | /s | 1/h |
| Scale factor | <1% | 150 ppm |
| Random walk |
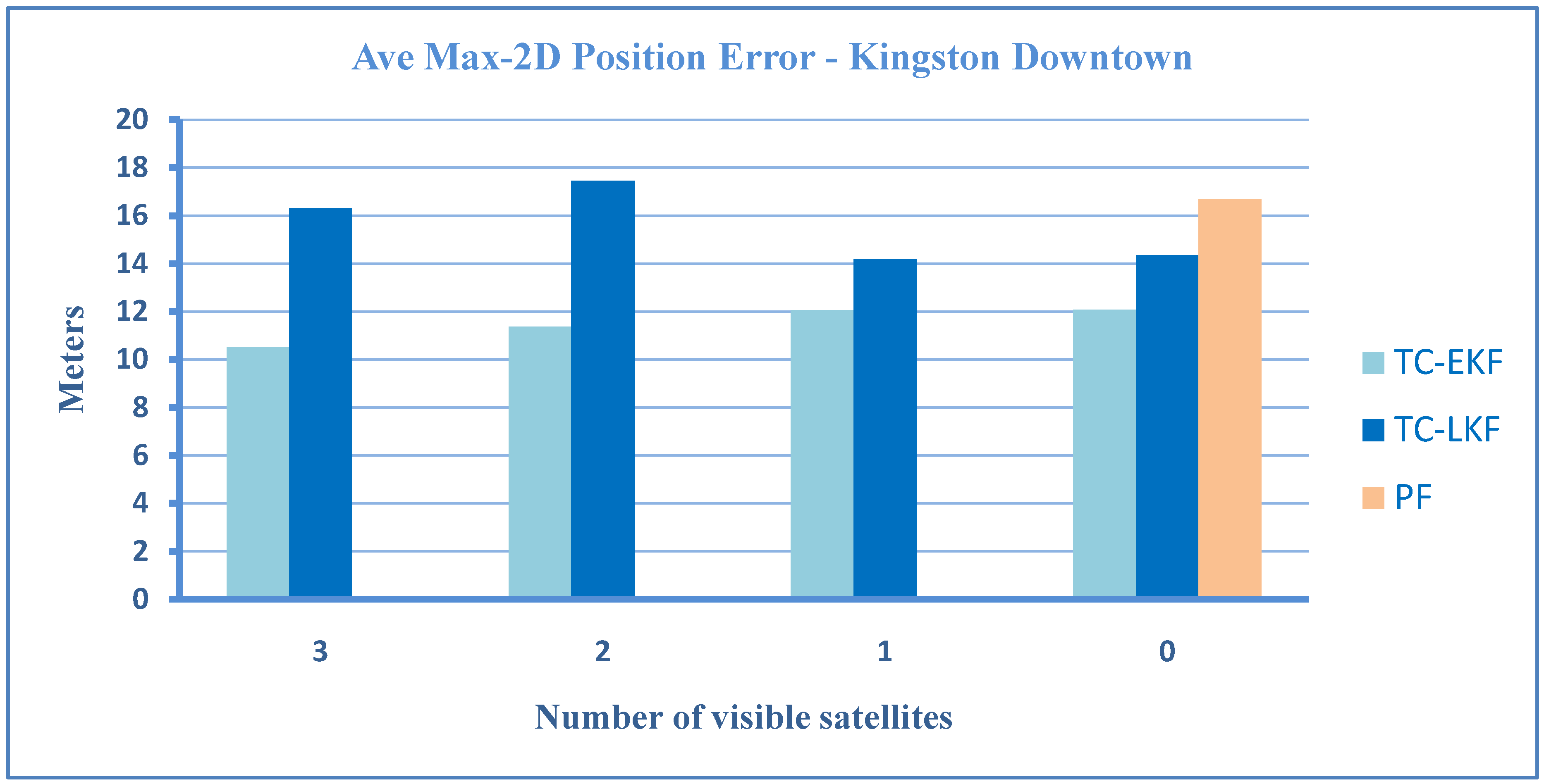
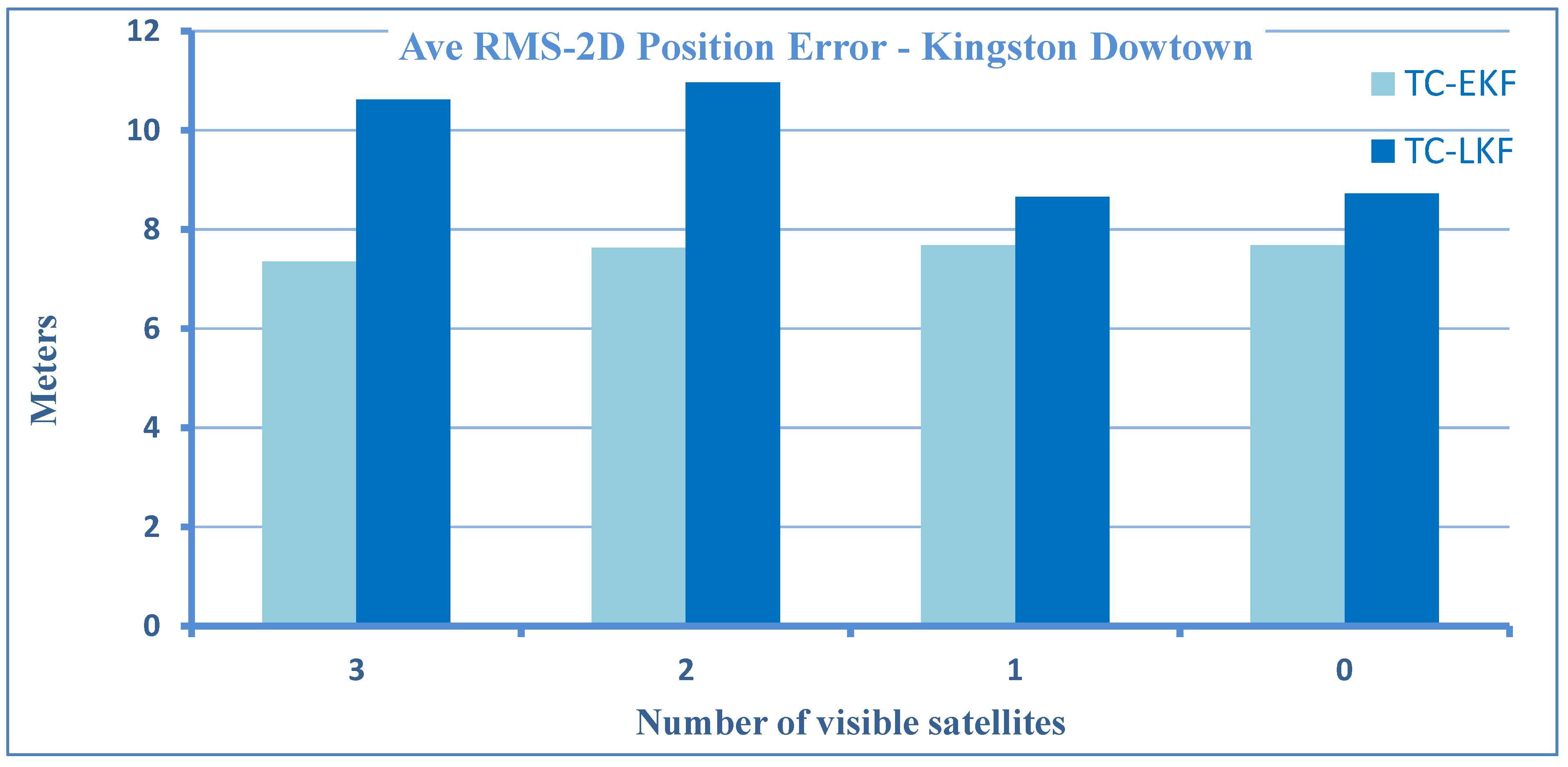
4.2. Evaluation and Comparison Criteria
4.3. Kingston Downtown Trajectory
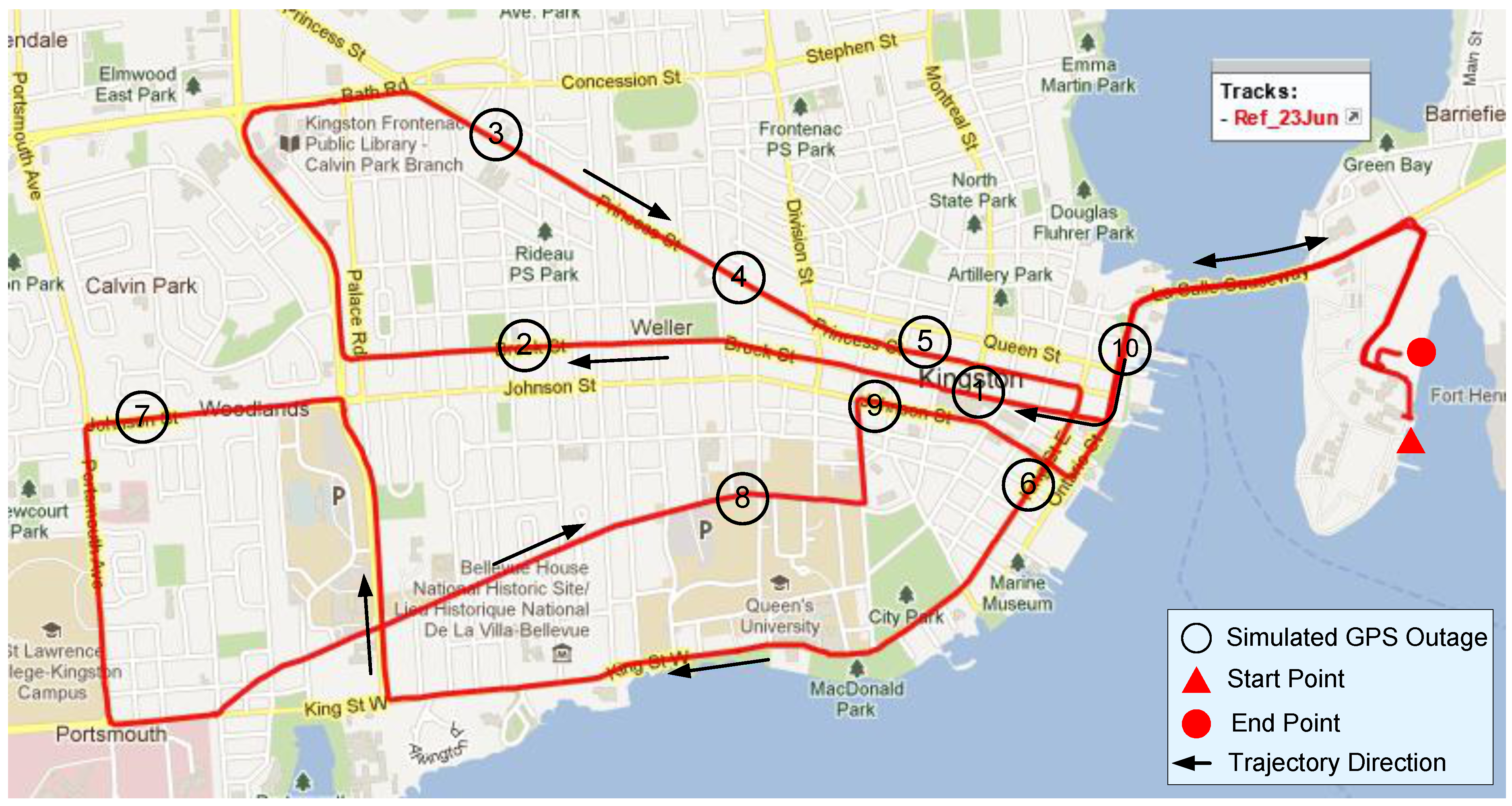
4.3.1. Positional Errors
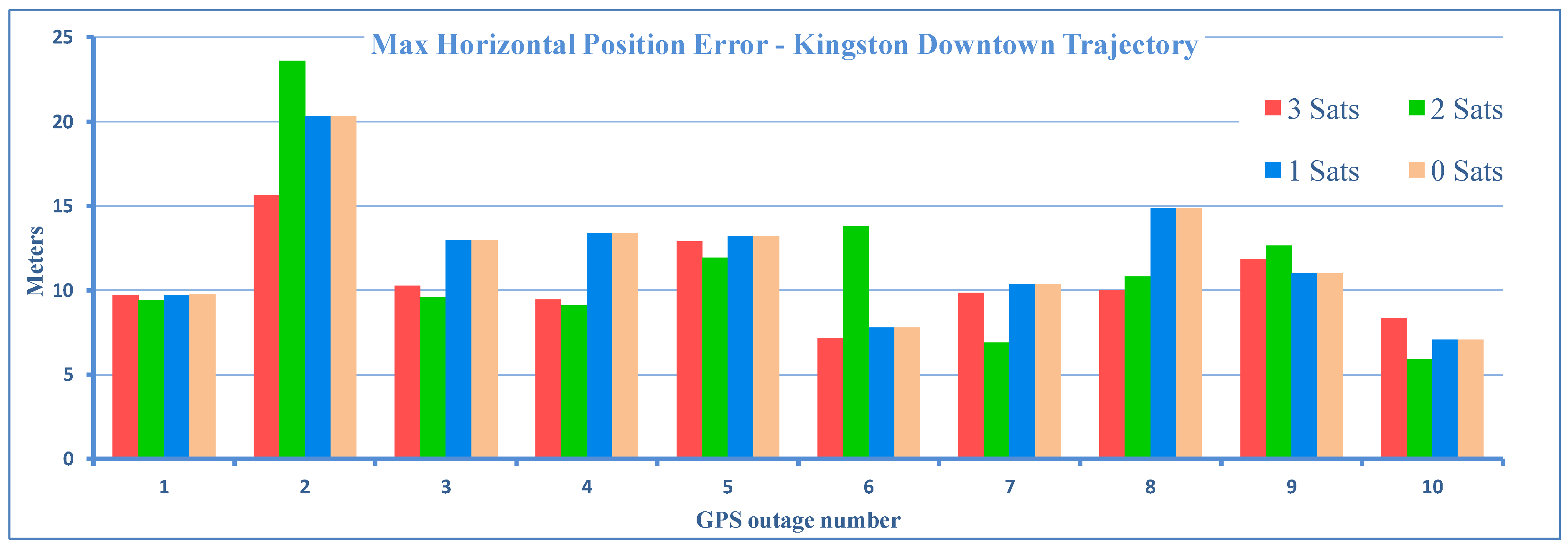
| Outage No. | Position (m) | Attitude () | Velocity (m/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Long | Alt | Pitch | Roll | Azi | Ve | Vn | Vu | |||
| 1 | 4.46 | 2.42 | 3.71 | 1.73 | 0.70 | 1.17 | 0.55 | 0.48 | 1.12 | ||
| 2 | 12.54 | 3.99 | 4.76 | 1.73 | 0.55 | 1.48 | 0.59 | 0.75 | 1.20 | ||
| 3 | 2.86 | 8.12 | 4.50 | 1.74 | 0.48 | 0.37 | 0.74 | 0.33 | 0.62 | ||
| 4 | 2.35 | 7.26 | 5.12 | 1.88 | 0.31 | 0.33 | 0.67 | 0.23 | 0.92 | ||
| 5 | 7.55 | 6.67 | 1.78 | 2.84 | 0.20 | 1.15 | 0.77 | 0.20 | 0.44 | ||
| 6 | 4.70 | 1.60 | 1.36 | 2.51 | 0.31 | 0.28 | 0.36 | 0.57 | 0.87 | ||
| 7 | 2.27 | 4.17 | 4.65 | 1.31 | 0.58 | 1.80 | 0.67 | 0.56 | 1.00 | ||
| 8 | 7.70 | 8.25 | 4.83 | 1.65 | 0.35 | 0.90 | 0.49 | 0.26 | 0.57 | ||
| 9 | 6.14 | 1.32 | 1.70 | 1.37 | 0.53 | 1.41 | 0.73 | 0.57 | 0.70 | ||
| 10 | 4.24 | 2.70 | 0.76 | 1.68 | 0.59 | 0.47 | 0.19 | 0.41 | 0.39 | ||
| Average | 5.48 | 4.65 | 3.32 | 1.84 | 0.46 | 0.94 | 0.58 | 0.44 | 0.78 | ||
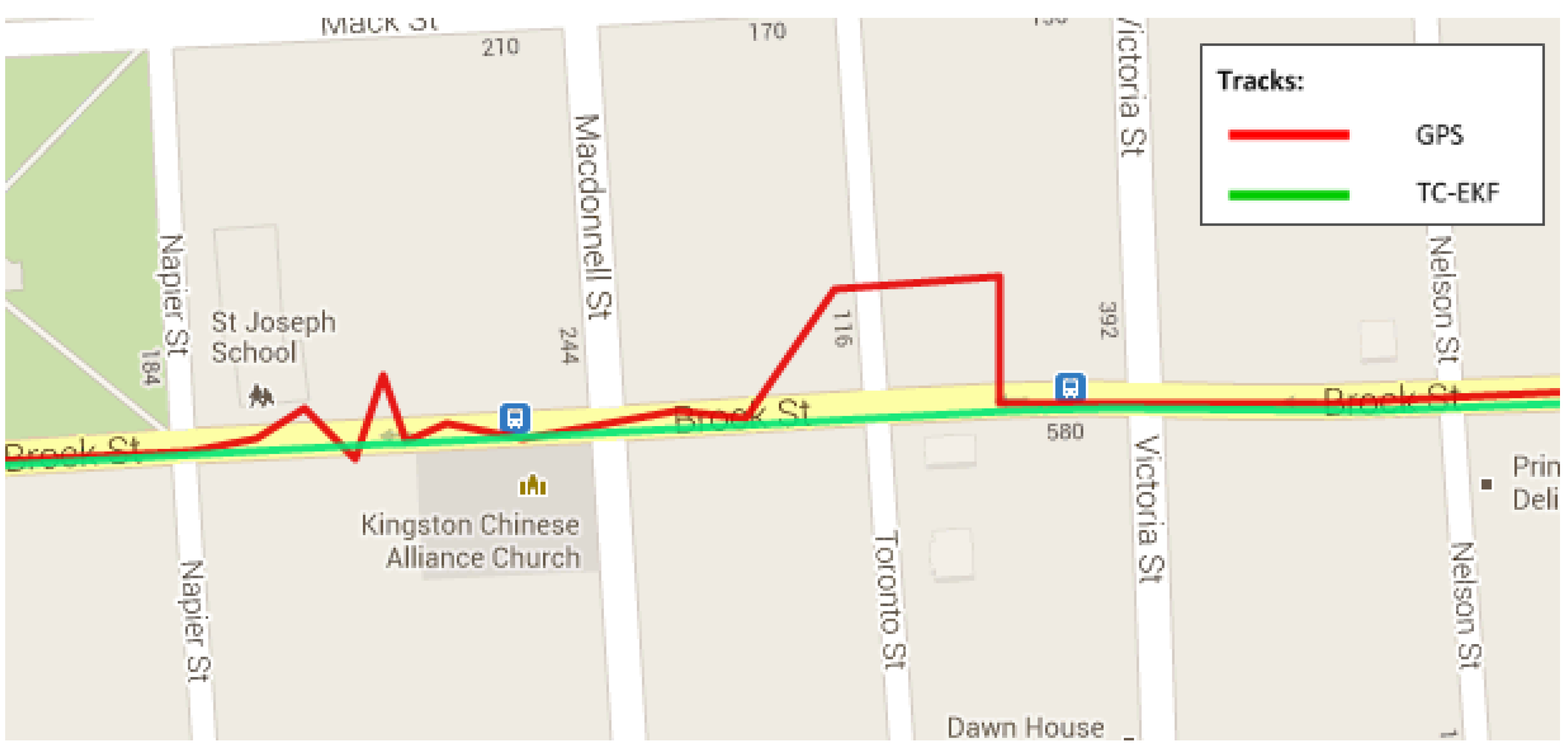
4.3.2. Tilt Angle Errors
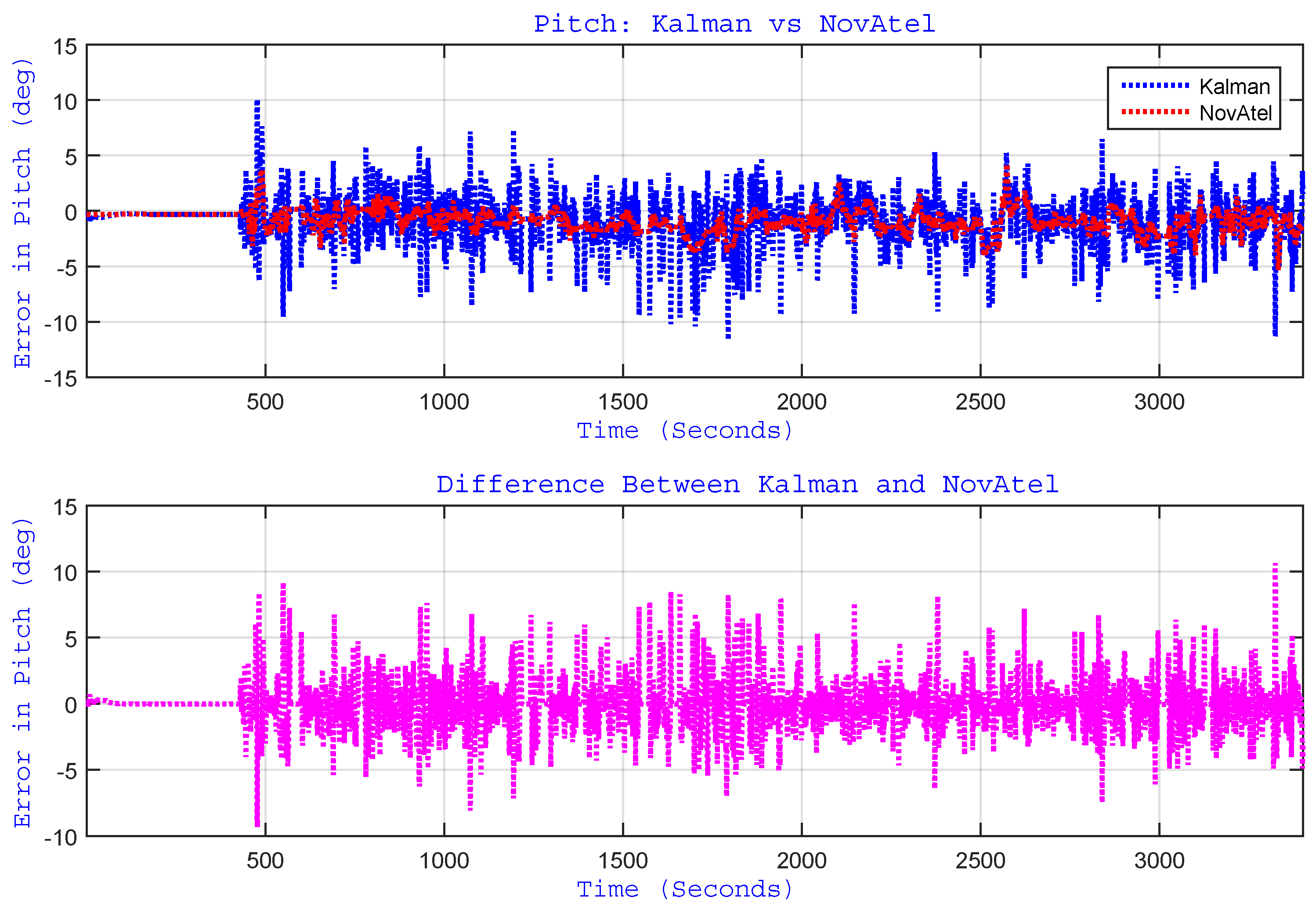
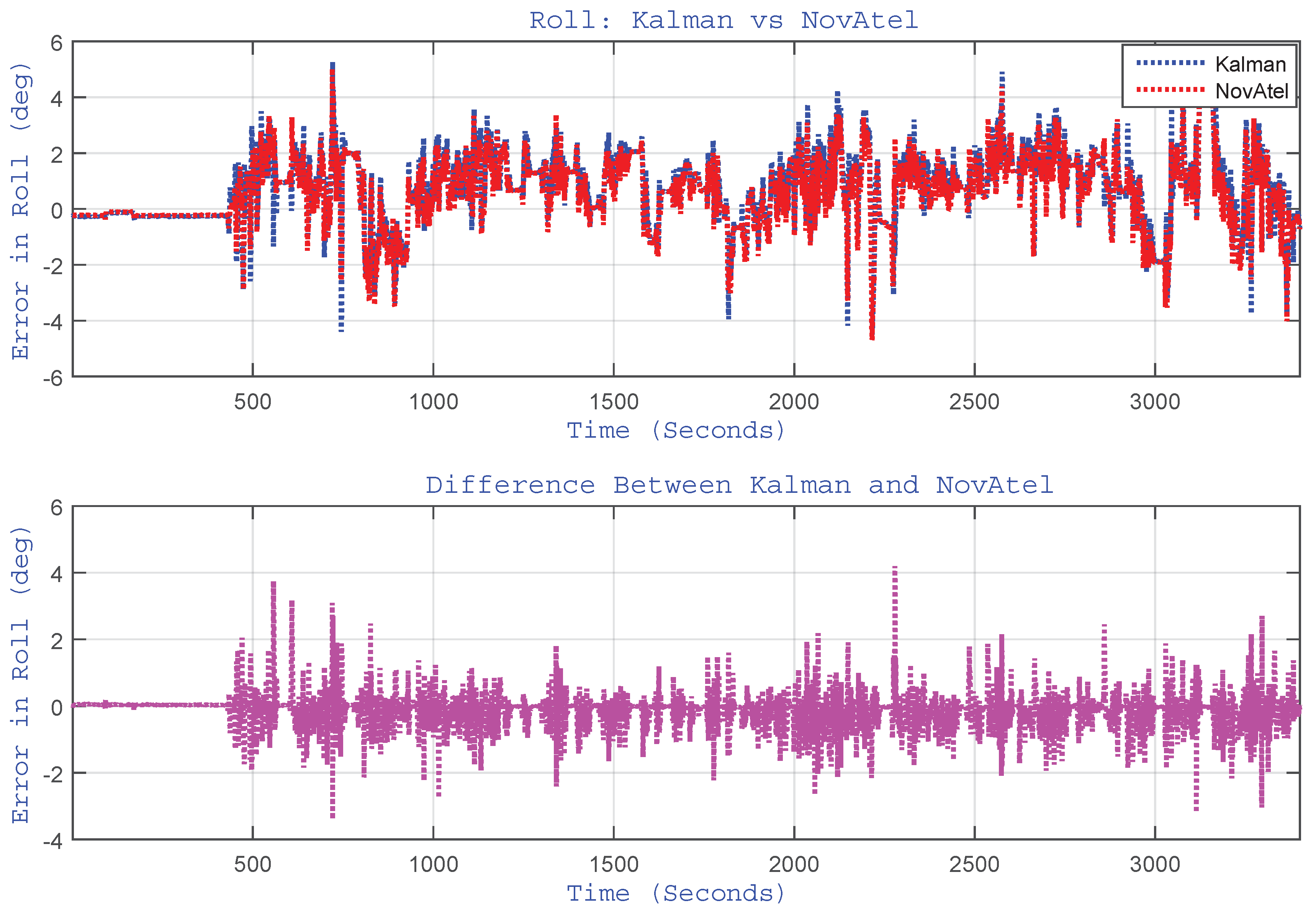
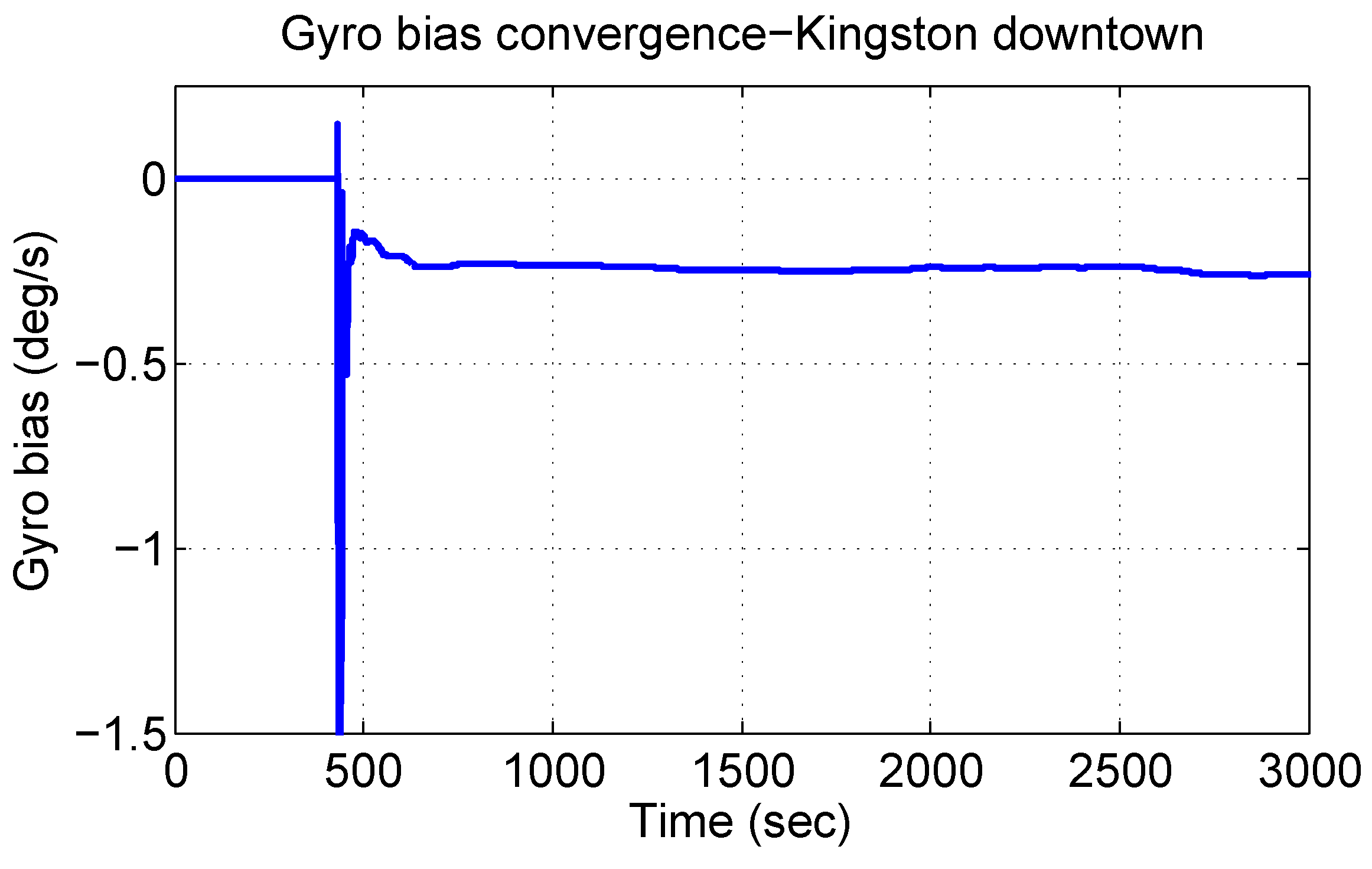
4.3.3. Gyroscope Bias
4.4. Toronto Downtown Trajectory
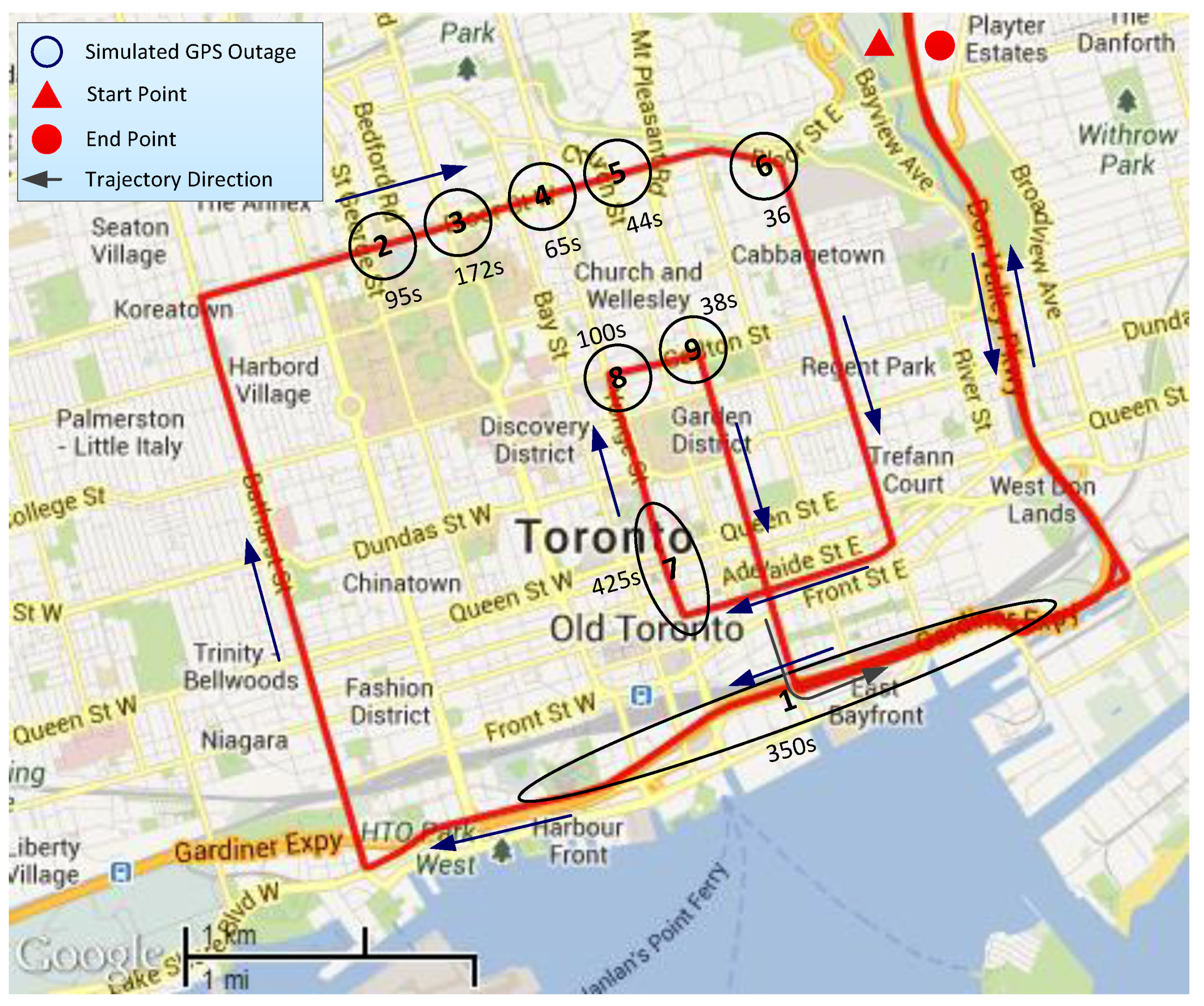
4.4.1. Positional Errors

| Outage No. | Outage Duration | Position (m) | Attitude (deg) | Velocity (m/s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Long | Alt | Pitch | Roll | Azi | Ve | Vn | Vu | ||||
| 1 | 350 | 9.05 | 14.24 | 12.18 | 3.17 | 0.61 | 2.31 | 1.28 | 1.92 | 1.94 | ||
| 2 | 95 | 8.34 | 5.18 | 3.16 | 3.05 | 0.35 | 1.99 | 0.62 | 0.58 | 0.98 | ||
| 3 | 172 | 15.77 | 6.10 | 10.60 | 2.94 | 0.32 | 3.80 | 0.64 | 0.41 | 0.55 | ||
| 4 | 65 | 7.77 | 11.78 | 42.20 | 1.63 | 0.14 | 2.08 | 0.34 | 0.10 | 0.35 | ||
| 5 | 44 | 7.82 | 2.53 | 5.35 | 4.34 | 0.23 | 1.28 | 0.64 | 0.24 | 1.06 | ||
| 6 | 36 | 2.44 | 1.64 | 4.73 | 3.59 | 0.86 | 4.18 | 1.97 | 1.76 | 2.04 | ||
| 7 | 425 | 9.42 | 14.37 | 9.70 | 3.43 | 0.41 | 3.56 | 0.76 | 0.75 | 0.94 | ||
| 8 | 100 | 5.36 | 2.04 | 3.54 | 4.28 | 0.96 | 48.79 | 1.24 | 1.40 | 1.58 | ||
| 9 | 38 | 1.83 | 6.36 | 4.25 | 3.26 | 1.41 | 7.59 | 1.49 | 2.13 | 0.32 | ||
| Average | 147 | 7.53 | 7.14 | 10.63 | 3.30 | 0.59 | 8.40 | 1.00 | 1.03 | 1.08 | ||
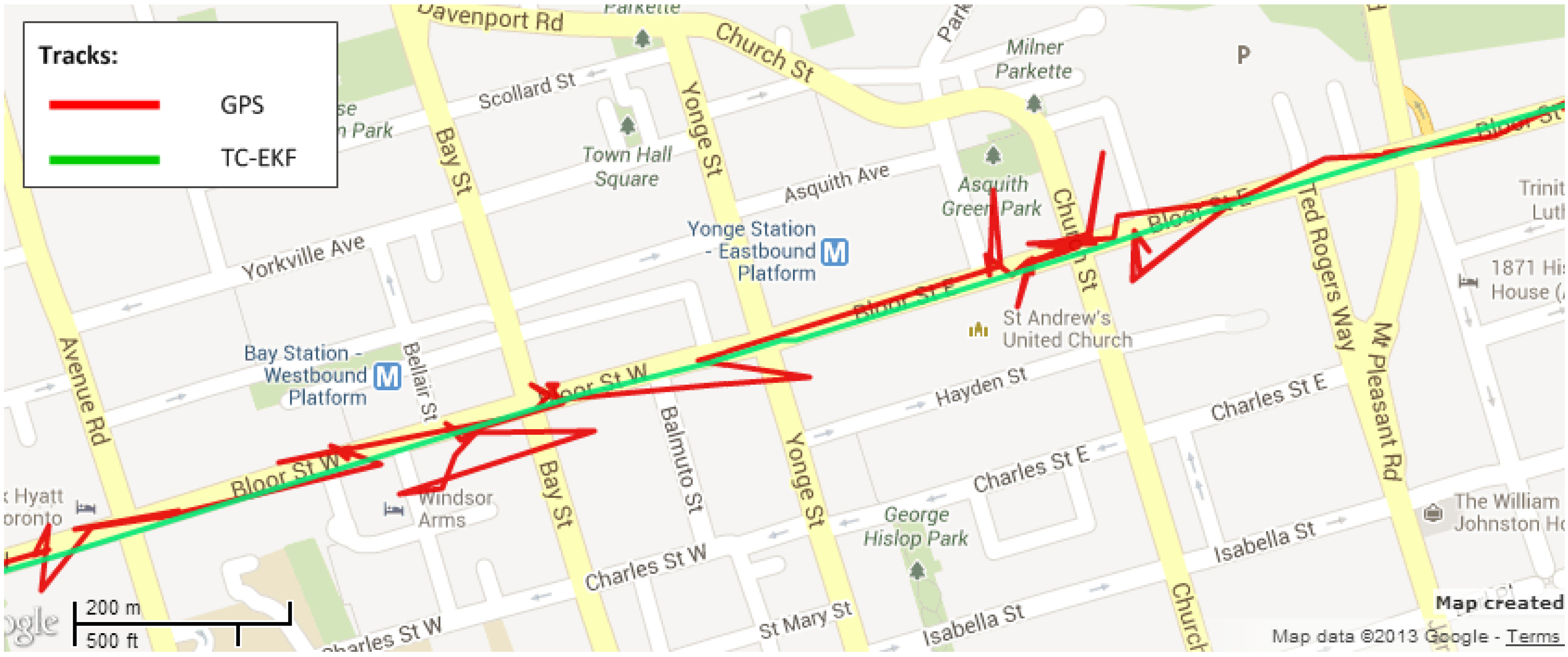
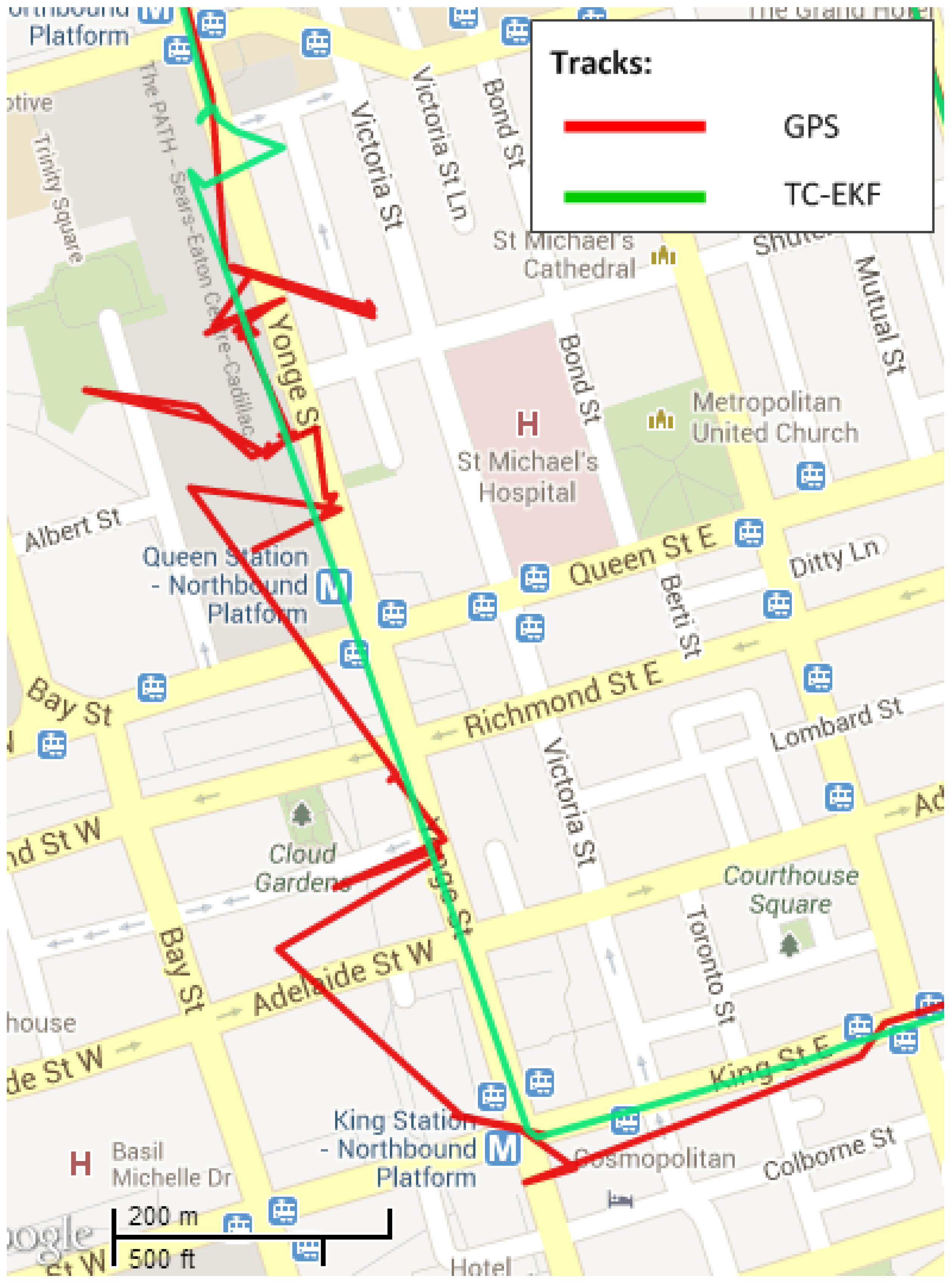
4.4.2. Tilt Angle Errors
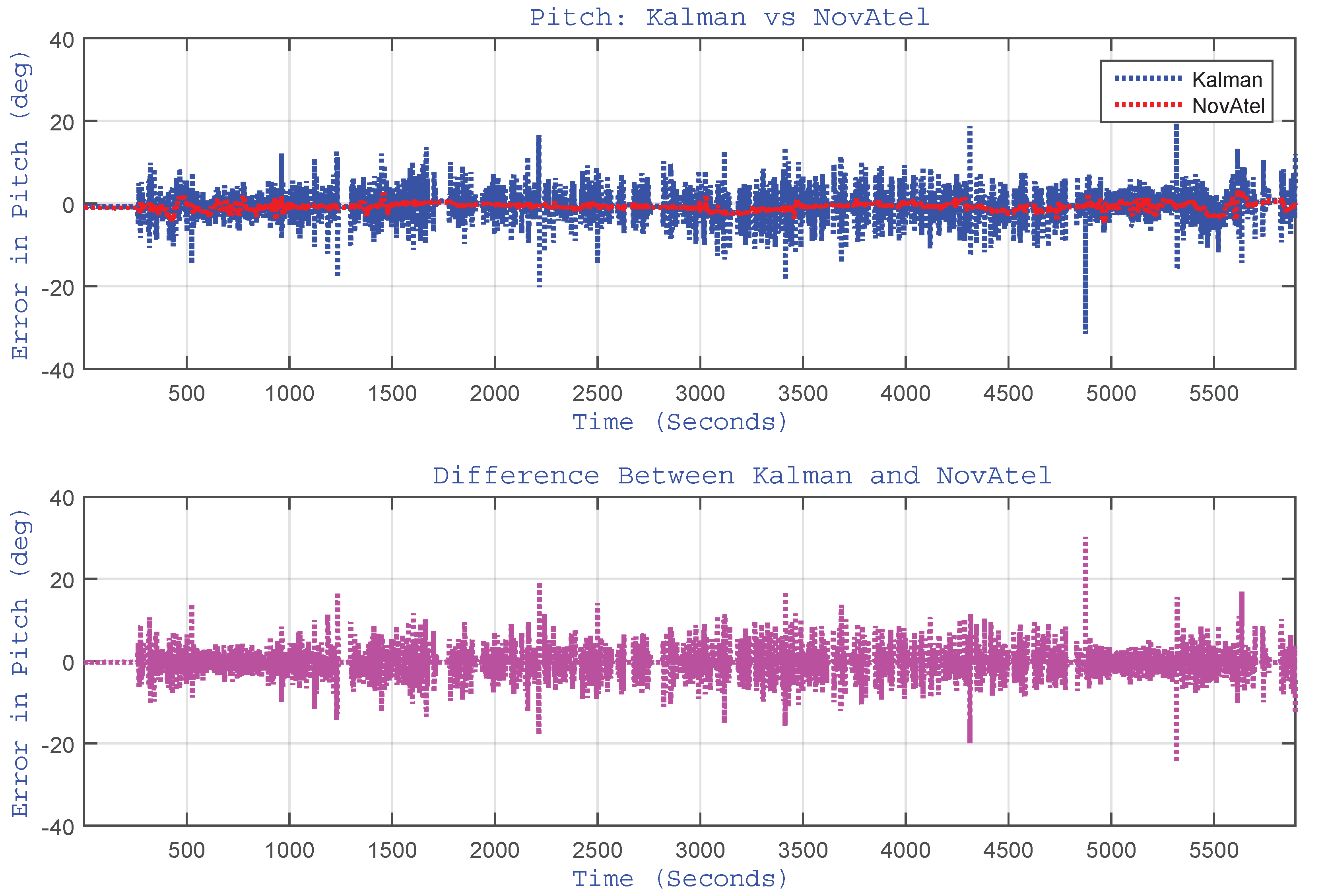
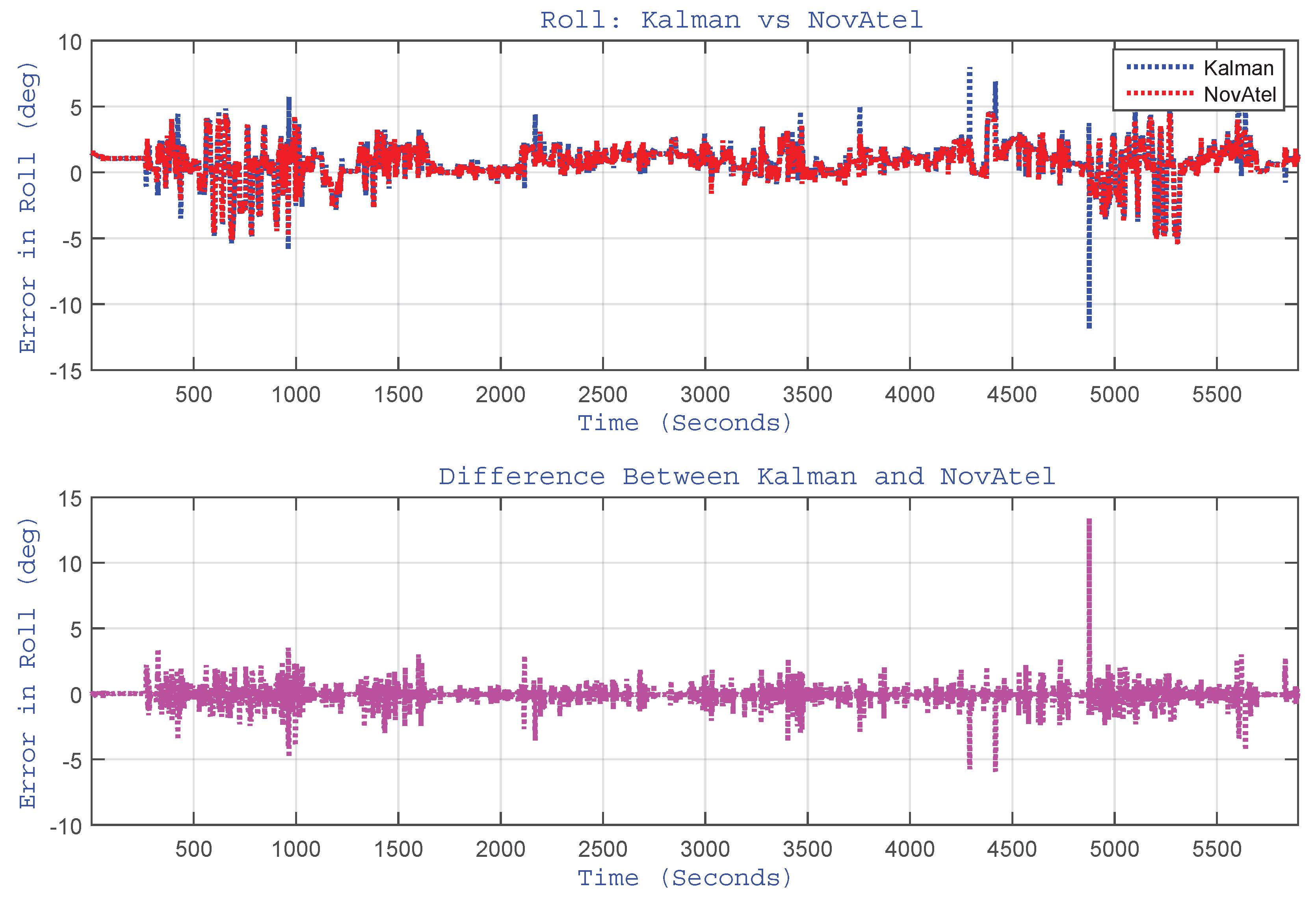
4.4.3. Gyroscope Bias
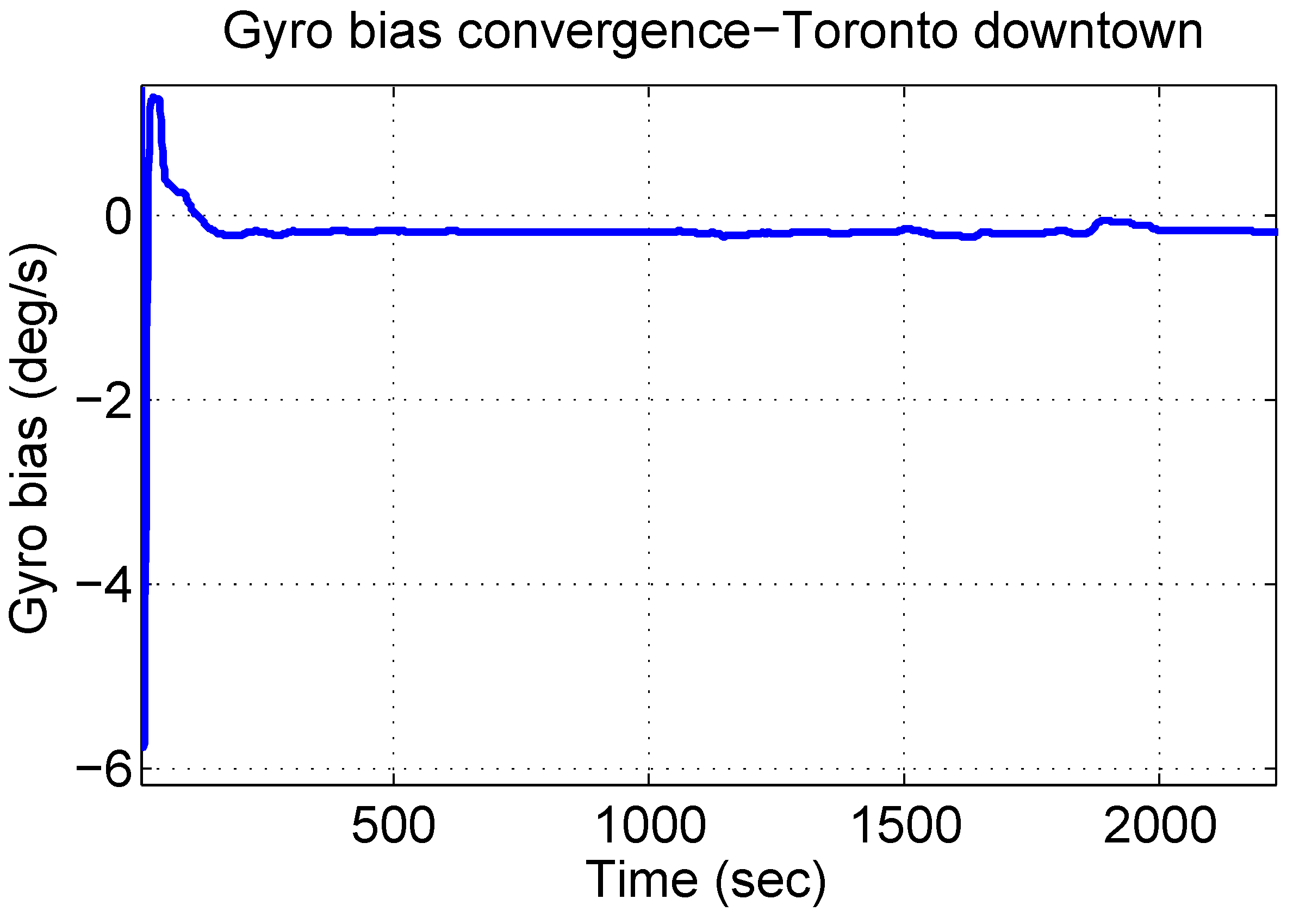
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Ganga-Jamuna Press: Lincoln, MA, USA, 2001. [Google Scholar]
- Hui, L.; Darabi, H.; Banerjee, P.; Jing, L. Survey of wireless indoor positioning techniques and systems. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2007, 37, 1067–1080. [Google Scholar]
- El-Rabbany, A. Introduction to GPS: The Global Positioning System, 2nd ed.; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Farrell, J.A. Aided Navigation: GPS with High Rate Sensors; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Groves, P.D. Principles of GNSS, Inertial, and Multi-sensor Integrated Navigation Systems; Artech House: Boston, MA, USA, 2008. [Google Scholar]
- Dissanayake, G.; Sukkarieh, S.; Nebot, E.; Durrant-Whyte, H. The aiding of a low-cost strapdown inertial measurement unit using vehicle model constraints for land vehicle applications. IEEE Trans. Robot. Autom. 2001, 17, 731–747. [Google Scholar] [CrossRef]
- Atia, M.M.; Georgy, J.; Korenberg, M.J.; Noureldin, A. Real-time implementation of mixture particle filter for 3D RISS/GPS integrated navigation solution. Electron. Lett. 2010, 46, 1083–1084. [Google Scholar] [CrossRef]
- Iqbal, U.; Okou, F.; Noureldin, A. An Integrated Reduced Inertial Sensor System-RISS/GPS for Land Vehicles. In Proceeding of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; The Institute of Navigation: Monterey, CA, USA; pp. 1014–1021.
- Wang, J.H.; Gao, Y. Land Vehicle Dynamics-Aided Inertial Navigation. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1638–1653. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Titterton, D.H.; Weston, J. Strapdown Inertial Navigation Technology, 2nd ed.; IEE Radar, Sonar, Navigation and Avionics Series; American Institute of Aeronautics and Astronautics: New York, NY, USA, 2005. [Google Scholar]
- Lawrence, A. Modern Inertial Technology: Navigation, Guidance, and Control, 2nd ed.; Springer: New York, NY, USA, 1998. [Google Scholar]
- Aggarwal, P.; Syed, Z.; Aboelmagd, N.; Naser, E.S. MEMS-Based Integrated Navigation; Technology and Applications, Artech House: Boston, MA, USA; London, UK, 2010. [Google Scholar]
- Karamat, T.B.; Georgy, J.; Iqbal, U.; Noureldin, A. A Tightly-Coupled Reduced Multi-Sensor System for Urban Navigation. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation-ION GNSS 2009, Savannah, GA, USA, 22–25 September 2009; pp. 582–592.
- Rezaei, S.; Sengupta, R. Kalman Filter-Based Integration of DGPS and Vehicle Sensors for Localization. IEEE Trans. Control Syst.Technol. 2007, 15, 1080–1088. [Google Scholar] [CrossRef]
- Adams, M.D. Lidar design, use, and calibration concepts for correct environmental detection. IEEE Trans. Robot. Autom. 2000, 16, 753–761. [Google Scholar] [CrossRef]
- Soloviev, A.; Bates, D.; van Graas, F. Tight coupling of laser scanner and inertial measurements for a fully autonomous relative navigation solution. Navig. J. Inst. Navig. 2007, 54, 189–205. [Google Scholar] [CrossRef]
- Degen, C.; El Mokni, H.; Govaers, F. Evaluation of a coupled laser inertial navigation system for pedestrian tracking. In Proceedings of the 15th International Conference on Information Fusion, FUSION 2012, Singapore, 9–12 July 2012; pp. 1292–1299.
- Soloviev, A.; Venable, D. Integration of GPS and vision measurements for navigation in GPS challenged environments. In Proceedings of the Position Location and Navigation Symposium (PLANS), 2010 IEEE/ION, Indian Wells, CA, USA, 4–6 May 2010; pp. 826–833.
- Gamallo, C.; Quintia, P.; Iglesias-Rodriguez, R.; Lorenzo, J.; Regueiro, C. Combination of a low cost GPS with visual localization based on a previous map for outdoor navigation. In Proceedings of the 2011 11th International Conference on Intelligent Systems Design and Applications (ISDA), Cordoba, Spain, 22–24 November 2011; pp. 1146–1151.
- Lin, F.; Chen, B.; Lee, T. Vision aided motion estimation for unmanned helicopters in GPS denied environments. In Proceedings of the 2010 IEEE Conference on Cybernetics and Intelligent Systems (CIS), Singapore, 28–30 June 2010; pp. 64–69.
- Mannings, R. Ubiquitous Positioning; Artech House: Boston, MA, USA, 2008. [Google Scholar]
- Miller, I.; Campbell, M. Particle filtering for map-aided localization in sparse GPS environments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2008), Pasadena, CA, USA, 19–23 May 2008; pp. 1834–1841.
- Jianjun, D.; Xiaohong, C. An improved map-matching model for GPS data with low polling rates to track vehicles. In Proceedings of the 2011 International Conference on Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011; pp. 299–302.
- Abdulrahim, K.; Hide, C.; Moore, T.; Hill, C. Aiding MEMS IMU with building heading for indoor pedestrian navigation. UPINLBS 2010, 2010, 1–6. [Google Scholar]
- Lou, L.; Xu, X.; Cao, J.; Chen, Z.; Xu, Y. Sensor fusion-based attitude estimation using low-cost MEMS-IMU for mobile robot navigation. In Proceedings of the 2011 6th IEEE Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 20–22 August 2011; Volume 2, pp. 465–468.
- Brandt, A.; Gardner, J. Constrained Navigation Algorithms for Strapdown Inertial Navigation Systems with Reduced Set of Sensors. In Proceedings of the 1998 American Control Conference (ACC), Philadelphia, PA, USA, 24–26 June 1998; American Autom. Control Council: Philadelphia, PA, USA; Volume 3, pp. 1848–1852.
- Iqbal, U.; Karamat, T.B.; Okou, A.F.; Noureldin, A. Experimental Results on an Integrated GPS and Multisensor System for Land Vehicle Positioning. Int. J. Navig. Observ. Hindawi Publ. Corp. 2009, 2009, 18. [Google Scholar] [CrossRef]
- Georgy, J.; Karamat, T.B.; Iqbal, U.; Noureldin, A. Enhanced MEMS-IMU/odometer/GPS integration using mixture particle filter. GPS Solut. 2010, 15, 239–252. [Google Scholar] [CrossRef]
- Cossaboom, M.; Georgy, J.; Karamat, T.B.; Noureldin, A. Augmented Kalman Filter and Map Matching for 3D RISS/GPS Integration for Land Vehicles. Int. J. Navig. Observ. 2012, 2012, 16. [Google Scholar] [CrossRef]
- Georgy, J.; Noureldin, A.; Korenberg, M.J.; Bayoumi, M.M. Low-cost three-dimensional navigation solution for RISS/GPS integration using mixture particle filter. IEEE Trans. Vehicul. Technol. 2010, 59, 599–615. [Google Scholar] [CrossRef]
- Iqbal, U. An Integrated Low Cost Reduced Inertial Sensor System/GPS for Land Vehicle Applications. Ph.D. Thesis, Royal Military College of Canada, Kingston, ON, Canada, 2008. [Google Scholar]
- Noureldin, A.; Irvine-Halliday, D.; Mintchev, M.P. Measurement-while-drilling surveying of highly inclined and horizontal well sections utilizing single-axis gyro sensing system. Meas. Sci. Technol. 2004, 15, 2426–2434. [Google Scholar] [CrossRef]
- Noureldin, A.; Irvine-Halliday, D.; Mintcheve, M. Accuracy Limitations of FOG-Based Continuous Measurement-While-Drilling Surveying Instruments for Horizontal Wells. IEEE Trans. Instrum. Meas. 2002, 51, 1177–1190. [Google Scholar] [CrossRef]
- Gelb, A. (Ed.) Applied Optimal Estimation; M.I.T. Press: Cambridge, MA, USA, 1974.
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering: With MATLAB Exercises and Solutions, 3rd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Grewal, M.S.; Andrews, A.P. Kalman Filtering: Theory and Practice Using MATLAB; Wiley: Oxford, UK, 2008. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley: Hoboken, NJ, USA; Chichester, UK, 2006. [Google Scholar]
- Kaplan, E.D.; Hegarty, C.J. Understanding GPS Principles and Applications, 2nd ed.; Artech House: Boston, MA, USA, 2006. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karamat, T.B.; Atia, M.M.; Noureldin, A. An Enhanced Error Model for EKF-Based Tightly-Coupled Integration of GPS and Land Vehicle’s Motion Sensors. Sensors 2015, 15, 24269-24296. https://doi.org/10.3390/s150924269
Karamat TB, Atia MM, Noureldin A. An Enhanced Error Model for EKF-Based Tightly-Coupled Integration of GPS and Land Vehicle’s Motion Sensors. Sensors. 2015; 15(9):24269-24296. https://doi.org/10.3390/s150924269
Chicago/Turabian StyleKaramat, Tashfeen B., Mohamed M. Atia, and Aboelmagd Noureldin. 2015. "An Enhanced Error Model for EKF-Based Tightly-Coupled Integration of GPS and Land Vehicle’s Motion Sensors" Sensors 15, no. 9: 24269-24296. https://doi.org/10.3390/s150924269
APA StyleKaramat, T. B., Atia, M. M., & Noureldin, A. (2015). An Enhanced Error Model for EKF-Based Tightly-Coupled Integration of GPS and Land Vehicle’s Motion Sensors. Sensors, 15(9), 24269-24296. https://doi.org/10.3390/s150924269







