A Novel Scheme for an Energy Efficient Internet of Things Based on Wireless Sensor Networks
Abstract
:1. Introduction
- (1)
- A hierarchical structure for placement of network components, that is objects/things in the IoT, is presented here. This structure has the scalability feature of the IoT to extend it up to any level. Direct communications between the relay nodes and sensor nodes at the cluster level, migrate the network load from local nodes to local relay nodes to provide energy efficient communication. Inter-cluster communication via cluster coordinators shifts the load from cluster heads (in a lower cluster) to the cluster coordinators (in upper clusters) thus enhancing the network lifetime.
- (2)
- An optimization problem is considered for the proposed network structure in terms of load balance and energy consumption for implementation of an efficient and scalable IoT. Thus, we propose, ME-CBCCP under the influence of clustering topology to resolve the optimization dilemma. This strategy facilitates the implementation of an energy efficient (green) IoT.
- (3)
- With extensive simulations on randomly deployed sensor nodes, the proposed scheme is validated in comparison to the traditional WSN schemes and found to be more favored for various applications of IoT.
2. Related Work
3. System Model and Framework
3.1. System Architecture
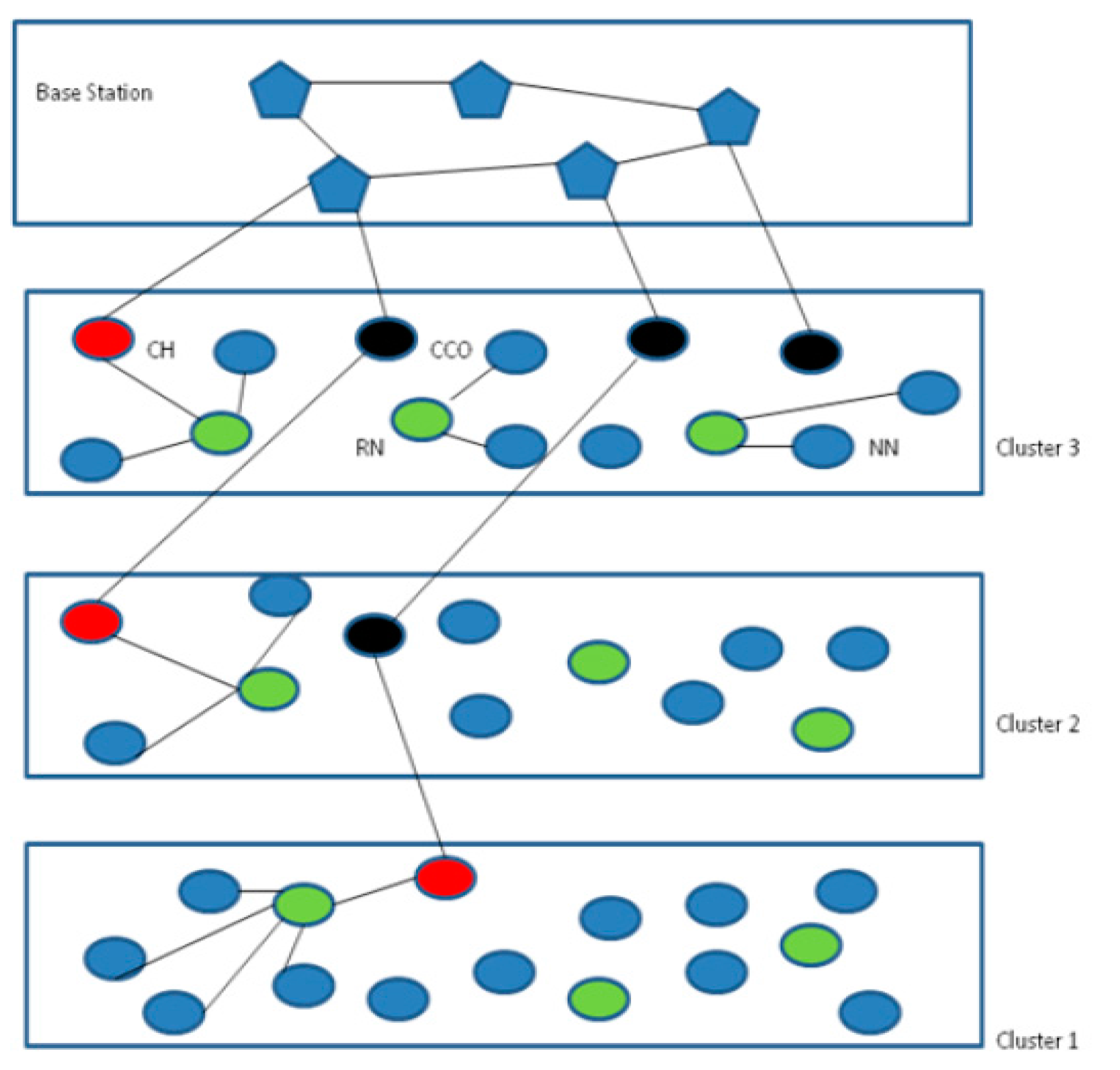
3.1.1. Communication within Clusters
- (1)
- (2)
- (3)
- (4)
- (5)
3.1.2. Communication among Clusters
- (1)
- (2)
- (3)
- (4)
- (5)
- (6)
- (7)
- (1)
- (2)
- (3)
- (a)
- The sensor nodes are stationary and symmetric. Nodes can communicate using the same transmission power level that means links are symmetrical and each node is allocated a unique ID .The importance and potential of all the nodes are equal to extend the lifetime of the network.
- (b)
- Routing techniques are required to balance the energy consumption among the nodes because the network supplies information to stationary observers positioned at the border of the area, which entails that energy consumption is not uniform for all nodes.
- (c)
- The number of transmission power levels are fixed for each node.
- (d)
- Nodes are equipped with GPS-capable antennae. The location of the nodes is tracked in the initial phase after that GPS will be turned off because the nodes are not mobile.
- (e)
- It is not possible to recharge the batteries of the nodes as they are left unattended after deployment. Hence there is requirement of energy efficient routing protocols.
- (f)
- Data is transmitted to the BS in multi-hop manner and BS layer are not constrained in energy while the other layers have the constraint of limited energy.
- (g)
- The network of IoT is fully connected as BS is reachable to each and every node.
3.2. Research Problem Foundation
4. Model for an Energy Efficient IoT
4.1. Constraints Imposed in IoT System
| Energy Consumption for data transmission | |
| Energy Consumption for data reception | |
| Energy Consumption for radio electronics | |
| Transmit amplifier of the normal node, relay node, and CH node and CC node respectively | |
| Cardinality of NN1, RN1, CH1, CC1 and BS1 | |
| Data rate from node u to v | |
| Maximum data rate | |
| Data length of the packet | |
| , , , , | Cost of CC, CH, RN, BS and NN |
| Cardinality of a set | |
| System budget | |
| Distance from node u to v |
4.2. Energy Expenditure Constraints
4.3. Wireless Links Constraints
4.4. Optimization Problem for Energy Efficient IoT
4.5. System Budget Constraints
| Algorithm 1. Minimum Energy Consumption Chain Based Algorithm (ME-CBCCP) |
| Input |
| Output |
| Enhanced network lifetime |
| 1: Deploy nodes randomly in the fixed area |
| 2: Apply subarea division algorithm to form the clusters () with fixed boundaries, allocate the cluster IDs to each layer of the cluster . That is for Select the closest within cluster . |
3: for each , repeat
|
| End for |
4: for each , repeat
|
| End for |
5: for each , repeat
|
| Continue with step 4. |
|
| End for |
5. Performance Evaluation and Results Discussion
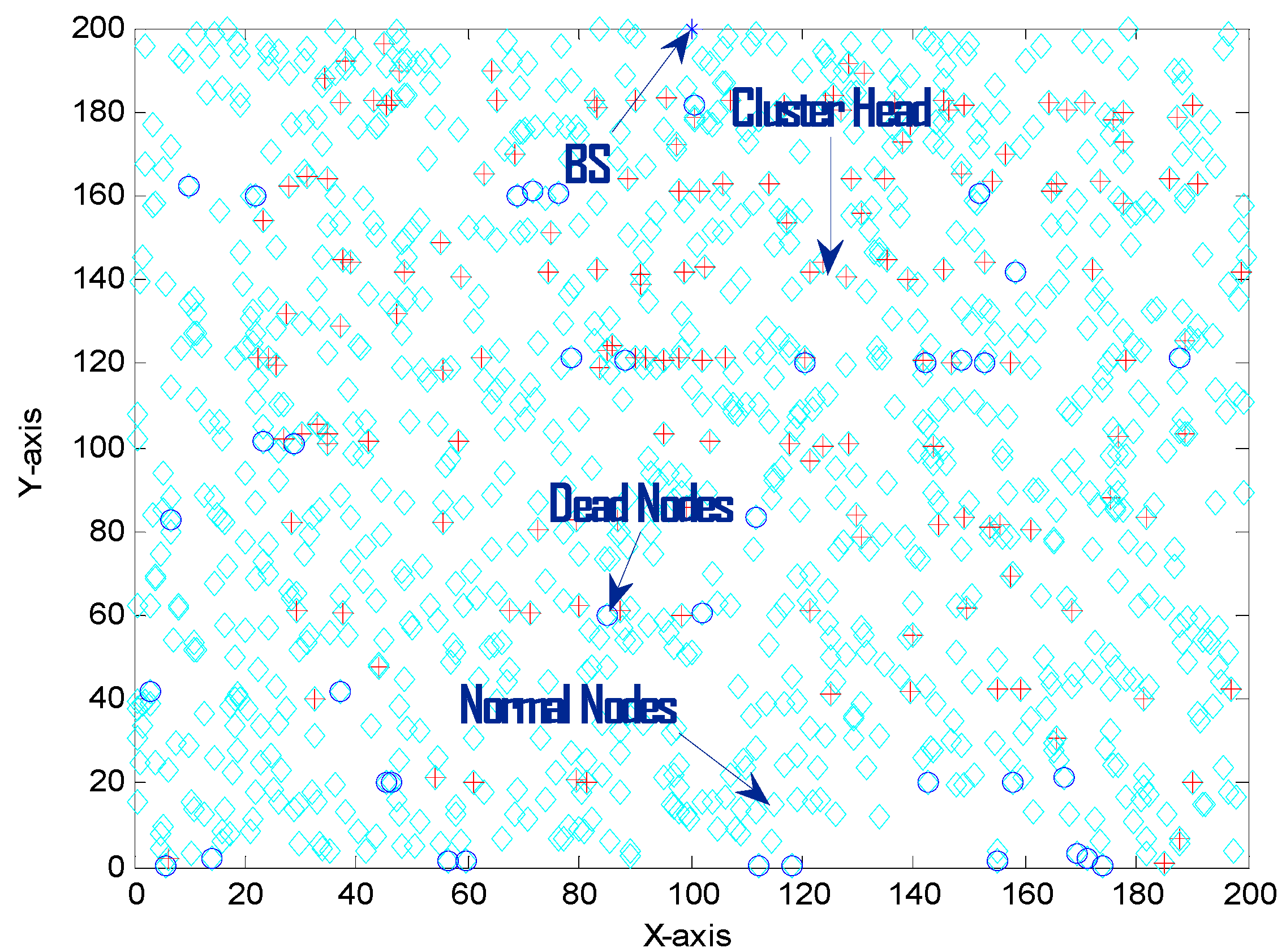
5.1. Setup Phase
5.2. Results Discussion
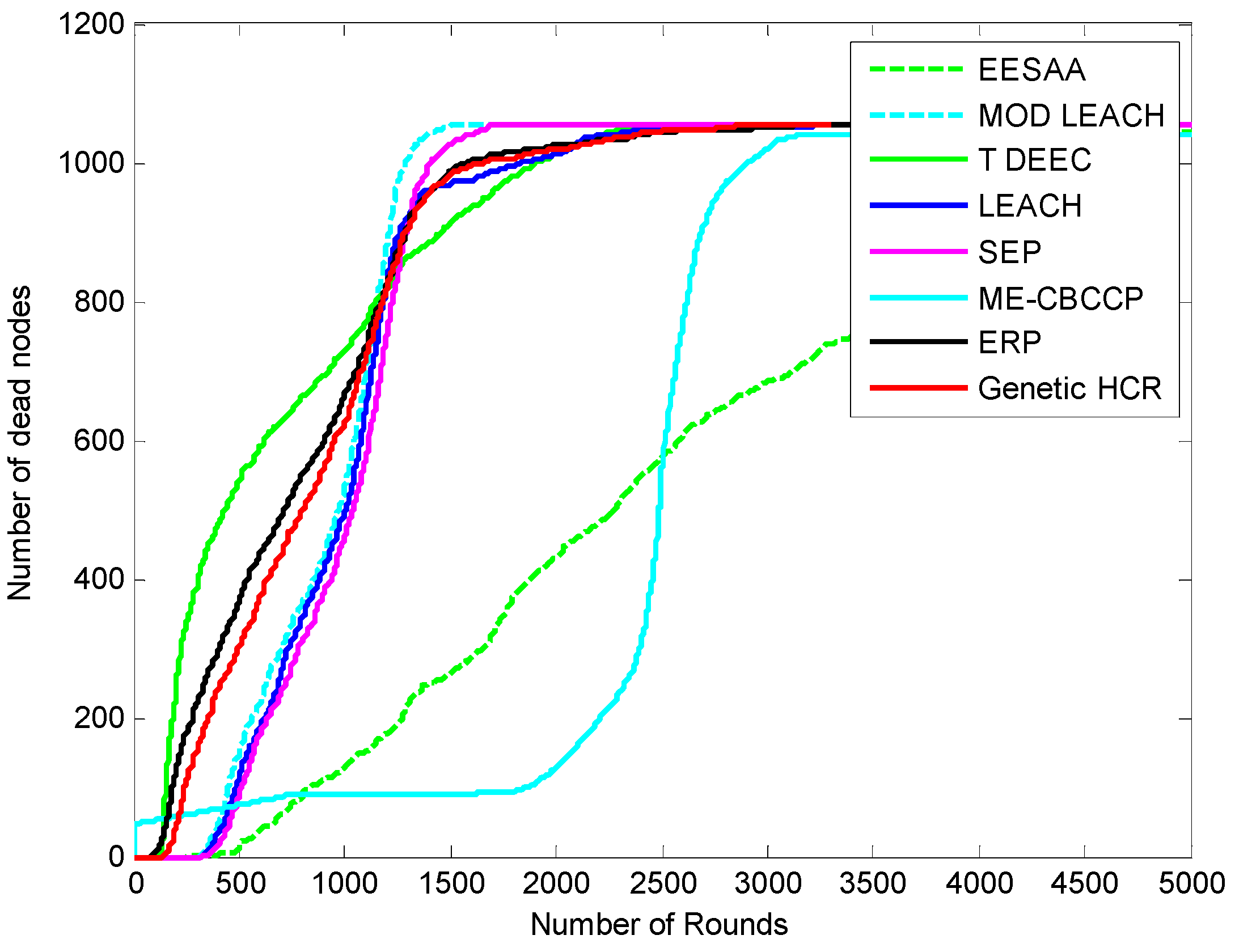
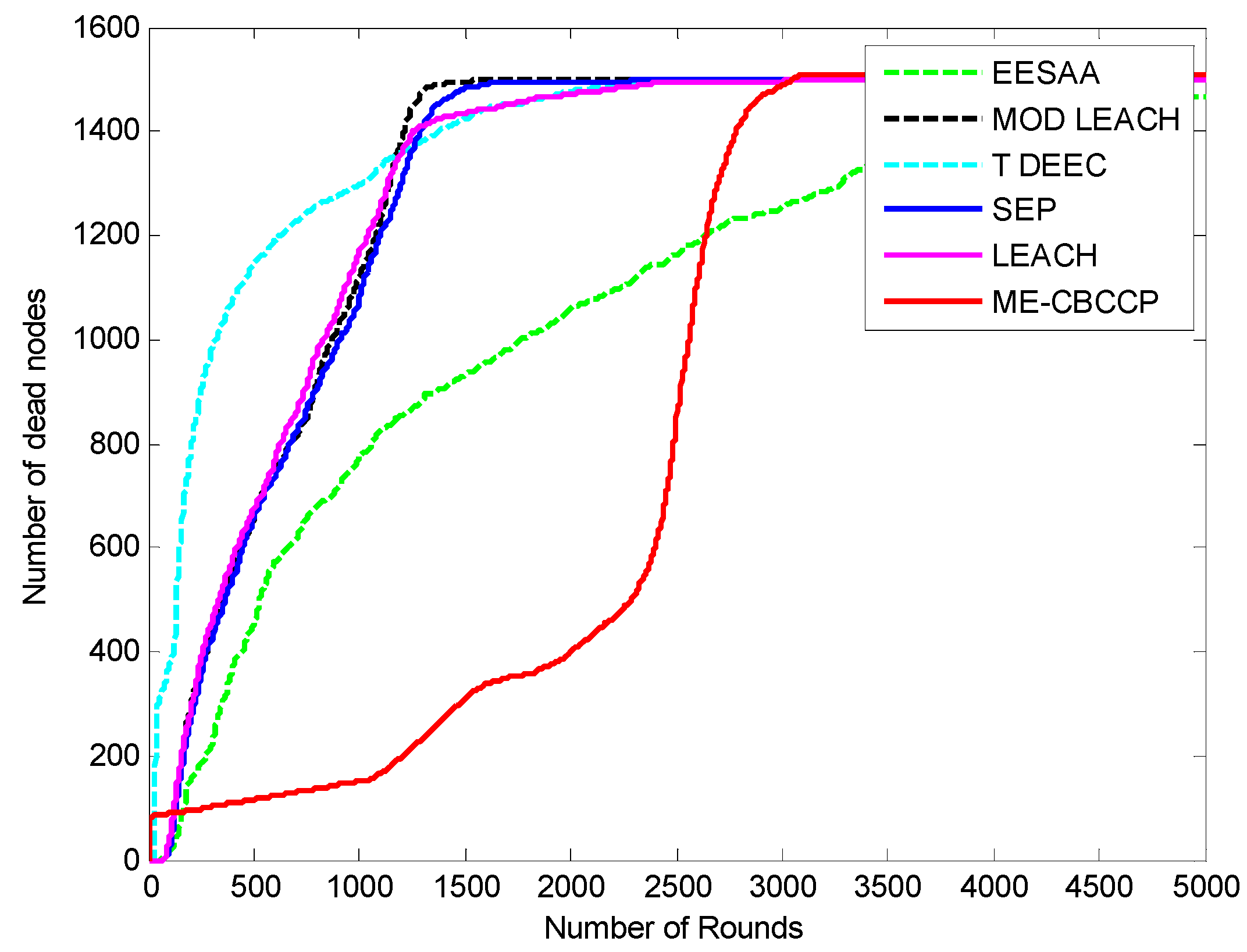
5.3. Comparison of Network Lifetime
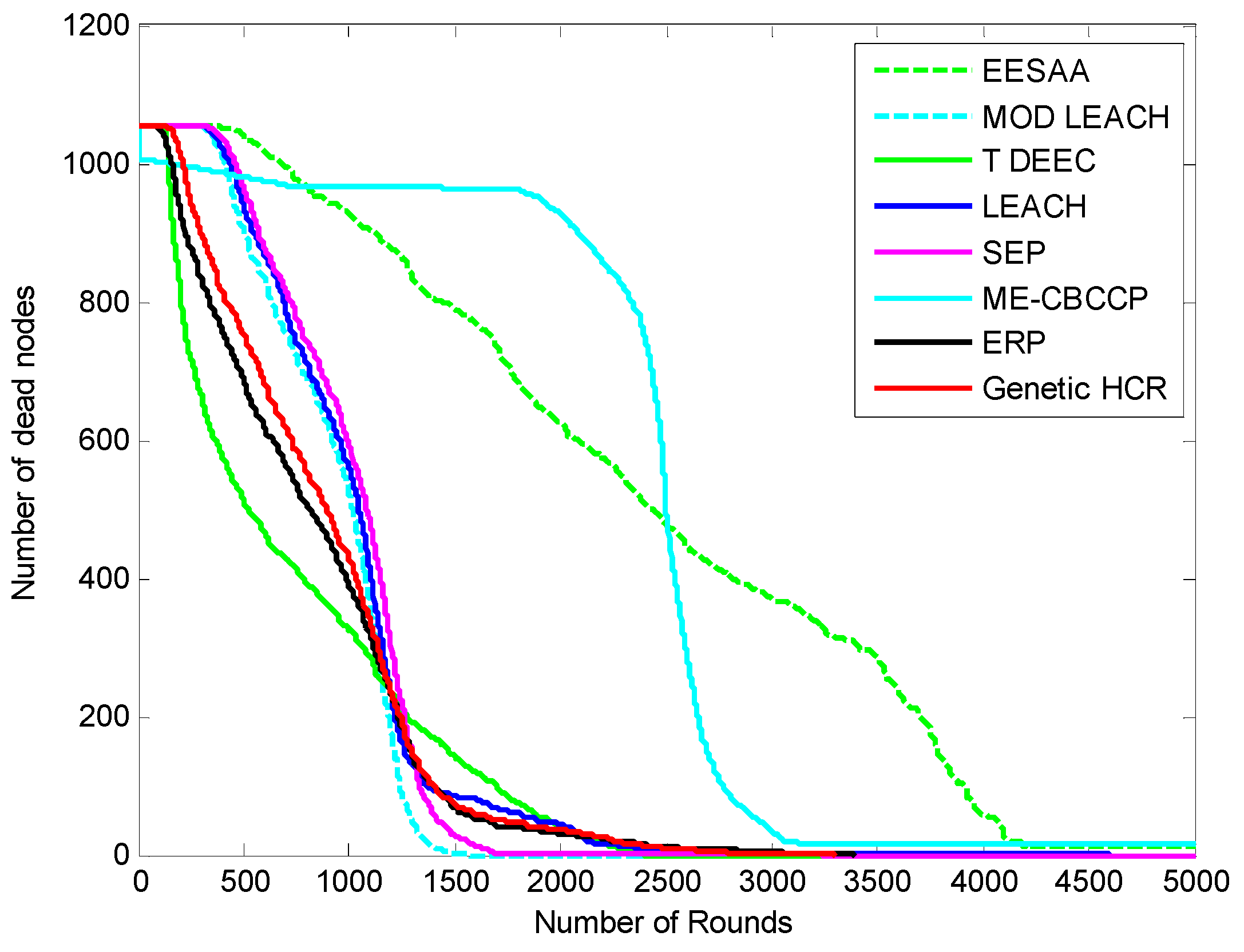
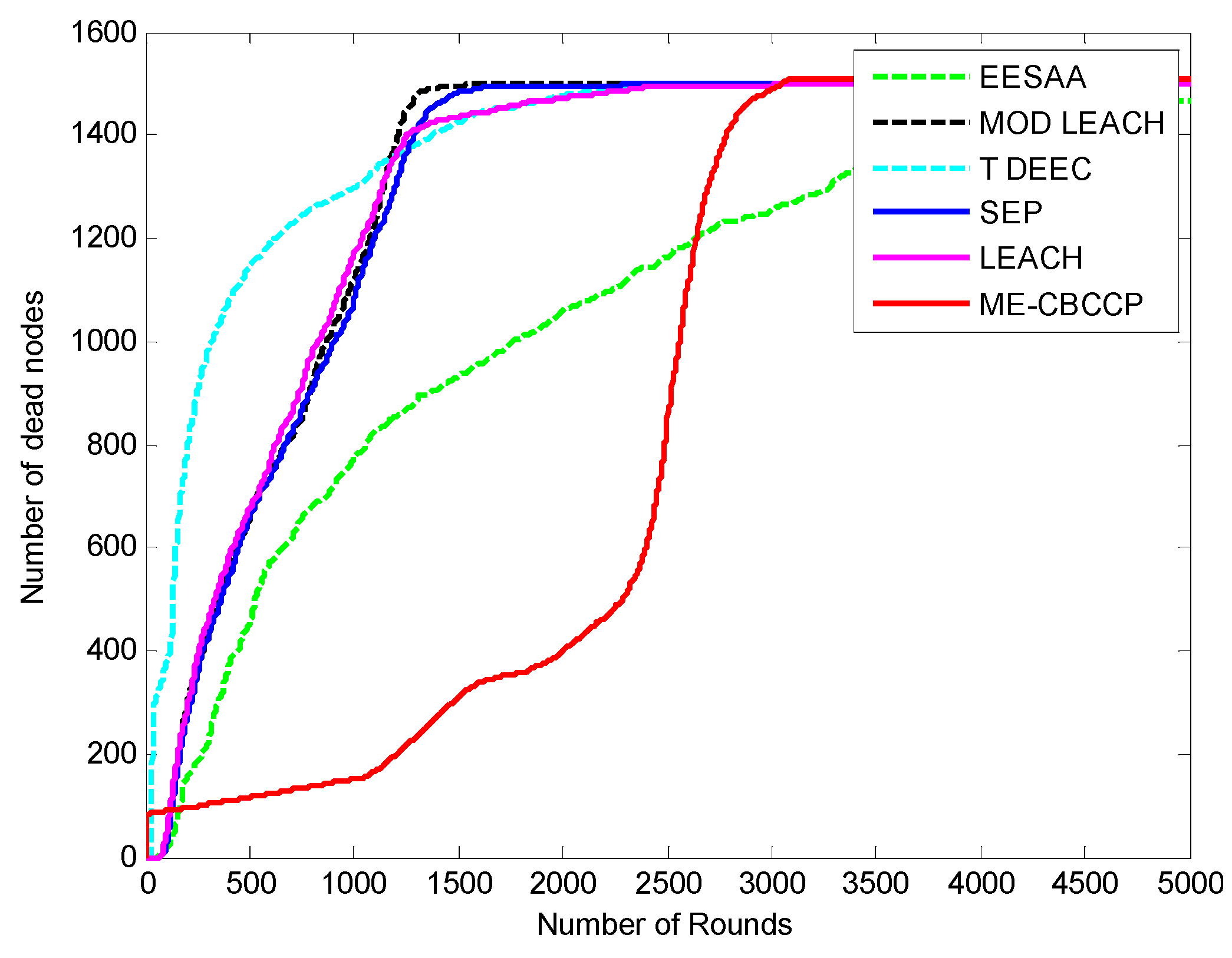
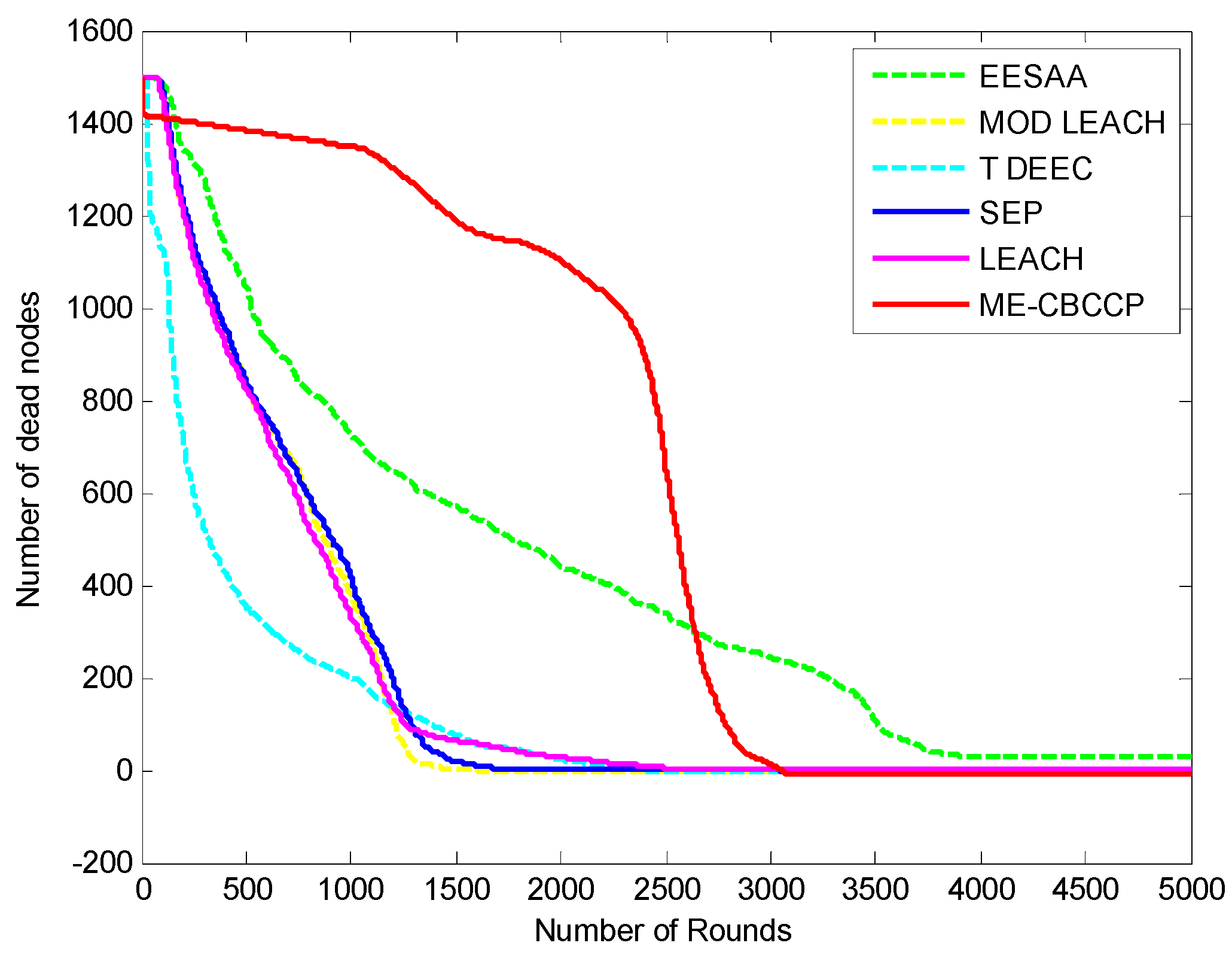
5.4. Comparison in Delay
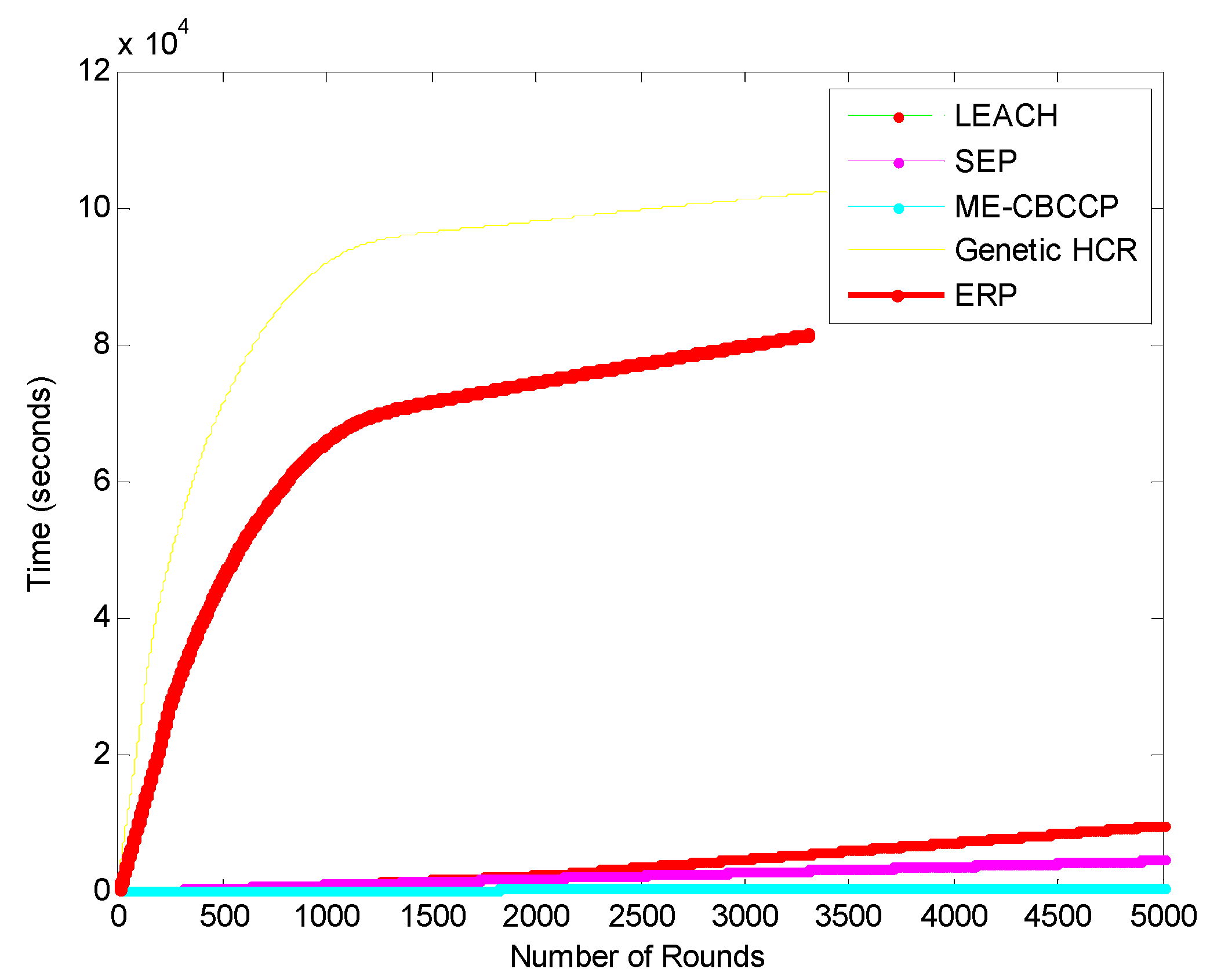
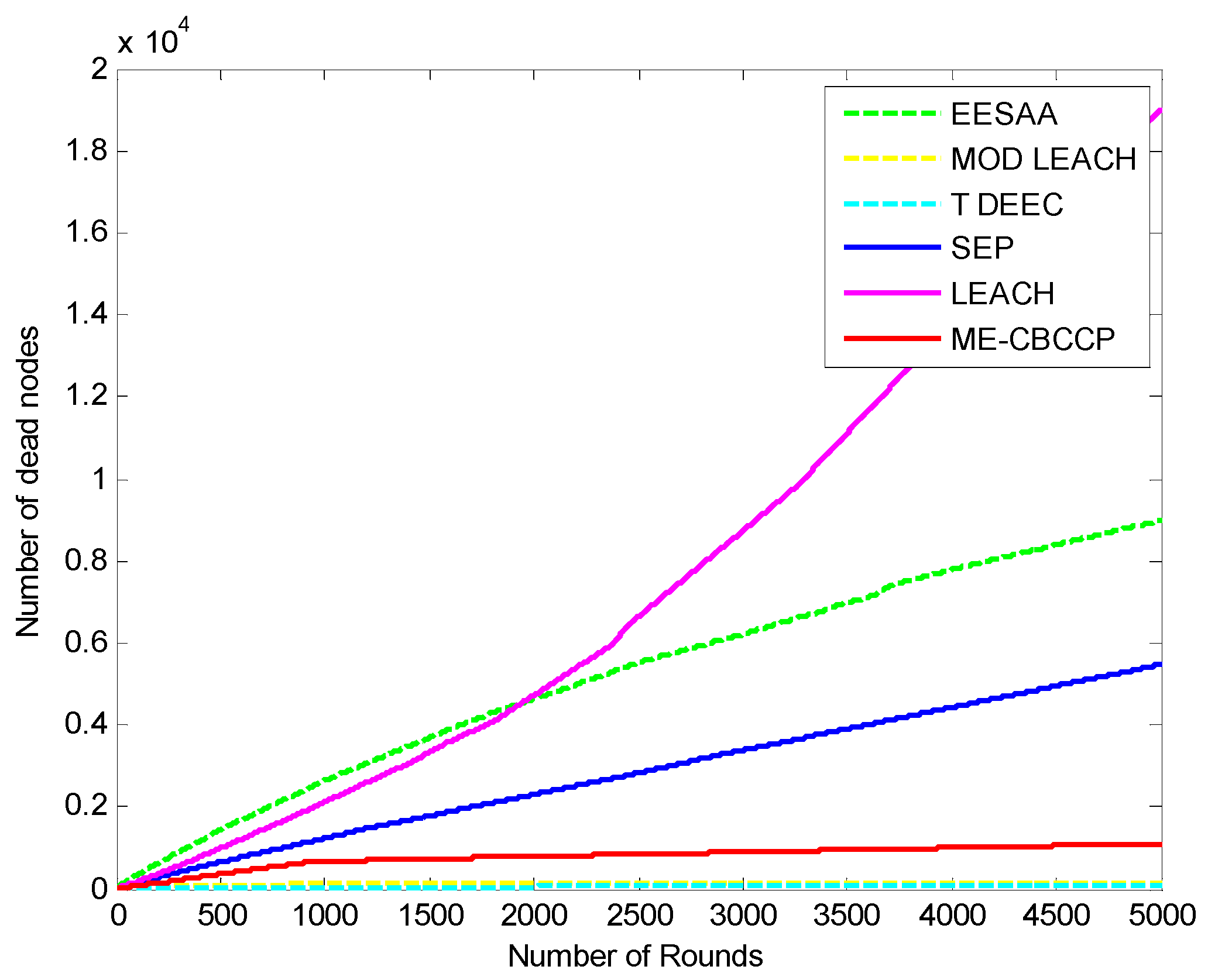
5.5. Comparison in Scalability
5.6. Analysis of ME-CBCCP in Terms of Other Parameters
6. Conclusions and Future Scope
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, J.; Meng, Y.; Gong, X.; Liu, Y.; Duan, Q. A novel deployment scheme for green Internet of Things. IEEE IoT J. 2014, 1, 196–205. [Google Scholar] [CrossRef]
- Jelicic, V.; Magno, M.; Brunelli, D.; Paci, G.; Benini, L. Context-adaptive multimodal wireless sensor network for energy-efficient gas monitoring. IEEE Sens. J. 2013, 13, 328–338. [Google Scholar] [CrossRef]
- Xiang, L.; Luo, J.; Deng, C.; Vasilakos, V.A.; Lin, W. DECA: Recovering fields of physical quantities from incomplete sensory data. In Proceedings of the 9th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks (SECON), Seoul, Korea, 18–21 June 2012; pp. 182–190.
- Sun, X.; Coyle, E.J. Quantization, channel compensation, and optimal energy allocation for estimation in sensor networks. ACM Trans. Sens. Netw. 2012, 8, 1–25. [Google Scholar] [CrossRef]
- Lee, S.; Younis, M. Eqar: Effective qos-aware relay node placement algorithm for connecting disjoint wireless sensor subnetworks. IEEE Trans. Comput. 2011, 60, 1772–1787. [Google Scholar] [CrossRef]
- Rani, S.; Malhotra, J.; Talwar, R. EEICCP—Energy Efficient Protocol for Wireless Sensor Networks. Wirel. Sens. Netw. 2013, 5, 127–136. [Google Scholar] [CrossRef]
- Rani, S.; Malhotra, J.; Talwar, J. Energy efficient protocol for densely deployed homogeneous network. In Proceedings of the IEEE International Conference on Issues and Challenges in Intelligent Computing Techniques (ICICT), Ghaziabad, India, 7–8 February 2014; pp. 292–298.
- Xu, M.; Leung, H. A joint fusion, power allocation and delay optimization approach for wireless sensor networks. IEEE Sens. J. 2011, 11, 737–744. [Google Scholar] [CrossRef]
- Lee, J.-S.; Cheng, W.-L. Fuzzy-logic-based clustering approach for wireless sensor networks using energy predication. IEEE Sens. J. 2012, 12, 2891–2897. [Google Scholar] [CrossRef]
- Shen, W.; Wu, Q. Exploring redundancy in sensor deployment to maximize network lifetime and coverage. In Proceedings of the 8th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, Salt Lake City, UT, USA, 27–30 June 2011; pp. 557–565.
- Li, F.; Luo, J.; Wang, W.; He, Y. Autonomous Deployment for Load Balancing-Surface Coverage in Sensor Networks Wireless Communications. IEEE Trans. Wirel. Commun. 2015, 14, 279–293. [Google Scholar] [CrossRef]
- Wei, P.; Chu, S.; Wang, X.; Zhou, Y. Deployment of a reinforcement backbone network with constraints of connection and resources. In Proceedings of the IEEE 30th International Conference on Distributed Computing System (ICDCS), Genova, Italy, 21–25 June 2010; pp. 10–19.
- Li, F.; Luo, J.; Xin, S.-Q.; Wang, W.-P.; He, Y. Laacad: Load balancing k-area coverage through autonomous deployment in wireless sensor networks. In Proceedings of the IEEE 32nd International Conference on Distributed Computing System (ICDCS), Macau, China, 18–21 June, 2012; pp. 566–575.
- Majumder, R.; Bag, G.; Kim, K.H. Power sharing and control in distributed generation with wireless sensor networks. IEEE Trans. Smart Grid 2012, 3, 618–634. [Google Scholar] [CrossRef]
- Yan, L.; Pan, W.; Luo, B.; Li, X.; Liu, J. Modified energy-efficient protocol for wireless sensor networks in the presence of distributed optical fiber senor link. IEEE Sens. J. 2011, 11, 1815–1819. [Google Scholar] [CrossRef]
- Cardei, M.; Thai, M.T.; Li, Y.; Wu, W. Energy-efficient target coverage in wireless sensor networks. In Proceedings of the 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March, 2005; pp. 1976–1984.
- Liu, C.; Cao, G. Distributed critical location coverage in wireless sensor networks with lifetime constraint. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012; pp. 1314–1322.
- Hodges, S.; Taylor, S.; Villar, N.; Scott, J.; Bial, D.; Fischer, P.T. Prototyping connected devices for the internet of things. Computer 2013, 46, 26–34. [Google Scholar] [CrossRef]
- Rohokale, V.M.; Prasad, N.R.; Prasad, R. A Cooperative Internet of Things (IoT) for rural healthcare monitoring and control. In Proceedings of the 2nd International Conference on Wireless Communications, Vehicular Technology, Information Theory and Aerospace & Electronics Systems Technology, Chennai, India, 28 February–3 March 2011; pp. 1–6.
- Ehsan, S.; Hamdaoui, B. A survey on energy-efficient routing techniques with QoS assurances for wireless multimedia sensor networks. IEEE Commun. Surv. Tutor. 2012, 14, 265–278. [Google Scholar] [CrossRef]
- Al-Fagih, A.E.; Al-Turjman, F.M.; Alsalih, W.M.; Hassanein, H.S. A priced public sensing framework for heterogeneous IoT architectures. IEEE Trans. Emerg. Top. Comput. 2013, 1, 133–147. [Google Scholar] [CrossRef]
- Rani, S.; Ahmed, S.H. Multi Hop Routing in Wireless Sensor Networks: An Overview, Taxonomy and Research Challenges; Springer: Berlin, Germany, 2015. [Google Scholar]
- Tyagi, S.; Kumar, N. A systematic review on clustering and routing techniques based upon LEACH protocol for wireless sensor networks. J. Netw. Comput. Appl. 2013, 36, 623–645. [Google Scholar] [CrossRef]
- Han, G.; Jiang, X.; Qian, A.; Rodrigues, J.J.; Cheng, L. A Comparative Study of Routing Protocols of Heterogeneous Wireless Sensor Networks. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Younis, O.; Fahmy, S. HEED: A hybrid, energy-efficient, distributed clustering approach for ad hoc sensor networks. IEEE Trans. Mob. Comput. 2004, 3, 366–379. [Google Scholar] [CrossRef]
- Jung, S.M.; Han, Y.J.; Chung, T.M. The concentric clustering scheme for efficient energy consumption in the PEGASIS. In Proceedings of the 9th International Conference on IEEE Advanced Communication Technology, Gangwon-Do, Korea, 12–14 February 2007; pp. 260–265.
- Lee, S.; Yoo, J.; Chung, T. Distance-based energy efficient clustering for wireless sensor networks. In Proceedings of the 29th Annual IEEE International Conference on Local Computer Networks, 16–18 November 2004; pp. 567–568.
- Hussain, S.; Matin, W.A. Energy Efficient Hierarchical Cluster-Based Routing for Wireless Sensor Networks; Jodrey School of Computer Science Acadia University: Wolfville, NS, Canada, 2005; pp. 1–33. [Google Scholar]
- Smaragdakis, G.; Matta, I.; Bestavros, A. SEP: A stable election protocol for clustered heterogeneous wireless sensor networks. In Proceedings of the 2nd IEEE International Workshop on Sensor and Actor Network Protocols and Applications, Boston, MA, USA, 22 August 2004; pp. 1–11.
- Kumar, D.; Patel, B.R. Multi-hop data communication algorithm for clustered wireless sensor networks. Int. J. Distrib. Sens. Netw. 2011. [Google Scholar] [CrossRef]
- Ye, M.; Li, C.; Chen, G.; Wu, J. EECS: An energy efficient clustering scheme in wireless sensor networks. In Proceedings of the 24th IEEE International Conference on Performance, Computing, and Communications, Phoenix, AZ, USA, 7–9 April 2005; pp. 535–540.
- Ding, P.; Holliday, J.; Celik, A. Distributed energy-efficient hierarchical clustering for wireless sensor networks. In Proceedings of the First IEEE International Conference on Distributed Computing in Sensor Systems, Springer-Verlag: Berlin, Germany, 30 June–1 July 2005; pp. 322–339.
- Li, C.; Ye, M.; Chen, G.; Wu, J. An energy-efficient unequal clustering mechanism for wireless sensor networks. In Proceedings of the IEEE International Conference on Mobile Ad hoc and Sensor Systems Conference, Washington, DC, USA, 7 November 2005.
- Buttyán, L.; Schaffer, P. Position-based aggregator node election in wireless sensor networks. Int. J. Distrib. Sens. Netw. 2010. [Google Scholar] [CrossRef]
- Liu, Y.; Hong, J.; Yue, G. An Energy-Efficient PEGASIS-Based Enhanced Algorithm in Wireless Sensor Networks. China Commun. 2006, 3, 91–97. [Google Scholar]
- Jung, S.M.; Han, Y.J.; Chung, T.M. The concentric clustering scheme for efficient energy consumption in the PEGASIS. In Proceedings of the 9th International Conference on Advanced Communication Technology, Gangwon, Korea, 12–14 February 2007; pp. 260–265.
- Muruganathan, S.D.; Ma, D.C.; Bhasin, R.; Fapojuwo, A.O. A centralized energy-efficient routing protocol for wireless sensor networks. IEEE Commun. Mag. 2005, 43, 8–13. [Google Scholar] [CrossRef]
- Dehni, L.; Krief, F.; Bennani, Y. Power control and clustering in wireless sensor networks. Chall. Ad Hoc Netw. 2006, 197, 31–40. [Google Scholar]
- Saini, P.; Sharma, A.K. Energy efficient scheme for clustering protocol prolonging the lifetime of heterogeneous wireless sensor networks. Int. J. Comput. Appl. 2010, 6, 30–36. [Google Scholar] [CrossRef]
- Shah, T.; Javaid, N.; Qureshi, T.N. Energy efficient sleep awake aware intelligent sensor network routing protocol. In Proceedings of the IEEE 15th International Multi-topic Conference (INMIC), Islamabad, Pakistan, 13–15 December 2012; pp. 317–322.
- Mahmood, D.; Javaid, N.; Mahmood, S.; Qureshi, S.; Memon, A.M.; Zaman, T. MODLEACH: A Variant of LEACH for WSNs. In Proceedings of the IEEE Eighth International Conference on Broadband and Wireless Computing, Communication and Applications (BWCCA), Compiegne, France, 28–30 October 2013; pp. 158–163.
- Rani, S.; Malhotra, J.; Talwar, R. On the Development of Realistic Cross Layer Communication Protocol for Wireless Sensor Networks. Wirel. Sens. Netw. 2014, 6, 57–66. [Google Scholar] [CrossRef]
- Tang, J.; Zhou, Z.; Niu, J.; Wang, Q. An energy efficient hierarchical clustering index tree for facilitating time-correlated region queries in the internet of things. J. Netw. Comput. Appl. 2014, 40, 1–11. [Google Scholar] [CrossRef]
- Diallo, C.; Marot, M.; Becker, M. Link Quality and Local Load Balancing Routing Mechanisms in Wireless Sensor Networks. In Proceedings of the Sixth Advanced International Conference on Telecommunications (AICT), Barcelona, Spain, 9–15 May 2010; pp. 306–315.
- Bara’a, A.A.; Khalil, E.A. A new evolutionary based routing protocol for clustered heterogeneous wireless sensor networks. Appl. Soft Comput. 2012, 12, 1950–1957. [Google Scholar] [CrossRef]
- Hussain, S.; Matin, A.W.; Islam, O. Genetic algorithm for hierarchical wireless sensor networks. J. Netw. 2007, 2, 87–97. [Google Scholar] [CrossRef]
- Liu, J.L.; Ravishankar, C.V. LEACH-GA: Genetic algorithm-based energy-efficient adaptive clustering protocol for wireless sensor networks. Int. J. Mach. Learn. Comput. 2011, 1, 79–85. [Google Scholar] [CrossRef]
- Norouzi, A.; Babamir, F.S.; Zaim, A.H. A new clustering protocol for wireless sensor networks using genetic algorithm approach. Wirel. Sens. Netw. 2011, 3, 362–370. [Google Scholar] [CrossRef]
- Xia, X.; Chen, Z.; Li, D.; Li, W. Proposal for Efficient Routing Protocol for Wireless Sensor Network in Coal Mine Goaf. Wirel. Pers. Commun. 2014, 77, 1699–1711. [Google Scholar] [CrossRef]
- Koç, M.; Korpeoglu, I. Controlled Sink Mobility Algorithms for Wireless Sensor Networks. Int. J. Distrib. Sens. Netw. 2014. [Google Scholar] [CrossRef]
- Kang, Y.; Hu, B.; Ding, Y.; Tan, J. A Hybrid Node Scheduling Approach Based on Energy Efficient Chain Routing for WSN. Adv. Mech. Eng. 2014. [Google Scholar] [CrossRef]
- Alia, O.M. A Decentralized Fuzzy C-Means-Based Energy-Efficient Routing Protocol for Wireless Sensor Networks. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Rani, S.; Malhotra, J.; Talwar, R. Energy Efficient Chain Based Cooperative Routing Protocol for WSN. Appl. Soft Comput. 2015, 35, 386–397. [Google Scholar] [CrossRef]
- Matheswaran, S.; Madheswaran, M. A Hybrid Optimized Weighted Minimum Spanning Tree for the Shortest Intra path Selection in Wireless Sensor Network. Math. Probl. Eng. 2014. [Google Scholar] [CrossRef]
- Amiri, E.; Keshavarz, H.; Alizadeh, M.; Zamani, M.; Khodadadi, T. Energy efficient routing in wireless sensor networks based on fuzzy ant colony optimization. Int. J. Distrib. Sens. Netw. 2014. [Google Scholar] [CrossRef]
- Zhong, Y.; Cheng, L.; Hang, L.; Song, Y.; Karimi, H.R. Energy-efficient routing control algorithm in large-scale WSN for water environment monitoring with application to three gorges reservoir area. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, S.H.; Bouk, S.H.; Javaid, N.; Sasase, I. Combined Human, Antenna Orientation in Elevation Direction and Ground Effect on RSSI in Wireless Sensor Networks. In Proceedings of the 10th International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 17–19 December 2012; pp. 46–49.
- Machado, K.; Rosário, D.; Cerqueira, E.; Loureiro, A.A.; Neto, A.; de Souza, J.N. A routing protocol based on energy and link quality for internet of things applications. Sensors 2013, 13, 1942–1964. [Google Scholar] [CrossRef] [PubMed]
- Butt, M.; Javed, M.; Akbar, A.; Taj, Q.; Lim, C.; Kim, K. Labile: Link Quality-Based Lexical Routing Metric for Reactive Routing Protocols. In Proceedings of the 5th International Conference on Future Information Technology IEEE 802.15.4 Networks, Busan, Korea, 21–23 May 2010; pp. 1–6.
- Perkins, C.; Belding-Royer, E.; Das, S. Ad hoc on-demand distance vector (AODV) routing. RFC 2003, 3561. [Google Scholar] [CrossRef]
- Chung, Y. An energy-efficient unicast routing protocol for wireless sensor Networks. Int. J. Comput. Sci. Emerg. Technol. 2011, 2, 60–64. [Google Scholar]
- Sheng, Z.; Yang, S.; Yu, Y.; Vasilakos, A.; McCann, J.; Leung, K. A survey on the ietf protocol suite for the internet of things: Standards, challenges, and opportunities. IEEE Trans. Wirel. Commun. 2013, 20, 91–98. [Google Scholar] [CrossRef]
- Mehmood, A.; Khan, S.; Zhang, D.; Lloret, J.; Ahmed, S.H. IoTEC: IoT based Efficient Clustering Protocol for Wireless Sensor Network. In Proceedings of the International Industrial Information Systems Conference, Chiang Mai, Thailand, 21–24 January 2014; pp. 10–11.
- Heinzelman, W.B.; Chandrakasan, A.P.; Balakrishnan, H. An application-specific protocol architecture for wireless micro sensor networks. IEEE Trans. Wirel. Commun. 2002, 1, 660–670. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rani, S.; Talwar, R.; Malhotra, J.; Ahmed, S.H.; Sarkar, M.; Song, H. A Novel Scheme for an Energy Efficient Internet of Things Based on Wireless Sensor Networks. Sensors 2015, 15, 28603-28626. https://doi.org/10.3390/s151128603
Rani S, Talwar R, Malhotra J, Ahmed SH, Sarkar M, Song H. A Novel Scheme for an Energy Efficient Internet of Things Based on Wireless Sensor Networks. Sensors. 2015; 15(11):28603-28626. https://doi.org/10.3390/s151128603
Chicago/Turabian StyleRani, Shalli, Rajneesh Talwar, Jyoteesh Malhotra, Syed Hassan Ahmed, Mahasweta Sarkar, and Houbing Song. 2015. "A Novel Scheme for an Energy Efficient Internet of Things Based on Wireless Sensor Networks" Sensors 15, no. 11: 28603-28626. https://doi.org/10.3390/s151128603
APA StyleRani, S., Talwar, R., Malhotra, J., Ahmed, S. H., Sarkar, M., & Song, H. (2015). A Novel Scheme for an Energy Efficient Internet of Things Based on Wireless Sensor Networks. Sensors, 15(11), 28603-28626. https://doi.org/10.3390/s151128603







