Front-Crawl Instantaneous Velocity Estimation Using a Wearable Inertial Measurement Unit
Abstract
: Monitoring the performance is a crucial task for elite sports during both training and competition. Velocity is the key parameter of performance in swimming, but swimming performance evaluation remains immature due to the complexities of measurements in water. The purpose of this study is to use a single inertial measurement unit (IMU) to estimate front crawl velocity. Thirty swimmers, equipped with an IMU on the sacrum, each performed four different velocity trials of 25 m in ascending order. A tethered speedometer was used as the velocity measurement reference. Deployment of biomechanical constraints of front crawl locomotion and change detection framework on acceleration signal paved the way for a drift-free integration of forward acceleration using IMU to estimate the swimmers velocity. A difference of 0.6 ± 5.4 cm·s−1 on mean cycle velocity and an RMS difference of 11.3 cm·s−1 in instantaneous velocity estimation were observed between IMU and the reference. The most important contribution of the study is a new practical tool for objective evaluation of swimming performance. A single body-worn IMU provides timely feedback for coaches and sport scientists without any complicated setup or restraining the swimmer's natural technique.1. Introduction
The advent of new technologies has changed the perception of athletic achievement. In swimming, the narrow gap between record holders, points to the growing importance of devising new tools to assess self-improvement and optimize the training process. However, the biomechanical analysis of swimming remains inadequately explored due to complications of kinematics measurements in water.
To date, the most common practice for performance monitoring in swimming is using video-based systems. A video sequence is captured and post-processed through digitization [1,2]. The main downside of such systems is being excessively time consuming and problematic to fully automate. The application of this class of methods can be severely restricted by factors such as light refraction in water or bubbles generated around the swimmers' bodies [3]. Recently a markerless 3D analysis method was proposed [4] based on extraction of a swimmer's silhouette. This method reduced the video processing time, while still being sensitive to different lighting condition that leads to misidentification of features [5].
The second category of techniques uses tethered monitoring. An early version of such a system was developed by Craig et al. [6]. Velocity is directly measured by a cord attached to the swimmer. The cord is tethered to a poolside shaft-encoder [7,8]. Although this system is considered as reference to assess swimming velocity, the device disturbs the swimmers' technique and measures the velocity only in the forward direction. Moreover, the system requires a resisting force to tighten the cord during the decelerations of swimmer for an accurate measurement. Hence, this force is constantly applied to the swimmer.
During the past two decades inertial measurement units (IMUs) have been proven to be powerful tools in human movement analysis [9]. First and foremost the portability of IMUs made them a viable system in daily life measurements, contrary to most other measurement systems which are restricted to laboratory conditions. Besides, the technological developments in microelectromechanical systems (MEMS) have made IMUs a low cost option compared to in-laboratory settings. The application of IMUs for sport analysis is a new trend in sport biomechanics [10–12]. A considerable number of studies have been conducted on the application of IMUs in the swimming context. Chronologically, Ohgi et al. [13] were probably the first to use a wrist-worn IMU to detect front crawl and breast stroke swimming phases automatically. A sacrum mounted 3D accelerometer was used by Davey et al. [14] to automatically extract simple metrics such as lap time and stroke rate. An IMU comprising a 3D accelerometer, 2D gyroscope and RF transceiver was used by Le Sage et al. [15] to characterize swimming strokes in real time. However, none of aforementioned works involved kinematic measurements using IMUs. Recently, Stamm et al. [16] published a method using a 3D accelerometer on the lower back to measure the front crawl velocity. However, a single 3D accelerometer generally is not capable of measuring the orientation of the body during dynamic movement. Consequently, the effect of lateral and vertical acceleration of swimmer's body cannot be removed from acceleration in the forward direction of swimming, therefore, calculating the integral of the acceleration signal in [16] to evaluate the velocity can be misleading. Besides, it is well known that the accuracy of IMU-based systems in velocity measurement rapidly degrades over time due to inherent sensor noises [17]. Hence special considerations are needed for a reliable assessment of velocity.
Considering the velocity as the most intuitive metric of swimmers' performance, this study aimed to propose a new method to measure swimming velocity in front crawl, using a single body-worn inertial sensor. We hypothesize that the swimmer's instantaneous velocity can be estimated accurately from IMU measurements when the average velocity of the swimmer over the trial is known. Drift-free integration of acceleration was certified in this study by assuming some simple locomotion constraints of the front crawl. Experimental protocols and statistical tools are introduced to assess the validity of the cycle and instantaneous velocity estimation method.
2. Experimental Section
2.1. Participants and Protocol
Eleven elite and nineteen recreational swimmers took part in this study. Their attributes are shown in Table 1. Each participant was informed of the procedures and risks associated with study participation and gave written informed consent prior to participation. This study was performed in accordance with the Declaration of Helsinki and was approved by the Ethics Committee of the Faculty of Biology and Medicine, University of Lausanne (protocol #87/10).
Each swimmer performed consecutive 25 m front-crawl trials in four different increasing velocity trials from 70% to 100% of their best personal 100 m timing recorded one month before the measurement. In case the performance time was different more than ±5% from the targeted time, the swimmer repeated the trial. They were asked to position in the water at the edge of the pool for starts.
2.2. Data Acquisition and Calibration
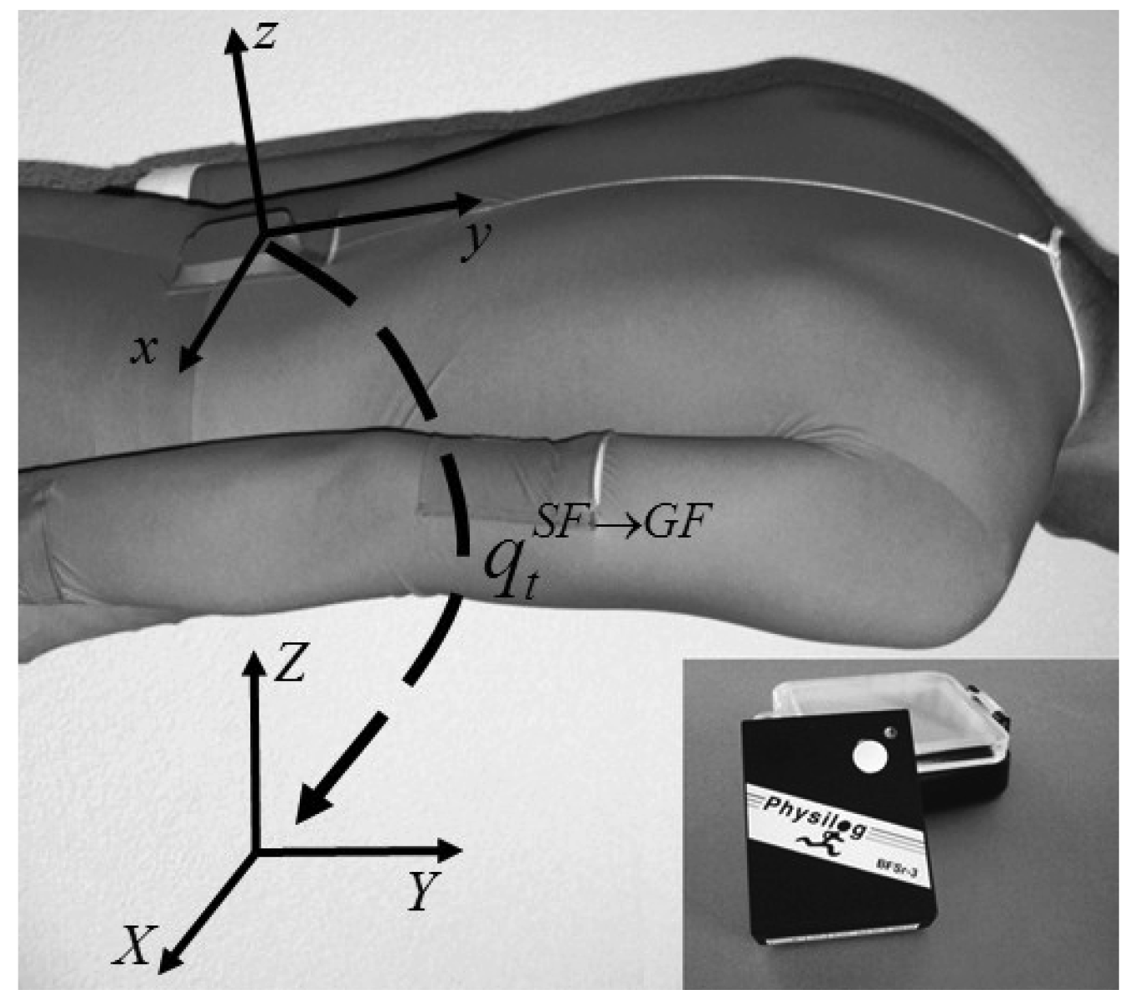
The swimmers were equipped with one waterproofed inertial sensor (Physilog®, BioAGM, La Tour-de-Peilz, Switzerland) including a 3D accelerometer (±11 g) and a 3D gyroscope (±900 °/s) and embedded data logger recording at 500 Hz. The sensor was worn on the sacrum inside the pocket of a custom designed swimming suit with a Velcro closing as shown in Figure 1. According to the feedback from swimmers, by wearing the sensor attachment in our study they did not feel the IMU imposed a noticeable drag during their training. The sensor was calibrated for offset, scale and non-orthogonality using in-field calibration procedure [18].
As reference system, a tethered apparatus (SpeedRT®, ApLab, Rome, Italy) [8] was attached to the waist of swimmers just beneath the lower end of the sensor with a belt. The system calculates the velocity by measuring the cord displacement through time at 100 Hz recording. The resistance applied to keep the cord tight is adjustable via a clutch on the pulley compartment of the apparatus. In our measurement, the resistance was set to 500 g [19]. Since the tethered reference is installed on the starting block above the swimming level, the SpeedRT® cord is not parallel to the direction of swimming and imposes the parallax problem [15]. By knowing the cord displacement at each time instant and the fact that the reference pulley was positioned 72 ± 1 cm above still pool water level, we calculated the instantaneous velocity measured by the reference in the swimming direction.
2.3. Estimation of Swimming Orientation Using IMU
Instantaneous velocity is estimated by integrating the forward acceleration signal in the global frame (GF: X, Y, Z) (Figure 1). Among the axes of GF the Z is assumed to be vertically upward and Y in parallel with the longitudinal edge of the pool. The acceleration in GF can be calculated from the acceleration measured in sensor frame (SF: x, y, z) by considering the orientation of SF relative to GF at each time sample. The following paragraphs describe the required steps.
By starting the trials from a relatively motionless posture in water, the initial sacrum acceleration has a magnitude equal to the gravity. Using quaternion based algebra to represent the orientation, the initial quaternion which aligns the z axis to Z, is given by:
At each time step t, the orientation of SF relative to GF, is updated using the previous orientation by integrating the angular velocity [20]:
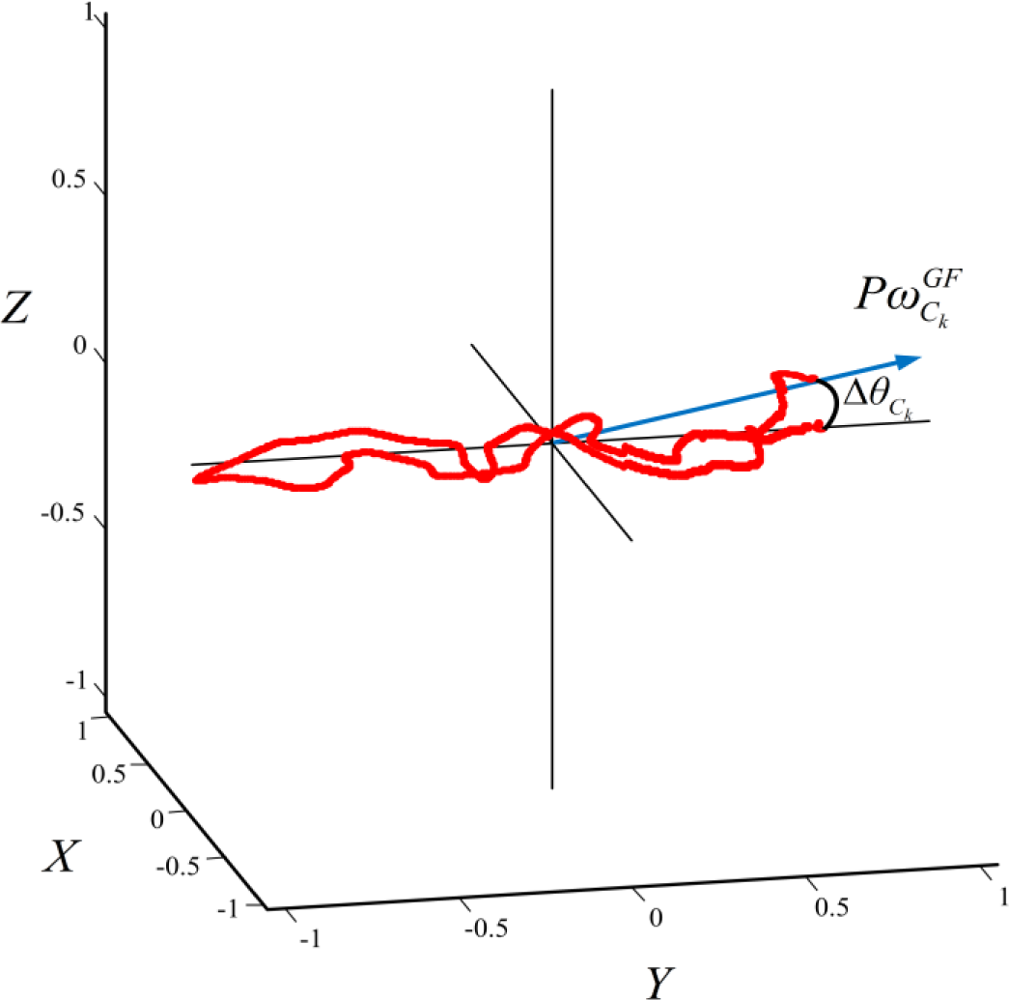
The time integration in Equation (4) suffers from an accumulative drift [17] due to gyroscopic noise. In order to reduce the effect of this drift we applied a dynamic biomechanical constraint, namely considering the swimmer sacrum rolls in average about forward direction Y. Therefore, for the data samples from cycle k to k + 1 (denoted by Ck and Ck+1 respectively), the principal component of angular velocity in GF (represented by ) should be aligned to Y. This can be mathematically written as:
Any deviation from the conditions of Equation (5) was assumed to be the effect of the orientation drift. Figure 2 shows the deviation of one cycle from this condition. The amplitude of the drifted angle is given by Equation (6):
Accordingly the rotation axis is presented as in Equation (7):
So if we suppose that the drift is linearly increased through one cycle with n data points, for the tth sample we can compute the corrective quaternion as in Equation (8):
Therefore, the corrected orientation of SF relative to GF, can be calculated from Equation (9):
The instantaneous forward acceleration in global frame can be calculated according to Equation (10), where g⃗ shows the gravity vector:
2.4. Instantaneous and Cycle Velocity Estimation
The instantaneous velocity Vt can be obtained by trapezoidal integration of . Nevertheless, this operation is not drift-free and results in a slow gradual trend in the cycle mean velocity V̄Ck. This velocity drift should be discriminated from the actual change originating from body action which accompanies a change in acceleration amplitude. Therefore, the forward acceleration is divided into segments where the range of acceleration remains within the same interval. Subsequently, at each segment we filter out the velocity drift.
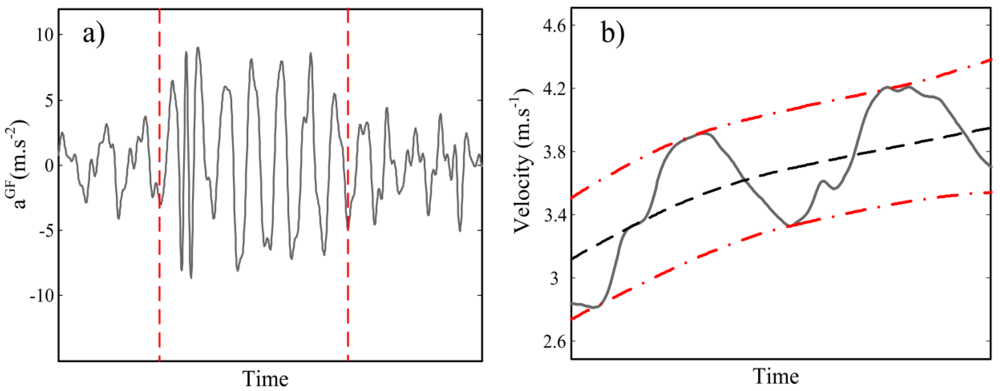
We used the geometric moving average (GMA) change detection algorithm [21] for segmentation. The algorithm is based on recursive estimation of signal variance and detecting if the variance change exceeds a predefined threshold. The threshold was selected empirically as 20% of the variance. Much smaller thresholds end up to detection of spurious signal segments while higher thresholds cannot recognize any changes of swimming regime. Figure 3(a) illustrates the result of this segmentation.
For velocity drift removal, we assumed the average trend of Vt peaks within each segment is quasi-constant due to the steady regime of swimming. Therefore, at each segment, cycle minimum and maximum peaks of Vt were extracted and a shape preserving spline [22] was fitted to these peaks [23].
De-trending was done by subtracting the average of upper and lower trend curves from the original velocity curve. Figure 3(b) depicts the extraction of the trend pattern. The instantaneous velocity curve then will be corrected for trial mean velocity by assuming that the average velocity of the trial is known from length of the pool and the duration of each trial. Finally, V̄Ck was estimated as the mean value of Vt for each cycle Ck. The algorithm development phase was completed by using the data of only 10 swimmers and then our algorithm was applied to the entire data set (30 swimmers).
2.5. Statistical Analysis
A twofold validation of the proposed velocity estimation method is presented in this section. In the first step, we provided the statistics to assess the cycle mean velocity estimated using our system . To this end, the mean (accuracy) and standard deviation (precision) of the difference between measured by SpeedRT system and obtained from IMU, , was calculated for different trials of each subject. Spearman's rank correlation was also used to verify the association between the two systems. Agreement between the two systems in V̄Ck measurement was assessed by use of Bland-Altman plot [24] and normalized pairwise variability index (nPVI) [25] as calculated by Equation (11):
In the second step we investigated the efficiency of our method in measuring the instantaneous velocity. The root mean squared (RMS), maximum and corresponding relative error of instantaneous velocity was calculated. As these calculations require similar time sampling of proposed and reference systems, the instantaneous velocity curve calculated by our method was downsampled to 100 Hz prior to error calculations. Besides, an indirect measure of accuracy of our system in instantaneous velocity measurement was provided by assessment of intra-cyclic velocity variation (IVV). In fact, the concurrent validity of our method was assessed by investigating IVV of the two groups of swimmers (Elite and Recreational), estimated by the two systems. IVV is computed as in Equation (12):
3. Results and Discussion
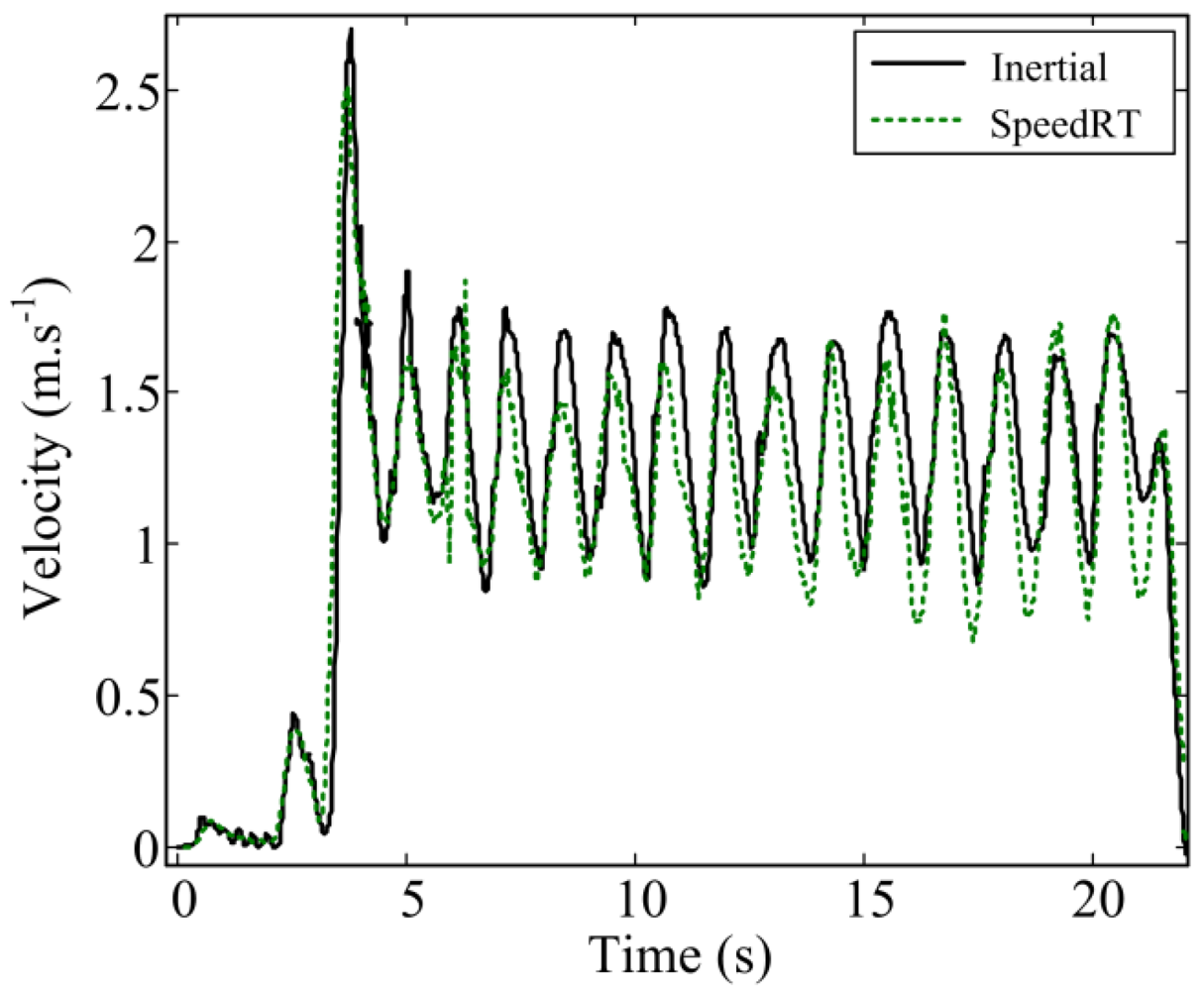
We have proposed a new wearable system and dedicated algorithms to measure front crawl velocity and described its validation procedure against a reference tethered device. Figure 4 illustrates a typical result of the instantaneous velocity obtained with our method and the reference system. A total number of N = 1,448 cycles were compared between the two systems.
A significant correlation was observed between the two systems (Spearman's rho = 0.94, p < 0.001) in V̄Ck assessment. The and the differed by 0.6 cm·s−1 and the precision was 5.4 cm·s−1 range [0.91, 1.95] cm.s−1). Table 2 summarizes the V̄Ck comparison between the two systems for all four different ranges of mean velocity (as measured by the reference and IMU). The results demonstrate that the proposed system is capable of measuring front-crawl velocity with acceptable accuracy (below 1.1 cm·s−1) and precision (below 5.8 cm·s−1) suggesting that our method can be reliably used for cycle mean velocity measurements. This accurate estimation of stroke cycle velocity was possible thanks to: (i) sensor orientation drift removal in GF using the principal component of swimming kinematics; (ii) velocity drift removal by introducing an appropriate segmentation of forward acceleration and by a spline shape modeling of the drift at each segment after integration of acceleration.
The two systems differed by 3.5% in assessment of V̄Ck variations as presented by nPVI in Table 2. The nPVI values in Table 2 shows that the difference in variability assessment of V̄Ck between the two systems in four ranges of velocity is less than 3.9%. This result as well as high V̄Ck correlation between the two systems confirms that our method detects the V̄Ck changes similar to the reference and supports the validity of our estimation.
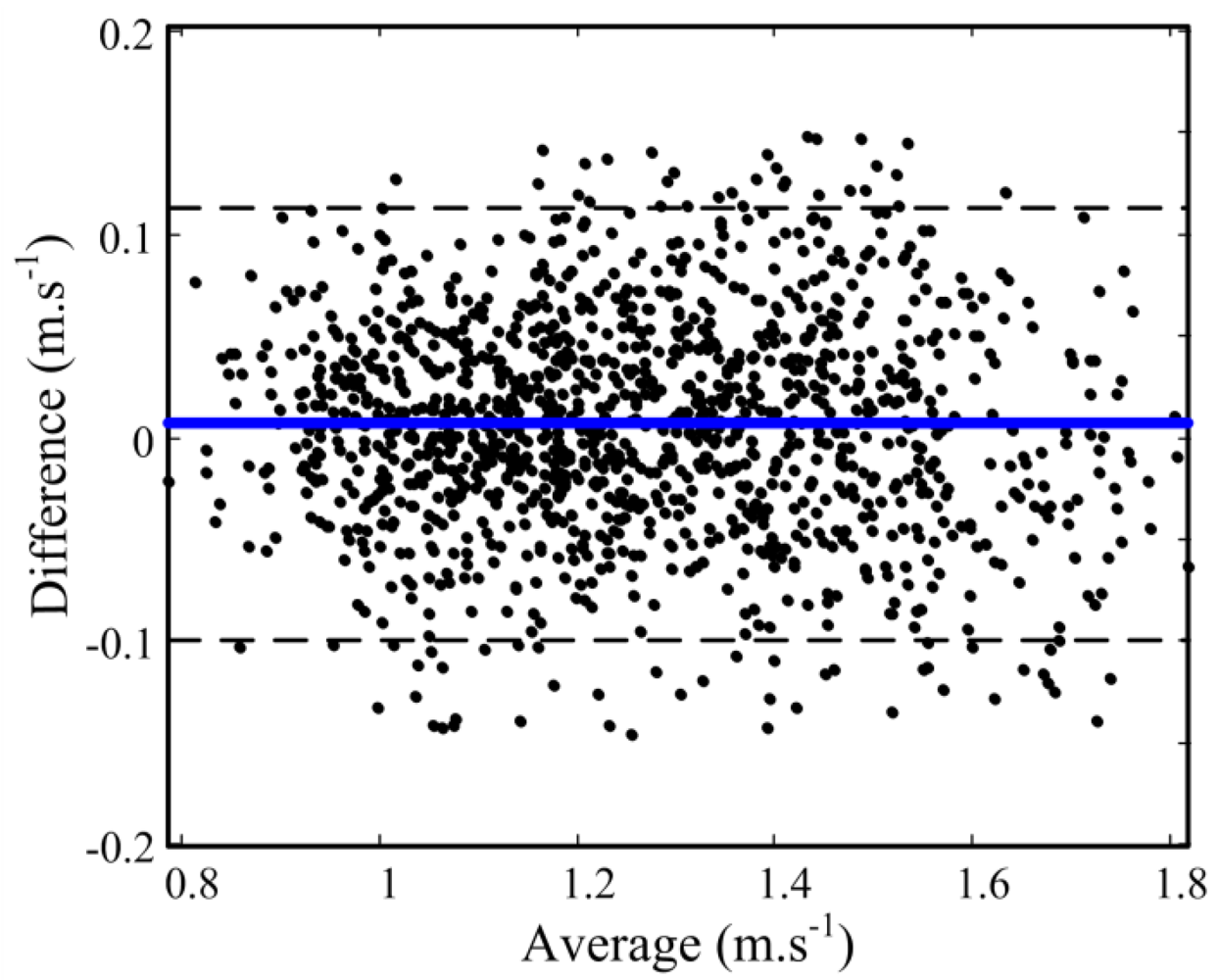
The Bland–Altman plot showed the 95% limits of agreement lower than 10.8 cm·s−1 between the two systems in V̄Ck assessment as depicted in Figure 5, where no significant difference and no heteroscedasticity (correlation = 0.03) were found. This finding, implies uniform performance of the method throughout the studied range of V̄Ck. It is noteworthy that by using the prior information about pool length to correct the velocity profile an error of 10.4 ± 39.7 cm is observed in estimating the sacrum's displacement. This error was expected since the sacrum does not necessarily travel a complete length of the swimming pool.
As regards validation of instantaneous velocity, an RMS difference of 11.3 cm·s−1 was observed that is comparable to the precision of the reference system. The maximum instantaneous error was 18.2 cm·s−1 that corresponds to a relative error of 9.7%. One source of the difference between the velocity estimated by our method and the velocity measured by the reference is a small artifact due to the non-rigidness of the swimming suit. Nevertheless, the custom designed swimming suit used to fix the sensor did not allow the sensor to move drastically and kept the artifact within a tolerable range. Moreover, during high accelerations when the artifact is more pronounced, the random bias of accelerometer is less significant (higher signal to noise ratio) which leads to acceptable results [28].
Indirect validation of instantaneous velocity by IVV in Table 3 through four different velocity ranges and the two different groups of participants, suggests that the IMU can be used for the study of instantaneous velocity variations. Indeed, our system, in accordance with the reference, showed a significant difference (p < 0.01, p < 0.001) to discriminate elite and recreational group based on IVV values (in different ranges of velocity). The reference showed an IVV change from 13.7% to 17.5% for the elite group and from 19.6% to 23.3% for the recreational group. Our method in accordance with the reference, showed significantly lower IVV values for elite swimmers (Table 3) that is consistent with previous studies [7,29].
Another observation from Table 3 is that the IMU tends to underestimate the IVV as presented by positive error values. However, the ANOVA shows that the small systematic difference between the two systems is not affected by group factor (p > 0.3). In a nutshell, using IMU the same systematic error can be seen for different groups of swimmers and can be compensated.
The ability of the inertial sensor to distinguish the variability of the movement of the subjects with different performance levels propounds the application of the inertial system in the study of swimming velocity. The capacity of our system to detect IVV changes also provides important evidence that our velocity drift removal method does not cancel out the velocity variations. Indeed, different swimming trial regimes were recognized based on changes of acceleration magnitude. These regimes are treated separately to mitigate the effect of the velocity drift and thereof variation of velocity signal was well maintained.
Signal segmentation using GMA is the core of drift removal in our method. Therefore, investigating the effect of changing the segmentation threshold in GMA can be illustrative of the method's robustness. To this end, the threshold in the GMA algorithm was shifted 5%. The effect of this change on the estimation is shown in Table 4. It can be seen that a decrement of 5% in the threshold led to a bigger error in the estimated velocity than equal increment. The small threshold caused many spurious segments on the signal which resulted in excessive localized correction on the velocity pattern; on the contrary, since during 25 m laps the actual acceleration profile of the swimmers does not change frequently, the higher threshold did not notably cut down on the algorithm performance.
Our dataset includes only one type of initial condition (swimming starts from a relatively motionless posture in water followed by a wall push) that is a subset of possible initial conditions in swimming. However, the study of other initial condition was not feasible within the scope of our experiment for practical reasons. Since the tethered reference only measures the velocity in forward direction of swimming, comparison of the multi lap data with turns between the IMU and the tethered device was not realizable. Although diving from the start block was a possibility, we avoided it for two practical considerations. Firstly, during the diving period calculation of the parallax effect on the velocity measured by the tethered reference is not possible. Secondly, avoiding the dives we could collect more stroke cycles which augments the statistical power of our study.
The algorithm we proposed in this paper, despite providing timely results, should not be misinterpreted as being real time. The data stream of one complete lap serves as the input of our algorithm since the correction is performed per lap. For a near real-time implementation of our method a crucial step is to determine the cycle mean velocity without using prior information about pool length.
4. Conclusions
The proposed method presents a reliable IMU-based system that can be practically used to measure the swimming velocity as the most intuitive metric of the athlete's performance. The system is user-centric meaning that several athletes can wear their own sensor at a time without interfering with the other athletes' measurements. Development of such a tool can help coaches pinpoint the strengths and weaknesses of the athletes during workout sessions and design an optimal personal training plan for athletes to improve their performance.
Accurate measurement of swimming velocity allowed the assessment of intra-cycle variability, an important determinant of swimming efficiency. Analysis of swimming velocity along with other parameters such as coordination [11] and energy expenditure can shed a new light on the biomechanics of locomotion in water. Further studies towards developing signal processing techniques for accurate assessment of velocity in the other swimming strokes are required. Estimation of cycle mean velocity independent of pool length information is also an interesting open problem in the future perspective of the study.
Acknowledgments
The authors wish to thank Arash Salarian for his technical advice. The work was supported by Swiss National Science Foundation (SNSF), grant No. 320030-127554.
References
- Puel, F.; Morlier, J.; Avalos, M.; Mesnard, M.; Cid, M.; Hellard, P. 3D kinematic and dynamic analysis of the front crawl tumble turn in elite male swimmers. J. Biomech. 2012, 45, 510–515. [Google Scholar]
- Vezos, N.; Gourgoulis, V.; Aggeloussis, N.; Kasimatis, P.; Christoforidis, C.; Mavromatis, G. Underwater stroke kinematics during breathing and breath-holding front crawl swimming. J. Sport Sci. Med. 2007, 6, 58–62. [Google Scholar]
- Callaway, A.J.; Cobb, J.E.; Jones, I. A comparison of video and accelerometer based approaches applied to performance monitoring in swimming. Int. J. Sports Sci. Coach. 2009, 4, 139–153. [Google Scholar]
- Ceseracciu, E.; Sawacha, Z.; Fantozzi, S.; Cortesi, M.; Gatta, G.; Corazza, S.; Cobelli, C. Markerless analysis of front crawl swimming. J. Biomech. 2011, 44, 2236–2242. [Google Scholar]
- Plaenkers, R.; Fua, P. Model-Based Silhouette Extraction for Accurate People Tracking. Proceedings of European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 325–339.
- Craig, A.B.; Termin, B.; Pendergast, D.R. Simultaneous recordings of velocity and video during swimming. Port. J. Sport Sci. 2006, 6, 32–35. [Google Scholar]
- Schnitzler, C.; Seifert, L.; Alberty, M.; Chollet, D. Hip velocity and arm coordination in front crawl swimming. Int. J. Sports Med. 2010, 31, 875–881. [Google Scholar]
- Justham, L.; Slawson, S.; West, A.; Conway, P.; Caine, M.; Harrison, R. Enabling Technologies for Robust Performance Monitoring (P10). Eng. Sport 2008, 7, 45–54. [Google Scholar]
- Yang, S.; Li, Q. Inertial sensor-based methods in walking speed estimation: A systematic review. Sensors 2012, 12, 6102–6116. [Google Scholar]
- Marsland, F.; Lyons, K.; Anson, J.; Waddington, G.; Macintosh, C.; Chapman, D. Identification of cross-country skiing movement patterns using micro-sensors. Sensors 2012, 12, 5047–5066. [Google Scholar]
- Dadashi, F.; Crettenand, F.; Millet, G.; Seifert, L.; Komar, J.; Aminian, K. Front Crawl Propulsive Phase Detection Using Inertial Sensors. Port. J. Sport Sci. 2011, 11, 855–858. [Google Scholar]
- Ayrulu-Erdem, B.; Barshan, B. Leg motion classification with artificial neural networks using wavelet-based features of gyroscope signals. Sensors 2011, 11, 1721–1743. [Google Scholar]
- Ohgi, Y. Microcomputer-based Acceleration Sensor Device for Sports Biomechanics—Stroke Evaluation by using Swimmers Wrist Acceleration. Sensors 2002, 1, 699–704. [Google Scholar]
- Davey, N.; Anderson, M.; James, D.A. Validation trial of an accelerometer-based sensor platform for swimming. Sports Technol. 2008, 1, 202–207. [Google Scholar]
- Le Sage, T.; Bindel, A.; Conway, P.P.; Justham, L.M.; Slawson, S.E.; West, A.A. Embedded programming and real-time signal processing of swimming strokes. Sports Eng. 2011, 14, 1–14. [Google Scholar]
- Stamm, A.; Thiel, D.V.; Burkett, B.; James, D.A. Towards Determining Absolute Velocity of Freestyle Swimming Using 3-Axis Accelerometers. Proceedings of the 5th Asia-Pacific Congress on Sports Technology, Melbourne, Australia, 28–31 August 2011; 13, pp. 120–125.
- Titterton, D.H.; Weston, J.L. Strapdown Inertial Navigation Technology; Peter Peregrinus Ltd.: London, UK, 2004. [Google Scholar]
- Ferraris, F.; Grimaldi, U.; Parvis, M. Procedure for effortless in-field calibration of three-axis rate gyros and accelerometers. Sens. Mater. 1995, 7, 311–330. [Google Scholar]
- Tella, V.; Toca-Herrera, J.L.; Gallach, J.E.; Benavent, J.; González, L.M.; Arellano, R. Effect of fatigue on the intra-cycle acceleration in front crawl swimming: A time-frequency analysis. J. Biomech. 2008, 41, 86–92. [Google Scholar]
- Bortz, J.E. New mathematical formulation for strapdown inertial navigation. IEEE Trans. Aerosp. Electr. Syst. 1971, AES-7, 61–66. [Google Scholar]
- Basseville, M.; Nikiforov, I.V. Detection of Abrupt Changes: Theory and Application; Prentice Hall Englewood Cliffs: New York, NY, USA, 1993. [Google Scholar]
- Fritsch, F.N.; Carlson, R.E. Monotone piecewise cubic interpolation. SIAM J. Numer. Anal. 1980, 238–246. [Google Scholar]
- Mariani, B.; Hoskovec, C.; Rochat, S.; Büla, C.; Penders, J.; Aminian, K. 3D gait assessment in young and elderly subjects using foot-worn inertial sensors. J. Biomech. 2010, 43, 2999–3006. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 1, 307–310. [Google Scholar]
- Sandnes, F.E.; Jian, H.L. Pair-wise variability index: Evaluating the cognitive difficulty of using mobile text entry systems. Proceedings of Mobile Human-Computer Interaction–Mobile HCI 2004, Glasgow, UK, 13–16 September 2004; pp. 25–37.
- Atkinson, G.; Nevill, A.M. Statistical methods for assessing measurement error (reliability) in variables relevant to sports medicine. Sports Med. 1998, 26, 217–238. [Google Scholar]
- Barbosa, T.M.; Bragada, J.A.; Reis, V.M.; Marinho, D.A.; Carvalho, C.; Silva, A.J. Energetics and biomechanics as determining factors of swimming performance: Updating the state of the art. J. Sci. Med. Sport 2010, 13, 262–269. [Google Scholar]
- Pang, G.; Liu, H. Evaluation of a low-cost MEMS accelerometer for distance measurement. J. Intel. Robot. Syst.: Theory Appl. 2001, 30, 249–265. [Google Scholar]
- Seifert, L.; Toussaint, H.M.; Alberty, M.; Schnitzler, C.; Chollet, D. Arm coordination, power, and swim efficiency in national and regional front crawl swimmers. Hum. Mov. Sci. 2010, 29, 426–439. [Google Scholar]
| Group | Male | Female | Age (yrs) | Height (cm) | Weight (kg) | V100 (m/s) |
|---|---|---|---|---|---|---|
| Elite | 6 | 5 | 20.3 ± 3.3 | 177.8 ± 9.6 | 69.2 ± 10.5 | 1.68 ± 0.17 |
| Recreational | 12 | 7 | 15.5 ± 2.8 | 171.3 ± 11.5 | 60.2 ± 12.2 | 1.34 ± 0.27 |
| Number of Cycles | Measured Mean Velocity | Evaluation of V̄Ck | |||
|---|---|---|---|---|---|
| Reference (m·s−1) | IMU (m·s−1) | Error (cm·s−1) | nPVI (%) | ||
| Trial1 | 333 | 1.1 ± 0.1 | 1.1 ± 0.1 | 0.8 ± 5.2 | 3.9 |
| Trial2 | 347 | 1.2 ± 0.1 | 1.2 ± 0.1 | 1.1 ± 5.4 | 3.6 |
| Trial3 | 370 | 1.4 ± 0.2 | 1.4 ± 0.2 | 0.7 ± 4.9 | 3.1 |
| Trial4 | 398 | 1.6 ± 0.2 | 1.6 ± 0.2 | −0.1 ± 5.8 | 3.4 |
| Total | 1448 | 1.4 ± 0.2 | 1.4 ± 0.2 | 0.6 ± 5.4 | 3.5 |
| Group | Number of Cycles | Reference (%) | Inertial (%) | IVV Error (%) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Accuracy | Precision | |||
| Trial1 | Elite | 109 | 14.4 a | 3.9 | 11.8 a | 3.7 | 2.6 * | 1.7 |
| Recreational | 224 | 19.7 a | 6.2 | 17.8 a | 7.1 | 1.8 | 4.5 | |
| Trial2 | Elite | 111 | 17.5 b | 2.7 | 12.3 b | 4.2 | 5.1 * | 2.3 |
| Recreational | 236 | 23.3 b | 4.6 | 20.6 b | 4.9 | 2.7 * | 3.5 | |
| Trial3 | Elite | 117 | 17.2 | 3.7 | 12.7 | 4.6 | 4.6 * | 3.1 |
| Recreational | 253 | 20.6 | 3.6 | 18.5 | 5.1 | 2.0 | 3.8 | |
| Trial4 | Elite | 120 | 13.7 b | 5.6 | 9.7 b | 6.6 | 4.1 * | 2.1 |
| Recreational | 278 | 19.6 b | 3.4 | 15.4 b | 6.2 | 4.2 * | 4.0 | |
| GMA Threshold | Velocity Estimation Error (cm·s−1) | |
|---|---|---|
| Cycle Mean (V̄Ck) | Instantaneous | |
| 0.15 | 0.3 ± 8.2 | 16.8 |
| 0.25 | 0.5 ± 6.8 | 12.9 |
Correction
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dadashi, F.; Crettenand, F.; Millet, G.P.; Aminian, K. Front-Crawl Instantaneous Velocity Estimation Using a Wearable Inertial Measurement Unit. Sensors 2012, 12, 12927-12939. https://doi.org/10.3390/s121012927
Dadashi F, Crettenand F, Millet GP, Aminian K. Front-Crawl Instantaneous Velocity Estimation Using a Wearable Inertial Measurement Unit. Sensors. 2012; 12(10):12927-12939. https://doi.org/10.3390/s121012927
Chicago/Turabian StyleDadashi, Farzin, Florent Crettenand, Grégoire P. Millet, and Kamiar Aminian. 2012. "Front-Crawl Instantaneous Velocity Estimation Using a Wearable Inertial Measurement Unit" Sensors 12, no. 10: 12927-12939. https://doi.org/10.3390/s121012927
APA StyleDadashi, F., Crettenand, F., Millet, G. P., & Aminian, K. (2012). Front-Crawl Instantaneous Velocity Estimation Using a Wearable Inertial Measurement Unit. Sensors, 12(10), 12927-12939. https://doi.org/10.3390/s121012927






