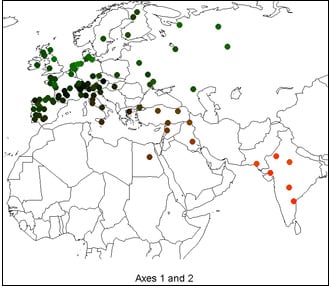
Spatial Trends of Genetic Variation of Domestic Ruminants in Europe
Abstract
:1. Introduction
2. Material and Methods
2.1. Spatial “Principal Components Analysis” (sPCA)
2.2. Spatial Analysis on metric Multidimensional Scaling (Principal Coordinates Analysis)
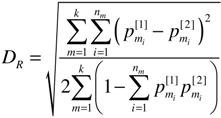
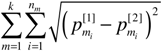 , is the canonical Euclidean distance, we use DR instead of DR2, for MDS analysis.
, is the canonical Euclidean distance, we use DR instead of DR2, for MDS analysis. 2.3. Data Sets
3. Results and Discussion
3.1. Comparison of Methods of Analyses
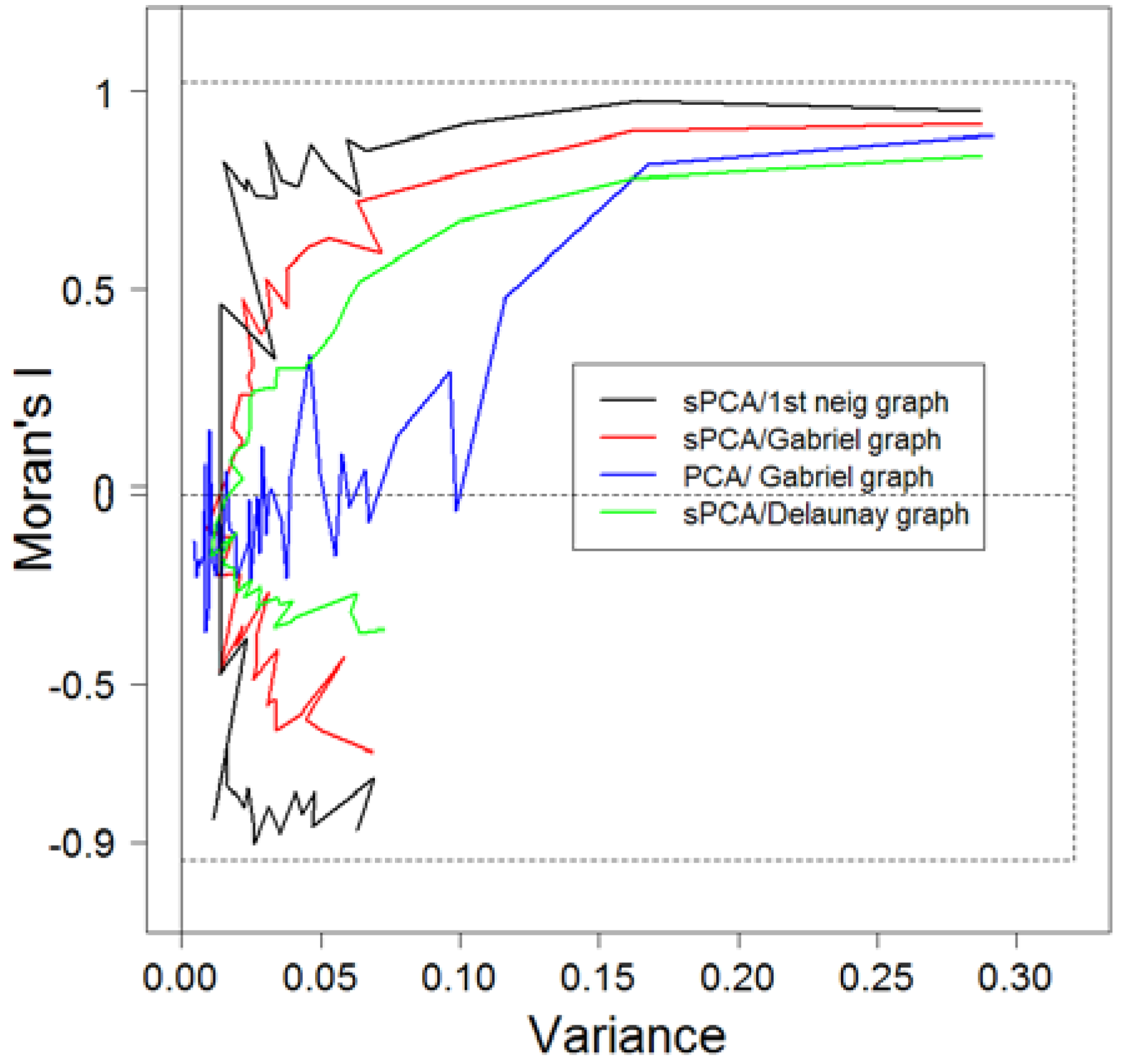
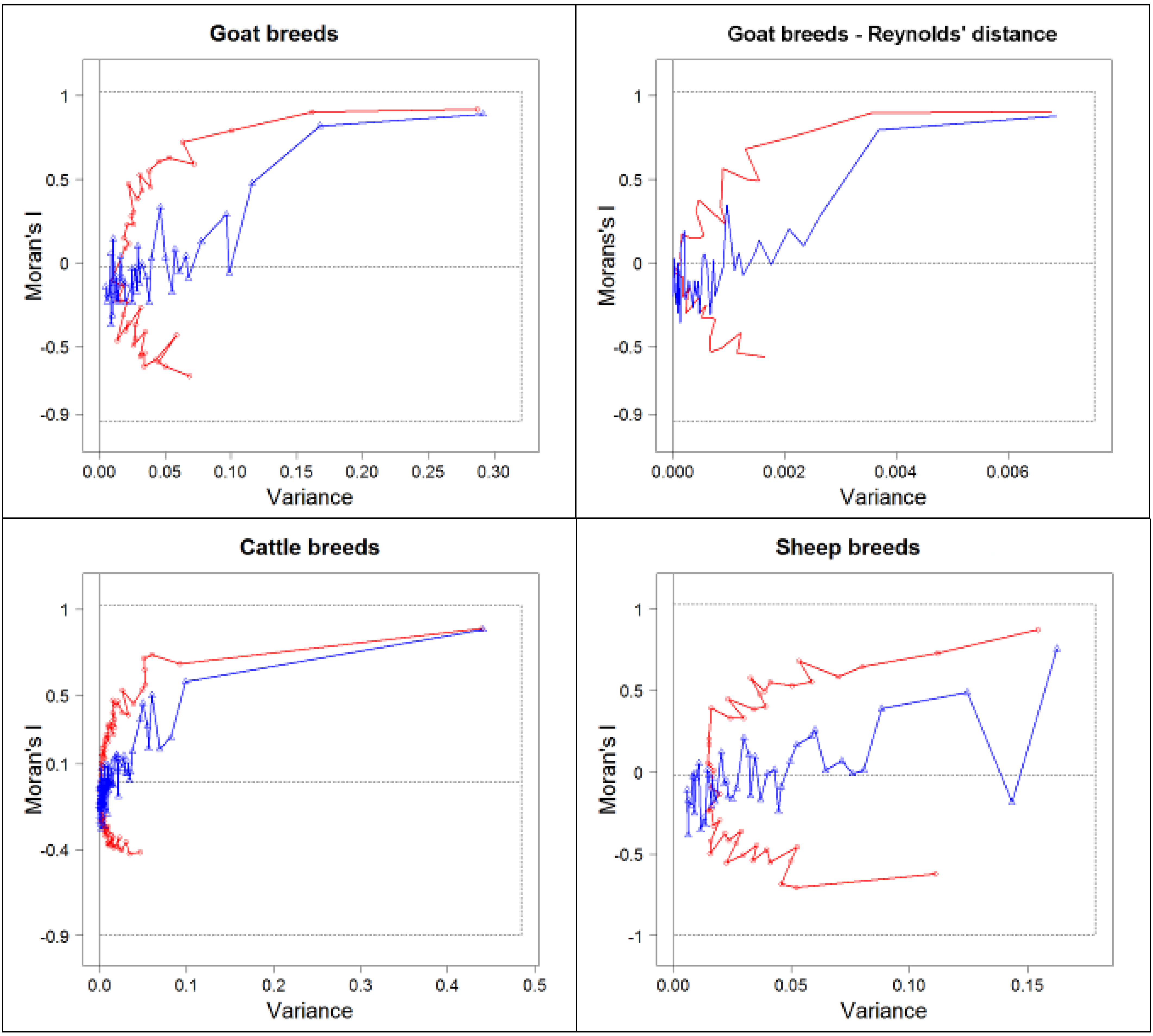
3.2. sPCA of Goat Allele Frequencies
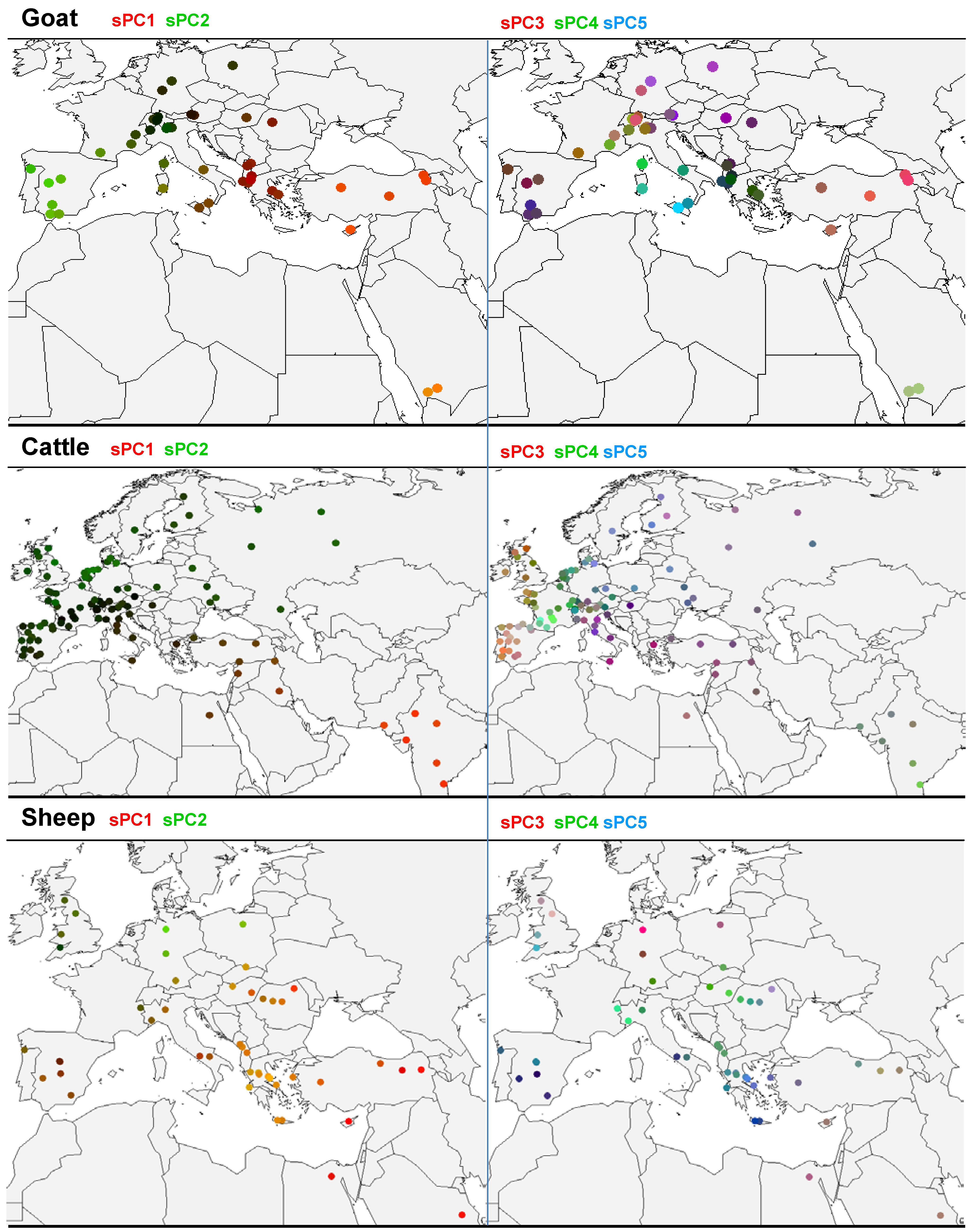
3.3. sPCA of Cattle Allelic Frequencies
3.4. sPCA of Sheep Allelic Frequencies
4. Conclusion
Supplementary Files
Supplementary File 1Acknowledgements
References
- Novembre, J.; Di Rienzo, A. Spatial patterns of variation due to natural selection in humans. Nat. Rev. Genet. 2009, 10, 745–755. [Google Scholar] [CrossRef] [PubMed]
- Diniz-Filho, J.A.F.; Nabout, J.C.; Telles, M.P.d.C.; Soares, T.N.; Rangel, T.F.L.V.B. A review of techniques for spatial modeling in geographical, conservation and landscape genetics. Genet. Mol. Biol. 2009, 32, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Manel, S.; Schwartz, M.K.; Luikart, G.; Taberlet, P. Landscape genetics: combining landscape ecology and population genetics. Trends Ecol. Evol. 2003, 18, 189–197. [Google Scholar] [CrossRef]
- Sokal, R.R.; Wartenberg, D.E. A test of spatial autocorrelation analysis using an isolation-by-distance model. Genetics 1983, 105, 219–237. [Google Scholar] [PubMed]
- Bertorelle, G.; Barbujani, G. Analysis of DNA diversity by spatial autocorrelation. Genetics 1995, 140, 811–819. [Google Scholar] [PubMed]
- Smouse, P.E.; Peakall, R. Spatial autocorrelation analysis of individual multiallele and multilocus genetic structure. Heredity 1999, 82, 561–573. [Google Scholar] [CrossRef] [PubMed]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Patterson, N.; Price, A.L.; Reich, D. Population structure and eigenanalysis. PLoS Genet. 2006, 2, 2074–2093. [Google Scholar] [CrossRef]
- Cavalli-Sforza, L.L. Population structure and human evolution. Proc. R. Soc. B 1966, 164, 362–379. [Google Scholar] [CrossRef]
- Hanotte, O.; Bradley, D.G.; Ochieng, J.W.; Verjee, Y.; Hill, E.W.; Rege, J.E.O. African pastoralism: Genetic imprints of origins and migrations. Science 2002, 296, 336–339. [Google Scholar] [CrossRef] [PubMed]
- Moazami-Goudarzi, K.; Laloe, D. Is a multivariate consensus representation of genetic relationships among populations always meaningful? Genetics 2002, 162, 473–484. [Google Scholar] [PubMed]
- Jombart, T.; Pontier, D.; Dufour, A.B. Genetic markers in the playground of multivariate analysis. Heredity 2009, 102, 330–341. [Google Scholar] [CrossRef] [PubMed]
- Novembre, J.; Johnson, T.; Bryc, K.; Kutalik, Z.; Boyko, A.R.; Auton, A.; Indap, A.; King, K.S.; Bergmann, S.; Nelson, M.R.; Stephens, M.; Bustamante, C.D. Genes mirror geography within Europe. Nature 2008, 456, 98–101. [Google Scholar] [CrossRef] [PubMed]
- Jombart, T.; Devillard, S.; Dufour, A.B.; Pontier, D. Revealing cryptic spatial patterns in genetic variability by a new multivariate method. Heredity 2008, 101, 92–103. [Google Scholar] [CrossRef] [PubMed]
- Thioulouse, J.; Chessel, D.; Champely, S. Multivariate analysis of spatial patterns: a unified approach to local and global structures. Environ. Ecol. Stat. 1995, 2, 1–14. [Google Scholar] [CrossRef]
- Wartenberg, D. Spatial autocorrelation as a criterion for retaining factors in ordinations of geographic data. Math. Geol. 1985, 17, 665–682. [Google Scholar] [CrossRef]
- Jombart, T. Adegenet: a R package for the multivariate analysis of genetic markers. Bioinformatics 2008, 24, 1403–1405. [Google Scholar] [CrossRef] [PubMed]
- Groeneveld, L.F.; Lenstra, J.A.; Eding, H.; Toro, M.A.; Scherf, B.; Pilling, D.; Negrini, R.; Finlay, E.K.; Jianlin, H.; Groeneveld, E.; Weigend, S. GLOBALDIV Consortium. Genetic diversity in farm animals - a review. Anim. Genet. 2010, 41, 6–31. [Google Scholar]
- Canon, J.; Garcia, D.; Garcia-Atance, M.A.; Obexer-Ruff, G.; Lenstra, J.A.; Ajmone-Marsan, P.; Dunner, S. ECONOGENE Consortium. Geographical partitioning of goat diversity in Europe and the Middle East. Anim. Genet. 2006, 37, 327–334. [Google Scholar]
- Lenstra, J.A. European Cattle Genetic Diversity Consortium. Marker-assisted conservation of European cattle breeds: an evaluation. Anim. Genet. 2006, 37, 475–481. [Google Scholar]
- Negrini, R.; Nijman, I.J.; Milanesi, E.; Moazami-Goudarzi, K.; Williams, J.L.; Erhardt, G.; Dunner, S.; Rodellar, C.; Valentini, A.; Bradley, D.G.; Olsaker, I.; Kantanen, J.; Ajmone-Marsan, P.; Lenstra, J.A. European Cattle Genetic Diversity Consortium. Differentiation of european cattle by AFLP fingerprinting. Anim. Genet. 2007, 38, 60–66. [Google Scholar]
- Peter, C.; Bruford, M.; Perez, T.; Dalamitra, S.; Hewitt, G.; Erhardt, G. ECONOGENE Consortium. Genetic diversity and subdivision of 57 European and Middle-Eastern sheep breeds. Anim. Genet. 2007, 38, 37–44. [Google Scholar]
- Legendre, P.; Legendre, L. Numerical Ecology, 2nd English ed.; Elsevier Science BV: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Piazza, A.; Menozzi, P.; Cavallisforza, L.L. Synthetic gene-frequency maps of man and selective effects of climate. Proc. Natl. Acad. Sci. USA. 1981, 78, 2638–2642. [Google Scholar] [CrossRef] [PubMed]
- Gower, J. Some distance properties of latent root and vector methods used in multivariate analysis. Biometrika 1966, 53, 325–338. [Google Scholar] [CrossRef]
- Gower, J.C.; Legendre, P. Metric and Euclidean properties of dissimilarity coefficients. J. Classif. 1986, 3, 5–48. [Google Scholar] [CrossRef]
- Lingoes, J. Some boundary conditions for a monotone analysis of symmetric matrices. Psychometrika 1971, 36, 195–203. [Google Scholar] [CrossRef]
- Cailliez, F. The analytic solution of the additive constant. Psychometrika 1983, 48, 305–310. [Google Scholar] [CrossRef]
- Baker, A.J.; Moeed, A. Rapid genetic differentiation and founder effect in colonizing populations of common mynas (acridotheres-tristis). Evolution 1987, 41, 525–538. [Google Scholar] [CrossRef]
- Zhivotovsky, L.A.; Rosenberg, N.A.; Feldman, M.W. Features of evolution and expansion of modern humans, inferred from genomewide microsatellite markers. Am. J. Hum. Genet. 2003, 72, 1171–1186. [Google Scholar] [CrossRef] [PubMed]
- Fullaondo, A.; Vicario, A.; Aguirre, A.; Barrena, I.; Salazar, A. Quantitative analysis of two-dimensional gel electrophoresis protein patterns: a method for studying genetic relationships among Globodera pallida populations. Heredity 2001, 87, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Reif, J.C.; Melchinger, A.E.; Frisch, M. Genetical and mathematical properties of similarity and dissimilarity coefficients applied in plant breeding and seed bank management. Crop Sci. 2005, 45, 1–7. [Google Scholar] [CrossRef]
- Reynolds, J.; Weir, B.S.; Cockerham, C.C. Estimation of the Coancestry Coefficient: Basis for a Short-Term Genetic Distance. Genetics 1983, 105, 767–779. [Google Scholar] [PubMed]
- Felsenstein, J. PHYLIP—Phylogeny Inference Package (Version 3.2). Cladistics 1989, 5, 164–166. [Google Scholar]
- Weir, B.S. Genetic Data Analysis; Sinauer Associates: Sunderland, MA, USA, 1990. [Google Scholar]
- Chessel, D.; Dufour, A.B.; Thioulouse, J. The ade4 package. I. One-table methods. R News 2004, 4, 5–10. [Google Scholar]
- Bivand, R. Implementing Spatial Data Analysis Software Tools in R. Geogr. Anal. 2006, 38, 23–40. [Google Scholar] [CrossRef]
- Loftus, R.T.; Ertugrul, O.; Harba, A.H.; El-Barody, M.A.A.; Machugh, D.E.; Park, S.D.E.; Bradley, D.G. A microsatellite survey of cattle from a center of origin: the Near East. Mol. Ecol. 1999, 8, 2015–2022. [Google Scholar] [CrossRef] [PubMed]
- Li, M.H.; Tapio, I.; Vilkki, J.; Ivanova, Z.; Kiselyova, T.; Marzanov, N.; Cinkulov, M.; Stojanovic, S.; Ammosov, I.; Popov, R.; Kantanen, J. The genetic structure of cattle populations (Bos taurus) in northern Eurasia and the neighboring Near Eastern regions: implications for breeding strategies and conservation. Mol. Ecol. 2007, 16, 3839–3853. [Google Scholar] [CrossRef] [PubMed]
- Luque, A.; Valera, M.; Azor, P.J.; Goyache, F.; Rodero, E.; Molina, A. La raza bovina autóctona española Pajuna: Situación actual y programa de recuperación. Anim. Genet. Resour. Inf. 2006, 39, 1–14. [Google Scholar] [CrossRef]
- Lenstra, J.A. ECONOGENE Consortium. Evolutionary and demographic history of sheep and goats suggested by nuclear, mtDNA and Y chromosome markers. In Proceedings of the International Workshop on the Role of Biotechnology for the Characterization and Conservation of Crop, Forestry, Animal and Fishery Genetic Resources, Torino, Italy, 5–7 March 2005; pp. 97–100.
- Pereira, F.; Queiros, S.; Gusmao, L.; Nijman, I.J.; Cuppen, E.; Lenstra, J.A.; Davis, S.J.M.; Nejmeddine, F.; Amorim, A. ECONOGENE Consortium. Tracing the History of Goat Pastoralism: New Clues from Mitochondrial and Y Chromosome DNA in North Africa. Mol. Biol. Evol. 2009, 26, 2765–2773. [Google Scholar]
- Luikart, G.; Gielly, L.; Excoffier, L.; Vigne, J.D.; Bouvet, J.; Taberlet, P. Multiple maternal origins and weak phylogeographic structure in domestic goats. Proc. Natl. Acad. Sci. USA 2001, 98, 5927–5932. [Google Scholar] [CrossRef] [PubMed]
- Naderi, S.; Rezaei, H.R.; Taberlet, P.; Zundel, S.; Rafat, S.A.; Naghash, H.R.; El-Barody, M.A.A.; Ertugrul, O.; Pompanon, F. Large-scale mitochondrial DNA analysis of the domestic goat reveals six haplogroups with high diversity. PLoS ONE 2007, 2, e1012. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Freeman, A.R.; Loftus, R.T.; Gaillard, C.; Fuller, D.Q.; Bradley, D.G. Admixture analysis of South Asian cattle. Heredity 2003, 91, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Payne, W.J.A.; Hodges, J. Tropical Cattle. Origins, Breeds and Breeding Policies; Blackwell Science: London, UK, 1997. [Google Scholar]
- Cymbron, T.; Freeman, A.R.; Malheiro, M.I.; Vigne, J.D.; Bradley, D.G. Microsatellite diversity suggests different histories for Mediterranean and Northern European cattle populations. Proc. R. Soc. B 2005, 272, 1837–1843. [Google Scholar] [CrossRef] [PubMed]
- Gotherstrom, A.; Anderung, C.; Hellborg, L.; Elburg, R.; Smith, C.; Bradley, D.G.; Ellegren, H. Cattle domestication in the Near East was followed by hybridization with aurochs bulls in Europe. Proc. R. Soc. B 2005, 272, 2345–2350. [Google Scholar] [CrossRef] [PubMed]
- Ibeagha-Awemu, E.M.; Jann, O.C.; Weimann, C.; Erhardt, G. Genetic diversity, introgression and relationships among West/Central African cattle breeds. Genet. Sel. Evol. 2004, 36, 673–690. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez-Gil, B.; Wiener, P.; Williams, J.L. Genetic effects on coat colour in cattle: dilution of eumelanin and phaeomelanin pigments in an F2-Backcross Charolais x Holstein population. BMC Genet. 2007, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Basarab, J.; Snelling, W.M.; Benkel, B.; Murdoch, B.; Hansen, C.; Moore, S.S. Assessment of positional candidate genes myf5 and igf1 for growth on bovine chromosome 5 in commercial lines of Bos taurus. J. Anim. Sci. 2004, 82, 1–7. [Google Scholar] [PubMed]
- Pariset, L.; Joost, S.; Marsan, P.A.; Valentini, A. Ec Landscape genomics and biased FST approaches reveal single nucleotide polymorphisms under selection in goat breeds of North-East Mediterranean. BMC Genet. 2009, 10, 7. [Google Scholar] [CrossRef] [PubMed]
- Manel, S.; Segelbacher, G. Perspectives and challenges in landscape genetics. Mol. Ecol. 2009, 18, 1821–1822. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Laloë, D.; Moazami-Goudarzi, K.; Lenstra, J.A.; Marsan, P.A.; Azor, P.; Baumung, R.; Bradley, D.G.; Bruford, M.W.; Cañón, J.; Dolf, G.; et al. Spatial Trends of Genetic Variation of Domestic Ruminants in Europe. Diversity 2010, 2, 932-945. https://doi.org/10.3390/d2060932
Laloë D, Moazami-Goudarzi K, Lenstra JA, Marsan PA, Azor P, Baumung R, Bradley DG, Bruford MW, Cañón J, Dolf G, et al. Spatial Trends of Genetic Variation of Domestic Ruminants in Europe. Diversity. 2010; 2(6):932-945. https://doi.org/10.3390/d2060932
Chicago/Turabian StyleLaloë, Denis, Katayoun Moazami-Goudarzi, Johannes A. Lenstra, Paolo Ajmone Marsan, Pedro Azor, Roswitha Baumung, Daniel G. Bradley, Michael W. Bruford, Javier Cañón, Gaudenz Dolf, and et al. 2010. "Spatial Trends of Genetic Variation of Domestic Ruminants in Europe" Diversity 2, no. 6: 932-945. https://doi.org/10.3390/d2060932
APA StyleLaloë, D., Moazami-Goudarzi, K., Lenstra, J. A., Marsan, P. A., Azor, P., Baumung, R., Bradley, D. G., Bruford, M. W., Cañón, J., Dolf, G., Dunner, S., Erhardt, G., Hewitt, G., Kantanen, J., Obexer-Ruff, G., Olsaker, I., Rodellar, C., Valentini, A., Wiener, P., & ECGDCEC. (2010). Spatial Trends of Genetic Variation of Domestic Ruminants in Europe. Diversity, 2(6), 932-945. https://doi.org/10.3390/d2060932