Machine Learning-Based Prediction of Rule Violations for Drug-Likeness Assessment in Peptide Molecules Using Random Forest Models
Abstract
1. Introduction
1.1. Drug-Likeness and the Evolution of Structural Filters for Oral Bioavailability
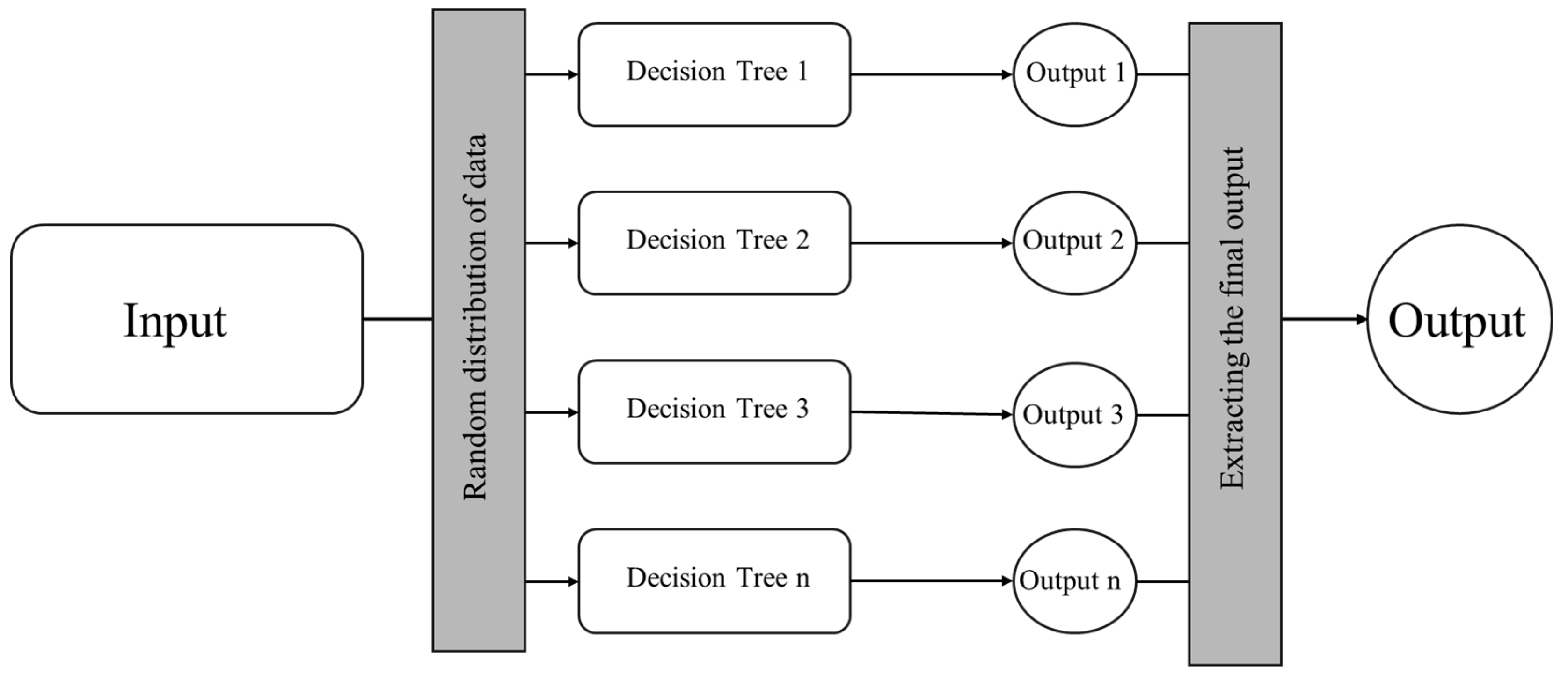
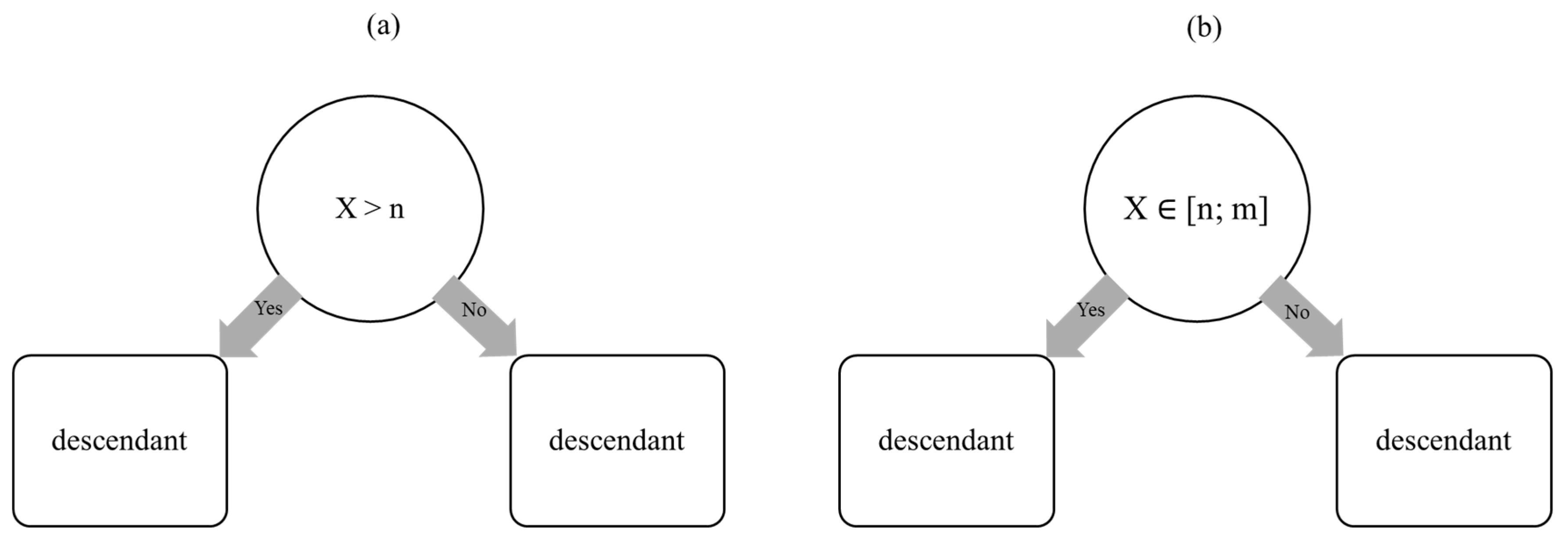
1.2. Random Forest Algorithm
2. Results
2.1. Metrics of the Created Models
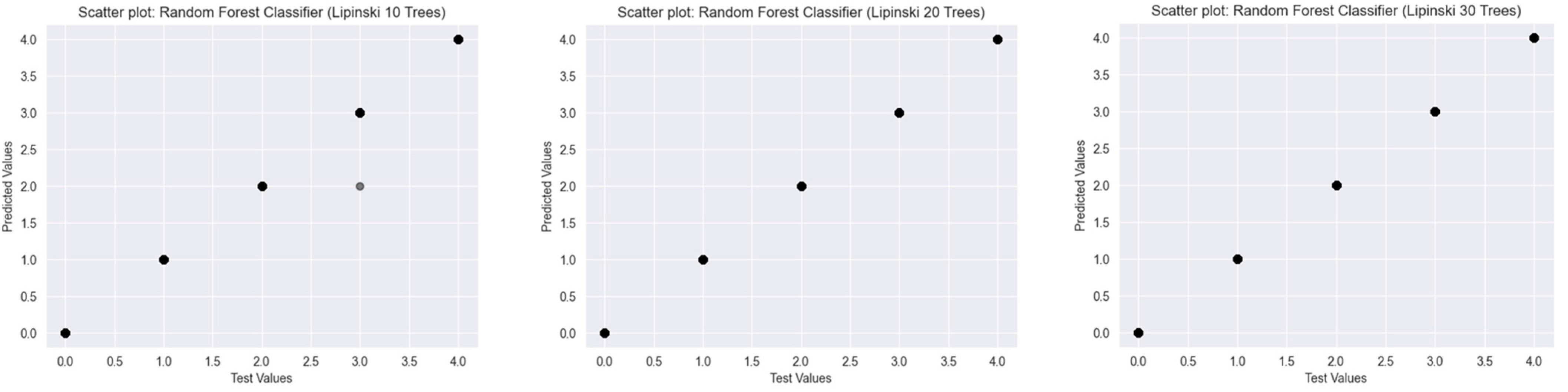
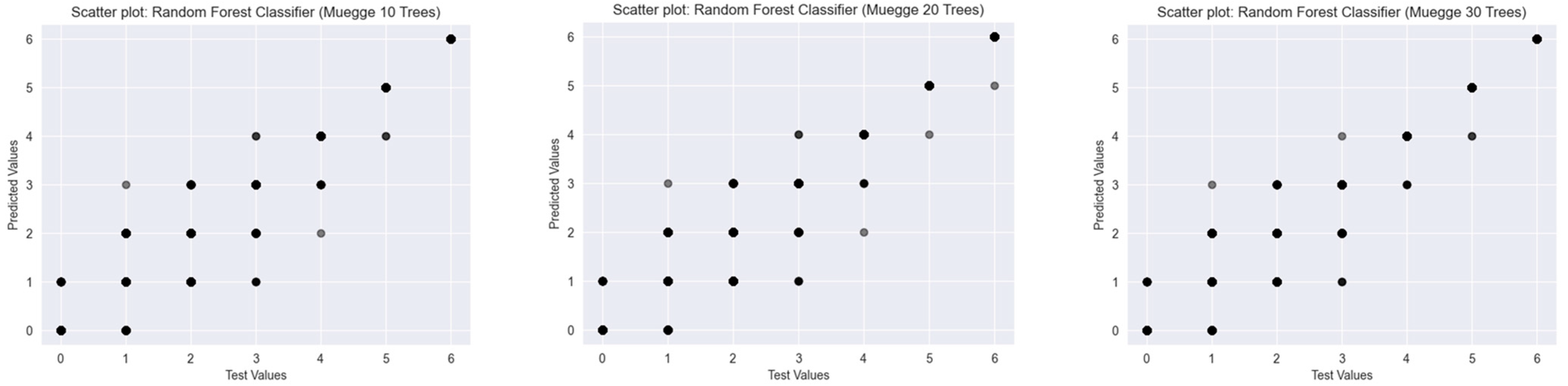
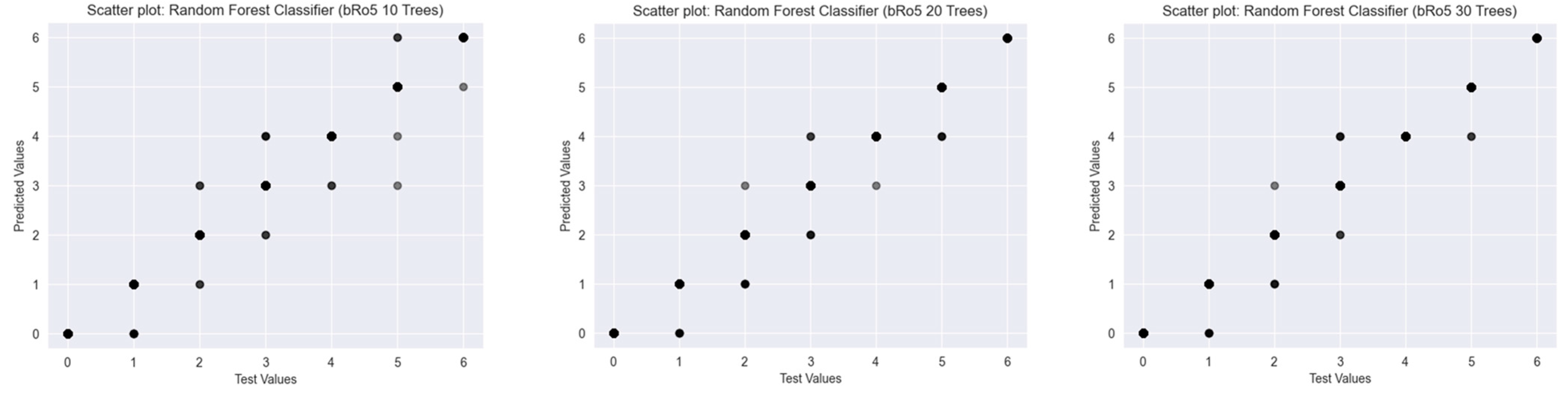
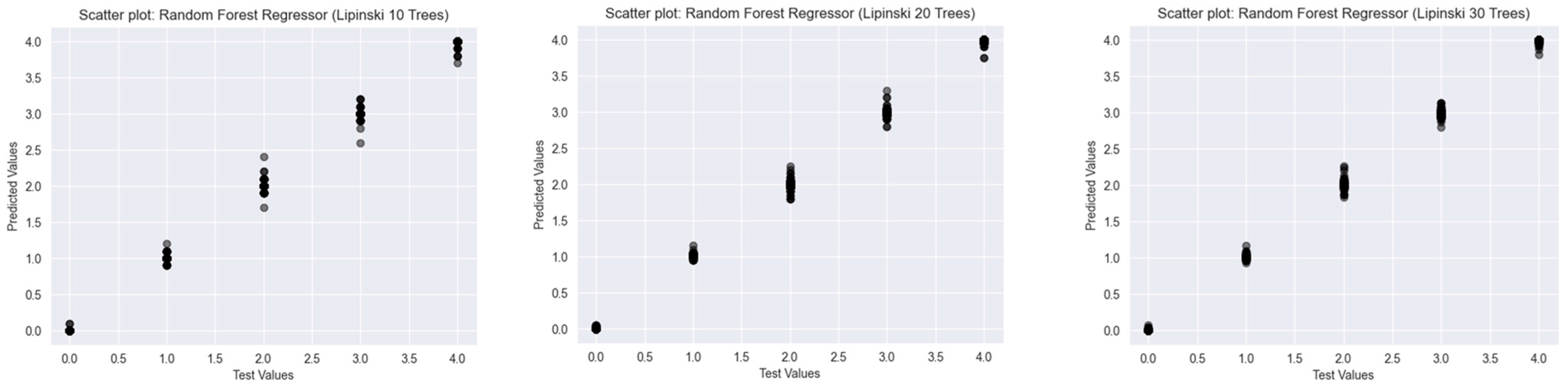
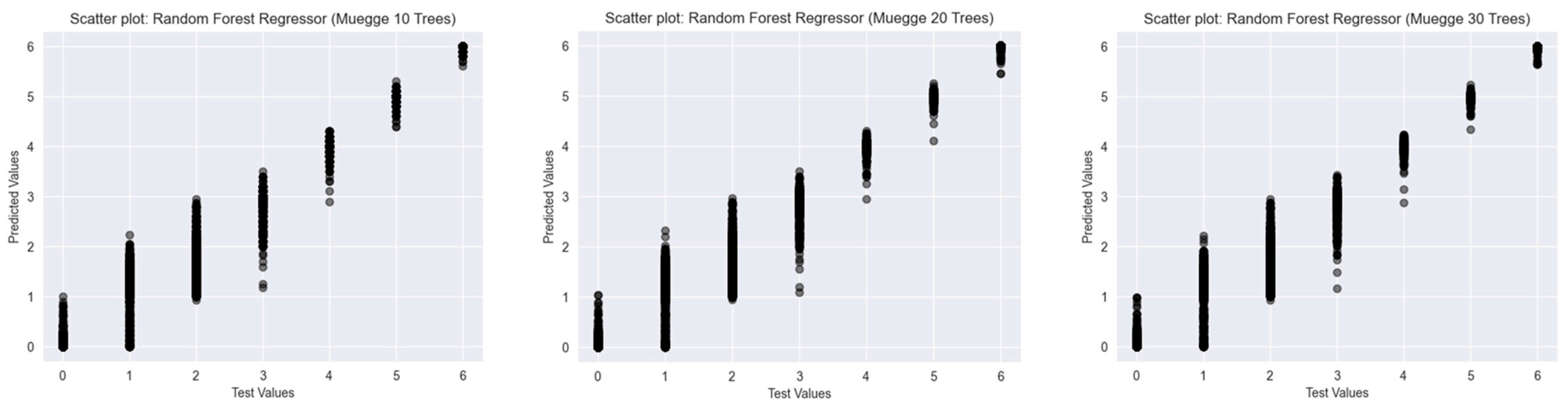
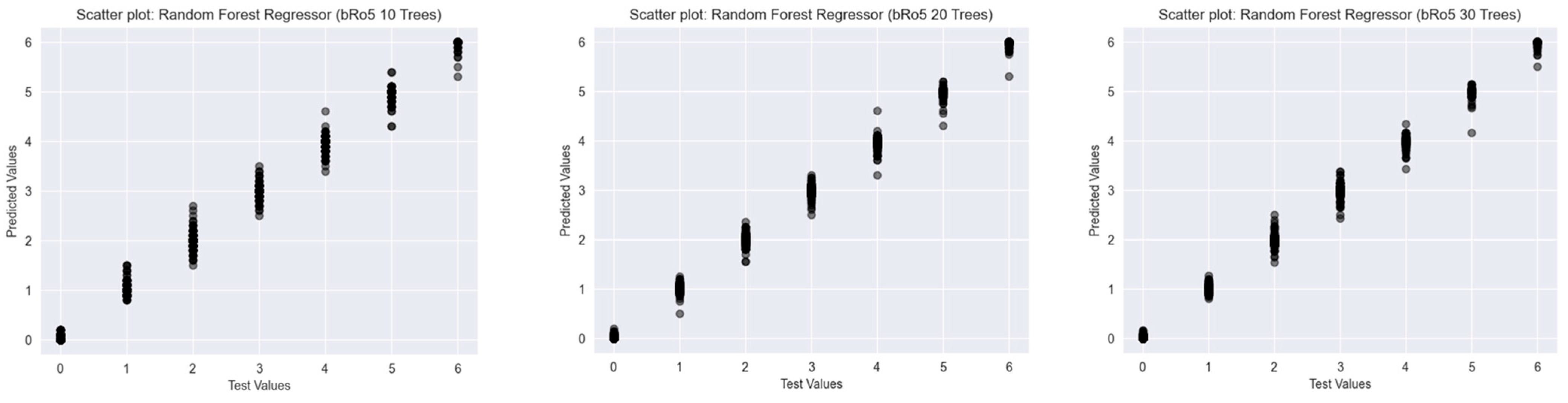
2.2. Results of the Predictions
2.2.1. Lipinski’s Rule of Five
2.2.2. Muegge’s Rule
2.2.3. Beyond Lipinski’s Rule of Five
2.2.4. Classifiers Working with Fingerprint Representations
3. Discussion
4. Materials and Methods
4.1. Software and Databases
4.2. Study Design
- (1)
- The models were trained using a dataset obtained from the PubChem database, which contains information on the chemical and physicochemical properties of drug and non-drug molecules.
- (2)
- The PubChem dataset (containing >300,000 drug (small and peptide) and non-drug molecules) was preprocessed to meet the objectives of the study. Only the following data were retained: molecule name, SMILES string, and values of molecular descriptors included in Lipinski’s rule (molecular weight, logP, number of hydrogen bond donors and acceptors), along with TPSA and rotatable bonds.
- (3)
- Three different counters were developed to quantify violations of Ro5, bRo5, and the criteria proposed by Muegge et al. [12] for the included molecules. The resulting values were added to a new dataset, which was subsequently used to train the ML models.
- (4)
- As the Random Forest Classifier is a supervised learning algorithm, the newly generated dataset was split into features (training data) and target values. The molecular descriptor values were used as input features, while the number of rule violations—calculated using the custom counters—served as target outputs. This dataset was further subdivided into training and evaluation sets to measure model performance, by train_test_split function which is included in scikit-learn. The parameters of splitting the data were test_size = 0.2 and random_state = 42. Data leakage prevented by applying strict train-validation-test separation prior to feature engineering, ensuring that all preprocessing steps were fitted only on the training data and applied to test data in a pipeline setting.
- (5)
- Following the data split, models were trained separately for each of the evaluated rules. Specifically, for Ro5, bRo5, and Muegge’s criteria, three models were created per rule using 10, 20, and 30 decision trees, respectively. We used grid search to help in optimising of hyper parameters values which was used. Especially tested hyper parameters was max_features = ‘sqrt’ or ‘log2’, min_samples_leaf = 1, min_samples_split = 2 or 5, but results yielded by default values of hyper parameters was better.
- (6)
- After training, model performance was evaluated using standard metrics to identify and potentially discard underperforming models.
- (7)
- To predict the number of rule violations for the studied peptide molecules, their molecular descriptor values first had to be determined. For this purpose, the RDKit library (https://www.rdkit.org, accessed on 5 June 2025) for Python 3.13 was used to calculate molecular descriptors from their SMILES strings. The resulting data were compiled into a test dataset containing descriptor values for all peptide candidates.
- (8)
- Once the models were trained and the test dataset constructed, predictions were made regarding violations of Ro5, bRo5, and Muegge’s rule for drug-likeness. The predicted values were then aggregated and compared with rule violation data obtained from two web-based platforms: SwissADME and Molinspiration. The SwissADME values were generated after model training, while the Molinspiration data were obtained in 2020.
- (9)
- For creating a models for comparison, we extract information about Morgan fingerprints from SMILES strings included in the training dataset. We combine them with the already calculated number of violations of each rule. After that we used again train_test_split function again, like in step 4.
- (10)
- Differentiated data were used for training of models (Random Forest Classifiers) with different numbers of estimators and evaluating their performance before predictions.
- (11)
- The next step was to obtain fingerprint representation of tested molecules and incorporating them in new dataset.
- (12)
- The final stage was the prediction of violations and comparing them with web-based platforms or manually calculated.
4.3. Evaluation of Created Classifier Models
4.4. Evaluation of Created Regressor Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lutz, M.W.; Menius, J.A.; Choi, T.D.; Gooding Laskody, R.; Domanico, P.L.; Goetz, A.S.; Saussy, D.L. Experimental Design for High-Throughput Screening. Drug Discov. Today 1996, 1, 277–286. [Google Scholar] [CrossRef]
- Gallop, M.A.; Barrett, R.W.; Dower, W.J.; Fodor, S.P.A.; Gordon, E.M. Applications of Combinatorial Technologies to Drug Discovery. 1. Background and Peptide Combinatorial Libraries. J. Med. Chem. 1994, 37, 1233–1251. [Google Scholar] [CrossRef]
- Gordon, E.M.; Barrett, R.W.; Dower, W.J.; Fodor, S.P.A.; Gallop, M.A. Applications of Combinatorial Technologies to Drug Discovery. 2. Combinatorial Organic Synthesis, Library Screening Strategies, and Future Directions. J. Med. Chem. 1994, 37, 1385–1401. [Google Scholar] [CrossRef] [PubMed]
- Martin, E.J.; Blaney, J.M.; Siani, M.A.; Spellmeyer, D.C.; Wong, A.K.; Moos, W.H. Measuring Diversity: Experimental Design of Combinatorial Libraries for Drug Discovery. J. Med. Chem. 1995, 38, 1431–1436. [Google Scholar] [CrossRef]
- Warr, W.A. Combinatorial Chemistry and Molecular Diversity. An Overview. J. Chem. Inf. Comput. Sci. 1997, 37, 134–140. [Google Scholar] [CrossRef]
- Brown, R.D.; Martin, Y.C. Designing Combinatorial Library Mixtures Using a Genetic Algorithm. J. Med. Chem. 1997, 40, 2304–2313. [Google Scholar] [CrossRef]
- Pötter, T.; Matter, H. Random or Rational Design? Evaluation of Diverse Compound Subsets from Chemical Structure Databases. J. Med. Chem. 1998, 41, 478–488. [Google Scholar] [CrossRef]
- Clark, D.E.; Pickett, S.D. Computational Methods for the Prediction of ‘Drug-Likeness’. Drug Discov. Today 2000, 5, 49–58. [Google Scholar] [CrossRef]
- Podlogar, B.L.; Muegge, I.; Brice, L.J. Computational Methods to Estimate Drug Development Parameters. Curr. Opin. Drug Discov. Dev. 2001, 4, 102–109. [Google Scholar] [PubMed]
- Lipinski, C.A.; Lombardo, F.; Dominy, B.W.; Feeney, P.J. Experimental and Computational Approaches to Estimate Solubility and Permeability in Drug Discovery and Development Settings. Adv. Drug Deliv. Rev. 2001, 46, 3–26. [Google Scholar] [CrossRef]
- Doak, B.C.; Over, B.; Giordanetto, F.; Kihlberg, J. Oral Druggable Space beyond the Rule of 5: Insights from Drugs and Clinical Candidates. Chem. Biol. 2014, 21, 1115–1142. [Google Scholar] [CrossRef]
- Muegge, I.; Heald, S.L.; Brittelli, D. Simple Selection Criteria for Drug-like Chemical Matter. J. Med. Chem. 2001, 44, 1841–1846. [Google Scholar] [CrossRef]
- Bemis, G.W.; Murcko, M.A. The Properties of Known Drugs. 1. Molecular Frameworks. J. Med. Chem. 1996, 39, 2887–2893. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhang, J. New Machine Learning Algorithm: Random Forest. In Information Computing and Applications; Liu, B., Ma, M., Chang, J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7473, pp. 246–252. ISBN 978-3-642-34061-1. [Google Scholar]
- Timofeev, R. Classification and Regression Trees (CART) Theory and Applications Theory and Applications. Master’s Thesis, Center of Applied Statistics and Economics Humboldt University, Berlin, Germany, 2004. [Google Scholar]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. ISBN 978-1-4419-9325-0. [Google Scholar]
- Salman, H.A.; Kalakech, A.; Steiti, A. Random Forest Algorithm Overview. Babylon. J. Mach. Learn. 2024, 2024, 69–79. [Google Scholar] [CrossRef]
- Nhlapho, S.; Nyathi, M.; Ngwenya, B.; Dube, T.; Telukdarie, A.; Munien, I.; Vermeulen, A.; Chude-Okonkwo, U. Druggability of Pharmaceutical Compounds Using Lipinski Rules with Machine Learning. Sci. Pharm. 2024, 3, 177–192. [Google Scholar] [CrossRef]
- Aqeel, I.; Majid, A. Hybrid Approach to Identify Druglikeness Leading Compounds against COVID-19 3CL Protease. Pharmaceuticals 2022, 15, 1333. [Google Scholar] [CrossRef]
- Mughal, H.; Wang, H.; Zimmerman, M.; Paradis, M.D.; Freundlich, J.S. Random Forest Model Prediction of Compound Oral Exposure in the Mouse. ACS Pharmacol. Transl. Sci. 2021, 4, 338–343. [Google Scholar] [CrossRef]
- Hu, Q.; Feng, M.; Lai, L.; Pei, J. Prediction of Drug-Likeness Using Deep Autoencoder Neural Networks. Front. Genet. 2018, 9, 585. [Google Scholar] [CrossRef] [PubMed]
- Abbas, K.; Abbasi, A.; Dong, S.; Niu, L.; Yu, L.; Chen, B.; Cai, S.-M.; Hasan, Q. Application of Network Link Prediction in Drug Discovery. BMC Bioinform. 2021, 22, 187. [Google Scholar] [CrossRef] [PubMed]
- Svetnik, V.; Liaw, A.; Tong, C.; Culberson, J.C.; Sheridan, R.P.; Feuston, B.P. Random Forest: A Classification and Regression Tool for Compound Classification and QSAR Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem 2025 Update. Nucleic Acids Res. 2025, 53, D1516–D1525. [Google Scholar] [CrossRef] [PubMed]
- Landrum, G.; Tosco, P.; Kelley, B.; Rodriguez, R.; Cosgrove, D.; Vianello, R.; Sriniker; Gedeck, P.; Jones, G.; Kawashima, E.; et al. RDKit: Open-Source Cheminformatics Software. Available online: https://www.rdkit.org (accessed on 16 July 2025).
- Daina, A.; Michielin, O.; Zoete, V. SwissADME: A Free Web Tool to Evaluate Pharmacokinetics, Drug-Likeness and Medicinal Chemistry Friendliness of Small Molecules. Sci. Rep. 2017, 7, 42717. [Google Scholar] [CrossRef] [PubMed]
- Molinspiration Cheminformatics 2006. Available online: https://www.molinspiration.com (accessed on 16 July 2025).
- Santafe, G.; Inza, I.; Lozano, J.A. Dealing with the Evaluation of Supervised Classification Algorithms. Artif. Intell. Rev. 2015, 44, 467–508. [Google Scholar] [CrossRef]
- Rainio, O.; Teuho, J.; Klén, R. Evaluation Metrics and Statistical Tests for Machine Learning. Sci. Rep. 2024, 14, 6086. [Google Scholar] [CrossRef]
- Geng, S. Analysis of the Different Statistical Metrics in Machine Learning. Highlights Sci. Eng. Technol. 2024, 88, 350–356. [Google Scholar] [CrossRef]
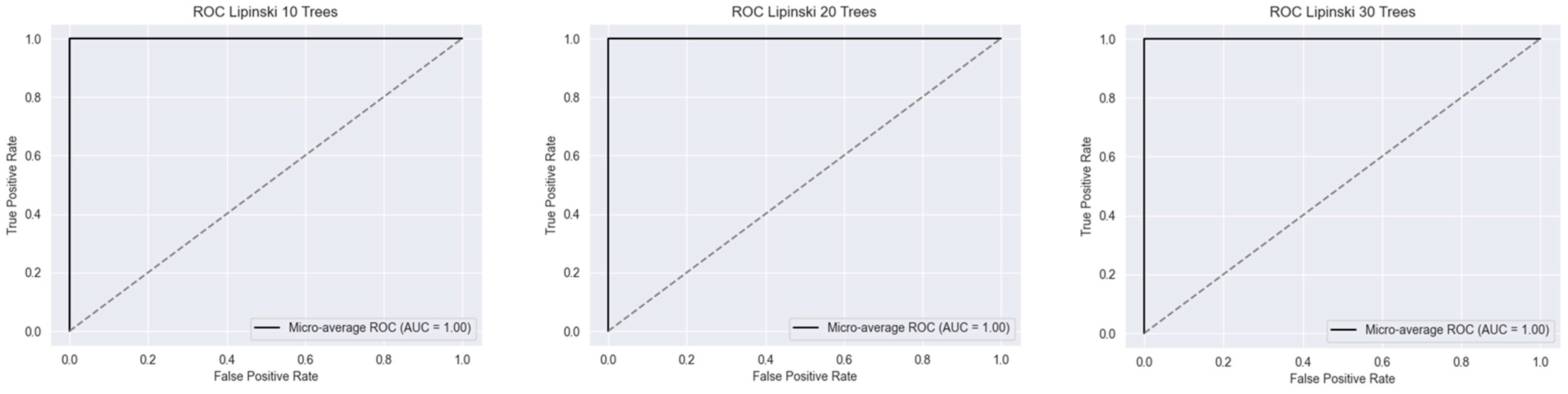
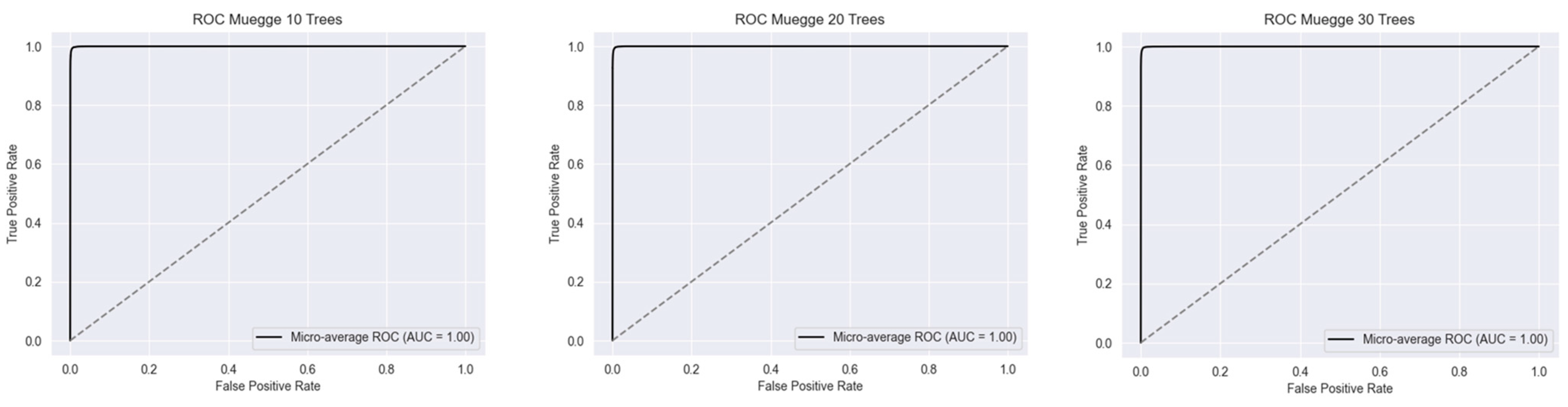

| RF Model (Number of Estimators) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | Ro5 (10) | Ro5 (20) | Ro5 (30) | bRo5 (10) | bRo5 (20) | bRo5 (30) | Muegge (10) | Muegge (20) | Muegge (30) |
| Classification models | |||||||||
| Accuracy | 1.0 | 1.0 | 1.0 | 0.999 | 0.999 | 0.999 | 0.985 | 0.986 | 0.986 |
| Precision | 1.0 | 1.0 | 1.0 | 0.999 | 0.999 | 0.999 | 0.985 | 0.986 | 0.986 |
| Sensitivity (Recall) | 1.0 | 1.0 | 1.0 | 0.999 | 0.999 | 0.999 | 0.985 | 0.986 | 0.986 |
| F1-score | 1.0 | 1.0 | 1.0 | 0.999 | 0.999 | 0.999 | 0.985 | 0.986 | 0.986 |
| Regression models | |||||||||
| MSE | 0.0 | 0.0 | 5.46 × 10−8 | 7.30 × 10−5 | 8.85 × 10−5 | 6.21 × 10−5 | 0.01 | 0.01 | 0.01 |
| MAE | 0.0 | 0.0 | 1.63 × 10−6 | 0.0002 | 0.0002 | 0.0002 | 0.019 | 0.019 | 0.019 |
| R2 | 1.0 | 1.0 | 0.999 | 0.999 | 0.999 | 0.999 | 0.996 | 0.996 | 0.996 |
| Peptide Molecule | Violations Ro5 (Estimators = 10) |
Violations Ro5
(Estimators = 20) |
Violations Ro5
(Estimators = 30) | Violations Ro5 (SwissADME) | Violations Ro5 (Molinspiration) |
|---|---|---|---|---|---|
| ML 1 | 2 | 2 | 2 | 2 | 2 |
| ML 2 | 2 | 2 | 2 | 2 | 2 |
| ML 3 | 2 | 2 | 2 | 2 | 2 |
| ML 4 | 2 | 2 | 2 | 2 | 2 |
| ML 5 | 2 | 2 | 2 | 2 | 2 |
| ML 6 | 2 | 2 | 2 | 2 | 2 |
| ML 7 | 2 | 2 | 2 | 2 | 2 |
| ML 8 | 2 | 2 | 2 | 2 | 2 |
| ML 9 | 2 | 2 | 2 | 2 | 2 |
| ML 10 | 2 | 2 | 2 | 2 | 2 |
| ML 11 | 2 | 2 | 2 | 2 | 2 |
| ML 12 | 2 | 2 | 2 | 2 | 2 |
| ML 13 | 0 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 | 0 |
| ML 15 | 1 | 1 | 1 | 1 | 1 |
| ML 16 | 0 | 0 | 0 | 0 | 0 |
| ML 17 | 3 | 3 | 3 | 3 | 3 |
| ML 18 | 4 | 4 | 4 | 3 | 3 |
| ML 19 | 4 | 4 | 4 | 3 | 3 |
| ML 20 | 4 | 4 | 4 | 3 | 3 |
| ML 21 | 4 | 4 | 4 | 3 | 3 |
| ML 22 | 4 | 4 | 4 | 3 | 3 |
| ML 23 | 3 | 3 | 3 | 3 | 3 |
| ML 24 | 4 | 4 | 4 | NaN | 3 |
| ML 25 | 4 | 4 | 4 | NaN | 3 |
| ML 26 | 4 | 4 | 4 | NaN | 3 |
| Peptide Molecule | Violations Ro5 (Estimators = 10) | Violations Ro5 (Estimators = 20) | Violations Ro5 (Estimators = 30) | Violations Ro5 (SwissADME) | Violations Ro5 (Molinspiration) |
|---|---|---|---|---|---|
| ML 1 | 2 | 2 | 2 | 2 | 2 |
| ML 2 | 2 | 2 | 2 | 2 | 2 |
| ML 3 | 2 | 2 | 2 | 2 | 2 |
| ML 4 | 2 | 2 | 2 | 2 | 2 |
| ML 5 | 2 | 2 | 2 | 2 | 2 |
| ML 6 | 2 | 2 | 2 | 2 | 2 |
| ML 7 | 2 | 2 | 2 | 2 | 2 |
| ML 8 | 2 | 2 | 2 | 2 | 2 |
| ML 9 | 2 | 2 | 2 | 2 | 2 |
| ML 10 | 2 | 2 | 2 | 2 | 2 |
| ML 11 | 2 | 2 | 2 | 2 | 2 |
| ML 12 | 2 | 2 | 2 | 2 | 2 |
| ML 13 | 0 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 | 0 |
| ML 15 | 1 | 1 | 1 | 1 | 1 |
| ML 16 | 0 | 0 | 0 | 0 | 0 |
| ML 17 | 3 | 3 | 3 | 3 | 3 |
| ML 18 | 4 | 4 | 4 | 3 | 3 |
| ML 19 | 4 | 4 | 4 | 3 | 3 |
| ML 20 | 4 | 4 | 4 | 3 | 3 |
| ML 21 | 4 | 4 | 4 | 3 | 3 |
| ML 22 | 4 | 4 | 4 | 3 | 3 |
| ML 23 | 3 | 3 | 3 | 3 | 3 |
| ML 24 | 4 | 4 | 4 | NaN | 3 |
| ML 25 | 4 | 4 | 4 | NaN | 3 |
| ML 26 | 4 | 4 | 4 | NaN | 3 |
| Peptide Molecule | Violations of Muegge’s Rule (Estimators = 10) | Violations of Muegge’s Rule (Estimators = 20) | Violations of Muegge’s Rule (Estimators = 30) | Violations of Muegge’s Rule (SwissADME) |
|---|---|---|---|---|
| ML 1 | 3 | 3 | 3 | 3 |
| ML 2 | 3 | 3 | 3 | 3 |
| ML 3 | 3 | 3 | 3 | 3 |
| ML 4 | 3 | 3 | 3 | 3 |
| ML 5 | 3 | 3 | 3 | 4 |
| ML 6 | 3 | 3 | 3 | 4 |
| ML 7 | 3 | 3 | 3 | 4 |
| ML 8 | 3 | 3 | 3 | 4 |
| ML 9 | 3 | 3 | 3 | 3 |
| ML 10 | 3 | 3 | 3 | 4 |
| ML 11 | 3 | 3 | 3 | 4 |
| ML 12 | 3 | 3 | 3 | 4 |
| ML 13 | 0 | 0 | 0 | 1 |
| ML 14 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 0 |
| ML 16 | 0 | 0 | 0 | 1 |
| ML 17 | 4 | 4 | 4 | 6 |
| ML 18 | 5 | 5 | 5 | 5 |
| ML 19 | 5 | 5 | 5 | 5 |
| ML 20 | 6 | 6 | 6 | 6 |
| ML 21 | 5 | 5 | 5 | 6 |
| ML 22 | 5 | 5 | 5 | 6 |
| ML 23 | 4 | 4 | 4 | 5 |
|
Peptide
Molecule |
Violations of Muegge’s Rule
(Estimators = 10) |
Violations of
Muegge’s Rule (Estimators = 20) |
Violations of
Muegge’s Rule (Estimators = 30) |
Violations of
Muegge’s Rule (SwissADME) |
|---|---|---|---|---|
| ML 1 | 3 | 3 | 3 | 3 |
| ML 2 | 3 | 3 | 3 | 3 |
| ML 3 | 3 | 3 | 3 | 3 |
| ML 4 | 3 | 3 | 3 | 3 |
| ML 5 | 3 | 3 | 3 | 4 |
| ML 6 | 3 | 3 | 3 | 4 |
| ML 7 | 3 | 3 | 3 | 4 |
| ML 8 | 3 | 3 | 3 | 4 |
| ML 9 | 3 | 3 | 3 | 3 |
| ML 10 | 3 | 3 | 3 | 4 |
| ML 11 | 3 | 3 | 3 | 4 |
| ML 12 | 3 | 3 | 3 | 4 |
| ML 13 | 0 | 0 | 0 | 1 |
| ML 14 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 0 |
| ML 16 | 0 | 0 | 0 | 1 |
| ML 17 | 4 | 4 | 4 | 6 |
| ML 18 | 5 | 5 | 5 | 5 |
| ML 19 | 5 | 5 | 5 | 5 |
| ML 20 | 5 | 5 | 5 | 6 |
| ML 21 | 5 | 5 | 5 | 6 |
| ML 22 | 5 | 5 | 5 | 6 |
| ML 23 | 4 | 4 | 4 | 5 |
| Peptide Molecule | Violations of bRo5 (Estimators = 10) | Violations of bRo5 (Estimators = 20) | Violations of bRo5 (Estimators = 30) | Manual |
| ML 1 | 2 | 2 | 2 | 2 |
| ML 2 | 2 | 2 | 2 | 2 |
| ML 3 | 2 | 2 | 2 | 2 |
| ML 4 | 2 | 2 | 2 | 2 |
| ML 5 | 2 | 2 | 2 | 2 |
| ML 6 | 2 | 2 | 2 | 2 |
| ML 7 | 2 | 2 | 2 | 2 |
| ML 8 | 2 | 2 | 2 | 2 |
| ML 9 | 2 | 2 | 2 | 2 |
| ML 10 | 2 | 2 | 2 | 2 |
| ML 11 | 2 | 2 | 2 | 2 |
| ML 12 | 2 | 2 | 2 | 2 |
| ML 13 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 0 |
| ML 16 | 0 | 0 | 0 | 0 |
| ML 17 | 3 | 3 | 3 | 3 |
| ML 18 | 3 | 3 | 3 | 3 |
| ML 19 | 3 | 3 | 3 | 3 |
| ML 20 | 3 | 4 | 4 | 4 |
| ML 21 | 3 | 4 | 3 | 3 |
| ML 22 | 3 | 4 | 3 | 3 |
| ML 23 | 3 | 3 | 3 | 3 |
| ML 24 | 6 | 6 | 6 | 6 |
| ML 25 | 5 | 5 | 5 | 5 |
| ML 26 | 4 | 4 | 4 | 4 |
| Peptide Molecule | Violations of bRo5 (Estimators = 10) | Violations of bRo5 (Estimators = 20) | Violations of bRo5 (Estimators = 30) | Manual |
|---|---|---|---|---|
| ML 1 | 2 | 2 | 2 | 2 |
| ML 2 | 2 | 2 | 2 | 2 |
| ML 3 | 2 | 2 | 2 | 2 |
| ML 4 | 2 | 2 | 2 | 2 |
| ML 5 | 2 | 2 | 2 | 2 |
| ML 6 | 2 | 2 | 2 | 2 |
| ML 7 | 2 | 2 | 2 | 2 |
| ML 8 | 2 | 2 | 2 | 2 |
| ML 9 | 2 | 2 | 2 | 2 |
| ML 10 | 2 | 2 | 2 | 2 |
| ML 11 | 2 | 2 | 2 | 2 |
| ML 12 | 2 | 2 | 2 | 2 |
| ML 13 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 0 |
| ML 16 | 0 | 0 | 0 | 0 |
| ML 17 | 3 | 3 | 3 | 3 |
| ML 18 | 3 | 3 | 3 | 3 |
| ML 19 | 3 | 3 | 3 | 3 |
| ML 20 | 3 | 3 | 3 | 4 |
| ML 21 | 3 | 3 | 3 | 3 |
| ML 22 | 3 | 3 | 3 | 3 |
| ML 23 | 3 | 3 | 3 | 3 |
| ML 24 | 6 | 5 | 5 | 6 |
| ML 25 | 5 | 5 | 5 | 5 |
| ML 26 | 4 | 4 | 4 | 4 |
| RF Model (Number of Estimators) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Metrics | Ro5 (10) | Ro5 (20) | Ro5 (30) | bRo5 (10) | bRo5 (20) | bRo5 (30) | Muegge (10) | Muegge (20) | Muegge (30) |
| Classification models | |||||||||
| Accuracy | 0.983 | 0.985 | 0.987 | 0.99 | 0.989 | 0.99 | 0.89 | 0.897 | 0.902 |
| Precision | 0.983 | 0.985 | 0.988 | 0.99 | 0.988 | 0.99 | 0.888 | 0.896 | 0.901 |
| Sensitivity (Recall) | 0.983 | 0.985 | 0.988 | 0.99 | 0.989 | 0.99 | 0.89 | 0.897 | 0.902 |
| F1-score | 0.983 | 0.985 | 0.988 | 0.99 | 0.988 | 0.990 | 0.889 | 0.896 | 0.901 |
| Peptide Molecule | Violations Ro5 (Estimators = 10) |
Violations Ro5
(Estimators = 20) |
Violations Ro5
(Estimators = 30) | Violations Ro5 (SwissADME) | Violations Ro5 (Molinspiration) |
|---|---|---|---|---|---|
| ML 1 | 0 | 0 | 0 | 2 | 2 |
| ML 2 | 0 | 0 | 0 | 2 | 2 |
| ML 3 | 0 | 0 | 0 | 2 | 2 |
| ML 4 | 0 | 0 | 0 | 2 | 2 |
| ML 5 | 0 | 0 | 0 | 2 | 2 |
| ML 6 | 0 | 0 | 0 | 2 | 2 |
| ML 7 | 0 | 0 | 0 | 2 | 2 |
| ML 8 | 0 | 0 | 0 | 2 | 2 |
| ML 9 | 0 | 0 | 0 | 2 | 2 |
| ML 10 | 0 | 0 | 0 | 2 | 2 |
| ML 11 | 0 | 0 | 0 | 2 | 2 |
| ML 12 | 0 | 0 | 0 | 2 | 2 |
| ML 13 | 0 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 1 | 1 |
| ML 16 | 0 | 0 | 0 | 0 | 0 |
| ML 17 | 0 | 0 | 0 | 3 | 3 |
| ML 18 | 0 | 0 | 0 | 3 | 3 |
| ML 19 | 0 | 0 | 0 | 3 | 3 |
| ML 20 | 0 | 0 | 0 | 3 | 3 |
| ML 21 | 0 | 0 | 0 | 3 | 3 |
| ML 22 | 0 | 0 | 0 | 3 | 3 |
| ML 23 | 0 | 0 | 0 | 3 | 3 |
| ML 24 | 0 | 0 | 0 | NaN | 3 |
| ML 25 | 0 | 0 | 0 | NaN | 3 |
| ML 26 | 0 | 0 | 0 | NaN | 3 |
| Peptide Molecule | Violations of Muegge’s Rule (Estimators = 10) | Violations of Muegge’s Rule (Estimators = 20) | Violations of Muegge’s Rule (Estimators = 30) | Violations of Muegge’s Rule (SwissADME) |
|---|---|---|---|---|
| ML 1 | 0 | 0 | 0 | 3 |
| ML 2 | 0 | 1 | 0 | 3 |
| ML 3 | 0 | 2 | 1 | 3 |
| ML 4 | 1 | 1 | 0 | 3 |
| ML 5 | 1 | 0 | 0 | 4 |
| ML 6 | 1 | 0 | 0 | 4 |
| ML 7 | 0 | 0 | 0 | 4 |
| ML 8 | 1 | 0 | 0 | 4 |
| ML 9 | 0 | 0 | 0 | 3 |
| ML 10 | 0 | 0 | 0 | 4 |
| ML 11 | 1 | 1 | 1 | 4 |
| ML 12 | 1 | 1 | 1 | 4 |
| ML 13 | 2 | 1 | 0 | 1 |
| ML 14 | 0 | 1 | 0 | 0 |
| ML 15 | 0 | 1 | 0 | 0 |
| ML 16 | 0 | 1 | 0 | 1 |
| ML 17 | 1 | 0 | 0 | 6 |
| ML 18 | 0 | 0 | 0 | 5 |
| ML 19 | 0 | 0 | 0 | 5 |
| ML 20 | 0 | 0 | 0 | 6 |
| ML 21 | 1 | 0 | 0 | 6 |
| ML 22 | 1 | 0 | 0 | 6 |
| ML 23 | 1 | 0 | 0 | 5 |
| Peptide Molecule | Violations of bRo5 (Estimators = 10) | Violations of bRo5 (Estimators = 20) | Violations of bRo5 (Estimators = 30) | Manual |
|---|---|---|---|---|
| ML 1 | 0 | 0 | 0 | 2 |
| ML 2 | 0 | 0 | 0 | 2 |
| ML 3 | 0 | 0 | 0 | 2 |
| ML 4 | 0 | 0 | 0 | 2 |
| ML 5 | 0 | 0 | 0 | 2 |
| ML 6 | 0 | 0 | 0 | 2 |
| ML 7 | 0 | 0 | 0 | 2 |
| ML 8 | 0 | 0 | 0 | 2 |
| ML 9 | 0 | 0 | 0 | 2 |
| ML 10 | 0 | 0 | 0 | 2 |
| ML 11 | 0 | 0 | 0 | 2 |
| ML 12 | 0 | 0 | 0 | 2 |
| ML 13 | 0 | 0 | 0 | 0 |
| ML 14 | 0 | 0 | 0 | 0 |
| ML 15 | 0 | 0 | 0 | 0 |
| ML 16 | 0 | 0 | 0 | 0 |
| ML 17 | 0 | 0 | 0 | 3 |
| ML 18 | 0 | 0 | 0 | 3 |
| ML 19 | 0 | 0 | 0 | 3 |
| ML 20 | 0 | 0 | 0 | 4 |
| ML 21 | 0 | 0 | 0 | 3 |
| ML 22 | 0 | 0 | 0 | 3 |
| ML 23 | 0 | 0 | 0 | 3 |
| ML 24 | 0 | 0 | 0 | 6 |
| ML 25 | 0 | 0 | 0 | 5 |
| ML 26 | 0 | 0 | 0 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lambev, M.; Dimitrova, D.; Mihaylova, S. Machine Learning-Based Prediction of Rule Violations for Drug-Likeness Assessment in Peptide Molecules Using Random Forest Models. Int. J. Mol. Sci. 2025, 26, 8407. https://doi.org/10.3390/ijms26178407
Lambev M, Dimitrova D, Mihaylova S. Machine Learning-Based Prediction of Rule Violations for Drug-Likeness Assessment in Peptide Molecules Using Random Forest Models. International Journal of Molecular Sciences. 2025; 26(17):8407. https://doi.org/10.3390/ijms26178407
Chicago/Turabian StyleLambev, Momchil, Dimana Dimitrova, and Silviya Mihaylova. 2025. "Machine Learning-Based Prediction of Rule Violations for Drug-Likeness Assessment in Peptide Molecules Using Random Forest Models" International Journal of Molecular Sciences 26, no. 17: 8407. https://doi.org/10.3390/ijms26178407
APA StyleLambev, M., Dimitrova, D., & Mihaylova, S. (2025). Machine Learning-Based Prediction of Rule Violations for Drug-Likeness Assessment in Peptide Molecules Using Random Forest Models. International Journal of Molecular Sciences, 26(17), 8407. https://doi.org/10.3390/ijms26178407






