Carrier Transport in Colloidal Quantum Dot Intermediate Band Solar Cell Materials Using Network Science
Abstract
1. Introduction
2. Materials and Methods
2.1. Hypotheses
- 1.
- 2.
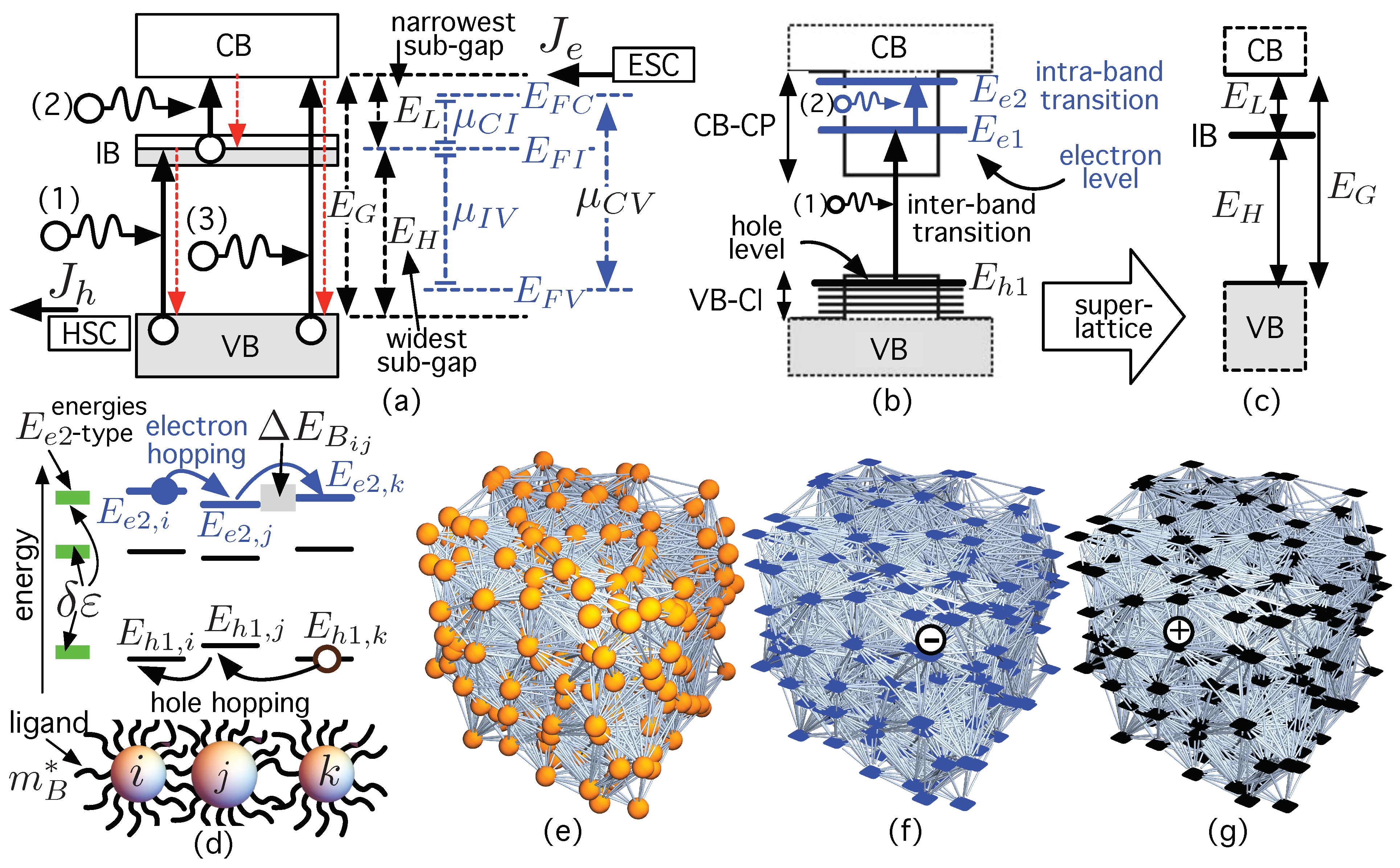
- The Fermi-level splits into three quasi-fermi levels, , , and , for describing the carrier concentration in the three bands.
- 3.
- and represent the carrier excess—with respect to the equilibrium ones, and , respectively—in the CB (electrons) and VB (holes) of the IB-material [136]. These are just the bands that inject current density (, ) via the selective contacts, ESC and HSC, the IB being isolated.
- 4.
- As no current is extracted from the IB, the net electron rate photo-excited from the VB to the IB (generation minus recombination, ) must equal the one from the IB to the CB, , that is, .
- 5.
- 6.
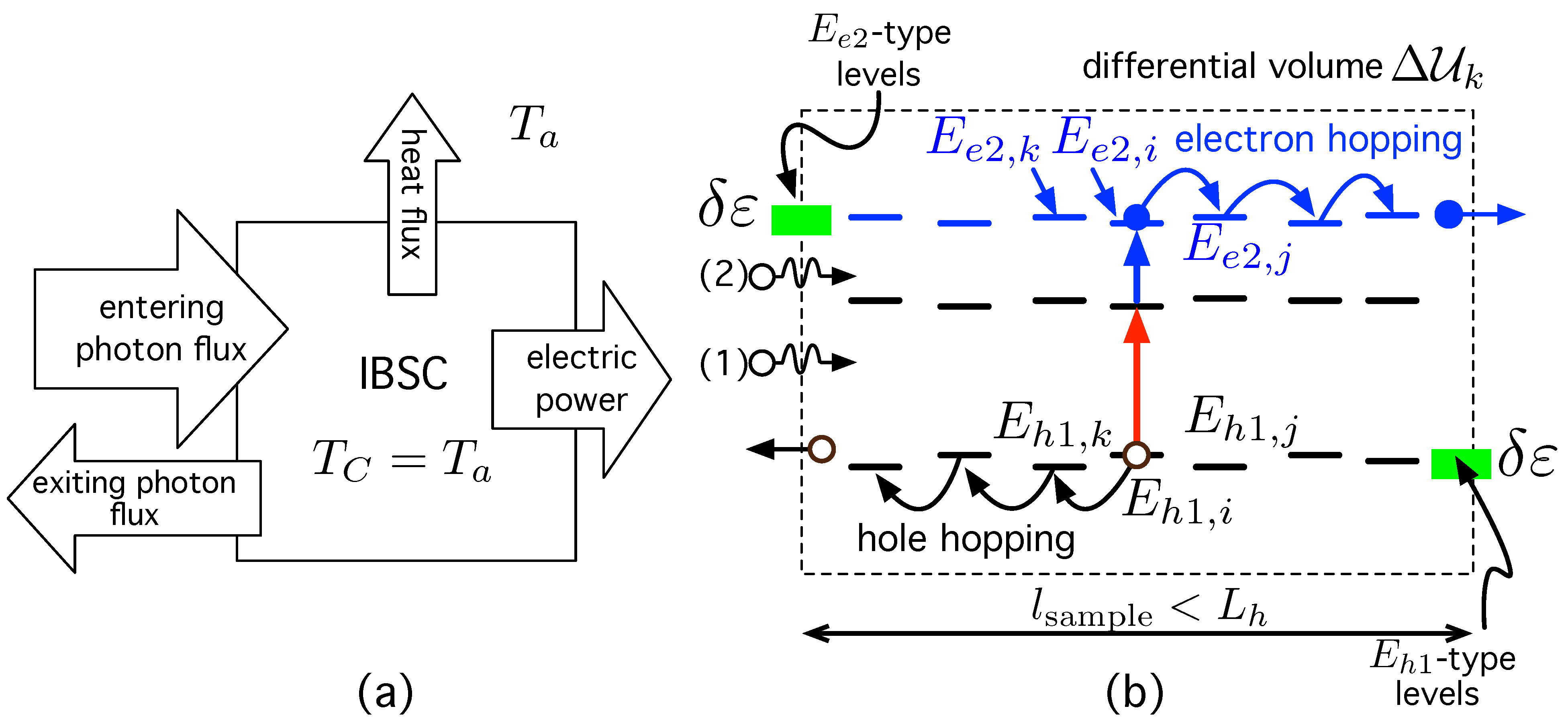
- The IBSC works under the low-injection approximation and, when carrier generation becomes uniform, then the electron and hole current densities and are described by a quasi-drift diffusion model, while that of the isolated IB, , becomes negligible [136]. Uniform carrier generation, as in SGSCs, can be accomplished by using light-trapping techniques, which randomize the light inside the material. Uniform recombination rates are reached as the diffusion length of the carriers involved (electrons in the CB, hole in the VB), and , increase [136].
2.2. Model: Incoherent Electron and Hole Hopping Transport in CQD-IB Materials and Their Corresponding Networks
2.2.1. Carrier Hopping Rates between Localized States i and j in a General Case
2.2.2. System: Electron and Hole Hopping Rates between Localized States in the CQD-IB Material
2.2.3. Defining the Associated Networks for Study Electron and Hole Hopping Transport
2.2.4. Continuous Time Random Walks on Networks
3. Results and Discussion
3.1. Methodology
3.2. Some Preliminary Considerations to Guide Carrier Transport Simulations in the Generated Networks
- 1.
- Reducing the inter-dot distance does not seem to have any drawback in principle: it would lead to a greater photon absorption per unit of volume/area and would also ease carrier transport. However, ref. [155] suggests that, at very small PbS-CQD radii, a relaxation of parity selection rules and a stronger electron-phonon coupling destroy the phonon bottleneck that helps electrons remain in excited states without thermalization. The study suggests that there could be an optimal dot size that, on the one hand, allows a sufficiently long energy separation between the ground () and the excited state (), and on the other hand, maintains the phonon bottleneck effect, avoiding thus fast thermalization. This is essential for the IBSC concept since it requires to have three electron gases with their corresponding quasi-Fermi levels, as stated by Hypothesis (2) in Section 2.
- 2.
- In the effort of reducing the value of the tunneling decay between localized states i and j—Equation (2)—we could try to decrease the value of the potential barrier and/or the value of the effective mass of the hopping particle . Decreasing the potential barrier , at first sight, would increase the probability for the carrier to hop to the nearby dot. However, there is a design restriction. The average barrier height cannot be less than the energy variation —Figure 3b—caused by the standard deviation in the dot size distribution (as stated by Equations (4)–(6)). The reason is that if then there will be many CQDs whose -type levels would be in the continuum. This would reduce the photon absorption causing transitions from the (localized) LIS with energy to the (now extended) at the energy continuum. That is, in the case of CQDs structures for IBSCs, it seems that what is good for photon absorption is not good for carrier transport and vice-versa.
- 3.
- The most obvious option, as pointed out in Section 1, is to reduce in Equation (3) by manufacturing CQD films that are as homogeneous as possible, both in the dots’ size and in the chemical composition of their surface. Although impressive advances are being made to obtain highly mono-dispersive samples (standard deviation, ∼ [81]), there seems to be a physical limit that is difficult to overcome [30,156]. In our simulations, we have considered , ).
3.2.1. Influence of the Dot Density
3.2.2. Influence of the Carrier Effective Mass in the Barrier/Ligand
3.2.3. The Combined Influence of and
3.2.4. Some Final Considerations and Future Long-Term Work
4. Conclusions
- 1.
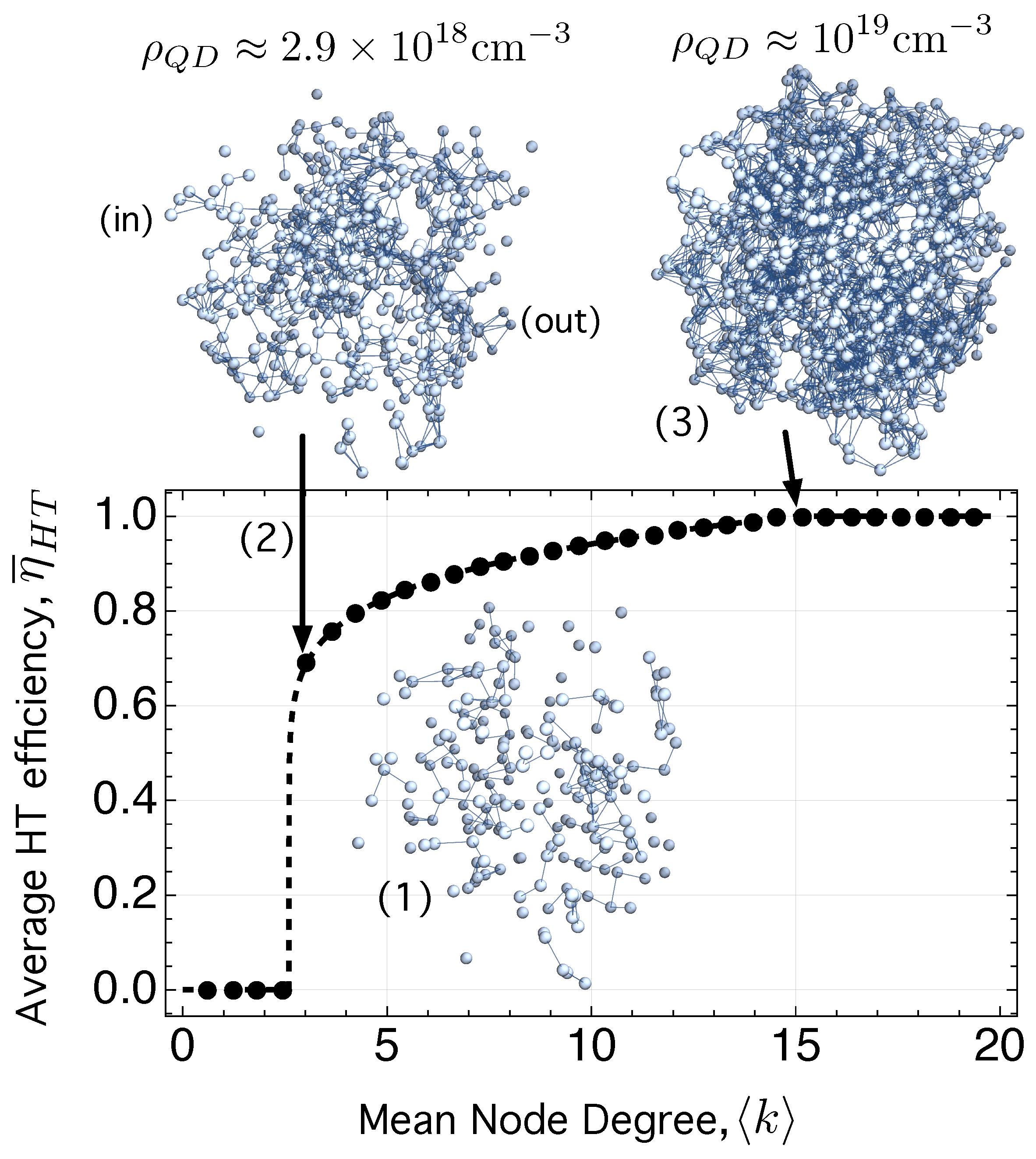
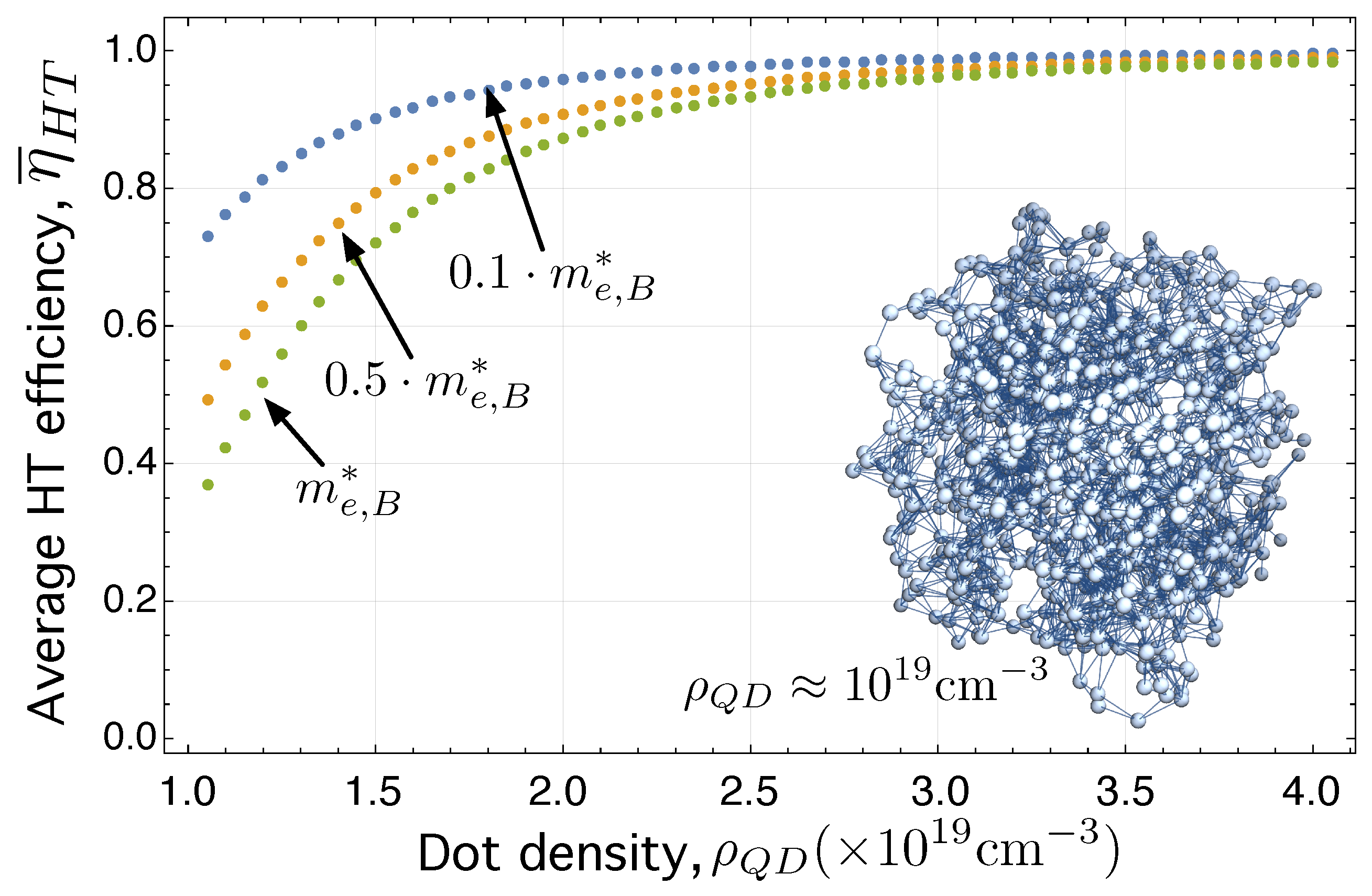
- We have studied the influence of the dot density on the average HT efficiency . Achieving higher , or equivalently, smaller inter-dot-distance, , is important not only for increasing sub-band-gap photon absorption but also for enhancing electron and hole HT (and, thus, for the injection of the increased photo-generated current). Reducing increases both electron and hole HT rates, and . We have found that, as increases, has a hybrid percolation transition at cm, in which changes abruptly from to . For dot densities cm all nodes are connected to at least one other, which allows any carrier to hop across the network a distance on the order of the hole diffusion length, . Although the proposed model predicts the beneficial feature of increasing by means of reducing , however, special care should be taken. This is because, as suggested in [155], there may be an optimal dot size that, on the one hand, allows a sufficiently long energy separation between the ground and the excited state and, on the other hand, maintains the phonon bottleneck effect, avoiding thus fast thermalization. This is essential for the CQD-IB solar cell, which requires to have three electron gases with their corresponding quasi-Fermi levels.
- 2.
- We have also explored how carrier hopping rate can be increased by reducing the tunneling decay between two any localized states i and j, . Prior to investigating the effect of the effective mass , we have found that decreasing the average barrier height has a design restriction. cannot be smaller than the energy variation caused by the standard deviation in the dot size distribution. The reason is that if then there will be CQDs whose -type levels would be in the continuum. This would reduce the photon absorption causing transitions from the (localized) LIS with energy to the (now extended stated) in the CB continuum.
- 3.
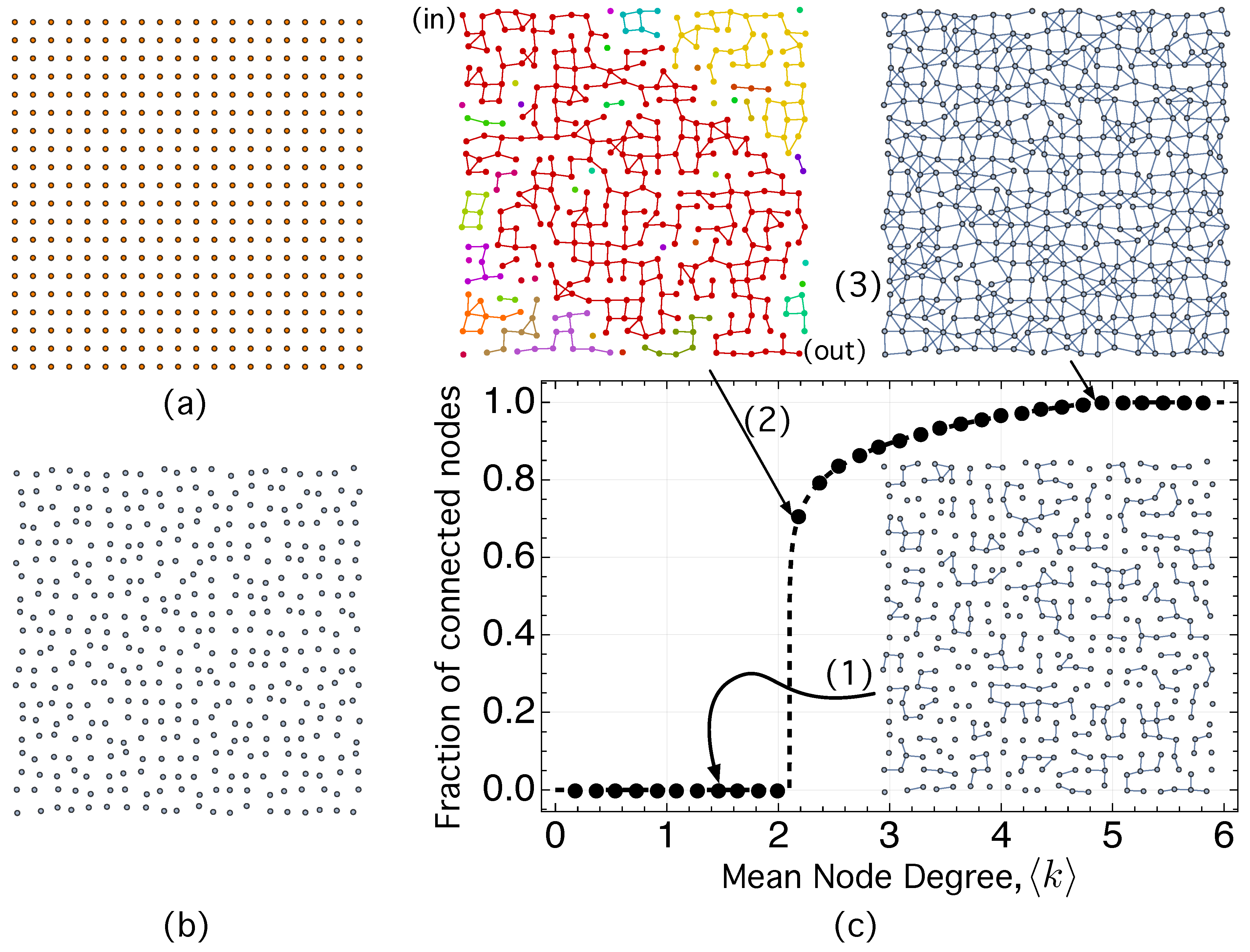
- By imposing the constraint , we have studied the effect of reducing the effective mass in the ligand/barrier, . For illustrative purposes, we first focused on a two-dimensional case that simulates a CQD film. Keeping the CQD positions constant, we have progressively reduced the value. Those networks that represent CQD films with smaller have more links because it is easier for the carrier to hop to the adjacent CQD. These results agree with those observed experimentally in the context of solar cells based on PbS CQD solids in which ligand exchange reduces and increases mobility [35].
- 4.
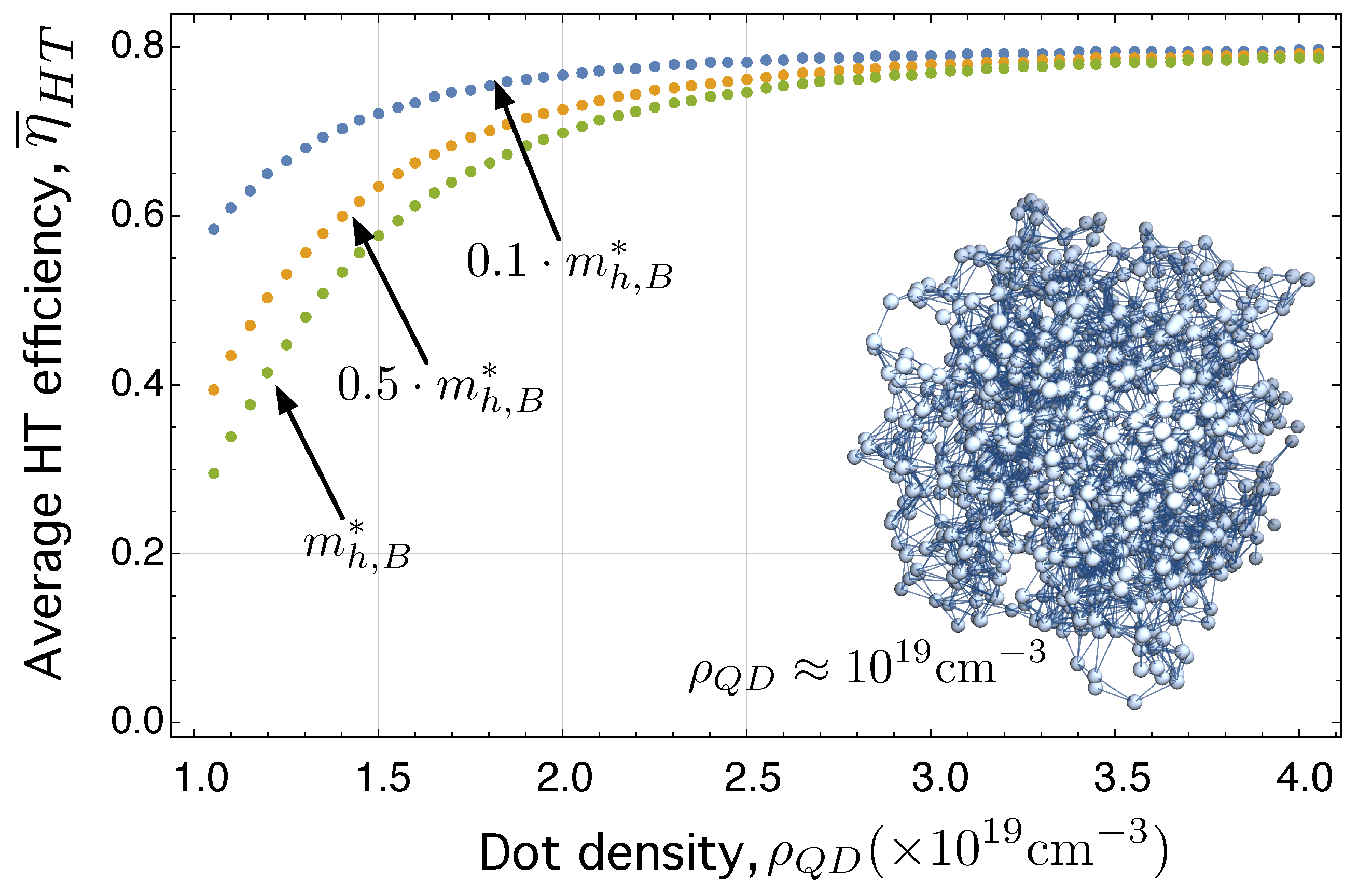
- Going one step further, we have carried out simulations to study the combined effect of increasing and decreasing , this time in samples of randomly distributed CQDs in a three-dimensional volume . We have computed the average value of the HT efficiency as increases, parametrized by decreasing values, for both the electron HT network, , and the hole HT network . The results point out that is smaller in the case of the hole HT network than in . This is because the Laplacian for holes contains elements that are smaller that those in the Laplacian for electrons. In turn, this is because ⇒⇒⇒.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, M.; Yazdani, N.; Yarema, M.; Jansen, M.; Wood, V.; Sargent, E.H. Colloidal quantum dot electronics. Nat. Electron. 2021, 4, 548–558. [Google Scholar] [CrossRef]
- Harrison, P.; Valavanis, A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Cotta, M.A. Quantum Dots and Their Applications: What Lies Ahead? ACS Appl. Nano Mater. 2020, 3, 4920–4924. [Google Scholar] [CrossRef]
- Zhao, Q.; Han, R.; Marshall, A.R.; Wang, S.; Wieliczka, B.M.; Ni, J.; Zhang, J.; Yuan, J.; Luther, J.M.; Hazarika, A.; et al. Colloidal Quantum Dot Solar Cells: Progressive Deposition Techniques and Future Prospects on Large-Area Fabrication. Adv. Mater. 2022, 34, 2107888. [Google Scholar] [CrossRef] [PubMed]
- Heuer-Jungemann, A.; Feliu, N.; Bakaimi, I.; Hamaly, M.; Alkilany, A.; Chakraborty, I.; Masood, A.; Casula, M.F.; Kostopoulou, A.; Oh, E.; et al. The role of ligands in the chemical synthesis and applications of inorganic nanoparticles. Chem. Rev. 2019, 119, 4819–4880. [Google Scholar] [CrossRef]
- Zito, J.; Infante, I. The future of ligand engineering in colloidal semiconductor nanocrystals. Accounts Chem. Res. 2021, 54, 1555–1564. [Google Scholar] [CrossRef]
- Sun, B.; Vafaie, M.; Levina, L.; Wei, M.; Dong, Y.; Gao, Y.; Kung, H.T.; Biondi, M.; Proppe, A.H.; Chen, B.; et al. Ligand-assisted reconstruction of colloidal quantum dots decreases trap state density. Nano Lett. 2020, 20, 3694–3702. [Google Scholar] [CrossRef]
- Boles, M.A.; Ling, D.; Hyeon, T.; Talapin, D.V. The surface science of nanocrystals. Nat. Mater. 2016, 15, 141–153. [Google Scholar] [CrossRef]
- Giansante, C.; Infante, I. Surface traps in colloidal quantum dots: A combined experimental and theoretical perspective. J. Phys. Chem. Lett. 2017, 8, 5209–5215. [Google Scholar] [CrossRef]
- Houtepen, A.J.; Hens, Z.; Owen, J.S.; Infante, I. On the origin of surface traps in colloidal II–VI semiconductor nanocrystals. Chem. Mater. 2017, 29, 752–761. [Google Scholar] [CrossRef]
- Bodnarchuk, M.I.; Boehme, S.C.; Ten Brinck, S.; Bernasconi, C.; Shynkarenko, Y.; Krieg, F.; Widmer, R.; Aeschlimann, B.; Gunther, D.; Kovalenko, M.V.; et al. Rationalizing and controlling the surface structure and electronic passivation of cesium lead halide nanocrystals. ACS Energy Lett. 2018, 4, 63–74. [Google Scholar] [CrossRef]
- Almeida, G.; Infante, I.; Manna, L. Resurfacing halide perovskite nanocrystals. Science 2019, 364, 833–834. [Google Scholar] [CrossRef]
- Talapin, D.V.; Murray, C.B. PbSe nanocrystal solids for n -and p-channel thin film field-effect transistors. Science 2005, 310, 86–89. [Google Scholar] [CrossRef]
- Talapin, D.V.; Lee, J.S.; Kovalenko, M.V.; Shevchenko, E.V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 2010, 110, 389–458. [Google Scholar] [CrossRef]
- Kovalenko, M.V.; Bodnarchuk, M.I.; Zaumseil, J.; Lee, J.S.; Talapin, D.V. Expanding the chemical versatility of colloidal nanocrystals capped with molecular metal chalcogenide ligands. J. Am. Chem. Soc. 2010, 132, 10085–10092. [Google Scholar] [CrossRef]
- Manzhos, S.; Chueh, C.C.; Giorgi, G.; Kubo, T.; Saianand, G.; Luder, J.; Sonar, P.; Ihara, M. Materials design and optimization for next-generation solar cell and light-emitting technologies. J. Phys. Chem. Lett. 2021, 12, 4638–4657. [Google Scholar] [CrossRef]
- Frederick, M.T.; Weiss, E.A. Relaxation of exciton confinement in CdSe quantum dots by modification with a conjugated dithiocarbamate ligand. ACS Nano 2010, 4, 3195–3200. [Google Scholar] [CrossRef]
- Brown, P.R.; Kim, D.; Lunt, R.R.; Zhao, N.; Bawendi, M.G.; Grossman, J.C.; Bulovic, V. Energy level modification in lead sulfide quantum dot thin films through ligand exchange. ACS Nano 2014, 8, 5863–5872. [Google Scholar] [CrossRef]
- Giansante, C. Surface chemistry control of colloidal quantum dot band gap. J. Phys. Chem. C 2018, 122, 18110–18116. [Google Scholar] [CrossRef]
- Giansante, C.; Infante, I.; Fabiano, E.; Grisorio, R.; Suranna, G.P.; Gigli, G. “Darker-than-Black” PbS quantum dots: Enhancing optical absorption of colloidal semiconductor nanocrystals via short conjugated ligands. J. Am. Chem. Soc. 2015, 137, 1875–1886. [Google Scholar] [CrossRef]
- Krieg, F.; Ochsenbein, S.T.; Yakunin, S.; Ten Brinck, S.; Aellen, P.; Suess, A.; Clerc, B.; Guggisberg, D.; Nazarenko, O.; Shynkarenko, Y.; et al. Colloidal CsPbX3 (X = Cl, Br, I) nanocrystals 2.0: Zwitterionic capping ligands for improved durability and stability. ACS Energy Lett. 2018, 3, 641–646. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, M.; Ghini, M.; Melcherts, A.E.; Zito, J.; Goldoni, L.; Infante, I.; Guizzardi, M.; Scotognella, F.; Kriegel, I.; et al. Colloidal Bi-Doped Cs2Ag1-xNaxInCl6 Nanocrystals: Undercoordinated Surface Cl Ions Limit their Light Emission Efficiency. ACS Mater. Lett. 2020, 2, 1442–1449. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, M.; Luijten, E. From predictive modeling to machine learning and reverse engineering of colloidal self-assembly. Nat. Mater. 2021, 20, 762–773. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Chu, X.; Sun, X.Y.; Xu, K.; Deng, H.X.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Voznyy, O.; Levina, L.; Fan, J.Z.; Askerka, M.; Jain, A.; Choi, M.J.; Ouellette, O.; Todorovi?, P.; Sagar, L.K.; Sargent, E.H. Machine learning accelerates discovery of optimal colloidal quantum dot synthesis. ACS Nano 2019, 13, 11122–11128. [Google Scholar] [CrossRef] [PubMed]
- Fong, A.Y.; Pellouchoud, L.; Davidson, M.; Walroth, R.C.; Church, C.; Tcareva, E.; Wu, L.; Peterson, K.; Meredig, B.; Tassone, C.J. Utilization of machine learning to accelerate colloidal synthesis and discovery. J. Chem. Phys. 2021, 154, 224201. [Google Scholar] [CrossRef]
- Kagan, C.R.; Lifshitz, E.; Sargent, E.H.; Talapin, D.V. Building devices from colloidal quantum dots. Science 2016, 353, aac5523. [Google Scholar] [CrossRef]
- Brett, M.W.; Gordon, C.K.; Hardy, J.; Davis, N.J. The Rise and Future of Discrete Organic–Inorganic Hybrid Nanomaterials. ACS Phys. Chem. Au 2022. [Google Scholar] [CrossRef]
- Park, Y.S.; Roh, J.; Diroll, B.T.; Schaller, R.D.; Klimov, V.I. Colloidal quantum dot lasers. Nat. Rev. Mater. 2021, 6, 382–401. [Google Scholar] [CrossRef]
- Qu, J. Colloidal Semiconductor Nanocrystals for Optoelectronic Applications: Photodetectors and Light Emitting Diodes. Ph.D. Thesis, Sorbonne Université, Paris, France, 2021. [Google Scholar]
- Kubo, T.; Wang, H.; Segawa, H. Solution-Processed Quantum-Dot Solar Cells. In Springer Handbook of Inorganic Photochemistry; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1215–1266. [Google Scholar]
- Lim, S.; Lee, G.; Han, S.; Kim, J.; Yun, S.; Lim, J.; Pu, Y.J.; Ko, M.J.; Park, T.; Choi, J.; et al. Monodisperse perovskite colloidal quantum dots enable high-efficiency photovoltaics. ACS Energy Lett. 2021, 6, 2229–2237. [Google Scholar] [CrossRef]
- Kramer, I.J.; Sargent, E.H. The architecture of colloidal quantum dot solar cells: Materials to devices. Chem. Rev. 2014, 114, 863–882. [Google Scholar] [CrossRef]
- Carey, G.H.; Abdelhady, A.L.; Ning, Z.; Thon, S.M.; Bakr, O.M.; Sargent, E.H. Colloidal quantum dot solar cells. Chem. Rev. 2015, 115, 12732–12763. [Google Scholar] [CrossRef]
- Saunina, A.Y.; Zvaigzne, M.A.; Aleksandrov, A.E.; Chistyakov, A.A.; Nikitenko, V.R.; Tameev, A.R.; Martynov, I.L. PbS Quantum Dots with Inorganic Ligands: Physical Modeling of the Charge and Excitation Transport in Photovoltaic Cells. J. Phys. Chem. C 2021, 125, 6020–6025. [Google Scholar] [CrossRef]
- Chen, H.; Pina, J.M.; Hou, Y.; Sargent, E.H. Synthesis, applications, and prospects of quantum-dot-in-perovskite solids. Adv. Energy Mater. 2022, 12, 2100774. [Google Scholar] [CrossRef]
- Mendes, M.J.; Hernández, E.; López, E.; García-Linares, P.; Ramiro, I.; Artacho, I.; Antolín, E.; Tobías, I.; Martí, A.; Luque, A. Self-organized colloidal quantum dots and metal nanoparticles for plasmon-enhanced intermediate-band solar cells. Nanotechnology 2013, 24, 345402. [Google Scholar] [CrossRef]
- Voros, M.; Galli, G.; Zimanyi, G.T. Colloidal nanoparticles for intermediate band solar cells. ACS Nano 2015, 9, 6882–6890. [Google Scholar] [CrossRef]
- Hahn, R.V.; Rodríguez-Bolívar, S.; Rodosthenous, P.; Skibinsky-Gitlin, E.S.; Califano, M.; Gómez-Campos, F.M. Optical Absorption in N-Dimensional Colloidal Quantum Dot Arrays: Influence of Stoichiometry and Applications in Intermediate Band Solar Cells. Nanomaterials 2022, 12, 3387. [Google Scholar] [CrossRef]
- Roy, S.; Mondol, N.; Hossain, M.S.; Howlader, A.H.; Hossain, M.J.; Islam, M.R.; Sarkar, A. Key photovoltaic parameters of organohalide lead perovskite quantum dot intermediate band solar cell: A numerical investigation. Mater. Today Commun. 2021, 29, 102884. [Google Scholar] [CrossRef]
- Hosokawa, H.; Tamaki, R.; Sawada, T.; Okonogi, A.; Sato, H.; Ogomi, Y.; Hayase, S.; Okada, Y.; Yano, T. Solution-processed intermediate-band solar cells with lead sulfide quantum dots and lead halide perovskites. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef]
- Ngo, T.T.; Mora-Seró, I. Interaction between colloidal quantum dots and halide perovskites: Looking for constructive synergies. J. Phys. Chem. Lett. 2019, 10, 1099–1108. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A. Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 1997, 78, 5014. [Google Scholar] [CrossRef]
- Green, M.A. Photovoltaic technology and visions for the future. Prog. Energy 2019, 1, 013001. [Google Scholar] [CrossRef]
- Green, M.A.; Bremner, S.P. Energy conversion approaches and materials for high-efficiency photovoltaics. Nat. Mater. 2017, 16, 23. [Google Scholar] [CrossRef] [PubMed]
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2019, 4, 1548305. [Google Scholar] [CrossRef]
- López, E.; Datas, A.; Ramiro, I.; Linares, P.; Antolín, E.; Artacho, I.; Martí, A.; Luque, A.; Shoji, Y.; Sogabe, T.; et al. Demonstration of the operation principles of intermediate band solar cells at room temperature. Sol. Energy Mater. Sol. Cells 2016, 149, 15–18. [Google Scholar] [CrossRef]
- Martí, A.; Cuadra, L.; Luque, A. Partial filling of a quantum dot intermediate band for solar cells. IEEE Trans. Electron Devices 2001, 48, 2394–2399. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; Cuadra, L. High efficiency solar cell with metallic intermediate band. In Proceedings of the 16th European Photovoltaic Solar Energy Conference, Glasgow, UK, 1–5 May 2000; pp. 59–61. [Google Scholar]
- Luque, A.; Martì, A. A metallic intermediate band high efficiency solar cell. Prog. Photovoltaics Res. Appl. 2001, 9, 73–86. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; Cuadra, L. Thermodynamic consistency of sub-bandgap absorbing solar cell proposals. IEEE Trans. Electron Devices 2001, 48, 2118–2124. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; Cuadra, L. Thermodynamics of solar energy conversion in novel structures. Phys. E Low-Dimens. Syst. Nanostructures 2002, 14, 107–114. [Google Scholar] [CrossRef]
- Araújo, G.L.; Martí, A. Absolute limiting efficiencies for photovoltaic energy conversion. Sol. Energy Mater. Sol. Cells 1994, 33, 213–240. [Google Scholar] [CrossRef]
- Luque, A.; Martí, A.; López, N.; Antolín, E.; Cánovas, E.; Stanley, C.; Farmer, C.; Caballero, L.; Cuadra, L.; Balenzategui, J. Experimental analysis of the quasi-Fermi level split in quantum dot intermediate-band solar cells. Appl. Phys. Lett. 2005, 87, 083505. [Google Scholar] [CrossRef]
- Martí, A.; Antolín, E.; Stanley, C.; Farmer, C.; López, N.; Díaz, P.; Cánovas, E.; Linares, P.; Luque, A. Production of photocurrent due to intermediate-to-conduction-band transitions: A demonstration of a key operating principle of the intermediate-band solar cell. Phys. Rev. Lett. 2006, 97, 247701. [Google Scholar] [CrossRef]
- Ramiro, I.; Antolin, E.; Linares, P.; Lopez, E.; Artacho, I.; Datas, A.; Marti, A.; Luque, A.; Steer, M.; Stanley, C. Two-photon photocurrent and voltage up-conversion in a quantum dot intermediate band solar cell. In Proceedings of the 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC), Denver, CO, USA, 8–13 June 2014; pp. 3251–3253. [Google Scholar]
- Tamaki, R.; Shoji, Y.; Okada, Y.; Miyano, K. Spectrally resolved interband and intraband transitions by two-step photon absorption in InGaAs/GaAs quantum dot solar cells. IEEE J. Photovoltaics 2014, 5, 229–233. [Google Scholar] [CrossRef]
- Antolin, E.; Martí, A.; Linares, P.G.; Ramiro, I.; Hernández, E.; Farmer, C.; Stanley, C.; Luque, A. Advances in quantum dot intermediate band solar cells. In Proceedings of the 2010 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 000065–000070. [Google Scholar]
- Datas, A.; López, E.; Ramiro, I.; Antolín, E.; Martí, A.; Luque, A.; Tamaki, R.; Shoji, Y.; Sogabe, T.; Okada, Y. Intermediate band solar cell with extreme broadband spectrum quantum efficiency. Phys. Rev. Lett. 2015, 114, 157701. [Google Scholar] [CrossRef]
- Ramiro, I.; Villa, J.; Tablero, C.; Antolín, E.; Luque, A.; Martí, A.; Hwang, J.; Phillips, J.; Martin, A.; Millunchick, J. Analysis of the intermediate-band absorption properties of type-II GaSb/GaAs quantum-dot photovoltaics. Phys. Rev. B 2017, 96, 125422. [Google Scholar] [CrossRef]
- Ekins-Daukes, N.; Honsberg, C.; Yamaguchi, M. Signature of intermediate band materials from luminescence measurements. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; pp. 49–54. [Google Scholar]
- Sautter, K.E.; Vallejo, K.D.; Simmonds, P.J. Strain-driven quantum dot self-assembly by molecular beam epitaxy. J. Appl. Phys. 2020, 128, 031101. [Google Scholar] [CrossRef]
- Martí, A.; Cuadra, L.; Luque, A. Quantum dot analysis of the space charge region of intermediate band solar cell. In Photovoltaics for the 21st Century II: Proceedings of the International Symposium; The Electrochemical Society: Washington, DC, USA, 2001; Volume 2001, p. 46. [Google Scholar]
- El Aouami, A.; Bikerouin, M.; El-Yadri, M.; Feddi, E.; Dujardin, F.; Courel, M.; Chouchen, B.; Gazzah, M.; Belmabrouk, H. Internal polarization electric field effects on the efficiency of InN/InxGa1-xN multiple quantum dot solar cells. Sol. Energy 2020, 201, 339–347. [Google Scholar] [CrossRef]
- Antolín, E.; Martí, A.; Farmer, C.; Linares, P.; Hernández, E.; Sánchez, A.; Ben, T.; Molina, S.; Stanley, C.; Luque, A. Reducing carrier escape in the InAs/GaAs quantum dot intermediate band solar cell. J. Appl. Phys. 2010, 108, 064513. [Google Scholar] [CrossRef]
- Ramiro, I.; Antolin, E.; Steer, M.; Linares, P.; Hernandez, E.; Artacho, I.; Lopez, E.; Ben, T.; Ripalda, J.; Molina, S.; et al. InAs/AlGaAs quantum dot intermediate band solar cells with enlarged sub-bandgaps. In Proceedings of the 2012 38th IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 000652–000656. [Google Scholar]
- Luque, A.; Martí, A.; Stanley, C. Understanding intermediate-band solar cells. Nat. Photonics 2012, 6, 146–152. [Google Scholar] [CrossRef]
- Luque, A.; Linares, P.; Antolín, E.; Ramiro, I.; Farmer, C.; Hernández, E.; Tobías, I.; Stanley, C.; Martí, A. Understanding the operation of quantum dot intermediate band solar cells. J. Appl. Phys. 2012, 111, 044502. [Google Scholar] [CrossRef]
- Ramiro, I.; Martí, A. Intermediate band solar cells: Present and Future. Prog. Photovoltaics Res. Appl. 2021, 29, 705–713. [Google Scholar] [CrossRef]
- Ramiro, I.; Kundu, B.; Dalmases, M.; Özdemir, O.; Pedrosa, M.; Konstantatos, G. Size-and temperature-dependent intraband optical properties of heavily n-doped PbS colloidal quantum dot solid-state films. ACS Nano 2020, 14, 7161–7169. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, L.; Yu, S.; Ding, T.; Xiang, D.; Wu, K. Spin blockade and phonon bottleneck for hot electron relaxation observed in n-doped colloidal quantum dots. Nat. Commun. 2021, 12, 550. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Chen, Z.; Liang, G.; Li, Y.; Lai, R.; Ding, T.; Wu, K. Observation of a phonon bottleneck in copper-doped colloidal quantum dots. Nat. Commun. 2019, 10, 4532. [Google Scholar] [CrossRef] [PubMed]
- Guyot-Sionnest, P. Electrical transport in colloidal quantum dot films. J. Phys. Chem. Lett. 2012, 3, 1169–1175. [Google Scholar] [CrossRef]
- Liu, H.; Pourret, A.; Guyot-Sionnest, P. Mott and Efros-Shklovskii variable range hopping in CdSe quantum dots films. ACS Nano 2010, 4, 5211–5216. [Google Scholar] [CrossRef]
- Liu, Y.; Gibbs, M.; Puthussery, J.; Gaik, S.; Ihly, R.; Hillhouse, H.W.; Law, M. Dependence of carrier mobility on nanocrystal size and ligand length in PbSe nanocrystal solids. Nano Lett. 2010, 10, 1960–1969. [Google Scholar] [CrossRef]
- Skinner, B.; Chen, T.; Shklovskii, B.I. Theory of hopping conduction in arrays of doped semiconductor nanocrystals. Phys. Rev. B 2012, 85, 205316. [Google Scholar] [CrossRef]
- Chen, W.; Zhong, J.; Li, J.; Saxena, N.; Kreuzer, L.P.; Liu, H.; Song, L.; Su, B.; Yang, D.; Wang, K.; et al. Structure and charge carrier dynamics in colloidal PbS quantum dot solids. J. Phys. Chem. Lett. 2019, 10, 2058–2065. [Google Scholar] [CrossRef]
- Ginsberg, N.S.; Tisdale, W.A. Spatially resolved photogenerated exciton and charge transport in emerging semiconductors. Annu. Rev. Phys. Chem. 2020, 71, 1–30. [Google Scholar] [CrossRef]
- Chen, M.; Shen, G.; Guyot-Sionnest, P. Size distribution effects on mobility and intraband gap of HgSe quantum dots. J. Phys. Chem. C 2020, 124, 16216–16221. [Google Scholar] [CrossRef]
- Jang, J.; Liu, W.; Son, J.S.; Talapin, D.V. Temperature-dependent Hall and field-effect mobility in strongly coupled all-inorganic nanocrystal arrays. Nano Lett. 2014, 14, 653–662. [Google Scholar] [CrossRef]
- Kagan, C.R.; Murray, C.B. Charge transport in strongly coupled quantum dot solids. Nat. Nanotechnol. 2015, 10, 1013–1026. [Google Scholar] [CrossRef]
- Ondry, J.C.; Philbin, J.P.; Lostica, M.; Rabani, E.; Alivisatos, A.P. Colloidal synthesis path to 2D crystalline quantum dot superlattices. ACS Nano 2020, 15, 2251–2262. [Google Scholar] [CrossRef]
- Weidman, M.C.; Nguyen, Q.; Smilgies, D.M.; Tisdale, W.A. Impact of size dispersity, ligand coverage, and ligand length on the structure of PbS nanocrystal superlattices. Chem. Mater. 2018, 30, 807–816. [Google Scholar] [CrossRef]
- Maier, A. There Must Be Order: Structure-Transport Correlations in Self-Assembled Nanocrystal Superlattices. Ph.D. Thesis, Eberhard Karls Universität Tübingen, Baden-Württemberg, Germany, 2021. [Google Scholar]
- Lee, J.S.; Kovalenko, M.V.; Huang, J.; Chung, D.S.; Talapin, D.V. Band-like transport, high electron mobility and high photoconductivity in all-inorganic nanocrystal arrays. Nat. Nanotechnol. 2011, 6, 348–352. [Google Scholar] [CrossRef]
- Choi, J.H.; Fafarman, A.T.; Oh, S.J.; Ko, D.K.; Kim, D.K.; Diroll, B.T.; Muramoto, S.; Gillen, J.G.; Murray, C.B.; Kagan, C.R. Bandlike transport in strongly coupled and doped quantum dot solids: A route to high-performance thin-film electronics. Nano Lett. 2012, 12, 2631–2638. [Google Scholar] [CrossRef]
- Lan, X.; Chen, M.; Hudson, M.H.; Kamysbayev, V.; Wang, Y.; Guyot-Sionnest, P.; Talapin, D.V. Quantum dot solids showing state-resolved band-like transport. Nat. Mater. 2020, 19, 323–329. [Google Scholar] [CrossRef]
- Barabási, A.L. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Spielman, D. Spectral graph theory. In Combinatorial Scientific Computing; Number 18; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Liu, W.; Liu, C.; Yang, Z.; Liu, X.; Zhang, Y.; Wei, Z. Modeling the propagation of mobile malware on complex networks. Commun. Nonlinear Sci. Numer. Simul. 2016, 37, 249–264. [Google Scholar] [CrossRef]
- Nicosia, V.; Tang, J.; Mascolo, C.; Musolesi, M.; Russo, G.; Latora, V. Graph metrics for temporal networks. In Temporal Networks; Springer: Berlin/Heidelberg, Germany, 2013; pp. 15–40. [Google Scholar]
- Viana, M.P.; Strano, E.; Bordin, P.; Barthelemy, M. The simplicity of planar networks. Sci. Rep. 2013, 3, 3495. [Google Scholar] [CrossRef]
- Cuadra, L.; Salcedo-Sanz, S.; Del Ser, J.; Jiménez-Fernández, S.; Geem, Z.W. A critical review of robustness in power grids using complex networks concepts. Energies 2015, 8, 9211–9265. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.R.; Lü, L.; Hu, M.B.; Xu, S.; Zhang, Y.C. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Zhang, X.; Liu, Z. Understanding the mechanisms of brain functions from the angle of synchronization and complex network. Front. Phys. 2022, 17, 1–23. [Google Scholar] [CrossRef]
- Montoya, J.M.; Solé, R.V. Small world patterns in food webs. J. Theor. Biol. 2002, 214, 405–412. [Google Scholar] [CrossRef]
- Chimal-Eguía, J.C.; Castillo-Montiel, E.; Paez-Hernández, R.T. Properties of the vascular networks in malignant tumors. Entropy 2020, 22, 166. [Google Scholar] [CrossRef]
- García-Sánchez, M.; Jiménez-Serra, I.; Puente-Sánchez, F.; Aguirre, J. The emergence of interstellar molecular complexity explained by interacting networks. Proc. Natl. Acad. Sci. USA 2022, 119, e2119734119. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2021, 896, 1–84. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, H.; Li, Z. On the resilience of modern power systems: A complex network perspective. Renew. Sustain. Energy Rev. 2021, 152, 111646. [Google Scholar] [CrossRef]
- Cuadra, L.; Pino, M.D.; Nieto-Borge, J.C.; Salcedo-Sanz, S. Optimizing the structure of distribution smart grids with renewable generation against abnormal conditions: A complex networks approach with evolutionary algorithms. Energies 2017, 10, 1097. [Google Scholar] [CrossRef]
- Doyle, J.C.; Alderson, D.L.; Li, L.; Low, S.; Roughan, M.; Shalunov, S.; Tanaka, R.; Willinger, W. The “robust yet fragile” nature of the Internet. Proc. Natl. Acad. Sci. USA 2005, 102, 14497–14502. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Li, K.; Wang, Y.; Zheng, Y.; Wang, D.; Yang, G.; Yu, X. A systematic mapping study for blockchain based on complex network. Concurr. Comput. Pract. Exp. 2022, 34, e5712. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; Number 92; American Mathematical Soc.: Fresno, CA, USA, 1997. [Google Scholar]
- Spielman, D.A. Algorithms, graph theory, and linear equations in Laplacian matrices. In Proceedings of the International Congress of Mathematicians 2010 (ICM 2010) (In 4 Volumes) Vol. I: Plenary Lectures and Ceremonies Vols. II–IV: Invited Lectures, Hyderabad, India, 19–27 August 2010; World Scientific: Singapore, 2010; pp. 2698–2722. [Google Scholar]
- Iannelli, F.; Koher, A.; Brockmann, D.; Hövel, P.; Sokolov, I.M. Effective distances for epidemics spreading on complex networks. Phys. Rev. E 2017, 95, 012313. [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; Niu, R.; Wu, X.; Fan, R. A new SAIR model on complex networks for analysing the 2019 novel coronavirus (COVID-19). Nonlinear Dyn. 2020, 101, 1777–1787. [Google Scholar] [CrossRef]
- Ding, L.; Liu, S.Y.; Yang, Q.; Xu, X.K. Uncovering the Dependence of Cascading Failures on Network Topology by Constructing Null Models. Entropy 2019, 21, 1119. [Google Scholar] [CrossRef]
- Dobson, I.; Carreras, B.A.; Lynch, V.E.; Newman, D.E. Complex systems analysis of series of blackouts: Cascading failure, critical points, and self-organization. Chaos Interdiscip. J. Nonlinear Sci. 2007, 17, 026103. [Google Scholar] [CrossRef]
- Pond, T.; Magsarjav, S.; South, T.; Mitchell, L.; Bagrow, J.P. Complex contagion features without social reinforcement in a model of social information flow. Entropy 2020, 22, 265. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casillas-Pérez, D.; Del Ser, J.; Casanova-Mateo, C.; Cuadra, L.; Piles, M.; Camps-Valls, G. Persistence in complex systems. Phys. Rep. 2022, 957, 1–73. [Google Scholar] [CrossRef]
- Cuadra, L.; Salcedo-Sanz, S.; Nieto-Borge, J.C. Organic Disordered Semiconductors as Networks Embedded in Space and Energy. Nanomaterials 2022, 12, 4279. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Continuous-time quantum walks: Models for coherent transport on complex networks. Phys. Rep. 2011, 502, 37–87. [Google Scholar] [CrossRef]
- Ma, R.; Yan, C.; Fong, P.W.K.; Yu, J.; Liu, H.; Yin, J.; Huang, J.; Lu, X.; Yan, H.; Li, G. In situ and ex situ investigations on ternary strategy and co-solvent effects towards high-efficiency organic solar cells. Energy Environ. Sci. 2022, 15, 2479–2488. [Google Scholar] [CrossRef]
- Ma, R.; Yan, C.; Yu, J.; Liu, T.; Liu, H.; Li, Y.; Chen, J.; Luo, Z.; Tang, B.; Lu, X.; et al. High-efficiency ternary organic solar cells with a good figure-of-merit enabled by two low-cost donor polymers. ACS Energy Lett. 2022, 7, 2547–2556. [Google Scholar] [CrossRef]
- Cuadra, L.; Nieto-Borge, J.C. Modeling Quantum Dot Systems as Random Geometric Graphs with Probability Amplitude-Based Weighted Links. Nanomaterials 2021, 11, 375. [Google Scholar] [CrossRef]
- Cuadra, L.; Nieto-Borge, J.C. Approaching disordered quantum dot systems by complex networks with spatial and physical-based constraints. Nanomaterials 2021, 11, 2056. [Google Scholar] [CrossRef]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Darázs, Z.; Kiss, T. Pólya number of the continuous-time quantum walks. Phys. Rev. A 2010, 81, 062319. [Google Scholar] [CrossRef]
- Mülken, O.; Volta, A.; Blumen, A. Asymmetries in symmetric quantum walks on two-dimensional networks. Phys. Rev. A 2005, 72, 042334. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Mülken, O. Dynamics of continuous-time quantum walks in restricted geometries. J. Phys. A Math. Theor. 2008, 41, 445301. [Google Scholar] [CrossRef]
- Mülken, O.; Bierbaum, V.; Blumen, A. Coherent exciton transport in dendrimers and continuous-time quantum walks. J. Chem. Phys. 2006, 124, 124905. [Google Scholar] [CrossRef]
- Agliari, E.; Blumen, A.; Muelken, O. Quantum-walk approach to searching on fractal structures. Phys. Rev. A 2010, 82, 012305. [Google Scholar] [CrossRef]
- Blumen, A.; Bierbaum, V.; Mülken, O. Coherent dynamics on hierarchical systems. Phys. A Stat. Mech. Its Appl. 2006, 371, 10–15. [Google Scholar] [CrossRef]
- Mülken, O.; Blumen, A. Slow transport by continuous time quantum walks. Phys. Rev. E 2005, 71, 016101. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.P.; Li, W.; Liu, F. Coherent transport on Apollonian networks and continuous-time quantum walks. Phys. Rev. E 2008, 78, 052103. [Google Scholar] [CrossRef]
- Salimi, S. Continuous-time quantum walks on star graphs. Ann. Phys. 2009, 324, 1185–1193. [Google Scholar] [CrossRef]
- Anishchenko, A.; Blumen, A.; Mülken, O. Enhancing the spreading of quantum walks on star graphs by additional bonds. Quantum Inf. Process. 2012, 11, 1273–1286. [Google Scholar] [CrossRef]
- Miller, A.; Abrahams, E. Impurity conduction at low concentrations. Phys. Rev. 1960, 120, 745. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random walks and diffusion on networks. Phys. Rep. 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Yang, J.; Hu, H.; Lv, Y.; Yuan, M.; Wang, B.; He, Z.; Chen, S.; Wang, Y.; Hu, Z.; Yu, M.; et al. Ligand-Engineered HgTe Colloidal Quantum Dot Solids for Infrared Photodetectors. Nano Lett. 2022, 22, 3465–3472. [Google Scholar] [CrossRef]
- Martí, A.; Cuadra, L.; Luque, A. Quasi-drift diffusion model for the quantum dot intermediate band solar cell. IEEE Trans. Electron Devices 2002, 49, 1632–1639. [Google Scholar] [CrossRef]
- Christodoulou, S.; Ramiro, I.; Othonos, A.; Figueroba, A.; Dalmases, M.; Ozdemir, O.; Pradhan, S.; Itskos, G.; Konstantatos, G. Single-exciton gain and stimulated emission across the infrared telecom band from robust heavily doped PbS colloidal quantum dots. Nano Lett. 2020, 20, 5909–5915. [Google Scholar] [CrossRef]
- Green, M.A. Solar Cells: Operating Principles, Technology, and System Applications; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Archer, M.D.; Green, M.A. Clean Electricity from Photovoltaics; World Scientific: Singapore, 2014; Volume 4. [Google Scholar]
- Pierret, R.F.; Neudeck, G.W. Advanced Semiconductor Fundamentals; Addison-Wesley: Reading, MA, USA, 1987; Volume 6. [Google Scholar]
- Baranovskii, S.D. Mott lecture: Description of charge transport in disordered organic semiconductors: Analytical theories and computer simulations. Phys. Status Solidi a 2018, 215, 1700676. [Google Scholar] [CrossRef]
- Baranovskii, S. Theoretical description of charge transport in disordered organic semiconductors. Phys. Status Solidi b 2014, 251, 487–525. [Google Scholar] [CrossRef]
- Pollak, M.; Shklovskii, B. Hopping Transport in Solids; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Marcus, R.A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Martínez, A.G.; Gómez, P.C.; de la Moya, S.; Siehl, H.U. Structural proton transfer rates in pure water according to Marcus theory and TD-DFT computations. J. Mol. Liq. 2022, 357, 119048. [Google Scholar] [CrossRef]
- Serdiuk, I.E.; Monka, M.; Kozakiewicz, K.; Liberek, B.; Bojarski, P.; Park, S.Y. Vibrationally Assisted Direct Intersystem Crossing between the Same Charge-Transfer States for Thermally Activated Delayed Fluorescence: Analysis by Marcus–Hush Theory Including Reorganization Energy. J. Phys. Chem. B 2021, 125, 2696–2706. [Google Scholar] [CrossRef]
- Sowa, J.K.; Mol, J.A.; Briggs, G.A.D.; Gauger, E.M. Beyond Marcus theory and the Landauer-Büttiker approach in molecular junctions: A unified framework. J. Chem. Phys. 2018, 149, 154112. [Google Scholar] [CrossRef]
- Koch, A.; Kinzel, D.; Dröge, F.; Gräfe, S.; Kupfer, S. Photochemistry and Electron Transfer Kinetics in a Photocatalyst Model Assessed by Marcus Theory and Quantum Dynamics. J. Phys. Chem. C 2017, 121, 16066–16078. [Google Scholar] [CrossRef]
- Roy, S.; Baer, M.D.; Mundy, C.J.; Schenter, G.K. Marcus theory of ion-pairing. J. Chem. Theory Comput. 2017, 13, 3470–3477. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Halperin, B.; Langer, J. Hopping conductivity in disordered systems. Phys. Rev. B 1971, 4, 2612. [Google Scholar] [CrossRef]
- Ding, X.; Jiang, T. Spectral distributions of adjacency and Laplacian matrices of random graphs. Ann. Appl. Probab. 2010, 20, 2086–2117. [Google Scholar] [CrossRef]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Kulvelis, N.; Dolgushev, M.; Mülken, O. Universality at breakdown of quantum transport on complex networks. Phys. Rev. Lett. 2015, 115, 120602. [Google Scholar] [CrossRef] [PubMed]
- Cuadra, L.; Martí, A.; López, N.; Luque, A. Phonon bottleneck effect and photon absorption in self-ordered quantum dot intermediate band solar cells. In Proceedings of the 19th European Photovoltaic Solar Energy Conference, Paris, France, 7–11 June 2004; WIP-Renewable Energies and ETA: Munich, Germany, 2004; pp. 250–254. [Google Scholar]
- Kennehan, E.R.; Doucette, G.S.; Marshall, A.R.; Grieco, C.; Munson, K.T.; Beard, M.C.; Asbury, J.B. Electron–Phonon Coupling and Resonant Relaxation from 1D and 1P States in PbS Quantum Dots. ACS Nano 2018, 12, 6263–6272. [Google Scholar] [CrossRef] [PubMed]
- Dodin, A. Transport and Fluctuations at the Nanoscale. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2020. [Google Scholar]
- Lee, D.; Kahng, B.; Cho, Y.; Goh, K.I.; Lee, D.S. Recent advances of percolation theory in complex networks. J. Korean Phys. Soc. 2018, 73, 152–164. [Google Scholar] [CrossRef]
- Böhme, G.A. Emergence and persistence of diversity in complex networks. Eur. Phys. J. Spec. Top. 2013, 222, 3089–3169. [Google Scholar] [CrossRef]
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]

| Parameter | Symbol | Value |
|---|---|---|
| Density of quantum dots | Variable | |
| Size of quantum dots | 4 nm | |
| Effective density of states in the CB | cm | |
| Effective density of states in the VB | cm | |
| Absorption coefficient causing transitions IB → CV | cm | |
| Absorption coefficient causing transitions VB → IB | cm | |
| Electron lifetime | 100 ps | |
| Hole lifetime | 50 ps | |
| Electron diffusivity | 10 cm s | |
| Hole diffusivity | 8 cm s | |
| Electron mobility | cm V s | |
| Hole mobility | cm V s | |
| Electron diffusion length | 316 nm | |
| Hole diffusion length | 200 nm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuadra, L.; Salcedo-Sanz, S.; Nieto-Borge, J.C. Carrier Transport in Colloidal Quantum Dot Intermediate Band Solar Cell Materials Using Network Science. Int. J. Mol. Sci. 2023, 24, 3797. https://doi.org/10.3390/ijms24043797
Cuadra L, Salcedo-Sanz S, Nieto-Borge JC. Carrier Transport in Colloidal Quantum Dot Intermediate Band Solar Cell Materials Using Network Science. International Journal of Molecular Sciences. 2023; 24(4):3797. https://doi.org/10.3390/ijms24043797
Chicago/Turabian StyleCuadra, Lucas, Sancho Salcedo-Sanz, and José Carlos Nieto-Borge. 2023. "Carrier Transport in Colloidal Quantum Dot Intermediate Band Solar Cell Materials Using Network Science" International Journal of Molecular Sciences 24, no. 4: 3797. https://doi.org/10.3390/ijms24043797
APA StyleCuadra, L., Salcedo-Sanz, S., & Nieto-Borge, J. C. (2023). Carrier Transport in Colloidal Quantum Dot Intermediate Band Solar Cell Materials Using Network Science. International Journal of Molecular Sciences, 24(4), 3797. https://doi.org/10.3390/ijms24043797









