Mechanical Properties of Twisted Carbon Nanotube Bundles with Carbon Linkers from Molecular Dynamics Simulations
Abstract
1. Introduction
2. Materials and Methods
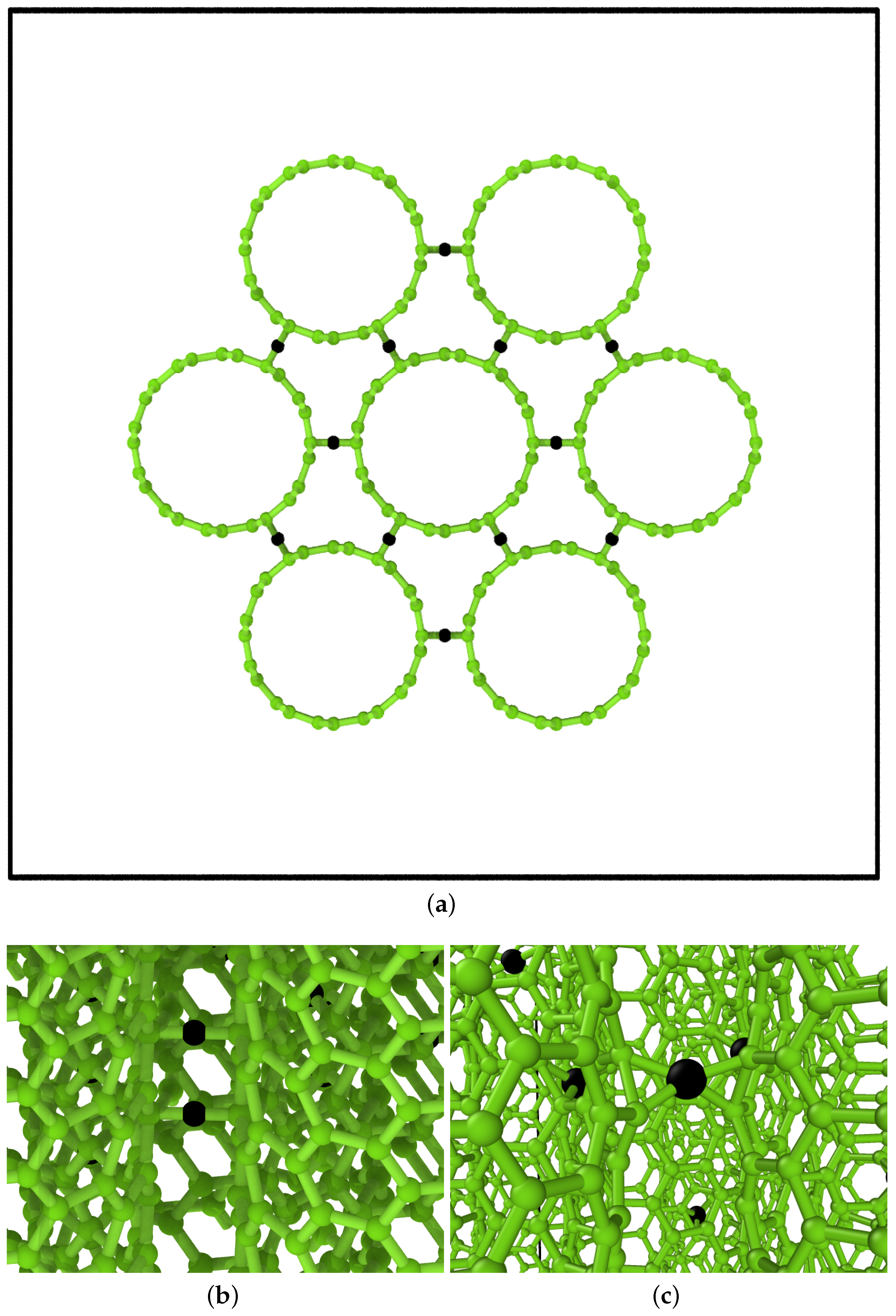
- a
- Finite-length bundles with or without linkers made by bare CNTs for the evaluation of the intertube interaction. We also used these samples for the assessment of the ReboScr2 and DRIP potentials. For this first type of system, we performed pull-out tests. The samples were set up in 20 nm-length bundles composed of seven CNTs.
- b
- Continuous straight and twisted CNT bundles with or without linkers. In these systems, the periodicity was added to the seven CNT bundles via a periodic supercell with a longitudinal dimension of 20 nm. The model represents the physical case of a bundle composed of extra-long nanotubes.
- c
- Periodic bundles composed of finite-length CNT bundles with or without linkers for the evaluation of linkers–twisting coupling. For these bundles composed of finite-length CNTs, we shifted the outer CNT of the bundle, alternatively, up and down for 5 nm, then set up a periodic cell of 20 nm. The model represents the physical case of a long bundle composed of short nanotubes.
3. Results
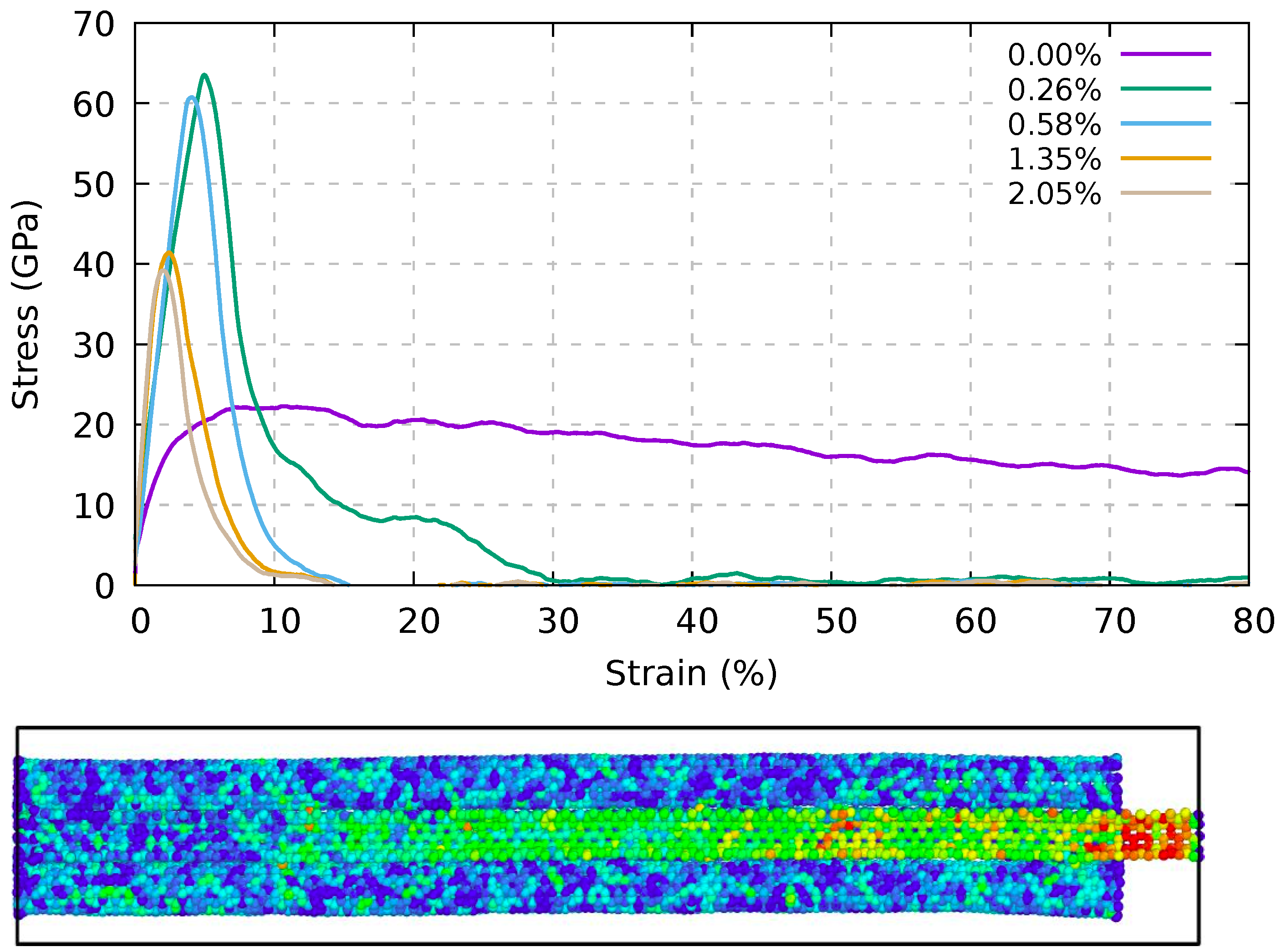
3.1. Pull-Out Test from a Nanotube Bundle
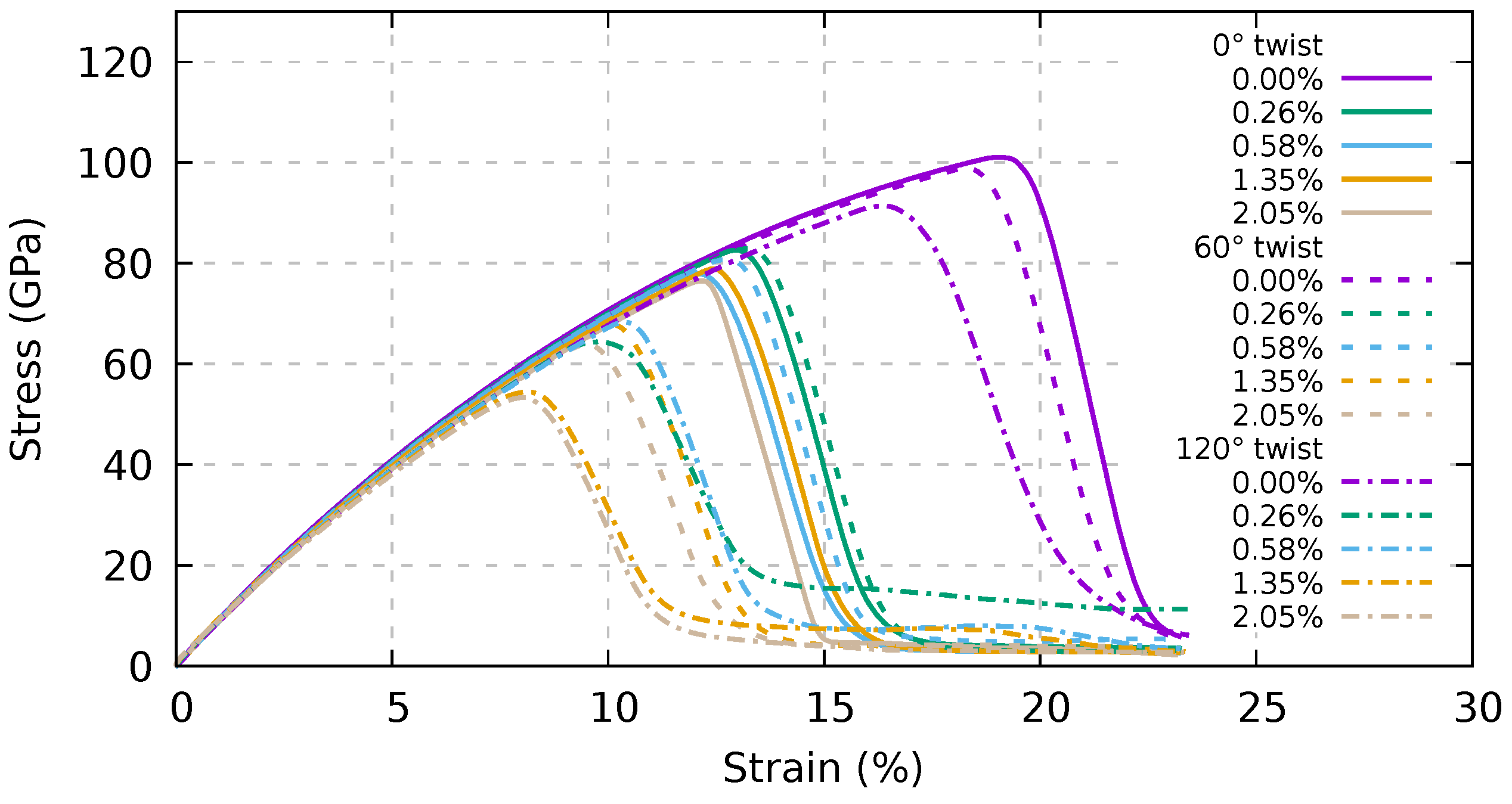
3.2. Twisted Bundles Composed of Extra-Long Nanotubes under Tension
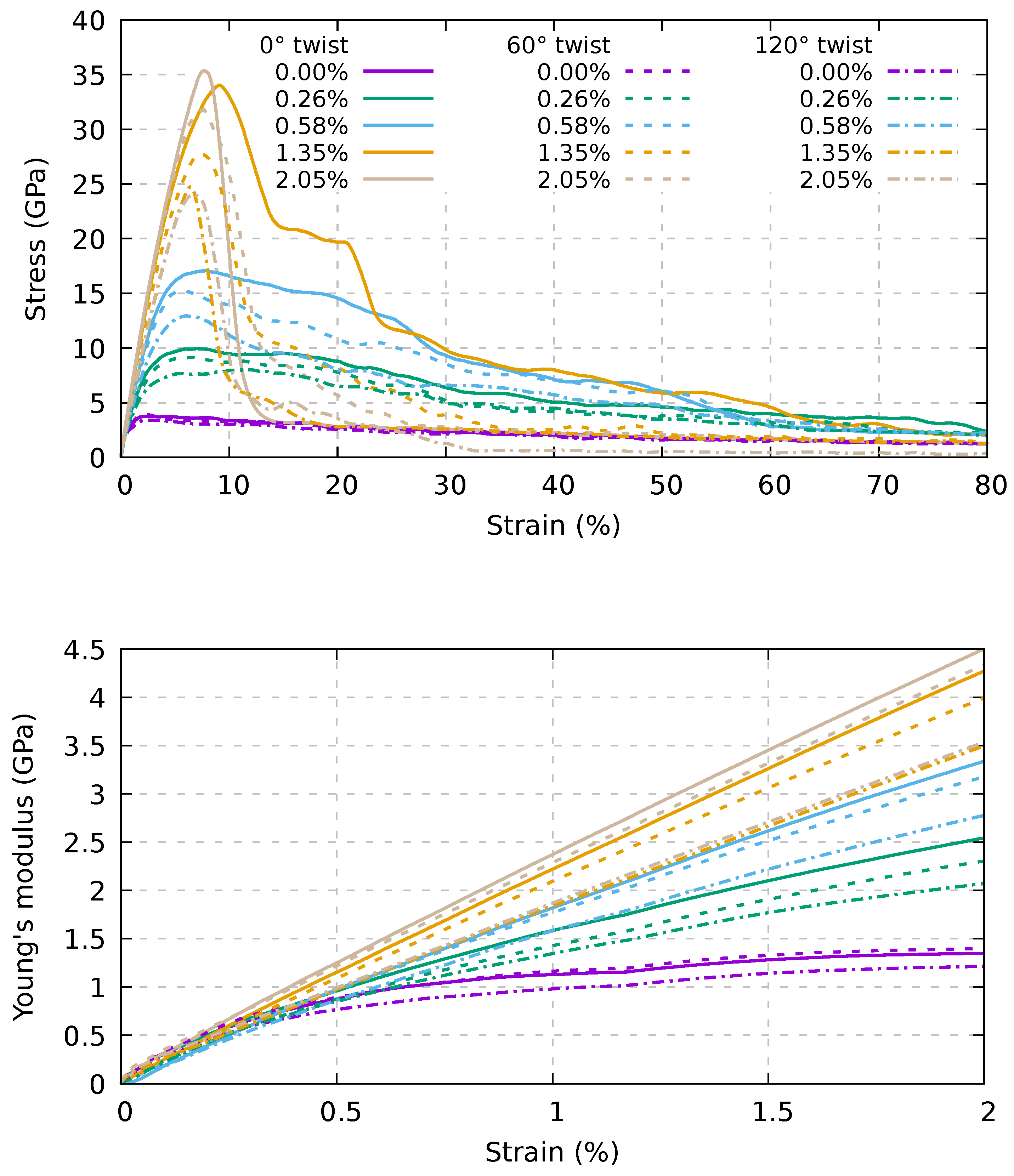
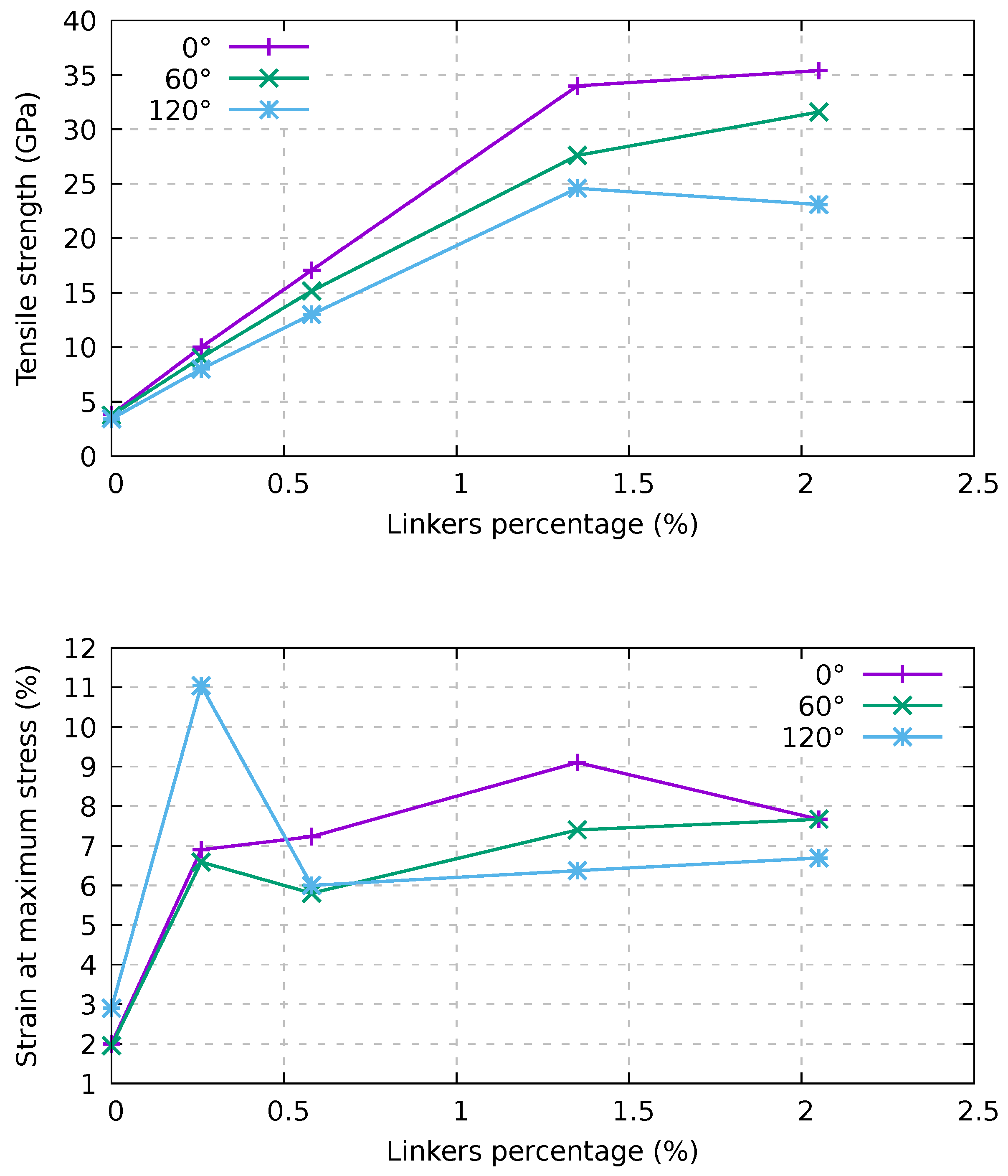
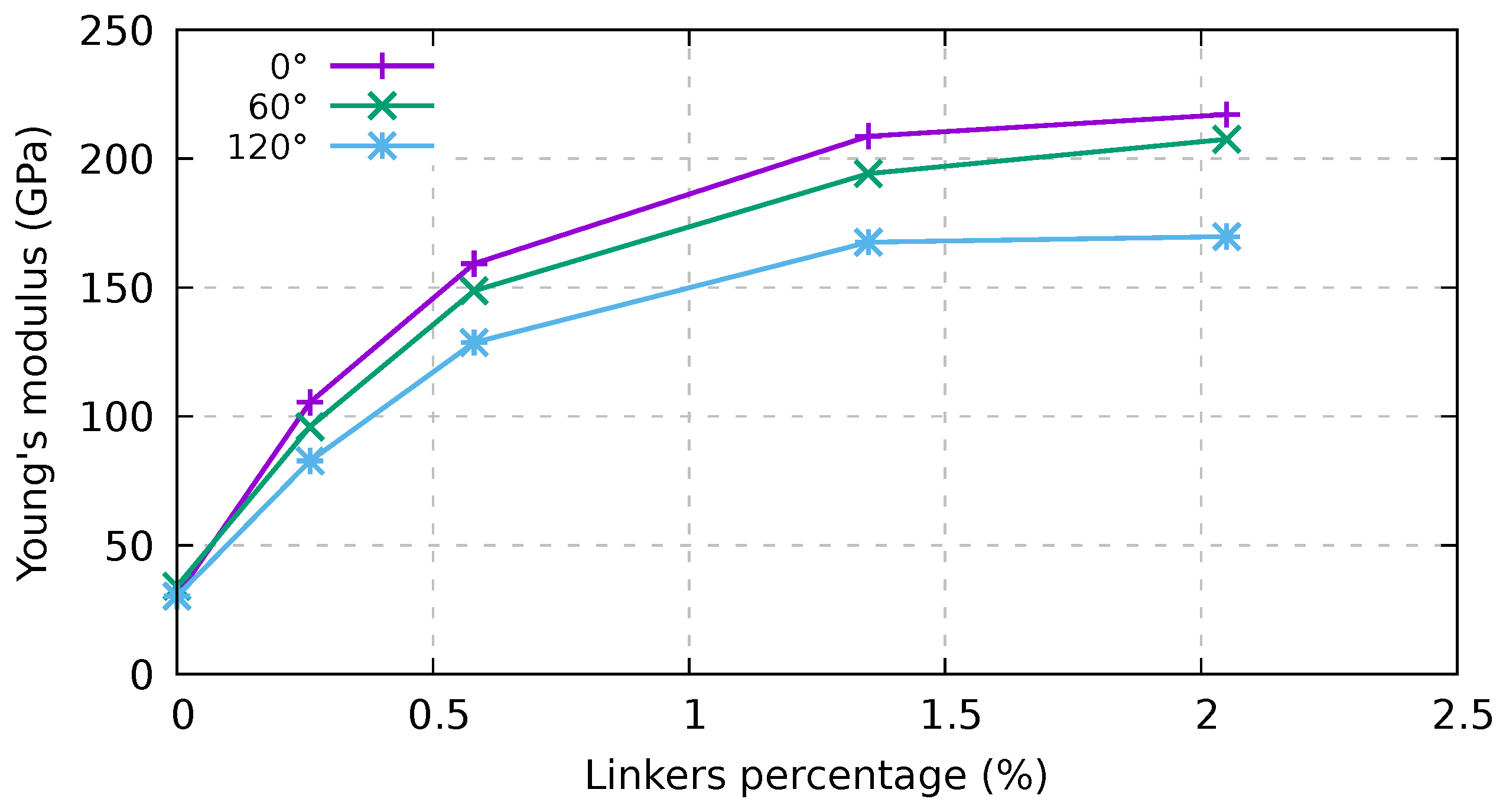
3.3. Twisted Bundles Composed of Short Nanotubes under Tension
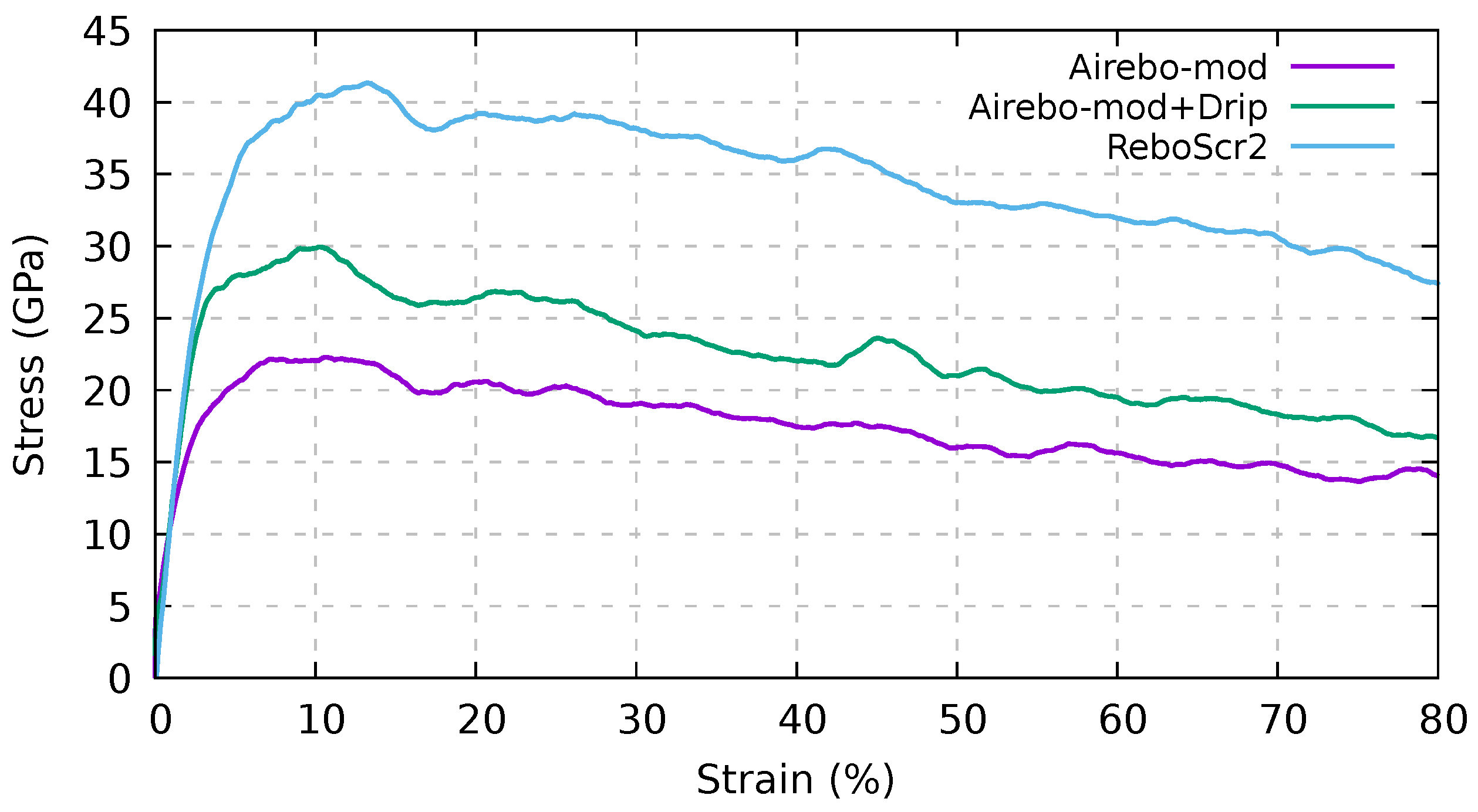
3.4. Test of Novel Potentials by Means of Pull-Out Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pugno, N.M. On the strength of the carbon nanotube-based space elevator cable: From nanomechanics to megamechanics. J. Phys. Condens. Matter 2006, 18, S1971–S1990. [Google Scholar] [CrossRef]
- Pugno, N. The role of defects in the design of space elevator cable: From nanotube to megatube. Acta Mater. 2007, 55, 5269–5279. [Google Scholar] [CrossRef]
- Pugno, N.M.; Bosia, F.; Carpinteri, A. Multiscale Stochastic Simulations for Tensile Testing of Nanotube-Based Macroscopic Cables. Small 2008, 4, 1044–1052. [Google Scholar] [CrossRef] [PubMed]
- Signetti, S.; Taioli, S.; Pugno, N.M. 2D Material Armors Showing Superior Impact Strength of Few Layers. ACS Appl. Mater. Interfaces 2017, 9, 40820–40830. [Google Scholar] [CrossRef] [PubMed]
- Taioli, S. Enabling Materials By Dimensionality: From 0D to 3D Carbon-Based Nanostructures. In Theoretical Chemistry for Advanced Nanomaterials: Functional Analysis by Computation and Experiment; Springer: Singapore, 2020; pp. 135–200. [Google Scholar]
- Azzolini, M.; Morresi, T.; Garberoglio, G.; Calliari, L.; Pugno, N.M.; Taioli, S.; Dapor, M. Monte Carlo simulations of measured electron energy-loss spectra of diamond and graphite: Role of dielectric-response models. Carbon 2017, 118, 299. [Google Scholar] [CrossRef]
- Krishnan, A.; Dujardin, E.; Ebbesen, T.W.; Yianilos, P.N.; Treacy, M.M.J. Young’s modulus of single-walled nanotubes. Phys. Rev. B 1998, 58, 14013–14019. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, R.; Ye, X.; Zhu, Z.; Xie, H.; Shen, B.; Cai, D.; Liu, B.; Zhang, C.; Jia, Z.; et al. Carbon nanotube bundles with tensile strength over 80 GPa. Nat. Nanotechnol. 2018, 13, 589–595. [Google Scholar] [CrossRef]
- Qian, D. Load transfer mechanism in carbon nanotube ropes. Compos. Sci. Technol. 2003, 63, 1561–1569. [Google Scholar] [CrossRef]
- Ericson, L.M. Macroscopic, Neat, Single-Walled Carbon Nanotube Fibers. Science 2004, 305, 1447–1450. [Google Scholar] [CrossRef]
- Koziol, K.; Vilatela, J.; Moisala, A.; Motta, M.; Cunniff, P.; Sennett, M.; Windle, A. High-Performance Carbon Nanotube Fiber. Science 2007, 318, 1892–1895. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, L.; Minus, M.L.; Chae, H.G.; Jagannathan, S.; Wong, C.P.; Kowalik, J.; Roberson, L.B.; Kumar, S. Solid-state spun fibers and yarns from 1-mm long carbon nanotube forests synthesized by water-assisted chemical vapor deposition. J. Mater. Sci. 2008, 43, 4356–4362. [Google Scholar] [CrossRef]
- Pugno, N.M. Young’s modulus reduction of defective nanotubes. Appl. Phys. Lett. 2007, 90, 043106. [Google Scholar] [CrossRef]
- Liu, X.; Lu, W.; Ayala, O.M.; Wang, L.P.; Karlsson, A.M.; Yang, Q.; Chou, T.W. Microstructural evolution of carbon nanotube fibers: Deformation and strength mechanism. Nanoscale 2013, 5, 2002–2008. [Google Scholar] [CrossRef] [PubMed]
- Mirzaeifar, R.; Qin, Z.; Buehler, M.J. Mesoscale mechanics of twisting carbon nanotube yarns. Nanoscale 2015, 7, 5435–5445. [Google Scholar] [CrossRef] [PubMed]
- Jiang, K.; Li, Q.; Fan, S. Spinning continuous carbon nanotube yarns. Nature 2002, 419, 801. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M. Multifunctional Carbon Nanotube Yarns by Downsizing an Ancient Technology. Science 2004, 306, 1358–1361. [Google Scholar] [CrossRef] [PubMed]
- Park, O.K.; Choi, H.; Jeong, H.; Jung, Y.; Yu, J.; Lee, J.K.; Hwang, J.Y.; Kim, S.M.; Jeong, Y.; Park, C.R.; et al. High-modulus and strength carbon nanotube fibers using molecular cross-linking. Carbon 2017, 118, 413–421. [Google Scholar] [CrossRef]
- Cornwell, C.F.; Welch, C.R. Brittle ductile transition in carbon nanotube bundles. Mol. Simul. 2012, 38, 1032–1037. [Google Scholar] [CrossRef]
- Kis, A.; Csányi, G.; Salvetat, J.P.; Lee, T.N.; Couteau, E.; Kulik, A.J.; Benoit, W.; Brugger, J.; Forró, L. Reinforcement of single-walled carbon nanotube bundles by intertube bridging. Nat. Mater. 2004, 3, 153–157. [Google Scholar] [CrossRef]
- Pregler, S.K.; Sinnott, S.B. Molecular dynamics simulations of electron and ion beam irradiation of multiwalled carbon nanotubes: The effects on failure by inner tube sliding. Phys. Rev. B 2006, 73, 224106. [Google Scholar] [CrossRef]
- Peng, K.; Jie, J.; Zhang, W.; Lee, S.T. Silicon nanowires for rechargeable lithium-ion battery anodes. Appl. Phys. Lett. 2008, 93, 033105. [Google Scholar] [CrossRef]
- Pomoell, J.A.V.; Krasheninnikov, A.V.; Nordlund, K.; Keinonen, J. Ion ranges and irradiation-induced defects in multiwalled carbon nanotubes. J. Appl. Phys. 2004, 96, 2864–2871. [Google Scholar] [CrossRef]
- Federizzi, R.L.; Moura, C.S.; Amaral, L. Polymerization of Carbon Nanotubes through Self-Irradiation. J. Phys. Chem. B 2006, 110, 23215–23220. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, N.; McCarthy, M.; Curtin, W. Improved inter-tube coupling in CNT bundles through carbon ion irradiation. Carbon 2013, 51, 173–184. [Google Scholar] [CrossRef]
- Meyer, J.C.; Girit, C.O.; Crommie, M.F.; Zettl, A. Imaging and dynamics of light atoms and molecules on graphene. Nature 2008, 454, 319–322. [Google Scholar] [CrossRef] [PubMed]
- Ataca, C.; Aktürk, E.; Şahin, H.; Ciraci, S. Adsorption of carbon adatoms to graphene and its nanoribbons. J. Appl. Phys. 2011, 109, 013704. [Google Scholar] [CrossRef]
- Liang, X.; Gao, Y.; Duan, J.; Liu, Z.; Fang, S.; Baughman, R.H.; Jiang, L.; Cheng, Q. Enhancing the strength, toughness, and electrical conductivity of twist-spun carbon nanotube yarns by π bridging. Carbon 2019, 150, 268–274. [Google Scholar] [CrossRef]
- Li, W.; Zhao, J.; Xue, Y.; Ren, X.; Zhang, X.; Li, Q. Merge multiple carbon nanotube fibers into a robust yarn. Carbon 2019, 145, 266–272. [Google Scholar] [CrossRef]
- Gupta, N.; Alred, J.M.; Penev, E.S.; Yakobson, B.I. Universal Strength Scaling in Carbon Nanotube Bundles with Frictional Load Transfer. ACS Nano 2020, 15, 1342–1350. [Google Scholar] [CrossRef]
- Silvestre, N.; Faria, B.; Canongia Lopes, J.N. A molecular dynamics study on the thickness and post-critical strength of carbon nanotubes. Compos. Struct. 2012, 94, 1352–1358. [Google Scholar] [CrossRef]
- Faria, B.; Silvestre, N.; Canongia Lopes, J.N. Interaction diagrams for carbon nanotubes under combined shortening–twisting. Compos. Sci. Technol. 2011, 71, 1811–1818. [Google Scholar] [CrossRef]
- Huhtala, M.; Krasheninnikov, A.V.; Aittoniemi, J.; Stuart, S.J.; Nordlund, K.; Kaski, K. Improved mechanical load transfer between shells of multiwalled carbon nanotubes. Phys. Rev. B 2004, 70, 045404. [Google Scholar] [CrossRef]
- Majure, D.; Haskins, R.; Lee, N.; Ebeling, R.; Maier, R.; Marsh, C.; Bednar, A.; Kirgan, R.; Welch, C.; Cornwell, C.F. Large-Scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) Simulations of the Effects of Chirality and Diameter on the Pullout Force in a Carbon Nanotube Bundle. In Proceedings of the 2008 DoD HPCMP Users Group Conference, Seattle, WA, USA, 14–17 July 2008. [Google Scholar]
- Cornwell, C.; Majure, D.; Haskins, R.; Lee, N.; Ebeling, R.; Maier, R.; Marsh, C.; Bednar, A.; Kirgan, R.; Welch, C. Critical Carbon Nanotube Length in Fibers. In Proceedings of the 2008 DoD HPCMP Users Group Conference, Seattle, WA, USA, 14–17 July 2008. [Google Scholar]
- Ke, C.; Zheng, M.; Zhou, G.; Cui, W.; Pugno, N.; Miles, R.N. Mechanical Peeling of Free-Standing Single-Walled Carbon-Nanotube Bundles. Small 2010, 6, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Pugno, N.M. The design of self-collapsed super-strong nanotube bundles. J. Mech. Phys. Solids 2010, 58, 1397–1410. [Google Scholar] [CrossRef]
- Pugno, N.; Bosia, F.; Carpinteri, A. Size effects on the strength of nanotube bundles. Meas. Sci. Technol. 2009, 20, 084028. [Google Scholar] [CrossRef]
- Filleter, T.; Bernal, R.; Li, S.; Espinosa, H. Ultrahigh Strength and Stiffness in Cross-Linked Hierarchical Carbon Nanotube Bundles. Adv. Mater. 2011, 23, 2855–2860. [Google Scholar] [CrossRef]
- Filleter, T.; Yockel, S.; Naraghi, M.; Paci, J.T.; Compton, O.C.; Mayes, M.L.; Nguyen, S.T.; Schatz, G.C.; Espinosa, H.D. Experimental-Computational Study of Shear Interactions within Double-Walled Carbon Nanotube Bundles. Nano Lett. 2012, 12, 732–742. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472. [Google Scholar] [CrossRef]
- Pedrielli, A.; Taioli, S.; Garberoglio, G.; Pugno, N.M. Designing graphene based nanofoams with nonlinear auxetic and anisotropic mechanical properties under tension or compression. Carbon 2017, 111, 796–806. [Google Scholar] [CrossRef]
- Pedrielli, A.; Taioli, S.; Garberoglio, G.; Pugno, N.M. Mechanical and thermal properties of graphene random nanofoams via Molecular Dynamics simulations. Carbon 2018, 132, 766–775. [Google Scholar] [CrossRef]
- Shenderova, O.A.; Brenner, D.W.; Omeltchenko, A.; Su, X.; Yang, L.H. Atomistic modeling of the fracture of polycrystalline diamond. Phys. Rev. B 2000, 61, 3877–3888. [Google Scholar] [CrossRef]
- Pastewka, L.; Pou, P.; Pérez, R.; Gumbsch, P.; Moseler, M. Describing bond-breaking processes by reactive potentials: Importance of an environment-dependent interaction range. Phys. Rev. B 2008, 78, 161402. [Google Scholar] [CrossRef]
- Wen, M.; Carr, S.; Fang, S.; Kaxiras, E.; Tadmor, E.B. Dihedral-angle-corrected registry-dependent interlayer potential for multilayer graphene structures. Phys. Rev. B 2018, 98, 235404. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 1988, 37, 6991–7000. [Google Scholar] [CrossRef]
- McCarthy, M.A.; Byrne, E.M.; O’Brien, N.P.; Murmu, T. Improved Mechanical Performance of CNTs and CNT Fibres in Nanocomposites Through Inter-Wall and Inter-Tube Coupling. In Springer Series in Materials Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; pp. 1–56. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B 2004, 69, 134103. [Google Scholar] [CrossRef]
- Tuckerman, M.E.; Alejandre, J.; López-Rendón, R.; Jochim, A.L.; Martyna, G.J. A Liouville-operator derived measure-preserving integrator for molecular dynamics simulations in the isothermal–isobaric ensemble. J. Phys. A Math. Gen. 2006, 39, 5629–5651. [Google Scholar] [CrossRef]
- Thompson, A.P.; Plimpton, S.J.; Mattson, W. General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions. J. Chem. Phys. 2009, 131, 154107. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- Nath, S.K.D.; Kim, S.G. Study of the Nanomechanics of CNTs under Tension by Molecular Dynamics Simulation Using Different Potentials. ISRN Condens. Matter Phys. 2014, 2014, 60601. [Google Scholar]
- Shiryaev, A.A.; Hinks, J.A.; Marks, N.A.; Greaves, G.; Valencia, F.J.; Donnelly, S.E.; González, R.I.; Kiwi, M.; Trigub, A.L.; Bringa, E.M.; et al. Ion implantation in nanodiamonds: Size effect and energy dependence. Sci. Rep. 2018, 8, 5099. [Google Scholar] [CrossRef] [PubMed]
- Tangarife, E.; Gonzalez, R.; Cardenas, C.; Bringa, E.; Munoz, F. Molecular simulations of carbon allotropes in processes with creation and destruction of chemical bonds. Carbon 2019, 144, 177–184. [Google Scholar] [CrossRef]
- Aparicio, E.; Tangarife, E.; Munoz, F.; Gonzalez, R.I.; Valencia, F.J.; Careglio, C.; Bringa, E.M. Simulated mechanical properties of finite-size graphene nanoribbons. Nanotechnology 2020, 32, 045709. [Google Scholar] [CrossRef]
- Pavia, F.; Curtin, W. Interfacial sliding in carbon nanotube/diamond matrix composites. Acta Mater. 2011, 59, 6700–6709. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pedrielli, A.; Dapor, M.; Gkagkas, K.; Taioli, S.; Pugno, N.M. Mechanical Properties of Twisted Carbon Nanotube Bundles with Carbon Linkers from Molecular Dynamics Simulations. Int. J. Mol. Sci. 2023, 24, 2473. https://doi.org/10.3390/ijms24032473
Pedrielli A, Dapor M, Gkagkas K, Taioli S, Pugno NM. Mechanical Properties of Twisted Carbon Nanotube Bundles with Carbon Linkers from Molecular Dynamics Simulations. International Journal of Molecular Sciences. 2023; 24(3):2473. https://doi.org/10.3390/ijms24032473
Chicago/Turabian StylePedrielli, Andrea, Maurizio Dapor, Konstantinos Gkagkas, Simone Taioli, and Nicola Maria Pugno. 2023. "Mechanical Properties of Twisted Carbon Nanotube Bundles with Carbon Linkers from Molecular Dynamics Simulations" International Journal of Molecular Sciences 24, no. 3: 2473. https://doi.org/10.3390/ijms24032473
APA StylePedrielli, A., Dapor, M., Gkagkas, K., Taioli, S., & Pugno, N. M. (2023). Mechanical Properties of Twisted Carbon Nanotube Bundles with Carbon Linkers from Molecular Dynamics Simulations. International Journal of Molecular Sciences, 24(3), 2473. https://doi.org/10.3390/ijms24032473







