Energy Deposition around Swift Carbon-Ion Tracks in Liquid Water
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Models for the Electronic Excitation Spectrum of Liquid Water
2.1.1. MELF-GOS Optical-Data Model
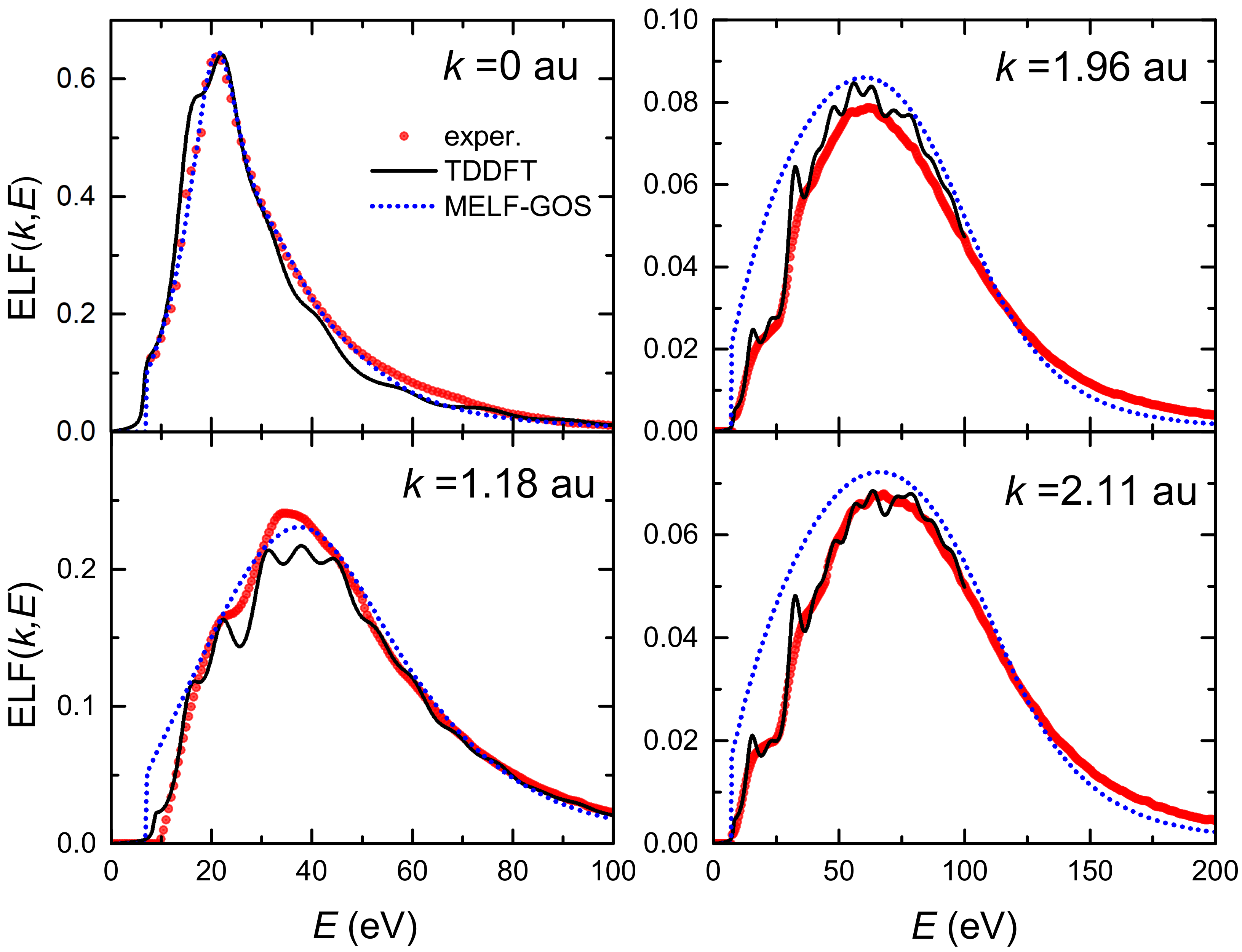
2.1.2. Linear-Response Time-Dependent Density Functional Theory
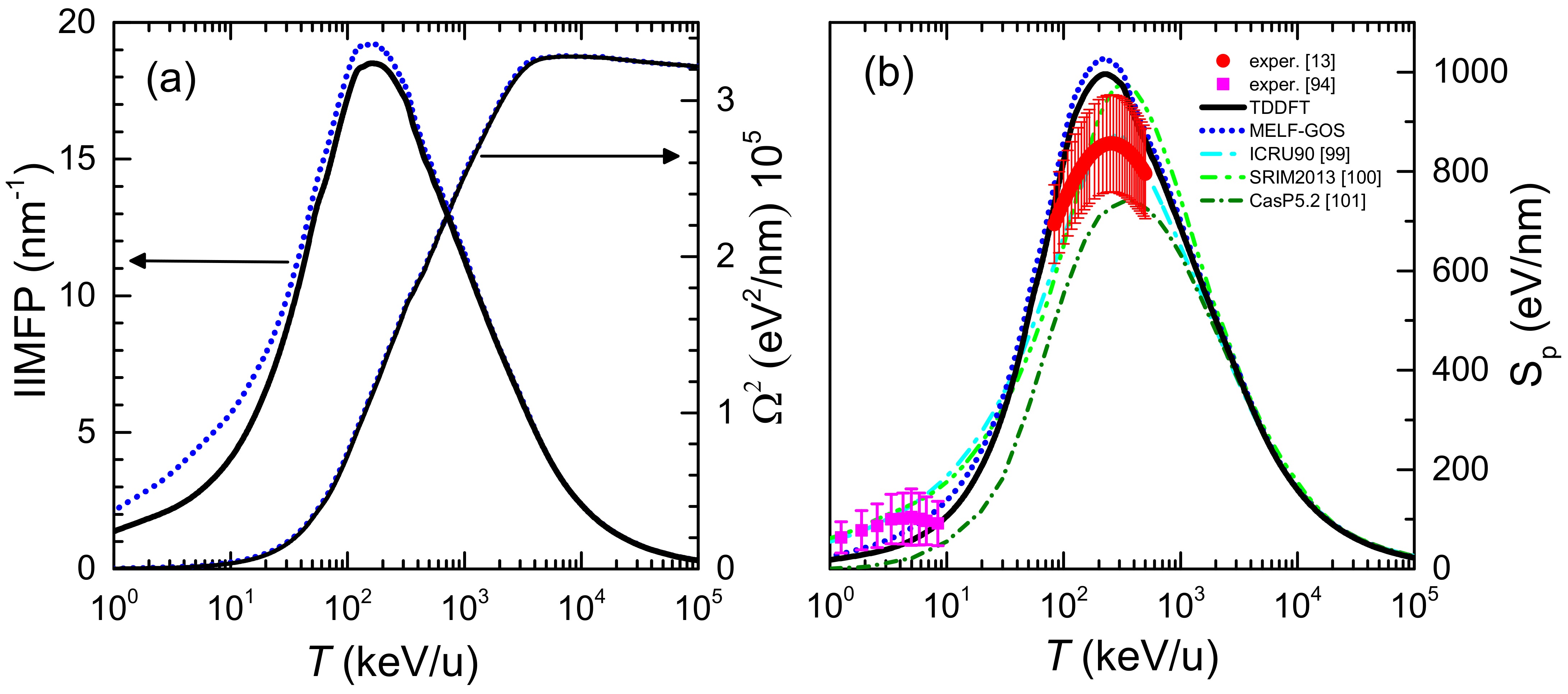
2.2. Energy Loss of Swift Carbon Ions in Liquid Water
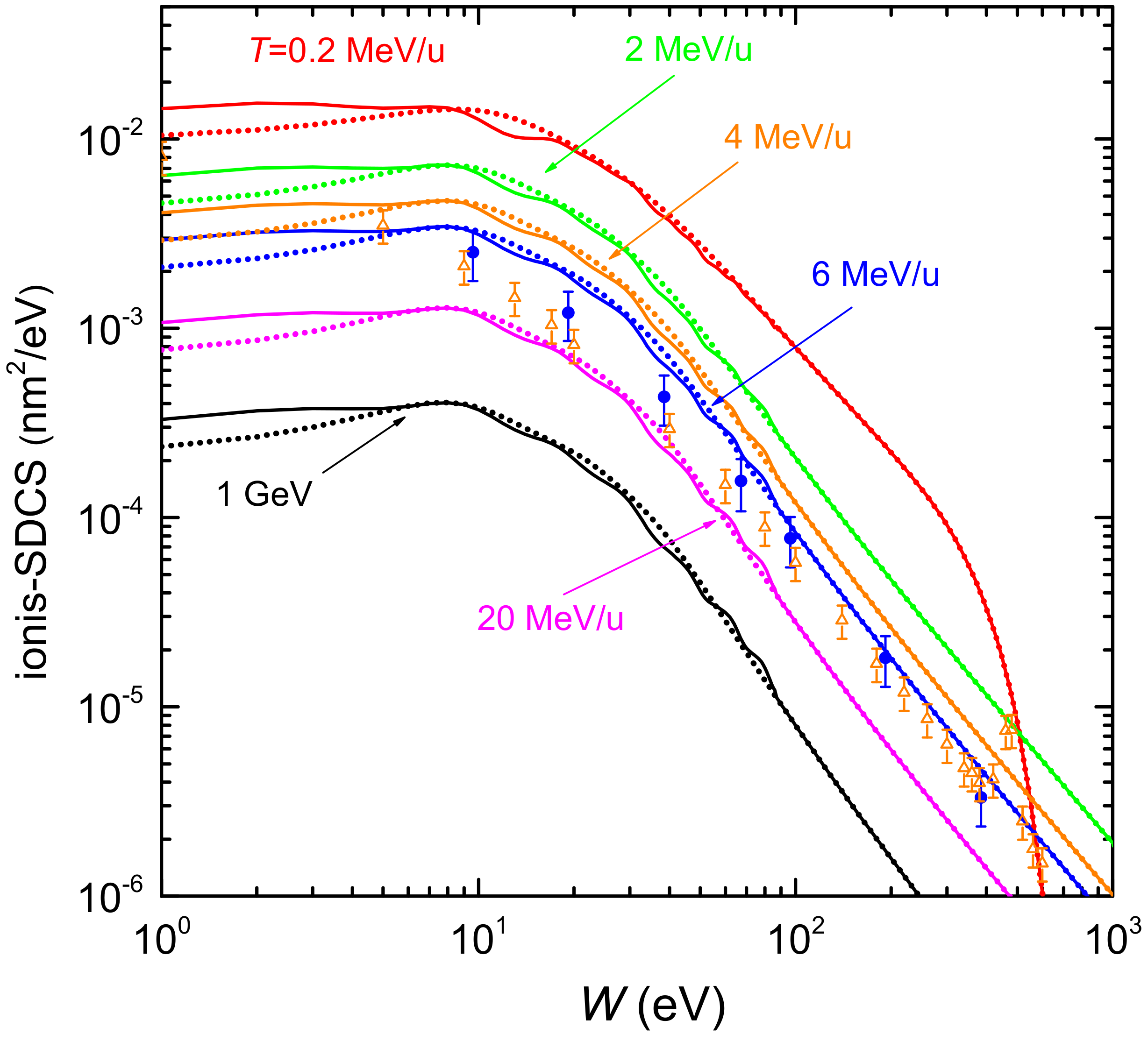
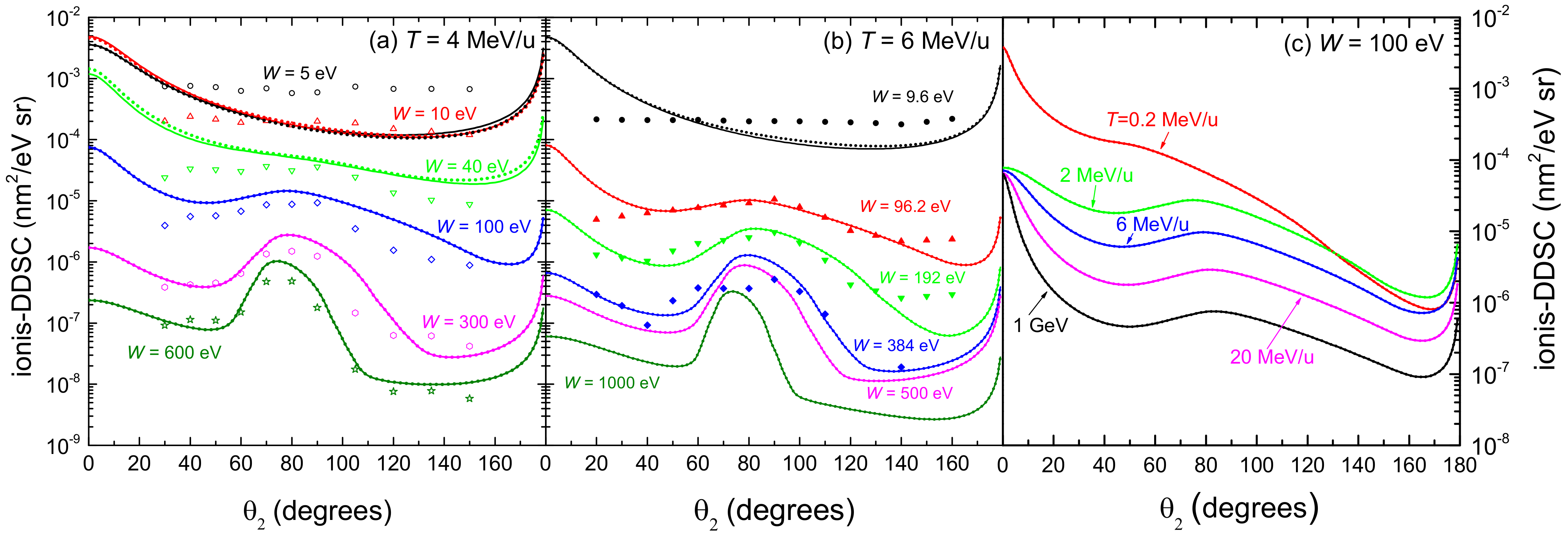
2.3. Angular and Energy cross Sections of Electrons Generated by Energetic Carbon Ions
2.4. Cross Sections for Electrons in Liquid Water
2.4.1. Elastic cross Section of an Electron with a Water Molecule Obtained by the Mott Theory
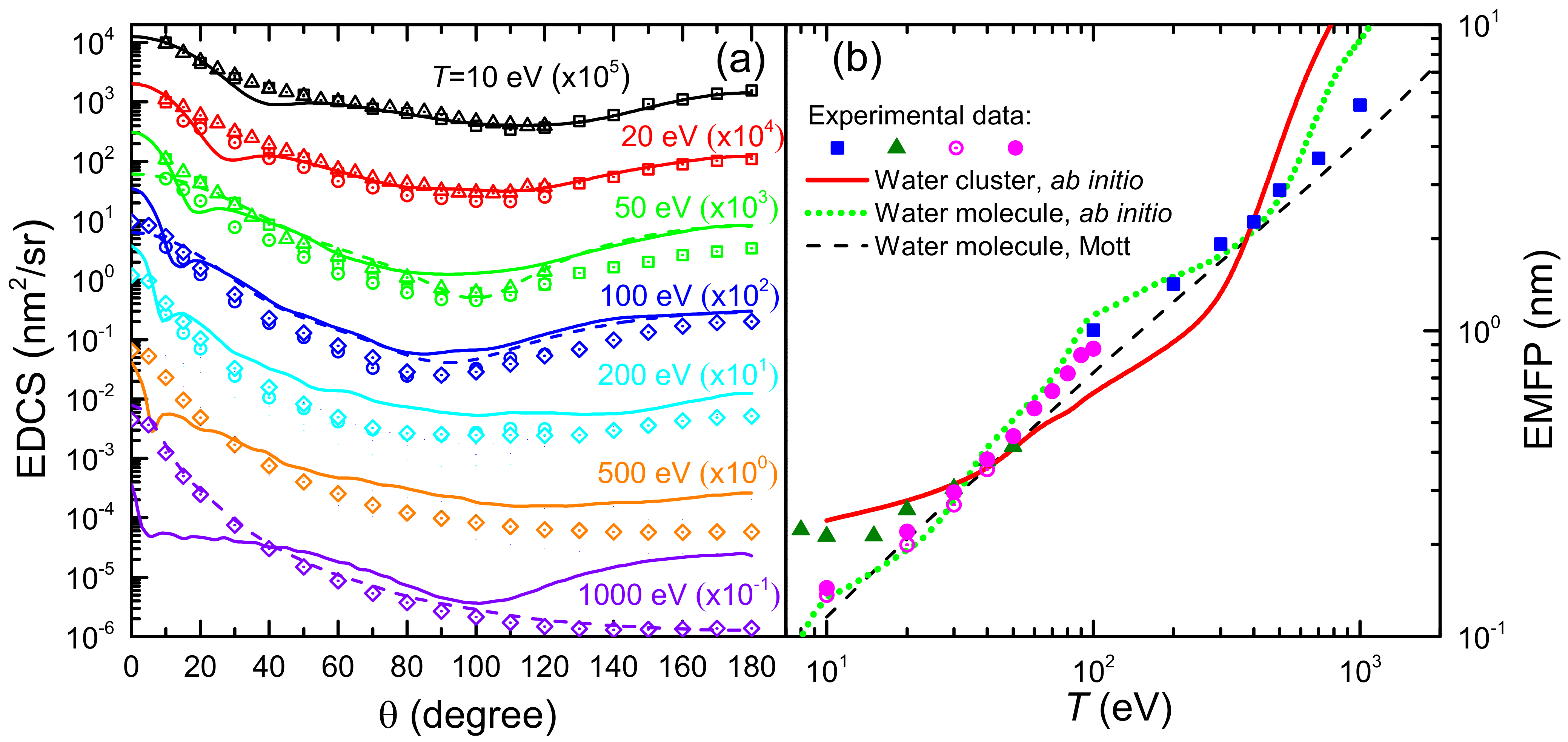
2.4.2. Elastic cross Section of an Electron with Liquid Water Molecules Obtained by the First Principles Approach
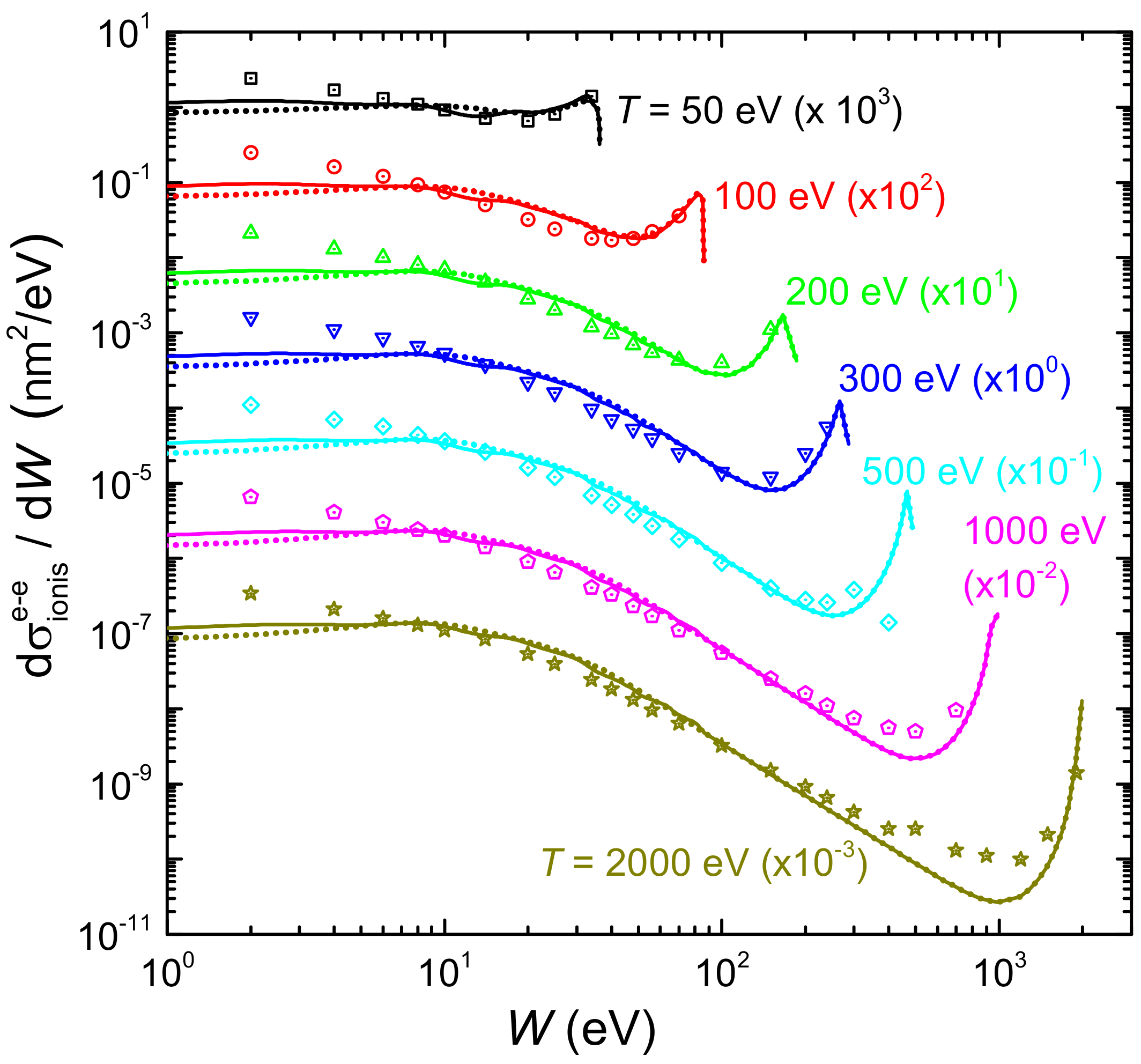
2.4.3. Inelastic cross Sections of Electrons in Liquid Water
2.5. Monte Carlo Simulation of Secondary Electron Transport around the Carbon Ion Path
3. Results and Discussion
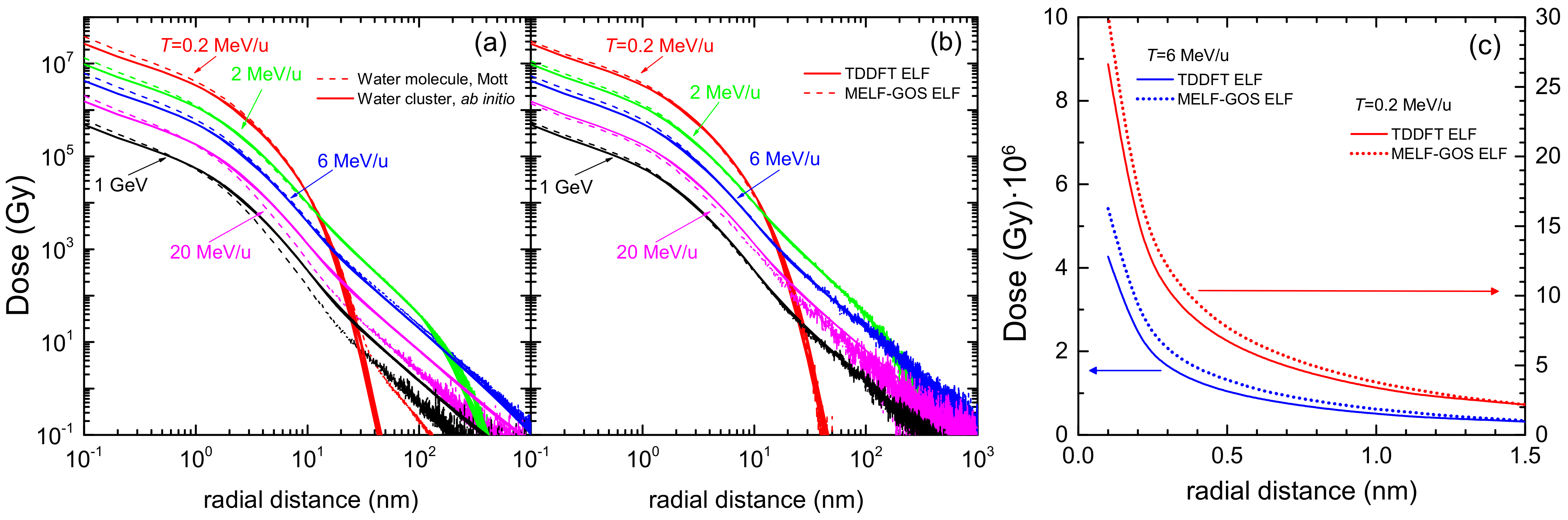
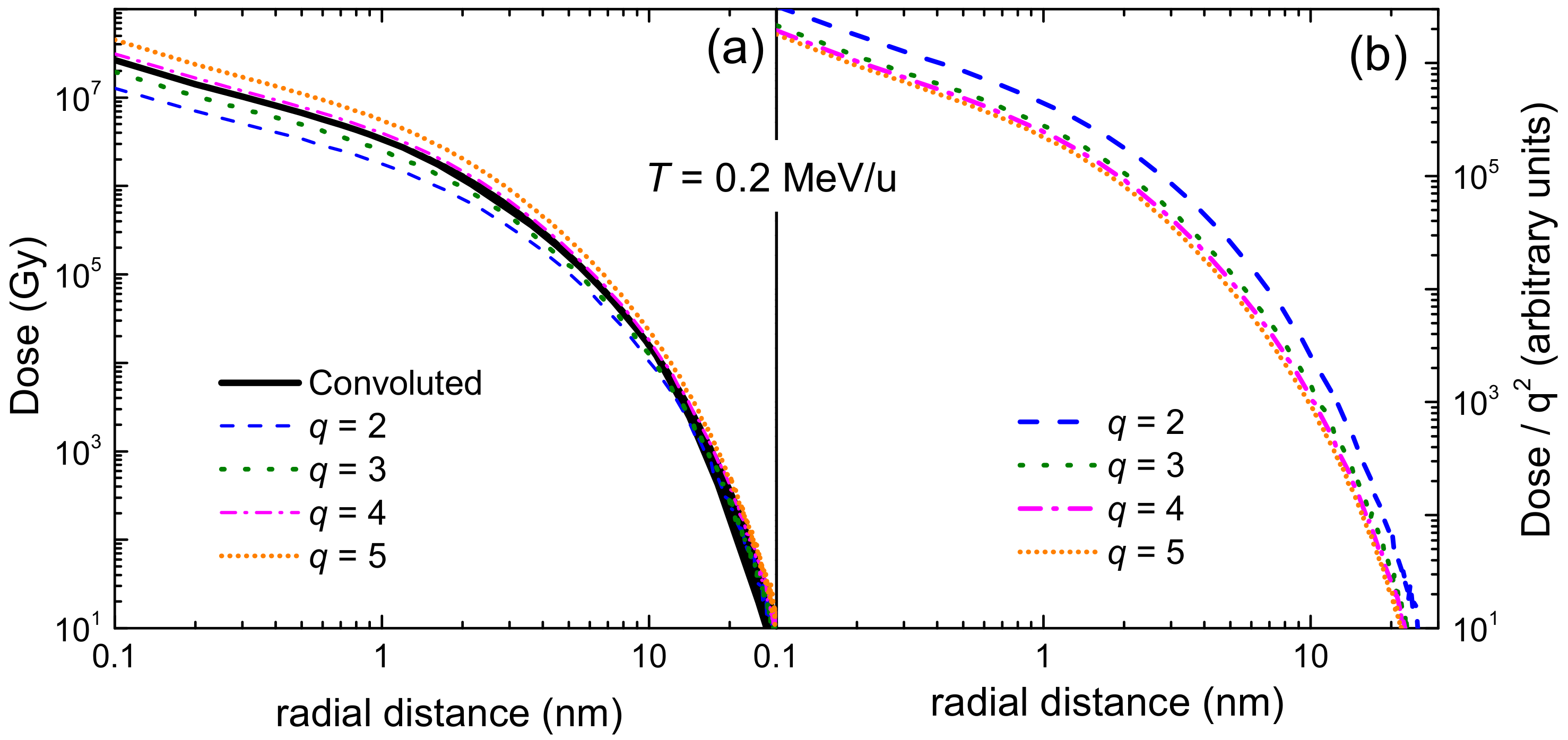
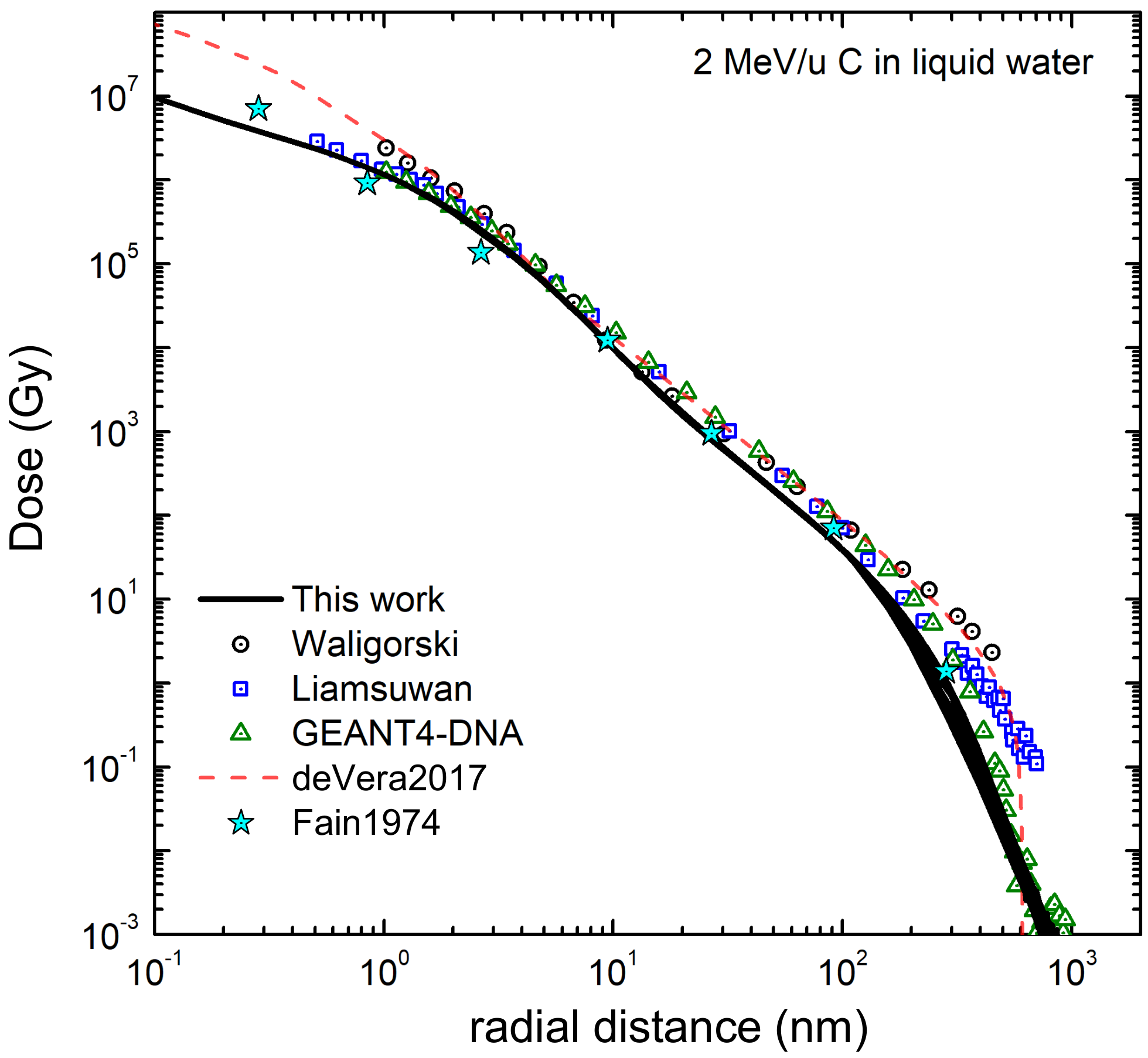
3.1. Simulation of the Radial Dose in Liquid Water around the Carbon Ion Path
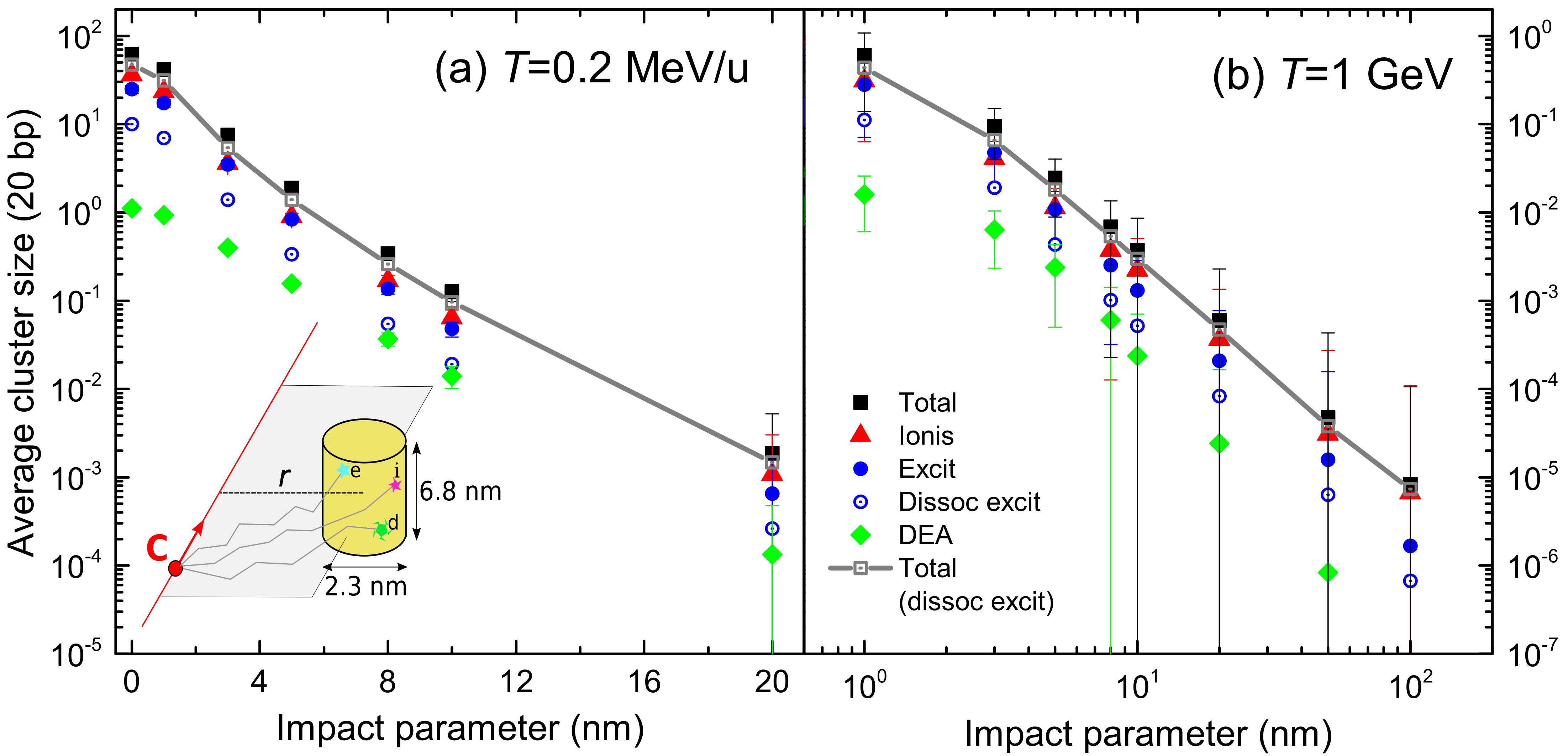
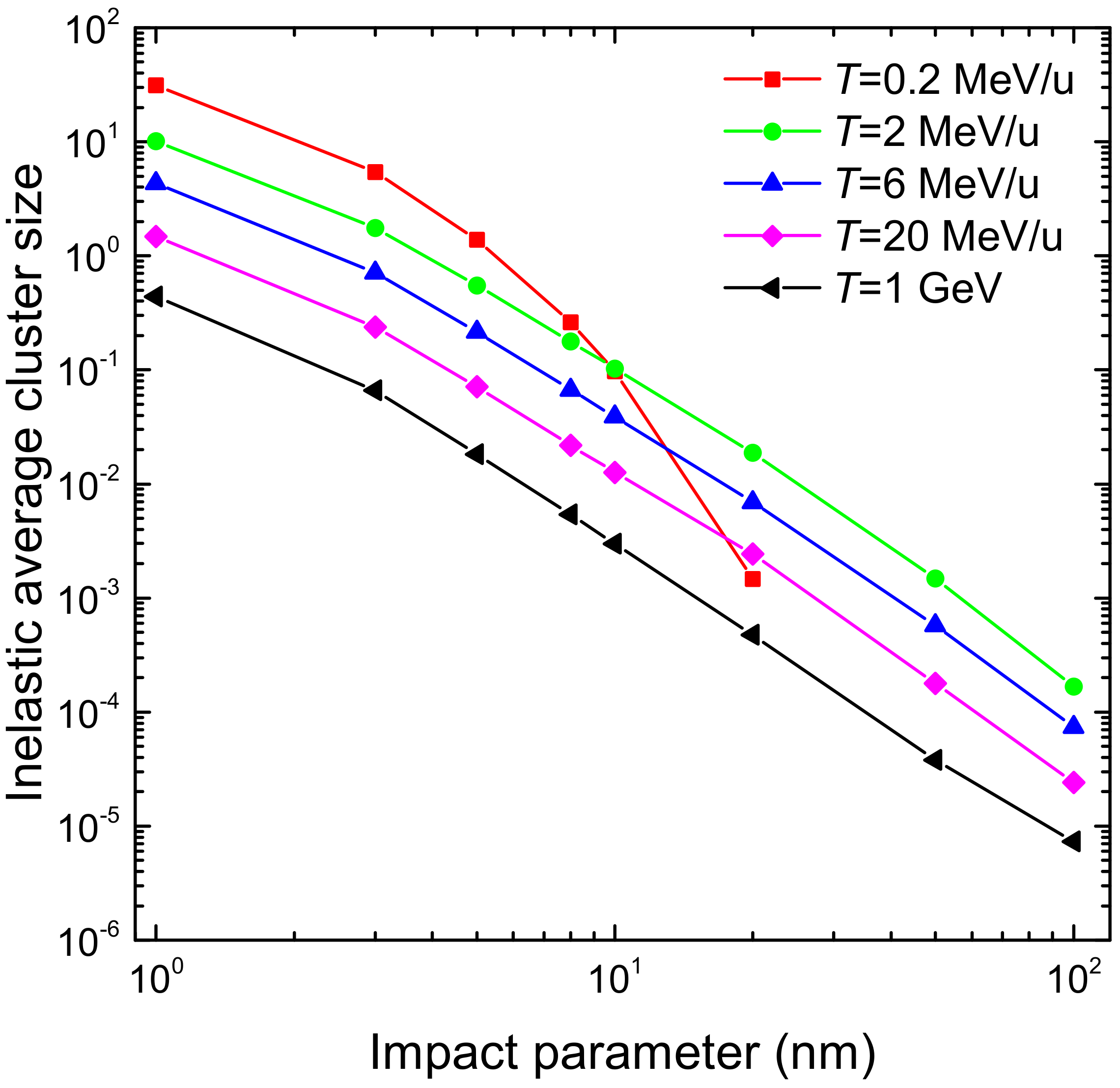
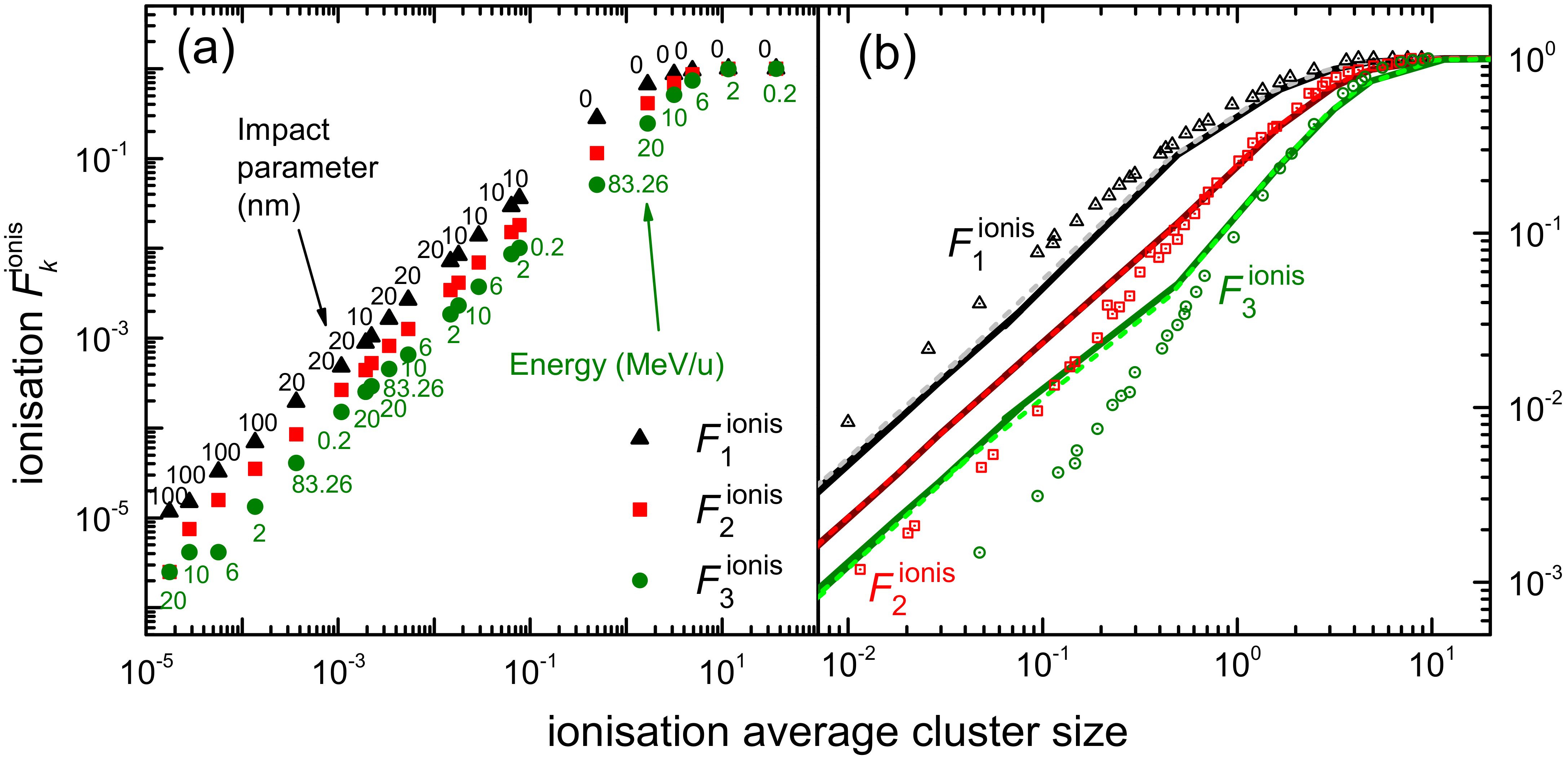
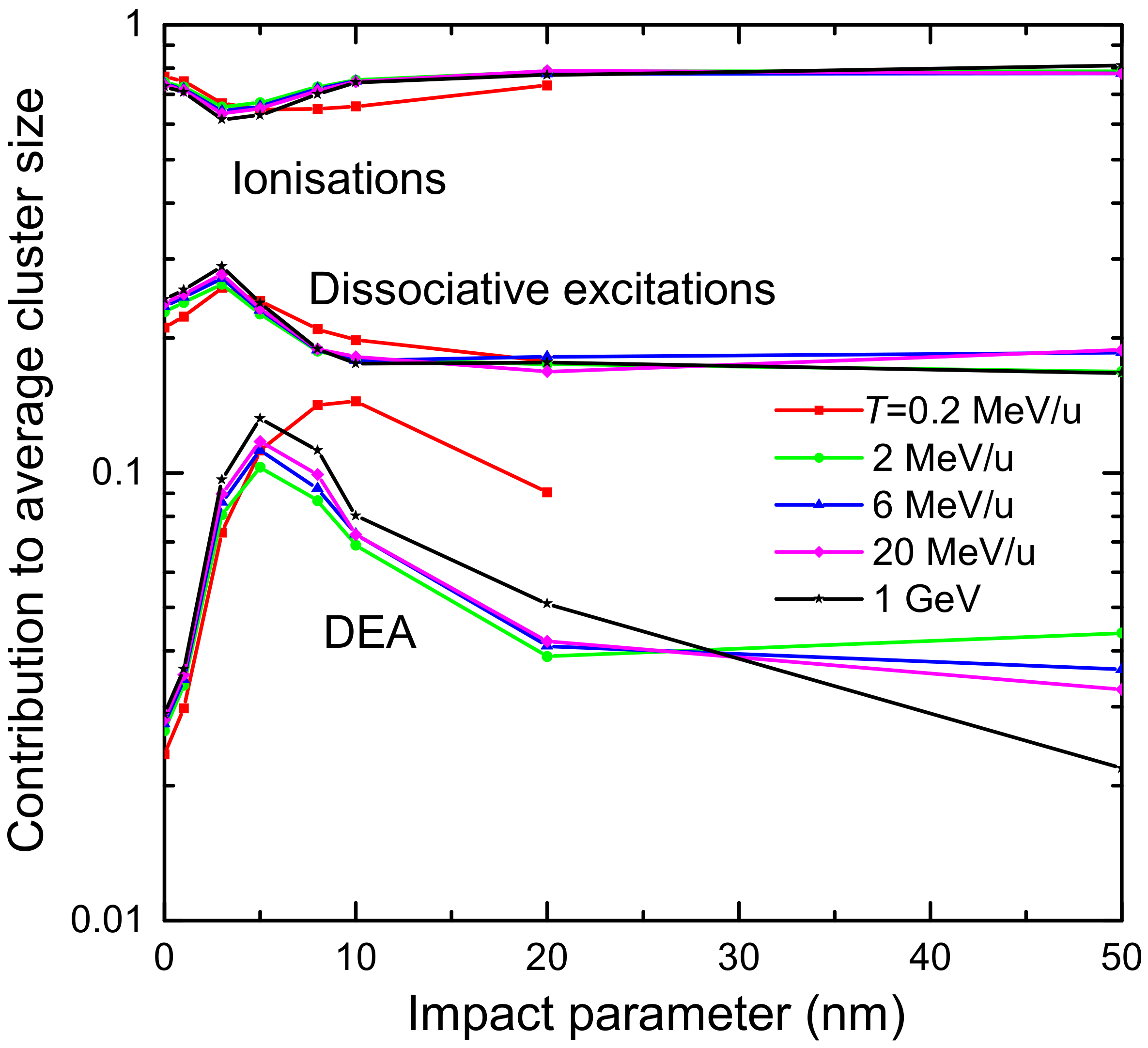
3.2. Simulation of Clustered Damage on the DNA Strand Scales
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DEA | Dissociative electron attachment |
| DFT | Density functional theory |
| ELF | Energy loss function |
| EMFP | Elastic mean free path |
| EDCS | Elastic differential cross section |
| excit-MFP | Excitation mean free path |
| excit-TCS | Excitation total cross section |
| IDDCS | Inelastic doubly differential cross section |
| IIMFP | Inverse inelastic mean free path |
| ionis-DDCS | Ionisation doubly differential cross section |
| ionis-MFP | Ionisation mean free path |
| ionis-SDCS | Ionisation singly differential cross section |
| ionis-TCS | Ionisation total cross section |
| LR-TDDFT | Linear-response time-dependent density functional theory |
| MC | Monte Carlo |
| MELF-GOS | Mermin Energy Loss Function – Generalised Oscillator Strengths |
| MFP | Mean free path |
| RBE | Relative biological effectiveness |
| SEED | Secondary Electrons Energy Deposition |
References
- ICRU. Report 46—Photon, Electron, Proton and Neutron Interaction Data for Body Tissues; International Commission on Radiation Units and Meassurements: Bethesda, MD, USA, 1992. [Google Scholar]
- Nikjoo, H.; Uehara, S.; Emfietzoglou, D. Interaction of Radiation with Matter; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar] [CrossRef]
- Durante, M.; Cucinotta, F.A. Physical basis of radiation protection in space travel. Rev. Mod. Phys. 2011, 83, 1245–1281. [Google Scholar] [CrossRef]
- Schardt, D.; Elsässer, T.; Schulz-Ertner, D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 2010, 82, 383–425. [Google Scholar] [CrossRef]
- Solov’yov, A.V. (Ed.) Nanoscale Insights into Ion-Beam Cancer Therapy; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Tsujii, H.; Kamada, T.; Baba, M.; Tsuji, H.; Kato, H.; Kato, S.; Yamada, S.; Yasuda, S.; Yanagi, T.; Kato, H.; et al. Clinical advantages of carbon-ion radiotherapy. New J. Phys. 2008, 10, 075009. [Google Scholar] [CrossRef]
- Ebner, D.K.; Kamada, T. The Emerging Role of Carbon-Ion Radiotherapy. Front. Oncol. 2016, 6, 140. [Google Scholar] [CrossRef]
- Besemer, A.; Paganetti, H.; Bednarz, B. The clinical impact of uncertainties in the mean excitation energy of human tissues during proton therapy. Phys. Med. Biol. 2013, 58, 887–902. [Google Scholar] [CrossRef]
- Paul, H. The mean ionization potential of water, and its connection to the range of energetic carbon ions in water. Nucl. Instrum. Methods Phys. Res. Sect. B 2007, 255, 435–437. [Google Scholar] [CrossRef]
- Paul, H. Recent results in stopping power for positive ions, and some critical comments. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2010, 268, 3421–3425. [Google Scholar] [CrossRef]
- Garcia-Molina, R.; Abril, I.; de Vera, P.; Paul, H. Comments on recent measurements of the stopping power of liquid water. Nucl. Instrum. Methods Phys. Res. Sect. B 2013, 299, 51–53. [Google Scholar] [CrossRef][Green Version]
- Paul, H. On the accuracy of stopping power codes and ion ranges used for hadron therapy. Adv. Quantum Chem. 2013, 65, 39. [Google Scholar]
- Baek, W.Y.; Braunroth, T.; De La Fuente Rosales, L.; Rahm, J.M.; Rabus, H. Stopping power of water for carbon ions with energies in the Bragg peak region. Phys. Rev. E 2020, 102, 62418. [Google Scholar] [CrossRef]
- Hunniford, C.A.; McCullough, R.W.; Davies, R.J.H.; Timson, D.J. DNA damage by low-energy ions. Biochem. Soc. Trans. 2009, 37, 893–896. [Google Scholar] [CrossRef] [PubMed]
- Loeffler, J.S.; Durante, M. Charged particle therapy–optimization, challenges and future directions. Nat. Rev. Clin. Oncol. 2013, 10, 411–424. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, H.; Ilicic, K.; Greubel, C.; Girst, S.; Reindl, J.; Sammer, M.; Schwarz, B.; Siebenwirth, C.; Walsh, D.W.M.; Schmid, T.E.; et al. DNA damage interactions on both nanometer and micrometer scale determine overall cellular damage. Sci. Rep. 2018, 8, 16063. [Google Scholar] [CrossRef]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 2000, 287, 1658–1660. [Google Scholar] [CrossRef]
- Nikjoo, H.; Uehara, S.; Emfietzoglou, D.; Cucinotta, F.A. Track-structure codes in radiation research. Radiat. Meas. 2006, 41, 1052–1074. [Google Scholar] [CrossRef]
- Surdutovich, E.; Solov’yov, A.V. Multiscale approach to the physics of radiation damage with ions. Eur. Phys. J. D 2014, 68, 7–11. [Google Scholar] [CrossRef]
- Verkhovtsev, A.; Surdutovich, E.; Solov’yov, A.V. Multiscale approach predictions for biological outcomes in ion-beam cancer therapy. Sci. Rep. 2016, 6, 27654. [Google Scholar] [CrossRef]
- De Nardo, L.; Colautti, P.; Conte, V.; Baek, W.Y.; Grosswendt, B.; Tornielli, G. Ionization-cluster distributions of α-particles in nanometric volumes of propane: Measurement and calculation. Radiat. Environ. Biophys. 2002, 41, 235–256. [Google Scholar] [CrossRef]
- Conte, V.; Selva, A.; Colautti, P.; Hilgers, G.; Rabus, H. Track structure characterization and its link to radiobiology. Radiat. Meas. 2017, 106, 506–511. [Google Scholar] [CrossRef]
- Conte, V.; Selva, A.; Colautti, P.; Hilgers, G.; Rabus, H.; Bantsar, A.; Pietrzak, M.; Pszona, S. Nanodosimetry: Towards a new concept of radiation quality. Radiat. Prot. Dosim. 2018, 180, 150–156. [Google Scholar] [CrossRef]
- Itikawa, Y.; Mason, N. Cross sections for electron collisions with water molecules. J. Phys. Chem. Ref. Data 2005, 34, 1–22. [Google Scholar] [CrossRef]
- Thorn, P.A. Electronic State Excitations in the Water Molecule by Collisions with Low Energy Electrons. Ph.D. Thesis, Flinders University of South Australia, Adelaide, Australia, 2008. [Google Scholar]
- Dal Cappello, C.; Champion, C.; Boudrioua, O.; Lekadir, H.; Sato, Y.; Ohsawa, D. Theoretical and experimental investigations of electron emission in C6+ + H2O collisions. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 781–790. [Google Scholar] [CrossRef]
- Song, M.Y.; Cho, H.; Karwasz, G.P.; Kokoouline, V.; Nakamura, Y.; Tennyson, J.; Faure, A.; Mason, N.J.; Itikawa, Y. Cross Sections for Electron Collisions with H2O. J. Phys. Chem. Ref. Data 2021, 50, 023103. [Google Scholar] [CrossRef]
- Michaud, M.; Wen, A.; Sanche, L. Cross Sections for Low-Energy (1–100 eV) Electron Elastic and Inelastic Scattering in Amorphous Ice. Radiat. Res. 2003, 159, 3–22. [Google Scholar] [CrossRef]
- Malerz, S.; Trinter, F.; Hergenhahn, U.; Ghrist, A.; Ali, H.; Nicolas, C.; Saak, C.M.; Richter, C.; Hartweg, S.; Nahon, L.; et al. Low-energy constraints on photoelectron spectra measured from liquid water and aqueous solutions. Phys. Chem. Chem. Phys. 2021, 23, 8246–8260. [Google Scholar] [CrossRef]
- Garcia-Molina, R.; Abril, I.; Kyriakou, I.; Emfietzoglou, D. Energy Loss of Swift Protons in Liquid Water: Role of Optical Data Input and Extension Algorithms. In Radiation Damage in Biomolecular Systems; García Gómez-Tejedor, G., Fuss, M.C., Eds.; Springer: Dordrecht, The Netherlands, 2012; Chapter 15; pp. 239–261. [Google Scholar] [CrossRef]
- Blanco, F.; Munoz, A.; Almeida, D.; Ferreira da Silva, F.; Limão-Vieira, P.; Fuss, M.C.; Sanz, A.G.; García, G. Modelling low energy electron and positron tracks in biologically relevant media. Eur. Phys. J. D 2013, 67, 199. [Google Scholar] [CrossRef]
- Blanco, F.; Munoz, A.; Almeida, D.; Silva, F.F.D.; Limão-Vieira, P.; García, G. Clustering and condensation effects in the electron scattering cross sections from water molecules. Int. J. Mass Spectrom. 2014, 365–366, 287–294. [Google Scholar] [CrossRef]
- Mermin, N.D. Lindhard dielectric function in the relaxation-time approximation. Phys. Rev. B 1970, 1, 2362–2363. [Google Scholar] [CrossRef]
- Abril, I.; Garcia-Molina, R.; Denton, C.D.; Pérez-Pérez, F.J.; Arista, N.R. Dielectric description of wakes and stopping powers in solids. Phys. Rev. A 1998, 58, 357–366. [Google Scholar] [CrossRef]
- Heredia-Avalos, S.; Garcia-Molina, R.; Fernández-Varea, J.M.; Abril, I. Calculated energy loss of swift He, Li, B, and N ions in SiO2, Al2O3, and ZrO2. Phys. Rev. A 2005, 72, 052902. [Google Scholar] [CrossRef]
- Hayashi, H.; Watanabe, N.; Udagawa, Y.; Kao, C.C. The complete optical spectrum of liquid water measured by inelastic x-ray scattering. Proc. Natl. Acad. Sci. USA 2000, 97, 6264–6266. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Molina, R.; Abril, I.; Denton, C.D.; Heredia-Avalos, S.; Kyriakou, I.; Emfietzoglou, D. Calculated depth-dose distributions for H+ and He+ beams in liquid water. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 2647–2652. [Google Scholar] [CrossRef]
- Garcia-Molina, R.; Abril, I.; Heredia-Avalos, S.; Kyriakou, I.; Emfietzoglou, D. A combined molecular dynamics and Monte Carlo simulation of the spatial distribution of energy deposition by proton beams in liquid water. Phys. Med. Biol. 2011, 56, 6475–6493. [Google Scholar] [CrossRef] [PubMed]
- De Vera, P.; Garcia-Molina, R.; Abril, I.; Solov’yov, A.V. Semiempirical Model for the Ion Impact Ionization of Complex Biological Media. Phys. Rev. Lett. 2013, 110, 148104. [Google Scholar] [CrossRef] [PubMed]
- De Vera, P.; Garcia-Molina, R.; Abril, I. Angular and Energy Distributions of Electrons Produced in Arbitrary Biomaterials by Proton Impact. Phys. Rev. Lett. 2015, 114, 018101. [Google Scholar] [CrossRef] [PubMed]
- De Vera, P.; Garcia-Molina, R. Electron Inelastic Mean Free Paths in Condensed Matter Down to a Few Electronvolts. J. Phys. Chem. C 2019, 123, 2075–2083. [Google Scholar] [CrossRef]
- De Vera, P.; Abril, I.; Garcia-Molina, R. Excitation and ionisation cross-sections in condensed-phase biomaterials by electrons down to very low energy: Application to liquid water and genetic building blocks. Phys. Chem. Chem. Phys. 2021, 23, 5079–5095. [Google Scholar] [CrossRef]
- Taioli, S.; Trevisanutto, P.E.; de Vera, P.; Simonucci, S.; Abril, I.; Garcia-Molina, R.; Dapor, M. Relative role of the physical mechanisms on complex biodamage induced by carbon irradiation. J. Phys. Chem. Lett. 2021, 12, 487–493. [Google Scholar] [CrossRef]
- Taioli, S.; Simonucci, S.; Dapor, M. SURPRISES: When ab initio meets statistics in extended systems. Comput. Sci. Discov. 2009, 2, 015002. [Google Scholar] [CrossRef]
- Taioli, S.; Simonucci, S.; Calliari, L.; Dapor, M. Electron spectroscopies and inelastic processes in nanoclusters and solids: Theory and experiment. Phys. Rep. 2010, 493, 237–319. [Google Scholar] [CrossRef]
- Morresi, T.; Taioli, S.; Simonucci, S. Nuclear Beta Decay: Relativistic Theory and Ab Initio Simulations of Electroweak Decay Spectra in Medium-Heavy Nuclei and of Atomic and Molecular Electronic Structure. Adv. Theory Simulations 2018, 1, 1870030. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Electrodynamics of Continuous Media; Pergamon: New York, NY, USA, 1984. [Google Scholar]
- Pines, D. Elementary Excitations in Solids; Perseus Books: Urbana, IL, USA, 1999. [Google Scholar]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope, 3rd ed.; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Planes, D.J.; Garcia-Molina, R.; Abril, I.; Arista, N.R. Wavenumber dependence of the energy loss function of graphite and aluminium. J. Electron Spectrosc. Relat. Phenom. 1996, 82, 23. [Google Scholar] [CrossRef]
- Moreno-Marín, J.C.; Abril, I.; Garcia-Molina, R. Stopping power calculation of rubidium and strontium for protons. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2002, 193, 30–35. [Google Scholar] [CrossRef]
- Denton, C.D.; Abril, I.; Moreno-Marín, J.C.; Heredia-Avalos, S.; Garcia-Molina, R. Energy loss of swift H and He projectiles in Al, Si, Ni and Cu targets. Phys. Status Solidi B Basic Res. 2008, 245, 1498–1504. [Google Scholar] [CrossRef]
- Behar, M.; Denton, C.D.; Fadanelli, R.C.; Abril, I.; Cantero, E.D.; Garcia-Molina, R.; Nagamine, L.C.C. Experimental and theoretical determination of the stopping power of ZrO2 films for protons and α-particles. Eur. Phys. J. D 2010, 59, 209–213. [Google Scholar] [CrossRef]
- Abril, I.; Denton, C.D.; de Vera, P.; Kyriakou, I.; Emfietzoglou, D.; Garcia-Molina, R. Effect of the Bethe surface description on the electronic excitations induced by energetic proton beams in liquid water and DNA. Nucl. Instrum. Methods Phys. Res. Sect. B 2010, 268, 1763–1767. [Google Scholar] [CrossRef]
- Abril, I.; Garcia-Molina, R.; Denton, C.D.; Kyriakou, I.; Emfietzoglou, D. Energy Loss of Hydrogen- and Helium-Ion Beams in DNA: Calculations Based on a Realistic Energy-Loss Function of the Target. Radiat. Res. 2011, 175, 247–255. [Google Scholar] [CrossRef]
- Heredia-Avalos, S.; Abril, I.; Denton, C.D.; Moreno-Marín, J.C.; Garcia-Molina, R. Target inner-shells contributions to the stopping power and straggling for H and He ions in gold. J. Phys. Condens. Matter 2007, 19, 466205. [Google Scholar] [CrossRef]
- Abril, I.; Garcia-Molina, R.; de Vera, P.; Kyriakou, I.; Emfietzoglou, D. Inelastic Collisions of Energetic Protons in Biological Media. Adv. Quantum Chem. 2013, 65, 129–164. [Google Scholar] [CrossRef]
- Fano, U. Penetration of Protons, Alpha Particles, and Mesons. Annu. Rev. Nucl. Sci. 1963, 13, 1–66. [Google Scholar] [CrossRef]
- Williams, G.P. X-ray Data Booklet; Lawrence Berkeley National Laboratory, University of California: Berkley, CA, USA, 2009; Chapter 1. [Google Scholar]
- Lindhard, J. On the properites of a gas of charged particles. Det K. Dan. Vidensk. Selsk.-Mat.-Fys. Meddelelser 1954, 28, 1–57. [Google Scholar]
- Sturm, K. Electron energy loss in simple metals and semiconductors. Adv. Phys. 1982, 31, 1–64. [Google Scholar] [CrossRef]
- Shiles, E.; Sasaki, T.; Inokuti, M.; Smith, D.Y. Self-consistency and sum-rule tests in the Kramers–Kronig analysis of optical data: Applications to aluminum. Phys. Rev. B 1980, 22, 1612–1628. [Google Scholar] [CrossRef]
- Watanabe, N.; Hayashi, H.; Udagawa, Y. Bethe surface of liquid water determined by inelastic X-ray scattering spectroscopy and electron correlation effects. Bull. Chem. Soc. Jpn. 1997, 70, 719–726. [Google Scholar] [CrossRef]
- Watanabe, N.; Hayashi, H.; Udagawa, Y. Inelastic X-ray scattering study on molecular liquids. J. Phys. Chem. Solids 2000, 61, 407–409. [Google Scholar] [CrossRef]
- Bethe, H. Bremsformel für Elektronen relativistischer Geschwindigkeit. Z. Für Phys. 1932, 76, 293–299. [Google Scholar] [CrossRef]
- Inokuti, M. Inelastic collisions of fast charged particles with atoms and molecules—The Bethe theory revisited. Rev. Mod. Phys. 1971, 43, 297. [Google Scholar] [CrossRef]
- Sigmund, P. Stopping of Heavy Ions. A theoretical Approach; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sigmund, P.; Schinner, A.; Paul, H. Errata and Addenda for ICRU Report 73, Stopping of Ions Heavier than Helium. J. ICRU 2009, 5, 1–10. [Google Scholar]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- Olsen, T.; Patrick, C.E.; Bates, J.E.; Ruzsinszky, A.; Thygesen, K.S. Beyond the RPA and GW methods with adiabatic xc-kernels for accurate ground state and quasiparticle energies. NPJ Comput. Mater. 2019, 5, 106. [Google Scholar] [CrossRef]
- Shukri, A.A.; Al-Qawasmeh, A.; Al Shorman, M.; Alsaad, A. Computational investigation of the valid valence state contribution in calculating the electronic stopping power of a proton in bulk Al within the linear response approach. Can. J. Phys. 2020, 98, 167–171. [Google Scholar] [CrossRef]
- Weissker, H.C.; Serrano, J.; Huotari, S.; Luppi, E.; Cazzaniga, M.; Bruneval, F.; Sottile, F.; Monaco, G.; Olevano, V.; Reining, L. Dynamic structure factor and dielectric function of silicon for finite momentum transfer: Inelastic x-ray scattering experiments and ab initio calculations. Phys. Rev. B 2010, 81, 085104. [Google Scholar] [CrossRef]
- Seidu, A.; Marini, A.; Gatti, M. Dynamical correlation effects in a weakly correlated material: Inelastic x-ray scattering and photoemission spectra of beryllium. Phys. Rev. B 2018, 97, 125144. [Google Scholar] [CrossRef]
- Paredes-Mellone, O.A.; Koskelo, J.; Ceppi, S.A.; Stutz, G.E. Dynamic Structure Factor and Dielectric Function of Valence Electrons in Lithium Hydride: An Inelastic X-Ray Scattering Study at Finite Momentum Transfer. Phys. Status Solidi B 2020, 257, 1900780. [Google Scholar] [CrossRef]
- Pedrielli, A.; de Vera, P.; Trevisanutto, P.E.; Pugno, N.M.; Garcia-Molina, R.; Abril, I.; Taioli, S.; Dapor, M. Electronic excitation spectra of cerium oxides: From ab initio dielectric response functions to Monte Carlo electron transport simulations. Phys. Chem. Chem. Phys. 2021, 23, 19173–19187. [Google Scholar] [CrossRef] [PubMed]
- Reining, L.; Olevano, V.; Rubio, A.; Onida, G. Excitonic Effects in Solids Described by Time-Dependent Density-Functional Theory. Phys. Rev. Lett. 2002, 88, 066404. [Google Scholar] [CrossRef] [PubMed]
- Takada, Y.; Yasuhara, H. Dynamical Structure Factor of the Homogeneous Electron Liquid: Its Accurate Shape and the Interpretation of Experiments on Aluminum. Phys. Rev. Lett. 2002, 89, 216402. [Google Scholar] [CrossRef]
- Cazzaniga, M.; Weissker, H.C.; Huotari, S.; Pylkkänen, T.; Salvestrini, P.; Monaco, G.; Onida, G.; Reining, L. Dynamical response function in sodium and aluminum from time-dependent density-functional theory. Phys. Rev. B 2011, 84, 075109. [Google Scholar] [CrossRef]
- Huotari, S.; Cazzaniga, M.; Weissker, H.C.; Pylkkänen, T.; Müller, H.; Reining, L.; Onida, G.; Monaco, G. Dynamical response function in sodium studied by inelastic x-ray scattering spectroscopy. Phys. Rev. B 2011, 84, 075108. [Google Scholar] [CrossRef]
- Adler, S.L. Quantum Theory of the Dielectric Constant in Real Solids. Phys. Rev. 1962, 126, 413–420. [Google Scholar] [CrossRef]
- Wiser, N. Dielectric Constant with Local Field Effects Included. Phys. Rev. 1963, 129, 62–69. [Google Scholar] [CrossRef]
- Garbuio, V.; Cascella, M.; Reining, L.; Sole, R.D.; Pulci, O. Ab Initio Calculation of Optical Spectra of Liquids: Many-Body Effects in the Electronic Excitations of Water. Phys. Rev. Lett. 2006, 97, 137402. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D. Empirical force fields for biological macromolecules: Overview and issues. J. Comput. Chem. 2004, 25, 1584–1604. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Koval, N.E.; Koval, P.; Pieve, F.D.; Kohanoff, J.; Artacho, E.; Emfietzoglou, D. Inelastic scattering of electrons in water from first-principles: Cross sections and inelastic mean free path for use in Monte Carlo track-structure simulations of biological damage. R. Soc. Open Sci. 2021, 9. [Google Scholar] [CrossRef]
- Timrov, I.; Vast, N.; Gebauer, R.; Baroni, S. turboEELS—A code for the simulation of the electron energy loss and inelastic X-ray scattering spectra using the Liouville–Lanczos approach to time-dependent density-functional perturbation theory. Comput. Phys. Commun. 2015, 196, 460–469. [Google Scholar] [CrossRef]
- Fermi, E. The ionization loss of energy in gases and in condensed materials. Phys. Rev. 1940, 57, 485. [Google Scholar] [CrossRef]
- Ritchie, R.H. Interaction of charged particles with a degenerate Fermi-Dirac electron gas. Phys. Rev. 1959, 114, 644–654. [Google Scholar] [CrossRef]
- Lindhard, J.; Winther, A. Stopping Power of Electron Gas and Equipartition Rule. Mat. Fys. Medd. Dan. Vid. Selsk. 1964, 34, 3–22. [Google Scholar]
- Brandt, W.; Kitagawa, M. Effective stopping-power charges of swift ions in condensed matter. Phys. Rev. B 1982, 25, 5631. [Google Scholar] [CrossRef]
- Rudd, M.E.; Kim, Y.K.; Madison, D.H.; Gay, T.J. Electron production in proton collisions with atoms and molecules: Energy distributions. Rev. Mod. Phys. 1992, 64, 441–490. [Google Scholar] [CrossRef]
- Montenegro, E.C.; Shah, M.B.; Luna, H.; Scully, S.W.; De Barros, A.L.; Wyer, J.A.; Lecointre, J. Water Fragmentation and Energy Loss by Carbon Ions at the Distal Region of the Bragg Peak. Phys. Rev. Lett. 2007, 99, 213201. [Google Scholar] [CrossRef]
- Grande, P.L.; Schiwietz, G. The unitary convolution approximation for heavy ions. Nucl. Instrum. Methods Phys. Res. Sect. B 2002, 195, 55–63. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Nikjoo, H. Cross sections for bare and dressed carbon ions in water and neon. Phys. Med. Biol. 2013, 58, 641–672. [Google Scholar] [CrossRef]
- Watt, D.E. Quantities for Dosimetry of Ionizing Radiations in Liquid Water; Taylor & Francis: London, UK, 1996. [Google Scholar]
- Rahm, J.M.; Baek, W.Y.; Rabus, H.; Hofsäss, H. Stopping power of liquid water for carbon ions in the energy range between 1 MeV and 6 MeV. Phys. Med. Biol. 2014, 59, 3683–3695. [Google Scholar] [CrossRef]
- ICRU Report 90. Key Data for Ionizing-Radiation Dosimetry: Measurement Standards and Applications. J. Int. Comm. Radiat. Units Meas. 2016, 14, 1–110. [Google Scholar] [CrossRef]
- Ziegler, J.F. SRIM—The Stopping and Range of Ions in Matter. 2013. Available online: http://www.srim.or (accessed on 14 February 2022).
- Schiwietz, G.; Grande, P.L. Stopping of protons—Improved accuracy of the UCA model. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2012, 273, 1–5. [Google Scholar] [CrossRef][Green Version]
- Bhattacharjee, S.; Biswas, S.; Monti, J.M.; Rivarola, R.D.; Tribedi, L.C. Double-differential cross section for ionization of H2O molecules by 4-MeV/u C6+ and Si13+ ions. Phys. Rev. A 2017, 96, 052707. [Google Scholar] [CrossRef]
- Salin, A. Ionization of atomic hydrogen by proton impact. J. Phys. B 1969, 2, 631–639. [Google Scholar] [CrossRef]
- Champion, C.; Dal Cappello, C. Theoretical investigations of electron emission after water vapour ionization by light ion impact. Nucl. Instrum. Methods Phys. Res. Sect. B 2009, 267, 881–884. [Google Scholar] [CrossRef]
- Jorge, A.; Horbatsch, M.; Illescas, C.; Kirchner, T. Classical-trajectory Monte Carlo calculations of differential electron-emission cross sections in fast heavy-ion collisions with water molecules. Phys. Rev. A 2019, 99, 062701. [Google Scholar] [CrossRef]
- Mott, N.F. The scattering of fast electrons by atomic nuclei. Proc. R. Soc. Lond. Ser. A 1929, 124, 425–442. [Google Scholar] [CrossRef]
- Jablonski, A.; Salvat, F.; Powell, C.J. Comparison of Electron Elastic-Scattering Cross Sections Calculated from Two Commonly Used Atomic Potentials. J. Phys. Chem. Ref. Data 2004, 33, 409. [Google Scholar] [CrossRef]
- Salvat, F.; Jablonski, A.; Powell, C. ELSEPA—Dirac partial-wave calculation of elastic scattering of electrons and positrons by atoms, positive ions and molecules. Comput. Phys. Commun. 2005, 165, 157–190. [Google Scholar] [CrossRef]
- Dapor, M. Polarized electron beams elastically scattered by atoms as a tool for testing fundamental predictions of quantum mechanics. Sci. Rep. 2018, 8, 5370. [Google Scholar] [CrossRef]
- Dapor, M. Electron–Atom Collisions: Quantum-Relativistic Theory and Exercises; De Gruyter: Berlin, Germany, 2022. [Google Scholar] [CrossRef]
- Furness, J.B.; McCarthy, I.E. The (e,2e) experiment as a probe for atomic structure. J. Phys. B 1973, 6, L204–L207. [Google Scholar] [CrossRef]
- Rehher, M.; Wolf, A. Relativistic Quantum Chemistry: The Fundamental Theory of Molecular Science; Wiley-VCH Verlag GmbH & Co. KGaA: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Hartweg, S.; Yoder, B.L.; Garcia, G.A.; Nahon, L.; Signorell, R. Size-Resolved Photoelectron Anisotropy of Gas Phase Water Clusters and Predictions for Liquid Water. Phys. Rev. Lett. 2017, 118, 103402. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Bromley, D.; Greiner, W. Relativistic Quantum Mechanics. Wave Equations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Taioli, S.; Simonucci, S. A computational perspective on multichannel scattering theory with applications to physical and nuclear chemistry. In Annual Reports in Computational Chemistry; Elsevier: Amsterdam, The Netherlands, 2015; Volume 11, pp. 191–310. [Google Scholar]
- Cho, H.; Park, Y.S.; Tanaka, H.; Buckman, S.J. Measurements of elastic electron scattering by water vapour extended to backward angles. J. Phys. B 2004, 37, 625–634. [Google Scholar] [CrossRef]
- Danjo, A.; Nishimura, H. Elastic scattering of electrons from H2O molecule. J. Phys. Soc. Jpn. 1985, 54, 1224–1227. [Google Scholar] [CrossRef]
- Johnstone, W.M.; Newell, W.R. Absolute vibrationally elastic cross sections for electrons scattered from water molecules between 6 eV and 50 eV. J. Phys. B 1991, 24, 3633–3643. [Google Scholar] [CrossRef]
- Katase, A.; Ishibashi, K.; Matsumoto, Y.; Sakae, T.; Maezono, S.; Murakami, E.; Watanabe, K.; Maki, H. Elastic scattering of electrons by water molecules over the range 100–1000 eV. J. Phys. B 1986, 19, 2715–2734. [Google Scholar] [CrossRef]
- García-Abenza, A.; Lozano, A.I.; Oller, J.C.; Blanco, F.; Gorfinkiel, J.D.; Limão-Vieira, P.; García, G. Evaluation of recommended cross sections for the simulation of electron tracks in water. Atoms 2021, 9, 98. [Google Scholar] [CrossRef]
- Ochkur, V.I. Ionization of the Hydrogen Atom By Electron Impact With Allowance for the Exchange. Sov. Phys.-JETP 1965, 20, 1175–1178. [Google Scholar]
- Prasad, S.S. Electron exchange in impact ionization of atomic hydrogen. Proc. Phys. Soc. 1965, 85, 57–59. [Google Scholar] [CrossRef]
- Inokuti, M. Excitation of the hydrogen atom by fast electrons in the Ochkur approximation. J. Phys. Soc. Jpn. 1967, 22, 971–973. [Google Scholar] [CrossRef]
- Rudge, M.R. Theory of the ionization of atoms by electron impact. Rev. Mod. Phys. 1968, 40, 564–590. [Google Scholar] [CrossRef]
- Emfietzoglou, D.; Nikjoo, H. The Effect of Model Approximations on Single-Collision Distributions of Low-Energy Electrons in Liquid Water. Radiat. Res. 2005, 163, 98–111. [Google Scholar] [CrossRef]
- Vriens, L. Binary-encounter electron-atom collision theory. Phys. Rev. 1966, 141, 88–92. [Google Scholar] [CrossRef]
- Bolorizadeh, M.A.; Rudd, M.E. Angular and energy dependence of cross sections for ejection of electrons from water vapor. I. 50-2000-eV electron impact. Phys. Rev. A 1986, 33, 882–887. [Google Scholar] [CrossRef] [PubMed]
- Schutten, J.; de Heer, F.J.; Moustafa, H.R.; Boerboom, A.J.H.; Kistemaker, J. Gross- and Partial-Ionization Cross Sections for Electrons on Water Vapor in the Energy Range 0.1–20 keV. J. Chem. Phys. 1966, 44, 3924–3928. [Google Scholar] [CrossRef]
- Bull, J.N.; Lee, J.W.; Vallance, C. Absolute electron total ionization cross-sections: Molecular analogues of DNA and RNA nucleobase and sugar constituents. Phys. Chem. Chem. Phys. 2014, 16, 10743–10752. [Google Scholar] [CrossRef]
- Thorn, P.A.; Brunger, M.J.; Teubner, P.J.O.; Diakomichalis, N.; Maddern, T.; Bolorizadeh, M.A.; Newell, W.R.; Kato, H.; Hoshino, M.; Tanaka, H.; et al. Cross sections and oscillator strengths for electron-impact excitation of the A1B1 electronic state of water. J. Chem. Phys. 2007, 126, 064306. [Google Scholar] [CrossRef] [PubMed]
- Brunger, M.J.; Thorn, P.A.; Campbell, L.; Diakomichalis, N.; Kato, H.; Kawahara, H.; Hoshino, M.; Tanaka, H.; Kim, Y.K. Excitation of the lowest lying 3B1, 1B1, 3A2, 1A2, 3A1 and 1A1 electronic states in water by 15 eV electrons. Int. J. Mass Spectrom. 2008, 271, 80–84. [Google Scholar] [CrossRef]
- Ralphs, K.; Serna, G.; Hargreaves, L.R.; Khakoo, M.A.; Winstead, C.; McKoy, V. Excitation of the six lowest electronic transitions in water by 9-20 eV electrons. J. Phys. B 2013, 46, 125201. [Google Scholar] [CrossRef]
- Matsui, M.; Hoshino, M.; Kato, H.; Da Silva, F.F.; Limão-Vieira, P.; Tanaka, H. Measuring electron-impact cross sections of water: Elastic scattering and electronic excitation of the a3B1 and A1B1 states. Eur. Phys. J. D 2016, 70, 77. [Google Scholar] [CrossRef]
- Harb, T.; Kedzierski, W.; McConkey, J.W. Production of ground state OH following electron impact on H2O. J. Chem. Phys. 2001, 115, 5507–5512. [Google Scholar] [CrossRef]
- Kreipl, M.S.; Friedland, W.; Paretzke, H.G. Time- and space-resolved Monte Carlo study of water radiolysis for photon, electron and ion irradiation. Radiat. Environ. Biophys. 2009, 48, 11–20. [Google Scholar] [CrossRef]
- Dapor, M.; Abril, I.; de Vera, P.; Garcia-Molina, R. Energy deposition around swift proton tracks in polymethylmethacrylate: How much and how far. Phys. Rev. B 2017, 96, 064113. [Google Scholar] [CrossRef]
- Dapor, M. Transport of Energetic Electrons in Solids. Computer Simulation with Applications to Materials Analysis and Characterization, 3rd ed.; Springer International Publishing AG: Cham, Switzerland, 2020. [Google Scholar]
- Fröhlich, H. Electrons in Lattice Fields. Adv. Phys. 1954, 3, 325–361. [Google Scholar] [CrossRef]
- Llacer, J.; Garwin, E.L. Electron-phonon interaction in alkali halides. I. The transport of secondary electrons with energies between 0.25 and 7.5 eV. J. Appl. Phys. 1969, 40, 2766–2775. [Google Scholar] [CrossRef]
- Ganachaud, J.P.; Mokrani, A. Theoretical study of the secondary electron emission of insulating targets. Surf. Sci. 1995, 334, 329–341. [Google Scholar] [CrossRef]
- Suszcynsky, D.; Borovsky, J. Secondary electron yields of solar system ices. J. Geophys. Res. 1992, 97, 2611–2619. [Google Scholar] [CrossRef]
- Suszcynsky, D.; Borovsky, J. Correction to “Secondary electron yields of solar system ices”. J. Geophys. Res. 1993, 98, 7499. [Google Scholar] [CrossRef]
- Thiel, B.; Stokes, D.; Phifer, D. Secondary electron yield of water. Microsc. Microanalisys 1999, 5, 282–283. [Google Scholar] [CrossRef]
- Baglin, V.; Bojko, J.; Gröbner, O.; Henrist, B.; Hilleret, N.; Scheuerlein, C.; Cern, M.T. The secondary electron yield of technical materials and its variations with surface treatment. In Proceedings of the EPAC, Vienna, Austria, 26–30 June 2000; pp. 217–221. [Google Scholar]
- Mehnaz; Yang, L.H.; Zou, Y.B.; Da, B.; Mao, S.F.; Li, H.M.; Zhao, Y.F.; Ding, Z.J. A comparative study on Monte Carlo simulations of electron emission from liquid water. Med. Phys. 2020, 47, 759–771. [Google Scholar] [CrossRef]
- Scholz, M.; Elsässer, T. Biophysical models in ion beam radiotherapy. Adv. Space Res. 2007, 40, 1381–1391. [Google Scholar] [CrossRef]
- De Vera, P.; Abril, I.; Garcia-Molina, R. Energy Spectra of Protons and Generated Secondary Electrons around the Bragg Peak in Materials of Interest in Proton Therapy. Radiat. Res. 2018, 190, 282. [Google Scholar] [CrossRef]
- Marquardt, J.; Heber, B.; Potgieter, M.S.; Strauss, R.D. Energy spectra of carbon and oxygen with HELIOS E6 - Radial gradients of anomalous cosmic ray oxygen within 1 AU. Astron. Astrphysics 2018, 610, A42. [Google Scholar] [CrossRef]
- De Vera, P.; Surdutovich, E.; Mason, N.J.; Solov’yov, A.V. Radial doses around energetic ion tracks and the onset of shock waves on the nanoscale. Eur. Phys. J. D 2017, 71, 281. [Google Scholar] [CrossRef]
- Faïn, J.; Monnin, M.; Montret, M. Spatial Energy Distribution around Heavy-Ion Path. Radiat. Res. 1974, 57, 379–389. [Google Scholar] [CrossRef]
- Waligórski, M.P.; Hamm, R.N.; Katz, R. The radial distribution of dose around the path of a heavy ion in liquid water. Nucl. Tracks Radiat. Meas. 1986, 11, 309–319. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Nikjoo, H. A Monte Carlo track structure simulation code for the full-slowing-down carbon projectiles of energies 1 keV u−1–10 MeV u−1 in water. Phys. Med. Biol. 2013, 58, 673–701. [Google Scholar] [CrossRef]
- Incerti, S.; Psaltaki, M.; Gillet, P.; Barberet, P.; Bardiès, M.; Bernal, M.A.; Bordage, M.C.; Breton, V.; Davidkova, M.; Delage, E.; et al. Simulating radial dose of ion tracks in liquid water simulated with Geant4-DNA: A comparative study. Nucl. Instrum. Methods Phys. Res. Sect. B 2014, 333, 92–98. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Vera, P.; Taioli, S.; Trevisanutto, P.E.; Dapor, M.; Abril, I.; Simonucci, S.; Garcia-Molina, R. Energy Deposition around Swift Carbon-Ion Tracks in Liquid Water. Int. J. Mol. Sci. 2022, 23, 6121. https://doi.org/10.3390/ijms23116121
de Vera P, Taioli S, Trevisanutto PE, Dapor M, Abril I, Simonucci S, Garcia-Molina R. Energy Deposition around Swift Carbon-Ion Tracks in Liquid Water. International Journal of Molecular Sciences. 2022; 23(11):6121. https://doi.org/10.3390/ijms23116121
Chicago/Turabian Stylede Vera, Pablo, Simone Taioli, Paolo E. Trevisanutto, Maurizio Dapor, Isabel Abril, Stefano Simonucci, and Rafael Garcia-Molina. 2022. "Energy Deposition around Swift Carbon-Ion Tracks in Liquid Water" International Journal of Molecular Sciences 23, no. 11: 6121. https://doi.org/10.3390/ijms23116121
APA Stylede Vera, P., Taioli, S., Trevisanutto, P. E., Dapor, M., Abril, I., Simonucci, S., & Garcia-Molina, R. (2022). Energy Deposition around Swift Carbon-Ion Tracks in Liquid Water. International Journal of Molecular Sciences, 23(11), 6121. https://doi.org/10.3390/ijms23116121






