Machine Learning Analysis of Longevity-Associated Gene Expression Landscapes in Mammals
Abstract
1. Introduction
2. Results and Discussion
2.1. Data Collection and Processing of Gene Expression across Mammalian Species
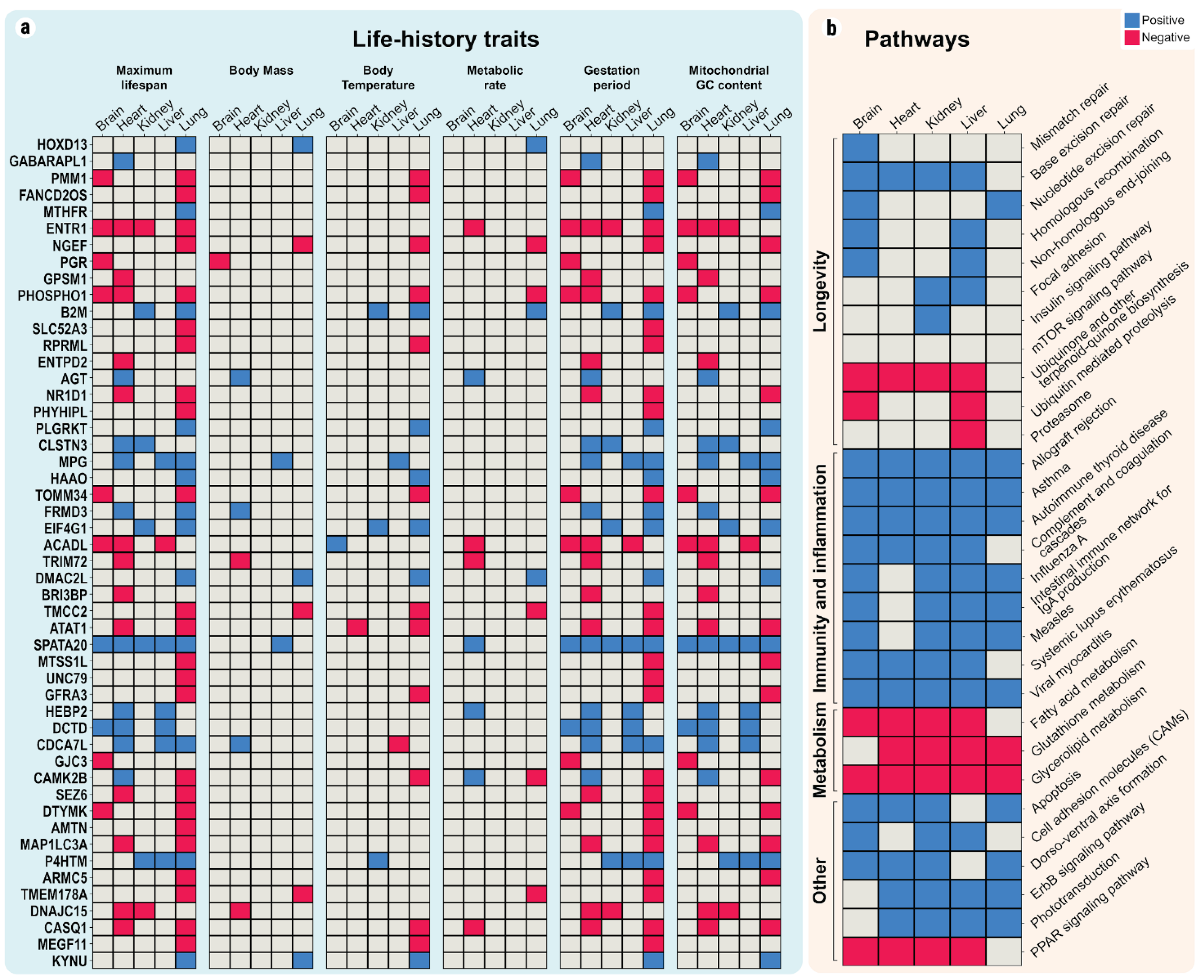
2.2. Linear Correlations between Gene Expression and Maximum Lifespan
2.3. Linear Relationships between Maximum Lifespan and Pathway Enrichment Scores
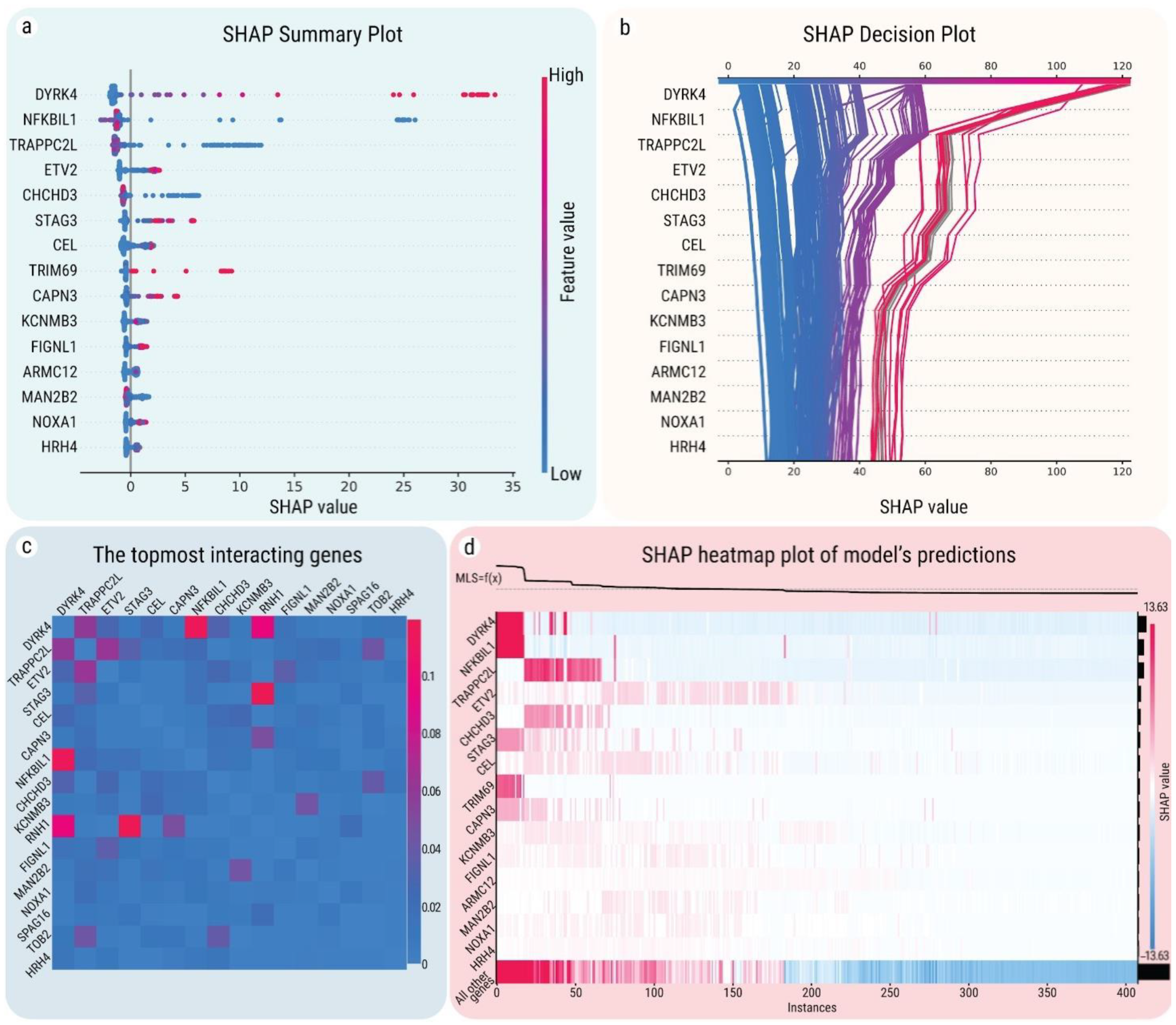
2.4. SHAP Explanations for Universal Gene Expression Patterns
2.5. Interactions between MLS-Associated Genes
2.6. Bayesian Networks
2.7. Integration of Linear, LightGBM-SHAP, and Bayesian Networks Models
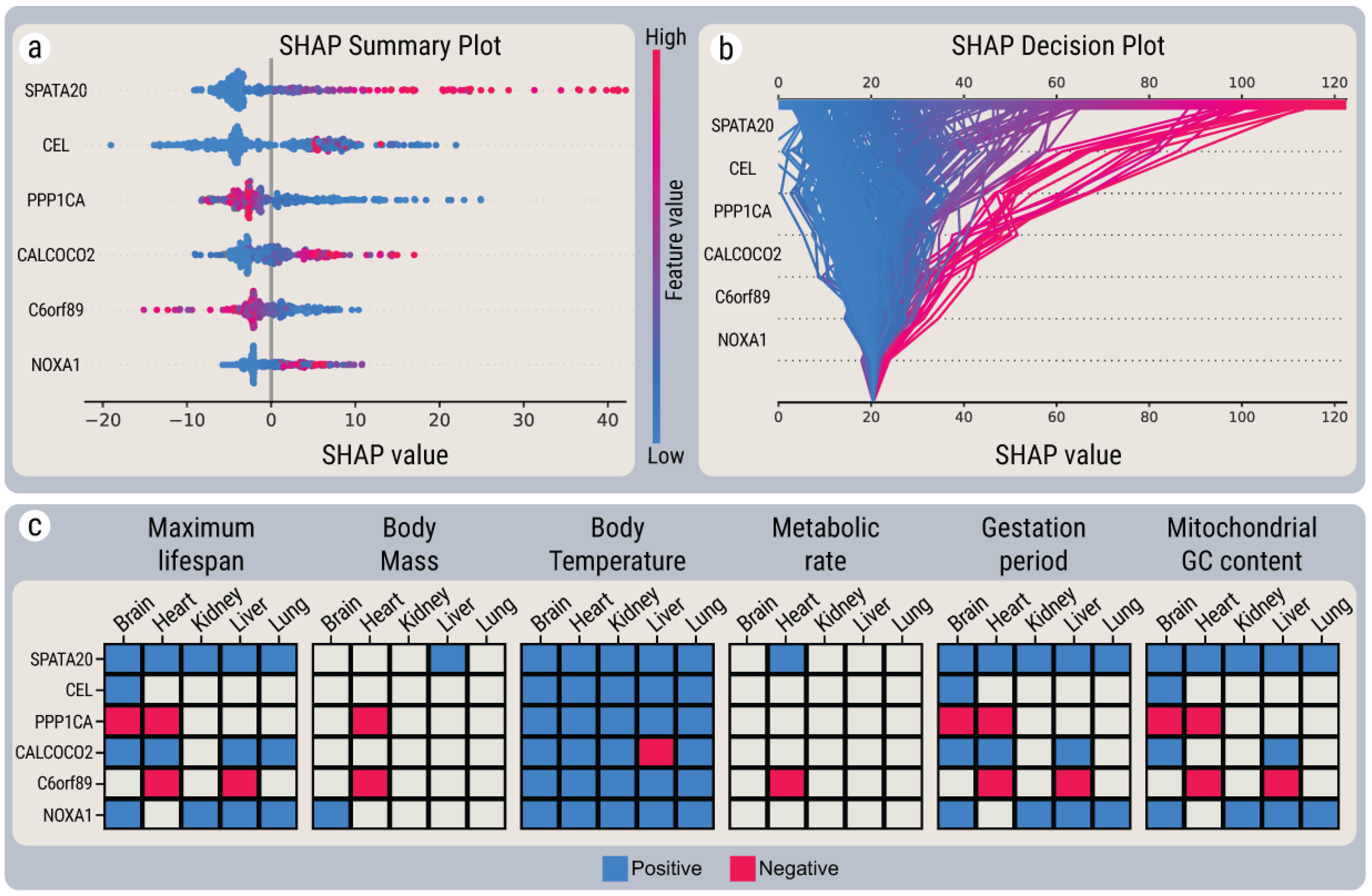
2.7.1. Joint Predictions in Linear and LightGBM-SHAP Models
2.7.2. Joint Predictions in Bayesian and LightGBM-SHAP Models
2.7.3. Joint Predictions in All Three Models
2.7.4. Composite Ranking
3. Materials and Methods
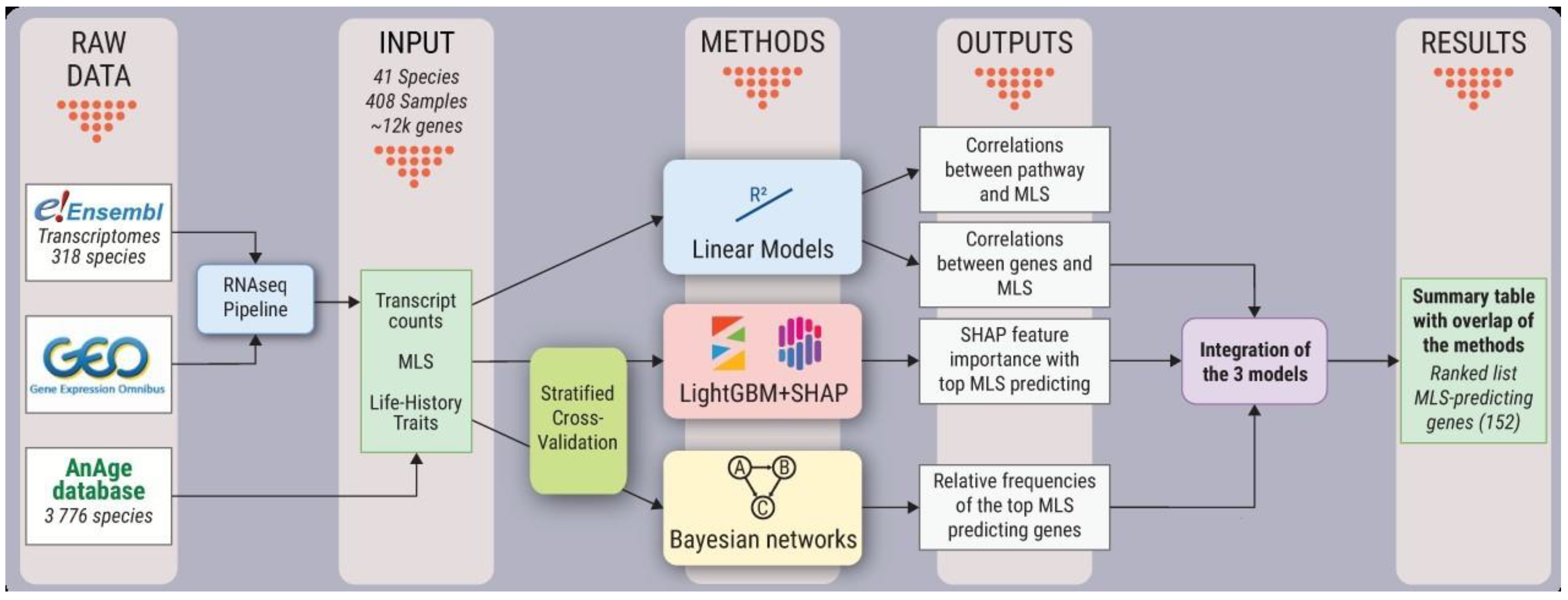
3.1. Bioinformatic Workflow and Analysis Design
3.2. Samples Selection and Data Quality
3.3. Orthology
3.4. Species Life-History Data
3.5. RNA-Seq Pipeline
3.6. Linear Models
3.7. Light GBM Models with SHAP Explanations
3.8. Bayesian Networks
3.9. Integration of Predicted Genes in the Linear, LightGBM-SHAP, and Bayesian Networks Models
3.10. An Explanatory Multilevel Linear Model for Composite Integration
3.11. Explanatory LightGBM-SHAP Model for Composite Integration
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Budovsky, A.; Abramovich, A.; Cohen, R.; Chalifa-Caspi, V.; Fraifeld, V. Longevity network: Construction and implications. Mech. Age. Dev. 2007, 128, 117–124. [Google Scholar] [CrossRef]
- Yanai, H.; Budovsky, A.; Barzilay, T.; Tacutu, R.; Fraifeld, V.E. Wide-scale comparative analysis of longevity genes and interventions. Aging Cell 2017, 16, 1267–1275. [Google Scholar] [CrossRef]
- Tacutu, R.; Thornton, D.; Johnson, E.; Budovsky, A.; Barardo, D.; Craig, T.; Diana, E.; Lehmann, G.; Toren, D.; Wang, J.; et al. Human ageing genomic resources: New and updated databases. Nucl. Acids Res. 2018, 46, D1083–D1090. [Google Scholar] [CrossRef]
- Sun, L.Y.; Spong, A.; Swindell, W.R.; Fang, Y.; Hill, C.; Huber, J.A.; Boehm, J.D.; Westbrook, R.; Salvatori, R.; Bartke, A. Growth hormone-releasing hormone disruption extends lifespan and regulates response to caloric restriction in mice. eLife 2013, 2, e01098. [Google Scholar] [CrossRef]
- Moskalev, A.; Chernyagina, E.; de Magalhães, J.P.; Barardo, D.; Thoppil, H.; Shaposhnikov, M.; Budovsky, A.; Fraifeld, V.E.; Garazha, A.; Tsvetkov, V.; et al. Geroprotectors.org: A new, structured and curated database of current therapeutic interventions in aging and age-related disease. Aging 2015, 7, 616–628. [Google Scholar] [CrossRef] [PubMed]
- Barardo, D.; Thornton, D.; Thoppil, H.; Walsh, M.; Sharifi, S.; Ferreira, S.; Anžič, A.; Fernandes, M.; Monteiro, P.; Grum, T.; et al. The DrugAge database of aging-related drugs. Aging Cell 2017, 16, 594–597. [Google Scholar] [CrossRef] [PubMed]
- Keane, M.; Semeiks, J.; Webb, A.E.; Li, Y.I.; Quesada, V.; Craig, T.; Madsen, L.B.; van Dam, S.; Brawand, D.; Marques, P.I.; et al. Insights into the evolution of longevity from the bowhead whale genome. Cell Rep. 2015, 10, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Gorbunova, V.; Seluanov, A.; Zhang, Z.; Gladyshev, V.N.; Vijg, J. Comparative genetics of longevity and cancer: Insights from long-lived rodents. Nat. Rev. Genet. 2014, 15, 531–540. [Google Scholar] [CrossRef] [PubMed]
- Fushan, A.A.; Turanov, A.A.; Lee, S.-G.; Kim, E.B.; Lobanov, A.V.; Yim, S.H.; Buffenstein, R.; Lee, S.-R.; Chang, K.-T.; Rhee, H.; et al. Gene expression defines natural changes in mammalian lifespan. Aging Cell 2015, 14, 352–365. [Google Scholar] [CrossRef]
- Ma, S.; Gladyshev, V.N. Molecular signatures of longevity: Insights from cross-species comparative studies. Semin. Cell Dev. Biol. 2017, 70, 190–203. [Google Scholar] [CrossRef]
- Toren, D.; Kulaga, A.; Jethva, M.; Rubin, E.; Snezhkina, A.V.; Kudryavtseva, A.V.; Nowicki, D.; Tacutu, R.; Moskalev, A.A.; Fraifeld, V.E. Gray whale transcriptome reveals longevity adaptations associated with DNA repair and ubiquitination. Aging Cell 2020, 19, e13158. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Upneja, A.; Galecki, A.; Tsai, Y.-M.; Burant, C.F.; Raskind, S.; Zhang, Q.; Zhang, Z.D.; Seluanov, A.; Gorbunova, V.; et al. Cell culture-based profiling across mammals reveals DNA repair and metabolism as determinants of species longevity. eLife 2016, 5, e19130. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Whelan, C.V.; Foley, N.M.; Jebb, D.; Touzalin, F.; Petit, E.J.; Puechmaille, S.J.; Teeling, E.C. Longitudinal comparative transcriptomics reveals unique mechanisms underlying extended healthspan in bats. Nat. Ecol. Evol. 2019, 3, 1110–1120. [Google Scholar] [CrossRef] [PubMed]
- Hilton, H.G.; Rubinstein, N.D.; Janki, P.; Ireland, A.T.; Bernstein, N.; Fong, N.L.; Wright, K.M.; Smith, M.; Finkle, D.; Martin-McNulty, B.; et al. Single-cell transcriptomics of the naked mole-rat reveals unexpected features of mammalian immunity. PLoS Biol. 2019, 17, e3000528. [Google Scholar] [CrossRef] [PubMed]
- Muradian, K.K.; Utko, N.A.; Mozzhukhina, T.G.; Litoshenko, A.Y.; Pishel, I.N.; Bezrukov, V.V.; Fraifield, V.E. Pair-wise linear and 3D nonlinear relationships between the liver antioxidant enzyme activities and the rate of body oxygen consumption in mice. Free Radic. Biol. Med. 2002, 33, 1736–1739. [Google Scholar] [CrossRef]
- Lehmann, G.; Segal, E.; Muradian, K.K.; Fraifeld, V.E. Do mitochondrial DNA and metabolic rate complement each other in determination of the mammalian maximum longevity? Rejuvenat. Res. 2008, 11, 409–417. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, G.; Muradian, K.K.; Fraifeld, V.E. Telomere length and body temperature-independent determinants of mammalian longevity? Front. Genet. 2013, 4, 111. [Google Scholar] [CrossRef]
- Tacutu, R.; Budovsky, A.; Yanai, H.; Fraifeld, V.E. Molecular links between cellular senescence, longevity and age-related diseases—A systems biology perspective. Aging 2011, 3, 1178–1191. [Google Scholar] [CrossRef]
- Wolfson, M.; Budovsky, A.; Tacutu, R.; Fraifeld, V. The signaling hubs at the crossroad of longevity and age-related disease networks. Int. J. Biochem. Cell Biol. 2009, 41, 516–520. [Google Scholar] [CrossRef]
- Kim, E.B.; Fang, X.; Fushan, A.A.; Huang, Z.; Lobanov, A.V.; Han, L.; Marino, S.M.; Sun, X.; Turanov, A.A.; Yang, P.; et al. Genome sequencing reveals insights into physiology and longevity of the naked mole rat. Nature 2011, 479, 223–227. [Google Scholar] [CrossRef]
- Hulbert, A.J. Metabolism and longevity: Is there a role for membrane fatty acids? Integr. Comp. Biol. 2010, 50, 808–817. [Google Scholar] [CrossRef]
- Lopez-Torres, M.; Perez-Campo, R.; Rojas, C.; Cadenas, S.; Barja, G. Maximum life span in vertebrates: Relationship with liver antioxidant enzymes, glutathione system, ascorbate, urate, sensitivity to peroxidation, true malondialdehyde, in vivo H2O2, and basal and maximum aerobic capacity. Mech. Ageing Dev. 1993, 70, 177–199. [Google Scholar] [CrossRef]
- Bozek, K.; Khrameeva, E.E.; Reznick, J.; Omerbašić, D.; Bennett, N.C.; Lewin, G.R.; Azpurua, J.; Gorbunova, V.; Seluanov, A.; Regnard, P.; et al. Lipidome determinants of maximal lifespan in mammals. Sci. Rep. 2017, 7, 5. [Google Scholar] [CrossRef] [PubMed]
- Chung, J.H.; Seo, A.Y.; Chung, S.W.; Kim, M.K.; Leeuwenburgh, C.; Yu, B.P.; Chung, H.Y. Molecular mechanism of PPAR in the regulation of age-related inflammation. Age. Res. Rev. 2008, 7, 126–136. [Google Scholar] [CrossRef] [PubMed]
- Pararasa, C.; Ikwuobe, J.; Shigdar, S.; Boukouvalas, A.; Nabney, I.T.; Brown, J.E.; Devitt, A.; Bailey, C.J.; Bennett, S.J.; Griffiths, H.R. Age-associated changes in long-chain fatty acid profile during healthy aging promote pro-inflammatory monocyte polarization via PPARγ. Aging Cell 2016, 15, 128–139. [Google Scholar] [CrossRef]
- Sibilia, M.; Steinbach, J.P.; Stingl, L.; Aguzzi, A.; Wagner, E.F. A strain-independent postnatal neurodegeneration in mice lacking the EGF receptor. EMBO J. 1998, 17, 719–731. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A highly efficient gradient boosting decision tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ricklefs, R.E. Life-history connections to rates of aging in terrestrial vertebrates. Proc. Natl. Acad. Sci. USA 2010, 107, 10314–10319. [Google Scholar] [CrossRef]
- Jylhävä, J.; Kananen, L.; Raitanen, J.; Marttila, S.; Nevalainen, T.; Hervonen, A.; Jylhä, M.; Hurme, M. Methylomic predictors demonstrate the role of NF-κB in old-age mortality and are unrelated to the aging-associated epigenetic drift. Oncotarget 2016, 7, 19228–19241. [Google Scholar] [CrossRef]
- Osorio, F.G.; Bárcena, C.; Soria-Valles, C.; Ramsay, A.J.; de Carlos, F.; Cobo, J.; Fueyo, A.; Freije, J.M.P.; López-Otín, C. Nuclear lamina defects cause ATM-dependent NF-κB activation and link accelerated aging to a systemic inflammatory response. Genes Dev. 2012, 26, 2311–2324. [Google Scholar] [CrossRef]
- Deng, Q.; Guo, T.; Zhou, X.; Xi, Y.; Yang, X.; Ge, W. Cross-talk between mitochondrial fusion and the hippo pathway in controlling cell proliferation during drosophila development. Genetics 2016, 203, 1777–1788. [Google Scholar] [CrossRef]
- Chaudhari, S.N.; Kipreos, E.T. Increased mitochondrial fusion allows the survival of older animals in diverse C. elegans longevity pathways. Nat. Commun. 2017, 8, 182. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, J.; Hwang, G.; Jacob, J.; Sapp, N.; Bedigian, R.; Oka, K.; Overbeek, P.; Murray, S.; Jordan, P.W. Meiosis-specific cohesin component, Stag3 is essential for maintaining centromere chromatid cohesion, and required for DNA repair and synapsis between homologous chromosomes. PLoS Genet. 2014, 10, e1004413. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, C.; Arato, K.; Lilienthal, E.; Zerweck, J.; Schutkowski, M.; Chatain, N.; Müller-Newen, G.; Becker, W.; de la Luna, S. Splice variants of the dual specificity tyrosine phosphorylation-regulated kinase 4 (DYRK4) differ in their subcellular localization and catalytic activity. J. Biol. Chem. 2011, 286, 5494–5505. [Google Scholar] [CrossRef] [PubMed]
- Kargbo, R.B. Selective DYRK1A inhibitor for the treatment of neurodegenerative diseases: Alzheimer, parkinson, huntington, and down syndrome. ACS Med. Chem. Lett. 2020, 11, 1795–1796. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, X.-Q.; Weber, H.C.; Xiang, Y.; Liu, C.; Liu, H.-J.; Yang, H.; Jiang, J.; Qu, X. Bombesin Receptor-Activated Protein (BRAP) Modulates NF-κB Activation in Bronchial Epithelial Cells by Enhancing HDAC Activity. J. Cell. Biochem. 2016, 117, 1069–1077. [Google Scholar] [CrossRef]
- Salminen, A.; Kaarniranta, K. Genetics vs. entropy: Longevity factors suppress the NF-kappaB-driven entropic aging process. Age. Res. Rev. 2010, 9, 298–314. [Google Scholar] [CrossRef]
- The PPP1CA Gene and Its Putative Association with Human Ageing. Available online: https://genomics.senescence.info/genes/entry.php?hgnc=PPP1CA (accessed on 11 December 2020).
- Bunu, G.; Toren, D.; Ion, C.F.; Barardo, D.; Sarghie, L.; Grigore, L.G.; de Magalhaes, J.P.; Fraifeld, V.; Tacutu, R. SynergyAge: A curated database for synergistic and antagonistic interactions of longevity-associated genes. Sci. Data 2020, 7, 366. [Google Scholar] [CrossRef]
- Cui, X.Y.; Fu, P.F.; Pan, D.N.; Zhao, Y.; Zhao, J.; Zhao, B.C. The antioxidant effects of ribonuclease inhibitor. Free Radic. Res. 2003, 37, 1079–1085. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.; Le, T.D. Practical approaches to causal relationship exploration. In Springerbriefs in Electrical and Computer Engineering; Springer International Publishing: Cham, Switzerland, 2015; ISBN 978-3-319-14432-0. [Google Scholar]
- Lagani, V.; Athineou, G.; Farcomeni, A.; Tsagris, M.; Tsamardinos, I. Feature Selection with the R PackageMXM: Discovering Statistically Equivalent Feature Subsets. J. Stat. Softw. 2017, 80. [Google Scholar] [CrossRef]
- Unable to find information for 10168452.
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2001; ISBN 9780262527927. [Google Scholar]
- Fanzani, A.; Giuliani, R.; Colombo, F.; Zizioli, D.; Presta, M.; Preti, A.; Marchesini, S. Overexpression of cytosolic sialidase Neu2 induces myoblast differentiation in C2C12 cells. FEBS Lett. 2003, 547, 183–188. [Google Scholar] [CrossRef]
- Emelyanova, L.; Preston, C.; Gupta, A.; Viqar, M.; Negmadjanov, U.; Edwards, S.; Kraft, K.; Devana, K.; Holmuhamedov, E.; O’Hair, D.; et al. Effect of aging on mitochondrial energetics in the human atria. J. Gerontol. A Biol. Sci. Med. Sci. 2018, 73, 608–616. [Google Scholar] [CrossRef] [PubMed]
- Alston, C.L.; Heidler, J.; Dibley, M.G.; Kremer, L.S.; Taylor, L.S.; Fratter, C.; French, C.E.; Glasgow, R.I.C.; Feichtinger, R.G.; Delon, I.; et al. Bi-allelic mutations in NDUFA6 establish its role in early-onset isolated mitochondrial complex I deficiency. Am. J. Hum. Genet. 2018, 103, 592–601. [Google Scholar] [CrossRef] [PubMed]
- Miwa, S.; Jow, H.; Baty, K.; Johnson, A.; Czapiewski, R.; Saretzki, G.; Treumann, A.; von Zglinicki, T. Low abundance of the matrix arm of complex I in mitochondria predicts longevity in mice. Nat. Commun. 2014, 5, 3837. [Google Scholar] [CrossRef] [PubMed]
- Zhai, L.; Wang, C.; Chen, Y.; Zhou, S.; Li, L. Rbm46 regulates mouse embryonic stem cell differentiation by targeting β-Catenin mRNA for degradation. PLoS ONE 2017, 12, e0172420. [Google Scholar] [CrossRef]
- Zheng, J.-S.; Arnett, D.K.; Parnell, L.D.; Lee, Y.-C.; Ma, Y.; Smith, C.E.; Richardson, K.; Li, D.; Borecki, I.B.; Tucker, K.L.; et al. Polyunsaturated fatty acids modulate the association between PIK3CA-KCNMB3 genetic variants and insulin resistance. PLoS ONE 2013, 8, e67394. [Google Scholar] [CrossRef]
- Chen, G.; Kroemer, G.; Kepp, O. Mitophagy: An emerging role in aging and age-associated diseases. Front. Cell Dev. Biol. 2020, 8, 200. [Google Scholar] [CrossRef]
- Wang, S.; Xia, W.; Qiu, M.; Wang, X.; Jiang, F.; Yin, R.; Xu, L. Atlas on substrate recognition subunits of CRL2 E3 ligases. Oncotarget 2016, 7, 46707–46716. [Google Scholar] [CrossRef]
- Martin, E.C.; Sukarta, O.C.A.; Spiridon, L.; Grigore, L.G.; Constantinescu, V.; Tacutu, R.; Goverse, A.; Petrescu, A.-J. LRRpredictor-A New LRR Motif Detection Method for Irregular Motifs of Plant NLR Proteins Using an Ensemble of Classifiers. Genes 2020, 11, 286. [Google Scholar] [CrossRef]
- Yuan, J.; Chen, J. FIGNL1-containing protein complex is required for efficient homologous recombination repair. Proc. Natl. Acad. Sci. USA 2013, 110, 10640–10645. [Google Scholar] [CrossRef]
- Kaneko, H. Histamime receptor H4 as a new therapeutic target for age-related macular degeneration. Nippon Ganka Gakkai Zasshi 2016, 120, 747–753. [Google Scholar]
- Li, Q.; Milenkovic, T. Improving supervised prediction of aging-related genes via dynamic network analysis. arXiv 2020, arXiv:2005.03659. [Google Scholar]
- Sahoo, S.; Meijles, D.N.; Pagano, P.J. NADPH oxidases: Key modulators in aging and age-related cardiovascular diseases? Clin. Sci. 2016, 130, 317–335. [Google Scholar] [CrossRef] [PubMed]
- Lalioti, V.S.; Vergarajauregui, S.; Villasante, A.; Pulido, D.; Sandoval, I.V. C6orf89 encodes three distinct HDAC enhancers that function in the nucleolus, the golgi and the midbody. J. Cell. Physiol. 2013, 228, 1907–1921. [Google Scholar] [CrossRef] [PubMed]
- Finger, Y.; Habich, M.; Gerlich, S.; Urbanczyk, S.; van de Logt, E.; Koch, J.; Schu, L.; Lapacz, K.J.; Ali, M.; Petrungaro, C.; et al. Proteasomal degradation induced by DPP9-mediated processing competes with mitochondrial protein import. EMBO J. 2020, 39, e103889. [Google Scholar] [CrossRef]
- Herrero, J.; Muffato, M.; Beal, K.; Fitzgerald, S.; Gordon, L.; Pignatelli, M.; Vilella, A.J.; Searle, S.M.J.; Amode, R.; Brent, S.; et al. Ensembl comparative genomics resources. Database 2016, 2016, bav096. [Google Scholar] [CrossRef]
- Toren, D.; Barzilay, T.; Tacutu, R.; Lehmann, G.; Muradian, K.K.; Fraifeld, V.E. MitoAge: A database for comparative analysis of mitochondrial DNA, with a special focus on animal longevity. Nucl. Acids Res. 2016, 44, D1262–D1265. [Google Scholar] [CrossRef]
- Chen, S.; Zhou, Y.; Chen, Y.; Gu, J. fastp: An ultra-fast all-in-one FASTQ preprocessor. Bioinformatics 2018, 34, i884–i890. [Google Scholar] [CrossRef]
- Patro, R.; Duggal, G.; Love, M.I.; Irizarry, R.A.; Kingsford, C. Salmon provides fast and bias-aware quantification of transcript expression. Nat. Methods 2017, 14, 417–419. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; pp. 92–96. [Google Scholar]
- Barbie, D.A.; Tamayo, P.; Boehm, J.S.; Kim, S.Y.; Moody, S.E.; Dunn, I.F.; Schinzel, A.C.; Sandy, P.; Meylan, E.; Scholl, C.; et al. Systematic RNA interference reveals that oncogenic KRAS-driven cancers require TBK1. Nature 2009, 462, 108–112. [Google Scholar] [CrossRef]
- Kanehisa, M.; Goto, S.; Sato, Y.; Furumichi, M.; Tanabe, M. KEGG for integration and interpretation of large-scale molecular data sets. Nucl. Acids Res. 2012, 40, D109–D114. [Google Scholar] [CrossRef]
- Subramanian, A.; Tamayo, P.; Mootha, V.K.; Mukherjee, S.; Ebert, B.L.; Gillette, M.A.; Paulovich, A.; Pomeroy, S.L.; Golub, T.R.; Lander, E.S.; et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc. Natl. Acad. Sci. USA 2005, 102, 15545–15550. [Google Scholar] [CrossRef] [PubMed]
- Chen, E.Y.; Tan, C.M.; Kou, Y.; Duan, Q.; Wang, Z.; Meirelles, G.V.; Clark, N.R.; Ma’ayan, A. Enrichr: Interactive and collaborative HTML5 gene list enrichment analysis tool. BMC Bioinformatics 2013, 14, 128. [Google Scholar] [CrossRef] [PubMed]
- Kuleshov, M.V.; Jones, M.R.; Rouillard, A.D.; Fernandez, N.F.; Duan, Q.; Wang, Z.; Koplev, S.; Jenkins, S.L.; Jagodnik, K.M.; Lachmann, A.; et al. Enrichr: A comprehensive gene set enrichment analysis web server 2016 update. Nucl. Acids Res. 2016, 44, W90–W97. [Google Scholar] [CrossRef] [PubMed]
- Lowe, S.C. Stratified Validation Splits for Regression Problems. Available online: https://scottclowe.com/2016-03-19-stratified-regression-partitions/ (accessed on 11 December 2020).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining—KDD ’19, Anchorage, AK, USA, 3–7 August 2019; ACM Press: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]
- Ozaki, Y.; Tanigaki, Y.; Watanabe, S.; Onishi, M. Multiobjective tree-structured parzen estimator for computationally expensive optimization problems. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020; ACM: New York, NY, USA, 2020; pp. 533–541. [Google Scholar]
- Stekhoven, D.J.; Bühlmann, P. MissForest--non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef]
- Guolin, K. Microsoft Research Welcome to LightGBM’s Documentation!—LightGBM 3.1.1.99 Documentation. 2016. Available online: github.com (accessed on 11 December 2020).
- McKinney, W. Pandas. 2008. Available online: github.com (accessed on 11 December 2020).
- JAGS—Just Another Gibbs Sampler. Available online: http://mcmc-jags.sourceforge.net/ (accessed on 11 December 2020).
- Peterson, R.A.; Cavanaugh, J.E. Ordered quantile normalization: A semiparametric transformation built for the cross-validation era. J. Appl. Stat. 2020, 47, 2312–2327. [Google Scholar] [CrossRef]
| Organ | Number of Samples | RMSE (Years) | R2 | MAE | Significant Genes for the Linear Regression |
|---|---|---|---|---|---|
| Brain | 132 | 15.47 | 0.79 | 8.72 | C1orf56, LRR1, C6orf89, CALCOCO2, CEL, DCTD, DNAJC15, PPP1CA, SPATA20, DPP9 |
| Heart | 39 | 12.43 | 0.78 | 7.12 | C1orf56, C6orf89, CALCOCO2, CEL, DCTD, DNAJC15, SPATA20, DPP9 |
| Kidney | 65 | 11.88 | 0.73 | 8.07 | C1orf56, C6orf89, CALCOCO2, CEL, DCTD, NOXA1, PPP1CA, SPATA20 |
| Liver | 139 | 8.92 | 0.71 | 4.32 | C1orf56, LRR1, C6orf89, CALCOCO2, CEL, DCTD, DNAJC15, NOXA1, PPP1CA, SPATA20, DPP9 |
| Lung | 33 | 21.04 | 0.73 | 13.40 | C1orf56, CALCOCO2, DCTD, NOXA1, SPATA20, DPP9 |
| All organs | 408 | 15.00 | 0.69 | 7.90 | NOXA1, CEL, CALCOCO2, C6orf89, PPP1CA, SPATA20, DPP9, DCTD, LRR1, DNAJC15, C1orf56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulaga, A.Y.; Ursu, E.; Toren, D.; Tyshchenko, V.; Guinea, R.; Pushkova, M.; Fraifeld, V.E.; Tacutu, R. Machine Learning Analysis of Longevity-Associated Gene Expression Landscapes in Mammals. Int. J. Mol. Sci. 2021, 22, 1073. https://doi.org/10.3390/ijms22031073
Kulaga AY, Ursu E, Toren D, Tyshchenko V, Guinea R, Pushkova M, Fraifeld VE, Tacutu R. Machine Learning Analysis of Longevity-Associated Gene Expression Landscapes in Mammals. International Journal of Molecular Sciences. 2021; 22(3):1073. https://doi.org/10.3390/ijms22031073
Chicago/Turabian StyleKulaga, Anton Y., Eugen Ursu, Dmitri Toren, Vladyslava Tyshchenko, Rodrigo Guinea, Malvina Pushkova, Vadim E. Fraifeld, and Robi Tacutu. 2021. "Machine Learning Analysis of Longevity-Associated Gene Expression Landscapes in Mammals" International Journal of Molecular Sciences 22, no. 3: 1073. https://doi.org/10.3390/ijms22031073
APA StyleKulaga, A. Y., Ursu, E., Toren, D., Tyshchenko, V., Guinea, R., Pushkova, M., Fraifeld, V. E., & Tacutu, R. (2021). Machine Learning Analysis of Longevity-Associated Gene Expression Landscapes in Mammals. International Journal of Molecular Sciences, 22(3), 1073. https://doi.org/10.3390/ijms22031073






