Fullerene Negative Ions: Formation and Catalysis
Abstract
1. Introduction
2. Results
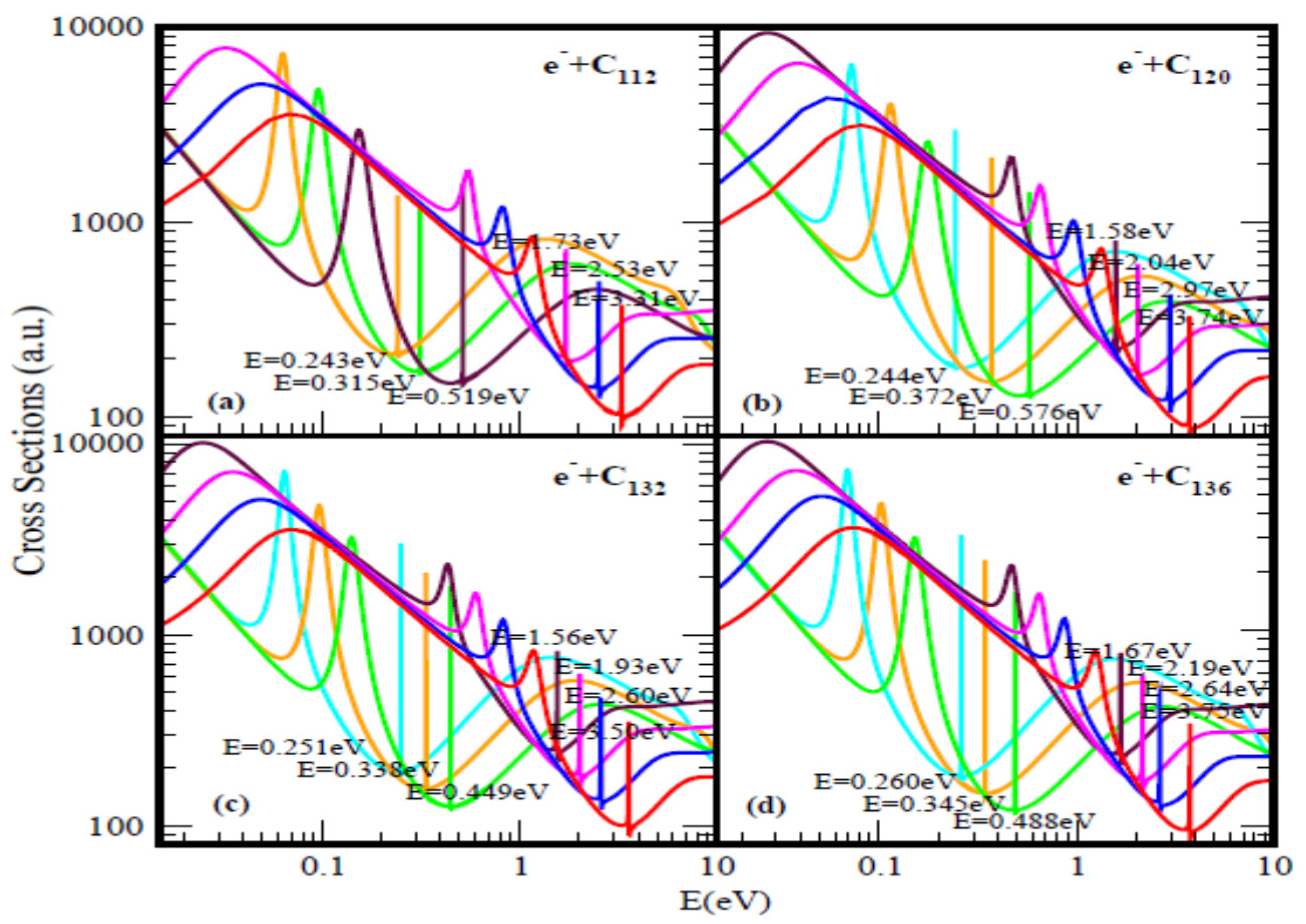
2.1. Fullerene Electron Scattering Total Cross Sections
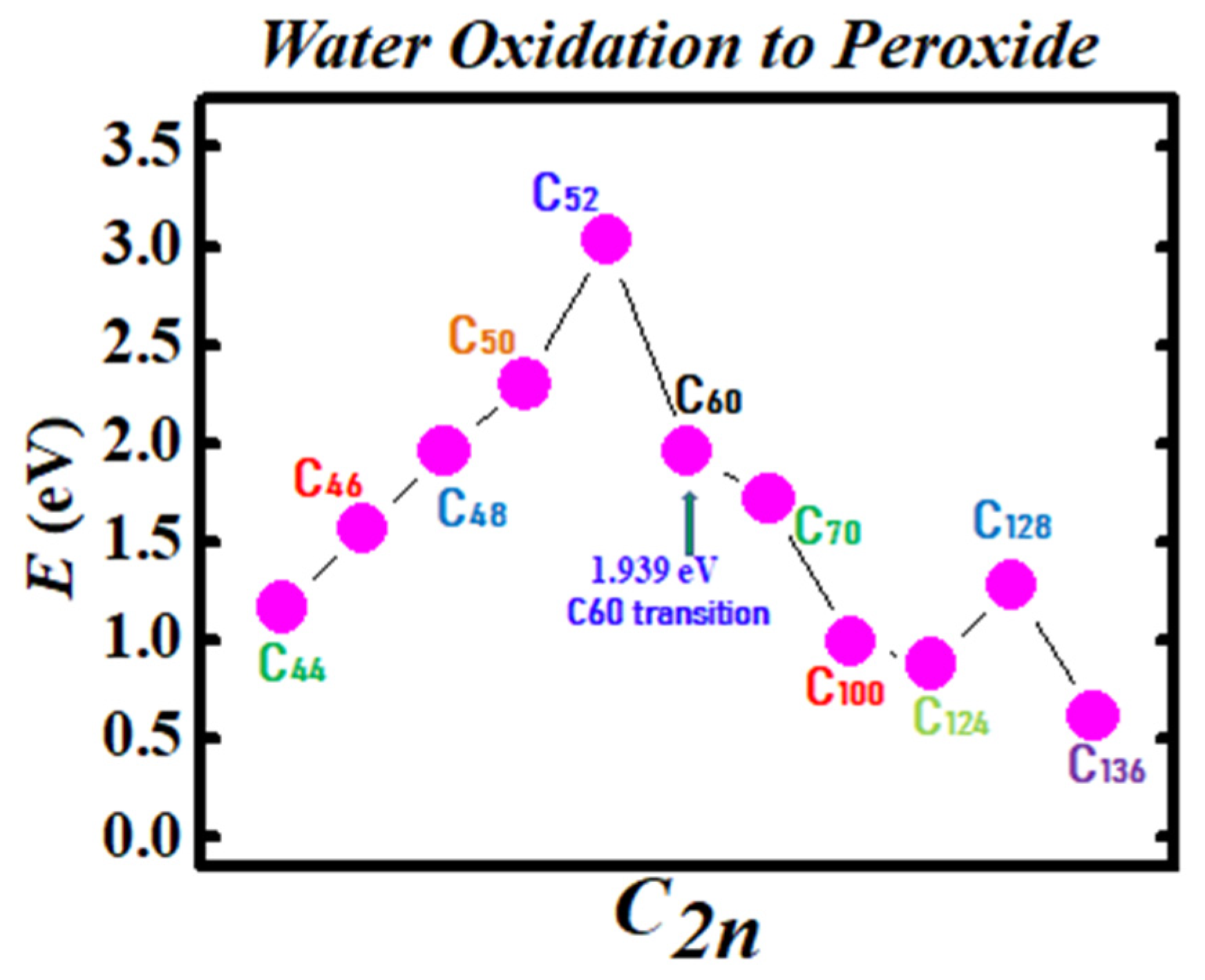
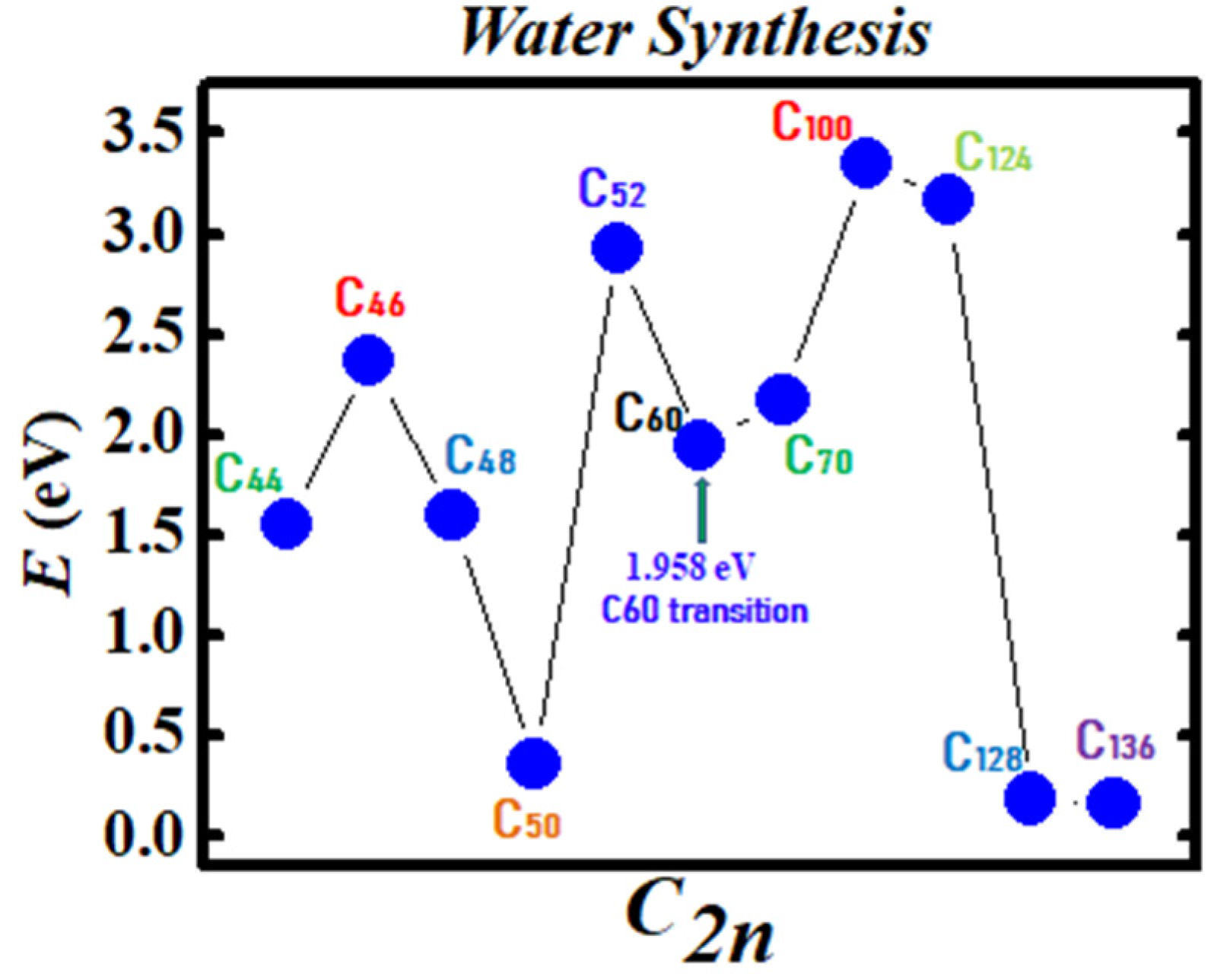
2.2. Fullerene Transition State Barriers
3. Method of Calculation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Year of the Periodic Table: Single Atoms as Active Catalysts. Available online: https://pubs.rsc.org/en/journals/articlecollectionlanding?sercode=nr&themeid=1fc90a67-e081-4265-99eb-2201eb17c286 (accessed on 12 January 2017).
- Msezane, A.Z.; Felfli, Z.; Sokolovski, D. Novel mechanism for nanoscale catalysis. J. Phys. B 2010, 43, 201001. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z.; Sokolovski, D. Cold fusion mechanism in nanoscale catalysis. Europhys News 2010, 41, 11. [Google Scholar]
- Edwards, J.K.; Carley, A.F.; Herzing, A.A.; Kiely, C.J.; Hutchings, G.J. Direct synthesis of hydrogen peroxide from H2 and O2 using supported Au–Pd catalysts. J. Chem. Soc. Faraday Discuss 2008, 138, 225. [Google Scholar] [CrossRef]
- Edwards, J.K.; Solsona, B.; Landon, P.; Carley, A.F.; Herzing, A.; Watanabe, M.; Kiely, C.J.; Hutchings, G.J. Direct synthesis of hydrogen peroxide from H2 and O2 using Au–Pd/Fe2O3 catalysts. J. Mater. Chem. 2005, 15, 4595. [Google Scholar] [CrossRef]
- Freakley, S.J.; He, Q.; Harrhy, J.H.; Lu, L.; Crole, D.A.; Morgan, D.J.; Ntainjua, E.N.; Edwards, J.K.; Carley, A.F.; Borisevich, A.Y.; et al. Palladium-tin catalysts for the direct synthesis of H2O2 with high selectivity. Science 2016, 351, 959. [Google Scholar] [CrossRef]
- Tesfamichael, A.; Suggs, K.; Felfli, Z.; Wang, X.-Q.; Msezane, A.Z. Atomic Gold and Palladium Negative-Ion Catalysis of Light, Intermediate, and Heavy Water to Corresponding Peroxides. J. Phys. Chem. C 2012, 116, 18698. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z.; Tesfamichael, A.; Suggs, K.; Wang, X.-Q. Gold anion catalysis of methane to methanol. Gold Bulletin 2012, 3, 127. [Google Scholar] [CrossRef][Green Version]
- Kasdan, K.; Lineberger, W.C. Alkali-metal negative ions. II. Laser photoelectron spectrometry. Phys. Rev. A 1974, 10, 1658. [Google Scholar] [CrossRef]
- Wang, L.-S.; Conceicao, J.J.; Jin, C.M.; Smalley, R.E. Threshold photodetachment of cold C−60. Chem. Phys. Lett. 1991, 182, 5. [Google Scholar] [CrossRef]
- Huang, D.-L.; Dau, P.D.; Liu, H.T.; Wang, L.-S. High-resolution photoelectron imaging of cold C₆₀⁻ anions and accurate determination of the electron affinity of C₆₀. J. Chem. Phys. 2014, 140, 224315. [Google Scholar] [CrossRef]
- Brink, C.; Andersen, L.H.; Hvelplund, P.; Mathur, D.; Voldstad, J.D. Laser photodetachment of C60− and C70− ions cooled in a storage ring. Chem. Phys. Lett. 1995, 233, 52. [Google Scholar] [CrossRef]
- Wang, X.B.; Woo, H.K.; Huang, X.; Kappes, M.M.; Wang, L.S. Direct Experimental Probe of the On-Site Coulomb Repulsion in the Doubly Charged Fullerene Anion C702-. Phys. Rev. Lett. 2006, 96, 143002. [Google Scholar] [CrossRef]
- Boltalina, O.V.; Sidorov, L.N.; Sukhanova, E.V.; Skokan, E.V. Electron affinities of higher fullerenes. Rapid Commun. Mass Spectrom. 1993, 7, 1009. [Google Scholar]
- Kietzmann, H.; Rochow, R.; Gantefor, G.; Eberhardt, W.; Vietze, K.; Seifert, G.; Fowler, P.W. Electronic structure of small fullerenes: Evidence for the high stability of C32. Phys. Rev. Lett. 1998, 81, 5378. [Google Scholar] [CrossRef]
- Wang, X.-B.; Woo, H.-K.; Yang, J.; Kappes, M.M.; Wang, L.S. Photoelectron Spectroscopy of Singly and Doubly Charged Higher Fullerenes at Low Temperatures: C76-, C78-, C84- and C762-, C782-, C842-. J. Phys. Chem. C 2007, 111, 17684. [Google Scholar] [CrossRef]
- Boltalina, O.V.; Ioffe, I.N.; Sorokin, I.D.; Sidorov, L.N. Electron Affinity of Some Endohedral Lanthanide Fullerenes. J. Phys. Chem. A 1997, 101, 9561. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z. New insights in low-energy electron-fullerene interactions. Chem. Phys. 2018, 503, 50. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z. Simple method for determining fullerene negative ion formation. Euro. Phys. J. D 2018, 72, 78. [Google Scholar] [CrossRef]
- Winstead, C.; McKoy, V. Elastic electron scattering by fullerene, C60. Phys. Rev. A 2006, 73, 012711. [Google Scholar] [CrossRef]
- Lucchese, R.R.; Gianturco, F.A.; Sanna, N. Low-energy electron scattering from C60 molecules. Chem. Phys. Lett. 1999, 305, 413. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Lucchese, R.R.; Sanna, N. Computed elastic cross sections and angular distributions of low-energy electron scattering from gas phase C60 fullerene. J. Phys. B 1999, 32, 2181. [Google Scholar] [CrossRef]
- Gianturco, F.A.; Lucchese, R.R. One-particle resonances in low-energy electron scattering from C60. J. Chem. Phys. 1999, 111, 6769. [Google Scholar] [CrossRef]
- Ipatov, A.N.; Ivanov, V.K.; Pacheco, J.M.; Ekardt, W. Exchange and polarization effects in elastic electron scattering by metallic clusters. J. Phys. B 1998, 31, L5119. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Cooper, M.B.; Hunter, M.E. Electron elastic scattering off endohedral fullerenes A@ C60: The initial insight. J. Phys. B 2014, 47, 15002. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Amusia, M.Y.; Chernysheva, L.V. Effects of target polarization in electron elastic scattering off endohedral A@C60. Phys. Rev. A 2017, 95, 012709. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V. On the behavior of scattering phases in collisions of electrons with multiatomic objects. JETP Letters 2015, 101, 503. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Chernysheva, L.V.; Dolmatov, V.K. Angle-differential elastic-electron scattering off C 60: A simple semi-empirical theory versus experiment. J. Phys. B 2019, 52, 085201. [Google Scholar] [CrossRef]
- Amusia, M.Y.; Baltenkov, A.S. Time delay in electron-C60 elastic scattering in a dirac bubble potential model. J. Phys. B 2019, 52, 015101. [Google Scholar] [CrossRef]
- Tanaka, H.; Boesten, L.; Onda, K.; Ohashi, O. Crossed-Beam Experiment for the Scattering of Low Energy Electrons from Gas Phase C60. J. Phys. Soc. Jpn. 1994, 63, 485. [Google Scholar] [CrossRef]
- Elhamidi, O.; Pommier, J.; Abouaf, R.J. Low energy electron impact on C76 and C84: Excitation, metastable anion formation, and lifetime. Int. J. Mass Spectr. 2001, 205, 17. [Google Scholar] [CrossRef]
- Elhamidi, O.; Pommier, J.; Abouaf, R.J. Low-energy electron attachment to fullerenes and in the gas phase. J. Phys B 1997, 30, 4633. [Google Scholar] [CrossRef]
- Viggiano, A.A.; Friedman, J.F.; Shuman, N.S.; Miller, T.M.; Schaffer, L.C.; Troe, J. Experimental and modeling study of thermal rate coefficients and cross sections for electron attachment to C60. J. Chem. Phys. 2010, 132, 194307. [Google Scholar] [CrossRef] [PubMed]
- Prabhudesai, V.S.; Nandi, D.; Krishnakumar, E. Low energy electron attachment to C60. Euro Phys. J. D 2005, 35, 261. [Google Scholar] [CrossRef]
- Msezane, A.Z.; Felfli, Z.; Shaginyan, V.R.; Amusia, M.Y. Anionic formation in low-energy electron scattering from large fullerenes: Their multiple functionalization. Int. J. Current Adv. Research 2017, 6, 8503–8509. [Google Scholar]
- Msezane, A.Z.; Felfli, Z. Low-energy electron scattering from fullerenes and heavy complex atoms: Negative ions formation. Eur. Phys. J. D 2018, 72, 173. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z. Negative Ion Formation in Low-Energy Electron Collisions with the Actinide Atoms Th, Pa, U, Np and Pu. Appl. Phys. Res. 2019, 11, 52. [Google Scholar] [CrossRef][Green Version]
- Felfli, Z.; Msezane, A.Z. Conundrum in Measured Electron Affinities of Complex Heavy Atoms. J. At. Mol. Condens. Nano Phys. 2018, 5, 73. [Google Scholar] [CrossRef][Green Version]
- Msezane, A.Z. Negative Ion Binding Energies in Complex Heavy Systems. J. At. Mol. Condens. Nano Phys. 2018, 5, 195. [Google Scholar] [CrossRef][Green Version]
- Ryzhkov, M.V.; Ivanovskii, A.L.; Delley, B. Electronic structure and stabilization of c60 fullerenes encapsulating actinide atom. Nanosyst. Phys. Chem. Math. 2014, 5, 494. [Google Scholar]
- Ryzhkov, M.V.; Ivanovskii, A.L.; Delley, B. Electronic structure of endohedral fullerenes An@ C28 (An = Th–Md). Comp. Theor. Chem. 2012, 985, 46. [Google Scholar] [CrossRef]
- Ryzhkov, M.V.; Delley, B. Electronic structure of predicted endohedral fullerenes An@ C40 (An = Th–Md). Comp. Theor. Chem. 2013, 1013, 70. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral Fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Morales-Martínez, R.; Zhang, X.; Yang, W.; Wang, Y.; Rodríguez-Fortea, A.; Poblet, J.M.; Feng, L.; Wang, S.; Chen, N. Unique Four-Electron Metal-to-Cage Charge Transfer of Th to a C82 Fullerene Cage: Complete Structural Characterization of Th@C3v(8)-C82. J. Am. Chem. Soc. 2017, 139, 5110. [Google Scholar] [CrossRef] [PubMed]
- Jin, P.; Lin, C.; Li, Y.; Li, L.; Zhao, Y. Th@C76. Computational characterization of larger actinide endohedral fullerenes. Int. J. Quant. Chem. 2018, 118, e25501. [Google Scholar] [CrossRef]
- Dunk, P.W.; Kaiser, N.K.; Mulet-Gas, M.; Rodriguez-Fortea, A.; Poblet, J.M.; Shinohara, H.; Hendrickson, C.L.; Marshall, A.G.; Kroto, H.W. The Smallest Stable Fullerene, M@C28 (M = Ti, Zr, U): Stabilization and Growth from Carbon Vapor. J. Am. Chem. Soc. 2012, 134, 9380. [Google Scholar] [CrossRef] [PubMed]
- Vital, S.; Marco-Martinez, J.; Filippone, S.; Martin, N. Fullerenes for catalysis: Metallofullerenes in hydrogen transfer reactions. Chem. Commun. 2017, 53, 4842. [Google Scholar] [CrossRef] [PubMed]
- Lezius, M.; Scheier, P.; Mark, T.D. Free electron attachment to C60 and C70. Chem. Phys. Lett. 1993, 203, 232. [Google Scholar] [CrossRef]
- Jaffke, T.; Illenberger, E.; Lezius, M.; Matejcik, S.; Smith, D.; Mark, T.D. Formation of C60− and C70− by free electron capture. Activation energy and effect of the internal energy on lifetime. Chem. Phys. Lett. 1994, 226, 213. [Google Scholar] [CrossRef]
- Huang, J.; Carman, H.S.; Compton, R.N. Low-Energy Electron Attachment to C60. J. Phys. Chem. 1995, 99, 1719. [Google Scholar] [CrossRef]
- Kronik, L.; Fromherz, R.; Ko, E.; Ganteför, G.; Chelikowsky, J.R. Highest electron affinity as a predictor of cluster anion structures. Nat. Mater. 2002, 1, 49. [Google Scholar] [CrossRef][Green Version]
- Hoke, E.T.; Sachs-Quintana, I.T.; Lloyd, M.T.; Kauvar, I.; Mateker, W.R.; Nardes, A.M.; Peters, C.H.; Kopidakis, N.; McGehee, M.D. The role of electron affinity in determining whether fullerenes catalyze or inhibit photooxidation of polymers for solar cells. Adv. Energy Mat. 2012, 2, 13. [Google Scholar] [CrossRef]
- Mateker, W.R.; McGehee, M.D. Progress in Understanding Degradation Mechanisms and Improving Stability in Organic Photovoltaics. Adv. Mater. 2016. [Google Scholar] [CrossRef] [PubMed]
- Baltenkov, A.; Manson, S.T.; Msezane, A.Z. Jellium model potentials for the C60 molecule and the photoionization of endohedral atoms, A@C60. J. Phys. B 2015, 48, 185103. [Google Scholar] [CrossRef]
- Nagase, S.; Kabayashi, K. Theoretical study of the lanthanide fullerene CeC82. Comparison with ScC82, YC82 and LaC82. Chem. Phys. Lett. 1999, 228, 106. [Google Scholar] [CrossRef]
- Tarento, R.J.; Joyes, P.Z. Size dependence of the electronic and magnetic properties of fullerenes (C60-C240). Phys. D 1996, 37, 165. [Google Scholar] [CrossRef]
- Zakrzewski, V.G.; Dolgounitcheva, O.; Ortiz, J.V. Electron Propagator Calculations on the Ground and Excited States of C60- . J. Phys. Chem. A 2014, 118, 7424. [Google Scholar] [CrossRef]
- Støchkel, K.; Andersen, J.U. Photo excitation and laser detachment of C60− anions in a storage ring. J. Chem. Phys. 2013, 139, 164304. [Google Scholar] [CrossRef]
- Palpant, B.; Otake, A.; Hayakawa, F.; Negishi, Y.; Lee, G.H.; Nakajima, A.; Kaya, K. Photoelectron spectroscopy of sodium-coated C60 and C70 cluster anions. Phys. Rev. B 1999, 60, 4509. [Google Scholar] [CrossRef]
- Johnson, W.R.; Guet, C. Elastic scattering of electrons from Xe, Cs+, and Ba2+. Phys. Rev. A 1994, 49, 1041. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 73005. [Google Scholar] [CrossRef]
- DMol3 2011 Accelrys Software Inc.: San Diego, CA.
- Hiscox, A.; Brown, B.M.; Marletta, M. On the low energy behavior of Regge poles. J. Math. Phys. 2010, 51, 102104. [Google Scholar] [CrossRef]
- Frautschi, S.C. Regge Poles and S-matrix Theory; W. A. Benjamin, Inc.: New York, NY, USA, 1963; Chapter X. [Google Scholar] [CrossRef]
- D’Alfaro, V.; Regge, T.E. Potential Scattering; Amsterdam: Amsterdam, The Netherlands, 1965. [Google Scholar]
- Mulholland, H.P. An asymptotic expansion for Σ(2n+1)exp (Àσ(n+1/2)2). Proc. Camb. Phil. Soc. (London) 1928, 24, 280–289. [Google Scholar] [CrossRef]
- Macek, J.H.; Krstic, P.S.; Ovchinnikov, S.Y. Regge Oscillations in Integral Cross Sections for Proton Impact on Atomic Hydrogen. Phys. Rev. Lett. 2004, 93, 183203. [Google Scholar] [CrossRef] [PubMed]
- Sokolovski, D.; Felfli, Z.; Ovchinnikov, S.Y.; Macek, J.H.; Msezane, A.Z. Regge oscillations in electron-atom elastic cross sections. Phys. Rev. A 2007, 76, 012705. [Google Scholar] [CrossRef]
- Felfli, Z.; Msezane, A.Z.; Sokolovski, D. Resonances in low-energy electron elastic cross sections for lanthanide atoms. Phys. Rev. A 2009, 79, 012714. [Google Scholar] [CrossRef]
- Felfli, Z.; Belov, S.; Avdonina, N.B.; Marletta, M.; Msezane, A.Z.; Naboko, S.N. Proceedings of the Third International Workshop on Contemporary Problems in Mathematical Physics; Govaerts, J., Hounkonnou, M.N., Msezane, A.Z., Eds.; World Scientific: Singapore, 2004; pp. 218–232. [Google Scholar]
- Belov, S.; Thylwe, K.-E.; Marletta, M.; Msezane, A.Z.; Naboko, S.N. On Regge pole trajectories for a rational function approximation of Thomas–Fermi potentials. J. Phys. A 2010, 43, 365301. [Google Scholar] [CrossRef]
- Burke, P.G.; Tate, C. A program for calculating regge trajectories in potential scattering. Comp. Phys. Commun. 1969, 1, 97. [Google Scholar] [CrossRef]
- Thylwe, K.W. On relativistic shifts of negative-ion resonances. Eur. Phys. J. D 2012, 66, 7. [Google Scholar] [CrossRef]

| Full. | Bes GR-S | BEs MS-1 | BEs MS-2 | BEs MS-3 | BEs EXT-1 | BEs EXT-2 | BEs EXT-3 | R-T GR-S | EA Expt. |
|---|---|---|---|---|---|---|---|---|---|
| C44 | 3.15 | 1.89 | 1.47 | - | 0.319 | 0.492 | - | 3.13 | 3.30 [15] |
| C60 | 2.663 [19] 2.57 [55] 2.23 [56] 2.63 [57] | 1.86 | 1.23 | - | 0.203 | 0.378 | - | 2.68 | 2.65 [10] 2.666 [12] 2.664 [58] 2.684 [11] |
| C70 | 2.70 | 1.77 | 1.27 | - | 0.230 | 0.364 | 0.528 | 2.72 | 2.676 [12] 2.72 [14] 2.765 [13] 2.74 [59] |
| C98 | 3.56 | 2.48 | 1.90 | - | 0.294 | 0.350 | 0.442 | 3.54 | - |
| C112 | 3.31 | 2.53 | 1.73 | - | 0.243 | 0.315 | 0.519 | 3.32 | - |
| C120 | 3.74 | 2.97 | 2.04 | 1.58 | 0.244 | 0.372 | 0.576 | 3.73 | - |
| C132 | 3.59 | 2.60 | 1.93 | 1.56 | 0.251 | 0.338 | 0.449 | 3.58 | - |
| C136 | 3.75 | 2.64 | 2.19 | 1.67 | 0.260 | 0.345 | 0.488 | 3.77 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felfli, Z.; Suggs, K.; Nicholas, N.; Msezane, A.Z. Fullerene Negative Ions: Formation and Catalysis. Int. J. Mol. Sci. 2020, 21, 3159. https://doi.org/10.3390/ijms21093159
Felfli Z, Suggs K, Nicholas N, Msezane AZ. Fullerene Negative Ions: Formation and Catalysis. International Journal of Molecular Sciences. 2020; 21(9):3159. https://doi.org/10.3390/ijms21093159
Chicago/Turabian StyleFelfli, Zineb, Kelvin Suggs, Nantambu Nicholas, and Alfred Z. Msezane. 2020. "Fullerene Negative Ions: Formation and Catalysis" International Journal of Molecular Sciences 21, no. 9: 3159. https://doi.org/10.3390/ijms21093159
APA StyleFelfli, Z., Suggs, K., Nicholas, N., & Msezane, A. Z. (2020). Fullerene Negative Ions: Formation and Catalysis. International Journal of Molecular Sciences, 21(9), 3159. https://doi.org/10.3390/ijms21093159





