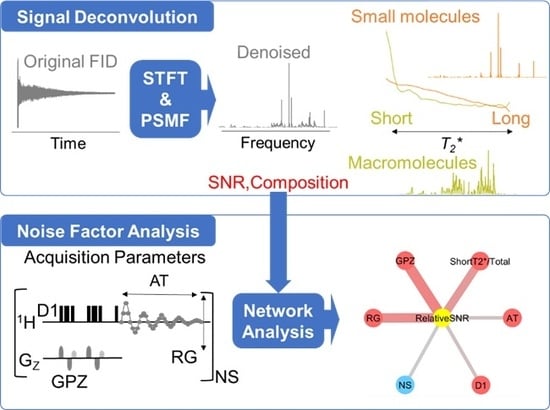
Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time–Frequency Analysis and Probabilistic Sparse Matrix Factorization
Abstract
1. Introduction
2. Results and Discussion
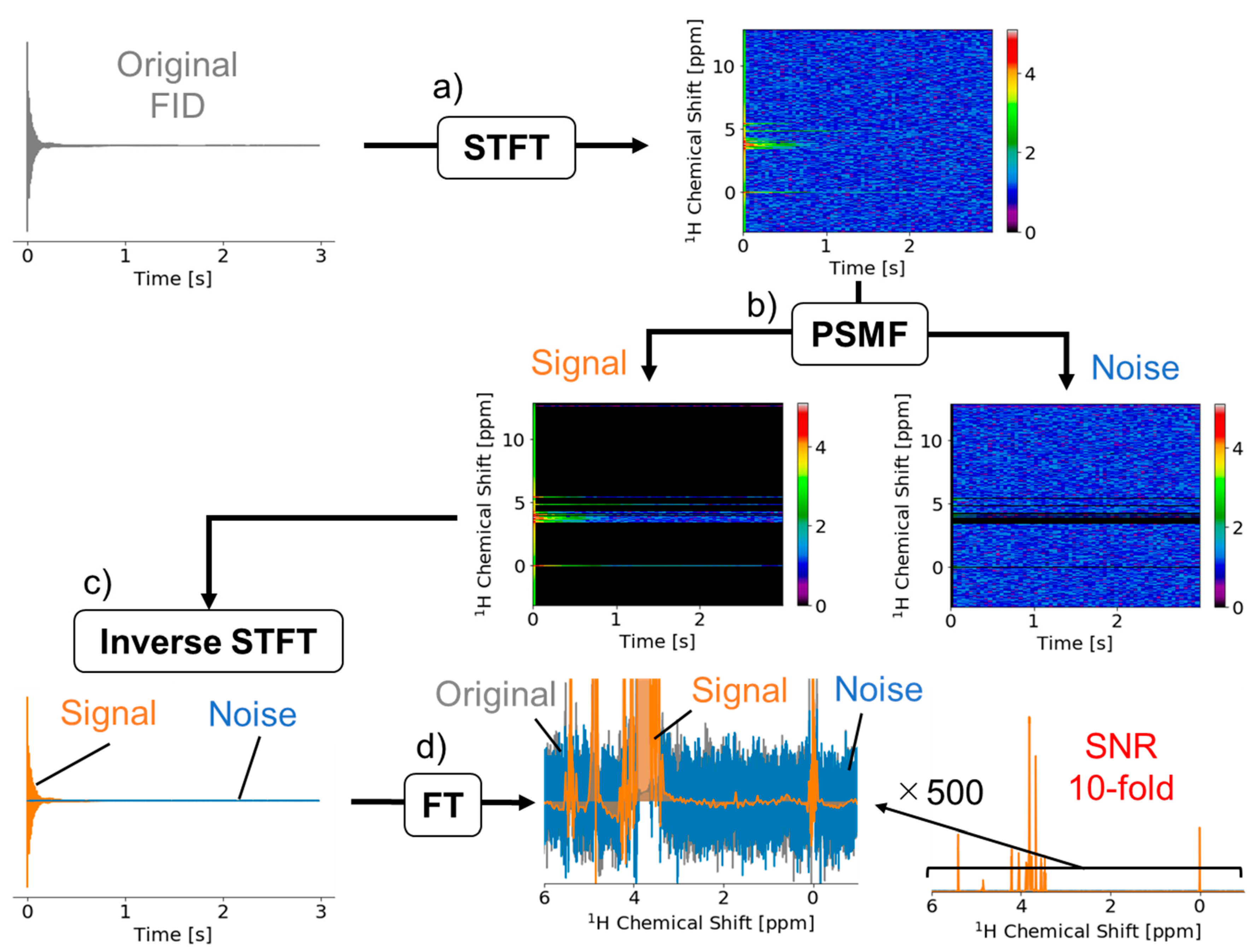
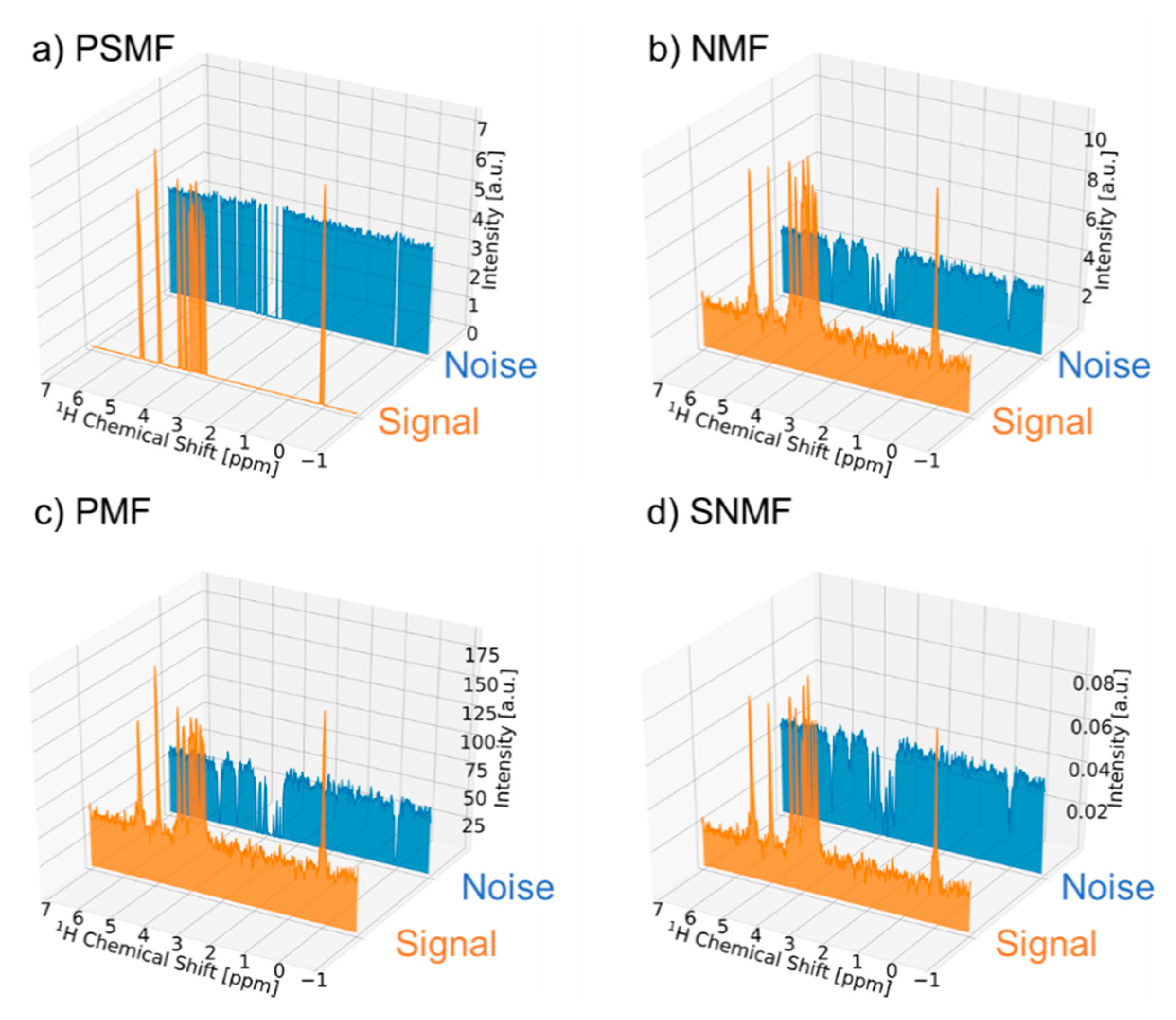
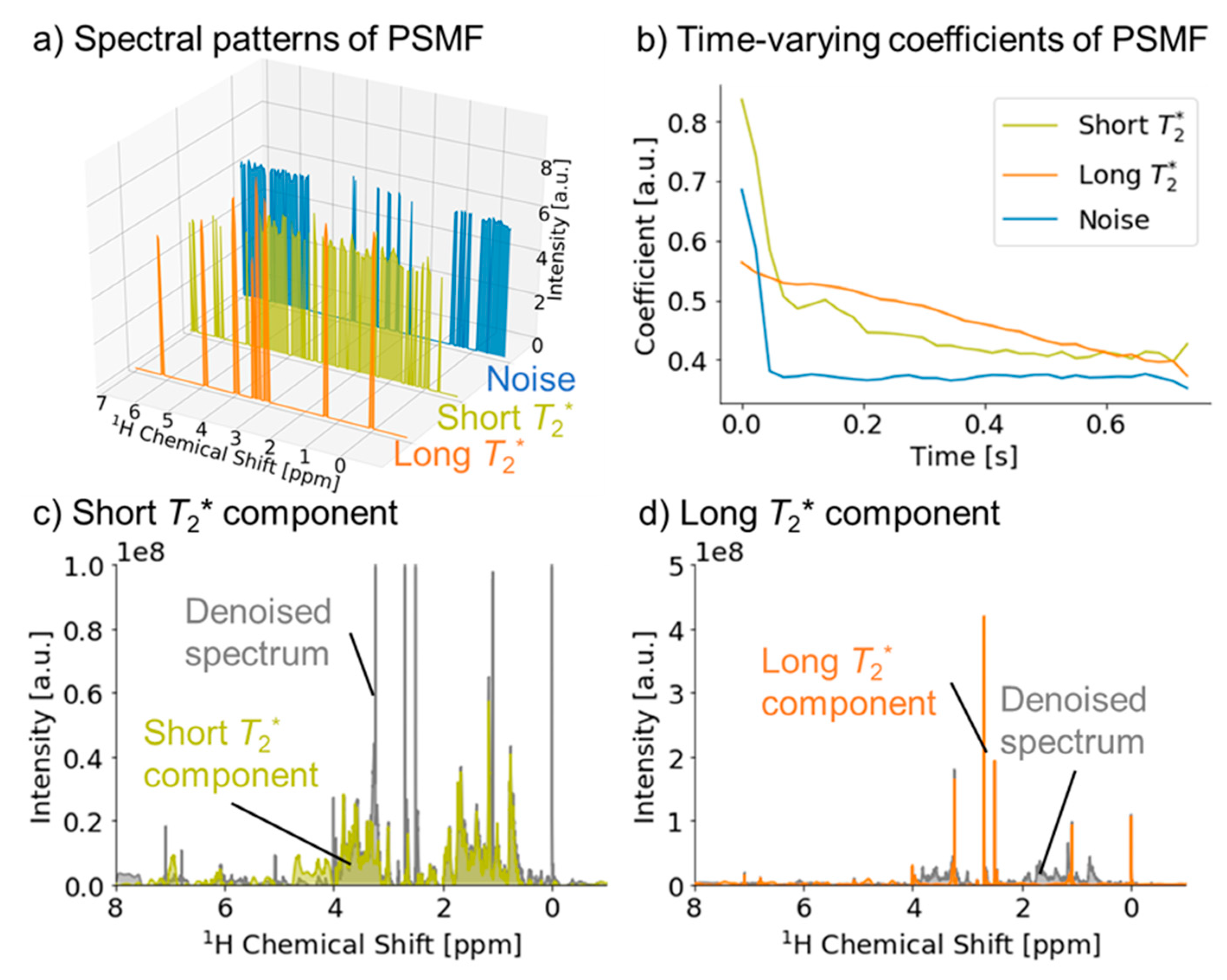
2.1. Signal Deconvolution Method
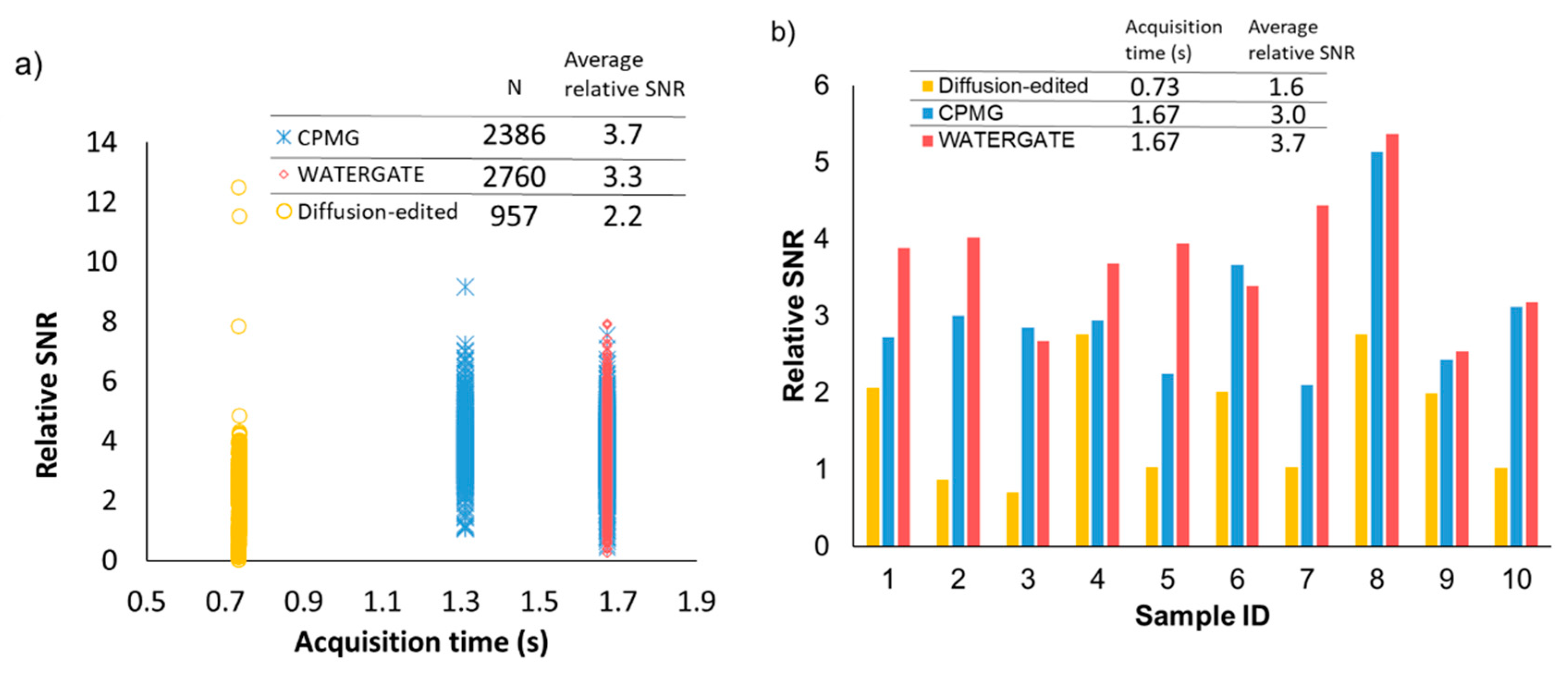
2.2. Noise Reduction in NMR Data Measured by Various Pulse Sequences
2.3. Application of Signal Deconvolution Method in Diffusion-Edited NMR
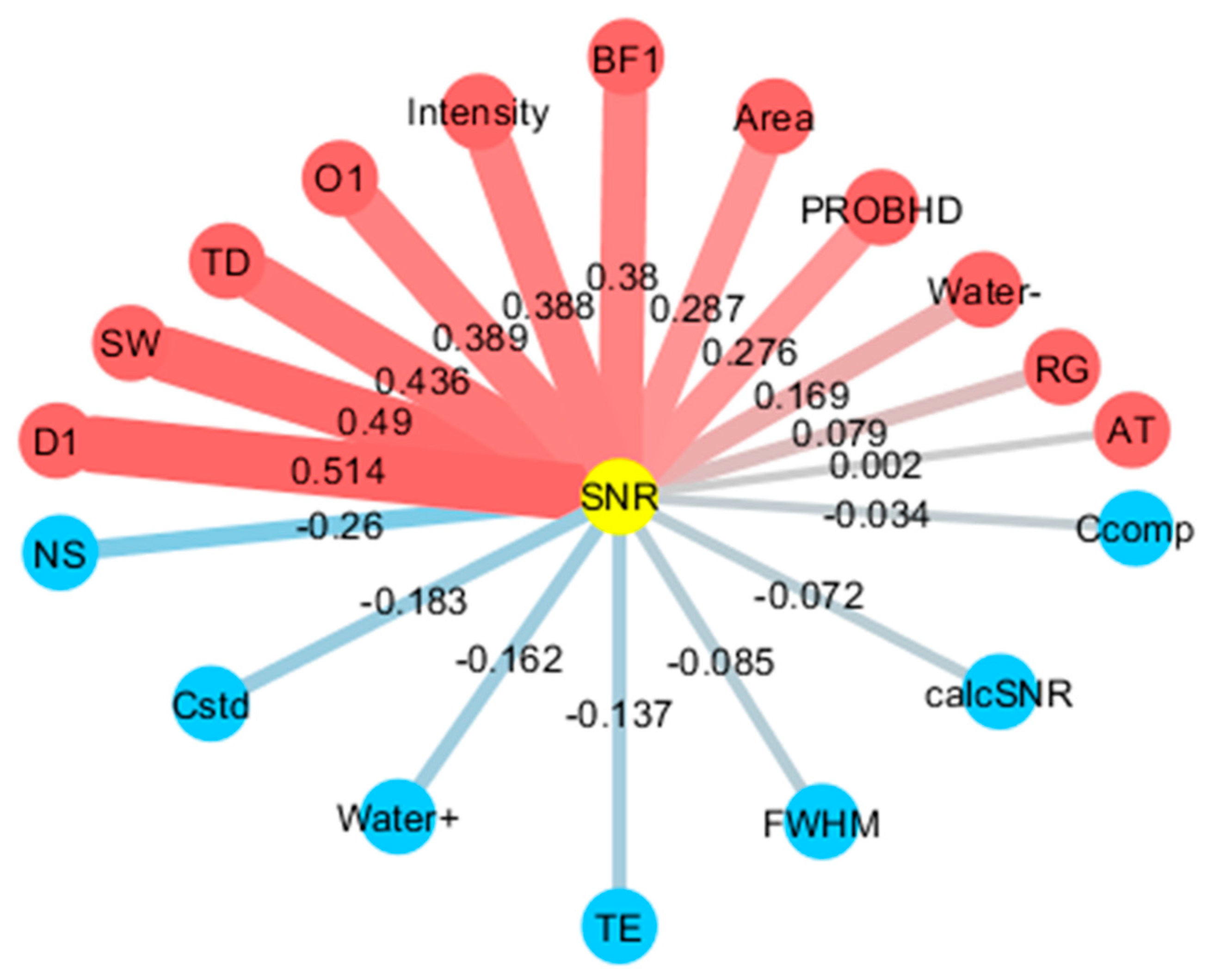
2.4. Noise Factor Analysis in Data Measured by Low- and High-Field NMR at Multiple Institutions
3. Materials and Methods
3.1. Signal Deconvolution Method
3.2. Noise Factor Analysis Method
3.3. NMR Data Acquisition
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Takeuchi, K.; Baskaran, K.; Arthanari, H. Structure determination using solution NMR: Is it worth the effort? J. Magn. Reson. 2019, 306, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, B.; Holmes, E.; Heude, C.; Tolson, R.F.M.; Harvey, N.; Lodge, S.L.; Chetwynd, A.J.; Cannet, C.; Fang, F.; Pearce, J.T.M.; et al. Quantitative Lipoprotein Subclass and Low Molecular Weight Metabolite Analysis in Human Serum and Plasma by 1H NMR Spectroscopy in a Multilaboratory Trial. Anal. Chem. 2018, 90, 11962–11971. [Google Scholar] [CrossRef] [PubMed]
- Chikayama, E.; Yamashina, R.; Komatsu, K.; Tsuboi, Y.; Sakata, K.; Kikuchi, J.; Sekiyama, Y. FoodPro: A Web-Based Tool for Evaluating Covariance and Correlation NMR Spectra Associated with Food Processes. Metabolites 2016, 6, 36. [Google Scholar] [CrossRef] [PubMed]
- Singh, K.; Kumar, S.P.; Blümich, B. Monitoring the mechanism and kinetics of a transesterification reaction for the biodiesel production with low field 1H NMR spectroscopy. Fuel 2019, 243, 192–201. [Google Scholar] [CrossRef]
- Kikuchi, J.; Ito, K.; Date, Y. Environmental metabolomics with data science for investigating ecosystem homeostasis. Prog. Nucl. Magn. Reson. Spectrosc. 2017, 104, 56–88. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S. NMR metabolomics: A look ahead. J. Magn. Reson. 2019, 306, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Maeda, H.; Yanagisawa, Y. Future prospects for NMR magnets: A perspective. J. Magn. Reson. 2019, 306, 80–85. [Google Scholar] [CrossRef]
- Kovacs, H.; Moskau, D.; Spraul, M. Cryogenically cooled probes—A leap in NMR technology. Prog. Nucl. Magn. Reson. Spectrosc. 2005, 46, 131–155. [Google Scholar] [CrossRef]
- Clos, L.J., II; Jofre, M.F.; Ellinger, J.; Westler, W.M.; Markley, J.L. NMRbot: Python scripts enable high-throughput data collection on current Bruker BioSpin NMR spectrometers. Metabolomics 2013, 9, 558–563. [Google Scholar] [CrossRef]
- Ardenkjær-Larsen, J.H.; Fridlund, B.; Gram, A.; Hansson, G.; Hansson, L.; Lerche, M.H.; Servin, R.; Thaning, M.; Golman, K. Increase in signal-to-noise ratio of >10,000 times in liquid-state NMR. Proc. Natl. Acad. Sci. USA 2003, 100, 10158–10163. [Google Scholar] [CrossRef]
- Kazimierczuk, K.; Orekhov, V. Non-uniform sampling: Post-Fourier era of NMR data collection and processing. Magn. Reson. Chem. 2015, 53, 921–926. [Google Scholar] [CrossRef] [PubMed]
- Pines, A.; Gibby, M.G.; Waugh, J.S. Proton-Enhanced Nuclear Induction Spectroscopy. A Method for High Resolution NMR of Dilute Spins in Solids. J. Chem. Phys. 1972, 56, 1776–1777. [Google Scholar] [CrossRef]
- Morris, G.A.; Freeman, R. Enhancement of nuclear magnetic resonance signals by polarization transfer. J. Am. Chem. Soc. 1979, 101, 760–762. [Google Scholar] [CrossRef]
- Blümich, B. Low-field and benchtop NMR. J. Magn. Reson. 2019, 306, 27–35. [Google Scholar] [CrossRef]
- Meiboom, S.; Gill, D. Modified Spin-Echo Method for Measuring Nuclear Relaxation Times. Rev. Sci. Instrum. 1958, 29, 688. [Google Scholar] [CrossRef]
- Piotto, M.; Saudek, V.; Sklenar, V. Gradient-tailored excitation for single-quantum NMR spectroscopy of aqueous solutions. J. Biomol. NMR 1992, 2, 661–665. [Google Scholar] [CrossRef]
- Vilén, E.M.; Klinger, M.; Sandström, C. Application of diffusion-edited NMR spectroscopy for selective suppression of water signal in the determination of monomer composition in alginates. Magn. Reson. Chem. 2011, 49, 584–591. [Google Scholar] [CrossRef]
- Chandrakumar, N. Chapter 3 1D Double Quantum Filter NMR Studies. Annu. Rep. NMR Spectrosc. 2009, 67, 265–329. [Google Scholar] [CrossRef]
- Lopez, J.; Cabrera, R.; Maruenda, H. Ultra-Clean Pure Shift 1H-NMR applied to metabolomics profiling. Sci. Rep. 2019, 9, 6900. [Google Scholar] [CrossRef]
- Gouilleux, B.; Rouger, L.; Giraudeau, P. Ultrafast 2D NMR: Methods and Applications. Annu. Rep. NMR Spectrosc. 2018, 93, 75–144. [Google Scholar] [CrossRef]
- Castañar, L.; Poggetto, G.D.; Colbourne, A.; Morris, G.A.; Nilsson, M. The GNAT: A new tool for processing NMR data. Magn. Reson. Chem. 2018, 56, 546–558. [Google Scholar] [CrossRef] [PubMed]
- Morris, G.A.; Barjat, H.; Home, T.J. Reference deconvolution methods. Prog. Nucl. Magn. Reson. Spectrosc. 1997, 31, 197–257. [Google Scholar] [CrossRef]
- Taylor, H.S.; Haiges, R.; Kershaw, A. Increasing Sensitivity in Determining Chemical Shifts in One Dimensional Lorentzian NMR Spectra. J. Phys. Chem. A 2013, 117, 3319–3331. [Google Scholar] [CrossRef]
- Krishnamurthy, K. CRAFT (complete reduction to amplitude frequency table)—Robust and time-efficient Bayesian approach for quantitative mixture analysis by NMR. Magn. Reson. Chem. 2013, 51, 821–829. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.; Pardi, C.; Brown, T.; McDonald, P.J. Active elimination of radio frequency interference for improved signal-to-noise ratio for in-situ NMR experiments in strong magnetic field gradients. J. Magn. Reson. 2018, 287, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Langmead, C.J.; Donald, B.R. Extracting structural information using time-frequency analysis of protein NMR data. In Proceedings of the Fifth Annual International Conference on Computing Machinery, Montreal, QC, Canada, 22–25 April 2001; pp. 164–175. [Google Scholar]
- Hirakawa, K.; Koike, K.; Kanawaku, Y.; Moriyama, T.; Sato, N.; Suzuki, T.; Furihata, K.; Ohno, Y. Short-time Fourier Transform of Free Induction Decays for the Analysis of Serum Using Proton Nuclear Magnetic Resonance. J. Oleo Sci. 2019, 68, 369–378. [Google Scholar] [CrossRef]
- Short, T.; Alzapiedi, L.; Brüschweiler, R.; Snyder, D. A covariance NMR toolbox for MATLAB and OCTAVE. J. Magn. Reson. 2010, 209, 75–78. [Google Scholar] [CrossRef]
- Manu, V.; Gopinath, T.; Wang, S.; Veglia, G. T2* weighted Deconvolution of NMR Spectra: Application to 2D Homonuclear MAS Solid-State NMR of Membrane Proteins. Sci. Rep. 2019, 9, 8225. [Google Scholar] [CrossRef]
- Yamada, S.; Ito, K.; Kurotani, A.; Yamada, Y.; Chikayama, E.; Kikuchi, J. InterSpin: Integrated Supportive Webtools for Low- and High-Field NMR Analyses Toward Molecular Complexity. ACS Omega 2019, 4, 3361–3369. [Google Scholar] [CrossRef]
- Kusaka, Y.; Hasegawa, T.; Kaji, H. Noise Reduction in Solid-State NMR Spectra Using Principal Component Analysis. J. Phys. Chem. A 2019, 123, 10333–10338. [Google Scholar] [CrossRef]
- Stilbs, P. Automated CORE, RECORD, and GRECORD processing of multi-component PGSE NMR diffusometry data. Eur. Biophys. J. 2012, 42, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Stilbs, P. RECORD processing–A robust pathway to component-resolved HR-PGSE NMR diffusometry. J. Magn. Reson. 2010, 207, 332–336. [Google Scholar] [CrossRef]
- Stilbs, P.; Paulsen, K.; Griffiths, P. Global Least-Squares Analysis of Large, Correlated Spectral Data Sets: Application to Component-Resolved FT-PGSE NMR Spectroscopy. J. Phys. Chem. 1996, 100, 8180–8189. [Google Scholar] [CrossRef]
- Kikuchi, J.; Yamada, S. NMR window of molecular complexity showing homeostasis in superorganisms. Analyst 2017, 142, 4161–4172. [Google Scholar] [CrossRef] [PubMed]
- Pupier, M.; Nuzillard, J.-M.; Wist, J.; Schlörer, N.E.; Kuhn, S.; Erdélyi, M.; Steinbeck, C.; Williams, A.; Butts, C.P.; Claridge, T.D.W.; et al. NMReDATA, a standard to report the NMR assignment and parameters of organic compounds. Magn. Reson. Chem. 2018, 56, 703–715. [Google Scholar] [CrossRef]
- Halouska, S.; Powers, R. Negative impact of noise on the principal component analysis of NMR data. J. Magn. Reson. 2006, 178, 88–95. [Google Scholar] [CrossRef]
- Becker, E.D.; Ferretti, J.A.; Gambhir, P.N. Selection of optimum parameters for pulse Fourier transform nuclear magnetic resonance. Anal. Chem. 1979, 51, 1413–1420. [Google Scholar] [CrossRef]
- Mo, H.; Harwood, J.; Zhang, S.; Xue, Y.; Santini, R.; Raftery, D. A quantitative measure of NMR signal receiving efficiency. J. Magn. Reson. 2009, 200, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Mo, H.; Harwood, J.S.; Raftery, D. A quick diagnostic test for NMR receiver gain compression. Magn. Reson. Chem. 2010, 48, 782–786. [Google Scholar] [CrossRef]
- Mo, H.; Harwood, J.S.; Raftery, D. Receiver gain function: The actual NMR receiver gain. Magn. Reson. Chem. 2010, 48, 235–238. [Google Scholar] [CrossRef]
- Mo, H.; Harwood, J.; Raftery, D. NMR quantitation: Influence of RF inhomogeneity. Magn. Reson. Chem. 2011, 49, 655–658. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Dong, H.; Ge, J.; Bai, B.; Yuan, Z.; Zhao, Z. Research on a secondary tuning algorithm based on SVD & STFT for FID signal. Meas. Sci. Technol. 2016, 27, 105006. [Google Scholar] [CrossRef]
- Zitnik, M.; Zupan, B. NIMFA: A python library for nonnegative matrix factorization. J. Mach. Learn. Res. 2012, 13, 849–853. [Google Scholar]
- Liu, H.; Dong, H.; Ge, J.; Liu, Z.; Yuan, Z.; Zhu, J.; Zhang, H. A fusion of principal component analysis and singular value decomposition based multivariate denoising algorithm for free induction decay transversal data. Rev. Sci. Instrum. 2019, 90, 035116. [Google Scholar] [CrossRef] [PubMed]
- Keeler, J. Understanding NMR Spectroscopy; Appollo—University of Cambridge Repository: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Dueck, D.; Morris, Q.; Frey, B.J. Multi-way clustering of microarray data using probabilistic sparse matrix factorization. Bioinformatics 2005, 21, 144–151. [Google Scholar] [CrossRef] [PubMed]
- Claridge, T. MNova: NMR data processing, analysis, and prediction software. J. Chem. Inf. Model. 2009, 49, 1136–1137. [Google Scholar] [CrossRef]
- Ulrich, E.L.; Akutsu, H.; Doreleijers, J.F.; Harano, Y.; Ioannidis, Y.E.; Lin, J.; Livny, M.; Mading, S.; Maziuk, D.; Miller, Z.; et al. BioMagResBank. Nucleic Acids Res. 2007, 36, D402–D408. [Google Scholar] [CrossRef]
- Ludwig, C.; Easton, J.; Lodi, A.; Tiziani, S.; Manzoor, S.E.; Southam, A.; Byrne, J.J.; Bishop, L.M.; He, S.; Arvanitis, T.N.; et al. Birmingham Metabolite Library: A publicly accessible database of 1-D 1H and 2-D 1H J-resolved NMR spectra of authentic metabolite standards (BML-NMR). Metabolomics 2011, 8, 8–18. [Google Scholar] [CrossRef]
- Wishart, D.S.; Feunang, Y.D.; Marcu, A.; Guo, A.C.; Liang, K.; Vázquez-Fresno, R.; Sajed, T.; Johnson, D.; Li, C.; Karu, N.; et al. HMDB 4.0: The human metabolome database for 2018. Nucleic Acids Res. 2018, 46, D608–D617. [Google Scholar] [CrossRef]
- Larive, C.K.; Jayawickrama, D.; Őrfi, L. Quantitative Analysis of Peptides with NMR Spectroscopy. Appl. Spectrosc. 1997, 51, 1531–1536. [Google Scholar] [CrossRef]
- Helmus, J.J.; Jaroniec, C.P. Nmrglue: An open source Python package for the analysis of multidimensional NMR data. J. Biomol. NMR 2013, 55, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Laurberg, H.; Christensen, M.G.; Plumbley, M.; Hansen, L.K.; Jensen, S.H. Theorems on Positive Data: On the Uniqueness of NMF. Comput. Intell. Neurosci. 2008, 2008, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef]
- Demchak, B.; Hull, T.; Reich, M.; Liefeld, T.; Smoot, M.; Ideker, T.; Mesirov, J.P. Cytoscape: The network visualization tool for GenomeSpace workflows. F1000Research 2014, 3, 151. [Google Scholar] [CrossRef] [PubMed]
- Yoshida, S.; Date, Y.; Akama, M.; Kikuchi, J. Comparative metabolomic and ionomic approach for abundant fishes in estuarine environments of Japan. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef]
- Misawa, T.; Wei, F.; Kikuchi, J. Application of Two-Dimensional Nuclear Magnetic Resonance for Signal Enhancement by Spectral Integration Using a Large Data Set of Metabolic Mixtures. Anal. Chem. 2016, 88, 6130–6134. [Google Scholar] [CrossRef]
- Asakura, T.; Sakata, K.; Date, Y.; Kikuchi, J. Regional feature extraction of various fishes based on chemical and microbial variable selection using machine learning. Anal. Methods 2018, 10, 2160–2168. [Google Scholar] [CrossRef]
- Wei, F.; Fukuchi, M.; Ito, K.; Sakata, K.; Asakura, T.; Date, Y.; Kikuchi, J. Large-Scale Evaluation of Major Soluble Macromolecular Components of Fish Muscle from Conventional 1H NMR Spectral Database. Molecules 2020, 25, 1966. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, S.; Kurotani, A.; Chikayama, E.; Kikuchi, J. Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time–Frequency Analysis and Probabilistic Sparse Matrix Factorization. Int. J. Mol. Sci. 2020, 21, 2978. https://doi.org/10.3390/ijms21082978
Yamada S, Kurotani A, Chikayama E, Kikuchi J. Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time–Frequency Analysis and Probabilistic Sparse Matrix Factorization. International Journal of Molecular Sciences. 2020; 21(8):2978. https://doi.org/10.3390/ijms21082978
Chicago/Turabian StyleYamada, Shunji, Atsushi Kurotani, Eisuke Chikayama, and Jun Kikuchi. 2020. "Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time–Frequency Analysis and Probabilistic Sparse Matrix Factorization" International Journal of Molecular Sciences 21, no. 8: 2978. https://doi.org/10.3390/ijms21082978
APA StyleYamada, S., Kurotani, A., Chikayama, E., & Kikuchi, J. (2020). Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time–Frequency Analysis and Probabilistic Sparse Matrix Factorization. International Journal of Molecular Sciences, 21(8), 2978. https://doi.org/10.3390/ijms21082978