Dynamics, a Powerful Component of Current and Future in Silico Approaches for Protein Design and Engineering
Abstract
1. Introduction
2. Tools to Facilitate Analyses of MD Simulation
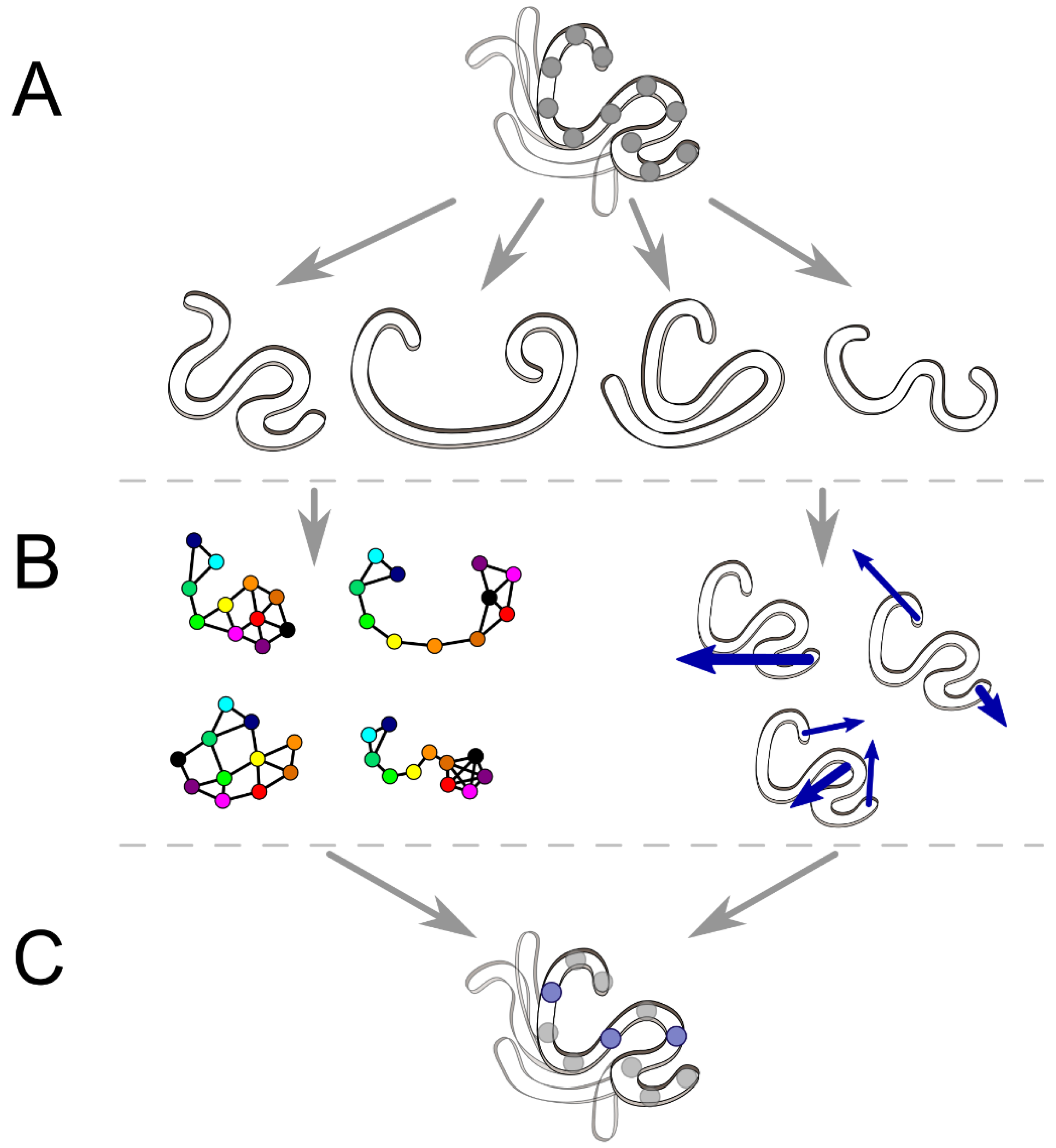
2.1. Interaction Network and Correlated Motion Analyses
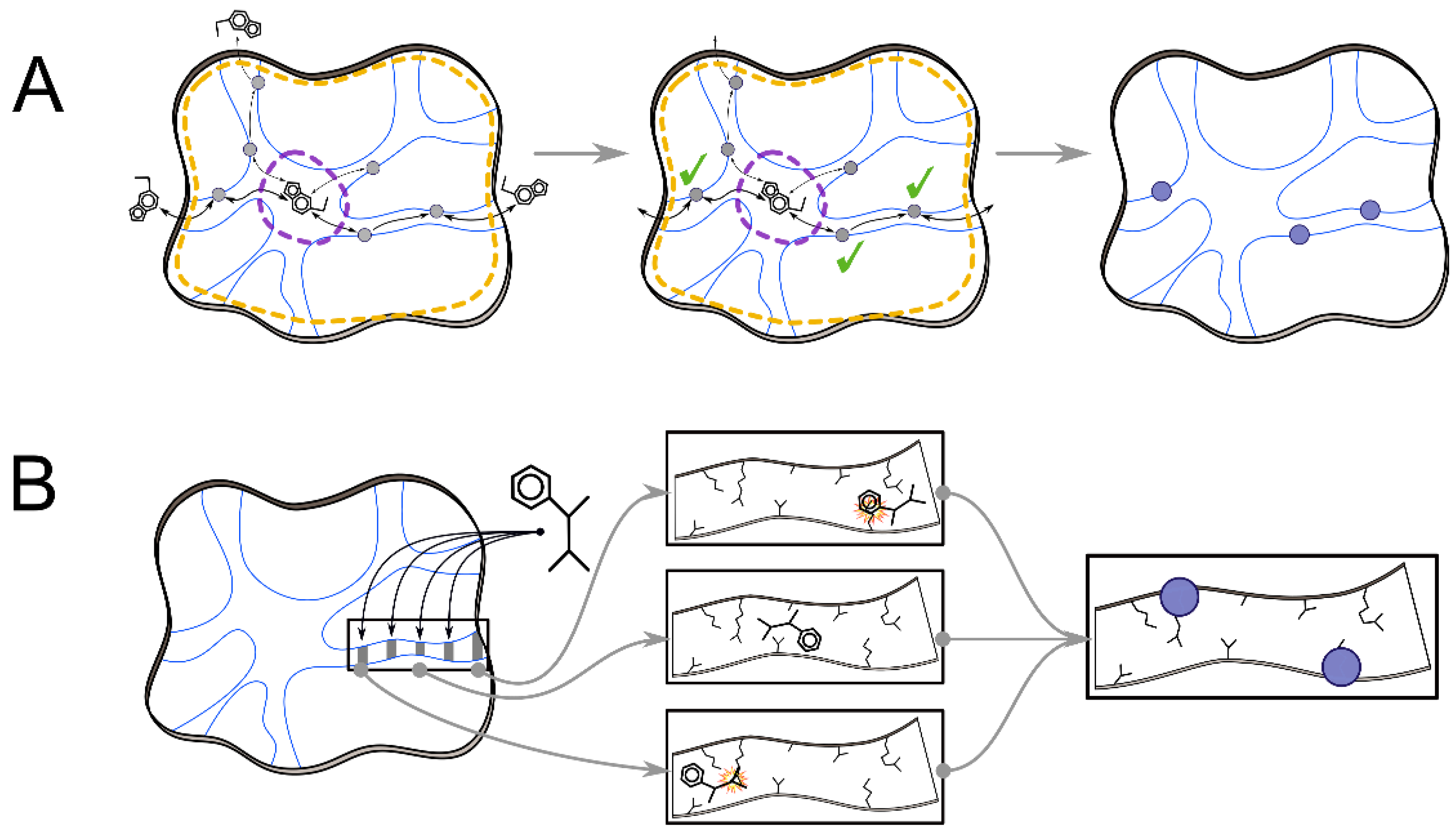
2.2. Analyses of Ligand Transport
3. Advances in the Integration of Protein Flexibility into Protein Design and Redesign Methods
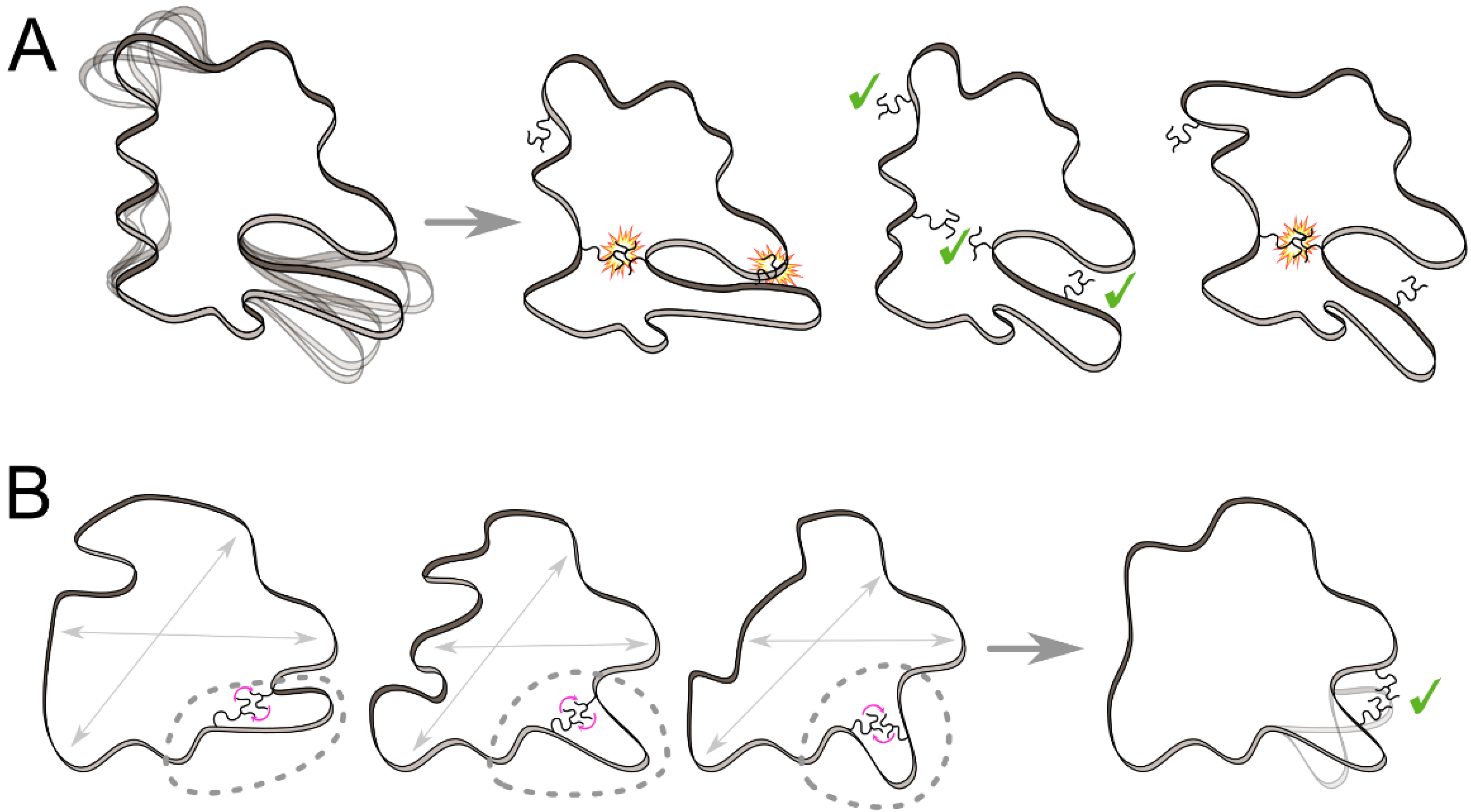
3.1. Ensemble-Based Approaches
3.2. Knowledge-Based Approaches
3.3. Provable Algorithms
4. Conclusions, Challenges, and Perspectives
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MD | molecular dynamics |
| GPU | graphics processing unit |
| PCA | principal component analysis |
| RIP-MD | residue interaction network in protein molecular dynamics |
| VMD | visual molecular dynamics |
| JED | Java-based Essential Dynamics |
| scFv | single-chain variable-fragment |
| PDB | protein data bank |
| RMSD | root-mean-square deviation |
| SPM | shortest path map |
| CAMERRA | computation of allosteric mechanism by evaluating residue–residue associations |
| DAAO | D-amino acid oxidase |
| MC | Monte Carlo |
| FixBB | fixed backbone |
| D&R | Design-and-relax |
| PCC | Pearson correlation coefficient |
| ΔΔG | change in binding free energy |
| RMSE | root-mean-square error |
| SSD | single-state design |
| MSD | multistate design |
| NMR | nuclear magnetic resonance |
| NSR | native sequence recovery |
| NSSR | native sequence similarity recovery |
| FlexiBaL-GP | flexible backbone learning by Gaussian processes |
| SHADES | structural homology algorithm for protein design |
| ITEM | In-contact amino acid residue tertiary motif |
| DEE | dead-end elimination |
| DEEPer | dead-end elimination with perturbations |
| CATS | coordinates of atoms by Taylor series |
| NMA | normal mode analysis |
References
- Kirk, O.; Borchert, T.V.; Fuglsang, C.C. Industrial enzyme applications. Curr. Opin. Biotechnol. 2002, 13, 345–351. [Google Scholar] [CrossRef]
- Bodansky, O. Diagnostic applications of enzymes in medicine. General enzymological aspects. Am. J. Med. 1959, 27, 861–874. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, M.; Mittal, A.; Mehta, P.K. Microbial enzymes: Industrial progress in 21st century. 3 Biotech 2016, 6, 174. [Google Scholar] [CrossRef]
- Sizer, I.W. Medical Applications of Microbial Enzymes. Adv. Appl. Microbiol. 1972, 15, 1–11. [Google Scholar] [CrossRef]
- Piotrowska-Długosz, A. Significance of Enzymes and Their Application in Agriculture. Biocatalysis 2019, 277–308. [Google Scholar] [CrossRef]
- Brannigan, J.A.; Wilkinson, A.J. Protein engineering 20 years on. Nat. Rev. Mol. Cell Biol. 2002, 3, 964–970. [Google Scholar] [CrossRef] [PubMed]
- Bornscheuer, U.T.; Huisman, G.W.; Kazlauskas, R.J.; Lutz, S.; Moore, J.C.; Robins, K. Engineering the third wave of biocatalysis. Nature 2012, 485, 185–194. [Google Scholar] [CrossRef] [PubMed]
- Kazlauskas, R.J.; Bornscheuer, U.T. Finding better protein engineering strategies. Nat. Chem. Biol. 2009, 5, 526–529. [Google Scholar] [CrossRef]
- Arnold, F.H. Innovation by Evolution: Bringing New Chemistry to Life (Nobel Lecture). Angew. Chem. Int. Ed. 2019, 58, 14420–14426. [Google Scholar] [CrossRef] [PubMed]
- Arnold, F.H. Directed Evolution: Bringing New Chemistry to Life. Angew. Chem. Int. Ed. 2018, 57, 4143–4148. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, A.J.; Fersht, A.R.; Blow, D.M.; Carter, P.; Winter, G. A large increase in enzyme-substrate affinity by protein engineering. Nature 1984, 307, 187–188. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.A.; Powers, D.B.; Bott, R.R.; Graycar, T.P.; Estell, D.A. Designing substrate specificity by protein engineering of electrostatic interactions. Proc. Natl. Acad. Sci. USA 1987, 84, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Thomas, P.G.; Russell, A.J.; Fersht, A.R. Tailoring the pH dependence of enzyme catalysis using protein engineering. Nature 1985, 318, 375–376. [Google Scholar] [CrossRef]
- Barrozo, A.; Borstnar, R.; Marloie, G.; Kamerlin, S.C.L. Computational Protein Engineering: Bridging the Gap between Rational Design and Laboratory Evolution. Int. J. Mol. Sci. 2012, 13, 12428–12460. [Google Scholar] [CrossRef] [PubMed]
- Hellinga, H.W. Computational protein engineering. Nat. Struct. Biol. 1998, 5, 525–527. [Google Scholar] [CrossRef]
- Wijma, H.J.; Janssen, D.B. Computational design gains momentum in enzyme catalysis engineering. FEBS J. 2013, 280, 2948–2960. [Google Scholar] [CrossRef]
- Looger, L.L.; Dwyer, M.A.; Smith, J.J.; Hellinga, H.W. Computational design of receptor and sensor proteins with novel functions. Nature 2003, 423, 185–190. [Google Scholar] [CrossRef]
- Saven, J.G. Computational protein design: Engineering molecular diversity, nonnatural enzymes, nonbiological cofactor complexes, and membrane proteins. Curr. Opin. Chem. Biol. 2011, 15, 452–457. [Google Scholar] [CrossRef]
- Huang, P.-S.; Boyken, S.E.; Baker, D. The coming of age of de novo protein design. Nature 2016, 537, 320. [Google Scholar] [CrossRef]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef]
- Agarwal, P.K. Enzymes: An integrated view of structure, dynamics and function. Microb. Cell Fact. 2006, 5, 2. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Gáspári, Z.; Perczel, A. Protein Dynamics as Reported by NMR. Annu. Rep. NMR Spectrosc. 2010, 71, 35–75. [Google Scholar] [CrossRef]
- Lewandowski, J.R.; Halse, M.E.; Blackledge, M.; Emsley, L. Direct observation of hierarchical protein dynamics. Science 2015, 348, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Gora, A.; Brezovsky, J.; Damborsky, J. Gates of enzymes. Chem. Rev. 2013, 113, 5871–5923. [Google Scholar] [CrossRef] [PubMed]
- Kokkonen, P.; Sykora, J.; Prokop, Z.; Ghose, A.; Bednar, D.; Amaro, M.; Beerens, K.; Bidmanova, S.; Slanska, M.; Brezovsky, J.; et al. Molecular Gating of an Engineered Enzyme Captured in Real Time. J. Am. Chem. Soc. 2018, 140, 17999–18008. [Google Scholar] [CrossRef]
- Pierce, L.C.T.; Salomon-Ferrer, R.; Augusto, F.; De Oliveira, C.; McCammon, J.A.; Walker, R.C. Routine access to millisecond time scale events with accelerated molecular dynamics. J. Chem. Theory Comput. 2012, 8, 2997–3002. [Google Scholar] [CrossRef]
- Noé, F. Beating the Millisecond Barrier in Molecular Dynamics Simulations. Biophys. J. 2015, 108, 228–229. [Google Scholar] [CrossRef][Green Version]
- Sultan, M.M.; Denny, R.A.; Unwalla, R.; Lovering, F.; Pande, V.S. Millisecond dynamics of BTK reveal kinome-wide conformational plasticity within the apo kinase domain. Sci. Rep. 2017, 7, 15604. [Google Scholar] [CrossRef]
- Silva, D.A.; Weiss, D.R.; Avila, F.P.; Da, L.T.; Levitt, M.; Wang, D.; Huang, X. Millisecond dynamics of RNA polymerase II translocation at atomic resolution. Proc. Natl. Acad. Sci. USA 2014, 111, 7665–7670. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Merz, K.M. Taking into account the ion-induced dipole interaction in the nonbonded model of ions. J. Chem. Theory Comput. 2014, 10, 289–297. [Google Scholar] [CrossRef] [PubMed]
- Jing, Z.; Liu, C.; Cheng, S.Y.; Qi, R.; Walker, B.D.; Piquemal, J.-P.; Ren, P. Polarizable Force Fields for Biomolecular Simulations: Recent Advances and Applications. Annu. Rev. Biophys. 2019, 48, 371–394. [Google Scholar] [CrossRef] [PubMed]
- Mongan, J.; Case, D.A. Biomolecular simulations at constant pH. Curr. Opin. Struct. Biol. 2005, 15, 157–163. [Google Scholar] [CrossRef]
- Panteva, M.T.; Giambaşu, G.M.; York, D.M. Comparison of structural, thermodynamic, kinetic and mass transport properties of Mg 2+ ion models commonly used in biomolecular simulations. J. Comput. Chem. 2015, 36, 970–982. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Z.; Li, G. Higher Accuracy Achieved in the Simulations of Protein Structure Refinement, Protein Folding, and Intrinsically Disordered Proteins Using Polarizable Force Fields. J. Phys. Chem. Lett. 2018, 9, 7110–7116. [Google Scholar] [CrossRef]
- Dobrev, P.; Vemulapalli, S.P.B.; Nath, N.; Griesinger, C.; Grubmüller, H. Probing the accuracy of explicit solvent constant pH molecular dynamics simulations for peptides. J. Chem. Theory Comput. 2020. [Google Scholar] [CrossRef]
- Smith, L.G.; Tan, Z.; Spasic, A.; Dutta, D.; Salas-Estrada, L.A.; Grossfield, A.; Mathews, D.H. Chemically Accurate Relative Folding Stability of RNA Hairpins from Molecular Simulations. J. Chem. Theory Comput. 2018, 14, 6598–6612. [Google Scholar] [CrossRef]
- Heo, L.; Feig, M. Experimental accuracy in protein structure refinement via molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2018, 115, 13276–13281. [Google Scholar] [CrossRef]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. Ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef]
- Childers, M.C.; Daggett, V. Insights from molecular dynamics simulations for computational protein design. Mol. Syst. Des. Eng. 2017, 2, 9–33. [Google Scholar] [CrossRef] [PubMed]
- Romero-Rivera, A.; Garcia-Borràs, M.; Osuna, S. Computational tools for the evaluation of laboratory-engineered biocatalysts. Chem. Commun. 2017, 53, 284–297. [Google Scholar] [CrossRef] [PubMed]
- Romero-Rivera, A.; Garcia-Borràs, M.; Osuna, S. Role of Conformational Dynamics in the Evolution of Retro-Aldolase Activity. ACS Catal. 2017, 7, 8524–8532. [Google Scholar] [CrossRef]
- Pabis, A.; Risso, V.A.; Sanchez-Ruiz, J.M.; Kamerlin, S.C. Cooperativity and flexibility in enzyme evolution. Curr. Opin. Struct. Biol. 2018, 48, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Buller, A.R.; Van Roye, P.; Cahn, J.K.B.; Scheele, R.A.; Herger, M.; Arnold, F.H. Directed Evolution Mimics Allosteric Activation by Stepwise Tuning of the Conformational Ensemble. J. Am. Chem. Soc. 2018, 140, 7256–7266. [Google Scholar] [CrossRef] [PubMed]
- Petrović, D.; Lynn, K.S.C. Molecular modeling of conformational dynamics and its role in enzyme evolution. Curr. Opin. Struct. Biol. 2018, 52, 50–57. [Google Scholar] [CrossRef]
- Maria-Solano, M.A.; Serrano-Hervás, E.; Romero-Rivera, A.; Iglesias-Fernández, J.; Osuna, S. Role of conformational dynamics in the evolution of novel enzyme function. Chem. Commun. 2018, 54, 6622–6634. [Google Scholar] [CrossRef]
- Jiménez-Osés, G.; Osuna, S.; Gao, X.; Sawaya, M.R.; Gilson, L.; Collier, S.J.; Huisman, G.W.; Yeates, T.O.; Tang, Y.; Houk, K.N. The role of distant mutations and allosteric regulation on LovD active site dynamics. Nat. Chem. Biol. 2014, 10, 431–436. [Google Scholar] [CrossRef]
- Yang, B.; Wang, H.; Song, W.; Chen, X.; Liu, J.; Luo, Q.; Liu, L. Engineering of the Conformational Dynamics of Lipase to Increase Enantioselectivity. ACS Catal. 2017, 7, 7593–7599. [Google Scholar] [CrossRef]
- Hong, N.S.; Petrović, D.; Lee, R.; Gryn’ova, G.; Purg, M.; Saunders, J.; Bauer, P.; Carr, P.D.; Lin, C.Y.; Mabbitt, P.D.; et al. The evolution of multiple active site configurations in a designed enzyme. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Campbell, E.; Kaltenbach, M.; Correy, G.J.; Carr, P.D.; Porebski, B.T.; Livingstone, E.K.; Afriat-Jurnou, L.; Buckle, A.M.; Weik, M.; Hollfelder, F.; et al. The role of protein dynamics in the evolution of new enzyme function. Nat. Chem. Biol. 2016, 12, 944–950. [Google Scholar] [CrossRef] [PubMed]
- Ollikainen, N.; de Jong, R.M.; Kortemme, T. Coupling Protein Side-Chain and Backbone Flexibility Improves the Re-design of Protein-Ligand Specificity. PLoS Comput. Biol. 2015, 11, e1004335. [Google Scholar] [CrossRef] [PubMed]
- Sevy, A.M.; Jacobs, T.M.; Crowe, J.E.; Meiler, J. Design of Protein Multi-specificity Using an Independent Sequence Search Reduces the Barrier to Low Energy Sequences. PLoS Comput. Biol. 2015, 11, e1004300. [Google Scholar] [CrossRef] [PubMed]
- Ludwiczak, J.; Jarmula, A.; Dunin-Horkawicz, S. Combining Rosetta with molecular dynamics (MD): A benchmark of the MD-based ensemble protein design. J. Struct. Biol. 2018, 203, 54–61. [Google Scholar] [CrossRef]
- Dawson, W.M.; Rhys, G.G.; Woolfson, D.N. Towards functional de novo designed proteins. Curr. Opin. Chem. Biol. 2019, 52, 102–111. [Google Scholar] [CrossRef]
- Marcos, E.; Silva, D.A. Essentials of de novo protein design: Methods and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1374. [Google Scholar] [CrossRef]
- Kuhlman, B.; Bradley, P. Advances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol. 2019, 20, 681–697. [Google Scholar] [CrossRef]
- Contreras-Riquelme, S.; Garate, J.; Perez-Acle, T.; Martin, A.J.M. RIP-MD: A tool to study residue interaction networks in protein molecular dynamics. PeerJ 2018, 6, e5998. [Google Scholar] [CrossRef]
- David, C.C.; Singam, E.R.A.; Jacobs, D.J. JED: A Java Essential Dynamics Program for comparative analysis of protein trajectories. BMC Bioinform. 2017, 18, 271. [Google Scholar] [CrossRef]
- Johnson, Q.R.; Lindsay, R.J.; Shen, T. CAMERRA: An analysis tool for the computation of conformational dynamics by evaluating residue-residue associations. J. Comput. Chem. 2018, 39, 1568–1578. [Google Scholar] [CrossRef]
- Lindsay, R.J.; Siess, J.; Lohry, D.P.; McGee, T.S.; Ritchie, J.S.; Johnson, Q.R.; Shen, T. Characterizing protein conformations by correlation analysis of coarse-grained contact matrices. J. Chem. Phys. 2018, 148, 025101. [Google Scholar] [CrossRef] [PubMed]
- Magdziarz, T.; Mitusińska, K.; Gołdowska, S.; Płuciennik, A.; Stolarczyk, M.; Lugowska, M.; Góra, A. AQUA-DUCT: A ligands tracking tool. Bioinformatics 2017, 33, 2045–2046. [Google Scholar] [CrossRef]
- Magdziarz, T.; Mitusińska, K.; Bzówka, M.; Raczyńska, A.; Stańczak, A.; Banas, M.; Bagrowska, W.; Góra, A. AQUA-DUCT 1.0: Structural and functional analysis of macromolecules from an intramolecular voids perspective. Bioinformatics 2019. [Google Scholar] [CrossRef]
- Filipovic, J.; Vavra, O.; Plhak, J.; Bednar, D.; Marques, S.M.; Brezovsky, J.; Matyska, L.; Damborsky, J. CaverDock: A Novel Method for the Fast Analysis of Ligand Transport. IEEE/ACM Trans. Comput. Biol. Bioinforma. 2019, 1. [Google Scholar] [CrossRef]
- Vavra, O.; Filipovic, J.; Plhak, J.; Bednar, D.; Marques, S.M.; Brezovsky, J.; Stourac, J.; Matyska, L.; Damborsky, J. CaverDock: A molecular docking-based tool to analyse ligand transport through protein tunnels and channels. Bioinformatics 2019, 35, 4986–4993. [Google Scholar] [CrossRef]
- Pace, C.N.; Martin Scholtz, J.; Grimsley, G.R. Forces stabilizing proteins. FEBS Lett. 2014, 588, 2177–2184. [Google Scholar] [CrossRef]
- Feher, V.A.; Durrant, J.D.; Van Wart, A.T.; Amaro, R.E. Computational approaches to mapping allosteric pathways. Curr. Opin. Struct. Biol. 2014, 25, 98–103. [Google Scholar] [CrossRef] [PubMed]
- Dokholyan, N.V. Controlling Allosteric Networks in Proteins. Chem. Rev. 2016, 116, 6463–6487. [Google Scholar] [CrossRef] [PubMed]
- Wodak, S.J.; Paci, E.; Dokholyan, N.V.; Berezovsky, I.N.; Horovitz, A.; Li, J.; Hilser, V.J.; Bahar, I.; Karanicolas, J.; Stock, G.; et al. Allostery in Its Many Disguises: From Theory to Applications. Structure 2019, 27, 566–578. [Google Scholar] [CrossRef]
- Glykos, N.M. Software news and updates carma: A molecular dynamics analysis program. J. Comput. Chem. 2006, 27, 1765–1768. [Google Scholar] [CrossRef]
- Brown, D.K.; Penkler, D.L.; Sheik Amamuddy, O.; Ross, C.; Atilgan, A.R.; Atilgan, C.; Tastan Bishop, Ö. MD-TASK: A software suite for analyzing molecular dynamics trajectories. Bioinformatics 2017, 33, 2768–2771. [Google Scholar] [CrossRef] [PubMed]
- David, C.C.; Jacobs, D.J. Principal component analysis: A method for determining the essential dynamics of proteins. Protein Dyn. Methods Mol. Biol. 2014, 1084, 193–226. [Google Scholar] [CrossRef]
- Peng, J.; Zhang, Z. Simulating large-scale conformational changes of proteins by accelerating collective motions obtained from principal component analysis. J. Chem. Theory Comput. 2014, 10, 3449–3458. [Google Scholar] [CrossRef] [PubMed]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Johnson, Q.R.; Lindsay, R.J.; Nellas, R.B.; Fernandez, E.J.; Shen, T. Mapping allostery through computational glycine scanning and correlation analysis of residue-residue contacts. Biochemistry 2015, 54, 1534–1541. [Google Scholar] [CrossRef]
- Johnson, Q.R.; Lindsay, R.J.; Nellas, R.B.; Shen, T. Pressure-induced conformational switch of an interfacial protein. Proteins Struct. Funct. Bioinform. 2016, 84, 820–827. [Google Scholar] [CrossRef]
- Brezovsky, J.; Chovancova, E.; Gora, A.; Pavelka, A.; Biedermannova, L.; Damborsky, J. Software tools for identification, visualization and analysis of protein tunnels and channels. Biotechnol. Adv. 2013, 31, 38–49. [Google Scholar] [CrossRef]
- Marques, S.M.; Daniel, L.; Buryska, T.; Prokop, Z.; Brezovsky, J.; Damborsky, J. Enzyme Tunnels and Gates As Relevant Targets in Drug Design. Med. Res. Rev. 2017, 37, 1095–1139. [Google Scholar] [CrossRef]
- Brezovsky, J.; Babkova, P.; Degtjarik, O.; Fortova, A.; Gora, A.; Iermak, I.; Rezacova, P.; Dvorak, P.; Smatanova, I.K.; Prokop, Z.; et al. Engineering a de Novo Transport Tunnel. ACS Catal. 2016, 6, 7597–7610. [Google Scholar] [CrossRef]
- Kokkonen, P.; Bednar, D.; Pinto, G.; Prokop, Z.; Damborsky, J. Engineering enzyme access tunnels. Biotechnol. Adv. 2019, 37, 107386. [Google Scholar] [CrossRef]
- Nunes-Alves, A.; Kokh, D.B.; Wade, R.C. Recent progress in molecular simulation methods for drug binding kinetics. arXiv 2020, arXiv:2002.08983v2. [Google Scholar]
- Schrödinger LLC. The PyMOL Molecular Graphics System; Version 2.0; Schrödinger LLC.: New York, NY, USA, 2017. [Google Scholar]
- Mitusińska, K.; Magdziarz, T.; Bzówka, M.; Stańczak, A.; Gora, A. Exploring solanum tuberosum epoxide hydrolase internal architecture by water molecules tracking. Biomolecules 2018, 8, 143. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, K.; Mitusińska, K.; Raedts, J.; Almourfi, F.; Joosten, H.J.; Hendriks, S.; Sedelnikova, S.E.; Kengen, S.W.M.; Hagen, W.R.; Góra, A.; et al. Distant non-obvious mutations influence the activity of a hyperthermophilic Pyrococcus furiosus phosphoglucose isomerase. Biomolecules 2019, 9, 212. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, K.; Góra, A.; Spruijt, R.; Mitusińska, K.; Suarez-Diez, M.; Martins dos Santos, V.; Schaap, P.J. Modulating D-amino acid oxidase (DAAO) substrate specificity through facilitated solvent access. PLoS ONE 2018, 13, e0198990. [Google Scholar] [CrossRef] [PubMed]
- Chovancova, E.; Pavelka, A.; Benes, P.; Strnad, O.; Brezovsky, J.; Kozlikova, B.; Gora, A.; Sustr, V.; Klvana, M.; Medek, P.; et al. CAVER 3.0: A Tool for the Analysis of Transport Pathways in Dynamic Protein Structures. PLoS Comput. Biol. 2012, 8, e1002708. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. Software news and update AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Pinto, G.P.; Vavra, O.; Filipovic, J.; Stourac, J.; Bednar, D.; Damborsky, J. Fast Screening of Inhibitor Binding/Unbinding Using Novel Software Tool CaverDock. Front. Chem. 2019, 7, 709. [Google Scholar] [CrossRef]
- Marques, S.M.; Bednar, D.; Damborsky, J. Computational Study of Protein-Ligand Unbinding for Enzyme Engineering. Front. Chem. 2019, 6, 650. [Google Scholar] [CrossRef]
- Pavlova, M.; Klvana, M.; Prokop, Z.; Chaloupkova, R.; Banas, P.; Otyepka, M.; Wade, R.C.; Tsuda, M.; Nagata, Y.; Damborsky, J. Redesigning dehalogenase access tunnels as a strategy for degrading an anthropogenic substrate. Nat. Chem. Biol. 2009, 5, 727–733. [Google Scholar] [CrossRef]
- Marques, S.M.; Dunajova, Z.; Prokop, Z.; Chaloupkova, R.; Brezovsky, J.; Damborsky, J. Catalytic Cycle of Haloalkane Dehalogenases Toward Unnatural Substrates Explored by Computational Modeling. J. Chem. Inf. Model. 2017, 57, 1970–1989. [Google Scholar] [CrossRef]
- Barlow, K.A.; Ó Conchúir, S.; Thompson, S.; Suresh, P.; Lucas, J.E.; Heinonen, M.; Kortemme, T. Flex ddG: Rosetta Ensemble-Based Estimation of Changes in Protein-Protein Binding Affinity upon Mutation. J. Phys. Chem. B 2018, 122, 5389–5399. [Google Scholar] [CrossRef]
- Löffler, P.; Schmitz, S.; Hupfeld, E.; Sterner, R.; Merkl, R. Rosetta:MSF: A modular framework for multi-state computational protein design. PLoS Comput. Biol. 2017, 13, e1005600. [Google Scholar] [CrossRef] [PubMed]
- Davey, J.A.; Damry, A.M.; Goto, N.K.; Chica, R.A. Rational design of proteins that exchange on functional timescales. Nat. Chem. Biol. 2017, 13, 1280–1285. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.G.F.; Kim, P.M. Data driven flexible backbone protein design. PLoS Comput. Biol. 2017, 13, e1005722. [Google Scholar] [CrossRef] [PubMed]
- Simoncini, D.; Zhang, K.Y.J.; Schiex, T.; Barbe, S. A structural homology approach for computational protein design with flexible backbone. Bioinformatics 2018, 35, 2418–2426. [Google Scholar] [CrossRef]
- Hallen, M.A.; Donald, B.R. CATS (Coordinates of Atoms by Taylor Series): Protein design with backbone flexibility in all locally feasible directions. Bioinformatics 2017, 33, i5–i12. [Google Scholar] [CrossRef]
- Keedy, D.A.; Georgiev, I.; Triplett, E.B.; Donald, B.R.; Richardson, D.C.; Richardson, J.S. The Role of Local Backrub Motions in Evolved and Designed Mutations. PLoS Comput. Biol. 2012, 8, e1002629. [Google Scholar] [CrossRef]
- Davey, J.A.; Chica, R.A. Multistate computational protein design with backbone ensembles. Comput. Protein Des. Methods Mol. Biol. 2017, 1529, 161–179. [Google Scholar] [CrossRef]
- Schreiber, G.; Fleishman, S.J. Computational design of protein–protein interactions. Curr. Opin. Struct. Biol. 2013, 23, 903–910. [Google Scholar] [CrossRef]
- Smith, C.A.; Kortemme, T. Backrub-Like Backbone Simulation Recapitulates Natural Protein Conformational Variability and Improves Mutant Side-Chain Prediction. J. Mol. Biol. 2008, 380, 742–756. [Google Scholar] [CrossRef]
- Kuhlman, B.; Dantas, G.; Ireton, G.C.; Varani, G.; Stoddard, B.L.; Baker, D. Design of a Novel Globular Protein Fold with Atomic-Level Accuracy. Science 2003, 302, 1364–1368. [Google Scholar] [CrossRef] [PubMed]
- Murphy, G.S.; Mills, J.L.; Miley, M.J.; Machius, M.; Szyperski, T.; Kuhlman, B. Increasing sequence diversity with flexible backbone protein design: The complete redesign of a protein hydrophobic core. Structure 2012, 20, 1086–1096. [Google Scholar] [CrossRef] [PubMed]
- Loshbaugh, A.L.; Kortemme, T. Comparison of Rosetta flexible-backbone computational protein design methods on binding interactions. Proteins Struct. Funct. Bioinform. 2020, 88, 206–226. [Google Scholar] [CrossRef]
- Khatib, F.; Cooper, S.; Tyka, M.D.; Xu, K.; Makedon, I.; Popović, Z.; Baker, D.; Players, F. Algorithm discovery by protein folding game players. Proc. Natl. Acad. Sci. USA 2011, 108, 18949–18953. [Google Scholar] [CrossRef] [PubMed]
- Tyka, M.D.; Keedy, D.A.; André, I.; Dimaio, F.; Song, Y.; Richardson, D.C.; Richardson, J.S.; Baker, D. Alternate states of proteins revealed by detailed energy landscape mapping. J. Mol. Biol. 2011, 405, 607–618. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.A.; Kortemme, T. Predicting the Tolerated Sequences for Proteins and Protein Interfaces Using RosettaBackrub Flexible Backbone Design. PLoS ONE 2011, 6, e20451. [Google Scholar] [CrossRef]
- Dourado, D.F.A.R.; Flores, S.C. A multiscale approach to predicting affinity changes in protein-protein interfaces. Proteins Struct. Funct. Bioinform. 2014, 82, 2681–2690. [Google Scholar] [CrossRef]
- Moal, I.H.; Fernández-Recio, J. SKEMPI: A Structural Kinetic and Energetic database of Mutant Protein Interactions and its use in empirical models. Bioinformatics 2012, 28, 2600–2607. [Google Scholar] [CrossRef]
- Benedix, A.; Becker, C.M.; de Groot, B.L.; Caflisch, A.; Böckmann, R.A. Predicting free energy changes using structural ensembles. Nat. Methods 2009, 6, 3–4. [Google Scholar] [CrossRef]
- Aldeghi, M.; Gapsys, V.; De Groot, B.L. Accurate Estimation of Ligand Binding Affinity Changes upon Protein Mutation. ACS Cent. Sci. 2018, 4, 1708–1718. [Google Scholar] [CrossRef]
- Aldeghi, M.; Gapsys, V.; De Groot, B.L. Predicting Kinase Inhibitor Resistance: Physics-Based and Data-Driven Approaches. ACS Cent. Sci. 2019, 5, 1468–1474. [Google Scholar] [CrossRef] [PubMed]
- Ibarra, A.A.; Bartlett, G.J.; Hegedüs, Z.; Dutt, S.; Hobor, F.; Horner, K.A.; Hetherington, K.; Spence, K.; Nelson, A.; Edwards, T.A.; et al. Predicting and Experimentally Validating Hot-Spot Residues at Protein-Protein Interfaces. ACS Chem. Biol. 2019, 14, 2252–2263. [Google Scholar] [CrossRef] [PubMed]
- Davey, J.A.; Chica, R.A. Improving the accuracy of protein stability predictions with multistate design using a variety of backbone ensembles. Proteins Struct. Funct. Bioinform. 2014, 82, 771–784. [Google Scholar] [CrossRef]
- de Groot, B.L.; van Aalten, D.M.F.; Scheek, R.M.; Amadei, A.; Vriend, G.; Berendsen, H.J.C. Prediction of protein conformational freedom from distance constraints. Proteins Struct. Funct. Genet. 1997, 29, 240–251. [Google Scholar] [CrossRef]
- Nivón, L.G.; Moretti, R.; Baker, D. A Pareto-Optimal Refinement Method for Protein Design Scaffolds. PLoS ONE 2013, 8, e59004. [Google Scholar] [CrossRef]
- Simoncini, D.; Allouche, D.; De Givry, S.; Delmas, C.; Barbe, S.; Schiex, T. Guaranteed Discrete Energy Optimization on Large Protein Design Problems. J. Chem. Theory Comput. 2015, 11, 5980–5989. [Google Scholar] [CrossRef]
- Gainza, P.; Roberts, K.E.; Donald, B.R. Protein Design Using Continuous Rotamers. PLoS Comput. Biol. 2012, 8, e1002335. [Google Scholar] [CrossRef]
- Gainza, P.; Nisonoff, H.M.; Donald, B.R. Algorithms for protein design. Curr. Opin. Struct. Biol. 2016, 39, 16–26. [Google Scholar] [CrossRef]
- Hallen, M.A.; Donald, B.R. Protein design by provable algorithms. Commun. ACM 2019, 62, 76–84. [Google Scholar] [CrossRef]
- Desmet, J.; De Maeyer, M.; Hazes, B.; Lasters, I. The dead-end elimination theorem and its use in protein side-chain positioning. Nature 1992, 356, 539–542. [Google Scholar] [CrossRef]
- Georgiev, I.; Lilien, R.H.; Donald, B.R. The minimized dead-end elimination criterion and its application to protein redesign in a hybrid scoring and search algorithm for computing partition functions over molecular ensembles. J. Comput. Chem. 2008, 29, 1527–1542. [Google Scholar] [CrossRef] [PubMed]
- Hallen, M.A.; Keedy, D.A.; Donald, B.R. Dead-end elimination with perturbations (DEEPer): A provable protein design algorithm with continuous sidechain and backbone flexibility. Proteins Struct. Funct. Bioinform. 2013, 81, 18–39. [Google Scholar] [CrossRef] [PubMed]
- Davis, I.W.; Arendall, W.B.; Richardson, D.C.; Richardson, J.S. The Backrub Motion: How Protein Backbone Shrugs When a Sidechain Dances. Structure 2006, 14, 265–274. [Google Scholar] [CrossRef]
- Hallen, M.A.; Gainza, P.; Donald, B.R. Compact representation of continuous energy surfaces for more efficient protein design. J. Chem. Theory Comput. 2015, 11, 2292–2306. [Google Scholar] [CrossRef]
- Hallen, M.A.; Jou, J.D.; Donald, B.R. LUTE (Local Unpruned Tuple Expansion): Accurate Continuously Flexible Protein Design with General Energy Functions and Rigid Rotamer-Like Efficiency. J. Comput. Biol. 2017, 24, 536–546. [Google Scholar] [CrossRef]
- Hallen, M.A. PLUG (Pruning of Local Unrealistic Geometries) removes restrictions on biophysical modeling for protein design. Proteins Struct. Funct. Bioinform. 2019, 87, 62–73. [Google Scholar] [CrossRef]
- Ojewole, A.A.; Jou, J.D.; Fowler, V.G.; Donald, B.R. BBK* (Branch and Bound Over K*): A Provable and Efficient Ensemble-Based Protein Design Algorithm to Optimize Stability and Binding Affinity Over Large Sequence Spaces. J. Comput. Biol. 2018, 25, 726–739. [Google Scholar] [CrossRef]
- Hallen, M.A.; Martin, J.W.; Ojewole, A.; Jou, J.D.; Lowegard, A.U.; Frenkel, M.S.; Gainza, P.; Nisonoff, H.M.; Mukund, A.; Wang, S.; et al. OSPREY 3.0: Open-source protein redesign for you, with powerful new features. J. Comput. Chem. 2018, 39, 2494–2507. [Google Scholar] [CrossRef]
- Frey, K.M.; Georgiev, I.; Donald, B.R.; Anderson, A.C. Predicting resistance mutations using protein design algorithms. Proc. Natl. Acad. Sci. USA 2010, 107, 13707–13712. [Google Scholar] [CrossRef]
- Roberts, K.E.; Cushing, P.R.; Boisguerin, P.; Madden, D.R.; Donald, B.R. Computational design of a PDZ domain peptide inhibitor that rescues CFTR activity. PLoS Comput. Biol. 2012, 8, e1002477. [Google Scholar] [CrossRef]
- Reevea, S.M.; Gainzab, P.; Freya, K.M.; Georgievb, I.; Donaldb, B.R.; Andersona, A.C. Protein design algorithms predict viable resistance to an experimental antifolate. Proc. Natl. Acad. Sci. USA 2015, 112, 749–754. [Google Scholar] [CrossRef]
- Rudicell, R.S.; Kwon, Y.D.; Ko, S.-Y.; Pegu, A.; Louder, M.K.; Georgiev, I.S.; Wu, X.; Zhu, J.; Boyington, J.C.; Chen, X.; et al. Enhanced Potency of a Broadly Neutralizing HIV-1 Antibody In Vitro Improves Protection against Lentiviral Infection In Vivo. J. Virol. 2014, 88, 12669–12682. [Google Scholar] [CrossRef]
- Sheik Amamuddy, O.; Veldman, W.; Manyumwa, C.; Khairallah, A.; Agajanian, S.; Oluyemi, O.; Verkhivker, G.M.; Tastan Bishop, Ö. Integrated Computational Approaches and Tools for Allosteric Drug Discovery. Int. J. Mol. Sci. 2020, 21, 847. [Google Scholar] [CrossRef]
- Bauer, J.A.; Pavlović, J.; Bauerová-Hlinková, V. Normal Mode Analysis as a Routine Part of a Structural Investigation. Molecules 2019, 24, 3293. [Google Scholar] [CrossRef]
- Kaushik, S.; Marques, S.M.; Khirsariya, P.; Paruch, K.; Libichova, L.; Brezovsky, J.; Prokop, Z.; Chaloupkova, R.; Damborsky, J. Impact of the access tunnel engineering on catalysis is strictly ligand-specific. FEBS J. 2018, 285, 1456–1476. [Google Scholar] [CrossRef]
- Musil, M.; Stourac, J.; Bendl, J.; Brezovsky, J.; Prokop, Z.; Zendulka, J.; Martinek, T.; Bednar, D.; Damborsky, J. FireProt: Web server for automated design of thermostable proteins. Nucleic Acids Res. 2017, 45, W393–W399. [Google Scholar] [CrossRef]
- Kim, D.E.; Chivian, D.; Baker, D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 2004, 32, W526–W531. [Google Scholar] [CrossRef]
- Vanquelef, E.; Simon, S.; Marquant, G.; Garcia, E.; Klimerak, G.; Delepine, J.C.; Cieplak, P.; Dupradeau, F.-Y. RED Server: A web service for deriving RESP and ESP charges and building force field libraries for new molecules and molecular fragments. Nucleic Acids Res. 2011, 39, W511–W517. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Y. Protein Structure and Function Prediction Using I-TASSER. Curr. Protoc. Bioinform. 2015, 52, 5.8.1–5.8.15. [Google Scholar] [CrossRef]
- Zimmermann, L.; Stephens, A.; Nam, S.Z.; Rau, D.; Kübler, J.; Lozajic, M.; Gabler, F.; Söding, J.; Lupas, A.N.; Alva, V. A Completely Reimplemented MPI Bioinformatics Toolkit with a New HHpred Server at its Core. J. Mol. Biol. 2018, 430, 2237–2243. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; De Groot, B.L.; Grubmüller, H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: A comparison to experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Stranges, P.B.; Kuhlman, B. A comparison of successful and failed protein interface designs highlights the challenges of designing buried hydrogen bonds. Protein Sci. 2013, 22, 74–82. [Google Scholar] [CrossRef]
- Maguire, J.B.; Boyken, S.E.; Baker, D.; Kuhlman, B. Rapid Sampling of Hydrogen Bond Networks for Computational Protein Design. J. Chem. Theory Comput. 2018, 14, 2751–2760. [Google Scholar] [CrossRef]
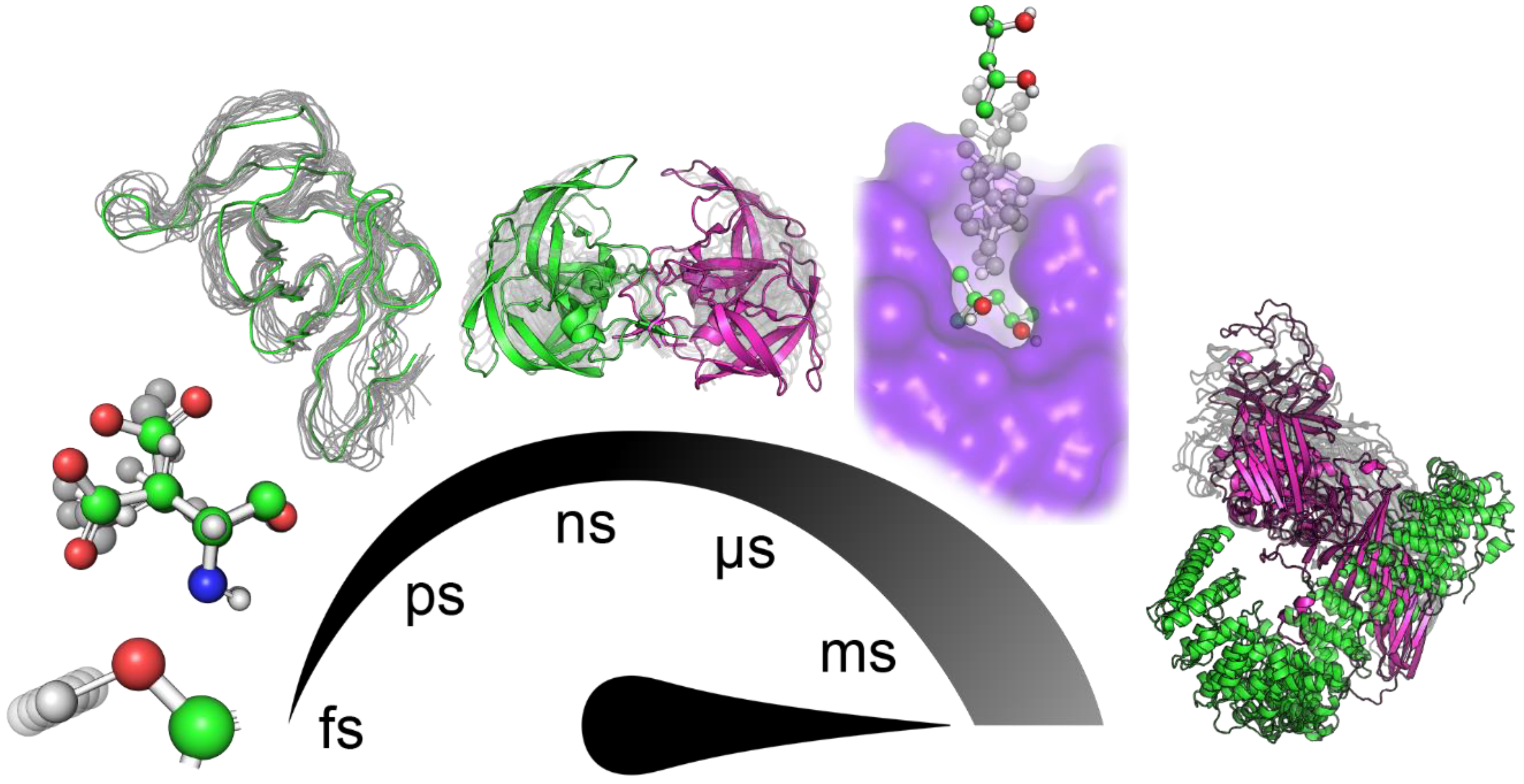
| Tool | Target Property | Availability | Code | Core Method(s) | Input | Link | Reference | ||
|---|---|---|---|---|---|---|---|---|---|
| Web Server | Standalone | Structure | Trajectory | ||||||
| Residue interaction network in protein molecular dynamics (RIP-MD) | Interaction network | + | + | Python | Residue interaction network | + | + | http://dlab.cl/ripmd/ | [58] |
| Java-based Essential Dynamics (JED) | Essential dynamics | - | + | Java | Principal component analysis (PCA) | - | + | https://github.com/charlesdavid/JED | [59] |
| DynaComm | Allostery | - | + | Python | Distance and correlation-based graphs, Dijkstra algorithm | + | + | https://silviaosuna.wordpress.com/tools/ | [43] |
| Computation of allosteric mechanism by evaluating residue–residue associations (CAMERRA) | Allostery | - | + | Perl, Python, C | PCA, contact analysis | - | + | shenlab.utk.edu/camerra.html | [60,61] |
| AQUA-DUCT | Ligand movement | - | + | Python | Geometry analysis | - | + | www.aquaduct.pl | [62,63] |
| CaverDock | Ligand movement | + | + | Python | Molecular docking | + | + | https://loschmidt.chemi.muni.cz/caverdock/ | [64,65] |
| Primary Package | Category | Method | Short Description | Input | Sampling of Side-Chain and Backbone Flexibility | Package | Add-Ons | Reference |
|---|---|---|---|---|---|---|---|---|
| Rosetta | Ensemble-based | Flex ddG | Estimating interface ∆∆G values upon mutation | Static structure | Backrub, torsion minimization, side-chain repacking | https://www.rosettacommons.org/software/ | https://github.com/Kortemme-Lab/flex_ddG_tutorial | [92] |
| Rosetta:MSF | Multistate framework using single-state protocols | Ensemble | Genetic algorithm based sequence optimizer and user-defined evaluator from Rosetta protocols | https://www.rosettacommons.org/software/ | - | [93] | ||
| Meta-multistate design (meta-MSD) | Engineering protein dynamics by meta-multistate design | Set of ensembles | Fast and accurate side-chain topology and energy refinement algorithm for sequence optimization; backbone-dependent rotamer library optimization for side-chains | https://www.rosettacommons.org/software/ | PHOENIX scripts upon request | [94] | ||
| Knowledge-based | Flexible backbone learning by Gaussian processes (FlexiBaL-GP) | Learning global protein backbone movements from multiple structures | Ensemble | Markov Chain Monte Carlo sampling—95% time spent on the side-chain selection and 5% time spent on the generation of the backbone movement | https://www.rosettacommons.org/software/ | - | [95] | |
| Structural homology algorithm for protein design (SHADES) | Protein design guided by local structural environments from known structures | Static structure | Sequence assembly from fragments followed by backbone optimization, side-chains repacking, and structure relaxation | https://www.rosettacommons.org/software/ | https://bitbucket.org/satsumaimo/shades/src/master/ | [96] | ||
| OSPREY 3.0 | Provable | Coordinates of atoms by Taylor series (CATS) | Enabling progressive backbone motions during protein design | Static structure | Continuous, strictly localized perturbations of the given segment of the backbone using a new internal coordinate system compatible with dead-end elimination workflows | https://github.com/donaldlab/OSPREY3 | - | [97] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Surpeta, B.; Sequeiros-Borja, C.E.; Brezovsky, J. Dynamics, a Powerful Component of Current and Future in Silico Approaches for Protein Design and Engineering. Int. J. Mol. Sci. 2020, 21, 2713. https://doi.org/10.3390/ijms21082713
Surpeta B, Sequeiros-Borja CE, Brezovsky J. Dynamics, a Powerful Component of Current and Future in Silico Approaches for Protein Design and Engineering. International Journal of Molecular Sciences. 2020; 21(8):2713. https://doi.org/10.3390/ijms21082713
Chicago/Turabian StyleSurpeta, Bartłomiej, Carlos Eduardo Sequeiros-Borja, and Jan Brezovsky. 2020. "Dynamics, a Powerful Component of Current and Future in Silico Approaches for Protein Design and Engineering" International Journal of Molecular Sciences 21, no. 8: 2713. https://doi.org/10.3390/ijms21082713
APA StyleSurpeta, B., Sequeiros-Borja, C. E., & Brezovsky, J. (2020). Dynamics, a Powerful Component of Current and Future in Silico Approaches for Protein Design and Engineering. International Journal of Molecular Sciences, 21(8), 2713. https://doi.org/10.3390/ijms21082713






