Downhill, Ultrafast and Fast Folding Proteins Revised
Abstract
1. Introduction
2. Results
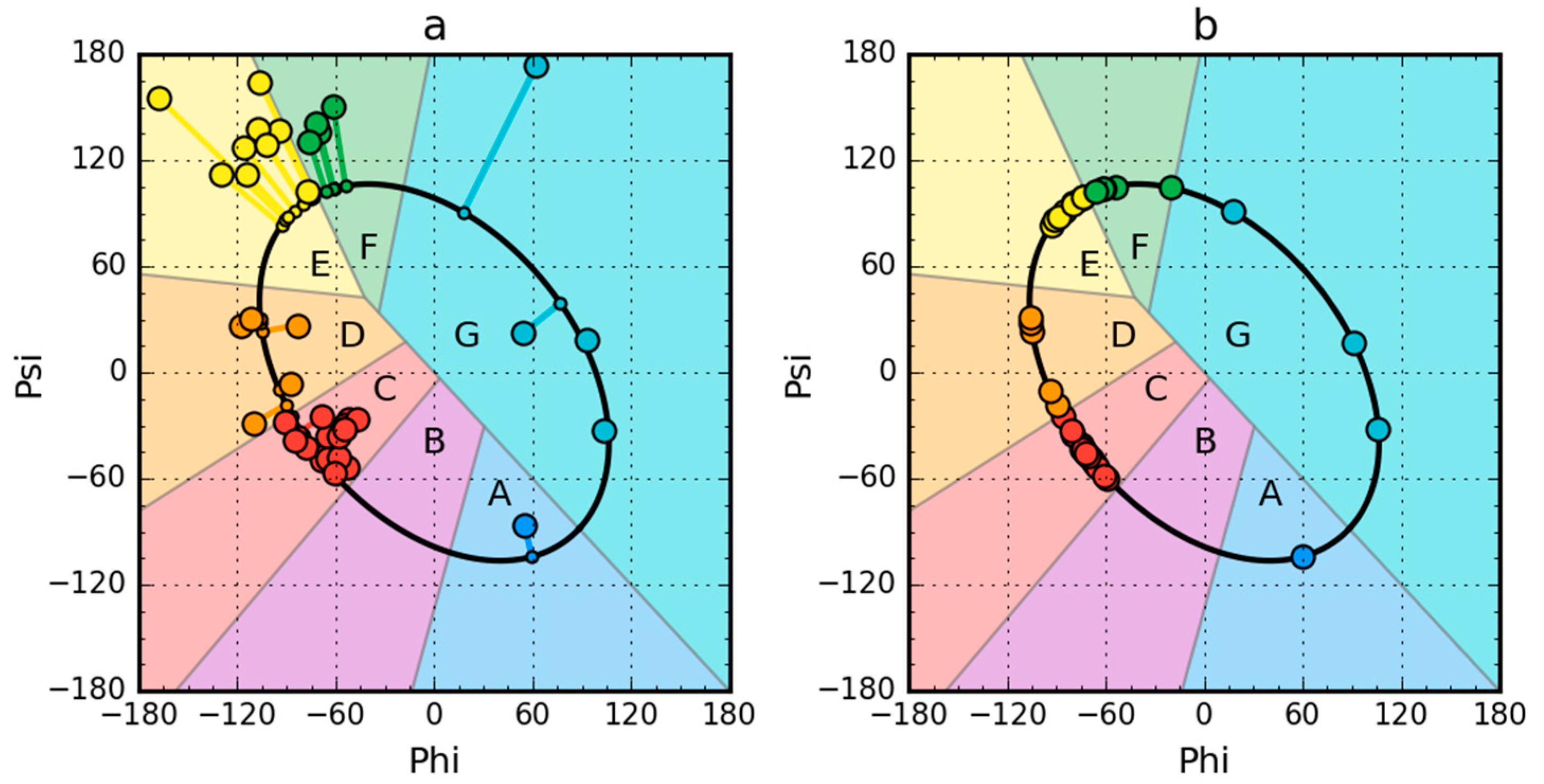
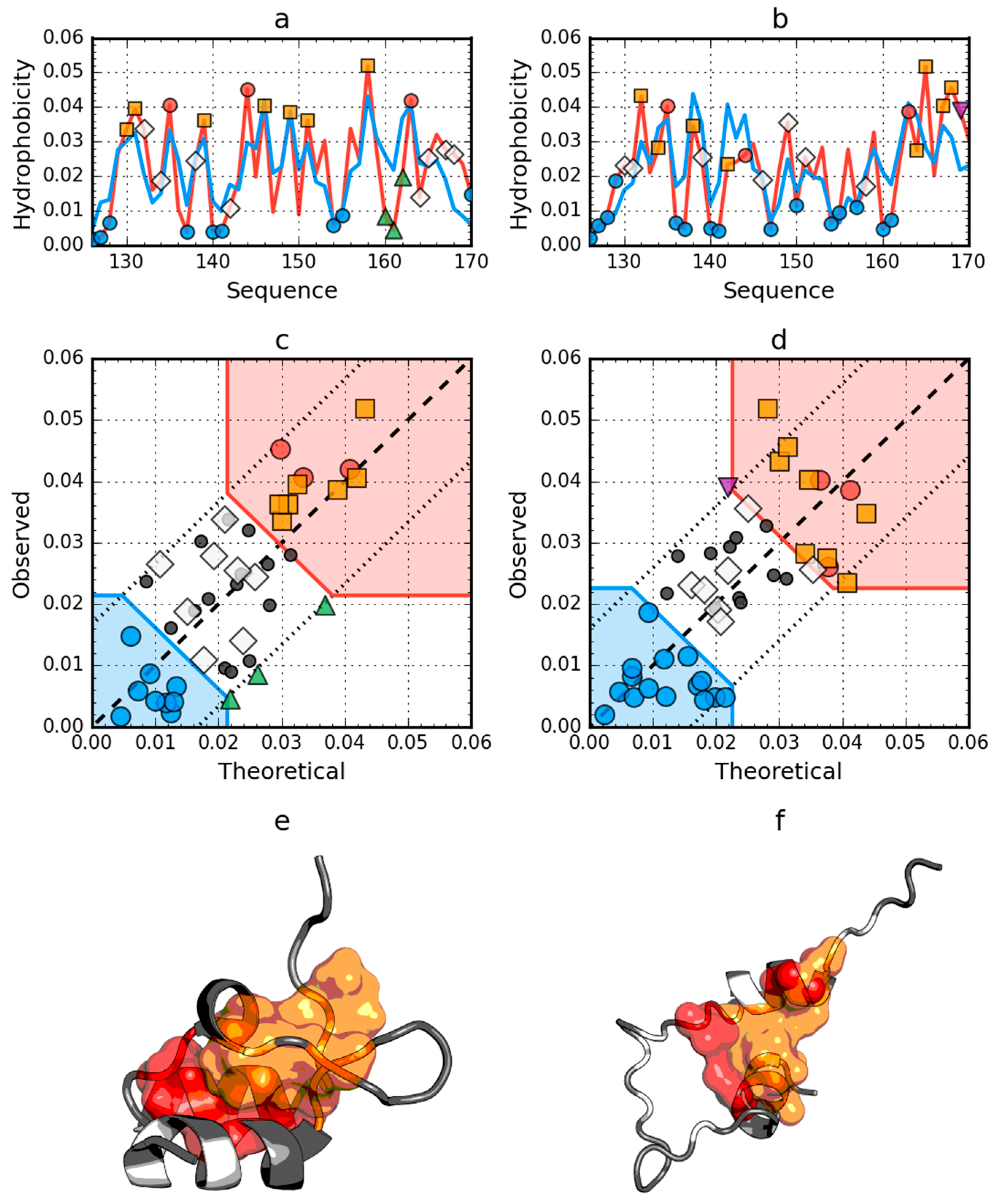
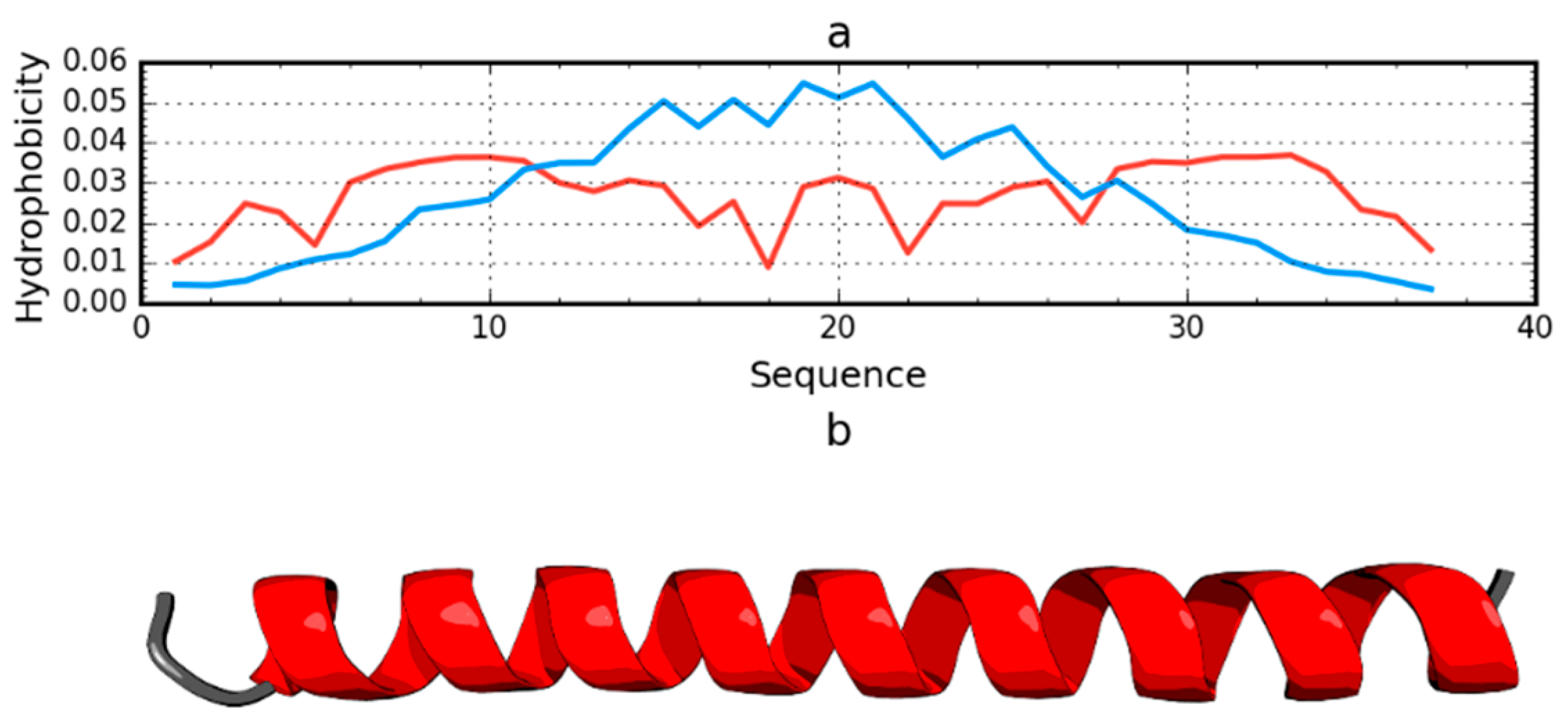
2.1. Peripheral-Subunit Binding Domain (1W4E)
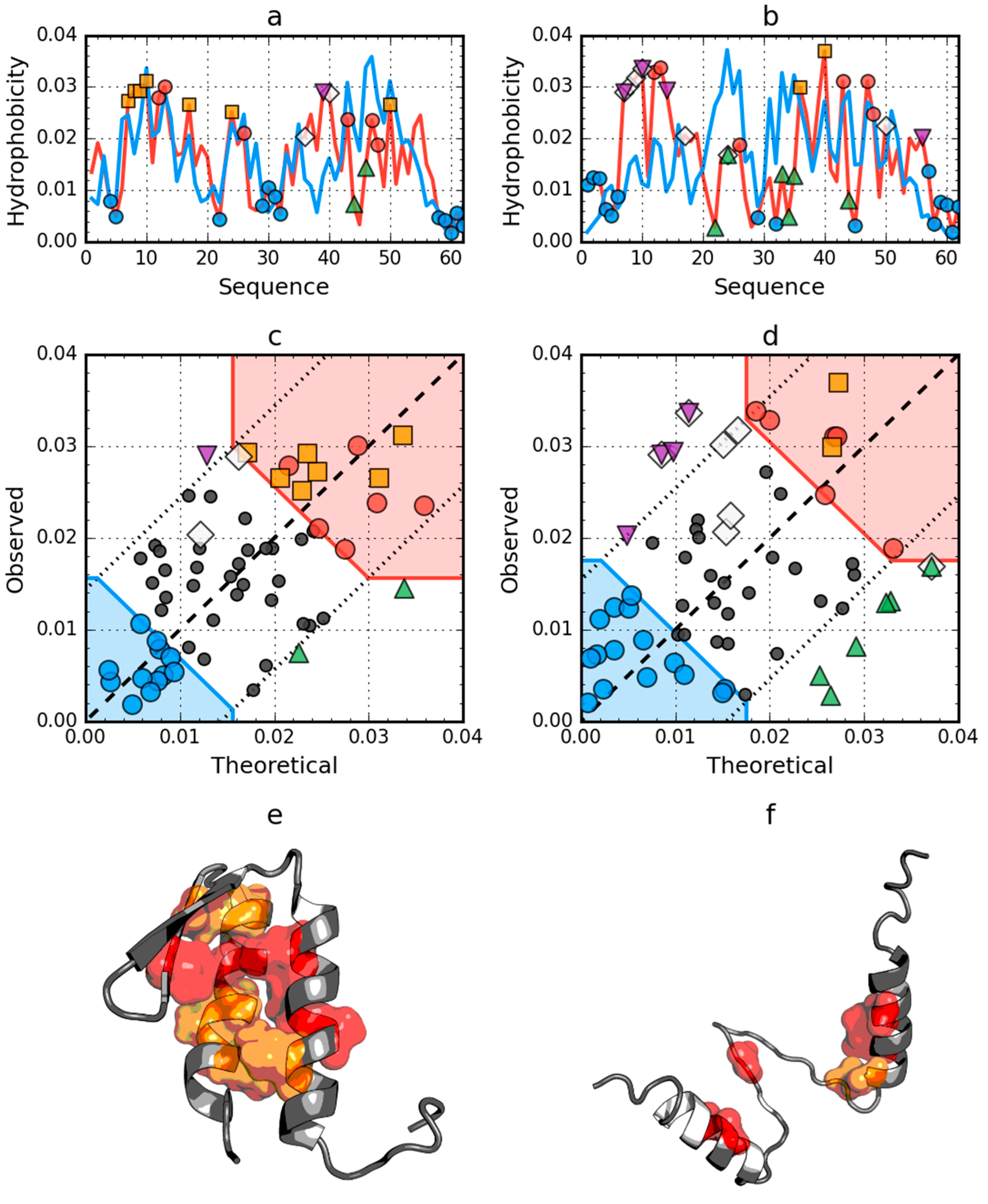
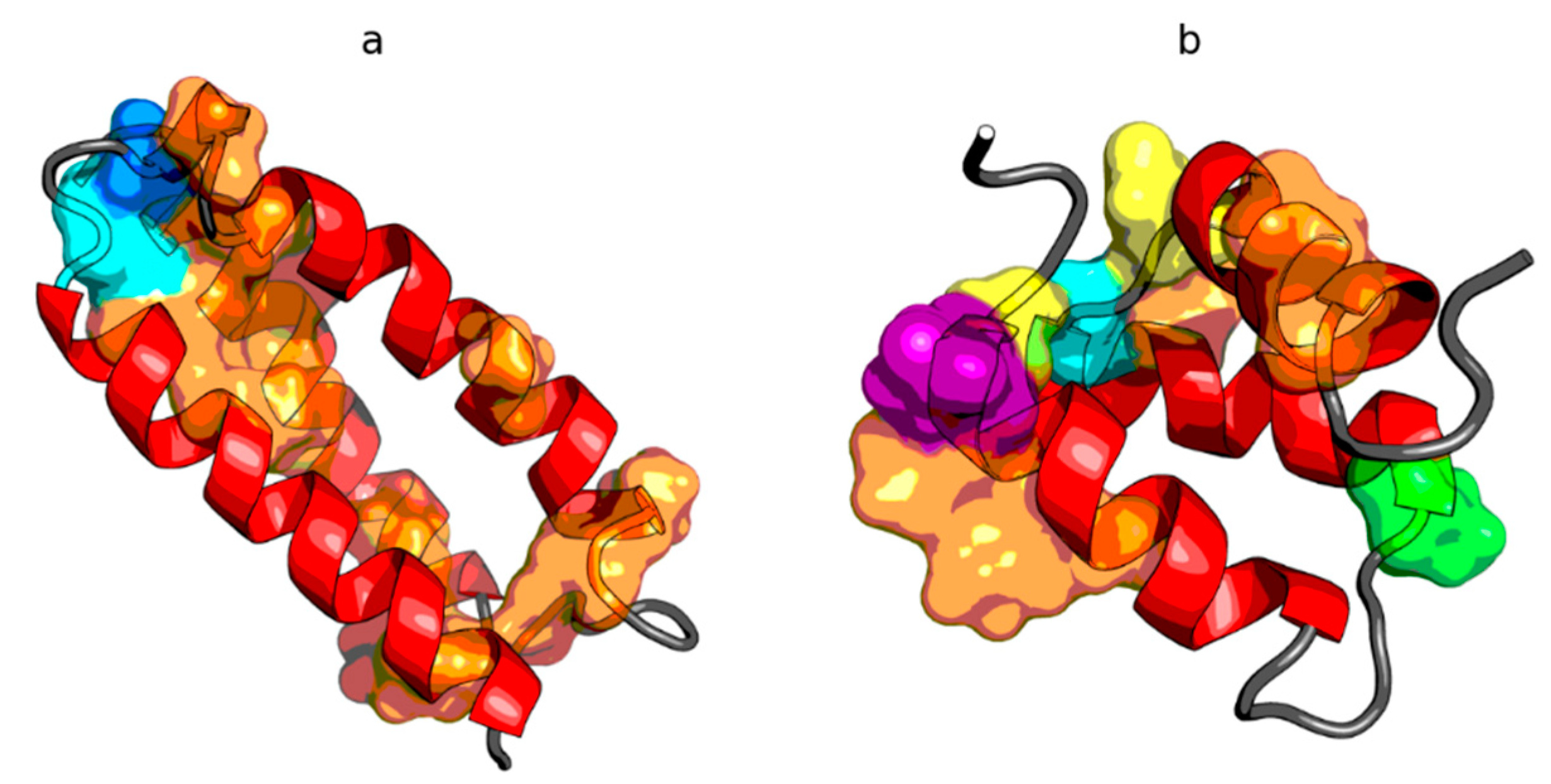
2.2. W Protein of Bacteriophage Lambda (2L6Q)
2.3. Other Proteins
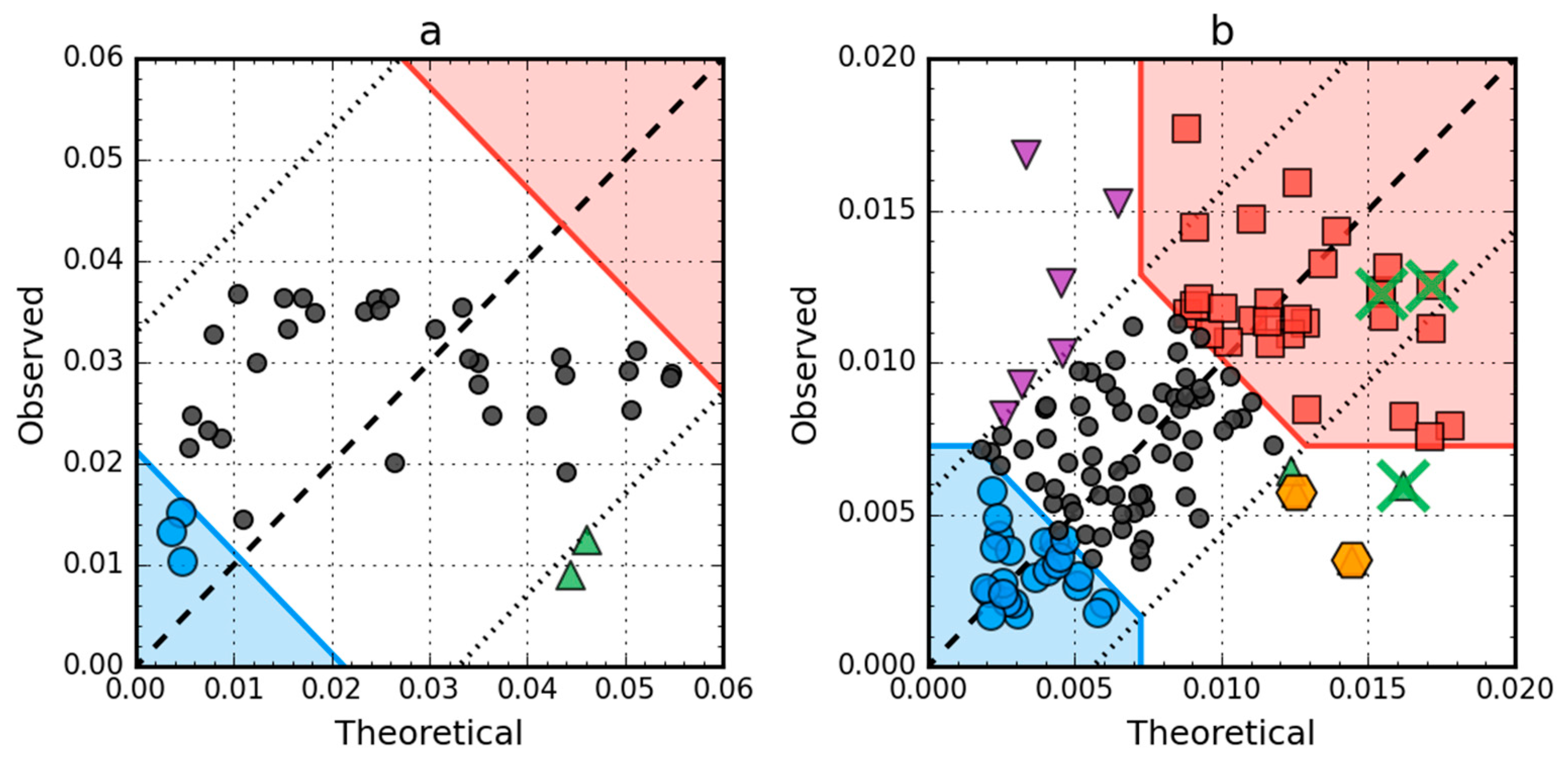
2.4. Comparative Analysis of Partially Unfolded Structures
2.5. Negative Control
3. Discussion
- Protein folding is the process of micellization of bipolar molecules (amino acids are molecules with different forms of bipolarity) with limited freedom of movement resulting from the presence of peptide bonds [42].
- Down-hill proteins (fast-folding, ultrafast-folding) are proteins with an amino acid sequence that allows construction of a micelle-like structure, which in the case of antifreeze proteins guarantees solubility (i.e., the basic condition enabling the performance of a biological function, which is the order of water molecules imposed by the distribution of charges on the protein surface preventing the structuring present in the ice structure). This issue is discussed in this paper.
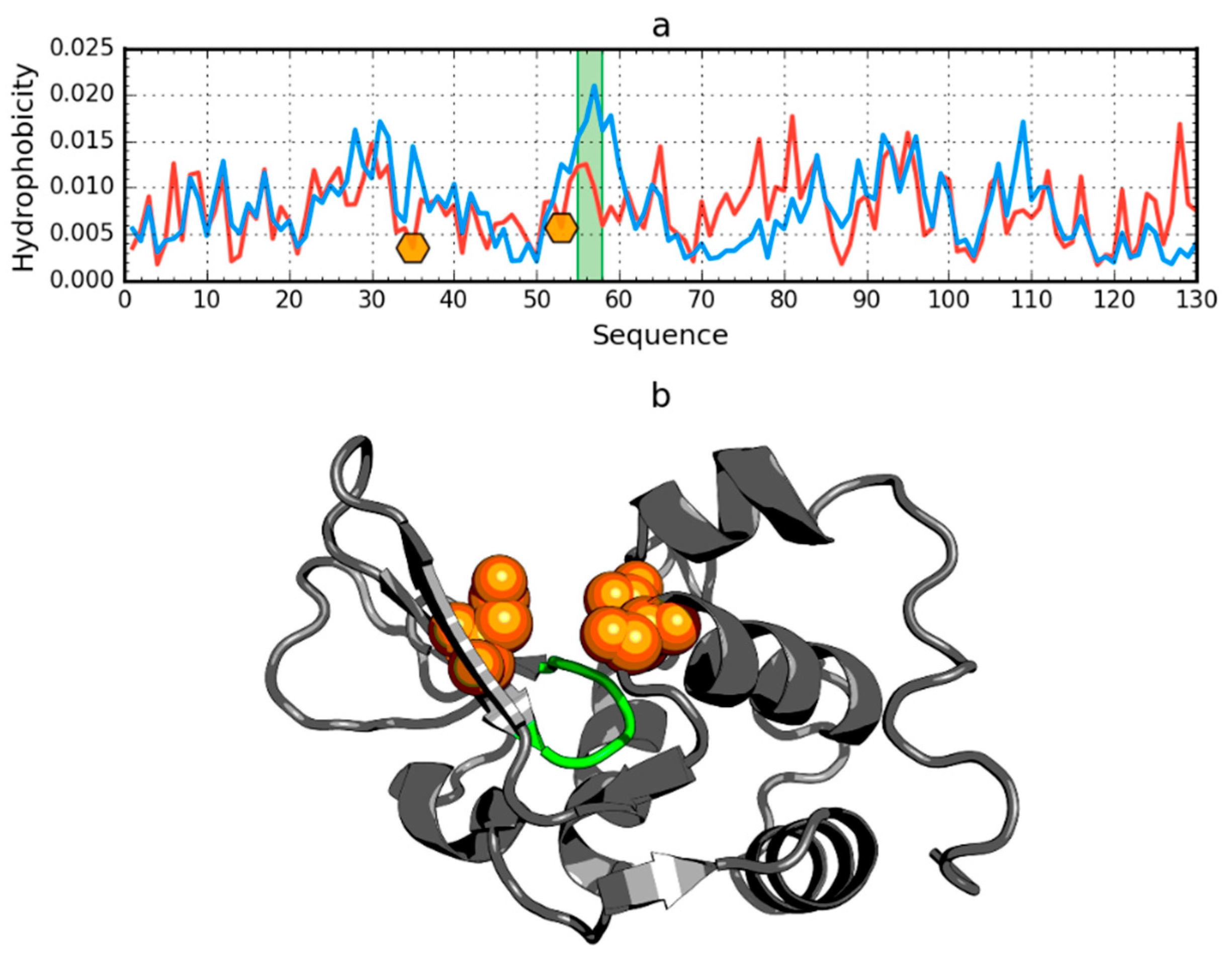
- Amino acid sequence determining the protein structure is a sequence with a specific coding system excluding the possibility of generating the perfect micelle, which is the local discordance versus 3D Gauss. The discordance is represented as local hydrophobicity deficiency and usually appears in the ligand or substrate binding cavity [32] or local hydrophobicity excess which is “used” by proteins to construct interfaces in protein–protein complexes [31]. Lysozyme is an example of cavity identification as shown in this paper.
- The form and degree of the encoded inability to reconstruct the micelle-like pattern determines the specificity of a given protein.
- In this context, amyloid (formed in physiological conditions) is also a result of micellization. The final product however takes the form of ribbon-like micelle since these polypeptides are not able to construct the globular forms [50].
4. Materials and Methods
4.1. Data
4.2. Late Stage Model—Fuzzy Oil Drop
4.3. Early-Stage Intermediate Model—Partially Unfolded Protein
4.4. Tools and Software
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FOD | Fuzzy oil drop |
| PDB | Protein data bank |
| RD | Relative distance |
References
- Dill, K.A.; Maccallum, J.L. The Protein-Folding Problem, 50 Years On. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, V. Conformational Dynamics and Ensembles in Protein Folding. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 395–412. [Google Scholar] [CrossRef]
- Schmeing, T.M.; Ramakrishnan, V. What recent ribosome structures have revealed about the mechanism of translation. Nat. Cell Biol. 2009, 461, 1234–1242. [Google Scholar] [CrossRef]
- Ellis, R.J.; Van Der Vies, S.M. Molecular Chaperones. Annu. Rev. Biochem. 1991, 60, 321–347. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J. Proteins as molecular chaperones. Nat. Cell Biol. 1987, 328, 378–379. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Fernández, M.R.; Valpuesta, J.M. Hsp70 chaperone: A master player in protein homeostasis. F1000Research 2018, 7, 1497. [Google Scholar] [CrossRef] [PubMed]
- Mayer, M.P.; Bukau, B. Hsp70 chaperones: Cellular functions and molecular mechanism. Cell. Mol. Life Sci. 2005, 62, 670–684. [Google Scholar] [CrossRef]
- Gruber, R.; Horovitz, A. Allosteric Mechanisms in Chaperonin Machines. Chem. Rev. 2016, 116, 6588–6606. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, C.J.; Dunker, A.K. Intrinsically Disordered Proteins and Intrinsically Disordered Protein Regions. Annu. Rev. Biochem. 2014, 83, 553–584. [Google Scholar] [CrossRef]
- Zwanzig, R.; Szabó, A.; Bagchi, B. Levinthal’s paradox. Proc. Natl. Acad. Sci. USA 1992, 89, 20–22. [Google Scholar] [CrossRef]
- Cavalli, A.; Haberthür, U.; Paci, E.; Caflisch, A. Fast protein folding on downhill energy landscape. Protein Sci. 2003, 12, 1801–1803. [Google Scholar] [CrossRef] [PubMed]
- Creighton, T.E.; Darby, N.J.; Kemmink, J. The roles of partly folded intermediates in protein folding. FASEB J. 1996, 10, 110–118. [Google Scholar] [CrossRef]
- Gelman, H.; Gruebele, M. Fast protein folding kinetics. Q. Rev. Biophys. 2014, 47, 95–142. [Google Scholar] [CrossRef] [PubMed]
- Eaton, W.A.; Muñoz, V.; Hagen, S.J.; Jas, G.S.; Lapidus, L.J.; Henry, E.R.; Hofrichter, J. Fast Kinetics and Mechanisms in Protein Folding. Annu. Rev. Biophys. Biomol. Struct. 2000, 29, 327–359. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, R.L. The Search for Folding Intermediates and the Mechanism of Protein Folding. Annu. Rev. Biophys. 2008, 37, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Creighton, T.E. How important is the molten globule for correct protein folding? Trends Biochem. Sci. 1997, 22, 6–10. [Google Scholar] [CrossRef]
- Kuwajima, K. The Molten Globule, and Two-State vs. Non-Two-State Folding of Globular Proteins. Biomolecules 2020, 10, 407. [Google Scholar] [CrossRef]
- Sanchez-Medina, C.; Sekhar, A.; Vallurupalli, P.; Cerminara, M.; Muñoz, V.; Kay, L.E. Probing the Free Energy Landscape of the Fast-Folding gpW Protein by Relaxation Dispersion NMR. J. Am. Chem. Soc. 2014, 136, 7444–7451. [Google Scholar] [CrossRef]
- Campos, L.A.; Liu, J.; Wang, X.; Ramanathan, R.; English, D.S.; Muñoz, V. A photoprotection strategy for microsecond-resolution single-molecule fluorescence spectroscopy. Nat. Methods 2011, 8, 143–146. [Google Scholar] [CrossRef]
- Ramanathan, R.; Muñoz, V. A Method for Extracting the Free Energy Surface and Conformational Dynamics of Fast-Folding Proteins from Single Molecule Photon Trajectories. J. Phys. Chem. B 2015, 119, 7944–7956. [Google Scholar] [CrossRef]
- Wang, Z.; Campos, L.A.; Muñoz, V. Single-Molecule Fluorescence Studies of Fast Protein Folding. In Methods in Enzymology; Elsevier BV: Amsterdam, The Netherlands, 2016; Volume 581, pp. 417–459. [Google Scholar] [CrossRef]
- Sadqi, M.; Lapidus, L.J.; Muñoz, V. How fast is protein hydrophobic collapse? Proc. Natl. Acad. Sci. USA 2003, 100, 12117–12122. [Google Scholar] [CrossRef] [PubMed]
- Oliva, F.Y.; Muñoz, V. A Simple Thermodynamic Test to Discriminate between Two-State and Downhill Folding. J. Am. Chem. Soc. 2004, 126, 8596–8597. [Google Scholar] [CrossRef] [PubMed]
- Doshi, U.R.; Muñoz, V. The Principles of α-Helix Formation: Explaining Complex Kinetics with Nucleation−Elongation Theory. J. Phys. Chem. B 2004, 108, 8497–8506. [Google Scholar] [CrossRef]
- Naganathan, A.N.; Muñoz, V. Scaling of Folding Times with Protein Size. J. Am. Chem. Soc. 2005, 127, 480–481. [Google Scholar] [CrossRef] [PubMed]
- Akmal, A.; Muñoz, V. The nature of the free energy barriers to two-state folding. Proteins Struct. Funct. Bioinform. 2004, 57, 142–152. [Google Scholar] [CrossRef] [PubMed]
- Naganathan, A.N.; Li, P.; Perez-Jimenez, R.; Sanchez-Ruiz, J.M.; Muñoz, V. Navigating the Downhill Protein Folding Regime via Structural Homologues. J. Am. Chem. Soc. 2010, 132, 11183–11190. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, V.; Thompson, P.A.; Hofrichter, J.; Eaton, W.A. Folding dynamics and mechanism of β-hairpin formation. Nat. Cell Biol. 1997, 390, 196–199. [Google Scholar] [CrossRef] [PubMed]
- Munoz, V.; Henry, E.; Hofrichter, J.; Eaton, W.A. A statistical mechanical model for -hairpin kinetics. Proc. Natl. Acad. Sci. USA 1998, 95, 5872–5879. [Google Scholar] [CrossRef] [PubMed]
- Muñoz, V.; Cerminara, M. When fast is better: Protein folding fundamentals and mechanisms from ultrafast approaches. Biochem. J. 2016, 473, 2545–2559. [Google Scholar] [CrossRef] [PubMed]
- Banach, M.; Konieczny, L.; Roterman, I. Protein-protein interaction encoded as an exposure of hydrophobic residues on the surface. In From Globular Proteins to Amyloids; Elsevier BV: Amsterdam, The Netherlands, 2020; pp. 79–89. [Google Scholar] [CrossRef]
- Banach, M.; Konieczny, L.; Roterman, I. Ligand binding cavity encoded as a local hydrophobicity deficiency. In From Globular Proteins to Amyloids; Elsevier BV: Amsterdam, The Netherlands, 2020; pp. 91–93. [Google Scholar] [CrossRef]
- Banach, M.; Konieczny, L.; Roterman, I. Why do antifreeze proteins require a solenoid? Biochimie 2018, 144, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Kalinowska, B.; Banach, M.; Król, M.; Irena, R. Application of Divergence Entropy to Characterize the Structure of the Hydrophobic Core in DNA Interacting Proteins. Entropy 2015, 17, 1477–1507. [Google Scholar] [CrossRef]
- Kalinowska, B.; Banach, M.; Wiśniowski, Z.; Konieczny, L.; Irena, R. Is the hydrophobic core a universal structural element in proteins? J. Mol. Model. 2017, 23, 205. [Google Scholar] [CrossRef] [PubMed]
- Banach, M.; Fabian, P.; Stapor, K.; Król, M.; Irena, R. Structure of the Hydrophobic Core Determines the 3D Protein Structure—Verification by Single Mutation Proteins. Biomolecules 2020, 10, 767. [Google Scholar] [CrossRef] [PubMed]
- Roterman, I. The geometrical analysis of peptide backbone structure and its local deformations. Biochimie 1995, 77, 204–216. [Google Scholar] [CrossRef]
- Roterman, I. Modelling the Optimal Simulation Path in the Peptide Chain Folding–Studies Based on Geometry of Alanine Heptapeptide. J. Theor. Biol. 1995, 177, 283–288. [Google Scholar] [CrossRef] [PubMed]
- Fabian, P.; Stapor, K.; Irena, R. Model of Early Stage Intermediate in Respect to Its Final Structure. Biomolecules 2019, 9, 866. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.D.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Hutchinson, E.G.; Thornton, J.M. PROMOTIF-A program to identify and analyze structural motifs in proteins. Protein Sci. 1996, 5, 212–220. [Google Scholar] [CrossRef]
- Konieczny, L.; Roterman, I. Introduction. In From Globular Proteins to Amyloids; Elsevier BV: Amsterdam, The Netherlands, 2020; pp. xiii–xx. [Google Scholar] [CrossRef]
- Banach, M.; Konieczny, L.; Roterman, I. The fuzzy oil drop model, based on hydrophobicity density distribution, generalizes the influence of water environment on protein structure and function. J. Theor. Biol. 2014, 359, 6–17. [Google Scholar] [CrossRef]
- Dułak, D.; Gadzała, M.; Stapor, K.; Fabian, P.; Konieczny, L.; Roterman, I. Folding with active participation of water. In From Globular Proteins to Amyloids; Elsevier BV: Amsterdam, The Netherlands, 2020; pp. 13–26. [Google Scholar] [CrossRef]
- Muñoz, V.; A Campos, L.; Sadqi, M. Limited cooperativity in protein folding. Curr. Opin. Struct. Biol. 2016, 36, 58–66. [Google Scholar] [CrossRef]
- Salapa, K.; Kalinowska, B.; Jadczyk, T.; Roterman, I. Measurement of Hydrophobicity Distribution in Proteins—Non-redundant Protein Data Bank. Bio-Algorithms Med.-Syst. 2012, 8, 327–338. [Google Scholar] [CrossRef]
- Dantas, G.; Kuhlman, B.; Callender, D.; Wong, M.; Baker, D. A Large Scale Test of Computational Protein Design: Folding and Stability of Nine Completely Redesigned Globular Proteins. J. Mol. Biol. 2003, 332, 449–460. [Google Scholar] [CrossRef]
- Banach, M.; Roterman, I. Solenoid—An amyloid under control. In From Globular Proteins to Amyloids; Elsevier: Amsterdam, The Netherlands, 2020; pp. 95–115. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Alexander, P.A.; Bryan, P.N.; Orban, J. Mutational Tipping Points for Switching Protein Folds and Functions. Structure 2012, 20, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Fabian, P.; Banach, M.; Stapor, K.; Król, M.; Ptak-Kaczor, M.; Irena, R. The Structure of Amyloid Versus the Structure of Globular Proteins. Int. J. Mol. Sci. 2020, 21, 4683. [Google Scholar] [CrossRef]
- Sadqi, M.; Fushman, D.; Muñoz, V. Atom-by-atom analysis of global downhill protein folding. Nat. Cell Biol. 2006, 442, 317–321. [Google Scholar] [CrossRef]
- Sborgi, L.; Verma, A.; Muñoz, V.; De Alba, E. Revisiting the NMR Structure of the Ultrafast Downhill Folding Protein gpW from Bacteriophage λ. PLoS ONE 2011, 6, e26409. [Google Scholar] [CrossRef]
- Sborgi, L.; Verma, A.; Muñoz, V.; De Alba, E. High Resolution NMR Structure of gpW (W Protein of Bacteriophage Lambda) at Acidic pH. 2011. Available online: https://www.rcsb.org/structure/2l6r (accessed on 7 October 2020). [CrossRef]
- Ferguson, N.; Sharpe, T.D.; Schartau, P.J.; Sato, S.; Allen, M.D.; Johnson, C.M.; Rutherford, T.J.; Fersht, A.R. Ultra-fast Barrier-limited Folding in the Peripheral Subunit-binding Domain Family. J. Mol. Biol. 2005, 353, 427–446. [Google Scholar] [CrossRef]
- Robien, M.A.; Clore, G.M.; Omichinski, J.G.; Perham, R.N.; Appella, E.; Sakaguchi, K.; Gronenborn, A.M. Three-dimensional solution structure of the E3-binding domain of the dihydrolipoamide succinyltransferase core from the 2-oxoglutarate dehydrogenase multienzyme complex of Escherichia coli. Biochemistry 1992, 31, 3463–3471. [Google Scholar] [CrossRef]
- Neuweiler, H.; Sharpe, T.D.; Rutherford, T.J.; Johnson, C.M.; Allen, M.D.; Ferguson, N.; Fersht, A.R. The Folding Mechanism of BBL: Plasticity of Transition-State Structure Observed within an Ultrafast Folding Protein Family. J. Mol. Biol. 2009, 390, 1060–1073. [Google Scholar] [CrossRef]
- Sicheri, F.; Yang, D.S.C. Ice-binding structure and mechanism of an antifreeze protein from winter flounder. Nat. Cell Biol. 1995, 375, 427–431. [Google Scholar] [CrossRef]
- Artymiuk, P.; Blake, C. Refinement of human lysozyme at 1.5 Å resolution analysis of non-bonded and hydrogen-bond interactions. J. Mol. Biol. 1981, 152, 737–762. [Google Scholar] [CrossRef]
- Banach, M.; Konieczny, L.; Roterman, I. Fuzzy Oil Drop Model Application—From Globular Proteins to Amyloids. In The Functional Role of Critical Dynamics in Neural Systems; Springer Science and Business Media LLC.: Berlin, Germany, 2018; pp. 639–658. [Google Scholar]
- Fabian, P.; Stapor, K.; Banach, M.; Ptak-Kaczor, M.; Król, M.; Irena, R. Alternative Hydrophobic Core in Proteins—The Effect of Specific Synergy. Symmetry 2020, 12, 273. [Google Scholar] [CrossRef]
- Jurkowski, W.; Baster, Z.; Dułak, D.; Roterman-Konieczna, I. The early-stage intermediate. In Protein Folding in Silico; Elsevier BV: Amsterdam, The Netherlands, 2012; pp. 1–20, ISBN-13: 9781907568176. [Google Scholar]
- Kauzmann, W. Some Factors in the Interpretation of Protein Denaturation. Adv. Protein Chem. 1959, 14, 1–63. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 1976, 104, 59–107. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Konieczny, L.; Brylinski, M.; Roterman, I. Gauss-function-based model of hydrophobicity density in proteins. In Silico Biol. 2006, 6, 15–22. [Google Scholar] [PubMed]
- The PyMOL Molecular Graphics System; Version 2.0; Schrödinger, LLC.: New York, NY, USA, 2015.
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Roterman, I.; Konieczny, L.; Jurkowski, W.; Prymula, K.; Banach, M. Two-intermediate model to characterize the structure of fast-folding proteins. J. Theor. Biol. 2011, 283, 60–70. [Google Scholar] [CrossRef]
- Mok, K.H.; Kuhn, L.T.; Goez, M.; Day, I.J.; Lin, J.C.; Andersen, N.H.; Hore, P.J. A pre-existing hydrophobic collapse in the unfolded state of an ultrafast folding protein. Nat. Cell Biol. 2007, 447, 106–109. [Google Scholar] [CrossRef]
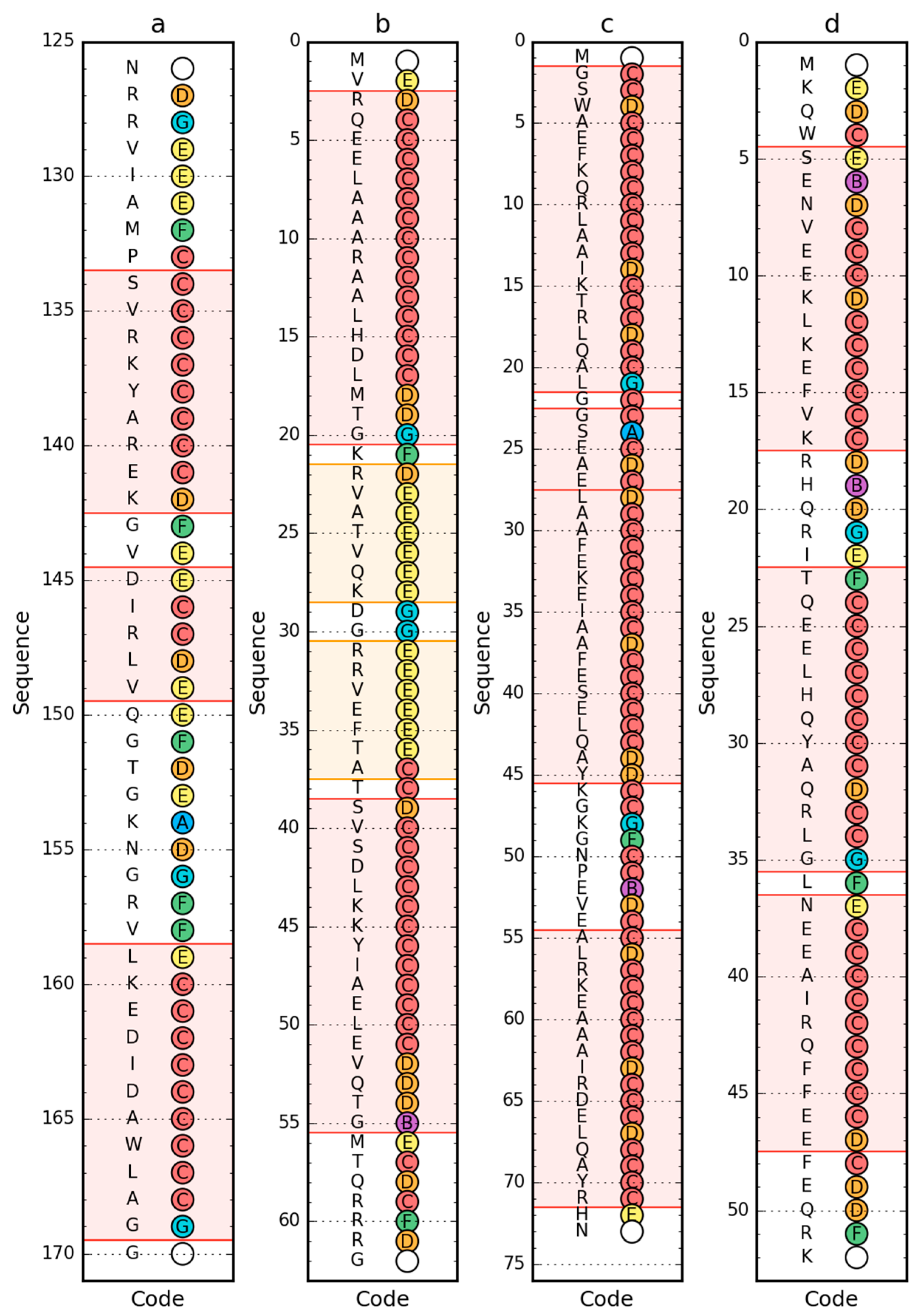
| PDB ID | RD—LS | RD—LS after Fragment Selection/Elimination | RD—ES | RD—ES after Fragment Selection/Elimination | ||
|---|---|---|---|---|---|---|
| 2CYU | 0.638 | 3-helix system | 0.493 | 0.540 | 18–23 | 0.431 |
| 2L6Q | 0.473 | 0.595 | 7–10,21–26 | 0.488 | ||
| 2L6R | 0.477 | 34–37 eliminated | 0.462 | 0.439 | ||
| 1BBL | 0.556 | 12–33 selected | 0.349 | |||
| 38–48 selected | 0.311 | |||||
| 2WXC | 0.382 | 0.525 | 165-C-term | 0.441 | ||
| 2A3D | 0.580 | 21–24 eliminated | 0.474 | 0.710 | 28–45 selected | 0.474 |
| 2F21 | 0.402 | 0.761 | ||||
| 1–49 selected | 0.520 | 0.657 | ||||
| 50–163 selected | 0.310 | 0.697 | ||||
| 2P6J | 0.298 | 0.504 | helix 5–17 | |||
| PDB-ID | Protein | Chain Length | Characteristics | Ref |
|---|---|---|---|---|
| 2CYU | e3-binding domain | 39 aa | Downhill | [51] |
| 2L6Q | Viral protein | 62 aa | [52] | |
| 2L6R | Viral protein | 62 aa | [53] | |
| 1W4E | Peripheral-subunit binding domain | 45 aa | Ultrafast | [54] |
| 1W4F | 45 aa | [54] | ||
| 1W4G | 45 aa | [54] | ||
| 1W4H | 45 aa | [54] | ||
| 2BTH | 45 aa | [54] | ||
| 1W4J | 51 aa | [54] | ||
| 1W4K | 51 aa | [54] | ||
| 1BBL | 37 aa | [55] | ||
| 2WXC | 47 aa | [56] | ||
| Negative Control | ||||
| 1WFA | Antifreeze | 37 aa | Antifreeze | [57] |
| 1LZ1 | Lysozyme | 130 aa | Enzyme | [58] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banach, M.; Stapor, K.; Konieczny, L.; Fabian, P.; Roterman, I. Downhill, Ultrafast and Fast Folding Proteins Revised. Int. J. Mol. Sci. 2020, 21, 7632. https://doi.org/10.3390/ijms21207632
Banach M, Stapor K, Konieczny L, Fabian P, Roterman I. Downhill, Ultrafast and Fast Folding Proteins Revised. International Journal of Molecular Sciences. 2020; 21(20):7632. https://doi.org/10.3390/ijms21207632
Chicago/Turabian StyleBanach, Mateusz, Katarzyna Stapor, Leszek Konieczny, Piotr Fabian, and Irena Roterman. 2020. "Downhill, Ultrafast and Fast Folding Proteins Revised" International Journal of Molecular Sciences 21, no. 20: 7632. https://doi.org/10.3390/ijms21207632
APA StyleBanach, M., Stapor, K., Konieczny, L., Fabian, P., & Roterman, I. (2020). Downhill, Ultrafast and Fast Folding Proteins Revised. International Journal of Molecular Sciences, 21(20), 7632. https://doi.org/10.3390/ijms21207632






