Polyelectrolyte-Nanoplatelet Complexation: Is It Possible to Predict the State Diagram?
Abstract
1. Introduction
2. Theoretical Section
2.1. The Coarse-Grained Model
2.2. Molecular Dynamics Simulations
2.3. Structural Analysis
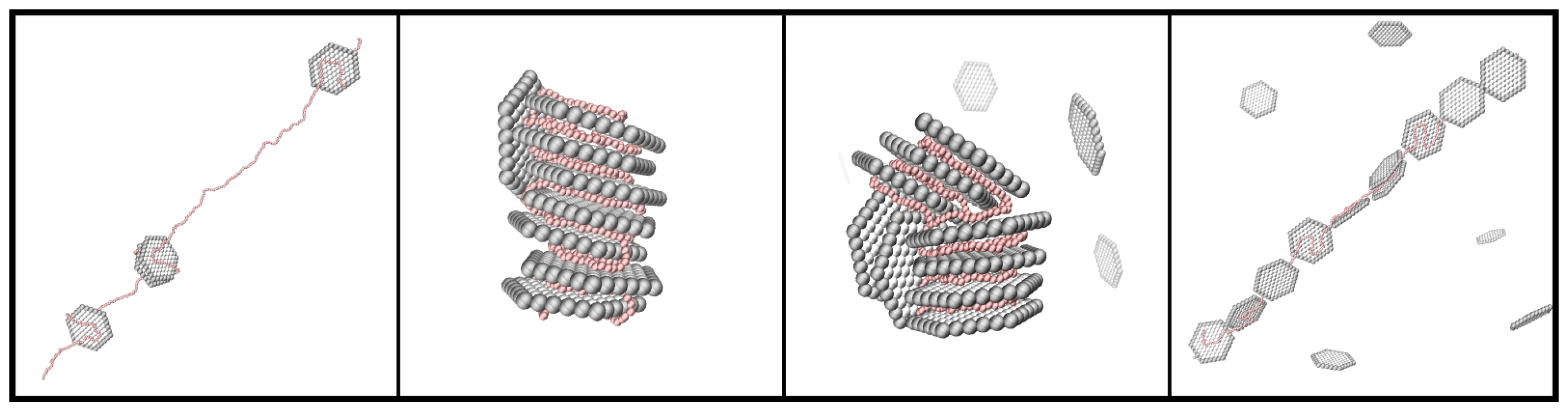
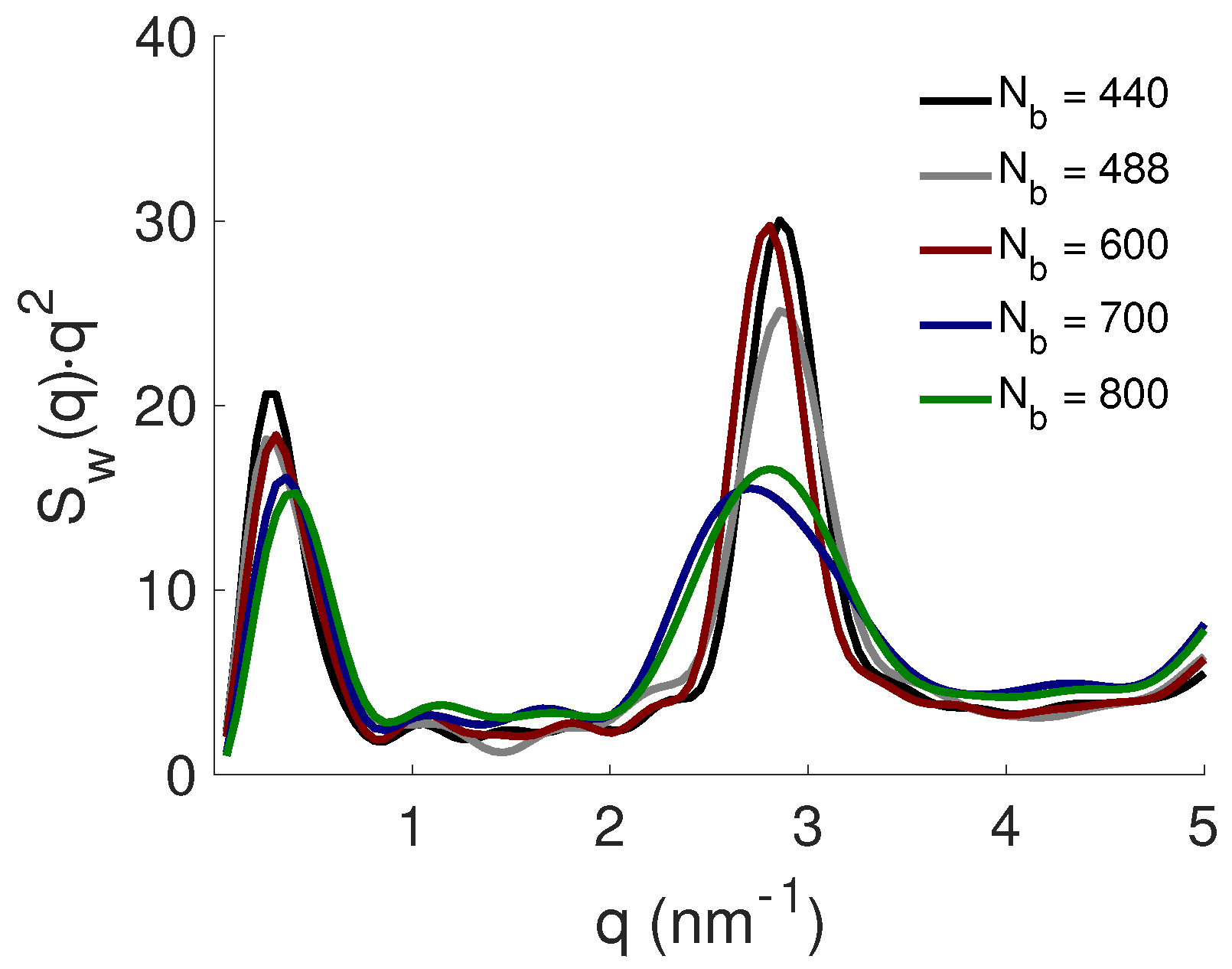
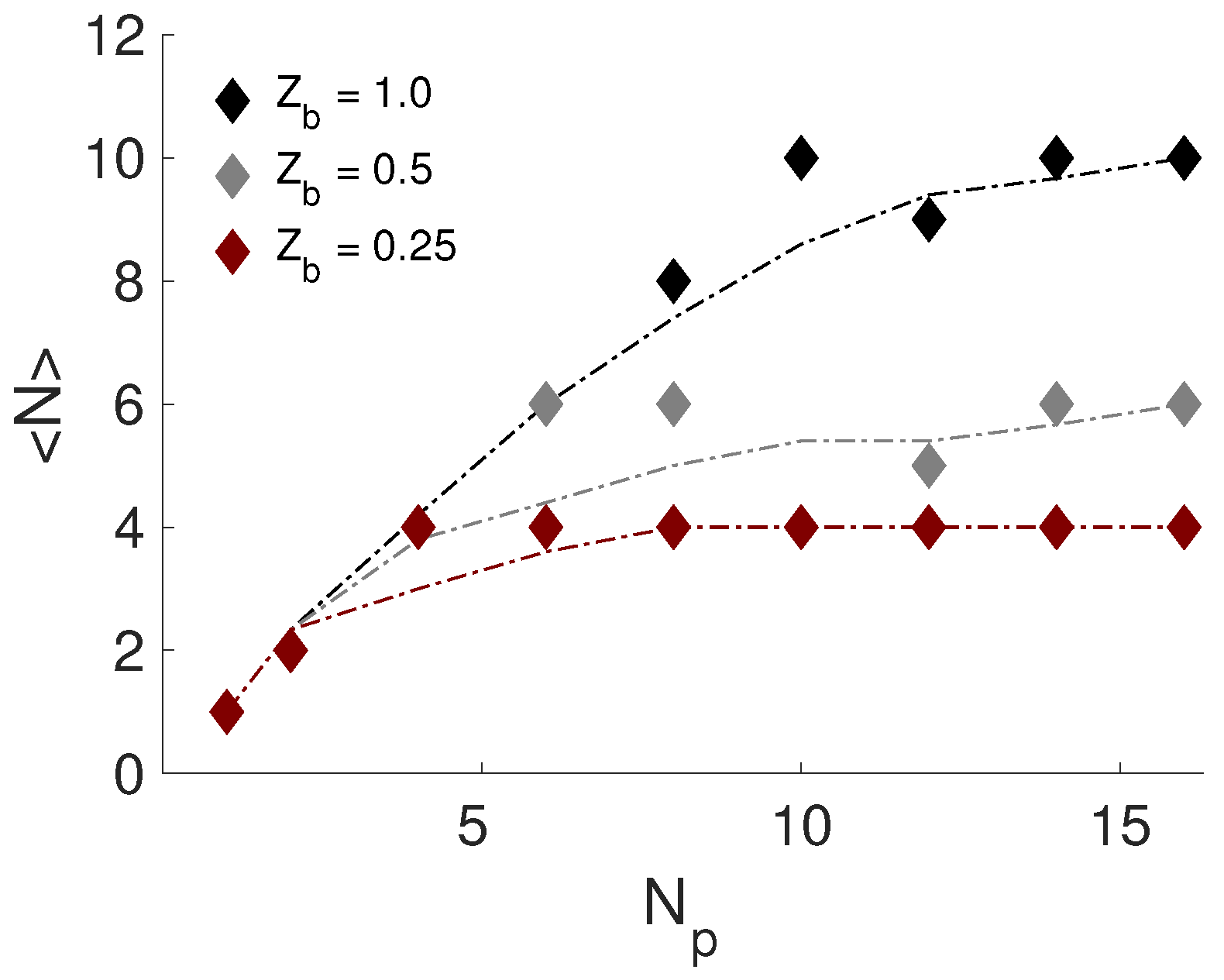
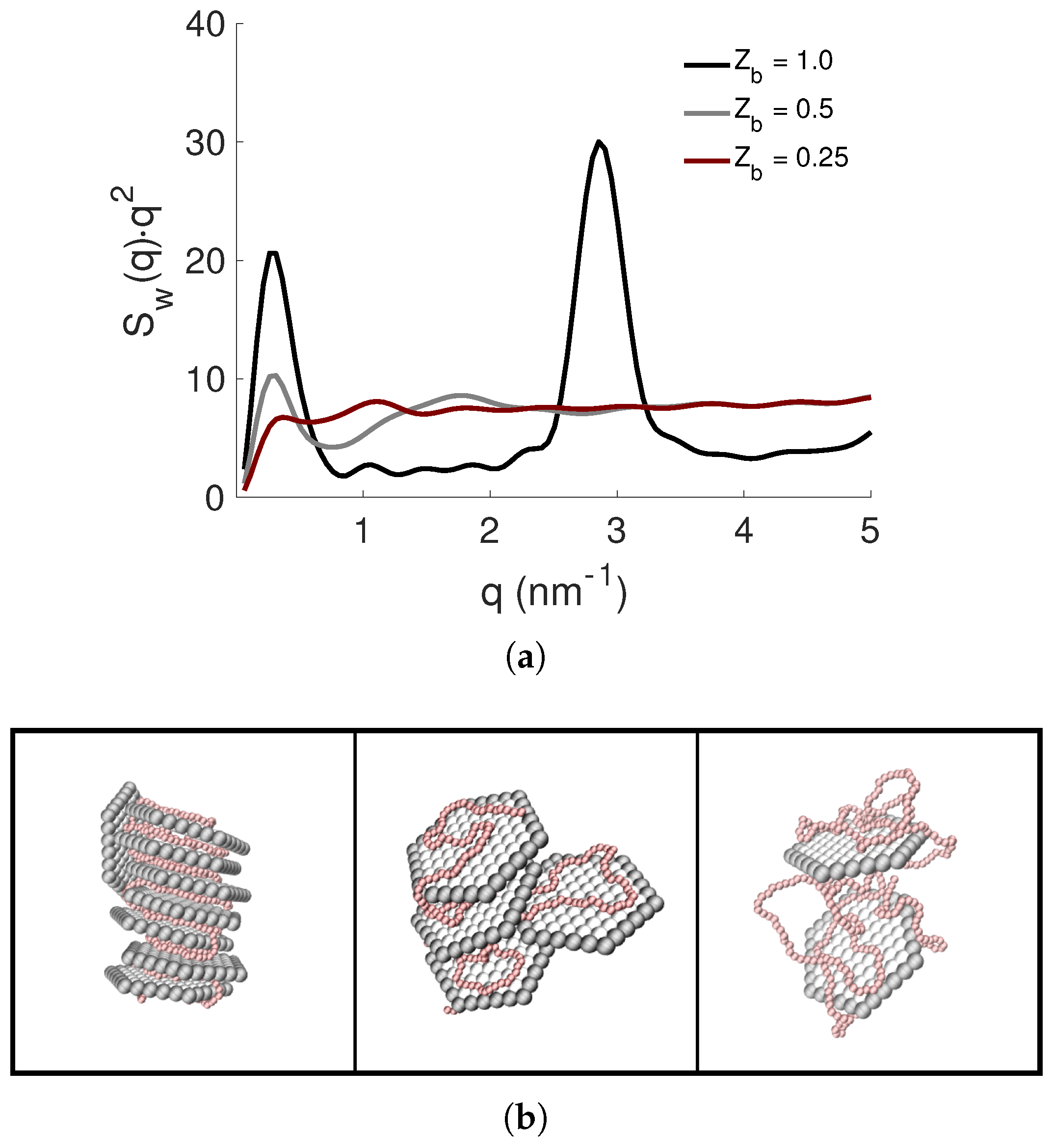
3. Results and Discussion
3.1. Composition of the PE-NP Complex
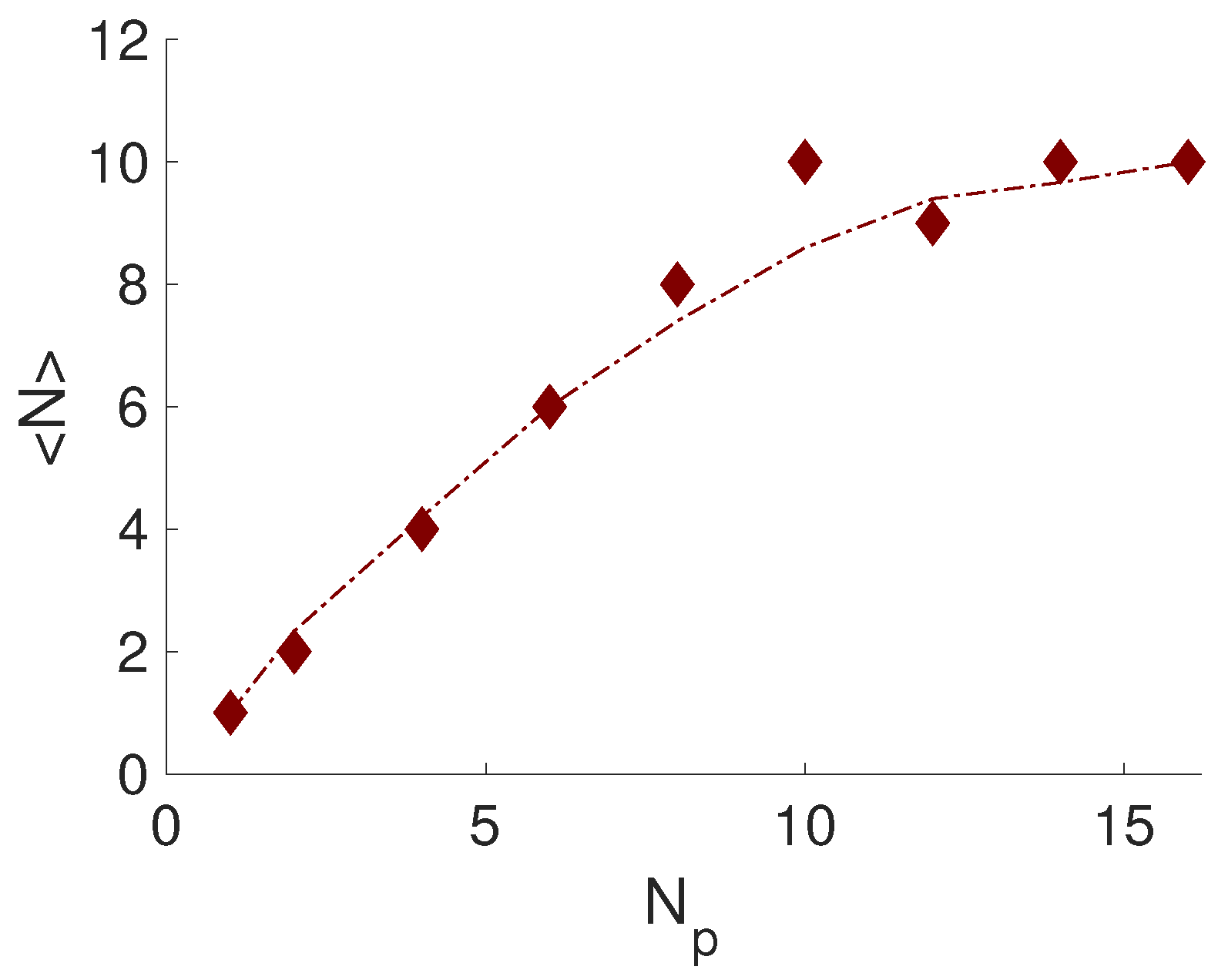
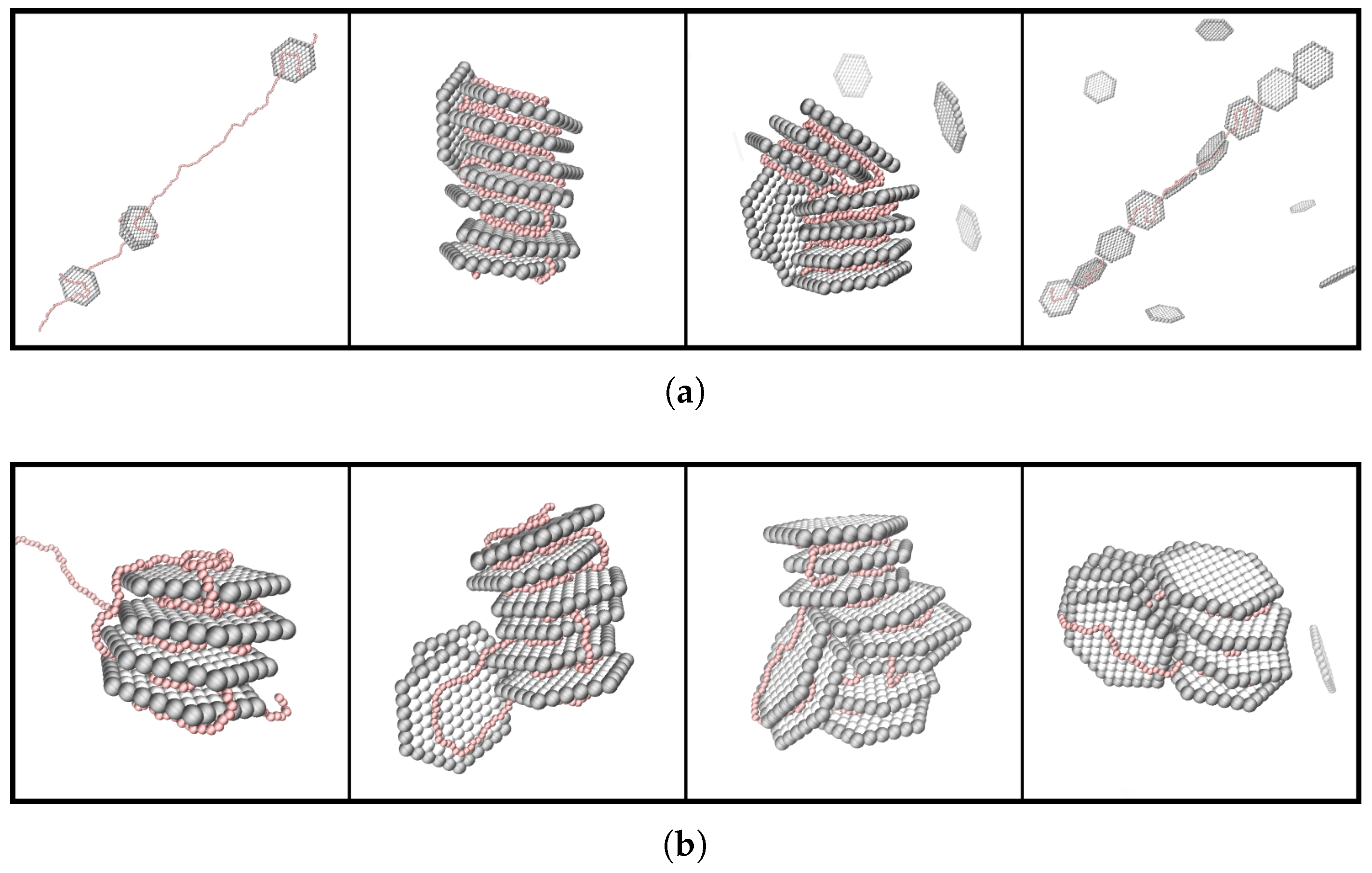
3.2. Effect of PE Length
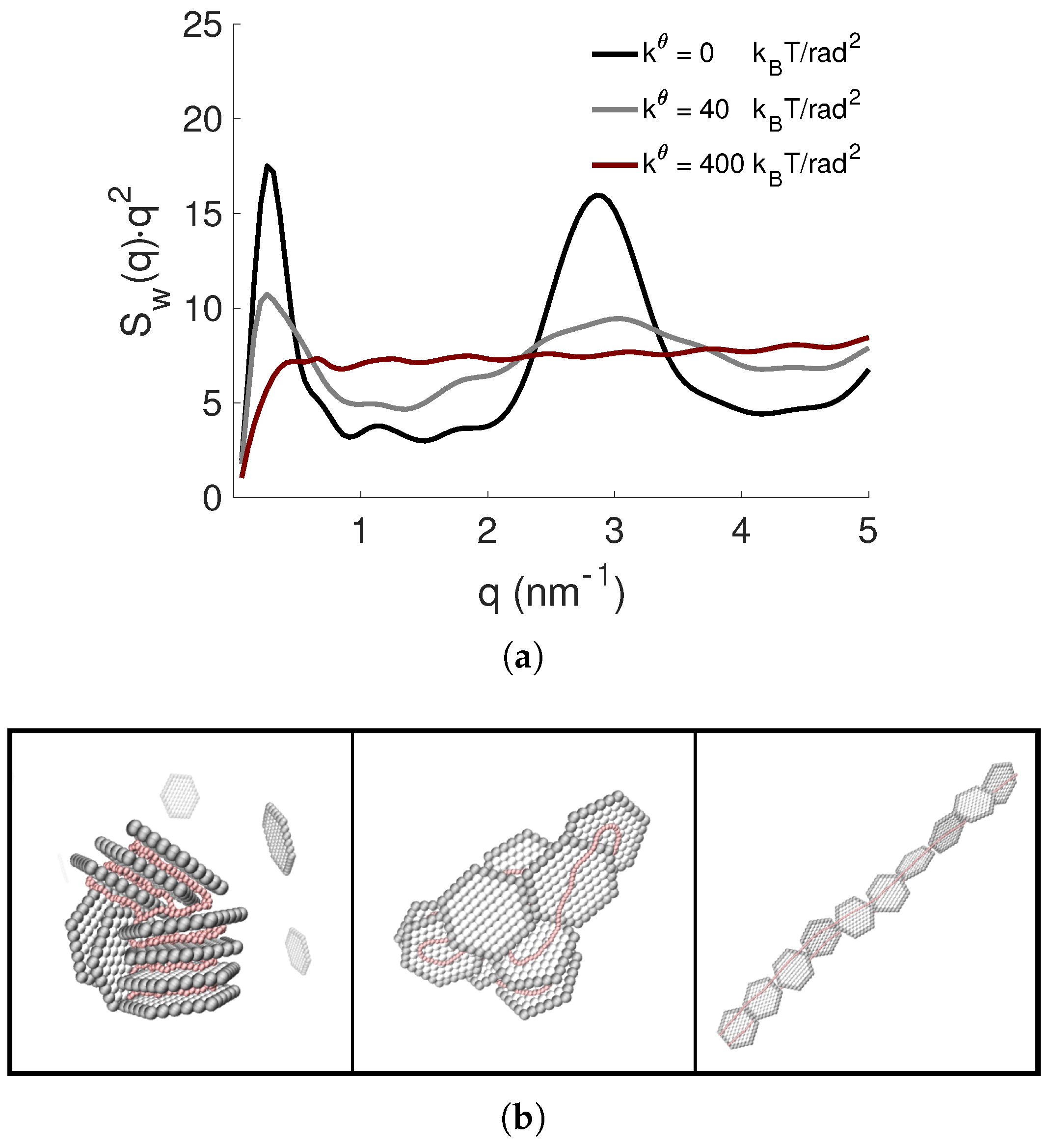
3.3. Effect of the PE Total Charge
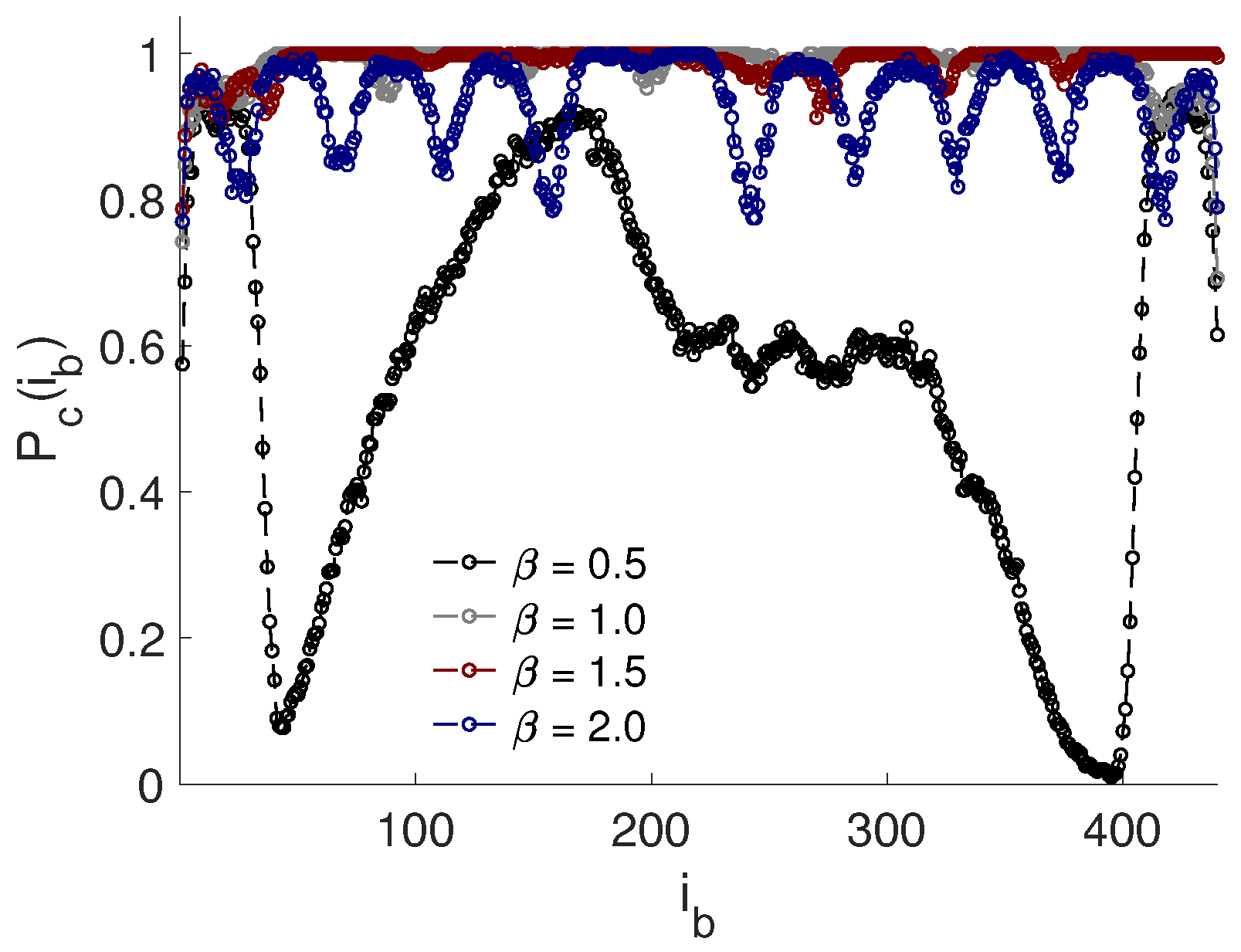
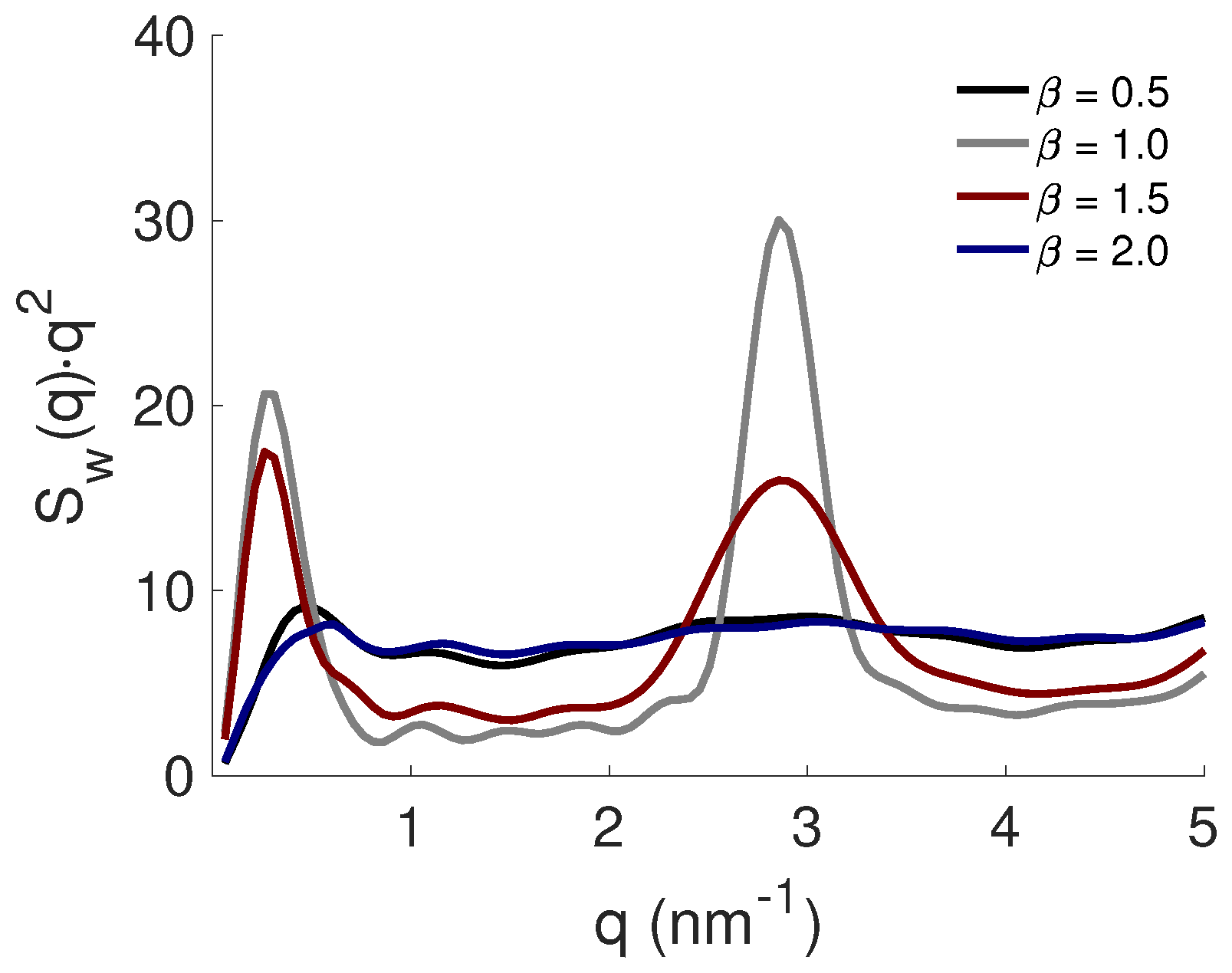
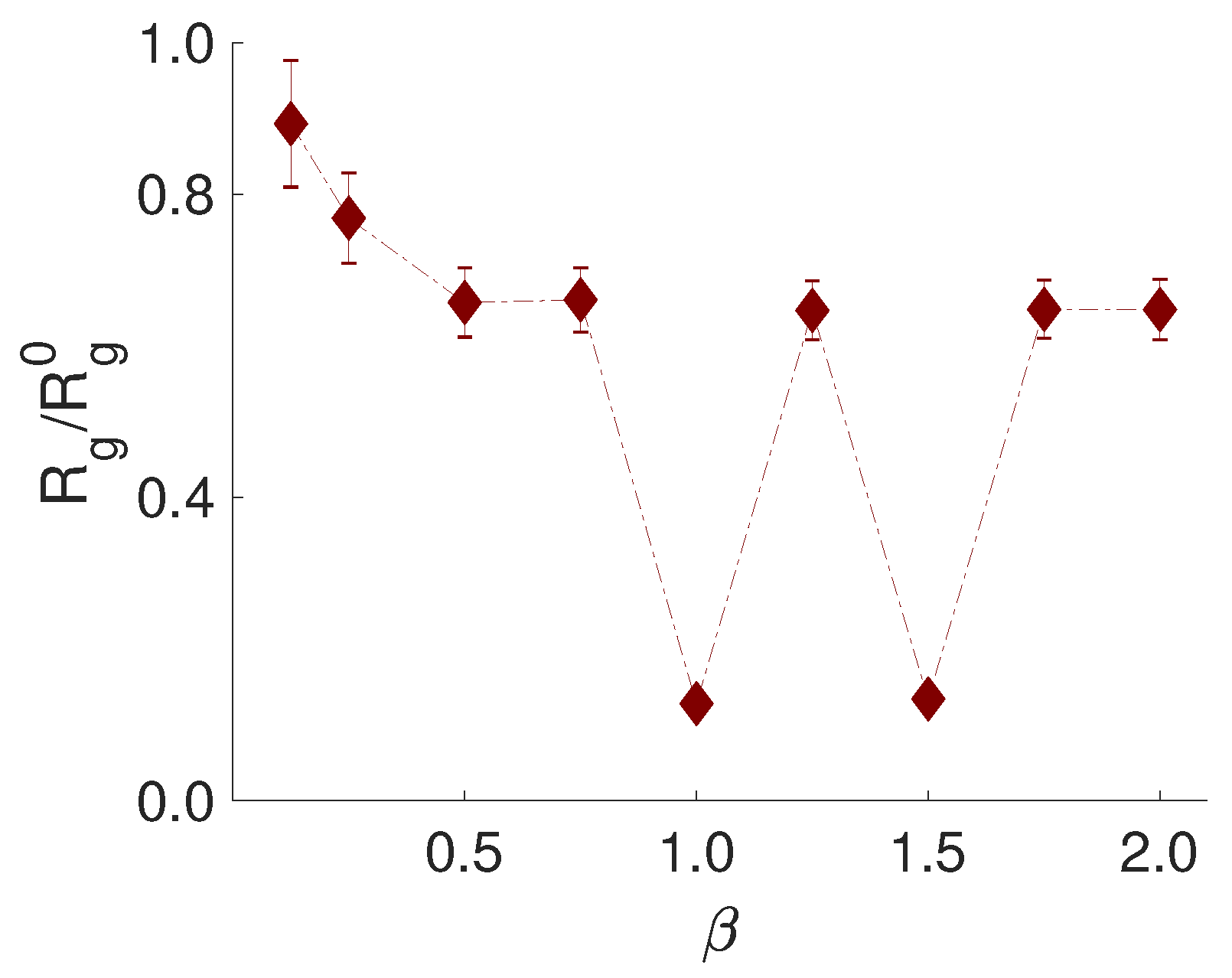
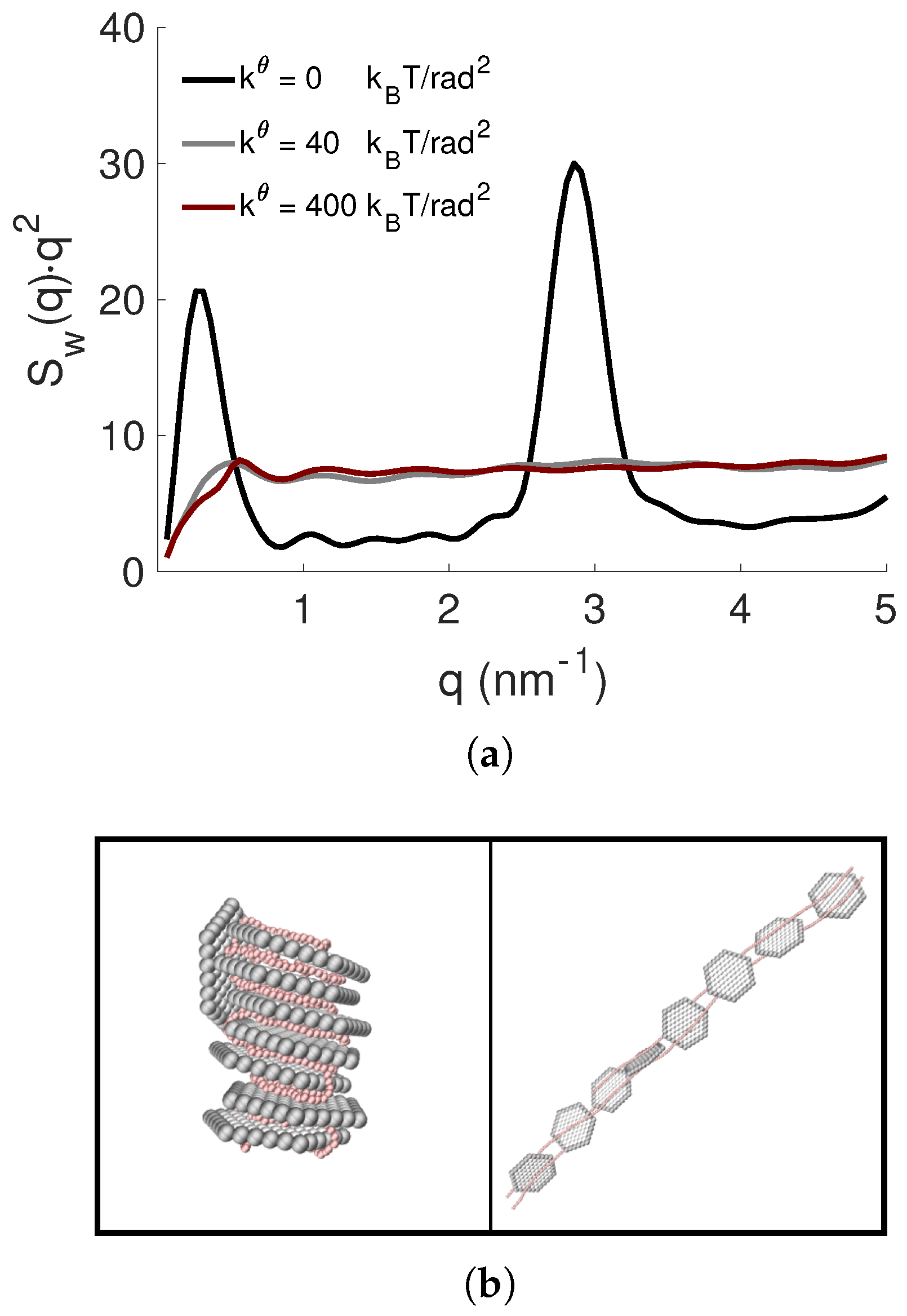
3.4. Effect of PE Flexibility
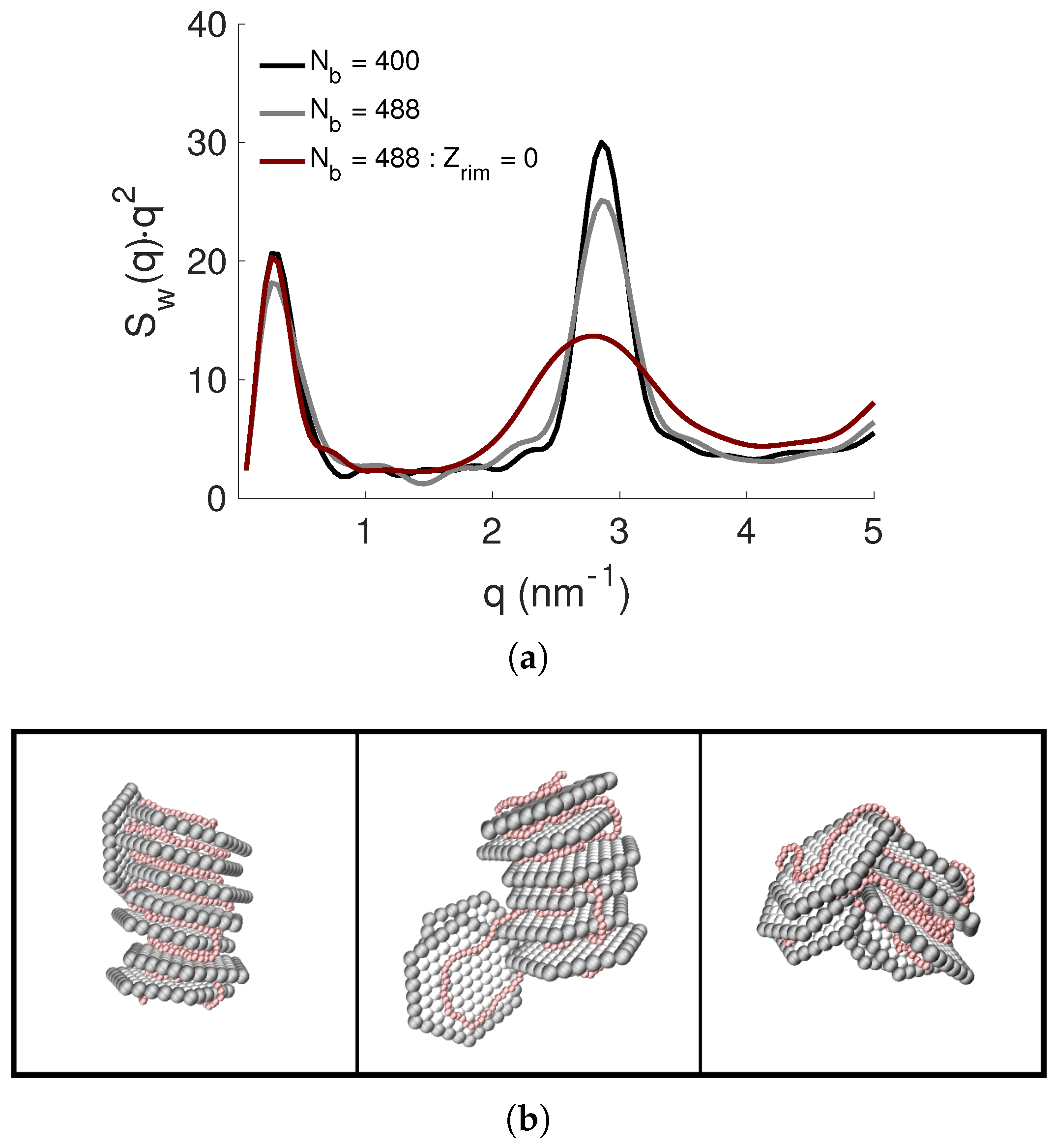
3.5. Effect of NP Charge and Rim
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PE | Polyelectrolyte |
| NP | Nanoplatelet |
| MD | Molecular dynamics |
References
- Böhm, N.; Kulicke, W.M. Optimization of the use of polyelectrolytes for dewatering industrial sludges of various origins. Colloid Polym. Sci. 1997, 275, 73–81. [Google Scholar] [CrossRef]
- Patel, H.A.; Somani, R.S.; Bajaj, H.C.; Jasra, R.V. Nanoclays for polymer nanocomposites, paints, inks, greases and cosmetics formulations, drug delivery vehicle and waste water treatment. Bull. Mater. Sci. 2006, 29, 133–145. [Google Scholar] [CrossRef]
- Netz, R.R.; Joanny, J.F. Complexation between a Semiflexible Polyelectrolyte and an Oppositely Charged Sphere. Macromolecules 1999, 32, 9026–9040. [Google Scholar] [CrossRef]
- Manias, E.; Touny, A.; Wu, L.; Strawhecker, K.; Lu, B.; Chung, T.C. Polypropylene/Montmorillonite Nanocomposites. Review of the Synthetic Routes and Materials Properties. Chem. Mater. 2001, 13, 3516–3523. [Google Scholar] [CrossRef]
- Stoll, S.; Chodanowski, P. Polyelectrolyte Adsorption on an Oppositely Charged Spherical Particle. Chain Rigidity Effects. Macromolecules 2002, 35, 9556–9562. [Google Scholar] [CrossRef]
- Messina, R.; Holm, C.; Kremer, K. Like-charge colloid–polyelectrolyte complexation. J. Chem. Phys. 2002, 117, 2947. [Google Scholar] [CrossRef]
- Messina, R.; Holm, C.; Kremer, K. Polyelectrolyte adsorption and multilayering on charged colloidal particles. J. Polym. Sci. B Polym. Phys. 2004, 42, 3557–3570. [Google Scholar] [CrossRef]
- Szilagyi, I.; Trefalt, G.; Tiraferri, A.; Maroni, P.; Borkovec, M. Polyelectrolyte adsorption, interparticle forces, and colloidal aggregation. J Polym. Sci. Pol. Phys. 2014, 42, 3557–3570. [Google Scholar] [CrossRef]
- Jiang, H.; Taranekar, P.; Reynolds, J.R.; Schanze, K.S. Conjugated Polyelectrolytes: Synthesis, Photophysics, and Applications. Angew. Chem. Int. 2009, 48, 4300–4316. [Google Scholar] [CrossRef]
- Mecerreyes, D. Polymeric ionic liquids: Broadening the properties and applications of polyelectrolytes. Prog. Polym. Sci. 2011, 36, 1629–1648. [Google Scholar] [CrossRef]
- Pefferkorn, E. The role of polyelectrolytes in the stabilisation and destabilisation of colloids. Adv. Colloid Interface Sci. 1995, 56, 33–104. [Google Scholar] [CrossRef]
- Hierrezuelo, J.; Sadeghpour, A.; Szilagyi, I.; Vaccaro, A.; Borkovec, M. Electrostatic Stabilization of Charged Colloidal Particles with Adsorbed Polyelectrolytes of Opposite Charge. Langmuir 2010, 26, 15109–15111. [Google Scholar] [CrossRef] [PubMed]
- Szilagyi, I.; Sadeghpour, A.; Borkovec, M. Destabilization of Colloidal Suspensions by Multivalent Ions and Polyelectrolytes: From Screening to Overcharging. Langmuir 2012, 28, 6211–6215. [Google Scholar] [CrossRef] [PubMed]
- Michot, L.J.; Bihannic, I.; Porsch, K.; Maddi, S.; Baravian, C.; Mougel, J.; Levitz, P. Phase Diagrams of Wyoming Na-Montmorillonite Clay. Influence of Particle Anisotropy. Langmuir 2004, 20, 10829–10837. [Google Scholar] [CrossRef]
- Tawari, S.L.; Koch, D.L.; Cohen, C. Electrical Double-Layer Effects on the Brownian Diffusivity and Aggregation Rate of Laponite Clay Particles. J. Colloid Interface Sci. 2001, 240, 54–66. [Google Scholar] [CrossRef]
- Delhorme, M.; Jönsson, B.; Labbez, C. Monte Carlo simulations of a clay inspired model suspension: The role of rim charge. Soft Matter 2012, 8, 9691. [Google Scholar] [CrossRef]
- Jonsson, M.; Linse, P. Polyelectrolyte-macroion complexation. I. Effect of linear charge density, chain length, and macroion charge. J. Chem. Phys. 2001, 115, 3406. [Google Scholar] [CrossRef]
- Jonsson, M.; Linse, P. Polyelectrolyte-macroion complexation. I. Effect of chain flexibility. J. Chem. Phys. 2001, 115, 10975. [Google Scholar] [CrossRef]
- BYK Additives & Instruments. BYK Technical Information B-RI 21 LAPONITE® Performance Additives; BYK Additives & Instruments: Wesel, Germany, 2016. [Google Scholar]
- Jansson, M.; Lenton, S.; Plivelic, T.S.; Skepö, M. Intercalation of cationic peptides within Laponite layered clay minerals in aqueous suspensions: The effect of stoichiometry and charge distance matching. J. Colloid Interface Sci. 2019, 557, 767–776. [Google Scholar] [CrossRef]
- Jönsson, B.; Labbez, C.; Cabane, B. Interaction of Nanometric Clay Platelets. Langmuir 2008, 24, 11406–11413. [Google Scholar] [CrossRef]
- Abraham, M.J.; van der Spoel, D.; Lindahl, E.; Hess, B.; The GROMACS development team. GROMACS User Manual Version 5.0.4. 2014. Available online: www.gromacs.org (accessed on October 2019).
- Gutiérrez, G.; Johansson, B. Molecular Dynamics Study of Structural Properties of Amorphous Al2O3. Phys. Rev. B 2002, 65, 104202. [Google Scholar] [CrossRef]
- Thuresson, A.; Jansson, M.; Plivelic, T.; Skpö, M. Temperature Response of Charged Colloidal Particles by Mixing Counterions Utilizing Ca2+/Na+ Montmorillonite as Model System. J. Phys. Chem. C 2017, 121, 7951–7958. [Google Scholar] [CrossRef]


| System | (/rad) | ||||||
|---|---|---|---|---|---|---|---|
| S.I | 1–16 | −61 | 6 | 1 | 440 | 1 | 0 |
| S.II | 8 | −61 | 6 | 1 | 440–800 | 1 | 0 |
| S.III | 1–16 | −61 | 6 | 1 | 440 | 0.25–1 | 0 |
| S.IV | 1–16 | −61 | 6 | 1 | 440 | 1 | 0–400 |
| S.V | 1–16 | −61 | 6 | 1 | 488 | 1 | 0 |
| S.VI | 1–16 | −61 | 0 | 1 | 488 | 1 | 0 |
| (nm) | |||||
|---|---|---|---|---|---|
| 440 | 1.00 | 1.00 | 8 | 0.13 | 2.21 |
| 488 | 0.90 | 0.90 | 8 | 0.14 | 2.22 |
| 600 | 0.73 | 0.73 | 8 | 0.19 | 2.27 |
| 700 | 0.63 | 0.63 | 8 | 0.37 | 2.41 |
| 800 | 0.55 | 0.55 | 8 | 0.60 | 2.34 |
| 1 | 1.0 | 0.13 | 0.13 | 0.89 | 0.5 | 0.25 | 0.25 | 0.76 | 0.25 | 0.50 | 0.50 | 0.47 |
| 2 | 0.25 | 0.25 | 0.77 | 0.50 | 0.50 | 0.47 | 1.00 | 1.00 | 0.18 | |||
| 4 | 0.50 | 0.50 | 0.66 | 1.00 | 1.00 | 0.15 | 2.00 | 2.00 | 0.39 | |||
| 6 | 0.75 | 0.75 | 0.66 | 1.50 | 1.50 | 0.73 | 3.00 | 2.00 | 0.37 | |||
| 8 | 1.00 | 1.00 | 0.13 | 2.00 | 1.50 | 0.76 | 4.00 | 2.00 | 0.37 | |||
| 10 | 1.25 | 1.25 | 0.65 | 2.50 | 1.00 | 0.76 | 5.00 | 2.00 | 0.36 | |||
| 12 | 1.50 | 1.13 | 0.13 | 3.00 | 1.25 | 0.19 | 6.00 | 2.00 | 0.34 | |||
| 14 | 1.75 | 1.25 | 0.65 | 3.50 | 1.50 | 0.27 | 7.00 | 2.00 | 0.34 | |||
| 16 | 2.00 | 1.25 | 0.65 | 4.00 | 1.50 | 0.26 | 8.00 | 2.00 | 0.36 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jansson, M.; Skepö, M. Polyelectrolyte-Nanoplatelet Complexation: Is It Possible to Predict the State Diagram? Int. J. Mol. Sci. 2019, 20, 6217. https://doi.org/10.3390/ijms20246217
Jansson M, Skepö M. Polyelectrolyte-Nanoplatelet Complexation: Is It Possible to Predict the State Diagram? International Journal of Molecular Sciences. 2019; 20(24):6217. https://doi.org/10.3390/ijms20246217
Chicago/Turabian StyleJansson, Maria, and Marie Skepö. 2019. "Polyelectrolyte-Nanoplatelet Complexation: Is It Possible to Predict the State Diagram?" International Journal of Molecular Sciences 20, no. 24: 6217. https://doi.org/10.3390/ijms20246217
APA StyleJansson, M., & Skepö, M. (2019). Polyelectrolyte-Nanoplatelet Complexation: Is It Possible to Predict the State Diagram? International Journal of Molecular Sciences, 20(24), 6217. https://doi.org/10.3390/ijms20246217






