Abstract
The adsorption of amyloidogenic peptides, amyloid beta 1–40 (Aβ1–40), alpha-synuclein (α-syn), and beta 2 microglobulin (β2m), was attempted over the surface of nano-gold colloidal particles, ranging from d = 10 to 100 nm in diameter (d). The spectroscopic inspection between pH 2 and pH 12 successfully extracted the critical pH point (pHo) at which the color change of the amyloidogenic peptide-coated nano-gold colloids occurred due to aggregation of the nano-gold colloids. The change in surface property caused by the degree of peptide coverage was hypothesized to reflect the ΔpHo, which is the difference in pHo between bare gold colloids and peptide coated gold colloids. The coverage ratio (Θ) for all amyloidogenic peptides over gold colloid of different sizes was extracted by assuming Θ = 0 at ΔpHo = 0. Remarkably, Θ was found to have a nano-gold colloidal size dependence, however, this nano-size dependence was not simply correlated with d. The geometric analysis and simulation of reproducing Θ was conducted by assuming a prolate shape of all amyloidogenic peptides. The simulation concluded that a spiking-out orientation of a prolate was required in order to reproduce the extracted Θ. The involvement of a secondary layer was suggested; this secondary layer was considered to be due to the networking of the peptides. An extracted average distance of networking between adjacent gold colloids supports the binding of peptides as if they are “entangled” and enclosed in an interfacial distance that was found to be approximately 2 nm. The complex nano-size dependence of Θ was explained by available spacing between adjacent prolates. When the secondary layer was formed, Aβ1–40 and α-syn possessed a higher affinity to a partially negative nano-gold colloidal surface. However, β2m peptides tend to interact with each other. This difference was explained by the difference in partial charge distribution over a monomer. Both Aβ1–40 and α-syn are considered to have a partial charge (especially δ+) distribution centering around the prolate axis. The β2m, however, possesses a distorted charge distribution. For a lower Θ (i.e., Θ <0.5), a prolate was assumed to conduct a gyration motion, maintaining the spiking-out orientation to fill in the unoccupied space with a tilting angle ranging between 5° and 58° depending on the nano-scale and peptide coated to the gold colloid.
1. Introduction
The interface of a solid surface and a protein at the nanoscale level are of interests for many applications including material science, biomedical science (e.g., implantation of artificial bones, heart, organs or blood clotting), industry (e.g., the manufacturing of biosensors, bio separation processes, and drug delivery), and research in the development of new materials. The functionalities of peptide coated nanomaterials have remarkably broad applications in areas where nano-size has a very significant effect [1], including nano-light switching devices [2], disease controlling materials combined with DNA [3], DNA sensors [4], control of human cell activity [5], photo dynamic therapy [6], and optical biosensors that quantify heavy metal pollution in water [7]. However, very little is known regarding how the proteins adhere to nanoscale solid surfaces.
Amyloidogenic peptides, such as Aβ1–40 or Aβ1–42, α-synuclein (α-syn), and β2 microglobulin (β2m) are all regarded as hallmark peptides associated with key onset mechanisms of neurodegenerative diseases, such as Alzheimer’s disease or Parkinson’s disease. Because of this, the formation process and characterization of amyloid fibrils have been extensively investigated. Fibrils are usually several hundreds of micrometers in size and consist of pre-fibrils, which are built of unit oligomers. Therefore, the formation of unit oligomers from soluble and nontoxic monomers is regarded as a key intermediate process of fibrillogenesis and is considered to be a reversible process. On the other hand, the formation of fibrils or pre-fibrils are considered non-reversible processes. The nuclei-based pre-fibril formation mechanism is considered to be the most reasonable method for interpreting the fibril formation process. A key stage in this fibrillogenesis is the formation of an intermediate oligomer through a reversible process which then leads to one-direction pre-fibril formation. A major conformational change of the monomer to an intermediate oligomer requires significant protein folding, requiring a Gibbs energy of −10 kcal/mol [8,9,10] based on computational calculations. The most important on-set process of any fibrillogenesis is networking between peptides. Considering that fibrils are formed irreversibly, the networking between peptides must be “effective” and occur due to a strong interaction. However, a direct investigation of this networking process is still lacking.
The PI’s group has been investigating the reversible self-assembly process (i.e., reversible networking process) on amyloidogenic peptide-coated gold colloidal nanoparticles. The peptides are relatively small, amphiphilic (i.e., consists of both hydrophilic and hydrophobic segments) peptides and the temperature/pH conditions for folded/unfolded conformations are well studied. The great advantage of this system is that a monomer peptide can be prepared on the nano-surface by orientating each peptide so that it may undergo the most effective networking process. Peptides are adsorbed over the nano-surface and are used to make connections between two nano-particle surfaces by making networks between peptides. Because of the networking between peptides, the assembly to the gold colloidal aggregates results in a drastic change in a spectroscopic feature, meaning that the networking process can thus be spectroscopically probed. Therefore, this work is viewed as the best prototype system to learn how nanoscale surface potentials interact with a peptide and if a specific structure can be selectively constructed [11,12,13]. Although these peptides eventually form irreversible insoluble amyloid fibrils, initial stages in fibrillogenesis are still reversible processes. We hypothesize that the peptide-peptide networking must be established by an unfolded conformation of each peptide and this unfolded conformation will be strongly enhanced at the nano-particle surface. As observed in negatively charged micelles and Teflon particles, β-sheet formation of Aβ on hydrophobic graphite surfaces [14] or at air–water interfaces [15] indicate an involvement of interfacial surface potential utilized for the conforming intermediate [16,17,18,19,20].
This study aims to clarify (1) an exact attaching sequence or portion of the peptide and (2) orientation of the peptide over the nano-scale surface, and (3) identify the probable conformation of peptides for successful networking. It is well known that the amyloidogenic peptides (e.g., amyloid beta: Aβ; beta 2 microglobulin: β2m; and alpha-synuclein: α-syn) adsorb onto a gold surface through a sulfur atom of a thiol (–SH) group. These amyloidogenic peptides undergo drastic structural changes (protein folding) to form many units of toxic polymers that eventually combine to create a few micron-sized fibers (i.e., amyloid fibrils), which are known to cause neurodegenerative diseases [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35]. However, Aβ and α-syn do not possess any sequences which contain a thiol group (i.e., Cysteine (Cys, C)). Contradicting the lack of a Cys sequence, the existence of gold nano-colloids were reported to enhance peptide-peptide networking using Aβ adsorbed on a nano-gold colloid as a “core” of a fiber [36].
There is no clear explanation of why amyloidogenic peptides adsorb onto gold so effectively. Since the detailed structural information of adsorbed peptides at the “core” is not known, contributing factors to the peptide-peptide networking needs to be fully investigated. This study describes a systematic method used to extract both a plausible peptide orientation and which segments interact with the colloidal surface. Based on these data, in Section 4.3.3 we describe a novel systematic procedure to extract the coverage ratio of peptide (Θ) onto the nano-gold colloids. Quite unexpectedly, the surface coverage conditions appeared to depend somewhat on the nano-particle size. While simulation does not explain the nano-size dependence on surface coverage, the observed trend suggests a plausible “packing” formation of the peptide due to a physical surface area condition.
2. Results
2.1. Extraction of Θ
This hypothesis stating a linear relationship between dpH and ΔpHo was clearly proved to be true when dpH was plotted as a function of ΔpHo for each tested gold colloidal size and in all three amyloidogenic peptides (Aβ1–40, α-syn, and β2m) as shown in Figure 1, while ovalbumin-coated gold colloid did not show any sign of linear relationship [36]. Each data point shown in Figure 1 corresponds to different gold colloidal sizes for a given peptide. It shows that the coverage area is determined by the size of the nano-particle and there must be an equilibrium electrostatic shielding value for a given nano-gold metal surface. The average coverage ratio, Θavg., for each amyloidogenic peptide was extracted as: Θavg (Aβ1–40) = 0.6 ± 0.2, Θavg (α-syn) = 0.6 ± 0.2, and Θavg (β2m) = 0.7 ± 0.2. By using the reported structural data most suited to the conditions of our work, the axial length a and b (a < b) of an approximated prolate for Aβ1–40 [17] α-syn [37], and β2m [38] were initially estimated to be: Aβ1–40 (a, b) = (2.1 nm, 4.1 nm), α-syn (a, b) = (3.1 nm, 8.5 nm), and β2m (a, b) = (2.5 nm, 4.6 nm).
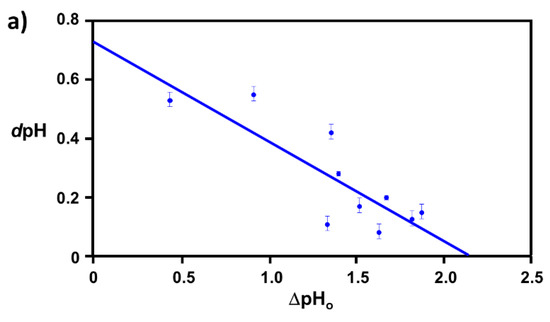

Figure 1.
A hypothesized linear relationship between dpH vs. ΔpHo was plotted for each amyloidogenic peptide-coated nano gold colloid, (a). Aβ1–40 in blue, (b). α-syn in red, and (c).β2m in green based on the values obtained from fitting sigmoidal plot with Equation (1). Each linear line was given as a guide for a correlation between dpH vs. ΔpHo. (dpH = m ΔpHo + b). Supporting information of this figure is available at Supplementary Materials.
2.2. Distance between Colloidal Particles
A representative TEM image of β2m-coated 30 nm gold colloids is shown in Figure 2a. As the magnified image clearly shows, distinct spacing noted as “Δ” between gold colloids were observed. (Figure 2b) The spaces between the gold particles was measured over multiple measurements per image for each size of gold particle and β2m. The morphology of the gold colloidal aggregates coated with Aβ1–40, α-syn, as well as albumin were also studied, and the aggregates formed were more extensive in size and number (size exceeded up to a few microns and the number of gold colloids far exceeded 500 or 1000) than those formed by β2m-coated gold colloid. Therefore, the density of the aggregates by Aβ1–40, as well as albumin coated gold colloid aggregates, extended in the longitudinal direction resulting in preventing the view the section of planar topology. In contrast, β2m formed relatively smaller aggregates, ranging within 500 nm with less than 100 colloids. This allowed us to visualize a two-dimensional view of the aggregate and made it possible to disclose the spacing between two adjacent gold colloids. While the peptide character of the studied peptides is not equivalent, we assume the networking character can be similar. Also, the physical dimension of the networking section compared to the diameter of each colloid can be approximated to be the same. Therefore, the information obtained for β2m will be shown as illustrative for the other two peptide coated gold colloids.

Figure 2.
(a) A TEM (transmission electron microscopy) image of 30 nm gold colloidal particles coated with β2m at pH 4. The scale bar for 100 nm is shown as a guide. (b) A magnified section of the red box showing the diameter of a gold colloid d and the distance between the adjacent colloidal particles (Δ). (Inset): A typical histogram showing the Δ and the observed numbers of the distribution. The distribution was fit by a Gaussian profile and shown by a dotted curve. This histogram is for the β2m-coated 30 nm gold colloid.
The average distances of adjacent nano-gold colloids and the average number of gold nano-particles to form one aggregate for d = 10, 30, 60, and 80 nm particles are summarized in Table 1. We can conclude that the average distance of the adjacent nano-gold colloids was extracted to be 2.0 ± 0.8 nm, indicating insignificant size dependence of the gold colloid and the number of nano-gold colloids forming a cluster.

Table 1.
The average distance, (Δ), of adjacent β2m-coated nano-gold colloids and the average number (η) of gold colloids consisting in an aggregate (gold colloid cluster) at pH 4.0 ± 0.3.
2.3. Simulation of Θ and Orientation
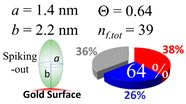
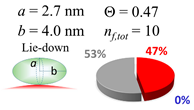
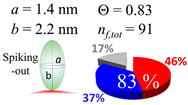
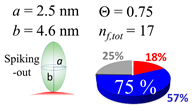
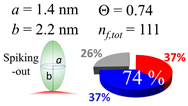
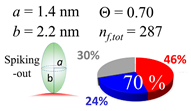
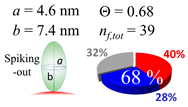
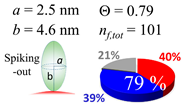
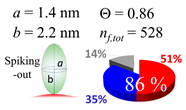
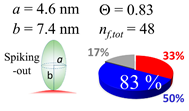
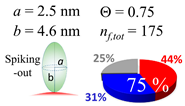
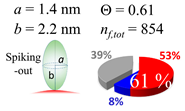
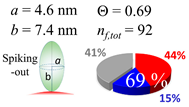
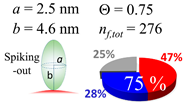
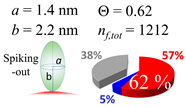
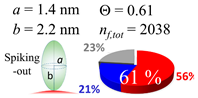
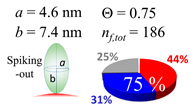
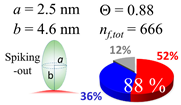
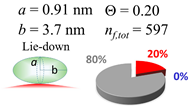
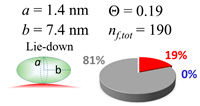
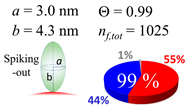
The procedures explained in Section 4.3.3 was applied to analyze the data points shown in Figure 3. The optimized axial lengths of prolate for three amyloidogenic peptides as a function of colloidal size are listed in Table 2. In order to reproduce extracted Θ, the spiking-out orientation need to be utilized for all cases except for d = 100 nm gold coated with Aβ1–40 and α-syn as well as d = 10, 20, 60 nm gold coated with β2m, which exhibited a lie-down orientation. For example, Aβ1–40 coated gold 20 nm diameter showed Θobs = 0.74 for a = 1.4 nm and b = 2.2 nm in order to reach maximum coverage ratio 0.37 under the first layer, Θf,cal, with total number of attached peptides to be ntotal = 111. After the second layer was added, it is calculated to have a maximum of Θs,cal = 0.72. In order to be consistent with the observed Θobs = 0.74, a contribution of the second layer, γ (Θs,cal) should be 0.51, so that Θobs = 0.74 = Θf,cal + γ (Θs,cal) × Θs,cal =0.37 + 0.51 × 0.72=0.37 + 0.37. There was almost no contribution of the second layer when Θobs < 0.5 for d = 100 nm of both Aβ1–40 and α-syn as well as d = 10, 20, and 60 nm for β2m.

Figure 3.
A plot for experimentally obtained Θ for (a) Aβ1–40 in blue (b) α-syn in red, and (c) β2m in green as a function of reported gold diameter d (nm). All data points were extracted by using Equation (2). Each dashed curve line is simulated by a method described in Section 4.3.3 with the parameters tabulate in Table 2. The dotted line shows an upper limit of the Θ value obtained by a single layer model. (d) The over-laid plots of all (a–c) are shown, and indicating (a,b) almost overlay each other.

Table 2.
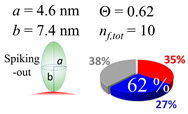
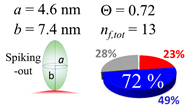
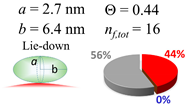
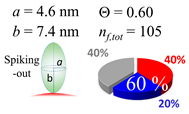
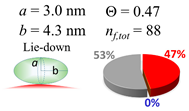
In each box, optimized axial length of a prolate (a and b), the sketches of orientation of adsorption, nf,tot(see Equation (3)), and circular graph indicating % of occupied surface area by adsorption (first layer in red, second layer in blue, and unoccupied in gray) for Aβ1–40, α-syn, and β2m as a function of gold size d (and d) nm.
In summary, as shown in Figure 4, all studied amyloidogenic peptides interacted with nano-gold surface at the original pH where a sample was prepared (~pH 7) with unfolded condition with spiking out condition.

Figure 4.
A picture of an illustrative model and sketch demonstrating a peptide aligning over the surface of a gold colloidal particle with a diameter, d. In the image on the left, the peptide and gold core are both shown with the same color, and a dotted oval indicates a prolate shaped peptide. In the sketch on the right, prolate shaped peptide is shown in blue and the core gold colloid with diameter d is shown in red sphere.
3. Discussions
3.1. Elucidation of Θ and Spectroscopic Measurement
The spectroscopic measurement used in this study exhibits the transition of dispersed peptide-coated gold colloid to aggregated gold colloid through a networking of peptides on the colloidal surface. The surface charge or surface charge potential of each colloid should ideally be neutral, in order to avoid mutual repulsions which would impede aggregation. It is speculated that an aggregation of Aβ1–40 coated gold colloid takes place at an isoelectric point, pI, of Aβ1–40 (pI = 5.2) [39]. If so, a constant pHo (~pI) is expected to be observed regardless of the sizes of gold colloid. However the observed pHo for Aβ1–40 coated gold colloid ranging from d = 10 nm to d = 100 nm scanned between pHo = 4.38 ± 0.06 for d = 100 nm and pHo = 6.20 ± 0.01 for d = 40 nm [40]. The extracted pHo implies the amount of positive charge, i.e., [H3O+], required to neutralize the colloidal surface. This work demonstrated the correlation between ΔpHo and dpH as a key concept in extracting the change of surface charge potential of the gold colloidal particle. Due to the fact that the bare gold colloid possesses surface plasmon (electrons) over its surface, the excess amount of [H3O+] needs to be supplied in order to neutralize the surface. Thus, the ΔpHo shows the difference of the amount of [H3O+] required between bare gold colloid and the peptide-coated gold colloid. Essentially, this means that the ΔpHo indirectly shows the amount of the negative charges quenched due to the attachment of the peptides over the surface and the changing surface charge potential of the colloidal surface.
The measured quantity dpH is defined in a method described in Section 4.3.1. Since λpeak(1) is the first derivative of λpeak(pH), it has the dimension of Δλ/ΔpH (Δλ indicates the wavelength change associated to the transition from a dispersed stage to an aggregated stage, and ΔpH indicates the amount of H3O+ ion needed for that transition). The marking wavelengths λmax and λmin indicate that the colloid is at the aggregated stage (λmax) or at the dispersed stage (λmin). In practice, the marking wavelengths can be treated as dimensionless numbers or as an index (or with arbitrary units), with the replacement of λpeak(1) by ΔΛ/ΔpH, where ΔΛ implies the difference of an index Λ. Overall, dpH indicates an inverse of λpeak(1) and it is proportional to ΔpH, if ΔΛ is treated as a constant. Therefore, because ΔpH ∝ –log Ω and dpH ∝ log Ω, where Ω is a constant associated with charge. Thus, in principle, there should be a linear correlation between dpH and ΔpH.
A. Wang et. al. reported a pH dependence in protein coverage [41], and it is presumable that the surface charge condition is fully influenced by the residual pH condition. This suggests that the peptides start occupying and aggregating at the gold surface as the pH point gets closer to pHo. If this is the case, peptides may not adsorb on the gold surface with our reported Θ values at pH > pHo. However, our work is designed to determine pHo, where the coverage of amyloidogenic peptide was already completed, our approach allows us to extract Θ only at pHo, and it limits a quantitative conclusion regarding the pH dependence of Θ.
3.2. Orientation of the Peptide over the Surface of Gold Colloidal Surface
Relatively high Θ (i.e., Θ >0.5) can be accommodated by filling the surface area with a greater number of smaller unit surface area. Thus, the most supported orientation of the prolates is a spiking-out orientation, as sketched in Figure 5. While a “lie-down” orientation was highly expected to establish more interaction between peptide and the gold surface, the higher coverage was only established by creating a larger amount of smaller contacting areas. As supporting evidence, a very similar orientation was reported by Stellaci’s group for bipolar polymer spiking out of gold nanoparticle sphere [42,43,44,45,46,47,48]. Considering that the gold colloid has a partially negative surface charge, any positively charged sequence can interact with it electrostatically. Since Aβ1–40 coated gold colloid is dissolved in an aqueous solution, hydrophobic segments of Aβ1–40 (sequences 23–40, C-terminal side) must be used for contacting the gold colloidal surface, causing hydrophilic segments of Aβ1–40 (sequences 1–22, N-terminal side) to face outside, making it soluble in water. Among the hydrophobic sequences (23–40), only 28Lysine (28Lys, 28K) can be positively charged at neutral conditions. Therefore, it is hypothesized that –N+– part of the 28Lysine is responsible for contacting on the gold colloidal surface as shown Figure 5.

Figure 5.
The proposed attachment structure of Aβ1–40 over the surface of a gold colloidal particle. At the left top sketch shows the proposed peptide orientation adsorbed over gold nano particle. In the middle the blow up of each peptide with a prolate shape is shown. Inside the prolate, a sketch of Aβ1–40 is shown within a prolate of a = 1.4 nm and b = 2.2 nm. On the top, a blow up and hypothesis of sequences responsible for the adsorption on the gold surface are shown and 28K was speculated to be in a direct contact with gold surface. At the further right, a structure of Lysine (K) is shown and -NH3+ group is estimated to be a central point for an adsorption.
Due to more complexities in structure, identification of binding sites for α-syn and β2m were less clear. Even so, a similar approach and rough estimation of the site is possible. For α-syn, residues 61–95, or the so-called NAC (Non-Aβ Component) region [49,50], is highly likely to be the region where the peptide is bound to the nano-gold surface. More specifically, 80K, 96K, and/or 97K are candidate residues that could be responsible for the colloidal attachment.
In a similar way, however, with a more complex situation, β2m is considered to possess hydrophobic (and aromatic-rich) region in residues 62–70 implying 63R (63Arginine), 66K, or 69H to be a plausible binding sites to the nano-surface [51]. If we assume multiple concurrent contacting spots are available, the mobility of β2m must be reduced and this can separate the binding property of β2m different from the other two peptides. In order to explain a negative correlation observed in Θ vs. Sd plot (Section 3.4), β2m was speculated to be a prolate with negative side facing outward. It is quite likely that the sequence from 50 to 58 are the section responsible for the above-mentioned section since the negatively charged section of 52D (52Aspartic Acid), 54E (54Glutamic Acid), and 56D are located therein.
The current model used for extracting Θ was tested for chicken ovalbumin as an example of a globular protein. There was no correlation found between dpH and ΔpH, and we assume that the model can be applied only for amyloidogenic peptides that clearly exhibits folded and unfolded conformations which are drastically different. Also the section of adsorption site has to be clearly determined no matter which size of the gold colloid was applied, otherwise clear mapping of charge distribution due to peptide (as explained in Section 3.4) cannot be obtained. The prolate shape localizes a partial charge in a relatively smaller region, which can become an adsorption point. In contrast, a globular protein takes a spherical shape creating a broader and more homogeneous partial charge distribution. This results in a less sensitive response in aggregation as a function of pH change, which results in a poorly defined dpH value in Equation (1), and reducing a correlation between ΔpHo and dpH.
3.3. Networking of the Peptide at an Interfacial Area
While the aggregation of Aβ1–40 coated gold colloid develops highly condensed networking which results in the mutual overlapping of gold colloids in both horizontal and latitudinal directions, the aggregation of β2m-coated gold colloid was less condensed, and TEM images enabled us to observe the spacing between adjacent gold colloids (Δ = 1.9 ± 0.7 nm), particularly around the edge area of the aggregates. Since Aβ1–40 and β2m both approximate as prolate tops with similar dimensions, the information on this spacing between adjacent gold colloid can be extrapolated to these two peptide systems. This result implies that the peptide layer covered the gold colloidal surface at a thickness of 0.95 nm [52]. If we consider a monolayer of peptide with spiking-out orientation, the adjacent distance between two gold colloid should correspond to 2b. This assumption strongly contradicts the extracted Δ (~2 nm) since calculated 2b value are 4.4 nm for Aβ1–40, 14.8 nm for α-syn, and 9.2 nm for β2m based on the values shown in Table 2. In order to allow peptides to be constrained within 2 nm spacing, the most probable conformation allows the peptides to be bent or spiraled around each other at the interface. Since amyloidogenic peptides studied in this work are all regarded as disordered proteins, it is reasonable to assume that disordered regions are flexible enough to take best suited configuration including a bent form in order to fit in 2 nm inter-colloidal surfaces. The process of gold colloidal aggregation is summarized as the process of a mixture (interaction) between monomer and gold colloidal surface, followed by the adsorption of each monomer over the nano-colloidal surface, and under acidic pH, the networking of peptides forming the gold colloid aggregation (Figure 6).

Figure 6.
A demonstrative picture of peptides being adsorbed over a surface of gold nano-particle (NP) and adsorption of peptide with spiking out orientation under pH 10 (bottom left) and forming a network with each other in order to form gold colloid aggregates at pH 4 (bottom right). The color of peptide and gold colloid are shown in the same color.
Based on the fact that all experimental observation needs to involve a second layer, we deduce that the first layer is responsible for the coverage of nano-gold surface and the second layer is the result of networking to the first layer of each peptide coated gold colloid. Due to the spiking-out orientation of the first layer, this would leave accessible another site for further networking as the peptide conformation becomes unfolded. The networking between dual peptides at an interface matches with a speculation of a dimer formation concluded in our previous work [53].
3.4. Verification of the Relationship between Physical Displacement and Coverage Ratio
Our first instinct was that Θ was dominated by the molecular interaction between gold surface and peptide’s terminus responsible for an electrostatic interaction. Therefore, the surface field reflecting from the surface curvature would be proportional to molecular interaction and may influence the surface interaction and coverage. However, by assuming that simple term of curvature is proportional to an inverse of radius, we did not see any correlation between a curvature and Θ, as also implied by the complex relationship between Θ and d shown in Figure 4. This implies that at least obvious chemical interaction does not explain the intrinsic reasoning of Θ and its nano-size dependence. While no correlation between the gold colloidal size and its coverage ratio of peptide (Θ) was found in our study, we attempted to find justification of Θ for a given nano-size of gold colloid by using a mathematical approach without involving intermolecular forces. The most simplified explanation of higher or lower coverage is gained from calculating how much space is wasted by a given unit adsorbent. However, the coverage ratio cannot be simply predicted as a function of surface area. For example, if the area to be covered increases, the unit area of an adsorbent may not utilize given space without leaving an unoccupied area, and so the coverage ratio may not increase. The equatorial belt area was used as an index of the effectiveness of space usage, and the spacing between each prolate (Sd) should be correlated with the coverage ratio (Θ). For example, a prolate of Aβ1–40 (a = 1.4 nm and b = 2.2 nm) covering a 40 nm (d = 40.6 nm) has Θ = 0.86), and 100 nm (d = 99.5 nm)has Θ of 0.20. When maximum prolate with dimension of (a = 1.4 nm and b = 2.2 nm) was distributed equatorial belt of each gold colloid, Sd = 0.051 nm for 40 nm with neq = 50 and Sd = 0.012 nm for 100 nm with neq = 175 demonstrating that the larger the Sd, the higher the Θ. A clear correlation between Θ and Sd was confirmed for Aβ1–40 and α-syn as shown in Figure 7a,b as a positive slope for β2m as shown in Figure 7c as a negative slope. The finalized fitting parameters and fitting procedures will be further detailed in a report by Yokoyama and Ichiki [54].
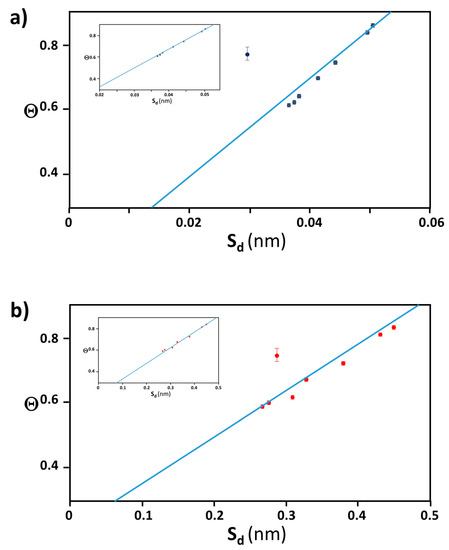

Figure 7.
The best optimized plot of Θ vs. Sd for (a) Aβ1–40 in blue, (b) α-syn in red, and (c) β2m in green, where fitting values for the linear relationship Θ = Φ Sd + ε. In each plot, there was always one deviating data point from the linear trend (d = 80 nm for Aβ1–40 and α-syn, d = 60 nm for β2m), and the insets show the plot when each outlier point was removed. Supporting information of this figure is available at Supplementary Materials.
A positive linear relationship between Θ and Sd is explained by considering that both Aβ1–40 (Figure 8(a-1)) and α-syn (Figure 8(a-2)) are simplified as a prolate with δ+ region at the adsorption side and opposite side (i.e., exposing side to the outward) as sketched in Figure 8(b-1), respectively. As the prolate attaches onto the gold surface through the δ+ region of a prolate, it also creates the δ+ region on the gold surface as indicated in Figure 8(b-1,b-2). So that an extra peptides are more invited for adsorption as the gold surface possesses more δ– region when Sd is longer. On the other hand, if Sd is relatively small, not enough δ– region is available for further adsorption of peptides causing the Θ decreased resulting in the positive linear relationship between Θ and Sd (Figure 8c). As it was speculated before, Aβ1–40 may be adsorbing on to the surface through 28K and α-syn adsorbs on to the surface through 80K or 96K97K. Since those sites are located at relatively close to the N-terminal, it is speculated that δ+ portion of C-terminal side must be exposing outward and away from the colloid surface. As for Aβ1–40, we speculate that 5R6H, 13H14H, or 16K are responsible for distributing δ+ region. The speculated region with δ+ and δ– are indicated by color coded areas in a prolate and bars in sequences as δ+ in blue and δ– in red, respectively (Figure 8(a-1)) As for α-syn, all lysines in the C-terminal region (i.e., 6K, 10K, 12K, 21K, 23K, 32K and 34K) are speculated to be exposing toward the outside and away from the colloidal surface side. While much more information is needed, crude estimation of charge distribution was shown in Figure 8(a-2). In a similar manner as shown in Figure 8(a-1), region with δ+ and δ– are indicated by color coded areas in a prolate and bars in sequences as δ+ in blue and δ– in red, respectively.

Figure 8.
A sketch explaining a positive linear proportionality between Θ vs. Sd, (a) simulation of prolate and charge distribution of Aβ1–40 ((a)-1) and of β2m ((a)-2). The sequences of each peptide are shown with the colored bar indicating δ– (in red) or δ+ (in blue). ((b)-1). A side view of a prolate top peptide with a partially positive side (δ+) of dipole attaching to the partially negative surface (δ–) of gold colloid. An extra prolate dipole attracted for the space of δ–, if Sd has enough length to let an extra prolate in. ((b)-2) The birds eye view of the surface showing area appears as δ– indicated by red is the highly probable are for an extra prolate to be interacted and may lead to an attachment. (c). A graph explaining the expected trend between Θ as a function of Sd.
Opposed to what we observed in Aβ1–40 and α-syn, β2m exhibited a negative linear slope for Θ vs. Sd plot. (Figure 7c). This is interpreted that as each β2m (sketched in Figure 9(b-1)) adsorbs onto the gold surface with δ+ segment as exposing more δ– area to the other side of gold surface as sketched in Figure 9(b-1,b-2). Thus, as Sd decreases, it creates a greater effective attraction to the extra β2m resulting in more coverage (i.e., a negative slope for Θ vs. Sd plot) as shown in Figure 9c. Since the adsorption site of β2m can be speculated to be at relatively toward the C-terminal side (i.e., 63R, 66K, or 69H), the exposing side away from the gold surface is speculated to be N-terminal side. Thus, it is estimated that18E is responsible for providing δ– region. In Figure 9a, region of δ+ and δ– are indicated by color coded areas in a prolate and bars in sequences as δ+ in blue and δ– in red, respectively.

Figure 9.
A sketch explaining negative linear relationship between Θ vs. Sd. (a) simulation of prolate and charge distribution of β2m. The sequences are shown with the colored bar indicating δ– (in red) or δ+ (in blue). ((b)-1). A side view of a prolate top peptide with δ+ side of dipole attaching to δ– surface of gold colloid. Because a distribution of δ– is expected to be spread from the top to the side toward outside, extra prolate is more attracted as more area of δ– is available. ((b)-2). A top view of a focused region in b)-1, where the area appears as δ– as the prolate locate close by shortening of Sd. (c). A graph explaining the expected trend between Θ as a function of Sd,.
In all three cases explained above, we claim that the spiking-out orientation of the first layer established a corresponding charge distribution seen in each peptide coated gold colloid. If the orientation was lie-down orientation, enhancement of self-adsorption would not take place. For example, a lie-down orientation of prolate dipole in the case of Aβ1–40 and α-syn would exhibit a significant amount of δ+ region and not effectively squeeze the prolate dipole with the same orientation. As for the case of β2m, the lie-down orientation exposes a greater amount of δ– region, resulting in a significant repulsion for the peptide attempts to adsorb with the same lie-down orientation.
3.5. Justification of Lower Coverage Ratio and Associated Prolate Shape
While the overall characteristic of the coverage of amyloidogenic peptides was relatively higher value (i.e., Θ ≥ 0.6), there were only five cases when Θ was < 0.5; Aβ1–40 coated d = 100 nm gold, α-syn coated d = 100 nm gold, β2m-coated d = 10, 20, and 60 nm gold. For all cases, the fit was not optimized with a prolate with spiking-out orientation but with lie-down orientation. Under the estimation that the spiking-out orientation is the best orientation to satisfy coverage stability (i.e., effective packing of the surface) and consistent with most of the coverage orientations observed in this experiment. Thus, it is hypothesized that each prolate takes a spiking-out orientation but tilts over the nano-gold surface as shown in Figure 10a and can rotate around the contact point on the nano-gold surface (Figure 10b) resulting in an occupied area with oblate shape as if it takes a lie-down orientation. In order to explain an oval shape occupying over the surface, a gyration type of motion is considered. So that the contact point of the prolate changes due to a change of tilting angle as it rotates over the surface, is plausible (Figure 10c).

Figure 10.
A sketch of the side view of a rotating prolate. (a) The tilting of a prolate over the nano-gold surface and approximation for radius () of the circular plane over the nano surface. Here, θα is a tangential angle between prolate axis and the surface line, and the tilting angle of a prolate against surface plane is given by an angle θτ. (b) A rotational motion of a prolate with a fixed contacting point, resulting in a circular occupied space over the surface. (c) A gyration motion of a prolate with a movable contacting point and tilting angle θτ, resulting in an oval (in green) occupied space with axial length of ag (blue circle) and bg (red circle).
From the geometry shown in Figure 10a, , where θα and θβ are the inner angles as shown in Figure 10a and the length was approximated as because θβ << 1. A tilting angle of a prolate, θτ = 90° – θα. The extracted θα and θβ are listed in Table 3.

Table 3.
The list of extracted tilting angles (θτ and θβ) for the lower coverage for (a) Aβ1–40, (b) α-syn, and (c) β2m. The average tilting angle for each peptide is shown at the bottom for each peptide in (θτ).
An example of extracted gyration motion was demonstrated and sketched in Figure 11 for the case of β2m adsorbed over d = 10 nm gold colloid (d = 9.80 nm). Focusing on one unit of prolate as shown in Figure 11a, the tilting angle, θτ, changes between 26° and 17° as it rotates, which modulates the surface area. The gyration of the prolate should be taking place simultaneously with the other prolates on the same surface as shown in Figure 11b. We cannot, however, deny that a stationary peptide in an unfolded conformation could occupy the space of the same size calculated by gyration motion. There is a possibility of that the adsorption is more randomized and is an ensemble of multiple orientations. For example, J. A. Yang and et. al., reported that α-syn adsorbs on the poly (allylamide hydrochloride) coated gold nanoparticles with random orientation with an increase in β-sheet and decrease in α-helix structure [55].

Figure 11.
(a) The sketch showing the gyration motion of a prolate (a = 2.7 nm and b = 4.0 nm) representing β2m over a gold nano-particle with a diameter of d = 10 nm, where the prolate major axis tilts between 26° and 17° as it rotates over the surface. It results in an oval occupied space with ag = 2.7 nm and bg = 4.0 nm. (See Table 3) (b) The sketch of a gyrating prolate over the nano-gold particle surface.
4. Materials and Methods
4.1. Materials
Lyophilized powder of Aβ1–40 peptide (MW; 4.2 kDa, 98% HPLC purity) and α-syn (MW: 14.4 kDa, purity >95% by SDS-PAGE) were purchased from r-Peptide (Bogart, GA, USA). Aqueous 220 μM stock solution of Aβ1–40 and 64.2 μM stock solution of α-syn were stored at –80 °C. The β2m (MW: 12 kDa/mol, purity >40% by SDS-PAGE) was purchased from AbD Serotec (Raleigh, NC, USA), and aqueous 77.0 μM stock solution was stored at –20 °C. Gold nanoparticles were purchased from Ted Pella, Inc. (Redding, CA, USA) and have the following estimated diameters (d), reported diameter (d), and particles per mL in O.D. (Optical Density, ϑ) where ϑ = 0.2 at 528 nm: d = 10 nm (d = 9.8 ± 1.0 nm, ϑ = 1.4 × 1012 particles mL−1), d = 15 nm (d = 15.2 ± 1.5 nm, ϑ = 2.8 × 1011 particles mL−1), d = 20 nm (d = 19.7 ± 1.1 nm, ϑ = 1.4 × 1011 particles mL−1), d = 30 nm (d = 30.7 ± 1.3 nm, ϑ = 4.0 × 1010 particles mL−1), d = 40 nm (d = 40.6 ± 1.1 nm, ϑ = 1.8 × 1010 particles mL−1), d = 50 nm (d = 51.5 ± 4 nm, ϑ = 8.2 × 109 particles mL−1), d = 60 nm (d = 60 ± 1.0 nm, ϑ = 4.3 × 109 particles mL−1), d = 80 nm (d = 80 ± 1.0 nm, ϑ = 2.2 × 109 particles mL−1), and d = 100 nm (d = 99.5 ± 1.3 nm, ϑ = 1.6 × 109 particles mL−1). The residual components in each colloidal particle can be regarded as identical. In order to maintain stability of the nano-gold colloids against salts, deionized and distilled water were used to prepare all aqueous solutions. All sizes of gold colloids were formed by Frens derived citrate reduction method possessing traces of citrate <10−5%, tannic acid <10−7% and potassium carbonate <10−8%. Thus, the observed size dependence in this study was not determined by the stabilizer of the gold colloids.12 The optimized ratio between all peptides and gold nanoparticles was set as 1000:1 so that the concentration of gold nanoparticles was roughly 300 pM [39]. Attachment of peptides to the gold colloidal surface was known to be achieved almost instantaneously and considered to reach equilibrium within a minute. The pH range of the solutions (between pH 2 and pH 12) was achieved by adding either HCl or NaOH to the solution. The UV–Vis absorption spectra were monitored between 200 and 800 nm as the pH value varied by an increment of 0.05 pH to acidic conditions.
4.2. TEM Imaging
The TEM (Transmission Electron Microscopy) experiment was conducted for β2m as well as for ovalbumin, Aβ1–40, and α-syn. The β2m samples were prepared with 2.8 μL of β2m stock aqueous solution mixed with 280 μL of gold colloids ranging between 10 nm, 30 nm, 60 nm, and 80 nm in diameter, with pH ranging from 6.5 to 7.5. Before plating on the grid, the sample pH was adjusted to either pH 10 or pH 4 under room temperature. 1 μL of the mixture was then plated onto Formvar Copper Film 400 Grids Mesh. The samples were incubated on the grid for two minutes, after which excess solution was removed from the grid with filter paper. All TEM images were collected on a Morgagni model 268 TEM (FEI Co., Hillsboro, OR, USA) operated at 80 kV and were taken under both 28,000× and 71,000× magnification using a model XR-40 four-megapixel CCD Digital camera. TEM image analysis was performed by converting the image to data consisting of pixel coordinates and corresponding color index using Image J. The threshold in color index was set to recognize the group of pixels corresponding to the gold particles and the average size of the gold particles, the distance between adjacent gold particles, ratio of the area occupied by the gold particles (occupancy, %), and the total numbers of gold particles were calculated. The β2m-coated gold colloid formed relatively small aggregates as opposed to ovalbumin or Aβ1–40. The number of gold colloidal particles was extracted by individually counting each particle rather than using the “occupancy” method. Because each gold colloid was easily identified for the β2m-coated gold colloid, in many cases, the space between each gold colloids in each aggregate were observed. In this study, the space between gold particles was focused and its distance was extensively analyzed whenever space between colloids was identified. Using the length of a pixel for calibration, the number of pixels between the colloids was transformed into nanometers. The distribution of the observed length in nm was fit with a Gaussian profile and the average distance was extracted.
4.3. Methods
4.3.1. pH-Dependent UV–Vis Absorption Band
Our group has been investigating the reversible self-assembly process of amyloidogenic peptide-coated colloidal gold nanoparticles extensively. These peptides are relatively small, amphiphilic peptides whose temperature/pH conditions for folded/unfolded conformations are well studied. Therefore, it has been viewed as a useful prototype system to learn how nanoscale surface potentials interact with a peptide, and if a specific oligomeric structure can be selectively constructed [11,12,13]. Although these peptides eventually form irreversible insoluble amyloids, the initial stage is still a reversible process. In temperature-dependent reversible processes [53], we found that a reversible process between folded and unfolded conformation took place under Aβ1–40 coated 20 nm gold colloid as pH externally changed well above or well below a critical pH point (pHo). The value of pHo for Aβ1–40 coated 20 nm gold was found to be pHo = 5.45 ± 0.05 at 20 °C, and a reversible process was observed between pH = 4 and pH 10. at 18 ± 0. 2 °C and above. Between 18 ± 0.2 °C and 6 ± 0.2 °C, only Aβ1–40 coated 30 nm gold colloid exhibited a reversible process. Under 6 ± 0.2 °C, only Aβ1–40 coated 40 nm gold colloid supported a reversible process between folded and unfolded conformations. The results from molecular dynamics (MD) calculations on Aβ10–35 suggested the temperature ranges are stable for dimer or trimer formation [56]. For example, the stable dimer formation temperature range matched with the temperature range of reversible process observed for Aβ1–40 coated 20 nm gold colloid (≥~18 °C). The trimers were predicted to be stable at the relatively lower temperature range, which reasonably matches temperature ranges for the reversible process over 30 or 40 nm gold colloid’s surface (i.e., <18 °C). Also, the stable temperature for trimer formation was in good agreement with the temperature range of the reversible process observed for Aβ1–40 coated 30 nm or 40 nm gold colloids. Since unfolded conformation leading to oligomerization is formed at only lower pH value than pHo, we concluded that this is evidence that oligomeric dimer units over 20 nm gold colloid particles or trimer units over 30 or 40 nm gold colloid particles were produced over a nano-gold colloidal surface at pH 4 [53]. The key intermediate oligomeric form in the reversible process has not been well studied due to its instability. We hypothesize that the activation energy required to form an intermediate oligomer can be gained from the nano-metal surface potential. While metastable folding intermediates (i.e., the oligomer form) for a folding pathway has been suggested and detected in solution [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71], a direct identification of an exact oligomer has not been shown. Oligomer observed in negatively charged micelles and Teflon particles, β-sheet formation of Aβ on hydrophobic graphite surfaces [14], or at air–water interfaces [15] indicate an involvement of interfacial surface potential utilized for the conforming intermediate [16,17,18,19,20]. Our group has established a way to reproduce and control the reversible self-assembly of Aβ on spherical gold nanoparticles. The average absorption peak shift (λpeak) at room temperature (Figure 12a) is plotted as a function of the continuous operation of an external pH change (Figure 12b). The value of λpeak corresponds to the color of the solution, which in turn corresponds to the morphology of the gold colloid aggregates. When the colloids assemble in an aggregated form at pH 4, the mixture is a blue color with λpeak ~650 nm or above. On the other hand, the gold colloids are widely dispersed at pH 10, and exhibit a reddish color with λpeak ~525 nm. Therefore, a repetitive pH change enables Aβ1–40 coated 20 nm gold colloid to exhibit an oscillating feature of λpeak between 525 nm and 625 nm as they reversibly form dispersed and aggregate forms, respectively.
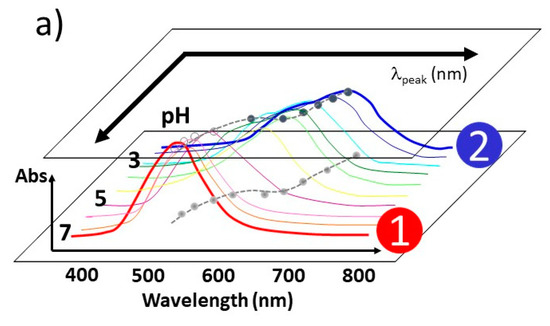

Figure 12.
A schematic diagram explaining the spectral analysis and construction of sigmoidal plots. (a) The average peak position of SPR, λpeak, was monitored as a function of the pH condition for both bare gold nano-particles and peptide-coated nano gold colloids. The λpeak was extracted by utilizing the method described in Section 4.3.1. Two representative spectrum marked by ① and ② represent that under pH 7 and pH 2, respectively. (b) The constructed sigmoidal plot was fit with the Boltzmann formula shown in Equation (1). Both dpH and ΔpHo were obtained. Here, the sigmoidal plot i indicates that of bare gold colloid, and the sigmoidal plot ii is a typical plot observed for amyloidogenic peptide coated gold nano-particles. The upper colored bar shows the corresponding solution color for regions ① and ②.
Each absorption spectrum was fit by the “Peak Fit” program in Origin (Version 9.5) and peak positions of i-th band (λi) and peak area of each band of i-th component were extracted (Ai). The observed band average peak position is correlated with the surface plasmon resonance (SPR) of gold colloids, and the peak position of the absorption band depends on the conformation of peptide attached on the gold colloidal surface. The folded or unfolded conformation can be prepared by setting the solution to be basic or acidic, respectively. When the solution is acidic, the absorption band commonly has two or more components. Thus, the average peak position, λpeak(pH), of the SPR band at given pH is extracted by the weighted average of two components as , where λi(pH) and ai(pH) are the peak position and fraction of the i-th component band, and the fraction ai was determined by the fraction of the area (Ai) of the band to the total area of the entire bands as: .
Then, the average peak position was surveyed as a function of pH, and the position of the peaks were plotted as a function of pH, as shown in Figure 12b. The constructed sigmoidal plot was then analyzed and fit with a Boltzmann formula (Equation (1)) as shown in Figure 12b.
The λmin and λmax stand for the minimum and maximum of the band peak positions, respectively. Here, pHo shows the pH where color change takes place, and λpeak (pHo) = (λ min + λ max)/2. Also, dpH = (λmax – λmin)/4λpeak(1), where λpeak(1) is the first derivative of the λpeak(pH).
λpeak(pH) = [λmin − λmax]/{1 + exp[(pH − pH0)/dpH]} + λmax
Absorption of a collective excitation of the electrons at the interface between a conductor and an insulator is hypothesized to account for the color of suspensions of these particles [72,73,74]. If the net anionic sites of the metal surface are neutralized by acid, aggregation should be enhanced, resulting in a color change from red to blue. As coverage increases, a shielding effect shifts pHo to the higher value. This ultimately means that greater coverage of peptide requires a less acidic condition to neutralize the surface. Bare gold colloids change their colors at lower pHs (pH < 4.5) while a peptide-coated colloidal surface shows a color change at pH = 4.5~6 depending on the degree of coverage. This pHo value change between bare gold and protein coated gold solution is direct evidence of protein adsorption on the metal colloid.
4.3.2. Correlation Relation between ΔpHo and dpH and Extraction of Coverage Ratio
As the protein covers more of the colloidal surface, a less negative net ionic charge can be achieved. In other words, the negative charge is partially quenched due to the coverage of the peptide over the gold surface. This indicates that a less acidic condition is required to neutralize the colloidal surface.
Assuming a linear relationship (i.e., y = mx = b, where m is a slope and b is an intercept), all data points are fit along the formula given by dpH = m ΔpHo + b, where dpH corresponds to y and ΔpHo corresponds to x in the above linear relationship as shown in Figure 13. We hypothesize that ΔpHo directly relates to the peptide coverage fraction, Θ, since ΔpHo exhibits the surface character change between peptide coated gold colloid and bare gold colloid. Thus, ΔpHo = 0 corresponds to Θ = 0 (i.e., no peptide coverage or bare gold colloid), and the x-axis intercept of dpH = m ΔpHo + b indicates the maximum value of ΔpHo, which occurs when Θ = 1 at dpH = 0 (i.e., λpeak (1) ~∞). The maximum coverage, therefore, can be achieved at the ΔpHo value given by . By replacing ΔpHo (max.) with Θ = 1, any Θ values in between ΔpHo = 0 and ΔpHo (max.) can then be calculated by

Figure 13.
For each amyloidogenic peptide, dpH obtained by Equation (1) by analyzing each sigmoidal plot (See Figure 12b) was plotted as a function of ΔpHo. The coverage ratio, Θ, for each gold colloidal size was obtained by scaling the data point, based on the x-axis intercept Θ =1 (See Equation (2)) Each data point corresponds to different nano-gold colloidal size and was obtained by analyzing sigmoidal plot shown in Figure 12b) for bare gold and amyloidogenic peptide coated gold.
4.3.3. Simulation Process for Calculating the Coverage Fraction
A full explanation of a simulation procedure of calculating peptide coverage fraction, Θ, will be described in a report by Yokoyama and Ichiki [54]. In this paper, an essential concepts for calculating Θ are briefly presented.
The adsorption orientation of a prolate (axial length of a and b, a < b) was selected from either spiking-out orientation (Figure 14a top) or lie-down orientation (Figure 14a bottom). In spiking-out orientation, b-axis of a prolate contacts tangentially at a nano-gold surface. On the other hand, in lie-down orientation, a-axis of a prolate contacts tangentially at a nano-gold surface. An area projected on the sphere surface as an occupying area (Asphere) is Asphere = πa2 for spiking-out orientation and Asphere = πab for lie-down orientation. Once adsorption orientation was selected, the numbers of adsorption points were calculated for the first layer and the second layer.

Figure 14.
(a) Sketches of two possible orientation of prolate and corresponding occupying area are shown. Top: spiking out orientation and occupying πa 2 on the surface. Bottom: lie-down orientation and occupying πab on the surface. (b) For spiking-out orientation, a procedure of counting total number of adsorption points for the first layer (nf,tot) and for the second layer (ns, tot) are shown. The nf,tot is an addition of top (nf,top) and bottom (nf,bot) adsorption points of a sphere, maximum adsorption position at equatorial positions (nf,eq), and the adsorption point along axial axis nf, ax added along each equatorial position j for a semi-sphere. For the second layer, the total number of adsorption points (ns,tot) is given by a summation of total number of equatorial adsorption position over a sphere of second layer (ns,,eq) and total number of adsorption points associated with axial positions, where total adsorption points of each axial line (ns,ax) is counted for each equatorial position of second layer, j.
For the first layer, the total adsorption points (nf,tot) is a sum of a top and a bottom spot of a sphere (nf,top and nf,bot), equatorial spots (nf,eq), and both hemi-sphere’s axial position for each equatorial spot j (nf,ax,j) as:
As for the second layer, avoiding the adsorption points taken by the first layer, the total adsorption points (ns,tot) are given by
where equatorial spots (ns,eq), and both hemi-sphere’s axial position for each equatorial spot j (ns,ax,j) are counted over a sphere corresponds to a second layer. The axial length a and b (a > b) of an approximated prolate for Aβ1–40 [17], α-synuclein [37] and β2m [38] are estimated to be: Aβ1–40 (a, b) = (2.1 nm, 4.1 nm), α-syn (a, b) = (2.9 nm, 6.0 nm), and β2m (a, b) = (2.1 nm, 4.6 nm). Each colloidal particle is approximated to be a sphere with diameter d (radius r = d/2).
In order to reproduce observed Θ, Θobs (= Θtotal), a combination of the first and second layers were calculated by Equation (5).
where Θf, total is a fraction of coverage contributed from the first layer, Θs, total is a fraction of coverage contributed from the second layer, and γ is an empirical factor indicating the weight of the second layer. Each of Θf, total and Θs, total is determined by Equation (6) and Equation (7), respectively.
Θtotal = Θf, total + γ Θs,total
Here, Aprolate indicates an area projected on the sphere surface as an occupying area. The areas to be covered for the first and the second layer are represented by Af,sphere and As,sphere, respectively. The values of Af,sphere and As,sphere are different depending the adsorption orientation. The total adsorption point for the first layer (nf,tot) and the second layer (ns,tot) are illustrated in Figure 14b and detailed in Equation (3) and (4), respectively.
5. Conclusions
The surface properties of nano-gold colloidal surfaces due to adsorption of amyloidogenic peptides were successfully monitored and characterized by observing the response of spectroscopic features as a function of an external pH change. This surface property change was found to be linearly correlated with the coverage ratio of the peptide onto the colloid, Θ. With the simplification of the space occupied by a peptide into a prolate, the Θ could be extracted through a simplified tessellation logic applied for a sphere. The simulation suggested that a prolate needs to have a spiking-out orientation with representative prolate axial length of (a, b) = (1.4 nm, 2.2 nm) for Aβ1–40, (a, b) = (4.6 nm, 7.4 nm) for α-syn, and (a, b) = (2.5 nm, 4.6 nm) for β2m. Of note, these values were similar to the values estimated by the reported protein structural data. However, the above-mentioned prolate dimensions could not reproduce the cases when Θ is less than ~0.50. A lower Θ is required to have less unit coverage area; this increase of unit area was interpreted as a gyration motion of each peptide, which kept a fixed contact spot but changed the tilting angle. The average tilting angle of the prolate was (θτ) (Aβ1–40) = 35 ± 2°, (θτ) (α-syn) = 18 ± 2°, and (θτ) (β2m) = 29 ± 6°, indicating that when the colloid coverage ratio is below 0.5 a prolate can possess high degree of freedom in mobility while still maintaining a high level of interaction with the gold nano-particle surface. At the same time, it indicated many other possibilities of conformation including multiple contacting points or an ensemble of different adsorption orientations. The resulting Θ was fully explained by a relationship between the distances of each unit monomer under a given colloidal area. However, the degree of affinity for a second layer required us to account for the distribution of partially positive charge (δ+) over a peptide. The segment possesses a δ+ that was considered to be highly used when Aβ1–40 and α-syn each interacted with a nano-gold colloidal surface. This possesses a distribution of centering around the prolate axis. On the other hand, the δ+ of β2m was used to interact with each monomer, and the charge distribution was spread around with a distortion, resulting in a high exposure for the counter acting monomer. Therefore, it guided us to predict that β2m possesses different charge distributions than Aβ1–40 and α-syn, and sequences or sections of peptide corresponding to δ+ or δ– thus postulated. In closing, we demonstrated that nano-scale geometrical simulation with a simplified protein structure (i.e., prolate) successfully represents peptide adsorption orientation, providing insights into interfacial conformation and indicating the presence of electrostatic intermolecular and interfacial interactions for these pathophysiologic peptide cases.
Supplementary Materials
Supplementary materials can be found at https://www.mdpi.com/1422-0067/20/21/5354/s1.
Author Contributions
Conceptualization, K.Y.; methodology, K.Y. and E.D.; software, K.Y. and J.J.; validation, K.Y., and A.I.; formal analysis, K.Y., K.B., P.S., J.J., E.D., N.R., J.B., I.D., and A.I.; investigation, K.Y., K.B., J.J. and A.I.; resources, K.Y., I.D., and A.I.; data curation, K.Y.; writing—original draft preparation, K.Y.; writing—review and editing, K.Y., J.B., N.R., and A.I.; visualization, K.Y., E.D., and N.R.; supervision, K.Y.; project administration, K.Y.; funding acquisition, K.Y.
Funding
This research received no external funding.
Acknowledgments
We are grateful for the support by Geneseo Foundation at the initial stage of this project. Ishan Deshmukh and Akane Ichiki thank for the gracious support by SUNY Geneseo Chemistry Department Alumni Summer Research Scholarship. We also thank Jonathan Bourne for helpful discussion during preparation of this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Norde, W. BioInterface Perspective-My voyage of discovery to proteins in flatland and beyond. Colloids Surf. B Biointerfaces 2008, 61, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Cook, N.P.; Kilpatrick, K.; Segatori, L.; Martí, A.A. Detection of α-Synuclein Amyloidogenic Aggregates in Vitro and in Cells using Light-Switching Dipyridophenazine Ruthenium(II) Complexes. J. Am. Chem. Soc. 2012, 134, 20776–20782. [Google Scholar] [CrossRef] [PubMed]
- Muangchuen, A.; Chaumpluk, P.; Suriyasomboon, A.; Ekgasit, S. Colorimetric detection of Ehrlichia canis via nucleic acid hybridization in gold nano-colloids. Sensors 2014, 14, 14472–14487. [Google Scholar] [CrossRef] [PubMed]
- Rasheed, P.A.; Sandhyarani, N. Femtomolar level detection of BRCA1 gene using a gold nanoparticle labeled sandwich type DNA sensor. Colloids Surf. B Biointerfaces 2014, 1, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Suarasan, S.; Focsan, M.; Soritau, O.; Maniu, D.; Astilean, S. One-pot, green synthesis of gold nanoparticles by gelatin and investigation of their biological effects on Osteoblast cells. Colloids Surf. B Biointerfaces 2015, 32, 122–131. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Yu, K.; Li, L.; Zhang, T.; Guan, Z.; Gao, N.; Yuan, P.; Li, S.; Yao, S.Q.; Xu, Q.H.; et al. Gold nanorod enhanced two-photon excitation fluorescence of photosensitizers for two-photon imaging and photodynamic therapy. ACS Appl. Mater. Interfaces 2014, 6, 2700–2708. [Google Scholar] [CrossRef]
- Politi, J.; Spadavecchia, J.; Iodice, M.; De Stefano, L. Oligopeptide–heavy metal interaction monitoring by hybrid gold nanoparticle based assay. Analyst 2015, 140, 149–155. [Google Scholar] [CrossRef]
- Heinz, H.; Farmer, B.L.; Pandey, R.B.; Slocik, J.M.; Patnaik, S.S.; Pachter, R.; Naik, R.R. Nature of Molecular Interactions of Peptides with Gold, Palladium, and Pd-Au Bimetal Surfaces in Aqueous Solution. J. Am. Chem. Soc. 2009, 131, 9704–9714. [Google Scholar] [CrossRef]
- Heinz, H.; Vaia, R.A.; Farmer, B.L.; Naik, R.R. Accurate Simulation of Surfaces and Interfaces of Face-Centered Cubic Metals Using 12-6 and 9-6 Lennard-Jones Potentials. J. Phys. Chem. C 2008, 112, 17281–17290. [Google Scholar] [CrossRef]
- Venditti, I.; Hassanein, T.F.; Fratoddi, I.; Fontana, L.; Battocchio, C.; Rinaldi, F.; Carafa, M.; Marianecci, C.; Diociaiuti, M.; Agostinelli, E.; et al. Bioconjugation of gold-polymer core-shell nanoparticles with bovine serum amine oxidase for biomedical applications. Colloids Surf. B Biointerfaces. 2015, 134, 314–321. [Google Scholar] [CrossRef]
- Yokoyama, K. Nanoscale Surface Size Dependence in Protein Conjugation. In Advances in Nanotechnology; Chen, E.J., Peng, N., Eds.; Nova Science Publishing: Hauppauge, NY, USA, 2010; pp. 65–104. [Google Scholar]
- Yokoyama, K. Modeling of Reversible Protein Conjugation on Nanoscale Surface. In Computational Nanotechnology: Modeling and Applications with MATLAB; Musa, S.M., Ed.; CRC Press-Taylor and Francis Group, LLC: Boca Raton, FL, USA, 2011; pp. 381–410. [Google Scholar]
- Yokoyama, K. Nano Size Dependent Properties of Colloidal Surfaces. In Colloids: Classification, Properties and Applications; Ray, P.C., Ed.; Nova Science Publishing: Hauppauge, NY, USA, 2012; pp. 25–58. [Google Scholar]
- Kowalewski, T.; Holtzman, D.M. In situ atomic force microscopy study of Alzheimer’s beta-amyloid peptide on different substrates: New insights into mechanism of beta-sheet formation. Proc. Natl. Acad. Sci. USA 1999, 96, 3688–3693. [Google Scholar] [CrossRef] [PubMed]
- Schladitz, C.; Vieira, E.P.; Hermel, H.; Mohwald, H. Amyloid-beta-sheet formation at the air-water interface. Biophys. J. 1999, 77, 3305–3310. [Google Scholar] [CrossRef]
- Kusumoto, Y.; Lomakin, A.; Teplow, D.B.; Benedek, G.B. Temperature dependence of amyloid beta-protein fibrillization. Proc. Natl. Acad. Sci. USA 1998, 95, 12277–12282. [Google Scholar] [CrossRef] [PubMed]
- Coles, M.; Bicknell, W.; Watson, A.A.; Fairlie, D.P.; Craik, D.J. Solution structure of amyloid beta-peptide(1–40) in a water-micelle environment. Is the membranespanning domain where we think it is? Biochemistry 1998, 37, 11064–11077. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.Y.; Jao, S.C.; Ma, K.; Zagorski, M.G. Solution structures of micelle-bound amyloid beta-(1–40) and beta-(1–42) peptides of Alzheimer’s disease. J. Mol. Biol. 1999, 285, 755–773. [Google Scholar] [CrossRef]
- Giacomelli, C.E.; Norde, W. Conformational changes of the amyloid beta-peptide(1-40) adsorbed on solid surfaces. Macromol. Biosci. 2005, 5, 401–407. [Google Scholar] [CrossRef]
- Rocha, S.; Krastev, R.; Thunemann, A.F.; Pereira, M.C.; Mohwald, H.; Brezesinski, G. Adsorption of amyloid beta-peptide at polymer surfaces: A neutron reflectivity study. Chem. Phys. Chem. 2005, 6, 2527–2534. [Google Scholar] [CrossRef]
- Moshe, A.; Landau, M.; Eisenberg, D. Preparation of Crystalline Samples of Amyloid Fibrils and Oligomers. Methods Mol. Biol. 2016, 1345, 201–210. [Google Scholar]
- Scarff, C.A.; Ashcroft, A.E.; Radford, S.E. Characterization of Amyloid Oligomers by Electrospray Ionization-Ion Mobility Spectrometry-Mass Spectrometry (ESI-IMS-MS). Methods Mol. Biol. 2016, 1345, 115–132. [Google Scholar]
- Pujol-Pina, R.; Vilapriny-Pascual, S.; Mazzucato, R.; Arcella, A.; Vilaseca, M.; Orozco, M.; Carulla, N. SDS-PAGE analysis of Aβ oligomers is disserving research into Alzheimer’s disease: Appealing for ESI-IM-MS. Sci. Rep. 2015, 5, 14809–14821. [Google Scholar]
- El-Shimy, I.A.; Heikal, O.A.; Hamdi, N. Minocycline attenuates Aβ oligomers-induced pro-inflammatory phenotype in primary microglia while enhancing Aβ fibrils phagocytosis. Neurosci. Lett. 2015, 609, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Attanasio, F.; Convertino, M.; Magno, A.; Caflisch, A.; Corazza, A.; Haridas, H.; Esposito, G.; Cataldo, S.; Pignataro, B.; Milardi, D.; et al. Carnosine Inhibits Ab42 Aggregation by Perturbing the HBond Network in and around the Central Hydrophobic Cluster. ChemBioChem 2013, 14, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Aliaga, L.; Cai, H. α-synuclein, LRRK2 and their interplay in Parkinson’s disease. Future Neurol. 2012, 7, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Paslawski, W.; Andreasen, M.; Nielsen, S.B.; Lorenzen, N.; Thomsen, K.; Kaspersen, J.D.; Pedersen, J.S.; Otzen, D.E. High Stability and Cooperative Unfolding of α-Synuclein Oligomers. Biochemistry 2014, 53, 6252–6263. [Google Scholar] [CrossRef]
- Pchelina, N.; Nuzhnyi, E.P.; Emelyanov, A.K.; Boukinac, T.M.; Usenko, T.S.; Nikolaev, M.A.; Salogub, G.N.; Yakimovskii, A.F.; Zakharova, E.Y. Increased plasma oligomeric alpha-synuclein in patients withlysosomal storage diseases. Neurosci. Lett. 2014, 583, 188–193. [Google Scholar] [CrossRef]
- van Rooijen, B.D.; Claessens, M.M.A.E.; Subramaniam, V. Lipid bilayer disruption by oligomeric α-synuclein depends on bilayer charge and accessibility of the hydrophobic core. Biochim. Biophys. Acta 2009, 1788, 1271–1278. [Google Scholar] [CrossRef]
- Vasudevaraiu, P.; Guerrero, E.; Hegda, M.L.; Collen, T.B.; Britton, G.B.; Rao, K.S. New evidence on alpha-synuclein and Tau binding to conformation and sequence specific GC* rich DNA: Relevance to neurological disorders. J. Pharm. Bioallied Sci. 2012, 4, 112–117. [Google Scholar]
- Comellas, G.; Lemkau, L.R.; Zhou, D.H.; George, J.M.; Rienstra, C.M. Structural Intermediates during α-Synuclein Fibrillogenesis on Phospholipid Vesicles. J. Am. Chem. Soc. 2012, 134, 5090–5099. [Google Scholar] [CrossRef]
- Fecchio, C.; De Franceschi, G.; Relini, A.; Greggio, E.; Dalla Serra, M.; Bubacco, L.; de Laureto, P.P. α-Synuclein Oligomers Induced by Docosahexaenoic Acid Affect Membrane Integrity. PLoS ONE 2013, 8, 1–12. [Google Scholar] [CrossRef]
- Esposito, G.; Garvey, M.; Alverdi, V.; Pettirossi, F.; Corazza, A.; Fogolari, F.; Polano, M.; Mangione, P.P.; Giorgetti, S.; Stoppini, M.; et al. Monitoring the Interaction between β2-Microglobulin and the Molecular Chaperone alpha B-crystallin by NMR and Mass Spectrometry: α B-Crystallin dissociates β2-Microglobulin Oligomers. J. Biol. Chem. 2013, 288, 17844–17858. [Google Scholar] [CrossRef]
- Esposito, G.; Corazza, A.; Bellotti, V. Pathological Self-Aggregation of β2-Microglobulin: A Challenge for Protein Biophysics. In Protein Aggregation and Fibrillogenesis in Cerebral and Systemic Amyloid Disease, Subcellular Biochemistry; Harris, J.R., Ed.; Springer: Berlin, Germany, 2012; Volume 65, pp. 165–182. [Google Scholar]
- Mustata, M.; Capone, R.; Jang, H.; Arce, F.T.; Ramachandran, S.; Lal, R.; Nussinov, R. K3 fragment of amyloidogenic β2-microglobulin forms ion channels: Implication for dialysis related amyloidosis. J. Am. Chem Soc. 2009, 131, 14938–14945. [Google Scholar] [CrossRef]
- Yokoyama, K.; Catalfamo, C.D.; Yuan, M. Reversible Peptide Oligomerization over Nanosclae Gold Surfaces. Aims Biophys. 2015, 2, 679–695. [Google Scholar] [CrossRef]
- Ulmer, T.S.; Bax, A.; Cole, N.B.; Nussbaum, R.L. Strcture and dynamics of micelle-bound human α-synuclein. J. Biol. Chem. 2005, 280, 9595–9603. [Google Scholar] [CrossRef] [PubMed]
- Verdone, G.; Corazza, A.; Viglino, P.; Pettirossi, F.; Giorgetti, S.; Mangione, P.; Andreola, A.; Stoppini, M.; Bellotti, V.; Esposito, G. The solution structure of human beta2-microglobulin reveals the prodromes of its amyloid transition. Protein Sci. 2002, 11, 487–499. [Google Scholar] [CrossRef] [PubMed]
- Yokoyama, K.; Welchons, D.R. The conjugation of amyloid beta protein on the gold colloidal nanoparticles’ surfaces. Nanotechnology 2007, 18, 105101–105107. [Google Scholar] [CrossRef]
- Yokoyama, K.; Briglio, N.M.; Sri Hartati, D.; Tsang, S.M.W.; MacCormac, J.E.; Welchons, D.R. Nanoscale size dependence in the conjugation of amyloid beta and ovalbumin proteins on the surface of gold colloidal particles. Nanotechnology 2008, 19, 375101–375108. [Google Scholar] [CrossRef]
- Wang, A.; Perera, Y.R.; Davidson, M.B.; Fitzkee, N.C. Electrostatic Interactions and Protein Competition Reveal a Dynamic Surface in Gold Nanoparticle–Protein Adsorption. J. Phys. Chem. C 2016, 120, 24231–24239. [Google Scholar] [CrossRef]
- Kuna, J.J.; Voïtchovsky, K.; Singh, C.; Jiang, H.; Mwenifumbo, S.; Ghorai, P.K.; Stevens, M.M.; Glotzer, S.C.; Stellacci, F. The effect of nanometre-scale structure on interfacial energy. Nat. Mater. 2009, 8, 837–842. [Google Scholar] [CrossRef]
- DeVries, G.A.; Brunnbauer, M.; Hu, Y.; Jackson, A.M.; Long, B.; Neltner, B.T.; Uzun, O.; Wunsch, B.H.; Stellacci, F. Divalent Metal Nanoparticles. Science 2007, 315, 358–361. [Google Scholar] [CrossRef]
- Jackson, A.M.; Myerson, J.W.; Stellacci, F. Spontaneous assembly of subnanometreordered domains in the ligand shell of monolayer-protected nanoparticles. Nat. Mater. 2004, 3, 330–336. [Google Scholar] [CrossRef]
- Singh, C.; Ghorai, P.K.; Horsch, M.A.; Jackson, A.M.; Larson, R.G.; Stellacci, F.; Glotzer, S.C. Entropy-Mediated Patterning of Surfactant-Coated Nanoparticles and Surfaces. Phys. Rev. Lett. 2007, 99, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Uzun, O.; Hu, Y.; Hu, Y.; Han, H.-S.; Watson, N.; Chen, S.; Irvine, D.J.; Stellacci, F. Surface-structure-regulated cell-membrane penetration by monolayer-protected nanoparticles. Nat. Mater. 2008, 7, 588–595. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Liu, X.; Akbulut, O.; Hu, J.; Suib, S.L.; Kong, J.; Stellacci, F. Superwetting nanowire membranes for selective absorption. Nat. Nanotechnol. 2008, 3, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Voı¨tchovsky, K.; Kuna, J.J.; Contera, S.A.; Tosatti, E.; Stellacci, F. Direct mapping of the solid–liquid adhesion energy with subnanometre resolution. Nat. Nanotechnol. 2010, 5, 401–405. [Google Scholar] [CrossRef]
- Davidson, W.S.; Jonas, A.; Clayton, D.F.; George, J.M. Stabilization of alpha-synuclein secondary structure upon binding to synthetic membranes. J. Biol. Chem. 1998, 273, 9443–9449. [Google Scholar] [CrossRef]
- George, J.M.; Jin, H.; Woods, W.S.; Clayton, D.F. Characterization of a novel protein regulated during the critical period for song learning in the zebra finch. Neuron 1995, 15, 361–372. [Google Scholar] [CrossRef]
- Platt, G.W.; Routledge, K.E.; Homans, S.W.; Radford, S.E. Fibril Growth Kinetics Reveal a Region of β2-microglobulin Important for Nucleation and Elongation of Aggregation. J. Mol. Biol. 2008, 378, 251–263. [Google Scholar] [CrossRef]
- D’Ambrosio, E.; Ralbovsky, N.; Yokoyama, K. Direct probing of the reversible selfassembly of amyloid beta peptide oligomers over nanoscale metal colloidal surfaces. In Proceedings of the 251st ACS National Meeting & Exposition, San Diego, CA, USA, March 13–17 2016. [Google Scholar]
- Yokoyama, K.; Gaulin, N.B.; Cho, H.; Briglio, N.M. Temperature Dependence of Conjugation of Amyloid Beta Peptide on the Gold Colloidal Nanoparticles. J. Phys. Chem. A 2010, 114, 1521–1528. [Google Scholar] [CrossRef]
- Yokoyama, K.; Ichiki, A. Peptide adsorption orientation. In Oligomerization; NOVA Science Publisher; In Preparation.
- Yang, J.A.; Johnson, B.J.; Wu, S.; Woods, W.S.; George, J.M.; Murphy, C.J. Study of Wild-Type α-Synuclein Binding and Orientation on Gold Nanoparticles. Langmuir 2013, 29, 4603–4615. [Google Scholar] [CrossRef]
- Jang, S.; Shin, S. Computational study on the structural diversity of amyloid beta peptide (Aβ10–35) Oligomers. J. Phys. Chem. B 2008, 112, 3479–3484. [Google Scholar] [CrossRef]
- Fraser, P.E.; Nguyen, J.T.; Surewicz, W.K.; Kirschner, D.A. pH-dependent structural transitions of Alzheimer amyloid peptides. Biophys. J. 1991, 60, 1190–1201. [Google Scholar] [CrossRef]
- Shen, C.L.; Scott, G.L.; Merchant, F.; Murphy, R.M. Light scattering analysis of fibril growth from the amino-terminal fragment beta(1-28) of beta-amyloid peptide. Biophys. J. 1993, 65, 2383–2395. [Google Scholar] [CrossRef]
- Inouye, H.; Fraser, P.E.; Kirshner, D.A. Structure of -crystallite assemblies formed by Alzheimer-amyloid protein analogues: Analysis by X-ray diffraction. Biophys. J. 1993, 64, 502–519. [Google Scholar] [CrossRef]
- Lomakin, A.; Chung, D.S.; Benedek, G.B.; Kirshner, D.A.; Teplow, D.B. On the nucleation and growth of amyloid -protein fibrils: Detection of nuclei and quantitation of rate constants. Proc. Natl. Acad. Sci. USA 1996, 93, 1125–1129. [Google Scholar] [CrossRef]
- Vine, H.L. Soluble multimeric Alzheimer (1-40) pre-amyloid complexes in dilute solution. Neurobiol. Aging 1995, 16, 755–764. [Google Scholar]
- Kuo, Y.M.; Emmerling, M.R.; Vigo-Pelfrey, C.; Kasunic, T.C.; Kirkpatrick, J.B.; Murdoch, G.H.; Ball, M.J.; Roher, A.E. Water-soluble A (N-40, N-42) oligomers in normal and Alzheimer disease brains. J. Biol. Chem. 1996, 271, 4077–4081. [Google Scholar] [CrossRef]
- Lambert, M.P.; Barlow, A.K.; Chromy, B.A.; Edwards, C.; Freed, R.; Liosatos, M.; Morgan, T.E.; Rozovsky, I.; Trommer, B.; Viola, K.L.; et al. Diffusible, nonfibrillar ligands derived from A 1-42 are potent central nervous system neurotoxins. Proc. Natl. Acad. Sci. USA 1998, 95, 6448–6453. [Google Scholar] [CrossRef]
- Teller, J.K.; Russo, C.; DeBusk, L.M.; Angelini, G.; Zaccheo, D.; Dagna-Bricarelli, F.; Scartezzini, P.; Bertolini, S.; Mann, D.M.; Tabaton, M.; et al. Presence of soluble amyloid beta-peptide precedes amyloid plaque formation in Down’s syndrome. Nat. Med. 1996, 2, 93–95. [Google Scholar] [CrossRef]
- Huang, T.H.J.; Yang, D.S.; Plaskos, N.P.; Go, S.; Yip, C.M.; Fraser, P.E.; Chakrabartty, A. Structural studies of soluble oligomers of the Alzheimer beta-amyloid peptide. J. Mol. Biol. 2000, 297, 73–87. [Google Scholar] [CrossRef]
- Garzon-Rodriguez, W.; Sepulveda-Bacerra, M.; Milton, S.; Glable, C.G. Soluble amyloid A-(1-40) exists as a stable dimer at low concentrations. J. Biol. Chem. 1997, 272, 21037–21044. [Google Scholar] [CrossRef]
- Barrow, C.J.; Zagorski, M.G. Solution structures of peptide and its constituent fragments: Relation to amyloid deposition. Science 1991, 253, 179–182. [Google Scholar] [CrossRef] [PubMed]
- Barrow, C.J.; Yasuda, A.; Kenny, P.T.; Zagorski, M.G. Solution conformations and aggregational properties of synthetic amyloid beta-peptides of Alzheimer’s disease. Analysis of circular dichroism spectra. J. Mol. Biol. 1992, 225, 1075–1093. [Google Scholar] [CrossRef]
- Zagorski, M.G.; Barrow, C.J. NMR studies of amyloid beta-peptides: Proton assignments, secondary structure, and mechanism of an alpha-helix----beta-sheet conversion for a homologous, 28-residue, N-terminal fragment. Biochemistry 1992, 31, 5621–5631. [Google Scholar] [CrossRef] [PubMed]
- Walsh, D.M.; Lomakin, A.; Benedek, G.B.; Condron, M.M.; Teplow, D.B. Amyloid -protein fibrillogenesis. J. Biol. Chem. 1997, 272, 22364–22372. [Google Scholar] [CrossRef]
- Crawford, F.; Soto, C.; Suo, Z.; Fang, C.; Parker, T.; Sawar, A.; Frangione, B.; Mullan, M. Alzheimer’s -amyloid vasoactivity: Identification of a novel -amyloid conformational intermediate. FEBS Lett. 1998, 436, 445–448. [Google Scholar] [CrossRef]
- Link, S.; El-Sayed, M. Spectral properties and relaxation dynamics of surface plasmon electronic oscillations in gold and silver nanodots and nanorods. J. Phys. Chem. B 1999, 103, 8410–8426. [Google Scholar] [CrossRef]
- Kelly, K.L.; Coronado, E.; Zhao, L.L.; Schatz, G.C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J. Phys. Chem. B 2003, 107, 668–677. [Google Scholar] [CrossRef]
- Jensen, T.R.; Schatz, G.C.; Van Duyne, R.P. Nanosphere lithography: Surface plasmon resonance spectrum of a periodic array of silver nanoparticles by ultraviolet–visible extinction spectroscopy and electrodynamic modeling. J. Phys. Chem. B 1999, 103, 2394–2401. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).