Future Preventive Gene Therapy of Polygenic Diseases from a Population Genetics Perspective
Abstract
1. Introduction
2. Results
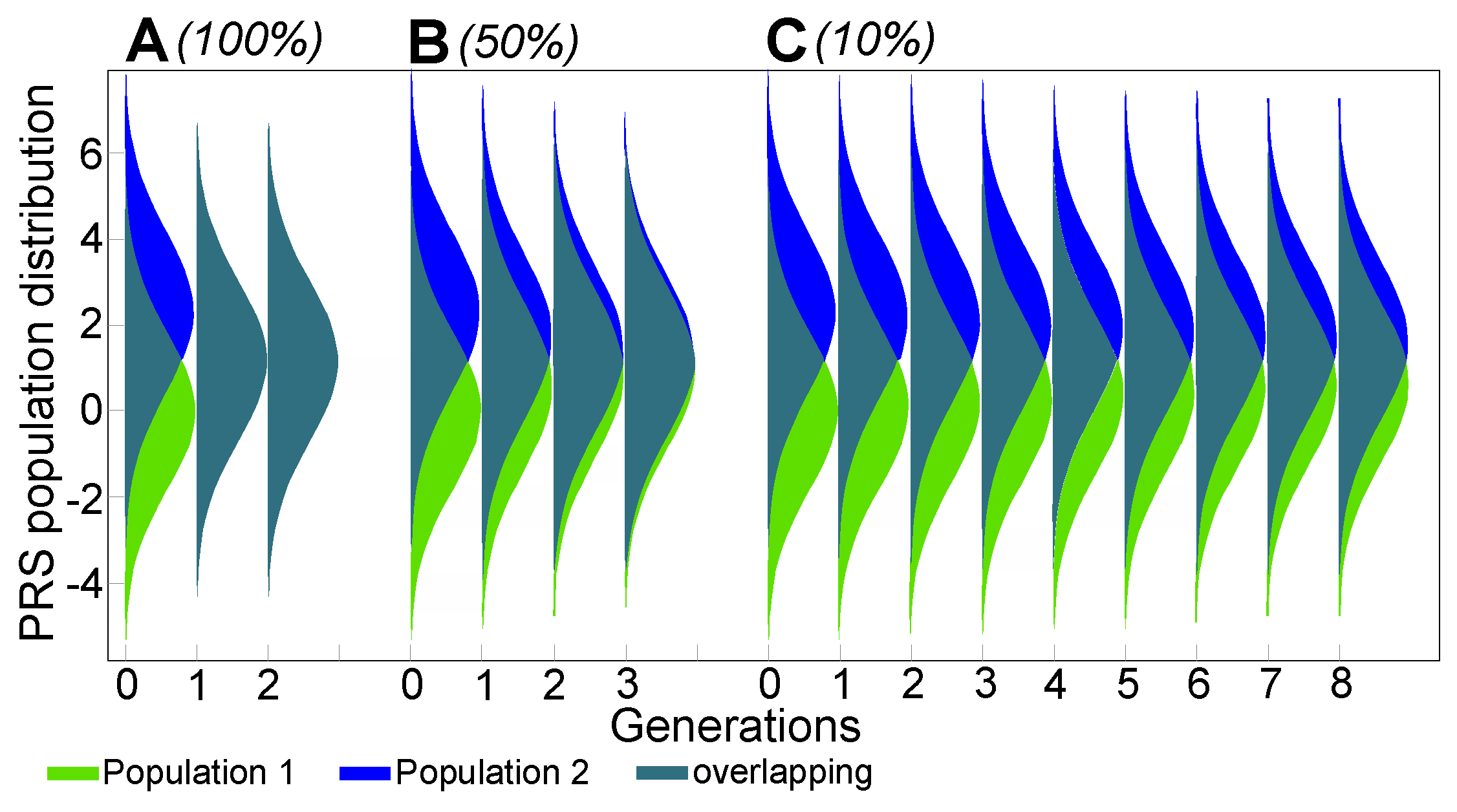
2.1. Admixture of Populations with Matching Mean PRSs: To What Extent Can Causal Risk Alleles of Polygenic Diseases Differ between Populations?
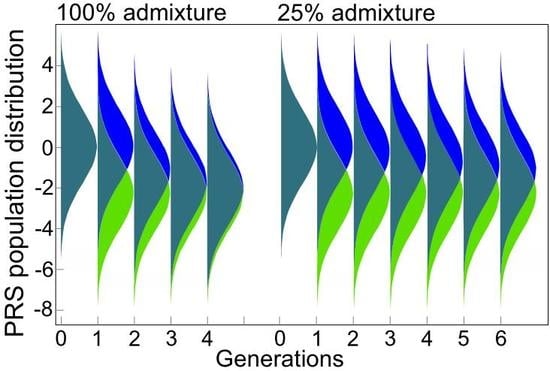
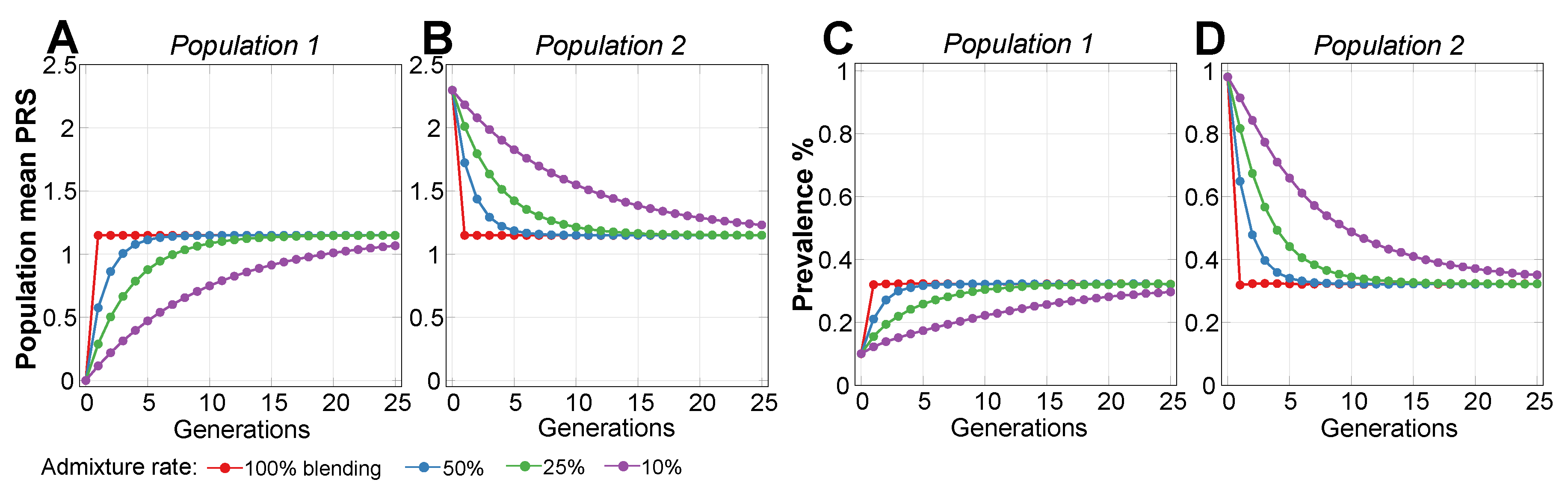
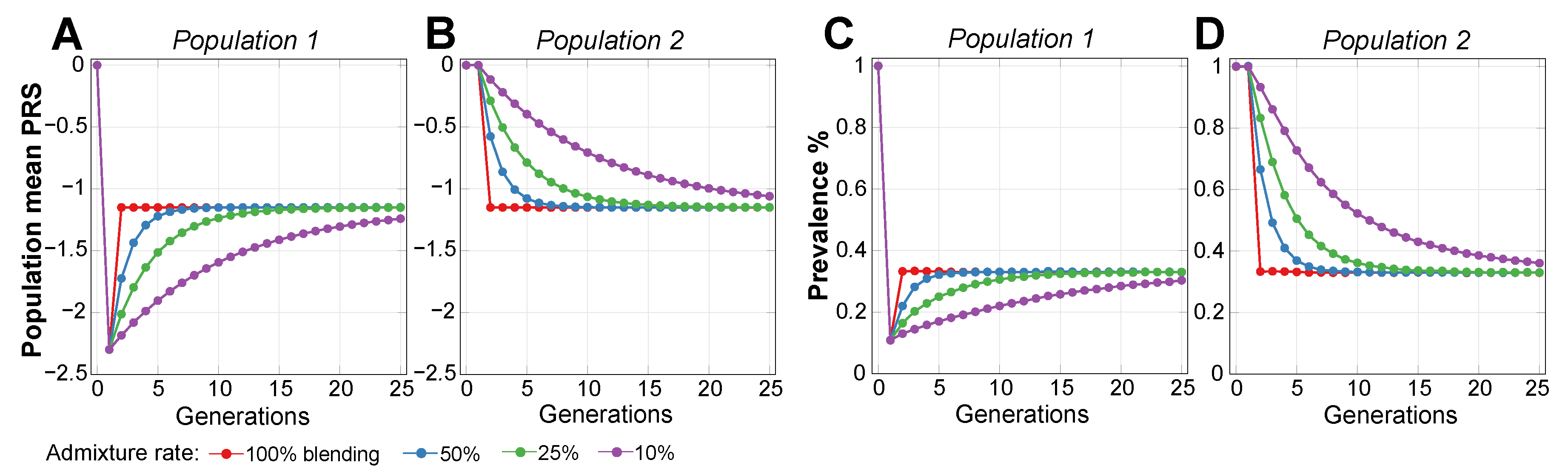
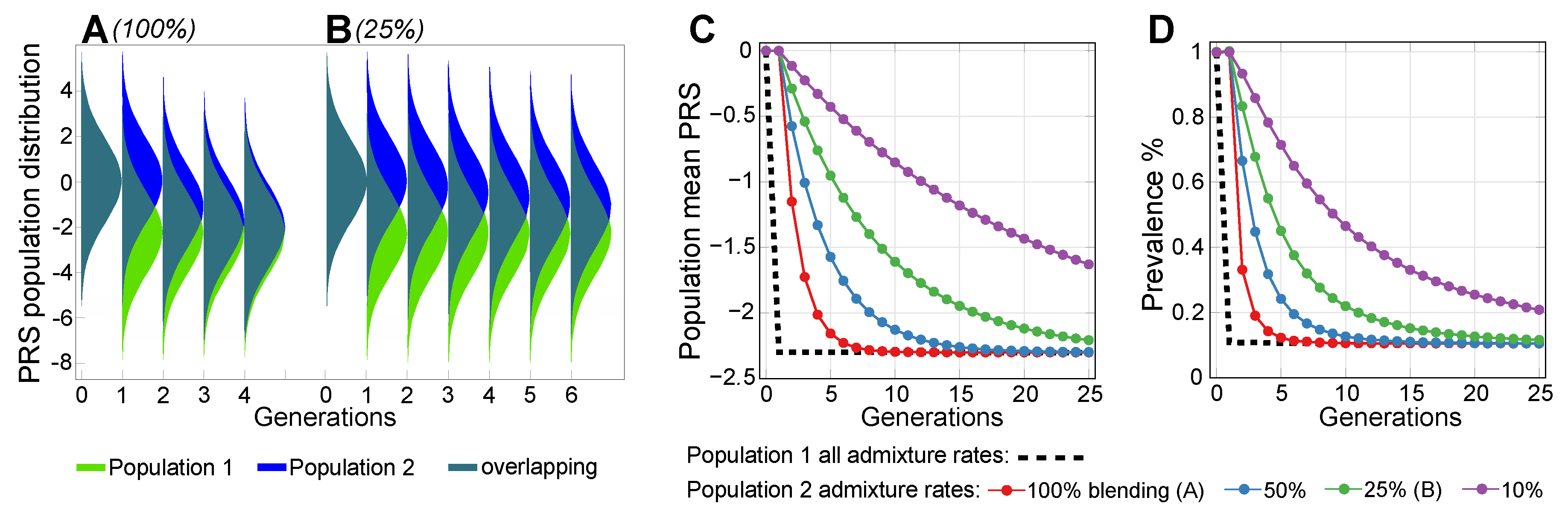
2.2. Admixture of Populations with Differing PRSs
2.3. Lowering Polygenic Disease Prevalence by Editing Effect SNPs
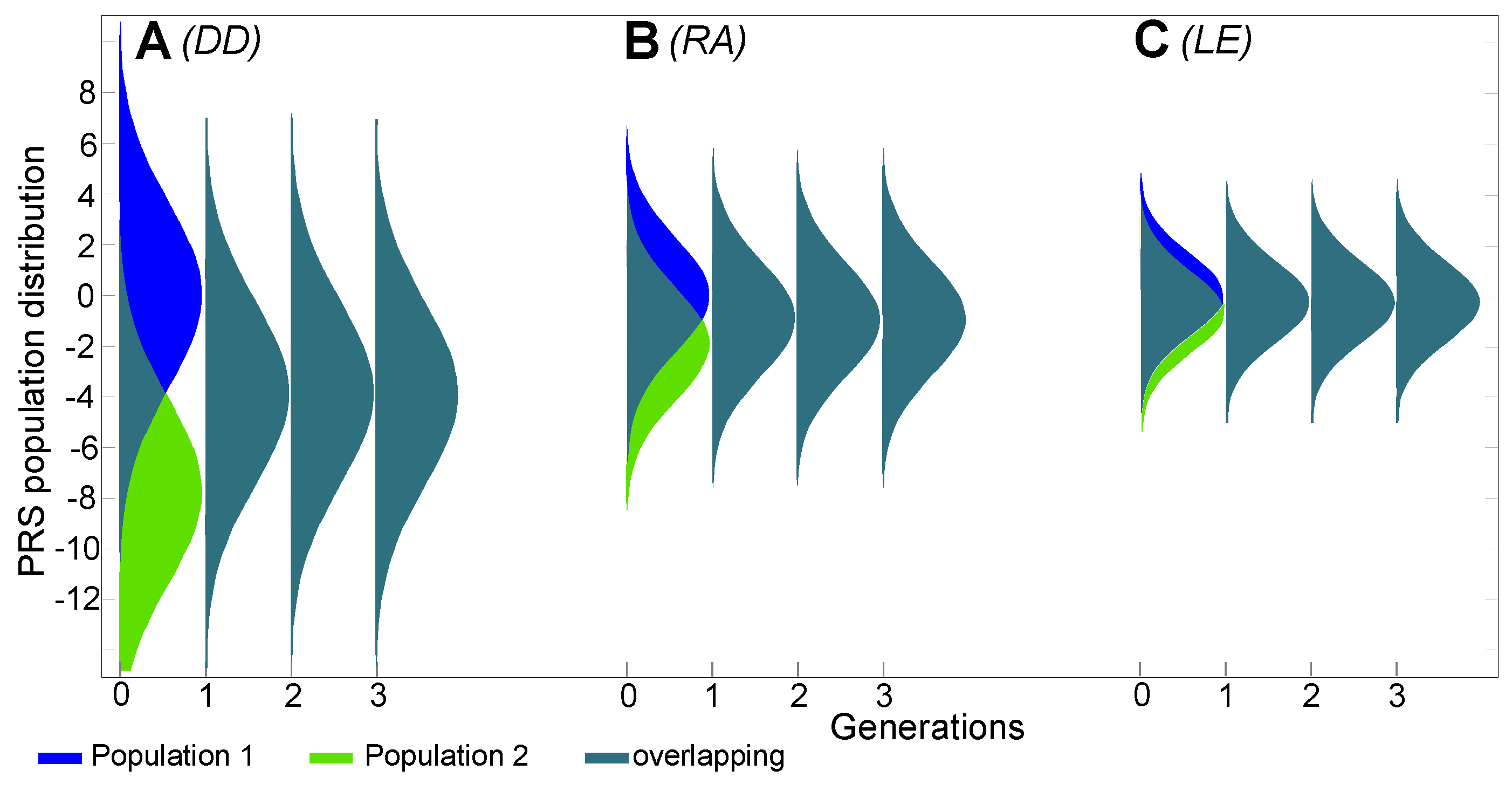
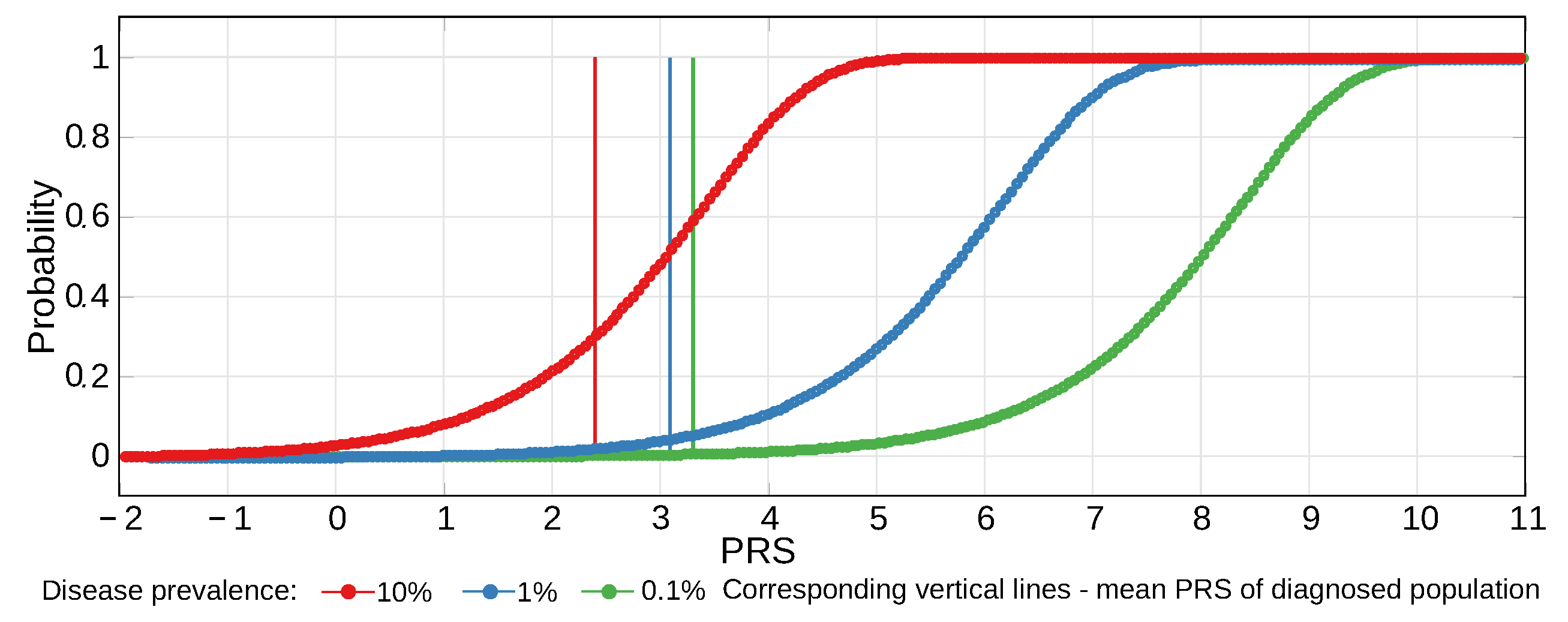
2.4. Estimates of Population Genomic Parameters for Diseases Known to Have Large Risk Differences between Ethnic Groups
2.5. An Estimate of Preventive Gene Therapy for Early- to Middle-Age-Onset Polygenic Diseases
3. Discussion
4. Methods
4.1. Considerations for Liability Threshold Models
4.2. Conceptual Summary
4.3. Allele Genetic Architecture
4.4. Disease Prevalence Analysis
4.5. Simulating Gene Therapy under Population Stratification and Admixture Scenarios
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AD | Alzheimer’s disease |
| AFD | allele frequency difference statistic [97] |
| CAD | coronary artery disease |
| DD | Dupuytren’s disease |
| EMOD | Early- to Middle-age-Onset polygenic Disease |
| Fst | F-statistics, originally conceived as te fixation index by Wright, implemented here using Hudson’s method [96] |
| GRS | genetic risk score; used synonymously with polygenic risk score, abbreviated below |
| GWAS | genome-wide association study |
| LE | lupus erythematosus |
| LOD | late-onset disease; herein, analyzed LODs are exclusively polygenic |
| MAF | minor allele frequency; customarily implies the effect allele frequency |
| OR | odds ratio |
| PRS | polygenic risk score; in this study, a normalized sum of logarithms of additional relative risk conferred by causal alleles |
| RA | rheumatoid arthritis |
| RR | relative risk or risk ratio |
| SNP | single nucleotide polymorphism; in the context of this study, SNP is used synonymously with the term ’allele’ |
| T2D | type 2 diabetes |
| WGS | whole genome sequencing ff |
Appendix A. Ancillary Chapters and Figures
Appendix A.1. Population Stratification and Admixture from the Perspective of Polygenic Disease Risk
Appendix A.2. A Concise Summary of Gene-Editing Techniques
Appendix A.3. Implementation of Common Low-Effect Genetic Architecture
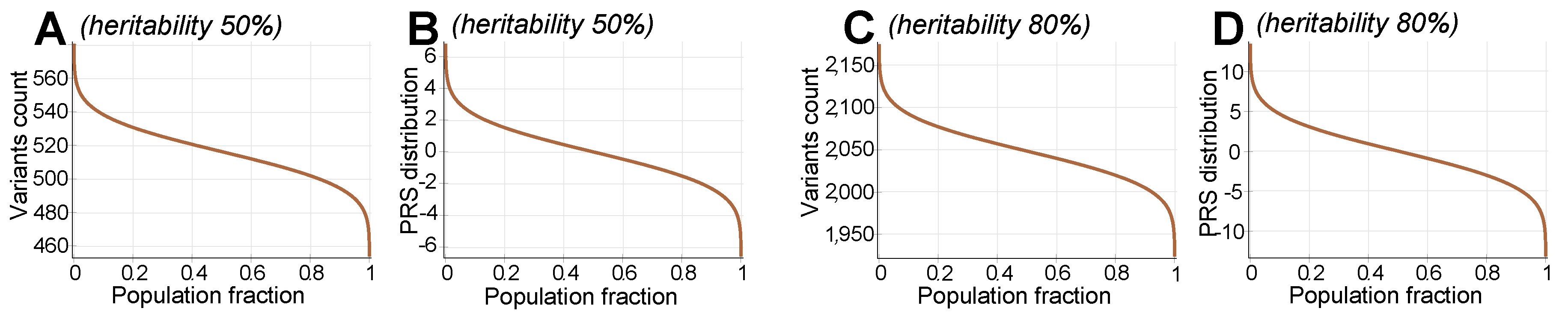
Appendix A.4. Ancillary Figures
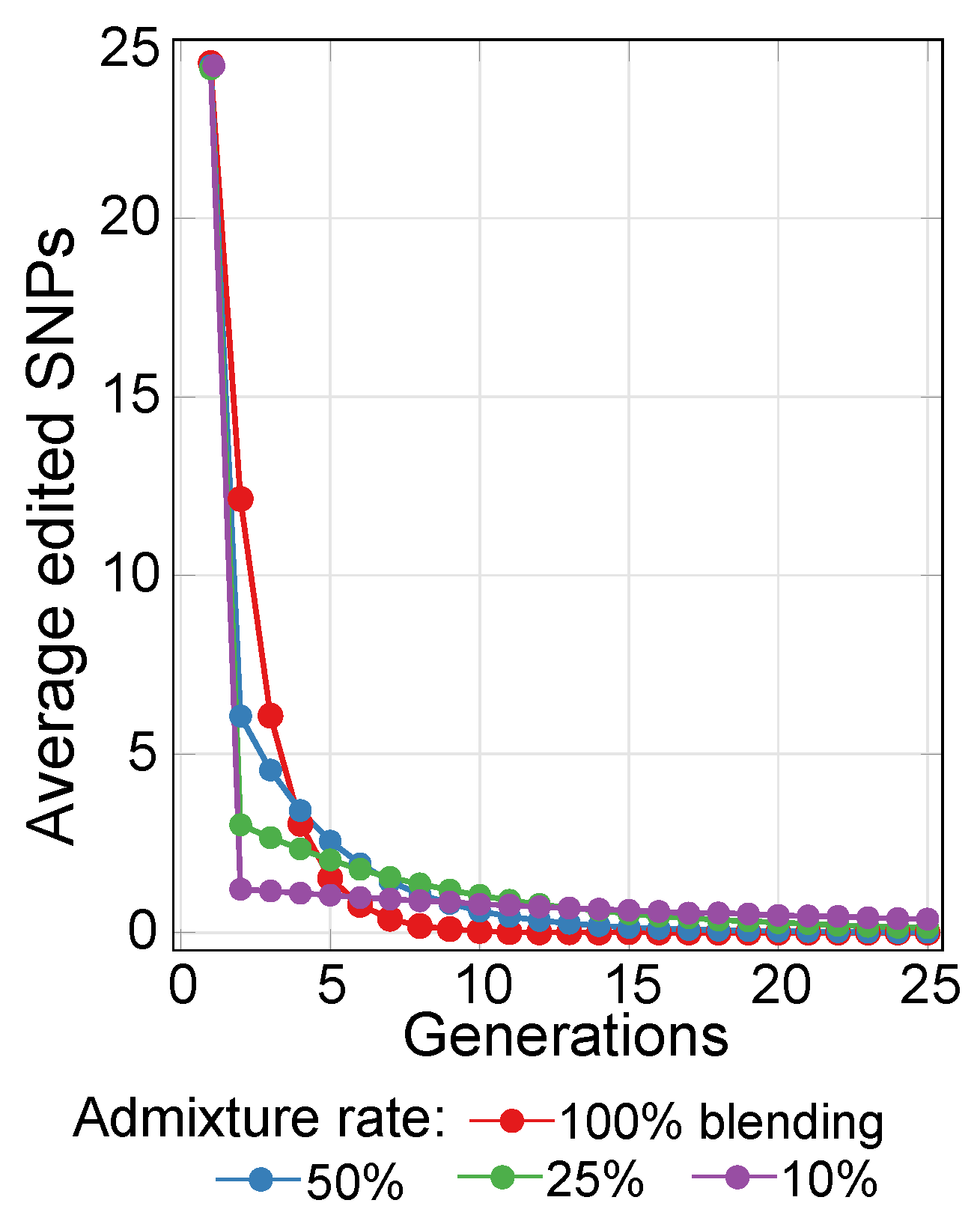
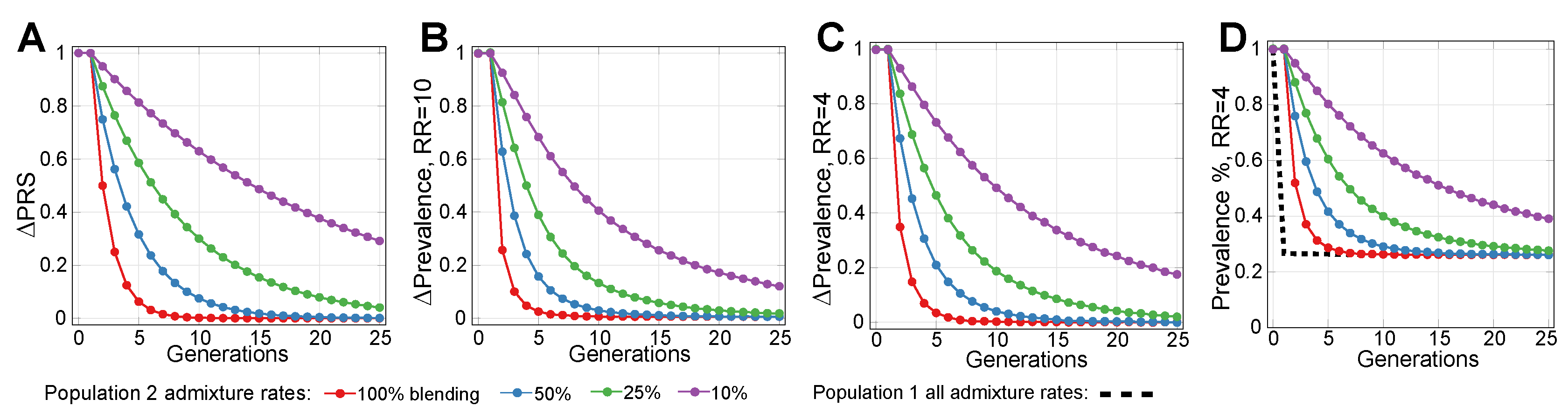
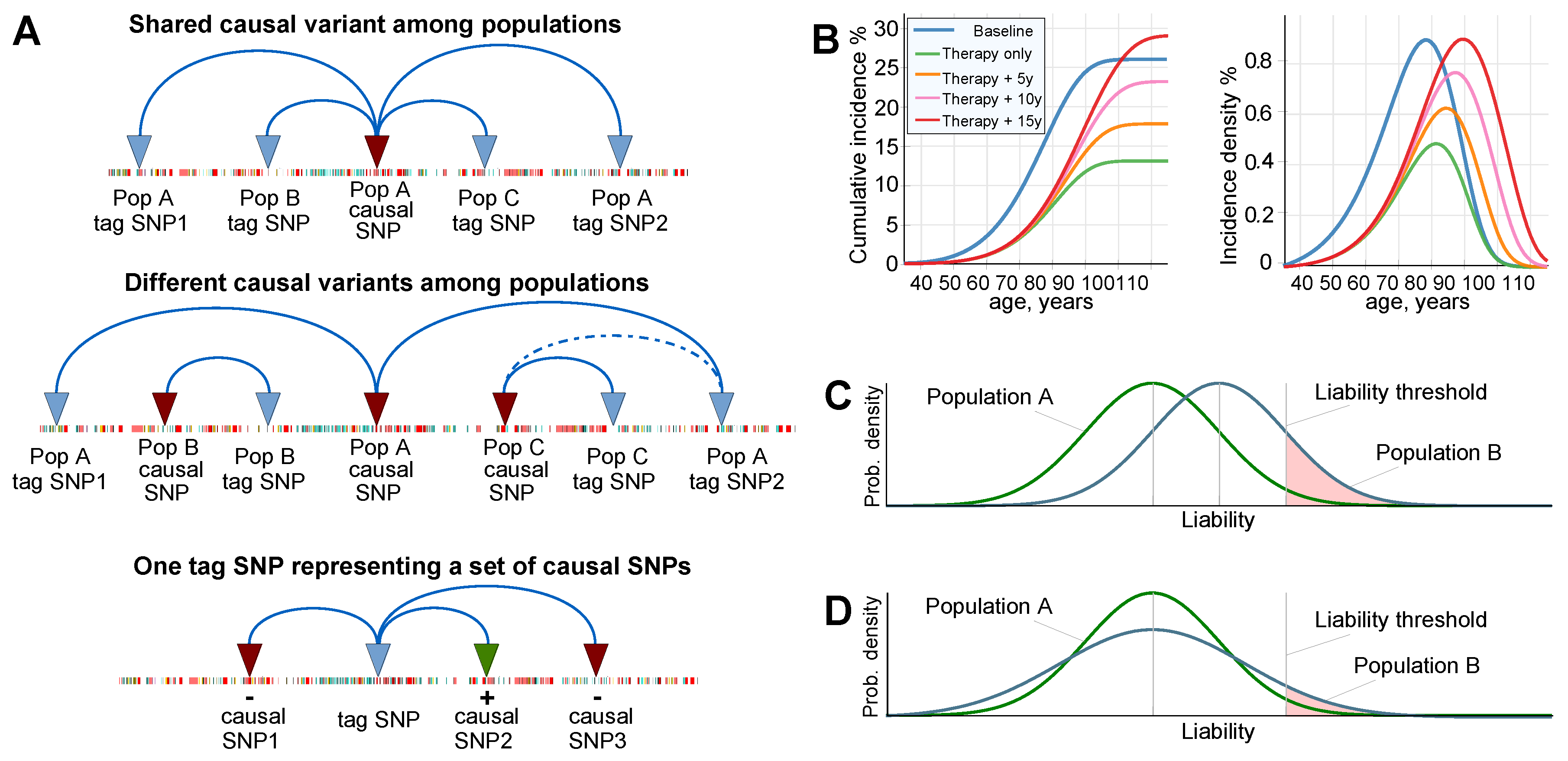
References
- Watson, J.D.; Crick, F.H. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature 1953, 171, 737. [Google Scholar] [CrossRef] [PubMed]
- Morton, N.E.; Crow, J.F.; Muller, H.J. An estimate of the mutational damage in man from data on consanguineous marriages. Proc. Natl. Acad. Sci. USA 1956, 42, 855–863. [Google Scholar] [CrossRef] [PubMed]
- Stein, L.D. Human genome: End of the beginning. Nature 2004, 431, 915. [Google Scholar] [CrossRef] [PubMed]
- Visscher, P.M.; Wray, N.R.; Zhang, Q.; Sklar, P.; McCarthy, M.I.; Brown, M.A.; Yang, J. 10 years of GWAS discovery: Biology, function, and translation. Am. J. Hum. Genet. 2017, 101, 5–22. [Google Scholar] [CrossRef] [PubMed]
- OMIM. 2019. Available online: http://omim.org/statistics/geneMap (accessed on 2 June 2019).
- Beckmann, J.S.; Estivill, X.; Antonarakis, S.E. Copy number variants and genetic traits: Closer to the resolution of phenotypic to genotypic variability. Nat. Rev. Genet. 2007, 8, 639. [Google Scholar] [CrossRef] [PubMed]
- Maroilley, T.; Tarailo-Graovac, M. Uncovering Missing Heritability in Rare Diseases. Genes 2019, 10, 275. [Google Scholar] [CrossRef] [PubMed]
- Stenson, P.D.; Mort, M.; Ball, E.V.; Evans, K.; Hayden, M.; Heywood, S.; Hussain, M.; Phillips, A.D.; Cooper, D.N. The Human Gene Mutation Database: Towards a comprehensive repository of inherited mutation data for medical research, genetic diagnosis and next-generation sequencing studies. Hum. Genet. 2017, 136, 665–677. [Google Scholar] [CrossRef]
- Gao, Z.; Waggoner, D.; Stephens, M.; Ober, C.; Przeworski, M. An estimate of the average number of recessive lethal mutations carried by humans. Genetics 2015, 199, 1243–1254. [Google Scholar] [CrossRef]
- Chong, J.X.; Buckingham, K.J.; Jhangiani, S.N.; Boehm, C.; Sobreira, N.; Smith, J.D.; Harrell, T.M.; McMillin, M.J.; Wiszniewski, W.; Gambin, T.; et al. The genetic basis of Mendelian phenotypes: Discoveries, challenges, and opportunities. Am. J. Hum. Genet. 2015, 97, 199–215. [Google Scholar] [CrossRef]
- Ginn, S.L.; Amaya, A.K.; Alexander, I.E.; Edelstein, M.; Abedi, M.R. Gene therapy clinical trials worldwide to 2017: An update. J. Gene Med. 2018, 20, e3015. [Google Scholar] [CrossRef]
- Philippidis, A. 25 Up-and-Coming Gene Therapies of 2019; Genetic Engineering and Biotechnology News (GEN): New York, NY, USA, 2019; Available online: https://www.genengnews.com/a-lists/25-up-and-coming-gene-therapies-of-2019 (accessed on 27 June 2019).
- Gyngell, C.; Bowman-Smart, H.; Savulescu, J. Moral reasons to edit the human genome: Picking up from the Nuffield report. J. Med. Ethics 2019. [Google Scholar] [CrossRef] [PubMed]
- Kemper, J.M.; Gyngell, C.; Savulescu, J. Subsidizing PGD: The Moral Case for Funding Genetic Selection. J. Bioethical Inq. 2019. [Google Scholar] [CrossRef] [PubMed]
- Nuffield Council on Bioethics. Genome Editing and Human Reproduction: Social and Ethical Issues; Nuffield Council on Bioethics: London, UK, 2018. [Google Scholar]
- Kofler, N.; Kraschel, K.L. Treatment of heritable diseases using CRISPR: Hopes, fears, and reality. Semin. Perinatol. 2018, 42, 515–521. [Google Scholar] [CrossRef] [PubMed]
- Pawitan, Y.; Seng, K.C.; Magnusson, P.K. How many genetic variants remain to be discovered? PLoS ONE 2009, 4, e7969. [Google Scholar] [CrossRef] [PubMed]
- Eyre-Walker, A. Genetic architecture of a complex trait and its implications for fitness and genome-wide association studies. Proc. Natl. Acad. Sci. USA 2010, 107, 1752–1756. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Ferreira, T.; Morris, A.P.; Medland, S.E.; Madden, P.A.; Heath, A.C.; Martin, N.G.; Montgomery, G.W.; Weedon, M.N.; Loos, R.J. Conditional and joint multiple-SNP analysis of GWAS summary statistics identifies additional variants influencing complex traits. Nat. Genet. 2012, 44, 369–375. [Google Scholar] [CrossRef] [PubMed]
- Gonzaga-Jauregui, C.; Lupski, J.R.; Gibbs, R.A. Human genome sequencing in health and disease. Annu. Rev. Med. 2012, 63, 35–61. [Google Scholar] [CrossRef]
- Lakatta, E.G. So! What’s aging? Is cardiovascular aging a disease? J. Mol. Cell. Cardiol. 2015, 83, 1–13. [Google Scholar] [CrossRef]
- Fuchsberger, C.; Flannick, J.; Teslovich, T.M.; Mahajan, A.; Agarwala, V.; Gaulton, K.J.; Ma, C.; Fontanillas, P.; Moutsianas, L.; McCarthy, D.J.; et al. The genetic architecture of type 2 diabetes. Nature 2016, 536, 41–47. [Google Scholar] [CrossRef]
- Mucci, L.A.; Hjelmborg, J.B.; Harris, J.R.; Czene, K.; Havelick, D.J.; Scheike, T.; Graff, R.E.; Holst, K.; Möller, S.; Unger, R.H.; et al. Familial risk and heritability of cancer among twins in Nordic countries. JAMA 2016, 315, 68–76. [Google Scholar] [CrossRef]
- Alzheimer’s Association. 2017 Alzheimer’s disease facts and figures. Alzheimers Dement. 2017, 13, 325–373. [Google Scholar] [CrossRef]
- Graff, R.E.; Möller, S.; Passarelli, M.N.; Witte, J.S.; Skytthe, A.; Christensen, K.; Tan, Q.; Adami, H.O.; Czene, K.; Harris, J.R. Familial risk and heritability of colorectal cancer in the nordic twin study of cancer. Clin. Gastroenterol. Hepatol. 2017, 15, 1256–1264. [Google Scholar] [CrossRef] [PubMed]
- Fedarko, N.S. Theories and Mechanisms of Aging. In Geriatric Anesthesiology; Nature Publishing Group: London, UK, 2018; pp. 19–25. [Google Scholar]
- Franceschi, C.; Garagnani, P.G.; Morsiani, C.; Conte, M.; Santoro, A.; Grignolio, A.; Monti, D.; Capri, M.; Salvioli, S. The continuum of aging and age-related diseases: Common mechanisms but different rates. Front. Med. 2018, 5, 61. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, T.J.; Turajlic, S.; Rowan, A.; Nicol, D.; Farmery, J.H.; O’Brien, T.; Martincorena, I.; Tarpey, P.; Angelopoulos, N.; Yates, L.R. Timing the landmark events in the evolution of clear cell renal cell cancer: TRACERx renal. Cell 2018, 173, 611–623. [Google Scholar] [CrossRef] [PubMed]
- Anderson, C.A.; Soranzo, N.; Zeggini, E.; Barrett, J.C. Synthetic associations are unlikely to account for many common disease genome-wide association signals. PLoS Biol. 2011, 9, e1000580. [Google Scholar] [CrossRef]
- Yang, J.; Bakshi, A.; Zhu, Z.; Hemani, G.; Vinkhuyzen, A.A.; Lee, S.H.; Robinson, M.R.; Perry, J.R.; Nolte, I.M.; van Vliet-Ostaptchouk, J.V. Genetic variance estimation with imputed variants finds negligible missing heritability for human height and body mass index. Nat. Genet. 2015, 47, 1114. [Google Scholar] [CrossRef] [PubMed]
- Song, M.; Kraft, P.; Joshi, A.D.; Barrdahl, M.; Chatterjee, N. Testing calibration of risk models at extremes of disease risk. Biostatistics 2014, 16, 143–154. [Google Scholar] [CrossRef]
- Langenberg, C.; Sharp, S.J.; Franks, P.W.; Scott, R.A.; Deloukas, P.; Forouhi, N.G.; Froguel, P.; Groop, L.C.; Hansen, T.; Palla, L.; et al. Gene-lifestyle interaction and type 2 diabetes: The EPIC interact case-cohort study. PLoS Med. 2014, 11, e1001647. [Google Scholar] [CrossRef]
- Chatterjee, N.; Shi, J.; García-Closas, M. Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 2016, 17, 392. [Google Scholar] [CrossRef]
- Prohaska, A.; Racimo, F.; Schork, A.J.; Sikora, M.; Stern, A.J.; Ilardo, M.; Allentoft, M.E.; Folkersen, L.; Buil, A.; Moreno-Mayar, J.V.; et al. Human Disease Variation in the Light of Population Genomics. Cell 2019, 177, 115–131. [Google Scholar] [CrossRef]
- Wong, K.H.; Levy-Sakin, M.; Kwok, P.Y. De novo human genome assemblies reveal spectrum of alternative haplotypes in diverse populations. Nat. Commun. 2018, 9, 3040. [Google Scholar] [CrossRef] [PubMed]
- Sirugo, G.; Williams, S.M.; Tishkoff, S.A. The Missing Diversity in Human Genetic Studies. Cell 2019, 177, 26–31. [Google Scholar] [CrossRef] [PubMed]
- Ballouz, S.; Dobin, A.; Gillis, J.A. Is it time to change the reference genome? Genome Biol. 2019, 20, 159. [Google Scholar] [CrossRef] [PubMed]
- Seyerle, A.A.; Young, A.M.; Jeff, J.M.; Melton, P.E.; Jorgensen, N.W.; Lin, Y.; Carty, C.L.; Deelman, E.; Heckbert, S.R.; Hindorff, L.A.; et al. Evidence of heterogeneity by race/ethnicity in genetic determinants of QT interval. Epidemiology 2014, 25, 790. [Google Scholar] [CrossRef] [PubMed]
- Marigorta, U.M.; Navarro, A. High Trans-ethnic Replicability of GWAS Results Implies Common Causal Variants. PLoS Genet. 2013, 9, e1003566. [Google Scholar] [CrossRef] [PubMed]
- Grimsby, J.L.; Porneala, B.C.; Vassy, J.L.; Yang, Q.; Florez, J.C.; Dupuis, J.; Liu, T.; Yesupriya, A.; Chang, M.H.; Ned, R.M.; et al. Race-ethnic differences in the association of genetic loci with HbA 1c levels and mortality in US adults: The third National Health and Nutrition Examination Survey (NHANES III). BMC Med Genet. 2012, 13, 30. [Google Scholar] [CrossRef] [PubMed]
- Mersha, T.B.; Abebe, T. Self-reported race/ethnicity in the age of genomic research: Its potential impact on understanding health disparities. Hum. Genom. 2015, 9, 1. [Google Scholar] [CrossRef] [PubMed]
- Belbin, G.M.; Nieves-Colón, M.A.; Kenny, E.E.; Moreno-Estrada, A.; Gignoux, C.R. Genetic diversity in populations across Latin America: Implications for population and medical genetic studies. Curr. Opin. Genet. Dev. 2018, 53, 98–104. [Google Scholar] [CrossRef]
- Zanetti, D.; Weale, M.E. Transethnic differences in GWAS signals: A simulation study. Ann. Hum. Genet. 2018, 82, 280–286. [Google Scholar] [CrossRef]
- Ntzani, E.E.; Liberopoulos, G.; Manolio, T.A.; Ioannidis, J.P. Consistency of genome-wide associations across major ancestral groups. Hum. Genet. 2012, 131, 1057–1071. [Google Scholar] [CrossRef]
- Martin, A.R.; Gignoux, C.R.; Walters, R.K.; Wojcik, G.L.; Neale, B.M.; Gravel, S.; Daly, M.J.; Bustamante, C.D.; Kenny, E.E. Human Demographic History Impacts Genetic Risk Prediction across Diverse Populations. Am. J. Hum. Genet. 2017, 100, 635–649. [Google Scholar] [CrossRef] [PubMed]
- Lappalainen, T.; Scott, A.J.; Brandt, M.; Hall, I.M. Genomic Analysis in the Age of Human Genome Sequencing. Cell 2019, 177, 70–84. [Google Scholar] [CrossRef] [PubMed]
- Abel, H.J.; Larson, D.E.; Chiang, C.; Das, I.; Kanchi, K.L.; Layer, R.M.; Neale, B.M.; Salerno, W.J.; Reeves, C.; Buyske, S.; et al. Mapping and characterization of structural variation in 17,795 deeply sequenced human genomes. bioRxiv 2018. [Google Scholar] [CrossRef]
- Zook, J.M.; Hansen, N.F.; Olson, N.D.; Chapman, L.M.; Mullikin, J.C.; Xiao, C.; Sherry, S.; Koren, S.; Phillippy, A.M.; Boutros, P.C.; et al. A robust benchmark for germline structural variant detection. bioRxiv 2019. [Google Scholar] [CrossRef]
- Oliynyk, R.T. Age-related late-onset disease heritability patterns and implications for genome-wide association studies. PeerJ 2019, 7, e7168. [Google Scholar] [CrossRef] [PubMed]
- Cox, D. Regression Models and Life-Tables. J. R. Stat. Soc. Ser. B Methodol. 1972, 34, 187–220. [Google Scholar] [CrossRef]
- Oliynyk, R.T. Quantifying the Potential for Future Gene Therapy to Lower Lifetime Risk of Polygenic Late-Onset Diseases. Int. J. Mol. Sci. 2019, 20, 3352. [Google Scholar] [CrossRef] [PubMed]
- Mars, N.J.; Koskela, J.T.; Ripatti, P.; Kiiskinen, T.T.; Havulinna, A.S.; Lindbohm, J.V.; Ahola-Olli, A.; Kurki, M.; Karjalainen, J.; Palta, P.; et al. Polygenic and clinical risk scores and their impact on age at onset of cardiometabolic diseases and common cancers. bioRxiv 2019. [Google Scholar] [CrossRef]
- Vicente, C.T.; Revez, J.A.; Ferreira, M.A.R. Lessons from ten years of genome-wide association studies of asthma. Clin. Transl. Immunol. 2017, 6, e165. [Google Scholar] [CrossRef]
- Willis-Owen, S.A.; Cookson, W.O.; Moffatt, M.F. The Genetics and Genomics of Asthma. Annu. Rev. Genom. Hum. Genet. 2018, 19, 223–246. [Google Scholar] [CrossRef]
- Lipton, R.B.; Bigal, M.E.; Diamond, M.; Freitag, F.; Reed, M.; Stewart, W.F. AMPP Advisory Group. Migraine prevalence, disease burden, and the need for preventive therapy. Neurology 2007, 68, 343–349. [Google Scholar] [CrossRef] [PubMed]
- Chalmer, M.A.; Esserlind, A.L.; Olesen, J.; Hansen, T.F. Polygenic risk score: Use in migraine research. J. Headache Pain 2018, 19, 29. [Google Scholar] [CrossRef] [PubMed]
- Riesmeijer, S.A.; Werker, P.M.; Nolte, I.M. Ethnic differences in prevalence of Dupuytren disease can partly be explained by known genetic risk variants. Eur. J. Hum. Genet. 2019. [Google Scholar] [CrossRef] [PubMed]
- Kurkó, J.; Besenyei, T.; Laki, J.; Glant, T.T.; Mikecz, K.; Szekanecz, Z. Genetics of rheumatoid arthritis—A comprehensive review. Clin. Rev. Allergy Immunol. 2013, 45, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.F.; Grainge, M.J.; Valdes, A.M.; See, L.C.; Luo, S.F.; Yu, K.H.; Zhang, W.; Doherty, M. Familial aggregation of systemic lupus erythematosus and coaggregation of autoimmune diseases in affected families. JAMA Intern. Med. 2015, 175, 1518–1526. [Google Scholar] [CrossRef] [PubMed]
- Bipolar Disorder and Schizophrenia Working Group of the Psychiatric Genomics Consortium. Genomic dissection of bipolar disorder and schizophrenia, including 28 subphenotypes. Cell 2018, 173, 1705–1715. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.Z.; Anderson, C.A. Genetic studies of Crohn’s disease: Past, present and future. Best Pract. Res. Clin. Gastroenterol. 2014, 28, 373–386. [Google Scholar] [CrossRef]
- Lee, J.C.; Biasci, D.; Roberts, R.; Gearry, R.B.; Mansfield, J.C.; Ahmad, T.; Prescott, N.J.; Satsangi, J.; Wilson, D.C.; Jostins, L.; et al. Genome-wide association study identifies distinct genetic contributions to prognosis and susceptibility in Crohn’s disease. Nat. Genet. 2017, 49, 262–268. [Google Scholar] [CrossRef]
- Gluckman, P.D.; Low, F.M.; Buklijas, T.; Hanson, M.A.; Beedle, A.S. How evolutionary principles improve the understanding of human health and disease. Evol. Appl. 2011, 4, 249–263. [Google Scholar] [CrossRef]
- Bergen, S.E.; O’Dushlaine, C.T.; Lee, P.H.; Fanous, A.H.; Ruderfer, D.M.; Ripke, S.; Sullivan, P.F.; Smoller, J.W.; Purcell, S.M.; International Schizophrenia Consortium, Swedish Schizophrenia Consortium; et al. Genetic modifiers and subtypes in schizophrenia: Investigations of age at onset, severity, sex and family history. Schizophr. Res. 2014, 154, 48–53. [Google Scholar] [CrossRef]
- Falconer, D. The inheritance of liability to diseases with variable age of onset, with particular reference to diabetes mellitus. Ann. Hum. Genet. 1967, 31, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Falconer, D.S. The inheritance of liability to certain diseases, estimated from the incidence among relatives. Ann. Hum. Genet. 1965, 29, 51–76. [Google Scholar] [CrossRef]
- Wray, N.R.; Goddard, M.E. Multi-locus models of genetic risk of disease. Genome Med. 2010, 2, 10. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Gaitsch, H.; Poon, H.; Cox, N.J.; Rzhetsky, A. Classification of common human diseases derived from shared genetic and environmental determinants. Nat. Genet. 2017, 49, 1319–1325. [Google Scholar] [CrossRef] [PubMed]
- Polubriaginof, F.C.; Vanguri, R.; Quinnies, K.; Belbin, G.M.; Yahi, A.; Salmasian, H.; Lorberbaum, T.; Nwankwo, V.; Li, L.; Shervey, M.M.; et al. Disease heritability inferred from familial relationships reported in medical records. Cell 2018, 173, 1692–1704. [Google Scholar] [CrossRef] [PubMed]
- Gravel, S. Population genetics models of local ancestry. Genetics 2012, 191, 607–619. [Google Scholar] [CrossRef]
- Huber, M.; Chen, Y.; Dinwoodie, I.; Dobra, A.; Nicholas, M. Monte carlo algorithms for Hardy–Weinberg proportions. Biometrics 2006, 62, 49–53. [Google Scholar] [CrossRef] [PubMed]
- Mayo, O. A century of Hardy–Weinberg equilibrium. Twin Res. Hum. Genet. 2008, 11, 249–256. [Google Scholar] [CrossRef]
- Chakraborty, R.; Weiss, K.M. Frequencies of complex diseases in hybrid populations. Am. J. Phys. Anthropol. 1986, 70, 489–503. [Google Scholar] [CrossRef]
- Borzecki, A.M.; Bridgers, D.K.; Liebschutz, J.M.; Kader, B.; Kazis, S.L.E.; Berlowitz, D.R. Racial differences in the prevalence of atrial fibrillation among males. J. Natl. Med Assoc. 2008, 100, 237–246. [Google Scholar] [CrossRef]
- Larsen, S.; Krogsgaard, D.; Larsen, L.A.; Iachina, M.; Skytthe, A.; Frederiksen, H. Genetic and environmental influences in Dupuytren’s disease: A study of 30,330 Danish twin pairs. J. Hand Surg. Eur. Vol. 2015, 40, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.H.; Kim, J.H.; Lee, C.H.; Kim, S.J.; Jo, Y.H.; Lee, M.; Choi, W.S. The epidemiology of Dupuytren’s disease in Korea: A nationwide population-based study. J. Korean Med. Sci. 2018, 33, e204. [Google Scholar] [CrossRef] [PubMed]
- Yeh, C.C.; Huang, K.F.; Ho, C.H.; Chen, K.T.; Liu, C.; Wang, J.J.; Chu, C.C. Epidemiological profile of Dupuytren’s disease in Taiwan (Ethnic Chinese): A nationwide population-based study. BMC Musculoskelet. Disord. 2015, 16, 20. [Google Scholar] [CrossRef] [PubMed]
- Molokhia, M.; McKeigue, P. Risk for rheumatic disease in relation to ethnicity and admixture. Arthritis Res. Ther. 2000, 2, 115. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Morris, D.L.; Vyse, T.J. Genetic advances in systemic lupus erythematosus: An update. Curr. Opin. Rheumatol. 2017, 29, 423–433. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.S.; Bayakly, A.R.; Helmick, C.G.; Gordon, C.; Easley, K.A.; Drenkard, C. The incidence and prevalence of systemic lupus erythematosus, 2002–2004: The Georgia Lupus Registry. Arthritis Rheumatol. 2014, 66, 357–368. [Google Scholar] [CrossRef]
- Herráez, D.L.; Martínez-Bueno, M.; Riba, L.; de la Torre, I.G.; Sacnún, M.; Goñi, M.; Berbotto, G.A.; Paira, S.; Musuruana, J.L.; Graf, C.E.; et al. Rheumatoid arthritis in Latin Americans enriched for Amerindian ancestry is associated with loci in chromosomes 1, 12, and 13, and the HLA class II region. Arthritis Rheum. 2013, 65, 1457–1467. [Google Scholar] [CrossRef]
- Dudbridge, F. Polygenic epidemiology. Genet. Epidemiol. 2016, 40, 268–272. [Google Scholar] [CrossRef]
- Hormozdiari, F.; Zhu, A.; Kichaev, G.; Ju, C.J.T.; Segrè, A.V.; Joo, J.W.J.; Won, H.; Sankararaman, S.; Pasaniuc, B.; Shifman, S.; et al. Widespread allelic heterogeneity in complex traits. Am. J. Hum. Genet. 2017, 100, 789–802. [Google Scholar] [CrossRef]
- Salzano, F.M.; Sans, M. Interethnic admixture and the evolution of Latin American populations. Genet. Mol. Biol. 2014, 37, 151–170. [Google Scholar] [CrossRef]
- Acuna-Hidalgo, R.; Veltman, J.A.; Hoischen, A. New insights into the generation and role of de novo mutations in health and disease. Genome Biol. 2016, 17, 241. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M. Mutation and human exceptionalism: Our future genetic load. Genetics 2016, 202, 869–875. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.; Ackerman, M.S.; Gout, J.F.; Long, H.; Sung, W.; Thomas, W.K.; Foster, P.L. Genetic drift, selection and the evolution of the mutation rate. Nat. Rev. Genet. 2016, 17, 704–714. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Wyman, M.J.; Sella, G.; Przeworski, M. Interpreting the dependence of mutation rates on age and time. PLoS Biol. 2016, 14, e1002355. [Google Scholar] [CrossRef] [PubMed]
- Engels, W.R. Exact tests for Hardy–Weinberg proportions. Genetics 2009, 183, 1431–1441. [Google Scholar] [CrossRef]
- Shifman, S.; Kuypers, J.; Kokoris, M.; Yakir, B.; Darvasi, A. Linkage disequilibrium patterns of the human genome across populations. Hum. Mol. Genet. 2003, 12, 771–776. [Google Scholar] [CrossRef]
- Martin, E.R.; Tunc, I.; Liu, Z.; Slifer, S.H.; Beecham, A.H.; Beecham, G.W. Properties of global-and local-ancestry adjustments in genetic association tests in admixed populations. Genet. Epidemiol. 2018, 42, 214–229. [Google Scholar] [CrossRef]
- Risch, N.; Merikangas, K. The future of genetic studies of complex human diseases. Science 1996, 273, 1516–1517. [Google Scholar] [CrossRef]
- Lu, Q.; Elston, R.C. Using the optimal receiver operating characteristic curve to design a predictive genetic test, exemplified with type 2 diabetes. Am. J. Hum. Genet. 2008, 82, 641–651. [Google Scholar] [CrossRef][Green Version]
- Stearns, F.W. One hundred years of pleiotropy: A retrospective. Genetics 2010, 186, 767–773. [Google Scholar] [CrossRef]
- Paaby, A.B.; Rockman, M.V. The many faces of pleiotropy. Trends Genet. 2013, 29, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Bhatia, G.; Patterson, N.; Sankararaman, S.; Price, A.L. Estimating and interpreting FST: The impact of rare variants. Genome Res. 2013, 23, 1514–1521. [Google Scholar] [CrossRef] [PubMed]
- Berner, D. Allele Frequency Difference AFD-An Intuitive Alternative to FST for Quantifying Genetic Population Differentiation. Genes 2019, 10, 308. [Google Scholar] [CrossRef] [PubMed]
- Wray, N.R.; Goddard, M.E.; Visscher, P.M. Prediction of individual genetic risk to disease from genome-wide association studies. Genome Res. 2007, 17, 1520–1528. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.R.; Daly, M.J.; Robinson, E.B.; Hyman, S.E.; Neale, B.M. Predicting polygenic risk of psychiatric disorders. Biol. Psychiatry 2019, 86, 97–109. [Google Scholar] [CrossRef] [PubMed]
- Gejman, P.V.; Sanders, A.R.; Duan, J. The role of genetics in the etiology of schizophrenia. Psychiatr. Clin. N. Am. 2010, 33, 35–66. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, M.A.; Mathur, R.; Vonk, J.M.; Szwajda, A.; Brumpton, B.; Granell, R.; Brew, B.K.; Ullemar, V.; Lu, Y.; Jiang, Y.; et al. Genetic Architectures of Childhood-and Adult-Onset Asthma Are Partly Distinct. Am. J. Hum. Genet. 2019, 104, 665–684. [Google Scholar] [CrossRef]
- Pardiñas, A.F.; Holmans, P.; Pocklington, A.J.; Escott-Price, V.; Ripke, S.; Carrera, N.; Legge, S.E.; Bishop, S.; Cameron, D.; Hamshere, M.L.; et al. Common schizophrenia alleles are enriched in mutation-intolerant genes and in regions under strong background selection. Nat. Genet. 2018, 50, 381. [Google Scholar] [CrossRef]
- Wray, N.R.; Visscher, P.M. Narrowing the boundaries of the genetic architecture of schizophrenia. Schizophr. Bull. 2009, 36, 14–23. [Google Scholar] [CrossRef]
- Ugowe, F.E.; Jackson, L.R.I.; Thomas, K.L. Racial and ethnic differences in the prevalence, management, and outcomes in patients with atrial fibrillation: A systematic review. Heart Rhythm 2018, 15, 1337–1345. [Google Scholar] [CrossRef]
- Musunuru, K.; Kathiresan, S. Genetics of Common, Complex Coronary Artery Disease. Cell 2019, 177, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Stern, M.C.; Fejerman, L.; Das, R.; Setiawan, V.W.; Cruz-Correa, M.R.; Perez-Stable, E.J.; Figueiredo, J.C. Variability in Cancer Risk and Outcomes Within US Latinos by National Origin and Genetic Ancestry. Curr. Epidemiol. Rep. 2016, 3, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Holley, A.; Northcott, H.; Gladding, P.; Harding, S.; Larsen, P. Significant Differences in Genetic Risk Profiles Between Maori and European Presenting with Myocardial Infarction. Hear. Lung Circ. 2017, 26, S307–S308. [Google Scholar] [CrossRef][Green Version]
- Gurdasani, D.; Carstensen, T.; Tekola-Ayele, F.; Pagani, L.; Tachmazidou, I.; Hatzikotoulas, K.; Karthikeyan, S.; Iles, L.; Pollard, M.O.; Choudhury, A.; et al. The African Genome Variation Project shapes medical genetics in Africa. Nature 2014, 517, 327. [Google Scholar] [CrossRef] [PubMed]
- National Academies of Sciences, Engineering, and Medicine. Human Genome Editing: Science, Ethics, and Governance; National Academies Press: Washington, DC, USA, 2017. [Google Scholar]
- Maurano, M.T.; Humbert, R.; Rynes, E.; Thurman, R.E.; Haugen, E.; Wang, H.; Reynolds, A.P.; Sandstrom, R.; Qu, H.; Brody, J.; et al. Systematic Localization of Common Disease-Associated Variation in Regulatory DNA. Science 2012, 337, 1190–1195. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Gorkin, D.U.; Baker, M.; Strober, B.J.; Asoni, A.L.; McCallion, A.S.; Beer, M.A. A method to predict the impact of regulatory variants from DNA sequence. Nat. Genet. 2015, 47, 955. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Tazearslan, C.; Suh, Y. Challenges and progress in interpretation of non-coding genetic variants associated with human disease. Exp. Biol. Med. 2017, 242, 1325–1334. [Google Scholar] [CrossRef]
- Dong, C.; Wei, P.; Jian, X.; Gibbs, R.; Boerwinkle, E.; Wang, K.; Liu, X. Comparison and integration of deleteriousness prediction methods for nonsynonymous SNVs in whole exome sequencing studies. Hum. Mol. Genet. 2014, 24, 2125–2137. [Google Scholar] [CrossRef]
- Ioannidis, N.M.; Rothstein, J.H.; Pejaver, V.; Middha, S.; McDonnell, S.K.; Baheti, S.; Musolf, A.; Li, Q.; Holzinger, E.; Karyadi, D.; et al. REVEL: An ensemble method for predicting the pathogenicity of rare missense variants. Am. J. Hum. Genet. 2016, 99, 877–885. [Google Scholar] [CrossRef]
- Jian, X.; Liu, X. In Silico Prediction of Deleteriousness for Nonsynonymous and Splice-Altering Single Nucleotide Variants in the Human Genome. In In Vitro Mutagenesis; Springer: Berlin/Heidelberg, Germany, 2017; pp. 191–197. [Google Scholar]
- Wagih, O.; Galardini, M.; Busby, B.P.; Memon, D.; Typas, A.; Beltrao, P. A resource of variant effect predictions of single nucleotide variants in model organisms. Mol. Syst. Biol. 2018, 14, e8430. [Google Scholar] [CrossRef]
- Yauy, K.; Baux, D.; Pegeot, H.; Van Goethem, C.; Mathieu, C.; Guignard, T.; Morales, R.J.; Lacourt, D.; Krahn, M.; Lehtokari, V.L.; et al. MoBiDiC Prioritization Algorithm, a Free, Accessible, and Efficient Pipeline for Single-Nucleotide Variant Annotation and Prioritization for Next-Generation Sequencing Routine Molecular Diagnosis. J. Mol. Diagn. 2018, 20, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Korvigo, I.; Afanasyev, A.; Romashchenko, N.; Skoblov, M. Generalising better: Applying deep learning to integrate deleteriousness prediction scores for whole-exome SNV studies. PLoS ONE 2018, 13, e0192829. [Google Scholar] [CrossRef] [PubMed]
- Wright, A.V.; Nuñez, J.K.; Doudna, J.A. Biology and applications of CRISPR systems: Harnessing nature’s toolbox for genome engineering. Cell 2016, 164, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Carroll, D. Genome engineering with zinc-finger nucleases. Genetics 2011, 188, 773–782. [Google Scholar] [CrossRef] [PubMed]
- Joung, J.K.; Sander, J.D. TALENs: A widely applicable technology for targeted genome editing. Nat. Rev. Mol. Cell Biol. 2013, 14, 49. [Google Scholar] [CrossRef] [PubMed]
- Kocak, D.D.; Josephs, E.A.; Bhandarkar, V.; Adkar, S.S.; Kwon, J.B.; Gersbach, C.A. Increasing the specificity of CRISPR systems with engineered RNA secondary structures. Nat. Biotechnol. 2019, 37, 657. [Google Scholar] [CrossRef]
- Smith, C.J.; Castanon, O.; Said, K.; Volf, V.; Khoshakhlagh, P.; Hornick, A.; Ferreira, R.; Wu, C.T.; Güell, M.; Garg, S.; et al. Enabling large-scale genome editing by reducing DNA nicking. bioRxiv 2019. [Google Scholar] [CrossRef]
- Strecker, J.; Ladha, A.; Gardner, Z.; Schmid-Burgk, J.L.; Makarova, K.S.; Koonin, E.V.; Zhang, F. RNA-guided DNA insertion with CRISPR-associated transposases. Science 2019. [Google Scholar] [CrossRef]
- Thompson, D.; Aboulhouda, S.; Hysolli, E.; Smith, C.; Wang, S.; Castanon, O.; Church, G. The future of multiplexed eukaryotic genome engineering. ACS Chem. Biol. 2017, 13, 313–325. [Google Scholar] [CrossRef]
- Kohman, R.E.; Kunjapur, A.M.; Hysolli, E.; Wang, Y.; Church, G.M. From Designing the Molecules of Life to Designing Life: Future Applications Derived from Advances in DNA Technologies. Angew. Chem. 2018, 57, 4313–4328. [Google Scholar] [CrossRef]
- Noh, M.; Yip, B.; Lee, Y.; Pawitan, Y. Multicomponent variance estimation for binary traits in family-based studies. Genet. Epidemiol. 2006, 30, 37–47. [Google Scholar] [CrossRef] [PubMed]
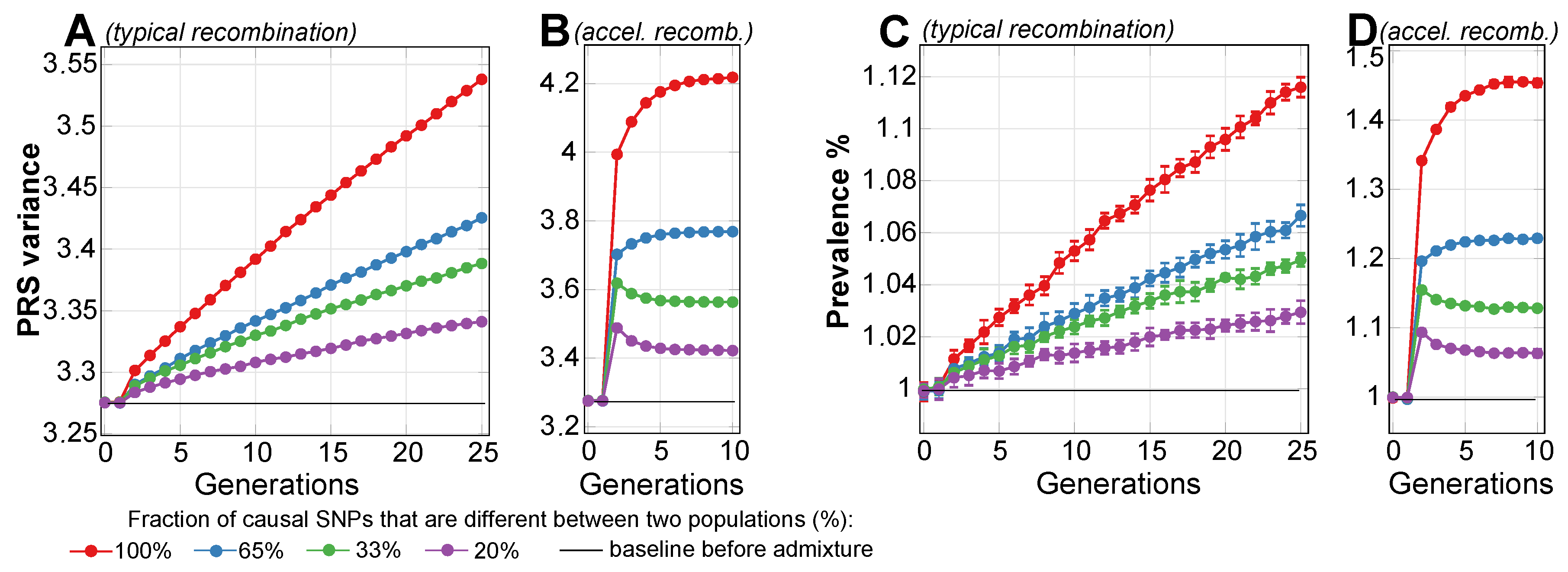
| Fraction of Differing Causal SNPs | 100% | 65% | 33% | 20% |
|---|---|---|---|---|
| Second-generation prevalence increase, % | 1 | <1 | <1 | <1 |
| Fifth-generation prevalence increase, % | 2.7 | 1.4 | 1.3 | 0.8 |
| Asymptotic prevalence increase limit, % | 45 | 22 | 11 | 6.3 |
| Disease | Prevalence in Pop 1 | Prevalence in Pop 2 | Admixed Prevalence | Relative Risk | PRS Change | Edited SNPs | SNPs in Disease Architecture |
|---|---|---|---|---|---|---|---|
| DD | 25% | 0.25% | 4.0% | 100 | 8.44 | 89.0 | 3575 |
| RA | 3.0% | 0.30% | 1.0% | 10 | 2.62 | 27.6 | 1350 |
| LE | 0.35% | 0.10% | 0.19% | 3.5 | 1.20 | 12.7 | 700 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliynyk, R.T. Future Preventive Gene Therapy of Polygenic Diseases from a Population Genetics Perspective. Int. J. Mol. Sci. 2019, 20, 5013. https://doi.org/10.3390/ijms20205013
Oliynyk RT. Future Preventive Gene Therapy of Polygenic Diseases from a Population Genetics Perspective. International Journal of Molecular Sciences. 2019; 20(20):5013. https://doi.org/10.3390/ijms20205013
Chicago/Turabian StyleOliynyk, Roman Teo. 2019. "Future Preventive Gene Therapy of Polygenic Diseases from a Population Genetics Perspective" International Journal of Molecular Sciences 20, no. 20: 5013. https://doi.org/10.3390/ijms20205013
APA StyleOliynyk, R. T. (2019). Future Preventive Gene Therapy of Polygenic Diseases from a Population Genetics Perspective. International Journal of Molecular Sciences, 20(20), 5013. https://doi.org/10.3390/ijms20205013