Reaction of Electrons with DNA: Radiation Damage to Radiosensitization
Abstract
1. Introduction
2. Various States of Radiation-Produced Electrons
2.1. Introduction
2.2. Structure of the Solvated Electron (e−aq)
2.3. Cavity Model of e−aq
2.4. Non-Cavity Model
3. Reaction of e−aq with DNA Bases
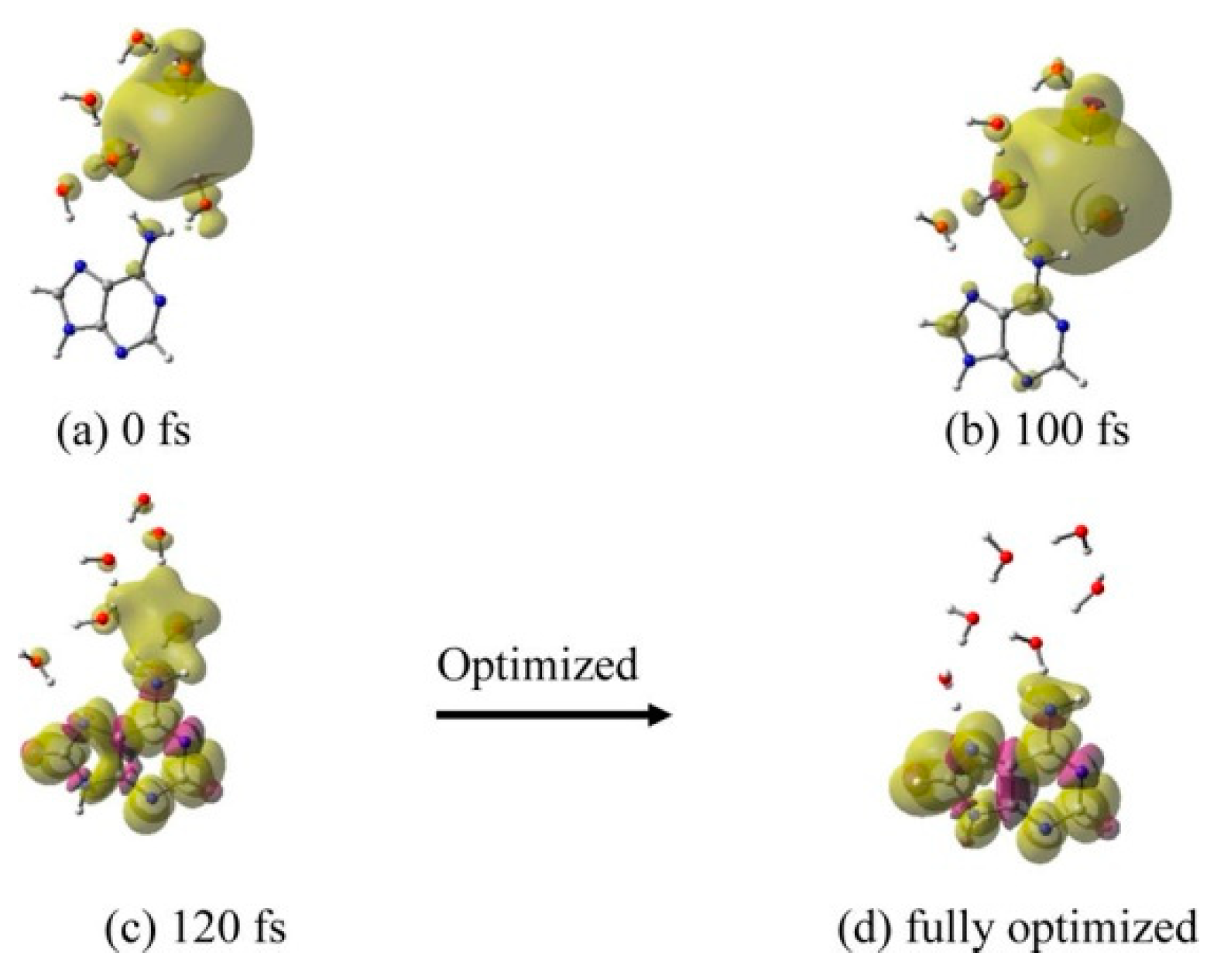
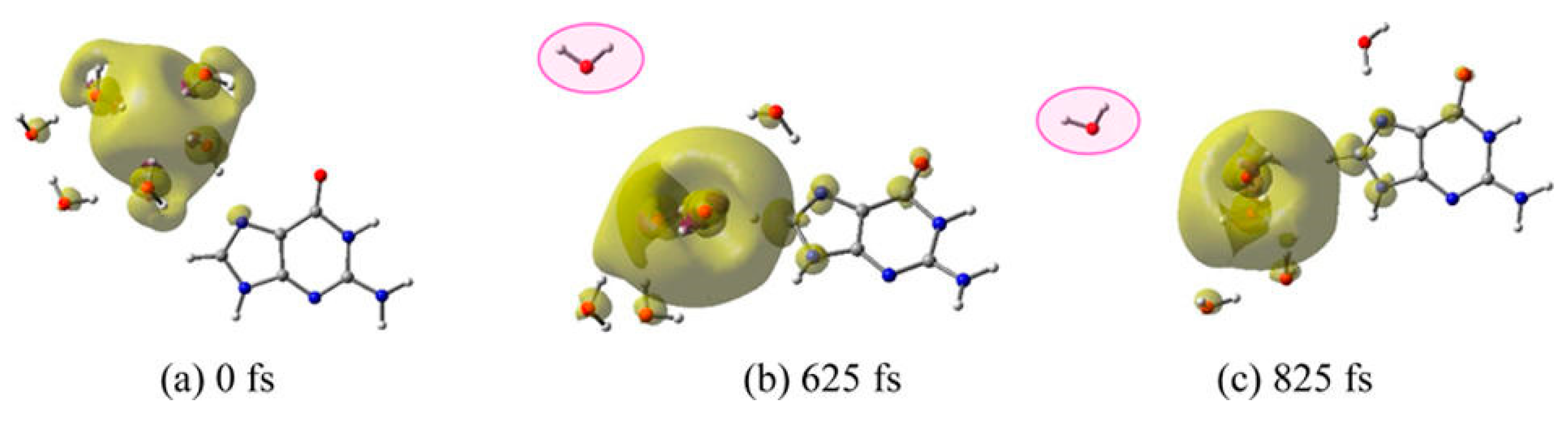
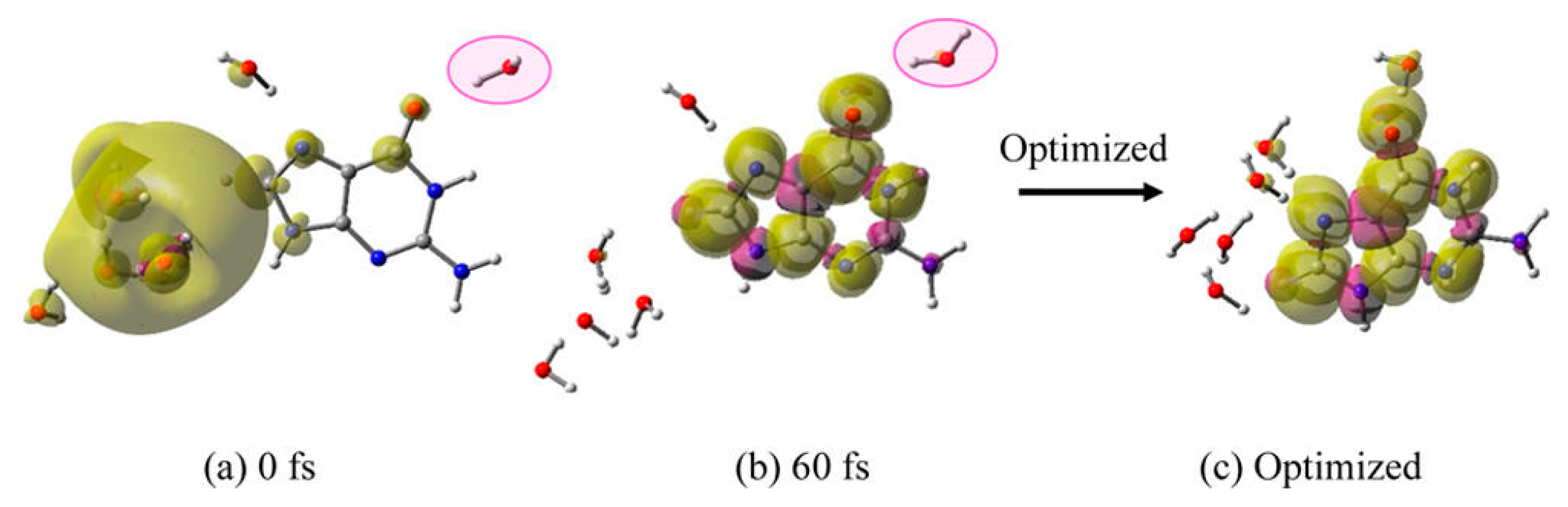
3.1. Simulation Studies of ab Initio Molecular Dynamics (MD)
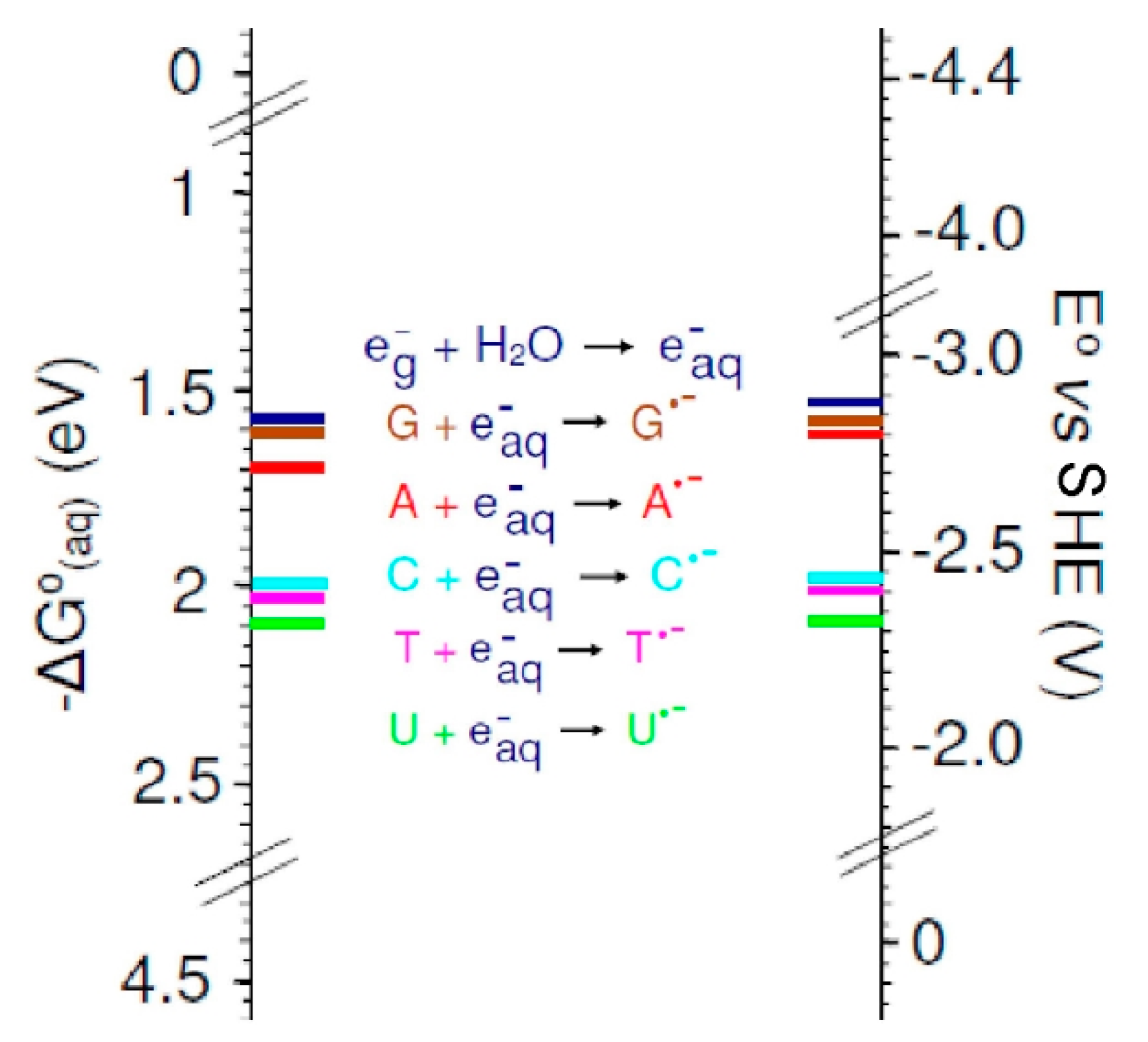
3.2. Base Reduction Potentials
4. Electron Reactions in Ion-Beam Irradiated DNA
4.1. Introduction
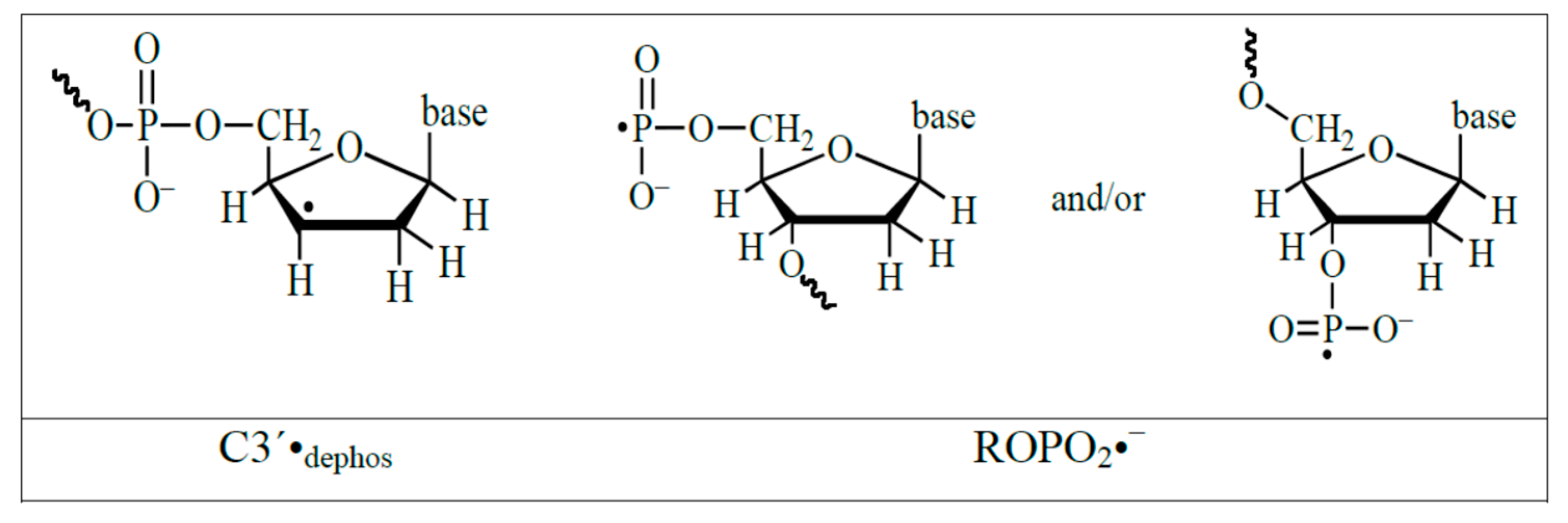
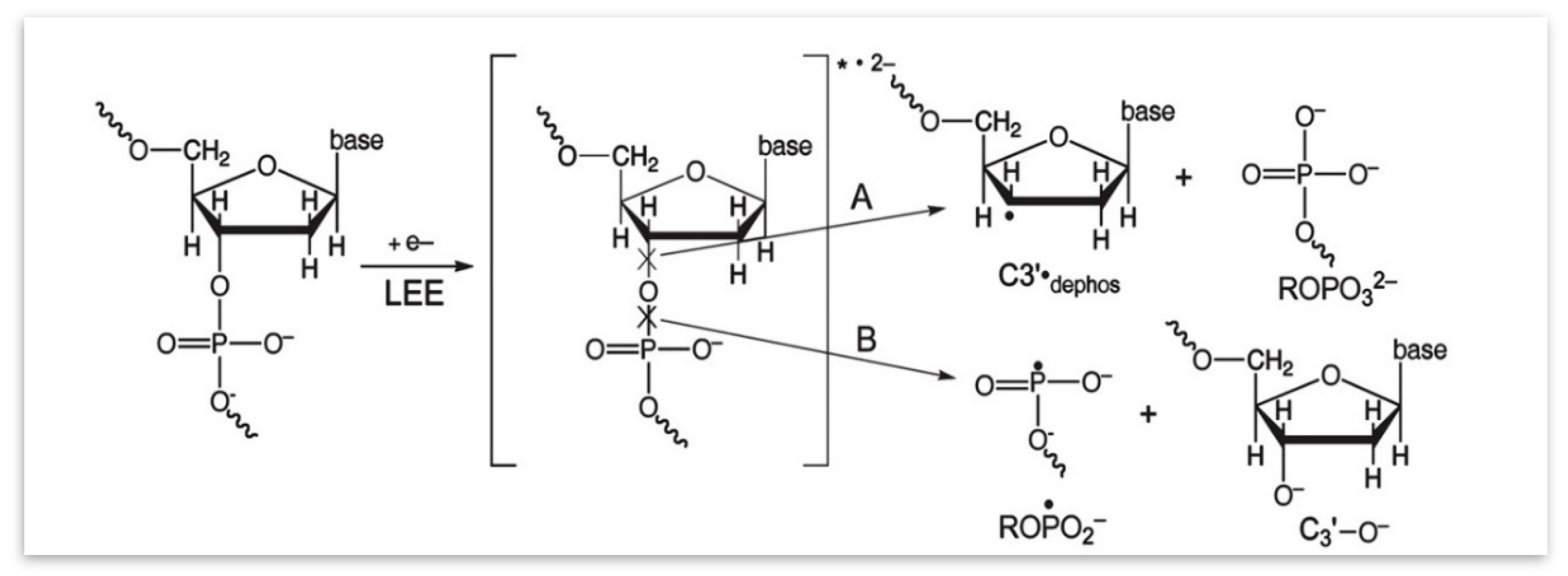
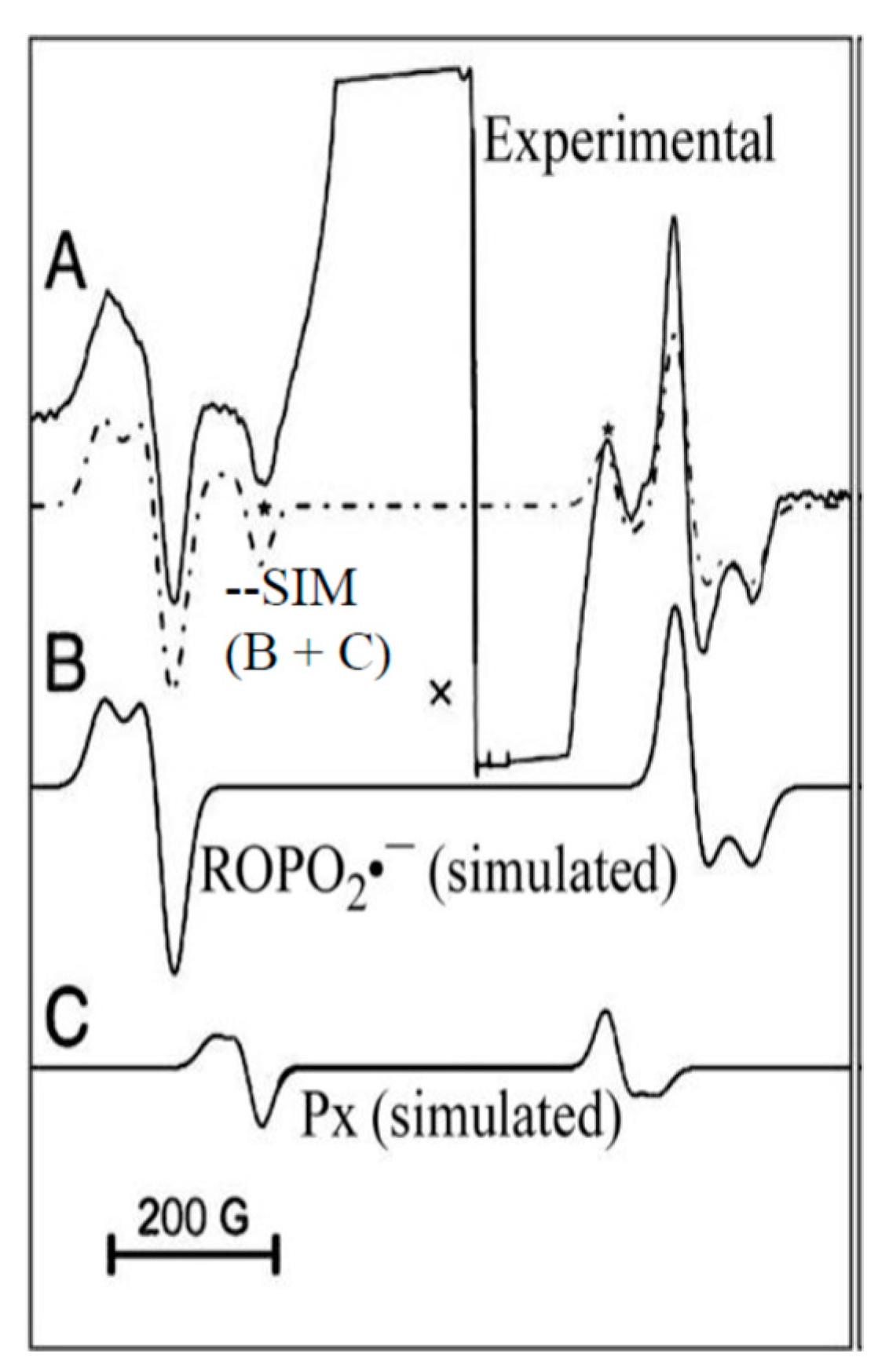
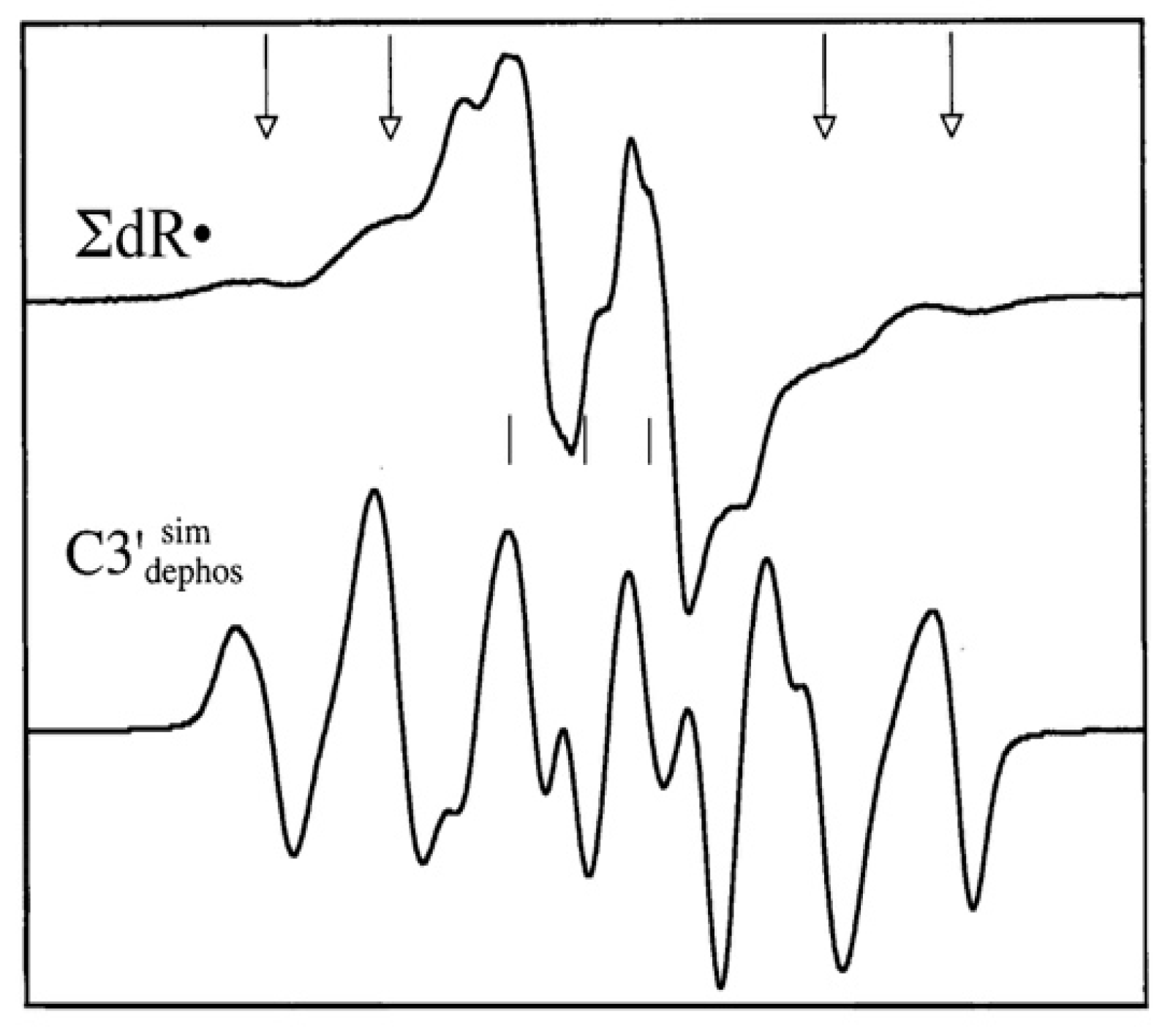
4.2. Low Energy Electron-Mediated Radicals in Ion-Beam Irradiated DNA
4.3. Mechanism of Formation of ROPO2•− and C3′•dephos via LEE-Mediated Dissociative Electron Attachment
4.4. The Relevance of the Solvated Electron (e−aq)
5. C5-Modified Pyrimidine Nucleosides as Radiosensitizers (Radiation Damage Enhancement Agents)
5.1. C5-Modified Pyrimidines as Radiosensitizers, a Short Summary
5.2. Formation of the Oxidizing Aminyl Radical under a Reductive Environment
5.3. Evidence of Radiosensitization by Azidonucleosides
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Herbert, J.M.; Coons, M.P. The Hydrated Electron. Annu. Rev. Phys. Chem. 2017, 68, 447–472. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wang, F.; Mostafavi, M. Ultrafast Chemistry of Water Radical Cation, H2O•+, in Aqueous Solutions. Molecules 2018, 23, 244. [Google Scholar]
- Kumar, A.; Sevilla, M.D. Proton-Coupled Electron Transfer in DNA on Formation of Radiation-Produced Ion Radicals. Chem. Rev. 2010, 110, 7002–7023. [Google Scholar] [CrossRef] [PubMed]
- Walker, D.C. The hydrated electron. Q. Rev. Chem. Soc. 1967, 21, 79–108. [Google Scholar] [CrossRef]
- Steenken, S. Purine bases, nucleosides, and nucleotides: Aqueous solution redox chemistry and transformation reactions of their radical cations and e- and OH adducts. Chem. Rev. 1989, 89, 503–520. [Google Scholar] [CrossRef]
- Ma, J.; Kumar, A.; Muroya, Y.; Yamashita, S.; Sakurai, T.; Denisov, S.A.; Sevilla, M.D.; Adhikary, A.; Seki, S.; Mostafavi, M. Observation of dissociative quasi-free electron attachment to nucleoside via excited anion radical in solution. Nat. Commun. 2019, 10, 102. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Low-Energy Electron (LEE)-Induced DNA Damage: Theoretical Approaches to Modeling Experiment. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Dordrecht, The Netherlands, 2015; pp. 1–63. ISBN 978-94-007-6169-8. [Google Scholar]
- Alizadeh, E.; Sanche, L. Precursors of Solvated Electrons in Radiobiological Physics and Chemistry. Chem. Rev. 2012, 112, 5578–5602. [Google Scholar] [CrossRef] [PubMed]
- Gauduel, Y.; Pommeret, S.; Migus, A.; Antonetti, A. Some Evidence of Ultrafast H2O+ -Water Molecule Reaction in Femtosecond Photoionization of Pure Liquid Water: Influence on Geminate Pair Recombination Dynamics. Chem. Phys. 1990, 149, 1–10. [Google Scholar] [CrossRef]
- Paik, D.H.; Lee, I.-R.; Yang, D.-S.; Baskin, J.S.; Zewail, A.H. Electrons in Finite-Sized Water Cavities: Hydration Dynamics Observed in Real Time. Science 2004, 306, 672–675. [Google Scholar] [CrossRef]
- Pimblott, S.M.; LaVerne, J.A. On the Radiation Chemical Kinetics of the Precursor to the Hydrated Electron. J. Phys. Chem. A 1998, 102, 2967–2975. [Google Scholar] [CrossRef]
- Savolainen, J.; Uhlig, F.; Ahmed, S.; Hamm, P.; Jungwirth, P. Direct observation of the collapse of the delocalized excess electron in water. Nat. Chem. 2014, 6, 697–701. [Google Scholar] [CrossRef] [PubMed]
- Von Sonntag, C. Free-radical-induced DNA damage and its repair: A chemical perspective; Springer: Berlin, Germany, 2006; ISBN 978-3-540-26120-9. [Google Scholar]
- Chomicz-Mańka, L.; Wityk, P.; Golon, Ł.; Zdrowowicz, M.; Wiczk, J.; Westphal, K.; Żyndul, M.; Makurat, S.; Rak, J. Consequences of Electron Attachment to Modified Nucleosides Incorporated into DNA. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Dordrecht, The Netherlands, 2015; pp. 1–22. ISBN 978-94-007-6169-8. [Google Scholar]
- Li, X.; Sevilla, M.D. DFT Treatment of Radiation Produced Radicals in DNA Model Systems. In Advances in Quantum Chemistry; John, S., Ed.; Academic Press: London, UK, 2007; Volume 52, pp. 59–87. [Google Scholar]
- Falcone, J.M.; Becker, D.; Sevilla, M.D.; Swarts, S.G. Products of the reactions of the dry and aqueous electron with hydrated DNA: Hydrogen and 5,6-dihydropyrimidines. Radiat. Phys. Chem. 2005, 72, 257–264. [Google Scholar] [CrossRef]
- Sevilla, M.D.; Becker, D.; Kumar, A.; Adhikary, A. Gamma and ion-beam irradiation of DNA: Free radical mechanisms, electron effects, and radiation chemical track structure. Radiat. Phys. Chem. 2016, 128, 60–74. [Google Scholar] [CrossRef] [PubMed]
- Boudaïffa, B.; Cloutier, P.; Hunting, D.; Huels, M.A.; Sanche, L. Resonant formation of DNA strand breaks by low-energy (3 to 20 eV) electrons. Science 2000, 287, 1658–1660. [Google Scholar]
- Kumar, A.; Sevilla, M.D. Role of Excited States in Low-Energy Electron (LEE) Induced Strand Breaks in DNA Model Systems: Influence of Aqueous Environment. ChemPhysChem 2009, 10, 1426–1430. [Google Scholar] [CrossRef]
- Kohanoff, J.; McAllister, M.; Tribello, G.A.; Gu, B. Interactions between low energy electrons and DNA: A perspective from first-principles simulations. J. Phys. Condens. Matter 2017, 29, 383001. [Google Scholar] [CrossRef]
- Nabben, F.J.; Karman, J.P.; Loman, H. Inactivation of Biologically Active DNA by Hydrated Electrons. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 1982, 42, 23–30. [Google Scholar] [CrossRef]
- Kuipers, K.; Lafleur, M.V.M. Characterization of DNA damage induced by gamma-radiationderived water radicals, using DNA repair enzymes. Int. J. Radiat. Biol. 1998, 74, 511–519. [Google Scholar] [CrossRef]
- Kočišek, J.; Sedmidubská, B.; Indrajith, S.; Fárník, M.; Fedor, J. Electron Attachment to Microhydrated Deoxycytidine Monophosphate. J. Phys. Chem. B 2018, 122, 5212–5217. [Google Scholar] [CrossRef]
- Ma, J.; Wang, F.; Denisov, S.A.; Adhikary, A.; Mostafavi, M. Reactivity of prehydrated electrons toward nucleobases and nucleotides in aqueous solution. Sci. Adv. 2017, 3, e1701669. [Google Scholar] [CrossRef]
- Coe, J.V.; Earhart, A.D.; Cohen, M.H.; Hoffman, G.J.; Sarkas, H.W.; Bowen, K.H. Using cluster studies to approach the electronic structure of bulk water: Reassessing the vacuum level, conduction band edge, and band gap of water. J. Chem. Phys. 1997, 107, 6023–6031. [Google Scholar] [CrossRef]
- Han, P.; Bartels, D.M. Hydrogen/deuterium isotope effects in water radiolysis. 2. Dissociation of electronically excited water. J. Phys. Chem. 1990, 94, 5824–5833. [Google Scholar] [CrossRef]
- Jortner, J. Theoretical Studies of Excess Electron States in Liquids. Ber. Bunsenges. Für Phys. Chem. 1971, 75, 696–714. [Google Scholar] [CrossRef]
- Grand, D.; Bernas, A.; Amouyal, E. Photoionization of aqueous indole: Conduction band edge and energy gap in liquid water. Chem. Phys. 1979, 44, 73–79. [Google Scholar] [CrossRef]
- Frank, A.J.; Grätzel, M.; Henglein, A. The 347.2 nm Laser Photolysis of Tetranitromethane in Polar, Nonpolar, and Micellar Solutions. Ber. Bunsenges. Für Phys. Chem. 1976, 80, 593–602. [Google Scholar] [CrossRef]
- Alizadeh, E.; Sanz, A.G.; García, G.; Sanche, L. Radiation Damage to DNA: The Indirect Effect of Low-Energy Electrons. J. Phys. Chem. Lett. 2013, 4, 820–825. [Google Scholar] [CrossRef] [PubMed]
- Gaiduk, A.P.; Pham, T.A.; Govoni, M.; Paesani, F.; Galli, G. Electron affinity of liquid water. Nat. Commun. 2018, 9, 247. [Google Scholar] [CrossRef]
- Kumar, A.; Walker, J.A.; Bartels, D.M.; Sevilla, M.D. A Simple ab Initio Model for the Hydrated Electron That Matches Experiment. J. Phys. Chem. A 2015, 119, 9148–9159. [Google Scholar] [CrossRef]
- Schwarz, H.A. Enthalpy and Entropy of Formation of the Hydrated Electron. J. Phys. Chem. 1991, 95, 6697–6701. [Google Scholar] [CrossRef]
- Hart, E.J.; Boag, J.W. Absorption Spectrum of the Hydrated Electron in Water and in Aqueous Solutions. J. Am. Chem. Soc. 1962, 84, 4090–4095. [Google Scholar] [CrossRef]
- Bartels, D.M.; Takahashi, K.; Cline, J.A.; Marin, T.W.; Jonah, C.D. Pulse Radiolysis of Supercritical Water. 3. Spectrum and Thermodynamics of the Hydrated Electron. J. Phys. Chem. A 2005, 109, 1299–1307. [Google Scholar] [CrossRef] [PubMed]
- Young, R.M.; Neumark, D.M. Dynamics of Solvated Electrons in Clusters. Chem. Rev. 2012, 112, 5553–5577. [Google Scholar] [CrossRef] [PubMed]
- Abel, B.; Buck, U.; Sobolewski, A.L.; Domcke, W. On the nature and signatures of the solvated electron in water. Phys Chem Chem Phys 2012, 14, 22–34. [Google Scholar] [CrossRef] [PubMed]
- Coe, J.V.; Williams, S.M.; Bowen, K.H. Photoelectron spectra of hydrated electron clusters vs. cluster size: Connecting to bulk. Int. Rev. Phys. Chem. 2008, 27, 27–51. [Google Scholar] [CrossRef]
- Boag, J.W.; Hart, E.J. Absorption Spectra in Irradiated Water and Some Solutions: Absorption Spectra of ‘Hydrated’ Electron. Nature 1963, 197, 45–47. [Google Scholar] [CrossRef]
- Feng, D.-F.; Kevan, L. Theoretical models for solvated electrons. Chem. Rev. 1980, 80, 1–20. [Google Scholar] [CrossRef]
- Larsen, R.E.; Glover, W.J.; Schwartz, B.J. Does the Hydrated Electron Occupy a Cavity? Science 2010, 329, 65–69. [Google Scholar] [CrossRef]
- Glover, W.J.; Schwartz, B.J. Short-Range Electron Correlation Stabilizes Noncavity Solvation of the Hydrated Electron. J. Chem. Theory Comput. 2016, 12, 5117–5131. [Google Scholar] [CrossRef]
- Casey, J.R.; Larsen, R.E.; Schwartz, B.J. Resonance Raman and temperature-dependent electronic absorption spectra of cavity and noncavity models of the hydrated electron. Proc. Natl. Acad. Sci. USA 2013, 110, 2712–2717. [Google Scholar] [CrossRef]
- Jacobson, L.D.; Herbert, J.M. Comment on “Does the Hydrated Electron Occupy a Cavity?”. Science 2011, 331, 1387. [Google Scholar] [CrossRef]
- Wilhelm, J.; VandeVondele, J.; Rybkin, V.V. Dynamics of the Bulk Hydrated Electron from Many-Body Wave-Function Theory. Angew. Chem. Int. Ed. 2019, 58, 3890–3893. [Google Scholar] [CrossRef]
- Uhlig, F.; Marsalek, O.; Jungwirth, P. Unraveling the Complex Nature of the Hydrated Electron. J. Phys. Chem. Lett. 2012, 3, 3071–3075. [Google Scholar] [CrossRef] [PubMed]
- Turi, L.; Madarasz, A. Comment on “Does the Hydrated Electron Occupy a Cavity?”. Science 2011, 331, 1387. [Google Scholar] [CrossRef] [PubMed]
- Herbert, J.M.; Jacobson, L.D. Structure of the Aqueous Electron: Assessment of One-Electron Pseudopotential Models in Comparison to Experimental Data and Time-Dependent Density Functional Theory. J. Phys. Chem. A 2011, 115, 14470–14483. [Google Scholar] [CrossRef] [PubMed]
- Turi, L. Hydrated Electrons in Water Clusters: Inside or Outside, Cavity or Noncavity? J. Chem. Theory Comput. 2015, 11, 1745–1755. [Google Scholar] [CrossRef]
- Turi, L.; Rossky, P.J. Theoretical Studies of Spectroscopy and Dynamics of Hydrated Electrons. Chem. Rev. 2012, 112, 5641–5674. [Google Scholar] [CrossRef]
- Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: Prediction of liquid-phase reduction potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068. [Google Scholar] [CrossRef]
- Du, Y.; Price, E.; Bartels, D.M. Solvated electron spectrum in supercooled water and ice. Chem. Phys. Lett. 2007, 438, 234–237. [Google Scholar] [CrossRef]
- Tauber, M.J.; Mathies, R.A. Structure of the Aqueous Solvated Electron from Resonance Raman Spectroscopy: Lessons from Isotopic Mixtures. J. Am. Chem. Soc. 2003, 125, 1394–1402. [Google Scholar] [CrossRef]
- Shiraishi, H.; Ishigure, K.; Morokuma, K. An ESR study on solvated electrons in water and alcohols: Difference in the g factor and related analysis of the electronic state by MO calculation. J. Chem. Phys. 1988, 88, 4637–4649. [Google Scholar] [CrossRef]
- Fessenden, R.W.; Verma, N.C. Time resolved electron spin resonance spectroscopy. III. Electron spin resonance emission from the hydrated electron. Possible evidence for reaction to the triplet state. J. Am. Chem. Soc. 1976, 98, 243–244. [Google Scholar] [CrossRef]
- Kevan, L. Solvated electron structure in glassy matrixes. Acc. Chem. Res. 1981, 14, 138–145. [Google Scholar] [CrossRef]
- Shkrob, I.A. The Structure of the Hydrated Electron. Part 1. Magnetic Resonance of Internally Trapping Water Anions: A Density Functional Theory Study. J. Phys. Chem. A 2007, 111, 5223–5231. [Google Scholar] [CrossRef] [PubMed]
- Pollard, T.P.; Beck, T.L. The thermodynamics of proton hydration and the electrochemical surface potential of water. J. Chem. Phys. 2014, 141, 18C512. [Google Scholar] [CrossRef] [PubMed]
- Shiraishi, H.; Sunaryo, G.R.; Ishigure, K. Temperature Dependence of Equilibrium and Rate Constants of Reactions Inducing Conversion between Hydrated Electron and Atomic Hydrogen. J. Phys. Chem. 1994, 98, 5164–5173. [Google Scholar] [CrossRef]
- Wardman, P. Reduction Potentials of One-Electron Couples Involving Free Radicals in Aqueous Solution. J. Phys. Chem. Ref. Data 1989, 18, 1637–1755. [Google Scholar] [CrossRef]
- Schwarz, H.A. Free radicals generated by radiolysis of aqueous solutions. J. Chem. Educ. 1981, 58, 101. [Google Scholar] [CrossRef]
- Tang, Y.; Shen, H.; Sekiguchi, K.; Kurahashi, N.; Mizuno, T.; Suzuki, Y.-I.; Suzuki, T. Direct measurement of vertical binding energy of a hydrated electron. Phys. Chem. Chem. Phys. 2010, 12, 3653. [Google Scholar] [CrossRef]
- Siefermann, K.R.; Liu, Y.; Lugovoy, E.; Link, O.; Faubel, M.; Buck, U.; Winter, B.; Abel, B. Binding energies, lifetimes and implications of bulk and interface solvated electrons in water. Nat. Chem. 2010, 2, 274–279. [Google Scholar] [CrossRef]
- Shreve, A.T.; Yen, T.A.; Neumark, D.M. Photoelectron spectroscopy of hydrated electrons. Chem. Phys. Lett. 2010, 493, 216–219. [Google Scholar] [CrossRef]
- Rossky, P.J.; Schnitker, J. The hydrated electron: Quantum simulation of structure, spectroscopy, and dynamics. J. Phys. Chem. 1988, 92, 4277–4285. [Google Scholar] [CrossRef]
- Schnitker, J.; Rossky, P.J. An electron–water pseudopotential for condensed phase simulation. J. Chem. Phys. 1987, 86, 3462–3470. [Google Scholar] [CrossRef]
- Turi, L.; Gaigeot, M.-P.; Levy, N.; Borgis, D. Analytical investigations of an electron–water molecule pseudopotential. I. Exact calculations on a model system. J. Chem. Phys. 2001, 114, 7805–7815. [Google Scholar] [CrossRef]
- Turi, L.; Borgis, D. Analytical investigations of an electron–water molecule pseudopotential. II. Development of a new pair potential and molecular dynamics simulations. J. Chem. Phys. 2002, 117, 6186–6195. [Google Scholar] [CrossRef]
- Jacobson, L.D.; Herbert, J.M. A one-electron model for the aqueous electron that includes many-body electron-water polarization: Bulk equilibrium structure, vertical electron binding energy, and optical absorption spectrum. J. Chem. Phys. 2010, 133, 154506. [Google Scholar] [CrossRef] [PubMed]
- Ambrosio, F.; Miceli, G.; Pasquarello, A. Electronic Levels of Excess Electrons in Liquid Water. J. Phys. Chem. Lett. 2017, 8, 2055–2059. [Google Scholar] [CrossRef] [PubMed]
- Walker, J.A.; Bartels, D.M. A Simple ab Initio Model for the Solvated Electron in Methanol. J. Phys. Chem. A 2016, 120, 7240–7247. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Adhikary, A.; Shamoun, L.; Sevilla, M.D. Do Solvated Electrons (eaq–) Reduce DNA Bases? A Gaussian 4 and Density Functional Theory-Molecular Dynamics Study. J. Phys. Chem. B 2016, 120, 2115–2123. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.-R.; Luo, T.; Lu, Q.-B. On the lifetimes and physical nature of incompletely relaxed electrons in liquid water. Phys. Chem. Chem. Phys. 2008, 10, 4463. [Google Scholar] [CrossRef]
- Cavanagh, M.C.; Martini, I.B.; Schwartz, B.J. Revisiting the pump–probe polarized transient hole-burning of the hydrated electron: Is its absorption spectrum inhomogeneously broadened? Chem. Phys. Lett. 2004, 396, 359–366. [Google Scholar] [CrossRef]
- Janik, I.; Lisovskaya, A.; Bartels, D.M. Partial Molar Volume of the Hydrated Electron. J. Phys. Chem. Lett. 2019, 10, 2220–2226. [Google Scholar] [CrossRef] [PubMed]
- Borsarelli, C.D.; Bertolotti, S.G.; Previtali, C.M. Thermodynamic changes associated with the formation of the hydrated electron after photoionization of inorganic anions: A time-resolved photoacoustic study. Photochem. Photobiol. Sci. 2003, 2, 791. [Google Scholar] [CrossRef] [PubMed]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical Review of rate constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (OH/O− in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef]
- Siefermann, K.R.; Abel, B. The Hydrated Electron: A Seemingly Familiar Chemical and Biological Transient. Angew. Chem. Int. Ed. 2011, 50, 5264–5272. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cai, Z.; Sevilla, M.D. DFT Calculations of the Electron Affinities of Nucleic Acid Bases: Dealing with Negative Electron Affinities. J. Phys. Chem. A 2002, 106, 1596–1603. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Low-Energy Electron Attachment to 5‘-Thymidine Monophosphate: Modeling Single Strand Breaks Through Dissociative Electron Attachment. J. Phys. Chem. B 2007, 111, 5464–5474. [Google Scholar] [CrossRef] [PubMed]
- Smyth, M.; Kohanoff, J. Excess Electron Localization in Solvated DNA Bases. Phys. Rev. Lett. 2011, 106, 238108. [Google Scholar] [CrossRef] [PubMed]
- Seidel, C.A.; Schulz, A.; Sauer, M.M.H. Nucleobase-specific quenching of fluorescent dyes. 1. Nucleobase one-electron redox potentials and their correlation with static and dynamic quenching efficiencies. J. Phys. Chem. 1996, 100, 5541–5553. [Google Scholar] [CrossRef]
- Ho, J. Are thermodynamic cycles necessary for continuum solvent calculation of pKas and reduction potentials? Phys. Chem. Chem. Phys. 2015, 17, 2859–2868. [Google Scholar] [CrossRef]
- Bartmess, J.E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. [Google Scholar] [CrossRef]
- Lewis, K.; Copeland, K.; Hill, G. One-electron redox properties of DNA nucleobases and common tautomers. Int. J. Quantum Chem. 2014, 114, 1678–1684. [Google Scholar] [CrossRef]
- Crespo-Hernández, C.E.; Close, D.M.; Gorb, L.; Leszczynski, J. Determination of Redox Potentials for the Watson–Crick Base Pairs, DNA Nucleosides, and Relevant Nucleoside Analogues. J. Phys. Chem. B 2007, 111, 5386–5395. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; Uehara, S.; Emfietzoglou, D. Interaction of Radiation with Matter; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Solov’yov, A.V. (Ed.) Nanoscale Insights into Ion-Beam Cancer Therapy; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Verkhovtsev, A.; Surdutovich, E.; Solov’yov, A.V. Multiscale approach predictions for biological outcomes in ion-beam cancer therapy. Sci. Rep. 2016, 6, 27654. [Google Scholar] [CrossRef] [PubMed]
- Hill, M.A. Radiation damage to DNA: The importance of track structure. Radiat. Meas. 1999, 31, 15–23. [Google Scholar] [CrossRef]
- Friedland, W.; Schmitt, E.; Kundrát, P.; Dingfelder, M.; Baiocco, G.; Barbieri, S.; Ottolenghi, A. Comprehensive Track-structure Based Evaluation of DNA Damage by Light Ions From Radiotherapy-relevant Energies Down to Stopping. Sci. Rep. 2017, 7, 45161. [Google Scholar] [CrossRef] [PubMed]
- Von Sonntag, C. The Chemical Basis of Radiation Biology; Taylor and Francis: London, UK, 1987. [Google Scholar]
- Adhikary, A.; Becker, D.; Sevilla, M.D. Electron spin resonance of radicals in irradiated DNA. In Applications of EPR in Radiation Research; Lund, A., Shiotani, M., Eds.; Springer: Berlin, Germany, 2016; pp. 299–352. [Google Scholar]
- Sanche, L. Interaction of low energy electrons with DNA: Applications to cancer radiation therapy. Radiat. Phys. Chem. 2016, 128, 36–43. [Google Scholar] [CrossRef]
- Huels, M.A.; Boudaïffa, B.; Cloutier, P.; Hunting, D.; Sanche, L. Single, double, and multiple double strand breaks induced in DNA by 3-100 eV electrons. J. Am. Chem. Soc. 2003, 125, 4467–4477. [Google Scholar] [CrossRef]
- Becker, D.; Adhikary, A.; Tetteh, S.T.; Bull, A.W.; Sevilla, M.D. Kr-86 Ion-Beam Irradiation of Hydrated DNA: Free Radical and Unaltered Base Yields. Radiat. Res. 2012, 178, 524–537. [Google Scholar] [CrossRef]
- Becker, D.; Razskazovskii, Y.; Callaghan, M.U.; Sevilla, M.D. Electron Spin Resonance of DNA Irradiated with a Heavy-Ion Beam (16O8+): Evidence for Damage to the Deoxyribose Phosphate Backbone. Radiat. Res. 1996, 146, 361–368. [Google Scholar] [CrossRef]
- Becker, D.; Bryant-Friedrich, A.; Trzasko, C.; Sevilla, M.D. Electron Spin Resonance Study of DNA Irradiated with an Argon-Ion Beam: Evidence for Formation of Sugar Phosphate Backbone Radicals. Radiat. Res. 2003, 160, 174–185. [Google Scholar] [CrossRef]
- Shukla, L.I.; Pazdro, R.; Becker, D.; Sevilla, M.D. Sugar radicals in DNA: Isolation of neutral radicals in gamma-irradiated DNA by hole and electron scavenging. Radiat. Res. 2005, 163, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Zheng, Y.; Cloutier, P.; Sanche, L.; Wagner, J.R. Low energy electron induced DNA damage: Effects of terminal phosphate and base moieties on the distribution of damage. J. Am. Chem. Soc. 2008, 130, 5612–5613. [Google Scholar] [CrossRef] [PubMed]
- Khorsandgolchin, G.; Sanche, L.; Cloutier, P.; Wagner, J.R. Strand Breaks Induced by Very Low Energy Electrons: Product Analysis and Mechanistic Insight into the Reaction with TpT. J. Am. Chem. Soc. 2019, 141, 10315–10323. [Google Scholar] [CrossRef] [PubMed]
- Adhikary, A.; Kumar, A.; Palmer, B.J.; Todd, A.D.; Heizer, A.N.; Sevilla, M.D. Reactions of 5-methylcytosine cation radicals in DNA and model systems: Thermal deprotonation from the 5-methyl group vs. excited state deprotonation from sugar. Int. J. Radiat. Biol. 2014, 90, 433–445. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. The Role of πσ* Excited States in Electron-Induced DNA Strand Break Formation: A Time-Dependent Density Functional Theory Study. J. Am. Chem. Soc. 2008, 130, 2130–2131. [Google Scholar] [CrossRef] [PubMed]
- Kopyra, J. Low energy electron attachment to the nucleotide deoxycytidine monophosphate: Direct evidence for the molecular mechanisms of electron-induced DNA strand breaks. Phys. Chem. Chem. Phys. 2012, 14, 8287–8289. [Google Scholar] [CrossRef]
- Sage, E.; Shikozono, N. Radiation-induced clustered DNA lesions: Repair and mutagenesis. Free Radic. Biol. Med. 2017, 107, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Theoretical Modeling of Radiation-Induced DNA Damage. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 1–40. ISBN 978-0-470-52627-9. [Google Scholar]
- Lehnert, S. Radiosensitizers and Radiochemotherapy in the Treatment of Cancer; CRC Press: Boca Raton, FL, USA, 2015; pp. 93–118. [Google Scholar]
- Rak, J.; Chomicz, L.; Wiczk, J.; Westphal, K.; Zdrowowicz, M.; Wityk, P.; Żyndul, M.; Makurat, S.; Golon, Ł. Mechanisms of damage to DNA labeled with electrophilic nucleobases induced by ionizing or uv radiation. J. Phys. Chem. B 2015, 119, 8227–8238. [Google Scholar] [CrossRef]
- Greenberg, M.M. Pyrimidine nucleobase radical reactivity in DNA and rna. Radiat. Phys. Chem. 2016, 128, 82–91. [Google Scholar] [CrossRef]
- Schurmann, R.; Vogel, S.; Ebel, K.; Bald, I. The physico-chemical basis of DNA radiosensitization-implications for cancer radiation therapy. Chem. Eur. J. 2018, 24, 1–10. [Google Scholar]
- Hong, I.S.; Ding, H.; Greenberg, M.M. Oxygen independent DNA interstrand cross-link formation by a nucleotide radical. J. Am. Chem. Soc. 2006, 128, 485–491. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.M.; Rode, A.B.; Han, E.J.; Hong, I.S.; Hong, S.H. 5-phenylselenyl- and 5-methylselenyl-methyl-2’-deoxyuridine induce oxidative stress, DNA damage, and caspase-2-dependent apoptosis in cancer cells. Apoptosis 2012, 17, 200–216. [Google Scholar] [CrossRef] [PubMed]
- Zdrowowicz, M.; Chomicz, L.; Żyndul, M.; Wityk, P.; Rak, J.; Wiegand, T.J.; Hanson, C.G.; Adhikary, A.; Sevilla, M.D. 5-thiocyanato-2’-deoxyuridine as a possible radiosensitizer: Electron-induced formation of uracil-c5-thiyl radical and its dimerization. Phys. Chem. Chem. Phys. 2015, 17, 16907–16916. [Google Scholar] [CrossRef] [PubMed]
- Makurat, S.; Zdrowowicz, M.; Chomicz-Ma’nka, L.; Kozak, W.; Serdiuk, I.E.; Wityk, P.; Kawecka, A.; Sosnowska, M.; Rak, J. 5-Selenocyanato and 5-trifluoromethanesulfonyl derivatives of 2′-deoxyuridine: Synthesis, radiation and computational chemistry as well as cytotoxicity. RSC Adv. 2018, 8, 21378–21388. [Google Scholar] [CrossRef]
- Bao, Q.; Chen, Y.; Zheng, Y.; Sanche, L. Cisplatin Radiosensitization of DNA Irradiated with 2–20 eV Electrons: Role of Transient Anions. J. Phys. Chem. C 2014, 118, 15516–15524. [Google Scholar] [CrossRef] [PubMed]
- Behmand, B.; Marignier, J.-L.; Mostafavi, M.; Wagner, J.R.; Hunting, D.J.; Sanche, L. Radiosensitization of DNA by Cisplatin Adducts Results from an Increase in the Rate Constant for the Reaction with Hydrated Electrons and Formation of Pt(I). J. Phys. Chem. B 2015, 119, 9496–9500. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Adhikary, A.; Kumar, A.; Becker, D.; Sevilla, M.D. Encyclopedia of Radicals in Chemistry, Biology and Materials; Chatgilialoglu, C., Struder, A., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2012; pp. 1371–1396. [Google Scholar]
- Bernhard, W.A. ‘Radical and Radical Ion Reactivity in Nucleic Acid Chemistry’; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 41–68. [Google Scholar]
- Close, D.M. ‘Radiation-induced Molecular Phenomena in Nucleic Acids: A Comprehensive Theoretical and Experimental Analysis’; Shukla, M.K., Leszczynski, J., Eds.; Springer: London, UK, 2008; pp. 493–529. [Google Scholar]
- Ma, J.; Marignier, J.-L.; Pernot, P.; Houée-Levin, C.; Kumar, A.; Sevilla, M.D.; Adhikary, A.; Mostafavi, M. Direct Observation of the Oxidation of DNA Bases by Phosphate Radical Formed Under Radiation: A Model of Backbone-to-base Hole Transfer. Phys. Chem. Chem. Phys. 2018, 20, 14927–14937. [Google Scholar] [CrossRef]
- Adhikary, A.; Kumar, A.; Bishop, C.T.; Wiegand, T.J.; Hindi, R.M.; Adhikary, A.; Sevilla, M.D. π-Radical to σ-Radical Tautomerization in One-Electron-Oxidized 1-Methylcytosine and Its Analogs. J. Phys. Chem. B 2015, 119, 11496–11505. [Google Scholar] [CrossRef]
- Adhikary, A.; Kumar, A.; Becker, D.; Sevilla, M.D. The Guanine Cation Radical: Investigation of Deprotonation States by ESR and DFT. J. Phys. Chem. B 2006, 110, 24171–24180. [Google Scholar] [CrossRef]
- Adhikary, A.; Khanduri, D.; Sevilla, M.D. Direct observation of the protonation state and hole localization site in DNA-oligomers. J. Am. Chem. Soc. 2009, 131, 8614–8619. [Google Scholar] [CrossRef]
- Adhikary, A.; Kumar, A.; Munafo, S.A.; Khanduri, D.; Sevilla, M.D. Prototropic Equilibria in DNA Containing One-electron Oxidized GC: Intra-duplex vs. Duplex to Solvent Deprotonation. Phys. Chem. Chem. Phys. 2010, 12, 5353–5368. [Google Scholar] [CrossRef] [PubMed]
- Adhikary, A.; Kumar, A.; Khanduri, D.; Sevilla, M.D. The effect of base stacking on the acid-base properties of the adenine cation radical [A•+] in solution: ESR and DFT studies. J. Am. Chem. Soc. 2008, 130, 10282–10292. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Adhikary, A.; Khanduri, D.; Pottiboyina, V.; Rice, C.T.; Sevilla, M.D. Formation of aminyl radicals on electron attachment to AZT: Abstraction from the sugar phosphate backbone vs. one-electron oxidation of Guanine. J. Phys. Chem. B 2010, 114, 9289–9299. [Google Scholar] [CrossRef] [PubMed]
- Mudgal, M.; Rishi, S.; Lumpuy, D.A.; Curran, K.A.; Varley, K.L.; Sobczak, A.J.; Dang, T.P.; Sulimoff, N.; Kumar, A.; Sevilla, M.D.; et al. Prehydrated One-electron Attachment to Azido-modified Pentofuranoses: Aminyl Radical Formation, Rapid H-atom Transfer and Subsequent Ring Opening. J. Phys. Chem. B 2017, 121, 4968–4980. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Peng, J.; Tuttle, P.; Ren, Y.; Garcia, C.; Debnath, D.; Rishi, S.; Hanson, C.; Ward, S.; Kumar, A.; et al. Electron-mediated Aminyl and Iminyl Radicals from C5-Azido-Modified Pyrimidine Nucleosides Augment Radiation Damage to Cancer Cells. Org. Lett. 2018, 20, 7400–7404. [Google Scholar] [CrossRef] [PubMed]
- Jagetia, G.C.; Aruna, R. Correlation of micronuclei-induction with the cell survival in HeLa cells treated with a base analogue, azidothymidine (AZT) before exposure to different doses of gamma-radiation. Toxicol. Lett. 2003, 139, 33–43. [Google Scholar] [CrossRef]
- Coucke, P.A.; Cottin, E.; Decosterd, L.A. Simultaneous alteration of de novo and salvage pathway to the deoxynucleoside triphosphate pool by (e)-2′-deoxy-(fluoromethylene)cytidine (fmdc) and zidovudine (azt) results in increased radiosensitivity in vitro. Acta Oncol. 2007, 46, 612–620. [Google Scholar] [CrossRef] [PubMed]
- Liao, Z.-K.; Zhou, F.-X.; Luo, Z.-G.; Zhang, W.-J.; Jie, X.; Bao, J.; Han, G.; Zhang, M.-S.; Xie, C.-H.; Zhou, Y.-F. Radio-activation of htert promoter in larynx squamous carcinoma cells: An ‘indirected-activator’ strategy in radio-gene-therapy. Oncol. Rep. 2008, 19, 281–286. [Google Scholar]
- Zhou, F.-X.; Liao, Z.-K.; Dai, J.; Jie, X.; Xie, C.-H.; Luo, Z.-G.; Liu, S.-Q.; Zhou, Y.-F. Radiosensitization effect of zidovudine on human malignant glioma cells. Biochem. Biophys. Res. Commun. 2007, 354, 351–356. [Google Scholar] [CrossRef]
- Westphal, E.M.; Blackstock, W.; Feng, W.; Israel, B.; Kenney, S.C. Activation of lytic Epstein-Barr virus (EBV) infection by radiation and sodium butyrate in vitro and in vivo: A potential method for treating EBV-positive malignancies. Cancer Res. 2000, 60, 5781–5788. [Google Scholar]
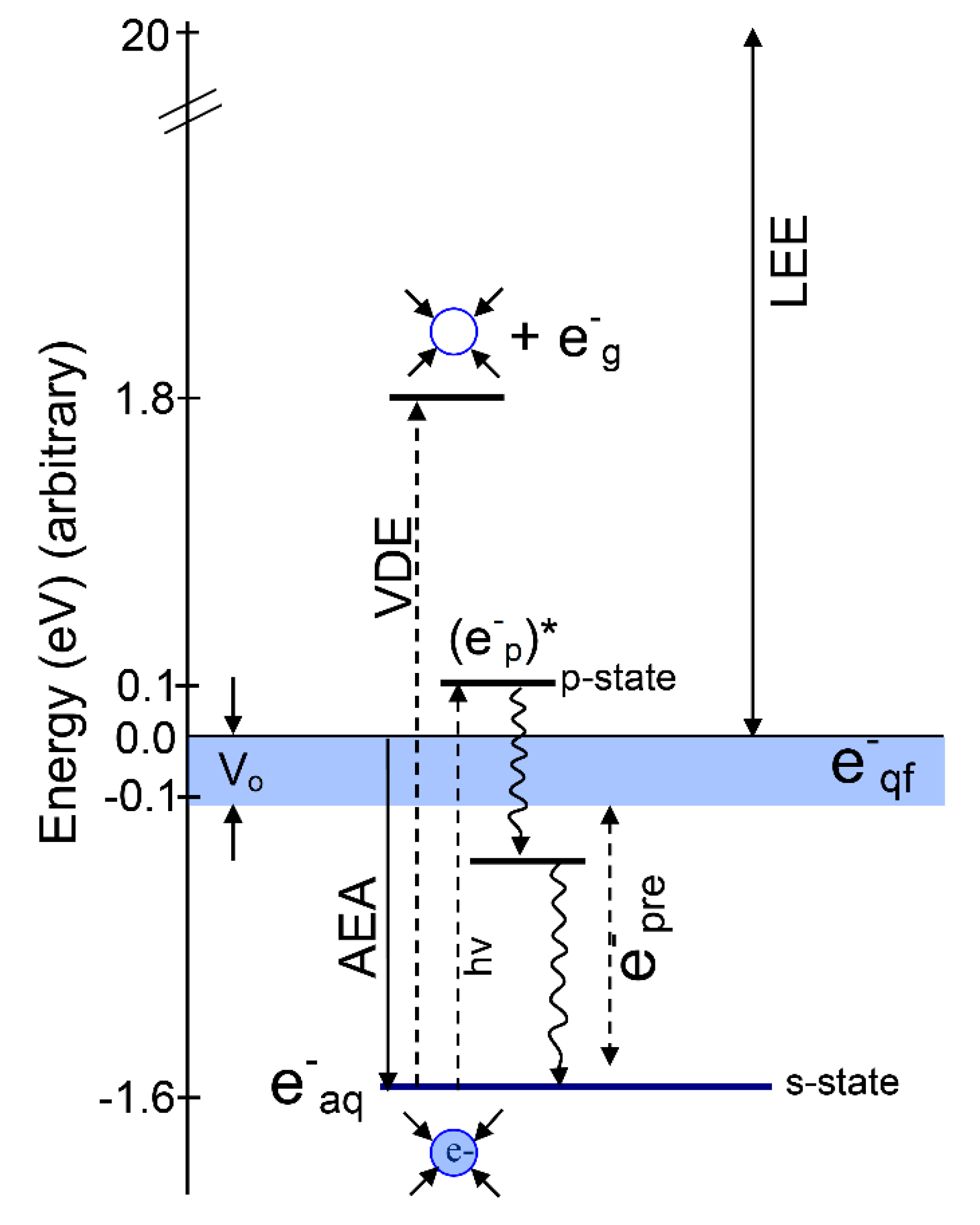
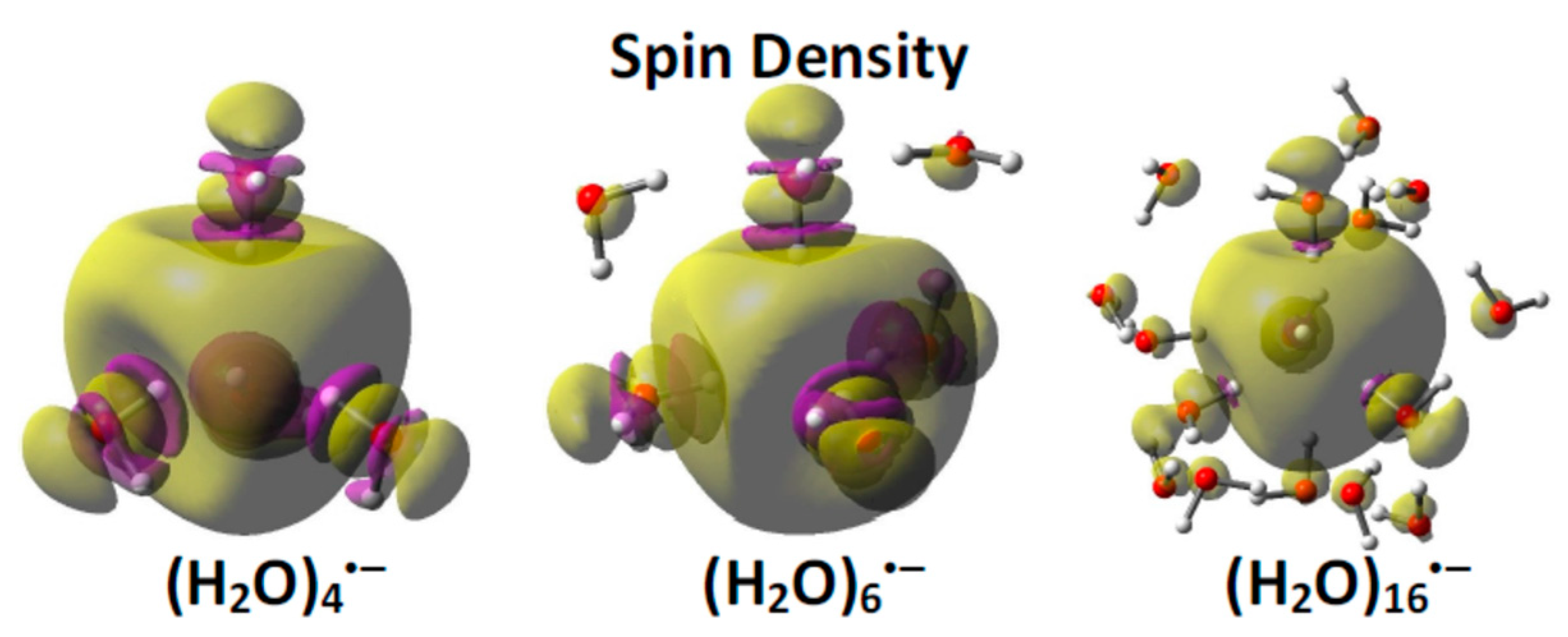
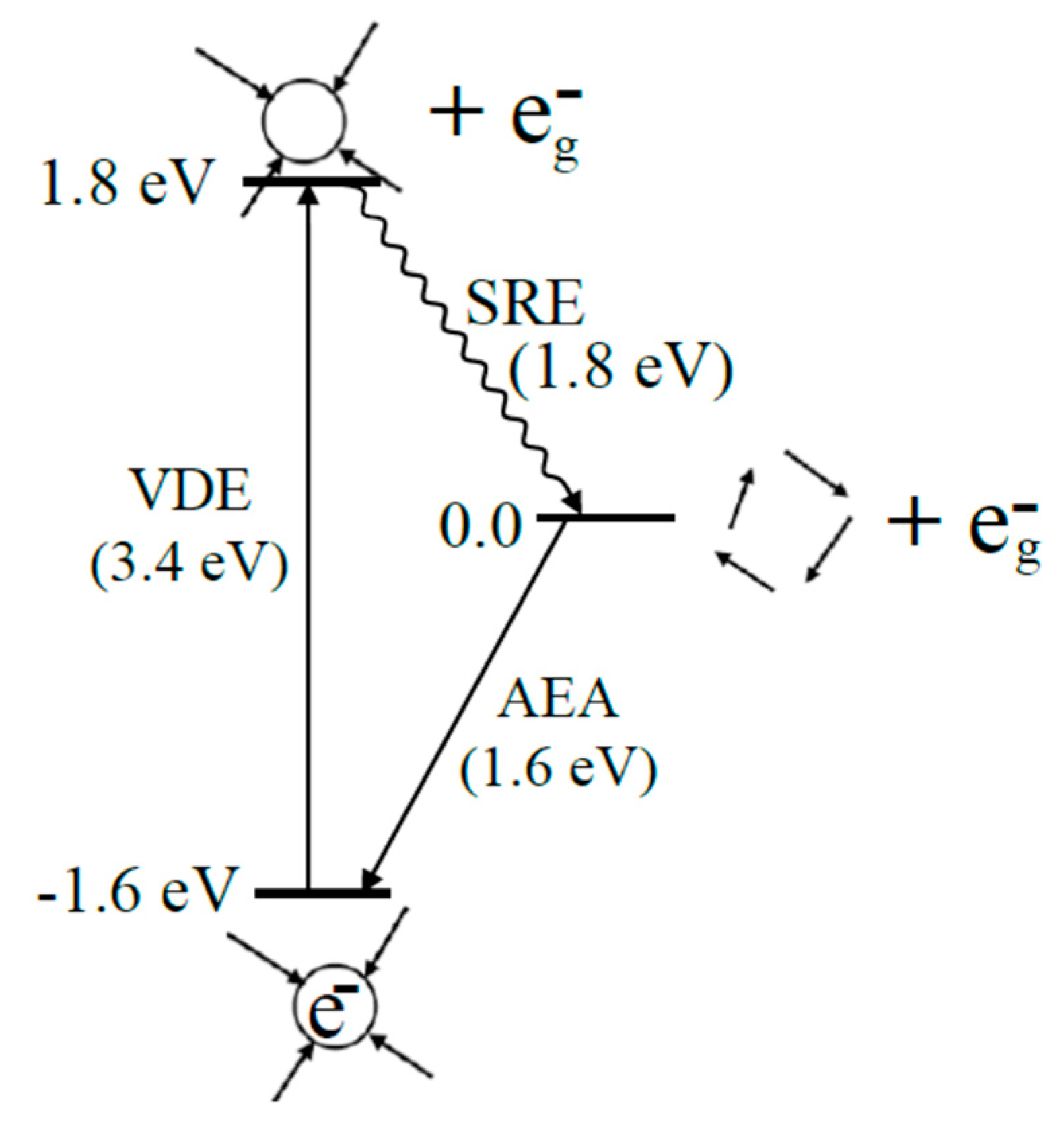
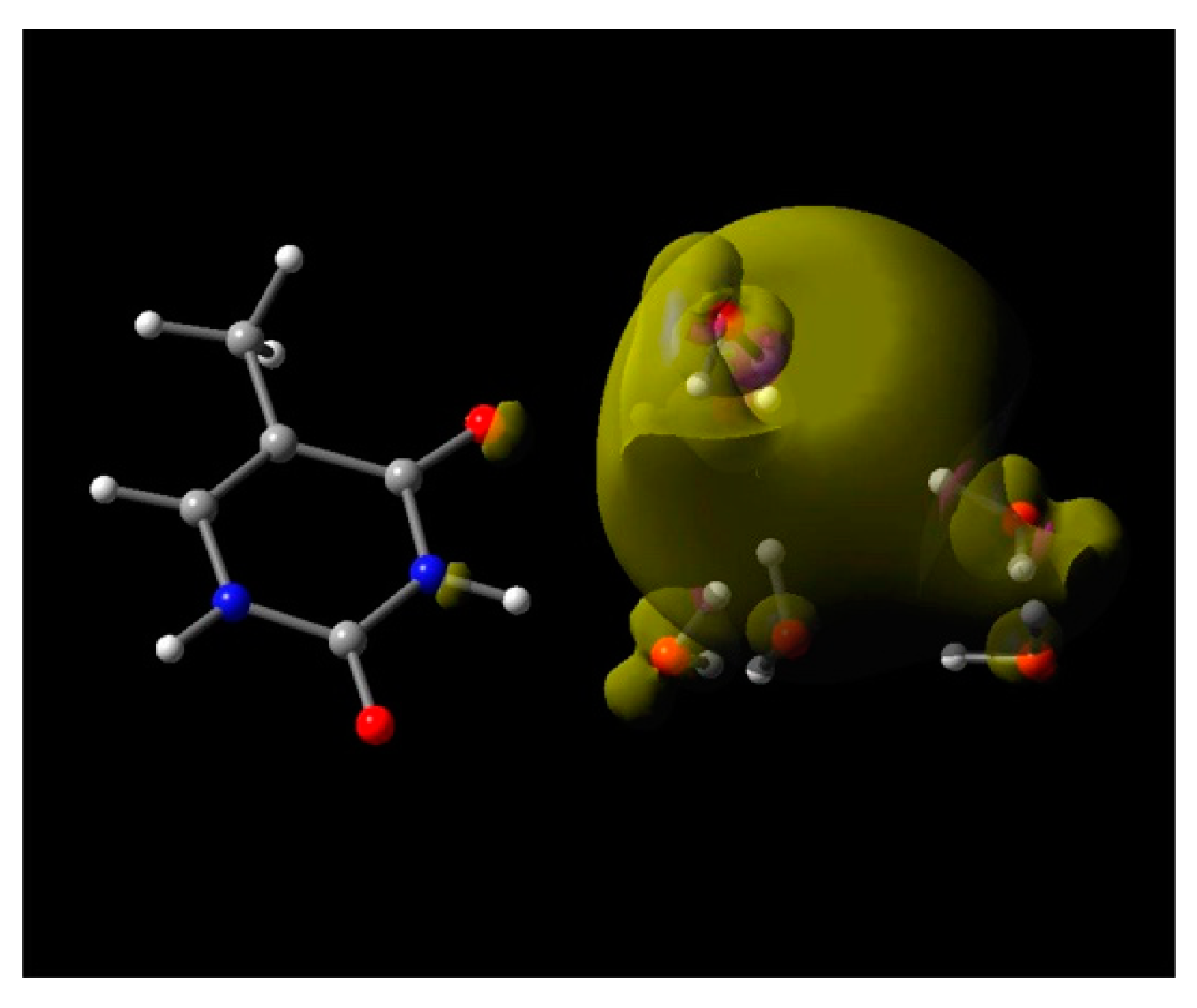
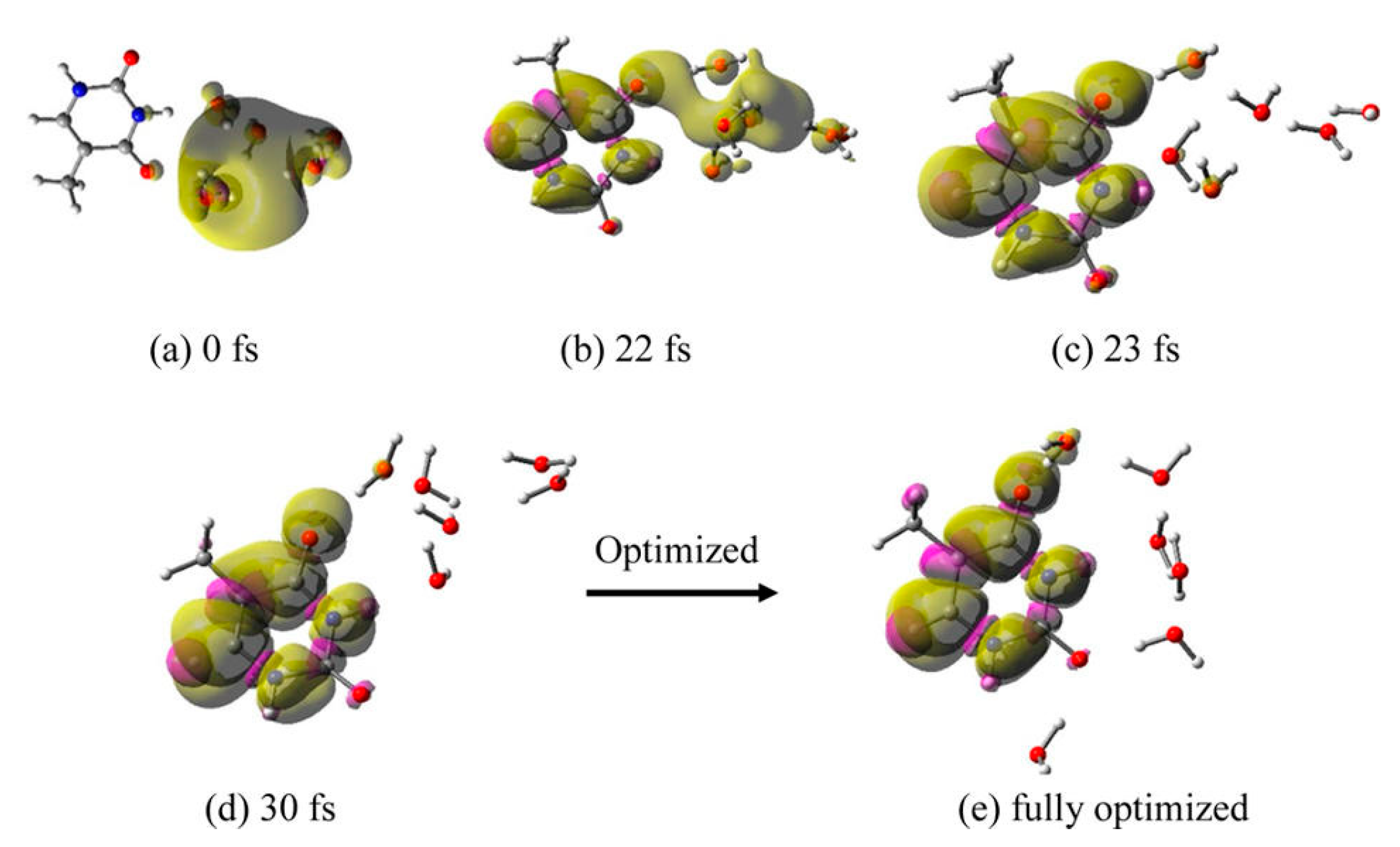
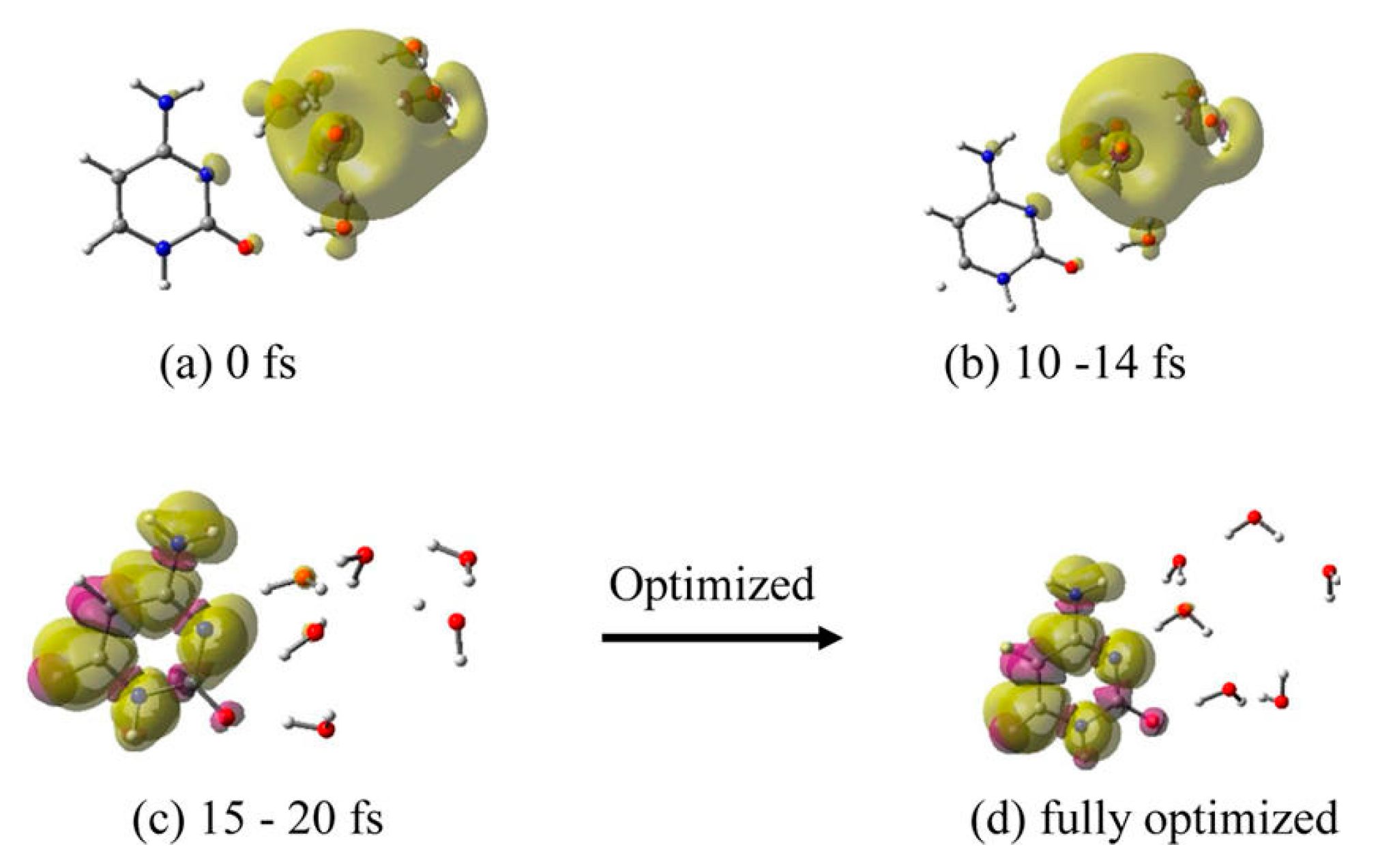
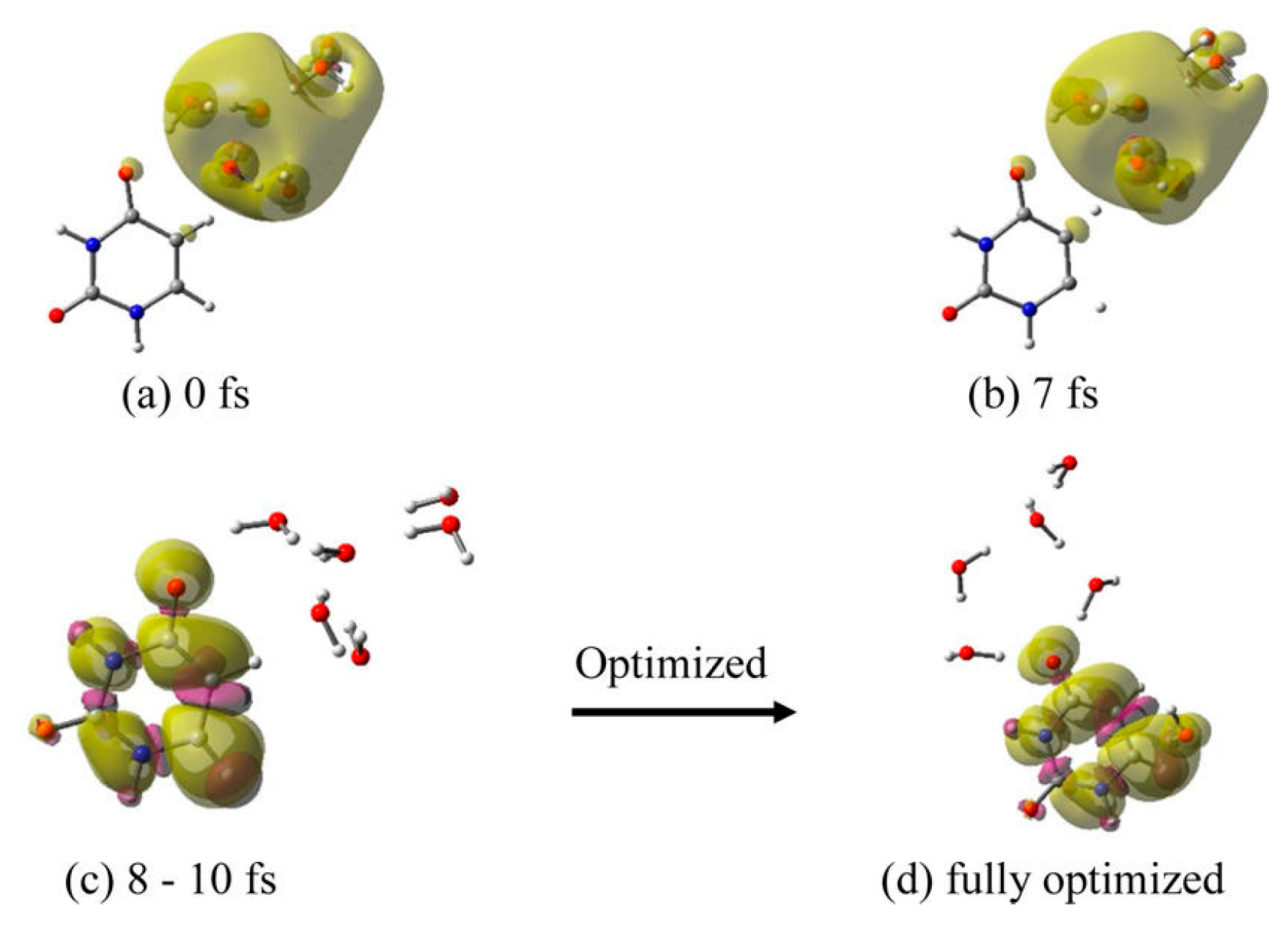
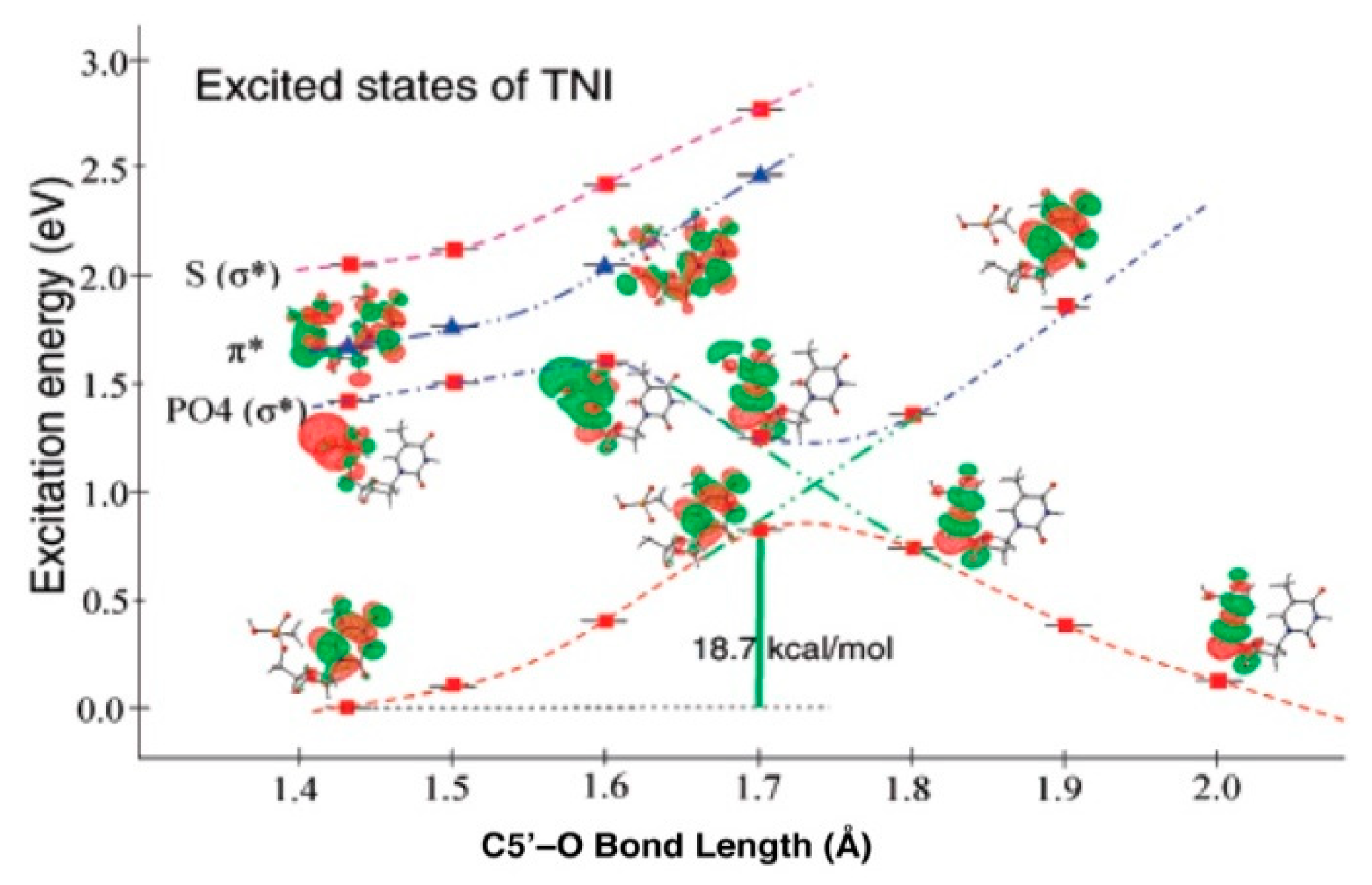
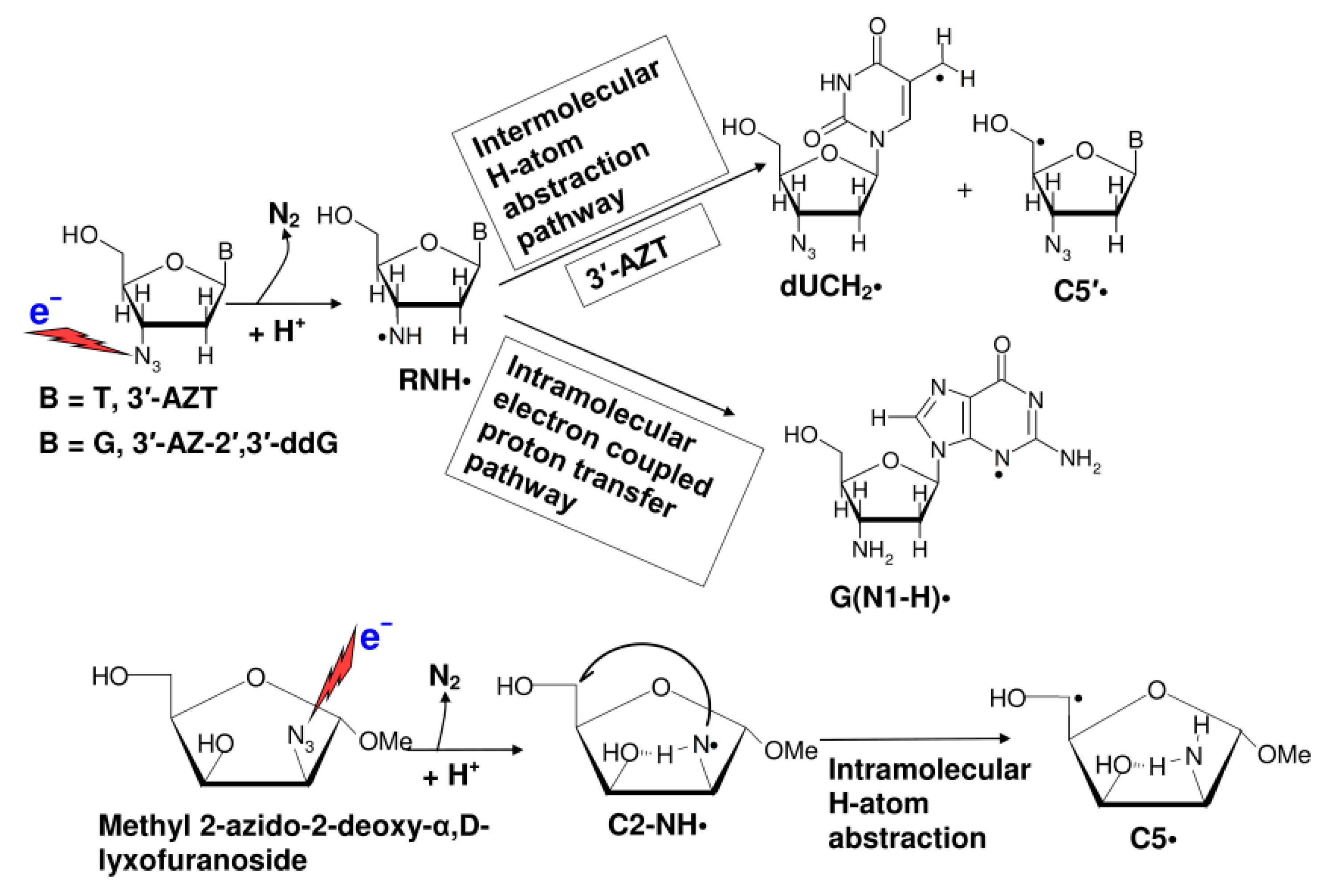
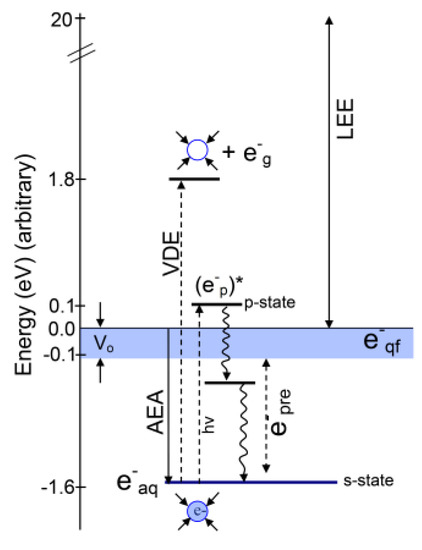
| Properties | Experiment | LGS (Non-Cavity) | TB (Cavity) | 4-H2O (Cavity) s |
|---|---|---|---|---|
| VDE (eV) | 3.3–3.6 d | 5.19 ± 0.07 r | 2.69 ± 0.01 r | 3.45 |
| Rg (Å) | 2.48 e; 2.35 f | 2.46 ± 0.04 r | 2.388 ± 0.003 r | 2.25–2.5 |
| λ (eV) a | 1.728 g,h | 1.71 ± 0.06 r | 1.940 ± 0.007 r | 1.72 t |
| dEMAX/dT (eV/K) b | −2.2 × 10−3 i | −5.2 × 10−3 r | −(1.9 ± 0.6) ×10−4 r | |
| V (cm3/mol) c | +26 j +26 ± 6 u | −116 ± 27 r | +31 ± 12 r | |
| Resonance Raman Shift (cm−1) | 200 k | ~200 | ||
| EPR g-factor shift (ppm) | −1900 l −1700 m | −1000 to −1350 | ||
| HFCC (Gauss) | Aiso = −0.92 n Bzz = 7.0 | Aiso = −0.6 Bzz = 7.0 | ||
| ΔhydG* (kcal/mol) | −36.3 o | −37.8 to −38.9 | ||
| ΔhydH* (kcal/mol) | −30.2 o | −29.9 to −31.7 | ||
| ΔhydS * (cal/(mol·deg)) | 20.5 o | 26.6–24.0 | ||
| Eo (V) | −2.95 p −2.87 q | −2.86 |
| Eo Versus SHE (V) | |||||
|---|---|---|---|---|---|
| Theory | |||||
| G4 | B3LYP b | Exp. a | |||
| PCM ε = 78 | PCM ε = 37 | PCM ε = 78 | |||
| Base | No water i | Waters (n) d | “DMF” f | No water i | DMF |
| G | −2.84 (−3.31) c | −2.62 (3); −2.66 (2) | −2.86 (ca.−3.0) g | −2.89 | < −2.76 |
| A | −2.78 (−2.86) c | −2.57 (3) e | −2.81 (−2.71) g | −2.78 | −2.52 |
| C | −2.44 (−2.41) c | −2.31 (2) | −2.48 (−2.56) g | −2.49 | −2.35 |
| T | −2.42 (−2.31) c | −2.34 (2) | −2.45 (−2.32) g | −2.37 | −2.18 |
| U | −2.33 | −2.05 (2) | −2.36 | −2.30 | −2.07 |
| MUE h | 0.24(0.20) V | 0.07 V | 0.22 (0.20V) | 0.16 V | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Becker, D.; Adhikary, A.; Sevilla, M.D. Reaction of Electrons with DNA: Radiation Damage to Radiosensitization. Int. J. Mol. Sci. 2019, 20, 3998. https://doi.org/10.3390/ijms20163998
Kumar A, Becker D, Adhikary A, Sevilla MD. Reaction of Electrons with DNA: Radiation Damage to Radiosensitization. International Journal of Molecular Sciences. 2019; 20(16):3998. https://doi.org/10.3390/ijms20163998
Chicago/Turabian StyleKumar, Anil, David Becker, Amitava Adhikary, and Michael D. Sevilla. 2019. "Reaction of Electrons with DNA: Radiation Damage to Radiosensitization" International Journal of Molecular Sciences 20, no. 16: 3998. https://doi.org/10.3390/ijms20163998
APA StyleKumar, A., Becker, D., Adhikary, A., & Sevilla, M. D. (2019). Reaction of Electrons with DNA: Radiation Damage to Radiosensitization. International Journal of Molecular Sciences, 20(16), 3998. https://doi.org/10.3390/ijms20163998