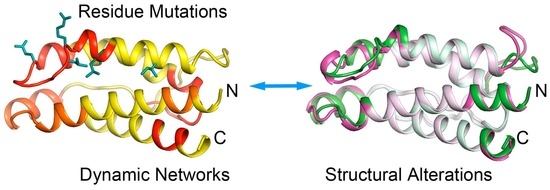
Site-Mutation of Hydrophobic Core Residues Synchronically Poise Super Interleukin 2 for Signaling: Identifying Distant Structural Effects through Affordable Computations
Abstract
1. Introduction
2. Results
2.1. The Correlation Pattern in CypA Detected by MD Simulation Coincides with the Experimentally Detected Dynamic Networks
2.2. The Cooperative Networks in CypA Are also Consistent with the Experimentally Detected Dynamic Networks
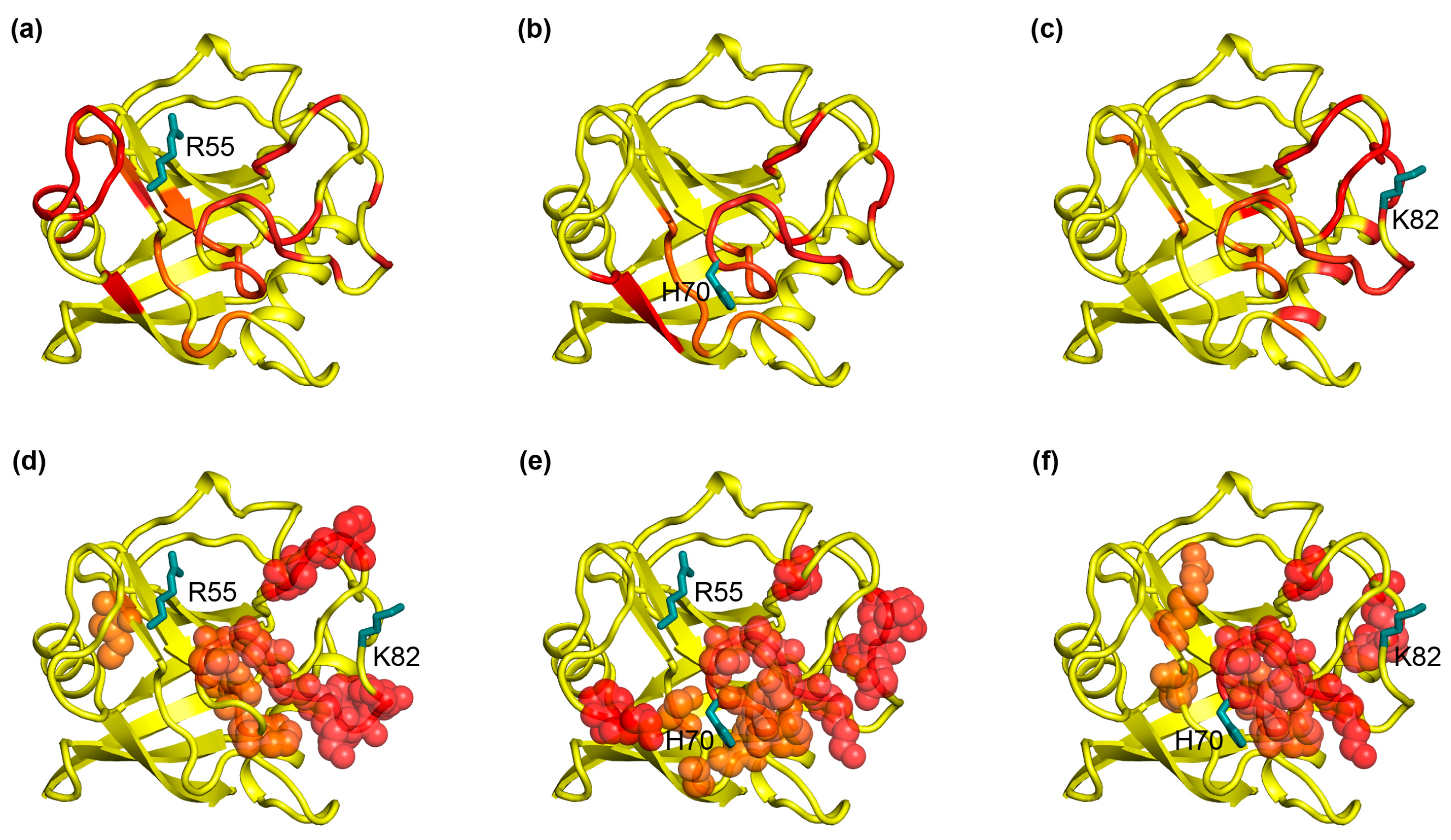
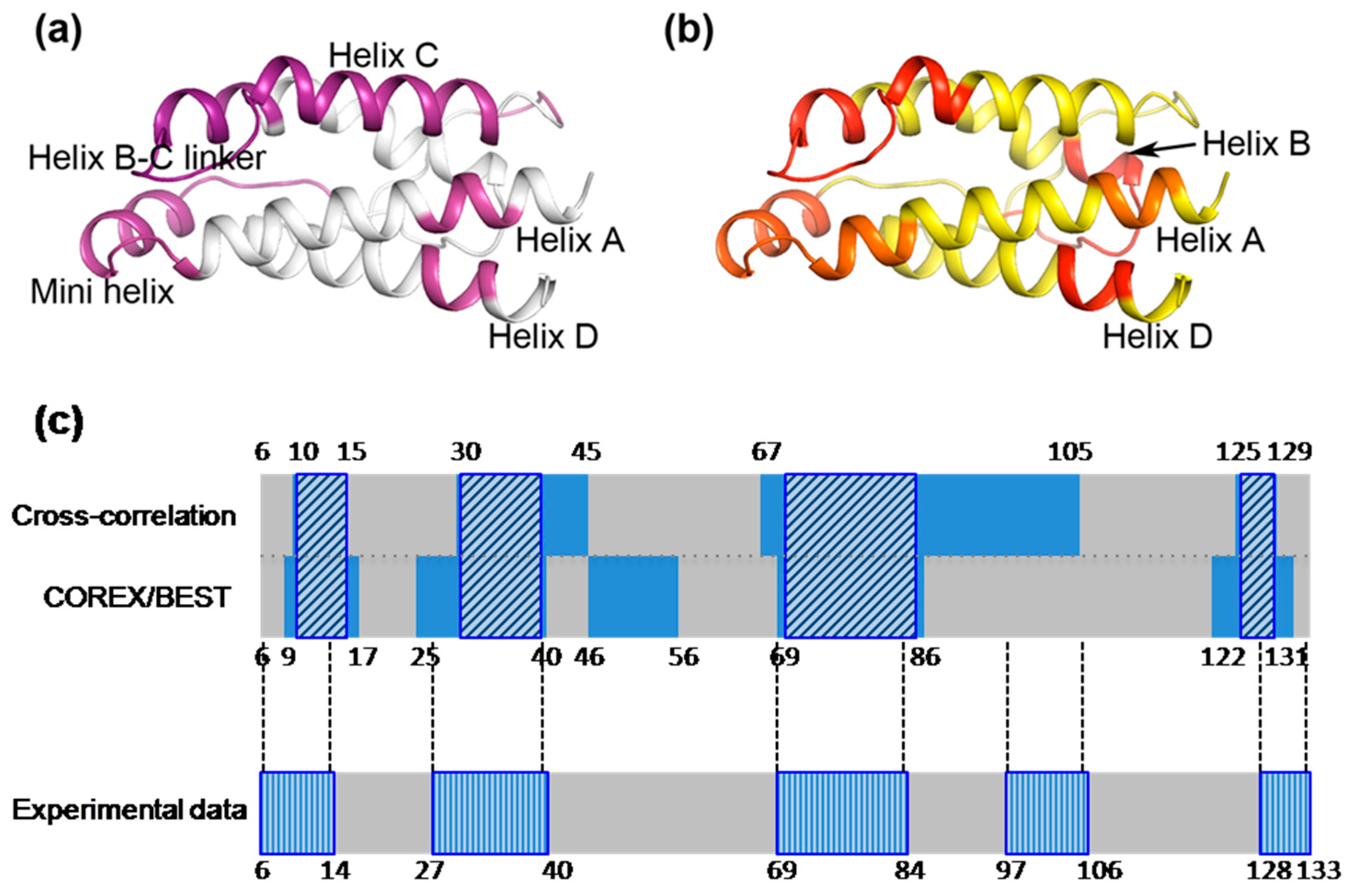
2.3. The Dynamic Networks in IL-2 Identified from Cross-Correlation Analysis
2.4. The Dynamic Networks in IL-2 Deduced According to COREX/BEST Algorithm
2.5. The Calculated Dynamic Networks in IL-2 Coincide with the Regions Undergoing Structure Alterations Caused by the Mutations
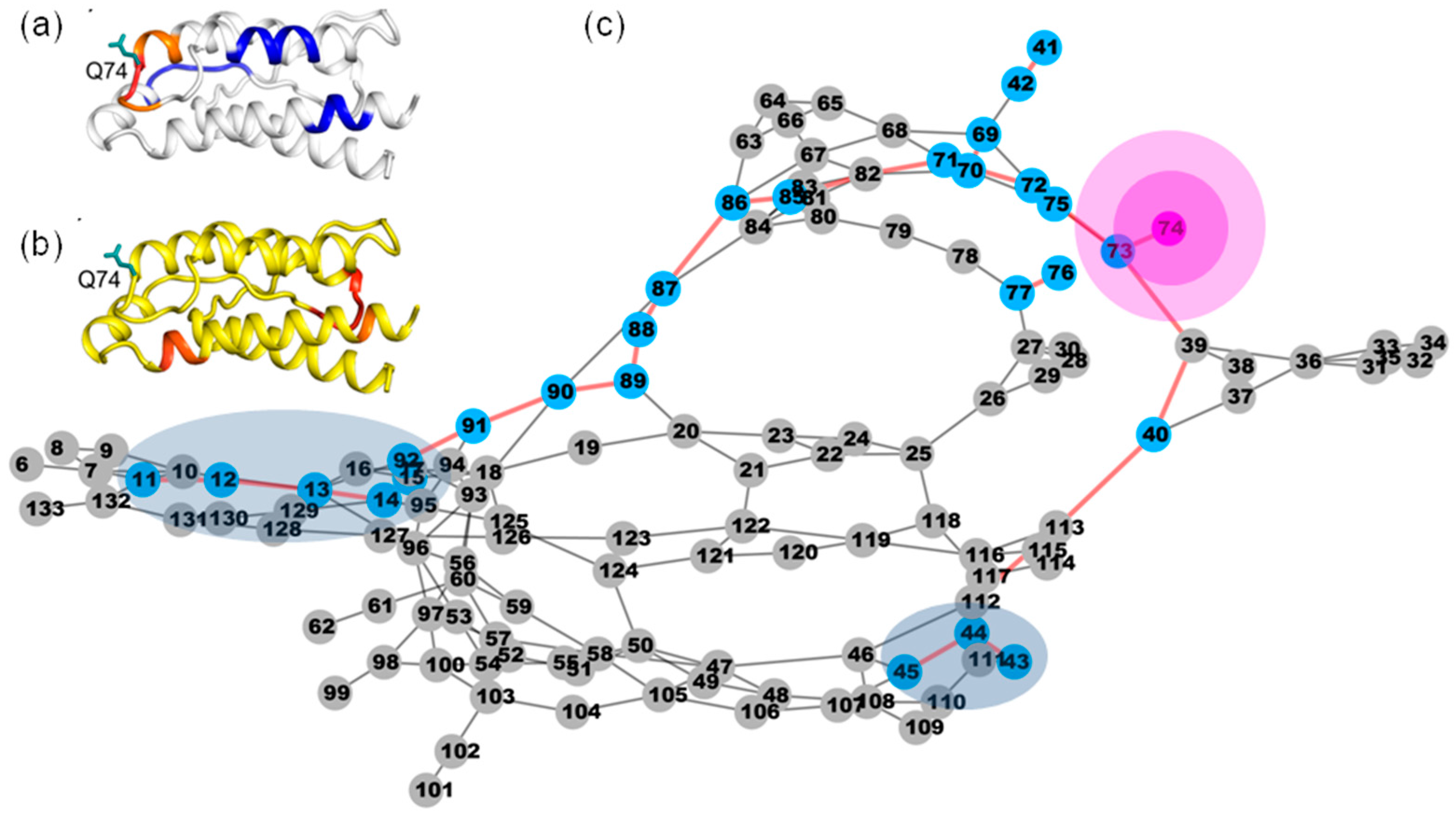
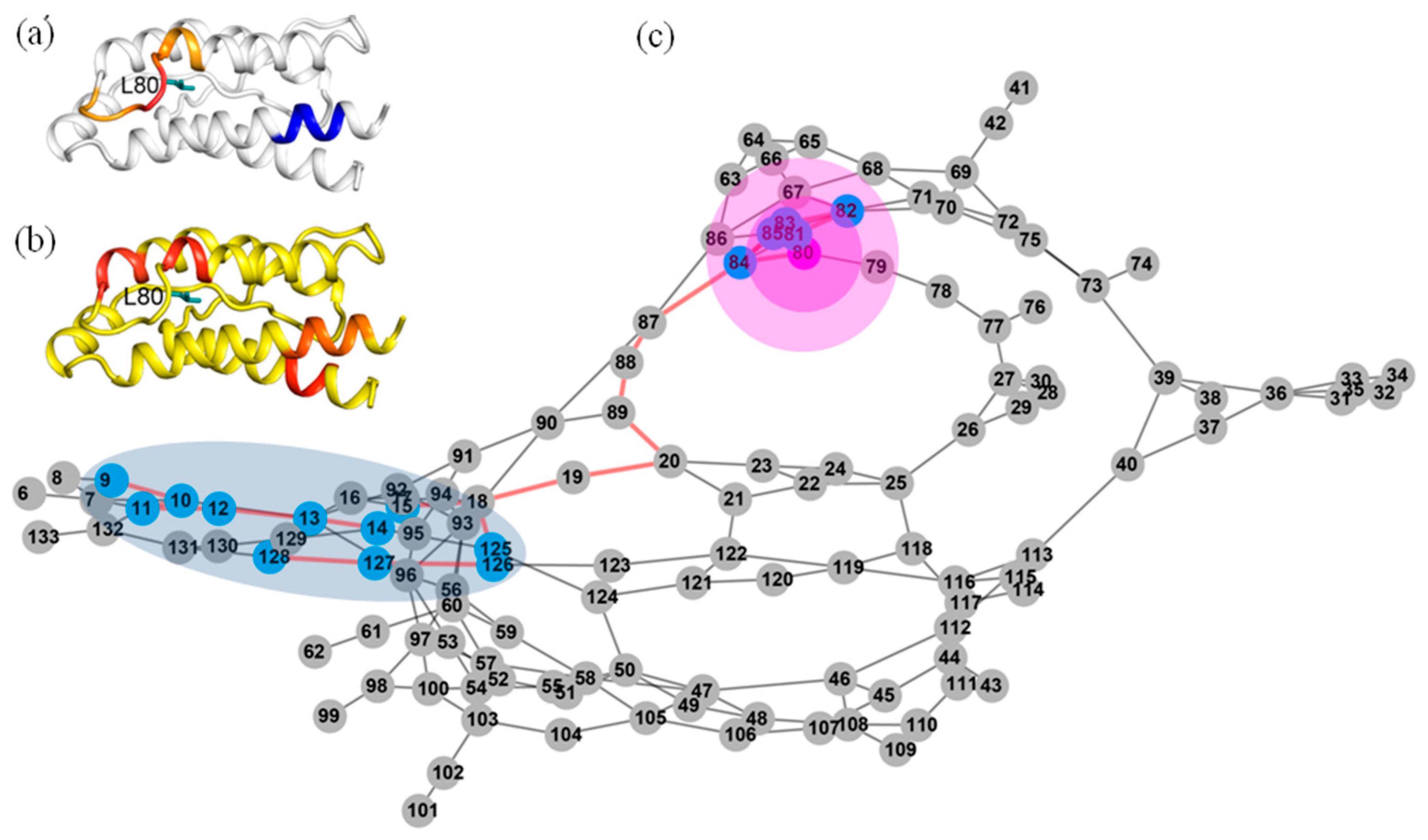
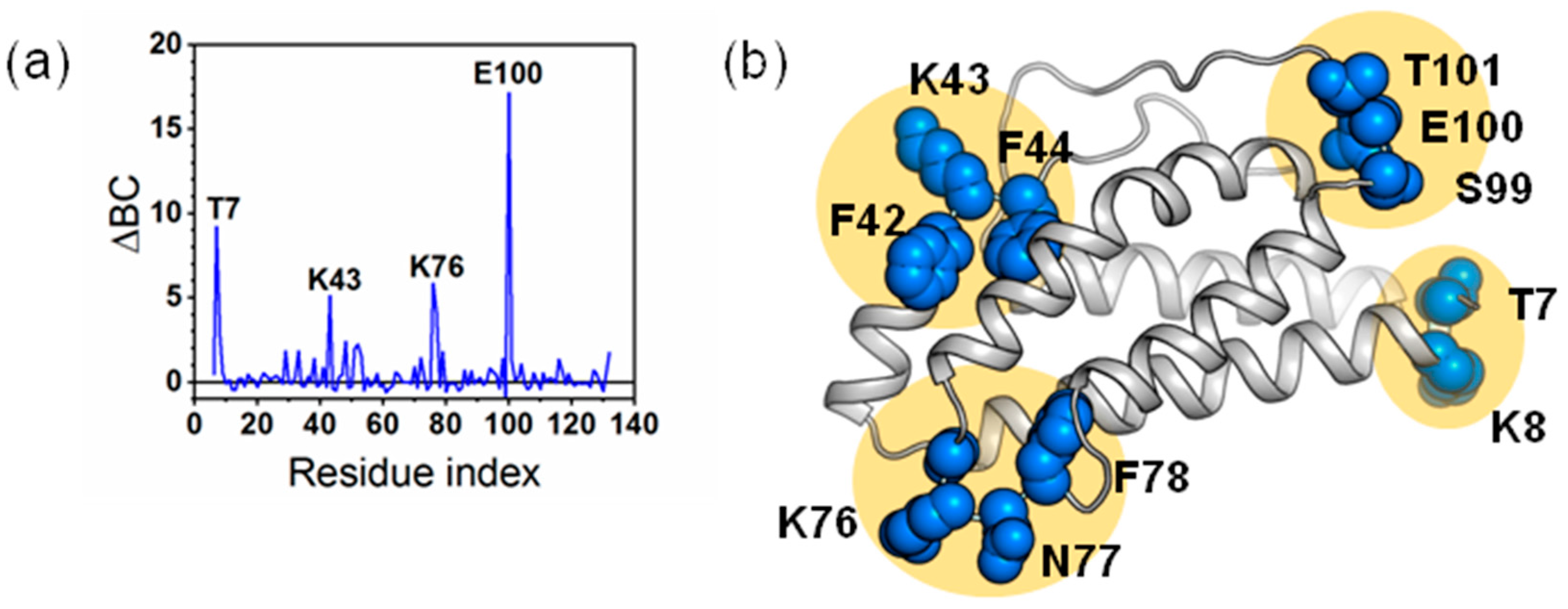
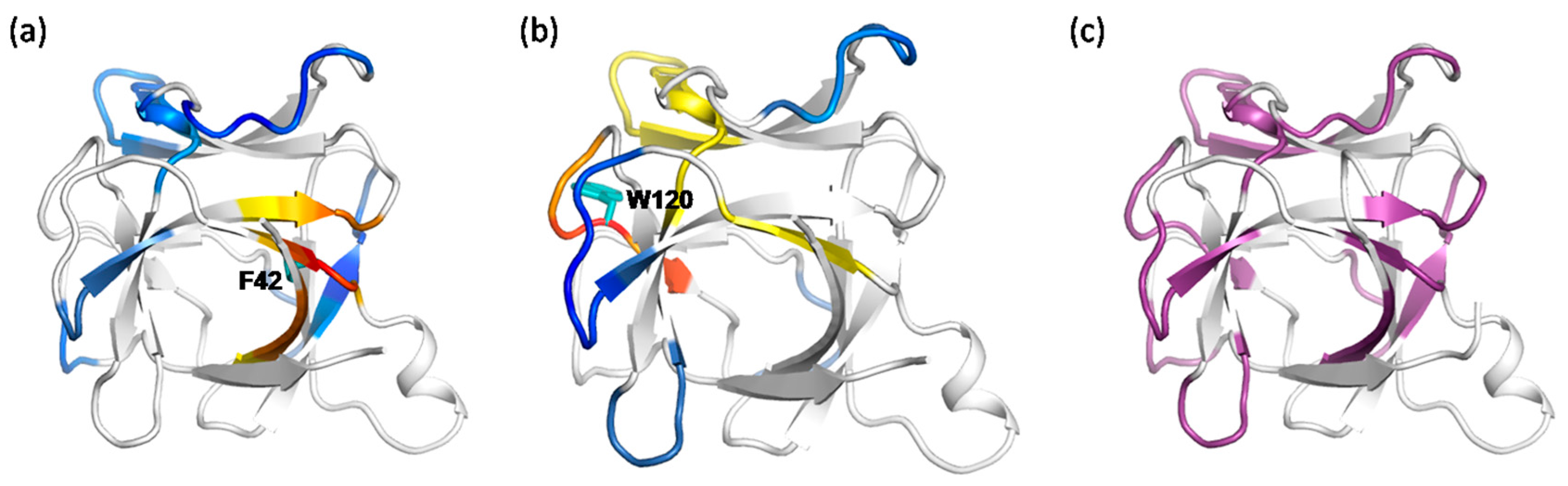
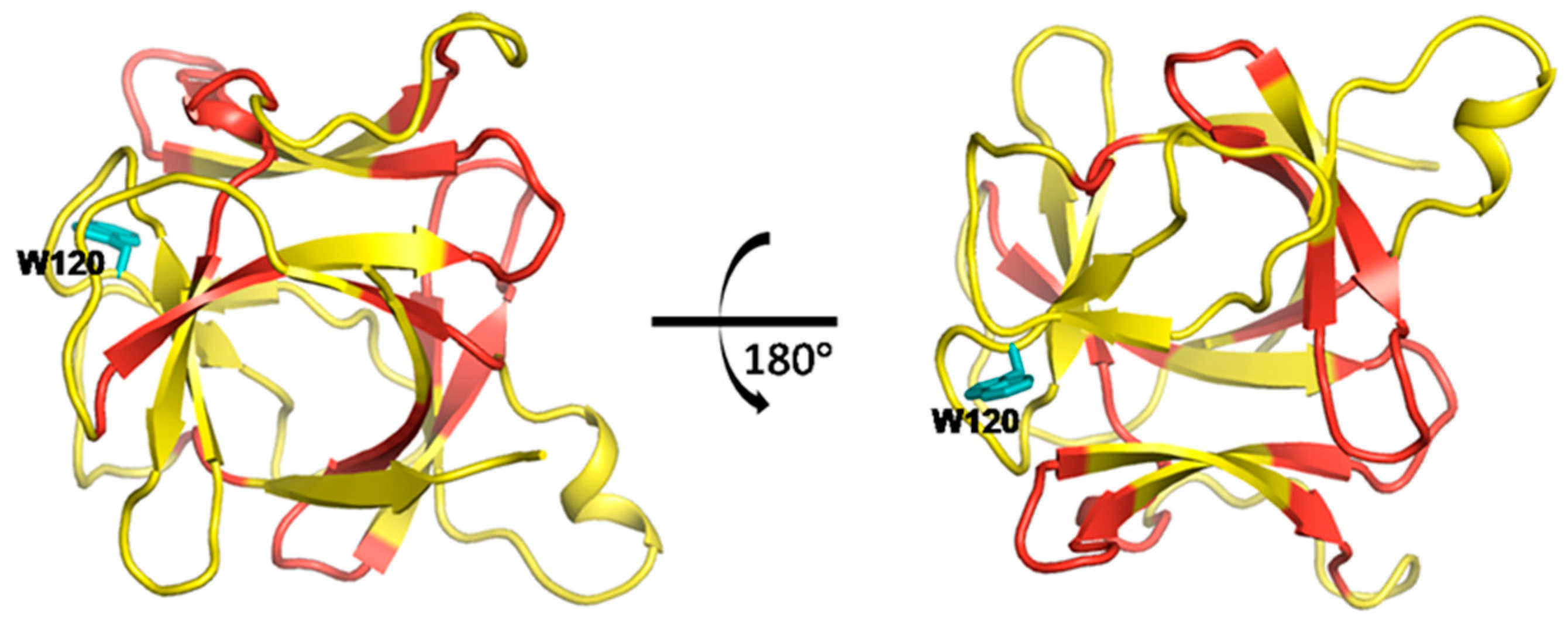
2.6. Identifying Allosteric Pathways in the Superkine
2.7. Most of the Mutated Residues in Superkine are Critical Ones in the Interaction Network
2.8. Application of Identifying Distant Structural Effect through Nanosecond Time Scale MD Simulations
2.8.1. The Dynamic Network in IL-1β Identified by Cross-Correlation Analysis
2.8.2. The Dynamic Network in IL-1β Deduced by COREX/BEST Algorithm
2.8.3. The Calculated Dynamic Networks in IL-1β Coincide with the Structural Alteration Regions Caused by the Mutations
3. Discussion
4. Materials and Methods
4.1. Structure Preparation
4.2. Molecular Dynamics Simulation and the Residue Dynamic Network Therein
4.2.1. Obtaining Trajectories from Nanosecond All-Atomic MD Simulations
4.2.2. Dynamical Network in Cross Correlation from MD Trajectory
4.3. Analysis of the Dynamic Network According to Graph Theory but from MD Simulation Data
4.3.1. Presentation of Dynamic Networks and Determination of Optimal Propagation Paths
4.3.2. Recognizing the Critical Residues in the Dynamic Network
4.4. Deriving the Dynamics Network from Cooperative Effects Based on Native State Ensembles
4.4.1. Generation of the Native State Ensemble
4.4.2. Quantization of Site Mutation Effects on All Other Residues
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| NMR | Nuclear Magnetic Resonance |
| CypA | cyclophilin A |
| IL-2 | Interleukin-2 |
| MD | Molecular dynamics |
| EAM | ensemble allosteric model |
References
- Rosenfeld, L.; Heyne, M.; Shifman, J.M.; Papo, N. Protein Engineering by Combined Computational and In Vitro Evolution Approaches. Trends Biochem. Sci. 2016, 41, 421–433. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, E.; Heyne, M.; Bakhman, A.; Kosloff, M.; Shifman, J.M.; Papo, N. Identifying Residues that Determine SCF Molecular-Level Interactions through a Combination of Experimental and In silico Analyses. J. Mol. Biol. 2017, 429, 97–114. [Google Scholar] [CrossRef] [PubMed]
- Murciano-Calles, J.; McLaughlin, M.E.; Erijman, A.; Hooda, Y.; Chakravorty, N.; Martinez, J.C.; Shifman, J.M.; Sidhu, S.S. Alteration of the C-terminal ligand specificity of the erbin PDZ domain by allosteric mutational effects. J. Mol. Biol. 2014, 426, 3500–3508. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-Oses, G.; Osuna, S.; Gao, X.; Sawaya, M.R.; Gilson, L.; Collier, S.J.; Huisman, G.W.; Yeates, T.O.; Tang, Y.; Houk, K.N. The role of distant mutations and allosteric regulation on LovD active site dynamics. Nat. Chem. Biol. 2014, 10, 431–436. [Google Scholar] [CrossRef] [PubMed]
- Humrich, J.Y.; Riemekasten, G. Clinical trials: The rise of IL-2 therapy—A novel biologic treatment for SLE. Nat. Rev. Rheumatol. 2016, 12, 695–696. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Zhang, X.; Wei, Y.; Sun, X.; Chen, Y.; Deng, J.; Jin, Y.; Gan, Y.; Hu, X.; Jia, R.; et al. Low-dose interleukin-2 treatment selectively modulates CD4(+) T cell subsets in patients with systemic lupus erythematosus. Nat. Med. 2016, 22, 991–993. [Google Scholar] [CrossRef] [PubMed]
- Klatzmann, D.; Abbas, A.K. The promise of low-dose interleukin-2 therapy for autoimmune and inflammatory diseases. Nat. Rev. Immunol. 2015, 15, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Koreth, J.; Matsuoka, K.; Kim, H.T.; McDonough, S.M.; Bindra, B.; Alyea, E.P., 3rd; Armand, P.; Cutler, C.; Ho, V.T.; Treister, N.S.; et al. Interleukin-2 and regulatory T cells in graft-versus-host disease. N. Engl. J. Med. 2011, 365, 2055–2066. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Strick-Marchand, H.; Lim, A.I.; Ren, J.; Masse-Ranson, G.; Dan, L.; Jouvion, G.; Rogge, L.; Lucas, S.; Bin, L.; et al. Regulatory T cells control toxicity in a humanized model of IL-2 therapy. Nat. Commun. 2017, 8, 1762. [Google Scholar] [CrossRef] [PubMed]
- Liao, W.; Lin, J.X.; Leonard, W.J. Interleukin-2 at the crossroads of effector responses, tolerance, and immunotherapy. Immunity 2013, 38, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Malek, T.R. The biology of interleukin-2. Annu. Rev. Immunol. 2008, 26, 453–479. [Google Scholar] [CrossRef] [PubMed]
- Levin, A.M.; Bates, D.L.; Ring, A.M.; Krieg, C.; Lin, J.T.; Su, L.; Moraga, I.; Raeber, M.E.; Bowman, G.R.; Novick, P.; et al. Exploiting a natural conformational switch to engineer an interleukin-2 ‘superkine’. Nature 2012, 484, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Lockless, S.W.; Ranganathan, R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science 1999, 286, 295–299. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.N.; Elfstrom, L.; Shi, Y.; Snall, T.; Engstrom, A.; Jemth, P. Reassessing a sparse energetic network within a single protein domain. Proc. Natl. Acad. Sci. USA 2008, 105, 4679–4684. [Google Scholar] [CrossRef] [PubMed]
- Fuentes, E.J.; Gilmore, S.A.; Mauldin, R.V.; Lee, A.L. Evaluation of energetic and dynamic coupling networks in a PDZ domain protein. J. Mol. Biol. 2006, 364, 337–351. [Google Scholar] [CrossRef] [PubMed]
- O’Rourke, K.F.; Gorman, S.D.; Boehr, D.D. Biophysical and computational methods to analyze amino acid interaction networks in proteins. Comput. Struct. Biotechnol. J. 2016, 14, 245–251. [Google Scholar] [CrossRef] [PubMed]
- Axe, J.M.; Yezdimer, E.M.; O’Rourke, K.F.; Kerstetter, N.E.; You, W.; Chang, C.E.; Boehr, D.D. Amino acid networks in a (β/α)(8) barrel enzyme change during catalytic turnover. J. Am. Chem. Soc. 2014, 136, 6818–6821. [Google Scholar] [CrossRef] [PubMed]
- Clarkson, M.W.; Gilmore, S.A.; Edgell, M.H.; Lee, A.L. Dynamic coupling and allosteric behavior in a nonallosteric protein. Biochemistry 2006, 45, 7693–7699. [Google Scholar] [CrossRef] [PubMed]
- Proctor, E.A.; Kota, P.; Aleksandrov, A.A.; He, L.; Riordan, J.R.; Dokholyan, N.V. Rational Coupled Dynamics Network Manipulation Rescues Disease-Relevant Mutant Cystic Fibrosis Transmembrane Conductance Regulator. Chem. Sci. 2015, 6, 1237–1246. [Google Scholar] [CrossRef] [PubMed]
- Vijayabaskar, M.S.; Vishveshwara, S. Interaction energy based protein structure networks. Biophys. J. 2010, 99, 3704–3715. [Google Scholar] [CrossRef] [PubMed]
- Eisenmesser, E.Z.; Millet, O.; Labeikovsky, W.; Korzhnev, D.M.; Wolf-Watz, M.; Bosco, D.A.; Skalicky, J.J.; Kay, L.E.; Kern, D. Intrinsic dynamics of an enzyme underlies catalysis. Nature 2005, 438, 117–121. [Google Scholar] [CrossRef] [PubMed]
- Manley, G.; Rivalta, I.; Loria, J.P. Solution NMR and computational methods for understanding protein allostery. J. Phys. Chem. B 2013, 117, 3063–3073. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yu, B.; Martins, I.R.; Li, P.; Amarasinghe, G.K.; Umetani, J.; Fernandez-Zapico, M.E.; Billadeau, D.D.; Machius, M.; Tomchick, D.R.; Rosen, M.K. Structural and energetic mechanisms of cooperative autoinhibition and activation of Vav1. Cell 2010, 140, 246–256. [Google Scholar] [CrossRef] [PubMed]
- Fraser, J.S.; Clarkson, M.W.; Degnan, S.C.; Erion, R.; Kern, D.; Alber, T. Hidden alternative structures of proline isomerase essential for catalysis. Nature 2009, 462, 669–673. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Louis, J.M.; Aniana, A.; Suh, J.Y.; Clore, G.M. Visualizing transient events in amino-terminal autoprocessing of HIV-1 protease. Nature 2008, 455, 693–696. [Google Scholar] [CrossRef] [PubMed]
- Clore, G.M. Visualizing lowly-populated regions of the free energy landscape of macromolecular complexes by paramagnetic relaxation enhancement. Mol. Biosyst. 2008, 4, 1058–1069. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cavalli, A.; Salvatella, X.; Dobson, C.M.; Vendruscolo, M. Protein structure determination from NMR chemical shifts. Proc. Natl. Acad. Sci. USA 2007, 104, 9615–9620. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Best, R.B.; Depristo, M.A.; Dobson, C.M.; Vendruscolo, M. Simultaneous determination of protein structure and dynamics. Nature 2005, 433, 128–132. [Google Scholar] [CrossRef] [PubMed]
- Estabrook, R.A.; Luo, J.; Purdy, M.M.; Sharma, V.; Weakliem, P.; Bruice, T.C.; Reich, N.O. Statistical coevolution analysis and molecular dynamics: Identification of amino acid pairs essential for catalysis. Proc. Natl. Acad. Sci. USA 2005, 102, 994–999. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.K.; Penkler, D.L.; Sheik Amamuddy, O.; Ross, C.; Atilgan, A.R.; Atilgan, C.; Tastan Bishop, O. MD-TASK: A software suite for analyzing molecular dynamics trajectories. Bioinformatics 2017, 33, 2768–2771. [Google Scholar] [CrossRef] [PubMed]
- Steiner, K.; Schwab, H. Recent advances in rational approaches for enzyme engineering. Comput. Struct. Biotechnol. J. 2012, 2, e201209010. [Google Scholar] [CrossRef] [PubMed]
- Motlagh, H.N.; Wrabl, J.O.; Li, J.; Hilser, V.J. The ensemble nature of allostery. Nature 2014, 508, 331–339. [Google Scholar] [CrossRef] [PubMed]
- Hilser, V.J.; Wrabl, J.O.; Motlagh, H.N. Structural and energetic basis of allostery. Annu. Rev. Biophys. 2012, 41, 585–609. [Google Scholar] [CrossRef] [PubMed]
- Del Sol, A.; Tsai, C.J.; Ma, B.; Nussinov, R. The origin of allosteric functional modulation: Multiple pre-existing pathways. Structure 2009, 17, 1042–1050. [Google Scholar] [CrossRef] [PubMed]
- Bowerman, S.; Wereszczynski, J. Detecting Allosteric Networks Using Molecular Dynamics Simulation. Methods Enzymol. 2016, 578, 429–447. [Google Scholar] [PubMed]
- Studer, R.A.; Dessailly, B.H.; Orengo, C.A. Residue mutations and their impact on protein structure and function: Detecting beneficial and pathogenic changes. Biochem. J. 2013, 449, 581–594. [Google Scholar] [CrossRef] [PubMed]
- Fiser, A.; Do, R.K.; Sali, A. Modeling of loops in protein structures. Protein Sci. 2000, 9, 1753–1773. [Google Scholar] [CrossRef] [PubMed]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Showalter, S.A.; Bruschweiler, R. Validation of Molecular Dynamics Simulations of Biomolecules Using NMR Spin Relaxation as Benchmarks: Application to the AMBER99SB Force Field. J. Chem. Theory Comput. 2007, 3, 961–975. [Google Scholar] [CrossRef] [PubMed]
- Price, D.J.; Brooks, C.R. A modified TIP3P water potential for simulation with Ewald summation. J. Chem. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Bakan, A.; Meireles, L.M.; Bahar, I. ProDy: Protein Dynamics Inferred from Theory and Experiments. Bioinformatics 2011, 27, 1575–1577. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Whitten, S.T.; Hilser, V.J. Ensemble-based signatures of energy propagation in proteins: A new view of an old phenomenon. Proteins 2006, 62, 728–738. [Google Scholar] [CrossRef] [PubMed]
- Vertrees, J.; Barritt, P.; Whitten, S.; Hilser, V.J. COREX/BEST server: A web browser-based program that calculates regional stability variations within protein structures. Bioinformatics 2005, 21, 3318–3319. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, L.; Zhou, Y.; Zhu, L.; Liu, C.; Wu, Z.; Wang, F.; Hao, G.; Yu, D.; Yuan, H.; Cui, Y. Site-Mutation of Hydrophobic Core Residues Synchronically Poise Super Interleukin 2 for Signaling: Identifying Distant Structural Effects through Affordable Computations. Int. J. Mol. Sci. 2018, 19, 916. https://doi.org/10.3390/ijms19030916
Mei L, Zhou Y, Zhu L, Liu C, Wu Z, Wang F, Hao G, Yu D, Yuan H, Cui Y. Site-Mutation of Hydrophobic Core Residues Synchronically Poise Super Interleukin 2 for Signaling: Identifying Distant Structural Effects through Affordable Computations. International Journal of Molecular Sciences. 2018; 19(3):916. https://doi.org/10.3390/ijms19030916
Chicago/Turabian StyleMei, Longcan, Yanping Zhou, Lizhe Zhu, Changlin Liu, Zhuo Wu, Fangkui Wang, Gefei Hao, Di Yu, Hong Yuan, and Yanfang Cui. 2018. "Site-Mutation of Hydrophobic Core Residues Synchronically Poise Super Interleukin 2 for Signaling: Identifying Distant Structural Effects through Affordable Computations" International Journal of Molecular Sciences 19, no. 3: 916. https://doi.org/10.3390/ijms19030916
APA StyleMei, L., Zhou, Y., Zhu, L., Liu, C., Wu, Z., Wang, F., Hao, G., Yu, D., Yuan, H., & Cui, Y. (2018). Site-Mutation of Hydrophobic Core Residues Synchronically Poise Super Interleukin 2 for Signaling: Identifying Distant Structural Effects through Affordable Computations. International Journal of Molecular Sciences, 19(3), 916. https://doi.org/10.3390/ijms19030916