Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods
Abstract
:1. Introduction
2. Physicochemical Mechanisms of Protein–Ligand Interaction
2.1. Protein–Ligand Binding Kinetics
2.2. Basic Concepts and Thermodynamic Relationships
2.3. Binding Driving Forces and Enthalpy-Entropy Compensation
3. Protein–Ligand Binding Models
3.1. Diffusion Followed by Collision Is the Prerequisite for Binding
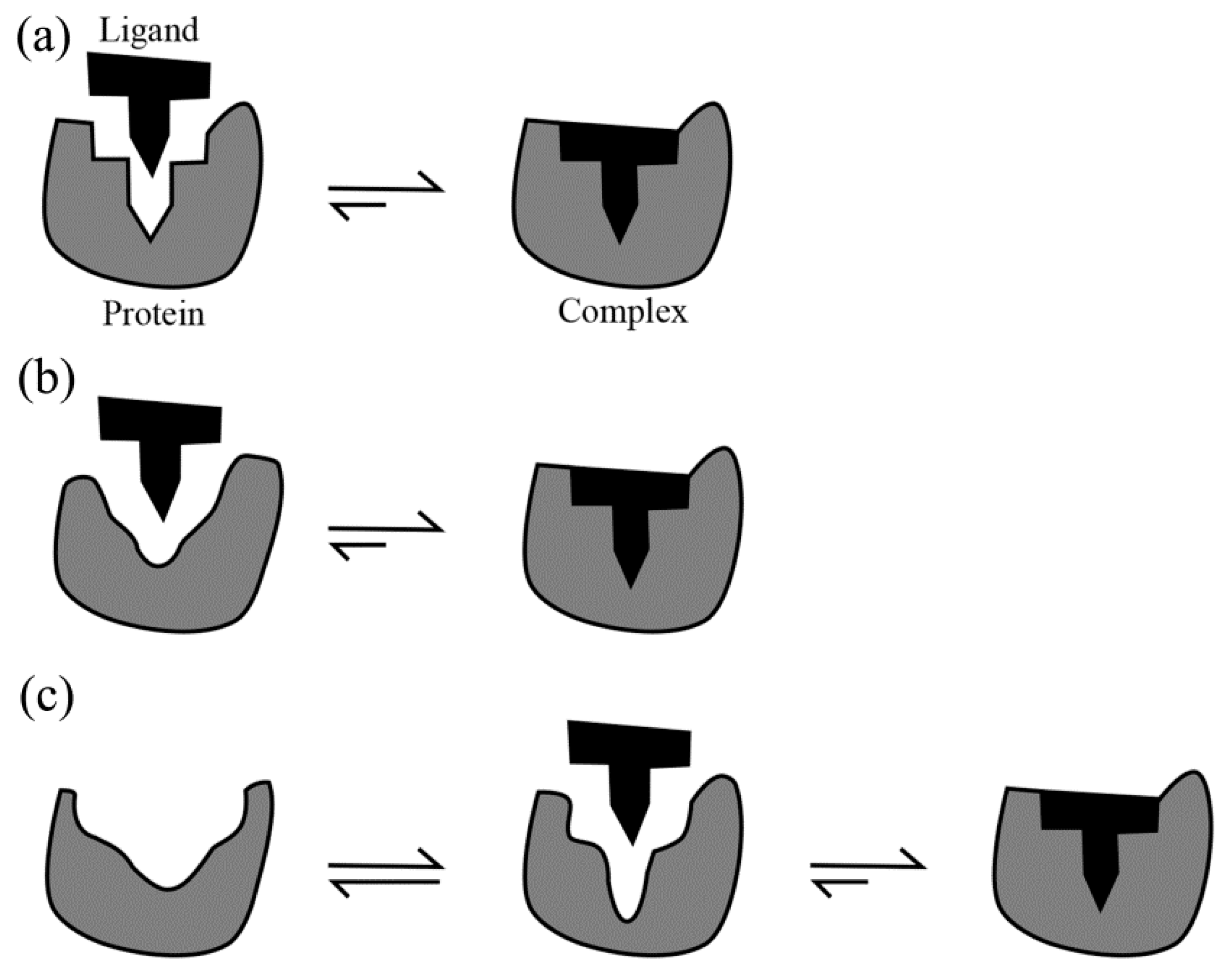
3.2. Lock-and-Key: An Entropy-Dominated Binding Process
3.3. Induced Fit
3.4. Conformational Selection: A Process in Which Entropy and Enthalpy Play Roles in a Sequential Manner
3.5. The Relationship between Lock-and-Key, Induced Fit and Conformational Selection
4. Methods Used to Investigate Protein–Ligand Binding Affinity
4.1. Experimental Methods
4.1.1. Isothermal Titration Calorimetry (ITC)
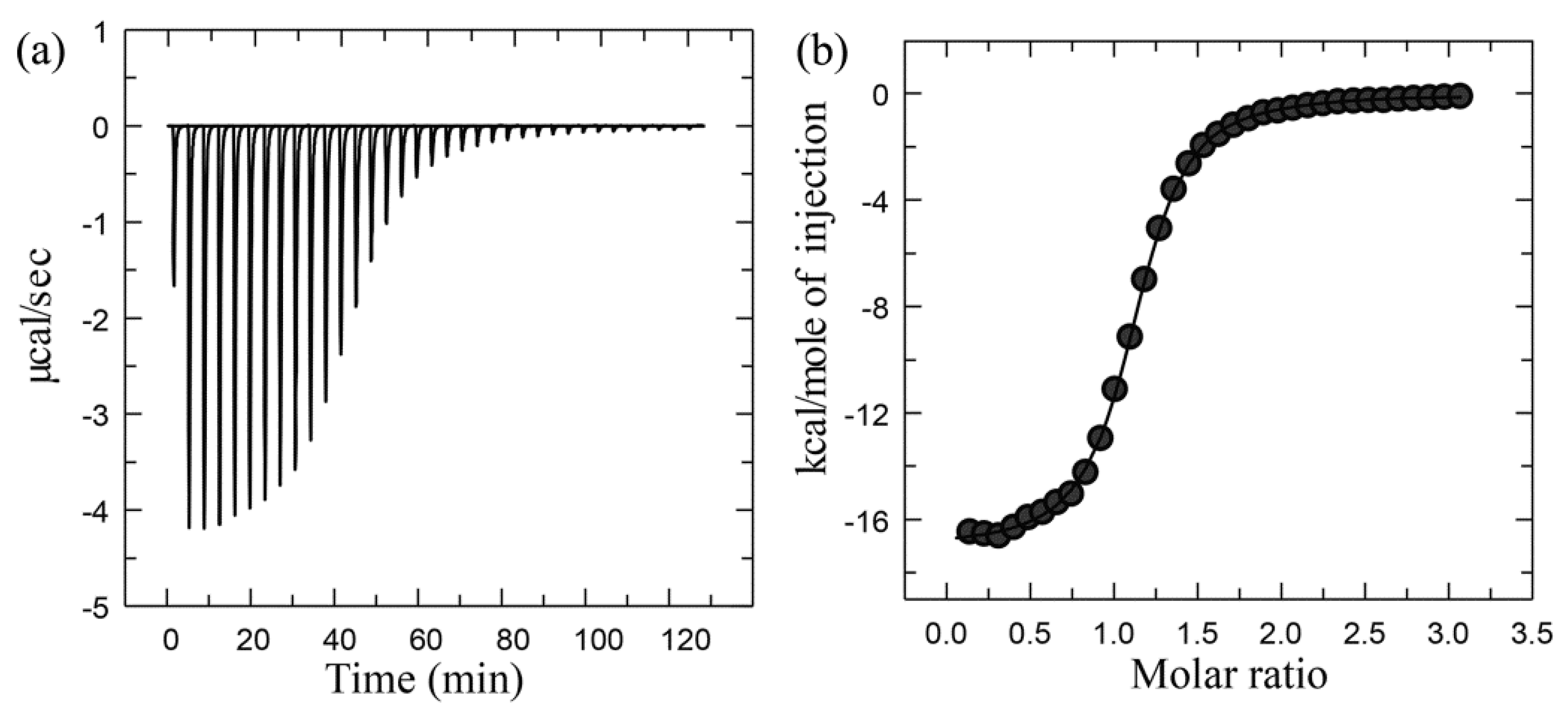
Experimental Setup, Principles, and Data Processing of ITC
Advantages and Disadvantages of ITC
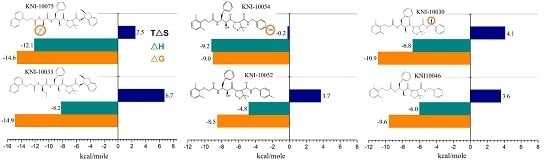
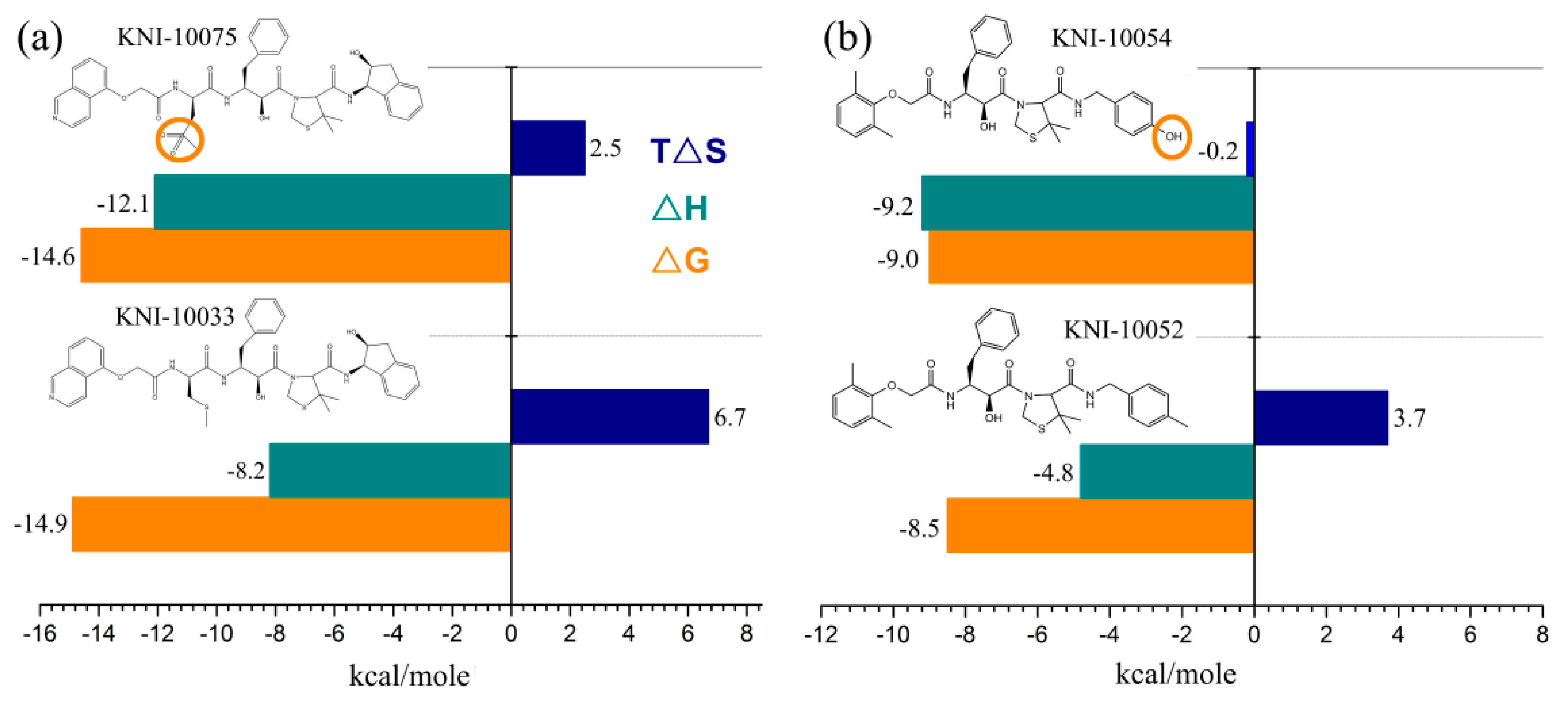
Case Study Using ITC
4.1.2. Surface Plasmon Resonance (SPR)
4.1.3. Fluorescence Polarization (FP)
4.2. Theoretical/Computational Methods
4.2.1. Protein–Ligand Docking
Search Algorithms and Their Challenges
Scoring Functions and Their Challenges
4.2.2. Free Energy Calculations
Alchemical Free Energy Calculations
Path Sampling
Endpoint Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Janin, J. Protein-protein recognition. Prog. Biophys. Mol. Biol. 1995, 64, 145–166. [Google Scholar] [CrossRef]
- Demchenko, A.P. Recognition between flexible protein molecules: Induced and assisted folding. J. Mol. Recognit. 2001, 14, 42–61. [Google Scholar] [CrossRef]
- Steinbrecher, T.; Labahn, A. Towards accurate free energy calculations in ligand protein-binding studies. Curr. Med. Chem. 2010, 17, 767–785. [Google Scholar] [CrossRef] [PubMed]
- Strogatz, S.H. Exploring complex networks. Nature 2001, 410, 268–276. [Google Scholar] [CrossRef] [PubMed]
- Acuner Ozbabacan, S.E.; Gursoy, A.; Keskin, O.; Nussinov, R. Conformational ensembles, signal transduction and residue hot spots: Application to drug discovery. Curr. Opin. Drug Discov. Dev. 2010, 13, 527–537. [Google Scholar]
- Perozzo, R.; Folkers, G.; Scapozza, L. Thermodynamics of protein-ligand interactions: History, presence, and future aspects. J. Recept. Signal. Transduct. Res. 2004, 24, 1–52. [Google Scholar] [CrossRef] [PubMed]
- Chaires, J.B. Calorimetry and thermodynamics in drug design. Annu. Rev. Biophys. 2008, 37, 135–151. [Google Scholar] [CrossRef] [PubMed]
- Ladbury, J.E.; Chowdhry, B.Z. Sensing the heat: The application of isothermal titration calorimetry to thermodynamic studies of biomolecular interactions. Chem. Biol. 1996, 3, 791–801. [Google Scholar] [CrossRef]
- Jönsson, U.; Fägerstam, L.; Ivarsson, B.; Johnsson, B.; Karlsson, R.; Lundh, K.; Löfås, S.; Persson, B.; Roos, H.; Rönnberg, I.; et al. Real-time biospecific interaction analysis using surface plasmon resonance and a sensor chip technology. Biotechniques 1991, 11, 620–627. [Google Scholar] [PubMed]
- Torreri, P.; Ceccarini, M.; Macioce, P.; Petrucci, T.C. Biomolecular interactions by Surface Plasmon Resonance technology. Ann. Ist. Super Sanita. 2005, 41, 437–441. [Google Scholar] [PubMed]
- Weber, G. Polarization of the fluorescence of macromolecules. I. Theory and experimental method. Biochem. J. 1952, 51, 145–155. [Google Scholar] [CrossRef] [PubMed]
- Rossi, A.; Taylor, C. Analysis of protein-ligand interactions by fluorescence polarization. Nat. Protoc. 2011, 6, 365–387. [Google Scholar] [CrossRef] [PubMed]
- Grinter, S.Z.; Zou, X. Challenges, applications, and recent advances of protein–ligand docking in structure-based drug design. Molecules 2014, 19, 10150–10176. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Ribeiro, A.J.; Coimbra, J.T.; Neves, R.P.; Martins, S.A.; Moorthy, N.S.; Fernandes, P.A.; Ramos, M.J. Protein-ligand docking in the new millennium-a retrospective of 10 years in the field. Curr. Med. Chem. 2013, 20, 2296–2314. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Zhou, H.X. Calculation of protein-ligand binding affinities. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 21–42. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, J.W. A method of geometrical representation of the thermodynamic properties of substances by means of surfaces. Trans. Conn. Acad. Arts Sci. 1873, 2, 382–404. [Google Scholar]
- Li, H.; Xie, Y.; Liu, C.; Liu, S. Physicochemical bases for protein folding, dynamics, and protein-ligand binding. Sci. China Life Sci. 2014, 57, 287–302. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Johnson, C.M. Introduction to microcalorimetry and biomolecular energetics. Methods Mol. Biol. 1994, 22, 109–124. [Google Scholar] [PubMed]
- Liu, S.Q.; Xie, Y.H.; Ji, X.L.; Tao, Y.; Tan, D.Y.; Zhang, K.Q.; Fu, Y.X. Protein folding, binding and energy landscape: A synthesis. In Protein Engineering; Kaumaya, P.T.P., Ed.; InTech: Rijeka, Croatia, 2012; pp. 207–252. [Google Scholar]
- MacRaild, C.A.; Daranas, A.H.; Bronowska, A.; Homans, S.W. Global changes in local protein dynamics reduce the entropic cost of carbohydrate binding in the arabinose-binding protein. J. Mol. Biol. 2007, 368, 822–832. [Google Scholar] [CrossRef] [PubMed]
- Bronowska, A.K. Thermodynamics of ligand-protein interactions: Implications for molecular design. In Thermodynamics—Interaction Studies—Solids, Liquids and Gases; Moreno-Piraján, J.C., Ed.; InTech: Rijeka, Croatia, 2011; pp. 1–48. [Google Scholar]
- Amzel, L.M. Loss of translational entropy in binding, folding, and catalysis. Proteins 1997, 28, 144–149. [Google Scholar] [CrossRef]
- Amzel, L.M. Calculation of entropy changes in biological processes: Folding, binding, and oligomerization. Methods Enzymol. 2000, 323, 167–177. [Google Scholar] [PubMed]
- Ma, B.; Kumar, S.; Tsai, C.J.; Nussinov, R. Folding funnels and binding mechanisms. Protein Eng. 1999, 12, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.J.; Xu, D.; Nussinov, R. Protein folding via binding and vice versa. Fold. Des. 1998, 3, R71–R80. [Google Scholar] [CrossRef]
- Tsai, C.J.; Kumar, S.; Ma, B.; Nussinov, R. Folding funnels, binding funnels, and protein function. Protein Sci. 1999, 8, 1181–1190. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.J.; Ma, B.; Nussinov, R. Folding and binding cascades: Shifts in energy landscapes. Proc. Natl. Acad. Sci. USA 1999, 96, 9970–9972. [Google Scholar] [CrossRef] [PubMed]
- Leopold, P.E.; Montal, M.; Onuchic, J.N. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.H.; Sang, P.; Tao, Y.; Liu, S.Q. 154 Protein folding and binding funnels: A common driving force and a common mechanism. J. Biomol. Struct. Dyn. 2013, 31, 100–101. [Google Scholar] [CrossRef]
- Dunitz, J.D. Win some, lose some: Enthalpy-entropy compensation in weak intermolecular interactions. Chem. Biol. 1995, 2, 709–712. [Google Scholar] [CrossRef]
- Krug, R.R.; Hunter, W.G.; Grieger, R.A. Statistical interpretation of enthalpy-entropy compensation. Nature 1976, 261, 566–567. [Google Scholar] [CrossRef]
- Cornish-Bowden, A. Enthalpy-entropy compensation: A phantom phenomenon. J. Biosci. 2002, 27, 121–126. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A.; Johnson, C.M.; Lakey, J.H.; Nöllmann, M. Heat does not come in different colours: Entropy-enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 2001, 93, 215–230. [Google Scholar] [CrossRef]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 1. The effect of random experimental errors. Phys. Chem. Chem. Phys. 2012, 14, 318–326. [Google Scholar] [CrossRef] [PubMed]
- Barrie, P.J. The mathematical origins of the kinetic compensation effect: 2. The effect of systematic errors. Phys. Chem. Chem. Phys. 2012, 14, 327–336. [Google Scholar] [CrossRef] [PubMed]
- Olsson, T.S.; Ladbury, J.E.; Pitt, W.R.; Williams, M.A. Extent of enthalpy-entropy compensation in protein-ligand interactions. Protein Sci. 2011, 20, 1607–1618. [Google Scholar] [CrossRef] [PubMed]
- Exner, O. Entropy-enthalpy compensation and anticompensation: Solvation and ligand binding. Chem. Commun. 2000, 2000, 1655–1656. [Google Scholar] [CrossRef]
- Gallicchio, E.; Kubo, M.M.; Levy, R.M. Entropy-enthalpy compensation in solvation and ligand binding revisited. J. Am. Chem. Soc. 1998, 120, 4526–4527. [Google Scholar] [CrossRef]
- Eftink, M.R.; Anusiem, A.C.; Biltonen, R.L. Enthalpy-entropy compensation and heat capacity changes for protein-ligand interactions: General thermodynamic models and data for the binding of nucleotides to ribonuclease A. Biochemistry 1983, 22, 3884–3896. [Google Scholar] [CrossRef] [PubMed]
- Lumry, R.; Rajender, S. Enthalpy-entropy compensation phenomena in water solutions of proteins and small molecules: A ubiquitous property of water. Biopolymers 1970, 9, 1125–1227. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M.; Krishnamurthy, V.M. Designing ligands to bind proteins. Q. Rev. Biophys. 2005, 38, 385–395. [Google Scholar] [CrossRef] [PubMed]
- Fenley, A.T.; Muddana, H.S.; Gilson, M.K. Entropy-enthalpy transduction caused by conformational shifts can obscure the forces driving protein-ligand binding. Proc. Natl. Acad. Sci. USA 2012, 109, 20006–20011. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, C.H.; Holloway, M.K. Thermodynamics of ligand binding and efficiency. ACS Med. Chem. Lett. 2011, 2, 433–437. [Google Scholar] [CrossRef] [PubMed]
- Qian, H. Entropy-enthalpy compensation: Conformational fluctuation and induced-fit. J. Chem. Phys. 1998, 109, 10015–10017. [Google Scholar] [CrossRef]
- Chang, C.E.; Gilson, M.K. Free energy, entropy, and induced fit in host-guest recognition: Calculations with the second-generation mining minima algorithm. J. Am. Chem. Soc. 2004, 126, 13156–13164. [Google Scholar] [CrossRef] [PubMed]
- Gilli, P.; Ferretti, V.; Gilli, G.; Borea, P.A. Enthalpy-entropy compensation in drug receptor binding. J. Phys. Chem. B 1994, 98, 1515–1518. [Google Scholar] [CrossRef]
- Chodera, J.D.; Mobley, D.L. Entropy-enthalpy compensation: Role and ramifications in biomolecular ligand recognition and design. Annu. Rev. Biophys. 2013, 42, 121–142. [Google Scholar] [CrossRef] [PubMed]
- Ryde, U. A fundamental view of enthalpy-entropy compensation. Med. Chem. Commun. 2014, 5, 1324–1336. [Google Scholar] [CrossRef]
- Breiten, B.; Lockett, M.R.; Sherman, W.; Fujita, S.; Al-Sayah, M.; Lange, H.; Bowers, C.M.; Heroux, A.; Krilov, G.; Whitesides, G.M. Water networks contribute to enthalpy/entropy compensation in protein-ligand binding. J. Am. Chem. Soc. 2013, 135, 15579–15584. [Google Scholar] [CrossRef] [PubMed]
- Fischer, E. Einfluss der configuration auf die wirkung der enzyme. Ber. Dtsch. Chem. Ges. 1894, 27, 2984–2993. [Google Scholar]
- Koshland, D.E.J. Application of a theory of enzyme specificity to protein synthesis. Proc. Natl. Acad. Sci. USA 1958, 44, 98–104. [Google Scholar] [CrossRef] [PubMed]
- Tobi, D.; Bahar, I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc. Natl. Acad. Sci. USA 2005, 102, 18908–18913. [Google Scholar] [CrossRef] [PubMed]
- Csermely, P.; Palotai, R.; Nussinov, R. Induced fit, conformational selection and independent dynamic segments: An extended view of binding events. Trends Biochem. Sci. 2010, 35, 539–546. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; Sligar, S.G.; Wolynes, P.G. The energy landscapes and motions of proteins. Science 1991, 254, 1598–1603. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.A.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein Folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef] [PubMed]
- Miller, D.W.; Dill, K.A. Ligand binding to proteins: The binding landscape model. Protein Sci. 1997, 6, 2166–2179. [Google Scholar] [CrossRef] [PubMed]
- Changeux, J.P.; Edelstein, S. Conformational selection or induced fit? 50 years of debate resolved. F1000 Biol. Rep. 2011, 3, 19. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D.; Nussinov, R.; Wright, P.E. The role of dynamic conformational ensembles in biomolecular recognition. Nat. Chem. Biol. 2009, 5, 789–796. [Google Scholar] [CrossRef] [PubMed]
- Nussinov, R.; Ma, B.; Tsai, C.J. Multiple conformational selection and induced fit events take place in allosteric propagation. Biophys. Chem. 2014, 186, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Bongrand, P. Ligand-receptor interactions. Rep. Prog. Phys. 1999, 62, 921–968. [Google Scholar] [CrossRef]
- Xie, Y.H.; Tao, Y.; Liu, S.Q. 153 Wonderful roles of the entropy in protein dynamics, binding and folding. J. Biomol. Struct. Dyn. 2013, 31, 98–100. [Google Scholar] [CrossRef]
- Held, M.; Metzner, P.; Prinz, J.H.; Noé, F. Mechanisms of protein-ligand association and its modulation by protein mutations. Biophys. J. 2011, 100, 701–710. [Google Scholar] [CrossRef] [PubMed]
- Schluttig, J.; Alamanova, D.; Helms, V.; Schwarz, U.S. Dynamics of protein-protein encounter: A Langevin equation approach with reaction patches. J. Chem. Phys. 2008, 129, 155106. [Google Scholar] [CrossRef] [PubMed]
- Northrup, S.H.; Allison, S.A.; McCammon, J.A. Brownian dynamics simulation of diffusion-influenced bimolecular reactions. J. Chem. Phys. 1984, 80, 1517–1524. [Google Scholar] [CrossRef]
- Spaar, A.; Dammer, C.; Gabdoulline, R.R.; Wade, R.C.; Helms, V. Diffusional encounter of barnase and barstar. Biophys. J. 2006, 90, 1913–1924. [Google Scholar] [CrossRef] [PubMed]
- Sacanna, S.; Irvine, W.T.; Chaikin, P.M.; Pine, D.J. Lock and key colloids. Nature 2010, 464, 575–578. [Google Scholar] [CrossRef] [PubMed]
- Sacanna, S.; Korpics, M.; Rodriguez, K.; Colon-Melendez, L.; Kim, S.-H.; Pine, D.J.; Yi, G.R. Shaping colloids for self-assembly. Nat. Commun. 2013, 4, 1688. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Wu, J. Hybrid MC-DFT method for studying multidimensional entropic forces. J. Phys. Chem. B 2011, 115, 1450–1460. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, M.; Oguni, T. Depletion effects on the lock and key steric interactions between macromolecules. Chem. Phys. Lett. 2002, 351, 79–84. [Google Scholar] [CrossRef]
- Kinoshita, M. Roles of entropic excluded-volume effects in colloidal and biological systems: Analyses using the three-dimensional integral equation theory. Chem. Eng. Sci. 2006, 61, 2150–2160. [Google Scholar] [CrossRef]
- Chang, H.Y.; Huang, C.W.; Chen, Y.F.; Chen, S.Y.; Sheng, Y.J.; Tsao, H.K. Assembly of lock-and-key colloids mediated by polymeric depletant. Langmuir 2015, 31, 13085–13093. [Google Scholar] [CrossRef] [PubMed]
- Odriozola, G.; Jiménez-Ángeles, F.; Lozada-Cassou, M. Entropy driven key-lock assembly. J. Chem. Phys. 2008, 129, 111101–111104. [Google Scholar] [CrossRef] [PubMed]
- Odriozola, G.; Lozada-Cassou, M. Statistical mechanics approach to lock-key supramolecular chemistry interactions. Phys. Rev. Lett. 2013, 110, 105701. [Google Scholar] [CrossRef] [PubMed]
- Asakura, S.; Oosawa, F. On interaction between two bodies immersed in a solution of macromolecules. J. Chem. Phys. 1954, 22, 1255–1256. [Google Scholar]
- Jiménez-Ángeles, F.; Odriozola, G.; Lozada-Cassou, M. Entropy effects in self-assembling mechanisms: Also a view from the information theory. J. Mol. Liq. 2011, 164, 87–100. [Google Scholar] [CrossRef]
- Zanella, M.; Bertoni, G.; Franchini, I.R.; Brescia, R.; Baranov, D.; Manna, L. Assembly of shape-controlled nanocrystals by depletion attraction. Chem. Commun. 2011, 47, 203–205. [Google Scholar] [CrossRef] [PubMed]
- Kraft, D.J.; Ni, R.; Smallenburg, F.; Hermes, M.; Yoon, K.; Weitz, D.A.; van Blaaderen, A.; Groenewold, J.; Dijkstra, M.; Kegel, W.K. Surface roughness directed self-assembly of patchy particles into colloidal micelles. Proc. Natl. Acad. Sci. USA 2012, 109, 10787–10792. [Google Scholar] [CrossRef] [PubMed]
- Oleinikova, A.; Smolin, N.; Brovchenko, I.A.G.; Winter, R. Formation of spanning water networks on protein surfaces via 2D percolation transition. J. Phys. Chem. B 2005, 109, 1988–1998. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.J. Limitations and extensions of the lock-and-key principle: Differences between gas state, solution and solid state structures. Int. J. Mol. Sci. 2015, 16, 6694–6717. [Google Scholar] [CrossRef] [PubMed]
- Corbett, P.T.; Tong, L.H.; Sanders, J.K.; Otto, S. Diastereoselective amplification of an induced-fit receptor from a dynamic combinatorial library. J. Am. Chem. Soc. 2005, 127, 8902–8903. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.E.; Potter, M.J.; Gilson, M.K. Calculation of molecular configuration integrals. J. Phys. Chem. B 2003, 107, 1048–1055. [Google Scholar] [CrossRef]
- Kumar, H.; Kasho, V.; Smirnova, I.; Finer-Moore, J.S.; Kaback, H.R.; Stroud, R.M. Structure of sugar-bound LacY. Proc. Natl. Acad. Sci. USA 2014, 111, 1784–1788. [Google Scholar] [CrossRef] [PubMed]
- Mirza, O.; Guan, L.; Verner, G.; Iwata, S.; Kaback, H.R. Structural evidence for induced fit and a mechanism for sugar/H+ symport in LacY. EMBO J. 2006, 25, 1177–1183. [Google Scholar] [CrossRef] [PubMed]
- Chaptal, V.; Kwon, S.; Sawaya, M.R.; Guan, L.; Kaback, H.R.; Abramson, J. Crystal structure of lactose permease in complex with an affinity inactivator yields unique insight into sugar recognition. Proc. Natl. Acad. Sci. USA 2011, 108, 9361–9366. [Google Scholar] [CrossRef] [PubMed]
- Hariharan, P.; Guan, L. Insights into the inhibitory mechanisms of the regulatory protein IIA(Glc) on melibiose permease activity. J. Biol. Chem. 2014, 289, 33012–33019. [Google Scholar] [CrossRef] [PubMed]
- Bosshard, H.R. Molecular recognition by induced fit: How fit is the concept? News Physiol. Sci. 2001, 16, 171–173. [Google Scholar] [PubMed]
- Foote, J.; Milstein, C. Conformational isomerism and the diversity of antibodies. Proc. Natl. Acad. Sci. USA 1994, 91, 10370–10374. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Ma, B.; Tsai, C.J.; Sinha, N.; Nussinov, R. Folding and binding cascades: Dynamic landscapes and population shifts. Protein Sci. 2000, 9, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Wlodarski, T.; Zagrovic, B. Conformational selection and induced fit mechanism underlie specificity in noncovalent interactions with ubiquitin. Proc. Natl. Acad. Sci. USA 2009, 106, 19346–19351. [Google Scholar] [CrossRef] [PubMed]
- Grünberg, R.; Leckner, J.; Nilges, M. Complementarity of structure ensembles in protein-protein binding. Structure 2004, 12, 2125–2136. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D.; McElheny, D.; Dyson, H.J.; Wright, P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science 2006, 313, 1638–1642. [Google Scholar] [CrossRef] [PubMed]
- Gsponer, J.; Christodoulou, J.; Cavalli, A.; Bui, J.M.; Richter, B.; Dobson, C.M.; Vendruscolo, M. A coupled equilibrium shift mechanism in calmodulin-mediated signal transduction. Structure 2008, 16, 736–746. [Google Scholar] [CrossRef] [PubMed]
- Junker, J.P.; Ziegler, F.; Rief, M. Ligand-dependent equilibrium fluctuations of single calmodulin molecules. Science 2009, 323, 633–637. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Wolfson, H.J.; Nussinov, R. Protein functional epitopes: Hot spots, dynamics and combinatorial libraries. Curr. Opin. Struct. Biol. 2001, 11, 364–369. [Google Scholar] [CrossRef]
- Vogt, A.D.; di Cera, E. Conformational selection or induced fit? A critical appraisal of the kinetic mechanism. Biochemistry 2012, 51, 5894–5902. [Google Scholar] [CrossRef] [PubMed]
- Hammes, G.G.; Chang, Y.C.; Oas, T.G. Conformational selection or induced fit: A flux description of reaction mechanism. Proc. Natl. Acad. Sci. USA 2009, 106, 13737–13741. [Google Scholar] [CrossRef] [PubMed]
- Greives, N.; Zhou, H.X. Both protein dynamics and ligand concentration can shift the binding mechanism between conformational selection and induced fit. Proc. Natl. Acad. Sci. USA 2014, 111, 10197–10202. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.X. From induced fit to conformational selection: A continuum of binding mechanism controlled by the timescale of conformational transitions. Biophys. J. 2010, 98, L15–L17. [Google Scholar] [CrossRef] [PubMed]
- Kastritis, P.L.; Bonvin, A.M. On the binding affinity of macromolecular interactions: Daring to ask why proteins interact. J. R. Soc. Interface 2012, 10, 20120835. [Google Scholar] [CrossRef] [PubMed]
- Mittermaier, A.; Kay, L.E. New tools provide new insights in NMR studies of protein dynamics. Science 2006, 312, 224–228. [Google Scholar] [CrossRef] [PubMed]
- Meyer, B.; Peters, T. NMR spectroscopy techniques for screening and identifying ligand binding to protein receptors. Angew. Chem. Int. Ed. Engl. 2003, 42, 864–890. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois, D.; Royant, A. Advances in kinetic protein crystallography. Curr. Opin. Struct. Biol. 2005, 15, 538–547. [Google Scholar] [CrossRef] [PubMed]
- Weiss, S. Measuring conformational dynamics of biomolecules by single molecule fluorescence spectroscopy. Nat. Struct. Biol. 2000, 7, 724–729. [Google Scholar] [CrossRef] [PubMed]
- Graf, C.; Stankiewicz, M.; Kramer, G.; Mayer, M.P. Spatially and kinetically resolved changes in the conformational dynamics of the Hsp90 chaperone machine. EMBO J. 2009, 28, 602–613. [Google Scholar] [CrossRef] [PubMed]
- Willander, M.; Al-Hilli, S. Analysis of biomolecules using surface plasmons. Methods Mol. Biol. 2009, 544, 201–229. [Google Scholar] [PubMed]
- Masi, A.; Cicchi, R.; Carloni, A.; Pavone, F.S.; Arcangeli, A. Optical methods in the study of protein-protein interactions. Adv. Exp. Med. Biol. 2010, 674, 33–42. [Google Scholar] [PubMed]
- Sturtevant, M. Biochemical applications of differential scanning calorimetry. Annu. Rev. Phys. Chem. 1987, 38, 463–488. [Google Scholar] [CrossRef]
- Celej, M.S.; Dassie, S.A.; González, M.; Bianconi, M.L.; Fidelio, G.D. Differential scanning calorimetry as a tool to estimate binding parameters in multiligand binding proteins. Anal. Biochem. 2006, 350, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Pierce, M.M.; Raman, C.S.; Nall, B.T. Isothermal titration calorimetry of protein-protein interactions. Methods 1999, 19, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Fisher, H.F.; Singh, N. Calorimetric methods for interpreting protein-ligand interactions. Methods Enzymol. 1995, 259, 194–221. [Google Scholar] [PubMed]
- Prabhu, N.V.; Sharp, K.A. Heat capacity in proteins. Annu. Rev. Phys. Chem. 2005, 56, 521–548. [Google Scholar] [CrossRef] [PubMed]
- Syme, N.R.; Dennis, C.; Phillips, S.E.; Homans, S.W. Origin of heat capacity changes in a “nonclassical” hydrophobic interaction. Chembiochem 2007, 8, 1509–1511. [Google Scholar] [CrossRef] [PubMed]
- Bouchemal, K. New challenges for pharmaceutical formulations and drug delivery systems characterization using isothermal titration calorimetry. Drug Discov. Today 2008, 13, 960–972. [Google Scholar] [CrossRef] [PubMed]
- Krell, T. Microcalorimetry: A response to challenges in modern biotechnology. Microb. Biotechnol. 2008, 1, 126–136. [Google Scholar] [CrossRef] [PubMed]
- Freyer, M.W.; Lewis, E.A. Isothermal titration calorimetry: Experimental design, data analysis, and probing macromolecule/ligand binding and kinetic interactions. Methods Cell Biol. 2008, 84, 79–113. [Google Scholar] [PubMed]
- Rajarathnam, K.; Rösgen, J. Isothermal titration calorimetry of membrane proteins—Progress and challenges. Biochim. Biophys. Acta. 2014, 1838, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Doyle, M.L.; Louie, G.; Dal Monte, P.R.; Sokoloski, T.D. Tight binding affinities determined from thermodynamic linkage to protons by titration calorimetry. Method Enzymol. 1995, 259, 183–194. [Google Scholar]
- Ghai, R.; Falconer, R.J.; Collins, B.M. Applications of isothermal titration calorimetry in pure and applied research - survey of the literature from 2010. J. Mol. Recognit. 2012, 25, 32–52. [Google Scholar] [CrossRef] [PubMed]
- Falconer, R.J.; Collins, B.M. Survey of the year 2009: Applications of isothermal titration calorimetry. J. Mol. Recognit. 2011, 24, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Falconer, R.J.; Penkova, A.; Jelesarov, I.; Collins, B.M. Survey of the year 2008: Applications of isothermal titration calorimetry. J. Mol. Recognit. 2010, 23, 395–413. [Google Scholar] [CrossRef] [PubMed]
- Freire, E. The binding thermodynamics of drug candidate. In Thermodynamics and Kinetics of Drug Binding; Keserü, G.M., Swinney, D.C., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015; pp. 1–13. [Google Scholar]
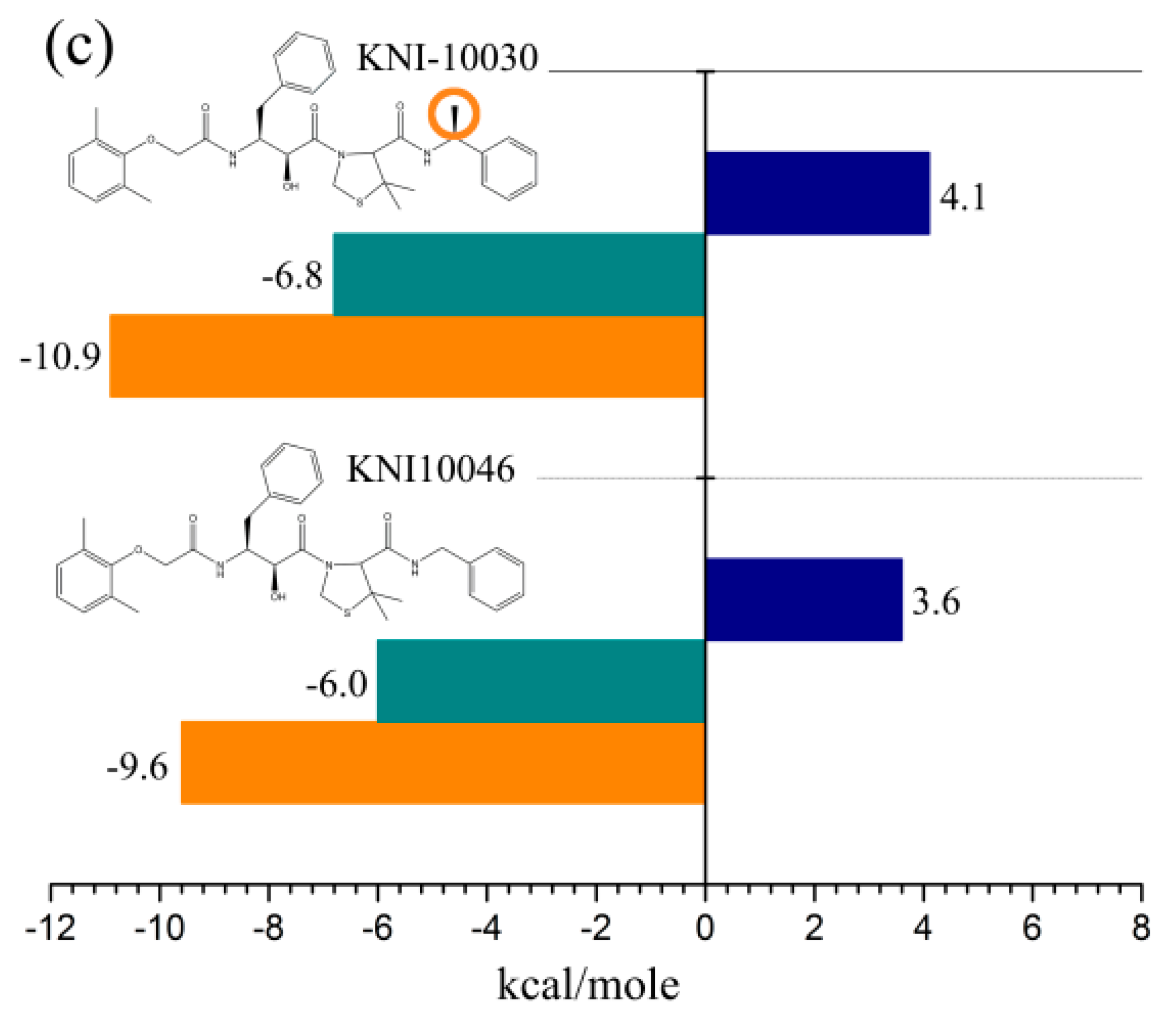
- Velazquez-Campoy, A.; Luque, I.; Todd, M.J.; Milutinovich, M.; Kiso, Y.; Freire, E. Thermodynamic dissection of the binding energetics of KNI-272, a potent HIV-1 protease inhibitor. Protein Sci. 2000, 9, 1801–1809. [Google Scholar] [CrossRef] [PubMed]
- Velazquez-Campoy, A.; Todd, M.J.; Freire, E. HIV-1 protease inhibitors: Enthalpic versus entropic optimization of the binding affinity. Biochemistry 2000, 39, 2201–2207. [Google Scholar] [CrossRef] [PubMed]
- Ohtaka, H.; Muzammil, S.; Schon, A.; Velazquez-Campoy, A.; Vega, S.; Freire, E. Thermodynamic rules for the design of high affinity HIV-1 protease inhibitors with adaptability to mutations and high selectivity towards unwanted targets. Int. J. Biochem. Cell Biol. 2004, 36, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Ohtaka, H.; Freire, E. Adaptive inhibitors of the HIV-1 protease. Prog. Biophys. Mol. Biol. 2005, 88, 193–208. [Google Scholar] [CrossRef] [PubMed]
- Lafont, V.; Armstrong, A.A.; Ohtaka, H.; Kiso, Y.; Mario Amzel, L.; Freire, E. Compensating enthalpic and entropic changes hinder binding affinity optimization. Chem. Biol. Drug Des. 2007, 69, 413–422. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, Y.; Freire, E. Finding a better path to drug selectivity. Drug Discov. Today 2011, 16, 985–990. [Google Scholar] [CrossRef] [PubMed]
- Tarcsay, Á.; Keserű, G.M. Is there a link between selectivity and binding thermodynamics profiles? Drug Discov. Today 2015, 20, 86–94. [Google Scholar] [CrossRef] [PubMed]
- Patching, S.G. Surface plasmon resonance spectroscopy for characterisation of membrane protein-ligand interactions and its potential for drug discovery. Biochim. Biophys. Acta 2014, 1838, 43–55. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, M.; Bjorkman, P.J. BIAcore: A microchip-based system for analyzing the formation of macromolecular complexes. Structure 1995, 3, 331–333. [Google Scholar] [CrossRef]
- Rich, R.L.; Myszka, D.G. BIACORE J: A new platform for routine biomolecular interaction analysis. J. Mol. Recognit. 2001, 14, 223–228. [Google Scholar] [CrossRef] [PubMed]
- Real-Fernández, F.; Rossi, G.; Panza, F.; Pratesi, F.; Migliorini, P.; Rovero, P. Surface plasmon resonance method to evaluate anti-citrullinated protein/peptide antibody affinity to citrullinated peptides. Methods Mol. Biol. 2015, 1348, 267–274. [Google Scholar] [PubMed]
- Van der Merwe, P.A. Surface plasmon resonance. In Protein-Ligand Interactions: Hydrodynamics and Calorimetry; Harding, S., Chowdhry, P.Z., Eds.; Oxford University Press: Bath, UK, 2001; pp. 137–170. [Google Scholar]
- Joshi, R. Biosensors; Isha Books: Dehli, India, 2006. [Google Scholar]
- Affinity Measurement with Biomolecular Interaction Analysis. Available online: www.iib.unibe.ch/wiki/files/biacore_slides.ppt (accessed on 6 December 2015).
- Willcox, B.E.; Gao, G.F.; Wyer, J.R.; Ladbury, J.E.; Bell, J.I.; Jakobsen, B.K.; van der Merwe, P.A. TCR binding to peptide-MHC stabilizes a flexible recognition interface. Immunity 1999, 10, 357–365. [Google Scholar] [CrossRef]
- Maynard, J.A.; Lindquist, N.C.; Sutherland, J.N.; Lesuffleur, A.; Warrington, A.E.; Rodriguez, M.; Oh, S.H. Surface plasmon resonance for high-throughput ligand screening of membrane-bound proteins. Biotechnol. J. 2009, 4, 1542–1558. [Google Scholar] [CrossRef] [PubMed]
- Owicki, J.C. Fluorescence polarization and anisotropy in high throughput screening: Perspectives and primer. J. Biomol. Screen. 2000, 5, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Lieto, A.; Cush, R.; Thompson, N. Ligand-receptor kinetics measured by total internal reflection with fluorescence correlation spectroscopy. Biophys. J. 2003, 85, 3294–3302. [Google Scholar] [CrossRef]
- Handl, H.; Gillies, R. Lanthanide-based luminescent assays for ligand-receptor interactions. Life Sci. 2005, 77, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Jameson, D.M.; Croney, J.C. Fluorescence polarization: Past, present and future. Comb. Chem. High Throughput Screen. 2003, 167–173. [Google Scholar] [CrossRef]
- Lea, W.A.; Simeonov, A. Fluorescence polarization assays in small molecule screening. Expert Opin. Drug Discov. 2011, 6, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Prusoff, W.H. Relationship between the inhibition constant (KI) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem. Pharmacol. 1973, 22, 3099–3108. [Google Scholar] [PubMed]
- Munson, P.J.; Rodbard, D. An exact correction to the ”Cheng-Prusoff” correction. J. Recept. Res. 1988, 8, 533–546. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, K.D. Quantitative analysis of protein-protein interactions. Methods Mol. Biol. 2004, 261, 15–32. [Google Scholar] [PubMed]
- Kastritis, P.L.; Moal, I.H.; Hwang, H.; Weng, Z.; Bates, P.A.; Bonvin, A.M.; Janin, J. A structure-based benchmark for protein-protein binding affinity. Protein Sci. 2011, 20, 482–491. [Google Scholar] [CrossRef] [PubMed]
- Pope, A.J.; Haupts, U.M.; Moore, K.J. Homogeneous fluorescence readouts for miniaturized high-throughput screening: Theory and practice. Drug Discov. Today 1999, 4, 350–362. [Google Scholar] [CrossRef]
- Arai, T.; Yatabe, M.; Furui, M.; Akatsuka, H.; Uehata, M.; Kamiyama, T. A fluorescence polarization-based assay for the identification and evaluation of calmodulin antagonists. Anal. Biochem. 2010, 405, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Manly, C.J.; Chandrasekhar, J.; Ochterski, J.W.; Hammer, J.D.; Warfield, B.B. Strategies and tactics for optimizing the Hit-to-Lead process and beyond—A computational chemistry perspective. Drug Discov. Today 2008, 13, 99–109. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Zou, X. Advances and challenges in protein-ligand docking. Int. J. Mol. Sci. 2010, 11, 3016–3034. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Cerqueira, N.M.; Fernandes, P.A.; Ramos, M.J. Virtual screening in drug design and development. Comb. Chem. High Throughput Screen. 2010, 13, 442–453. [Google Scholar] [CrossRef] [PubMed]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [PubMed]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, S.; Balius, T.E.; Rizzo, R.C. Docking validation resources: Protein family and ligand flexibility experiments. J. Chem. Inf. Model. 2010, 50, 1986–2000. [Google Scholar] [CrossRef] [PubMed]
- Ewing, T.J.; Makino, S.; Skillman, A.G.; Kuntz, I.D. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule databases. J. Comput. Aided Mol. Des. 2001, 15, 411–428. [Google Scholar] [CrossRef] [PubMed]
- Rarey, M.; Kramer, B.; Lengauer, T.; Klebe, G. A fast flexible docking method using an incremental construction algorithm. J. Mol. Biol. 1996, 261, 470–489. [Google Scholar] [CrossRef] [PubMed]
- Friesner, R.A.; Murphy, R.B.; Repasky, M.P.; Frye, L.L.; Greenwood, J.R.; Halgren, T.A.; Sanschagrin, P.C.; Mainz, D.T. Extra Precision Glide: Docking and Scoring Incorporating a Model of Hydrophobic Enclosure for Protein-Ligand Complexes. J. Med. Chem. 2006, 49, 6177–6196. [Google Scholar] [CrossRef] [PubMed]
- Halperin, I.; Ma, B.; Wolfson, H.; Nussinov, R. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 2002, 47, 409–443. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Fernandes, P.A.; Ramos, M.J. Protein-ligand docking: Current status and future challenges. Proteins 2006, 65, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Li, L.; Weng, Z. ZDOCK: An initial-stage protein-docking algorithm. Proteins 2003, 52, 80–87. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Zou, X. An iterative knowledge-based scoring function to predict protein-ligand interactions: I. Derivation of interaction potentials. J. Comput. Chem. 2006, 27, 1866–1875. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Zou, X. An iterative knowledge-based scoring function to predict protein-ligand interactions: II. Validation of the scoring function. J. Comput. Chem. 2006, 27, 1876–1882. [Google Scholar] [CrossRef] [PubMed]
- Shoichet, B.K.; Kuntz, I.D.; Bodian, D.L. Molecular docking using shape descriptors. J. Comput. Chem. 1992, 13, 380–397. [Google Scholar] [CrossRef]
- Kearsley, S.K.; Underwood, D.J.; Sheridan, R.P.; Miller, M.D. Flexibases: A way to enhance the use of molecular docking methods. J. Comput. Aided Mol. Des. 1994, 8, 565–582. [Google Scholar] [CrossRef] [PubMed]
- Leach, A.R.; Kuntz, I.D. Conformational analysis of flexible ligands in macromolecular receptor sites. J. Comput. Chem. 1992, 13, 730–748. [Google Scholar] [CrossRef]
- Böhm, H.J. The computer program LUDI: A new method for the de novo design of enzyme inhibitors. J. Comput. Aided Mol. Des. 1992, 6, 61–78. [Google Scholar] [CrossRef] [PubMed]
- Klebe, G.; Mietzner, T. A fast and efficient method to generate biologically relevant conformations. J. Comput. Aided Mol. Des. 1994, 8, 583–606. [Google Scholar] [CrossRef] [PubMed]
- Lorber, D.M.; Shoichet, B.K. Hierarchical docking of databases of multiple ligand conformations. Curr. Top. Med. Chem. 2005, 5, 739–749. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Pang, Y.P. Preference of small molecules for local minimum conformations when binding to proteins. PLoS ONE 2007, 2, e820. [Google Scholar] [CrossRef] [PubMed]
- Totrov, M.; Abagyan, R. Flexible ligand docking to multiple receptor conformations: A practical alternative. Curr. Opin. Struct. Biol. 2008, 18, 178–184. [Google Scholar] [CrossRef] [PubMed]
- Apostolakis, J.; Plückthun, A.; Caflisch, A. Docking small ligands in flexible binding sites. J. Comput. Chem. 1998, 19, 21–37. [Google Scholar] [CrossRef]
- Dixon, J.S.; Oshiro, C.M. Flexible ligand docking using a genetic algorithm. J. Comput. Aided Mol. Des. 1995, 9, 113–130. [Google Scholar]
- Desmet, J.; Maeyer, M.D.; Hazes, B.; Lasters, I. The dead end eliminatino theorem and its use in protein side-chain positioning. Nature 1992, 356, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, C.; Antes, I.; Lengauer, T. Docking and scoring with alternative side-chain conformations. Proteins 2009, 74, 712–726. [Google Scholar] [CrossRef] [PubMed]
- Beier, C.; Zacharias, M. Tackling the challenges posed by target flexibility in drug design. Exp. Opin. Drug Discov. 2010, 5, 347–359. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.; Kalyanaraman, C.; Irwin, J.J.; Jacobson, M.P. Physics-based scoring of protein-ligand complexes: Enrichment of known inhibitors in large-scale virtual screening. J. Chem. Inf. Model. 2006, 46, 243–253. [Google Scholar] [CrossRef] [PubMed]
- Rocchia, W.; Sridharan, S.; Nicholls, A.; Alexov, E.; Chiabrera, A.; Honig, B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. J. Comput. Chem. 2002, 23, 128–137. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Morin, P.; Wang, W.; Kollman, P.A. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 2001, 123, 5221–5230. [Google Scholar] [CrossRef] [PubMed]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Hawkins, G.D.; Cramer, C.J.; Truhlar, D.G. Pairwise solute descreening of solute charges from a dielectric medium. Chem. Phys. Lett. 1995, 246, 122–129. [Google Scholar] [CrossRef]
- Eldridge, M.D.; Murray, C.W.; Auton, T.R.; Paolini, G.V.; Mee, R.P. Empirical scoring functions: I. The development of a fast empirical scoring function to estimate the binding affinity of ligands in receptor complexes. J. Comput. Aided Mol. Des. 1997, 11, 425–445. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Y.; Grinter, S.Z.; Zou, X. Scoring functions and their evaluation methods for protein-ligand docking: Recent advances and future directions. Phys. Chem. Chem. Phys. 2010, 12, 12899–12908. [Google Scholar] [CrossRef] [PubMed]
- Muegge, I. PMF scoring revisited. J. Med. Chem. 2006, 49, 5895–5902. [Google Scholar] [CrossRef] [PubMed]
- Charifson, P.S.; Corkery, J.J.; Murcko, M.A.; Walters, W.P. Consensus scoring: A method for obtaining improved hit rates from docking databases of three-dimensional structures into proteins. J. Med. Chem. 1999, 42, 5100–5109. [Google Scholar] [CrossRef] [PubMed]
- Verkhivker, G.M.; Bouzida, D.; Gehlhaar, D.K.; Rejto, P.A.; Arthurs, S.; Colson, A.B.; Freer, S.T.; Larson, V.; Luty, B.A.; Marrone, T.; et al. Deciphering common failures in molecular docking of ligand-protein complexes. J. Comput. Aided Mol. Des. 2000, 14, 731–751. [Google Scholar] [CrossRef] [PubMed]
- De Ruiter, A.; Oostenbrink, C. Free energy calculations of protein-ligand interactions. Curr. Opin. Chem. Biol. 2011, 15, 547–552. [Google Scholar] [CrossRef] [PubMed]
- Hansen, N.; van Gunsteren, W.F. Practical aspects of free-energy calculations: A review. J. Chem. Theory Comput. 2014, 10, 2632–2647. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Mobley, D.L.; Chodera, J.D. Chapter 4 alchemical free energy calculations: Ready for prime Time? In Annual Reports in Computational Chemistry; Spellmeyer, D.C., Wheeler, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; Volume 3, pp. 41–59. [Google Scholar]
- Brandsdal, B.O.; Österberg, F.; Almlöf, M.; Feierberg, I.; Luzhkov, V.B.; Åqvist, J. Free energy calculations and ligand binding. Adv. Prot. Chem. 2003, 66, 123–158. [Google Scholar]
- Christ, C.D.; Mark, A.E.; van Gunsteren, W.F. Basic ingredients of free energy calculations: A review. J. Comput. Chem. 2010, 31, 1569–1582. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Mobley, D.L.; Shirts, M.R.; Dixon, R.W.; Branson, K.; Pande, V.S. Alchemical free energy methods for drug discovery: Progress and challenges. Curr. Opin. Struct. Biol. 2011, 21, 150–160. [Google Scholar] [CrossRef] [PubMed]
- Tembe, B.L.; McCammon, J.A. Ligand-receptor interactions. Comput. Chem. 1984, 8, 281–283. [Google Scholar] [CrossRef]
- Deng, Y.; Roux, B. Computations of standard binding free energies with molecular dynamics simulations. J. Phys. Chem. B 2009, 113, 2234–2246. [Google Scholar] [CrossRef] [PubMed]
- Aleksandrov, A.; Thompson, D.; Simonson, T. Alchemical free energy simulations for biological complexes: Powerful but temperamental. J. Mol. Recognit. 2009, 23, 117–127. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Buckner, J.K.; Boudon, S.; Tirado-Rives, J. Efficient computation of absolute free energies of binding by computer simulations. Application to the methane dimer in water. J. Chem. Phys. 1988, 89, 3742–3746. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Darve, E.; Rodríguez-Gómez, D.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 2008, 128, 144120. [Google Scholar] [CrossRef] [PubMed]
- Maragliano, L.; Vanden-Eijnden, E. A temperature-accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem. Phys. Lett. 2006, 426, 168–175. [Google Scholar] [CrossRef]
- St-Pierre, J.-F.; Karttunen, M.; Mousseau, N.; Róg, T.; Bunker, A. Use of umbrella sampling to calculate the entrance/exit pathway for Z-Pro-Prolinal inhibitor in prolyl oligopeptidase. J. Chem. Theory Comput. 2011, 7, 1583–1594. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Fajer, M.; Hamelberg, D.; McCammon, J.A. Replica-exchange accelerated molecular dynamics (REXAMD) applied to thermodynamic integration. J. Chem. Theory Comput. 2008, 4, 1565–1569. [Google Scholar] [CrossRef] [PubMed]
- Fukunishi, Y.; Mitomo, D.; Nakamura, H. Protein-ligand binding free energy calculation by the smooth reaction path generation (SRPG) method. J. Chem. Inf. Model. 2009, 49, 1944–1951. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Given, J.A.; Bush, B.L.; McCammon, J.A. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J. 1997, 72, 1047–1769. [Google Scholar] [CrossRef]
- Hermans, J.; Shankar, S. The free energy of xenon binding to myoglobin from molecular dynamics simulation. Isr. J. Chem. 1986, 27, 225–227. [Google Scholar] [CrossRef]
- Woo, H.J.; Roux, B. Calculation of absolute protein-ligand binding free energy from computer simulations. Proc. Natl. Acad. Sci. USA 2005, 102, 6825–6830. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Cossins, B.P.; Foucher, S.; Edge, C.M.; Essex, J.W. Protein-ligand binding affinity by nonequilibrium free energy methods. J. Phys. Chem. B 2008, 112, 14985–14992. [Google Scholar] [CrossRef] [PubMed]
- Narambuena, C.F.; Beltramo, D.M.; Leiva, E.P.M. Polyelectrolyte adsorption on a charged surface. Free energy calculation from Monte Carlo simulations using Jarzynski equality. Macromolecules 2008, 41, 8267–8274. [Google Scholar] [CrossRef]
- Minh, D.D.L.; Chodera, J.D. Estimating equilibrium ensemble averages using multiple time slices from driven nonequilibrium processes: Theory and application to free energies, moments, and thermodynamic length in singlemolecule pulling experiments. J. Chem. Phys. 2011, 134, 024111. [Google Scholar] [CrossRef] [PubMed]
- Cossins, B.P.; Foucher, S.; Edge, C.M.; Essex, J.W. Assessment of nonequilibrium free energy methods. J. Phys. Chem. B 2009, 113, 5508–5519. [Google Scholar] [CrossRef] [PubMed]
- Åqvist, J.; Medina, C.; Samuelsson, J.E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng. 1994, 7, 385–391. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, J.; Ander, M.; Nervall, M.; Åqvist, J. Continuum solvation models in the linear interaction energy method. J. Phys. Chem. B 2006, 110, 12034–12041. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, J.; Kollman, P.A. What determines the van der Waals coefficient beta in the LIE (linear interaction energy) method to estimate binding free energies using molecular dynamics simulations? Proteins 1999, 34, 395–402. [Google Scholar] [CrossRef]
- Valiente, P.A.; Gil, A.; Batista, P.R.; Caffarena, E.R.; Pons, T.; Pascutti, P.G. New parameterization approaches of the LIE method to improve free energy calculations of PlmII-inhibitors complexes. J. Comput. Chem. 2010, 31, 2723–2734. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, J.; Cheatham, T.E.; Cieplak, P.; Kollman, P.A.; Case, D.A. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate-DNA helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Swanson, J.M.; Henchman, R.H.; McCammon, J.A. Revisiting free energy calculations: A theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 2004, 86, 67–74. [Google Scholar] [CrossRef]
- Brown, S.P.; Muchmore, S.W. High-throughput calculation of protein-ligand binding affinities: Modification and adaptation of the MM-PBSA protocol to enterprise grid computing. J. Chem. Inf. Model. 2006, 46, 999–1005. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Wang, J.; Li, Y.; Wang, W. Assessing the performance of the MM/PBSA and MM/GBSA methods. 1. The accuracy of binding free energy calculations based on molecular dynamics simulations. J. Chem. Inf. Model. 2011, 51, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; Kushick, J. Method for estimating the configurational entropy of macromolecules. Macromolecules 1981, 14, 325–332. [Google Scholar] [CrossRef]
- Gohlke, H.; Case, D.A. Converging free energy estimates: MM-PB(GB)SA studies on the protein-protein complex Ras-Raf. J. Comput. Chem. 2004, 25, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Li, Y.; Xia, Y.-L.; Ai, S.-M.; Liang, J.; Sang, P.; Ji, X.-L.; Liu, S.-Q. Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods. Int. J. Mol. Sci. 2016, 17, 144. https://doi.org/10.3390/ijms17020144
Du X, Li Y, Xia Y-L, Ai S-M, Liang J, Sang P, Ji X-L, Liu S-Q. Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods. International Journal of Molecular Sciences. 2016; 17(2):144. https://doi.org/10.3390/ijms17020144
Chicago/Turabian StyleDu, Xing, Yi Li, Yuan-Ling Xia, Shi-Meng Ai, Jing Liang, Peng Sang, Xing-Lai Ji, and Shu-Qun Liu. 2016. "Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods" International Journal of Molecular Sciences 17, no. 2: 144. https://doi.org/10.3390/ijms17020144
APA StyleDu, X., Li, Y., Xia, Y.-L., Ai, S.-M., Liang, J., Sang, P., Ji, X.-L., & Liu, S.-Q. (2016). Insights into Protein–Ligand Interactions: Mechanisms, Models, and Methods. International Journal of Molecular Sciences, 17(2), 144. https://doi.org/10.3390/ijms17020144