First-Principles Investigation of Ag-Doped Gold Nanoclusters
Abstract
:1. Introduction
2. Results and Discussion
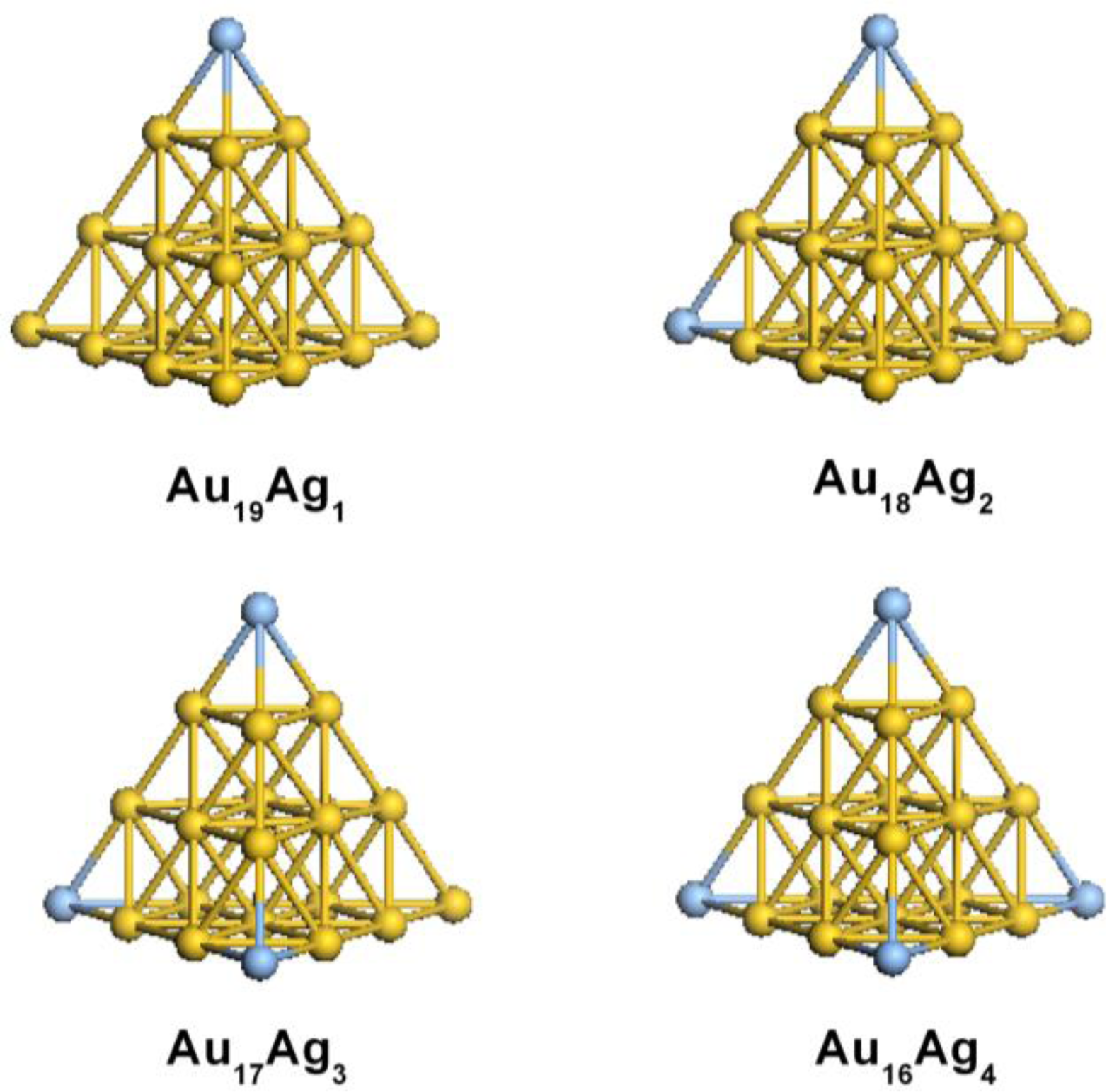
2.1. Structural Properties of Ag-Doped Gold Clusters
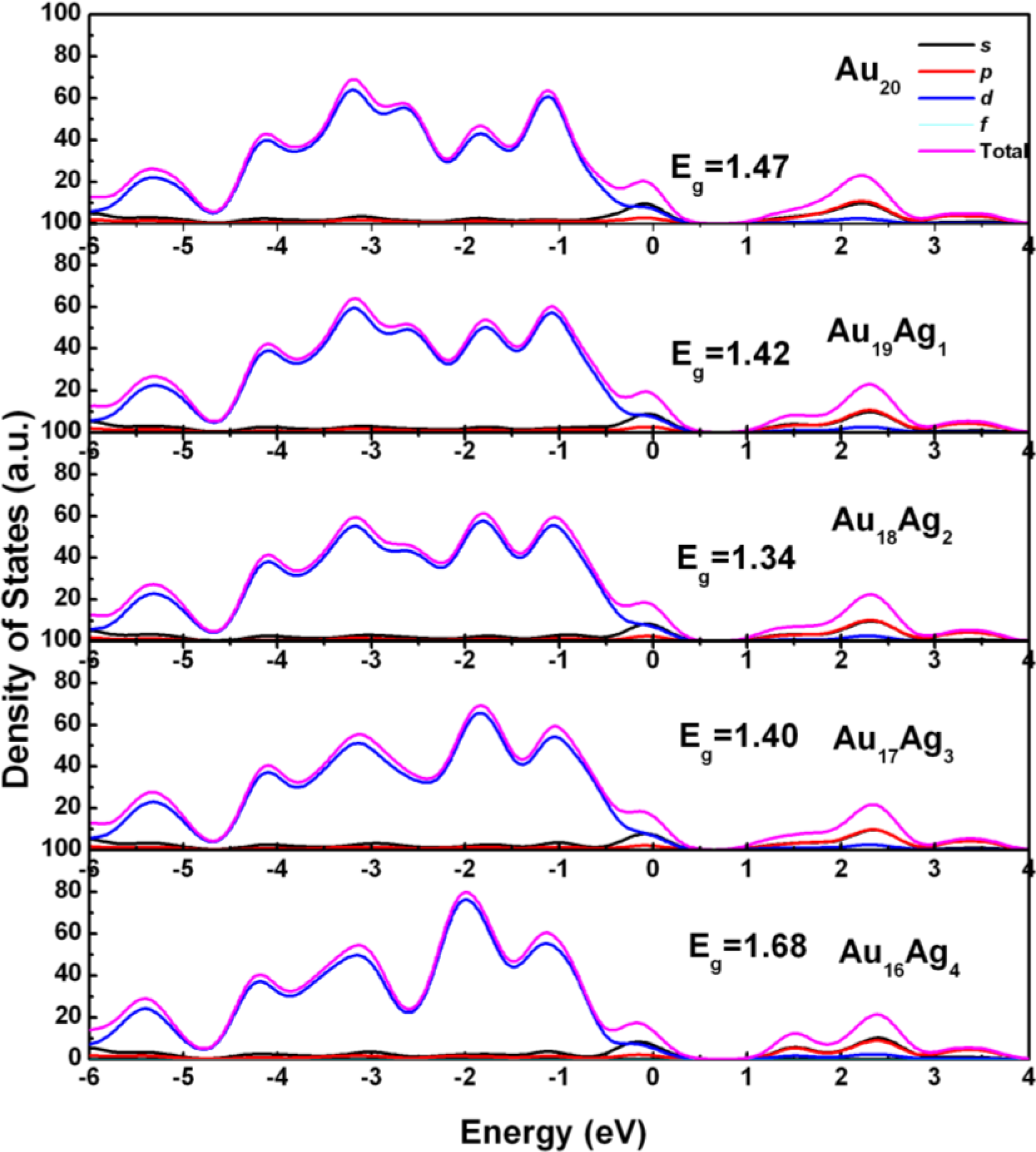
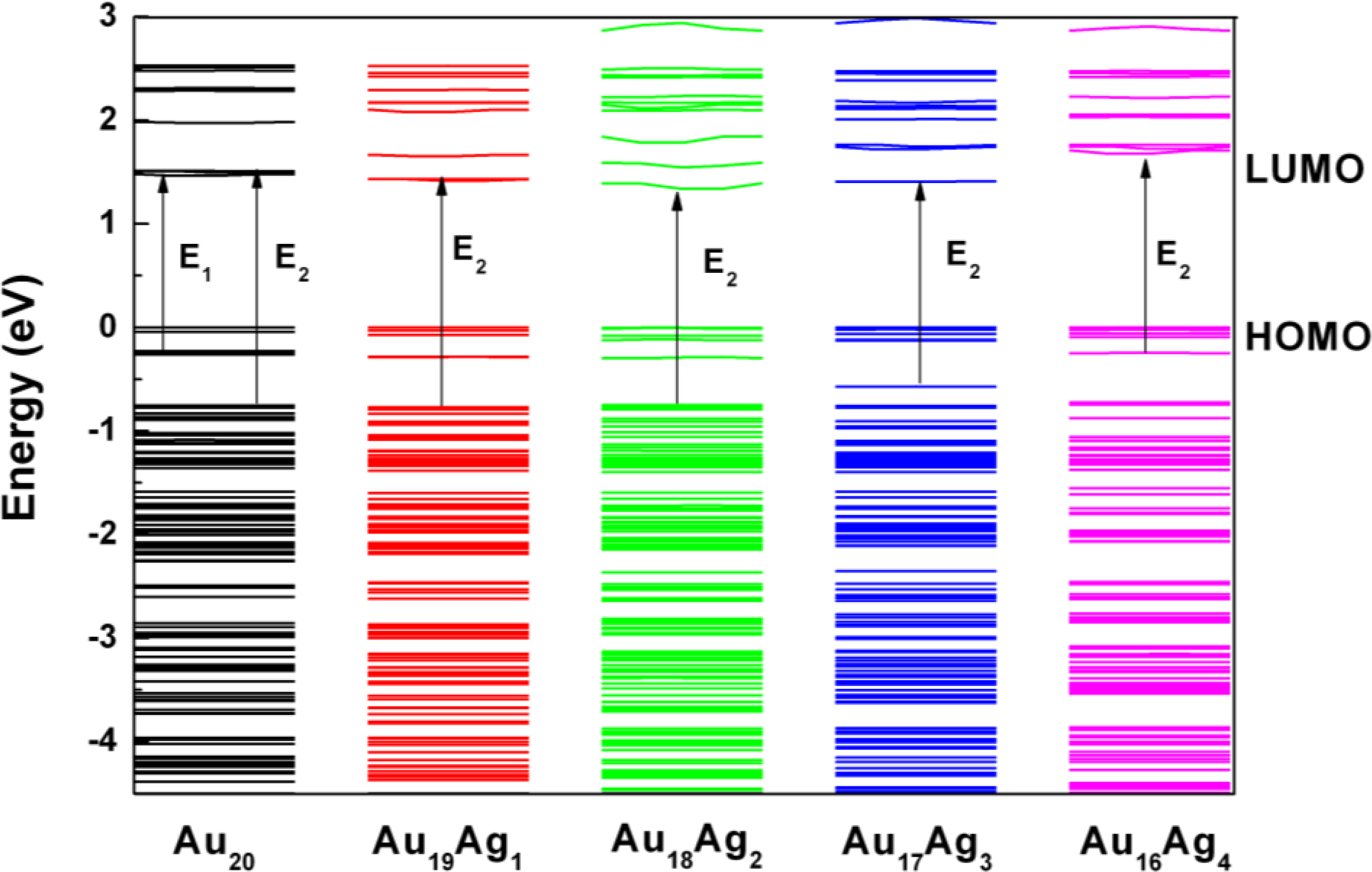
2.2. Electronic Structure of Ag-Doped Au20 Clusters
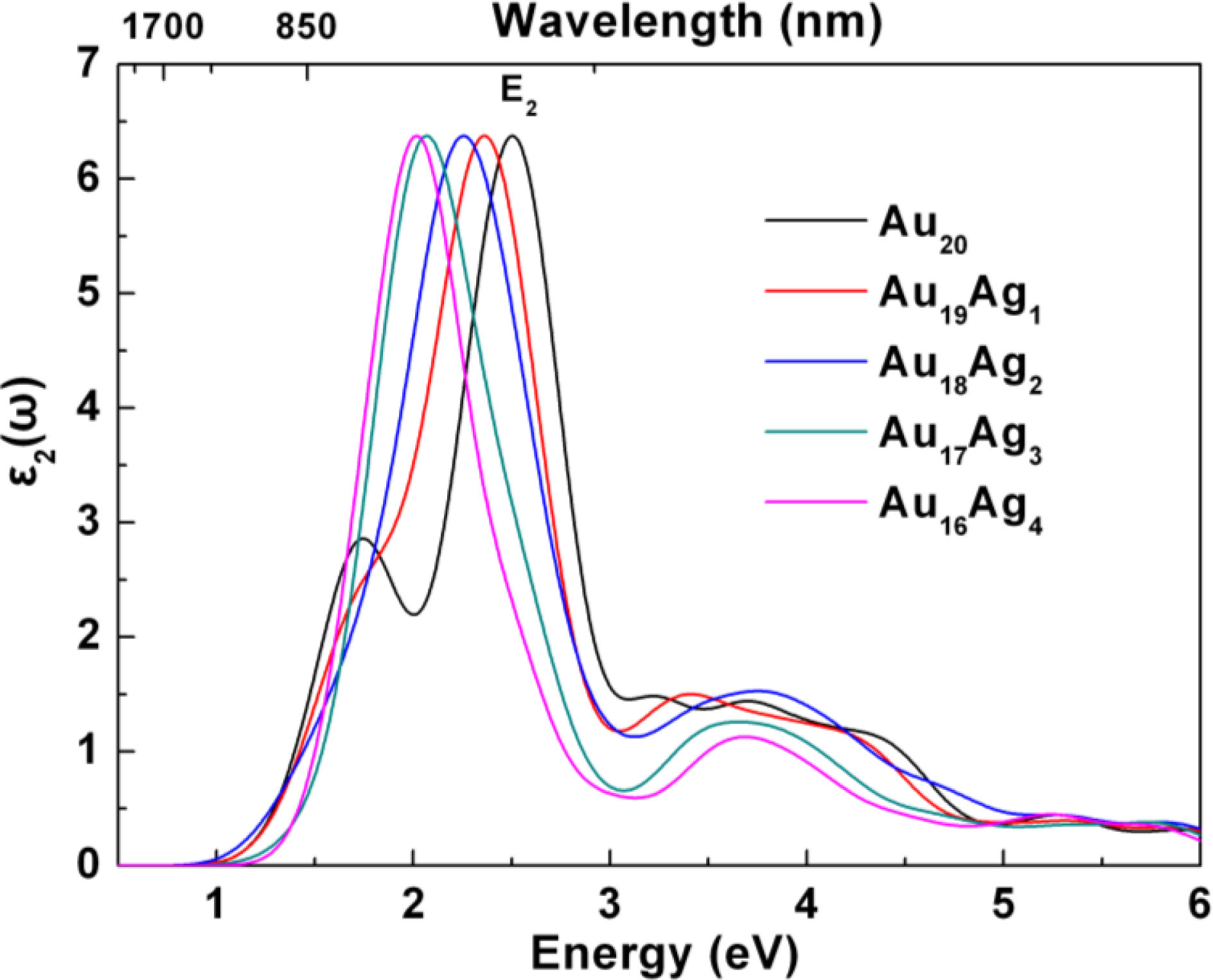
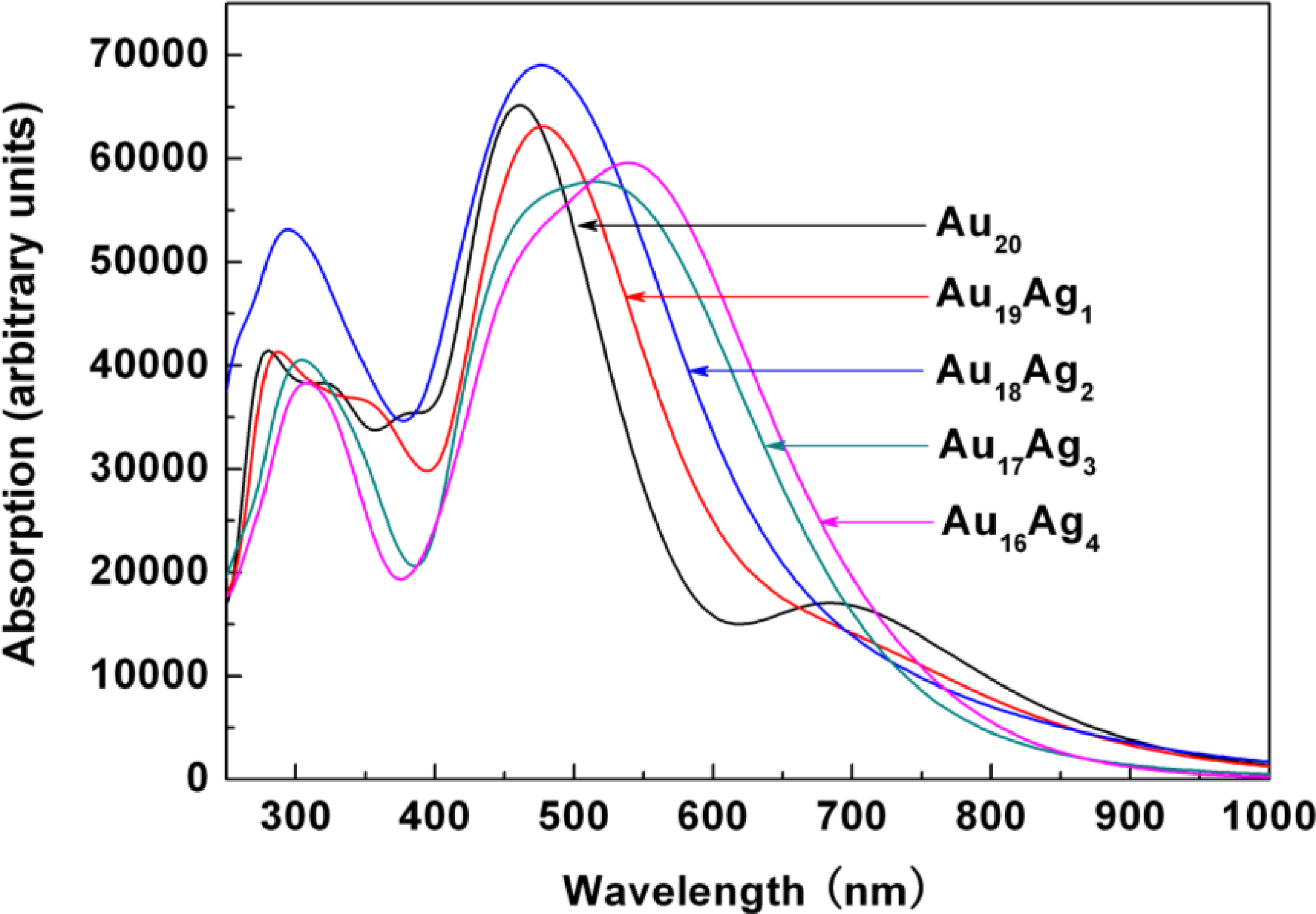
2.3. Tunable Optical Properties of Gold Clusters
3. Computational Section
4. Conclusions
Acknowledgments
References
- Huang, X; El-Sayed, I; Qian, W; El-Sayed, M. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J. Am. Chem. Soc 2006, 128, 2115–2020. [Google Scholar]
- Hainfeld, J; Slatkin, D; Smilowitz, H. The use of gold nanoparticles to enhance radiotherapy in mice. Phys. Med. Biol 2004, 49, N309–N315. [Google Scholar]
- Wu, D; Zhang, X; Liu, P; Zhang, L; Fan, F; Guo, M. Gold Nanostructure: Fabrication, Surface Modification, Targeting Imaging, and Enhanced Radiotherapy. Curr. Nanosci 2011, 7, 110–118. [Google Scholar]
- Murphy, C; Gole, A; Stone, J; Sisco, P; Alkilany, A; Goldsmith, E; Baxter, S. Gold nanoparticles in biology: beyond toxicity to cellular imaging. Acc. Chem. Res 2008, 41, 1721–1730. [Google Scholar]
- Zhang, X; Wu, H. Toxicologic effects of gold nanoparticles in vivo by different administration routes. Int. J. Nanomed 2010, 5, 771–781. [Google Scholar]
- Zhang, XD; Guo, ML; Wu, HY; Sun, YM; Ding, YQ; Feng, X; Zhang, LA. Irradiation stability and cytotoxicity of gold nanoparticles for radiotherapy. Int. J. Nanomed 2009, 4, 165–173. [Google Scholar]
- Loo, C; Lowery, A; Halas, N; West, J; Drezek, R. Immunotargeted nanoshells for integrated cancer imaging and therapy. Nano Lett 2005, 5, 709–711. [Google Scholar]
- Chen, J; Wang, D; Xi, J; Au, L; Siekkinen, A; Warsen, A; Li, Z; Zhang, H; Xia, Y; Li, X. Immuno gold nanocages with tailored optical properties for targeted photothermal destruction of cancer cells. Nano. Lett 2007, 7, 1318–1322. [Google Scholar]
- Sun, Q; Wang, Q; Rao, B; Jena, P. Electronic Structure and Bonding of Au on a SiO2 Cluster: A Nanobullet for Tumors. Phys. Rev. Lett 2004, 93, 186803. [Google Scholar]
- Gruene, P; Rayner, D; Redlich, B; van der Meer, A; Lyon, J; Meijer, G; Fielicke, A. Structures of neutral Au7, Au19, and Au20 clusters in the gas phase. Science 2008, 321, 674–676. [Google Scholar]
- Li, X; Wang, H; Yang, X; Zhu, Z; Tang, Y. Size dependence of the structures and energetic and electronic properties of gold clusters. J. Chem. Phys 2007, 126, 084505. [Google Scholar]
- Zheng, X; Shi, X; Dai, Z; Zeng, Z. Transport properties of the Au32 cluster with fullerene symmetry. Phys. Rev. B 2006, 74, 85418. [Google Scholar]
- Li, J; Li, X; Zhai, H; Wang, L. Au20: A tetrahedral cluster. Science 2003, 299, 864–867. [Google Scholar]
- Wu, K; Li, J; Lin, C. Remarkable second-order optical nonlinearity of nano-sized Au20 cluster: a TDDFT study. Chem. Phys. Lett 2004, 388, 353–357. [Google Scholar]
- Guo, JJ; Yang, JX; Die, D. First Principle Calculation on AunAg2 (n = 1∼4) Clusters. Commun. Theor. Phys 2007, 48, 348–352. [Google Scholar]
- Zhang, XD; Guo, ML. Electronic structure and optical transitions of Au20−xCux nanoclusters. J. Nanosci. Nanotechnol 2010, 10, 7192–7195. [Google Scholar]
- Bona čić-Koutecký, V; Burda, J; Mitri, R; Ge, M; Zampella, G; Fantucci, P. Density functional study of structural and electronic properties of bimetallic silver-gold clusters: Comparison with pure gold and silver clusters. J. Chem. Phys 2002, 117, 3120–3131. [Google Scholar]
- Wang, L; Pal, R; Huang, W; Zeng, X; Wang, L. Observation of earlier two-to-three dimensional structural transition in gold cluster anions by isoelectronic substitution: MAu (n = 8–11; M = Ag, Cu). J. Chem. Phys 2010, 132, 114306. [Google Scholar]
- Ghanty, T; Banerjee, A; Chakrabarti, A. Structures and the Electronic Properties of Au19X Clusters (X = Li, Na, K, Rb, Cs, Cu, and Ag). J. Phys. Chem. C 2009, 114, 20. [Google Scholar]
- Li, S; Shao, Z; Han, S; Xue, X; Wang, F; Sun, Q; Jia, Y; Guo, Z. Role of Ag-doping in small transition metal clusters from first-principles simulations. J. Chem. Phys 2009, 131, 184301. [Google Scholar]
- Idrobo, J; Walkosz, W; Yip, S; Üğüt, S; Wang, J; Jellinek, J. Static polarizabilities and optical absorption spectra of gold clusters (Aun, n = 2–14 and 20) from first principles. Phys. Rev. B 2007, 76, 205422. [Google Scholar]
- Zhang, X; Guo, M; Li, W; Liu, C. First-principles study of electronic and optical properties in wurtzite ZnCdO. J. Appl. Phys 2008, 103, 063721. [Google Scholar]
- Chen, F; Johnston, R. Structure and spectral characteristics of the nanoalloy Ag3Au10. Appl. Phys. Lett 2007, 90, 153123. [Google Scholar]
- Lee, H; Ge, M; Sahu, B; Tarakeshwar, P; Kim, K. Geometrical and electronic structures of gold, silver, and gold-silver binary clusters: Origins of ductility of gold and gold-silver alloy formation. J. Phys. Chem. B 2003, 107, 9994–10005. [Google Scholar]
- Zorriasatein, S; Joshi, K; Kanhere, D. Electronic and structural investigations of gold clusters doped with copper: AuCu (n = 13–19). J. Chem. Phys 2008, 128, 184314. [Google Scholar]
- Rossi, G; Ferrando, R; Rapallo, A; Fortunelli, A; Curley, BC; Lloyd, LD; Johnston, RL. Global optimization of bimetallic cluster structures. II. Size-matched Ag–Pd, Ag–Au, and Pd–Pt systems. J. Chem. Phys 2005, 122, 194309. [Google Scholar]
- Curley, B; Rossi, G; Ferrando, R; Johnston, R. Theoretical study of structure and segregation in 38-atom Ag–Au nanoalloys. Eur. Phys. J. D 2007, 43, 53–56. [Google Scholar]
- Payne, M; Teter, M; Allan, D; Arias, T; Joannopoulos, J. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys 1992, 64, 1045–1097. [Google Scholar]
- Perdew, J; Burke, K; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett 1996, 77, 3865. [Google Scholar]
- Monkhorst, H; Pack, J. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar]
- Zhang, X; Guo, M; Liu, C; Li, W; Hong, X. Electronic and optical properties of TiCdO: A first-principles prediction. Appl. Phys. Lett 2008, 93, 012103. [Google Scholar]

© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, X.-D.; Guo, M.-L.; Wu, D.; Liu, P.-X.; Sun, Y.-M.; Zhang, L.-A.; She, Y.; Liu, Q.-F.; Fan, F.-Y. First-Principles Investigation of Ag-Doped Gold Nanoclusters. Int. J. Mol. Sci. 2011, 12, 2972-2981. https://doi.org/10.3390/ijms12052972
Zhang X-D, Guo M-L, Wu D, Liu P-X, Sun Y-M, Zhang L-A, She Y, Liu Q-F, Fan F-Y. First-Principles Investigation of Ag-Doped Gold Nanoclusters. International Journal of Molecular Sciences. 2011; 12(5):2972-2981. https://doi.org/10.3390/ijms12052972
Chicago/Turabian StyleZhang, Xiao-Dong, Mei-Li Guo, Di Wu, Pei-Xun Liu, Yuan-Ming Sun, Liang-An Zhang, Yi She, Qing-Fen Liu, and Fei-Yue Fan. 2011. "First-Principles Investigation of Ag-Doped Gold Nanoclusters" International Journal of Molecular Sciences 12, no. 5: 2972-2981. https://doi.org/10.3390/ijms12052972
APA StyleZhang, X.-D., Guo, M.-L., Wu, D., Liu, P.-X., Sun, Y.-M., Zhang, L.-A., She, Y., Liu, Q.-F., & Fan, F.-Y. (2011). First-Principles Investigation of Ag-Doped Gold Nanoclusters. International Journal of Molecular Sciences, 12(5), 2972-2981. https://doi.org/10.3390/ijms12052972



