Geometrical Evolution Pattern and Spectroscopic Properties of Terbium-Doped Germanium Anionic TbGen (n = 6–17) Nanoclusters: From Tb-Lined to Tb-Encapsulated Structures
Abstract
1. Introduction
2. Computational Details
3. Result and Discussion
3.1. GM Configurations of Anionic TbGen (n = 6–17) Nanoclusters
3.2. The Charge Transfer and Magnetic Moment of TbGen− (n = 6–17) Nanoclusters
3.3. The Evaluated Photoelectron Spectroscopy of TbGen− (n = 6–17)
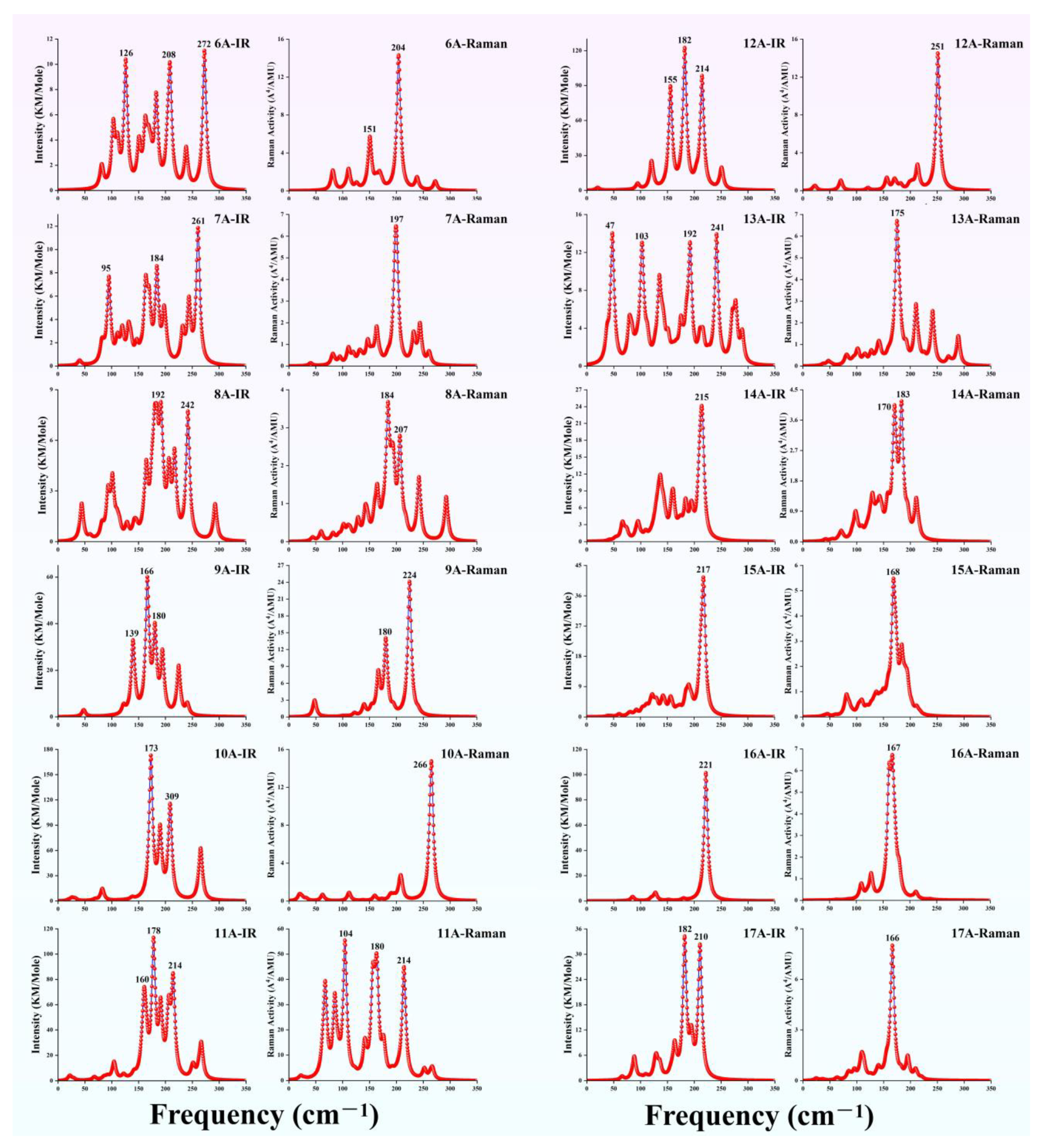
3.4. The Simulated Infrared and Raman Spectra of TbGen− (n = 6–17)
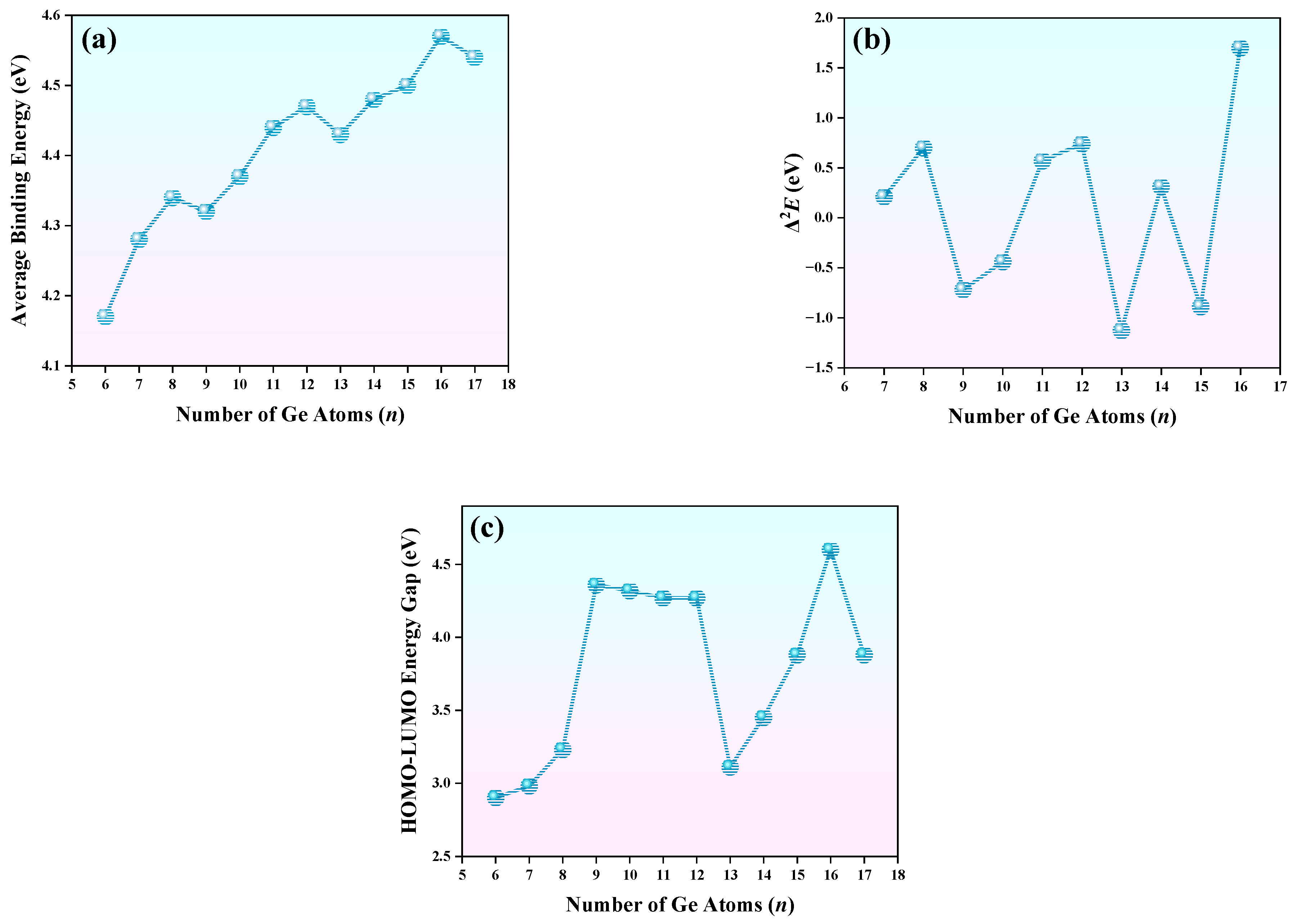
3.5. The Relative and Chemical Stabilities of TbGen− (n = 6–17)
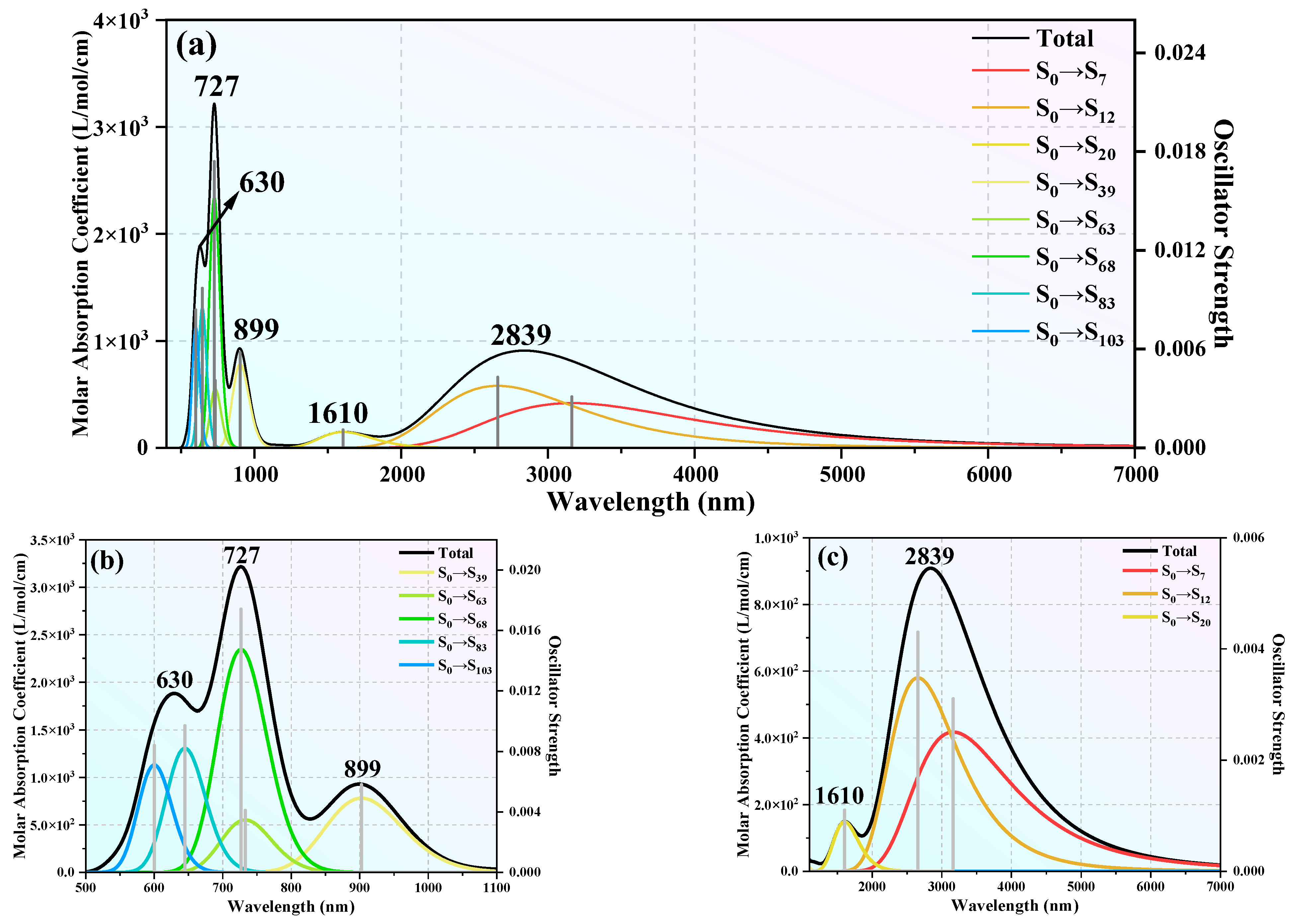
3.6. UV–Vis Spectra of the TbGe12− and TbGe16− Clusters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shvartsburg, A.A.; Liu, B.; Lu, Z.Y.; Wang, C.Z.; Jarrold, M.F.; Ho, K.M. Structures of germanium clusters: Where the growth patterns of silicon and germanium clusters diverge. Phys. Rev. Lett. 1999, 83, 2167. [Google Scholar] [CrossRef]
- Wang, J.; Wang, G.; Zhao, J. Structure and electronic properties of Gen(n = 2–25) clusters from density-functional theory. Phys. Rev. B 2001, 64, 205411. [Google Scholar] [CrossRef]
- Bulusu, S.; Yoo, S.; Zeng, X.C. Search for global minimum geometries for medium sized germanium clusters: Ge12–Ge20. J. Chem. Phys. 2005, 122, 164305. [Google Scholar] [CrossRef] [PubMed]
- An, W. Predicting the structural evolution of Gen− (3≤ n ≤ 20) clusters: An anion photoelectron spectroscopy simulation. Phys. Chem. Chem. 2018, 20, 25746–25751. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Lu, J.; Li, S.; Zhang, Y. Endohedral group-14 clusters Au@X12 (X = Ge, Sn, Pb) and their anions: A first-principles study. J. Mol. Liq. 2023, 376, 121477. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Cuong, N.T.; Lan, N.T.; Tung, N.T.; Nguyen, M.T.; Tam, N.M. First-row transition metal doped germanium clusters Ge16M: Some remarkable superhalogens. RSC Adv. 2022, 12, 13487–13499. [Google Scholar] [CrossRef]
- Li, X.J.; Ren, H.J.; Yang, L.M. An Investigation of Electronic Structure and Aromaticity in Medium-Sized Nanoclusters of Gold-Doped Germanium. J. Nanomater. 2012, 2012, 518593. [Google Scholar] [CrossRef]
- Mahtout, S.; Siouani, C.; Rabilloud, F. Growth behavior and electronic structure of noble metal-doped germanium clusters. J. Phys. Chem. A 2018, 122, 662–677. [Google Scholar] [CrossRef]
- Siouani, C.; Mahtout, S.; Rabilloud, F. Structure, stability, and electronic properties of niobium-germanium and tantalum-germanium clusters. J. Mol. Model. 2019, 25, 113. [Google Scholar] [CrossRef]
- Zhao, J.; Du, Q.; Zhou, S.; Kumar, V. Endohedrally doped cage clusters. Chem. Rev. 2020, 120, 9021–9163. [Google Scholar] [CrossRef]
- Cheshnovsky, O.; Yang, S.H.; Pettiette, C.L.; Craycraft, M.J.; Liu, Y.; Smalley, R.E. Ultraviolet photoelectron spectroscopy of semiconductor clusters: Silicon and germanium. Chem. Phys. Lett. 1987, 138, 119–124. [Google Scholar] [CrossRef]
- Burton, G.R.; Xu, C.; Neumark, D.M. study of small semiconductor clusters using anion photoelectron spectroscopy: Germanium clusters (Gen, n = 2–15). Surf. Rev. Lett. 1996, 3, 383–388. [Google Scholar] [CrossRef]
- Burton, G.R.; Xu, C.; Arnold, C.C.; Neumark, D.M. Photoelectron spectroscopy and zero electron kinetic energy spectroscopy of germanium cluster anions. J. Chem. Phys. 1996, 104, 2757–2764. [Google Scholar] [CrossRef]
- Negishi, Y.; Kawamata, H.; Hayakawa, F.; Nakajima, A.; Kaya, K. The infrared HOMO–LUMO gap of germanium clusters. Chem. Phys. Lett. 1998, 294, 370–376. [Google Scholar] [CrossRef]
- Deng, X.; Kong, X.; Xu, X.L.; Xu, H.G.; Zheng, W.J. Photoelectron Spectroscopy and Density Functional Calculations of TiGen− (n = 7–12) Clusters. Chin. J. Chem. Phys. 2016, 29, 123–128. [Google Scholar] [CrossRef]
- Atobe, J.; Koyasu, K.; Furuse, S.; Nakajima, A. Anion photoelectron spectroscopy of germanium and tin clusters containing a transition-or lanthanide-metal atom; MGen− (n = 8–20) and MSnn− (n = 15–17) (M = Sc–V, Y–Nb, and Lu–Ta). Phys. Chem. Chem. Phys. 2012, 14, 9403–9410. [Google Scholar] [CrossRef]
- Borshch, N.A.; Pereslavtseva, N.S.; Kurganskii, S.I. Spatial structure and electron energy spectra of ScGen− (n = 6–16) clusters. Russ. J. Phys. Chem. B 2015, 9, 9–18. [Google Scholar] [CrossRef]
- Wang, H.; Yang, J.; Lin, L. Geometric evolution, electronic structure, and vibrational properties of ScGen− (n = 6–17) anion clusters: A DFT insight. Int. J. Quantum Chem. 2022, 122, e27002. [Google Scholar] [CrossRef]
- Wang, H.; Dong, C.; Yang, J. Theoretical Insights into the Geometrical Evolution, Photoelectron Spectra, and Vibrational Properties of YGen– (n = 6–20) Anions: From Y-Linked to Y-Encapsulated Structures. ACS Omega 2022, 7, 36330–36342. [Google Scholar] [CrossRef]
- Yang, Z.; Cao, Z.; Rehman, A.U.; Yang, J. Structural Evolution, Electronic Structures, and Vibrational Properties of Anionic LuGen (n = 5–17) Clusters: From Lu-Linked to Lu-Encapsulated Configurations. Inorg. Chem. 2021, 60, 14446–14456. [Google Scholar] [CrossRef]
- Zhao-Feng, Y.; Zhen-Zhu, C.; Aziz, U.R.; Ju-Cai, Y. Structural and Electronic Properties of Lutetium Doped Germanium Clusters LuGen(+/0/−)(n = 6~19): A Density Functional Theory Investigation. Chin. J. Struc. Chem. 2022, 41, 2203155–2203165. [Google Scholar]
- Yang, Z.; Cao, Z.; Bano, R.; Yang, J.; Gilani, M.A. A systematic investigation of structural growth patterns and electronic properties of [LuGen]+/0 and [Gen+1]+/0 (n = 1–17) nanoalloy clusters. Mater. Today Commun. 2022, 30, 103018. [Google Scholar] [CrossRef]
- Zhang, J.M.; Wang, H.Q.; Li, H.F.; Xie, B.; Han, C.; Jiang, L.Y. Insights into the structure and growth of Lu-doped germanium clusters: Comparing density functional theory calculations with photoelectron spectroscopy experiments. Mol. Phys. 2022, 120, e2131644. [Google Scholar] [CrossRef]
- Li, A.; Li, H.; Li, Z.; Qin, L.; Mei, X.; Zhang, J.; Zhang, Y.; Zheng, H.; Jiang, K.; Wu, W.; et al. Structural evolution and electronic properties of the La-doped germanium clusters. Mol. Phys. 2024, 123, e2356191. [Google Scholar] [CrossRef]
- Trivedi, R.; Banerjee, A.; Bandyopadhyay, D. Insight into stabilities and magnetism of EuGen (n = 1–20) nanoclusters: An assessment of electronic aromaticity. J. Mater. Sci. 2022, 57, 19338–19355. [Google Scholar] [CrossRef]
- Hao, C.; Dong, C.; Yang, Z. Structural evolution and electronic properties of cerium doped germanium anionic nanocluster CeGen− (n = 5–17): Theoretical investigation. Int. J. Quantum. Chem. 2024, 124, e27315. [Google Scholar] [CrossRef]
- Yang, Z.; Rehman, A.U.; Cao, Z.; Yang, J. Structural evolution, photoelectron spectra and vibrational properties of anionic GdGen− (n = 5–18) nanoalloy clusters: A DFT insight. RSC Adv. 2022, 12, 22020–22030. [Google Scholar] [CrossRef]
- Hao, C.; Dong, X.; Li, C.; Dong, C.; Yang, Z.; Yang, J. Structural behaviors, optical properties and electronic structures of rare earth samarium doped germanium anion nanocluster SmGen− (n = 4–20): A density functional theory investigation. Mater. Sci. Eng. B 2025, 315, 118095. [Google Scholar] [CrossRef]
- Hao, C.; Dong, X.; Li, C.; Dong, C.; Yang, Z.; Yang, J. Structural, Electronic, and Nonlinear Optical Characteristics of Europium-Doped Germanium Anion Nanocluster EuGen− (n = 7–20): A Theoretical Investigation. Molecules 2025, 30, 1377. [Google Scholar] [CrossRef]
- Zhang, J.; Dolg, M. ABCluster: The artificial bee colony algorithm for cluster global optimization. Phys. Chem. Chem. Phys. 2015, 17, 24173–24181. [Google Scholar] [CrossRef]
- Zhang, J.; Dolg, M. Global optimization of clusters of rigid molecules using the artificial bee colony algorithm. Phys. Chem. Chem. Phys. 2016, 18, 3003–3010. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Glezakou, V.A.; Rousseau, R.; Nguyen, M.T. NWPEsSe: An adaptive-learning global optimization algorithm for nanosized cluster systems. J. Chem. Theory Comput. 2020, 16, 3947–3958. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian~09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Savin, A.; Preuss, H. Energy-adjusted pseudopotentials for the rare earth elements. Theor. Chim. Acta 1989, 75, 173–194. [Google Scholar] [CrossRef]
- Dolg, M.; Stoll, H.; Preuss, H. A combination of quasirelativistic pseudopotential and ligand field calculations for lanthanoid compounds. Theor. Chim. Acta 1993, 85, 441–450. [Google Scholar] [CrossRef]
- Bergner, A.; Dolg, M.; Küchle, W.; Stoll, H.; Preuß, H. Ab initio energy-adjusted pseudopotentials for elements of groups 13–17. Mol. Phys. 1993, 80, 1431–1441. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New basis set exchange: An open, up-to-date resource for the molecular sciences community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- Metz, B.; Stoll, H.; Dolg, M. Small-core multiconfiguration-Dirac–Hartree–Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563–2569. [Google Scholar] [CrossRef]
- Peterson, K.A. Systematically convergent basis sets with relativistic pseudopotentials. I. Correlation consistent basis sets for the post-d group 13–15 elements. J. Chem. Phys. 2003, 119, 11099–11112. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Towards chemical accuracy for the thermodynamics of large molecules: New hybrid density functionals including non-local correlation effects. Phys. Chem. Chem. Phys. 2006, 8, 4398–4401. [Google Scholar] [CrossRef]
- Wilson, A.K.; Woon, D.E.; Peterson, K.A.; Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667–7676. [Google Scholar] [CrossRef]
- Ortiz, J.V. Electron binding energies of anionic alkali metal atoms from partial fourth order electron propagator theory calculations. J. Chem. Phys. 1988, 89, 6348–6352. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Lu, T. A comprehensive electron wavefunction analysis toolbox for chemists, Multiwfn. J. Comput. Chem. 2024, 161, 082503. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Liu, B.; Yang, J. Thermochemical Properties and Growth Mechanism of the Ag-Doped Germanium Clusters, AgGenλ with n = 1–13 and λ = −1, 0, and +1. ACS Omega 2021, 6, 9813–9827. [Google Scholar] [CrossRef]
- Feng, Y.; Yang, J.; Liu, Y. Study on the structures and properties of praseodymium-doped silicon clusters PrSin (n = 3–9) and their anions with density functional schemes. Theor. Chem. Acc. 2016, 135, 258. [Google Scholar] [CrossRef]
- Jaiswal, S.; Babar, V.P.; Kumar, V. Growth behavior, electronic structure, and vibrational properties of SinY anion clusters (n = 4–20): Metal atom as linker and endohedral dopant. Phys. Rev. B 2013, 88, 085412. [Google Scholar] [CrossRef]
- Baerends, E.J.; Gritsenko, O.V.; Van Meer, R. The KohnSham Gap, the Fundamental Ggap and the Optical Gap: The Physical Meaning of Occupied and Virtual Kohn-Sham Orbital Energies. Phys. Chem. Chem. Phys. 2013, 15, 16408–16425. [Google Scholar] [CrossRef]



| Clusters | Charge (a.u.) | Electron Configuration | Magnetic Moment of Tb Atom | Molecule (μB) | |||||
|---|---|---|---|---|---|---|---|---|---|
| 6s | 4f | 5d | 6p | 7s | Total | ||||
| TbGe6− | 0.07 | [core]6s0.824f7.365d2.216p0.317s0.24 | −0.50 | 6.59 | 0.28 | 0.01 | −0.04 | 6.34 | 6 |
| TbGe7− | 0.17 | [core]6s0.754f7.365d2.176p0.297s0.25 | −0.52 | 6.44 | 0.26 | 0.01 | −0.03 | 6.16 | 6 |
| TbGe8− | 0.19 | [core]6s0.784f7.385d2.086p0.367s0.21 | −0.54 | 6.58 | 0.26 | 0.01 | −0.03 | 6.28 | 6 |
| TbGe9− | 0.39 | [core]6s1.284f7.005d1.736p0.437s0.17 | 0.46 | 6.96 | −0.50 | −0.27 | −0.04 | 6.61 | 6 |
| TbGe10− | 0.32 | [core]6s1.014f7.015d1.966p0.587s0.11 | −0.74 | 6.95 | 0.04 | 0.02 | 0.01 | 6.28 | 6 |
| TbGe11− | 0.12 | [core]6s0.714f7.365d1.886p0.687s0.25 | −0.53 | 6.60 | 0.15 | 0.02 | −0.07 | 6.17 | 6 |
| TbGe12− | −0.27 | [core]6s0.714f7.355d2.156p0.817s0.24 | −0.54 | 6.61 | 0.15 | 0.01 | −0.06 | 6.17 | 6 |
| TbGe13− | 0.10 | [core]6s0.734f7.345d2.356p0.397s0.13 | −0.57 | 6.62 | 0.26 | −0.01 | −0.01 | 6.29 | 6 |
| TbGe14− | −2.94 | [core]6s0.704f7.355d4.176p1.377s0.33 | −0.71 | 6.94 | 0.15 | 0.02 | −0.01 | 6.16 | 6 |
| TbGe15− | −3.94 | [core]6s0.824f6.995d5.066p1.747s0.27 | −0.60 | 6.95 | 0.26 | 0.02 | −0.05 | 6.58 | 6 |
| TbGe16− | −4.76 | [core]6s0.664f7.355d5.286p2.007s0.41 | −0.43 | 6.61 | 0.20 | 0.01 | −0.18 | 6.21 | 6 |
| TbGe17− | −3.93 | [core]6s0.674f7.355d4.816p1.687s0.37 | −0.46 | 6.61 | 0.19 | 0.01 | −0.15 | 6.20 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, C.; Yang, J. Geometrical Evolution Pattern and Spectroscopic Properties of Terbium-Doped Germanium Anionic TbGen (n = 6–17) Nanoclusters: From Tb-Lined to Tb-Encapsulated Structures. Molecules 2025, 30, 2066. https://doi.org/10.3390/molecules30092066
Hao C, Yang J. Geometrical Evolution Pattern and Spectroscopic Properties of Terbium-Doped Germanium Anionic TbGen (n = 6–17) Nanoclusters: From Tb-Lined to Tb-Encapsulated Structures. Molecules. 2025; 30(9):2066. https://doi.org/10.3390/molecules30092066
Chicago/Turabian StyleHao, Chenliang, and Jucai Yang. 2025. "Geometrical Evolution Pattern and Spectroscopic Properties of Terbium-Doped Germanium Anionic TbGen (n = 6–17) Nanoclusters: From Tb-Lined to Tb-Encapsulated Structures" Molecules 30, no. 9: 2066. https://doi.org/10.3390/molecules30092066
APA StyleHao, C., & Yang, J. (2025). Geometrical Evolution Pattern and Spectroscopic Properties of Terbium-Doped Germanium Anionic TbGen (n = 6–17) Nanoclusters: From Tb-Lined to Tb-Encapsulated Structures. Molecules, 30(9), 2066. https://doi.org/10.3390/molecules30092066








