Orientational Structure and Electro-Optical Properties of Chiral Nematic Droplets with Conical Anchoring
Abstract
1. Introduction
2. Results
2.1. CLC Droplets Structures
2.2. The Electro-Optical Response of PDLC Cells
3. Discussion
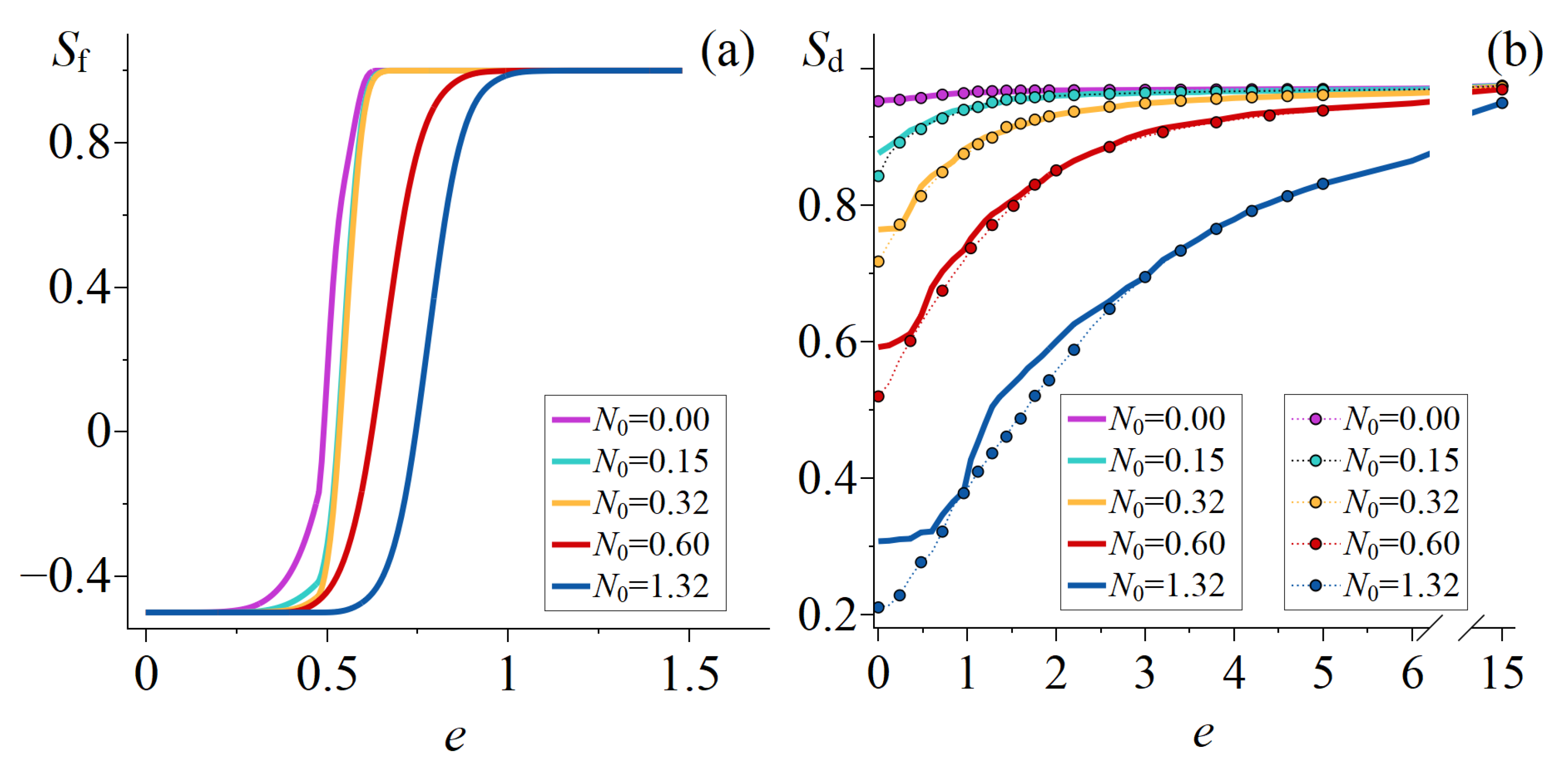
3.1. The Calculated Dependencies
3.2. The Measured Dependencies
4. Materials and Methods
4.1. Samples Fabrication
4.2. Electro-Optical Measurement
4.3. Calculating Droplets Structures
4.4. Calculating Light Transmittance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Drzaic, P.S. Liquid Crystal Dispersions; World Scientific: Singapore, 1995. [Google Scholar]
- Jinqian, L.; Zhao, Y.; Gao, H.; Wang, D.; Miao, Z.; Cao, H.; Yang, Z.; He, W. Polymer dispersed liquid crystals doped with CeO2 nanoparticles for the smart window. Liq. Cryst. 2021, 49, 29–38. [Google Scholar] [CrossRef]
- Meng, X.; Li, J.; Lin, Y.; Liu, X.; Zhao, J.; Li, D.; He, Z. Periodic Electro-Optical Characteristics of PDLC Film Driven by a Low-Frequency Square Wave Voltage. Crystals 2022, 12, 163. [Google Scholar] [CrossRef]
- Mahar, M.; Muhammad, J.; Ali, M.; Mangi, K.H.; Murad, A.; Iqbal, M. Preparation of silver nanoparticles (AgNPs)-doped epoxy-based thin PDLC films (smart glass). Polym. Bull. 2022, 79, 3135–3153. [Google Scholar]
- Sharma, V.; Kumar, P.; Jaggi, C.; Malik, P.; Raina, K. Preparation and electrooptic study of reverse mode polymer dispersed liquid crystal: Performance augmentation with the doping of nanoparticles and dichroic dye. J. Appl. Polym. Sci. 2019, 137, 48745. [Google Scholar] [CrossRef]
- Yin, S.; Ge, S.; Zhao, Y.; Lu, W.; Ma, H.; Sun, Y. Influence of different small styryl molecules on electro-optical characteristics of reverse-mode polymer stabilised cholesteric liquid crystal devices. Liq. Cryst. 2023, 50, 2458–2467. [Google Scholar] [CrossRef]
- Islam, M.S.; Chan, K.Y.; Thien, G.S.H.; Low, P.L.; Lee, C.L.; Wong, S.K.; Noor, E.E.M.; Au, B.W.C.; Ng, Z.N. Performances of Polymer-Dispersed Liquid Crystal Films for Smart Glass Applications. Polymers 2023, 15, 3420. [Google Scholar] [CrossRef]
- Deng, Y.; Yang, Y.; Xiao, Y.; Zeng, X.; Xie, H.L.; Lan, R.; Lanying, Z.; Yang, H. Annual Energy-Saving Smart Windows with Actively Controllable Passive Radiative Cooling and Multimode Heating Regulation. Adv. Mater. 2024, 36, e2401869. [Google Scholar] [CrossRef]
- Agarwal, S.; Srivastava, S.; Joshi, S.; Tripathi, S.; Singh, B.P.; Pandey, K.K.; Manohar, R. A Comprehensive Review on Polymer-Dispersed Liquid Crystals: Mechanisms, Materials, and Applications. ACS Mater. Au 2025, 5, 88–114. [Google Scholar] [CrossRef]
- Sun, S.; Li, J.; Li, X.; Zhao, X.; Li, K.; Chen, L. Dynamic 3D metasurface holography via cascaded polymer dispersed liquid crystal. Microsyst. Nanoeng. 2024, 10, 203. [Google Scholar] [CrossRef]
- Jiang, J.; McGraw, G.; Ma, R.; Brown, J.; Yang, D.K. Selective scattering polymer dispersed liquid crystal film for light enhancement of organic light emitting diode. Opt. Express 2017, 25, 3327–3335. [Google Scholar] [CrossRef]
- He, Z.; Yin, K.; Hsiang, E.L.; Wu, S.T. Volumetric light-shaping polymer-dispersed liquid crystal films for mini-LED backlights. Liq. Cryst. 2020, 47, 1458–1463. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, S.; Miao, X.; Xie, P.; Sun, N.; Xu, Z.; Zhong, T.; Zhang, L.; Shen, Y. Advancements and Applications of Liquid Crystal/Polymer Composite Films. ACS Mater. Lett. 2023, 5, 2760–2775. [Google Scholar] [CrossRef]
- Hsiao, V.K.; Lu, C.; He, G.S.; Pan, M.; Cartwright, A.N.; Prasad, P.N.; Jakubiak, R.; Vaia, R.A.; Bunning, T.J. High contrast switching of distributed-feedback lasing in dye-doped H-PDLC transmission grating structures. Opt. Express 2005, 13, 3787–3794. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, F.K.; Jamil, M.M.A.; Lee, J.W.; Kim, S.R.; Jeon, Y.J. The effect of UV intensities and curing time on polymer dispersed liquid crystal (PDLC) display: A detailed analysis study. Electron. Mater. Lett. 2016, 12, 685–692. [Google Scholar] [CrossRef]
- Kalkar, A.; Kunte, V.; Bhamare, S. Electrooptic studies on polymer-dispersed liquid-crystal composite films. III. Poly(methyl methacrylate-co-butyl acrylate)/E7 and poly(methyl methacrylate-co-butyl acrylate)/E8 composites. J. Appl. Polym. Sci. 2008, 107, 689–699. [Google Scholar] [CrossRef]
- Koo, J.J.; No, Y.S.; Jeon, C.; Kim, J.H. Improvement of Electro-Optic Properties in PDLC Device by Using New Cross-Linker for the Control of the Contrast Ratio, Response Time and Driving Voltage. Mol. Cryst. Liq. Cryst. 2008, 491, 58–66. [Google Scholar] [CrossRef]
- Qinqin, W.; Wang, Y. Low driving voltage ITO doped polymer-dispersed liquid crystal film and reverse voltage pulse driving method. Appl. Opt. 2017, 56, 8159. [Google Scholar] [CrossRef]
- Cupelli, D.; Nicoletta, F.; Filpo, G.; Chidichimo, G.; Fazio, A.; Gabriele, B.; Salerno, G. Fine adjustment of conductivity in polymer-dispersed liquid crystals. Appl. Phys. Lett. 2004, 85, 3292–3294. [Google Scholar] [CrossRef]
- Ahmad, F.K.; Jeon, A.; Jeon, Y.J.; Jamil, M.M.A. A novel technique of fabrication of nanoparticle acrylate doped polymer dispersed liquid crystal (PDLC) film. J. Dispers. Sci. Technol. 2021, 43, 1506–1511. [Google Scholar] [CrossRef]
- Kumari, A.; Sinha, A. Role of BaTiO3 nanoparticles on electro-optic performance of epoxy-resin-based PDLC devices. Liq. Cryst. 2020, 48, 23–34. [Google Scholar] [CrossRef]
- Mhatre, M.; Katariya-Jain, A.; Deshmukh, R. Improved electro-optical and dielectric properties of polymer dispersed liquid crystal doped with disperse dye red 1 and carbon nanoparticles. Liq. Cryst. 2023, 50, 957–976. [Google Scholar] [CrossRef]
- Hsu, C.C.; Chen, Y.X.; Li, H.W.; Hsu, J.S. Low switching voltage ZnO quantum dots doped polymer-dispersed liquid crystal film. Opt. Express 2016, 24, 7063–7068. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, R.; Katariya-Jain, A. The complete morphological, electro-optical and dielectric study of dichroic dye-doped polymer-dispersed liquid crystal. Liq. Cryst. 2014, 41, 960–975. [Google Scholar] [CrossRef]
- Zhao, C.; Hu, Y.; Xu, J.; Yu, M.; Zou, C.; Qian, W.; Gao, Y.; Yang, H. Research on the Morphology, Electro-Optical Properties and Mechanical Properties of Electrochromic Polymer-Dispersed Liquid Crystalline Films Doped with Anthraquinone Dyes. Crystals 2023, 13, 735. [Google Scholar] [CrossRef]
- Boussoualem, M.; Ismaili, M.; Roussel, F. Influence of surface anchoring conditions on the dielectric and electro-optical properties of nematic droplets dispersed in a polymer network. Soft Matter 2014, 10, 367–373. [Google Scholar] [CrossRef]
- Sharma, V.; Kumar, P. Electric Field Dependent Textural Variation inside the Liquid Crystal Droplets with Homeotropic Alignment. J. Phys. Conf. Ser. 2021, 2070, 012038. [Google Scholar] [CrossRef]
- Liang, Z.Y.; Tu, C.Y.; Yang, T.H.; Liu, C.K.; Cheng, K.T. Low-Threshold-Voltage and Electrically Switchable Polarization-Selective Scattering Mode Liquid Crystal Light Shutters. Polymers 2018, 10, 1354. [Google Scholar] [CrossRef]
- Malik, P.; Raina, K. Droplet orientation and optical properties of polymer dispersed liquid crystal composite films. Opt. Mater. 2004, 27, 613–617. [Google Scholar] [CrossRef]
- Deshmukh, R.R.; Katariya-Jain, A. Novel techniques of PDLC film preparation furnishing manifold properties in a single device. Liq. Cryst. 2016, 43, 256–267. [Google Scholar] [CrossRef]
- Kumar, P.; Sharma, V.; Jaggi, C.; Raina, K.K. Dye-dependent studies on droplet pattern and electro-optic behaviour of polymer dispersed liquid crystal. Liq. Cryst. 2017, 44, 757–767. [Google Scholar] [CrossRef]
- Krakhalev, M.N.; Prishchepa, O.O.; Sutormin, V.S.; Zyryanov, V.Y. Polymer dispersed nematic liquid crystal films with conical boundary conditions for electrically controllable polarizers. Opt. Mater. 2019, 89, 1–4. [Google Scholar] [CrossRef]
- Seč, D.; Porenta, T.; Ravnik, M.; Žumer, S. Geometrical frustration of chiral ordering in cholesteric droplets. Soft Matter 2012, 8, 11982–11988. [Google Scholar] [CrossRef]
- Gardymova, A.; Krakhalev, M.; Zyryanov, V. Optical Textures and Orientational Structures in Cholesteric Droplets with Conical Boundary Conditions. Molecules 2020, 25, 1740. [Google Scholar] [CrossRef] [PubMed]
- Feizer, K.; Krakhalev, M.; Zyryanov, V. Electrically induced optical and structural response of cholesteric and nematic droplets with conical boundary conditions. Liq. Cryst. Their Appl. 2022, 22, 55–62. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.; Zhang, L.; Xu, J.; Yuan, B.; Chen, C.; Zou, C.; Wang, Q.; Gao, Y.; Yu, M.; et al. A novel low-voltage fast-response electrically controlled dimming film based on fluorinated PDLC for smart window applications. Chem. Eng. J. 2024, 479, 147668. [Google Scholar] [CrossRef]
- Yu, M.; Xu, J.; Wang, T.; Zhang, L.; Wei, H.; Zou, C.; Gao, Y.; Yang, H. Effects of acrylate monomers with different alkyl chain structure on the electro-optical properties and microstructure of polymer dispersed liquid crystals. J. Appl. Polym. Sci. 2022, 139, e53056. [Google Scholar] [CrossRef]
- Sun, N.; Zhang, Z.; Yang, H. Effects of Diverse Acrylates on the Electro-Optical Performance of Polymer-Dispersed Liquid Crystal Films. Molecules 2025, 30, 2284. [Google Scholar] [CrossRef]
- Zhao, J.; He, Z.; Yu, P.; Ma, Z.; Chen, B.; Yao, W.; Miao, Z. Functionalized mesoporous silica composites for the modulation of polymer dispersed liquid crystals. Surfaces Interfaces 2025, 68, 106755. [Google Scholar] [CrossRef]
- Ren, Y.; Hu, W. Effects of Multi-Fluorinated Liquid Crystals with High Refractive Index on the Electro-Optical Properties of Polymer-Dispersed Liquid Crystals. Materials 2025, 18, 1406. [Google Scholar] [CrossRef]
- Lin, Y.H.; Ren, H.; Wu, S.T. High contrast polymer-dispersed liquid crystal in a 90° twisted cell. Appl. Phys. Lett. 2004, 84, 4083–4085. [Google Scholar] [CrossRef]
- Wu, B.G.; Erdmann, J.H.; Doane, J.W. Response times and voltages for PDLC light shutters. Liq. Cryst. 1989, 5, 1453–1465. [Google Scholar] [CrossRef]
- Ramdane, O.O.; Auroy, P.; Forget, S.; Raspaud, E.; Martinot-Lagarde, P.; Dozov, I. Memory-free conic anchoring of liquid crystals on a solid substrate. Phys. Rev. Lett. 2000, 84, 3871. [Google Scholar] [CrossRef] [PubMed]
- Kostikov, D.A.; Krakhalev, M.N.; Prishchepa, O.O.; Zyryanov, V.Y. Nematic Structures under Conical Anchoring at Various Director Tilt Angles Specified by Polymethacrylate Compositions. Polymers 2021, 13, 2993. [Google Scholar] [CrossRef] [PubMed]
- Yan, B.; He, J.; Du, X.; Zhang, K.; Wang, S.; Pan, C.; Wang, Y. Control of liquid crystal droplet configuration in polymer dispersed liquid crystal with macro-iniferter polystyrene. Liq. Cryst. 2009, 36, 933–938. [Google Scholar] [CrossRef]
- Balenko, N.; Shibaev, V.; Bobrovsky, A. Polymer dispersed cholesteric liquid crystals with combined photo- and mechanochromic response. J. Mol. Liq. 2024, 401, 124637. [Google Scholar] [CrossRef]
- Yang, Z.H.; Hsiao, Y.C.; Shen, D.; Lee, W. A thermally tunable narrowband selector based on a chiral nematic containing a binary thermosensitive chiral dopant mixture. Mol. Cryst. Liq. Cryst. 2017, 644, 19–25. [Google Scholar] [CrossRef]
- Drzaic, P.S.; Scheffer, T.J. Liquid Crystal Dispersions. J. Soc. Inf. Disp. 1995, 5, 413–415. [Google Scholar] [CrossRef]
- Rudyak, V.Y.; Emelyanenko, A.V.; Loiko, V.A. Structure transitions in oblate nematic droplets. Phys. Rev. E 2013, 88, 052501. [Google Scholar] [CrossRef]
- Nastishin, Y.; Polak, R.; Shiyanovskii, S.; Lavrentovich, O. Determination of nematic polar anchoring from retardation versus voltage measurements. Appl. Phys. Lett. 1999, 75, 202–204. [Google Scholar] [CrossRef]
- Žumer, S. Light scattering from nematic droplets: Anomalous-diffraction approach. Phys. Rev. A 1988, 37, 4006–4015. [Google Scholar] [CrossRef]
- Kelly, J.R.; Palffy-Muhoray, P. The Optical Response of Polymer Dispersed Liquid Crystals. Mol. Cryst. Liq. Cryst. 1994, 243, 11–29. [Google Scholar] [CrossRef]
- Simoni, F.; Francescangeli, O. Optical Properties of Polymer-dispersed Liquid Crystals. Int. J. Polym. Mater. Polym. Biomater. 2000, 45, 381–449. [Google Scholar] [CrossRef]
- Sutormin, V.S.; Krakhalev, M.N.; Timofeev, I.V.; Bikbaev, R.G.; Prishchepa, O.O.; Zyryanov, V.Y. Cholesteric layers with tangential-conical surface anchoring for an electrically controlled polarization rotator. Opt. Mater. Express 2021, 11, 1527–1536. [Google Scholar] [CrossRef]



| Parameter | Definition |
|---|---|
| The relative chirality parameter | |
| The measured transmittance of the PDLC cell in the initial state (before applying voltage) | |
| The measured transmittance of the PDLC cell at the turned-on high voltage | |
| The measured transmittance of the PDLC cell at the turned-off high voltage | |
| The contrast ratio | |
| The measured turn-on time is the time to switch to the transparent state | |
| The measured turn-off time is the time to switch to the opaque state | |
| The calculated transmittance of the PDLC cell | |
| The calculated sampling order parameter | |
| The calculated droplet order parameter |
| CR | , ms | , ms | ||||
|---|---|---|---|---|---|---|
| 0.0 | 0.0027 | 0.840 | 0.91 | 1.08 | – | – |
| 0.15 | 0.0032 | 0.370 | 0.91 | 2.46 | – | – |
| 0.32 | 0.0031 | 0.045 | 0.91 | 20 | 70 | 80 |
| 0.60 | 0.0032 | 0.006 | 0.89 | 148 | 68 | 35 |
| 1.32 | 0.0029 | 0.003 | 0.91 | 303 | 60 | 12 |
| C,% | d, μm | Value |
|---|---|---|
| 0.0 | 2.3 | 0.0 |
| 0.5 | 2.2 | 0.15 |
| 1.0 | 2.3 | 0.32 |
| 2.0 | 2.2 | 0.60 |
| 4.0 | 2.4 | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feizer, K.A.; Krakhalev, M.N.; Rudyak, V.Y.; Zyryanov, V.Y. Orientational Structure and Electro-Optical Properties of Chiral Nematic Droplets with Conical Anchoring. Molecules 2025, 30, 4761. https://doi.org/10.3390/molecules30244761
Feizer KA, Krakhalev MN, Rudyak VY, Zyryanov VY. Orientational Structure and Electro-Optical Properties of Chiral Nematic Droplets with Conical Anchoring. Molecules. 2025; 30(24):4761. https://doi.org/10.3390/molecules30244761
Chicago/Turabian StyleFeizer, Kristina A., Mikhail N. Krakhalev, Vladimir Yu. Rudyak, and Victor Ya. Zyryanov. 2025. "Orientational Structure and Electro-Optical Properties of Chiral Nematic Droplets with Conical Anchoring" Molecules 30, no. 24: 4761. https://doi.org/10.3390/molecules30244761
APA StyleFeizer, K. A., Krakhalev, M. N., Rudyak, V. Y., & Zyryanov, V. Y. (2025). Orientational Structure and Electro-Optical Properties of Chiral Nematic Droplets with Conical Anchoring. Molecules, 30(24), 4761. https://doi.org/10.3390/molecules30244761








