Rovibrational Analysis of the ν1, ν4, ν1 + ν4 and ν1 − ν4 Bands of 13CF4
Abstract
1. Introduction
2. Results
2.1. Line Positions Analysis
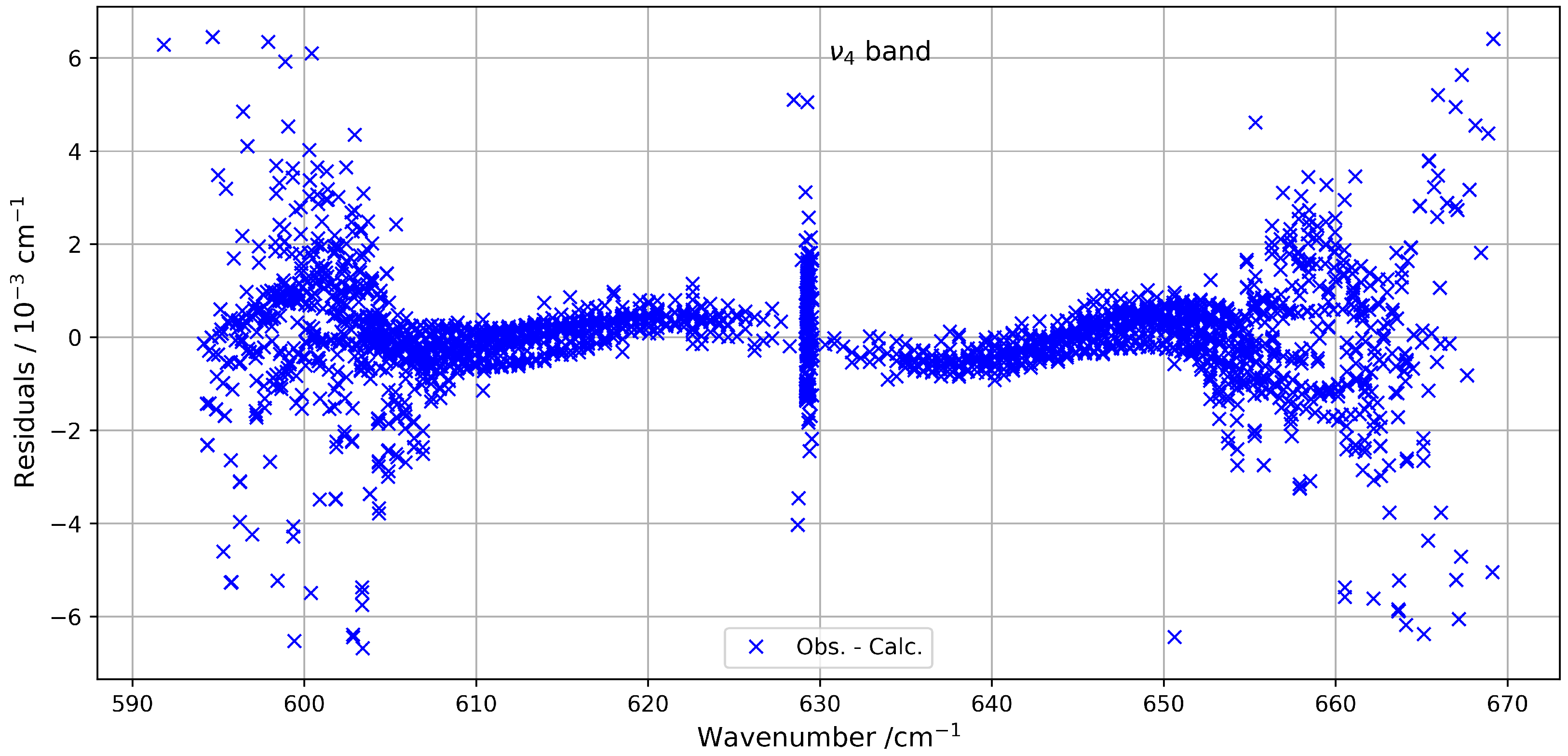
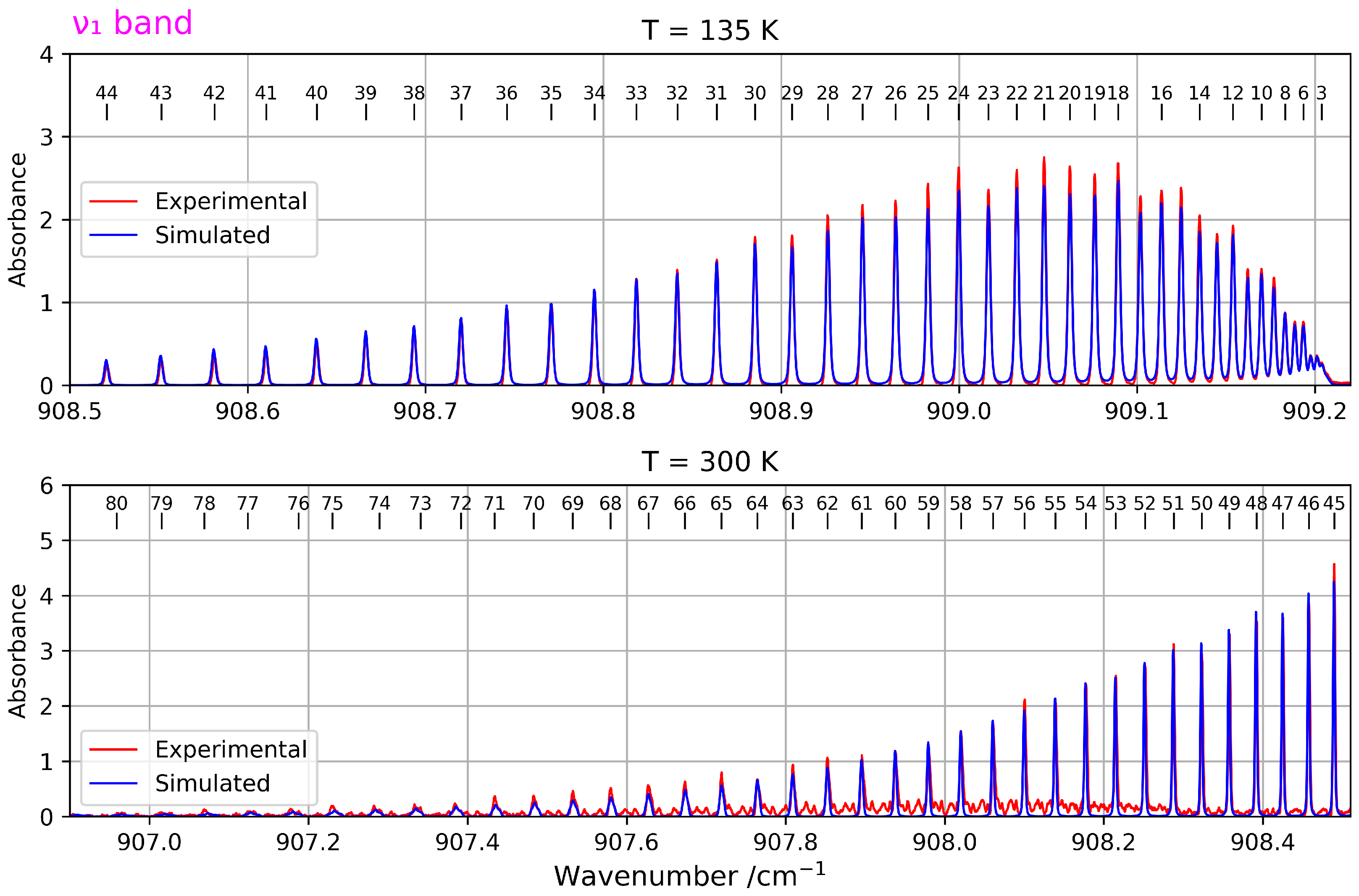
2.1.1. Band
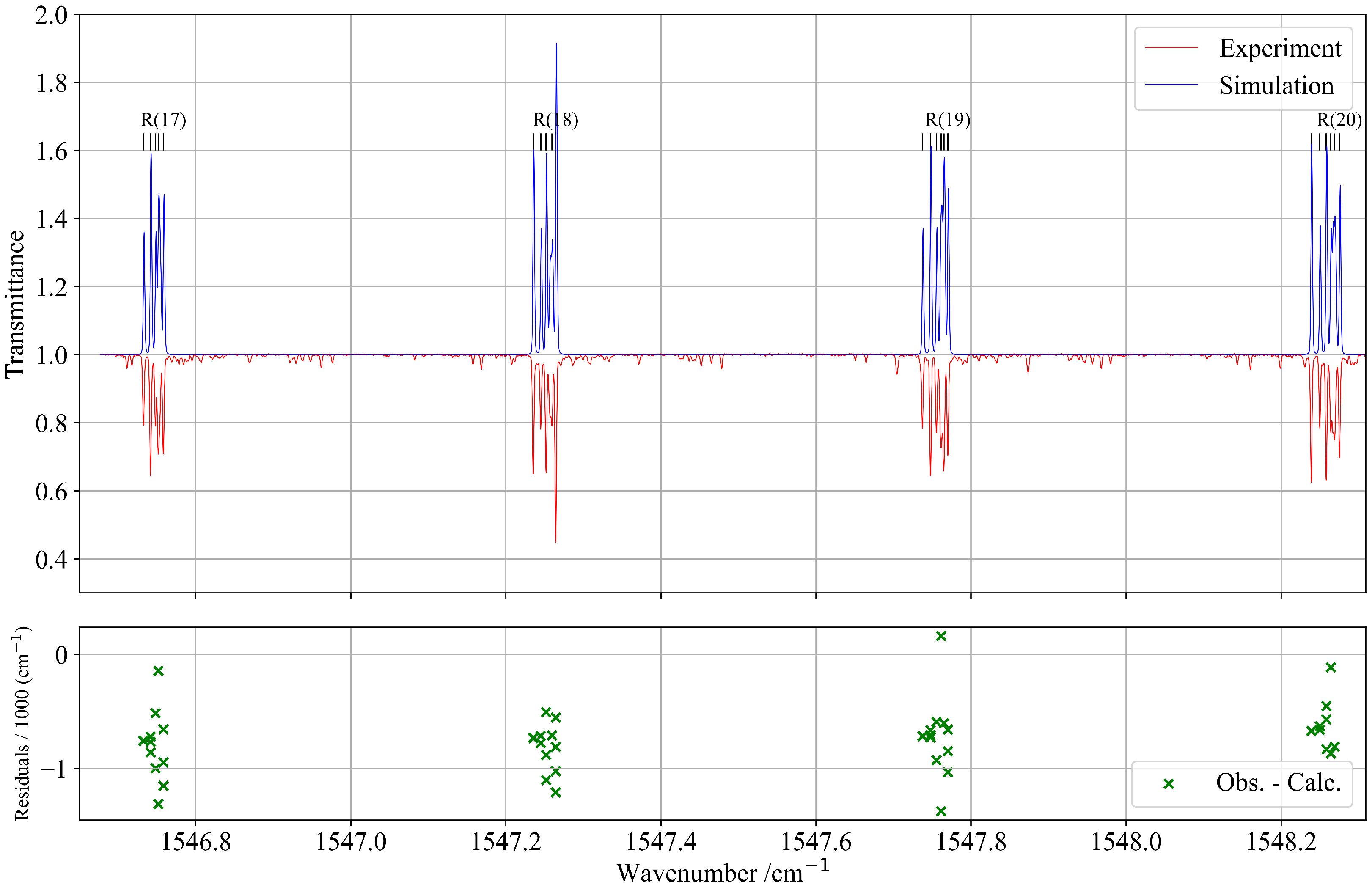
2.1.2. Band
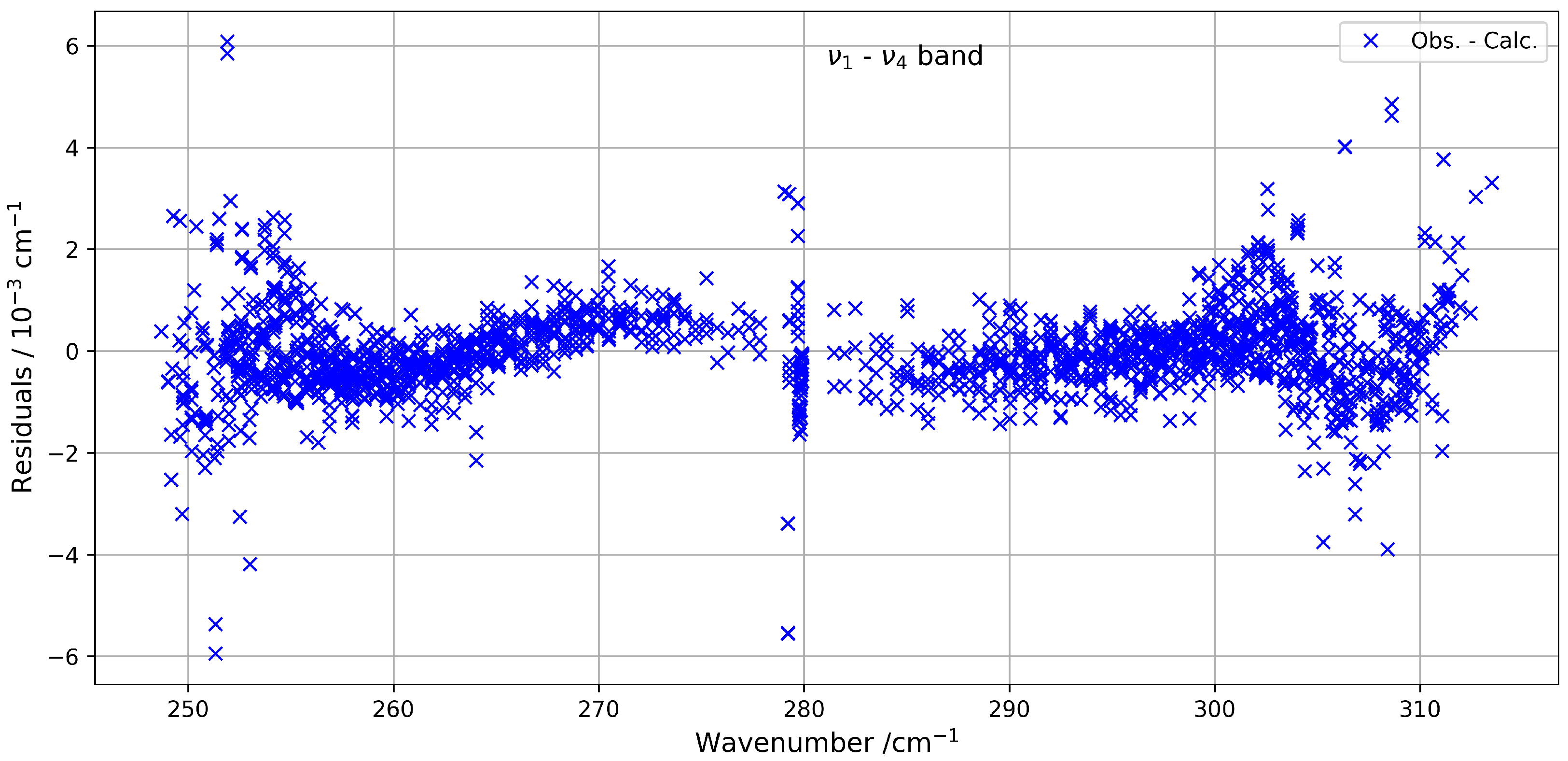
2.1.3. and Bands
Hot Band
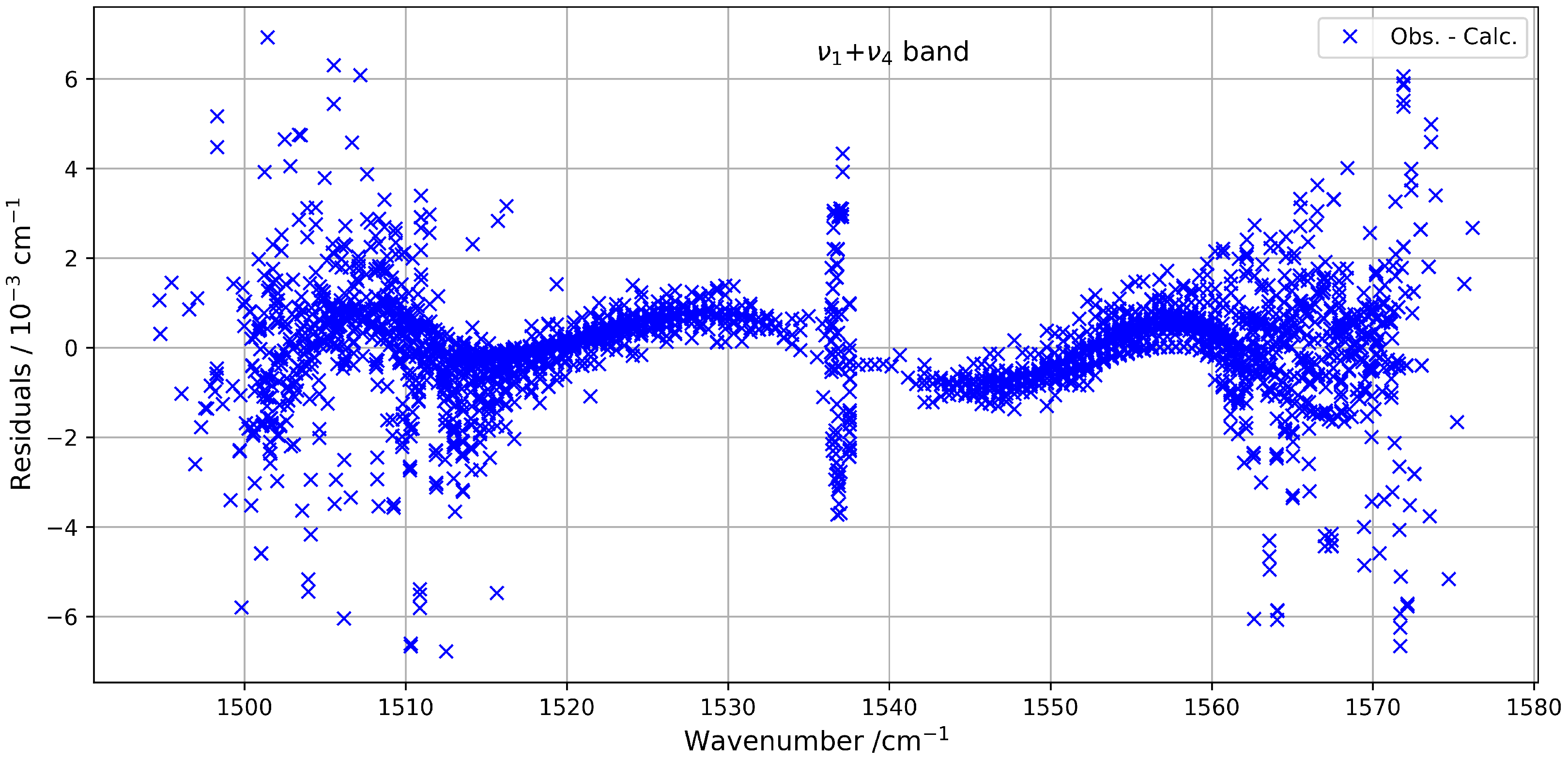
+ Combination Band
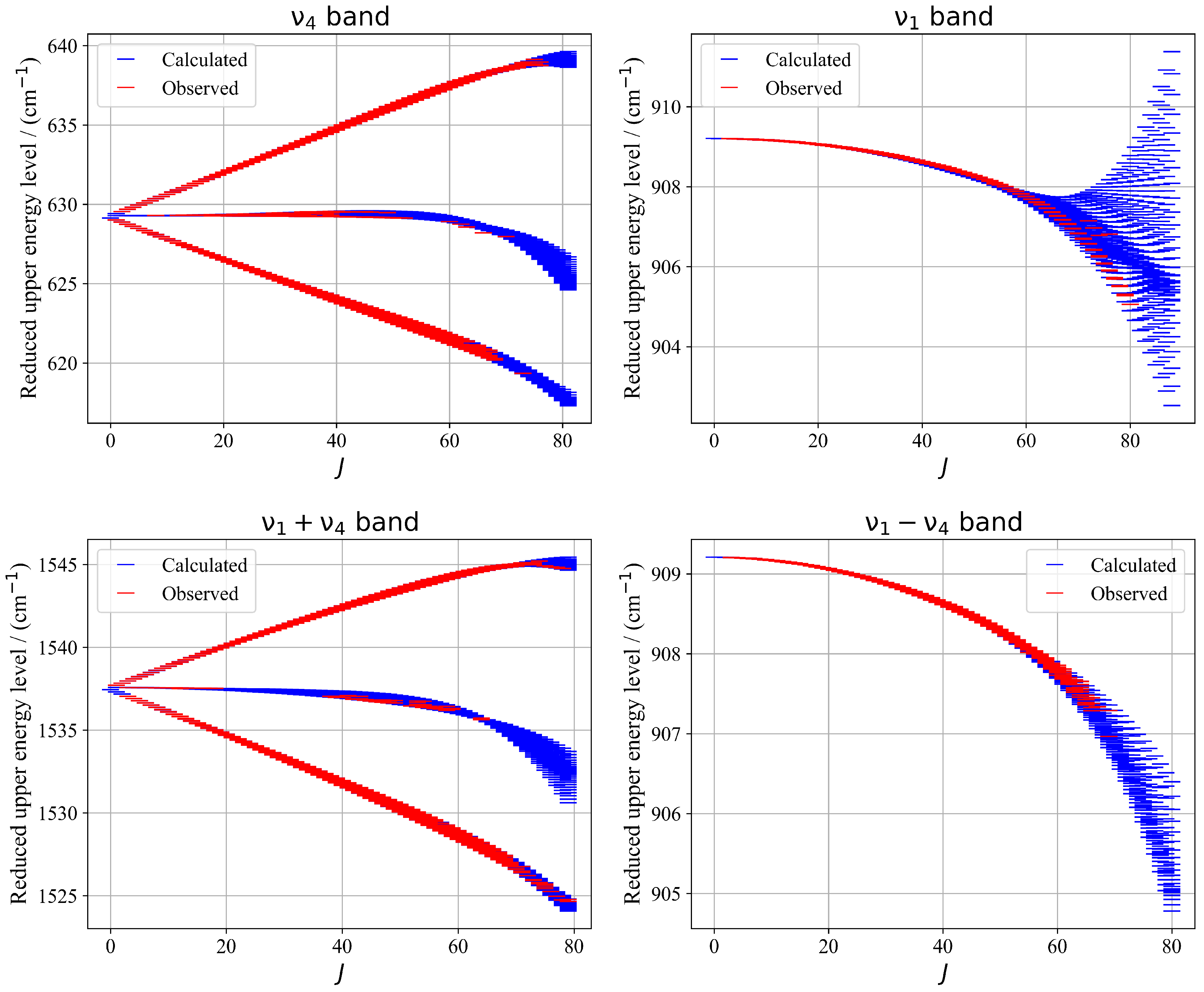
2.2. Energy Levels
3. Experimental and Theoretical Methodology
3.1. Experimental Section
3.2. Theoretical Model
- The GS effective Hamiltonian:
- The effective Hamiltonian:
- The effective Hamiltonian:
- The effective Hamiltonian:
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Carlos, M.; Gruson, O.; Richard, C.; Boudon, V.; Rotger, M.; Daumont, L.; Perrin, A. High-resolution spectroscopy and global analysis of CF4 rovibrational bands to model its atmospheric absorption. J. Quant. Spectrosc. Radiat. Transf. 2017, 201, 75–93. [Google Scholar] [CrossRef]
- Burkholder, J.B.; Sander, S.P. Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies: Evaluation Number 18; Technical Report Evaluation Number 18; Jet Propulsion Laboratory: La Cañada Flintridge, CA, USA; California Institute of Technology: Pasadena, CA, USA; JPL Publication: Pasadena, CA, USA, 2015. [Google Scholar]
- Say, D.; Manning, A.J.; Western, L.; Young, D.; Wisher, A.; Rigby, M.; Reimann, S.; Vollmer, M.K.; Maione, M.; Arduini, J.; et al. Global trends and European emissions of tetrafluoromethane (CF4), hexafluoroethane (C2F6) and octafluoropropane (C3F8). Atmos. Chem. Phys. 2021, 21, 2149–2164. [Google Scholar] [CrossRef]
- Kim, J.; Fraser, P.J.; Li, S.; Mühle, J.; Ganesan, A.L.; Krummel, P.B.; Steele, L.P.; Park, S.; Kim, S.; Park, M.; et al. Quantifying aluminum and semiconductor industry perfluorocarbon emissions from atmospheric measurements. Geophys. Res. Lett. 2014, 41, 4787–4794. [Google Scholar] [CrossRef]
- Llewellyn, H.J.; Craig, K.; Scott, E. Potential constants of CF4. J. Chem. Phys. 1978, 69, 833–838. [Google Scholar] [CrossRef]
- Boudon, V.; Mitchell, J.C.; Domanskaya, A.; Maul, C.; Robert, G.; Benidar, A.; William, G.H. High-resolution spectroscopy and analysis of the nu3/2nu4 dyad of CF4. Mol. Phys. 2011, 109, 2473–2484. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hargreaves, E.R.; Hashemi, R.; Karlovets, E.V.; Skinner, F.M.; Yurchenko, S.N. The HITRAN2020 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2022, 277, 107949. [Google Scholar] [CrossRef]
- McDowell, R.S.; Reisfeld, M.J.; Galbraith, H.W.; Krohn, B.J.; Flicker, H.; Kennedy, R.C.; Ldridge, J.P.; Nereson, N.G. High-resolution spectroscopy of the 16-micron bending fundamental of CF4. J. Mol. Spectrosc. 1980, 83, 440–450. [Google Scholar] [CrossRef]
- Domanskaya, A.V.; Tonkov, M.V.; Boissoles, J. The nu4 fundamental band of tetrafluoromethane: Structure and broadening coefficients. In Proceedings of the Proceedings SPIE 14th Symposium High-Resolution Molecular Spectroscopy, Krasnoyarsk, Russia, 6–11 July 2003; Volume 5311, pp. 185–190. [Google Scholar] [CrossRef]
- Tabyaoui, A.; Lavorel, B.; Saint-Loup, R.; Rotger, M. Stimulated Raman and CARS spectroscopy of nu1 and 2nu2 (A1) bands of 12CF4. J. Raman Spectrosc. 1994, 25, 299–304. [Google Scholar] [CrossRef]
- Martínez, R.Z.; Bermejo, D.; Boudon, V. Stimulated Raman spectroscopy of 13CF4. J. Mol. Spectrosc. 2018, 348, 47–56. [Google Scholar] [CrossRef]
- Boudon, V.; Bermejo, D.; Martínez, R.Z. High-resolution stimulated Raman spectroscopy and analysis of the nu1, 2nu1-nu1, nu2, 2nu2, and 3nu2-nu2 bands of CF4. J. Raman Spectrosc. 2013, 44, 731–738. [Google Scholar] [CrossRef]
- Simon, F.; Cuisset, A.; Elmaleh, C.; Hindle, F.; Gaël, M.; Rey, M.; Richard, C.; Boudon, V. Unrivaled accuracy in measuring rotational transitions of greenhouse gases: THz CRDS of CF4. Phys. Chem. Chem. Phys. 2024, 26, 12345–12357. [Google Scholar] [CrossRef] [PubMed]
- Wenger, C.; Boudon, V.; Champion, J.P.; Pierre, G. Highly-spherical Top Data System (HTDS) software for spectrum simulation of octahedral XY6 molecules. J. Quant. Spectrosc. Radiat. Transf. 2000, 66, 1–16. [Google Scholar] [CrossRef]
- Wenger, C.; Champion, J.P. Spherical top data system (STDS) software for the simulation of spherical top spectra. J. Quant. Spectrosc. Radiat. Transf. 1998, 59, 471–480. [Google Scholar] [CrossRef]
- Wenger, C.; Rotger, M.; Boudon, V. C4v Top Data System (C4vTDS) software for infrared spectrum simulation of XY5Z symmetric molecules. J. Quant. Spectrosc. Radiat. Transf. 2002, 74, 621–636. [Google Scholar] [CrossRef]
- Wenger, C.; Rotger, M.; Boudon, V. C2v Top Data System (C2vTDS) software for infrared spectrum simulation of XY2Z2 asymmetric molecules: Some improvements to the TDS packages. J. Quant. Spectrosc. Radiat. Transf. 2004, 93, 429–446. [Google Scholar] [CrossRef]
- Richard, C.; Fathallah, O.B.; Hardy, P.; Kamel, R.; Merkulova, M.; Rotger, M.; Ulenikov, O.; Boudon, V. CaSDa24: Latest updates to the Dijon calculated spectroscopic databases. J. Quant. Spectrosc. Radiat. Transf. 2024, 327, 109127. [Google Scholar] [CrossRef]
- Brubach, J.B.; Manceron, L.; Rouzières, M.; Pirali, O.; Balcon, D.; Kwabia Tchana, F.; Boudon, V.; Tudorie, M.; Huet, T.; Cuisset, A.; et al. Performance of the AILES THz-Infrared beamline at SOLEIL for high resolution spectroscopy. AIP Conf. Proc. 2010, 1214, 81–84. [Google Scholar] [CrossRef]
- Roy, P.; Brubach, J.B.; Rouzières, M.; Pirali, O.; Manceron, L.; Kwabia Tchana, F. AILES: The infrared and THz beamline on SOLEIL synchrotron radiation source; AILES: La ligne infrarouge et THz sur rayonnement synchrotron SOLEIL. Rev. Électr. Électron. 2008, 3, 23–30. [Google Scholar]
- Boudon, V.; Champion, J.P.; Gabard, T.; Loëte, M.; Wenger, M.R.C. Spherical Top Theory and Molecular Spectra. In Handbook of High-Resolution Spectroscopy; Quack, M., Merkt, F., Eds.; Wiley: Chichester, UK, 2011; Volume 3, pp. 1437–1460. [Google Scholar]
- Champion, J.P.; Loëte, M.; Pierre, G. Spherical top spectra. In Spectroscopy of the Earth’s Atmosphere and Interstellar Medium; Rao, K.N., Weber, A., Eds.; Academic Press: San Diego, CA, USA, 1992; pp. 339–422. [Google Scholar]




| Level | Order | Ω() | {} | {} | This Work 13CF4 | Ref. [6] 12CF4 |
|---|---|---|---|---|---|---|
| Value/cm−1 | Value/cm−1 | |||||
| GS | 0 | |||||
| GS | 2 | |||||
| GS | 2 | |||||
| GS | 4 | |||||
| GS | 4 | |||||
| GS | 4 | |||||
| GS | 6 | |||||
| GS | 6 | |||||
| GS | 6 | |||||
| GS | 6 | |||||
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 2 | ||||||
| 2 | ||||||
| 3 | ||||||
| 3 | ||||||
| 4 | ||||||
| 4 | ||||||
| 4 | ||||||
| 4 | ||||||
| 4 | ||||||
| 4 | ||||||
| 5 | ||||||
| 5 | ||||||
| 5 | ||||||
| 5 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 |
| Level | Order | Ω() | {} C1 | {} C2 | This Work | Ref. [11] |
|---|---|---|---|---|---|---|
| Value/cm−1 | Value/cm−1 | |||||
| 0 | ||||||
| 2 | ||||||
| 4 | ||||||
| 4 | ||||||
| 6 | ||||||
| 6 | ||||||
| 6 |
| Level | Order | Ω() | {} C1 | {} C2 | Value/cm−1 |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 2 | |||||
| 2 | |||||
| 3 | |||||
| 3 | |||||
| 4 | |||||
| 4 | |||||
| 4 | |||||
| 4 | |||||
| 4 | |||||
| 4 | |||||
| 5 | |||||
| 5 | |||||
| 5 | |||||
| 5 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 | |||||
| 6 |
| Level | Number of Assigned Transitions | ||
|---|---|---|---|
| 987 | 80 | 0.54 | |
| 2783 | 75 | 1.27 | |
| 2964 | 80 | 1.27 | |
| 2258 | 68 | 0.88 |
| Vibrational Bands | Pressure (hPa) | Path Length (m) | Resolution (cm−1) | Beamsplitter | Source | Detector | Lowpass Filter (kHz) | Optical Velocity (cm/s) |
|---|---|---|---|---|---|---|---|---|
| 0.515 | 0.845 | 0.00102 | KBr/Ge | Globar + iris 1.15 mm | HgCdTe 4K + Cold filter 1 | 80 | 5.08 | |
| 6.31 | 0.051 | 0.00102 | KBr/Ge | Globar + iris 1.15 mm | HgCdTe 4K + Cold filter 1 | 80 | 5.08 | |
| 20.05 | 96 | 0.0017 | Mylar/Si | Synchrotron | Bolometer 4K + 700 cm−1 cold filter | 40 | 2.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Fathallah, O.; Terrier, R.; Manceron, L.; Richard, C.; Boudon, V. Rovibrational Analysis of the ν1, ν4, ν1 + ν4 and ν1 − ν4 Bands of 13CF4. Molecules 2025, 30, 4267. https://doi.org/10.3390/molecules30214267
Ben Fathallah O, Terrier R, Manceron L, Richard C, Boudon V. Rovibrational Analysis of the ν1, ν4, ν1 + ν4 and ν1 − ν4 Bands of 13CF4. Molecules. 2025; 30(21):4267. https://doi.org/10.3390/molecules30214267
Chicago/Turabian StyleBen Fathallah, Ons, Romain Terrier, Laurent Manceron, Cyril Richard, and Vincent Boudon. 2025. "Rovibrational Analysis of the ν1, ν4, ν1 + ν4 and ν1 − ν4 Bands of 13CF4" Molecules 30, no. 21: 4267. https://doi.org/10.3390/molecules30214267
APA StyleBen Fathallah, O., Terrier, R., Manceron, L., Richard, C., & Boudon, V. (2025). Rovibrational Analysis of the ν1, ν4, ν1 + ν4 and ν1 − ν4 Bands of 13CF4. Molecules, 30(21), 4267. https://doi.org/10.3390/molecules30214267







