The Next Frontier in the Study of Noncovalent Bonding: Transition Metals
Abstract
1. Introduction
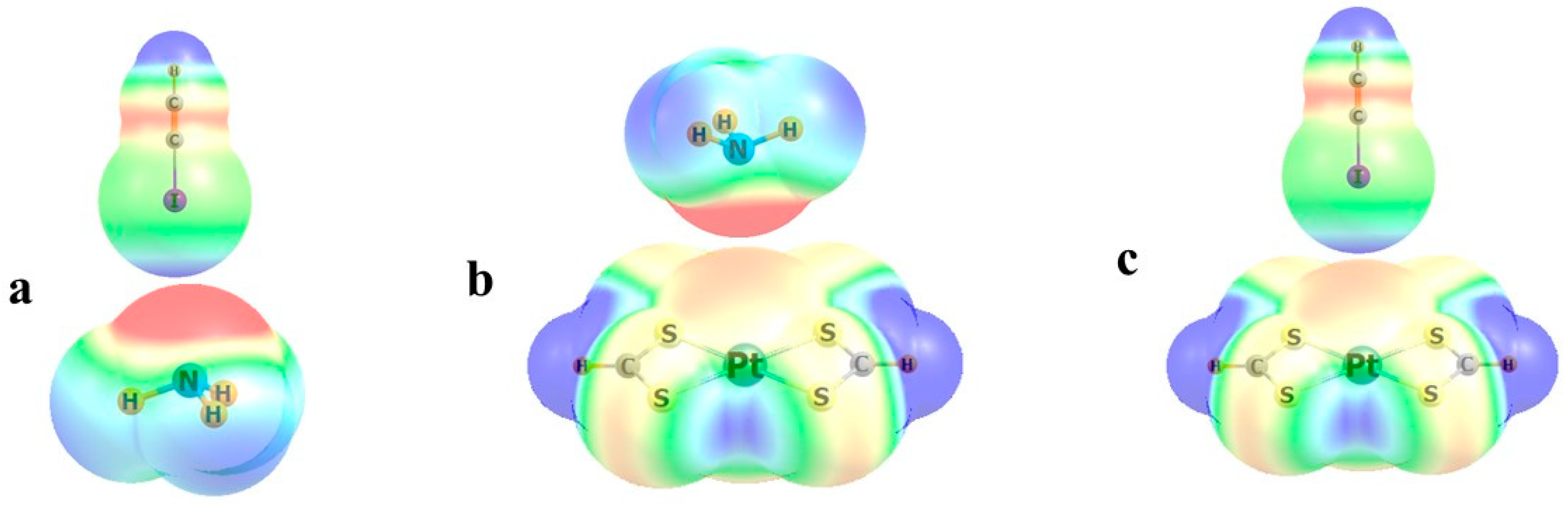
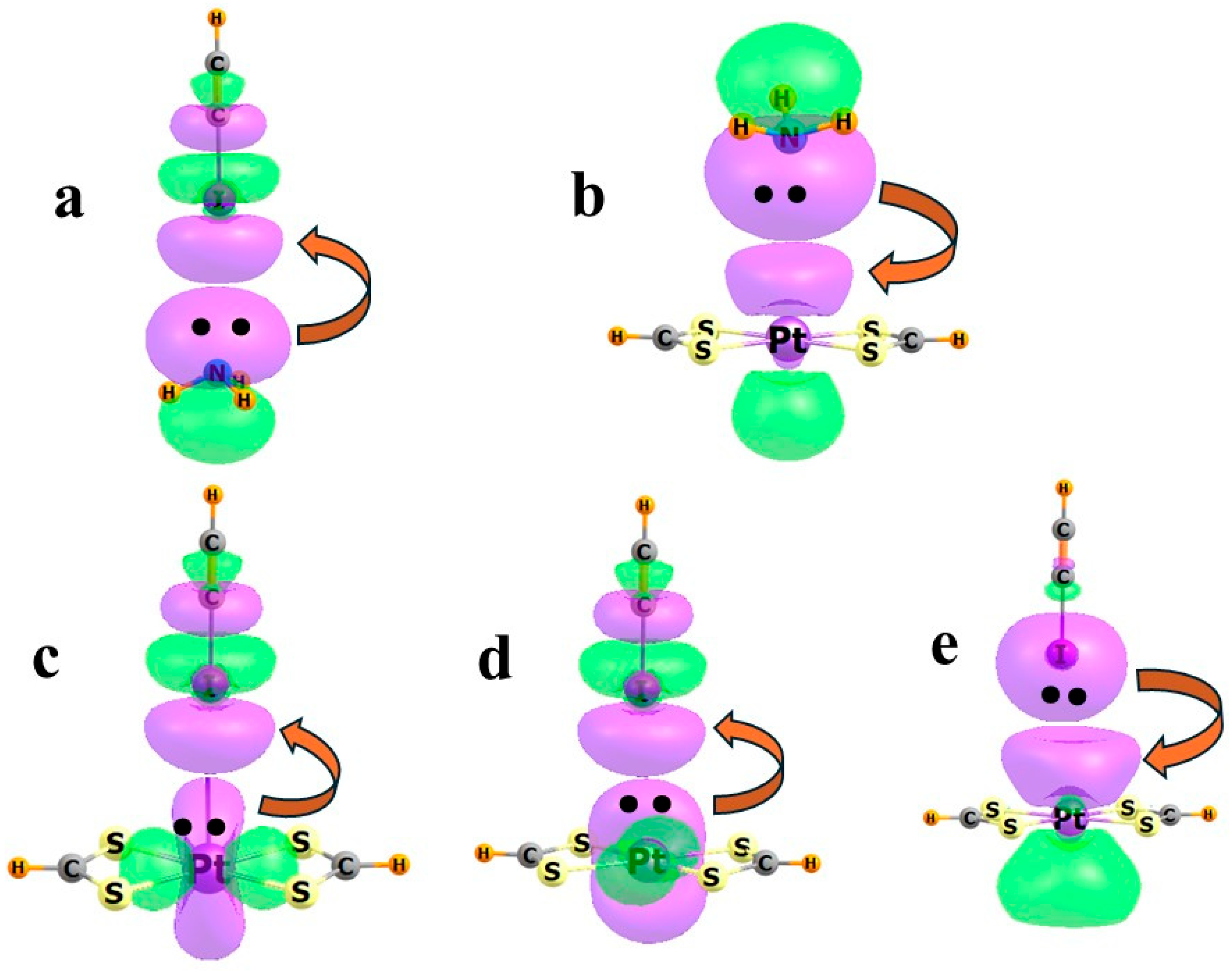
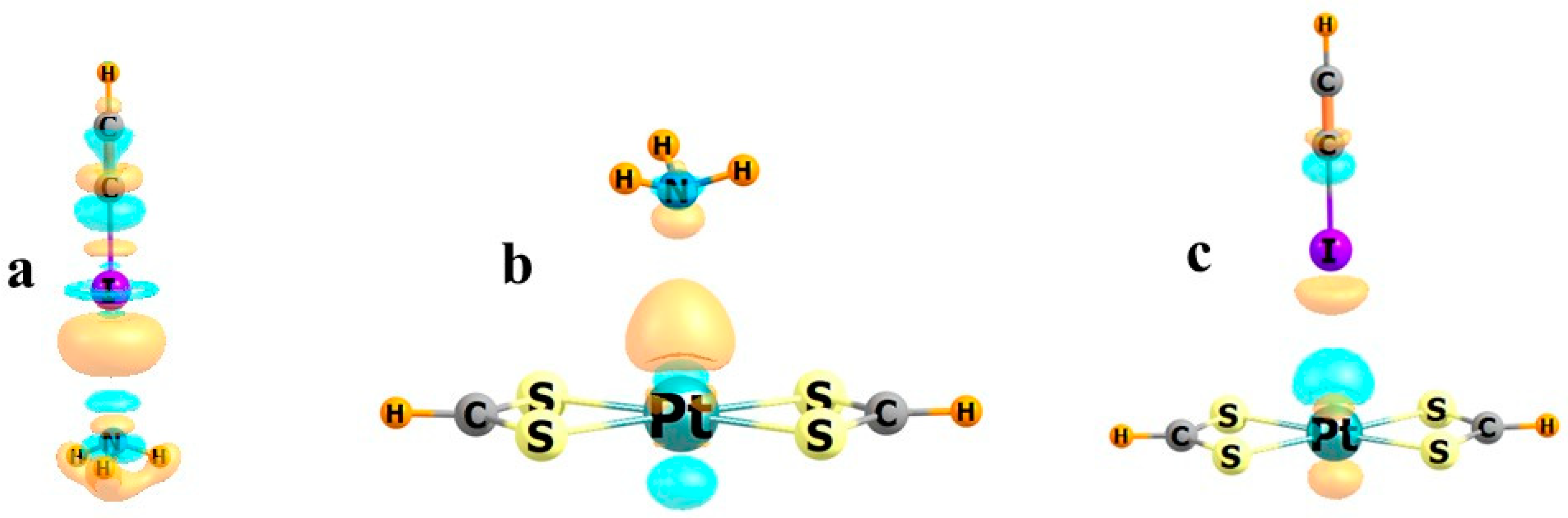
2. Participation of Transition Metals
3. Resolving Direction of Electron Transfer
4. Examples
5. Covalent or Noncovalent
6. Spin Multiplicity
7. Nomenclature
8. Guidance for the Future
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QTAIM | Quantum Theory of Atoms in Molecules analyzes topology of electron density [56]. |
| AIM | Atoms in Molecules: shortened version of the preceding. |
| NCI | Noncovalent Interactions: pictoral description of reduced density gradient [57]. |
| NBO | Natural Bond Orbital: means of localization of electron density accenting orbitals involved in charge transfer [110]. |
| vdW radius | van der Waals, referring to approximate atom size [79,111,112]. |
References
- Pimentel, G.C.; McClellan, A.L. The Hydrogen Bond; Freeman: San Francisco, CA, USA, 1960. [Google Scholar]
- Hamilton, W.C.; Ibers, J.A. Hydrogen Bonding in Solids; W. A. Benjamin: New York, NY, USA, 1968. [Google Scholar]
- Vinogradov, S.N.; Linnell, R.H. Hydrogen Bonding; Van Nostrand-Reinhold: New York, NY, USA, 1971. [Google Scholar]
- Green, R.D. Hydrogen Bonding by C-H Groups; Wiley Interscience: New York, NY, USA, 1974. [Google Scholar]
- Joesten, M.D.; Schaad, L.J. Hydrogen Bonding; Marcel Dekker: New York, NY, USA, 1974. [Google Scholar]
- Schuster, P.; Zundel, G.; Sandorfy, C. The Hydrogen Bond. Recent Developments in Theory and Experiments; North-Holland Publishing Co.: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Schuster, P. Hydrogen Bonds; Springer-Verlag: Berlin, Germany, 1984. [Google Scholar]
- Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer-Verlag: Berlin, Germany, 1991. [Google Scholar]
- Scheiner, S. Hydrogen Bonding: A Theoretical Perspective; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond in Structural Chemistry and Biology; Oxford: New York, NY, USA, 1999. [Google Scholar]
- Grabowski, S.J. Hydrogen Bonding—New Insights; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Del Bene, J.E.; Alkorta, I.; Sanchez-Sanz, G.; Elguero, J. Structures, energies, bonding, and NMR properties of pnicogen complexes H2XP:NXH2 (X = H, CH3, NH2, OH, F, Cl). J. Phys. Chem. A 2011, 115, 13724–13731. [Google Scholar] [CrossRef]
- Scheiner, S.; Lu, J. Halogen, Chalcogen, and Pnicogen Bonding Involving Hypervalent Atoms. Chem. Eur. J. 2018, 24, 8167–8177. [Google Scholar] [CrossRef]
- Bauzá, A.; Quiñonero, D.; Frontera, A.; Deyà, P.M. Substituent effects in halogen bonding complexes between aromatic donors and acceptors: A comprehensive ab initio study. Phys. Chem. Chem. Phys. 2011, 13, 20371–20379. [Google Scholar] [CrossRef]
- Dong, W.; Li, Q.; Scheiner, S. Comparative Strengths of Tetrel, Pnicogen, Chalcogen, and Halogen Bonds and Contributing Factors. Molecules 2018, 23, 1681. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Halogen bond and its counterparts: Bent’s rule explains the formation of nonbonding interactions. J. Phys. Chem. A 2011, 115, 12340–12347. [Google Scholar] [CrossRef]
- Grabowski, S.J. Tetrel bond–s-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
- Shields, Z.P.; Murray, J.S.; Politzer, P. Directional tendencies of halogen and hydrogen bonds. Int. J. Quantum Chem. 2010, 110, 2823–2832. [Google Scholar] [CrossRef]
- Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Disc. 2017, 203, 485–507. [Google Scholar] [CrossRef]
- Pizzi, A.; Terraneo, G.; Lo Iacono, C.; Beccaria, R.; Dhaka, A.; Resnati, G. Taxonomy of Chemical Bondings: Opportunities and Challenges. Angew. Chem. Int. Ed. 2025, 64, e202506525. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the Hydrogen Bond. Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon Anthony, C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Aakeroy, C.B.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Legon Anthony, C.; Nicotra, F.; Rissanen, K.; Scheiner, S.; Terraneo, G.; Metrangolo, P.; et al. Definition of the chalcogen bond (IUPAC Recommendations 2019). Pure Appl. Chem. 2019, 91, 1889. [Google Scholar] [CrossRef]
- Resnati, G.; Bryce, D.L.; Desiraju, G.R.; Frontera, A.; Krossing, I.; Legon, A.C.; Metrangolo, P.; Nicotra, F.; Rissanen, K.; Scheiner, S.; et al. Definition of the pnictogen bond (IUPAC Recommendations 2023). Pure Appl. Chem. 2024, 96, 135–145. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P. s-Holes, p-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef]
- Bauzá, A.; Ramis, R.; Frontera, A. A Combined Theoretical and Cambridge Structural Database Study of p-Hole Pnicogen Bonding Complexes between Electron Rich Molecules and Both Nitro Compounds and Inorganic Bromides (YO2Br, Y = N, P, and As). J. Phys. Chem. A 2014, 118, 2827–2834. [Google Scholar] [CrossRef]
- Scheiner, S. Dissection of the Origin of π-Holes and the Noncovalent Bonds in Which They Engage. J. Phys. Chem. A 2021, 125, 6514–6528. [Google Scholar] [CrossRef]
- Sun, J.; Decato, D.A.; Bryantsev, V.S.; John, E.A.; Berryman, O.B. The interplay between hydrogen and halogen bonding: Substituent effects and their role in the hydrogen bond enhanced halogen bond. Chem. Sci. 2023, 14, 8924–8935. [Google Scholar] [CrossRef] [PubMed]
- Decato, D.A.; Sun, J.; Boller, M.R.; Berryman, O.B. Pushing the limits of the hydrogen bond enhanced halogen bond—The case of the C–H hydrogen bond. Chem. Sci. 2022, 13, 11156–11162. [Google Scholar] [CrossRef] [PubMed]
- Decato, D.A.; Riel, A.M.S.; May, J.H.; Bryantsev, V.S.; Berryman, O.B. Theoretical, Solid-State, and Solution Quantification of the Hydrogen Bond-Enhanced Halogen Bond. Angew. Chem. Int. Ed. 2021, 60, 3685–3692. [Google Scholar] [CrossRef]
- Scheiner, S. Ability of Peripheral H Bonds to Strengthen a Halogen Bond. J. Phys. Chem. A 2022, 126, 9691–9698. [Google Scholar] [CrossRef]
- Tian, R.; Zeng, Y.; Li, X.; Zhang, X. The nature of π-hole spodium bonds in the HgLCl2(L = pyrrole, pyrazole, imidazole, pyridine, pyridazine, and pyrimidine) complexes: From noncovalent to covalent interactions. New J. Chem. 2024, 48, 6582–6589. [Google Scholar] [CrossRef]
- Gomila, R.M.; Tiekink, E.R.T.; Frontera, A. A Computational Chemistry Investigation of the Influence of Steric Bulk of Dithiocarbamato-Bound Organic Substituents upon Spodium Bonding in Three Homoleptic Mercury(II) Bis(N,N-dialkyldithiocarbamato) Compounds for Alkyl = Ethyl, Isobutyl, and Cyclohexyl. Inorganics 2023, 11, 468. [Google Scholar] [CrossRef]
- Jabłoński, M. Study of Beryllium, Magnesium, and Spodium Bonds to Carbenes and Carbodiphosphoranes. Molecules 2021, 26, 2275. [Google Scholar] [CrossRef]
- Gomila, R.M.; Bauzá, A.; Mooibroek, T.J.; Frontera, A. Spodium bonding in five coordinated Zn(ii): A new player in crystal engineering? CrystEngComm 2021, 23, 3084–3093. [Google Scholar] [CrossRef]
- Bauzá, A.; Alkorta, I.; Elguero, J.; Mooibroek, T.J.; Frontera, A. Spodium Bonds: Noncovalent Interactions Involving Group 12 Elements. Angew. Chem. Int. Ed. 2020, 59, 17482–17487. [Google Scholar] [CrossRef]
- Burguera, S.; Bauzá, A.; Frontera, A. A novel approach for estimating the strength of argentophilic and aurophilic interactions using QTAIM parameters. Phys. Chem. Chem. Phys. 2024, 26, 16550–16560. [Google Scholar] [CrossRef]
- Li, J.; Feng, Q.; Wang, C.; Mo, Y. On the nature of inter-anion coinage bonds. Phys. Chem. Chem. Phys. 2023, 25, 15371–15381. [Google Scholar] [CrossRef]
- de las Nieves Piña, M.; Mooibroek, T.J.; Frontera, A.; Bauzá, A. Importance of Cu and Ag regium–π bonds in supramolecular chemistry and biology: A combined crystallographic and ab initio study. Phys. Chem. Chem. Phys. 2022, 24, 24983–24991. [Google Scholar] [CrossRef] [PubMed]
- Pizzi, A.; Calabrese, M.; Daolio, A.; Ursini, M.; Frontera, A.; Resnati, G. Expanding the toolbox of the coinage bond: Adducts involving new gold(iii) derivatives and bioactive molecules. CrystEngComm 2022, 24, 3846–3851. [Google Scholar] [CrossRef]
- Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Rivalry between Regium and Hydrogen Bonds Established within Diatomic Coinage Molecules and Lewis Acids/Bases. ChemPhysChem. 2020, 21, 2557–2563. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Wang, Z.; Yu, X.; Li, Q. Synergistic and Diminutive Effects between Regium and Aerogen Bonds. ChemPhysChem. 2020, 21, 2426–2431. [Google Scholar] [CrossRef]
- Daolio, A.; Pizzi, A.; Calabrese, M.; Terraneo, G.; Bordignon, S.; Frontera, A.; Resnati, G. Molecular Electrostatic Potential and Noncovalent Interactions in Derivatives of Group 8 Elements. Angew. Chem. Int. Ed. 2021, 60, 20723–20727. [Google Scholar] [CrossRef]
- Calabrese, M.; Pizzi, A.; Daolio, A.; Beccaria, R.; Lo Iacono, C.; Scheiner, S.; Resnati, G. Osme Bond: Geometric and Energetic Features in the Adducts between OsO4 and Lewis Bases. Chem. Eur. J. 2024, 30, e202304240. [Google Scholar] [CrossRef] [PubMed]
- Burguera, S.; Sahu, A.K.; Chávez Romero, M.J.; Biswal, H.S.; Bauzá, A. Manganese matere bonds in biological systems: PDB inspection and DFT calculations. Phys. Chem. Chem. Phys. 2024, 26, 18606–18613. [Google Scholar] [CrossRef]
- Grödler, D.; Burguera, S.; Frontera, A.; Strub, E. Investigating Recurrent Matere Bonds in Pertechnetate Compounds. Chem. Eur. J. 2024, 30, e202400100. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Calabrese, M.; Demitri, N.; Pizzi, A.; Nag, T.; Hung, I.; Gan, Z.; Resnati, G.; Bryce, D.L. Non-covalent matere bonds in perrhenates probed via ultrahigh field rhenium-185/187 NMR and zero-field NQR spectroscopy. Chem. Commun. 2023, 59, 12609–12612. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Cryst. 2020, 10, 180. [Google Scholar] [CrossRef]
- Michalczyk, M.; Zierkiewicz, W.; Scheiner, S. Wolfium bonds in homodimers of MX4Y (M = Mo, W.; X = F, Cl, Br; Y = O, S, Se). Phys. Chem. Chem. Phys. 2024, 26, 5836–5847. [Google Scholar] [CrossRef]
- Calabrese, M.; Gomila, R.M.; Pizzi, A.; Frontera, A.; Resnati, G. Erythronium Bonds: Noncovalent Interactions Involving Group 5 Elements as Electron-Density Acceptors. Chem. Eur. J. 2023, 29, e202302176. [Google Scholar] [CrossRef]
- Giordana, A.; Priola, E.; Mahmoudi, G.; Doustkhah, E.; Gomila, R.M.; Zangrando, E.; Diana, E.; Operti, L.; Frontera, A. Exploring coinage bonding interactions in [Au(CN)4]− assemblies with silver and zinc complexes: A structural and theoretical study. Phys. Chem. Chem. Phys. 2025, 27, 5395–5402. [Google Scholar] [CrossRef]
- Gomila, R.M.; Frontera, A. The matere bond. Dalton Trans. 2025, 54, 3095–3105. [Google Scholar] [CrossRef]
- Karmakar, M.; Gomila, R.M.; Frontera, A.; Chattopadhyay, S. On the Existence of Matere Bonds in Pentacoordinated Manganese Complexes: A Combined Experimental and Theoretical Investigation. Cryst. Growth Des. 2024, 24, 5990–6000. [Google Scholar] [CrossRef]
- Scheiner, S. Semicoordinate and halogen bonding to group 10 and group 8 metals. Phys. Chem. Chem. Phys. 2025, 27, 12416–12426. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules, A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-Garcia, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Lu, T. Visualization Analysis of Covalent and Noncovalent Interactions in Real Space. Angew. Chem. Int. Ed. 2025, 64, e202504895. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Physical Review B 1986, 33, 8800–8802. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinhold, F.; Curtiss, L.A.; Pochatko, D.J. Natural bond orbital analysis of molecular interactions: Theoretical studies of binary complexes of HF, H2O, NH3, N2, O2, F2, CO and CO2 with HF, H2O, and NH3. J. Chem. Phys. 1986, 84, 5687–5705. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Amonov, A.; Scheiner, S. Semicoordinate versus σ-Hole Bonding of Group 10 Metal Atoms in a Square Planar Motif. Inorg. Chem. 2025. [Google Scholar] [CrossRef]
- Bikbaeva, Z.M.; Ivanov, D.M.; Novikov, A.S.; Ananyev, I.V.; Bokach, N.A.; Kukushkin, V.Y. Electrophilic–Nucleophilic Dualism of Nickel(II) toward Ni···I Noncovalent Interactions: Semicoordination of Iodine Centers via Electron Belt and Halogen Bonding via σ-Hole. Inorg. Chem. 2017, 56, 13562–13578. [Google Scholar] [CrossRef] [PubMed]
- Kryukova, M.A.; Kostareva, M.B.; Cheranyova, A.M.; Khazanova, M.A.; Rozhkov, A.V.; Ivanov, D.M. Metal-Involving Bifurcated Halogen Bonding with Iodide and Platinum(II) Center. Int. J. Mol. Sci. 2025, 26, 4555. [Google Scholar] [CrossRef]
- Eliseeva, A.A.; Ivanov, D.M.; Rozhkov, A.V.; Kukushkin, V.Y.; Bokach, N.A. Engineering metal site behavior: Electrophilic-nucleophilic dualism in square-planar platinum(ii) through geometry-controlled switching. Dalton Trans. 2025, 54, 9076–9087. [Google Scholar] [CrossRef]
- Lin, T.-P.; Gabbaï, F.P. Telluronium Ions as σ-Acceptor Ligands. Angew. Chem. Int. Ed. 2013, 52, 3864–3868. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Katlenok, E.A.; Zhmykhova, M.V.; Ivanov, A.Y.; Kuznetsov, M.L.; Bokach, N.A.; Kukushkin, V.Y. Metal-Involving Chalcogen Bond. The Case of Platinum(II) Interaction with Se/Te-Based σ-Hole Donors. J. Am. Chem. Soc. 2021, 143, 15701–15710. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Kizior, B.; Michalczyk, M.; Jezierska, A.; Scheiner, S. Pd and Pt metal atoms as electron donors in σ-hole bonded complexes. Phys. Chem. Chem. Phys. 2023, 25, 26172–26184. [Google Scholar] [CrossRef] [PubMed]
- Zelenkov, L.E.; Ivanov, D.M.; Sadykov, E.K.; Bokach, N.A.; Galmés, B.; Frontera, A.; Kukushkin, V.Y. Semicoordination Bond Breaking and Halogen Bond Making Change the Supramolecular Architecture of Metal-Containing Aggregates. Cryst. Growth Des. 2020, 20, 6956–6965. [Google Scholar] [CrossRef]
- Fachini, L.G.; Baptistella, G.B.; Postal, K.; Santana, F.S.; de Souza, E.M.; Ribeiro, R.R.; Nunes, G.G.; Sá, E.L. A new approach to study semi-coordination using two 2-methyl-5-nitroimidazole copper(ii) complexes of biological interest as a model system. RSC Advances 2023, 13, 27997–28007. [Google Scholar] [CrossRef]
- Burguera, S.; Bauzá, A.; Frontera, A. Tuning the Nucleophilicity and Electrophilicity of Group 10 Elements through Substituent Effects: A DFT Study. Int. J. Mol. Sci. 2023, 24, 15597. [Google Scholar] [CrossRef]
- Siddiqui, R.; Burguera, S.; de las Nieves Piña, M.; Dhamija, S.; Titi, H.M.; Frontera, A.; Bauzá, A.; Patra, R. From Coordination to π-Hole Chemistry of Transition Metals: Metalloporphyrins as a Case of Study. Angew. Chem. Int. Ed. 2024, 63, e202409963. [Google Scholar] [CrossRef]
- Ivanov, D.M.; Bokach, N.A.; Kukushkin, V.Y.; Frontera, A. Metal Centers as Nucleophiles: Oxymoron of Halogen Bond-Involving Crystal Engineering. Chem. Eur. J. 2022, 28, e202103173. [Google Scholar] [CrossRef]
- Rozhkov, A.V.; Burguera, S.; Frontera, A.; Kukushkin, V.Y. Formal Metal-Dependent (M = Pt, Pd) Switching between Arene π-Hole and σ-(Te)-Hole in the Arenetellurium(II) Noncovalent Binding. Cryst. Growth Des. 2024, 24, 9581–9589. [Google Scholar] [CrossRef]
- Shen, Z.; Li, X.; Zeng, Y.; Zhang, X. Influence of Noncovalent Interaction on the Nucleophilicity and Electrophilicity of Metal Centers in [MII(S2CNEt2)2] (M = Ni, Pd, Pt). J. Phys. Chem. A 2024, 128, 10796–10807. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalczyk, M.; Maris, T.; Wysokiński, R.; Scheiner, S. Experimental and theoretical evidence of attractive interactions between dianions: [PdCl4]2−⋯[PdCl4]2−. Chem. Commun. 2021, 57, 13305–13308. [Google Scholar] [CrossRef]
- Lo Iacono, C.; Pizzi, A.; Mahmudov, K.T.; Gomila, R.M.; Frontera, A.; Resnati, G. When CuCl42– and CuBr42– Form Anion···Anion Networks Assembled via Cu···Cl/Br Regium Bonds. Cryst. Growth Des. 2025, 25, 4338–4347. [Google Scholar] [CrossRef]
- Scheiner, S. Participation of transition metal atoms in noncovalent bonds. Phys. Chem. Chem. Phys. 2024, 26, 27382–27394. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S. A cartography of the van der Waals territories. Dalton Trans. 2013, 42, 8617–8636. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. Halogen and Chalcogen Bond Energies Evaluated Using Electron Density Properties. ChemPhysChem. 2020, 21, 26–31. [Google Scholar] [CrossRef]
- Vener, M.V.; Egorova, A.N.; Churakov, A.V.; Tsirelson, V.G. Intermolecular hydrogen bond energies in crystals evaluated using electron density properties: DFT computations with periodic boundary conditions. J. Comput. Chem. 2012, 33, 2303–2309. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density—Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. Engl. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Matta, C.F.; Hernández-Trujillo, J.; Tang, T.-H.; Bader, R.F.W. Hydrogen–Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals. Chem. Eur. J. 2003, 9, 1940–1951. [Google Scholar] [CrossRef]
- Burguera, S.; Frontera, A. Osme Bonds in Molecular Crystals: Structural Insights, Substituent Effects, and Energetic Features. Cryst. Growth Des. 2025, 25, 3949–3957. [Google Scholar] [CrossRef]
- Saha, S.; Sastry, G.N. Cooperative or Anticooperative: How Noncovalent Interactions Influence Each Other. J. Phys. Chem. B 2015, 119, 11121–11135. [Google Scholar] [CrossRef]
- Legon, A. The Hydrogen Bond, the Halogen Bond and Rotational Spectroscopy: A Personal Retrospective. J. Indian Inst. Sci. 2020, 100, 191–202. [Google Scholar] [CrossRef]
- Legon, A.C.; Walker, N.R. What’s in a name? ‘Coinage-metal’ non-covalent bonds and their definition. Phys. Chem. Chem. Phys. 2018, 20, 19332–19338. [Google Scholar] [CrossRef] [PubMed]
- Taylor, R. Aerogen Bond, Halogen Bond, Chalcogen Bond, Pnictogen Bond, Tetrel Bond, Triel Bond ... Why So Many Names? Cryst. Growth Des. 2024, 24, 4003–4012. [Google Scholar] [CrossRef]
- Middya, P.; Karmakar, M.; Gomila, R.M.; Drew, M.G.B.; Frontera, A.; Chattopadhyay, S. The importance of spodium bonds, H-bonds and π-stacking interactions in the solid state structures of four zinc complexes with tetradentate secondary diamine ligands. New J. Chem. 2023, 47, 9346–9363. [Google Scholar] [CrossRef]
- Yang, Q.; Wu, Q.; Zhang, X.; Yang, X.; Li, Q. Hydrogen and halogen bonds formed by MCO3 (M = Zn, Cd) and their enhancement by a spodium bond. Mol. Phys. 2022, 120, e2102548. [Google Scholar] [CrossRef]
- Llull, R.; Montalbán, G.; Vidal, I.; Gomila, R.M.; Bauzá, A.; Frontera, A. Theoretical study of spodium bonding in the active site of three Zn-proteins and several model systems. Phys. Chem. Chem. Phys. 2021, 23, 16888–16896. [Google Scholar] [CrossRef]
- Amonov, A.; Scheiner, S. Spodium Bonding to Dicoordinated Group 12 Atoms. J. Phys. Chem. A 2024, 128, 8751–8761. [Google Scholar] [CrossRef]
- Yan, J.; Zeng, Y.; Meng, L.; Li, X.; Zhang, X. Gold(III) derivatives as the noncovalent interaction donors: Theoretical study of the π-hole regium bonds. Phys. Chem. Chem. Phys. 2023, 25, 29155–29164. [Google Scholar] [CrossRef]
- Shan, A.; Li, X.; Zeng, Y.; Meng, L.; Zhang, X. Theoretical investigation on the nature of substituted benzene⋯AuX interactions: Covalent or noncovalent? New J. Chem. 2022, 46, 3315–3324. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. Noncovalent Interactions Involving Group 6 in Biological Systems: The Case of Molybdopterin and Tungstopterin Cofactors. Chem. Eur. J. 2022, 28, e202201660. [Google Scholar] [CrossRef]
- Katlenok, E.A.; Kuznetsov, M.L.; Semenov, N.A.; Bokach, N.A.; Kukushkin, V.Y. A new look at the chalcogen bond: π-hole-based chalcogen (Se, Te) bonding which does not include a σ-hole interaction. Inorganic Chemistry Frontiers 2023, 10, 3065–3081. [Google Scholar] [CrossRef]
- Civiš, S.; Lamanec, M.; Špirko, V.; Kubišta, J.; Špet’ko, M.; Hobza, P. Hydrogen Bonding with Hydridic Hydrogen–Experimental Low-Temperature IR and Computational Study: Is a Revised Definition of Hydrogen Bonding Appropriate? J. Am. Chem. Soc. 2023, 145, 8550–8559. [Google Scholar] [CrossRef] [PubMed]
- Lamanec, M.; Zienertová, J.; Špeťko, M.; Nachtigallová, D.; Hobza, P. Similarities and Differences of Hydridic and Protonic Hydrogen Bonding. ChemPhysChem. 2024, 25, e202400403. [Google Scholar] [CrossRef] [PubMed]
- de Azevedo Santos, L.; Vermeeren, P.; Bickelhaupt, F.M.; Fonseca Guerra, C. “Hydridic Hydrogen-Bond Donors” Are Not Hydrogen-Bond Donors. J. Am. Chem. Soc. 2024, 146, 25701–25709. [Google Scholar] [CrossRef]
- Arunan, E.; Metrangolo, P.; Resnati, G.; Scheiner, S. IUPAC Recommendations: (Un)equivocal Understanding of Hydrogen and Halogen Bonds and Their (Un)equivocal Naming! Cryst. Growth Des. 2024, 24, 8153–8158. [Google Scholar] [CrossRef]
- Scheiner, S. Lower limits on hydrogen bond strength. Charge of bridging H atom. Phys. Chem. Chem. Phys. 2025, 27, 10283–10290. [Google Scholar] [CrossRef]
- Roberts, D.W.; Mao, Y. Probing “hydridic hydrogen bonds” using energy decomposition analysis based on absolutely localized molecular orbitals. Phys. Chem. Chem. Phys. 2025, 27, 14370–14378. [Google Scholar] [CrossRef] [PubMed]
- Gomila, R.M.; Beccaria, R.; Iacono, C.L.; Frontera, A.; Renati, G. Naming Matters: Hydridic Hydrogen Atoms are Halogen, Chalcogen, and Pnictogen Bond Acceptors not “Hydridic Hydrogen Bond” Donors. Chem. Eur. J. 2025, e02074. [Google Scholar] [CrossRef]
- Scheiner, S. Transition between the Noncovalency and Covalency of σ–Hole Bonds. J. Phys. Chem. A 2023, 127, 9760–9770. [Google Scholar] [CrossRef]
- Scheiner, S. Transition from covalent to noncovalent bonding between tetrel atoms. Phys. Chem. Chem. Phys. 2024, 26, 15978–15986. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Regium bonds between Mn clusters (M = Cu, Ag, Au and n = 2–6) and nucleophiles NH3 and HCN. Phys. Chem. Chem. Phys. 2018, 20, 22498–22509. [Google Scholar] [CrossRef] [PubMed]
- Reed, A.E.; Weinhold, F. Natural bond orbital analysis of near Hartree-Fock water dimer. J. Chem. Phys. 1983, 78, 4066–4073. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Mantina, M.; Chamberlin, A.C.; Valero, R.; Cramer, C.J.; Truhlar, D.G. Consistent van der Waals Radii for the Whole Main Group. J. Phys. Chem. A 2009, 113, 5806–5812. [Google Scholar] [CrossRef]

| Group | M | n | −Eb | RCl | RN |
|---|---|---|---|---|---|
| 3 | Y | 1 | 25.55 | 2.440 | 2.455 |
| 3 | 39.01 | 2.475 | 2.428 | ||
| 5 | Nb | 1 | 42.98 | 2.283 | 2.261 |
| 3 | 27.80 | 2.294 | 2.302 | ||
| 5 | 29.38 | 2.321 | 2.356 | ||
| 6 | Mo | 2 | 37.28 | 2.279 | 2.174 |
| 4 | 30.20 | 2.262 | 2.301 | ||
| 7 | Tc | 1 | 41.91 | 2.234 | 2.196 |
| 3 | 54.40 | 2.241 | 2.086 | ||
| 5 | 23.22 | 2.262 | 2.283 | ||
| 8 | Ru | 2 | 54.16 | 2.246 | 2.054 |
| 4 | 27.53 | 2.207 | 2.206 | ||
| 10 | Pd | 2 | 38.03 | 2.237 | 2.145 |
| 4 | 40.15 | 2.255 | 2.132 | ||
| 11 | Ag | 1 | 30.06 | 2.328 | 2.246 |
| 3 | 40.01 | 2.292 | 2.147 | ||
| 12 | Cd | 2 | 20.92 | 2.351 | 2.412 |
| 4 | 22.75 | 2.390 | 2.422 |
| Group | A | n | ρBCP | HBCP | ||
|---|---|---|---|---|---|---|
| M-Cl | M··N | M-Cl | M··N | |||
| 3 | Y | 1 | 0.0734 | 0.0500 | −0.0171 | −0.0055 |
| 3 | 0.0652 | 0.0503 | −0.0120 | −0.0047 | ||
| 5 | Nb | 1 | 0.1066 | 0.0781 | −0.0407 | −0.0182 |
| 3 | 0.1016 | 0.0669 | −0.0377 | −0.0126 | ||
| 5 | 0.1009 | 0.0634 | −0.0378 | −0.0121 | ||
| 6 | Mo | 2 | 0.1008 | 0.0833 | −0.0394 | −0.0174 |
| 4 | 0.1064 | 0.0638 | −0.0403 | −0.0095 | ||
| 7 | Tc | 1 | 0.1181 | 0.0781 | −0.0461 | −0.0155 |
| 3 | 0.1066 | 0.0978 | −0.0370 | −0.0215 | ||
| 5 | 0.1109 | 0.0721 | −0.0415 | −0.0137 | ||
| 8 | Ru | 2 | 0.1035 | 0.1041 | −0.0335 | −0.0245 |
| 4 | 0.1192 | 0.0743 | −0.0454 | −0.0113 | ||
| 10 | Pd | 2 | 0.1036 | 0.0801 | −0.0315 | −0.0122 |
| 4 | 0.1029 | 0.0881 | −0.0317 | −0.0165 | ||
| 11 | Ag | 1 | 0.0807 | 0.0652 | −0.0181 | −0.0078 |
| 3 | 0.0912 | 0.0840 | −0.0240 | −0.0142 | ||
| 12 | Cd | 2 | 0.0770 | 0.0466 | −0.0170 | −0.0045 |
| 4 | 0.0700 | 0.0457 | −0.0146 | −0.0044 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scheiner, S. The Next Frontier in the Study of Noncovalent Bonding: Transition Metals. Molecules 2025, 30, 3643. https://doi.org/10.3390/molecules30173643
Scheiner S. The Next Frontier in the Study of Noncovalent Bonding: Transition Metals. Molecules. 2025; 30(17):3643. https://doi.org/10.3390/molecules30173643
Chicago/Turabian StyleScheiner, Steve. 2025. "The Next Frontier in the Study of Noncovalent Bonding: Transition Metals" Molecules 30, no. 17: 3643. https://doi.org/10.3390/molecules30173643
APA StyleScheiner, S. (2025). The Next Frontier in the Study of Noncovalent Bonding: Transition Metals. Molecules, 30(17), 3643. https://doi.org/10.3390/molecules30173643






