Hetero-Disubstituted Sugarcane Bagasse as an Efficient Bioadsorbent for Cationic Dyes
Abstract
1. Introduction
2. Results and Discussion
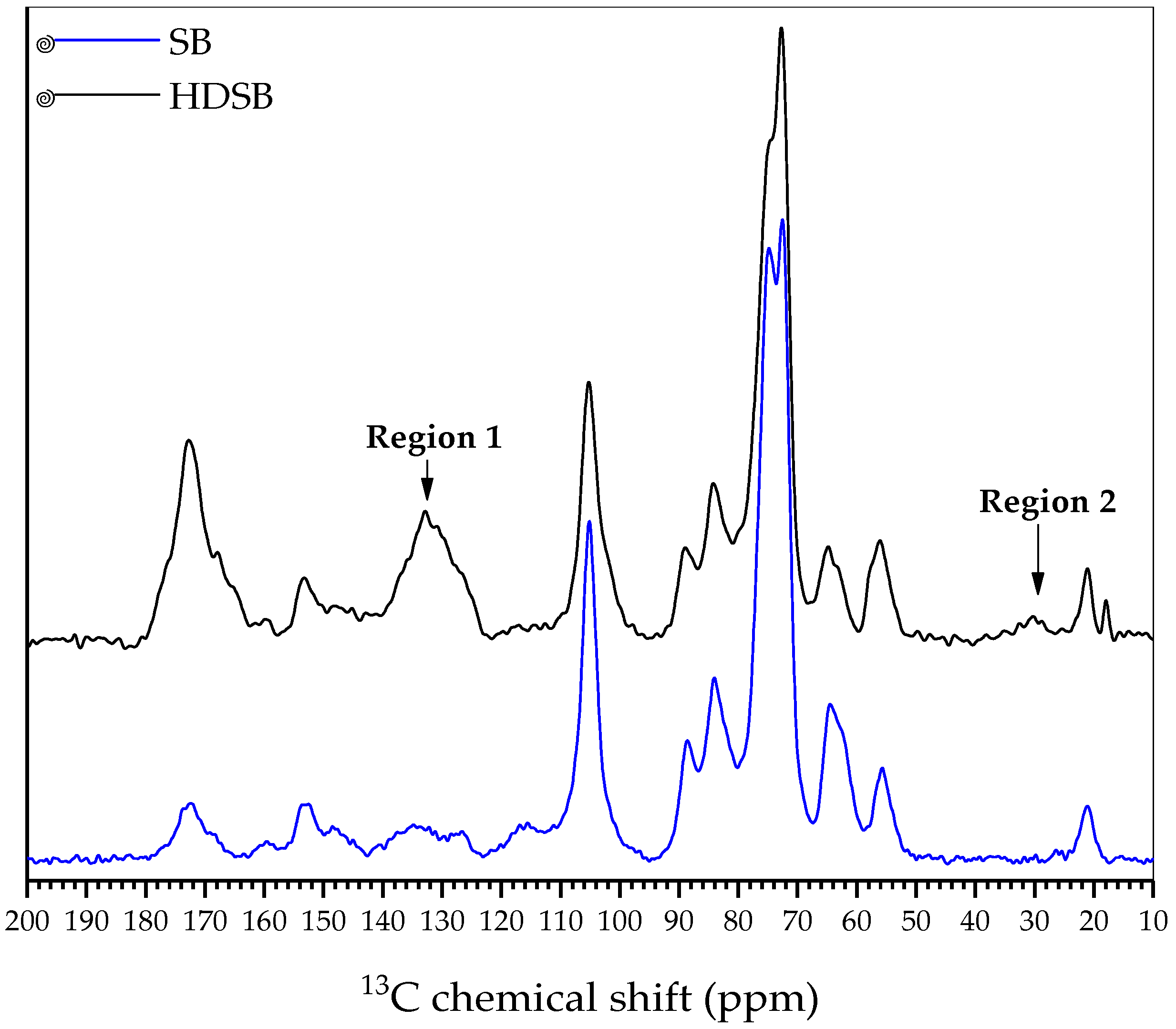
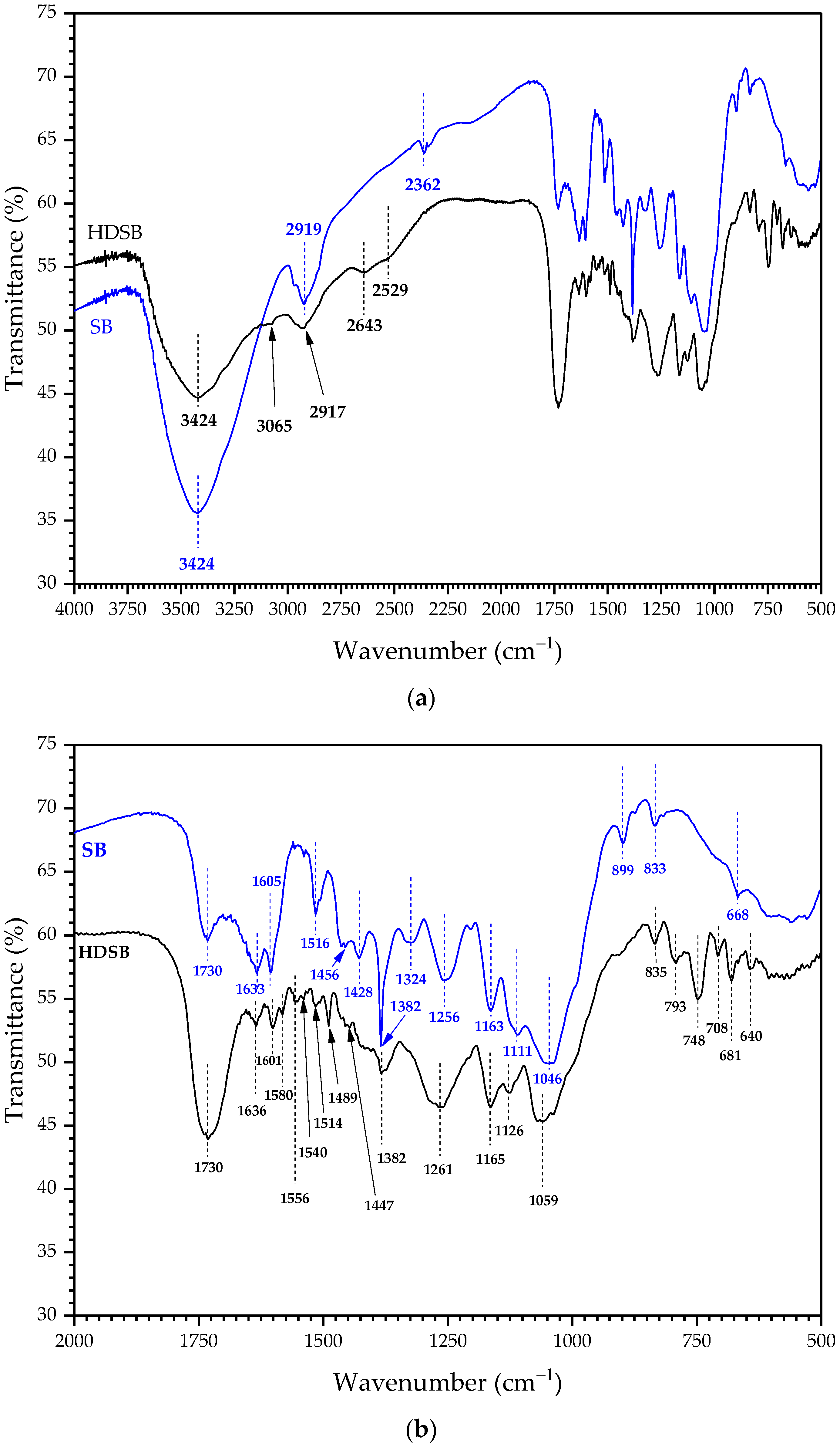
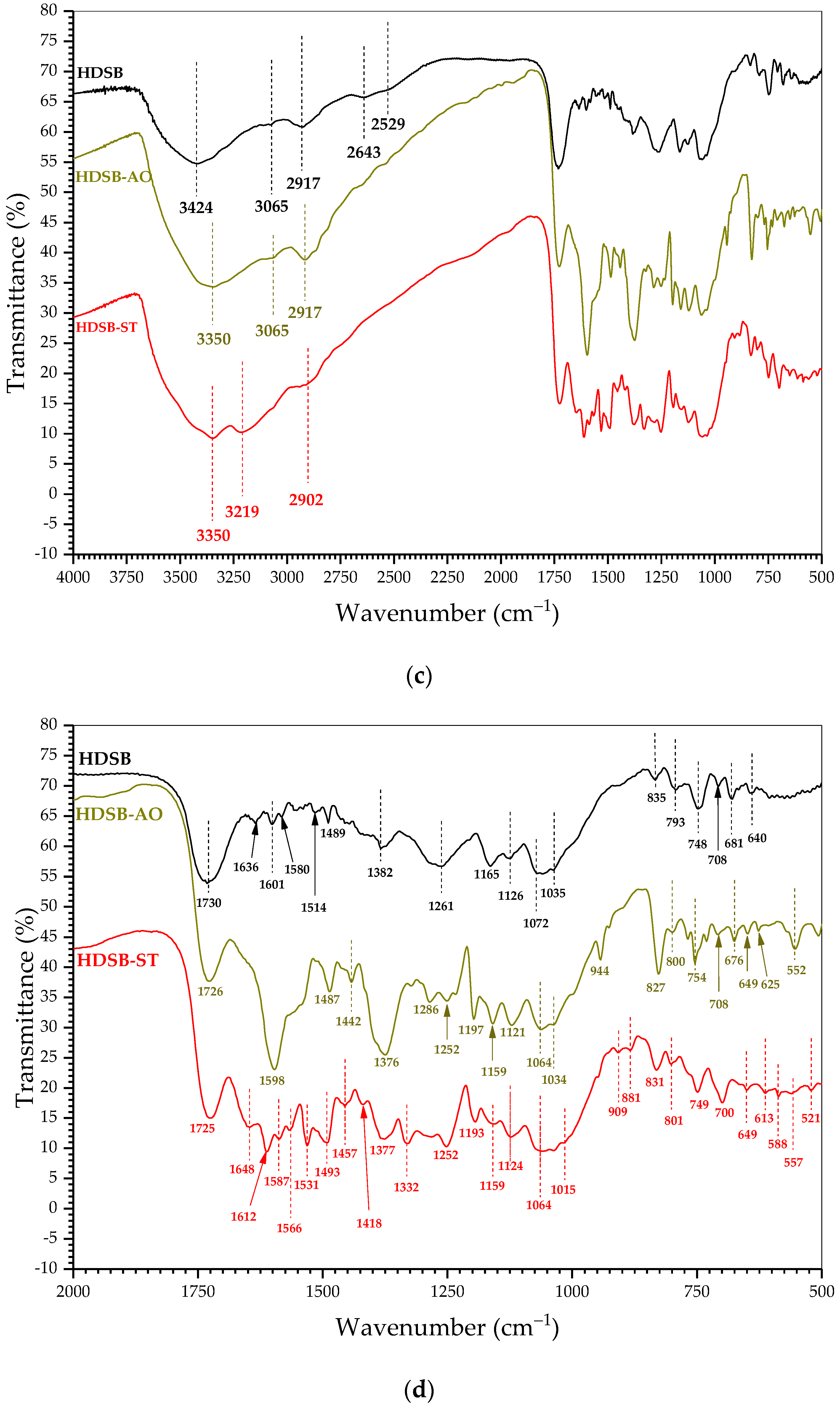
2.1. Characterization of the Biomaterials
2.2. Batch Adsorption Studies
2.2.1. Effect of Adsorbent Dosage
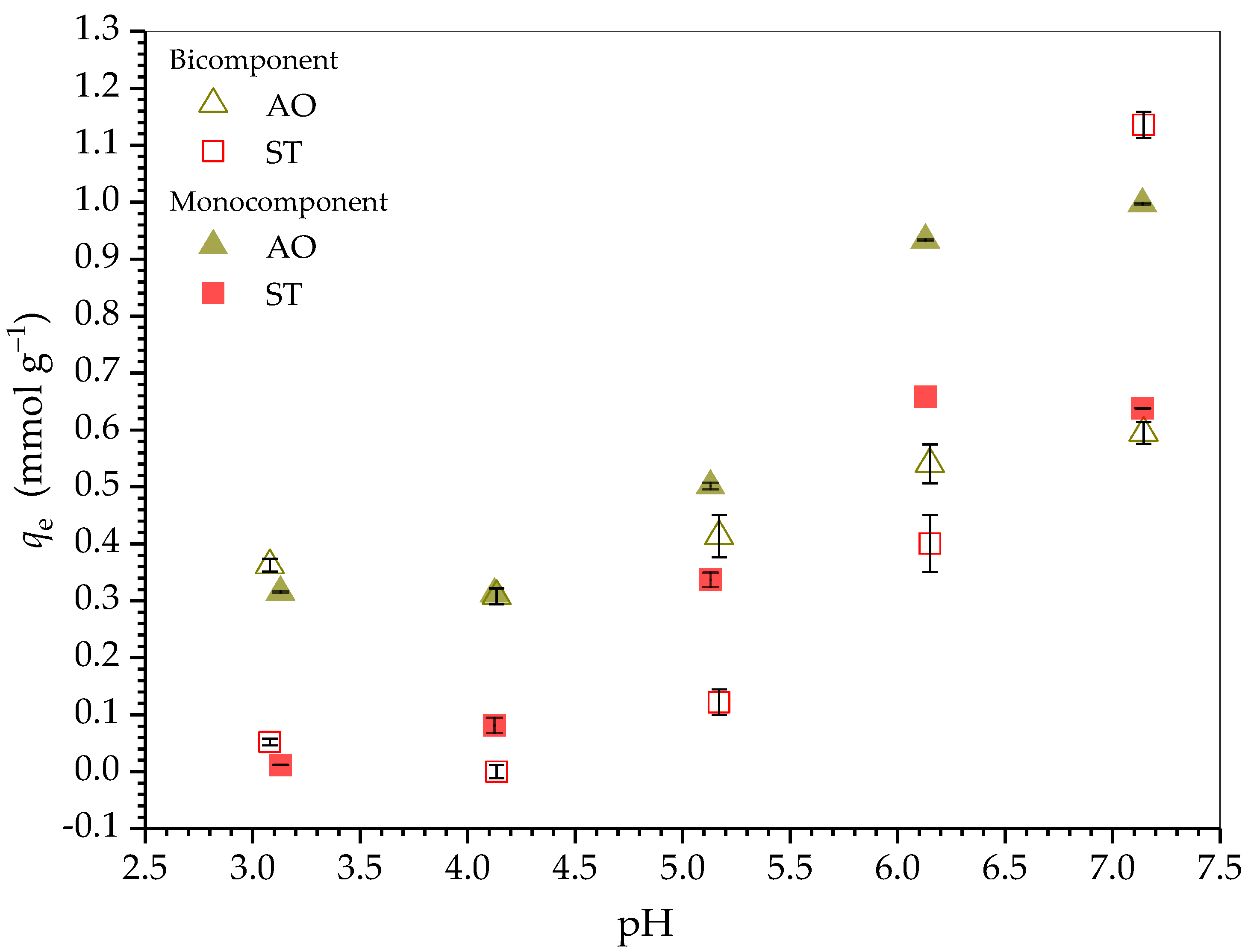
2.2.2. Effect of Solution pH
2.2.3. Adsorption Kinetics
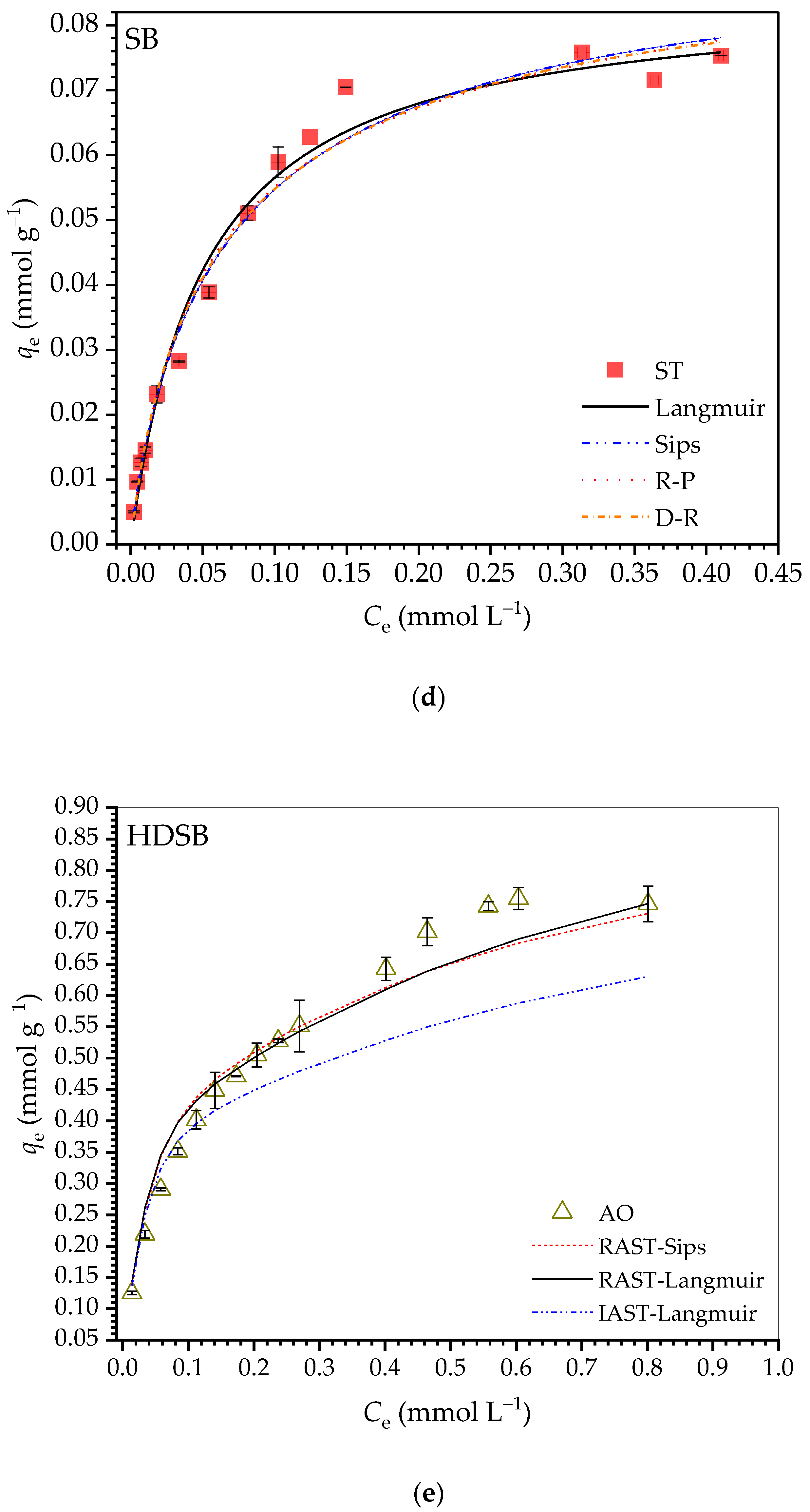
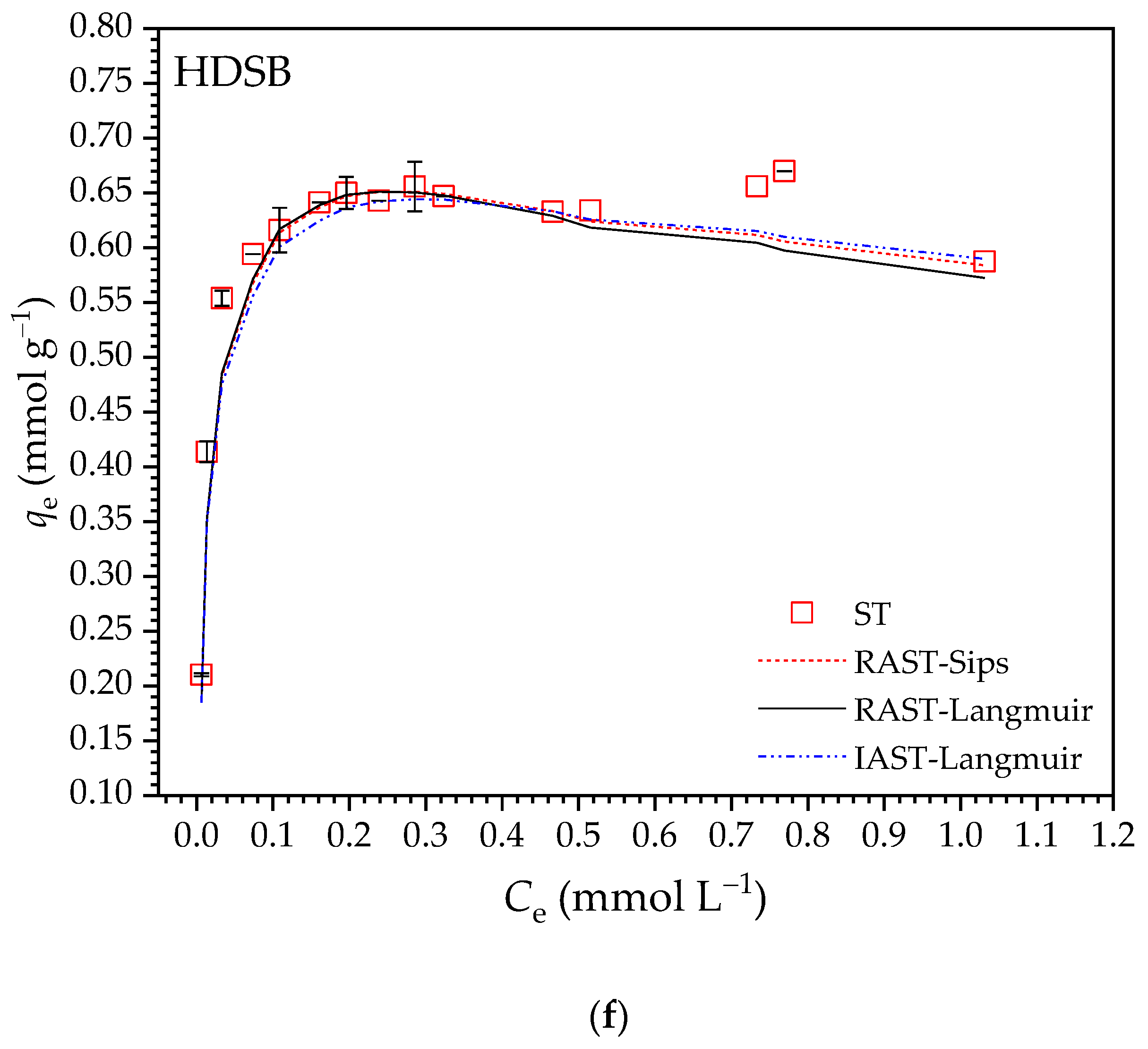
2.2.4. Adsorption Isotherms
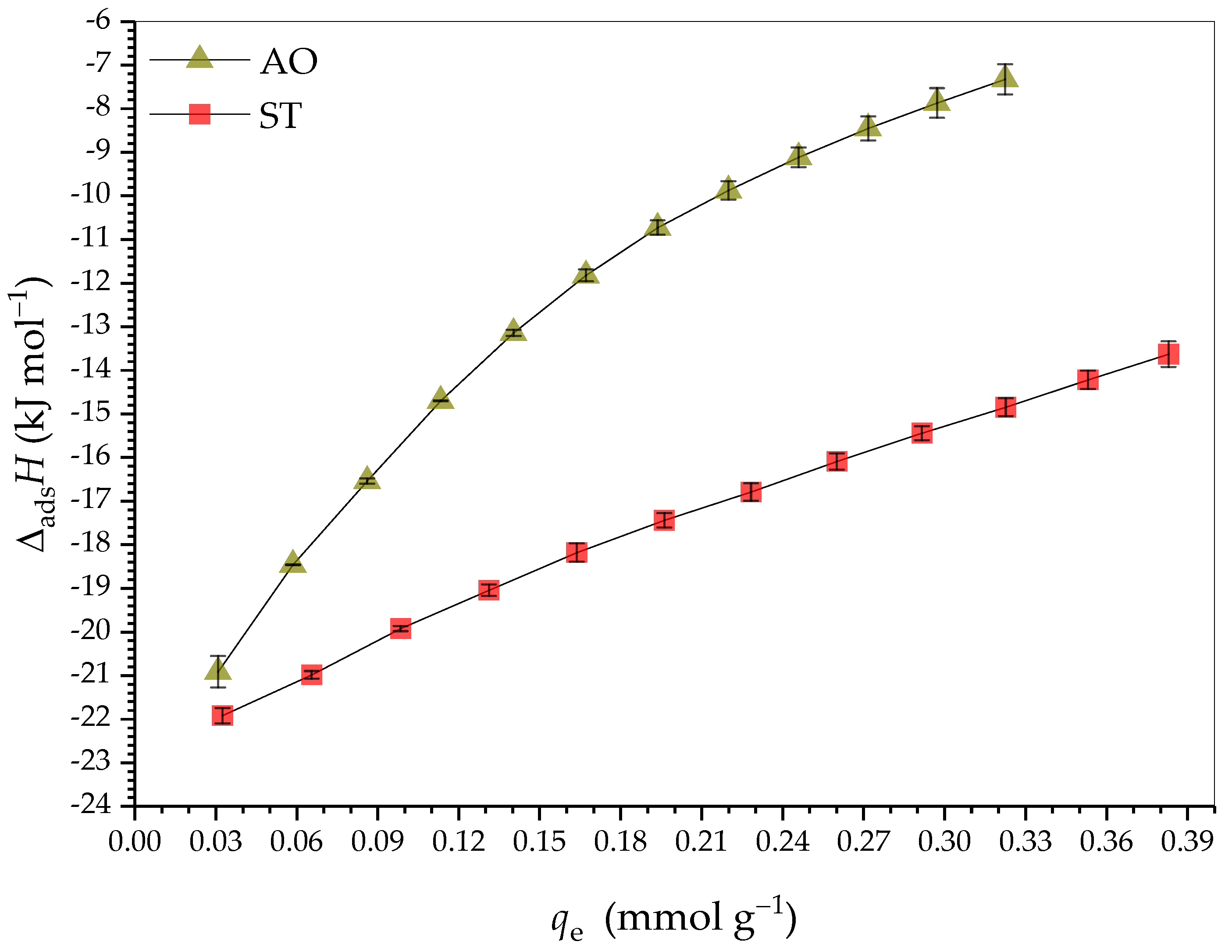
2.3. Adsorption Thermodymanics
| Adsorbent | Dye | qe (mmol g−1) | pH | T (°C) | Particle Size (mm) | Dose (g L−1) | Reference |
|---|---|---|---|---|---|---|---|
| Cellulose modified with trimellitic anhydride | AO | 2.63 1 | 4.5 | 25 | 0.25 | 0.2 | [43] |
| 5.18 1 | 7.0 | ||||||
| Sugarcane bagasse modified with trimellitic anhydride | AO | 1.01 1 | 4.5 | 25 | 0.5 | 0.2 | [42] |
| 1.73 1 | 7.0 | ||||||
| Sugarcane bagasse ash | AO | 0.12 2 | 7.0 | 30 | - | 0.2 | [68] |
| Activated carbon | AO | 0.35 2 | 7.0 | 25 | - | 0.04 | [10] |
| Guava leaves | AO | 0.03 2 | 9.0 | 30 | 0.2 | - | [69] |
| Sugarcane bagasse modified with phthalic and succinic anhydrides | AO | 1.37 1 | 7.0 | 25 | 0.5 | 0.2 | This work |
| Sugarcane bagasse | AO | 0.10 1 | 7.0 | 25 | 0.5 | 0.2 | This work |
| Nano Carbon/Polyurethane Tubes | ST | 1.59 2 | 7.0 | 30 | (1.0–3.0) × 10−5 | 0.1 | [70] |
| HDTMA-algae | ST | 0.17 2 | 4.0 | 25 | 9.3 × 10−5 | 5 | [71] |
| Rice husks | ST | 0.21 2 | 6.5 | 40 | 0.15–0.3 | 2 | [72] |
| Sugarcane bagasse modified with trimellitic anhydride | ST | 0.64 1 | 4.5 | 25 | 0.5 | 0.2 | [42] |
| 1.23 1 | 7.0 | 25 | |||||
| Cellulose modified with trimellitic anhydride | ST | 3.18 1 | 4.5 | 25 | 0.25 | 0.2 | [43] |
| 3.74 1 | 7.0 | 25 | |||||
| Sugarcane bagasse modified with phthalic and succinic anhydrides | ST | 0.93 1 | 7.0 | 25 | 0.5 | 0.2 | This work |
| Sugarcane bagasse | ST | 0.07 1 | 7.0 | 25 | 0.5 | 0.2 | This work |
2.4. Evaluation of Reuse of the Hetero-Disubstituted Sugarcane Bagasse
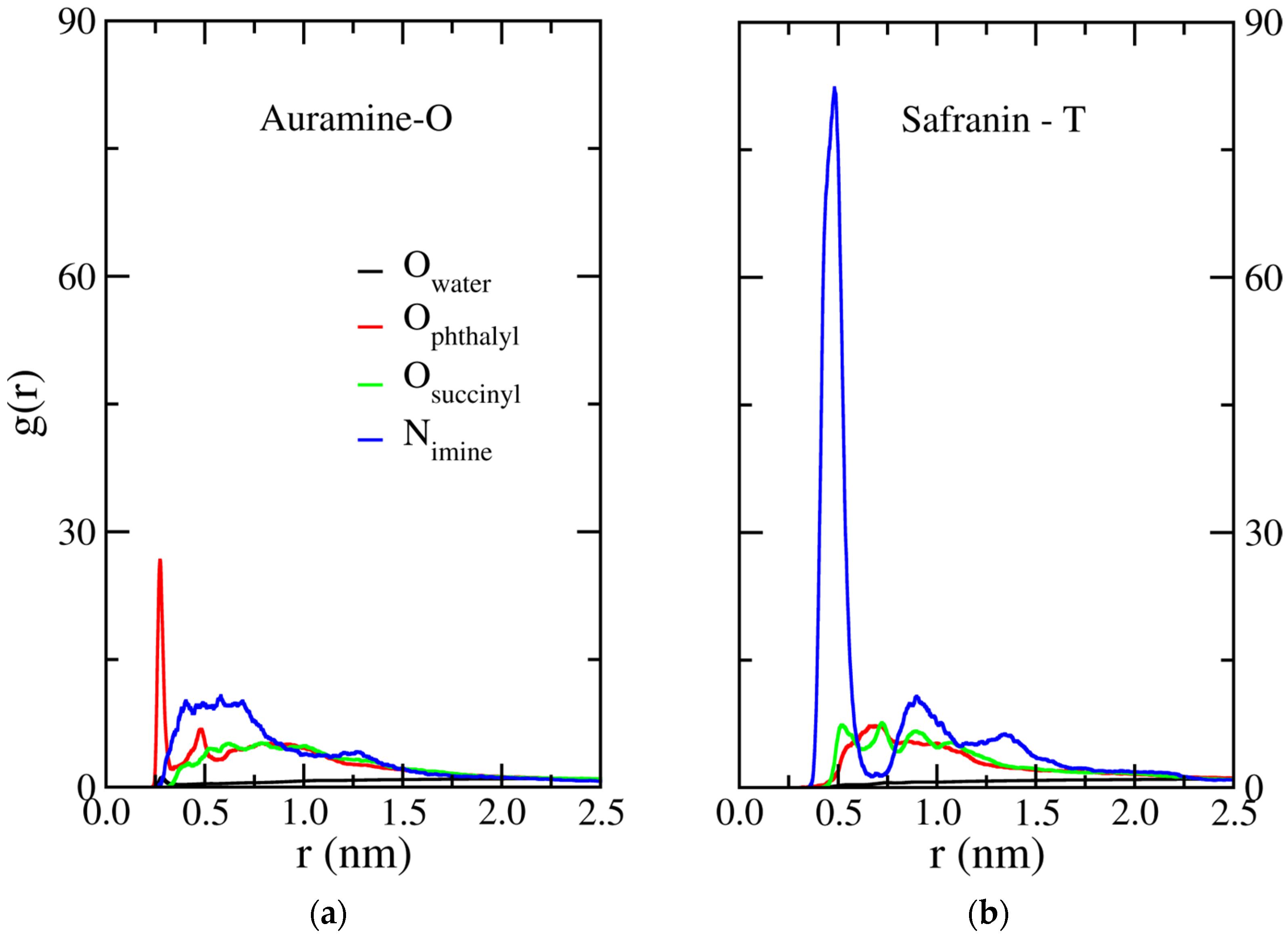
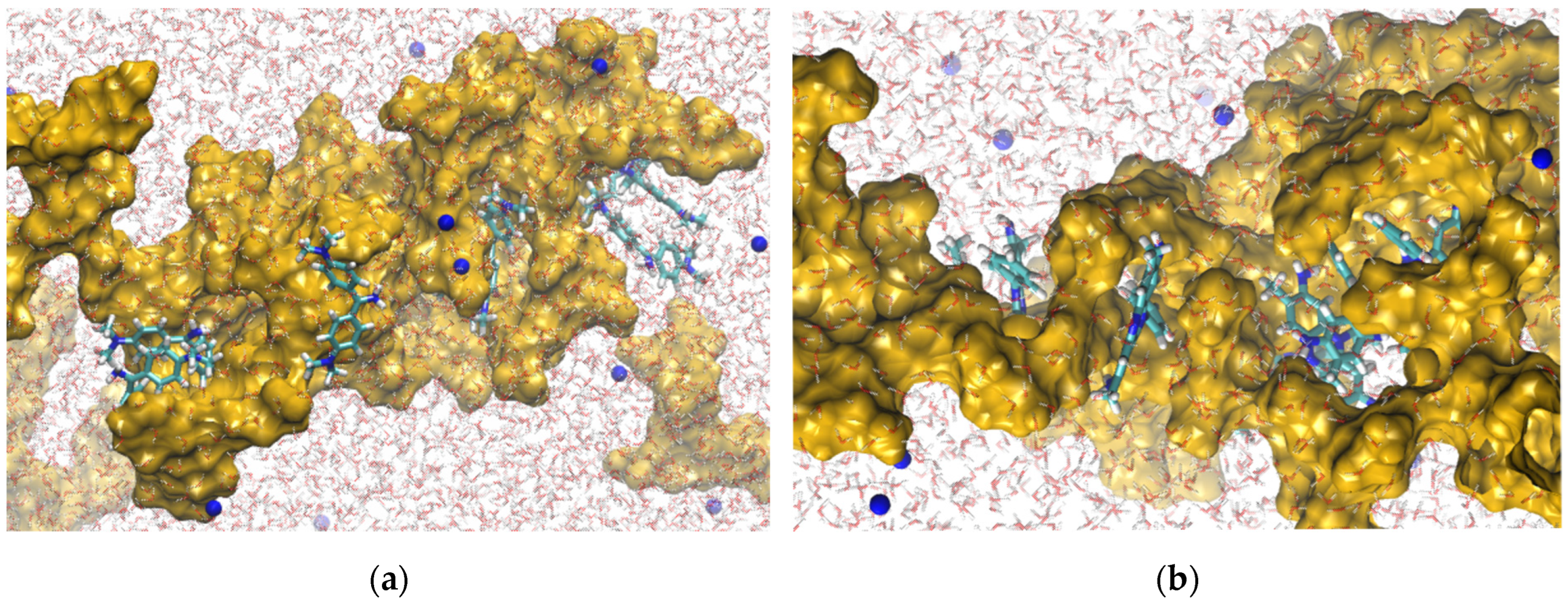
2.5. Radial Distribution Functions
3. Materials and Methods
3.1. Material
3.2. Preparation of Raw Sugarcane Bagasse and Hetero-Disubstituted Sugarcane Bagasse
3.3. Characterization of Raw Sugarcane Bagasse and Hetero-Disubstituted Sugarcane Bagasse
3.4. Batch Mono- and Bicomponent Adsorption Studies
3.5. Modeling of Single and Binary Batch Adsorption Data
3.6. Calculation of Adsorption Thermodynamic Parameters
3.7. Desorption and Re-Adsorption of the Hetero-Disubstituted Sugarcane Bagasse
3.8. Molecular Dynamics Simulations
4. Conclusions
5. Patents
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AO | Auramine-O |
| b | Langmuir constant (L mol−1) |
| B | Boyd plot slope |
| Ci,AO | Auramine-O solution concentration at time t (x = t) or equilibrium (x = e) (mmol L−1) |
| Ci,ST | Safranin-T solution concentration at time t (x = t) or equilibrium (x = e) (mmol L−1) |
| ∆adsG° | Change in standard free energy of adsorption (kJ mol−1 or J mol−1) |
| ∆adsH | Change in enthalpy of adsorption (kJ mol−1 or J mol−1) |
| ∆adsH° | Change in standard enthalpy of adsorption (kJ mol−1 or J mol−1) |
| ΔadsS° | Change in standard entropy of adsorption (J K−1 mol−1) |
| Ds | Surface diffusion coefficient (m2 min−1) of the Corsel model |
| Di | Effective diffusion coefficient of species i (m2 min−1) of the Boyd model |
| Edes | Desorption efficiency (%) |
| Ere-ads | Re-adsorption efficiency (%) |
| HDSB | Hetero-disubstituted sugarcane bagasse |
| HDSB-AO | Hetero-disubstituted sugarcane bagasse loaded with AO |
| HDSB-ST | Hetero-disubstituted sugarcane bagasse loaded with ST |
| IAST | Ideal Adsorbed Solution Theory |
| IPD | Intraparticle diffusion model |
| k,di | Intraparticle diffusion rate constant (mmol g−1 min−1/2) of step i |
| µ | Ionic strength (mol L−1) |
| n | Sips parameter (heterogeneity of the adsorption system) |
| pHPZC | Point of zero charge |
| qe | Equilibrium adsorption capacity (mmol g−1) |
| Qmax | Maximum adsorption capacity (mmol g−1) |
| qx,AO | Adsorption capacity at time t (x = t) or at equilibrium (x = e) of AO on HDSB (mmol g−1) |
| qx,ST | Adsorption capacity at time t (x = t) or at equilibrium (x = e) of ST on HDSB (mmol g−1) |
| R | Gas constant (J K−1 mol−1) |
| R2 | Coefficient of determination |
| R2adj | Adjusted coefficient of determination |
| RAST | Real Adsorbed Solution Theory |
| RDF | Radial Distribution Function |
| RSS | Residual sum of squares |
| ST | Safranin-T |
| SB | Sugarcane bagasse |
| T | Temperature (K or °C) |
| t | Time |
| TΔadsS° | Entropic contribution (kJ mol−1) |
| Vdye | Volume (L) of the dye (AO or ST) |
| wg | Weight gain (%) |
| wHDSB | Weight of HDSB (g) |
| γe | Activity coefficient at equilibrium |
| χ2red | Reduced chi-square |
Appendix A
| Kinetic Model | Model Equation | Parameter | Reference |
|---|---|---|---|
| Pseudo-first order (PFO) | k1 (min−1): pseudo-first order rate constant | [50] | |
| h (mmol g−1min−1): initial adsorption rate | |||
| Pseudo-second order (PSO) | k2 (g mmol−1 min−1): pseudo-second order rate constant | [51] | |
| h (mmol g−1min−1): initial adsorption rate | |||
| Elovich | α (mmol g−1 min−1): initial adsorption rate β (g mmol−1): desorption rate constant. | [52] | |
| Intraparticle diffusion (IPD) | ki (mmol g−1min−1/2): intraparticle diffusion rate constant C (mmol g−1): model constant | [53] | |
| Boyd | f (f = qt qe−1): fractional surface coverage | [54] | |
| Di (m2 min−1): effective diffusion coefficient |
| Isotherm Model | Model Equation | Parameter | Reference |
|---|---|---|---|
| Langmuir | Qmax (mmol g−1): maximum adsorption capacity b (L mmol−1): Langmuir binding constant | [60] | |
| Sips | n (dimensionless): heterogeneity of the adsorption system | [61] | |
| Redlich–Peterson (R-P) | KR (L g−1): model constant aR (L mmol−1): model constant β (dimensionless): model exponent | [62] | |
| Dubinin–Radushkevich (D-R) | with | qs (mmol g−1): maximum adsorption capacity B (mol2 kJ−2): constant related to the adsorption energy ɛ (kJ mol−1): Polanyi potential R: gas constant (8.314 J K−1 mol−1) T (K): temperature E (kJ mol−1): adsorption energy | [63] |
| Error function | |||
| Reduce Chi-square (χ2red) | wi: weighting coefficient υ (υ = N − P): number of degrees of freedom N: number of experimental data points P: number of variables of the model | [42] | |
| Kinetic Model | Model Equation | Parameter | Reference |
|---|---|---|---|
| Corsel | with and For a binary system: with and | Γ(t) (mmol m−2): concentration of dye on the adsorbent surface Γmax (mmol m−2): maximum surface coverage k(Γ)on (L mmol−1 min−1): adsorption rate function k(Γ)off (min−1): desorption rate function Cb (mmol L−1): dye concentration in the bulk Ds (m2 min−1): Surface diffusion coefficient δ (m): unstirred layer thickness k+1 (L mmol−1min−1): initial intrinsic rate constant k−1 (min−1): initial intrinsic desorption rate constants α: adsorption interaction constant β: desorption interaction constant K: association constant | [55] |
| Isotherm Model | Model Equation | Parameter | Reference |
|---|---|---|---|
| Real Adsorbed Solution Theory (RAST) | For RAST model fed with the Langmuir isotherm: For RAST model fed with the Sips isotherm: Approximation proposed by Erto et al. [64]: | N: number of dyes in the mixture Ce (mmol L−1): dye equilibrium concentration in the liquid phase C0e,i (mmol L−1): dye concentration in the liquid phase in equilibrium with dye concentration adsorbed on the solid phase [q0e,i (mmol g−1] T: temperature P: pressure Ψ: reduced spreading pressure γi: adsorbed dye activity coefficient xi: adsorbed dye mole fraction qT (mmol g−1): total dye solid phase concentration V (L): volume w (g): adsorbent weight c: adjustable model parameter Λij: interaction effect parameter CT (mmol L−1): total solute concentration xi = mole fraction of the species i a and b: adjustment constants of the approximation proposed by Erto et al. [64] | [64] |
| Error function | |||
| Residual Sum of Squares (RSS) | yi: experimental data point ŷi: estimated data point | [42] | |
References
- Future, M.R. Dyes & Pigments Market Research Report Information By Type (Dyes, Pigments), By End-Use (Textile, Leather, Paper, Paint, Printing Inks, Plastics) and by Region (North America, Europe, Asia-Pacific, And Rest Of The World)—Market Forecast Till 2032. Available online: https://www.marketresearchfuture.com/reports/dyes-pigments-market-10294?utm_term=&utm_campaign=&utm_source=adwords&utm_medium=ppc&hsa_acc=2893753364&hsa_cam=20269362920&hsa_grp=148912616334&hsa_ad=661977011274&hsa_src=g&hsa_tgt=dsa-2086491750467&hsa_kw=&hsa_mt=&hsa_net=adwords&hsa_ver=3&gad_source=1 (accessed on 8 May 2025).
- European Union. The Impact of Textile Production and Waste on the Environment (Infographics). Available online: https://www.europarl.europa.eu/news/en/headlines/society/20201208STO93327/the-impact-of-textile-production-and-waste-on-the-environment-infographic (accessed on 8 May 2025).
- Karthik, T.; Gopalakrishnan, D. Roadmap to Sustainable Textiles and Clothing: Environmental and Social Aspects of Textiles and Clothing Supply Chain. In Environmental Analysis of Textile Value Chain: An Overview; Muthu, S.S., Ed.; Springer: Singapore, 2014; pp. 153–188. [Google Scholar]
- Chapman, D. Water Quality Assessments: A Guide to the use of Biota, Sediments and Water in Environmental Monitoring, 2nd ed.; E & FN Spon: London, UK, 1996. [Google Scholar]
- Yaseen, D.A.; Scholz, M. Textile dye wastewater characteristics and constituents of synthetic effluents: A critical review. Int. J. Environ. Sci. Technol. 2019, 16, 1193–1226. [Google Scholar] [CrossRef]
- IARC. Monographs on the Evaluation of the Carcinogenic Risks to Humans, Supplement No. 7: Overall Evaluations of Carcinogenicity: An Updating of IARC Monographs; IARC: Lyon, France, 1987; p. 40. [Google Scholar]
- Gupta, V.K.; Kumar, R.; Nayak, A.; Saleh, T.A.; Barakat, M. Adsorptive removal of dyes from aqueous solution onto carbon nanotubes: A review. Adv. Colloid Interface Sci. 2013, 193, 24–34. [Google Scholar] [CrossRef]
- Arslan, I.; Balcioǧlu, I.A.; Bahnemann, D.W. Advanced chemical oxidation of reactive dyes in simulated dyehouse effluents by ferrioxalate-Fenton/UV-A and TiO2/UV-A processes. Dyes Pigm. 2000, 47, 207–218. [Google Scholar] [CrossRef]
- Kasiri, M.B.; Modirshahla, N.; Mansouri, H. Decolorization of organic dye solution by ozonation; Optimization with response surface methodology. Int. J. Ind. Chem. 2013, 4, 3. [Google Scholar] [CrossRef]
- Asfaram, A.; Ghaedi, M.; Agarwal, S.; Tyagi, I.; Gupta, V.K. Removal of basic dye Auramine-O by ZnS: Cu nanoparticles loaded on activated carbon: Optimization of parameters using response surface methodology with central composite design. RSC Adv. 2015, 5, 18438–18450. [Google Scholar] [CrossRef]
- Foorginezhad, S.; Zerafat, M.M. Microfiltration of cationic dyes using nano-clay membranes. Ceram. Int. 2017, 43, 15146–15159. [Google Scholar] [CrossRef]
- Kasperchik, V.; Yaskevich, A.; Bil’dyukevich, A. Wastewater treatment for removal of dyes by coagulation and membrane processes. Pet. Chem. 2012, 52, 545–556. [Google Scholar] [CrossRef]
- Konicki, W.; Hełminiak, A.; Arabczyk, W.; Mijowska, E. Adsorption of cationic dyes onto Fe@ graphite core–shell magnetic nanocomposite: Equilibrium, kinetics and thermodynamics. Chem. Eng. Res. Des. 2018, 129, 259–270. [Google Scholar] [CrossRef]
- Nawaz, M.S.; Ahsan, M. Comparison of physico-chemical, advanced oxidation and biological techniques for the textile wastewater treatment. Alex. Eng. J. 2014, 53, 717–722. [Google Scholar] [CrossRef]
- Martins, L.R.; Rodrigues, J.A.V.; Adarme, O.F.H.; Melo, T.M.S.; Gurgel, L.V.A.; Gil, L.F. Optimization of cellulose and sugarcane bagasse oxidation: Application for adsorptive removal of crystal violet and auramine-O from aqueous solution. J. Colloid Interface Sci. 2017, 494, 223–241. [Google Scholar] [CrossRef] [PubMed]
- Demirbas, A. Heavy metal adsorption onto agro-based waste materials: A review. J. Hazard. Mater. 2008, 157, 220–229. [Google Scholar] [CrossRef]
- do Gurgel, M.N.A.; Freire, F.J.; da Silva, F.C.; Abreu Junior, C.H.; Marchiori, L.F.S.; Raizer, A.J. Gerenciamento, tratamento e disposição de resíduos na cana-de-açúcar. In Inovação E Desenvolvimento Em Cana-De-Açúcar: Manejo, Nutrição, Bioinsumos, Recomendação De Corretivos E Fertilizantes; da Silva, F.C., Freire, F.J., Eds.; Embrapa: Brasília, Brazil, 2024; pp. 339–385. [Google Scholar]
- USDA Foreign Agricultural Service. U. S. Department of Agriculture. Production–Sugar. Available online: https://www.fas.usda.gov/data/production/commodity/0612000 (accessed on 16 July 2025).
- Xu, F. Structure, Ultrastructure, and Chemical Composition. In Cereal Straw as a Resource for Sustainable Biomaterials and Biofuels; Sun, R.-C., Ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 9–47. [Google Scholar] [CrossRef]
- Fengel, D.; Wegener, G. Wood: Chemistry, Ultrastructure, Reactions; Walter De Gruyter: Berlin, Germany, 1989. [Google Scholar]
- Raj, V.; Chauhan, M.S.; Pal, S.L. Potential of sugarcane bagasse in remediation of heavy metals: A review. Chemosphere 2022, 307, 135825. [Google Scholar] [CrossRef] [PubMed]
- Ullmann, F.; Bohnet, M. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Zeikus, J.G.; Jain, M.K.; Elankovan, P. Biotechnology of succinic acid production and markets for derived industrial products. Appl. Microbiol. Biotechnol. 1999, 51, 545–552. [Google Scholar] [CrossRef]
- van Es, D.S.; van der Klis, F.; van Haveren, J. Succinic Acid from Biomass. WO2012044168A1, 5 April 2012. Available online: https://patentimages.storage.googleapis.com/f0/3b/c0/0b58794c76af8f/WO2012044168A1.pdf (accessed on 16 July 2025).
- Gao, X.; Tong, X.; Zhang, Y.; Xue, S. The sustainable production of succinic anhydride from renewable biomass. iScience 2023, 26, 107203. [Google Scholar] [CrossRef]
- Mahmoud, E.; Watson, D.A.; Lobo, R.F. Renewable production of phthalic anhydride from biomass-derived furan and maleic anhydride. Green Chem. 2014, 16, 167–175. [Google Scholar] [CrossRef]
- Shao, X.; Su, L.; Zhang, J.; Tian, Z.; Zhang, N.; Wang, Y.; Wang, H.; Cui, X.; Hou, X.; Deng, T. Green Production of Phthalic Anhydride from Biobased Furan and Maleic Anhydride by an Acid Resin Catalyst. ACS Sustain. Chem. Eng. 2021, 9, 14385–14394. [Google Scholar] [CrossRef]
- Xu, L.; Han, Z.; Yao, Q.; Deng, J.; Zhang, Y.; Fu, Y.; Guo, Q. Towards the sustainable production of pyridines via thermo-catalytic conversion of glycerol with ammonia over zeolite catalysts. Green Chem. 2015, 17, 2426–2435. [Google Scholar] [CrossRef]
- Jassem, A.M.; Almashal, F.A.K.; Mohammed, M.Q.; Jabir, H.A.S. A catalytic and green method for one-pot synthesis of new Hantzsch 1,4-dihydropyridines. SN Appl. Sci. 2020, 2, 359. [Google Scholar] [CrossRef]
- Kasana, S.; Das Kurmi, B.; Patel, P. Green Synthesis of Pyridine and their Fused System: Harnessing the Catalytic Power of Ionic Liquids for Sustainable and Efficient Multicomponent Reaction. Curr. Org. Chem. 2025, 29, 713–729. [Google Scholar] [CrossRef]
- Rezende, C.A.; de Lima, M.A.; Maziero, P.; Ribeiro de Azevedo, E.; Garcia, W.; Polikarpov, I. Chemical and morphological characterization of sugarcane bagasse submitted to a delignification process for enhanced enzymatic digestibility. Biotechnol. Biofuels 2011, 4, 54. [Google Scholar] [CrossRef]
- Stael, G.C.; D’Almeida, J.R.M.; Tavares, M.I.B. A solid state NMR carbon-13 high resolution study of natural fiber from sugar cane and their composites with EVA. Polym. Test. 2000, 19, 251–259. [Google Scholar] [CrossRef]
- de Melo, J.C.; da Silva Filho, E.C.; Santana, S.A.; Airoldi, C. Exploring the favorable ion-exchange ability of phthalylated cellulose biopolymer using thermodynamic data. Carbohydr. Res. 2010, 345, 1914–1921. [Google Scholar] [CrossRef] [PubMed]
- de Melo, J.C.; Silva Filho, E.C.; Santana, S.A.A.; Airoldi, C. Synthesized cellulose/succinic anhydride as an ion exchanger. Calorimetry of divalent cations in aqueous suspension. Thermochim. Acta 2011, 524, 29–34. [Google Scholar] [CrossRef]
- Smith, B.C. Infrared Spectral Interpretation: A Systematic Approach; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kumar, A.; Negi, Y.S.; Choudhary, V.; Bhardwaj, N.K. Characterization of Cellulose Nanocrystals Produced by Acid-Hydrolysis from Sugarcane Bagasse as Agro-Waste. J. Mat. Phys. Chem. 2014, 2, 1–8. [Google Scholar] [CrossRef]
- Chen, M.-J.; Shi, Q.-S. Transforming Sugarcane Bagasse into Bioplastics via Homogeneous Modification with Phthalic Anhydride in Ionic Liquid. ACS Sustain. Chem. Eng. 2015, 3, 2510–2515. [Google Scholar] [CrossRef]
- Hase, Y.; Davanzo, C.U.; Kawai, K.; Sala, O. The vibrational spectra of phthalic anhydride. J. Mol. Struct. 1976, 30, 37–44. [Google Scholar] [CrossRef]
- Chemical Book AURAMINE O(2465-27-2) IR1. Available online: https://www.chemicalbook.com/SpectrumEN_2465-27-2_IR1.htm (accessed on 16 July 2025).
- Chemical Book Basic Red 2(477-73-6) IR1. Available online: https://www.chemicalbook.com/ChemicalProductProperty_EN_CB8141392.htm (accessed on 16 July 2025).
- Harada, N.; Uyama, H. Surface modification of cellulose with succinic anhydride in dimethyl sulfoxide using potassium carbonate as a catalyst. Carbohydr. Res. 2023, 528, 108812. [Google Scholar] [CrossRef]
- Fideles, R.A.; Ferreira, G.M.D.; Teodoro, F.S.; Adarme, O.F.H.; da Silva, L.H.M.; Gil, L.F.; Gurgel, L.V.A. Trimellitated sugarcane bagasse: A versatile adsorbent for removal of cationic dyes from aqueous solution. Part I: Batch adsorption in a monocomponent system. J. Colloid Interface Sci. 2018, 515, 172–188. [Google Scholar] [CrossRef]
- Teodoro, F.S.; Elias, M.M.C.; Ferreira, G.M.D.; Adarme, O.F.H.; Savedra, R.M.L.; Siqueira, M.F.; da Silva, L.H.M.; Gil, L.F.; Gurgel, L.V.A. Synthesis and application of a new carboxylated cellulose derivative. Part III: Removal of auramine-O and safranin-T from mono-and bi-component spiked aqueous solutions. J. Colloid Interface Sci. 2018, 512, 575–590. [Google Scholar] [CrossRef]
- Ferreira, B.C.S.; Teodoro, F.S.; Mageste, A.B.; Gil, L.F.; de Freitas, R.P.; Gurgel, L.V.A. Application of a new carboxylate-functionalized sugarcane bagasse for adsorptive removal of crystal violet from aqueous solution: Kinetic, equilibrium and thermodynamic studies. Ind. Crops Prod. 2015, 65, 521–534. [Google Scholar] [CrossRef]
- Zhang, Z.; Moghaddam, L.; O’Hara, I.M.; Doherty, W.O. Congo Red adsorption by ball-milled sugarcane bagasse. Chem. Eng. J. 2011, 178, 122–128. [Google Scholar] [CrossRef]
- Zhang, Z.; O’Hara, I.M.; Kent, G.A.; Doherty, W.O. Comparative study on adsorption of two cationic dyes by milled sugarcane bagasse. Ind. Crops Prod. 2013, 42, 41–49. [Google Scholar] [CrossRef]
- Huber, R.G.; Margreiter, M.A.; Fuchs, J.E.; von Grafenstein, S.; Tautermann, C.S.; Liedl, K.R.; Fox, T. Heteroaromatic π-Stacking Energy Landscapes. J. Chem. Inf. Model. 2014, 54, 1371–1379. [Google Scholar] [CrossRef]
- Saragi, R.T.; Calabrese, C.; Juanes, M.; Pinacho, R.; Rubio, J.E.; Pérez, C.; Lesarri, A. π-Stacking Isomerism in Polycyclic Aromatic Hydrocarbons: The 2-Naphthalenethiol Dimer. J. Phys. Chem. Lett. 2023, 14, 207–213. [Google Scholar] [CrossRef]
- Abbaz, A.; Arris, S.; Viscusi, G.; Ayat, A.; Aissaoui, H.; Boumezough, Y. Adsorption of Safranin O Dye by Alginate/Pomegranate Peels Beads: Kinetic, Isotherm and Thermodynamic Studies. Gels 2023, 9, 916. [Google Scholar] [CrossRef]
- Lagergren, S. Zur theorie der sogenannten adsorption gelöster stoffe. K. Sven. Vetenskapsakademiens Handl. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.-S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Roginsky, S.; Zeldovich, Y. Die katalische oxidation von kohlenmonoxyd auf mangandioxyd. Acta Physioch. URSS 1934, 1, 554–594. [Google Scholar]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. J. San. Eng. Div. 1963, 89, 31–59. [Google Scholar] [CrossRef]
- Boyd, G.E.; Adamson, A.W.; Myers, L.S. The exchange adsorption of ions from aqueous solutions by organic zeolites. II. Kinetics. J. Am. Chem. Soc. 1947, 69, 2836–2848. [Google Scholar] [CrossRef]
- Corsel, J.W.; Willems, G.M.; Kop, J.M.; Cuypers, P.A.; Hermens, W.T. The role of intrinsic binding rate and transport rate in the adsorption of prothrombin, albumin, and fibrinogen to phospholipid bilayers. J. Colloid Interface Sci. 1986, 111, 544–554. [Google Scholar] [CrossRef]
- Revellame, E.D.; Fortela, D.L.; Sharp, W.; Hernandez, R.; Zappi, M.E. Adsorption kinetic modeling using pseudo-first order and pseudo-second order rate laws: A review. Clean. Eng. Technol. 2020, 1, 100032. [Google Scholar] [CrossRef]
- Cuypers, P.A.; Willems, G.M.; Hemker, H.C.; Hermens, W.T. Adsorption Kinetics of Protein Mixtures A Tentative Explanation of the Vroman Effect. Ann. N. Y. Acad. Sci. 1987, 516, 244–252. [Google Scholar] [CrossRef]
- Hlady, V. Adsorption Kinetics of Low Density Lipoprotein onto a Hydrophobic-Hydrophilic Gradient Surface. In Supramolecular Structure and Function 7; Pifat-Mrzljak, G., Ed.; Springer: Boston, MA, USA, 2001; pp. 45–61. [Google Scholar] [CrossRef]
- Teodoro, F.S.; Adarme, O.F.H.; Gil, L.F.; Gurgel, L.V.A. Synthesis and application of a new carboxylated cellulose derivative. Part II: Removal of Co2+, Cu2+ and Ni2+ from bicomponent spiked aqueous solution. J. Colloid Interface Sci. 2017, 487, 266–280. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Sips, R. On the structure of a catalyst surface. J. Chem. Phys. 1948, 16, 490–495. [Google Scholar] [CrossRef]
- Redlich, O.; Peterson, D.L. A useful adsorption isotherm. J. Phys. Chem. 1959, 63, 1024. [Google Scholar] [CrossRef]
- Dubinin, M.M.; Radushkevich, L.V. Equation of the characteristic curve of the activated charcoal. USSR Phys. Chem. Sect. 1947, 55, 331–333. [Google Scholar]
- Erto, A.; Lancia, A.; Musmarra, D. A Real Adsorbed Solution Theory model for competitive multicomponent liquid adsorption onto granular activated carbon. Microporous Mesoporous Mater. 2012, 154, 45–50. [Google Scholar] [CrossRef]
- Costa, E.; Sotelo, J.L.; Calleja, G.; Marrón, C. Adsorption of binary and ternary hydrocarbon gas mixtures on activated carbon: Experimental determination and theoretical prediction of the ternary equilibrium data. AIChE J. 1981, 27, 5–12. [Google Scholar] [CrossRef]
- Erto, A.; Lancia, A.; Musmarra, D. A modelling analysis of PCE/TCE mixture adsorption based on Ideal Adsorbed Solution Theory. Sep. Purif. Technol. 2011, 80, 140–147. [Google Scholar] [CrossRef]
- Teodoro, F.S.; do Carmo Ramos, S.N.; Elias, M.M.C.; Mageste, A.B.; Ferreira, G.M.D.; da Silva, L.H.M.; Gil, L.F.; Gurgel, L.V.A. Synthesis and application of a new carboxylated cellulose derivative. Part I: Removal of Co2+, Cu2+ and Ni2+ from monocomponent spiked aqueous solution. J. Colloid Interface Sci. 2016, 483, 185–200. [Google Scholar] [CrossRef]
- Mall, I.D.; Srivastava, V.C.; Agarwal, N.K. Adsorptive removal of Auramine-O: Kinetic and equilibrium study. J. Hazard. Mater. 2007, 143, 386–395. [Google Scholar] [CrossRef]
- Gaikwad, R.W.; Kinldy, S.A.M. Studies on auramine dye adsorption on psidium guava leaves. Korean J. Chem. Eng. 2009, 26, 102–107. [Google Scholar] [CrossRef]
- Khan, T.A.; Nazir, M.; Khan, E.A.; Riaz, U. Multiwalled carbon nanotube–polyurethane (MWCNT/PU) composite adsorbent for safranin T and Pb(II) removal from aqueous solution: Batch and fixed-bed studies. J. Mol. Liq. 2015, 212, 467–479. [Google Scholar] [CrossRef]
- Guler, U.A.; Ersan, M.; Tuncel, E.; Dügenci, F. Mono and simultaneous removal of crystal violet and safranin dyes from aqueous solutions by HDTMA-modified Spirulina sp. Process Saf. Environ. Prot. 2016, 99, 194–206. [Google Scholar] [CrossRef]
- Gupta, V.K.; Mittal, A.; Jain, R.; Mathur, M.; Sikarwar, S. Adsorption of Safranin-T from wastewater using waste materials-activated carbon and activated rice husks. J. Colloid Interface Sci. 2006, 303, 80–86. [Google Scholar] [CrossRef]
- Ramos, S.N.C.; Xavier, A.L.P.; Teodoro, F.S.; Elias, M.M.C.; Gonçalves, F.J.; Gil, L.F.; de Freitas, R.P.; Gurgel, L.V.A. Modeling mono-and multi-component adsorption of cobalt(II), copper(II), and nickel(II) metal ions from aqueous solution onto a new carboxylated sugarcane bagasse. Part I: Batch adsorption study. Ind. Crops Prod. 2015, 74, 357–371. [Google Scholar] [CrossRef]
- McKay, G.; Al-Duri, B. Prediction of bisolute adsorption isotherms using single-component data for dye adsorption onto carbon. Chem. Eng. Sci. 1988, 43, 1133–1142. [Google Scholar] [CrossRef]
- Pereira, A.R.; Soares, L.C.; Teodoro, F.S.; Elias, M.M.C.; Ferreira, G.M.D.; Savedra, R.M.L.; Siqueira, M.F.; Martineau-Corcos, C.; da Silva, L.H.M.; Prim, D. Aminated cellulose as a versatile adsorbent for batch removal of As(V) and Cu(II) from mono-and multicomponent aqueous solutions. J. Colloid Interface Sci. 2020, 576, 158–175. [Google Scholar] [CrossRef]
- Liu, Y. Is the free energy change of adsorption correctly calculated? J. Chem. Eng. Data 2009, 54, 1981–1985. [Google Scholar] [CrossRef]
- Ghosal, P.S.; Gupta, A.K. Determination of thermodynamic parameters from Langmuir isotherm constant-revisited. J. Mol. Liq. 2017, 225, 137–146. [Google Scholar] [CrossRef]
- Davies, C.W. Ion Association, 1st ed.; Butterworths: London, UK, 1962. [Google Scholar]
- Neese, F. The ORCA program system. WIREs Comp. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLS-AA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Dias, K.S.; Savedra, R.M.L.; de Magalhães, C.E.T.; Siqueira, M.F. Solvent influence on molecular interactions in the bulk of fluorene copolymer films. RSC Adv. 2020, 10, 20772–20777. [Google Scholar] [CrossRef]
- de Magalhães, C.E.T.; Savedra, R.M.L.; Dias, K.S.; Ramos, R.; Siqueira, M.F. Structural dependence of MEH-PPV chromism in solution. J. Mol. Model. 2017, 23, 91. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Johnson, R.L.; Schmidt-Rohr, K. Quantitative solid-state 13C NMR with signal enhancement by multiple cross polarization. J. Magn. Reson. 2014, 239, 44–49. [Google Scholar] [CrossRef]
- Bernardinelli, O.D.; Lima, M.A.; Rezende, C.A.; Polikarpov, I.; deAzevedo, E.R. Quantitative 13C MultiCP solid-state NMR as a tool for evaluation of cellulose crystallinity index measured directly inside sugarcane biomass. Biotechnol. Biofuels 2015, 8, 110. [Google Scholar] [CrossRef]
- Noh, J.S.; Schwarz, J.A. Effect of HNO3 treatment on the surface-acidity of activated carbons. Carbon 1990, 28, 675–682. [Google Scholar] [CrossRef]
- Guo, J.; Catchmark, J.M. Surface area and porosity of acid hydrolyzed cellulose nanowhiskers and cellulose produced by Gluconacetobacter xylinus. Carbohydr. Polym. 2012, 87, 1026–1037. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The determination of pore volume and area distributions in porous substances. I. Computations from nitrogen isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Sabnis, R.W. Handbook of Biological Dyes and Stains: Synthesis and Industrial Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010; p. 521. [Google Scholar] [CrossRef]
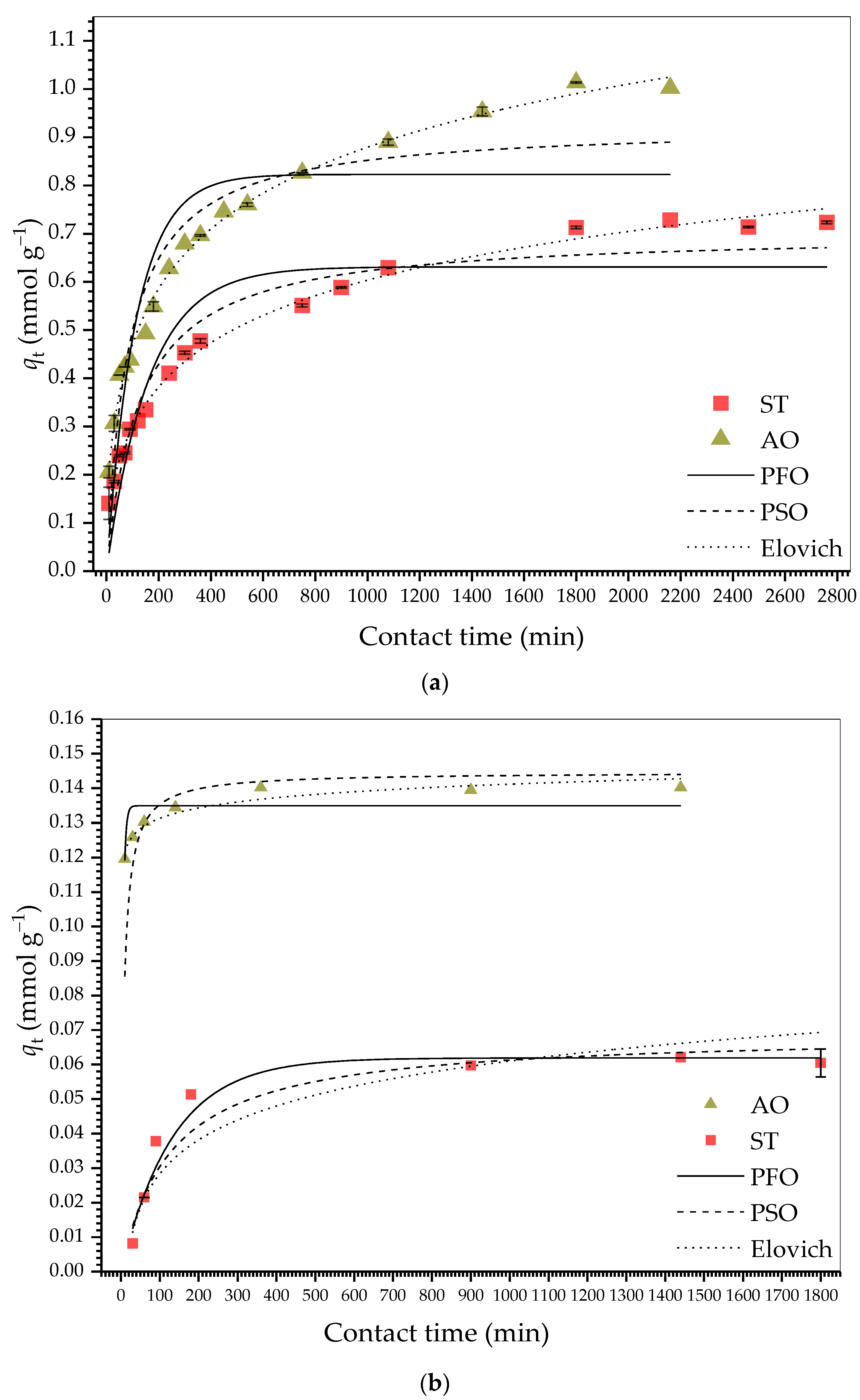
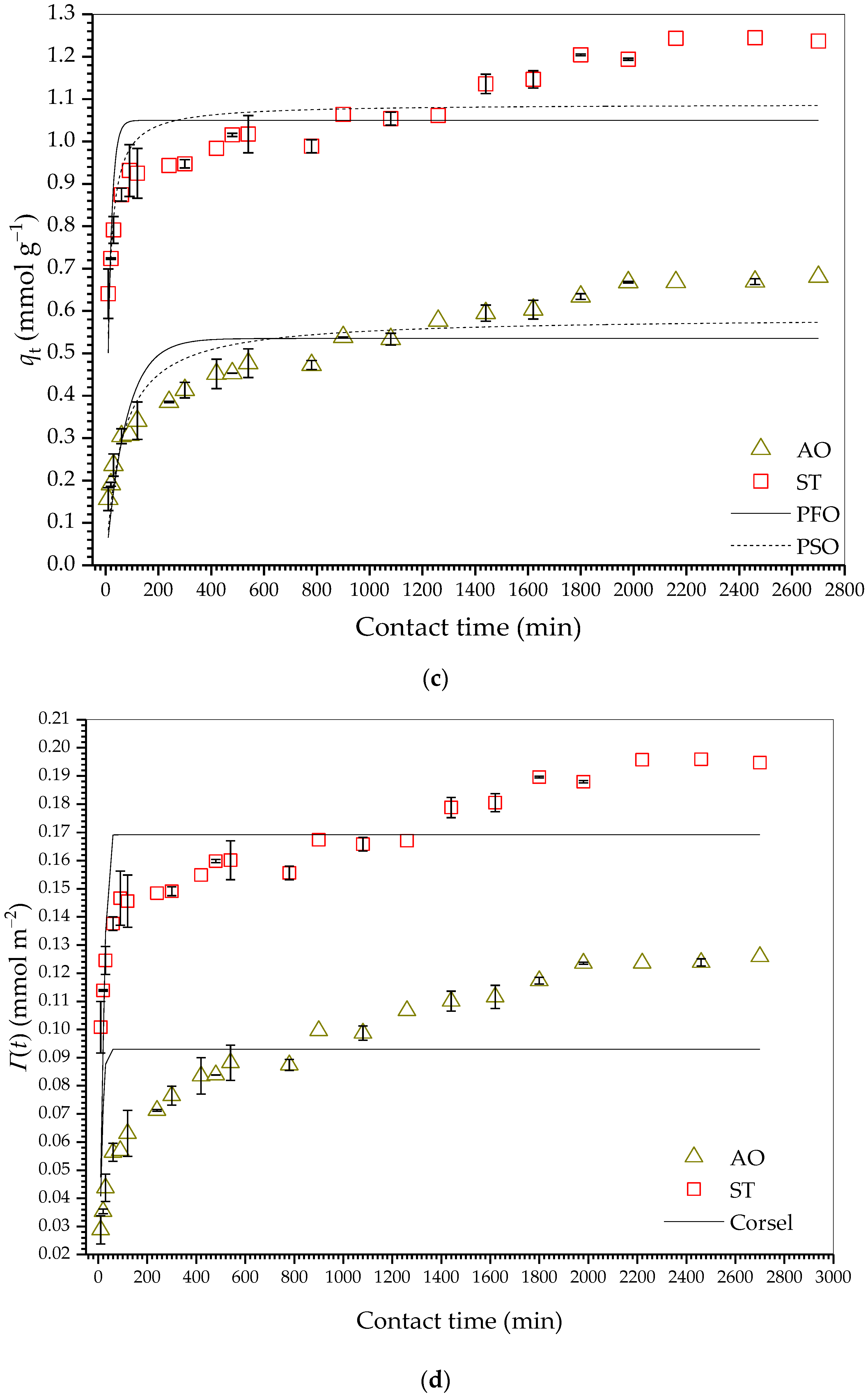
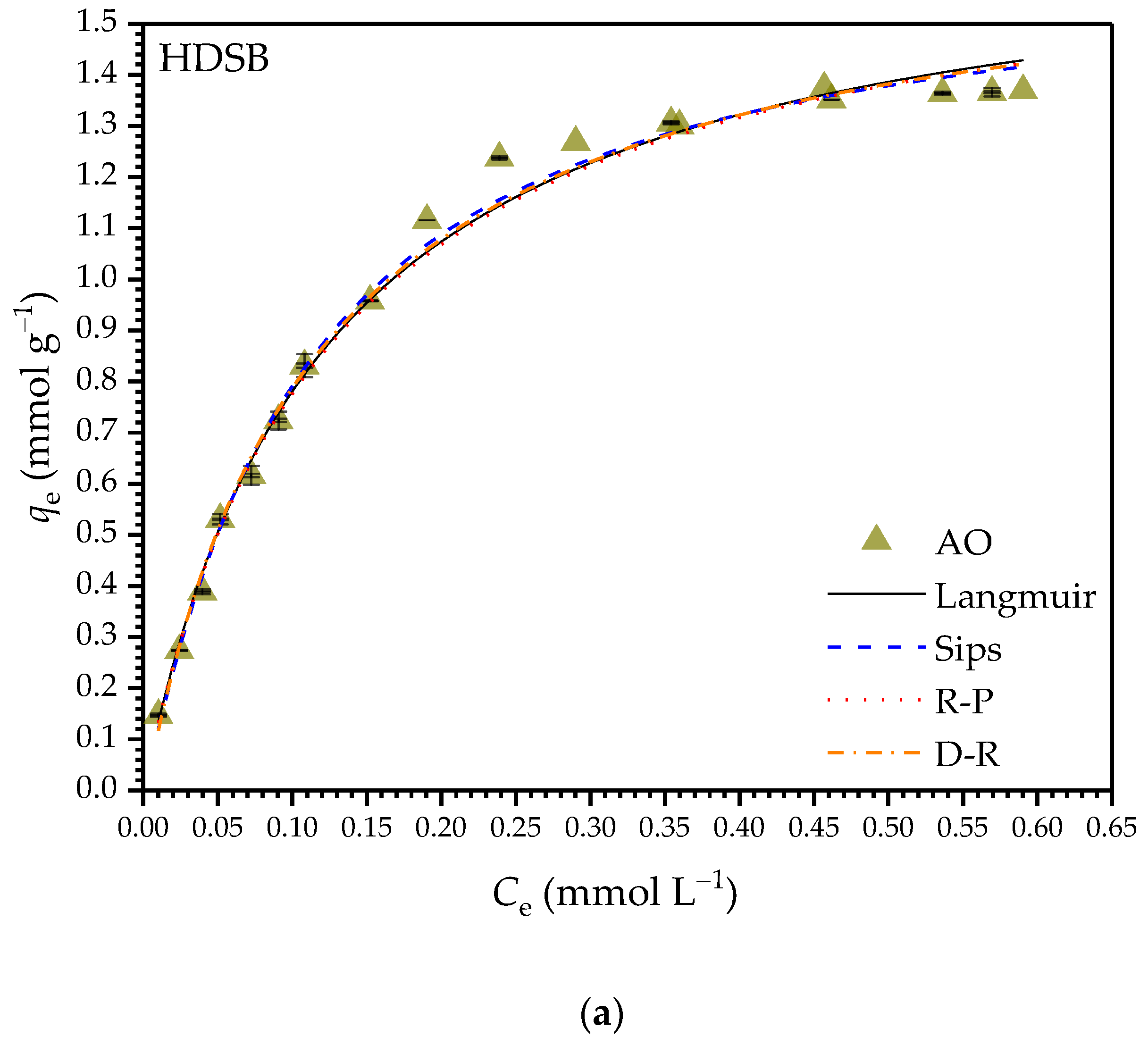
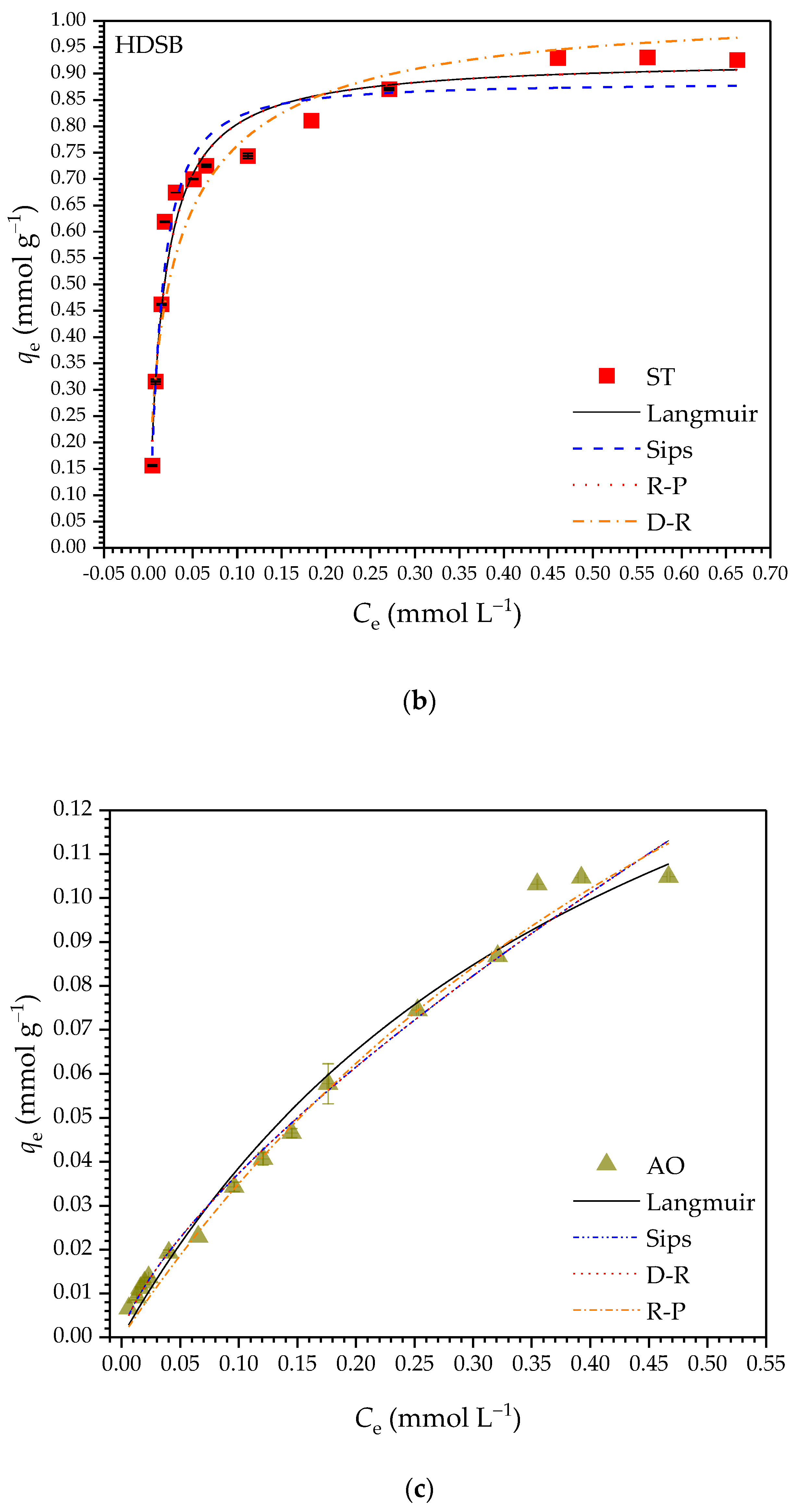
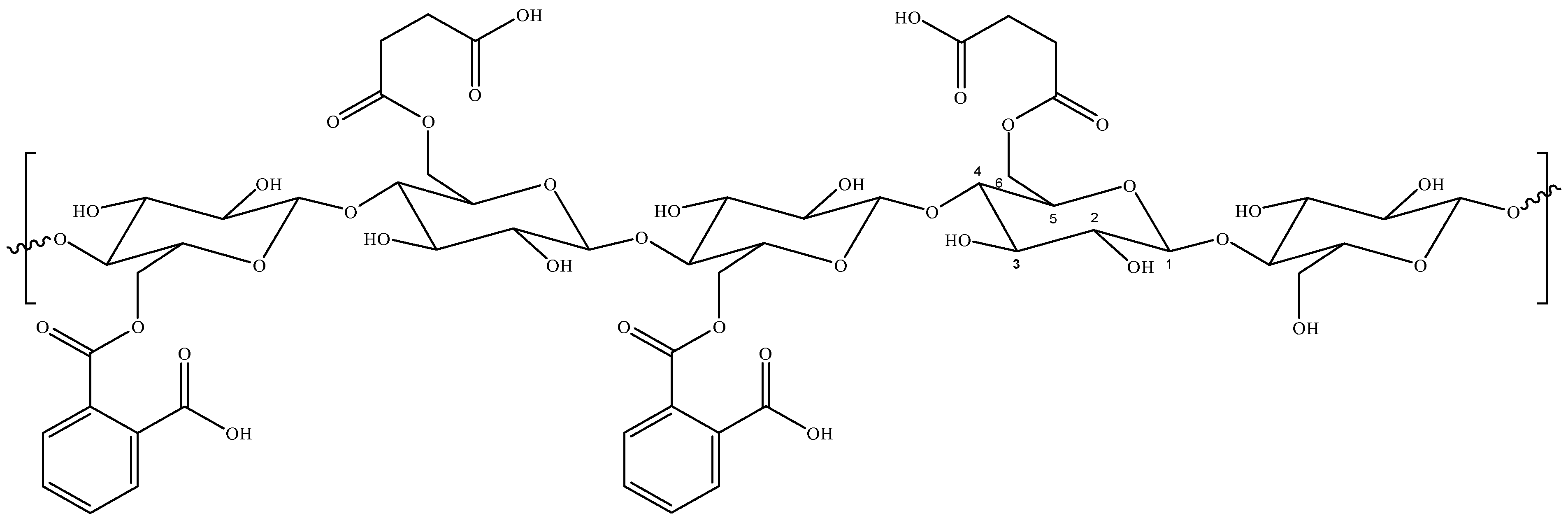
| Parameter | HDSB | SB | ||
|---|---|---|---|---|
| AO | ST | AO | ST | |
| qe,exp (mmol g−1) | 1.008 ± 0.006 | 0.862 ± 0.001 | 0.140 ± 0.000 | 0.061 ± 0.001 |
| te (min) | 1800 | 2460 | 360 | 900 |
| Pseudo-first order (PFO) | ||||
| qe,est (mmol g−1) | 0.82 ± 0.05 | 0.74 ± 0.03 | 0.135 ± 0.003 | 0.062 ± 0.004 |
| k1 (min−1) | (9 ± 2) × 10−3 | (1.1 ± 0.2) × 10−2 | (2.15 ± 0.04) × 10−1 | (8 ± 1) × 10−3 |
| R2 | 0.812 | 0.748 | 0.558 | 0.961 |
| R2adj | 0.799 | 0.736 | 0.469 | 0.954 |
| χ2red | 2.4 × 10−2 | 2.1 × 10−2 | 3.0 × 10−4 | 9.0 × 10−4 |
| Pseudo-second order (PSO) | ||||
| qe,est (mmol g−1) | 0.93 ± 0.05 | 0.79 ± 0.03 | 0.138 ± 0.002 | 0.069 ± 0.007 |
| k2 (g mmol−1min−1) | (1.3 ± 0.3) × 10−2 | (2.4 ± 0.5) × 10−2 | 4.1 ± 0.9 | 0.11 ± 0.04 |
| R2 | 0.911 | 0.881 | 0.850 | 0.931 |
| R2adj | 0.905 | 0.875 | 0.820 | 0.918 |
| χ2red | 1.1 × 10−2 | 1.0 × 10−2 | 9.0 × 10−5 | 1.6 × 10−3 |
| Elovich | ||||
| t0 (min) | 21 ± 5 | 13 ± 5 | (2.78 ± 0.00) ×10−14 | (8.64 ± 0.00) × 10−13 |
| α (mmol g−1min−1) | (1.8 ± 0.3) × 10−2 | (3.78 ± 0.73) × 10−2 | (8.3 ± 0.3) ×10−8 | (1.1 ± 0.3) × 10−3 |
| β (g mmol−1) | 5.2 ± 0.2 | 7.6 ± 0.3 | (23 ± 3) × 101 | (7 ± 1) × 101 |
| R2 | 0.994 | 0.992 | 0.933 | 0.913 |
| R2adj | 0.993 | 0.991 | 0.899 | 0.869 |
| χ2red | 8.0 × 10−4 | 7.0 × 10−4 | 5.0 × 10−5 | 2.5 × 10−3 |
| Intraparticle diffusion (IPD) | ||||
| Step 1 | ||||
| kd,1 (mmol g−1 min−1/2) | (2.9 ± 0.2) × 10−2 | (2.7 ± 0.1) × 10−2 | (1.6 ± 0.3) × 10−3 | (5.5 ± 0.8) × 10−3 |
| C (mmol g−1) | (1.6 ± 0.3) × 10−1 | (1.7 ± 0.1) × 10−1 | (1.2 ± 0.0) × 10−1 | −(2.0 ± 0.8) × 10−2 |
| R2 | 0.975 | 0.991 | 0.944 | 0.960 |
| R2adj | 0.969 | 0.989 | 0.916 | 0.939 |
| Step 2 | ||||
| kd,2 (mmol g−1 min−1/2) | (1.3 ± 0.0) × 10−2 | (6.8 ± 0.3) × 10−3 | - | - |
| C | (4.6 ± 0.1) × 10−1 | (5.2 ± 0.1) × 10−1 | - | - |
| R2 | 0.994 | 0.979 | ||
| R2adj | 0.992 | 0.977 | - | - |
| Boyd plot | ||||
| B | (1.9 ± 0.1) × 10−3 | (2.4 ± 0.1) × 10−3 | (9 ± 1) × 10−3 | (9.2 ± 0.7) × 10−4 |
| Di (m2 min−1) | 1.17 × 10−11 | 1.50 × 10−11 | 6.00 × 10−11 | 5.84 × 10−11 |
| Parameter | AO | ST |
|---|---|---|
| qe,exp (mmol g−1) | 0.672 ± 0.006 | 1.242 ± 0.004 |
| te (min) | 1980 | 2160 |
| Pseudo-first order (PFO) | ||
| qe,est (mmol g−1) | 0.55 ± 0.03 | 1.05 ± 0.03 |
| k1 (min−1) | 0.013 ± 0.003 | 0.07 ± 0.01 |
| R2 | 0.760 | 0.567 |
| R2adj | 0.748 | 0.545 |
| χ2red | 0.019 | 0.014 |
| Pseudo-second order (PSO) | ||
| qe,est (mmol g−1) | 0.59 ± 0.02 | 1.09 ± 0.02 |
| k2 (g mmol−1 min−1) | 0.028 ± 0.006 | 0.09 ± 0.02 |
| R2 | 0.873 | 0.752 |
| R2adj | 0.866 | 0.739 |
| χ2red | 0.010 | 0.008 |
| Corsel | ||
| α | 0.170 | 6.668 |
| β | 0.529 | 1.954 |
| γ (α + β) | 0.700 | 8.622 |
| γi − γj | −7.921 | |
| Γmax (mmol m−2) | 0.125 | 0.195 |
| k+1 (L mmol−1 min−1) | 74.3 | 710 |
| k−1 (min−1) | 8.938 | 8.209 |
| K = k+1/k−1 (L mmol−1) | 8.314 | 86.5 |
| Ds (m2 min−1) | 1.17 × 10−11 | 1.50 × 10−11 |
| R2 | 0.300 | 0.315 |
| χ2red | 0.010 | 0.003 |
| Parameter | HDSB | SB | ||
|---|---|---|---|---|
| AO | ST | AO | ST | |
| Qmax,exp (mmol g−1) | 1.362 ± 0.009 | 0.929 ± 0.003 | 0.1042 ± 0.0009 | 0.074 ± 0.002 |
| Ie (mol L−1) | 0.1507 | 0.1507 | - | - |
| γe | 0.7593 | 0.7593 | - | - |
| Langmuir | ||||
| Qmax,est (mmol g−1) | 1.72 ± 0.03 | 0.93 ± 0.03 | 0.21 ± 0.03 | 0.085 ± 0.004 |
| b (L mmol−1) | 8.3 ± 0.4 | 65 ± 8 | 2.3 ± 0.5 | 20 ± 2 |
| Keq | 10,944 ± 593 | 85,062 ± 9996 | - | - |
| R2 | 0.9950 | 0.9950 | 0.9752 | 0.9857 |
| R2adj | 0.9947 | 0.9708 | 0.9734 | 0.9845 |
| χ2red | 0.0017 | 0.0048 | 0.0007 | 0.0003 |
| RSS | 0.0273 | 0.0533 | 0.0100 | 0.0043 |
| Sips | ||||
| Qmax,est (mmol g−1) | 1.64 ± 0.06 | 0.88 ± 0.03 | 0.15 ± 0.08 | 0.096 ± 0.009 |
| b (L mmol−1) | 9.4 ± 0.9 | 76 ± 8 | 3 ± 3 | 14 ± 4 |
| n | 0.93 ± 0.05 | 0.8 ± 0.1 | 1.0 ± 0.2 | 1.2 ± 0.1 |
| R2 | 0.9959 | 0.9785 | 0.9411 | 0.9893 |
| R2adj | 0.9953 | 0.9741 | 0.9321 | 0.9874 |
| χ2red | 0.0016 | 0.0043 | 0.0018 | 0.0003 |
| RSS | 0.0243 | 0.0779 | 0.0040 | 0.0032 |
| Redlich–Peterson (R-P) | ||||
| KR (L g−1) | 14 ± 1 | 60 ± 9 | 0.4 ± 0.1 | 1.9 ± 0.3 |
| aR (L mmol−1) | 8.3 ± 0.6 | 65 ± 9 | 1.4 ± 0.6 | 21 ± 3 |
| Qmax,est (mmol g−1) | 1.7 ± 0.2 | 0.9 ± 0.2 | 0.3 ± 0.1 | 0.09 ± 0.02 |
| β | 1.00 ± 0.06 | 1.00 ± 0.04 | 1.0 ± 0.9 | 0.92 ± 0.07 |
| R2 | 0.9953 | 0.9732 | 0.9692 | 0.9871 |
| R2adj | 0.9946 | 0.9679 | 0.964 | 0.9843 |
| χ2red | 0.0019 | 0.0018 | 0.0095 | 0.0004 |
| RSS | 0.0279 | 0.0533 | 0.0024 | 0.0018 |
| Dubinin–Radushkevich (D-R) | ||||
| Qmax,est (mmol g−1) | 1.61 ± 0.02 | 1.01 ± 0.05 | 0.12 ± 0.01 | 0.088 ± 0.003 |
| k (mmol2 kJ−2) | 0.0202 ± 0.0005 | 0.0079 ± 0.0008 | 0.0284 ± 0.003 | 0.0133 ± 0.0006 |
| R2 | 0.9949 | 0.9383 | 0.9328 | 0.9867 |
| R2adj | 0.9945 | 0.9326 | 0.9280 | 0.9870 |
| χ2red | 0.0019 | 0.0112 | 0.0019 | 0.0003 |
| RSS | 0.0304 | 0.1231 | 0.0273 | 0.0040 |
| Type of Dye | Model-Isotherm | RSS | χ2red | R2 |
|---|---|---|---|---|
| AO | IAST-Langmuir | 0.122 | 0.013 | 0.777 |
| RAST-Sips | 0.012 | 0.003 | 0.964 | |
| RAST-Langmuir | 0.022 | 0.004 | 0.959 | |
| ST | IAST-Langmuir | 0.019 | 0.003 | 0.910 |
| RAST-Sips | 0.017 | 0.002 | 0.920 | |
| RAST-Langmuir | 0.018 | 0.002 | 0.913 |
| Dye | Desorption Time (min) 1 | ||
|---|---|---|---|
| 60 | 180 | 360 | |
| AO | 32.3 ± 0.9 | 38.6 ± 0.2 | 42.8 ± 0.2 |
| ST | 40 ± 1 | 51 ± 1 | 54 ± 2 |
| Dye | qe,initial (mmol g−1) | qe,re-adsorbed (mmol g−1) | Ere-ad (%) |
|---|---|---|---|
| AO | 0.97 ± 0.01 | 0.96 ± 0.08 | 99 |
| ST | 0.71 ± 0.02 | 0.55 ± 0.07 | 77 |
| Parameter | Type of Single Adsorption Experiment | Type of Binary Adsorption Experiment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Adsorbent Dosage | Solution pH | Contact Time | Initial Dye Concentration | Solution pH | Contact Time | Initial Dye Concentration | |||
| AO or ST | AO or ST | AO | ST | AO | ST | AO-ST | |||
| Initial pH | 7.00 | 3.13–7.14 2 | 7.00 | 7.00 | 7.00 | 7.00 | 3.13–7.14 2 | 7.00 | 7.00 |
| Weight of HDSB (g) | 0.0100–0.0800 (±0.0001) | 0.0200 (±0.0001) | 0.0200 (±0.0001) | ||||||
| Dye concentration (mmol L−1) | 0.374 | 0.037–0.845 | 0.033–0.834 | 0.374 1 | 0.037–0.894 (AO)/0.045–1.085 (ST) 1 | ||||
| Agitation time (min) | 1440 | 1440 | 10–2160 | 10–2760 | 1800 | 2460 | 1440 | 10–2700 | 2280 |
| Parameter | Dye | |
|---|---|---|
| AO | ST | |
| Initial dye concentration in the syringe (mg L−1) | 282.2 | 336.9 |
| Solution pH 1 | 7.00 | |
| Temperature (°C) | 25.0000 ± 0.0001 | |
| Agitation speed (rpm) | 180 | |
| Initial volume of buffer in the calorimetric cells (mL) | 2.70 ± 0.01 | |
| Weight of HDSB in the sample calorimetric cell (g) | 0.00800 ± 0.00001 | |
| Injection volume (µL) | 40 | |
| Interval of time between two consecutive injections (min) | 35 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elias Carvalho, M.M.C.; Soares, L.C.; Adarme, O.F.H.; Ferreira, G.M.D.; Savedra, R.M.L.; Siqueira, M.F.; Azevedo, E.R.d.; Gurgel, L.V.A. Hetero-Disubstituted Sugarcane Bagasse as an Efficient Bioadsorbent for Cationic Dyes. Molecules 2025, 30, 3163. https://doi.org/10.3390/molecules30153163
Elias Carvalho MMC, Soares LC, Adarme OFH, Ferreira GMD, Savedra RML, Siqueira MF, Azevedo ERd, Gurgel LVA. Hetero-Disubstituted Sugarcane Bagasse as an Efficient Bioadsorbent for Cationic Dyes. Molecules. 2025; 30(15):3163. https://doi.org/10.3390/molecules30153163
Chicago/Turabian StyleElias Carvalho, Megg Madonyk Cota, Liliane Catone Soares, Oscar Fernando Herrera Adarme, Gabriel Max Dias Ferreira, Ranylson Marcello Leal Savedra, Melissa Fabíola Siqueira, Eduardo Ribeiro de Azevedo, and Leandro Vinícius Alves Gurgel. 2025. "Hetero-Disubstituted Sugarcane Bagasse as an Efficient Bioadsorbent for Cationic Dyes" Molecules 30, no. 15: 3163. https://doi.org/10.3390/molecules30153163
APA StyleElias Carvalho, M. M. C., Soares, L. C., Adarme, O. F. H., Ferreira, G. M. D., Savedra, R. M. L., Siqueira, M. F., Azevedo, E. R. d., & Gurgel, L. V. A. (2025). Hetero-Disubstituted Sugarcane Bagasse as an Efficient Bioadsorbent for Cationic Dyes. Molecules, 30(15), 3163. https://doi.org/10.3390/molecules30153163










