Investigation of the Adsorption and Reactions of Methyl Radicals on Transition Metal (M = Co, Ni, Pd, Pt) (111) Surfaces in Aqueous Suspensions
Abstract
1. Introduction
2. Result Analysis
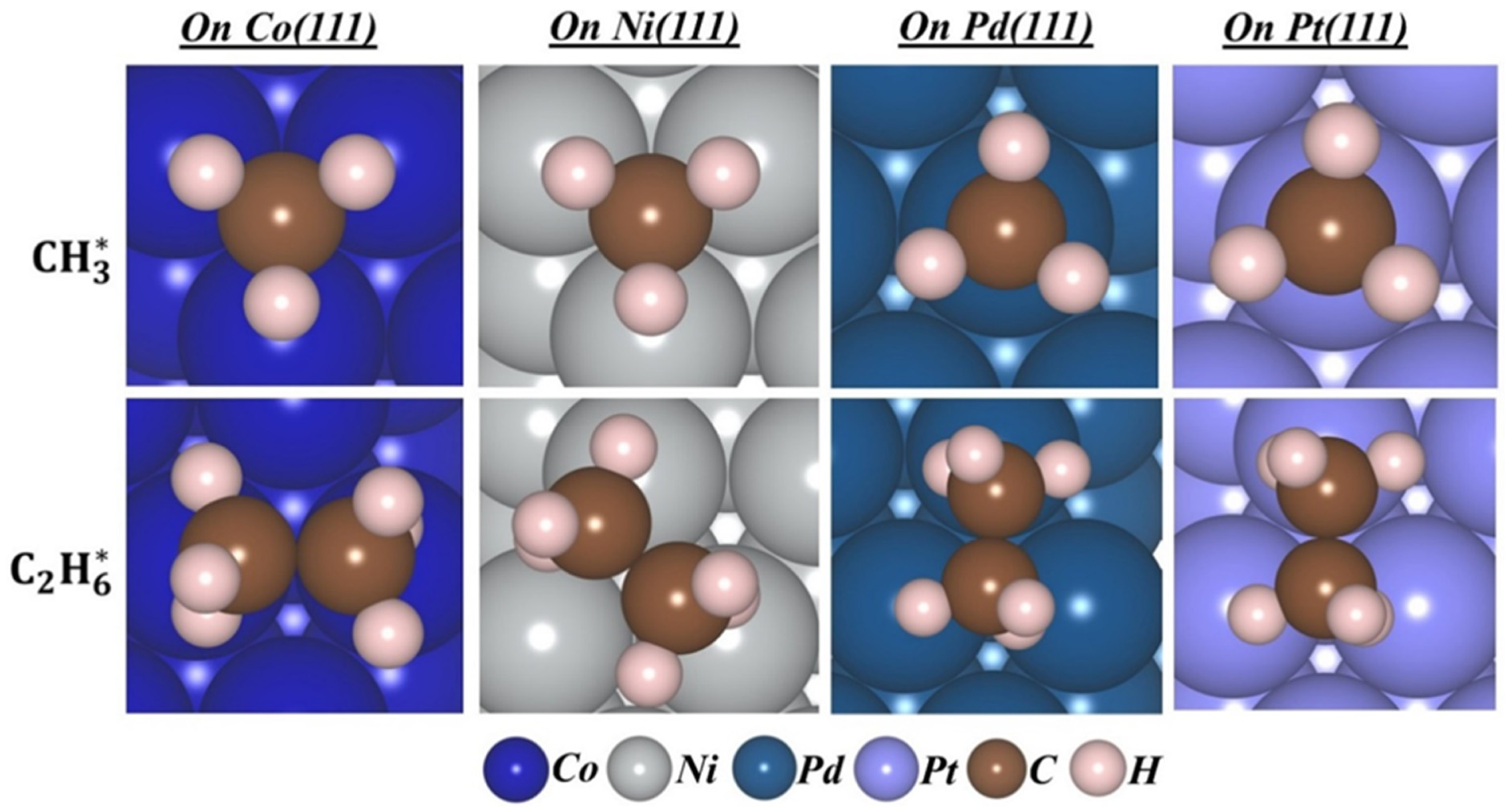
2.1. The Adsorption of Methyl Radicals on M(111) Surfaces
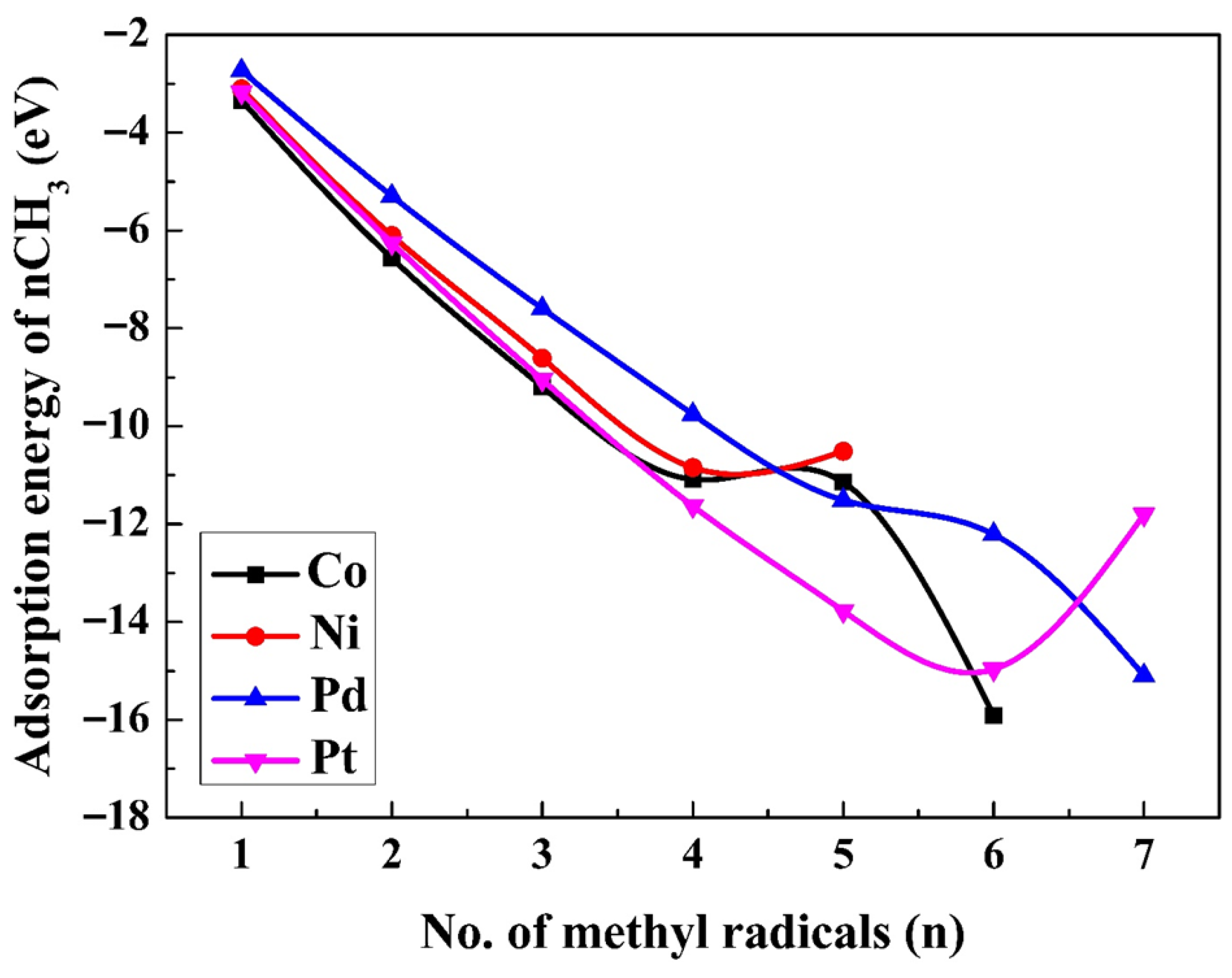
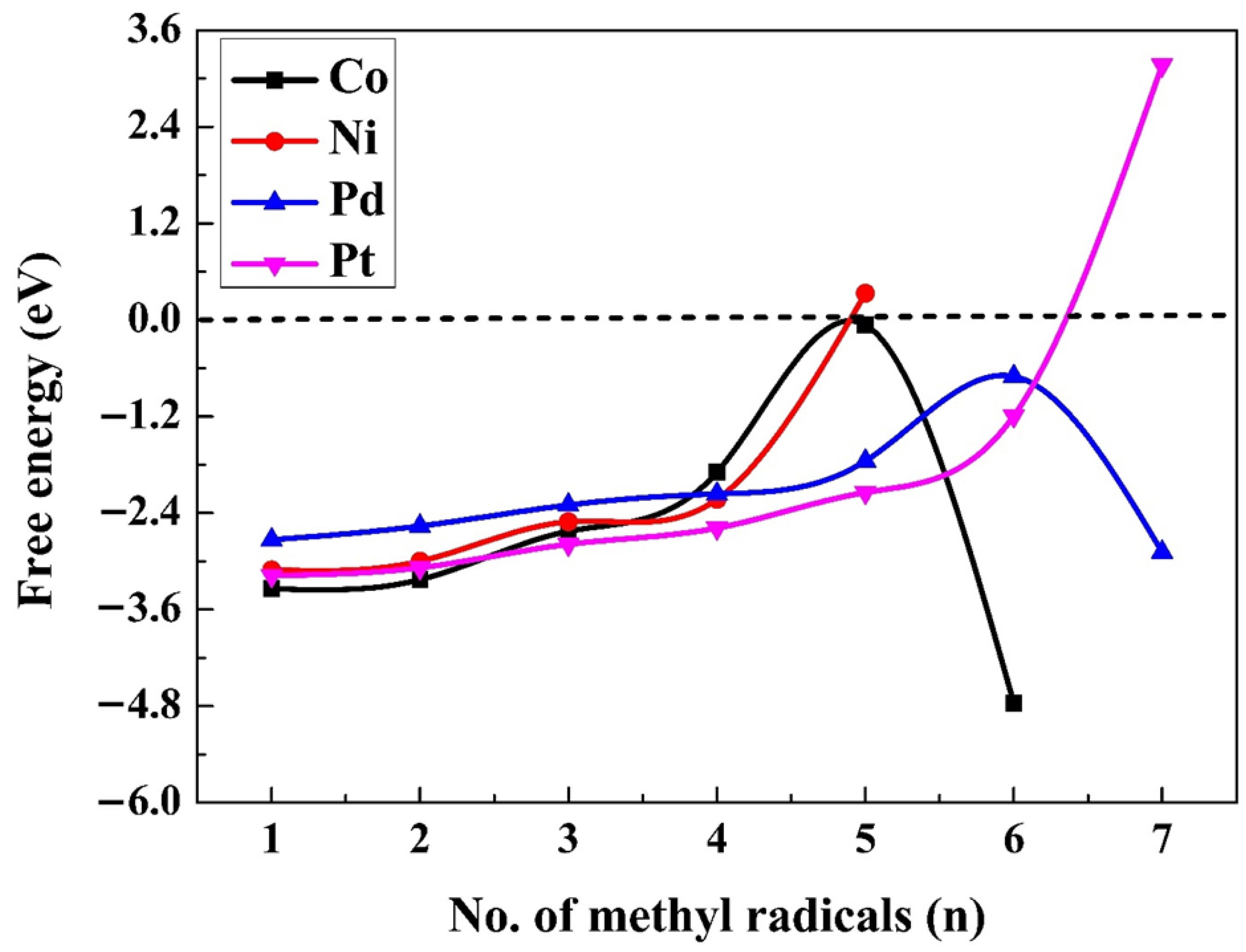
2.2. Adsorption of Methyl Radicals at Higher Coverage
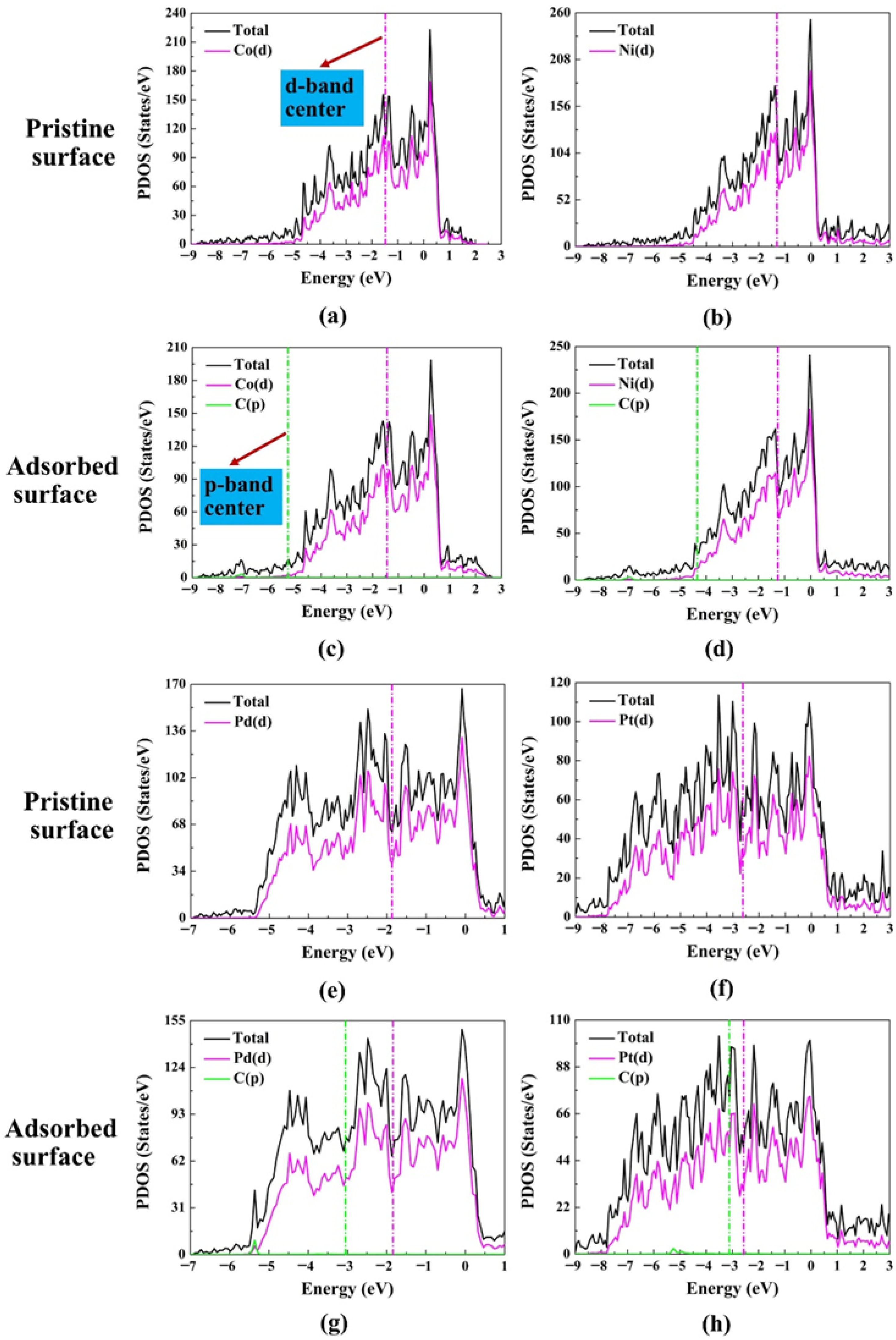
2.3. Projected Density of States
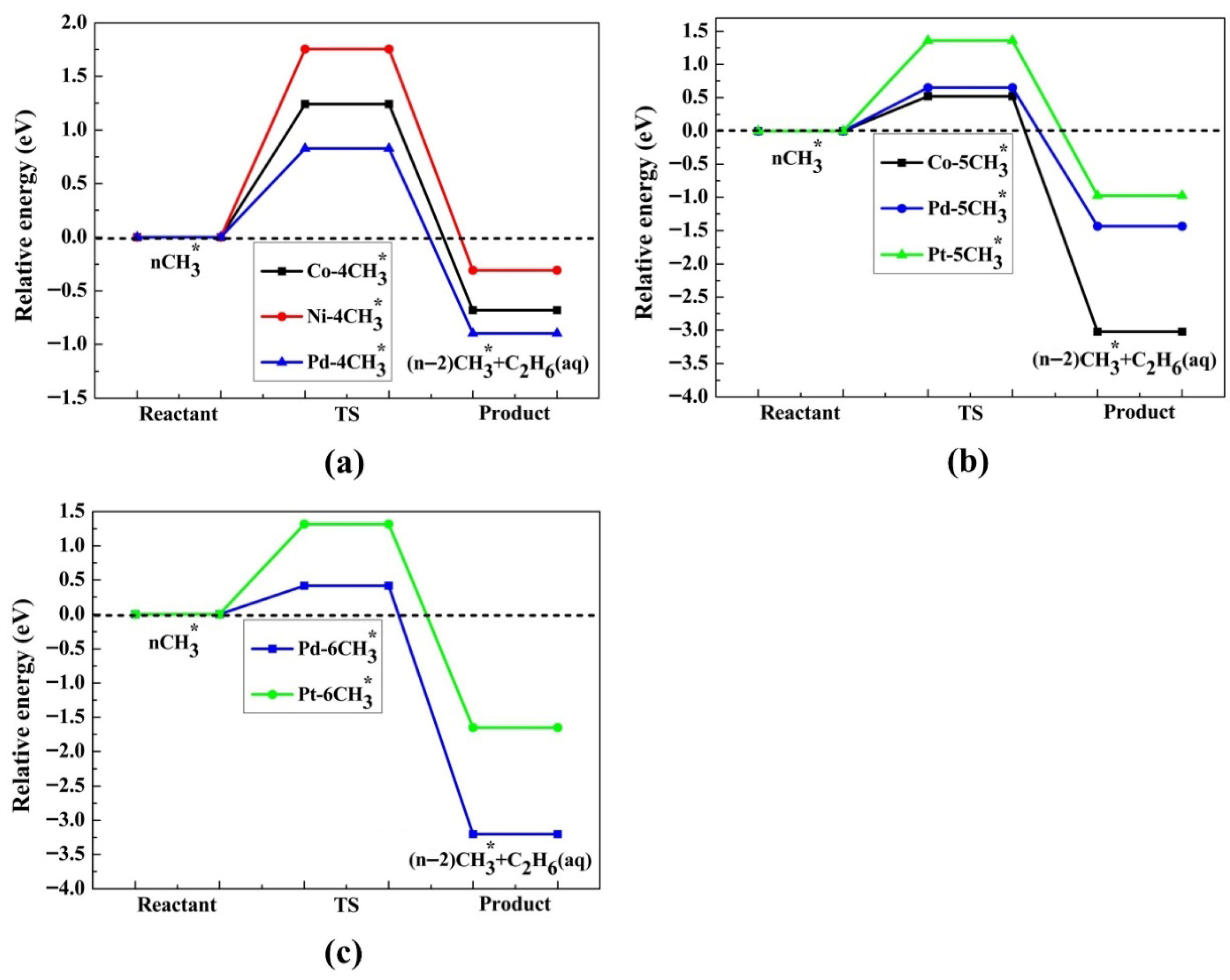
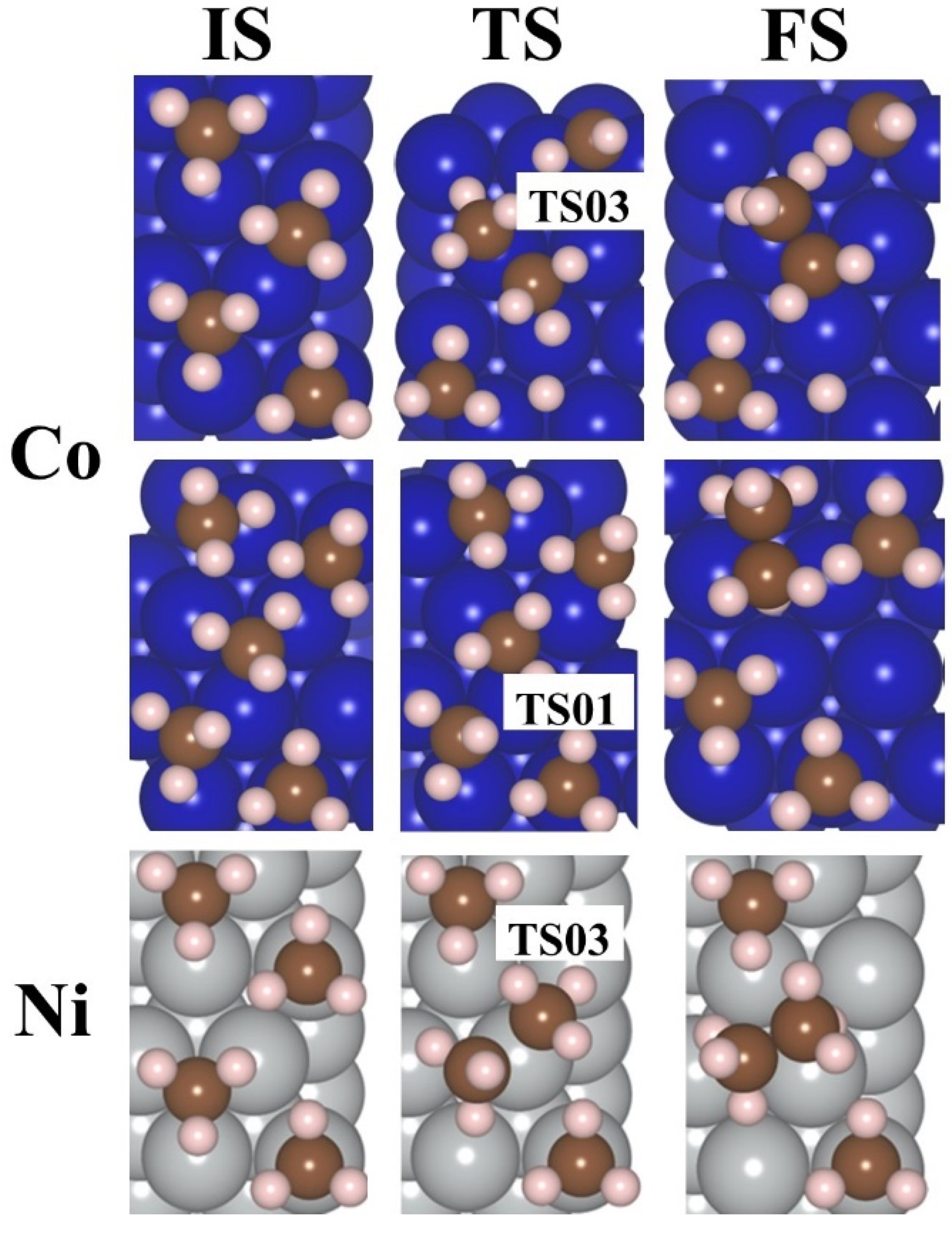
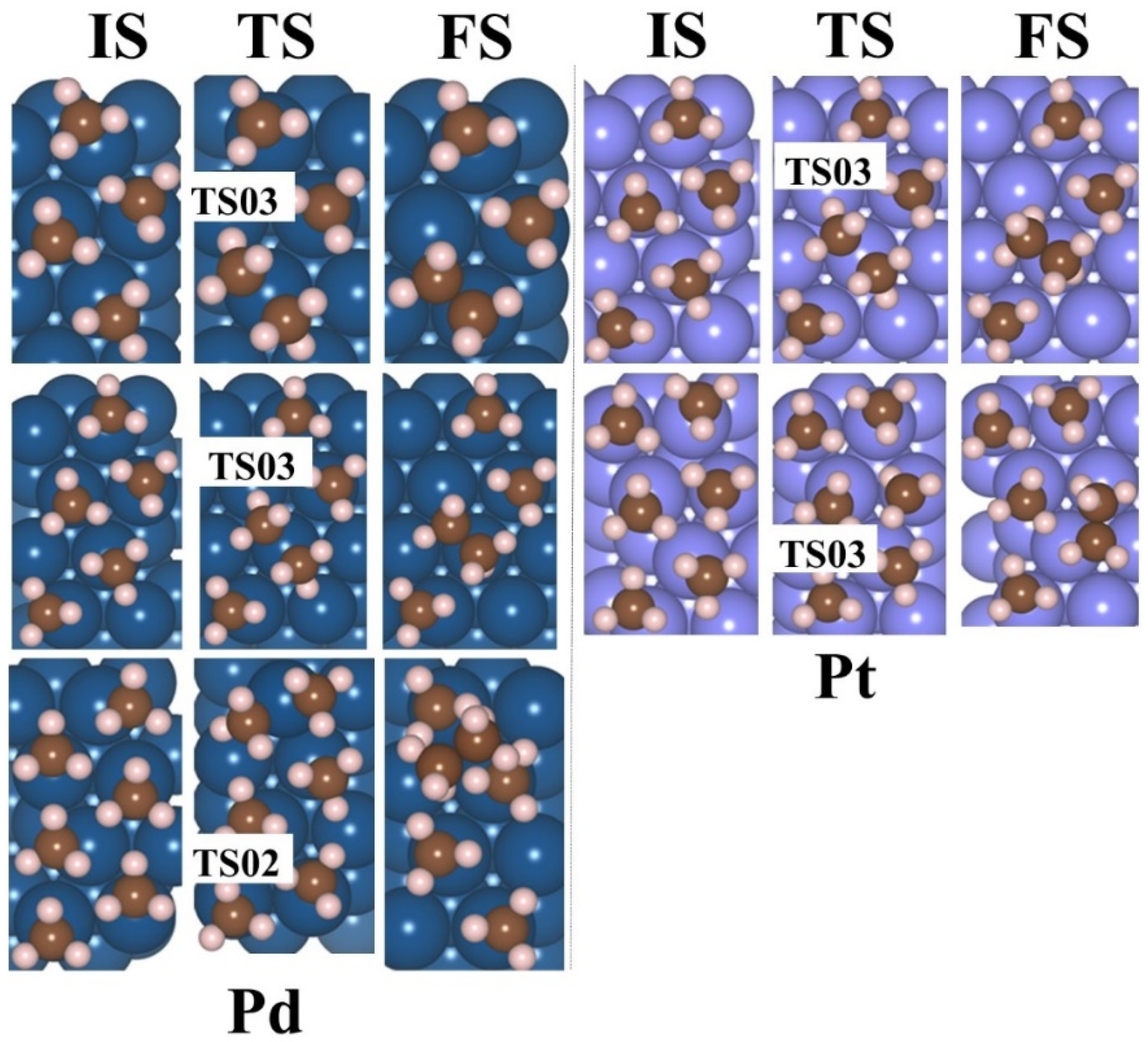
2.4. Production of Ethane via the LH Mechanism—A Reaction of Two out of n Adsorbed Radicals
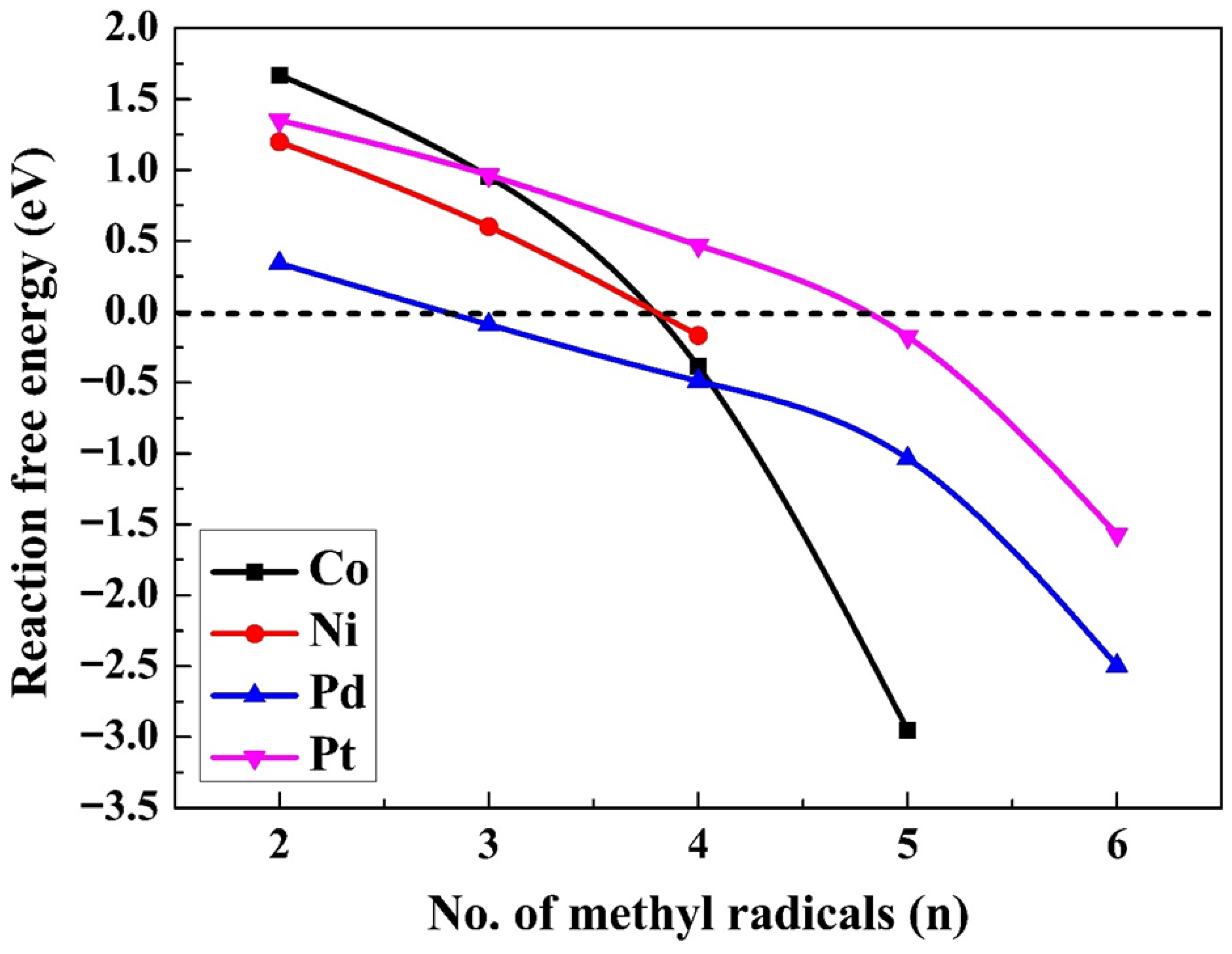
2.5. Ethane Production via the RE Mechanism—Reaction Between One Adsorbed Methyl Radical and Another One in Solution
2.6. Formation of Methanol (CH3OH) on M(111) Surfaces
2.7. The Diffusion of Adsorbed CH2 and CH3 on M(111) Surfaces
3. Computational Methods
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gomberg, M. Triphenylmethyl, Ein Fall von Dreiwerthigem Kohlenstoff. Berichte Dtsch. Chem. Ges. 1900, 33, 3150–3163. [Google Scholar] [CrossRef]
- Gansäuer, A.; Bluhm, H. Reagent-Controlled Transition-Metal-Catalyzed Radical Reactions. Chem. Rev. 2000, 100, 2771–2788. [Google Scholar] [CrossRef] [PubMed]
- Easton, C.J. Free-Radical Reactions in the Synthesis of α-Amino Acids and Derivatives. Chem. Rev. 1997, 97, 53–82. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Van Der Donk, W.A.; Liu, W. Radical-Mediated Enzymatic Methylation: A Tale of Two SAMS. Acc. Chem. Res. 2012, 45, 555–564. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, E.J.; Kümmerle, A.E.; Fraga, C.A. The Methylation Effect in Medicinal Chemistry. Chem. Rev. 2011, 111, 5215–5246. [Google Scholar] [CrossRef] [PubMed]
- Feng, B.; Yang, Y.; You, J. A Methylation Platform of Unconventional Inert Aryl Electrophiles: Trimethylboroxine as a Universal Methylating Reagent. Chem. Sci. 2020, 11, 6031–6035. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y. Recent Advances in Methylation: A Guide for Selecting Methylation Reagents. Chem. A Eur. J. 2019, 25, 3405–3439. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Chen, Z.; Wu, J. Recent Progress in Methyl-Radical-Mediated Methylation or Demethylation Reactions. ACS Catal. 2021, 11, 10713–10732. [Google Scholar] [CrossRef]
- Kolb, D.M. Electrochemical Surface Science. Angew. Chem. Int. Ed. 2001, 40, 1162–1181. [Google Scholar] [CrossRef]
- Hou, Z.-W.; Xu, H.-C.; Wang, L. Electrochemical Generation and Utilization of Radical Intermediates. Curr. Opin. Electrochem. 2024, 44, 101447. [Google Scholar] [CrossRef]
- Zeng, X. The Strategies towards Electrochemical Generation of Aryl Radicals. Chem. A Eur. J. 2024, 30, e202402220. [Google Scholar] [CrossRef] [PubMed]
- Albo, Y.; Shandalov, E.; Hayoun, L.; Zilbermann, I.; Maimon, E.; Meyerstein, D. Homogeneous and Heterogeneous Electrocatalytic Reduction of Halo-Organic Compounds by (NiIILi)2+ (Li=Tetraaza-Macrocyclic Ligand) in Aqueous Solutions. Inorganica Chim. Acta 2017, 466, 502–509. [Google Scholar] [CrossRef]
- Nowotny, M.K.; Sheppard, L.R.; Bak, T.; Nowotny, J. Defect Chemistry of Titanium Dioxide. Application of Defect Engineering in Processing of TiO2-Based Photocatalysts. J. Phys. Chem. C 2008, 112, 5275–5300. [Google Scholar] [CrossRef]
- Quach, V.; Wojcieszak, R.; Ghazzal, M.N. Strong Metal-support Interactions in Photocatalysis: Fundamentals and Design Methods. ChemNanoMat 2023, 9, e202300329. [Google Scholar] [CrossRef]
- Bar-Ziv, R.; Zilbermann, I.; Oster-Golberg, O.; Zidki, T.; Yardeni, G.; Cohen, H.; Meyerstein, D. On the Lifetime of the Transients (NP)—(CH3) n (NP=Ag0, Au0, TiO2 Nanoparticles) Formed in the Reactions Between Methyl Radicals and Nanoparticles Suspended in Aqueous Solutions. Chem. A Eur. J. 2012, 18, 4699–4705. [Google Scholar] [CrossRef] [PubMed]
- Golberg-Oster, O.; Bar-Ziv, R.; Yardeni, G.; Zilbermann, I.; Meyerstein, D. On the Reactions of Methyl Radicals with TiO2 Nanoparticles and Granular Powders Immersed in Aqueous Solutions. Chem. A Eur. J. 2011, 17, 9226–9231. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Nosaka, Y. Mechanism of the OH Radical Generation in Photocatalysis with TiO2 of Different Crystalline Types. J. Phys. Chem. C 2014, 118, 10824–10832. [Google Scholar] [CrossRef]
- Nosaka, Y.; Komori, S.; Yawata, K.; Hirakawa, T.; Nosaka, A.Y. Photocatalytic OH Radical Formation in TiO2 Aqueous Suspension Studied by Several Detection Methods. Phys. Chem. Chem. Phys. 2003, 5, 4731–4735. [Google Scholar] [CrossRef]
- Kisch, H. Semiconductor Photocatalysis for Chemoselective Radical Coupling Reactions. Acc. Chem. Res. 2017, 50, 1002–1010. [Google Scholar] [CrossRef] [PubMed]
- Hori, M.; Goto, T. Progress of Radical Measurements in Plasmas for Semiconductor Processing. Plasma Sources Sci. Technol. 2006, 15, S74. [Google Scholar] [CrossRef]
- Zidki, T.; Bar-Ziv, R.; Green, U.; Cohen, H.; Meisel, D.; Meyerstein, D. The Effect of the Nano-Silica Support on the Catalytic Reduction of Water by Gold, Silver and Platinum Nanoparticles–Nanocomposite Reactivity. Phys. Chem. Chem. Phys. 2014, 16, 15422–15429. [Google Scholar] [CrossRef] [PubMed]
- Rostamikia, G.; Janik, M.J. First Principles Mechanistic Study of Borohydride Oxidation over the Pt (1 1 1) Surface. Electrochimica Acta 2010, 55, 1175–1183. [Google Scholar] [CrossRef]
- Akça, A.; Genç, A.; Kutlu, B. BH4 Dissociation on Various Metal (1 1 1) Surfaces: A DFT Study. Appl. Surf. Sci. 2019, 473, 681–692. [Google Scholar] [CrossRef]
- Raju Karimadom, B.; Varshney, S.; Zidki, T.; Meyerstein, D.; Kornweitz, H. DFT Study of the BH4− Hydrolysis on Au (111) Surface. ChemPhysChem 2022, 23, e202200069. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.; Baltrusaitis, J. Destruction of Emerging Organophosphate Contaminants in Wastewater Using the Heterogeneous Iron-Based Photo-Fenton-like Process. J. Hazard. Mater. Lett. 2021, 2, 100012. [Google Scholar] [CrossRef]
- Herney-Ramirez, J.; Vicente, M.A.; Madeira, L.M. Heterogeneous Photo-Fenton Oxidation with Pillared Clay-Based Catalysts for Wastewater Treatment: A Review. Appl. Catal. B Environ. 2010, 98, 10–26. [Google Scholar] [CrossRef]
- Miller, C.J.; Wadley, S.; Waite, T.D. Fenton, Photo-Fenton and Fenton-like Processes. In Advanced Oxidation Processes for Water Treatment: Fundamentals and Applications; IWA Publishing: London, UK, 2017; Volume 297. [Google Scholar]
- Steinfeld, J.I. Reactions of Photogenerated Free Radicals at Surfaces of Electronic Materials. Chem. Rev. 1989, 89, 1291–1301. [Google Scholar] [CrossRef]
- Rusonik, I.; Polat, H.; Cohen, H.; Meyerstein, D. Reaction of Methyl Radicals with Metal Powders Immersed in Aqueous Solutions. Eur. J. Inorg. Chem. 2003, 2003, 4227–4233. [Google Scholar] [CrossRef]
- Bar-Ziv, R.; Zilbermann, I.; Shandalov, M.; Shevchenko, V.; Meyerstein, D. Coating Platinum Nanoparticles with Methyl Radicals: Effects on Properties and Catalytic Implications. Chem. A Eur. J. 2015, 21, 19000–19009. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Maynard, K.; Johnson, A.; Ceyer, S. The Structure and Chemistry of CH3 and CH Radicals Adsorbed on Ni (111). J. Chem. Phys. 1995, 102, 7734–7749. [Google Scholar] [CrossRef]
- Toyoda, H.; Kojima, H.; Sugai, H. Mass Spectroscopic Investigation of the CH3 Radicals in a Methane Rf Discharge. Appl. Phys. Lett. 1989, 54, 1507–1509. [Google Scholar] [CrossRef]
- Gavin Jr, R.M.; Reutt, J.; Muetterties, E.L. Metal-Hydrogen Bridge Bonding of Hydrocarbons on Metal Surfaces. Proc. Natl. Acad. Sci. USA 1981, 78, 3981–3985. [Google Scholar] [CrossRef] [PubMed]
- Schüle, J.; Siegbahn, P.; Wahlgren, U. A Theoretical Study of Methyl Chemisorption on Ni (111). J. Chem. Phys. 1988, 89, 6982–6988. [Google Scholar] [CrossRef]
- Siegbahn, P.E.; Panas, I. A Theoretical Study of CHx Chemisorption on the Ni (100) and Ni (111) Surfaces. Surf. Sci. 1990, 240, 37–49. [Google Scholar] [CrossRef]
- Yang, H.; Whitten, J.L. Ab Initio Chemisorption Studies of Methyl on Nickel (111). J. Am. Chem. Soc. 1991, 113, 6442–6449. [Google Scholar] [CrossRef]
- Yang, H.; Whitten, J.L. Chemisorption of Atomic H and CHx Fragments on Ni (111). Surf. Sci. 1991, 255, 193–207. [Google Scholar] [CrossRef]
- De Koster, A.; Van Santen, R. Molecular Orbital Studies of the Adsorption of CH3, CH2, and CH on Rh (111) and Ni (111) Surfaces. J. Catal. 1991, 127, 141–166. [Google Scholar] [CrossRef]
- Burghgraef, H.; Jansen, A.; Van Santen, R. Electronic Structure Calculations and Dynamics of the Chemisorption of Methane on a Ni (111) Surface. Chem. Phys. 1993, 177, 407–420. [Google Scholar] [CrossRef]
- Brookhart, M.; Green, M.L. Carbon Hydrogen-Transition Metal Bonds. J. Organomet. Chem. 1983, 250, 395–408. [Google Scholar] [CrossRef]
- Bar-Ziv, R.; Zidki, T. The Effect of Negatively Charged Metallic Nanocatalysts on Their Reactions with Alkyl Radicals. J. Coord. Chem. 2018, 71, 1791–1798. [Google Scholar] [CrossRef]
- Zidki, T.; Cohen, H.; Meyerstein, D. Reactions of Alkyl-Radicals with Gold and Silver Nanoparticles in Aqueous Solutions. Phys. Chem. Chem. Phys. 2006, 8, 3552–3556. [Google Scholar] [CrossRef] [PubMed]
- Zidki, T.; Elisseev, A.; Cohen, H.; Meyerstein, D. Reactions of Methyl Radicals with Cu Nanoparticles in Aqueous Suspensions. In The Optimization of Composition, Structure and Properties of Metals, Oxides, Composites, Nano and Amorphous Materials; Russian Academy of Sciences: Moscow, Russia, 2014; pp. 259–276. [Google Scholar]
- Shaham, N.; Masarwa, A.; Matana, Y.; Cohen, H.; Meyerstein, D. Kinetics and Reaction Mechanisms of Complexes with Cobalt− Carbon σ Bonds of the Type {(NH3)5Co− R}N+ in Aqueous Solutions, a Pulse Radiolysis Study. Eur. J. Inorg. Chem. 2002, 2002, 87–92. [Google Scholar] [CrossRef]
- Kumar, P.; Meyerstein, D.; Mizrahi, A.; Kornweitz, H. Exploring the Adsorption and Reactions of Methyl Radicals on M (111) Surfaces (M=Cu, Ag, Au): A DFT Study. ChemPhysChem 2025, 26, e202400979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Density Functional Theory (DFT). Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.; Burke, K.; Ernzerhof, M. Perdew, Burke, and Ernzerhof Reply. Phys. Rev. Lett. 1998, 80, 891. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Mathew, K.; Kolluru, V.; Mula, S.; Steinmann, S.N.; Hennig, R.G. Implicit Self-Consistent Electrolyte Model in Plane-Wave Density-Functional Theory. J. Chem. Phys. 2019, 151, 234101. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A Three-Dimensional Visualization System for Electronic and Structural Analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory; Clarendon: Oxford, UK, 1990. [Google Scholar]
- Brandbyge, M.; Mozos, J.-L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-Functional Method for Nonequilibrium Electron Transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Brown, M.E.; Dollimore, D.; Galwey, A.K. Reactions in the Solid State; Elsevier: Amsterdam, The Netherlands, 1980; Volume 22, ISBN 0-08-086816-9. [Google Scholar]
- Grunze, M.; Brundle, C.; Tomanek, D. Adsorption and Decomposition of Ammonia on a W (110) Surface: Photoemission Fingerprinting and Interpretation of the Core Level Binding Energies Using the Equivalent Core Approximation. Surf. Sci. 1982, 119, 133–149. [Google Scholar] [CrossRef]
- Rao, C.N.R.; Rao, G.R. Nature of Nitrogen Adsorbed on Transition Metal Surfaces as Revealed by Electron Spectroscopy and Cognate Techniques. Surf. Sci. Rep. 1991, 13, 223–263. [Google Scholar] [CrossRef]
- Ruban, A.; Hammer, B.; Stoltze, P.; Skriver, H.L.; Nørskov, J.K. Surface Electronic Structure and Reactivity of Transition and Noble Metals. J. Mol. Catal. Chem. 1997, 115, 421–429. [Google Scholar] [CrossRef]
- Deubel, D.V. Theoretical Aspects of Transition Metal Catalysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; Volume 12, ISBN 3-540-23510-8. [Google Scholar]
- Cheng, H.; Reiser, D.B.; Mathias, P.M.; Baumert, K.; Dean Jr, S.W. Investigation of Nitriding Mechanism at Transition Metal Surfaces: NH3 Adsorption and Decomposition on Fe (100), Ni (100), and Cr (100). J. Phys. Chem. 1995, 99, 3715–3722. [Google Scholar] [CrossRef]
- Xin, H.; Vojvodic, A.; Voss, J.; Nørskov, J.K.; Abild-Pedersen, F. Effects of D-Band Shape on the Surface Reactivity of Transition-Metal Alloys. Phys. Rev. B 2014, 89, 115114. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Electronic Factors Determining the Reactivity of Metal Surfaces. Surf. Sci. 1995, 343, 211–220. [Google Scholar] [CrossRef]
- Hammer, B.; Norskov, J.K. Why Gold Is the Noblest of All the Metals. Nature 1995, 376, 238–240. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theoretical Surface Science and Catalysis—Calculations and Concepts. In Advances in Catalysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 45, pp. 71–129. ISBN 0360-0564. [Google Scholar]
- Gross, A. Theoretical Surface Science: A Microscopic Perspective; Originally published in the series: Advanced Texts in Physics; Springer: Berlin/Heidelberg, Germany, 2003; Volume 132. [Google Scholar]
- Nørskov, J.K.; Studt, F.; Abild-Pedersen, F.; Bligaard, T. Fundamental Concepts in Heterogeneous Catalysis; John Wiley and Sons: Hoboken, NJ, USA, 2014; ISBN 1-118-88895-2. [Google Scholar]
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
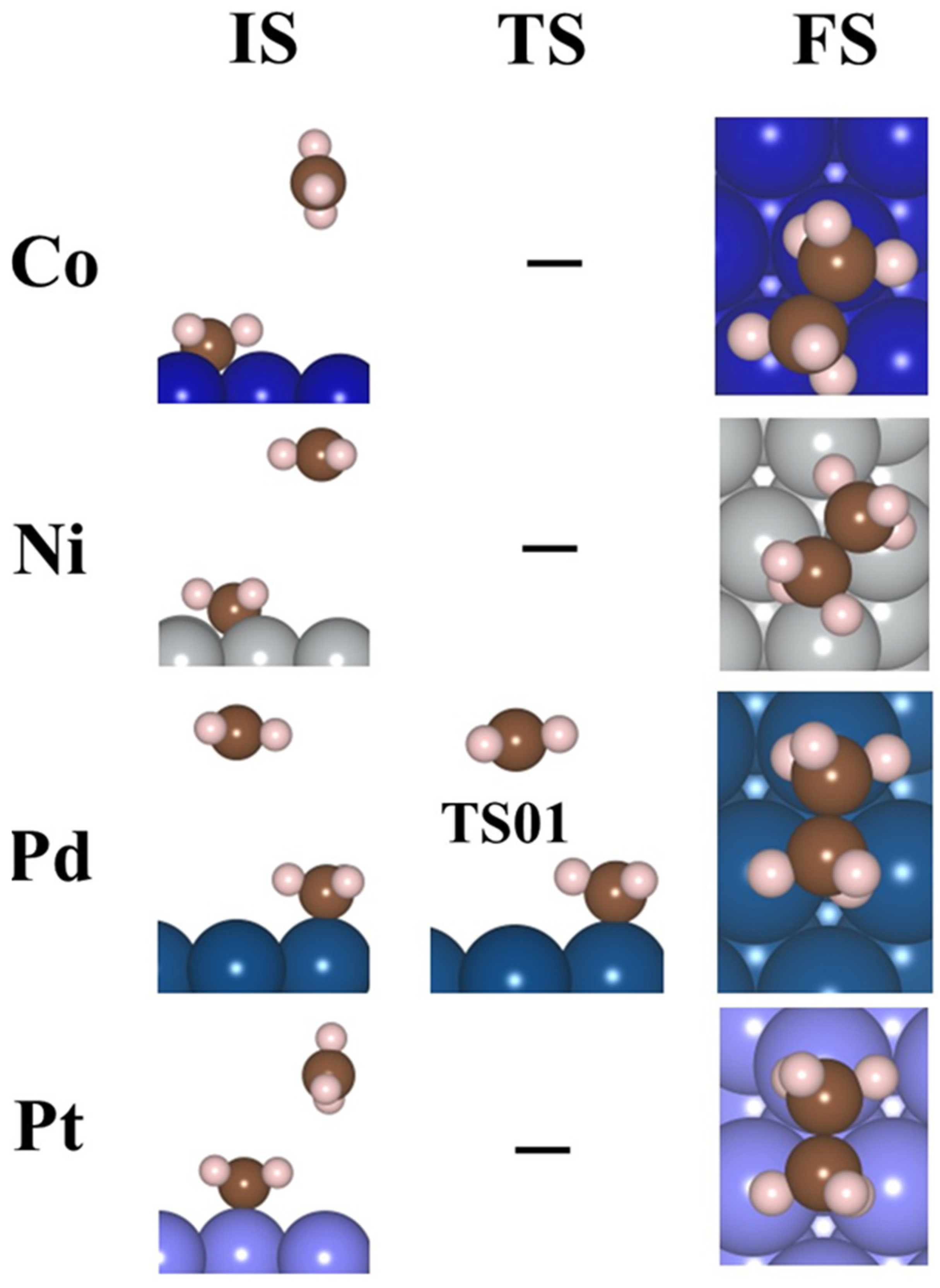
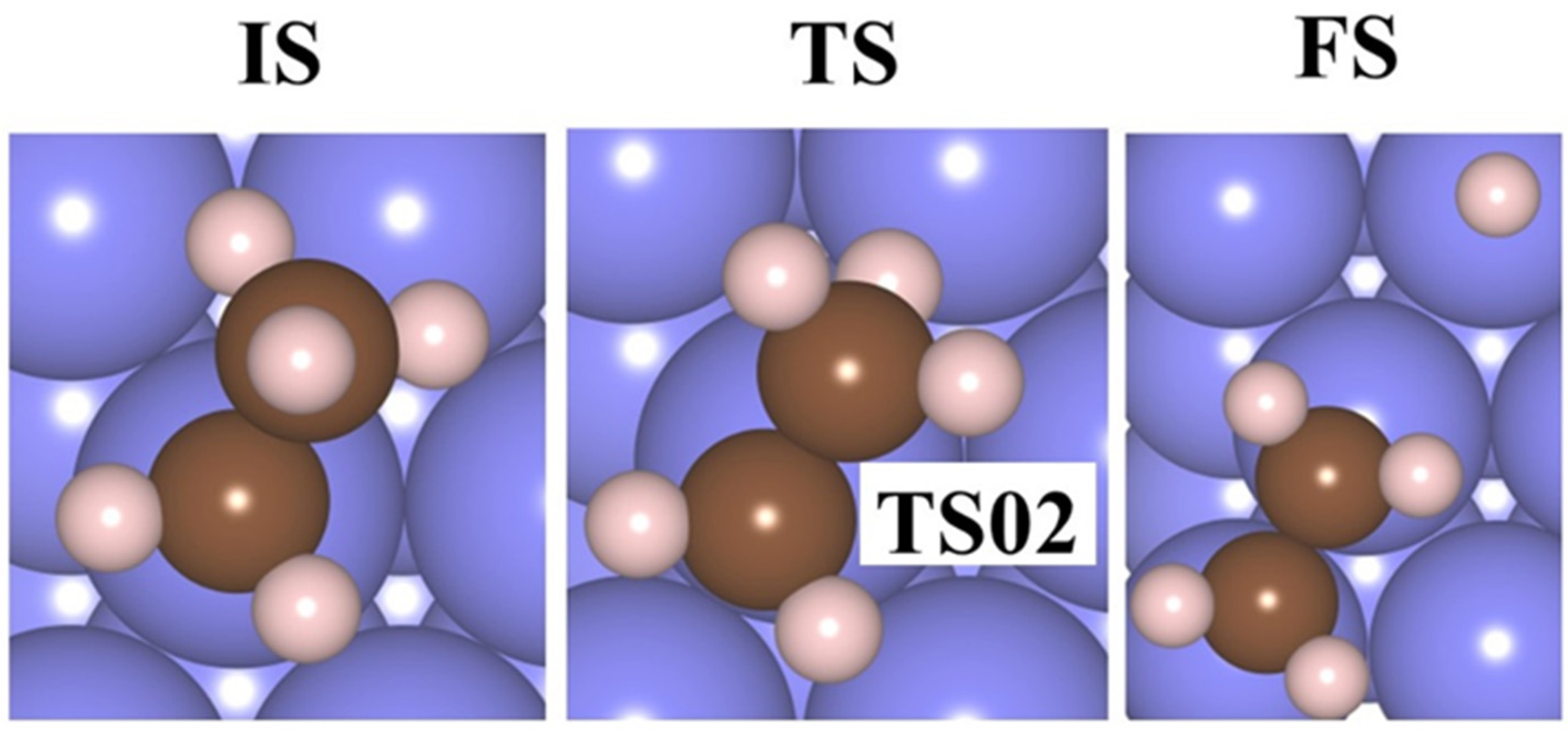
| Metals | Adsorbates | Adsorption Sites | Adsorption | Charge Transfer a (e) | M(111)-C Distance (Å) |
|---|---|---|---|---|---|
| Co | fcc | −3.34 | 0.40 | 2.03 | |
| bridge | −0.55 | 0.01 | 2.91 | ||
| Ni | fcc | −3.11 | 0.37 | 2.06 | |
| hcp | −0.75 | 0.03 | 3.16 | ||
| Pd | top | −2.73 | 0.07 | 2.03 | |
| hcp | −0.68 | −0.02 | 2.89 | ||
| Pt | top | −3.18 | 0.04 | 2.07 | |
| hcp | −0.69 | −0.04 | 3.08 |
| Metal Surfaces | pbc () (eV) | dbc-pbc (eV) | ||
|---|---|---|---|---|
| Pristine Surfaces | ||||
| Co(111) | −1.47 | −1.43 | −5.31 | 3.88 |
| Ni(111) | −1.30 | −1.28 | −4.33 | 3.05 |
| Pd(111) | −1.87 | −1.85 | −3.06 | 1.21 |
| Pt(111) | −2.62 | −2.59 | −3.09 | 0.50 |
| M(111) Surfaces | No. of Methyl Radicals Adsorb | C-C Bond (Å) in IS | C-C Bond (Å) in TS | ||
|---|---|---|---|---|---|
| Co | −0.39 | 1.24 | 3.46 | 1.85 | |
| Ni | −0.17 | 1.75 | 3.72 | 1.93 | |
| Pd | −0.49 | 0.83 | 3.21 | 2.01 | |
| Co | −2.95 | 0.52 | 3.21 | 3.15 | |
| Pd | −1.04 | 0.65 | 3.00 | 2.04 | |
| Pt | −0.18 | 1.36 | 3.05 | 1.93 | |
| Pd | −2.50 | 0.41 | 3.09 | 2.48 | |
| Pt | −1.57 | 1.32 | 3.09 | 3.03 |
| Reaction Numbers | Reactions | Co(111) (eV) | Ni(111) (eV) | Pd(111) (eV) | Pt(111) (eV) | ||||
|---|---|---|---|---|---|---|---|---|---|
| 8 | −2.11 | 0.56 | −2.36 | 0.16 | −2.86 | 0.21 | −2.72 | NB | |
| 9 | −2.93 | NB | −2.89 | NB | - | - | −2.69 | NB | |
| 10 | 0.82 | NC | 0.52 | NC | NC | NC | −0.03 | 1.60 | |
| 11 | 0.48 | NC | 0.13 | NC | NC | NC | −0.61 | 1.48 | |
| 12 | 0.67 | NC | 0.72 | NC | NC | NC | −0.13 | 1.36 | |
| Adsorbates on M(111) | Diffusion Barrier (Ea) (eV) | |||
|---|---|---|---|---|
| Co(111) | Ni(111) | Pd(111) | Pt(111) | |
| 0.48 | 0.46 | 1.03 | 0.67 | |
| 0.04 | 0.50 | 0.28 | 0.65 | |
| Processes | Rate Constants (k) (M−1 s−1) | |||
|---|---|---|---|---|
| Co(111) | Ni(111) | Pd(111) | Pt(111) | |
| Diffusion of | 6.19 × 103 | 1.68 × 104 | 3.15 × 10−6 | 4.18 |
| Diffusion of | 9.65 × 1011 | 3.07 × 103 | 2.25 × 107 | 1.26 × 101 |
| Reaction 7 () | 1.06 × 10−9 | 2.18 × 10−18 | 9.38 × 10−3 | NC |
| Reaction 7 (5) | 1.69 × 103 | NC | 1.03 × 101 | 1.06 × 10−11 |
| Reaction 7 (6) | NC | NC | 1.02 × 105 | 4.76 × 10−11 |
| Reaction 11 () | NC | NC | NC | 9.65 × 10−14 |
| Reaction 12 () | NC | NC | NC | 1.06 × 10−11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Meyerstein, D.; Mizrahi, A.; Kornweitz, H. Investigation of the Adsorption and Reactions of Methyl Radicals on Transition Metal (M = Co, Ni, Pd, Pt) (111) Surfaces in Aqueous Suspensions. Molecules 2025, 30, 3065. https://doi.org/10.3390/molecules30153065
Kumar P, Meyerstein D, Mizrahi A, Kornweitz H. Investigation of the Adsorption and Reactions of Methyl Radicals on Transition Metal (M = Co, Ni, Pd, Pt) (111) Surfaces in Aqueous Suspensions. Molecules. 2025; 30(15):3065. https://doi.org/10.3390/molecules30153065
Chicago/Turabian StyleKumar, Pankaj, Dan Meyerstein, Amir Mizrahi, and Haya Kornweitz. 2025. "Investigation of the Adsorption and Reactions of Methyl Radicals on Transition Metal (M = Co, Ni, Pd, Pt) (111) Surfaces in Aqueous Suspensions" Molecules 30, no. 15: 3065. https://doi.org/10.3390/molecules30153065
APA StyleKumar, P., Meyerstein, D., Mizrahi, A., & Kornweitz, H. (2025). Investigation of the Adsorption and Reactions of Methyl Radicals on Transition Metal (M = Co, Ni, Pd, Pt) (111) Surfaces in Aqueous Suspensions. Molecules, 30(15), 3065. https://doi.org/10.3390/molecules30153065







