The Role of Exchange Energy in Modeling Core-Electron Binding Energies of Strongly Polar Bonds
Abstract
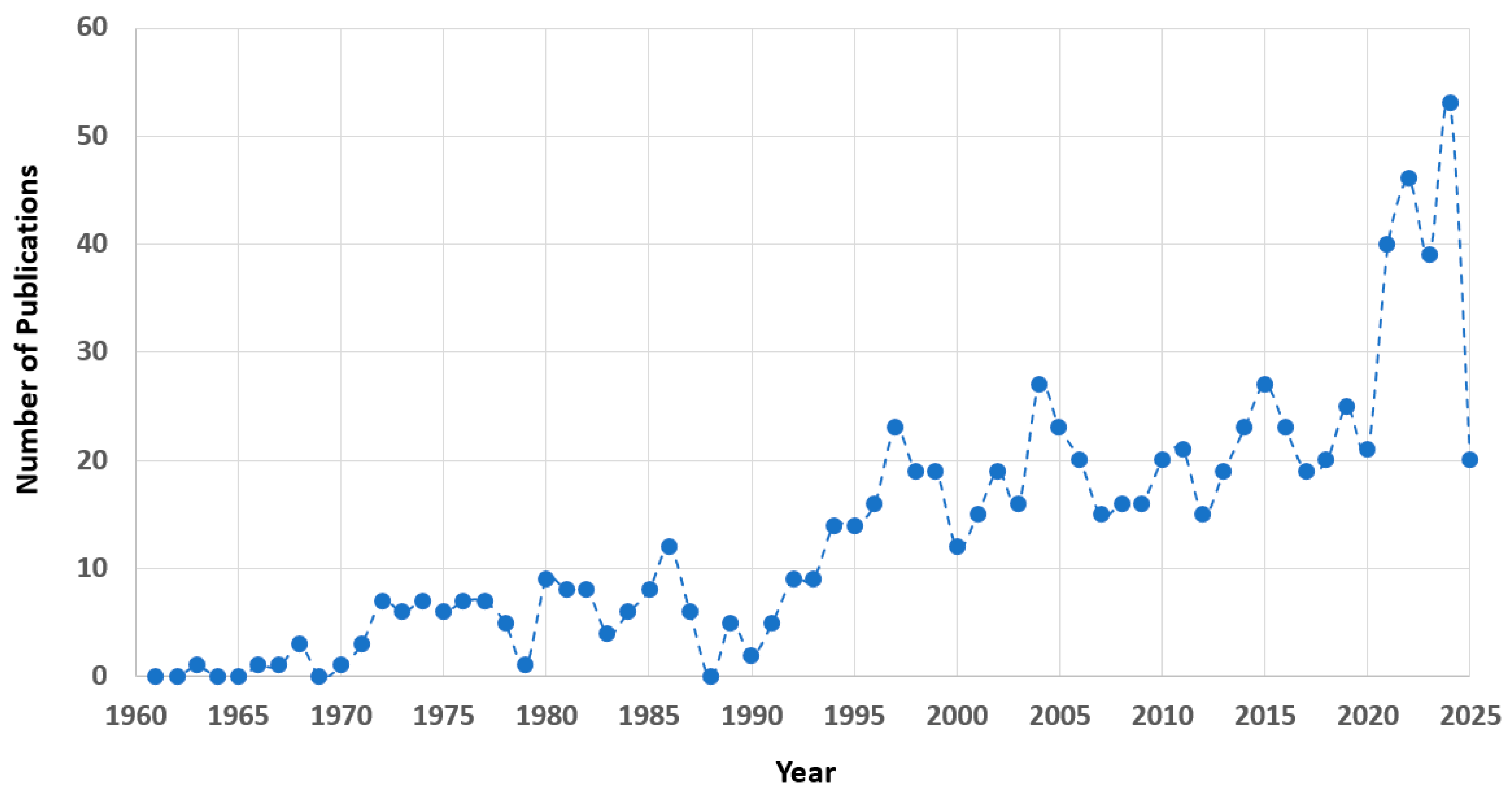
1. Introduction
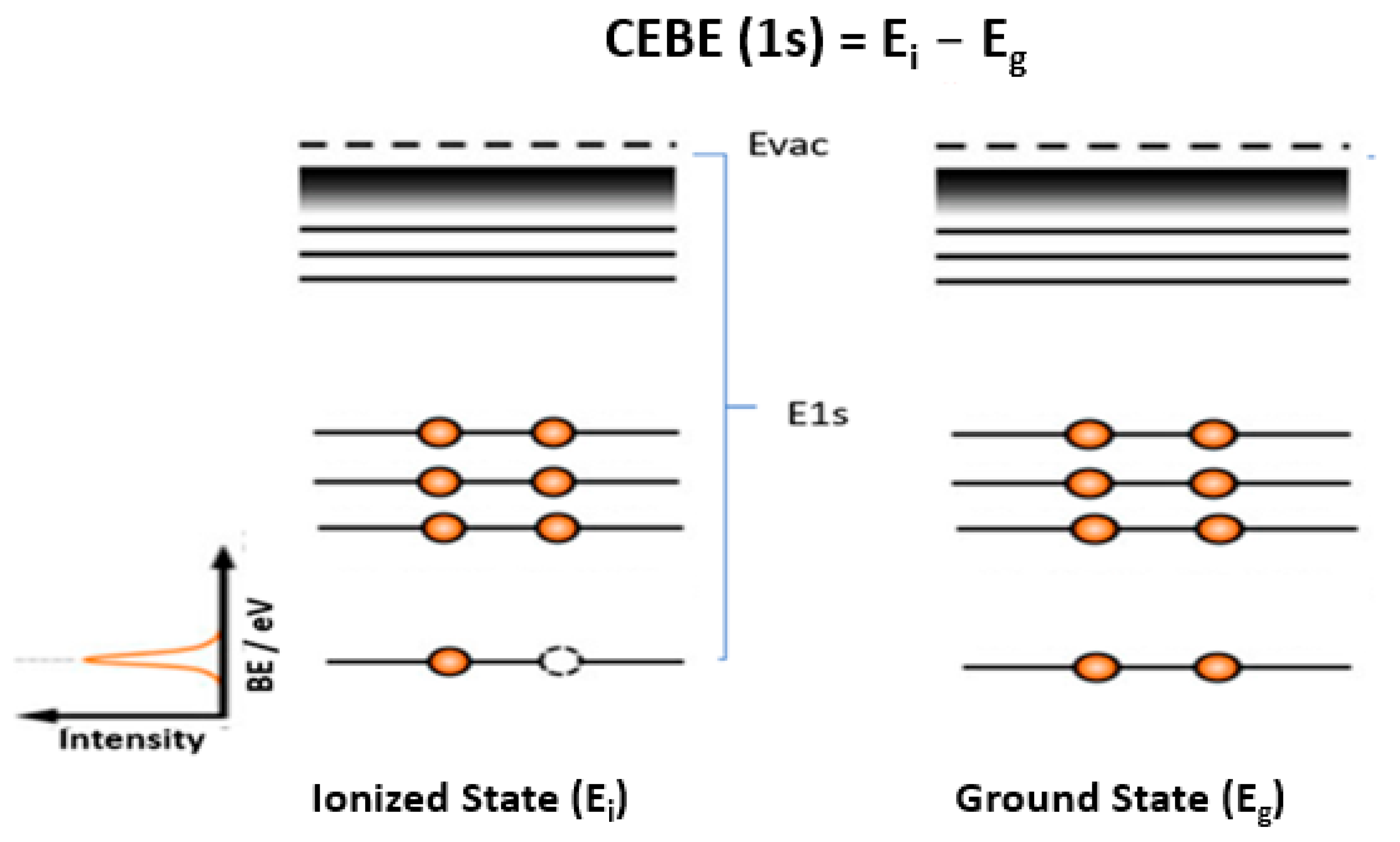
2. Core-Electron Binding Energy (CEBE) of Molecules
3. Development of CEBE Methods
4. Overview of DFT Methods for Accurate CEBEs
5. Computational Details
6. Materials and Methods
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F. Future of computational molecular spectroscopy—From supporting interpretation to leading the innovation. Phys. Chem. Chem. Phys. 2023, 25, 7090–7105. [Google Scholar] [CrossRef]
- Wang, F. Perspectives in Future Applications and Advancements of NMR Spectroscopy. Curr. Org. Chem. 2023, 27, 1563–1566. [Google Scholar] [CrossRef]
- Fahlman, A.; Hamrin, K.; Hedman, J.; Nordberg, R.; Nordling, C.; Siegbahn, K. Electron spectroscopy and chemical binding. Nature 1966, 210, 4–8. [Google Scholar] [CrossRef]
- Siegbahn, K. Electron spectroscopy for atoms, molecules, and condensed matter. Rev. Mod. Phys. 1982, 54, 709. [Google Scholar] [CrossRef]
- Gelius, U.; Heden, P.; Hedman, J.; Lindberg, B.; Manne, R.; Nordberg, R.; Nordling, C.; Siegbahn, K. Molecular spectroscopy by means of ESCA III. Carbon compounds. Phys. Scr. 1970, 2, 70. [Google Scholar] [CrossRef]
- Bagus, P.S.; Illas, F.; Pacchioni, G.; Parmigiani, F. Mechanisms responsible for chemical shifts of core-level binding energies and their relationship to chemical bonding. J. Electron Spectrosc. Relat. Phenom. 1999, 100, 215–236. [Google Scholar] [CrossRef]
- Ewald, P.; Pauling, L.; Robertson, J.; Hume-Rothery, W.; Wyckoff, R.; Lonsdale, K.; Siegbahn, M. 50 Years of X-Ray Diffraction. International Union of Crystallography. 1962. Available online: https://www.iucr.org/publ/50yearsofxraydiffraction (accessed on 23 February 2025).
- Besley, N.A. Modeling of the spectroscopy of core electrons with density functional theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1527. [Google Scholar] [CrossRef]
- Elettra. Gas Phase Beamline. Available online: https://www.elettra.eu/lightsources/elettra/elettra-beamlines/gas-phase (accessed on 11 April 2025).
- Zhu, Q.; Wang, F.; Ivanova, E.P. Impact of ketone and amino on the inner shell of guanine. J. Synchrotron Radiat. 2009, 16, 545–552. [Google Scholar] [CrossRef]
- Karlsen, T.; Børve, K.J.; Sæthre, L.J.; Wiesner, K.; Bässler, M.; Svensson, S. Toward the Spectrum of Free Polyethylene: Linear Alkanes Studied by Carbon 1s Photoelectron Spectroscopy and Theory. J. Am. Chem. Soc. 2002, 124, 7866–7873. [Google Scholar] [CrossRef]
- Ahmed, M.; Ganesan, A.; Wang, F.; Feyer, V.; Plekan, O.; Prince, K.C. Photoelectron spectra of some antibiotic building blocks: 2-azetidinone and thiazolidine-carboxylic acid. J. Phys. Chem. A 2012, 116, 8653–8660. [Google Scholar] [CrossRef]
- Wickrama Arachchilage, A.P.; Wang, F.; Feyer, V.; Plekan, O.; Prince, K.C. Photoelectron spectra and structures of three cyclic dipeptides: PhePhe, TyrPro, and HisGly. J. Chem. Phys. 2012, 136, 124301. [Google Scholar] [CrossRef]
- Iakhnenko, M.; Feyer, V.; Tsud, N.; Plekan, O.; Wang, F.; Ahmed, M.; Slobodyanyuk, O.V.; Acres, R.G.; Matolin, V.; Prince, K.C. Adsorption of cytosine and AZA derivatives of cytidine on Au single crystal surfaces. J. Phys. Chem. C 2013, 117, 18423–18433. [Google Scholar] [CrossRef]
- Wang, F.; Zhu, Q.; Ivanova, E.P. Inner-shell chemical shift of DNA/RNA bases and inheritance from their parent purine and pyrimidine. J. Synchrotron Radiat. 2008, 15, 624–631. [Google Scholar] [CrossRef]
- Saha, S.; Wang, F. NK spectra of adenine amino tautomers. In Journal of Physics: Conference Series, Proceedings of the 8th Asian International Seminar on Atomic and Molecular Physics, Perth, Australia, 24–28 November 2008; IOP Publishing: Bristol, UK, 2008; p. 12040. [Google Scholar]
- Aarva, A.; Deringer, V.L.; Sainio, S.; Laurila, T.; Caro, M.A. Understanding X-ray spectroscopy of carbonaceous materials by combining experiments, density functional theory, and machine learning. Part I: Fingerprint spectra. Chem. Mater. 2019, 31, 9243–9255. [Google Scholar] [CrossRef]
- Aarva, A.; Deringer, V.L.; Sainio, S.; Laurila, T.; Caro, M.A. Understanding X-ray Spectroscopy of Carbonaceous Materials by Combining Experiments, Density Functional Theory, and Machine Learning. Part II: Quantitative Fitting of Spectra. Chem. Mater. 2019, 31, 9256–9267. [Google Scholar] [CrossRef]
- Ohno, K.; Ishida, T.; Naitoh, Y.; Izumi, Y. Through-Space/Through-Bond Interactions on Electron. J. Am. Chem. Soc. 1985, 107, 8082–8086. [Google Scholar] [CrossRef]
- Yoneyama, K.; Noguchi, Y.; Ohno, K. All-electron first-principles GWΓ simulations for accurately predicting core-electron binding energies considering first-order three-point vertex corrections. J. Chem. Phys. 2024, 161, 154102. [Google Scholar] [CrossRef]
- Li, J.; Jin, Y.; Rinke, P.; Yang, W.; Golze, D. Benchmark of GW methods for core-level binding energies. J. Chem. Theory Comput. 2022, 18, 7570–7585. [Google Scholar] [CrossRef]
- Yu, J.; Mei, Y.; Chen, Z.; Fan, Y.; Yang, W. Accurate Prediction of Core-Level Binding Energies from Ground-State Density Functional Calculations: The Importance of Localization and Screening. J. Phys. Chem. Lett. 2025, 16, 2492–2500. [Google Scholar] [CrossRef]
- Rijal, D.; Vasilyev, V.; Wang, F. Advancing Sustainable Aviation Fuel Design: Machine Learning for High-Energy-Density Liquid Polycyclic Hydrocarbons. Energy Fuels 2025, 39, 3243–3255. [Google Scholar] [CrossRef]
- Wang, F.; Chong, D.P. Polycycloalkanes at the Helm: Exploring high energy density eFuel with norbornyl derivatives. Mater. Today Chem. 2024, 41, 102264. [Google Scholar] [CrossRef]
- Chong, D.P. Density functional theory study of the electron spectra of formamide vapor. J. Electron Spectrosc. Relat. Phenom. 2011, 184, 164–169. [Google Scholar] [CrossRef]
- Cavigliasso, G.; Chong, D.P. Accurate density-functional calculation of core-electron binding energies by a total-energy difference approach. J. Chem. Phys. 1999, 111, 9485–9492. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yue, W. Accurate and simple density functional for the electronic exchange energy: Generalized gradient approximation. Phys. Rev. B 1986, 33, 8800. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Gritsenko, O.; Braïda, B.; Baerends, E. Physical interpretation and evaluation of the kohn-sham and dyson components of the δε relations between the kohn-sham orbital energies and the ionization potentials. J. Chem. Phys. 1937, 119, 2003. [Google Scholar]
- Kahk, J.M.; Lischner, J. Accurate absolute core-electron binding energies of molecules, solids, and surfaces from first-principles calculations. Phys. Rev. Mater. 2019, 3, 100801. [Google Scholar] [CrossRef]
- Reiher, M. Relativistic douglas–kroll–hess theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 139–149. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Öhrn, Y. How quantitative is the concept of maximum overlap? Theor. Chim. Acta 1971, 21, 215–234. [Google Scholar] [CrossRef]
- Gilbert, A.T.; Besley, N.A.; Gill, P.M. Self-consistent field calculations of excited states using the maximum overlap method (MOM). J. Phys. Chem. A 2008, 112, 13164–13171. [Google Scholar] [CrossRef]
- Besley, N.A.; Gilbert, A.T.; Gill, P.M. Self-consistent-field calculations of core excited states. J. Chem. Phys. 2009, 130, 124308. [Google Scholar] [CrossRef]
- Chong, D.P. Accurate calculation of core-electron binding energies by the density-functional method. Chem. Phys. Lett. 1995, 232, 486–490. [Google Scholar] [CrossRef]
- Chong, D.P.; Aplincourt, P.; Bureau, C. DFT Calculations of Core− Electron Binding Energies of the Peptide Bond. J. Phys. Chem. A 2002, 106, 356–362. [Google Scholar] [CrossRef]
- Takahata, Y.; Chong, D.P. DFT calculation of core-electron binding energies. J. Electron Spectrosc. Relat. Phenom. 2003, 133, 69–76. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; et al. ADF; SCM Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, 2025. [Google Scholar]
- Koopmans, T. Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Phillips, J. Generalized Koopmans’ Theorem. Phys. Rev. 1961, 123, 420. [Google Scholar] [CrossRef]
- Smith, D.W.; Day, O.W. Extension of Koopmans’ theorem. I. Derivation. J. Chem. Phys. 1975, 62, 113–114. [Google Scholar] [CrossRef]
- Zheng, X.; Cheng, L. Performance of delta-coupled-cluster methods for calculations of core-ionization energies of first-row elements. J. Chem. Theory Comput. 2019, 15, 4945–4955. [Google Scholar] [CrossRef]
- Halbert, L.; Vidal, M.L.; Shee, A.; Coriani, S.; Severo Pereira Gomes, A. Relativistic EOM-CCSD for Core-Excited and Core-Ionized State Energies Based on the Four-Component Dirac–Coulomb (− Gaunt) Hamiltonian. J. Chem. Theory Comput. 2021, 17, 3583–3598. [Google Scholar] [CrossRef]
- Delgado, A.A.A.; Matthews, D.A. Enhancing the accuracy of XPS calculations: Exploring hybrid basis set schemes for CVS-EOMIP-CCSD calculations. J. Chem. Phys. 2025, 162, 34112. [Google Scholar] [CrossRef]
- Golze, D.; Wilhelm, J.; Van Setten, M.J.; Rinke, P. Core-level binding energies from GW: An efficient full-frequency approach within a localized basis. J. Chem. Theory Comput. 2018, 14, 4856–4869. [Google Scholar] [CrossRef]
- Golze, D.; Keller, L.; Rinke, P. Accurate absolute and relative core-level binding energies from GW. J. Phys. Chem. Lett. 2020, 11, 1840–1847. [Google Scholar] [CrossRef]
- Kas, J.J.; Vila, F.D.; Rehr, J.J.; Chambers, S.A. Real-time cumulant approach for charge-transfer satellites in x-ray photoemission spectra. Phys. Rev. B 2015, 91, 121112. [Google Scholar] [CrossRef]
- Janak, J.; Williams, A. Method for calculating wave functions in a nonspherical potential. Phys. Rev. B 1981, 23, 6301. [Google Scholar] [CrossRef]
- Williams, A.; Lang, N. Core-level binding-energy shifts in metals. Phys. Rev. Lett. 1978, 40, 954. [Google Scholar] [CrossRef]
- Pueyo Bellafont, N.; Bagus, P.S.; Illas, F. Prediction of core level binding energies in density functional theory: Rigorous definition of initial and final state contributions and implications on the physical meaning of Kohn-Sham energies. J. Chem. Phys. 2015, 142, 214102. [Google Scholar] [CrossRef]
- Chong, D.P. Density-functional calculation of core-electron binding energies of C, N, O, and F. J. Chem. Phys. 1995, 103, 1842–1845. [Google Scholar] [CrossRef]
- Chong, D.P. Density-functional calculation of core-electron binding energies of glycine conformers. Can. J. Chem. 1996, 74, 1005–1007. [Google Scholar] [CrossRef]
- Stener, M.; Lisini, A.; Decleva, P. Density functional calculations of excitation energies and oscillator strengths for C1s→ π∗ and O1s→ π∗ excitations and ionization potentials in carbonyl containing molecules. Chem. Phys. 1995, 191, 141–154. [Google Scholar] [CrossRef]
- Hu, C.-H.; Chong, D.P. Density functional calculation of core-electron binding energies of transition metal carbonyl and nitrosyl complexes. Chem. Phys. Lett. 1996, 262, 733–736. [Google Scholar] [CrossRef]
- Chong, D.P.; Hu, C.-H.; Duffy, P. Accurate density-functional calculation of core-electron binding energies with a scaled polarized triple-zeta basis set. Twelve test cases and application to three C2H4O2 isomers. Chem. Phys. Lett. 1996, 249, 491–495. [Google Scholar] [CrossRef]
- Triguero, L.; Pettersson, L.; Ågren, H. Calculations of near-edge x-ray-absorption spectra of gas-phase and chemisorbed molecules by means of density-functional and transition-potential theory. Phys. Rev. B 1998, 58, 8097. [Google Scholar] [CrossRef]
- Takahata, Y.; Chong, D.P. Estimation of Hammett sigma constants of substituted benzenes through accurate density-functional calculation of core-electron binding energy shifts. Int. J. Quantum Chem. 2005, 103, 509–515. [Google Scholar] [CrossRef]
- Yang, L.; Ågren, H.; Carravetta, V.; Pettersson, L.G. Static exchange and quantum defect analysis of x-ray absorption spectra of carbonyl compounds. Phys. Scr. 1996, 54, 614. [Google Scholar] [CrossRef]
- Chong, D.P.; Minato, T.; Mukherjee, P.K. Calculations of core-electron binding energies by transition operator method followed by Rayleigh–Schröudinger perturbation theory. Int. J. Quantum Chem. 1983, 23, 1903–1914. [Google Scholar] [CrossRef]
- Duffy, P.; Chong, D.P.; Casida, M.E.; Salahub, D.R. Assessment of Kohn-Sham density-functional orbitals as approximate Dyson orbitals for the calculation of electron-momentum-spectroscopy scattering cross sections. Phys. Rev. A 1994, 50, 4707. [Google Scholar] [CrossRef]
- Chong, D.P.; Gritsenko, O.V.; Baerends, E.J. Interpretation of the Kohn–Sham orbital energies as approximate vertical ionization potentials. J. Chem. Phys. 2002, 116, 1760–1772. [Google Scholar] [CrossRef]
- Domagała, M.; Jabłoński, M.; Dubis, A.T.; Zabel, M.; Pfitzner, A.; Palusiak, M. Testing of Exchange-Correlation Functionals of DFT for a Reliable Description of the Electron Density Distribution in Organic Molecules. Int. J. Mol. Sci. 2022, 23, 14719. [Google Scholar] [CrossRef]
- Bureau, C.; Chong, D.P. Density functional calculations of core-electron binding energies of amines. Application to (CH3) 3N Ni and (CH3) 4N+ Ni. Chem. Phys. Lett. 1997, 264, 186–192. [Google Scholar] [CrossRef]
- Bureau, C.; Chong, D.P.; Lecayon, G.; Delhalle, J. Accurate density functional calculation of core electron binding energies: Part V: Application to nitriles. Model molecules for polyacrylonitrile revisited. J. Electron Spectrosc. Relat. Phenom. 1997, 83, 227–234. [Google Scholar] [CrossRef]
- Chong, D.P. Accurate Dft Calculation of Core-Electron Binding Energies. Reviews of Modern Quantum Chemistry: A Celebration of the Contributions of Robert G Parr. World Sci. 2002, 2, 1106–1139. [Google Scholar]
- Bakke, A.A.; Chen, H.-W.; Jolly, W.L. A table of absolute core-electron binding-energies for gaseous atoms and molecules. J. Electron Spectrosc. Relat. Phenom. 1980, 20, 333–366. [Google Scholar] [CrossRef]
- Jolly, W.; Bomben, K.; Eyermann, C. Core-electron binding energies for gaseous atoms and molecules. At. Data Nucl. Data Tables 1984, 31, 433–493. [Google Scholar] [CrossRef]
- Chong, D.P. Localized and delocalized 1s core-holes in DFT calculations. J. Electron Spectrosc. Relat. Phenom. 2007, 159, 94–96. [Google Scholar] [CrossRef]
- Pueyo Bellafont, N.; Álvarez Saiz, G.; Viñes, F.; Illas, F. Performance of Minnesota functionals on predicting core-level binding energies of molecules containing main-group elements. Theor. Chem. Acc. 2016, 135, 35. [Google Scholar] [CrossRef]
- Chong, D.P. Computational study of the electron spectra of vapor-phase indole and four azaindoles. Molecules 2021, 26, 1947. [Google Scholar] [CrossRef]
- Parr, R.G. Reviews of Modern Quantum Chemistry: A Celebration of the Contributions of Robert G. Parr; World Scientific: Singapore, 2002; Volume 1. [Google Scholar]
- Powis, I.; Rennie, E.E.; Hergenhahn, U.; Kugeler, O.; Bussy-Socrate, R. Investigation of the gas-phase amino acid alanine by synchrotron radiation photoelectron spectroscopy. J. Phys. Chem. A 2003, 107, 25–34. [Google Scholar] [CrossRef]
- Pi, J.M.; Stella, M.; Fernando, N.K.; Lam, A.Y.; Regoutz, A.; Ratcliff, L.E. Predicting core level photoelectron spectra of amino acids using density functional theory. J. Phys. Chem. Lett. 2020, 11, 2256–2262. [Google Scholar] [CrossRef]
- Ganesan, A.; Wang, F.; Brunger, M.; Prince, K. Effects of alkyl side chains on properties of aliphatic amino acids probed using quantum chemical calculations. Synchrotron Radiat. 2011, 18, 733–742. [Google Scholar] [CrossRef]
- Saha, S.; Wang, F.; Brunger, M.J. Intramolecular proton transfer in adenine imino tautomers. Mol. Simul. 2006, 32, 1261–1270. [Google Scholar] [CrossRef]
- Saha, S.; Wang, F.; Guerra, C.F.; Bickelhaupt, F.M. Outer valence orbital response to proton positions in prototropic tautomers of adenine. J. Comput. Methods Sci. Eng. 2006, 6, 251–267. [Google Scholar] [CrossRef]
- Saha, S.; Wang, F.; MacNaughton, J.B.; Moewes, A.; Chong, D.P. The attachment of amino fragment to purine: Inner-shell structures and spectra. J. Synchrotron Radiat. 2008, 15, 151–157. [Google Scholar] [CrossRef]
- Jones, D.B.; Wang, F.; Winkler, D.A.; Brunger, M.J. Orbital based electronic structural signatures of the guanine keto G-7H/G-9H tautomer pair as studied using dual space analysis. Biophys. Chem. 2006, 121, 105–120. [Google Scholar] [CrossRef]
- Arachchilage, A.P.W.; Wang, F.; Feyer, V.; Plekan, O.; Prince, K.C. Correlation of electronic structures of three cyclic dipeptides with their photoemission spectra. J. Chem. Phys. 2010, 133, 174319. [Google Scholar] [CrossRef]
- Hill, A.; Sa’adeh, H.; Cameron, D.; Wang, F.; Trofimov, A.B.; Larionova, E.Y.; Richter, R.; Prince, K.C. Positional and conformational isomerism in hydroxybenzoic acid: A core-level study and comparison with phenol and benzoic acid. J. Phys. Chem. A 2021, 125, 9877–9891. [Google Scholar] [CrossRef]
- Hill, A.; Wang, F. Intramolecular O··· H Hydrogen Bonding of Salicylic Acid: Further Insights from O 1s XPS and 1H NMR Spectra Using DFT Calculations. J. Phys. Chem. A 2023, 127, 2705–2716. [Google Scholar] [CrossRef]
- Sa’adeh, H.; Prince, K.C.; Richter, R.; Vasilyev, V.; Chong, D.P.; Wang, F. A photoelectron spectroscopic investigation of aspirin, paracetamol and ibuprofen in the gas phase. Phys. Chem. Chem. Phys. 2023, 25, 10946–10955. [Google Scholar] [CrossRef]
- Sa’adeh, H.; Backler, F.; Wang, F.; Piccirillo, S.; Ciavardini, A.; Richter, R.; Coreno, M.; Prince, K.C. Experimental and theoretical soft X-ray study of nicotine and related compounds. J. Phys. Chem. A 2020, 124, 4025–4035. [Google Scholar] [CrossRef]
- Ahmed, M.; Wang, F.; Acres, R.G.; Prince, K.C. Structures of cycloserine and 2-oxazolidinone probed by X-ray photoelectron spectroscopy. arXiv 2013, arXiv:1305.6384. [Google Scholar]
- Islam, S.; Ganesan, A.; Auchettl, R.; Plekan, O.; Acres, R.G.; Wang, F.; Prince, K.C. Electronic structure and intramolecular interactions in three methoxyphenol isomers. J. Chem. Phys. 2018, 149, 134312. [Google Scholar] [CrossRef]
- Feketeová, L.; Plekan, O.; Goonewardane, M.; Ahmed, M.; Albright, A.L.; White, J.; O’Hair, R.A.; Horsman, M.R.; Wang, F.; Prince, K.C. Photoelectron spectra and electronic structures of the radiosensitizer nimorazole and related compounds. J. Phys. Chem. A 2015, 119, 9986–9995. [Google Scholar] [CrossRef]
- Sa’adeh, H.; Mohamed, A.E.; Richter, R.; Coreno, M.; Wang, F.; Prince, K.C. Photoemission and X-ray Absorption Investigation of Ammonia-Borane in the Gas Phase. ACS Omega 2023, 8, 45970–45975. [Google Scholar] [CrossRef]
- Wang, F.; Chong, D.P. Electronic structure study of H3BXH3 (X═ B, N and P) as hydrogen storage materials using calculated NMR and XPS spectra. Aust. J. Chem. 2023, 76, 854–863. [Google Scholar] [CrossRef]
- Chong, D.P.; Wang, F. Dehydrogenation of ammonia borane impacts valence and core electrons: A photoemission spectroscopic study. ACS Omega 2022, 7, 35924–35932. [Google Scholar] [CrossRef]
- Padrao, S.; Fiuza, S.M.; Amado, A.M.; Amorim da Costa, A.M.; Batista de Carvalho, L.A. Validation of the mPW1PW Quantum chemical calculations for the vibrational study of organic molecules–re-assignment of the isopropylamine vibrational spectra. J. Phys. Org. Chem. 2011, 24, 110–121. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The m PW and m PW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- Liptak, M.D.; Shields, G.C. Comparison of density functional theory predictions of gas-phase deprotonation data. Int. J. Quantum Chem. 2005, 105, 580–587. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Akter, S. Effect of Self-Interaction Correction on Molecular Polarizabilities and Core Ionization Energies. Ph.D. Thesis, The University of Texas at El Paso, El Paso, TX, USA, 2023. [Google Scholar]
- Segala, M.; Chong, D.P. Further study of exchange-correlation functionals for the calculations of outer-valence ionization potentials of gas-phase molecules. J. Electron Spectrosc. Relat. Phenom. 2024, 274, 147459. [Google Scholar] [CrossRef]
- Defonsi Lestard, M.E.; Tuttolomondo, M.E.; Wann, D.A.; Robertson, H.E.; Rankin, D.W.; Altabef, A.B. Experimental and theoretical structure and vibrational analysis of ethyl trifluoroacetate, CF3CO2CH2CH3. J. Raman Spectrosc. 2010, 41, 1357–1368. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chong, D.P. Exchange energy in DFT functional for core electrons. Personal communication, 2024. [Google Scholar]
- Körzdörfer, T.; Marom, N. Strategy for finding a reliable starting point for G0W0 demonstrated for molecules. Phys. Rev. B—Condens. Matter Mater. Phys. 2012, 86, 041110. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Kanungo, B.; Kaplan, A.D.; Shahi, C.; Gavini, V.; Perdew, J.P. Unconventional Error Cancellation Explains the Success of Hartree–Fock Density Functional Theory for Barrier Heights. J. Phys. Chem. Lett. 2024, 15, 323–328. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Fox, D.J. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Chong, D.P. DFT computation of the electron spectra of thiophene. Can. J. Chem. 2024, 102, 425–430. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Watts, J.D.; Gauss, J.; Bartlett, R.J. Coupled-cluster methods with noniterative triple excitations for restricted open-shell Hartree–Fock and other general single determinant reference functions. Energies and analytical gradients. J. Chem. Phys. 1993, 98, 8718–8733. [Google Scholar] [CrossRef]
- Becke, A.D. Densityfunctional thermochemistry. III. the role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Ambroise, M.A.; Jensen, F. Probing basis set requirements for calculating core ionization and core excitation spectroscopy by the Δ self-consistent-field approach. J. Chem. Theory Comput. 2018, 15, 325–337. [Google Scholar] [CrossRef]
- Thomas, T.D.; Sæthre, L.J.; Børve, K.J.; Gundersen, M.; Kukk, E. Reactivity and core-ionization energies in conjugated dienes. Carbon 1s photoelectron spectroscopy of 1,3-pentadiene. J. Phys. Chem. A 2005, 109, 5085–5092. [Google Scholar] [CrossRef]
- Segala, M.; Chong, D.P. An evaluation of exchange-correlation functionals for the calculations of the ionization energies for atoms and molecules. J. Electron Spectrosc. Relat. Phenom. 2009, 171, 18–23. [Google Scholar] [CrossRef]
- Klues, M.; Hermann, K.; Witte, G. Analysis of the near-edge X-ray-absorption fine-structure of anthracene: A combined theoretical and experimental study. J. Chem. Phys. 2014, 140, 14302. [Google Scholar] [CrossRef]
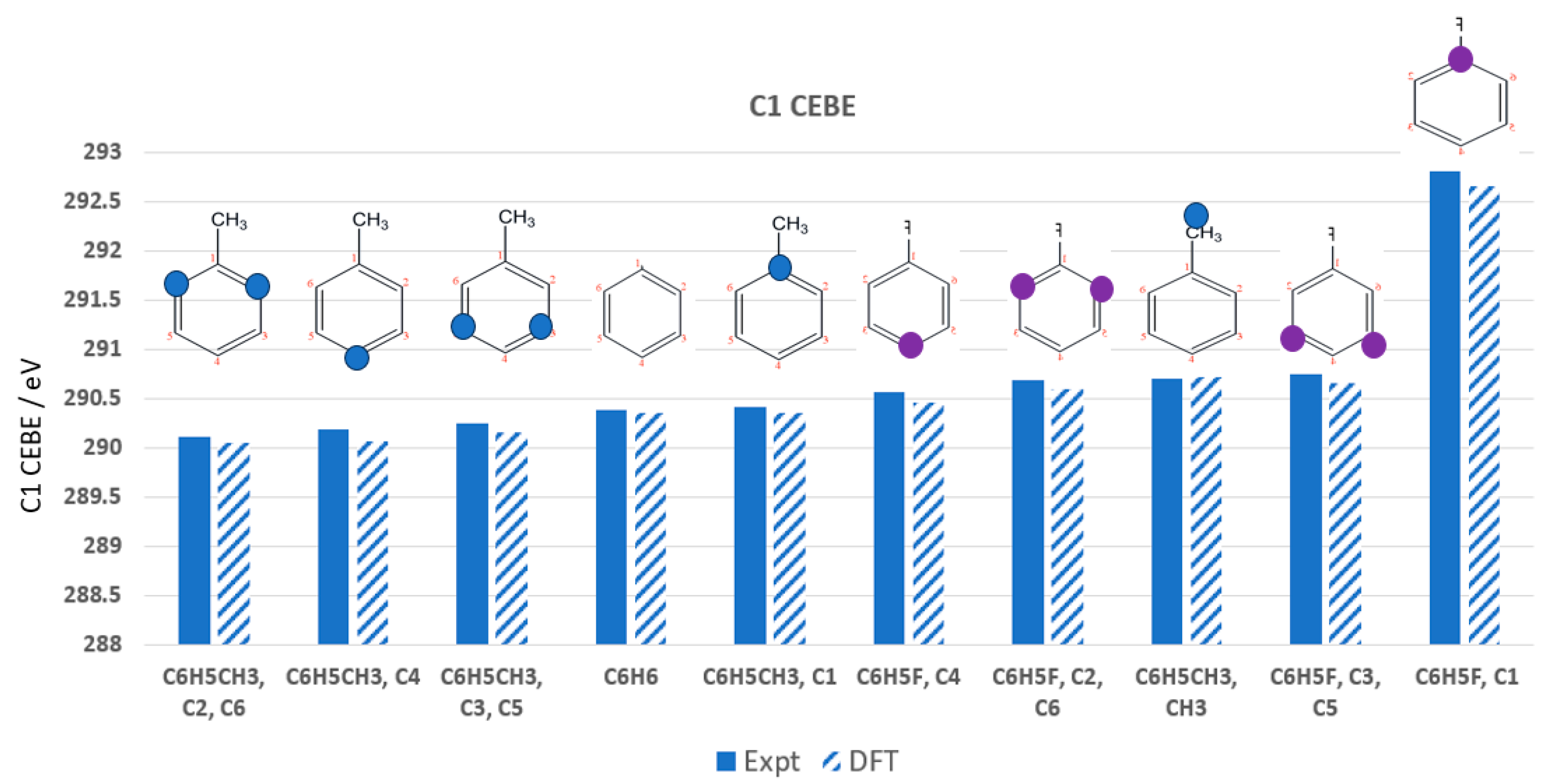
- Myrseth, V.; Sæthre, L.J.; Børve, K.J.; Thomas, T.D. The substituent effect of the methyl group. Carbon 1s ionization energies, proton affinities, and reactivities of the methylbenzenes. J. Org. Chem. 2007, 72, 5715–5723. [Google Scholar] [CrossRef]
- Sæthre, L.J.; Børve, K.J.; Thomas, T.D. Chemical shifts of carbon 1s ionization energies. J. Electron Spectrosc. Relat. Phenom. 2011, 183, 2–9. [Google Scholar] [CrossRef]
- Sæthre, L.J.; Berrah, N.; Bozek, J.D.; Børve, K.J.; Carroll, T.X.; Kukk, E.; Gard, G.L.; Winter, R.; Thomas, T.D. Chemical insights from high-resolution X-ray photoelectron spectroscopy and ab initio theory: Propyne, trifluoropropyne, and ethynylsulfur pentafluoride. J. Am. Chem. Soc. 2001, 123, 10729–10737. [Google Scholar] [CrossRef]
- Myrseth, V.; Børve, K.; Wiesner, K.; Bässler, M.; Svensson, S.; Sæthre, L. Vibrational structure and vibronic coupling in the carbon 1s photoelectron spectra of benzene and deuterobenzene. Phys. Chem. Chem. Phys. 2002, 4, 5937–5943. [Google Scholar] [CrossRef]
- Carroll, T.X.; Thomas, T.D.; Bergersen, H.; Børve, K.J.; Sæthre, L.J. Fluorine as a π donor. Carbon 1s photoelectron spectroscopy and proton affinities of fluorobenzenes. J. Org. Chem. 2006, 71, 1961–1968. [Google Scholar] [CrossRef]
- Myrseth, V.; Bozek, J.; Kukk, E.; Sæthre, L.; Thomas, T. Adiabatic and vertical carbon 1s ionization energies in representative small molecules. J. Electron Spectrosc. Relat. Phenom. 2002, 122, 57–63. [Google Scholar] [CrossRef]
- Zahl, M.G.; Fossheim, R.; Børve, K.J.; Sæthre, L.J.; Thomas, T.D. Electronic Properties of Chlorine, Methyl, and Chloromethyl as Substituents to the Ethylene Group—Viewed from the Core of Carbon. J. Phys. Chem. A 2015, 119, 9481–9493. [Google Scholar] [CrossRef]
- Thomas, T.D.; Saethre, L.J.; Børve, K.J.; Bozek, J.D.; Huttula, M.; Kukk, E. Carbon 1s photoelectron spectroscopy of halomethanes. Effects of electronegativity, hardness, charge distribution, and relaxation. J. Phys. Chem. A 2004, 108, 4983–4990. [Google Scholar] [CrossRef]
- Thomas, T.D. (Department of Chemistry, University of Bergen, Bergen, Norway); Chong, D.P. (Department of Chemistry, University of British Columbia, Vancouver, BC, Canada). The C1s Energy Measurement of CCl3Br. Personal communication, 2021. [Google Scholar]


| Factor | CEBE Challenges | Valence IPs Challenges |
|---|---|---|
| Electron Correlation | Stronger effects | Moderate effects |
| Orbital Relaxation | Critical | Less significant |
| Relativistic Effects | Significant (especially for heavy elements) | Small (except for heavy elements) |
| Charge Localization | Core-hole localization needed | Less problematic |
| Basis Set Dependence | Core-optimized basis required | Standard valence basis sufficient |
| Experimental Uncertainty | Higher (XPS calibration issues) | More precise |
 | Calculated ΔDFT | Thomas et al. [110] Expt | ||
|---|---|---|---|---|
| Method-A * | Method-C # | Adiabatic | Vertical | |
| C1 | 289.743 (−0.230) | 289.800 (−0.173) | 289.762 | 289.973 |
| C2 | 290.514 (−0.147) | 290.571 (−0.090) | 290.501 | 290.661 |
| C3 | 290.276 (−0.136) | 290.333 (−0.079) | 290.247 | 290.412 |
| C4 | 290.096 (−0.154) | 290.153 (−0.097) | 290.093 | 290.250 |
| C5 | 290.727 (−0.029) + 0.057 c | 290.784 (+0.028) | 290.565 | 290.756, 290.784 a |
| RMSD | 0.1533 | 0.1044 | 0.1780 b | - |
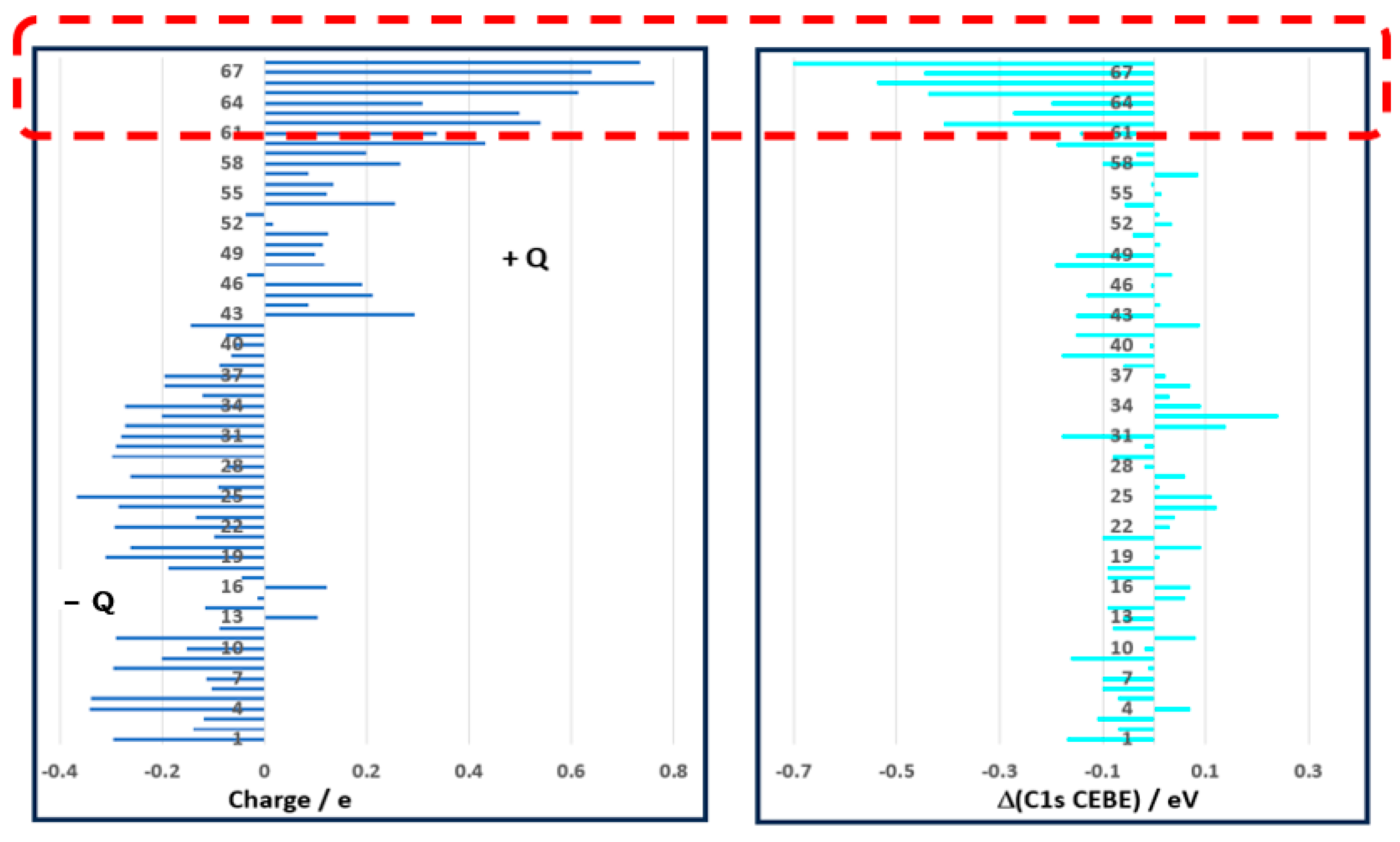
| No | Molecule | Expt | Ref | Charge Q (C) | DFT a | Δ (DFT−Expt) | μ/Debye c,d |
|---|---|---|---|---|---|---|---|
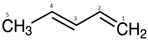
| 1 | CH2=CHCH=CHCH3 | 289.97 | [110] | −0.2951 b | 289.80 b | −0.17 | 0.6437 |
| 2 | C6H5CH3, C2, C6 | 290.11 | [113] | −0.1393 | 290.05 | −0.07 | 0.3688 |
| 3 | C6H5CH3, C4 | 290.18 | [113] | −0.1196 | 290.07 | −0.11 | 0.3688 |
| 4 | CH2=CHCH3 | 290.23 | [110] | −0.3416 | 290.30 | 0.07 | 0.3799 |
| 5 | CH2=CHCH=CH2 | 290.25 | [110] | −0.3378 | 290.17 | −0.07 | 0 |
| 6 | C6H5CH3, C3, C5 | 290.25 | [113] | −0.1020 | 290.15 | −0.10 | 0.3688 |
| 7 | CH2=CHCH=CHCH3 | 290.25 | [110] | −0.1142 b | 290.15 b | −0.10 | 0.6437 |
| 8 | C(CH3)4 | 290.37 | [114] | −0.2942 b | 291.36 b | −0.01 | 0 |
| 9 | HCCCH3 | 290.37 | [115] | −0.1997 | 290.21 | −0.16 | 0.7852 |
| 10 | C6H6 | 290.38 | [116] | −0.1519 | 290.35 | −0.02 | 0 |
| 11 | CH(CH3)3 | 290.39 | [114] | −0.2896 b | 290.47 b | 0.08 | 0.1307 |
| 12 | CH2=CHCH=CHCH3 | 290.41 | [110] | −0.0872 b | 290.33 b | −0.08 | 0.6437 |
| 13 | C6H5CH3, C1 | 290.41 | [113] | 0.1041 | 290.35 | −0.06 | 0.3688 |
| 14 | C6H5F, C4 | 290.56 | [117] | −0.1148 b | 290.46 b | −0.09 | 1.4773 |
| 15 | CH(CH3)3 | 290.63 | [114] | −0.0141 b | 290.69 b | 0.06 | 0.1307 |
| 16 | C(CH3)4 | 290.66 | [114] | 0.1231 b | 290.73 b | 0.07 | 0 |
| 17 | CH2=CHCH=CHCH3 | 290.66 | [110] | −0.0437 b | 290.00 h | −0.09 | 0.6437 |
| 18 | C6H5F, C2, C6 | 290.69 | [117] | −0.1876 b | 290.60 b | −0.09 | 1.4773 |
| 19 | C6H5CH3, CH3 | 290.70 | [113] | −0.3099 | 290.71 | 0.01 | 0.3688 |
| 20 | C2H6 | 290.71 | [118] | −0.2624 | 290.80 | 0.09 | 0 |
| 21 | C6H5F, C3, C5 | 290.75 | [117] | −0.0981 | 290.66 | −0.10 | 1.4773 |
| 22 | CH2=CHCH=CHCH3 | 290.76 | [110] | −0.2931 b | 290.78 b | 0.03 | 0.6437 |
| 23 | CH2=CHCH3 | 290.76 | [110] | −0.1331 | 290.80 | 0.04 | 0.3799 |
| 24 | C2H4 | 290.82 | [118] | −0.2838 | 290.94 | 0.12 | 0 |
| 25 | CH4 | 290.84 | [118] | −0.3664 | 290.96 | 0.11 | 0 |
| 26 | CH2=CHCH=CH2 | 290.85 | [110] | −0.0900 | 290.85 | 0.01 | 0 |
| 27 | CH2=CHCH3 | 290.86 | [110] | −0.2617 | 290.93 | 0.06 | 0.3799 |
| 28 | HCCCH3 | 290.93 | [115] | −0.0736 | 290.91 | −0.02 | 0.7852 |
| 29 | CH2=CHCl | 290.93 | [119] | −0.2973 | 290.85 | −0.08 | 1.6863 |
| 30 | CH3CHFCH3 | 290.97 | [114] | −0.2895 | 290.95 | −0.02 | 1.8801 |
| 31 | CH2=CCl2 | 290.99 | [119] | −0.2795 | 290.81 | −0.18 | 1.6013 |
| 32 | CH3CH2F | 291.13 | [114] | −0.2713 | 291.26 | 0.14 | 2.0770 |
| 33 | C2H2 | 291.25 | [118] | −0.2008 | 291.48 | 0.24 | 0 |
| 34 | HCCCH3 | 291.76 | [115] | −0.2725 | 291.85 | 0.09 | 0.7852 |
| 35 | HCCCF3 | 292.03 | [115] | −0.1213 | 292.05 | 0.03 | 2.5410 |
| 36 | CH3Br | 292.06 | [120] | −0.1950 | 292.13 | 0.07 | 2.1523 |
| 37 | HCCCF3 | 292.14 | [115] | −0.1954 | 292.17 | 0.02 | 2.5410 |
| 38 | cis CHCl=CHCl | 292.27 | [119] | −0.0873 | 292.21 | −0.06 | 2.1910 |
| 39 | CHCl=CCl2 | 292.29 | [119] | −0.0646 | 292.11 | −0.18 | 2.0770 |
| 40 | CH2=CHCl | 292.29 | [119] | −0.0590 | 292.28 | −0.01 | 1.0352 |
| 41 | Trans CHCl=CHCl | 292.34 | [119] | −0.0741 | 292.19 | −0.15 | 1.6863 |
| 42 | CH3Cl | 292.43 | [114] | −0.1439 | 292.52 | 0.09 | 0 |
| 43 | C6H5F, C1 | 292.81 | [117] | 0.2941 | 292.66 | −0.15 | 2.1375 |
| 44 | CH2Br2 | 293.10 | [120] | 0.0856 | 293.11 | 0.01 | 1.4773 |
| 45 | CH3CHFCH3 | 293.15 | [114] | 0.2113 b | 293.02 b | −0.13 | 1.7209 |
| 46 | CH3CH2F | 293.28 | [114] | 0.1915 | 293.28 | −0.01 | 1.8801 |
| 47 | CH2ClBr | 293.46 | [120] | −0.0343 | 293.49 | 0.03 | 2.0770 |
| 48 | C2Cl4 | 293.51 | [119] | 0.1178 | 293.32 | −0.19 | 1.8105 |
| 49 | CHCl=CCl2 | 293.53 | [119] | 0.0987 | 293.38 | −0.15 | 1.0352 |
| 50 | CH3F | 293.56 | [118] | 0.1151 | 293.57 | 0.01 | 2.0326 |
| 51 | CH2=CCl2 | 293.56 | [119] | 0.1249 | 293.52 | −0.04 | 1.6013 |
| 52 | CH2Cl2 | 293.86 | [114] | 0.0173 | 293.89 | 0.03 | 1.8889 |
| 53 | CHBr3 | 293.99 | [120] | −0.0371 | 294.00 | 0.0 | 1.0487 |
| 54 | CH2FCl | 295.04 | [120] | 0.2545 | 294.98 | −0.06 | 2.0708 |
| 55 | CHCl3 | 295.14 | [114] | 0.1226 | 295.13 | 0.02 | 1.2548 |
| 56 | CCl3Br | 295.91 | G | 0.1343 | 295.90 | −0.01 | 0.1678 |
| 57 | CO | 296.23 | [118] | 0.0856 | 296.31 | 0.09 | 0.2838 |
| 58 | CFBr3 | 296.28 | [120] | 0.2643 | 296.18 | −0.10 | 0.6251 |
| 59 | CCl4 | 296.32 | [114] | 0.1991 | 296.28 | −0.03 | 0 |
| 60 | CH2F2 | 296.35 | [120] | 0.4331 | 296.16 | −0.19 | 2.1557 |
| 61 | CHFCl2 | 296.37 | [120] | 0.3371 | 296.23 | −0.14 | 1.4649 |
| 62 | CO2 | 297.70 | [118] | 0.5394 | 297.29 | −0.41 | 0 |
| 63 | CHF2Cl | 297.70 | [120] | 0.4977 | 297.43 | −0.27 | 1.6383 |
| 64 | CF2Br2 | 297.87 | [114] | 0.3103 | 297.67 | −0.20 | 0.6795 |
| 65 | CHF3 | 299.16 | [118] | 0.6132 | 298.72 | −0.44 | 1.8030 |
| 66 | HCCCF3 | 299.55 | [115] | 0.7613 | 299.01 | −0.54 | 2.5410 |
| 67 | CF3Br | 299.74 | [114] | 0.6398 | 299.29 | −0.45 | 0.6395 |
| 68 | CF4 | 301.90 | [118] | 0.7352 | 301.19 | −0.71 | 0 |
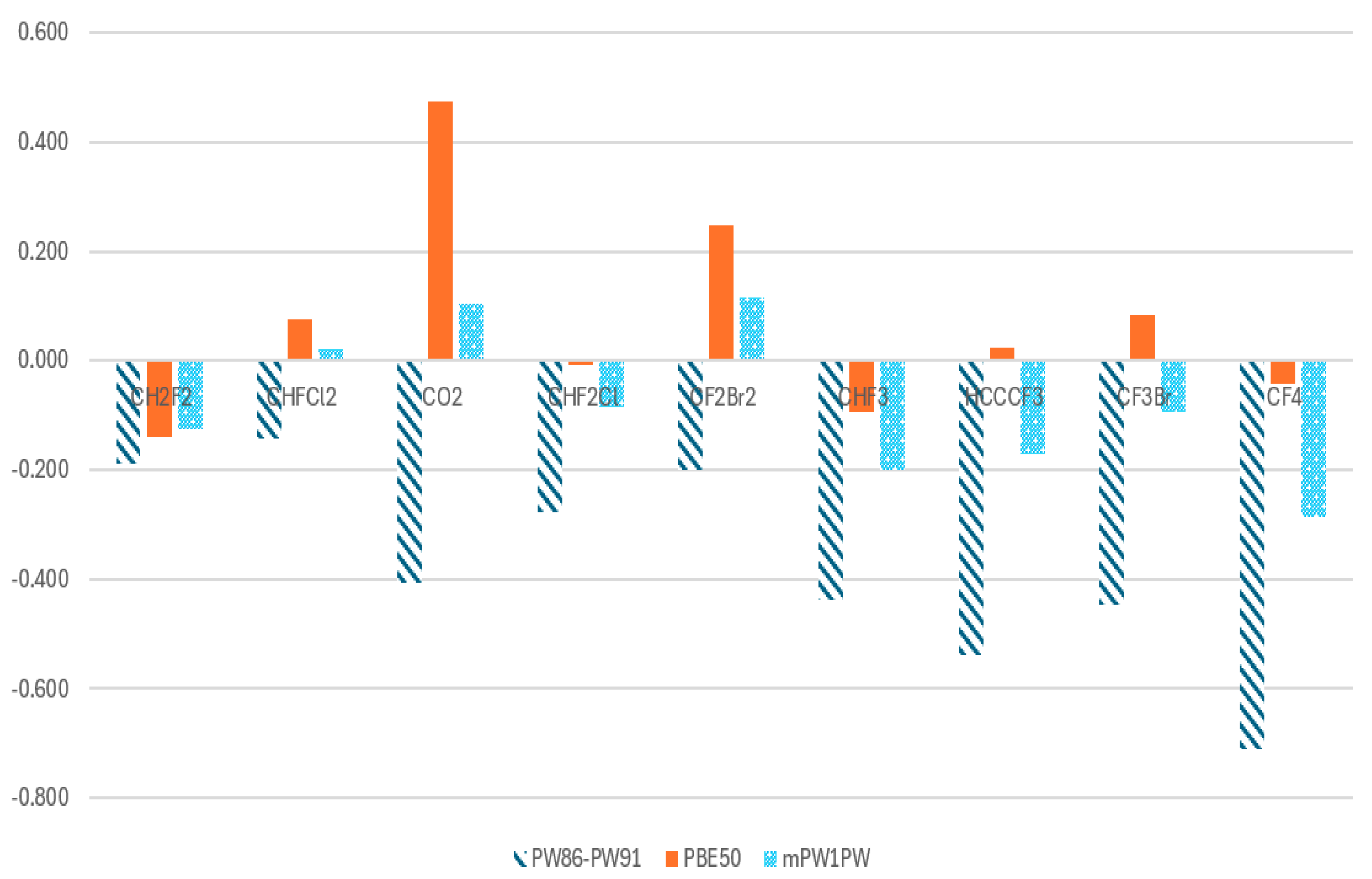
| Case | Molecule | PW86-PW91 (DFTpw) | Abs | PBE50 | Abs | mPW1PW | Abs |
|---|---|---|---|---|---|---|---|
| 60 | CH2F2 | −0.188 | 0.188 | −0.140 | 0.140 | −0.125 | 0.125 |
| 61 | CHFCl2 | −0.143 | 0.143 | 0.076 | 0.076 | 0.020 | 0.020 |
| 62 | CO2 | −0.407 | 0.407 | 0.475 | 0.475 | 0.104 | 0.104 |
| 63 | CHF2Cl | −0.278 | 0.278 | −0.007 | 0.007 | −0.085 | 0.085 |
| 64 | CF2Br2 | −0.200 | 0.200 | 0.247 | 0.247 | 0.115 | 0.115 |
| 65 | CHF3 | −0.439 | 0.439 | −0.093 | 0.093 | −0.201 | 0.201 |
| 66 | HCCCF3 | −0.538 | 0.538 | 0.024 | 0.024 | −0.171 | 0.171 |
| 67 | CF3Br | −0.446 | 0.446 | 0.084 | 0.084 | −0.093 | 0.093 |
| 68 | CF4 | −0.710 | 0.710 | −0.042 | 0.042 | −0.286 | 0.286 |
| Sum | 3.349 | 1.188 | 1.200 | ||||
| AAD | 0.372 | 0.132 | 0.133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Chong, D.P. The Role of Exchange Energy in Modeling Core-Electron Binding Energies of Strongly Polar Bonds. Molecules 2025, 30, 2887. https://doi.org/10.3390/molecules30132887
Wang F, Chong DP. The Role of Exchange Energy in Modeling Core-Electron Binding Energies of Strongly Polar Bonds. Molecules. 2025; 30(13):2887. https://doi.org/10.3390/molecules30132887
Chicago/Turabian StyleWang, Feng, and Delano P. Chong. 2025. "The Role of Exchange Energy in Modeling Core-Electron Binding Energies of Strongly Polar Bonds" Molecules 30, no. 13: 2887. https://doi.org/10.3390/molecules30132887
APA StyleWang, F., & Chong, D. P. (2025). The Role of Exchange Energy in Modeling Core-Electron Binding Energies of Strongly Polar Bonds. Molecules, 30(13), 2887. https://doi.org/10.3390/molecules30132887








