Accurate Prediction of Drug Activity by Computational Methods: Importance of Thermal Capacity
Abstract
1. Introduction
2. Results
2.1. Theoretical Background
2.2. Heat Capacity of Water
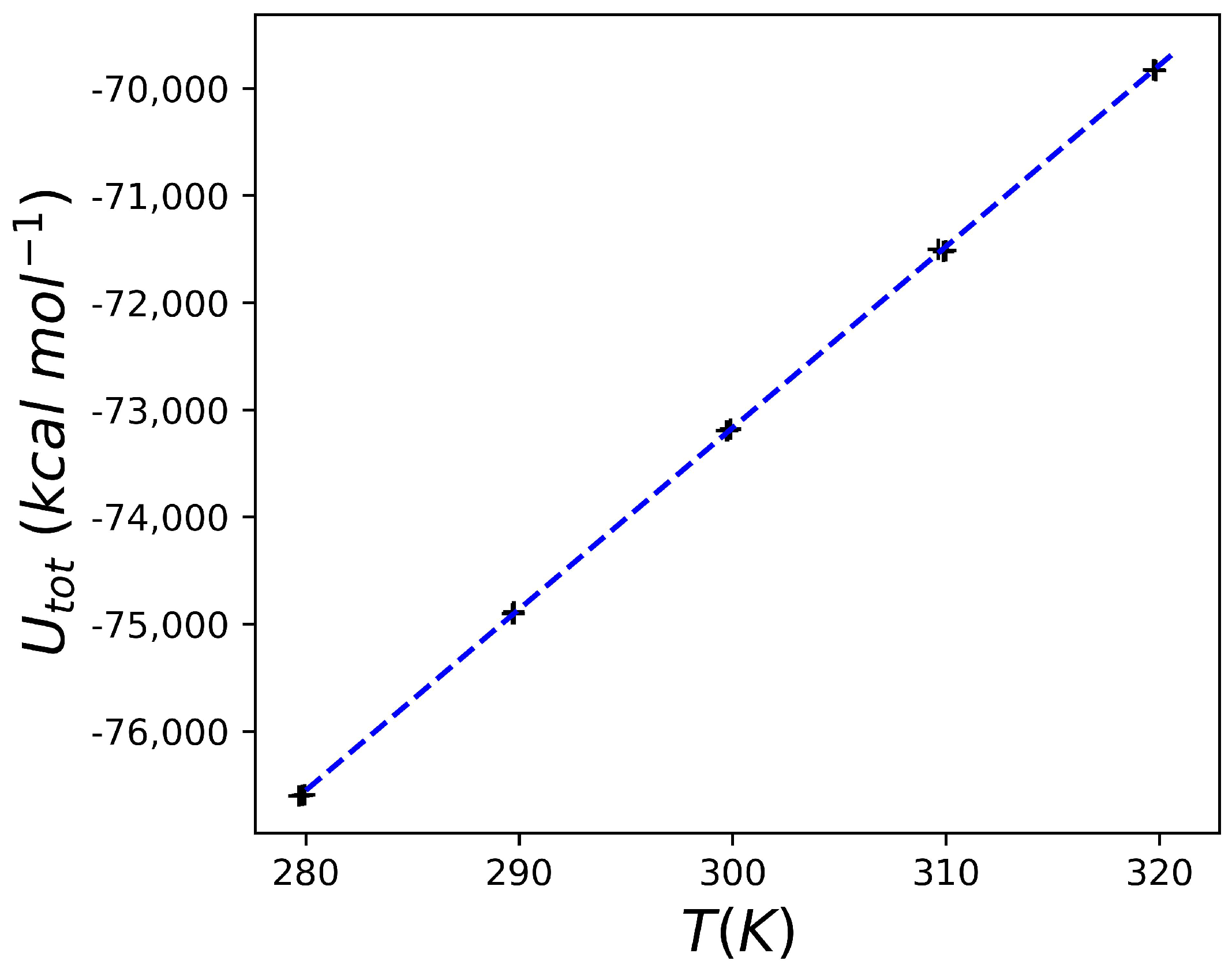
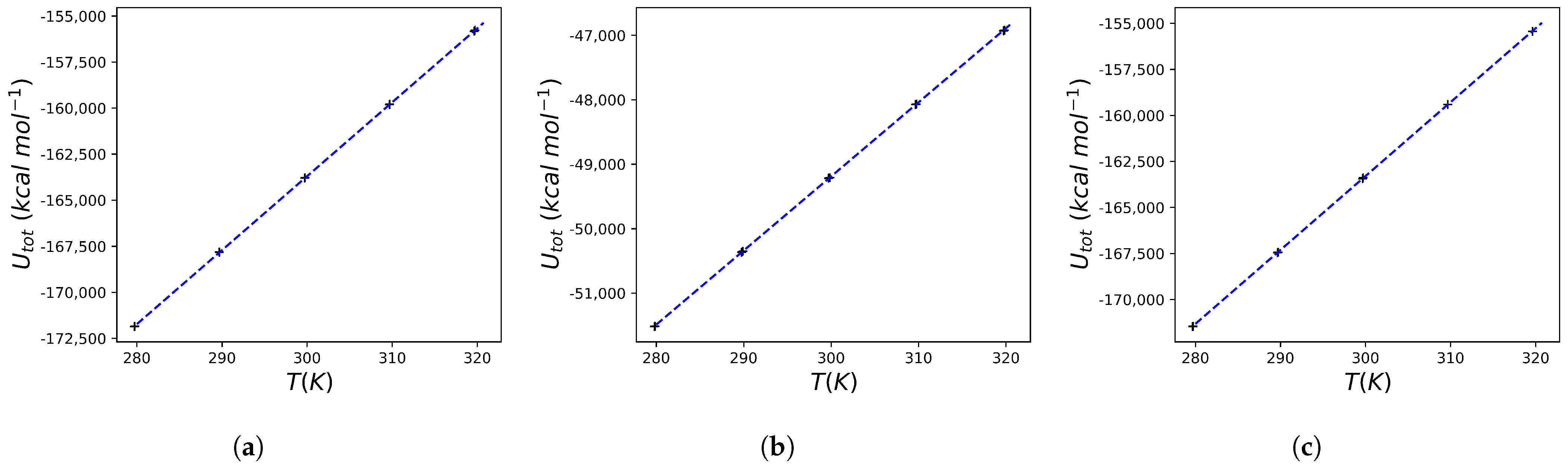
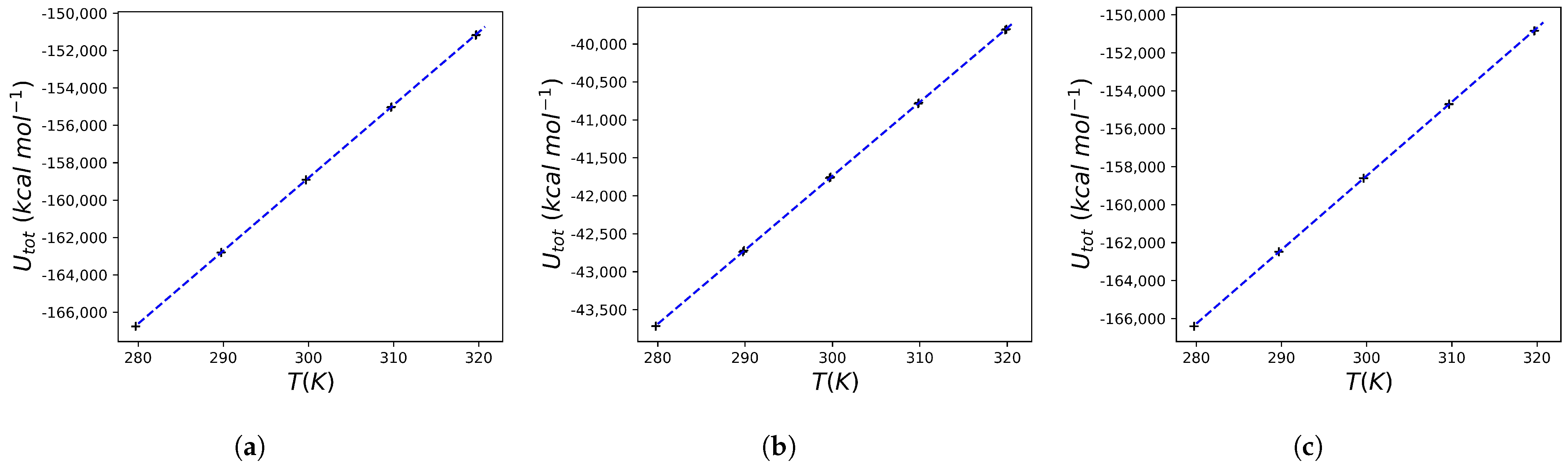
2.3. Heat Capacity Calculations of Protein Systems
3. Discussion
4. Materials and Methods
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIDS | Acquired ImmunoDeficiency Syndrome |
| PDB | Protein Data Bank |
| PME | Particle-Mesh Ewald |
| RMSD | Root Mean Squared Deviations |
| RMSF | Root Mean Squared Fluctuations |
| SDF | Structured Data Files |
Appendix A
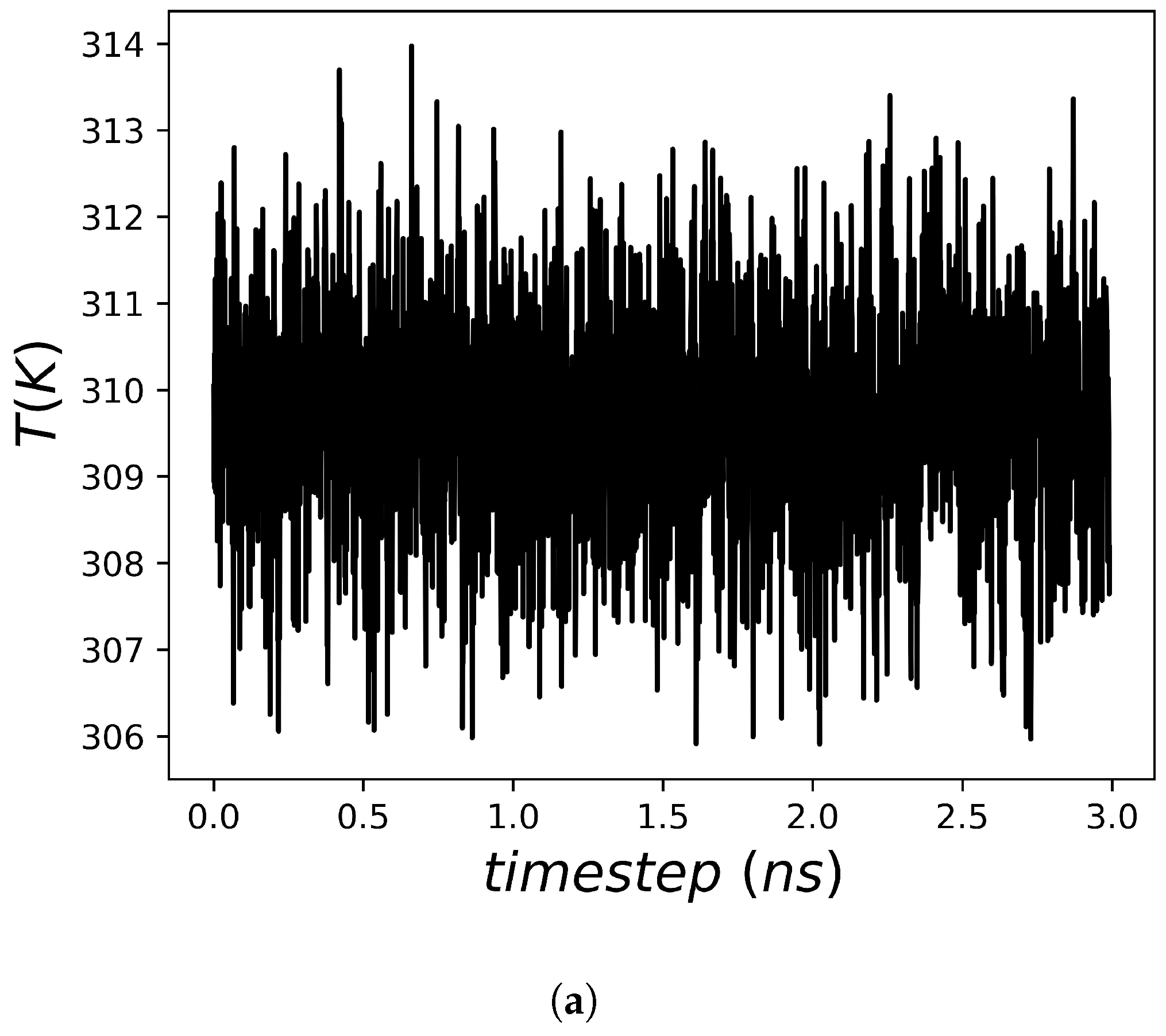
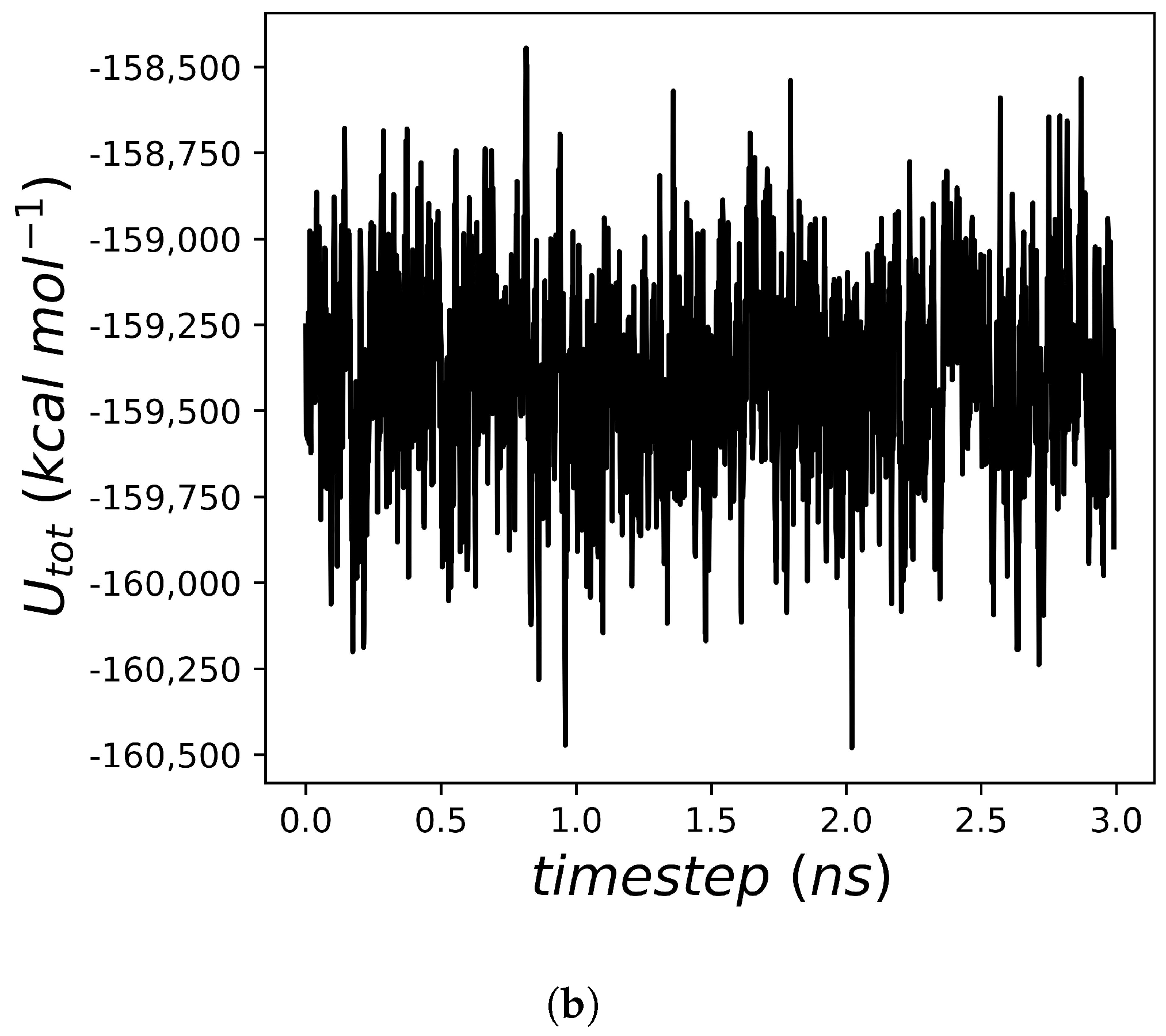
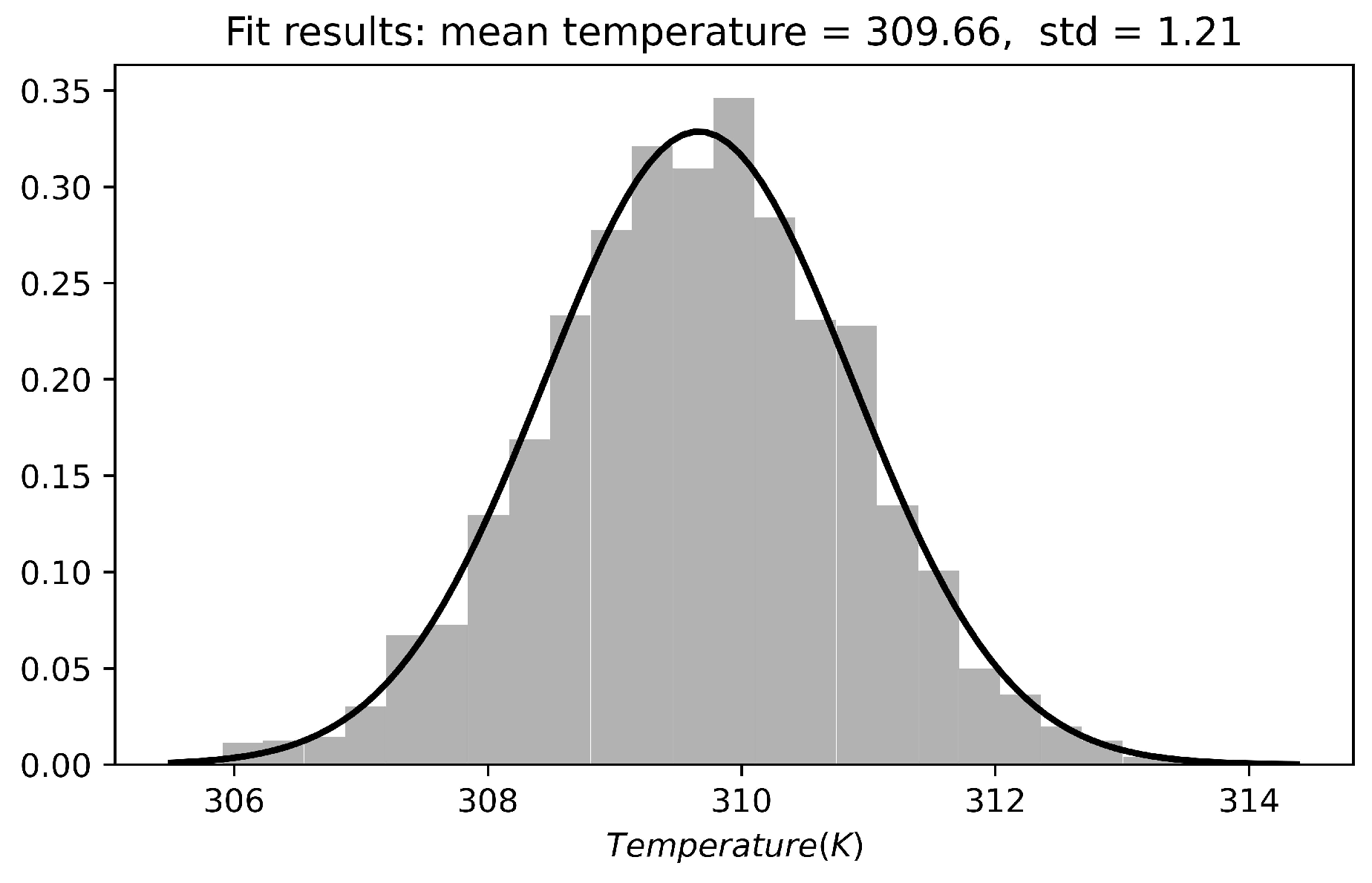
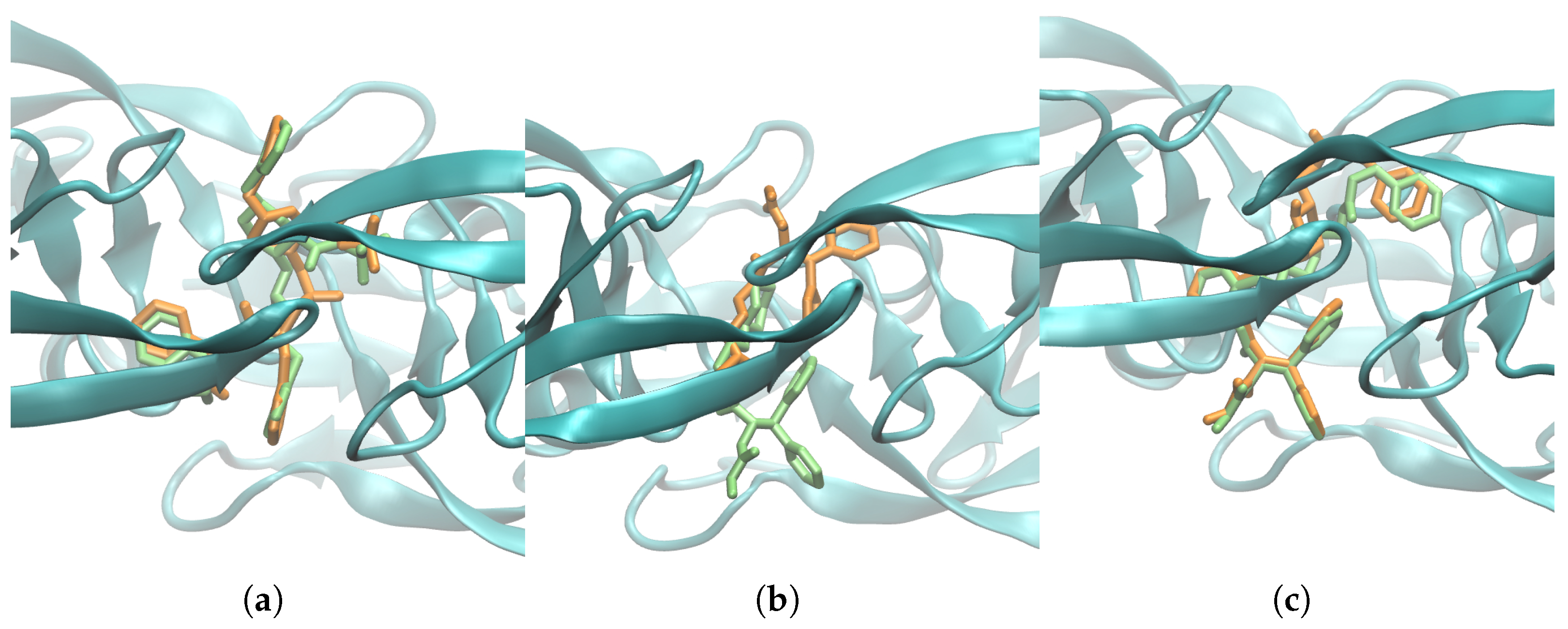
References
- Jorgensen, W.L. The many roles of computation in drug discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.; Li, X.; Lin, X. A review on applications of computational methods in drug screening and design. Molecules 2020, 25, 1375. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of drug–target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 2008, 24, i232–i240. [Google Scholar] [CrossRef] [PubMed]
- Bakheet, T.M.; Doig, A.J. Properties and identification of human protein drug targets. Bioinformatics 2009, 25, 451–457. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J.; et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef]
- Borkakoti, N.; Thornton, J.M. AlphaFold2 protein structure prediction: Implications for drug discovery. Curr. Opin. Struct. Biol. 2023, 78, 102526. [Google Scholar] [CrossRef]
- Karplus, M. Development of Multiscale Models for Complex Chemical Systems: From H+ H 2 to Biomolecules (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 2014, 53, 9992–10005. [Google Scholar] [CrossRef]
- De Vivo, M.; Masetti, M.; Bottegoni, G.; Cavalli, A. Role of molecular dynamics and related methods in drug discovery. J. Med. Chem. 2016, 59, 4035–4061. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, Y.; Qi, Z.; Hou, S.; Chen, J. Machine learning empowering drug discovery: Applications, opportunities and challenges. Molecules 2024, 29, 903. [Google Scholar] [CrossRef]
- Deng, J.; Yang, Z.; Ojima, I.; Samaras, D.; Wang, F. Artificial intelligence in drug discovery: Applications and techniques. Brief. Bioinform. 2022, 23, bbab430. [Google Scholar] [CrossRef] [PubMed]
- Ehrlich, P. Über den jetzigen Stand der Chemotherapie. Ber. Dtsch. Chem. Ges. 1909, 42, 17–47. [Google Scholar] [CrossRef]
- Yang, S.Y. Pharmacophore modeling and applications in drug discovery: Challenges and recent advances. Drug Discov. Today 2010, 15, 444–450. [Google Scholar] [CrossRef] [PubMed]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. QSAR without borders. Chem. Soc. Rev. 2020, 49, 3525–3564. [Google Scholar] [CrossRef]
- Paggi, J.M.; Pandit, A.; Dror, R.O. The art and science of molecular docking. Annu. Rev. Biochem. 2024, 93, 389–410. [Google Scholar] [CrossRef]
- Guterres, H.; Im, W. Improving protein-ligand docking results with high-throughput molecular dynamics simulations. J. Chem. Inf. Model. 2020, 60, 2189–2198. [Google Scholar] [CrossRef]
- Sardanelli, A.M.; Isgrò, C.; Palese, L.L. SARS-CoV-2 main protease active site ligands in the human metabolome. Molecules 2021, 26, 1409. [Google Scholar] [CrossRef]
- Limongelli, V. Ligand binding free energy and kinetics calculation in 2020. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1455. [Google Scholar] [CrossRef]
- Miller, D.W.; Dill, K.A. Ligand binding to proteins: The binding landscape model. Protein Sci. 1997, 6, 2166–2179. [Google Scholar] [CrossRef]
- Ikeguchi, M.; Ueno, J.; Sato, M.; Kidera, A. Protein structural change upon ligand binding: Linear response theory. Phys. Rev. Lett. 2005, 94, 078102. [Google Scholar] [CrossRef]
- Prabhu, N.V.; Sharp, K.A. Heat capacity in proteins. Annu. Rev. Phys. Chem. 2005, 56, 521–548. [Google Scholar] [CrossRef] [PubMed]
- Cooper, A. Protein heat capacity: An anomaly that maybe never was. J. Phys. Chem. Lett. 2010, 1, 3298–3304. [Google Scholar] [CrossRef]
- Vega, S.; Abian, O.; Velazquez-Campoy, A. On the link between conformational changes, ligand binding and heat capacity. Biochim. Biophys. Acta-Gen. Subj. 2016, 1860, 868–878. [Google Scholar] [CrossRef]
- Cooper, A.; Johnson, C.M.; Lakey, J.H.; Nöllmann, M. Heat does not come in different colours: Entropy–enthalpy compensation, free energy windows, quantum confinement, pressure perturbation calorimetry, solvation and the multiple causes of heat capacity effects in biomolecular interactions. Biophys. Chem. 2001, 93, 215–230. [Google Scholar] [CrossRef]
- Geschwindner, S.; Ulander, J.; Johansson, P. Ligand binding thermodynamics in drug discovery: Still a hot tip? J. Med. Chem. 2015, 58, 6321–6335. [Google Scholar] [CrossRef]
- Reynolds, C.H.; Holloway, M.K. Thermodynamics of ligand binding and efficiency. ACS Med. Chem. Lett. 2011, 2, 433–437. [Google Scholar] [CrossRef]
- Weber, P.C.; Salemme, F.R. Applications of calorimetric methods to drug discovery and the study of protein interactions. Curr. Opin. Struct. Biol. 2003, 13, 115–121. [Google Scholar] [CrossRef]
- Abian, O.; Vega, S.; Velazquez-Campoy, A. Biological calorimetry: Old friend, new insights. Biophysica 2023, 3, 21–34. [Google Scholar] [CrossRef]
- Winquist, J.; Geschwindner, S.; Xue, Y.; Gustavsson, L.; Musil, D.; Deinum, J.; Danielson, U.H. Identification of structural–kinetic and structural–thermodynamic relationships for thrombin inhibitors. Biochemistry 2013, 52, 613–626. [Google Scholar] [CrossRef]
- Todd, M.J.; Freire, E. The effect of inhibitor binding on the structural stability and cooperativity of the HIV-1 protease. Proteins 1999, 36, 147–156. [Google Scholar] [CrossRef]
- Todd, M.J.; Luque, I.; Velázquez-Campoy, A.; Freire, E. Thermodynamic basis of resistance to HIV-1 protease inhibition: Calorimetric analysis of the V82F/I84V active site resistant mutant. Biochemistry 2000, 39, 11876–11883. [Google Scholar] [CrossRef] [PubMed]
- Åqvist, J.; van der Ent, F. Calculation of heat capacity changes in enzyme catalysis and ligand binding. J. Chem. Theory Comput. 2022, 18, 6345–6353. [Google Scholar] [CrossRef] [PubMed]
- Koenekoop, L.; Åqvist, J. Computational Analysis of Heat Capacity Effects in Protein–Ligand Binding. J. Chem. Theory Comput. 2024, 20, 5708–5716. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Weast, R.C. CRC Handbook of Chemistry and Physics; CRC Press Inc.: Boca Raton, FL, USA, 1986. [Google Scholar]
- Vacca, J.P.; Dorsey, B.; Schleif, W.; Levin, R.; McDaniel, S.; Darke, P.; Zugay, J.; Quintero, J.; Blahy, O.; Roth, E. L-735,524: An orally bioavailable human immunodeficiency virus type 1 protease inhibitor. Proc. Natl. Acad. Sci. USA 1994, 91, 4096–4100. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Chen, E.; Hall, D.L.; Darke, P.L.; Culberson, C.; Shafer, J.A.; Kuo, L.C. Crystal structure at 1.9-A resolution of human immunodeficiency virus (HIV) II protease complexed with L-735,524, an orally bioavailable inhibitor of the HIV proteases. J. Biol. Chem. 1994, 269, 26344–26348. [Google Scholar] [CrossRef]
- Munshi, S.; Chen, Z.; Li, Y.; Olsen, D.B.; Fraley, M.E.; Hungate, R.W.; Kuo, L.C. Rapid X-ray diffraction analysis of HIV-1 protease–inhibitor complexes: Inhibitor exchange in single crystals of the bound enzyme. Acta Crystallogr. D 1998, 54, 1053–1060. [Google Scholar] [CrossRef]
- Munshi, S.; Chen, Z.; Yan, Y.; Li, Y.; Olsen, D.B.; Schock, H.B.; Galvin, B.B.; Dorsey, B.; Kuo, L.C. An alternate binding site for the P1–P3 group of a class of potent HIV-1 protease inhibitors as a result of concerted structural change in the 80s loop of the protease. Acta Crystallogr. D 2000, 56, 381–388. [Google Scholar] [CrossRef]
- King, N.M.; Melnick, L.; Prabu-Jeyabalan, M.; Nalivaika, E.A.; Yang, S.S.; Gao, Y.; Nie, X.; Zepp, C.; Heefner, D.L.; Schiffer, C.A. Lack of synergy for inhibitors targeting a multi-drug-resistant HIV-1 protease. Protein Sci. 2002, 11, 418–429. [Google Scholar] [CrossRef]
- Mahalingam, B.; Wang, Y.F.; Boross, P.I.; Tozser, J.; Louis, J.M.; Harrison, R.W.; Weber, I.T. Crystal structures of HIV protease V82A and L90M mutants reveal changes in the indinavir-binding site. Eur. J. Biochem. 2004, 271, 1516–1524. [Google Scholar] [CrossRef]
- Clemente, J.C.; Moose, R.E.; Hemrajani, R.; Whitford, L.R.; Govindasamy, L.; Reutzel, R.; McKenna, R.; Agbandje-McKenna, M.; Goodenow, M.M.; Dunn, B.M. Comparing the accumulation of active-and nonactive-site mutations in the HIV-1 protease. Biochemistry 2004, 43, 12141–12151. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Boross, P.I.; Wang, Y.F.; Tozser, J.; Louis, J.M.; Harrison, R.W.; Weber, I.T. Kinetic, stability, and structural changes in high-resolution crystal structures of HIV-1 protease with drug-resistant mutations L24I, I50V, and G73S. J. Mol. Biol. 2005, 354, 789–800. [Google Scholar] [CrossRef] [PubMed]
- Coman, R.M.; Robbins, A.H.; Fernandez, M.A.; Gilliland, C.T.; Sochet, A.A.; Goodenow, M.M.; McKenna, R.; Dunn, B.M. The contribution of naturally occurring polymorphisms in altering the biochemical and structural characteristics of HIV-1 subtype C protease. Biochemistry 2008, 47, 731–743. [Google Scholar] [CrossRef] [PubMed]
- Kuhnert, M.; Steuber, H.; Diederich, W.E. Structural basis for HTLV-1 protease inhibition by the HIV-1 protease inhibitor indinavir. J. Med. Chem. 2014, 57, 6266–6272. [Google Scholar] [CrossRef]
- Chen, X.; Liu, M.; Gilson, M.K. BindingDB: A web-accessible molecular recognition database. Comb. Chem. High Throughput Screen. 2001, 4, 719–725. [Google Scholar] [CrossRef]
- Liu, T.; Hwang, L.; Burley, S.K.; Nitsche, C.I.; Southan, C.; Walters, W.P.; Gilson, M.K. BindingDB in 2024: A FAIR knowledgebase of protein-small molecule binding data. Nucleic Acids Res. 2025, 53, D1633–D1644. [Google Scholar] [CrossRef]
- Bungard, C.J.; Williams, P.D.; Ballard, J.E.; Bennett, D.J.; Beaulieu, C.; Bahnck-Teets, C.; Carroll, S.S.; Chang, R.K.; Dubost, D.C.; Fay, J.F.; et al. Discovery of MK-8718, an HIV protease inhibitor containing a novel morpholine aspartate binding group. ACS Med. Chem. Lett. 2016, 7, 702–707. [Google Scholar] [CrossRef]
- Lervik, A.; Bresme, F.; Kjelstrup, S.; Bedeaux, D.; Rubi, J.M. Heat transfer in protein–water interfaces. Phys. Chem. Chem. Phys. 2010, 12, 1610–1617. [Google Scholar] [CrossRef]
- Eftink, M.R.; Anusiem, A.; Biltonen, R.L. Enthalpy-entropy compensation and heat capacity changes for protein-ligand interactions: General thermodynamic models and data for the binding of nucleotides to ribonuclease A. Biochemistry 1983, 22, 3884–3896. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Burley, S.K.; Bhikadiya, C.; Bi, C.; Bittrich, S.; Chen, L.; Crichlow, G.V.; Christie, C.H.; Dalenberg, K.; Di Costanzo, L.; Duarte, J.M.; et al. RCSB Protein Data Bank: Powerful new tools for exploring 3D structures of biological macromolecules for basic and applied research and education in fundamental biology, biomedicine, biotechnology, bioengineering and energy sciences. Nucleic Acids Res. 2021, 49, D437–D451. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Jo, S.; Brooks, C.L., III; Lee, H.S.; Im, W. CHARMM-GUI ligand reader and modeler for CHARMM force field generation of small molecules. J. Comput. Chem. 2017, 38, 1879–1886. [Google Scholar] [CrossRef]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Kalé, L.; Skeel, R.; Bhandarkar, M.; Brunner, R.; Gursoy, A.; Krawetz, N.; Phillips, J.; Shinozaki, A.; Varadarajan, K.; Schulten, K. NAMD2: Greater scalability for parallel molecular dynamics. J. Comput. Phys. 1999, 151, 283–312. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; De Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys 1994, 101, 10–1063. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2010, 31, 455–461. [Google Scholar] [CrossRef]
- Eberhardt, J.; Santos-Martins, D.; Tillack, A.F.; Forli, S. AutoDock Vina 1.2.0: New docking methods, expanded force field, and python bindings. J. Chem. Inf. Model. 2021, 61, 3891–3898. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef]
- Gasteiger, J.; Marsili, M. A new model for calculating atomic charges in molecules. Tetrahedron Lett. 1978, 19, 3181–3184. [Google Scholar] [CrossRef]
- Bell, E.W.; Zhang, Y. DockRMSD: An open-source tool for atom mapping and RMSD calculation of symmetric molecules through graph isomorphism. J. Cheminform. 2019, 11, 1–9. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 1–14. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
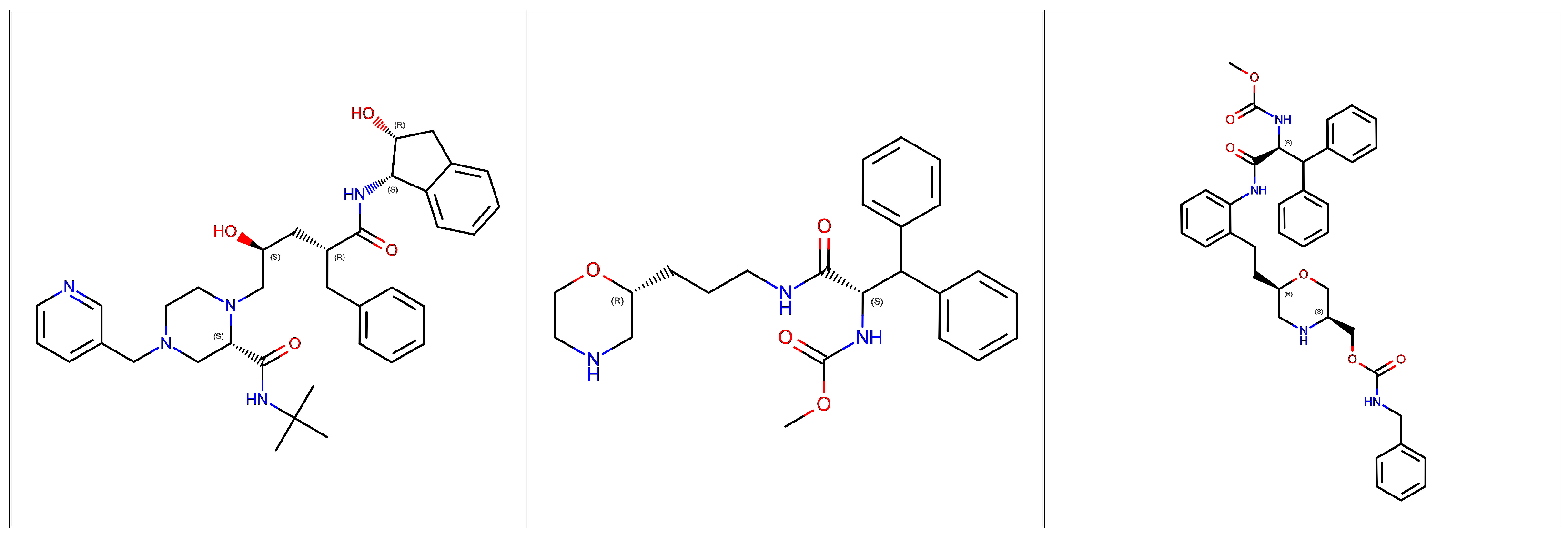

| Ligand ID | 1SDT | 5IVQ | 5IVS |
|---|---|---|---|
| MK1 | −11.89 (0.20) | −10.16 (0.21) | −11.33 (0.26) |
| 6EF | −10.93 (0.40) | −10.79 (0.47) | −11.73 (0.04) |
| 6EH | −9.35 (0.03) | −9.15 (0.15) | −9.41 (0.47) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palese, L.L. Accurate Prediction of Drug Activity by Computational Methods: Importance of Thermal Capacity. Molecules 2025, 30, 2563. https://doi.org/10.3390/molecules30122563
Palese LL. Accurate Prediction of Drug Activity by Computational Methods: Importance of Thermal Capacity. Molecules. 2025; 30(12):2563. https://doi.org/10.3390/molecules30122563
Chicago/Turabian StylePalese, Luigi Leonardo. 2025. "Accurate Prediction of Drug Activity by Computational Methods: Importance of Thermal Capacity" Molecules 30, no. 12: 2563. https://doi.org/10.3390/molecules30122563
APA StylePalese, L. L. (2025). Accurate Prediction of Drug Activity by Computational Methods: Importance of Thermal Capacity. Molecules, 30(12), 2563. https://doi.org/10.3390/molecules30122563










