Surface Charge Effects for the Hydrogen Evolution Reaction on Pt(111) Using a Modified Grand-Canonical Potential Kinetics Method
Abstract
1. Introduction
2. Results and Discussions
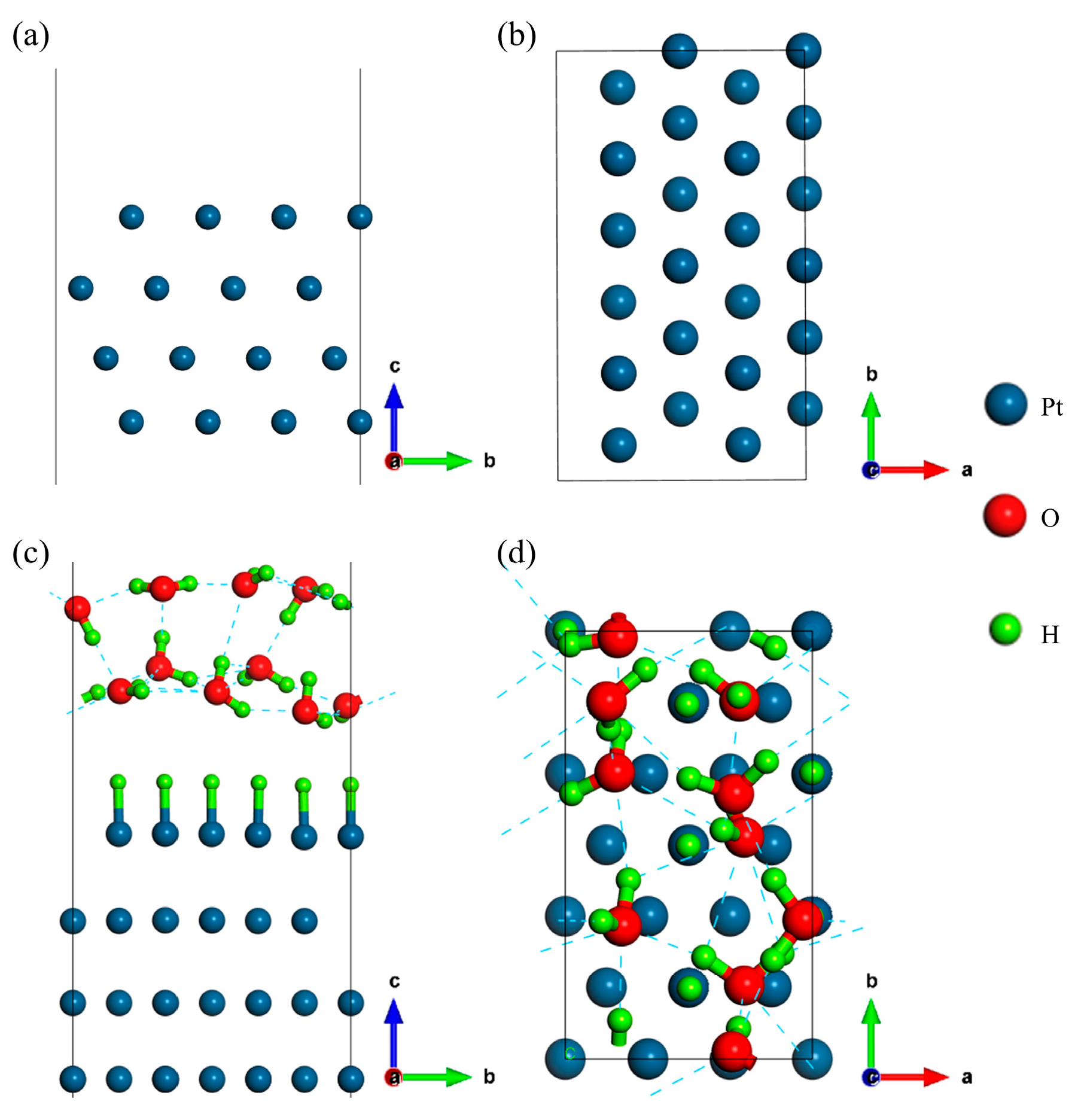
2.1. Structure Models
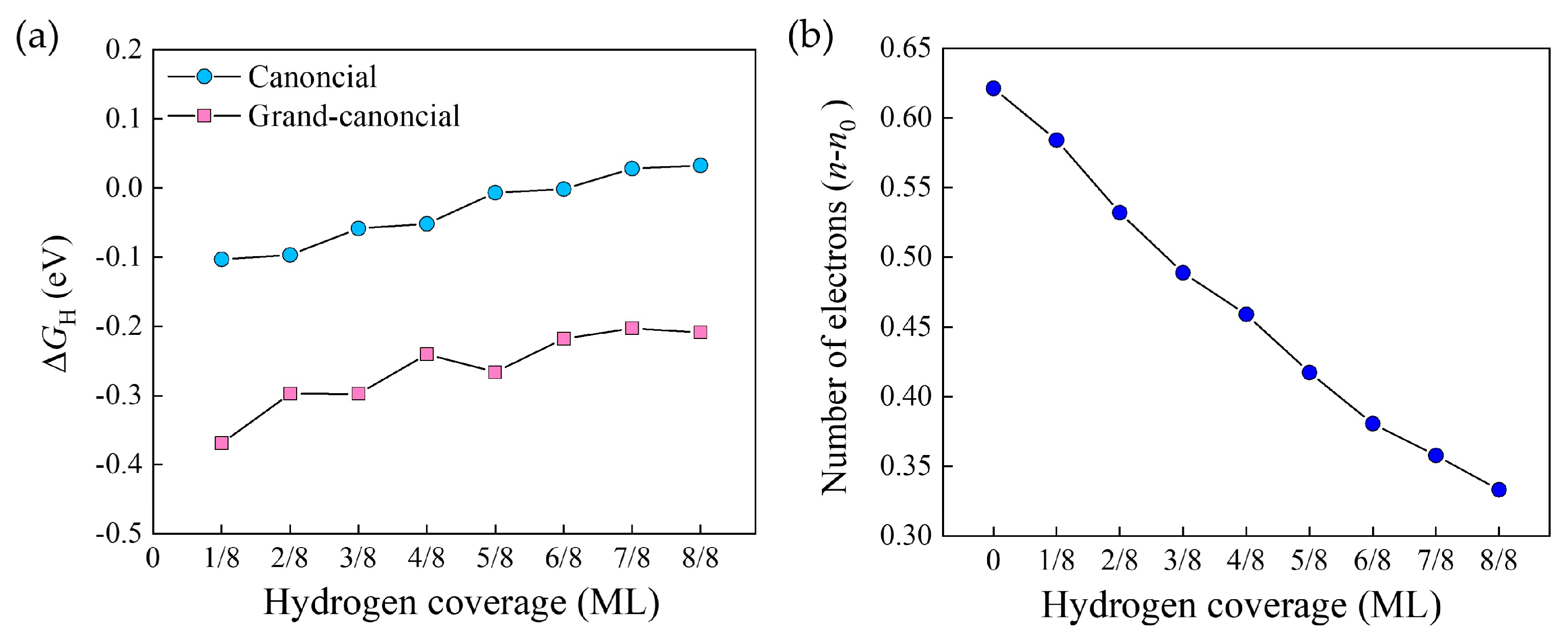
2.2. Hydrogen Adsorption Energies
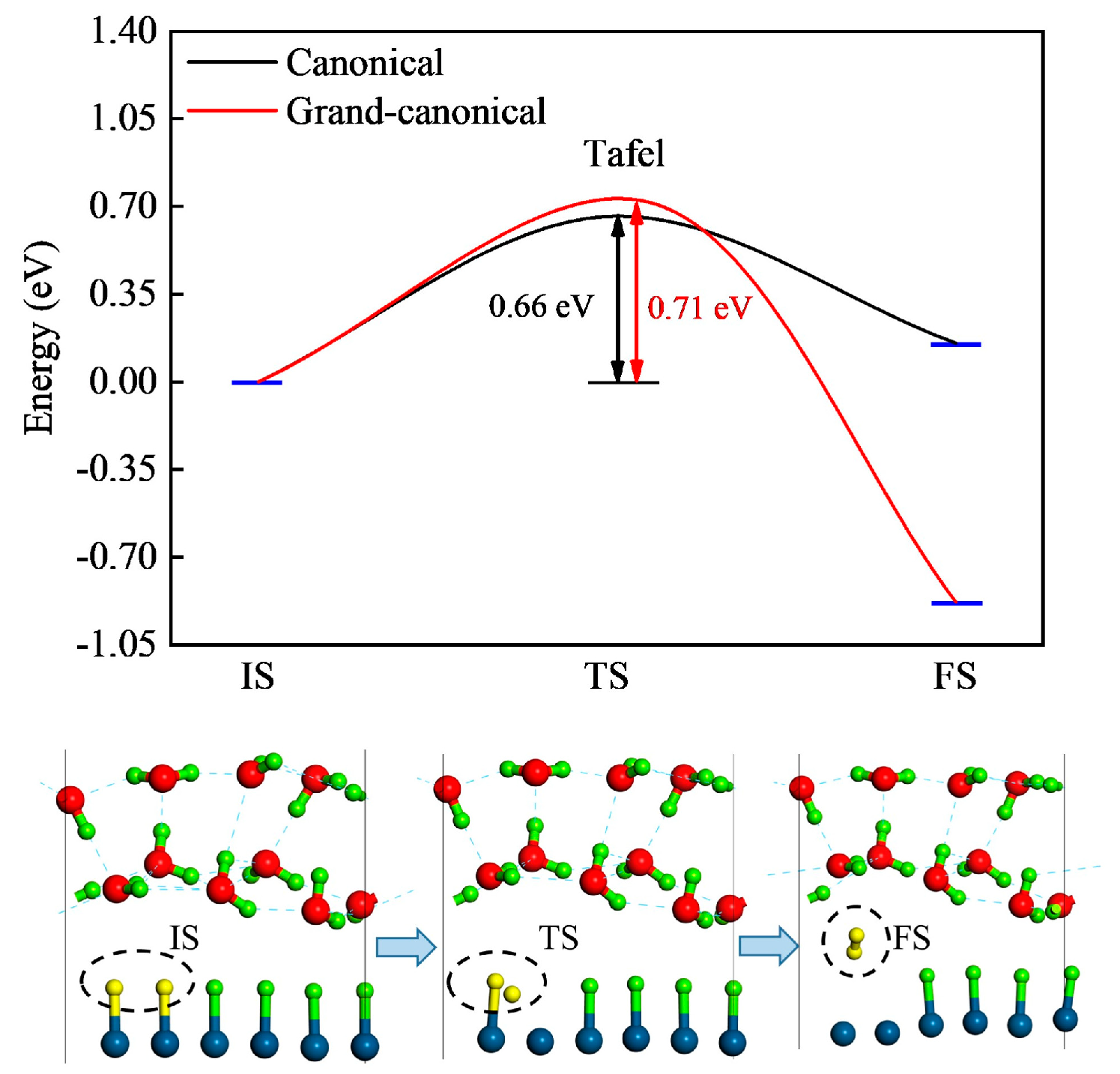
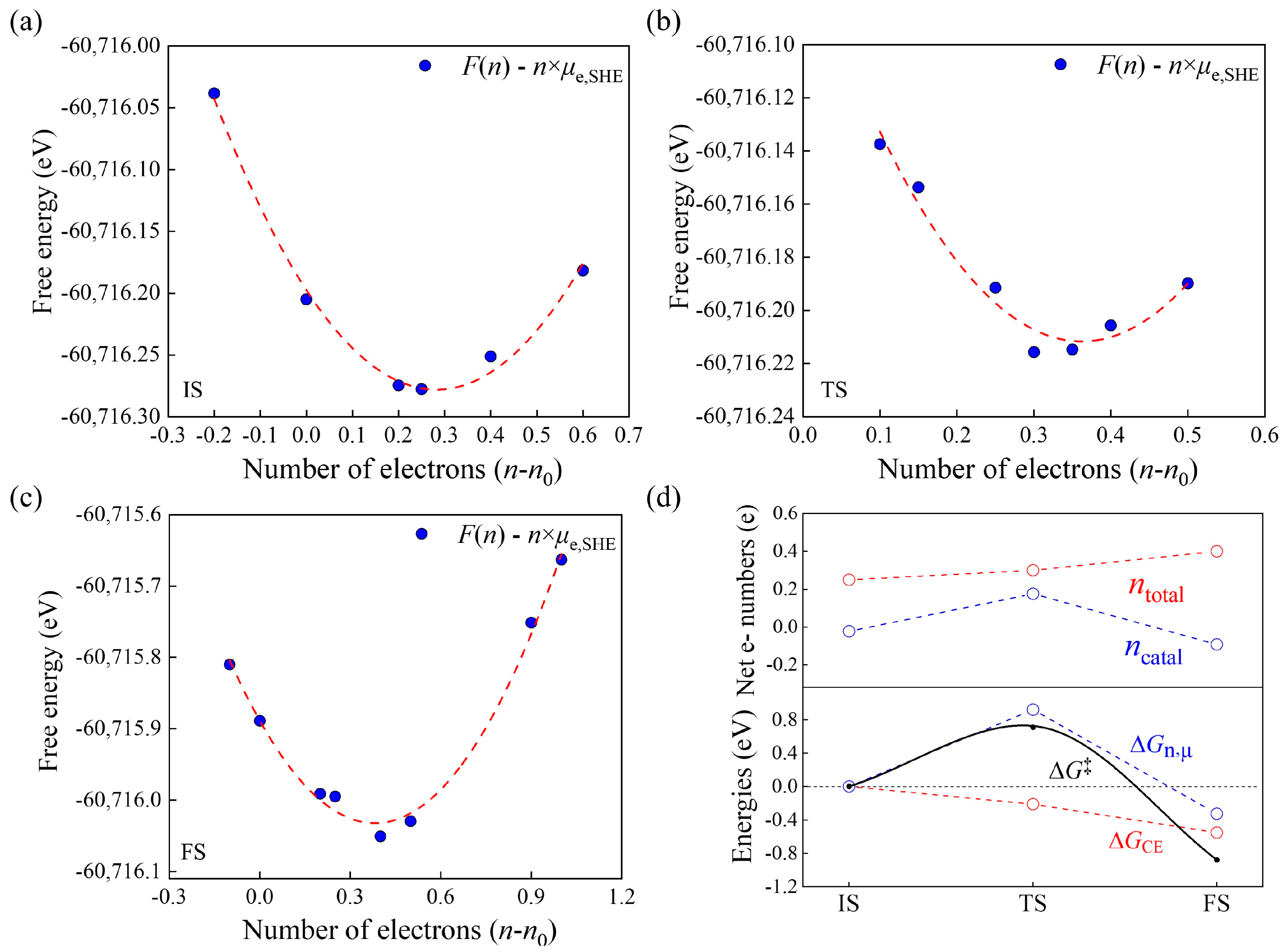
2.3. Reaction Kinetics
3. Methods
3.1. DFT Computational Details
3.2. Canonical Calculation of Hydrogen Adsorption Energy
3.3. Grand-Canonical Calculation of Hydrogen Adsorption Energy
3.4. Modified GCP-K Method
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kreuter, W.; Hofmann, H. Electrolysis: The important energy transformer in a world of sustainable energy. Int. J. Hydrogen Energy 1998, 23, 661–666. [Google Scholar] [CrossRef]
- Christopher, K.; Dimitrios, R. A review on exergy comparison of hydrogen production methods from renewable energy sources. Energy Environ. Sci. 2012, 5, 6640–6651. [Google Scholar] [CrossRef]
- Wang, J.; Xu, F. Non-Noble Metal-based Carbon Composites in Hydrogen Evolution Reaction: Fundamentals to Applications. Adv. Mater. 2017, 29, 1605838. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T. Towards the computational design of solid catalysts. Nat. Chem. 2009, 1, 37–46. [Google Scholar] [CrossRef]
- Conway, B.E.; Bockris, J.O.M. Electrolytic Hydrogen Evolution Kinetics and Its Relation to the Electronic and Adsorptive Properties of the Metal. J. Chem. Phys. 2004, 26, 532–541. [Google Scholar] [CrossRef]
- Hansen, H.A.; Rossmeisl, J. Surface Pourbaix diagrams and oxygen reduction activity of Pt, Ag and Ni(111) surfaces studied by DFT. Phys. Chem. Chem. Phys. 2008, 10, 3722–3730. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Skúlason, E. Modeling the electrified solid–liquid interface. Chem. Phys. Lett. 2008, 466, 68–71. [Google Scholar] [CrossRef]
- Skúlason, E.; Karlberg, G.S. Density functional theory calculations for the hydrogen evolution reaction in an electrochemical double layer on the Pt(111) electrode. Phys. Chem. Chem. Phys. 2007, 9, 3241–3250. [Google Scholar] [CrossRef]
- Lamoureux, P.S.; Singh, A.R. pH Effects on Hydrogen Evolution and Oxidation over Pt(111): Insights from First-Principles. ACS Catal. 2019, 9, 6194–6201. [Google Scholar] [CrossRef]
- Kronberg, R.; Laasonen, K. Reconciling the Experimental and Computational Hydrogen Evolution Activities of Pt(111) through DFT-Based Constrained MD Simulations. ACS Catal. 2021, 11, 8062–8078. [Google Scholar] [CrossRef]
- Kim, D.; Shi, J. Substantial Impact of Charge on Electrochemical Reactions of Two-Dimensional Materials. J. Am. Chem. Soc. 2018, 140, 9127–9131. [Google Scholar] [CrossRef]
- Kim, K.Y.; Lee, J. Role of Hyper-Reduced States in Hydrogen Evolution Reaction at Sulfur Vacancy in MoS2. ACS Catal. 2018, 8, 4508–4515. [Google Scholar] [CrossRef]
- Huang, Y.; Nielsen, R.J. Reaction Mechanism for the Hydrogen Evolution Reaction on the Basal Plane Sulfur Vacancy Site of MoS2 Using Grand Canonical Potential Kinetics. J. Am. Chem. Soc. 2018, 140, 16773–16782. [Google Scholar] [CrossRef]
- Melander, M.M.; Kuisma, M.J. Grand-canonical approach to density functional theory of electrocatalytic systems: Thermodynamics of solid-liquid interfaces at constant ion and electrode potentials. J. Chem. Phys. 2018, 150, 041706. [Google Scholar] [CrossRef]
- Huang, J.; Climent, V. Understanding surface charge effects in electrocatalysis. Part 2: Hydrogen peroxide reactions at platinum. Chin. J. Catal. 2022, 43, 2837–2849. [Google Scholar] [CrossRef]
- An, Y.; Cao, W. Substantial impact of surface charges on electrochemical reaction kinetics on S vacancies of MoS2 using grand-canonical iteration method. J. Chem. Phys. 2023, 159, 144702. [Google Scholar] [CrossRef]
- Rossmeisl, J.; Chan, K. pH in atomic scale simulations of electrochemical interfaces. Phys. Chem. Chem. Phys. 2013, 15, 10321–10325. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 152, J23. [Google Scholar] [CrossRef]
- Jaramillo, T.F.; Jørgensen, K.P. Identification of Active Edge Sites for Electrochemical H2 Evolution from MoS2 Nanocatalysts. Science 2007, 317, 100–102. [Google Scholar] [CrossRef]
- Chen, X.; Gu, Y. Origin of hydrogen evolution activity on MS 2 (M = Mo or Nb) monolayers. J. Mater. Chem. A 2015, 3, 18898–18905. [Google Scholar] [CrossRef]
- Strmcnik, D.; Uchimura, M. Improving the hydrogen oxidation reaction rate by promotion of hydroxyl adsorption. Nat. Chem. 2013, 5, 300–306. [Google Scholar] [CrossRef]
- Skúlason, E.; Tripkovic, V. Modeling the Electrochemical Hydrogen Oxidation and Evolution Reactions on the Basis of Density Functional Theory Calculations. J. Phys. Chem. C 2010, 114, 18182–18197. [Google Scholar] [CrossRef]
- Sarwar, S.; Ali, A. Towards thermoneutral hydrogen evolution reaction using noble metal free molybdenum ditelluride/graphene nanocomposites. J. Colloid Interface Sci. 2021, 581, 847–859. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Dion, M.; Rydberg, H. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed]
- Román-Pérez, G.; Soler, J.M. Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes. Phys. Rev. Lett. 2009, 103, 096102. [Google Scholar] [CrossRef] [PubMed]
- Klimes, J.; Bowler, D. Van der Waals density functional applied to solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar] [CrossRef]
- Sheppard, D.; Henkelman, G. Paths to which the nudged elastic band converges. J. Comput. Chem. 2011, 32, 1769–1771. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, D.; Xiao, P. A generalized solid-state nudged elastic band method. J. Chem. Phys. 2012, 136, 074103. [Google Scholar] [CrossRef]
- Sheppard, D.; Terrell, R. Optimization methods for finding minimum energy paths. J. Chem. Phys. 2008, 128, 134106. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
- Jónsson, H.; Mills, G. Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Chan, K.; Nørskov, J.K. Electrochemical Barriers Made Simple. J. Phys. Chem. Lett. 2015, 6, 2663–2668. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X. Reaction Mechanism with Thermodynamic Structural Screening for Electrochemical Hydrogen Evolution on Monolayer 1T′ Phase MoS2. Chem. Mater. 2018, 30, 5404–5411. [Google Scholar] [CrossRef]
- Sundararaman, R.; Goddard, W.A., III. The charge-asymmetric nonlocally determined local-electric (CANDLE) solvation model. J. Chem. Phys. 2015, 142, 064107. [Google Scholar] [CrossRef]
- An, Y.; Ouyang, M. Electronegativity principle for hydrogen evolution activity using first-principles calculations. Phys. Chem. Chem. Phys. 2023, 25, 13289–13296. [Google Scholar] [CrossRef]
| Species | nIS,total | nTS,total | Δntotal |
|---|---|---|---|
| H2O-1 | 7.94 | 7.90 | −0.04 |
| H2O-2 | 7.95 | 7.95 | −0.004 |
| H2O-3 | 8.04 | 7.98 | −0.06 |
| H2O-4 * | 7.95 | 8.01 | +0.06 |
| H2O-5 | 8.04 | 8.03 | −0.01 |
| H2O-6 | 8.05 | 8.01 | −0.04 |
| H2O-7 | 8.00 | 7.97 | −2.04 |
| H2O-8 * | 8.03 | 8.04 | +0.01 |
| H2O-9 * | 7.96 | 7.99 | +0.03 |
| H2O-10 * | 8.00 | 8.05 | +0.05 |
| Catalyst | 390.04 | 390.08 | +0.05 |
| Total | 470.0002 | 470.0001 | −2.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, S.; Ouyang, M.; An, Y.; Cao, W.; Chen, X. Surface Charge Effects for the Hydrogen Evolution Reaction on Pt(111) Using a Modified Grand-Canonical Potential Kinetics Method. Molecules 2024, 29, 1813. https://doi.org/10.3390/molecules29081813
Kong S, Ouyang M, An Y, Cao W, Chen X. Surface Charge Effects for the Hydrogen Evolution Reaction on Pt(111) Using a Modified Grand-Canonical Potential Kinetics Method. Molecules. 2024; 29(8):1813. https://doi.org/10.3390/molecules29081813
Chicago/Turabian StyleKong, Shaoyu, Min Ouyang, Yi An, Wei Cao, and Xiaobo Chen. 2024. "Surface Charge Effects for the Hydrogen Evolution Reaction on Pt(111) Using a Modified Grand-Canonical Potential Kinetics Method" Molecules 29, no. 8: 1813. https://doi.org/10.3390/molecules29081813
APA StyleKong, S., Ouyang, M., An, Y., Cao, W., & Chen, X. (2024). Surface Charge Effects for the Hydrogen Evolution Reaction on Pt(111) Using a Modified Grand-Canonical Potential Kinetics Method. Molecules, 29(8), 1813. https://doi.org/10.3390/molecules29081813







