High-Precision Determination of NMR Interaction Parameters by Measurement of Single Crystals: A Review of Classical and Advanced Methods
Abstract
1. Introduction
2. The NMR Resonance Line: The Origins of Orientation Dependence
2.1. The Chemical Shift
2.2. The Quadrupole Interaction
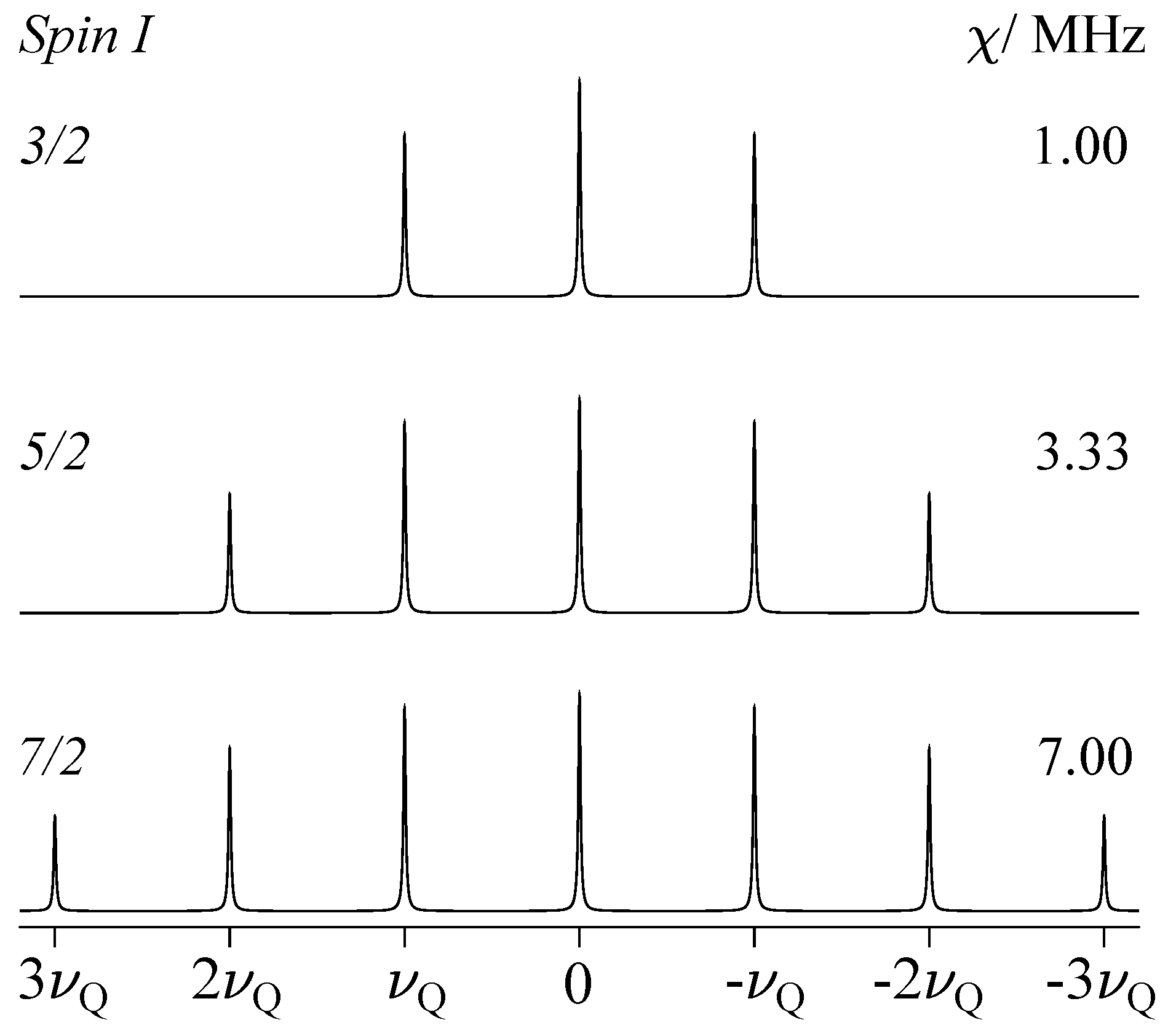
2.2.1. Quadrupole Interaction for Half-Integer Spin
2.2.2. Quadrupole Interaction for Integer Spin
- (i)
- The tensors of a deuterium atom in a covalent bond are nearly axially symmetric, with the asymmetry parameter remaining in the range of .
- (ii)
- The direction of the eigenvector associated with the largest principal component of the tensor () is parallel to the bond direction of the deuteron.
- (iii)
- If the deuteron is part of a planar structure (e.g., aromatic rings), the eigenvector of the second-largest principal component () is perpendicular to this plane.
2.3. The Dipolar Interaction
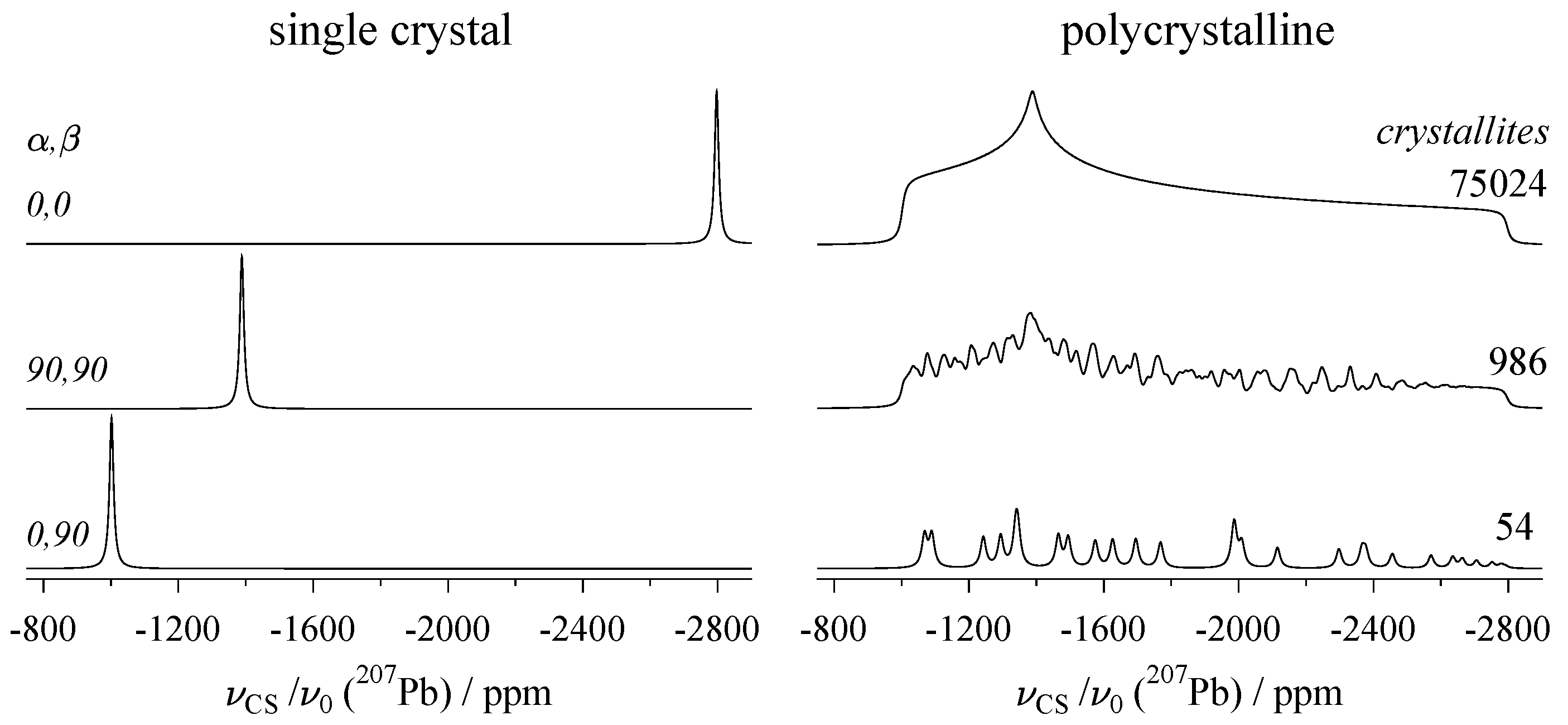
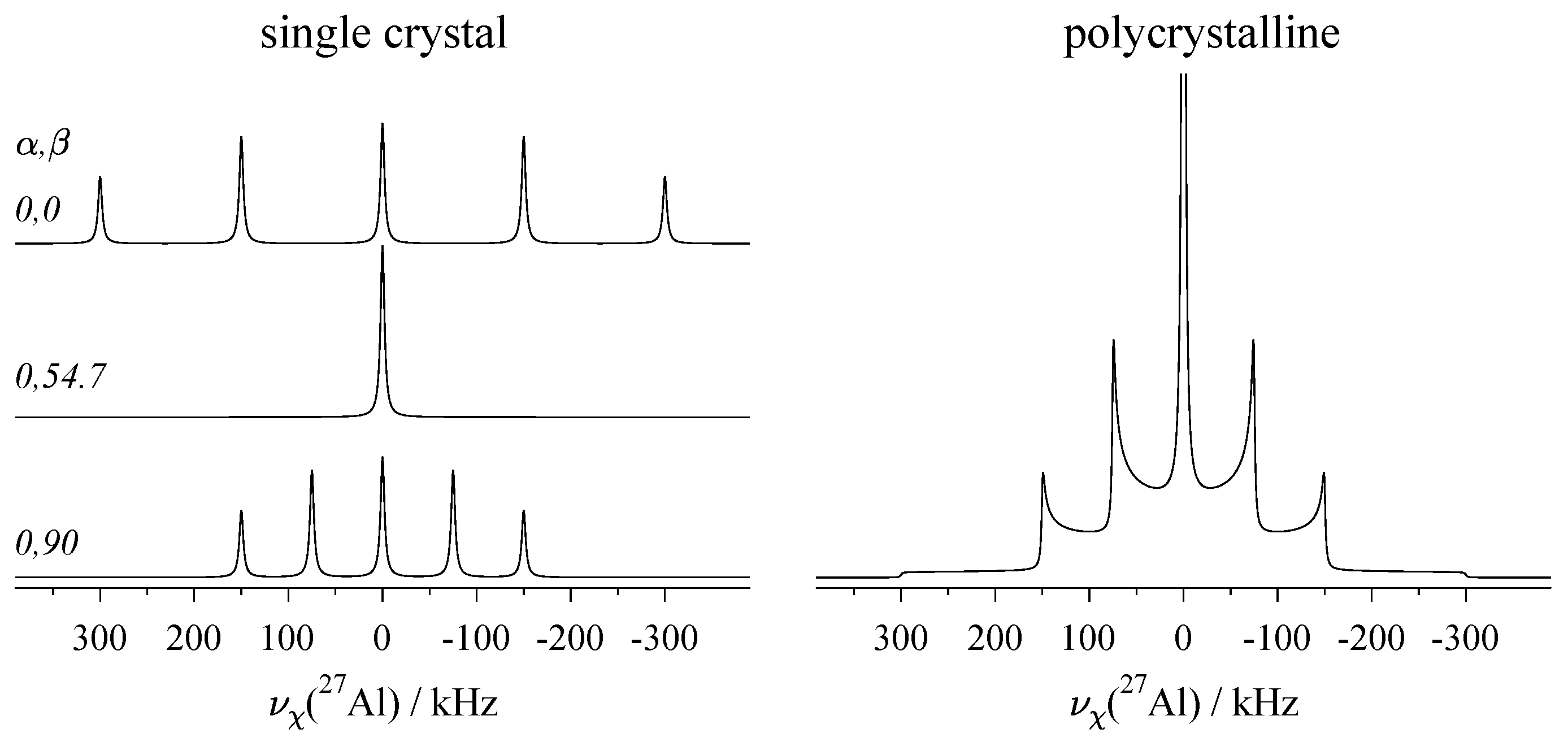
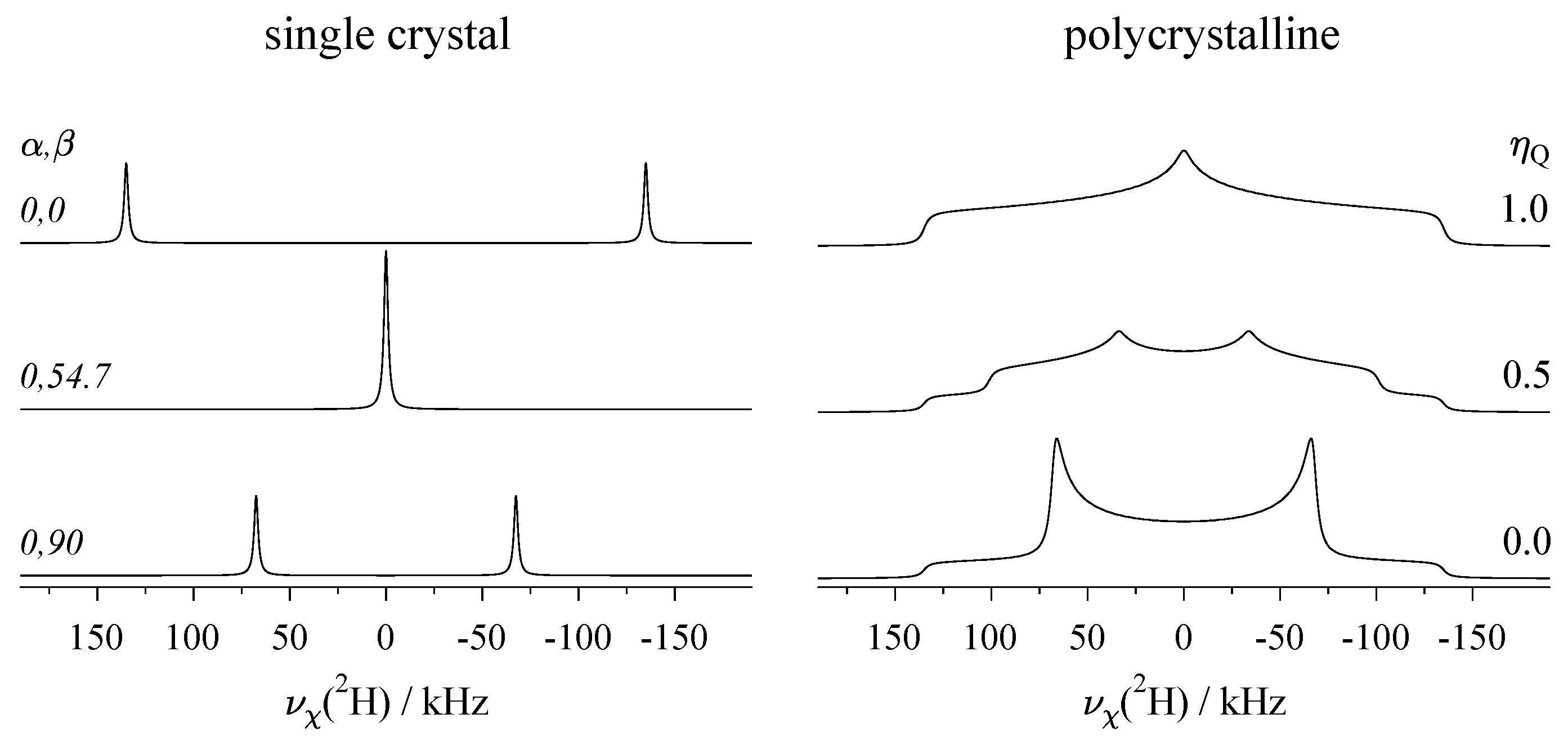
2.4. Effect of the Various Interactions on Single-Crystal Spectra
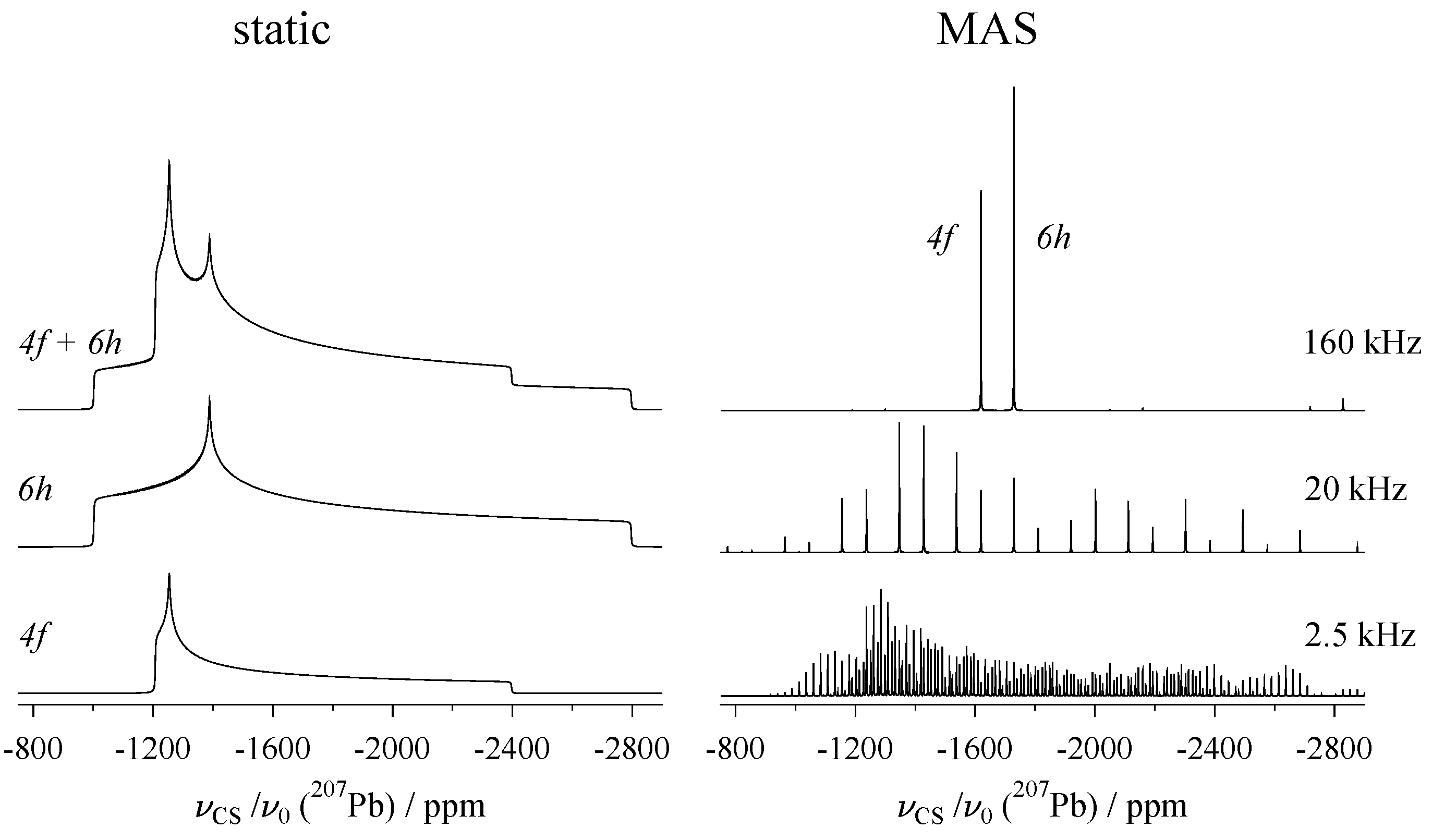
3. Averaging the Orientation Dependence: Magic-Angle-Spinning (MAS)
3.1. MAS of Polycrystalline Samples
3.2. MAS of Single Crystals
4. Expressing the Orientation Dependence: The Tensor Representation
4.1. Deriving the Resonance Position from the Interaction Tensor
4.2. Equivalence of Interaction Tensors in the Crystal Structure
- Crystallograpic Equivalence:
- Spins are connected by any symmetry element.
- Magnetic Equivalence:
- Spins are connected by either inversion or translation.
4.3. Effects of Crystal Symmetry on Tensor Shape
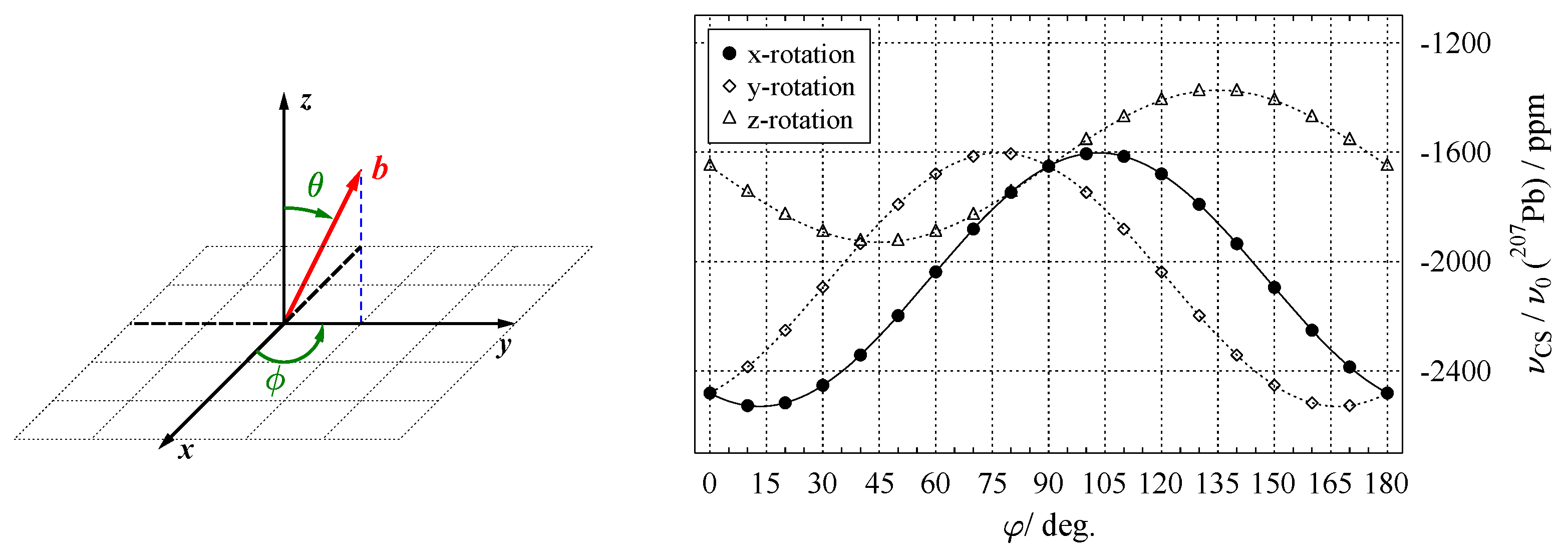
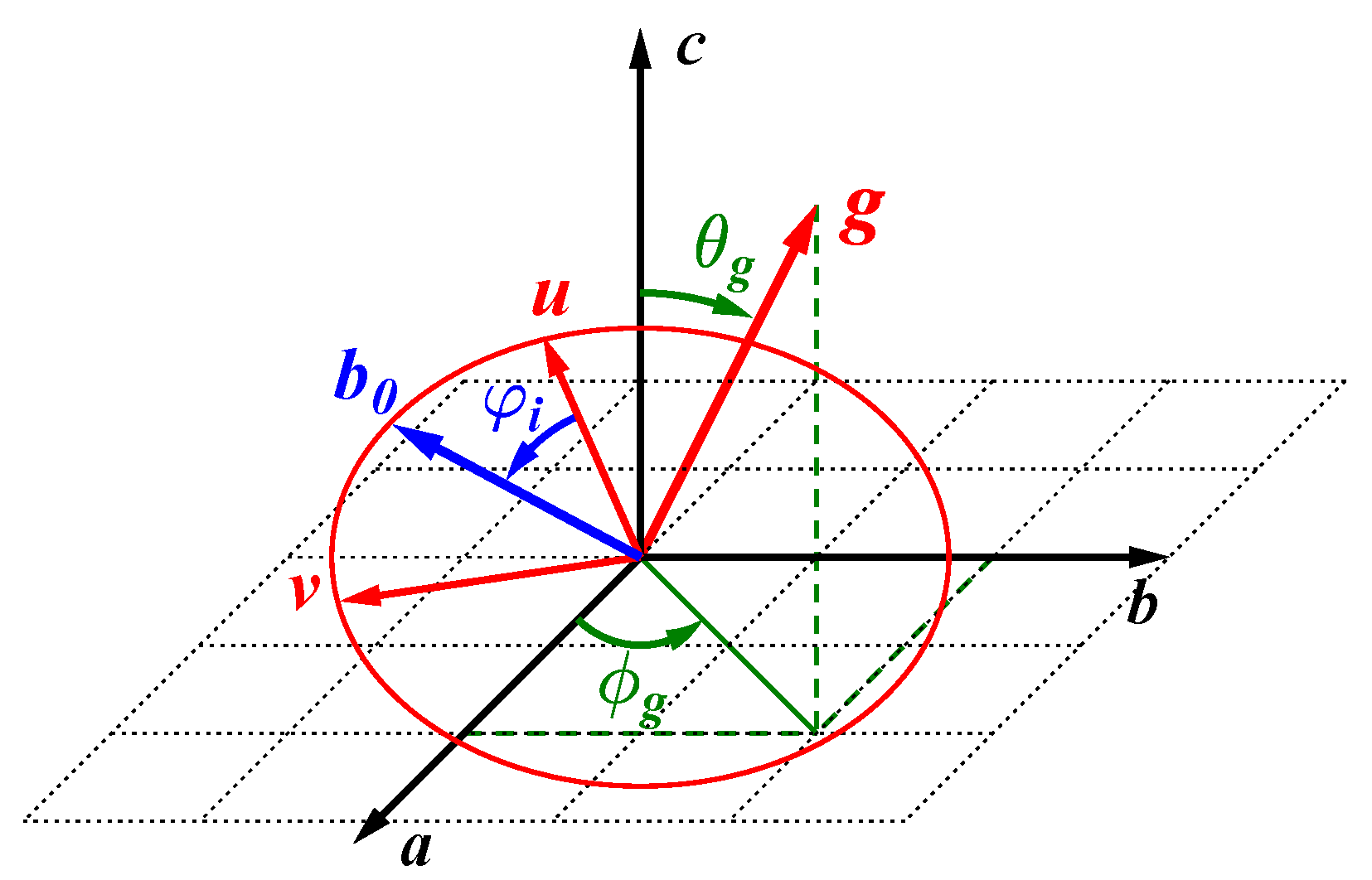
5. Recording the Orientation Dependence: The Rotation Pattern
5.1. Goniometer Axis Perpendicular to the Magnetic Field
5.2. Other Goniometer Geometries
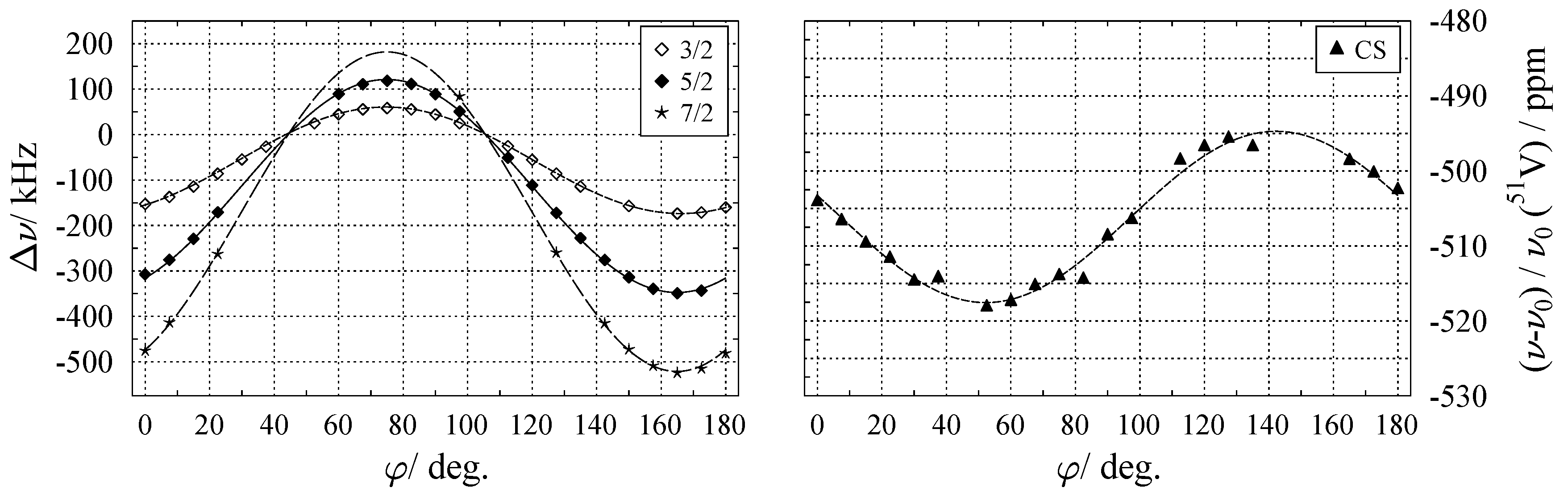
6. Analysing the Orientation Dependence: From Rotation Pattern to Tensor
6.1. Chemical Shift Tensor
6.2. Quadrupole Coupling Tensor
6.3. The Single-Rotation Method
6.4. The Minimal-Rotation Method
7. Predicting the Future of Orientation Dependence: Outlook
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tensor Transformations
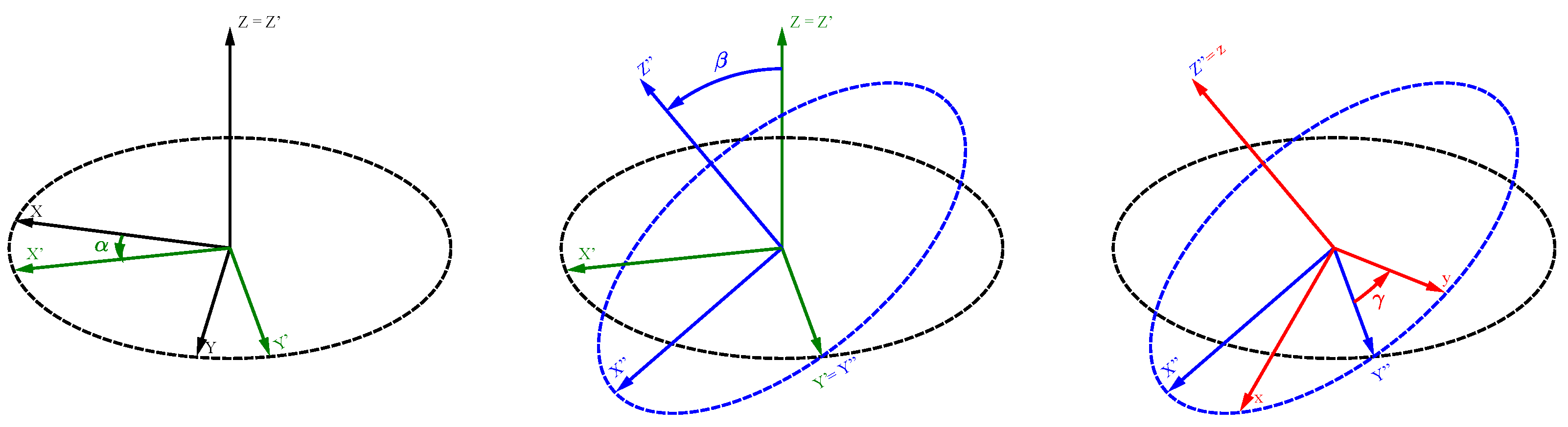
Appendix A.1. The Euler Angles
Appendix A.2. Euler Rotation Matrices
Appendix A.3. General Rotation Matrix
Appendix A.4. Active vs. Passive Rotations
Appendix A.5. Inversion and Reflection
Appendix B. NMR Interaction Tensors from Single-Crystal Experiments
| Compound | Wyckoff | Ref. | ||||
|---|---|---|---|---|---|---|
| (Mineral) | Position | (in ppm) | ||||
| PbCO3 (cerussite) | [10] | |||||
| Pb5(VO4)3Cl | [124] | |||||
| (vanadinite) | ||||||
| PbMoO4 (wulfenite) | [129] | |||||
| Pb2Cl2CO3 (phosgenite) | [129] | |||||
| PbSO4 (anglesite) | [130] | |||||
| Pb5(PO4)3Cl | [143] | |||||
| (pyromorphite) | ||||||
| Nuclide | Spin I | Compound | Ref. | |||
|---|---|---|---|---|---|---|
| (Mineral) | (in MHz) | (in ppm) | ||||
| 7Li | LiH2PO4 | a | [144] | |||
| -LiAlO2 | 82 a | [145,146] | ||||
| 9Be | Be3Al2Si6O18 | a | [5,147] | |||
| (beryl) | ||||||
| 11B | CaB3O4 (OH)3 H2O | [126] | ||||
| (colemanite) | ||||||
| Na2B4O7 10H2O | ||||||
| (borax) | ||||||
| 69Ga | CdGa2Te4 | 0 | 120 | [148] | ||
| 0 | 290 | |||||
| 71Ga | Y3Ga5O12 | [149] | ||||
| 87Rb | RbClO4 | [150] | ||||
| Rb2SO4 | ||||||
| [150] | ||||||
| Rb2CrO4 | ||||||
| [151] | ||||||
| RbVO3 | [152] | |||||
| 27Al | AlN | 0 | [81] | |||
| -Al2O3 | [153] | |||||
| -LiAlO2 | [127] | |||||
| Al2SiO5 | [154] | |||||
| (andalusite) | ||||||
| 67Zn | Zn(CH3COO)2 · 2H2O | [155] | ||||
| Zn(HCOO)2 · 2H2O | [156] | |||||
| 45Sc | [{Sc(H2O)5(-OH)}2]Cl4H2O | [157] | ||||
| 51V | V2O5 | a | [125,158] | |||
| Pb5(VO4)3Cl | [124] | |||||
| 133Cs | Cs2CrO4 | [159] | ||||
| Compound | Deuteron(s) a | (in kHz) | Ref. | ||
|---|---|---|---|---|---|
| Name | Formula | ||||
| Benzene | C6D6 | all | 187 b | 0 b | [160] |
| Pyromellitic acid | C6D2(COOD)4 | D3, D3′ | 168 | 0.075 | [161] |
| Azulene | C10H6D2 | D1, D3 | 182 | 0.06 | [162] |
| 2,3-Dimethyl-naphthalene | C10H6(CH3)2 | D1,2,3 | 177 | 0 | [163] |
| Fluorene | C13D10 | D1,4 | 0.047 | [136] | |
| D5,8 | 0.040 | ||||
| D2 | 0.047 | ||||
| D3 | 0.047 | ||||
| Anthracene | C14D10 | (B, F, D) | 179.0 | 0.058 | [164] |
| A | 183.7 | 0.067 | |||
| G | 181.3 | 0.055 | |||
Appendix C. Coefficients for Quadrupole Interaction 2nd and 3rd Order
Appendix D. Equivalence of Tensor and Polar/Azimuthal Angle Notation
References
- Purcell, E.M.; Bloembergen, N.; Pound, R.V. Resonance absorption by nuclear magnetic moments in a single crystal of CaF2. Phys. Rev. 1946, 70, 988. [Google Scholar] [CrossRef]
- Pound, R.V. Nuclear electric quadrupole interaction in crystals. Phys. Rev. 1950, 79, 685–702. [Google Scholar] [CrossRef]
- Itoh, J.; Kusaka, R.; Yamagata, Y.; Kiriyama, R.; Ibamoto, H. Nuclear magnetic resonance experiment on a four-proton system in a single crystal of K2HgCl4· H2O. J. Chem. Phys. 1952, 20, 1503–1504. [Google Scholar] [CrossRef]
- Volkoff, G.M.; Petch, H.E.; Smellie, D.W.L. Nuclear electric quadrupole interactions in single crystals. Can. J. Phys. 1952, 30, 270–289. [Google Scholar] [CrossRef]
- Brown, C.L.; Williams, D. Quadrupolar splitting of the Al27 and Be9 magnetic resonances in beryl crystals. J. Chem. Phys. 1956, 24, 751–756. [Google Scholar] [CrossRef]
- Sherwood, M.H.; Facelli, J.C.; Alderman, D.W.; Grant, D.M. Carbon-13 chemical shift tensors in polycyclic aromatic compounds. 2. Single-crystal study of naphthalene. J. Am. Chem. Soc. 1991, 113, 750–753. [Google Scholar] [CrossRef]
- Bräuniger, T.; Poupko, R.; Luz, Z.; Reichert, D.; Zimmermann, H.; Schmitt, H.; Haeberlen, U. Orientational disorder in 1,2,3-trichloro-4,5,6-trimethylbenzene. A single crystal deuterium NMR study of the site populations and dynamics. Phys. Chem. Chem. Phys. 2001, 3, 1891–1903. [Google Scholar] [CrossRef]
- Odin, C. Critical behavior of KDCO3 from 2H and 39K single crystal NMR. Magn. Reson. Chem. 2008, 46, 9–16. [Google Scholar] [CrossRef]
- Vosegaard, T.; Byriel, I.P.; Binet, L.; Massiot, D.; Jakobsen, H.J. Crystal structure studies by single-crystal NMR spectroscopy. 71Ga and 69Ga single-crystal NMR of β-Ga2O3 twins. J. Am. Chem. Soc. 1998, 120, 8184–8188. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Steinadler, J.; Hochleitner, R.; Bräuniger, T. Characterisation of contact twinning for cerussite, PbCO3, by single-crystal NMR spectroscopy. Phys. Chem. Miner. 2021, 48, 40. [Google Scholar] [CrossRef]
- Verkhovskii, S.V.; Yakubovsky, A.Y.; Malkin, B.Z. Saikin, S.K.; Cardona, M.; Trokiner, A.; Ozhogin, V.I. Isotopic disorder in Ge single crystals probed with 73Ge NMR. Phys. Rev. B 2003, 68, 104201. [Google Scholar] [CrossRef]
- Vosegaard, T. Single-Crystal NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2021, 123, 51–72. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.A.; Palke, W.E.; Gerig, J.T. The Hamiltonians of NMR Part I. Concepts Magn. Reson. 1992, 4, 107–144. [Google Scholar] [CrossRef]
- Smith, S.A.; Palke, W.E.; Gerig, J.T. The Hamiltonians of NMR Part II. Concepts Magn. Reson. 1992, 4, 181–204. [Google Scholar]
- Haeberlen, U. High Resolution NMR in Solids: Selective Averaging. In Advances in Magnetic Resonance; Waugh, J., Ed.; Academic Press: New York, NY, USA, 1976; ISBN 0-12-025561-8. [Google Scholar]
- Jazwinski, J. Advances in understanding and use of NMR scalar couplings. Ann. Rep. NMR Spectrosc. 2022, 107, 185–254. [Google Scholar] [CrossRef]
- Rose, M.E. Elementary Theory of Angular Momentum; John Wiley & Sons: New York, NY, USA, 1957; ISBN 0-486-68480-6. [Google Scholar]
- Millot, Y.; Man, P.P. Active and passive rotations with Euler angles in NMR. Concepts Magn. Reson. 2012, 40A, 215–252. [Google Scholar] [CrossRef]
- Wigner, E. Gruppentheorie und ihre Anwendung auf die Quantenmechanik der Atomspektren; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1931. [Google Scholar] [CrossRef]
- Man, P.P. Wigner active and passive rotation matrices applied to NMR tensor. Concepts Magn. Reson. Part A 2017, 45A, e21385. [Google Scholar] [CrossRef]
- McConnell, A.J. Applications of Tensor Analysis; Dover Publications, Inc.: New York, NY, USA, 1957; ISBN 0-486-60373-3. [Google Scholar]
- Mueller, L.J. Tensors and rotations in NMR. Concepts Magn. Reson. 2011, 38A, 221–235. [Google Scholar] [CrossRef]
- Proctor, W.G.; Yu, F.C. The dependence of a nuclear magnetic resonance frequency upon chemical compound. Phys. Rev. 1950, 77, 717. [Google Scholar] [CrossRef]
- Arnold, J.T.; Dharmatti, S.S.; Packard, M.E. Chemical effects on nuclear induction signals from organic compounds. J. Chem. Phys. 1951, 19, 507. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Goodfellow, R.; Granger, P. NMR Nomenclature: Nuclear Spin Properties and Conventions for Chemical Shifts (IUPAC Recommendations 2001). Concepts Magn. Reson. 2002, 14, 326–346. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Malm, S.M. Asymmetry in the nuclear magnetic shielding tensor. Mol. Phys. 1971, 22, 1127–1130. [Google Scholar] [CrossRef]
- Anet, F.A.L.; O’Leary, D.J. The shielding tensor. Part I: Understanding its symmetry properties. Concepts Magn. Reson. 1991, 3, 193–214. [Google Scholar] [CrossRef]
- Herzfeld, J.; Berger, A.E. Sideband intensities in NMR spectra of samples spinning at the magic angle. J. Chem. Phys. 1980, 73, 6021–6030. [Google Scholar] [CrossRef]
- Dybowski, C.; Neue, G. Solid state 207Pb NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2002, 41, 153–170. [Google Scholar] [CrossRef]
- Bielecki, A.; Burum, D.P. Temperature dependence of 207Pb MAS spectra of solid lead nitrate. An accurate, sensitive thermometer for variable-temperature MAS. J. Magn. Reson. A 1995, 116, 215–220. [Google Scholar] [CrossRef]
- Neue, G.; Dybowski, C.; Smith, M.L.; Hepp, M.A.; Perry, D.L. Determination of 207Pb2+ chemical shift tensors from precise powder lineshape analysis. Solid State Nucl. Magn. Reson. 1996, 6, 241–250. [Google Scholar] [CrossRef]
- Bak, M.; Rasmussen, J.T.; Nielsen, N.C. SIMPSON: A general simulation program for solid-state NMR spectroscopy. J. Magn. Reson. 2000, 147, 296–330. [Google Scholar] [CrossRef]
- Zaremba, S.K. Good lattice points, discrepancy, and numerical integration. Ann. Mat. Pura. Appl. 1966, 73, 293–317. [Google Scholar] [CrossRef]
- Conroy, H. Molecular Schrödinger equation. VIII. A new method for the evaluation of multidimensional integrals. J. Chem. Phys. 1967, 47, 5307–5318. [Google Scholar] [CrossRef]
- Cheng, V.B.; Suzukawa, H.H., Jr.; Wolfsberg, M. Investigations of a nonrandom numerical method for multidimensional integration. J. Chem. Phys. 1973, 59, 3992–3999. [Google Scholar] [CrossRef]
- Edén, M. Computer simulations in solid-state NMR. III. Powder averaging. Concepts Magn. Reson. 2003, 18A, 24–55. [Google Scholar] [CrossRef]
- Facelli, J.C. Chemical shift tensors: Theory and application to molecular structural problems. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 58, 176–201. [Google Scholar] [CrossRef]
- Harris, R.K. NMR crystallography: The use of chemical shifts. Solid State Sci. 2004, 6, 1025–1037. [Google Scholar] [CrossRef]
- Martineau, C.; Senker, J.; Taulelle, F. NMR Crystallography. Ann. Rep. NMR Spectrosc. 2014, 82, 1–57. [Google Scholar] [CrossRef]
- Ye, D.; Jia, D.-C.; Yang, Z.-H.; Sun, Z.-L.; Zhang, P.-F. Microstructure and thermal stability of amorphous SiBCNAl powders fabricated by mechanical alloying. J. Alloys Compd. 2010, 506, 88–92. [Google Scholar] [CrossRef]
- Keller, K.; Brendler, E.; Schmerler, S.; Röder, C.; Heide, G.; Kortus, J.; Kroke, E. Spectroscopic characterization of rocksalt-type aluminum nitride. J. Phys. Chem. C 2015, 119, 12581–12588. [Google Scholar] [CrossRef]
- Neudert, L.; Heinke, F.; Bräuniger, T.; Pucher, F.J.; Vaughan, G.B.; Oeckler, O.; Schnick, W. An unusual nitride network of aluminum-centered octahedra and phosphorus-centered tetrahedra and structure determination from microcrystalline samples. Chem. Commun. 2017, 53, 2709–2712. [Google Scholar] [CrossRef]
- Pointner, M.M.; Pritzl, R.M.; Albrecht, J.M.; Blahusch, L.; Wright, J.P.; Bright, E.L.; Giacobbe, C.; Oeckler, O.; Schnick, W. Multicationic tetrahedra networks: Alkaline-earth-centered polyhedra and non-condensed AlNl6-octahedra in the imidonitridophosphates AE2AlP8N15(NH) (AE = Ca, Sr, Ba). Chem. Eur. J. 2024, 30, e202400766. [Google Scholar] [CrossRef]
- Schurko, R.W.; Wasylishen, R.E.; Foerster, H. Characterization of anisotropic aluminum magnetic shielding tensors. Distorted octahedral complexes and linear molecules. J. Phys. Chem. A 1998, 102, 9750–9760. [Google Scholar] [CrossRef]
- van Wüllen, L.; Kalwei, M. 13C–27Al TRAPDOR and REDOR experiments for the detection of 13C–27Al dipolar interactions in solids. J. Magn. Reson. 1999, 139, 250–257. [Google Scholar] [CrossRef] [PubMed]
- Freude, D.; Behrens, H.-J. Investigation of 27Al-NMR chemical shifts in zeolites of the faujasite type. Cryst. Res. Tech. 1981, 16, K36–K38. [Google Scholar] [CrossRef]
- Müller, D.; Gessner, W.; Behrens, H.-J.; Scheler, G. Determination of the aluminium coordination in aluminium-oxygen compounds by solid-state high-resolution 27Al NMR. Chem. Phys. Lett. 1981, 79, 59–62. [Google Scholar] [CrossRef]
- Müller, D.; Grunze, I.; Hallas, E.; Ladwig, G. Hochfeld-27Al-NMR-Untersuchungen zur Aluminiumkoordination in kristallinen Aluminiumphosphaten. Z. Anorg. Allg. Chem. 1983, 500, 80–88. [Google Scholar] [CrossRef]
- Müller, D.; Gessner, W.; Scheler, G. Solid-state 27Al NMR studies on polycrystalline aluminates of the system CaO–Al2O3. Polyhedron 1986, 5, 779–785. [Google Scholar] [CrossRef]
- Morris, H.D.; Ellis, P.D. 27Al cross polarization of aluminas. The NMR spectroscopy of surface aluminum atoms. J. Am. Chem. Soc. 1989, 111, 6045–6049. [Google Scholar] [CrossRef]
- Lippmaa, E.; Samoson, A.; Mägi, M. High-resolution 27Al NMR of aluminosilicates. J. Am. Chem. Soc. 1986, 108, 1730–1735. [Google Scholar] [CrossRef]
- Alemany, L.B.; Kirker, G.W. First observation of 5-coordinate aluminum by MAS 27Al NMR in well-characterized solids. J. Am. Chem. Soc. 1986, 108, 6158–6162. [Google Scholar] [CrossRef]
- Cruickshank, M.C.; Glasser, L.S.D.; Barri, S.A.I.; Poplett, I.J.F. Penta-co-ordinated aluminium: A solid-state 27Al N.M.R. study. J. Chem. Soc. Chem. Commun. 1986, 1, 23–24. [Google Scholar] [CrossRef]
- Du, L.-S.; Stebbins, J.F. Calcium and strontium hexaluminates: NMR evidence that “pentacoordinate” cation sites are four-coordinated. J. Phys. Chem. B 2004, 108, 3681–3685. [Google Scholar] [CrossRef]
- Dressler, M.; Nofz, M.; Malz, F.; Pauli, J.; Jäger, C.; Reinsch, S.; Scholz, G. Aluminum speciation and thermal evolution of aluminas resulting from modified Yoldas sols. J. Solid State Chem. 2007, 180, 2409–2419. [Google Scholar] [CrossRef]
- Harindranath, K.; Viswanath, K.A.; Chandran, C.V.; Bräuniger, T.; Madhu, P.K.; Ajithkumar, T.G.; Joy, P.A. Evidence for the co-existence of distorted tetrahedral and trigonal bipyramidal aluminium sites in SrAl12O19 from 27Al NMR studies. Solid State Commun. 2010, 150, 262–266. [Google Scholar] [CrossRef]
- Müller, D.; Gessner, W.; Samoson, A.; Lippmaa, E.; Scheler, G. Solid-state aluminium-27 nuclear magnetic resonance chemical shift and quadrupole coupling data for condensed AlO4 tetrahedra. J. Chem. Soc. Dalton Trans. 1986, 6, 1277–1281. [Google Scholar] [CrossRef]
- Goswami, M.; Nayak, P.K.; Periasamy, N.; Madhu, P.K. Characterisation of different polymorphs of tris(8-hydroxyquinolinato) aluminium(III) using solid-state NMR and DFT calculations. Chem. Central J. 2009, 3, 15. [Google Scholar] [CrossRef]
- Smith, M.E. Observation of Mixed Al(O,N)4 structural units by 27Al magic angle spinning NMR. J. Phys. Chem. 1992, 96, 1444–1448. [Google Scholar] [CrossRef]
- Kempgens, P.; Harris, R.K.; Yu, Z.; Thompson, D.P. Structural characterization of Li α-sialon ceramics by high-resolution 27Al and 29Si NMR spectroscopy. J. Mater. Chem. 2001, 11, 2507–2512. [Google Scholar] [CrossRef]
- Bräuniger, T.; Kempgens, P.; Harris, R.K.; Howes, A.P.; Liddell, K.; Thompson, D.P. A combined 14N/27Al nuclear magnetic resonance and powder X-ray diffraction study of impurity phases in β-sialon ceramics. Solid State Nucl. Magn. Reson. 2003, 23, 62–76. [Google Scholar] [CrossRef]
- Butler, N.D.; Dupree, R.; Lewis, M.H. The use of magic-angle-spinning NMR in structural studies of Si–Al–O–N phases. J. Mater. Sci. Lett. 1984, 3, 469–470. [Google Scholar] [CrossRef]
- Klinowski, J.; Thomas, J.M.; Thompson, D.P.; Korgul, P.; Jack, K.H.; Fyfe, C.A.; Gobbi, G.C. Structural studies of sialon ceramics by high-resolution solid-state NMR. Polyhedron 1984, 3, 1267–1269. [Google Scholar] [CrossRef]
- Dupree, R.; Lewis, M.H.; Smith, M.E. Structural characterization of ceramic phases with high-resolution 27Al NMR. J. Appl. Cryst. 1988, 21, 109–116. [Google Scholar] [CrossRef]
- Haase, J.; Freude, D.; Fröhlich, T.; Himpel, G.; Kerbe, F.; Lippmaa, E.; Pfeifer, H.; Sarv, P.; Schäfer, H.; Seiffert, B. 27Al magic-angle-spinning NMR studies of aluminium nitride ceramics. Chem. Phys. Lett. 1989, 156, 328–332. [Google Scholar] [CrossRef]
- Bastow, T.J.; Massiot, D.; Coutures, J.P. 14N NMR in AlN and BN. Solid State Nucl. Magn. Reson. 1998, 10, 241–245. [Google Scholar] [CrossRef] [PubMed]
- Bräuniger, T.; Chandran, C.V.; Wedig, U.; Jansen, M. NMR chemical shift and quadrupolar interaction parameters of carbon-coordinated 27Al in aluminium carbide, Al4C3. Z. Anorg. Allg. Chem. 2011, 637, 530–535. [Google Scholar] [CrossRef]
- Cohen, M.H.; Reif, F. Quadrupole Effects in Nuclear Magnetic Resonance Studies of Solids. Solid State Phys. 1957, 5, 321–438. [Google Scholar] [CrossRef]
- Pyykkö, P. Year-2017 nuclear quadrupole moments. Mol. Phys. 2018, 116, 1328–1338. [Google Scholar] [CrossRef]
- Kemble, E.C. The Fundamental Principles of Quantum Mechanics; McGraw-Hill Book Company, Inc.: New York, NY, USA; London, UK, 1937. [Google Scholar]
- Bain, A.D. Exact calculation, using angular momentum, of combined Zeeman and quadrupolar interactions in NMR. Mol. Phys. 2003, 101, 3163–3175. [Google Scholar] [CrossRef]
- Perras, F.A.; Widdifield, C.M.; Bryce, D.L. QUEST—QUadrupolar Exact SofTware: A fast graphical program for the exact simulation of NMR and NQR spectra for quadrupolar nuclei. Solid State Nucl. Magn. Reson. 2012, 45–46, 36–44. [Google Scholar] [CrossRef]
- Bain, A.D. A simple proof that third-order quadrupole perturbations of the NMR central transition of half-integral spin nuclei are zero. J. Magn. Reson. 2006, 179, 308–310. [Google Scholar] [CrossRef]
- Mantsch, H.H.; Saito, H.; Smith, I.C.P. Deuterium magnetic resonance, applications in chemistry, physics and biology. Prog. Nucl. Magn. Reson. Spectrosc. 1977, 11, 211–271. [Google Scholar] [CrossRef]
- Lesot, P.; Courtieu, J. Natural abundance deuterium NMR spectroscopy: Developments and analytical applications in liquids, liquid crystals and solid phases. Prog. Nucl. Magn. Reson. Spectrosc. 2009, 55, 128–159. [Google Scholar] [CrossRef]
- O’Dell, L.A. Direct detection of nitrogen-14 in NMR spectroscopy. Prog. Nucl. Magn. Reson. Spectrosc. 2011, 59, 295–318. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, H.; Zimmermann, H.; Körner, O.; Stumber, M.; Meinel, C.; Haeberlen, U. Precision measurement of the quadrupole coupling and chemical shift tensors of the deuterons in α-calcium formate. J. Magn. Reson. 2001, 151, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Bräuniger, T.; Poukpo, R.; Luz, Z.; Zimmermann, H.; Haeberlen, U. Quantification of the orientational disorder in ortho-dichlorotetramethylbenzene: A single crystal deuterium nuclear magnetic resonance and X-ray study of the site populations. J. Chem. Phys. 2001, 115, 8049–8059. [Google Scholar] [CrossRef]
- Detken, A.; Focke, P.; Zimmermann, H.; Haeberlen, U.; Olejniczak, Z.; Lalowicz, Z.T. Deuteron NMR of methyl groups in the tunneling regime. A single crystal study of aspirin-CD3. Z. Naturforsch. A 1995, 50, 95–116. [Google Scholar] [CrossRef]
- Detken, A.; Zimmermann, H. Geometry and tunneling dynamics of CHD2 groups in aspirin: A single-crystal deuteron nuclear magnetic resonance study. J. Chem. Phys. 1998, 109, 6791–6799. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Moudrakovski, I.L.; Hartmann, C.; Indris, S.; Bräuniger, T. Local Electronic Structure in AlN Studied by Single-Crystal 27Al and 14N NMR and DFT Calculations. Molecules 2020, 25, 469. [Google Scholar] [CrossRef]
- Marburger, S.P.; Fung, B.M.; Khitrin, A.K. 14N chemical shifts and quadrupole coupling constants of inorganic nitrates. J. Magn. Reson. 2002, 154, 205–209. [Google Scholar] [CrossRef]
- Kempgens, P.; Britton, J. Powder-XRD and 14N magic angle-spinning solid-state NMR spectroscopy of some metal nitrides. Magn. Reson. Chem. 2016, 54, 371–378. [Google Scholar] [CrossRef]
- Steinadler, J.; Eisenburger, L.; Bräuniger, T. Characterization of the binary nitrides VN and ScN by solid-state NMR spectroscopy. Z. Anorg. Allg. Chem. 2022, 648, e202200201. [Google Scholar] [CrossRef]
- Pake, G.E. Nuclear resonance absorption in hydrated crystals: Fine structure of the proton line. J. Chem. Phys. 1948, 16, 327–336. [Google Scholar] [CrossRef]
- Eichele, K.; Wasylishen, R.E. 31P NMR study of powder and single-crystal samples of ammonium dihydrogen phosphate: Effect of homonuclear dipolar coupling. J. Phys. Chem. 1994, 98, 3108–3113. [Google Scholar] [CrossRef]
- Eichele, K.; Wasylishen, R.E. The Dipolar-Splitting-Ratio Method—A Convenient Approach to the Analysis of Dipolar-Chemical-Shift NMR Spectra of Static Powder Samples. J. Magn. Reson. A 1994, 106, 46–56. [Google Scholar] [CrossRef]
- Bloom, A.L.; Shoolery, J.N. Effects of perturbing radiofrequency fields on nuclear spin coupling. Phys. Rev. 1955, 97, 1261–1265. [Google Scholar] [CrossRef]
- Hodgkinson, P. Heteronuclear decoupling in the NMR of solids. Prog. Nucl. Magn. Reson. Spectrosc. 2005, 46, 197–222. [Google Scholar] [CrossRef]
- Madhu, P.K. Heteronuclear spin decoupling in solid state nuclear magnetic resonance: Overview and outlook. Isr. J. Chem. 2014, 54, 25–38. [Google Scholar] [CrossRef]
- Andrew, E.R. Magic angle spinning in solid state n.m.r. spectroscopy. Phil. Trans. R. Soc. A 1981, 299, 505–520. [Google Scholar]
- Brunner, E.; Fenzke, D.; Freude, D.; Pfeifer, H. The influence of homonuclear dipolar interaction on the residual linewidths of MAS NMR spectra. Chem. Phys. Lett. 1990, 169, 591–594. [Google Scholar] [CrossRef]
- Hodgkinson, P.; Emsley, L. The reliability of the determination of tensor parameters by solid-state nuclear magnetic resonance. J. Chem. Phys. 1997, 107, 4808–4816. [Google Scholar] [CrossRef]
- Ernst, M.; Bush, S.; Kolbert, A.C.; Pines, A. Second-order recoupling of chemical-shielding and dipolar-coupling tensors under spin decoupling in solid-state NMR. J. Chem. Phys. 1996, 105, 3387–3397. [Google Scholar] [CrossRef]
- Zax, D.B. Field-dependent isotropic shifts and limitations to linewidths in solid state nuclear magnetic resonance: A Floquet treatment. J. Chem. Phys. 1996, 105, 6616–6625. [Google Scholar] [CrossRef]
- Wi, S.; Frydman, L. Quadrupolar-shielding cross-correlations in solid state nuclear magnetic resonance: Detecting antisymmetric components in chemical shift tensors. J. Chem. Phys. 2002, 116, 1551–1561. [Google Scholar] [CrossRef]
- Samoson, A.; Lippmaa, E.; Pines, A. High-resolution solid-state N.M.R. Averaging of second-order effects by means of a double rotor. Mol. Phys. 1988, 65, 1013–1018. [Google Scholar] [CrossRef]
- Kunath-Fandrei, G.H.; Kelbauskas, L.; Döring, D.; Rager, H.; Jäger, C. Determination of the orientation of 29Si chemical shift tensors using rotorsynchronized MAS NMR of single crystals: Forsterite (Mg2SiO4). Phys. Chem. Miner. 1998, 26, 55–62. [Google Scholar] [CrossRef]
- Vasa, S.K.; van Eck, E.R.H.; Janssen, J.W.G.; Kentgens, A.P.M. Full quadrupolar tensor determination by NMR using a micro-crystal spinning at the magic angle. Phys. Chem. Chem. Phys. 2010, 12, 4813–4820. [Google Scholar] [CrossRef]
- Avadhut, Y.S.; Weber, J.; Schmedt auf der Günne, J. Accurate determination of chemical shift tensor orientations of single-crystals by solid-state magic angle spinning NMR. J. Magn. Reson. 2017, 282, 89–103. [Google Scholar] [CrossRef] [PubMed]
- VanderHart, D.L.; Earl, W.L.; Garroway, A.N. Resolution in 13C NMR of organic solids using high-power proton decoupling and magic-angle sample spinning. J. Magn. Reson. 1981, 44, 361–401. [Google Scholar] [CrossRef]
- Freitas, J.C.C.; Emmerich, F.G.; Cernicchiaro, G.R.C.; Sampaio, L.C.; Bonagamba, T.J. Magnetic susceptibility effects on 13C MAS NMR spectra of carbon materials and graphite. Solid State Nucl. Magn. Reson. 2001, 20, 61–73. [Google Scholar] [CrossRef]
- Spiess, H.W.; Zimmermann, H.; Haeberlen, U. Proton magnetic shielding and susceptibility effects in single crystals of ferrocene. Chem. Phys. 1976, 12, 123–130. [Google Scholar] [CrossRef]
- Schönborn, F.; Schmitt, H.; Zimmermann, H.; Haeberlen, U.; Corminboeuf, C.; Grossmann, G.; Heine, T. The proton nuclear magnetic shielding tensors in biphenyl: Experiment and theory. J. Magn. Reson. 2005, 175, 52–64. [Google Scholar] [CrossRef]
- Pell, A.J.; Pintacuda, G.; Emsley, L. Single crystal nuclear magnetic resonance in spinning powders. J. Chem. Phys. 2011, 135, 144201. [Google Scholar] [CrossRef]
- Popp, T.M.O.; Alaniva, N.H.; Barnes, A.B. Setting the magic angle using single crystal sapphire rotors. J. Magn. Reson. Open 2021, 8–9, 100019. [Google Scholar] [CrossRef]
- Weil, J.A.; Anderson, J.H. Determination of the g Tensor in Paramagnetic Resonance. J. Chem. Phys. 1958, 28, 864–866. [Google Scholar] [CrossRef]
- Weil, J.A. Use of symmetry-related crystal sites for measuring tensor properties in magnetic resonance. J. Magn. Reson. 1973, 10, 391–393. [Google Scholar] [CrossRef]
- Hahn, T. (Ed.) International Tables for Crystallography. Volume A. Space-Group Symmetry; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Laufek, F.; Skála, R.; Haloda, J.; Císařová, I. Crystal structure of vanadinite: Refinement of anisotropic displacement parameters. J. Czech Geolog. Soc. 2006, 51, 271–275. [Google Scholar] [CrossRef]
- Kennedy, M.A.; Ellis, P.D. The single-crystal NMR experiment: An experimentalist’s guide. Part I: Experimental aspects and symmetry considerations. Concepts Magn. Reson. 1989, 1, 35–47. [Google Scholar] [CrossRef]
- Kennedy, M.A.; Ellis, P.D. The single-crystal NMR experiment: An experimentalist’s guide. Part II: Data analysis and assignment of symmetry-related tensors. Concepts Magn. Reson. 1989, 1, 109–129. [Google Scholar] [CrossRef]
- Lugli, C.; Medici, L.; Saccardo, D. Natural wulfenite: Structural refinement by single-crystal X-ray diffraction. Neues Jb. Miner. Monat. 1999, 6, 281–288. [Google Scholar]
- Vosegaard, T.; Hald, E.; Daugaard, P.; Jakobsen, H.J. A two-axis goniometer for sensitivity enhancement in single-crystal nuclear magnetic resonance spectroscopy. Rev. Sci. Instrum. 1999, 70, 1771–1779. [Google Scholar] [CrossRef]
- Sherwood, M.H.; Alderman, D.W.; Grant, D.M. Two-dimensional chemical-shift tensor correlation spectroscopy. Multiple-axis sample-reorientation mechanism. J. Magn. Reson. 1989, 84, 466–489. [Google Scholar] [CrossRef]
- Heuer, A. A new method for an automatic analysis of rotation patterns. J. Magn. Reson. 1990, 89, 287–296. [Google Scholar] [CrossRef]
- Vosegaard, T.; Hald, E.; Langer, V.; Skov, H.J.; Daugaard, P.; Bildsøe, H.; Jakobsen, H.J. Improved hardware and software for single-crystal NMR spectroscopy. J. Magn. Reson. 1998, 135, 126–132. [Google Scholar] [CrossRef] [PubMed]
- Vinding, M.S.; Kessler, T.O.; Vosegaard, T. A simple low-cost single-crystal NMR setup. J. Magn. Reson. 2016, 269, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Bryce, D.L. SCFit: Software for single-crystal NMR analysis. Free vs constrained fitting. Solid State Nucl. Magn. Reson. 2019, 102, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Berglund, B.; Tegenfeldt, J. The determination of quadrupole coupling tensors from single-crystal NMR data. J. Magn. Reson. 1978, 30, 451–455. [Google Scholar] [CrossRef]
- El Saffar, Z.M. The determination of the quadrupole coupling tensor using nuclear magnetic resonance. J. Magn. Reson. 1975, 19, 233–239. [Google Scholar] [CrossRef]
- Kind, R. Exploring crystal symmetry for the determination of EFG-tensors from NMR-NQR rotation patterns. Z. Naturforsch. 1986, 41a, 122–128. [Google Scholar] [CrossRef]
- Tesche, B.; Zimmermann, H.; Poupko, R.; Haeberlen, U. The Single-Rotation Method of Determining Quadrupole Coupling Tensors in Monoclinic Crystals. Error Analysis and Application to Bullvalene. J. Magn. Reson., Ser. A 1993, 104, 68–77. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Hoch, C.; Hochleitner, R.; Bräuniger, T. NMR interaction tensors of 51V and 207Pb in vanadinite, Pb5(VO4)3Cl, determined from DFT calculations and single-crystal NMR measurements, using only one general rotation axis. Solid State Nucl. Magn. Reson. 2018, 89, 11–20. [Google Scholar] [CrossRef]
- Gornostansky, S.D.; Stager, C.V. Nuclear magnetic resonance study of V2O5. J. Chem. Phys. 1966, 46, 4959–4962. [Google Scholar] [CrossRef]
- Hansen, M.R.; Vosegaard, T.; Jakobsen, H.J.; Skibsted, J. 11B chemical shielding anisotropies in borates from 11B MAS, MQMAS, and single-crystal NMR spectroscopy. J. Phys. Chem. A 2004, 108, 586–594. [Google Scholar] [CrossRef]
- Bräuniger, T.; Groh, B.; Moudrakovski, I.L.; Indris, S. Local electronic structure in γ-LiAlO2 studied by single-crystal 27Al NMR and DFT calculations. J. Phys. Chem. A 2016, 120, 7839–7846. [Google Scholar] [CrossRef] [PubMed]
- Giuseppetti, G.; Tadini, C. Reexamination of the crystal structure of phosgenite, Pb2Cl2(CO3). Tscher. Miner. Petr. Mitt. 1974, 21, 101–109. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Steinadler, J.; Hochleitner, R.; Bräuniger, T. Single-crystal 207Pb-NMR of wulfenite, PbMoO4, aided by simultaneous measurement of phosgenite, Pb2Cl2CO3. Solid State Nucl. Magn. Reson. 2019, 103, 17–24. [Google Scholar] [CrossRef] [PubMed]
- Zeman, O.E.O.; Steinadler, J.; Hochleitner, R.; Bräuniger, T. Determination of the full 207Pb chemical shift tensor of anglesite, PbSO4, and correlation of the isotropic shift to lead-oxygen distance in natural minerals. Crystals 2019, 9, 43. [Google Scholar] [CrossRef]
- Kye, Y.-S.; Zhao, X.; Harbison, G.S. Orientation of single crystals using linear approximations to NMR transits. J. Magn. Reson. 2005, 174, 54–59. [Google Scholar] [CrossRef][Green Version]
- Yamauchi, K.; Janssen, J.W.G.; Kentgens, A.P.M. Implementing solenoid microcoils for wide-line solid-state NMR. J. Magn. Reson. 2004, 167, 87–96. [Google Scholar] [CrossRef]
- Takeda, K. Microcoils and microsamples in solid-state NMR. Solid State Nucl. Magn. Reson. 2012, 47–48, 1–9. [Google Scholar] [CrossRef]
- Carver, T.R.; Slichter, C.P. Experimental verification of the Overhauser nuclear polarization effect. Phys. Rev. 1956, 102, 975–980. [Google Scholar] [CrossRef]
- Abragam, A.; Proctor, W.G. Une nouvelle methode de polarisation dynamique des noyaux atomiques dans les solides. Comptes Rendus Hebd. Seances L’Acad. Sci. 1958, 246, 2253–2256. [Google Scholar]
- Buntkowsky, G.; Hoffmann, W.; Vieth, H.-M. Optical nuclear polarization for sensitivity enhancement of 2H NMR single-crystal studies. Appl. Magn. Reson. 1999, 17, 489–502. [Google Scholar] [CrossRef]
- Nevzorov, A.A.; Milikisiyants, S.; Marek, A.N.; Smirnov, A.I. Multi-resonant photonic band-gap/saddle coil DNP probehead for static solid state NMR of microliter volume samples. J. Magn. Reson. 2018, 297, 113–123. [Google Scholar] [CrossRef] [PubMed]
- Perras, F.A.; Paterson, A.L.; Syed, Z.H.; Kropf, A.J.; Kaphan, D.M.; Delferro, M.; Pruski, M. Revealing the configuration and conformation of surface organometallic catalysts with DNP-enhanced NMR. J. Phys. Chem. C 2021, 125, 13433–13442. [Google Scholar] [CrossRef]
- Shimon, D.; Cantwell, K.A.; Joseph, L.; Williams, E.Q.; Peng, Z.L.; Takahashi, S.; Ramanathan, C. Large room temperature bulk DNP of 13C via P1 centers in diamond. J. Phys. Chem. C 2022, 126, 17777–17787. [Google Scholar] [CrossRef]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review; reprint from 1968; Dover: Mineola, NY, USA, 1957; p. 473. [Google Scholar]
- Schmidt-Rohr, K.; Spiess, H.W. Multidimensional Solid-State NMR and Polymers; Academic Press Ltd.: London, UK, 1994. [Google Scholar]
- Householder, A.S. Unitary triangularization of a nonsymmetric matrix. J. ACM 1958, 5, 339–342. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Moudrakovski, I.L.; Hoch, C.; Hochleitner, R.; Schmahl, W.W.; Karaghiosoff, K.; Bräuniger, T. Determination of the 31P and 207Pb Chemical Shift Tensors in Pyromorphite, Pb5(PO4)3Cl, by Single-Crystal NMR Measurements and DFT Calculations. Z. Anorg. Allg. Chem. 2017, 643, 1635–1641. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Kainz, V.; Bräuniger, T. Single-Crystal 31P and 7Li NMR of the ionic conductor LiH2PO4. Crystals 2020, 10, 302. [Google Scholar] [CrossRef]
- Indris, S.; Heitjans, P.; Uecker, R.; Bredow, T. Local Electronic Structure in a LiAlO2 single crystal studied with 7Li NMR spectroscopy and comparison with quantum chemical calculations. Phys. Rev. B 2006, 74, 245120. [Google Scholar] [CrossRef]
- Müller, D.; Gessner, W.; Scheler, G. Chemical shift and quadrupole coupling of the 27Al NMR spectra of LiAlO2 polymorphs. Polyhedron 1983, 2, 1195–1198. [Google Scholar] [CrossRef]
- Skibsted, J.; Norby, P.; Bildsøe, H.; Jakobsen, H.J. Line shapes and widths of MAS sidebands for 27Al satellite transitions. Multinuclear MAS NMR of tugtupite Na8Al2Be2Si8O24Cl2. Solid State Nucl. Magn. Reson. 1995, 5, 239–255. [Google Scholar] [CrossRef]
- Breuer, A.; Siebert, D. 69Ga NMR and 115In NMR in AB2X4. Ber. Bunsenges. Phys. Chem. 1996, 100, 1736–1739. [Google Scholar] [CrossRef]
- Vosegaard, T.; Massiot, D.; Gautier, N.; Jakobsen, H.J. 71Ga chemical shielding and quadrupole coupling tensors of the garnet Y3Ga5O12 from single-crystal 71Ga NMR. Inorg. Chem. 1997, 36, 2446–2450. [Google Scholar] [CrossRef] [PubMed]
- Vosegaard, T.; Skibsted, J.; Bildsøe, H.; Jakobsen, H.J. Quadrupole Coupling and Anisotropic Shielding from Single-Crystal NMR of the Central Transition for Quadrupolar Nuclei. 87Rb NMR of RbClO4 and Rb2SO4. J. Magn. Reson. A 1996, 122, 111–119. [Google Scholar] [CrossRef]
- Vosegaard, T.; Byriel, I.P.; Jakobsen, H.J. Characterization of the two rubidium sites in Rb2CrO4 by 87Rb single-crystal NMR. J. Phys. Chem. A 1997, 101, 8955–8958. [Google Scholar] [CrossRef]
- Vosegaard, T.; Skibsted, J.; Bildsøe, H.; Jakobsen, H.J. Solid-state 87Rb of RbVO3. A comparison of experiments for retrieving chemical shielding and quadrupole coupling tensorial interactions. Solid State Nucl. Magn. Reson. 1999, 14, 203–210. [Google Scholar] [CrossRef]
- Vosegaard, T.; Jakobsen, H.J. 27Al chemical shielding anisotropy. J. Magn. Reson. 1997, 128, 135–137. [Google Scholar] [CrossRef]
- Bryant, P.L.; Harwell, C.R.; Wu, K.; Fronczek, F.R.; Hall, R.W.; Butler, L.G. Single-crystal 27Al NMR of andalusite and calculated electric field gradients: The first complete NMR assignment for a 5-coordinate aluminum site. J. Phys. Chem. A 1999, 103, 5246–5252. [Google Scholar] [CrossRef]
- Vosegaard, T.; Andersen, U.; Jakobsen, H.J. Improved 67Zn solid-state NMR from single-crystal studies. Zn(CH3COO)2· 2H2O. J. Am. Chem. Soc. 1999, 121, 1970–1971. [Google Scholar] [CrossRef]
- Lipton, A.S.; Smith, M.D.; Adams, R.D.; Ellis, P.D. 67Zn solid-state and single-crystal NMR spectroscopy and x-ray crystal structure of zinc formate dihydrate. J. Am. Chem. Soc. 2001, 124, 410–414. [Google Scholar] [CrossRef]
- Zeman, O.E.O.; Bräuniger, T. Quantifying the Quadrupolar Interaction by 45Sc-NMR Spectroscopy of Single Crystals. Solid State Nucl. Magn. Reson. 2022, 117, 101775. [Google Scholar] [CrossRef]
- Shubin, A.A.; Lapina, O.B.; Courcot, D. Characterization by solid state 51V NMR spectroscopy. Catal. Today 2000, 56, 379–387. [Google Scholar] [CrossRef]
- Power, W.P.; Mooibroek, S.; Wasylishen, R.E.; Stanley Cameron, T. Cesium-133 single-crystal NMR study of cesium chromate. J. Phys. Chem. 1994, 98, 1552–1560. [Google Scholar] [CrossRef]
- Pyykkö, P.; Lähteenmäki, U. Measurement of the deuteron quadrupole coupling constant in C6D6 single crystals. Ann. Univ. Turku Ser. A 1966, 93, 1–7. [Google Scholar]
- Schajor, W.; Tegenfeldt, J.; Haeberlen, U. The EFG tensors and the positions of the deuterons in deuterated pyromellitic acid dihydrate. J. Magn. Reson. 1981, 44, 285–293. [Google Scholar] [CrossRef]
- Bräuniger, T.; Poukpo, R.; Luz, Z.; Gutsche, P.; Meinel, C.; Zimmermann, H.; Haeberlen, U. The dynamic disorder of azulene. A single crystal deuterium study. J. Chem. Phys. 2000, 112, 10858–10870. [Google Scholar] [CrossRef]
- Speier, P.; Zimmermann, H.; Haeberlen, U.; Luz, Z. Dynamic disorder in 2,3-dimethylnaphthalene: A single crystal deuteron nuclear magnetic resonance study. Mol. Phys. 1998, 95, 1153–1167. [Google Scholar] [CrossRef]
- Ellis, D.M.; Bjorkstam, J.L. Deuteron nuclear magnetic resonance in anthracene crystals. J. Chem. Phys. 1967, 46, 4460–4463. [Google Scholar] [CrossRef]
- Volkoff, G.M. Second order nuclear quadrupole effects in single crystals. Part I. Theoretical. Can. J. Phys. 1953, 31, 820–836. [Google Scholar] [CrossRef]
- Volkoff, G.M. Second order nuclear quadrupole effects in single crystals. Part II. Experimental results for spodumene. Can. J. Phys. 1953, 31, 837–858. [Google Scholar]
- Narita, K.; Umeda, J.-I.; Kusumoto, H. Nuclear magnetic resonance powder patterns of the second-order nuclear quadrupole interaction in solids with asymmetric field gradient. J. Chem. Phys. 1966, 44, 2719–2723. [Google Scholar] [CrossRef]
- Wolf, F.; Kline, D.; Story, H.S. 93Nb and 23Na NMR in polycrystalline sodium niobate. J. Chem. Phys. 1970, 53, 3538–3543. [Google Scholar] [CrossRef]
- Müller, D. Zur Bestimmung chemischer Verschiebungen der NMR-Frequenzen bei Quadrupolkernen aus den MAS-NMR-Spektren. Ann. Phys. 1982, 39, 451–460. [Google Scholar]





| 27Al Coordination | Range a | References |
|---|---|---|
| AlN6 | to 5 ppm | [40,41,42,43] |
| AlO6 | to 37 ppm | [44,45,46,47,48,49,50] |
| AlO5 | 20 to 52 ppm b | [51,52,53,54,55,56] |
| AlO4 | 39 to 85 ppm | [46,47,48,49,50,57] |
| AlO3N3 | 43 to 55 ppm | [58] |
| AlOyN4−y | 66 to 103 ppm | [59,60,61] |
| AlN4 | 100 to 115 ppm | [61,62,63,64,65,66] |
| Al4C3 | 111 to 120 ppm | [67] |
| 1st Order | 2nd Order | 3rd Order | Chemical Shift | Cross Term | |
|---|---|---|---|---|---|
| CT frequency | ✗ | ✓ | ✗ | ✓ | ✓ |
| ST frequencies | ✓ | ✓ | ✓ | ✓ | ✓ |
| Signs for terms | ≠ | = | ≠ | = | = |
| ST difference (splittings) | ✓ | ✗ | ✓ | ✗ | ✗ |
| ST sum (centres) | ✗ | ✓ | ✗ | ✓ | ✓ |
| Scales with | ✗ | ↓ | ↓ | ↑ | ↓ |
| Nuclide | Compound | Ref. | ||||
|---|---|---|---|---|---|---|
| (spin I) | (Formula) | (in ppm) | ||||
| 29Si | Forsterite | [98] | ||||
| () | (Mg2SiO4) | |||||
| 13C () | L-alanine (C3H7NO2) | [100] | ||||
| Atom | Wyckoff | Site | Atomic Coordinates | ||
|---|---|---|---|---|---|
| Position | Symmetry | x | y | z | |
| Pb1 | |||||
| Pb2 | |||||
| V1 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bräuniger, T. High-Precision Determination of NMR Interaction Parameters by Measurement of Single Crystals: A Review of Classical and Advanced Methods. Molecules 2024, 29, 4148. https://doi.org/10.3390/molecules29174148
Bräuniger T. High-Precision Determination of NMR Interaction Parameters by Measurement of Single Crystals: A Review of Classical and Advanced Methods. Molecules. 2024; 29(17):4148. https://doi.org/10.3390/molecules29174148
Chicago/Turabian StyleBräuniger, Thomas. 2024. "High-Precision Determination of NMR Interaction Parameters by Measurement of Single Crystals: A Review of Classical and Advanced Methods" Molecules 29, no. 17: 4148. https://doi.org/10.3390/molecules29174148
APA StyleBräuniger, T. (2024). High-Precision Determination of NMR Interaction Parameters by Measurement of Single Crystals: A Review of Classical and Advanced Methods. Molecules, 29(17), 4148. https://doi.org/10.3390/molecules29174148






