Thermochemical Research on Furfurylamine and 5-Methylfurfurylamine: Experimental and Computational Insights
Abstract
1. Introduction
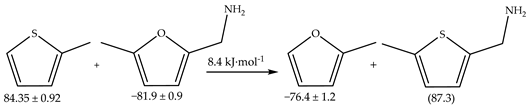
2. Results
2.1. Experimental Results
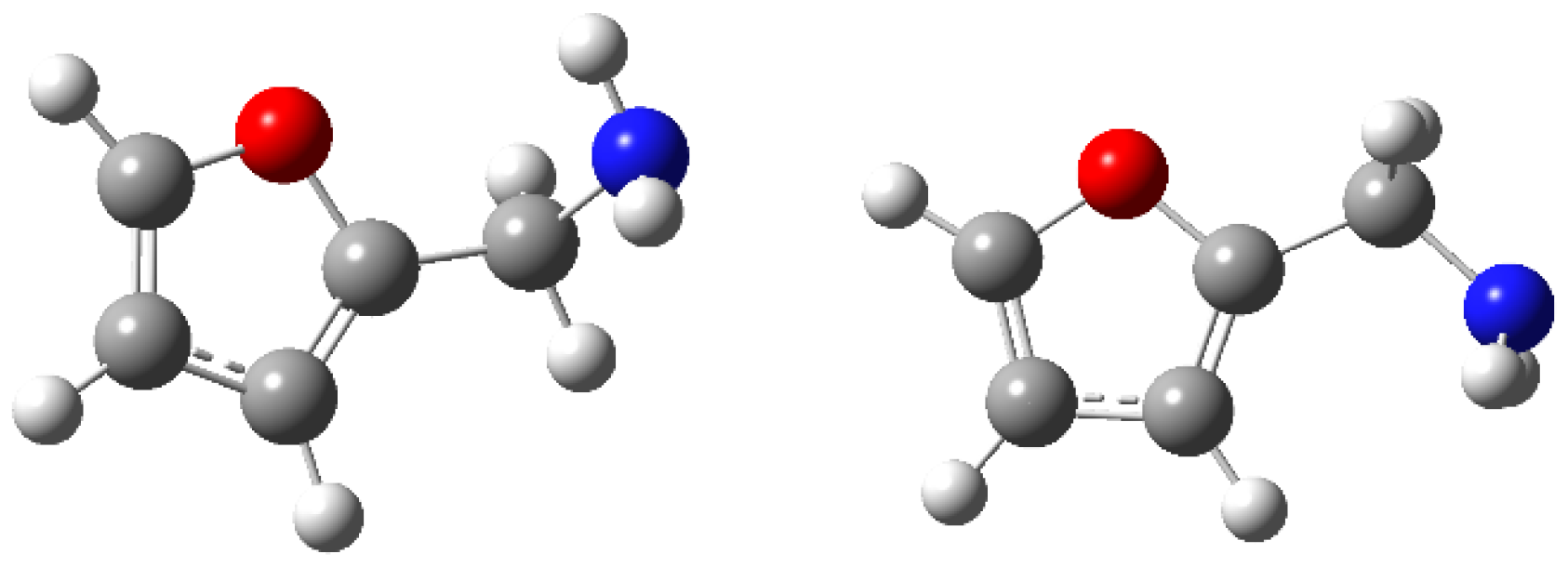
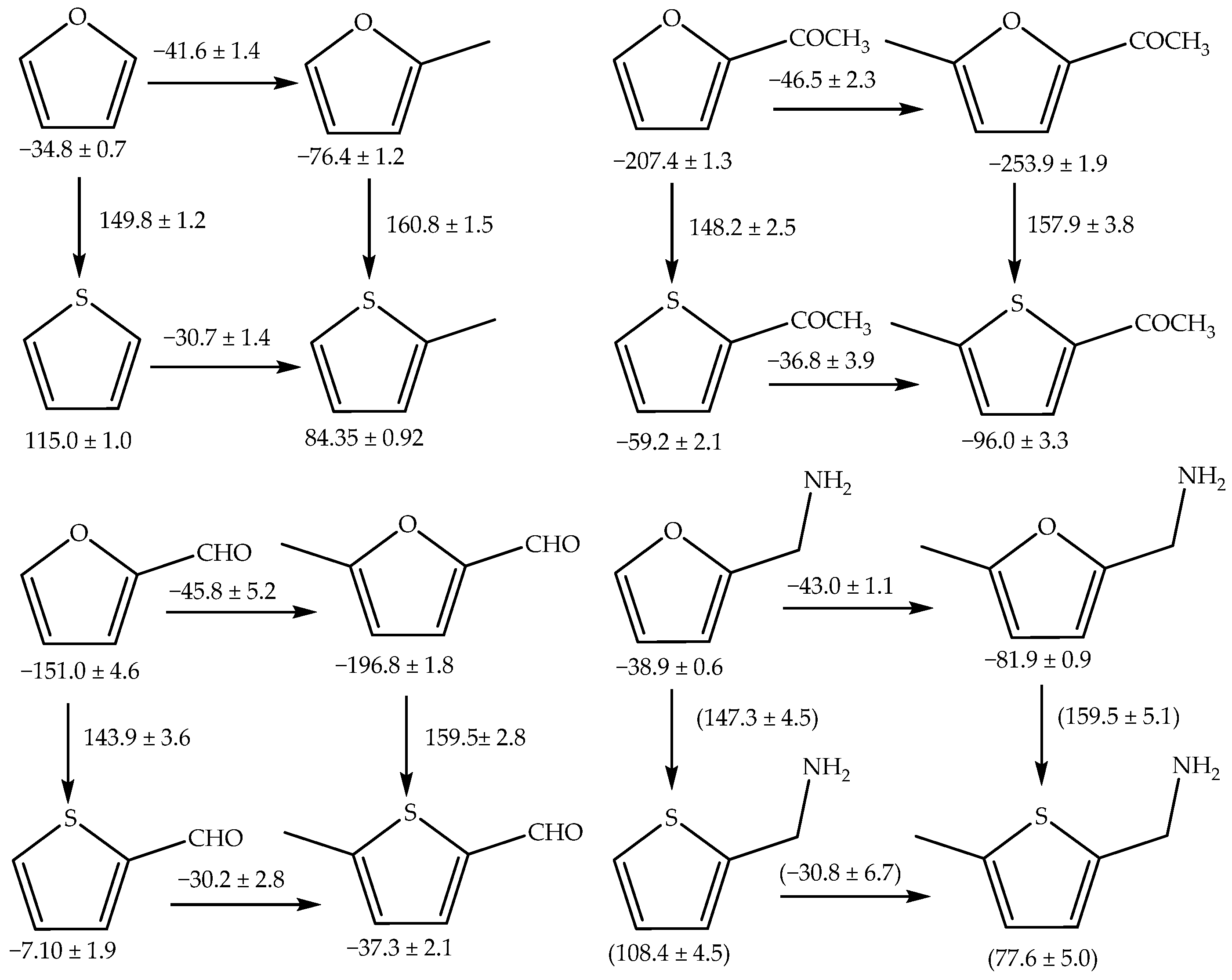
2.2. Computational Results
3. Discussion

4. Materials and Methods
4.1. Materials and Purity Control
4.2. Combustion Calorimetry
4.3. High Temperature Microcalorimetry
4.4. Computational Approach
5. Conclusions
- Using combustion calorimetry, the enthalpies of formation in the liquid phase were derived for both compounds as −(92.6 ± 1.1) kJ·mol−1 for furfurylamine and −(134.5 ± 1.5) kJ·mol−1 for 5-methylfurfurylamine.
- The enthalpy of formation of furfurylamine in the liquid phase derived in this work is quite different from the value reported before in the literature
- Through high-temperature Calvet microcalorimetry, the enthalpies of vaporization of the compounds studied at 298.15 K were obtained: (49.1 ± 0.8) kJ·mol−1 for furfurylamine and (53.3 ± 0.9) kJ·mol−1 for 5-methylfurfurylamine.
- Combining these data, their gas-phase enthalpy of formation was determined as −(43.5 ± 14) kJ·mol−1 for furfurylamine, and −(81.2 ± 1.7) kJ·mol−1 for 5-methylfurfurylamine.
- The enthalpies of formation in the gaseous phase were also estimated by a theoretical analysis using G3 level calculations.
- An excellent agreement between the experimental and computational results of the standard enthalpy of formation in gaseous phase was achieved.
- The evaluation and the comparison of the enthalpic contribution of the methyl group as a substituent on the structure of similar compounds were performed in the gas phase.
- The enthalpies of formation in the gaseous phase of 2-thiophenemethylamine and 5-methyl-2-thiophenemethylamine were estimated using both empirical and computational methods.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, A.; Olsen, S.I. Key issues in life cycle assessment of biofuels. In Sustainable Bioenergy and Bioproducts. Green Energy and Technology; Gopalakrishnan, K., van Leeuwen, J., Brown, R., Eds.; Springer: London, UK, 2012. [Google Scholar] [CrossRef]
- Jaswal, A.; Singh, P.P.; Mondal, T. Furfural—A versatile, biomass-derived platform chemical for the production of renewable chemicals. Green Chem. 2022, 24, 510–551. [Google Scholar] [CrossRef]
- Islama, A.K.M.S.; Ahiduzzaman, M. Biomass energy: Sustainable solution for greenhouse gas emission. AIP Conf. Proc. 2012, 1440, 23–32. [Google Scholar] [CrossRef]
- Di, J.; Li, Q.; Ma, C.; He, Y.-C. An efficient and sustainable furfurylamine production from biomass-derived furfural by a robust mutant ω-transaminase biocatalyst. Bioresour. Technol. 2023, 369, 128425. [Google Scholar] [CrossRef]
- Cao, L.; Yu, I.K.M.; Chen, S.S.; Tsang, D.C.W.; Wang, L.; Xiong, X.; Zhang, S.; Ok, Y.S.; Kwon, E.E.; Song, H.; et al. Production of 5-hydroxymethylfurfural from starch-rich food waste catalyzed by sulfonated biochar. Bioresour. Technol. 2018, 252, 76–82. [Google Scholar] [CrossRef]
- Yadav, V.G.; Yadav, G.D.; Patankar, S.C. The production of fuels and chemicals in the new world: Critical analysis of the choice between crude oil and biomass vis-à-vis sustainability and the environment. Clean Technol. Environ. Policy 2020, 22, 1757–1774. [Google Scholar] [CrossRef]
- Deng, W.; Feng, Y.; Fu, J.; Guo, H.; Guo, Y.; Han, B.; Jiang, Z.; Kong, L.; Li, C.; Liu, H.; et al. Catalytic conversion of lignocellulosic biomass into chemicals and fuels. Green Energy Environ. 2023, 8, 10–114. [Google Scholar] [CrossRef]
- Yong, K.J.; Wu, T.Y.; Lee, C.B.T.L.; Lee, Z.J.; Liu, Q.; Jahim, J.M.; Zhou, Q.; Zhang, L. Furfural production from biomass residues: Current technologies, challenges and future prospects. Biomass Bioenergy 2022, 161, 106458. [Google Scholar] [CrossRef]
- He, W.; He, Y.-C.; Ye, J. Efficient synthesis of furfurylamine from biomass via a hybrid strategy in an EaCl:Gly–water medium. Front. Bioeng. Biotechnol. 2023, 11, 1144787. [Google Scholar] [CrossRef]
- Dunbabin, A.; Subrizi, F.; Ward, J.M.; Sheppard, T.D.; Hailes, H.C. Furfurylamines from biomass: Transaminase catalysed upgrading of furfurals. Green Chem. 2017, 19, 397. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Li, X.; Liu, H.; Yao, X.; Xia, C.; Huang, Z. Recent advances in the efficient synthesis of useful amines from biomass-based furan compounds and their derivatives over heterogeneous catalysts. Catalysts 2023, 13, 528. [Google Scholar] [CrossRef]
- Hea, W.; Nib, J.; Heb, Y.-C.; Ye, J. Chemoenzymatic catalytic synthesis of furfurylamine from hemicellulose in biomasses. Int. J. Biol. Macromol. 2022, 22, 1201–1210. [Google Scholar] [CrossRef]
- Shi, S.; Zhao, X.; Wang, Q.; Shan, H.; Xu, Y. Synthesis and evaluation of polyaspartic acid/furfurylamine graft copolymer as scale and corrosion inhibitor. RSC Adv. 2016, 6, 102406–102412. [Google Scholar] [CrossRef]
- Lankenaua, A.W.; Kanan, M.W. Polyamide monomers via carbonate-promoted C–H carboxylation of furfurylamine. Chem. Sci. 2020, 11, 248–252. [Google Scholar] [CrossRef]
- Nikul’shin, P.A.; Ershov, M.A.; Grigor’yeva, E.V.; Tarazanov, S.V.; Kuznetsova, S.N.; Repina, O.V. Furfural derivatives as fuel components. Chem. Technol. Fuels Oils 2020, 55, 720–725. [Google Scholar] [CrossRef]
- Tarabanko, V.E.; Chernyak, M.Y.; Simakova, I.L.; Kaigorodov, K.L.; Bezborodov, Y.N.; Orlovskaya, N.F. Antiknock properties of furfural derivatives. Russ. J. Appl. Chem. 2015, 88, 1778–1782. [Google Scholar] [CrossRef]
- Ji, F.; Yi, W.B.; Sun, M.; Lv, M.F.; Cai, C. Synthesis of novel isoquinolinone and 1,2-dihydroisoquinoline scaffolds via Ugi reaction and ring opening reaction of furans. Mol. Divers. 2013, 17, 295–305. [Google Scholar] [CrossRef]
- Chen, W.-T.; Han, S.; Dai, Z.-H.; Fu, Y.-X.; Sun, M.-S.; Li, Z.-M.; Zhou, Y.; Tao, D.-J. Porous nitrogen-doped carbon supported MoO2/Mo2C hybrid catalyst for efficient oxidative coupling of primary amines to imines. J. Porous Mater. 2023, 30, 705–712. [Google Scholar] [CrossRef]
- Stroganova, T.A.; Butin, A.V.; Vasilin, V.K.; Nevolina, T.A.; Krapivin, G.D. A new strategy for Pyrrolo[1,2-a][1,4]diazepine structure formation. Synlett 2007, 7, 1106–1108. [Google Scholar] [CrossRef]
- Divyashree, N.R.; Revanasiddappa, H.D.; Jayalakshmi, B.; Iqbal, M.; Amachawadi, R.; Shivamallu, C.; Kollur, S.P. Turn-ON’ furfurylamine-based fluorescent sensor for Cd2+ ion detection and its application in real water samples. Polyhedron 2023, 238, 116411. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Amaral, L.M.P.F. Standard molar enthalpies of formation of 2-furancarbonitrile, 2-acetylfuran, and 3-furaldehyde. J. Chem. Thermodyn. 2009, 41, 26–29. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Amaral, L.M.P.F. Standard molar enthalpies of formation of some vinylfuran derivatives. J. Chem. Thermodyn. 2009, 41, 349–354. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Amaral, L.M.P.F. Standard molar enthalpies of formation of some methylfuran derivatives. J. Therm. Anal. Calorim. 2010, 100, 375–380. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Amaral, L.M.P.F. Thermochemical study of 2,5-dimethyl-3-furancarboxilic acid, 4,5-dimethyl-2-furaldehyde and 3-acetyl-2,5-dimethylfuran. J. Chem. Thermodyn. 2011, 43, 1–8. [Google Scholar] [CrossRef]
- Rossini, F.D. (Ed.) Experimental Thermochemistry; Interscience: New York, NY, USA, 1956; Chapter 14; Volume 1. [Google Scholar]
- Olofson, G. Combustion Calorimetry; Sunner, S., Månsson, M., Eds.; Pergamon Press: Oxford, UK, 1979; Chapter 6. [Google Scholar]
- Cox, J.D.; Wagman, D.D.; Medvedev, V.A. CODATA Key Values for Thermodynamics; Hemisphere Publishing Corp.: New York, NY, USA, 1989. [Google Scholar]
- Hagen, K.; Postmyr, L. Structure and conformation of furfurylamine determined by gas-phase electron diffraction, microwave spectroscopy data, and ab initio molecular orbital calculations. J. Phys. Chem. A 1999, 103, 11460–11464. [Google Scholar] [CrossRef]
- Levine, I.N. Physical Chemistry; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Lukyanova, V.A.; Tarazanov, S.V.; Dorofeeva, O.V.; Druzhinina, A.I.; Ilin, D.Y. Enthalpy of formation and hydrogen bonded dimerization of furfurylamine: Experimental and computational study. Thermochim. Acta 2023, 725, 179536. [Google Scholar] [CrossRef]
- Kolska, Z.; Ruzicka, V.; Gani, R. Estimation of the enthalpy of vaporization and the entropy of vaporization for pure organic compounds at 298.15 K and at normal boiling temperature by a group contribution method. Ind. Eng. Chem. Res. 2005, 44, 8436–8454. [Google Scholar] [CrossRef]
- Naef, R.; Acree, W.E., Jr. Calculation of five thermodynamic molecular descriptors by means of a general computer algorithm based on the group-additivity method: Standard enthalpies of vaporization, sublimation and solvation, and entropy of fusion of ordinary organic molecules and total phase-change entropy of liquid crystals. Molecules 2017, 22, 1059. [Google Scholar] [CrossRef]
- Seidel, R.W.; Goddard, R.; Nöthling, N.; Lehmann, C.W. In situ cryocrystallization and solid-state structures of furfural and some derivatives. CrystEngComm 2019, 21, 3295. [Google Scholar] [CrossRef]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermochemical Data of Organic Compounds; Chapman and Hall: New York, NY, USA, 1986; pp. 1–792. [Google Scholar]
- Ribeiro da Silva, M.A.V.; Santos, A.F.L.O.M. Energetics of thiophenecarboxaldehydes and some of its alkyl derivatives. J. Chem. Thermodyn. 2008, 40, 917–923. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Santos, A.F.L.O.M. Experimental thermochemical study of the three methyl substituted 2-acetylthiophene isomers. J. Chem. Thermodyn. 2008, 40, 1309–1313. [Google Scholar] [CrossRef]
- Freitas, V.L.S.; Gomes, J.R.B.; Ribeiro da Silva, M.D.M.C. Dibenzofuran and methyldibenzofuran derivatives: Assessment of thermochemical data. Struct. Chem. 2013, 24, 1923–1933. [Google Scholar] [CrossRef]
- Freitas, V.L.S.; Ribeiro da Silva, M.D.M.C.; Gomes, J.R.B. A computational study on the thermochemistry of methylbenzo- and methyldibenzothiophenes. J. Mol. Struct Theochem 2010, 946, 20–25. [Google Scholar] [CrossRef]
- Simmie, J.M.; Somers, K.P.; Metcalfe, W.K.; Curran, H.J. Substituent effects in the thermochemistry of furans: A theoretical (CBS-QB3, CBS-APNO and G3) study. J. Chem. Thermodyn. 2013, 58, 117–128. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Ribeiro da Silva, M.D.M.C.; Pilcher, G. The construction, calibration and use of a new high precision static bomb calorimeter. Rev. Port. Quim. 1984, 26, 163–172. Available online: https://www.spq.pt/magazines/RPQuimica/312 (accessed on 3 March 2024).
- Ribeiro da Silva, M.A.V.; Ribeiro da Silva, M.D.M.C.; Pilcher, G. Enthalpies of combustion of 1,2-dihydroxybenzene and of six alkylsubstituted 1,2-dihydroxybenzenes. J. Chem. Thermodyn. 1984, 16, 1149–1155. [Google Scholar] [CrossRef]
- Certificate of Analysis Standard Reference Material 39j Benzoic Acid Calorimetric Standard; NBS: Washington, DC, USA, 1995.
- Skinner, H.A.; Snelson, A. The heats of combustion of the four isomeric butyl alcohols. Trans. Faraday Soc. 1960, 6, 1776–1783. [Google Scholar] [CrossRef]
- Coops, J.; Jessup, R.S.; van Nes, K.G. Calibration of calorimeters for reactions in a bomb at constant volume. In Experimental Thermochemistry; Rossini, F.D., Ed.; Intercience: New York, NY, USA, 1956; Chapter 3; Volume 1. [Google Scholar]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I.; Bailey, S.M.; Churney, K.L.; Nuttall, R.L. The NBS tables of chemical thermodynamic properties. Selected values for inorganic and C1 and C2 organic substances in SI units. J. Phys. Chem. Ref. Data 1982, 11 (Suppl. S2). Available online: https://srd.nist.gov/JPCRD/jpcrdS2Vol11.pdf (accessed on 3 March 2024).
- Washburn, E.W. Standard states for bomb calorimetry. J. Res. Nalt. Bur. Stand. 1933, 10, 525–558. [Google Scholar] [CrossRef]
- Hubbard, W.N.; Scott, D.W.; Waddington, G. Experimental Thermochemistry; Rossini, F.D., Ed.; Interscience: New York, NY, USA, 1956; Chapter 5; Volume 1. [Google Scholar]
- Aldrich. Chemical Handbook of Fine Chemicals and Laboratory Equipment; Sigma-Aldrich Chemical Co.: Gillingham, UK, 2008–2009.
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, W.A.; De Bièvre, P.; Gröning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T.; et al. Atomic weights of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 265–291. [Google Scholar] [CrossRef]
- Santos, L.M.N.B.; Schröder, B.; Fernandes, O.O.P.; Ribeiro da Silva, M.A.V. Measurement of enthalpies of sublimation by drop method in a Calvet type calorimeter: Design and test of a new system. Thermochim. Acta 2004, 415, 15–20. [Google Scholar] [CrossRef]
- Adedeji, F.A.; Larange, D.; Brown, S.; Connor, J.A.; Leung, M.L.; Paz-Andrade, I.M.; Skinner, H.A. Thermochemistry of arene chromium tricarbonyls and the strenghts of arene-chromium bonds. J. Organomet. Chem. 1975, 97, 221–228. [Google Scholar] [CrossRef]
- NIST Computational Chemistry Comparison and Benchmark Database. 2013. NIST Standard Reference Database Number 101, Release 16a; Johnson, R.D., III, Ed.; NIST Chemistry Webbook. SRD 69. Available online: http://cccbdb.nist.gov/vibscalejust.asp (accessed on 23 May 2023).
- Sabbah, R.; Xu-Wu, A.; Chickos, J.S.; Leitão, M.L.P.; Roux, M.V.; Torres, L.A. Reference materials for calorimetry and differential thermal analysis. Thermochim. Acta 1999, 331, 93. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Raghavachari, K.; Redfern, P.C.; Rassolov, V.; Pople, J.A. Gaussian-3 (G3) theory for molecules containing first and second-row atoms. J. Chem. Phys. 1998, 109, 7764–7776. [Google Scholar] [CrossRef]
- Feller, D.; Franz, J.A. A Theoretical determination of the heats of formation of furan, tetrahydrofuran, THF-2-yl, and THF-3-yl. J. Phys. Chem. A 2000, 104, 9017–9025. [Google Scholar] [CrossRef]
- Simmie, J.M.; Curran, H.J. Formation Enthalpies and Bond Dissociation Energies of Alkylfurans. The Strongest C—X Bonds Known? J. Phys. Chem. A 2009, 113, 5128–5137. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Roux, M.V.; Temprado, M.; Chickos, J.S.; Nagano, Y. Critically Evaluated Thermochemical Properties of Polycyclic Aromatic Hydrocarbons. J. Phys. Chem. Ref. Data 2008, 37, 1855–1996. [Google Scholar] [CrossRef]
- Verevkin, S.P. Thermochemical study of the ortho interactions in alkyl substituted anilines. J. Chem. Thermodyn. 2000, 32, 247–259. [Google Scholar] [CrossRef]
- Gomez, L.A.T.; Sabbah, R. Thermodynamique de substances azotees. IX. Etude thermochimique de la benzamide. Comparaison des grandeurs energetiques liees a la structure de quelques amides et thioamides. Thermochim. Acta 1982, 58, 311–315. [Google Scholar] [CrossRef]
- Manion, J.A. Evaluated Enthalpies of Formation of the Stable Closed Shell C1 and C2 Chlorinated Hydrocarbons. J. Phys. Chem. Ref. Data 2002, 31, 123–172. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Welle, F.M. Thermochemical Studies for Determination of the Standard Molar Enthalpies of Formation of Alkyl-Substituted Furans and Some Ethers. Struct. Chem. 1998, 9, 215–221. [Google Scholar] [CrossRef]
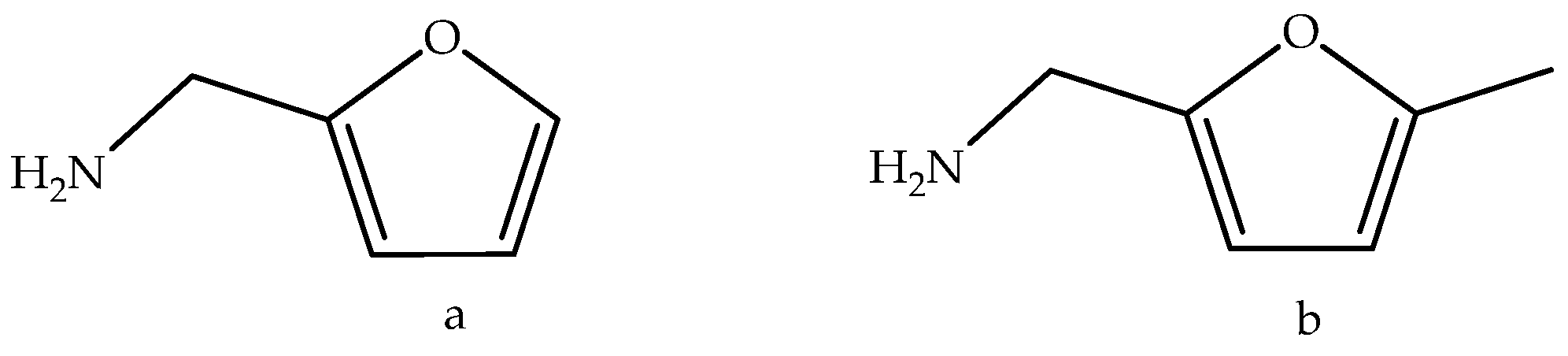

| Furfurylamine | 5-Methylfurfurylamine |
|---|---|
| −29,591.73 | −31,577.92 |
| −29,582.70 | −31,568.06 |
| −29,589.96 | −31,562.26 |
| −29,589.56 | −31,577.61 |
| −29,593.49 | −31,586.75 |
| −29,581.42 | −31,579.48 |
| −31,589.80 | |
| −31,584.93 | |
| a | |
| −29,588.1 ± 2.0 | −31,577.4 ± 3.3 |
| Compound | |||
|---|---|---|---|
| Furfurylamine | 2873.5 ± 0.9 | 2875.4 ± 0.9 | 92.6 ± 1.1 |
| 5-Methylfurfurylamine | 3509.7 ± 1.3 | 3512.8 ± 1.3 | 134.5 ± 1.5 |
| Compound | ||||
|---|---|---|---|---|
| Furfurylamine | 344.5 | 54.5 ± 0.4 | 5.4 | 49.1 ± 0.8 |
| 5-Methylfurfurylamine | 339.9 | 59.3 ± 0.4 | 6.0 | 53.3 ± 0.9 |
| Compound | ||||
|---|---|---|---|---|
| Experimental a | G3 b | |||
| Furfurylamine | –92.6 ± 1.1 | 49.1 ± 0.8 | –43.5 ± 1.4 | –38.9 ± 0.6 |
| 5-Methylfurfurylamine | –134.5 ± 1.5 | 53.3 ± 0.9 | –81.2 ± 1.7 | –81.9 ± 0.9 |
| /kJ·mol−1 | ||
|---|---|---|
| This Work | Lukyanova et al. [30] | |
| Furfurylamine (monomer) | 53.7 | 66.5 |
| Furfurylamine (dimer) | 83.4 | 109.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaral, L.M.P.F.; Almeida, A.R.R.P.; Ribeiro da Silva, M.A.V. Thermochemical Research on Furfurylamine and 5-Methylfurfurylamine: Experimental and Computational Insights. Molecules 2024, 29, 2729. https://doi.org/10.3390/molecules29122729
Amaral LMPF, Almeida ARRP, Ribeiro da Silva MAV. Thermochemical Research on Furfurylamine and 5-Methylfurfurylamine: Experimental and Computational Insights. Molecules. 2024; 29(12):2729. https://doi.org/10.3390/molecules29122729
Chicago/Turabian StyleAmaral, Luísa M. P. F., Ana R. R. P. Almeida, and Manuel A. V. Ribeiro da Silva. 2024. "Thermochemical Research on Furfurylamine and 5-Methylfurfurylamine: Experimental and Computational Insights" Molecules 29, no. 12: 2729. https://doi.org/10.3390/molecules29122729
APA StyleAmaral, L. M. P. F., Almeida, A. R. R. P., & Ribeiro da Silva, M. A. V. (2024). Thermochemical Research on Furfurylamine and 5-Methylfurfurylamine: Experimental and Computational Insights. Molecules, 29(12), 2729. https://doi.org/10.3390/molecules29122729







