Electronic and Nuclear Quantum Effects on Proton Transfer Reactions of Guanine–Thymine (G-T) Mispairs Using Combined Quantum Mechanical/Molecular Mechanical and Machine Learning Potentials
Abstract
1. Introduction
2. Results and Discussion
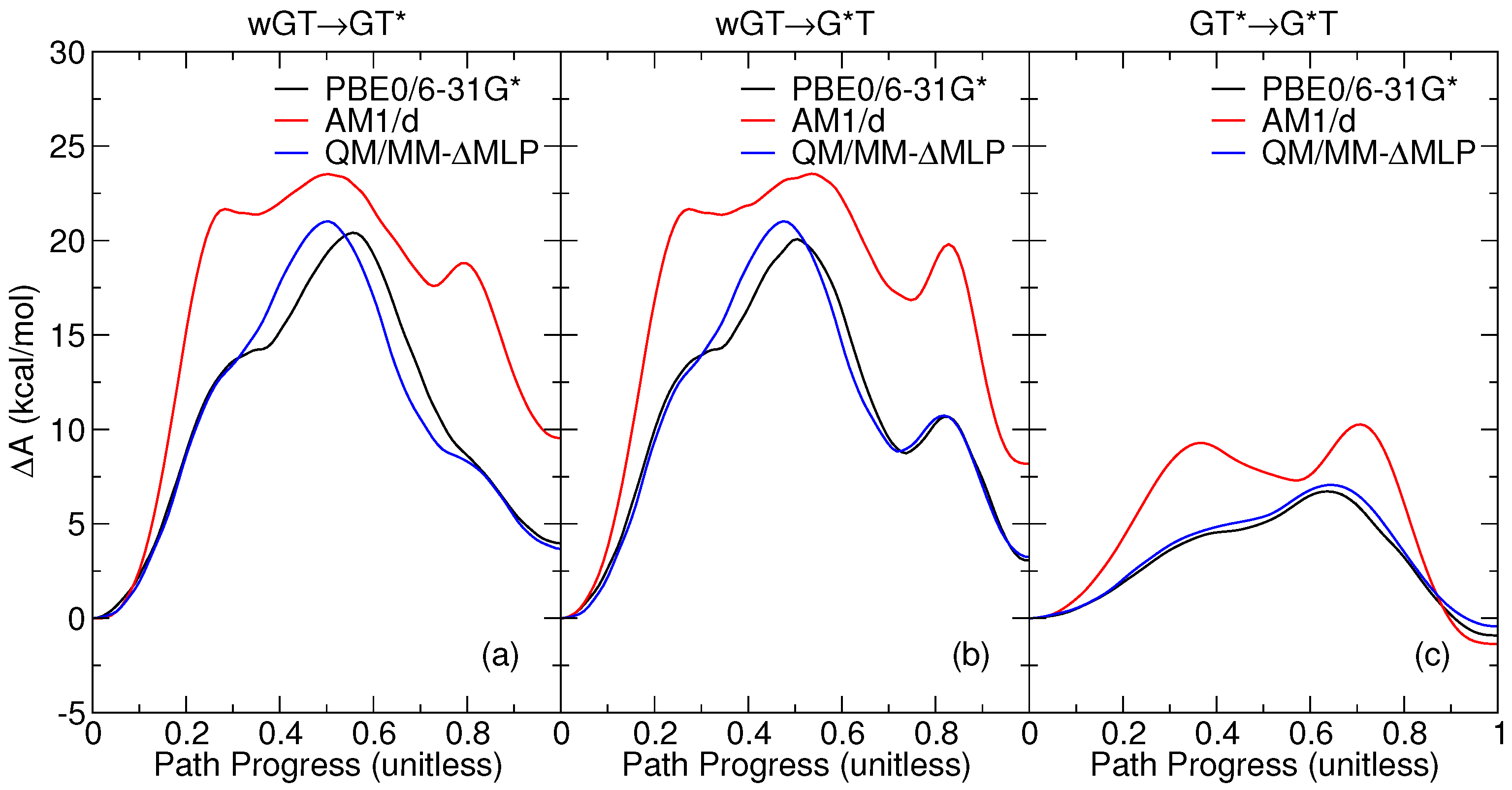
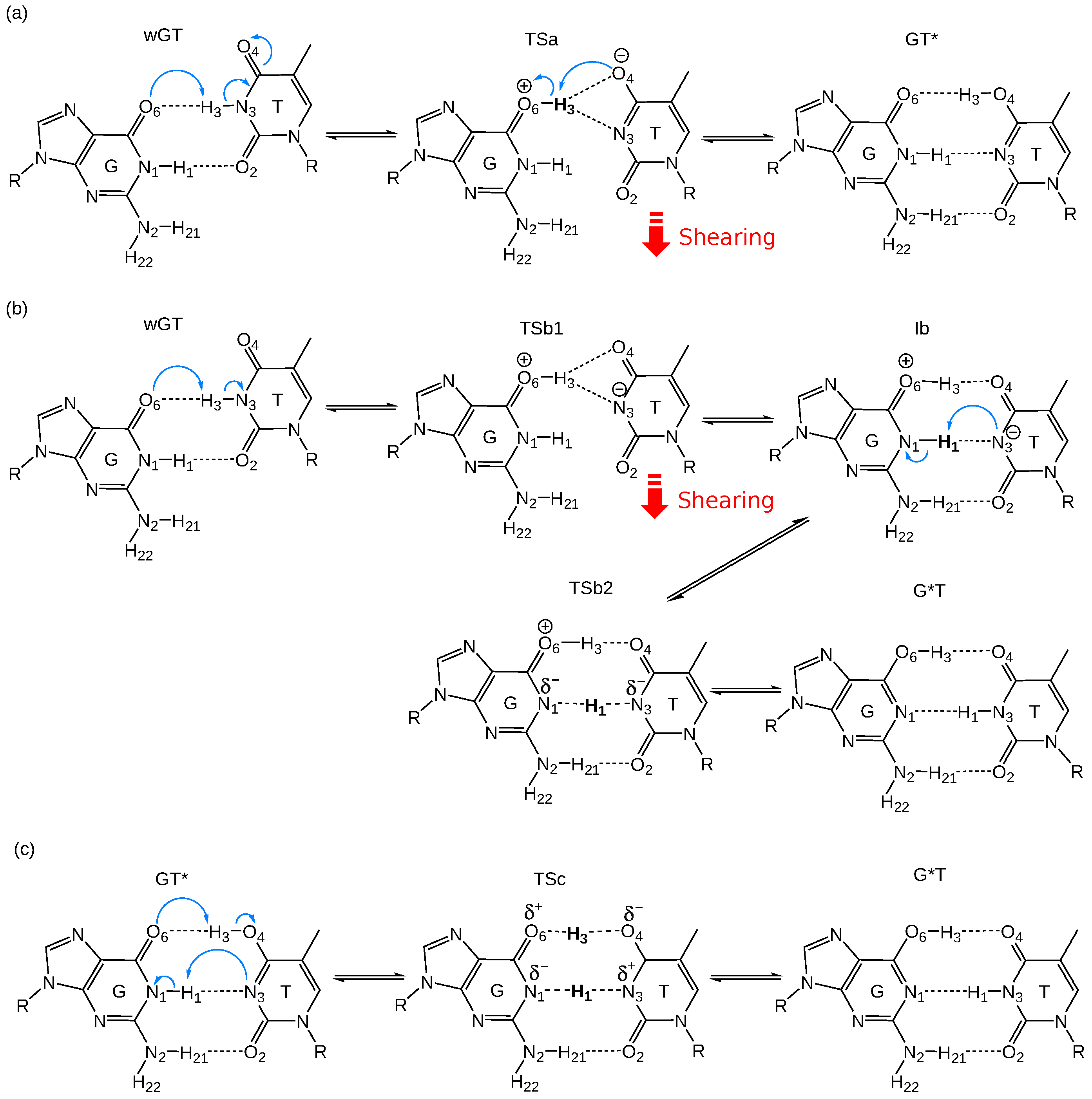
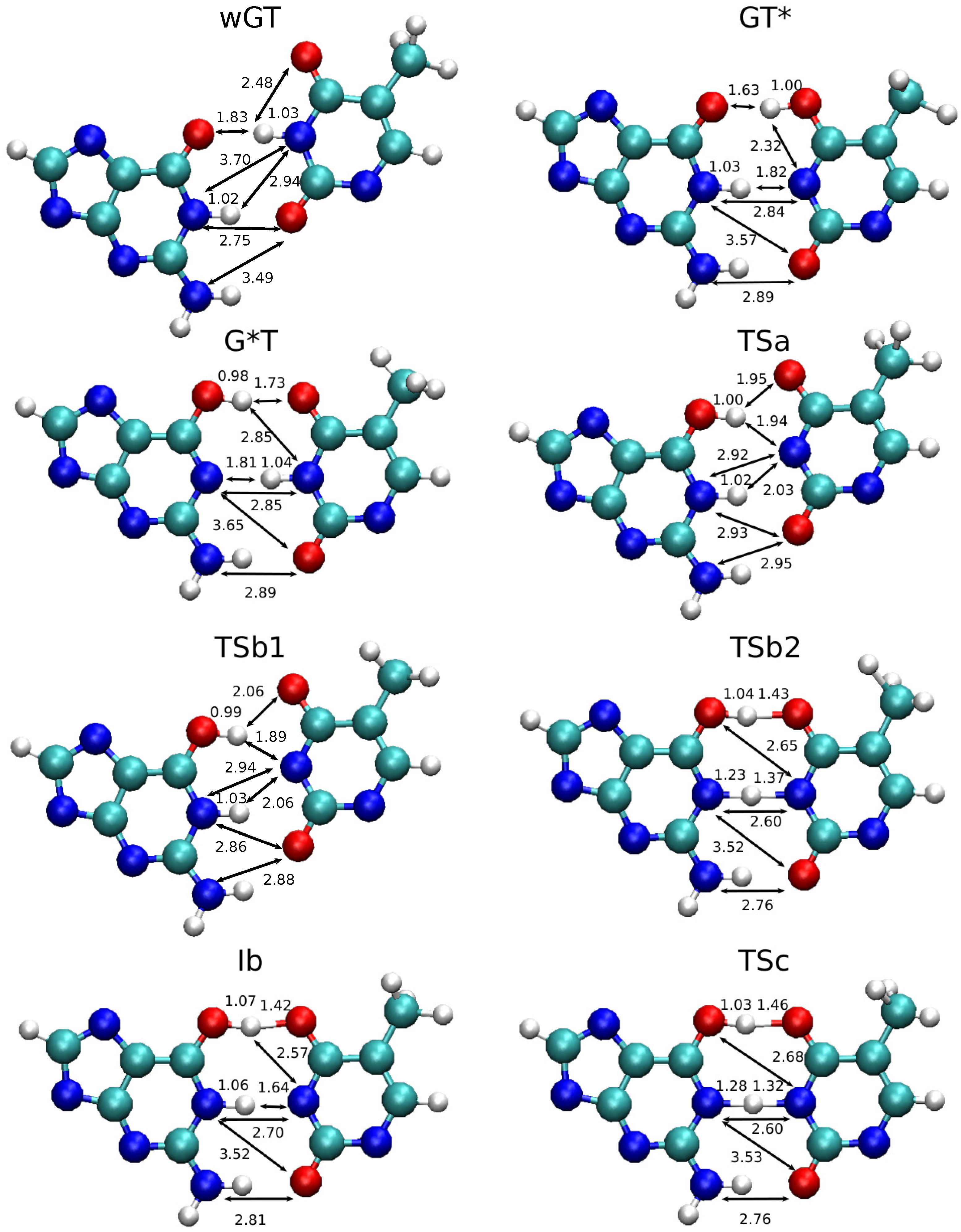
2.1. Free Energy Profiles of G-T Mispair from Classical Molecular Dynamics
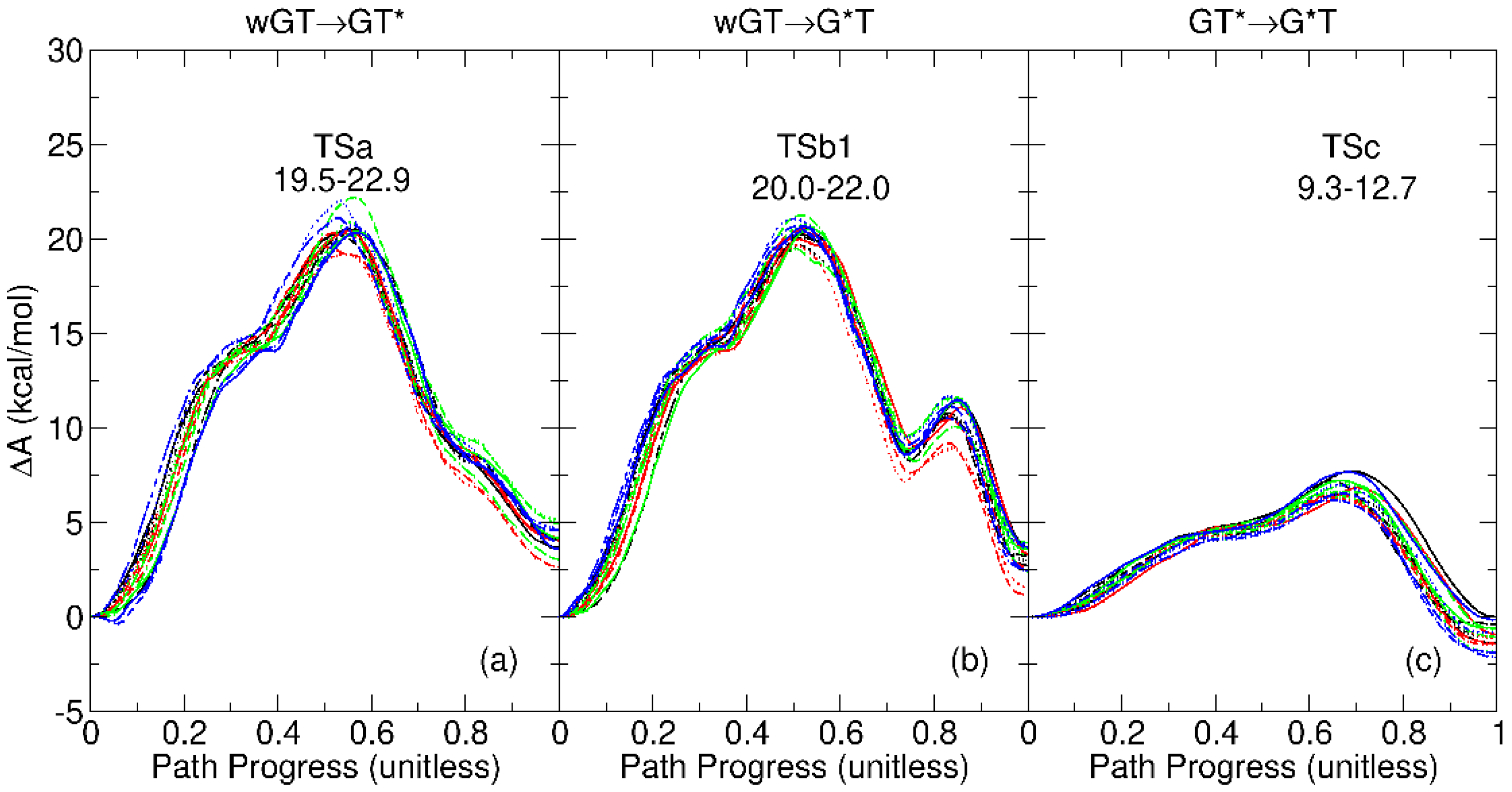
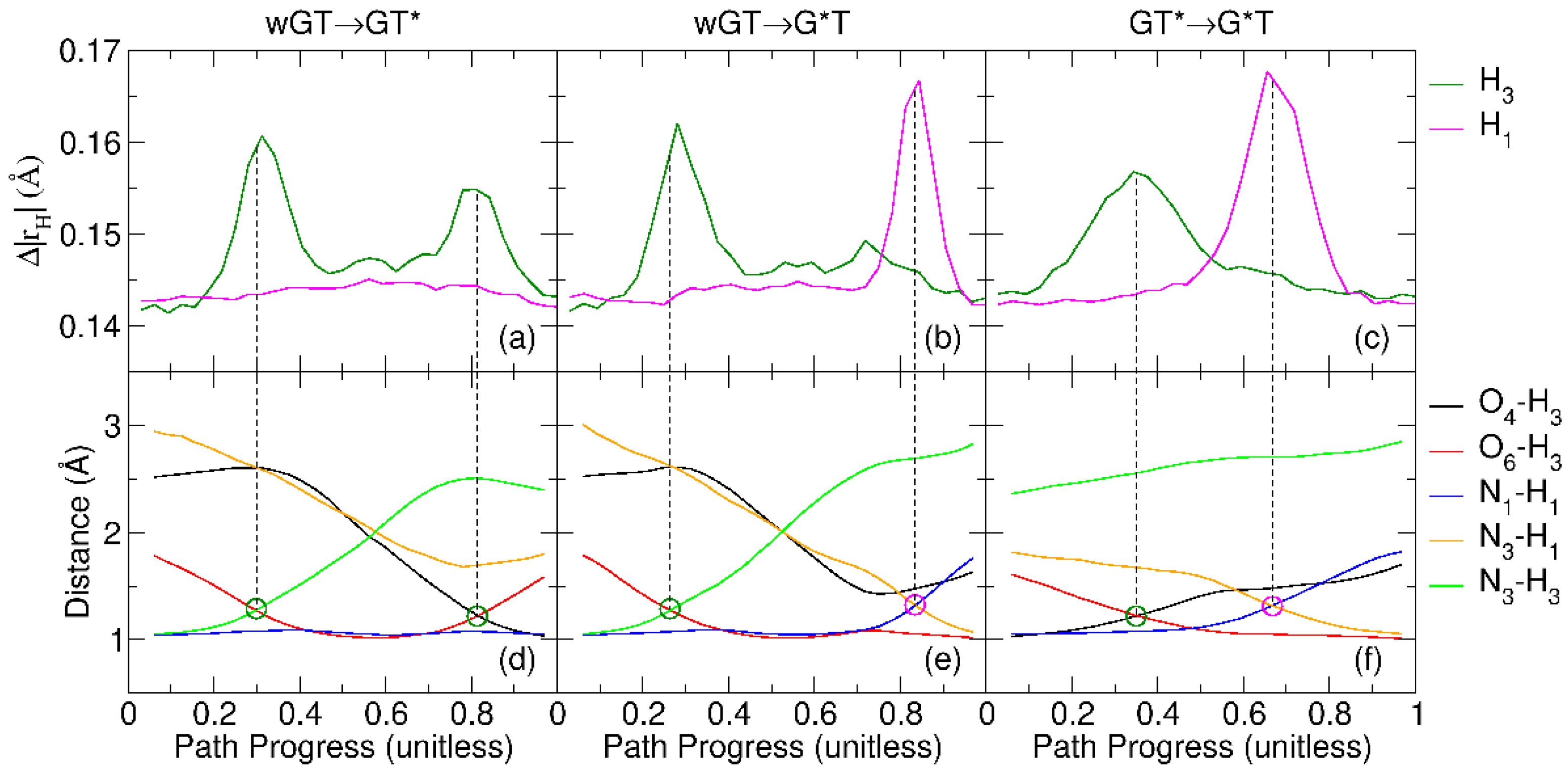
2.2. Sensitivity of Free Energy Profiles to Sampling
2.3. Free Energy Profiles of G-T Mispair from Path Integral Molecular Dynamics
2.4. Comparison of Various Models with Experiment
2.5. Benefits and Pitfalls of the QM/MM+MLP Approach
| Reaction | Method | ||||||
|---|---|---|---|---|---|---|---|
| wGT→GT* | Expt. [21] | 4.43 | 16.88 | 12.45 | |||
| PBE0/6-31G* | 3.97 (0.04) | −0.46 | 20.41 (0.05) | 3.53 | 16.45 (0.04) | 4.00 | |
| AM1/d | 9.54 (0.04) | 5.11 | 23.51 (0.06) | 6.63 | 13.98 (0.05) | 1.53 | |
| QM/MM-MLP | 3.6 7(0.07) | −0.76 | 21.01 (0.07) | 4.13 | 17.34 (0.07) | 4.89 | |
| PIMD | 3.48 (0.03) | −0.95 | 20.65 (0.04) | 3.77 | 17.16 (0.03) | 4.71 | |
| Li et al. [23] | 6.00 | 1.57 | 15.70 | −1.18 | 9.70 | −2.75 | |
| wGT→G*T | Expt. [21] | 3.82 | |||||
| PBE0/6-31G* | 3.06 (0.04) | −0.76 | 20.08 (0.05) | 17.02 (0.05) | |||
| AM1/d | 8.19 (0.04) | 4.37 | 23.55 (0.04) | 15.36 (0.04) | |||
| QM/MM-MLP | 3.24 (0.07) | −0.58 | 21.02 (0.07) | 17.78(0.07) | |||
| PIMD | 3.75 (0.04) | −0.07 | 20.63 (0.04) | 16.88 (0.04) | |||
| Li et al. [23] | N/A | N/A | N/A | ||||
| GT*→G*T | Expt. [21] | −0.62 | 9.21 | 9.83 | |||
| PBE0/6-31G* | −0.91 (0.03) | −0.29 | 6.72 (0.05) | −2.49 | 7.63 (0.05) | −2.20 | |
| AM1/d | −1.36 (0.03) | −0.74 | 10.26 (0.03) | 1.05 | 11.62 (0.04) | 1.79 | |
| QM/MM-MLP | −0.43 (0.07) | 0.19 | 7.06 (0.07) | −2.15 | 7.49 (0.07) | −2.34 | |
| PIMD | 0.26 (0.03) | 0.88 | 4.21 (0.03) | −5.00 | 3.95 (0.04) | −5.88 | |
| Li et al. [23] | −0.20 | 0.42 | 5.70 | −3.51 | 5.90 | −3.93 |
3. Materials and Methods
3.1. Background
3.2. Free Energy Profiles of Tautomer Reactions from Classical Molecular Dynamics
3.3. Free Energy Profiles of Tautomer Reactions from PIMD
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QM | Quantum mechanics |
| MM | Molecular mechanics |
| MLP | Machine learning potential correction |
| PIMD | Path integral molecular dynamics |
References
- Serrano-Andrés, L.; Merchán, M. Are the five natural DNA/RNA base monomers a good choice from natural selection? J. Photochem. Photobiol. C 2009, 10, 21–32. [Google Scholar] [CrossRef]
- Eberlein, L.; Beierlein, F.R.; van Eikema Hommes, N.J.R.; Radadiya, A.; Heil, J.; Benner, S.A.; Clark, T.; Kast, S.M.; Richards, N.G.J. Tautomeric Equilibria of Nucleobases in the Hachimoji Expanded Genetic Alphabet. J. Chem. Theory Comput. 2020, 16, 2766–2777. [Google Scholar] [CrossRef] [PubMed]
- Eichler, E.E. Genetic Variation, Comparative Genomics, and the Diagnosis of Disease. N. Engl. J. Med. 2019, 381, 64–74. [Google Scholar] [CrossRef] [PubMed]
- Gregory, T.R. Understanding Natural Selection: Essential Concepts and Common Misconceptions. Evo Edu Outreach 2009, 2, 156–175. [Google Scholar] [CrossRef]
- Gheorghiu, A.; Coveney, P.V.; Arabi, A.A. The influence of base pair tautomerism on single point mutations in aqueous DNA. Interface Focus 2020, 10, 20190120. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, R. The Role of Proton Transfer on Mutations. Front. Chem. 2019, 7, 536. [Google Scholar] [CrossRef] [PubMed]
- Bebenek, K.; Pedersen, L.C.; Kunkel, T.A. Replication infidelity via a mismatch with Watson–Crick geometry. Proc. Natl. Acad. Sci. USA 2011, 108, 1862–1867. [Google Scholar] [CrossRef] [PubMed]
- Perera, R.L.; Torella, R.; Klinge, S.; Kilkenny, M.L.; Maman, J.D.; Pellegrini, L. Mechanism for priming DNA synthesis by yeast DNA Polymerase α. elife 2013, 2, 00482. [Google Scholar] [CrossRef]
- Topal, M.D.; Fresco, J.R. Complementary base pairing and the origin of substitution mutations. Nature 1976, 263, 285–289. [Google Scholar] [CrossRef]
- Tomasetti, C.; Li, L.; Vogelstein, B. Stem cell divisions, somatic mutations, cancer etiology, and cancer prevention. Science 2017, 355, 1330–1334. [Google Scholar] [CrossRef]
- Mendiratta, G.; Ke, E.; Aziz, M.; Liarakos, D.; Tong, M.; Stites, E.C. Cancer gene mutation frequencies for the U.S. population. Nat. Commun. 2021, 12, 5961. [Google Scholar] [CrossRef]
- Watson, J.D.; Crick, F.H.C. Molecular structure of nucleic acids. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef]
- Rozov, A.; Demeshkina, N.; Westhof, E.; Yusupov, M.; Yusupova, G. New Structural Insights into Translational Miscoding. Trends Biochem. Sci. 2016, 41, 798–814. [Google Scholar] [CrossRef]
- de Vries, M.S. Gas-Phase IR Spectroscopy of Nucleobases. Top. Curr. Chem. 2014, 364, 271–297. [Google Scholar]
- Allawi, H.T.; SantaLucia, J., Jr. Thermodynamics and NMR of Internal G·T Mismatches in DNA. Biochemistry 1997, 36, 10581–10594. [Google Scholar] [CrossRef] [PubMed]
- Waters, T.R.; Swann, P.F. Kinetics of the Action of Thymine DNA Glycosylase. J. Biol. Chem. 1998, 273, 20007–20014. [Google Scholar] [CrossRef]
- Fox, K.R.; Allinson, S.L.; Sahagun-Krause, H.; Brown, T. Recognition of GT mismatches by Vsr mismatch endonuclease. Nucleic Acids Res. 2000, 28, 2535–2540. [Google Scholar] [CrossRef] [PubMed]
- Osakada, Y.; Kawai, K.; Fujitsuka, M.; Majima, T. Kinetics of charge transfer in DNA containing a mismatch. Nucleic Acids Res. 2008, 36, 5562–5570. [Google Scholar] [CrossRef]
- Koag, M.C.; Nam, K.; Lee, S. The spontaneous replication error and the mismatch discrimination mechanisms of human DNA polymerase β. Nucleic Acids Res. 2014, 42, 11233–11245. [Google Scholar] [CrossRef] [PubMed]
- Kimsey, I.J.; Petzold, K.; Sathyamoorthy, B.; Stein, Z.W.; Al-Hashimi, H.M. Visualizing transient Watson–Crick-like mispairs in DNA and RNA duplexes. Nature 2015, 519, 315–320. [Google Scholar] [CrossRef]
- Kimsey, I.J.; Szymanski, E.S.; Zahurancik, W.J.; Shakya, A.; Xue, Y.; Chu, C.C.; Sathyamoorthy, B.J.; Suo, Z.; Al-Hashimi, H.M. Dynamic basis for dG.dT misincorporation via tautomerization and ionization. Nature 2018, 554, 195–201. [Google Scholar] [CrossRef]
- Szymanski, E.S.; Kimsey, I.J.; Al-Hashimi, H.M. Direct NMR Evidence that Transient Tautomeric and Anionic States in dG·dT Form Watson–Crick-like Base Pairs. J. Am. Chem. Soc. 2017, 139, 4326–4329. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Rangadurai, A.; Al-Hashimi, H.M.; Hammes-Schiffer, S. Environmental Effects on Guanine-Thymine Mispair Tautomerization Explored with Quantum Mechanical/Molecular Mechanical Free Energy Simulations. J. Am. Chem. Soc. 2020, 142, 11183–11191. [Google Scholar] [CrossRef] [PubMed]
- Maximoff, S.N.; Kamerlin, S.C.L.; Florián, J. DNA Polymerase lambda Active Site Favors a Mutagenic Mispair between the Enol Form of Deoxyguanosine Triphosphate Substrate and the Keto Form of Thymidine Template: A Free Energy Perturbation Study. J. Phys. Chem. B 2017, 121, 7813–7822. [Google Scholar] [CrossRef]
- Chandorkar, S.; Raghunathan, S.; Jaganade, T.; Priyakumar, U.D. Multiscale Modeling of Wobble to Watson–Crick-Like Guanine–Uracil Tautomerization Pathways in RNA. Int. J. Mol. Sci. 2021, 22, 5411. [Google Scholar] [CrossRef] [PubMed]
- Slocombe, L.; Winokan, M.; Al-Khalili, J.; Sacchi, M. Quantum Tunnelling Effects in the Guanine-Thymine Wobble Misincorporation via Tautomerism. J. Phys. Chem. Lett. 2023, 14, 9–15. [Google Scholar] [CrossRef] [PubMed]
- Hunter, W.N.; Brown, T.; Kneale, G.; Anand, N.N.; Rabinovich, D.; Kennard, O. The Structure of Guanosine-Thymidine Mismatches in B-DNA at 2.5 Angstroms Resolution. J. Biol. Chem. 1993, 262, 9962–9970. [Google Scholar] [CrossRef]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Lin, Y.S.; Li, G.D.; Mao, S.P.; Chai, J.D. Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections. J. Chem. Theory Comput. 2013, 9, 263–272. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Giese, T.J.; York, D.M. Ambient-Potential Composite Ewald Method for ab Initio Quantum Mechanical/Molecular Mechanical Molecular Dynamics Simulation. J. Chem. Theory Comput. 2016, 12, 2611–2632. [Google Scholar] [CrossRef] [PubMed]
- Giese, T.J.; Zeng, J.; Ekesan, Ş.; York, D.M. Combined QM/MM, Machine Learning Path Integral Approach to Compute Free Energy Profiles and Kinetic Isotope Effects in RNA Cleavage Reactions. J. Chem. Theory Comput. 2022, 18, 4304–4317. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Giese, T.J.; Ekesan, Ş.; Zeng, J.; Aradi, B.; Hourahine, B.; Aktulga, H.M.; Götz, A.W.; Merz, K.M., Jr.; York, D.M. Amber free energy tools: Interoperable software for free energy simulations using generalized quantum mechanical/molecular mechanical and machine learning potentials. J. Chem. Phys. 2024; in press. [Google Scholar]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.Y.; Berryman, J.T.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cisneros, G.A.; Cruzeiro, V.W.D.; et al. Amber 2023; University of California: San Francisco, CA, USA, 2023. [Google Scholar]
- Kapil, V.; Rossi, M.; Marsalek, O.; Petraglia, R.; Litman, Y.; Spura, T.; Cheng, B.; Cuzzocrea, A.; Meißner, R.H.; Wilkins, D.M.; et al. i-PI 2.0: A universal force engine for advanced molecular simulations. Comput. Phys. Commun. 2019, 236, 214–223. [Google Scholar] [CrossRef]
- Rosta, E.; Nowotny, M.; Yang, W.; Hummer, G. Catalytic Mechanism of RNA Backbone Cleavage by Ribonuclease H from Quantum Mechanics/Molecular mechanics simulations. J. Am. Chem. Soc. 2011, 133, 8934–8941. [Google Scholar] [CrossRef] [PubMed]
- Giese, T.J.; Ekesan, Ş.; McCarthy, E.; Tao, Y.; York, D.M. Surface-Accelerated String Method for Locating Minimum Free Energy Paths. J. Chem. Theory Comput. 2024, 20, 2058–2073. [Google Scholar] [CrossRef] [PubMed]
- Dickerson, R. Definitions and nomenclature of nucleic acid structure components. Nucleic Acids Res. 1989, 17, 1797–1803. [Google Scholar] [CrossRef] [PubMed]
- Kosugi, K.; Nakano, H.; Sato, H. SCC-DFTB-PIMD Method To Evaluate a Multidimensional Quantum Free-Energy Surface for a Proton-Transfer Reaction. J. Chem. Theory Comput. 2019, 15, 4965–4973. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Behara, P.K.; Dotson, D.L.; Galvelis, R.; Herr, J.E.; Horton, J.T.; Mao, Y.; Chodera, J.D.; Pritchard, B.P.; Wang, Y.; et al. SPICE, A Dataset of Drug-like Molecules and Peptides for Training Machine Learning Potentials. Sci. Data 2023, 10, 11. [Google Scholar] [CrossRef]
- Giese, T.J.; Zeng, J.; Lerew, L.; McCarthy, E.; Tao, Y.; Ekesan, Ş.; York, D.M. Software infrastructure for next-generation QM/MM–ΔMLP force fields. J. Phys. Chem. 2024; in press. [Google Scholar]
- Li, P.; Jia, X.; Pan, X.; Shao, Y.; Mei, Y. Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput. 2018, 14, 5583–5596. [Google Scholar] [CrossRef]
- Giese, T.J.; Zeng, J.; York, D.M. Multireference Generalization of the Weighted Thermodynamic Perturbation Method. J. Phys. Chem. A 2022, 126, 8519–8533. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef]
- Colominas, C.; Luque, F.J.; Orozco, M. Tautomerism and protonation of guanine and cytosine. Implications in the formation of hydrogen-bonded complexes. J. Am. Chem. Soc. 1996, 118, 6811–6821. [Google Scholar] [CrossRef]
- Leszczynski, J. The Potential Energy Surface of Guanine Is Not Flat: An ab Initio Study with Large Basis Sets and Higher Order Electron Correlation Contributions. J. Phys. Chem. A 1998, 102, 2357–2362. [Google Scholar] [CrossRef]
- Zhanpeisov, N.U.; Šponer, J.; Leszczynski, J. Reverse Watson-Crick isocytosine-cytosine and guanine-cytosine base pairs stabilized by the formation of the minor tautomers of bases. An ab initio study in the gas phase and in a water cluster. J. Phys. Chem. A 1998, 102, 10374–10379. [Google Scholar] [CrossRef]
- Šponer, J.; Šponer, J.E.; Gorb, L.; Leszczynski, J.; Lippert, B. Metal-stabilized rare tautomers and mispairs of DNA bases: N6-metalated adenine and N4-metalated cytosine, theoretical and experimental views. J. Phys. Chem. A 1999, 103, 11406–11413. [Google Scholar] [CrossRef]
- Bezbaruah, B.; Medhi, C. Quantum Mechanical Study on the Proton Transfer Mechanism within Adenine-thymine and Guanine-cytosine Base Pairs of DNA Nucleobase. Indian J. Adv. Chem. Sci. 2016, 4, 314–320. [Google Scholar]
- Dwi Hartono, Y.; Pabon-Martinez, Y.V.; Uyar, A.; Wengel, J.; Lundin, K.E.; Zain, R.; Smith, C.I.E.; Nilsson, L.; Villa, A. Role of Pseudoisocytidine Tautomerization in Triplex-Forming Oligonucleotides: In Silico and in Vitro Studies. ACS Omega 2017, 2, 2165–2177. [Google Scholar] [CrossRef]
- Slocombe, L.; Al-Khalili, J.S.; Sacchi, M. Quantum and classical effects in DNA point mutations: Watson–Crick tautomerism in AT and GC base pairs. Phys. Chem. Chem. Phys. 2021, 23, 4141–4150. [Google Scholar] [CrossRef]
- Fang, W.; Chen, J.; Rossi, M.; Feng, Y.; Li, X.Z.; Michaelides, A. Inverse Temperature Dependence of Nuclear Quantum Effects in DNA Base Pairs. J. Phys. Chem. Lett. 2016, 7, 2125–2131. [Google Scholar] [CrossRef]
- Pohl, R.; Socha, O.; Slavíček, P.; Šála, M.; Hodgkinson, P.; Dračínský, M. Proton transfer in guanine–cytosine base pair analogues studied by NMR spectroscopy and PIMD simulations. Faraday Discuss. 2018, 212, 331–344. [Google Scholar] [CrossRef]
- Voth, G.A. Feynman path integral formulation of quantum mechanical transition-state theory. J. Phys. Chem. 1993, 97, 8365–8377. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. How important are quantum mechanical nuclear motions in enzyme catalysis? J. Am. Chem. Soc. 1996, 118, 11745–11751. [Google Scholar] [CrossRef]
- Wang, L.; Fried, S.D.; Boxer, S.G.; Markland, T.E. Quantum delocalization of protons in the hydrogen-bond network of an enzyme active site. Proc. Natl. Acad. Sci. USA 2014, 111, 18454–18459. [Google Scholar] [CrossRef]
- Vardi-Kilshtain, A.; Nitoker, N.; Major, D.T. Nuclear quantum effects and kinetic isotope effects in enzyme reactions. Arch. Biochem. Biophys. 2015, 582, 18–27. [Google Scholar] [CrossRef]
- Gao, J. Chapter Fourteen—Enzymatic Kinetic Isotope Effects from Path-Integral Free Energy Perturbation Theory. Methods Enzymol. 2016, 577, 359–388. [Google Scholar]
- Sauceda, H.E.; Vassilev-Galindo, V.; Chmiela, S.; Müller, K.R.; Tkatchenko, A. Dynamical strengthening of covalent and non-covalent molecular interactions by nuclear quantum effects at finite temperature. Nat. Commun. 2021, 12, 442. [Google Scholar] [CrossRef]
- Chmiela, S.; Tkatchenko, A.; Sauceda, H.E.; Poltavsky, I.; Schütt, K.T.; Müller, K.R. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 2017, 3, 1603015. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.E.; Müller, K.R.; Tkatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.E.; Tkatchenko, A.; Müller, K.R. Accurate Molecular Dynamics Enabled by Efficient Physically Constrained Machine Learning Approaches. In Machine Learning Meets Quantum Physics; Schütt, K.T., Chmiela, S., von Lilienfeld, O.A., Tkatchenko, A., Tsuda, K., Müller, K.R., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 968, pp. 129–154. [Google Scholar]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; von Lilienfeld, O. Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef]
- Blum, L.C.; Reymond, J.L. 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13. J. Am. Chem. Soc. 2009, 131, 8732–8733. [Google Scholar] [CrossRef] [PubMed]
- Giese, T.J.; Huang, M.; Chen, H.; York, D.M. Recent Advances toward a General Purpose Linear-Scaling Quantum Force Field. Acc. Chem. Res. 2014, 47, 2812–2820. [Google Scholar] [CrossRef] [PubMed]
- Giese, T.J.; York, D.M. Quantum mechanical force fields for condensed phase molecular simulations. J. Phys. Condens. Matter 2017, 29, 383002. [Google Scholar] [CrossRef] [PubMed]
- Margraf, J.T.; Hennemann, M.; Clark, T. EMPIRE: A highly parallel semiempirical molecular orbital program: 3: Born-Oppenheimer molecular dynamics. J. Mol. Model. 2020, 26, 43. [Google Scholar] [CrossRef] [PubMed]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafe, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrica, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Truhlar, D.G.; Wang, Y.; Mazack, M.J.; Löffler, P.; Provorse, M.R.; Rehak, P. Explicit polarization: A quantum mechanical framework for developing next generation force fields. Acc. Chem. Res. 2014, 47, 2837–2845. [Google Scholar] [CrossRef]
- Lindsey, R.K.; Fried, L.E.; Goldman, N. ChIMES: A Force Matched Potential with Explicit Three-Body Interactions for Molten Carbon. J. Chem. Theory Comput. 2017, 13, 6222–6229. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, R.K.; Kroonblawd, M.P.; Fried, L.E.; Goldman, N. Computational Approaches for Chemistry Under Extreme Conditions; Springer International Publishing: Cham, Switzerland, 2019; Chapter Force Matching Approaches to Extend Density Functional Theory to Large Time and Length Scales; pp. 71–93. [Google Scholar] [CrossRef]
- Goldman, N.; Kweon, K.E.; Sadigh, B.; Heo, T.W.; Lindsey, R.K.; Pham, C.H.; Fried, L.E.; Aradi, B.; Holliday, K.; Jeffries, J.R.; et al. Semi-Automated Creation of Density Functional Tight Binding Models through Leveraging Chebyshev Polynomial-Based Force Fields. J. Chem. Theory Comput. 2021, 17, 4435–4448. [Google Scholar] [CrossRef]
- Behler, J. First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems. Angew. Chem. Engl. 2017, 56, 12828–12840. [Google Scholar] [CrossRef]
- Meuwly, M. Machine Learning for Chemical Reactions. Chem. Rev. 2021, 121, 10218–10239. [Google Scholar] [CrossRef]
- Zeng, J.; Giese, T.J.; Ekesan, Ş.; York, D.M. Development of Range-Corrected Deep Learning Potentials for Fast, Accurate Quantum Mechanical/Molecular Mechanical Simulations of Chemical Reactions in Solution. J. Chem. Theory Comput. 2021, 17, 6993–7009. [Google Scholar] [CrossRef]
- Pan, X.; Yang, J.; Van, R.; Epifanovsky, E.; Ho, J.; Huang, J.; Pu, J.; Mei, Y.; Nam, K.; Shao, Y. Machine-Learning-Assisted Free Energy Simulation of Solution-Phase and Enzyme Reactions. J. Chem. Theory Comput. 2021, 17, 5745–5758. [Google Scholar] [CrossRef]
- Snyder, R.; Kim, B.; Pan, X.; Shao, Y.; Pu, J. Bridging semiempirical and ab initio QM/MM potentials by Gaussian process regression and its sparse variants for free energy simulation. J. Chem. Phys. 2023, 159, 054107. [Google Scholar] [CrossRef]
- Zeng, J.; Tao, Y.; Giese, T.J.; York, D.M. QDπ: A Quantum Deep Potential Interaction Model for Drug Discovery. J. Chem. Theory Comput. 2023, 19, 1261–1275. [Google Scholar] [CrossRef]
- Zeng, J.; Tao, Y.; Giese, T.J.; York, D.M. Modern semiempirical electronic structure methods and machine learning potentials for drug discovery: Conformers, tautomers, and protonation states. J. Chem. Phys. 2023, 158, 124110. [Google Scholar] [CrossRef]
- Han, Y.; Wang, Z.; Wei, Z.; Liu, J.; Li, J. Machine learning builds full-QM precision protein force fields in seconds. Brief. Bioinform. 2021, 22, bbab158. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Khorshidi, A.; Kastlunger, G.; Peterson, A.A. The potential for machine learning in hybrid QM/MM calculations. J. Chem. Phys. 2018, 148, 241740. [Google Scholar] [CrossRef]
- Böselt, L.; Thürlemann, M.; Riniker, S. Machine Learning in QM/MM Molecular Dynamics Simulations of Condensed- Phase Systems. J. Chem. Theory Comput. 2021, 17, 2641–2658. [Google Scholar] [CrossRef] [PubMed]
- Shen, L.; Wu, J.; Yang, W. Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef]
- Shen, L.; Yang, W. Molecular Dynamics Simulations with Quantum Mechanics/Molecular Mechanics and Adaptive Neural Networks. J. Chem. Theory Comput. 2018, 14, 1442–1455. [Google Scholar] [CrossRef]
- Ekesan, Ş.; York, D.M. Dynamical ensemble of the active state and transition state mimic for the RNA-cleaving 8-17 DNAzyme in solution. Nucleic Acids Res. 2019, 47, 10282–10295. [Google Scholar] [CrossRef]
- Loncharich, R.J.; Brooks, B.R.; Pastor, R.W. Langevin dynamics of peptides: The frictional dependence of isomerization rates of N-acetylalanyl-N’-methylamide. Biopolymers 1992, 32, 523–535. [Google Scholar] [CrossRef] [PubMed]
- Galindo-Murillo, R.; Robertson, J.C.; Zgarbova, M.; Sponer, J.; Otyepka, M.; Jurecka, P.; Cheatham, T.E., III. Assessing the current state of AMBER force field modifications for DNA. J. Chem. Theory Comput. 2016, 12, 4114–4127. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Roberts, B.P.; Chakravorty, D.K.; Merz, K.M., Jr. Rational design of Particle Mesh Ewald compatible Lennard-Jones parameters for +2 metal cations in explicit solvent. J. Chem. Theory Comput. 2013, 9, 2733–2748. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Lopez, X.; York, D.M. Parameterization of semiempirical methods to treat nucleophilic attacks to biological phosphates: AM1/d parameters for phosphorus. Theor. Chem. Acc. 2003, 109, 149–159. [Google Scholar] [CrossRef]
- Nam, K.; Cui, Q.; Gao, J.; York, D.M. Specific reaction parametrization of the AM1/d Hamiltonian for phosphoryl transfer reactions: H, O, and P atoms. J. Chem. Theory Comput. 2007, 3, 486–504. [Google Scholar] [CrossRef]
- Nam, K.; Gao, J.; York, D.M. An efficient linear-scaling Ewald method for long-range electrostatic interactions in combined QM/MM calculations. J. Chem. Theory Comput. 2005, 1, 2–13. [Google Scholar] [CrossRef]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Giese, T.J.; Ekesan, Ş.; York, D.M. Extension of the Variational Free Energy Profile and Multistate Bennett Acceptance Ratio Methods for High-Dimensional Potential of Mean Force Profile Analysis. J. Phys. Chem. A 2021, 125, 4216–4232. [Google Scholar] [CrossRef]
- Giese, T.J.; York, D.M. FE-ToolKit: The Free Energy Analysis Toolkit. Available online: https://gitlab.com/RutgersLBSR/fe-toolkit (accessed on 3 March 2024).
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Cerutti, D.S.; Cisneros, G.A.; Cruzeiro, V.W.D.; Forouzesh, N.; Giese, T.J.; Götz, A.W.; Gohlke, H.; et al. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef]
- Ceriotti, M.; More, J.; Manolopoulos, D.E. i-PI: A Python interface for ab initio path integral molecular dynamics simulations. Comput. Phys. Commun. 2014, 185, 1019–1026. [Google Scholar] [CrossRef]
- Ceriotti, M.; Manolopoulos, D.E. Efficient first-principles calculation of the quantum kinetic energy and momentum distribution of nuclei. Phys. Rev. Lett. 2012, 109, 100604. [Google Scholar] [CrossRef]
- Ceriotti, M.; Markland, T.E. Efficient methods and practical guidelines for simulating isotope effects. J. Chem. Phys. 2013, 138, 014112. [Google Scholar] [CrossRef]
- Ceriotti, M.; Manolopoulos, D.E.; Parrinello, M. Accelerating the convergence of path integral dynamics with a generalized Langevin equation. J. Chem. Phys. 2011, 134, 084104. [Google Scholar] [CrossRef]
- Ceriotti, M.; Bussi, G.; Parrinello, M. Colored-Noise Thermostats à la Carte. J. Chem. Theory Comput. 2010, 6, 1170–1180. [Google Scholar] [CrossRef]
- Ceriotti, M.; Bussi, G.; Parrinello, M. Langevin Equation with Colored Noise for Constant-Temperature Molecular Dynamics Simulations. Phys. Rev. Lett. 2009, 102, 020601. [Google Scholar] [CrossRef]
- Bonomi, M.; Branduardi, D.; Bussi, G.; Camilloni, C.; Provasi, D.; Raiteri, P.; Donadio, D.; Marinelli, F.; Pietrucci, F.; Broglia, R.; et al. PLUMED: A portable plugin for free energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180, 1961–1972. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- McCarthy, E.; Ekesan, Ş.; Giese, T.J.; Wilson, T.J.; Deng, J.; Huang, L.; Lilley, D.M.J.; York, D.M. Catalytic mechanism and pH dependence of a methyltransferase ribozyme (MTR1) from computational enzymology. Nucleic Acids Res. 2023, 51, 4508–4518. [Google Scholar] [CrossRef] [PubMed]
- Chipot, C.; Pohorille, A. (Eds.) Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer Series in Chemical Physics; Springer: New York, NY, USA, 2007; Volume 86. [Google Scholar]
- Zeng, J.; Zhang, D.; Lu, D.; Mo, P.; Li, Z.; Chen, Y.; Rynik, M.; Huang, L.; Li, Z.; Shi, S.; et al. DeePMD-kit v2: A software package for deep potential models. J. Chem. Phys. 2023, 159, 054801. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Chen, W.; Zeng, J.; Zhang, L.; Han, W.; E, W. DP-GEN: A concurrent learning platform for the generation of reliable deep learning based potential energy models. Comput. Phys. Commun. 2020, 253, 107206. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Stanzione, D.; West, J.; Evans, R.T.; Minyard, T.; Ghattas, O.; Panda, D.K. Frontera: The Evolution of Leadership Computing at the National Science Foundation. In PEARC’20: Practice and Experience in Advanced Research Computing; Association for Computing Machinery: New York, NY, USA, 2020; pp. 106–111. [Google Scholar]
- Boerner, T.J.; Deems, S.; Furlani, T.R.; Knuth, S.L.; Towns, J. ACCESS: Advancing Innovation: NSF’s Advanced Cyberinfrastructure Coordination Ecosystem: Services & Supports. In PEARC’23: Practice and Experience in Advanced Research Computing; Romanella, R.S.A., Knuth, S., Hackworth, K., Pummill, J., Eds.; Association for Computing Machinery: New York, NY, USA, 2023; pp. 173–176. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Giese, T.J.; York, D.M. Electronic and Nuclear Quantum Effects on Proton Transfer Reactions of Guanine–Thymine (G-T) Mispairs Using Combined Quantum Mechanical/Molecular Mechanical and Machine Learning Potentials. Molecules 2024, 29, 2703. https://doi.org/10.3390/molecules29112703
Tao Y, Giese TJ, York DM. Electronic and Nuclear Quantum Effects on Proton Transfer Reactions of Guanine–Thymine (G-T) Mispairs Using Combined Quantum Mechanical/Molecular Mechanical and Machine Learning Potentials. Molecules. 2024; 29(11):2703. https://doi.org/10.3390/molecules29112703
Chicago/Turabian StyleTao, Yujun, Timothy J. Giese, and Darrin M. York. 2024. "Electronic and Nuclear Quantum Effects on Proton Transfer Reactions of Guanine–Thymine (G-T) Mispairs Using Combined Quantum Mechanical/Molecular Mechanical and Machine Learning Potentials" Molecules 29, no. 11: 2703. https://doi.org/10.3390/molecules29112703
APA StyleTao, Y., Giese, T. J., & York, D. M. (2024). Electronic and Nuclear Quantum Effects on Proton Transfer Reactions of Guanine–Thymine (G-T) Mispairs Using Combined Quantum Mechanical/Molecular Mechanical and Machine Learning Potentials. Molecules, 29(11), 2703. https://doi.org/10.3390/molecules29112703





