The Effect of β-Sheet Secondary Structure on All-β Proteins by Molecular Dynamics Simulations
Abstract
1. Introduction
2. Results and Discussion
2.1. Effect of the Chain Length
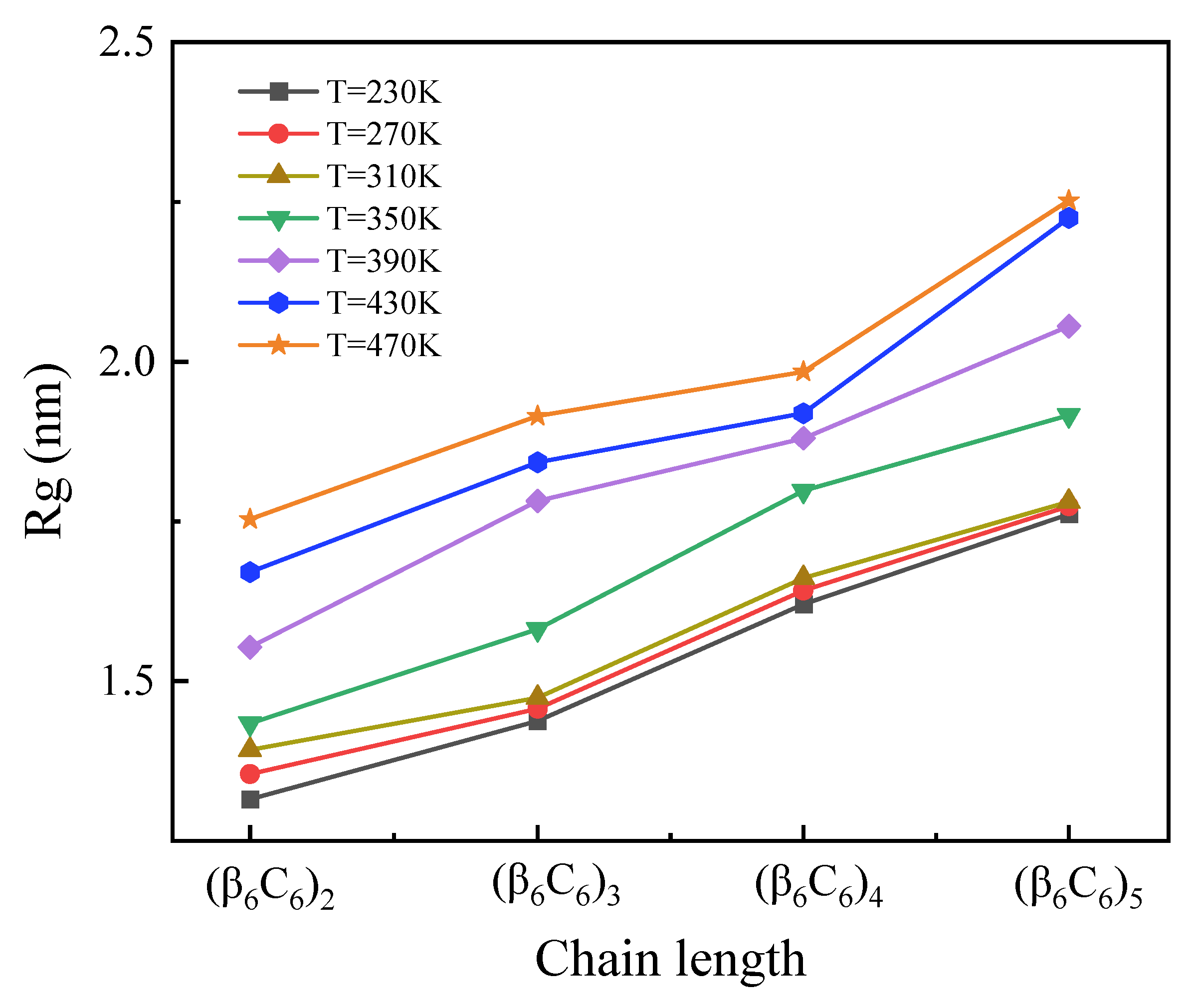
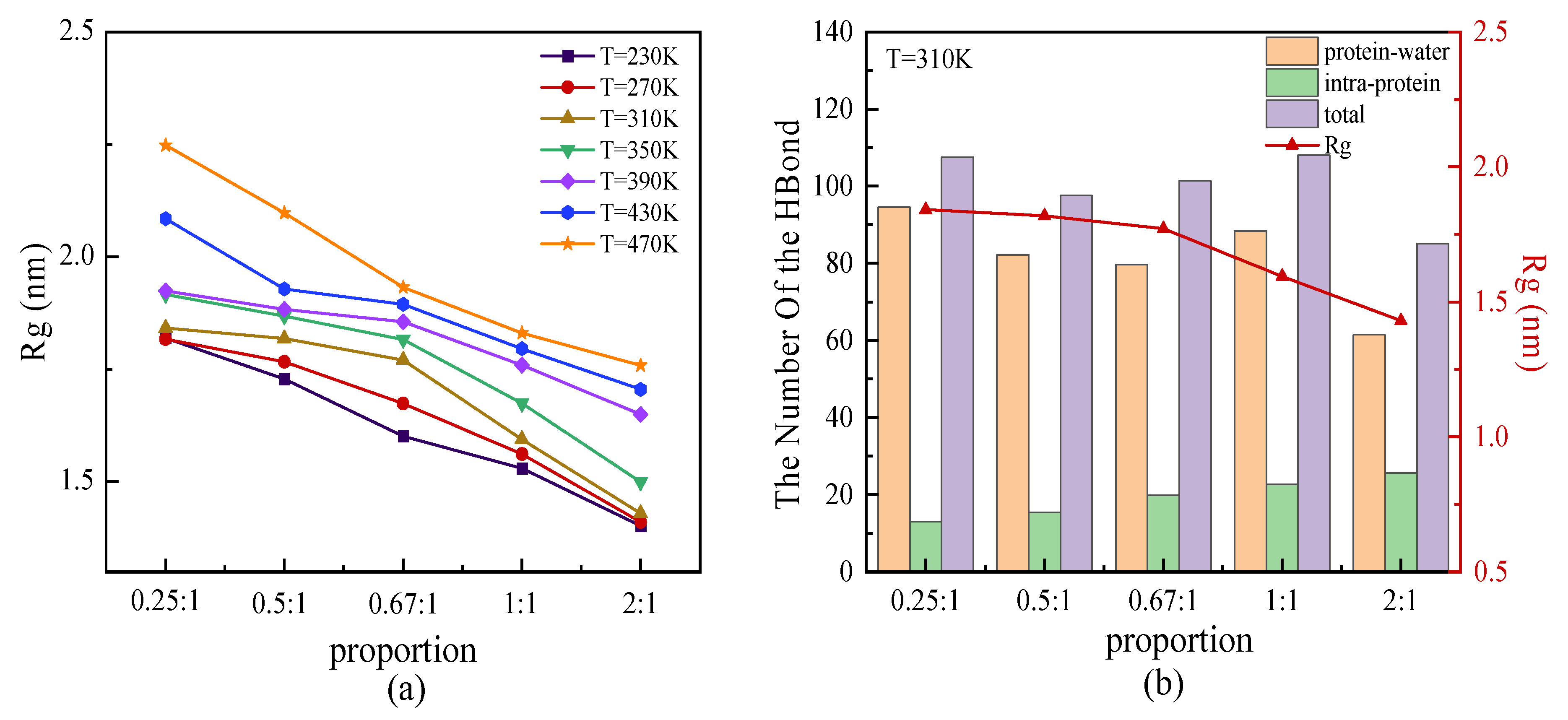
2.1.1. Radius of Gyration
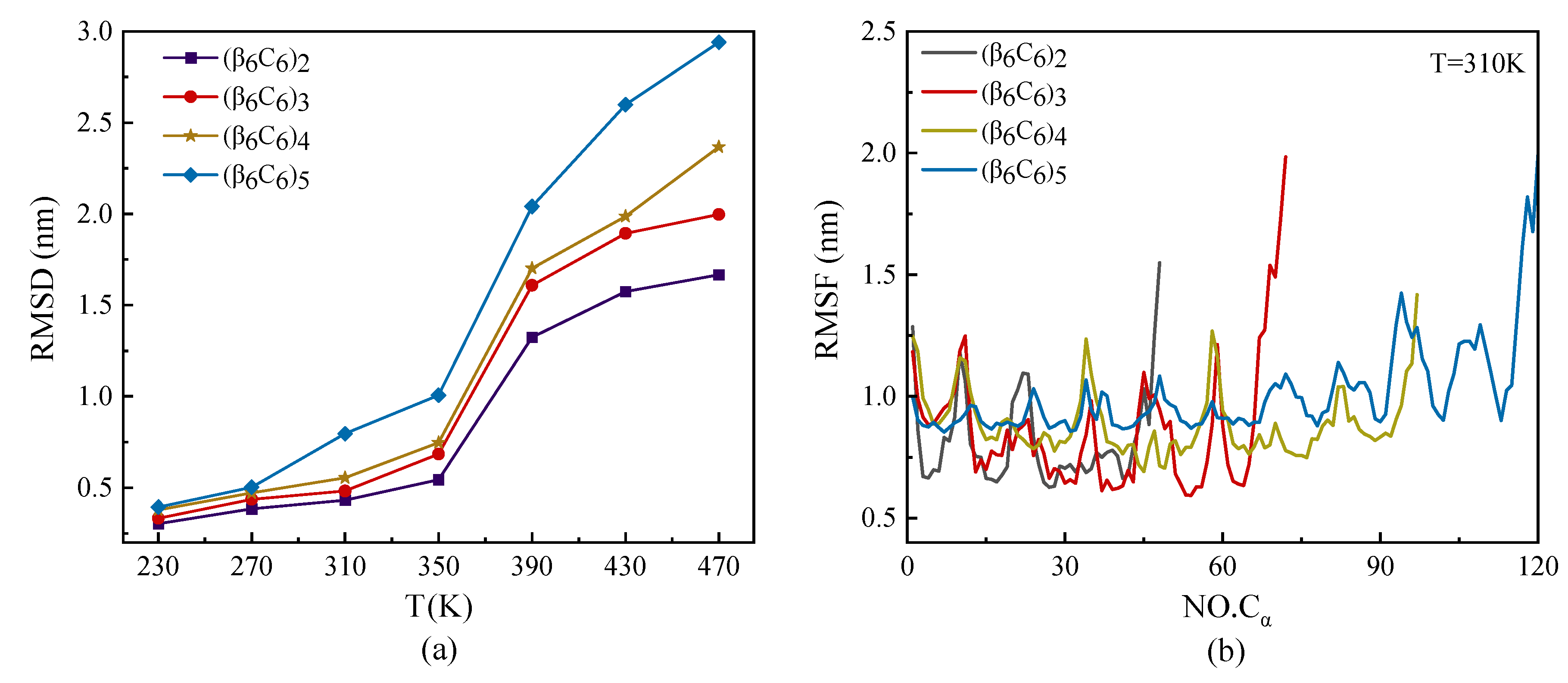
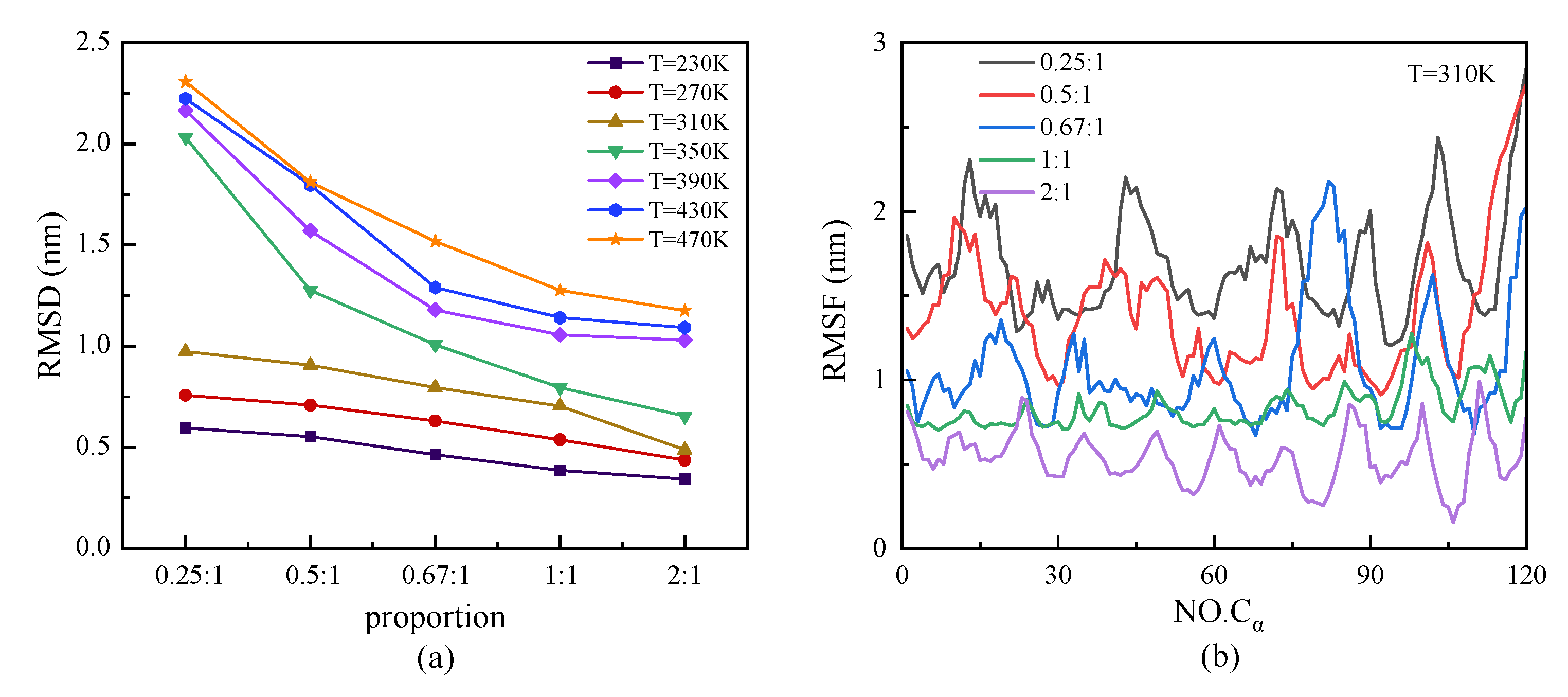
2.1.2. Root Mean Square Deviation and Root Mean Square Fluctuation
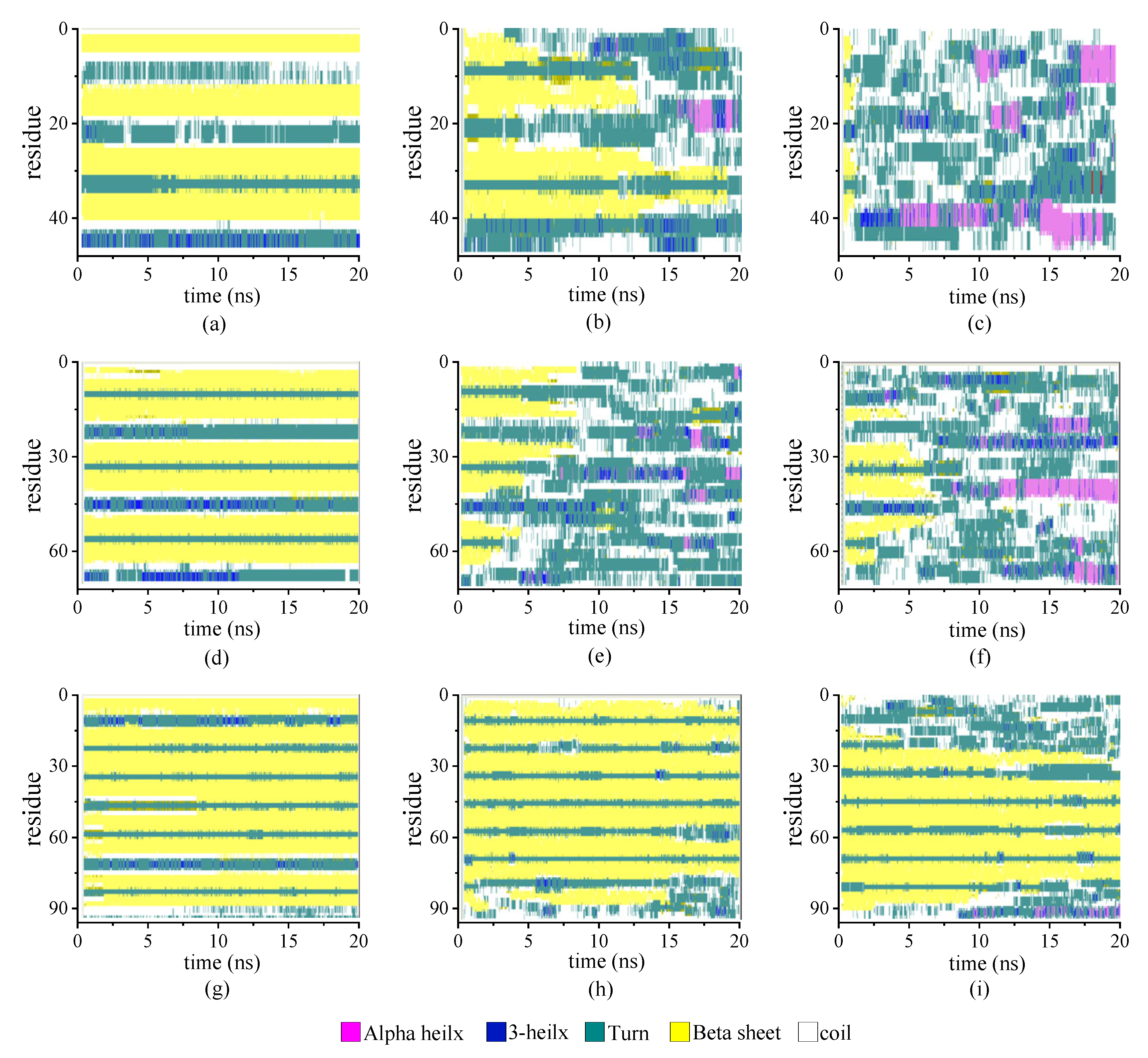
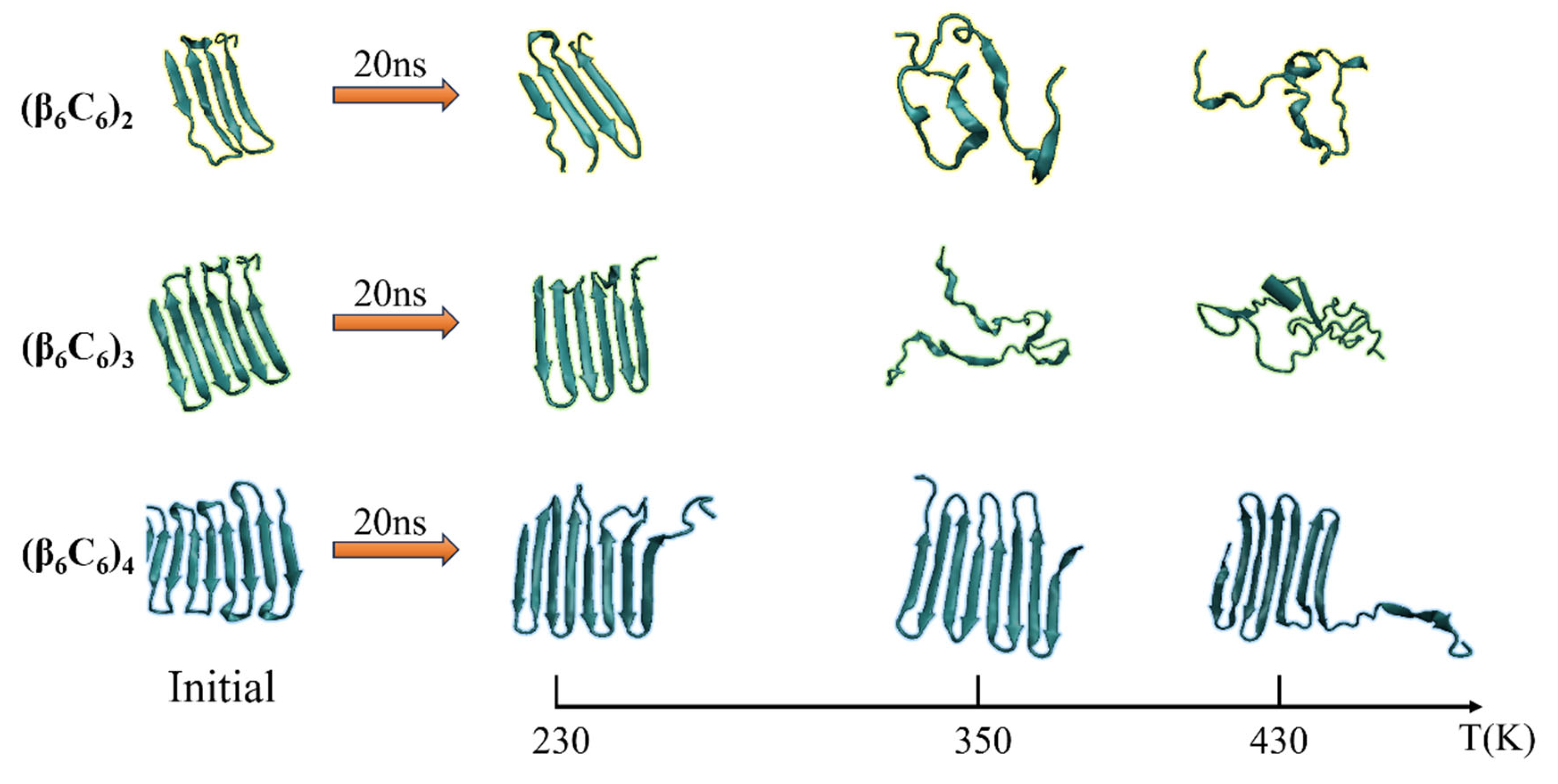
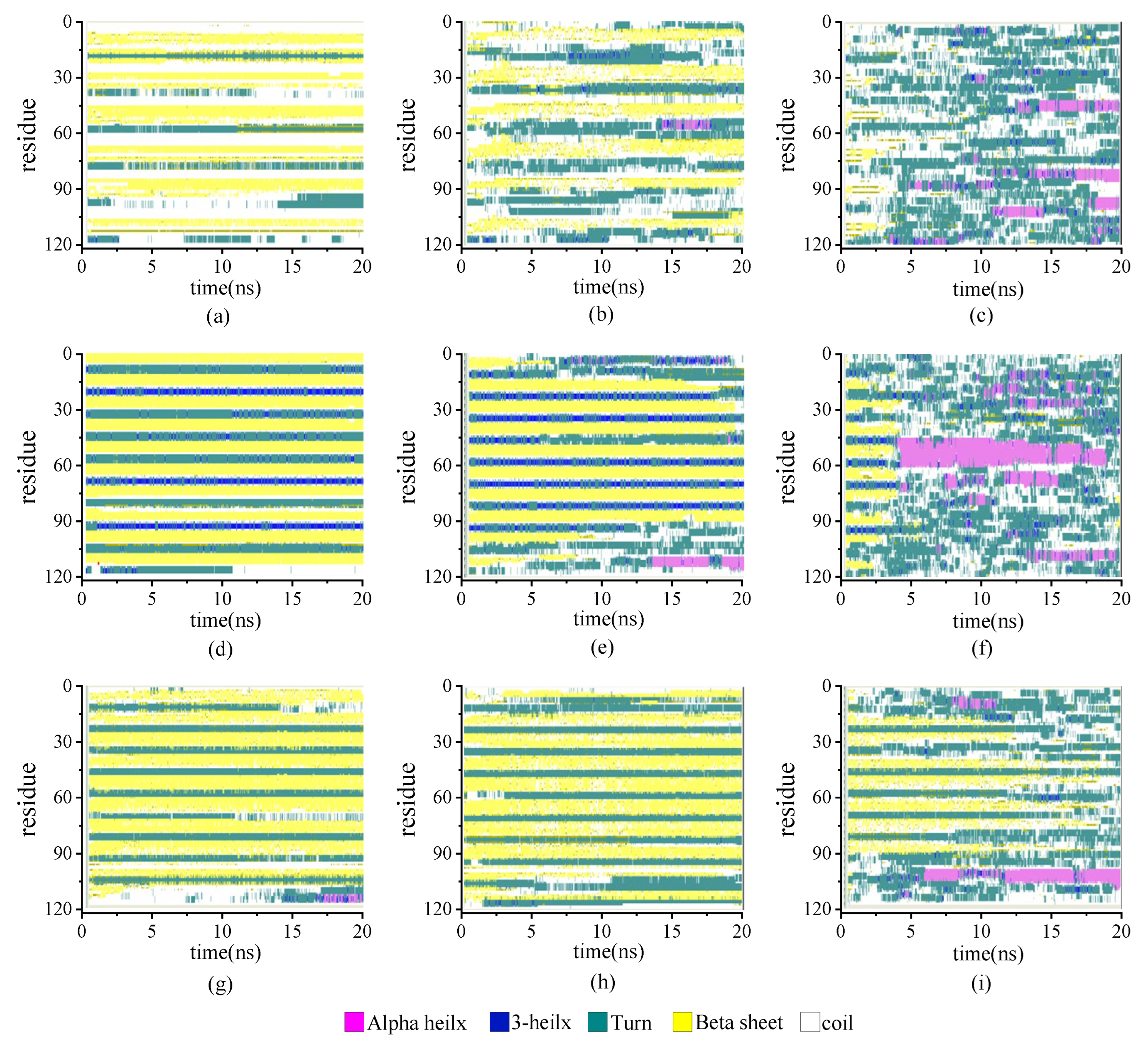
2.1.3. Secondary Structure Analysis
2.2. Effect of the β-Sheet Proportion
2.2.1. Energy
2.2.2. Structural Characteristics
2.2.3. Secondary Structure Analysis
3. Materials and Methods
4. Conclusions
- (1)
- The radius of gyration, Rg, increased with the chain length as well as the temperature. But it had the negative effect of the β-sheet proportions, i.e., in the protein with the same chain length but higher proportion of the β-sheet secondary structure, the lower Rg observed indicated the compact structure.
- (2)
- The root mean square deviation, RMSD, of different chain lengths at various temperature showed that RMSD increased with temperature, especially in the case of the longer chain. Meanwhile, the longer chain presented the higher value of RMSF at a certain temperature. The visible period was also shown according to the repeated secondary structures. Several minimum values of RMSF were located on the skeleton Cα atoms participating in the β-sheets, which indicated a kind of stable secondary structure rather than random coil.
- (3)
- Comparing the protein chains with the same length at the certain temperature, the protein with the higher proportion of the β-sheet structure in a repeating unit presented the lower nonbonded energy with more HBs within the protein, the smaller Rg, as well as the small value of RMSD. It also concluded that the protein with the lower ratio of β-sheet could easily transform its oriented and compact structures to others, such as random coils, turns, and even α-helices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prince, M.; Bryce, R.; Albanese, E. The global prevalence of dementia: A systematic review and metaanalysis. Alzheimer’s Dement. 2013, 9, 63–75. [Google Scholar] [CrossRef]
- Watters, A.L.; Deka, P.; Corrent, C. The highly cooperative folding of small naturally occurring proteins is likely the result of natural selection. Cell 2007, 128, 613–624. [Google Scholar] [CrossRef] [PubMed]
- Marcos, E.; Chidyausiku, T.M.; McShan, A.C.; Evangelidis, T.; Nerli, S.; Carter, L.; Nivón, L.G.; Davis, A.; Oberdorfer, G.; Tripsianes, K.; et al. De novo design of a non-local β-sheet protein with high stability and accuracy. Nat. Struct. Mol. Biol. 2018, 25, 1028–1034. [Google Scholar] [CrossRef] [PubMed]
- Shifman, J.M. Intricacies of β Sheet Protein Design. Structure 2008, 16, 1751–1752. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Butterfield, G.; Lajoie, M.; Gustafson, H. Evolution of a designed protein assembly encapsulating its own RNA genome. Nature 2017, 552, 415–420. [Google Scholar] [CrossRef] [PubMed]
- Freire, F.; Almeida, A.M.; Fisk, J.D. Impact of strand length on the stability of parallel-β-sheet secondary structure. Angew. Chem. 2011, 123, 8894–8897. [Google Scholar] [CrossRef]
- Syud, F.A.; Stanger, H.E.; Mortell, H.S. Influence of Strand Number on Antiparallel β-Sheet Stability in Designed Three- and Four-stranded β-Sheets. J. Mol. Biol. 2003, 326, 553–568. [Google Scholar] [CrossRef]
- Chidyausiku, T.M.; Mendes, S.R.; Klima, J.C.; Nadal, M.; Eckhard, U.; Roel-Touris, J.; Houliston, S.; Guevara, T.; Haddox, H.K.; Moyer, A.; et al. De novo design of immunoglobulin-like domains. Nat. Commun. 2022, 13, 5661. [Google Scholar] [CrossRef]
- Bermudez, M.; Mortier, J.; Rakers, C. More than a look into a crystal ball: Protein structure elucidation guided by molecular dynamics simulations. Drug Discov. Today 2016, 21, 1799–1805. [Google Scholar] [CrossRef]
- Raval, A.; Piana, S.; Eastwood, M.P. Assessment of the utility of contact-based restraints in accelerating the prediction of protein structure using molecular dynamics simulations. Protein Sci. 2016, 25, 19–29. [Google Scholar] [CrossRef]
- Johnson, S.M.; Connelly, S.; Fearns, C. The Transthyretin Amyloidoses: From Delineating the Molecular Mechanism of Aggregation Linked to Pathology to a Regulatory-Agency-Approved Drug. J. Mol. Biol. 2012, 421, 185–203. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Hu, J.; Kapral, R. Chemical Logic Gates on Active Colloids. Adv. Sci. 2024, 18, 2305695. [Google Scholar] [CrossRef]
- Ferreon, A.C.; Deniz, A.A. Protein folding at single-molecule resolution. Biochim. Biophys. Acta (BBA)-Proteins Protomics 2011, 1814, 1021–1029. [Google Scholar] [CrossRef] [PubMed]
- Meier, K.; van Gunsteren, W.F. Cyclic beta-helical/beta-hairpin D,L-alpha-peptide: Study of its folding properties and structure refinement using molecular dynamics. J. Phys. Chem. A 2010, 114, 1852–1859. [Google Scholar] [CrossRef] [PubMed]
- Soto, P.; Colombo, G. Characterization of the conformational space of a triple-stranded β-sheet forming peptide with molecular dynamics simulations. Proteins Struct. 2004, 57, 734–746. [Google Scholar] [CrossRef] [PubMed]
- Xia, K.; Shen, H.; Wang, P. Investigation of the conformation of human prion protein in ethanol solution using molecular dynamics simulations. J. Biomol. Struct. Dyn. 2022, 41, 5872–5881. [Google Scholar] [CrossRef] [PubMed]
- Man, V.H.; He, X.; Gao, J. Effects of All-Atom Molecular Mechanics Force Fields on Amyloid Peptide Assembly: The Case of PHF6 Peptide of Tau Protein. J. Chem. Theory Comput. 2021, 17, 6458–6471. [Google Scholar] [CrossRef]
- Guo, K.; Zhang, X.; Zhao, D. Identification and characterization of sericin5 reveals non-cocoon silk sericin components with high β-sheet content and adhesive strength. Acta Biomater. 2022, 150, 96–110. [Google Scholar] [CrossRef] [PubMed]
- Erickson, D.P.; Ozturk, O.K.; Selling, G.W. Corn zein undergoes conformational changes to higher β-sheet content during its self-assembly in an increasingly hydrophilic solvent. Int. J. Biol. Macromol. 2020, 157, 232–239. [Google Scholar] [CrossRef]
- Afkhami, R.; Varidi, M.J.; Varidi, M. Boosting emulsion properties: The role of β-sheet content and fibril length in soy protein isolate emulsions. Food Hydrocoll. 2024, 149, 109513. [Google Scholar] [CrossRef]
- Xie, C.; Li, W.; Liang, Q. Fabrication of robust silk fibroin film by controlling the content of β-sheet via the synergism of UV-light and ionic liquids. Appl. Surf. Sci. 2019, 492, 55–65. [Google Scholar] [CrossRef]
- Shao, D.; Zhang, Q.; Xu, P. Effects of the Temperature and Salt Concentration on the Structural Characteristics of the Protein (PDB Code 1BBL). Polymers 2022, 14, 2134. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD-visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Wu, Z.; Jiang, Z. Effects of Residual Composition and Distribution on the Structural Characteristics of the Protein. Int. J. Mol. Sci. 2022, 23, 14263. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; You, L.; Dou, W. Effects of an Electric Field on the Conformational Transition of the Protein: A Molecular Dynamics Simulation Study. Polymers 2019, 11, 282. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Shao, D.; Jiang, Z. Effects of an Electric Field on the Conformational Transition of the Protein: Pulsed and Oscillating Electric Fields with Different Frequencies. Polymers 2022, 14, 123. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Xia, F.; Jiang, Z. The Effect of β-Sheet Secondary Structure on All-β Proteins by Molecular Dynamics Simulations. Molecules 2024, 29, 2967. https://doi.org/10.3390/molecules29132967
Feng Z, Xia F, Jiang Z. The Effect of β-Sheet Secondary Structure on All-β Proteins by Molecular Dynamics Simulations. Molecules. 2024; 29(13):2967. https://doi.org/10.3390/molecules29132967
Chicago/Turabian StyleFeng, Zhou, Fang Xia, and Zhouting Jiang. 2024. "The Effect of β-Sheet Secondary Structure on All-β Proteins by Molecular Dynamics Simulations" Molecules 29, no. 13: 2967. https://doi.org/10.3390/molecules29132967
APA StyleFeng, Z., Xia, F., & Jiang, Z. (2024). The Effect of β-Sheet Secondary Structure on All-β Proteins by Molecular Dynamics Simulations. Molecules, 29(13), 2967. https://doi.org/10.3390/molecules29132967




