Measurements of Nuclear Magnetic Shielding in Molecules
Abstract
1. Introduction
2. NMR Chemical Shifts
3. Nuclear Magnetic Shielding in Molecules
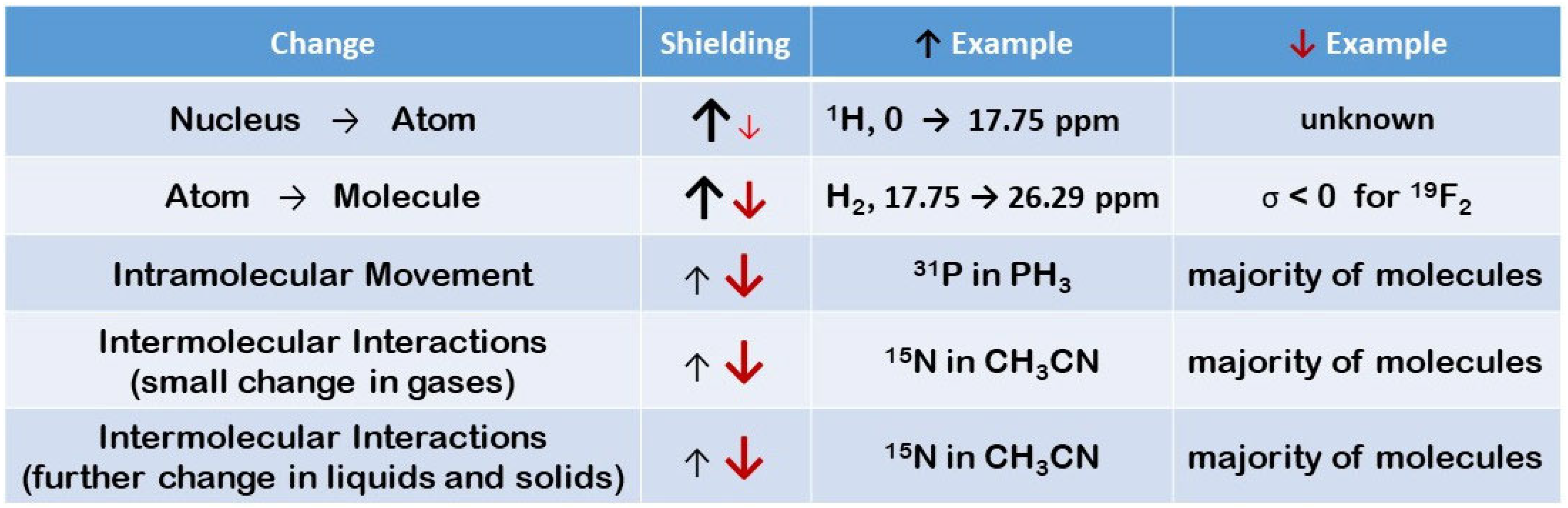
3.1. General Insight
3.2. Theoretical Approach to Shielding
4. Determination of Absolute Shielding
4.1. The Ramsey–Flygare Method
4.2. Methods Based on 1H NMR Signal of Liquid Water and Shielding Transfers
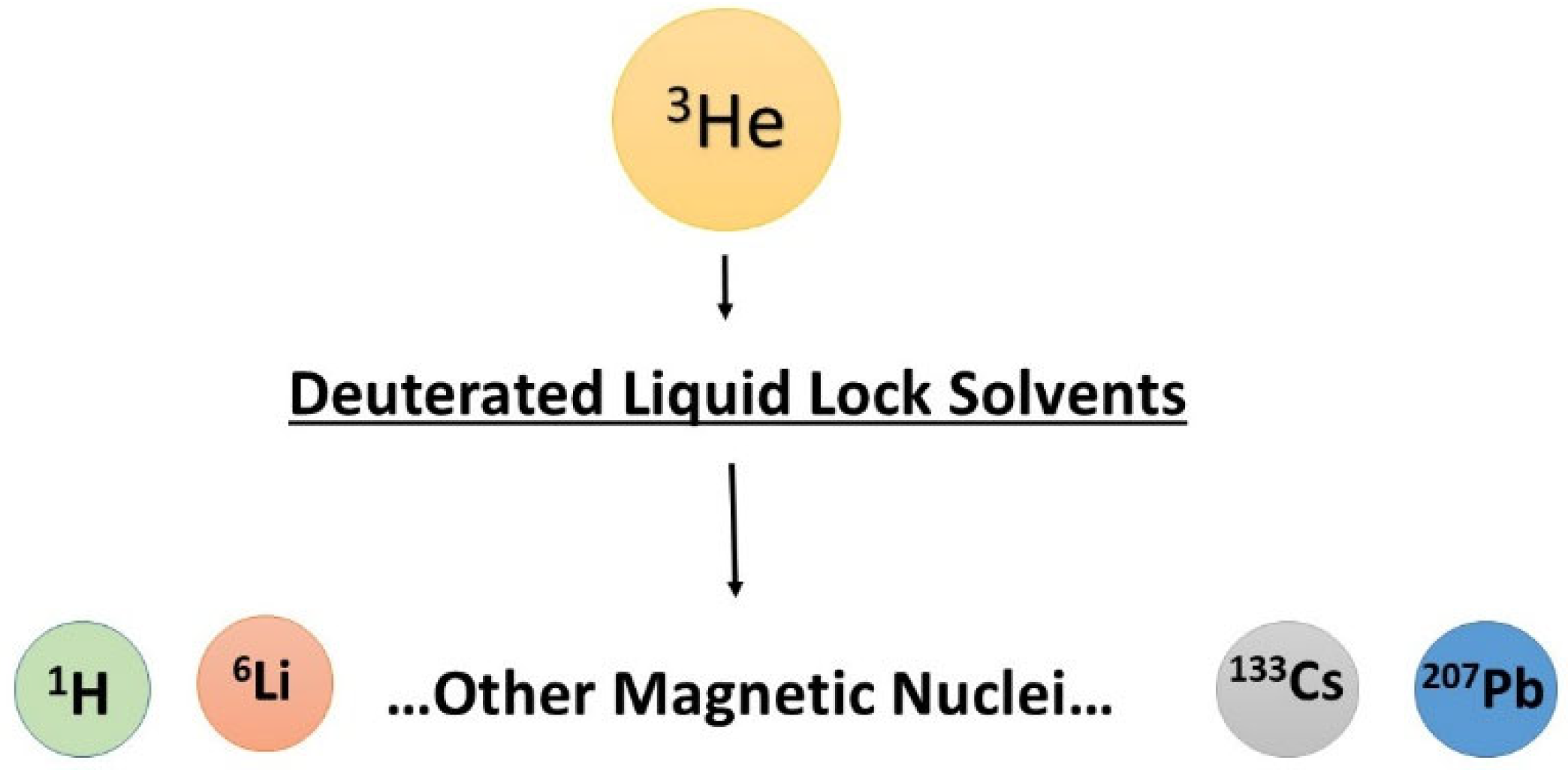
4.3. Helium-3 Atom as the Universal Shielding Reference
5. Nuclear Magnetic Dipole Moments
6. Universal Approach to Shielding Measurements
7. Conclusions
Funding
Conflicts of Interest
References
- Lamb, W.E. Internal Diamagnetic Fields. Phys. Rev. 1941, 60, 817–819. [Google Scholar] [CrossRef]
- Pople, J.A.; Schneider, W.G.; Bernstein, H.J. High-Resolution Nuclear Magnetic Resonance; McGraw-Hill: New York, NY, USA, 1959; Chapter 7; pp. 165–183. [Google Scholar] [CrossRef]
- Ramsey, N.F. Magnetic Shielding of Nuclei in Molecules. Phys. Rev. 1950, 78, 699–703. [Google Scholar] [CrossRef]
- Ramsey, N.F. Dependence of Magnetic Shielding of Nuclei upon Molecular Orientation. Phys. Rev. 1951, 83, 540–541. [Google Scholar] [CrossRef]
- Saika, A.; Slichter, C.P. A Note on the Fluorine Resonance Shifts. J. Chem. Phys. 1954, 22, 26–28. [Google Scholar] [CrossRef]
- Pople, J.A. Nuclear Magnetic Resonance in Diamagnetic Materials. The Theory of Chemical Shifts. Disc. Faraday Soc. 1962, 34, 7–14. [Google Scholar] [CrossRef]
- Karplus, M.; Pople, J.A. Theory of Carbon NMR Chemical Shifts in Conjugated Molecules. J. Chem. Phys. 1963, 38, 2803–2807. [Google Scholar] [CrossRef]
- Baker, M.R.; Anderson, C.H.; Ramsey, N.F. Nuclear Magnetic Antishielding of Nuclei in Molecules. Magnetic Moments of F19, N14 and N15. Phys. Rev. 1964, 133, A1533–A1536. [Google Scholar] [CrossRef]
- Kalinowski, H.-O.; Berger, S.; Braun, S. Carbon-13 NMR Spectroscopy, 1st ed.; John Wiley & Sons: Chichester, UK; New York, NY, USA; Brisbane, Australia; Toronto, ON, Canada; Singapore, 1988; pp. 91–92. ISBN 0-471-96763-7. [Google Scholar] [CrossRef]
- Jameson, C.J. Effects of Intermolecular Interactions and Intramolecular Dynamics on Nuclear Resonance. Bull. Magn. Reson. 1981, 3, 3–29. Available online: https://ismar.org/wp-content/uploads/2021/09/BMR_03_003-028_1981.pdf (accessed on 28 March 2024).
- Jameson, C.J. Fundamental Intramolecular and Intermolecular Information from NMR in the Gas Phase. In New Developments in NMR: Gas Phase NMR; Price, W.S., Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016; Chapter 1; pp. 1–51. [Google Scholar] [CrossRef]
- Woliński, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Gauss, J. Calculation of NMR Chemical Shifts at Second-order Many-body Perturbation Theory Using Gauge-including Atomic Orbitals. Chem. Phys. Lett. 1992, 191, 614–620. [Google Scholar] [CrossRef]
- Watts, J.D.; Gauss, J.; Bartlett, R.J. Coupled-cluster Methods with Noniterative Triple Excitations for Restricted Open-shell Hartree–Fock and other General Single Determinant Reference Functions. Energies and Analytical Gradients. J. Chem. Phys. 1993, 98, 8718–8733. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Coupled-cluster Calculations of Nuclear Magnetic Resonance Chemical Shifts. J. Chem. Phys. 1995, 103, 3561–3577. [Google Scholar] [CrossRef]
- Bühl, M.; Kaupp, M.; Malkina, O.L.; Malkin, V.G. The DFT Route to NMR Chemical Shifts. J. Comput. Chem. 1999, 20, 91–105. [Google Scholar] [CrossRef]
- Halgaker, T.; Jaszuński, M.; Ruud, K. Ab Initio Methods for the Calculation of NMR Shielding and Indirect Spin−Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef] [PubMed]
- Vaara, J. Theory and Computation of Nuclear Magnetic Resonance Parameters. Phys. Chem. Chem. Phys. 2007, 9, 5399–5418. [Google Scholar] [CrossRef]
- Jackowski, K.; Słowiński, M.A. Searching for the Best Values of NMR Shielding and Spin-Spin Coupling Parameters: CH4-nFn Series of Molecules as the Example. Molecules 2023, 28, 1499. [Google Scholar] [CrossRef] [PubMed]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Goodfellow, R.; Granger, P. NMR Nomenclature. Nuclear Spin Properties and Conventions for Chemical Shifts (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 1795–1818, reprinted in Magn. Reson. Chem. 2002, 40, 489–505. [Google Scholar] [CrossRef]
- Harris, R.K.; Becker, E.D.; Cabral de Menezes, S.M.; Granger, P.; Hoffman, R.E.; Zilm, K.W. Further Conventions for NMR Shielding and Chemical Shifts (IUPAC Recommendations). Pure Appl. Chem. 2008, 80, 59–84, reprinted in Magn. Reson. Chem. 2008, 46, 582–598. [Google Scholar] [CrossRef]
- Proctor, W.G.; Yu, F.C. The Dependence of a Nuclear Magnetic Resonance Frequency upon Chemical Compound. Phys. Rev. 1950, 77, 717. [Google Scholar] [CrossRef]
- Dickinson, W.C. Dependence of the F19 Nuclear Resonance Position on Chemical Compound. Phys. Rev. 1950, 77, 736–737. [Google Scholar] [CrossRef]
- Jackowski, K.; Garbacz, P. Nuclear Magnetic Moments and Measurements of Shielding. In New Developments in NMR: Gas Phase NMR; Price, W.S., Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016; Chapter 3; pp. 93–125. ISBN 978-1-78262-722-7. [Google Scholar] [CrossRef]
- Makulski, W.; Jackowski, K. 1H, 13C and 29Si Magnetic Shielding in Gaseous and Liquid Tetramethylsilane. J. Magn. Reson. 2020, 313, 106716. [Google Scholar] [CrossRef] [PubMed]
- Wehrli, D.; Spyszkiewicz-Kaczmarek, M.; Puchalski, M.; Pachucki, K. QED Effects on the Nuclear Magnetic Shielding of 3He. Phys. Rev. Lett. 2021, 127, 263001. [Google Scholar] [CrossRef] [PubMed]
- Jameson, C.J.; Jameson, A.K.; Oppusunggu, D.; Wille, S.; Burell, P.M. 15N Nuclear Magnetic Shielding Scale from Gas Phase Studies. J. Chem. Phys. 1981, 74, 81–88. [Google Scholar] [CrossRef]
- Komorovsky, S.; Repisky, M.; Malkin, E.; Ruud, K.; Gauss, J. Communication: The Absolute Shielding Scales of Oxygen and Sulfur Revisited. J. Chem. Phys. 2015, 142, 091102. [Google Scholar] [CrossRef] [PubMed]
- Makulski, W.; Wilczek, M.; Jackowski, K. 17O and 1H NMR spectral parameters in isolated water molecules. Phys. Chem. Chem. Phys. 2018, 20, 22468–22476. [Google Scholar] [CrossRef] [PubMed]
- Jameson, C.J.; Jameson, A.K.; Honarbakhsh, J. 19F Nuclear Magnetic Shielding Scales from Gas Phase Studies. J. Chem. Phys. 1984, 81, 5266–5267. [Google Scholar] [CrossRef]
- Jameson, C.J.; De Dios, A.; Jameson, A.K. Absolute Shielding Scale for 31P from Gas-phase NMR Studies. Chem. Phys. Lett. 1990, 167, 575–582. [Google Scholar] [CrossRef]
- Jameson, C.J.; Jameson, A.K. Concurrent 19F and 77Se or 19F and 125Te NMR T1 Measurements for Determination of 77Se and 125Te Absolute Shielding Scales. Chem. Phys. Lett. 1987, 135, 254–259. [Google Scholar] [CrossRef]
- McFarlane, W. A Magnetic Double Resonance Study of Some Aryl and Pentafluoroaryl Mercury Compounds. J. Chem. Soc. A 1968, 2280–2285. [Google Scholar] [CrossRef]
- McFarlane, W. The Determination of Carbon-13 Chemical Shifts in Esters by Hetero-nuclear Magnetic Double Resonance. J. Chem. Soc. B 1969, 28–30. [Google Scholar] [CrossRef]
- Garbacz, P.; Jackowski, K.; Makulski, W.; Wasylishen, R.E. Nuclear Magnetic Shielding for Hydrogen in Selected Isolated Molecules. J. Phys. Chem. A 2012, 118, 11896–11904. [Google Scholar] [CrossRef] [PubMed]
- Raynes, W.T.; Panteli, N. The Extraction of a Nuclear Magnetic Shielding Function for the H2 Molecule from Spin-Rotation and Isotope Shift Data. Mol. Phys. 1983, 48, 439–449. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Mroczkowski, S.; Freedberg, D.J.; Anet, F.A.L. Probing the Interior of Fullerenes by 3He NMR Spectroscopy of Endohedral 3He@C60 and 3He@C70. Nature 1994, 367, 256–258. [Google Scholar] [CrossRef]
- Saunders, M.; Jiménez-Vázquez, H.A.; Bangerter, B.W.; Cross, R.J.; Mroczkowski, S.; Freedberg, D.J.; Anet, F.A.L. 3He NMR. A Powerful Tool for Following Fullerene Chemistry. J. Am. Chem. Soc. 1994, 116, 3621–3622. [Google Scholar] [CrossRef]
- Guan-Wu, W.; Xin-Hao, Z.; Huan, Z.; Qing-Xiang, G.; Yun-Dong, W. Accurate Calculation, Prediction, and Assignment of 3He NMR. Chemical Shifts of Helium-3-Encapsulated Fullerenes and Fullerene Derivatives. J. Org. Chem. 2003, 68, 6732–6738. [Google Scholar] [CrossRef] [PubMed]
- Kupka, T.; Stachów, M.; Stobiński, L.; Kaminsky, J. 3He NMR: From Free Gas to its Encapsulation in Fullerene. Magn. Reson. Chem. 2013, 51, 463–468. [Google Scholar] [CrossRef] [PubMed]
- Kupka, T. Noble Gases as Magnetic Probes in Fullerene Chemistry. eMagRes 2016, 5, 959–966. [Google Scholar] [CrossRef]
- Krivdin, L.B. An Overview of Helium-3 NMR: Recent Developments and Applications. Prog. Nucl. Magn. Reson. Spect. 2023, 136–137, 83–109. [Google Scholar] [CrossRef]
- Bruker Almanac 2010, pp. 73–76. Available online: http://www.pascal-man.com/pulseprogram/Almanac2010.pdf (accessed on 28 March 2024).
- Schneider, W.G.; Bernstein, H.J.; Pople, J.A. Proton Magnetic Resonance Chemical Shift of Free (Gaseous) and Associated (Liquid) Hydride Molecules. J. Chem. Phys. 1958, 28, 601–607. [Google Scholar] [CrossRef]
- Spiesecke, H.; Schneider, W.G. Effect of Electronegativity and Magnetic Anisotropy of Substituents on C13 and H1 Chemical Shifts in CH3X and CH3CH2X Compounds. J. Chem. Phys. 1961, 35, 722–731. [Google Scholar] [CrossRef]
- Samultsev, D.O.; Rusakov, Y.Y.; Krivdin, L.B. Normal Halogen Dependence of 13C NMR Chemical Shifts of Halogenomethanes Revisited at the Four-Component Relativistic Level. Magn. Reson. Chem. 2016, 54, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Niemann, U.; Marsmann, H.C. Si-Kernresonanzmessungen an Siliciumhalogeniden. 29Si NMR Studies on Silicon Halogenides. Z. Naturforsch. B 1975, 30, 202–206. [Google Scholar] [CrossRef]
- Mason, J. The Interpretation of Carbon Nuclear Magnetic Resonance Shifts. J. Chem. Soc. A 1971, 1038–1047. [Google Scholar] [CrossRef]
- Wehrli, F.W.; Wirthlin, T. Interpretation of Carbon-13 NMR Spectra; Heyden & Son Ltd.: London, UK; Philadelphia, PA, USA; Reine, Norway, 1978; pp. 34–36. [Google Scholar] [CrossRef]
- Jackowski, K.; Kęcki, Z. Molecular Interaction of Hydrocarbon Alkyl Groups with Carbon Tetrachloride Observed in 13C NMR chemical shifts. Ber. Bunsenges. Phys. Chem. 1981, 85, 143–145. [Google Scholar] [CrossRef]
- Jackowski, K. Effect of Collision Interactions on 13C Nuclear Magnetic Shielding in Monosubstituted Benzenes in Halogen-Containing Solvents. Org. Magn. Reson. 1984, 22, 263–268. [Google Scholar] [CrossRef]
- Tiers, G.D.V. Proton Nuclear Resonance Spectroscopy: I. Reliable Shielding Values by Internal Referencing with Tetramethylsilane. J. Phys. Chem. 1958, 62, 1151–1152. [Google Scholar] [CrossRef]
- Antušek, A.; Jaszuński, M. Accurate Non-Relativistic Calculations of NMR Shielding Constants. In New Developments in NMR: Gas Phase NMR; Price, W.S., Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016; Chapter 6; pp. 186–217. [Google Scholar] [CrossRef]
- Faber, R.; Kaminsky, J.; Sauer, S.P.A. Rovibrational and Temperature Effects in Theoretical Studies of NMR Parameters. In New Developments in NMR: Gas Phase NMR; Price, W.S., Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016; Chapter 7; pp. 218–266. [Google Scholar] [CrossRef]
- Repisky, M.; Komorovsky, S.; Bast, R.; Ruud, K. Relativistic Calculations of Nuclear Magnetic Resonance Parameters. In New Developments in NMR: Gas Phase NMR; Price, W.S., Jackowski, K., Jaszuński, M., Eds.; Royal Society of Chemistry: Cambridge, UK, 2016; Chapter 8; pp. 267–303. [Google Scholar] [CrossRef]
- Field-Theodore, T.E.; Olejniczak, M.; Jaszuński, M.; Wilson, D.J.D. NMR Shielding Constants in Group 15 Trifluorides. Phys. Chem. Chem. Phys. 2018, 20, 23025–23033. [Google Scholar] [CrossRef]
- Hindermann, D.K.; Cornwell, C.D. Vibrational Corrections to the Nuclear-Magnetic Shielding and Spin–Rotation Constants for Hydrogen Fluoride. Shielding Scale for 19F. J. Chem. Phys. 1968, 48, 4154–4161. [Google Scholar] [CrossRef]
- Jackowski, K.; Kubiszewski, M.; Makulski, W. 13C and 19F Nuclear Magnetic Shielding and Spin-Spin Coupling in Gaseous Fluoromethane-d3. J. Mol. Struct. 2002, 614, 267–272. [Google Scholar] [CrossRef]
- Sundholm, D.; Gauss, J. Isotope and Temperature Effects on Nuclear Magnetic Shieldings and Spin-Rotation Constants Calculated at the Coupled-Cluster Level. Mol. Phys. 1997, 92, 1007–1014. [Google Scholar] [CrossRef]
- Jaszuński, M.; Łach, G.; Strasburger, K. NMR Shielding Constants in Hydrogen Molecule Isotopomers. Theor. Chem. Acc. 2011, 129, 325–330. [Google Scholar] [CrossRef]
- Karadakov, P.B.; Morokuma, K. ONIOM as an Efficient Tool for Calculating NMR Chemical Shielding Constants in Large Molecules. Chem. Phys. Lett. 2000, 317, 589–596. [Google Scholar] [CrossRef]
- Poidevin, C.; Stoychev, G.L.; Riplinger, C.; Auer, A.A. High Level Electronic Structure Calculation of Molecular Solid-State NMR Shielding Constants. J. Chem. Theory Comput. 2022, 18, 2408–2417. [Google Scholar] [CrossRef] [PubMed]
- Flygare, W.H. Spin—Rotation Interaction and Magnetic Shielding in Molecules. J. Chem. Phys. 1964, 41, 793–800. [Google Scholar] [CrossRef]
- Gierke, T.D.; Flygare, W.H. An Empirical Evaluation of the Individual Elements in the Nuclear Diamagnetic Shielding Tensor by the Atom Dipole Methodology. J. Am. Chem. Soc. 1972, 94, 7277–7283. [Google Scholar] [CrossRef]
- Bryce, D.L.; Wasylishen, R.E. Microwave Spectroscopy and Nuclear Magnetic Resonance Spectroscopy-What Is the Connection? Acc. Chem. Res. 2003, 36, 327–334. [Google Scholar] [CrossRef]
- Ozier, I.; Crapo, L.M.; Ramsey, N.F. Spin Rotation Constant and Rotational Magnetic Moment of 13C16O. J. Chem. Phys. 1968, 49, 2314–2321. [Google Scholar] [CrossRef]
- Jameson, C.J.; Jameson, A.K. Gas Phase 13C Chemical Shifts in the Zero Pressure Limit: Refinements to the Absolute Shielding Scale for 13C. Chem. Phys. Lett. 1987, 134, 461–466. [Google Scholar] [CrossRef]
- Raynes, W.T.; McVey, R.; Wright, S.J. An Improved Carbon-13 Nuclear Shielding Scale. J. Chem. Soc. Faraday Trans. 2 1989, 85, 759–763. [Google Scholar] [CrossRef]
- Wasylishen, R.E.; Bryce, D.L. A Revised Experimental Absolute Magnetic Shielding Scale for Oxygen. J. Chem. Phys. 2002, 117, 10061–10066. [Google Scholar] [CrossRef]
- Wasylishen, R.E.; Mooibroek, S.; Mcdonald, J.B. A More Reliable Oxygen-17 Absolute Chemical Shielding Scale. J. Chem. Phys. 1984, 81, 1057–1059. [Google Scholar] [CrossRef]
- Frerking, M.A.; Langer, W.D. A Measurement of the Hyperfine Structure of C17O. J. Chem. Phys. 1981, 74, 6990–6991. [Google Scholar] [CrossRef]
- Cazzoli, G.; Dore, L.; Puzzarini, C.; Beninati, S. Millimeter- and Submillimeter-Wave Spectrum of C17O. Rotational Hyperfine Structure Analyzed Using the Lamb-Dip Techniques. Phys. Chem. Chem. Phys. 2002, 4, 3575–3577. [Google Scholar] [CrossRef]
- Kukolich, S.G. Proton Magnetic Shielding Tensors from Spin-Rotation Measurements on H2CO and NH3. J. Am. Chem. Soc. 1975, 97, 5704–5707. [Google Scholar] [CrossRef]
- Davies, P.B.; Neumann, R.M.; Wofsy, S.C.; Klemperer, W. Radio-Frequency Spectrum of Phosphine (PH3). J. Chem. Phys. 1971, 55, 3564–3568. [Google Scholar] [CrossRef]
- Jameson, C.J. Chemical Shift Scales on an Absolute Basis. In Encyclopedia of Nuclear Magnetic Resonance; Grant, D.M., Harris, R.K., Eds.; John Wiley: London, UK, 1996; pp. 1273–1281. [Google Scholar] [CrossRef]
- Winkler, P.F.; Kleppner, D.; Myint, T.; Walther, F.G. Magnetic Moment of the Proton in Bohr Magnetons. Phys. Rev. A 1972, 5, 83–114. [Google Scholar] [CrossRef]
- Phillips, W.D.; Cooke, W.E.; Kleppner, D. Magnetic Moment of the Proton in H2O in Bohr Magnetons. Phys. Rev. Lett. 1975, 35, 1619–1622. [Google Scholar] [CrossRef]
- Jameson, C.J.; Jameson, A.K. Absolute Shielding Scale for 29Si. Chem. Phys. Lett. 1988, 149, 300–305. [Google Scholar] [CrossRef]
- Jackowski, K.; Jaszuński, M.; Kamieński, B.; Wilczek, M. NMR Frequency and Magnetic Dipole Moment of 3He Nucleus. J. Magn. Reson. 2008, 193, 147–149. [Google Scholar] [CrossRef]
- Mohr, P.J.; Taylor, B.N.; Newell, C.B. CODATA Recommended Values of the Fundamental Physical Constants: 2006. Rev. Mod. Phys. 2008, 80, 633–730. [Google Scholar] [CrossRef]
- Mohr, P.J.; Taylor, B.N.; Newell, C.B. CODATA recommended values of the fundamental physical constants: 2010. Rev. Mod. Phys. 2012, 84, 1527–1605. [Google Scholar] [CrossRef]
- Jackowski, K.; Jaszuński, M.; Wilczek, M. Alternative Approach to the Standardization of NMR Spectra. Direct Measurement of Nuclear Magnetic Shielding in Molecules. J. Phys. Chem. A 2010, 114, 2471–2475. [Google Scholar] [CrossRef] [PubMed]
- Antušek, A.; Jackowski, K.; Jaszuński, M.; Makulski, W.; Wilczek, M. Nuclear Magnetic Dipole Moments from NMR Spectra. Chem. Phys. Lett. 2005, 411, 111–116. [Google Scholar] [CrossRef]
- Stone, N.J. Table of Nuclear Magnetic Dipole and Electric Quadrupole Moments. At. Data Nucl. Data Tables 2005, 90, 75–176. [Google Scholar] [CrossRef]
- Flowers, J.L.; Petley, B.W.; Richards, M.G. A Measurement of the Nuclear Magnetic Moment of the Helium-3 Atom in Terms of that of the Proton. Metrologia 1993, 30, 75–87. [Google Scholar] [CrossRef]
- Makulski, W.; Jackowski, K.; Antušek, A.; Jaszuński, M. Gas-phase NMR measurements, absolute shielding scales and magnetic dipole moments of 29Si and 73Ge nuclei. J. Phys. Chem. A 2006, 110, 11462–11466. [Google Scholar] [CrossRef] [PubMed]
- Jackowski, K.; Makulski, W.; Szyprowska, A.; Antušek, A.; Jaszuński, M.; Jusélius, J. NMR Shielding Constants in BF3 and Magnetic Dipole Moments of 11B and 10B Nuclei. J. Chem. Phys. 2009, 130, 044309. [Google Scholar] [CrossRef] [PubMed]
- Makulski, W.; Szyprowska, A.; Jackowski, K. Precise Determination of the 13C Nuclear Magnetic Moment from 13C, 3He and 1H NMR Measurements in the Gas Phase. Chem. Phys. Lett. 2011, 511, 224–228. [Google Scholar] [CrossRef]
- Lantto, P.; Jackowski, K.; Makulski, W.; Olejniczak, M.; Jaszuński, M. NMR Shielding Constants in PH3, Absolute Shielding Scale and the Nuclear Magnetic Moment of 31P. J. Phys. Chem. A 2011, 115, 10617–10623. [Google Scholar] [CrossRef]
- Jaszuński, M.; Repisky, M.; Demissie, T.B.; Komorovsky, S.; Malkin, E.; Ruud, K.; Garbacz, P.; Jackowski, K.; Makulski, W. Spin-Rotation and NMR Shielding Constants in HCl. J. Chem. Phys. 2013, 139, 234302. [Google Scholar] [CrossRef] [PubMed]
- Adrjan, B.; Makulski, W.; Jackowski, K.; Demissie, T.B.; Ruud, K.; Antušek, A.; Jaszuński, M. NMR Absolute Shielding Scale and Nuclear Magnetic Moment of 207Pb. Phys. Chem. Chem. Phys. 2016, 18, 16483–16490. [Google Scholar] [CrossRef]
- Jaszuński, M.; Olejniczak, M. NMR Shielding Constants in SeH2 and TeH2. Mol. Phys. 2013, 111, 1355–1363. [Google Scholar] [CrossRef]
- Makulski, W. 83Kr Nuclear Magnetic Moment in Terms of that of 3He. Magn. Reson. Chem. 2014, 52, 430–434. [Google Scholar] [CrossRef]
- Makulski, W. 129Xe and 131Xe Nuclear Magnetic Dipole Moments from Gas Phase NMR Spectra. Magn. Reson. Chem. 2015, 53, 273–279. [Google Scholar] [CrossRef]
- Antušek, A.; Kȩdziera, D.; Kaczmarek-Kȩdziera, A.; Jaszuński, M. Coupled Cluster Study of NMR Shielding of Alkali Metal Ions in Water Complexes and Magnetic Moments of Alkali Metal Nuclei. Chem. Phys. Lett. 2012, 532, 1–8. [Google Scholar] [CrossRef]
- Antušek, A.; Rodziewicz, P.; Kȩdziera, D.; Kaczmarek-Kȩdziera, A.; Jaszuński, M. Ab Initio Study of NMR Shielding of Alkali Earth Metal Ions in Water Complexes and Magnetic Moments of Alkali Earth Metal Nuclei. Chem. Phys. Lett. 2013, 588, 57–62. [Google Scholar] [CrossRef]
- Antušek, A.; Holka, F. Absolute Shielding Scales for Al, Ga, and In and revised nuclear magnetic dipole moments of 27Al, 69Ga, 71Ga, 113In, and 115In nuclei. J. Chem. Phys. 2015, 143, 074301. [Google Scholar] [CrossRef]
- Antušek, A.; Šulka, M. Ab Initio Calculations of NMR Shielding of Sc3+, Y3+ and La3+ Ions in the Water Solution and 45Sc, 89Y, 138La and 139La Nuclear Magnetic Dipole Moments. Chem. Phys. Lett. 2016, 660, 127–131. [Google Scholar] [CrossRef]
- Stone, N.J. Table of Recommended Nuclear Magnetic Dipole Moments. In IAEA Nuclear Data Section; Vienna International Centre: Vienna, Austria, 2019; Available online: http://www-nds.iaea.org/publications (accessed on 28 March 2024).
- Harding, R.D.; Pallada, S.; Croese, J.; Antušek, A.; Baranowski, M.; Bissell, M.L.; Cerato, L.; Dziubinska-Kühn, K.M.; Gins, W.; Gustafsson, F.P.; et al. Magnetic Moments of Short-Lived Nuclei with Part-per-Million Accuracy:Toward Novel Applications of β-Detected NMR in Physics, Chemistry, and Biology. Phys. Rev. X 2020, 10, 041061. [Google Scholar] [CrossRef]
- Garbacz, P.; Makulski, W. 183W Nuclear Dipole Moment Determined by Gas-Phase NMR Spectroscopy. Chem. Phys. 2017, 498–499, 7–11. [Google Scholar] [CrossRef]
- Antušek, A.; Repisky, M.; Jaszuński, M.; Jackowski, K.; Makulski, W.; Misiak, M. Nuclear Magnetic Dipole Moment of 209Bi from NMR experiments. Phys. Rev. A 2018, 98, 052509. [Google Scholar] [CrossRef]
- Makulski, W.; Garbacz, P. Gas-Phase 21Ne NMR Studies and the Nuclear Magnetic Dipole Moment of Neon-21. Magn. Res. Chem. 2020, 58, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Makulski, W.; Aucar, J.J.; Aucar, G.A. Ammonia: The Molecule for Establishing 14N and 15N Absolute Shielding Scales and a Source of Information on Nuclear Magnetic Moments. J. Chem. Phys. 2022, 157, 084306. [Google Scholar] [CrossRef] [PubMed]
- Makulski, W. Probing Nuclear Dipole Moments and Magnetic Shielding Constants through 3-Helium NMR Spectroscopy. Physchem 2022, 2, 116–130. [Google Scholar] [CrossRef]
- Makulski, W.; Słowiński, M.A.; Garbacz, P. Nuclear Dipole Moments and Shielding Constants of Light Nuclei Measured in Magnetic Fields. Magnetochemistry 2023, 9, 148. [Google Scholar] [CrossRef]
- Garbacz, P.; Jackowski, K. Referencing of 1H and 13C NMR shielding measurements. Chem. Phys. Lett. 2019, 728, 148–152. [Google Scholar] [CrossRef]
- Garbacz, P.; Piszczatowski, K.; Jackowski, K.; Moszyński, R.; Jaszuński, M. Weak intermolecular interactions in gas-phase NMR. J. Chem. Phys. 2011, 135, 084310. [Google Scholar] [CrossRef] [PubMed]
- Altman, L.J.; Laungani, D.; Gunnarsson, G.; Wennerstrom, H.; Forsén, S. Proton, deuterium, and tritium nuclear magnetic resonance of intramolecular hydrogen bonds. Isotope effects and the shape of the potential energy function. J. Am. Chem. Soc. 1978, 100, 8264–8266. [Google Scholar] [CrossRef]
- Jameson, C.J.; Mason, J. The Chemical Shift. In Multinuclear NMR; Mason, J., Ed.; Plenum Press: New York, NY, USA, 1987; Chapter 3; p. 81. [Google Scholar] [CrossRef]
- Jackowski, K.; Makulski, W. 13C shielding scale for MAS NMR spectroscopy. Magn. Reson. Chem. 2011, 49, 600–602. [Google Scholar] [CrossRef]
- Yi, Y.; Adrjan, B.; Włodarz, J.; Li, J.; Jackowski, K.; Roszak, S. NMR Measurements and DFT Studies of Nuclear Magnetic Shielding in Emodin and Chuanxiongzine Molecules. J. Mol. Struct. 2018, 1166, 304–310. [Google Scholar] [CrossRef]
- Yi, Y.; Adrjan, B.; Li, J.; Hu, B.; Roszak, S. NMR Studies of Daidzein and Puerarin: Active Anti-oxidants in Traditional Chinese Medicine. J. Mol. Model. 2019, 25, 202. [Google Scholar] [CrossRef] [PubMed]
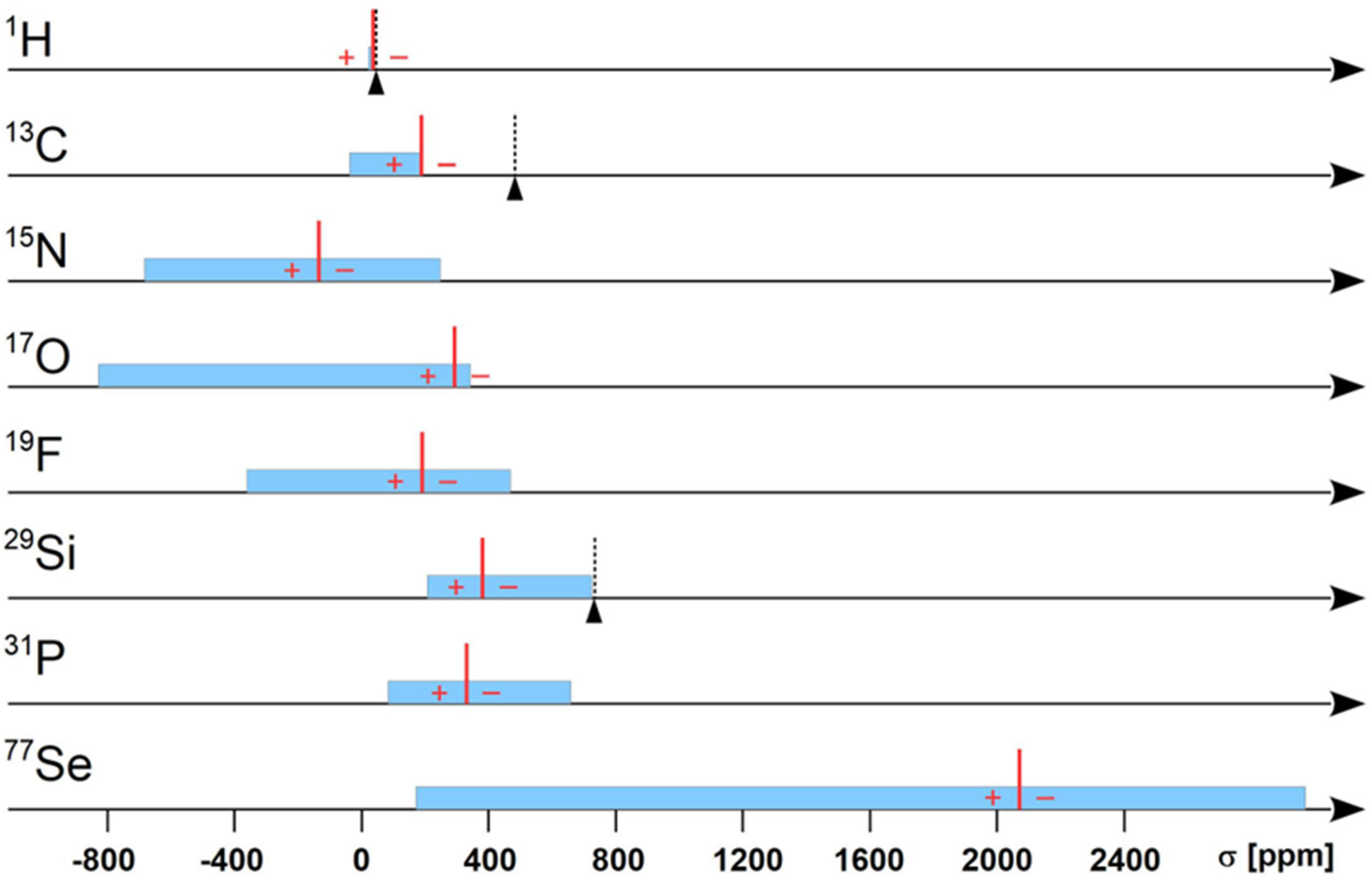


| NMR | Natural Abundance a [%] | gX Factor b,c | Absolute Frequency a ΞX [MHz] | Reference Shielding σ [ppm] | Recommended Reference Standard a |
|---|---|---|---|---|---|
| 1H | 99.9885 | 5.585 694 70 | 100.000 000 | 33.480(5) d | TMS in CDCl3 |
| 2H | 0.0115 | 0.857 438 231 | 15.350 609 | 33.568(5) e | TMS-d12 in CDCl3 |
| 3He | 1.37 × 10−4 | −4.255 250 62 | 76.179 437 | 59.967 f | 3He gas |
| 13C | 1.07 | 1.404 739 | 25.145 020 | 186.42(10) g | TMS in CDCl3 |
| 15N | 0.368 | −0.566 141 | 10.136 767 | −135.8 h | CH3NO2 liquid |
| 17O | 0.038 | −0.757 418 8 | 13.556 457 | 290.2 i | D2O liquid |
| 19F | 100 | 5.256 68 | 94.094 011 | 188.7 j | CCl3F liquid |
| 29Si | 4.6832 | −1.110 104 | 19.867 187 | 379.0(20) g | TMS in CDCl3 |
| 31P | 100 | 2.261 85 | 40.480742 | 328.35 k | H3PO4 85% in H2O |
| 77Se | 7.63 | 1.06 1 | 19.071 513 | 2069 l | (CH3)2Se liquid |
| Applied NMR Methods | µX Transfer | Observed Molecules | Magnetic Moments, µX/µN | More Details |
|---|---|---|---|---|
| 1H and 13C | 1H → 13C | 13CH4 | 0.7023694(7) | Refs. [83,88] |
| 1H and 14N | 1H → 14N | 14NH3 | 0.4035723(5) | Ref. [83] |
| 1H and 15N | 1H → 15N | 15NH3 | −0.283057(1) | Ref. [83] |
| 1H and 17O | 1H → 17O | H217O | −1.893547(2) | Ref. [83] |
| 1H and 19F | 1H → 19F | CH319F | 2.62834(1) | Ref. [83] |
| 1H and 29Si | 1H → 29Si | 29SiH4 | −0.555052(3) | Ref. [86] |
| 1H and 31P | 1H → 31P | 31PH3 | 1.130925(5) | Refs. [83,89] |
| 19F and 33S | 19F → 33S | 33SF6 | 0.64325(2) | Ref. [83] |
| 1H and 35Cl | 1H → 35Cl | H35Cl | 0.82170(1) | Ref. [90] |
| 1H and 37Cl | 1H → 37Cl | H37Cl | 0.68398(1) | Ref. [90] |
| 1H and 73Ge | 1H → 73Ge | 73GeH4 | −0.87824(5) | Ref. [86] |
| 1H and 77Se | 1H → 77Se | H277Se | 0.53356(5) | Ref. [92] |
| 1H and 207Pb | 1H → 207Pb | 207Pb(CH3)4 | 0.5906(4) | Ref. [91] |
| 3He and 10B | 3He → 10B | 10BF3 + 3He | 1.8004636(8) | Ref. [87] |
| 3He and 11B | 3He → 11B | 11BF3 + 3He | 2.688378(1) | Ref. [87] |
| 3He and 83Kr | 3He → 83Kr | 83Kr + 3He | −0.970730(3) | Ref. [93] |
| 3He and 129Xe | 3He → 129Xe | 129Xe + 3He | −0.77796(2) | Ref. [94] |
| 3He and 131Xe | 3He → 131Xe | 131Xe + 3He | 0.691845(7) | Ref. [94] |
| No | Lock Solvent | Observed 2H Signal | σD [ppm] |
|---|---|---|---|
| 1 | Cyclohexane-d12 | -CD2- | 31.834 |
| 2 | Toluene-d8 | -CD3 | 31.525 |
| 3 | Acetonitrile-d3 | -CD3 | 30.864 |
| 4 | DMSO-d6 | -CD3 | 30.574 |
| 5 | Acetone-d6 | -CD3 | 30.570 |
| 6 | Methanol-d4 | -CD3 | 29.593 |
| 7 | Water-d2 | -OD | 28.837 |
| 8 | Nitromethane-d3 | -CD3 | 28.041 |
| 9 | Benzene-d6 | =CD- | 26.441 |
| 10 | Chloroform-d | -CD | 26.389 |
| Observed NMR Parameters | Primary Isotope Effects | Secondary Isotope Effects |
|---|---|---|
| Shielding in H2 and HD molecules | σ0(H2) = 26.293 ppm σ0(HD) = 26.239 ppm | σ0(H2) = 26.293 ppm σ0(HD) = 26.327 ppm |
| Isotope effects | 0Δ(2/1H) = −0.046 ppm | 1Δ(2/1H) = −0.034 ppm |
| Shielding in HD and D2 molecules | σ0(HD) = 26.327 ppm σ0(D2) = 26.388 ppm | σ0(HD) = 26.339 ppm σ0(D2) = 26.388 ppm |
| Isotope effects | 0Δ(2/1H) = −0.061 ppm | 1Δ(2/1H) = −0.049 ppm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackowski, K.; Wilczek, M. Measurements of Nuclear Magnetic Shielding in Molecules. Molecules 2024, 29, 2617. https://doi.org/10.3390/molecules29112617
Jackowski K, Wilczek M. Measurements of Nuclear Magnetic Shielding in Molecules. Molecules. 2024; 29(11):2617. https://doi.org/10.3390/molecules29112617
Chicago/Turabian StyleJackowski, Karol, and Marcin Wilczek. 2024. "Measurements of Nuclear Magnetic Shielding in Molecules" Molecules 29, no. 11: 2617. https://doi.org/10.3390/molecules29112617
APA StyleJackowski, K., & Wilczek, M. (2024). Measurements of Nuclear Magnetic Shielding in Molecules. Molecules, 29(11), 2617. https://doi.org/10.3390/molecules29112617





