The Effect of Different Substances Embedded in Fullerene Cavity on Surfactant Self-Assembly Behavior through Molecular Dynamics Simulation
Abstract
1. Introduction
2. Discussion
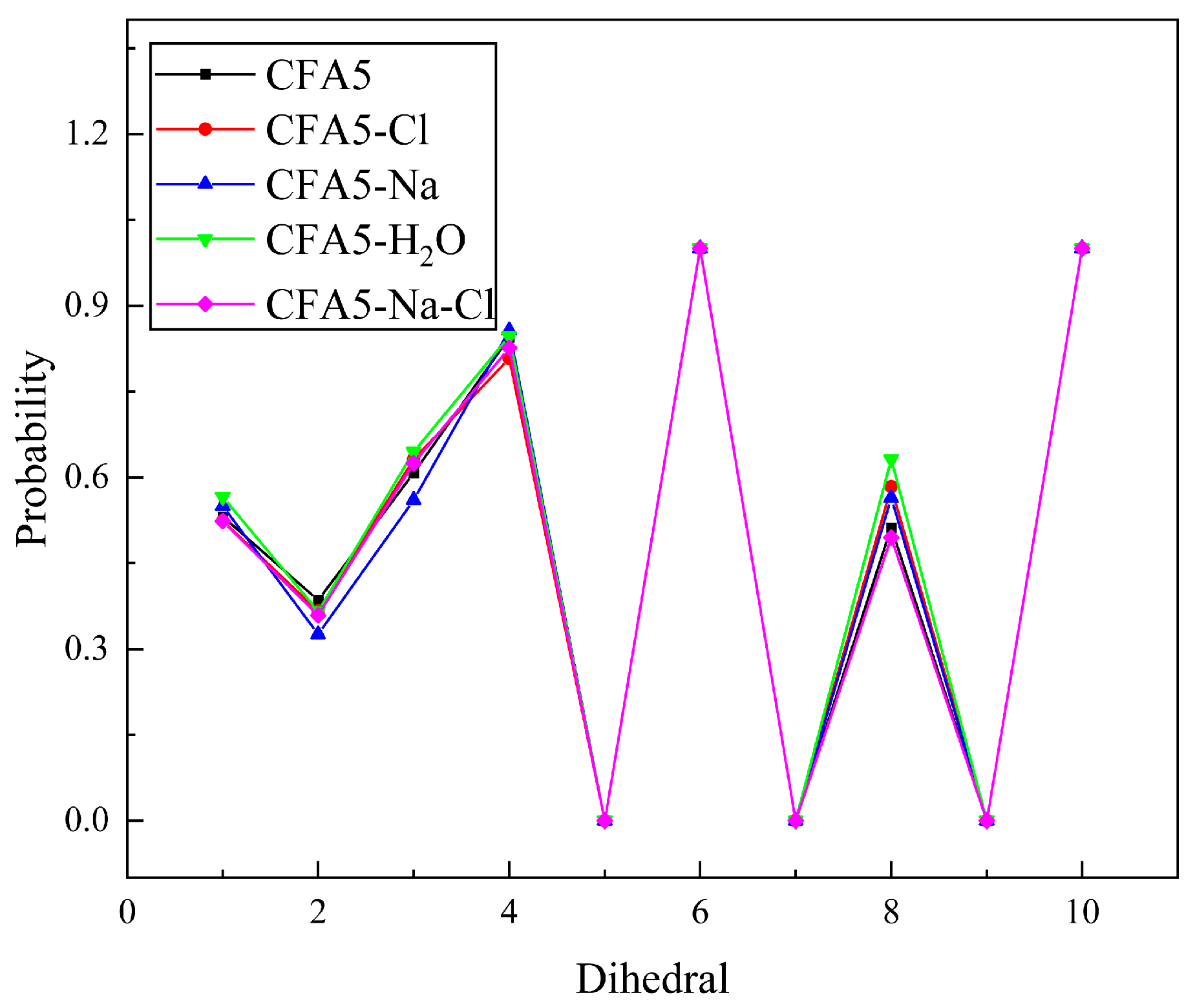
2.1. Conformation of Surfactant Alkyl Chain
2.2. Structure of Micelles
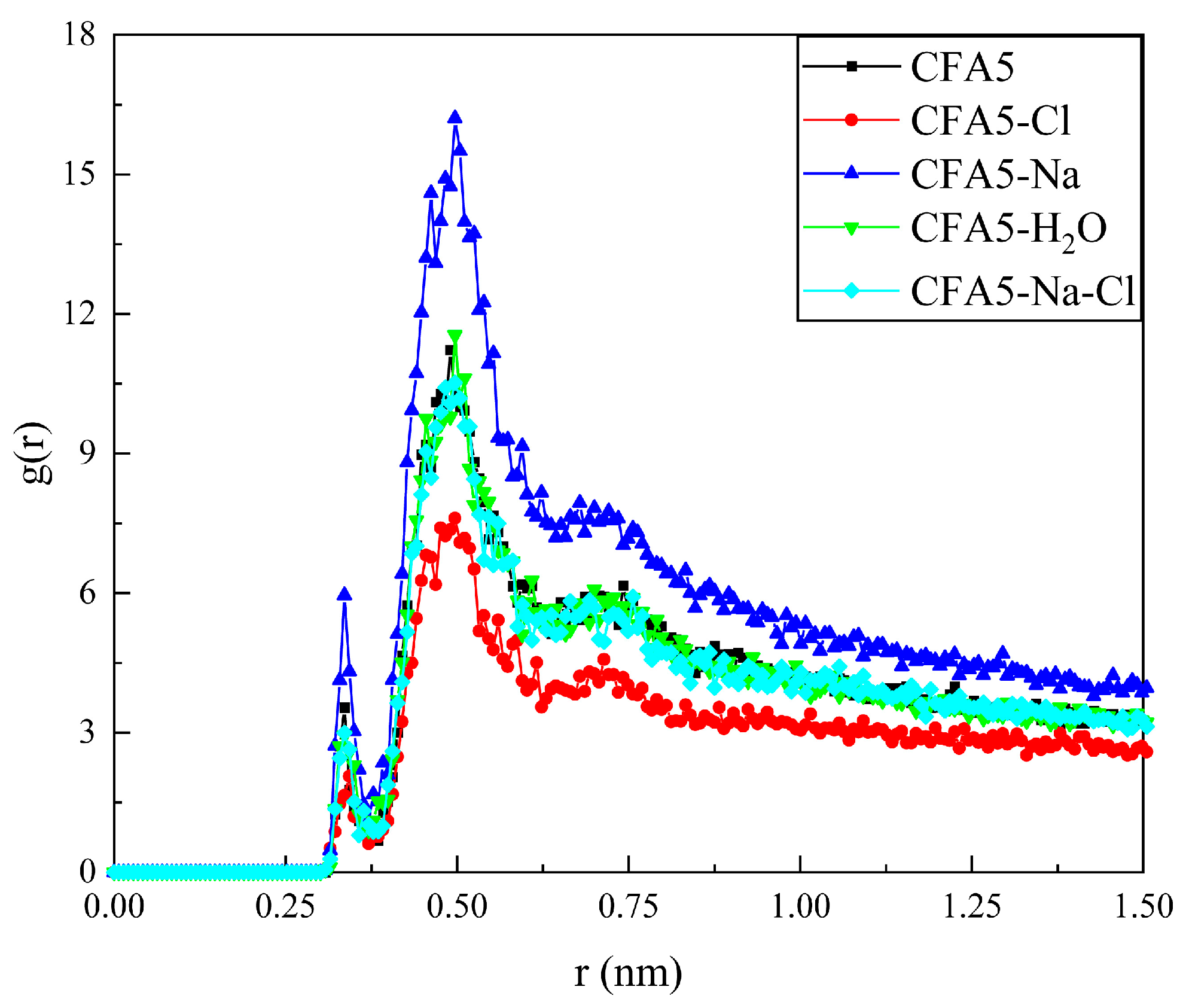
2.2.1. Micelle Size
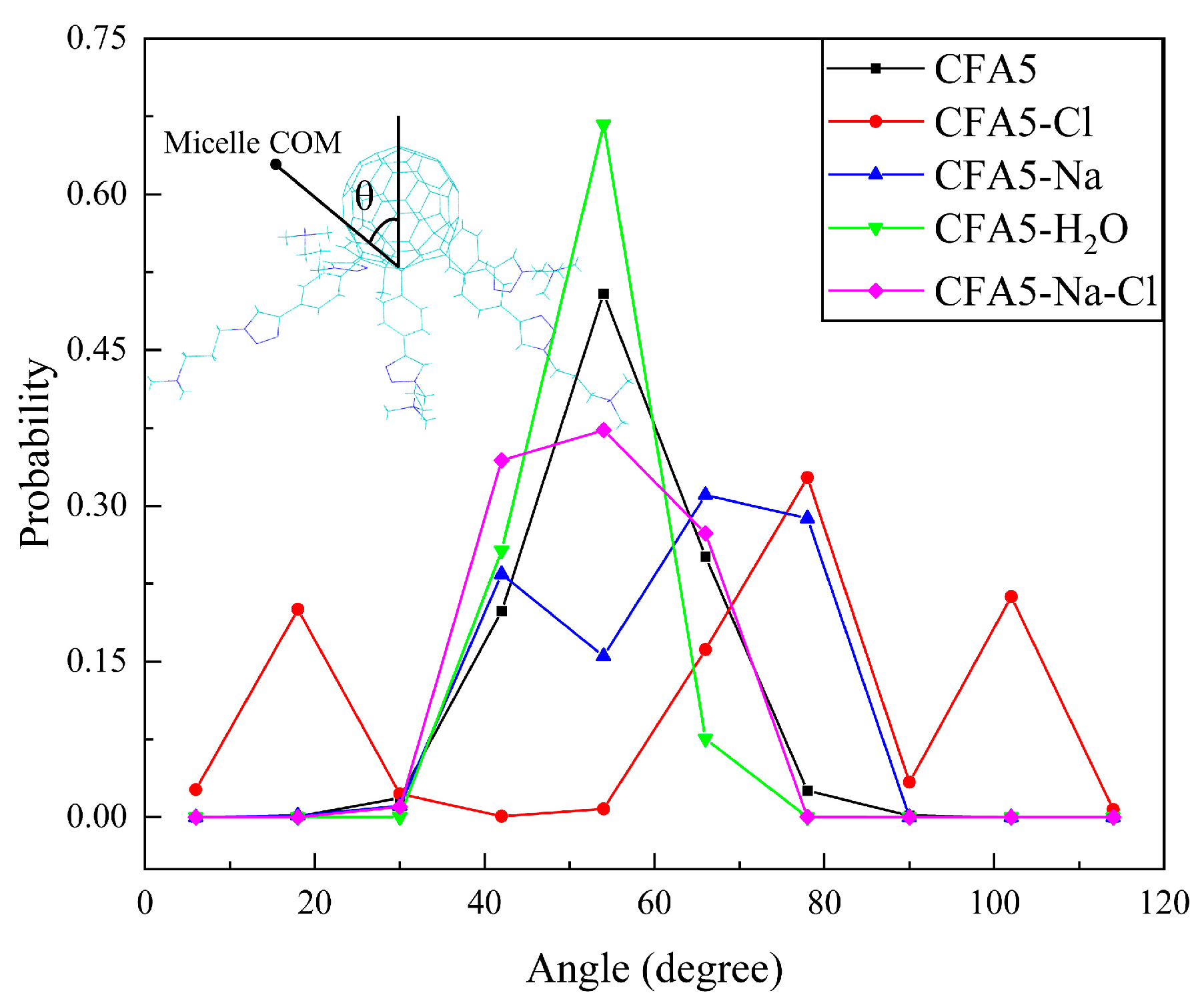
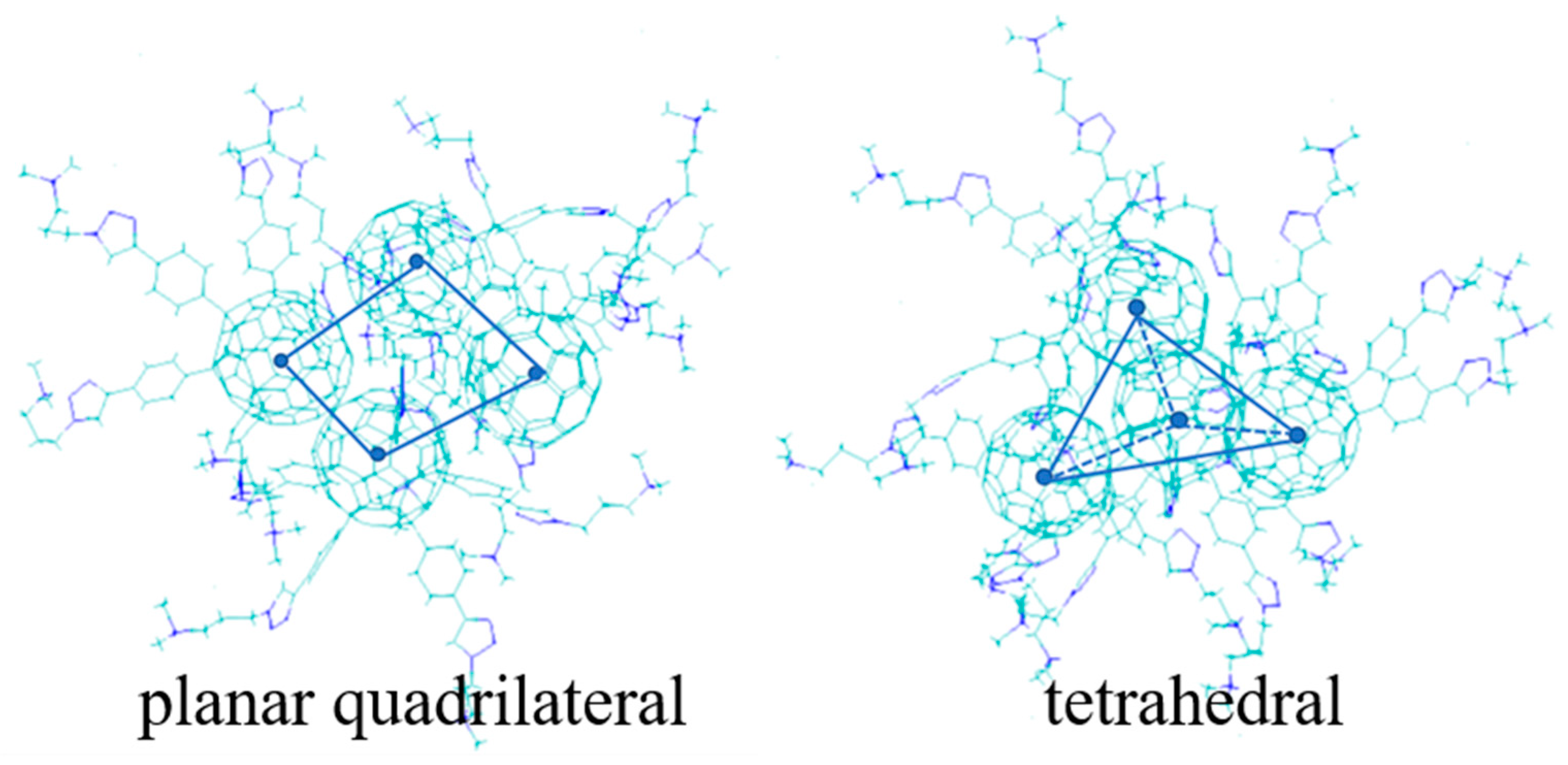
2.2.2. Micelle Shape
2.2.3. Solvent Accessible Surface Area
2.3. Molecular Polarity
2.4. Conformation of Surfactant Alkyl Chain
2.5. Interactions between Cl− Ions in Solution and Fullerene Surfactant Headgroups
2.6. Interactions between Micelles and Water
2.6.1. Hydration Numbers of Selected Atoms
2.6.2. Hydrogen Bond Interactions between Surfactant and Water Molecules
2.7. Distance between COMs of Fullerene Spheres
2.8. Representative Configurations of Fullerene Micelles
3. Computational Details
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Krätschmer, W.; Lamb, L.D.; Fostiropoulos, K.; Huffman, D.R. Solid C60: A new form of carbon. Nature 1990, 347, 354–358. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Murata, Y. Cobalt-functionalized open-[60] fullerenes. Organometallics 2024, 43, 227–232. [Google Scholar] [CrossRef]
- Hashikawa, Y.; Sadai, S.; Ikemoto, Y.; Murata, Y. Open-[60] fullerenols with water adsorbed both inside and outside. Chem. Commun. 2024, 60, 1261–1264. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Popov, A.A. Capturing unstable metallofullerenes. Inorganics 2024, 12, 48–63. [Google Scholar] [CrossRef]
- Li, B.C.; Wang, W.; An, Y.; Xu, Z.Y. Compensation behaviors and phase transitions of a 3D fullerene-like polymer. J. Mater. Sci. 2024, 59, 698–714. [Google Scholar] [CrossRef]
- Siringan, M.J.; Dawar, A.; Zhang, J. Interactions between fullerene derivatives and biological systems. Mater. Chem. Front. 2023, 7, 2153–2174. [Google Scholar] [CrossRef]
- Zhang, E.-Y.; Wang, C.-R. Fullerene self-assembly and supramolecular nanostructures. Curr. Opin. Colloid Interface Sci. 2009, 14, 148–156. [Google Scholar] [CrossRef]
- Jeng, U.; Lin, T.; Chang, T.; Lee, H.; Hsu, C.; Hsieh, Y.; Canteenwala, T.; Chiang, L. Self Assembly of Amphiphiles-Comparison of the aggregation behavior of water-soluble hexa (sulfobutyl) fullerenes and polyhydroxylated fullerenes for their free-radical scavenging activity. Prog. Colloid Polym. Sci. 2001, 118, 232–237. [Google Scholar]
- Zhao, Y.; Chen, G. C60 fullerene amphiphiles as supramolecular building blocks for organized and well-defined nanoscale objects. In Fullerenes and Other Carbon-Rich Nanostructures; Nierengarten, J.-F., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 23–53. [Google Scholar]
- Angelini, G.; De Maria, P.; Fontana, A.; Pierini, M.; Maggini, M.; Gasparrini, F.; Zappia, G. Study of the Aggregation Properties of a Novel Amphiphilic C60 Fullerene Derivative. Langmuir 2001, 17, 6404–6407. [Google Scholar] [CrossRef]
- Guldi, D.M.; Maggini, M.; Mondini, S.; Guérin, F.; Fendler, J.H. Formation, Characterization, and Properties of Nanostructured [Ru(bpy)3]2+-C60 Langmuir-Blodgett Films in Situ at the Air-Water Interface and ex Situ on Substrates. Langmuir 2000, 16, 1311–1318. [Google Scholar] [CrossRef]
- Nakamura, E.; Isobe, H. In vitro and in vivo gene delivery with tailor-designed aminofullerenes. Chem. Rec. 2010, 10, 260–270. [Google Scholar] [CrossRef]
- Kumar, K.S.; Patnaik, A. Tunable one-, two-, and three-dimensional self-assemblies from an acceptor-donor fullerene-N,N-dimethylaminoazobenzene dyad: Interfacial geometry and temporal evolution. Langmuir 2011, 27, 11017–11026. [Google Scholar] [CrossRef]
- Coelho, E.; de Andrade, D.X.; Colherinhas, G. Exploring fullerenol-C60(OH)24 interactions with lipid bilayers: Molecular dynamics study of agglomeration and surface deposition. J. Mol. Liq. 2023, 391, 123205–123215. [Google Scholar] [CrossRef]
- Shaikh, N.; Bernhard, S.P.; Walker, R.A. Surface Activity and Aggregation Behavior of Polyhydroxylated Fullerenes in Aqueous Solutions. Langmuir 2022, 38, 10412–10418. [Google Scholar] [CrossRef]
- Sawamura, M.; Iikura, H.; Nakamura, E. The first pentahaptofullerene metal complexes. J. Am. Chem. Soc. 1996, 118, 12850–12851. [Google Scholar] [CrossRef]
- Matsuo, Y.; Nakamura, E. Selective Multiaddition of Organocopper Reagents to Fullerenes. Chem. Rev. 2008, 108, 3016–3028. [Google Scholar] [CrossRef]
- Mohanta, V.; Dey, D.; Ramakumar, S.; Patil, S. Vesicular Nanostructure Formation by Self-Assembly of Anisotropic Penta-phenol-Substituted Fullerene in Water. Langmuir 2015, 31, 13600–13608. [Google Scholar] [CrossRef]
- Sawamura, M.; Nagahama, N.; Toganoh, M.; Hackler, U.E.; Isobe, H.; Nakamura, E.; Zhou, S.-Q.; Chu, B. Pentaorgano [60] fullerene R5C60−. A water soluble hydrocarbon anion. Chem. Lett. 2000, 29, 1098–1099. [Google Scholar] [CrossRef]
- Homma, T.; Harano, K.; Isobe, H.; Nakamura, E. Preparation and properties of vesicles made of nonpolar/polar/nonpolar fullerene amphiphiles. J. Am. Chem. Soc. 2011, 133, 6364–6370. [Google Scholar] [CrossRef]
- Isobe, H.; Homma, T.; Nakamura, E. Energetics of water permeation through fullerene membrane. Proc. Natl. Acad. Sci. USA 2007, 104, 14895–14899. [Google Scholar] [CrossRef] [PubMed]
- Harano, K.; Narita, A.; Nakamura, E. Photocrosslinking of Fullerene Vesicles that Prevents Phase Transition and Decreases Water Permeation. Chem. Lett. 2013, 42, 1176–1178. [Google Scholar] [CrossRef]
- Harano, K.; Nakamura, E. Interfacial Chemistry of Conical Fullerene Amphiphiles in Water. Acc. Chem. Res. 2019, 52, 2090–2100. [Google Scholar] [CrossRef]
- Zhou, S.; Burger, C.; Chu, B.; Sawamura, M.; Nagahama, N.; Toganoh, M.; Hackler, U.E.; Isobe, H.; Nakamura, E. Spherical Bilayer Vesicles of Fullerene-Based Surfactants in Water: A Laser Light Scattering Study. Science 2001, 291, 1944–1947. [Google Scholar] [CrossRef]
- Li, C.Z.; Matsuo, Y.; Nakamura, E. Octupole-like supramolecular aggregates of conical iron fullerene complexes into a three-dimensional liquid crystalline lattice. J. Am. Chem. Soc. 2010, 132, 15514–15515. [Google Scholar] [CrossRef]
- Nitta, H.; Harano, K.; Isomura, M.; Backus, E.H.G.; Bonn, M.; Nakamura, E. Conical Ionic Amphiphiles Endowed with Micellization Ability but Lacking Air-Water and Oil-Water Interfacial Activity. J. Am. Chem. Soc. 2017, 139, 7677–7680. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, Y.; Leng, X.; Liu, G.; Xia, Q.; Wang, H. Molecular dynamics simulations on fullerene surfactants with different charges at the air–water interface. Phys. Chem. Chem. Phys. 2020, 22, 16353–16358. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, H. Self-aggregation of the SDS surfactant at a solid-liquid interface. J. Phys. Chem. B 2007, 111, 4054–4059. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Srinivasan, H.; Mukhopadhyay, R.; Sakai, V.G.; Mitra, S. Microscopic insights on the structural and dynamical aspects of Imidazolium-based surface active ionic liquid micelles. J. Mol. Liq. 2021, 332, 115722–115733. [Google Scholar] [CrossRef]
- Bogusz, S.; Venable, R.M.; Pastor, R.W. Molecular dynamics simulations of octyl glucoside micelles: Structural properties. J. Phys. Chem. B 2000, 104, 5462–5470. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Koenig, P.H.; Larson, R.G. Molecular Dynamics Simulations of Sodium Dodecyl Sulfate Micelles in Water-The Effect of the Force Field. J. Phys. Chem. B 2014, 118, 3864–3880. [Google Scholar] [CrossRef] [PubMed]
- Theodorou, D.N.; Suter, U.W. Shape of unperturbed linear polymers: Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar] [CrossRef]
- Lee, B.; Richards, F.M. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379–404. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanian, S.; Pal, S.; Bagchi, B. Hydrogen-bond dynamics near a micellar surface: Origin of the universal slow relaxation at complex aqueous interfaces. Phys. Rev. Lett. 2002, 89, 115505–115509. [Google Scholar] [CrossRef] [PubMed]
- Luzar, A.; Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Heiney, P.A.; Fischer, J.E.; McGhie, A.R.; Romanow, W.J.; Denenstein, A.M.; McCauley, J.P., Jr.; Smith, A.B.; Cox, D.E. Orientational ordering transition in solid C60. Phys. Rev. Lett. 1991, 66, 2911–2915. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision, B.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Jakalian, A.; Bush, B.L.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: I. Method. J. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Berendsen, H.J.; Postma, J.P.M.; Van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
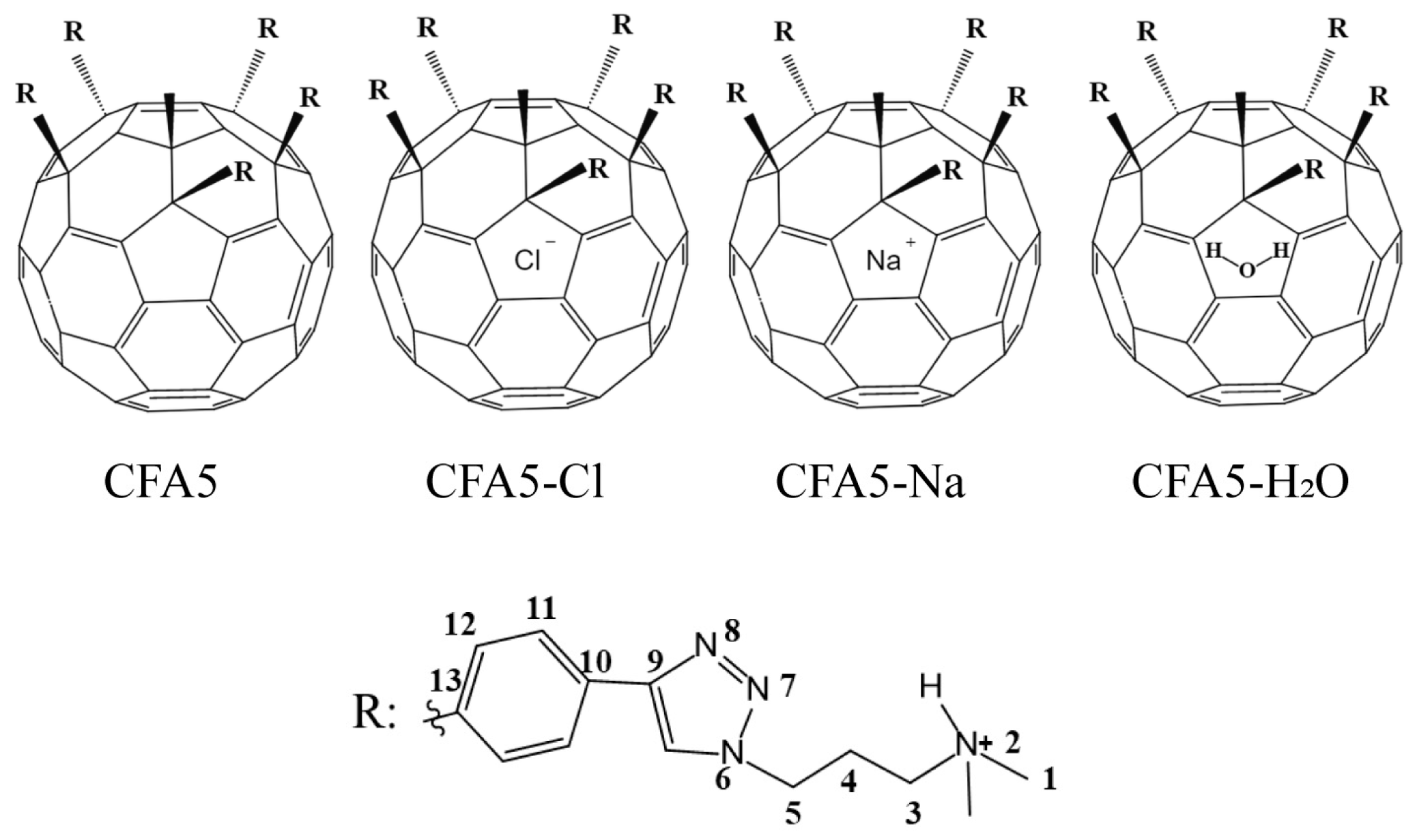

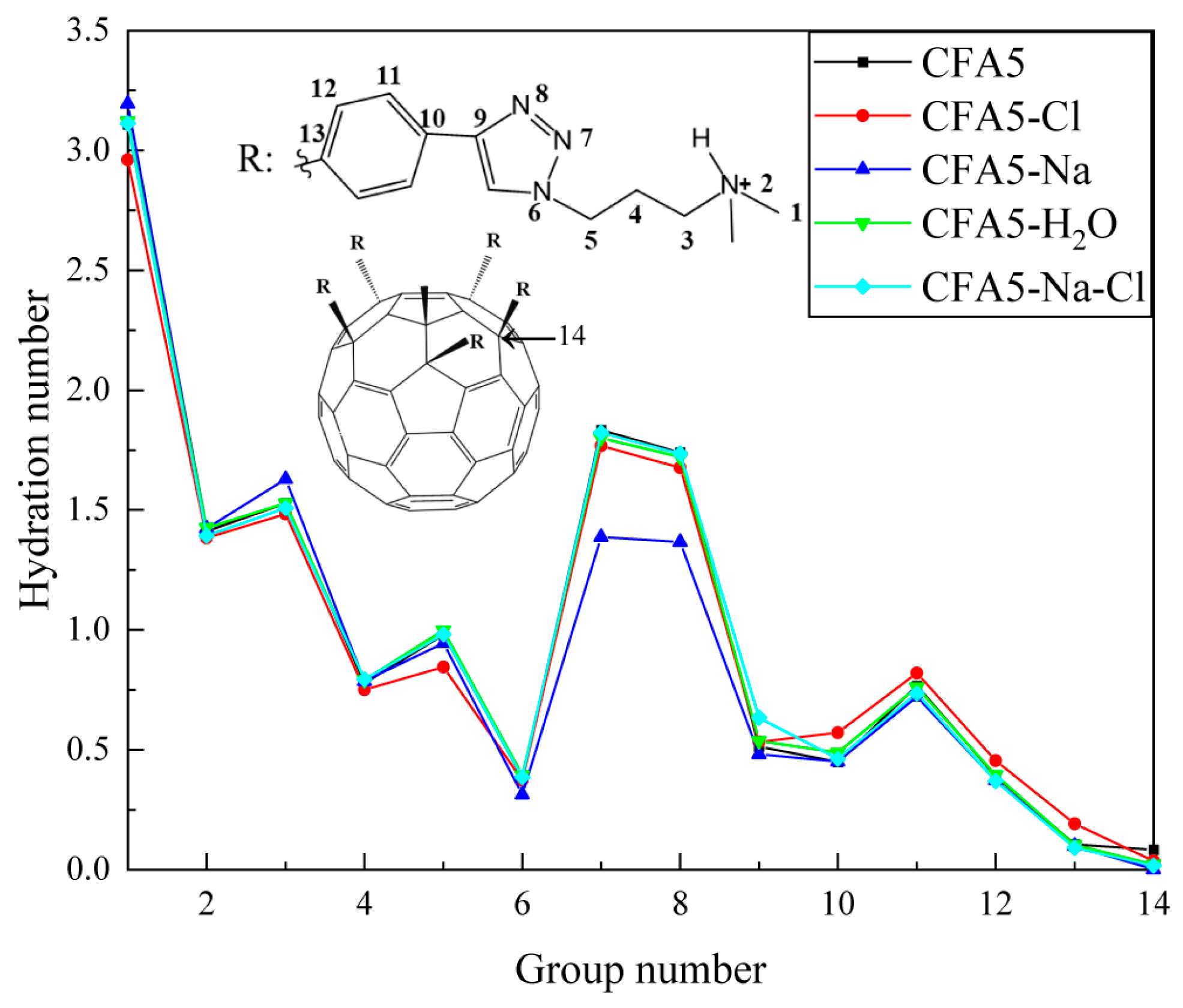
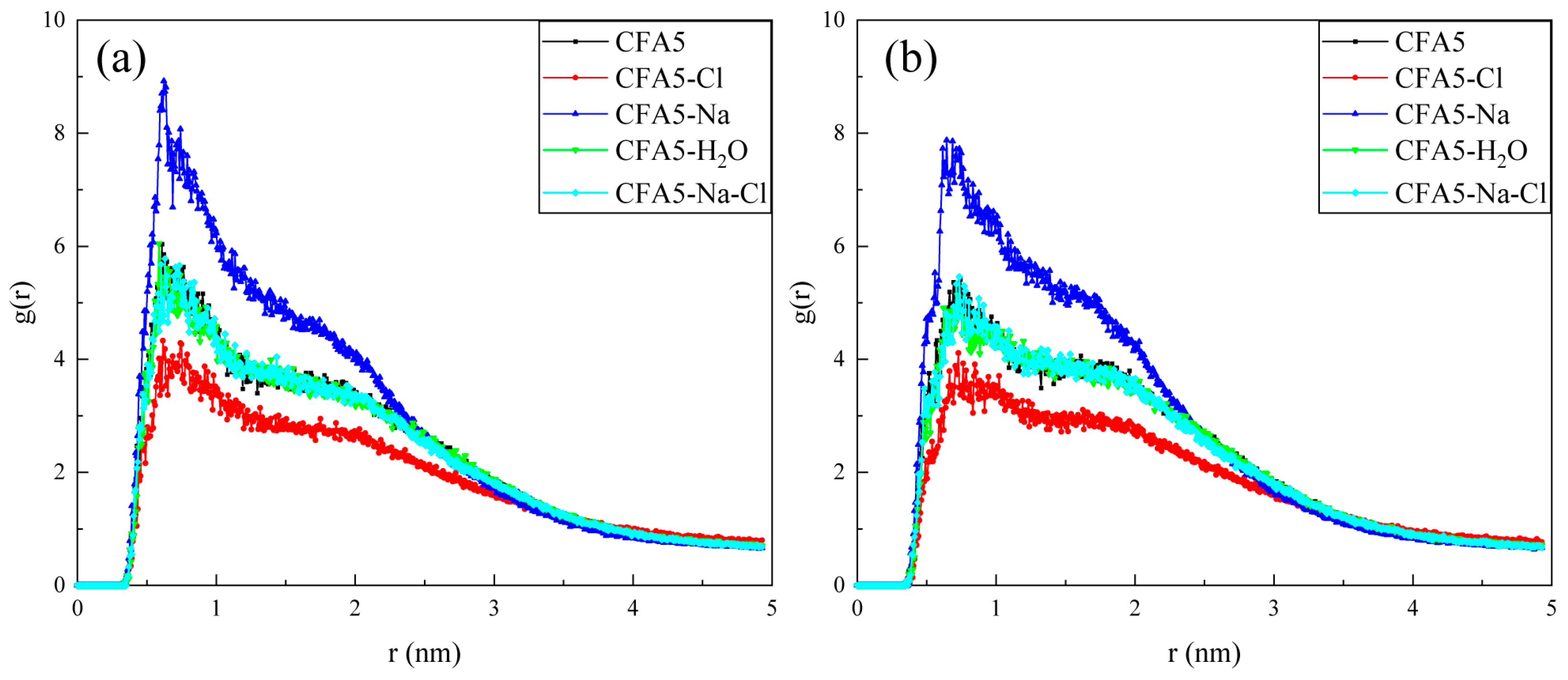
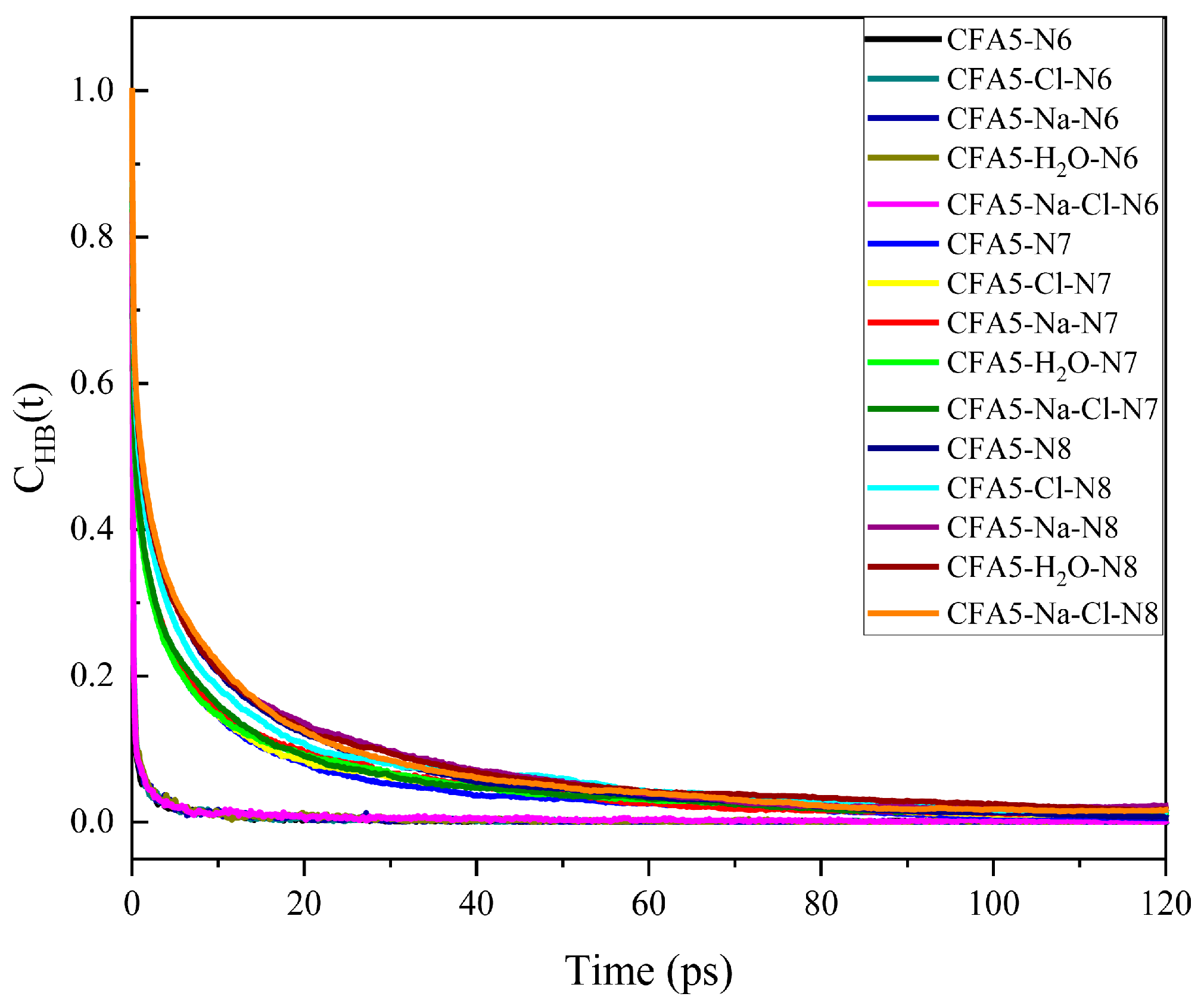
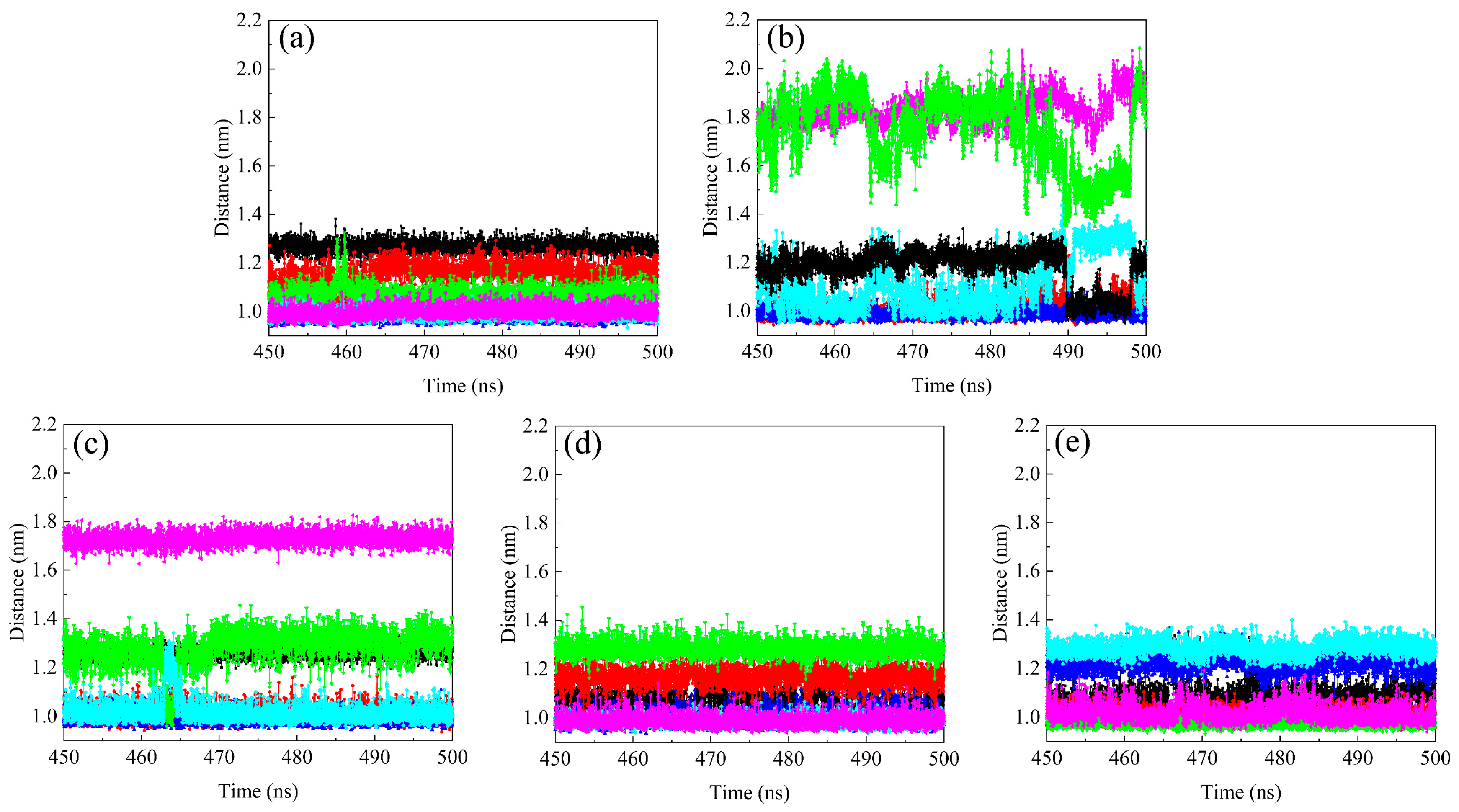

| CFA5 | CFA5-Cl | CFA5-Na | CFA5-H2O | CFA5-Na-Cl | |
|---|---|---|---|---|---|
| Imax/Imin | 1.27 ± 0.04 | 1.52 ± 0.11 | 1.6 ± 0.05 | 1.30 ± 0.05 | 1.37 ± 0.07 |
| e | 0.14 ± 0.02 | 0.22 ± 0.03 | 0.24 ± 0.02 | 0.15 ± 0.02 | 0.18 ± 0.03 |
| Rg11/Rg22 | 1.02 ± 0.01 | 1.06 ± 0.03 | 1.08 ± 0.01 | 1.02 ± 0.02 | 1.03 ± 0.01 |
| Rg22/Rg33 | 1.10 ± 0.02 | 1.16 ± 0.03 | 1.17 ± 0.02 | 1.11 ± 0.02 | 1.14 ± 0.03 |
| Rg/nm | 1.13 ± 0.01 | 1.18 ± 0.01 | 1.17 ± 0.01 | 1.13 ± 0.01 | 1.14 ± 0.01 |
| Rs/nm | 1.46 ± 0.01 | 1.52 ± 0.01 | 1.51 ± 0.01 | 1.46 ± 0.01 | 1.48 ± 0.01 |
| SASA/nm2 | 60.11 ± 1.42 | 60.77 ± 1.53 | 63.09 ± 1.34 | 61.17 ± 1.39 | 60.64 ± 1.40 |
| CFA5 | CFA5-Cl | CFA5-Na | CFA5-H2O | CFA5-Na-Cl | |
|---|---|---|---|---|---|
| N6-H2O | 0.04 ± 0.04 | 0.05 ± 0.05 | 0.03 ± 0.04 | 0.05 ± 0.05 | 0.05 ± 0.05 |
| N7-H2O | 0.70 ± 0.15 | 0.68 ± 0.15 | 0.51 ± 0.12 | 0.75 ± 0.14 | 0.75 ± 0.15 |
| N8-H2O | 0.93 ± 0.15 | 0.85 ± 0.15 | 0.69 ± 0.13 | 0.94 ± 0.15 | 0.92 ± 0.14 |
| CFA5 | CFA5-Cl | CFA5-Na | CFA5-H2O | CFA5-Na-Cl | |
|---|---|---|---|---|---|
| Fullerene | 4 | 4 | 4 | 4 | 4 |
| Na+ | 0 | 4 | 4 | 0 | 2 |
| Cl− | 20 | 24 | 24 | 20 | 22 |
| H2O | 32,390 | 32,417 | 32,413 | 32,407 | 32,413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Jiang, Y.; Wei, Y.; Wang, Y.; Zhu, X.; Liu, G.; Xia, Q. The Effect of Different Substances Embedded in Fullerene Cavity on Surfactant Self-Assembly Behavior through Molecular Dynamics Simulation. Molecules 2024, 29, 2355. https://doi.org/10.3390/molecules29102355
Li X, Jiang Y, Wei Y, Wang Y, Zhu X, Liu G, Xia Q. The Effect of Different Substances Embedded in Fullerene Cavity on Surfactant Self-Assembly Behavior through Molecular Dynamics Simulation. Molecules. 2024; 29(10):2355. https://doi.org/10.3390/molecules29102355
Chicago/Turabian StyleLi, Xin, Yongkang Jiang, Yaoyao Wei, Yulu Wang, Xinqi Zhu, Guokui Liu, and Qiying Xia. 2024. "The Effect of Different Substances Embedded in Fullerene Cavity on Surfactant Self-Assembly Behavior through Molecular Dynamics Simulation" Molecules 29, no. 10: 2355. https://doi.org/10.3390/molecules29102355
APA StyleLi, X., Jiang, Y., Wei, Y., Wang, Y., Zhu, X., Liu, G., & Xia, Q. (2024). The Effect of Different Substances Embedded in Fullerene Cavity on Surfactant Self-Assembly Behavior through Molecular Dynamics Simulation. Molecules, 29(10), 2355. https://doi.org/10.3390/molecules29102355






