Impacts of Mutations in the P-Loop on Conformational Alterations of KRAS Investigated with Gaussian Accelerated Molecular Dynamics Simulations
Abstract
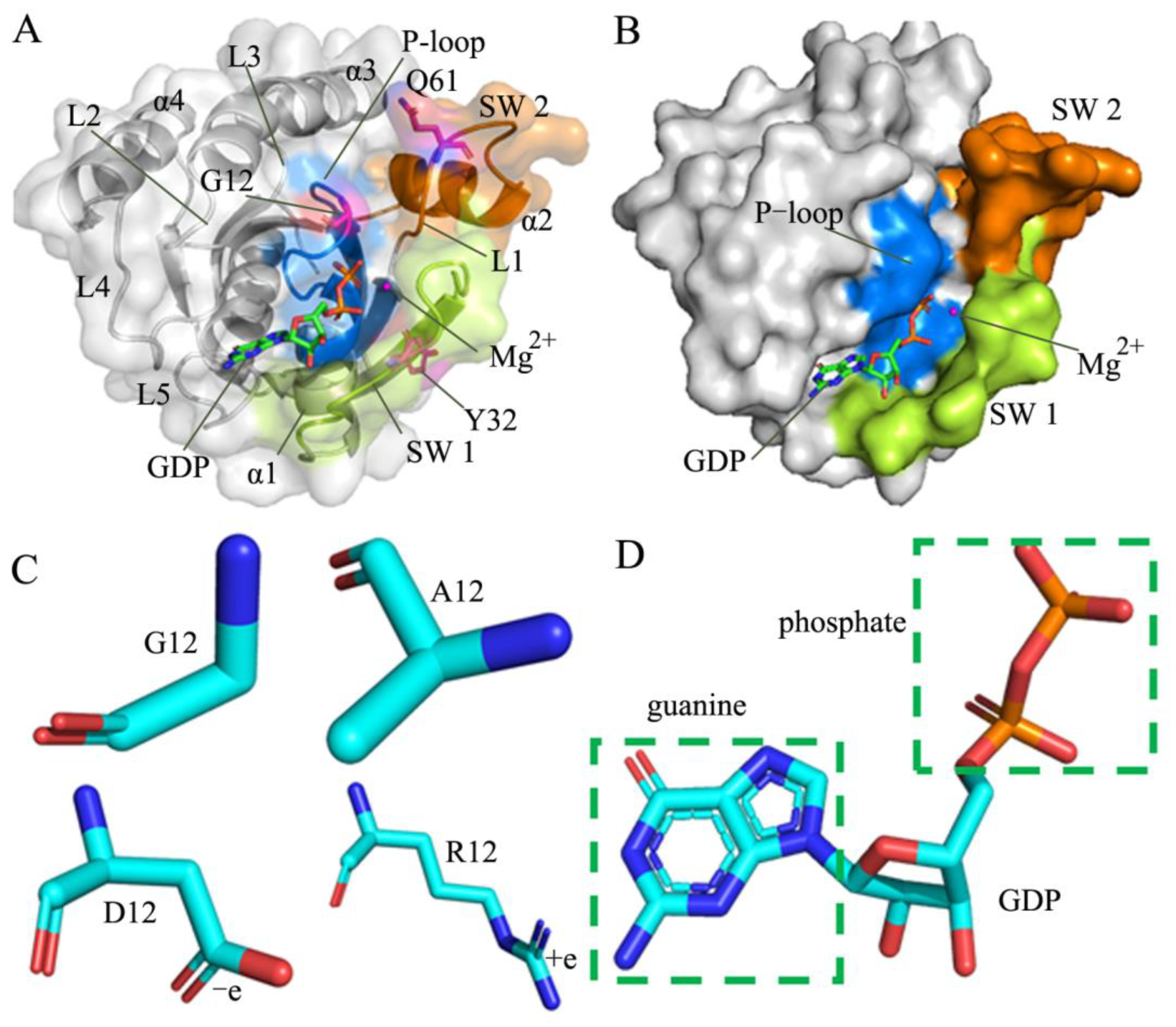
1. Introduction
2. Results and Discussion
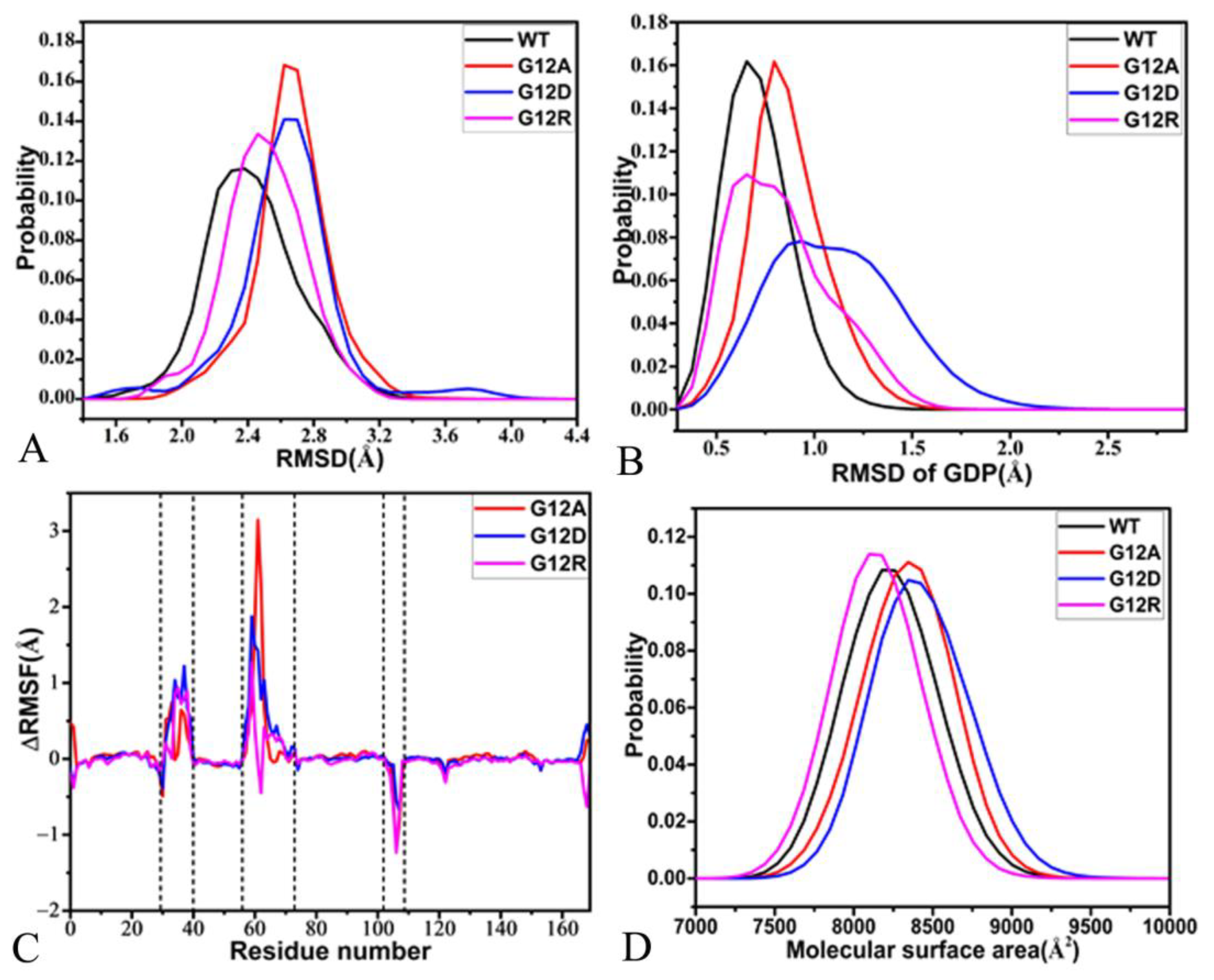
2.1. Structural Fluctuations and Internal Dynamics of KRAS
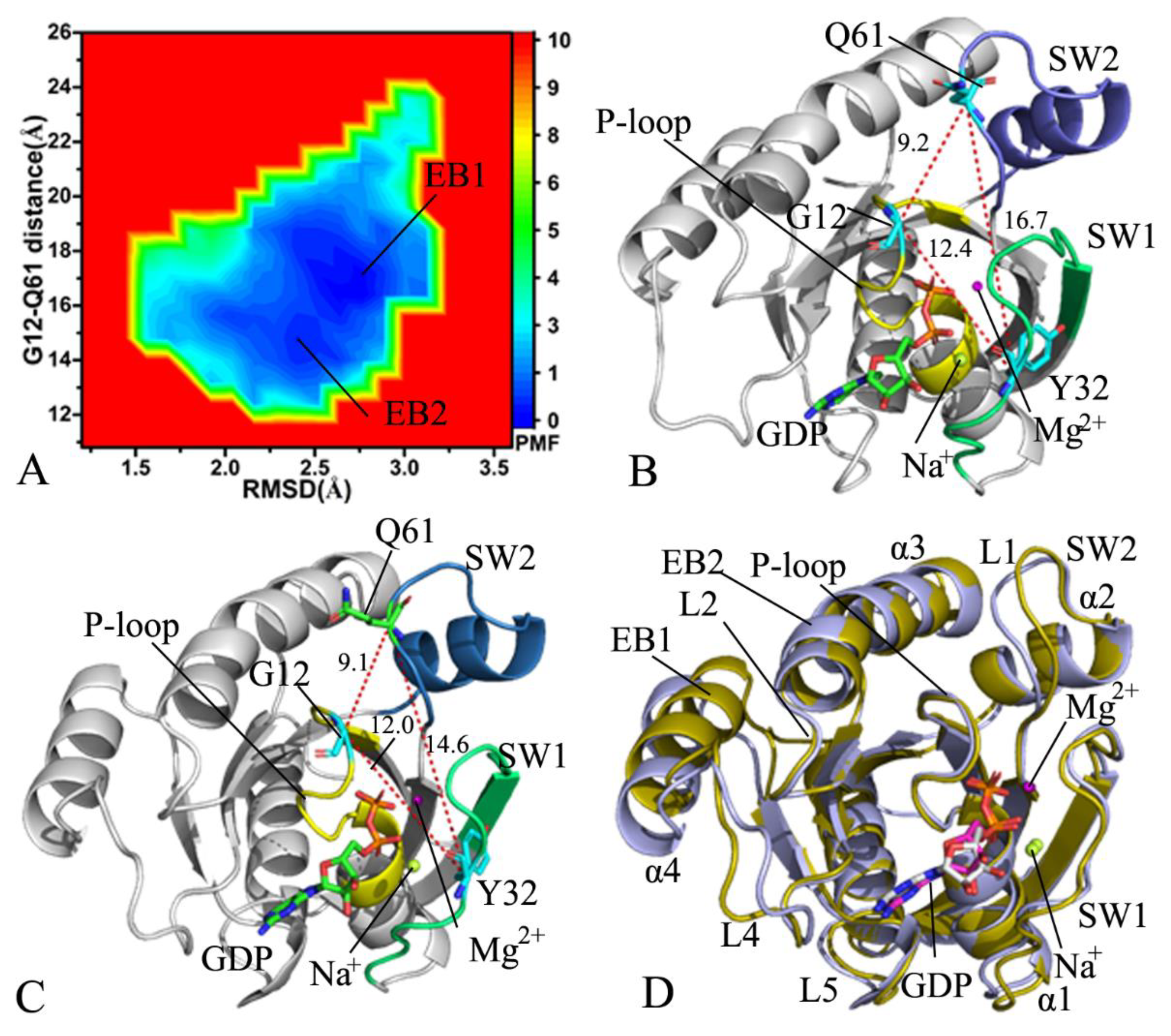
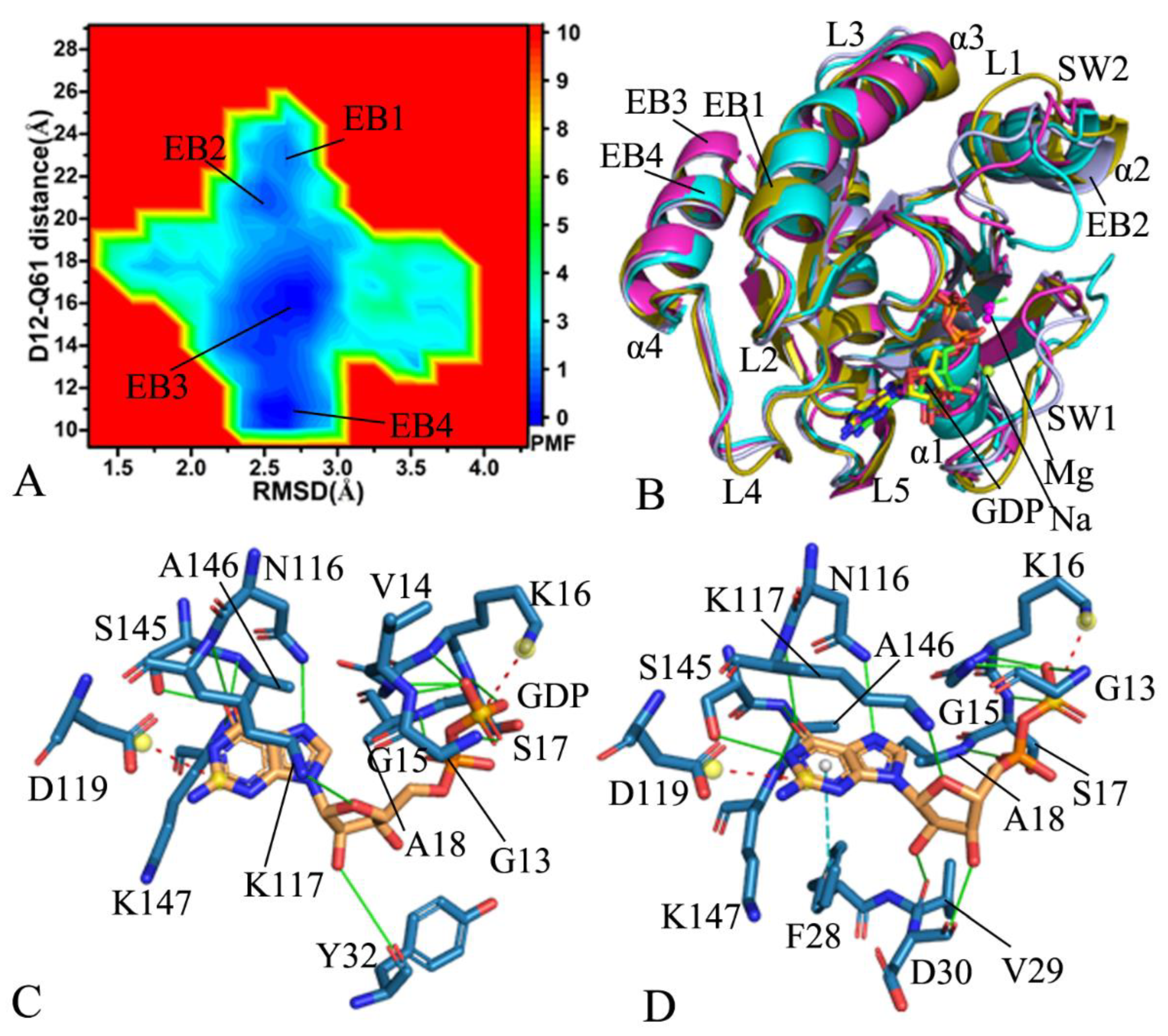
2.2. Free Energy Profile of Mutation-Induced Conformational Transitions of KRAS
2.3. Dynamics Behavior Revealed by PCA
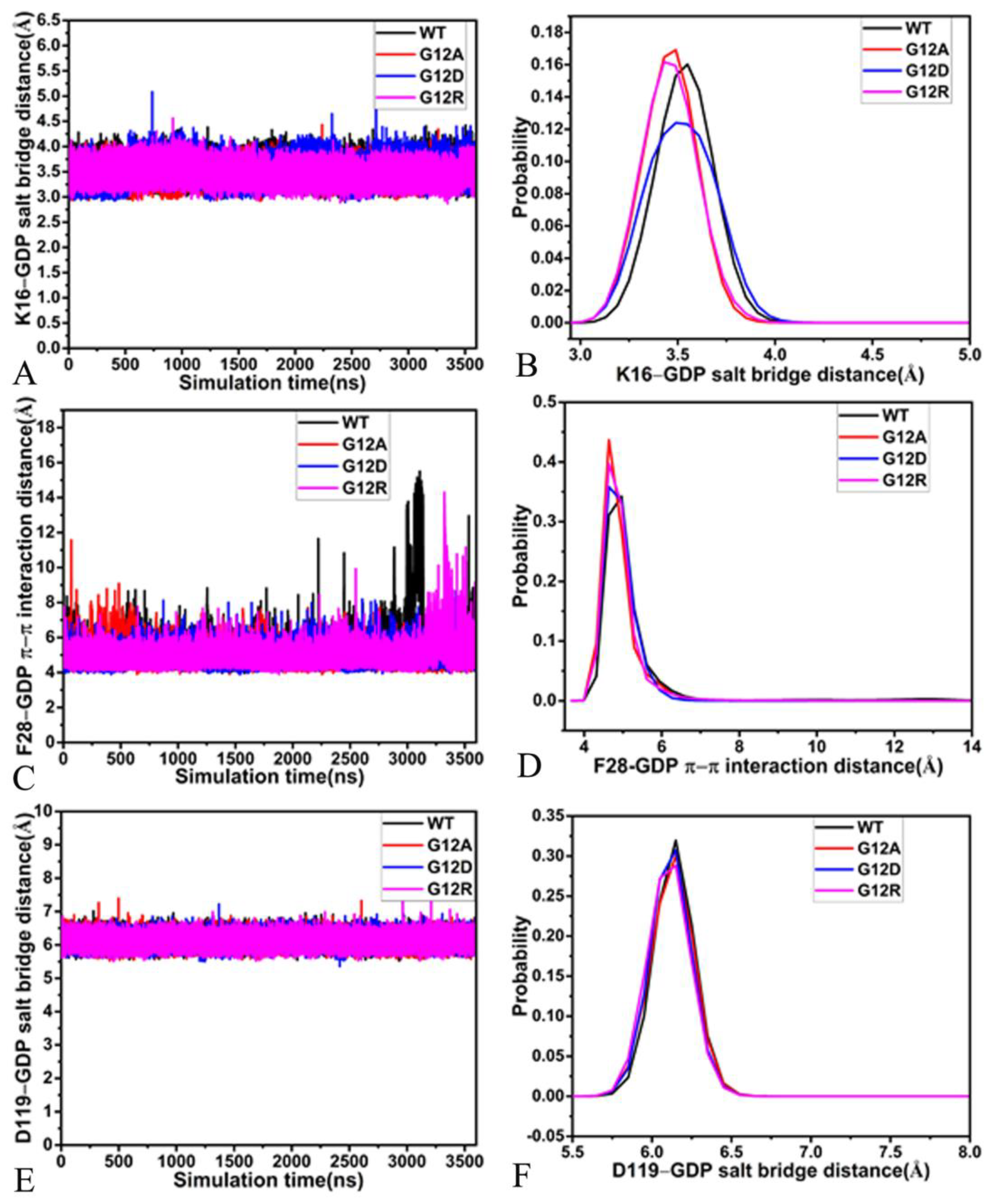
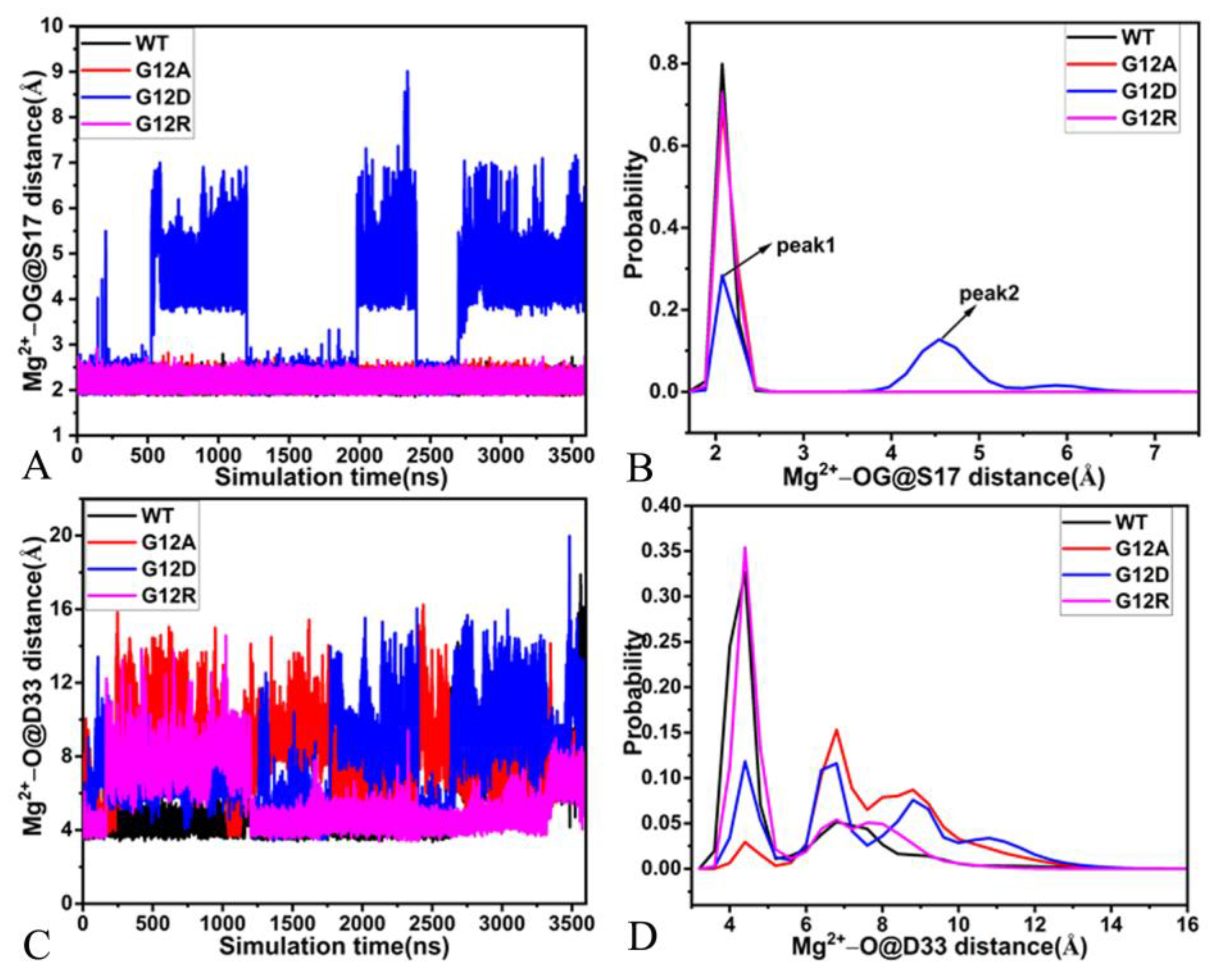
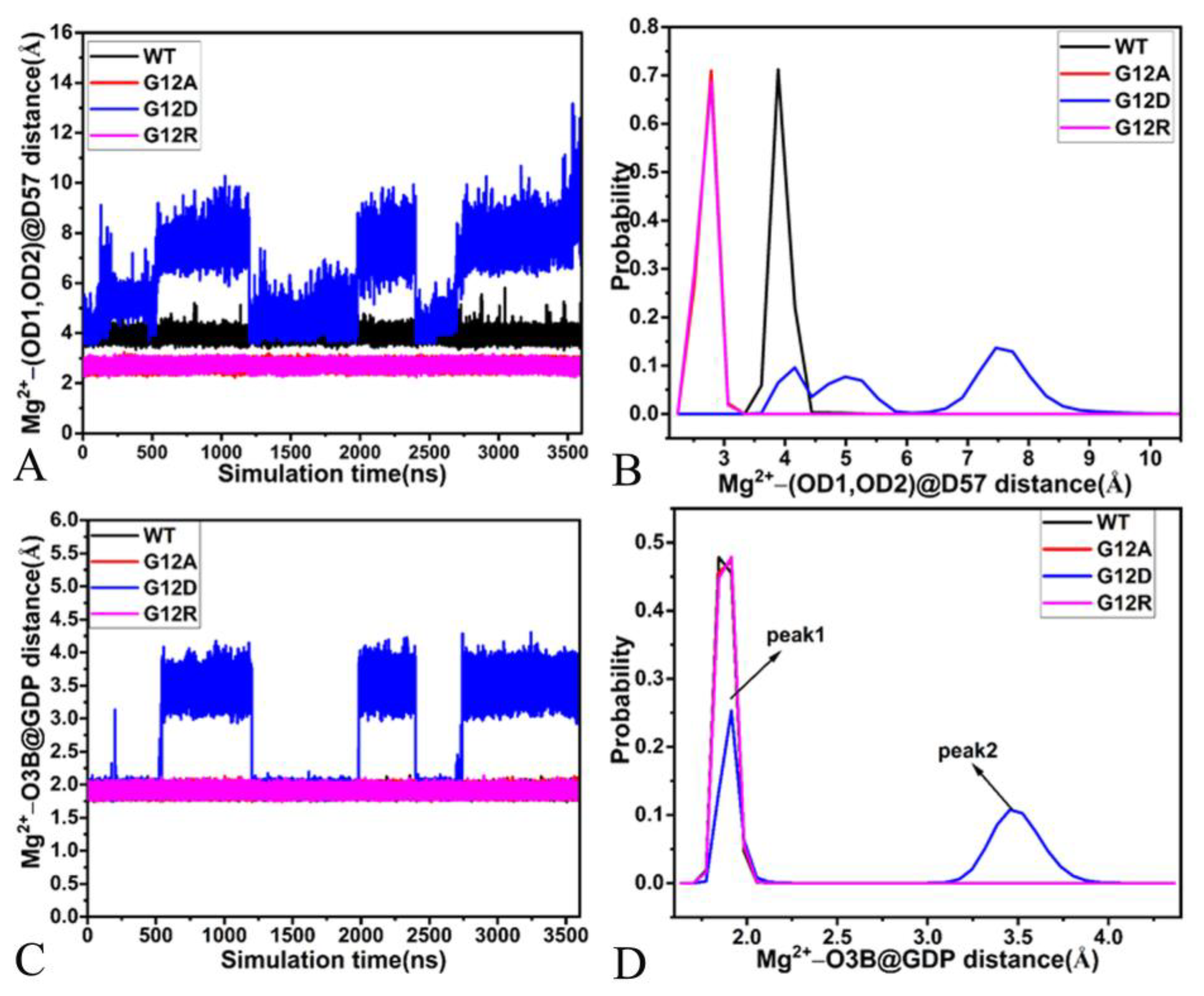
2.4. Interaction Network of GDP with KRAS
3. Theory and Methods
3.1. Preparation of Simulated Systems
3.2. GaMD Simulations
3.3. Principal Component Analysis
3.4. Dynamics Cross-Correlation Maps
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cox, A.D.; Fesik, S.W.; Kimmelman, A.C.; Luo, J.; Der, C.J. Drugging the undruggable RAS: Mission Possible? Nat. Rev. Drug Discov. 2014, 13, 828–851. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Migoni, A.; Canning, P.; Quevedo, C.E.; Bataille, C.J.R.; Bery, N.; Miller, A.; Russell, A.J.; Phillips, S.E.V.; Carr, S.B.; Rabbitts, T.H. Structure-based development of new RAS-effector inhibitors from a combination of active and inactive RAS-binding compounds. Proc. Natl. Acad. Sci. USA 2019, 116, 2545–2550. [Google Scholar] [CrossRef]
- Ito, Y.; Yamasaki, K.; Iwahara, J.; Terada, T.; Kamiya, A.; Shirouzu, M.; Muto, Y.; Kawai, G.; Yokoyama, S.; Laue, E.D.; et al. Regional Polysterism in the GTP-Bound Form of the Human c-Ha-Ras Protein. Biochemistry 1997, 36, 9109–9119. [Google Scholar] [CrossRef]
- Lu, S.; Jang, H.; Muratcioglu, S.; Gursoy, A.; Keskin, O.; Nussinov, R.; Zhang, J. Ras Conformational Ensembles, Allostery, and Signaling. Chem. Rev. 2016, 116, 6607–6665. [Google Scholar] [CrossRef] [PubMed]
- Gysin, S.; Salt, M.; Young, A.; McCormick, F. Therapeutic Strategies for Targeting Ras Proteins. Genes Cancer 2011, 2, 359–372. [Google Scholar] [CrossRef] [PubMed]
- Boriack-Sjodin, P.A.; Margarit, S.M.; Bar-Sagi, D.; Kuriyan, J. The structural basis of the activation of Ras by Sos. Nature 1998, 394, 337–343. [Google Scholar] [CrossRef]
- Settleman, J.; Albright, C.F.; Foster, L.C.; Weinberg, R.A. Association between GTPase activatorsfor Rho and Ras families. Nature 1992, 359, 153–154. [Google Scholar] [CrossRef]
- Hunter, J.C.; Manandhar, A.; Carrasco, M.A.; Gurbani, D.; Gondi, S.; Westover, K.D. Biochemical and Structural Analysis of Common Cancer-Associated KRAS Mutations. Mol. Cancer Res. 2015, 13, 1325–1335. [Google Scholar] [CrossRef]
- McCormick, F. ras GTPase activating protein: Signal transmitter and signal terminator. Cell 1989, 56, 5–8. [Google Scholar] [CrossRef]
- Prior, I.A.; Lewis, P.D.; Mattos, C. A Comprehensive Survey of Ras Mutations in Cancer. Cancer Res. 2012, 72, 2457–2467. [Google Scholar] [CrossRef]
- Simanshu, D.K.; Nissley, D.V.; McCormick, F. RAS Proteins and Their Regulators in Human Disease. Cell 2017, 170, 17–33. [Google Scholar] [CrossRef] [PubMed]
- Poulin, E.J.; Bera, A.K.; Lu, J.; Lin, Y.-J.; Strasser, S.D.; Paulo, J.A.; Huang, T.Q.; Morales, C.; Yan, W.; Cook, J.; et al. Tissue-Specific Oncogenic Activity of KRASA146T. Cancer Discov. 2019, 9, 738–755. [Google Scholar] [CrossRef]
- Franken, S.M.; Scheidig, A.J.; Krengel, U.; Rensland, H.; Lautwein, A.; Geyer, M.; Scheffzek, K.; Goody, R.S.; Kalbitzer, H.R. Three-dimensional structures and properties of a transforming and a nontransforming glycine-12 mutant of p21H-ras. Biochemistry 1993, 32, 8411–8420. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Jang, H.; Gu, S.; Zhang, J.; Nussinov, R. Drugging Ras GTPase: A comprehensive mechanistic and signaling structural view. Chem. Soc. Rev. 2016, 45, 4929–4952. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian, M.R.; Zor, T.; Vogt, D.; Kabsch, W.; Selinger, Z.; Wittinghofer, A.; Scheffzek, K. Guanosine triphosphatase stimulation of oncogenic Ras mutants. Proc. Natl. Acad. Sci. USA 1999, 96, 7065–7070. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, G.A.; Der, C.J.; Rossman, K.L. RAS isoforms and mutations in cancer at a glance. J. Cell Sci. 2016, 129, 1287–1292. [Google Scholar] [CrossRef]
- Xu, S.; Long, B.N.; Boris, G.H.; Chen, A.; Ni, S.; Kennedy, M.A. Structural insight into the rearrangement of the switch I region in GTP-bound G12A K-Ras. Acta Crystallog. D 2017, 73, 970–984. [Google Scholar] [CrossRef] [PubMed]
- Eberhard, D.A.; Johnson, B.E.; Amler, L.C.; Goddard, A.D.; Heldens, S.L.; Herbst, R.S.; Ince, W.L.; Jänne, P.A.; Januario, T.; Johnson, D.H.; et al. Mutations in the Epidermal Growth Factor Receptor and in KRAS Are Predictive and Prognostic Indicators in Patients With Non–Small-Cell Lung Cancer Treated With Chemotherapy Alone and in Combination With Erlotinib. J. Clin. Oncol. 2005, 23, 5900–5909. [Google Scholar] [CrossRef]
- Chen, S.; Shu, L.; Zhao, R.; Zhao, Y. Molecular dynamics simulations reveal the activation mechanism of mutations G12V and Q61L of Cdc42. Proteins 2022, 90, 1376–1389. [Google Scholar] [CrossRef]
- Parker, J.A.; Volmar, A.Y.; Pavlopoulos, S.; Mattos, C. K-Ras Populates Conformational States Differently from Its Isoform H-Ras and Oncogenic Mutant K-RasG12D. Structure 2018, 26, 810–820.e814. [Google Scholar] [CrossRef]
- Fraser, J.S.; van den Bedem, H.; Samelson, A.J.; Lang, P.T.; Holton, J.M.; Echols, N.; Alber, T. Accessing protein conformational ensembles using room-temperature X-ray crystallography. Proc. Natl. Acad. Sci. USA 2011, 108, 16247–16252. [Google Scholar] [CrossRef]
- Gentile, D.R.; Rathinaswamy, M.K.; Jenkins, M.L.; Moss, S.M.; Siempelkamp, B.D.; Renslo, A.R.; Burke, J.E.; Shokat, K.M. Ras Binder Induces a Modified Switch-II Pocket in GTP and GDP States. Cell Chem. Biol. 2017, 24, 1455–1466.e1414. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, S.; Zeng, Q.; Wang, W.; Zhang, Q.; Liu, X. Free Energy Profiles Relating With Conformational Transition of the Switch Domains Induced by G12 Mutations in GTP-Bound KRAS. Front. Mol. Biosci. 2022, 9, 912518. [Google Scholar] [CrossRef]
- Lu, J.; Harrison, R.A.; Li, L.; Zeng, M.; Gondi, S.; Scott, D.; Gray, N.S.; Engen, J.R.; Westover, K.D. KRAS G12C Drug Development: Discrimination between Switch II Pocket Configurations Using Hydrogen/Deuterium-Exchange Mass Spectrometry. Structure 2017, 25, 1442–1448.e1443. [Google Scholar] [CrossRef]
- Eren, M.; Tuncbag, N.; Jang, H.; Nussinov, R.; Gursoy, A.; Keskin, O. Normal Mode Analysis of KRas4B Reveals Partner Specific Dynamics. J. Phys. Chem. B 2021, 125, 5210–5221. [Google Scholar] [CrossRef] [PubMed]
- Buhrman, G.; Wink, G.; Mattos, C. Transformation Efficiency of RasQ61 Mutants Linked to Structural Features of the Switch Regions in the Presence of Raf. Structure 2007, 15, 1618–1629. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zeng, Q.; Wang, W.; Hu, Q.; Bao, H. Q61 mutant-mediated dynamics changes of the GTP-KRAS complex probed by Gaussian accelerated molecular dynamics and free energy landscapes. RSC Adv. 2022, 12, 1742–1757. [Google Scholar] [CrossRef]
- Sayyed-Ahmad, A.; Prakash, P.; Gorfe, A.A. Distinct dynamics and interaction patterns in H- and K-Ras oncogenic P-loop mutants. Proteins 2017, 85, 1618–1632. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, W.; Chen, G.; Wang, P.; Chen, Z.; Zhou, Y.; Ogasawara, M.; Trachootham, D.; Feng, L.; Pelicano, H.; et al. K-rasG12V transformation leads to mitochondrial dysfunction and a metabolic switch from oxidative phosphorylation to glycolysis. Cell Res. 2012, 22, 399–412. [Google Scholar] [CrossRef]
- Mehaffey, M.R.; Schardon, C.L.; Novelli, E.T.; Cammarata, M.B.; Webb, L.J.; Fast, W.; Brodbelt, J.S. Investigation of GTP-dependent dimerization of G12X K-Ras variants using ultraviolet photodissociation mass spectrometry. Chem. Sci. 2019, 10, 8025–8034. [Google Scholar] [CrossRef]
- Pálfy, G.; Vida, I.; Perczel, A. 1H, 15N backbone assignment and comparative analysis of the wild type and G12C, G12D, G12V mutants of K-Ras bound to GDP at physiological pH. Biomol. NMR Assign. 2020, 14, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.W.; Lin, Y.-J.; Reid, D.; Parker, J.; Pavlopoulos, S.; Dischinger, P.; Graveel, C.; Aguirre, A.J.; Steensma, M.; Haigis, K.M.; et al. Isoform-Specific Destabilization of the Active Site Reveals a Molecular Mechanism of Intrinsic Activation of KRas G13D. Cell Rep. 2019, 28, 1538–1550.e1537. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, L.; Wang, W.; Sun, H.; Pang, L.; Bao, H. Conformational transformation of switch domains in GDP/K-Ras induced by G13 mutants: An investigation through Gaussian accelerated molecular dynamics simulations and principal component analysis. Comput. Biol. Med. 2021, 135, 104639. [Google Scholar] [CrossRef]
- Tran, T.H.; Chan, A.H.; Young, L.C.; Bindu, L.; Neale, C.; Messing, S.; Dharmaiah, S.; Taylor, T.; Denson, J.-P.; Esposito, D.; et al. KRAS interaction with RAF1 RAS-binding domain and cysteine-rich domain provides insights into RAS-mediated RAF activation. Nat. Commun. 2021, 12, 1176. [Google Scholar] [CrossRef]
- Yu, Z.; Su, H.; Chen, J.; Hu, G. Deciphering Conformational Changes of the GDP-Bound NRAS Induced by Mutations G13D, Q61R, and C118S through Gaussian Accelerated Molecular Dynamic Simulations. Molecules 2022, 27, 5596. [Google Scholar] [CrossRef] [PubMed]
- Ting, P.Y.; Johnson, C.W.; Fang, C.; Cao, X.; Graeber, T.G.; Mattos, C.; Colicelli, J. Tyrosine phosphorylation of RAS by ABL allosterically enhances effector binding. FASEB J. 2015, 29, 3750–3761. [Google Scholar] [CrossRef]
- Ostrem, J.M.; Peters, U.; Sos, M.L.; Wells, J.A.; Shokat, K.M. K-Ras(G12C) inhibitors allosterically control GTP affinity and effector interactions. Nature 2013, 503, 548–551. [Google Scholar] [CrossRef]
- Kim, E.; Ilic, N.; Shrestha, Y.; Zou, L.; Kamburov, A.; Zhu, C.; Yang, X.; Lubonja, R.; Tran, N.; Nguyen, C.; et al. Systematic Functional Interrogation of Rare Cancer Variants Identifies Oncogenic Alleles. Cancer Discov. 2016, 6, 714–726. [Google Scholar] [CrossRef]
- Bera, A.K.; Lu, J.; Wales, T.E.; Gondi, S.; Gurbani, D.; Nelson, A.; Engen, J.R.; Westover, K.D. Structural basis of the atypical activation mechanism of KRASV14I. J. Biol. Chem. 2019, 294, 13964–13972. [Google Scholar] [CrossRef]
- Ash, M.-R.; Maher, M.J.; Guss, J.M.; Jormakka, M. A suite of Switch I and Switch II mutant structures from the G-protein domain of FeoB. Acta Crystallog. D 2011, 67, 973–980. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, S.; Wang, W.; Pang, L.; Zhang, Q.; Liu, X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J. Chem. Inf. Model. 2021, 61, 1954–1969. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Chen, J.; Xia, F.; Cui, Q.; Deng, X.; Xu, X. Identification of functional substates of KRas during GTP hydrolysis with enhanced sampling simulations. Phys. Chem. Chem. Phys. 2022, 24, 7653–7665. [Google Scholar] [CrossRef]
- Sun, Z.; Gong, Z.; Xia, F.; He, X. Ion dynamics and selectivity of Nav channels from molecular dynamics simulation. Chem. Phys. 2021, 548, 111245. [Google Scholar] [CrossRef]
- Liang, S.S.; Liu, X.G.; Cui, Y.X.; Zhang, S.L.; Zhang, Q.G.; Chen, J.Z. Molecular mechanism concerning conformational changes of CDK2 mediated by binding of inhibitors using molecular dynamics simulations and principal component analysis. SAR QSAR Environ. Res. 2021, 32, 573–594. [Google Scholar] [CrossRef] [PubMed]
- Hou, T.; Zhang, W.; Case, D.A.; Wang, W. Characterization of Domain–Peptide Interaction Interface: A Case Study on the Amphiphysin-1 SH3 Domain. J. Mol. Biol. 2008, 376, 1201–1214. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Yang, F.; Wang, P.; Zheng, G.; Chen, Y.; Yao, X.; Zhu, F. What Contributes to Serotonin–Norepinephrine Reuptake Inhibitors’ Dual-Targeting Mechanism? The Key Role of Transmembrane Domain 6 in Human Serotonin and Norepinephrine Transporters Revealed by Molecular Dynamics Simulation. ACS Chem. Neurosci. 2018, 9, 1128–1140. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Shen, M.; Tian, S.; Xu, L.; Pan, P.; Guan, Y.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 5. Improved docking performance using high solute dielectric constant MM/GBSA and MM/PBSA rescoring. Phys. Chem. Chem. Phys. 2014, 16, 22035–22045. [Google Scholar] [CrossRef]
- Li, M.; Liu, X.; Zhang, S.; Sun, J.; Zhang, Q.; Chen, J. Selective Mechanism of Inhibitors to Two Bromodomains of BRD4 Revealed by Multiple Replica Molecular Dynamics Simulations and Free Energy Analyses. Chin. J. Chem. Phys. 2022. [Google Scholar] [CrossRef]
- Leonis, G.; Steinbrecher, T.; Papadopoulos, M.G. A Contribution to the Drug Resistance Mechanism of Darunavir, Amprenavir, Indinavir, and Saquinavir Complexes with HIV-1 Protease Due to Flap Mutation I50V: A Systematic MM–PBSA and Thermodynamic Integration Study. J. Chem. Inf. Model. 2013, 53, 2141–2153. [Google Scholar] [CrossRef]
- Su, J.; Liu, X.; Zhang, S.; Yan, F.; Zhang, Q.; Chen, J. A theoretical insight into selectivity of inhibitors toward two domains of bromodomain-containing protein 4 using molecular dynamics simulations. Chem. Biol. Drug Des. 2018, 91, 828–840. [Google Scholar] [CrossRef]
- Chen, J.; Wang, X.; Pang, L.; Zhang, J.Z.H.; Zhu, T. Effect of mutations on binding of ligands to guanine riboswitch probed by free energy perturbation and molecular dynamics simulations. Nucleic Acids Res. 2019, 47, 6618–6631. [Google Scholar] [CrossRef]
- Sun, H.; Li, Y.; Tian, S.; Xu, L.; Hou, T. Assessing the performance of MM/PBSA and MM/GBSA methods. 4. Accuracies of MM/PBSA and MM/GBSA methodologies evaluated by various simulation protocols using PDBbind data set. Phys. Chem. Chem. Phys. 2014, 16, 16719–16729. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Liu, X.; Zhang, S.; Liang, S.; Zhang, Q.; Chen, J. Deciphering the binding mechanism of inhibitors of the SARS-CoV-2 main protease through multiple replica accelerated molecular dynamics simulations and free energy landscapes. Phys. Chem. Chem. Phys. 2022, 24, 22129–22143. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.; Wang, P.; Tu, G.; Yang, F.; Zheng, G.; Li, X.; Li, X.; Chen, Y.; Yao, X.; Zhu, F. Computational identification of the binding mechanism of a triple reuptake inhibitor amitifadine for the treatment of major depressive disorder. Phys. Chem. Chem. Phys. 2018, 20, 6606–6616. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Huai, Z.; He, Q.; Liu, Z. A General Picture of Cucurbit[8]uril Host–Guest Binding. J. Chem. Inf. Model. 2021, 61, 6107–6134. [Google Scholar] [CrossRef]
- Vatansever, S.; Erman, B.; Gümüş, Z.H. Comparative effects of oncogenic mutations G12C, G12V, G13D, and Q61H on local conformations and dynamics of K-Ras. Comput. Struct. Biotech. 2020, 18, 1000–1011. [Google Scholar] [CrossRef]
- Prakash, P.; Hancock, J.F.; Gorfe, A.A. Binding hotspots on K-ras: Consensus ligand binding sites and other reactive regions from probe-based molecular dynamics analysis. Proteins 2015, 83, 898–909. [Google Scholar] [CrossRef]
- Wang, X. Conformational Fluctuations in GTP-Bound K-Ras: A Metadynamics Perspective with Harmonic Linear Discriminant Analysis. J. Chem. Inf. Model. 2021, 61, 5212–5222. [Google Scholar] [CrossRef]
- Vatansever, S.; Erman, B.; Gümüş, Z.H. Oncogenic G12D mutation alters local conformations and dynamics of K-Ras. Sci. Rep. 2019, 9, 11730. [Google Scholar] [CrossRef]
- Lu, S.; Jang, H.; Nussinov, R.; Zhang, J. The Structural Basis of Oncogenic Mutations G12, G13 and Q61 in Small GTPase K-Ras4B. Sci. Rep. 2016, 6, 21949. [Google Scholar] [CrossRef]
- Gorfe, A.A.; Grant, B.J.; McCammon, J.A. Mapping the Nucleotide and Isoform-Dependent Structural and Dynamical Features of Ras Proteins. Structure 2008, 16, 885–896. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wang, L.; Bao, H.; Chen, J. Cluster analysis on conformational changes of the GDP/KRAS complex induced by A59G and D33E. Chem. Phys. Lett. 2021, 781, 138995. [Google Scholar] [CrossRef]
- Pierce, L.C.T.; Salomon-Ferrer, R.; Augusto, F.; de Oliveira, C.; McCammon, J.A.; Walker, R.C. Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics. J. Chem. Theory Comput. 2012, 8, 2997–3002. [Google Scholar] [CrossRef]
- Wang, J.; Arantes, P.R.; Bhattarai, A.; Hsu, R.V.; Pawnikar, S.; Huang, Y.-M.M.; Palermo, G.; Miao, Y. Gaussian accelerated molecular dynamics: Principles and applications. WIREs Comput. Mol. Sci. 2021, 11, e1521. [Google Scholar] [CrossRef]
- Miao, Y.; Feher, V.A.; McCammon, J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J. Chem. Theory Comput. 2015, 11, 3584–3595. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Miao, Y. Peptide Gaussian accelerated molecular dynamics (Pep-GaMD): Enhanced sampling and free energy and kinetics calculations of peptide binding. J. Chem. Phys. 2020, 153, 154109. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Protein–Protein Interaction-Gaussian Accelerated Molecular Dynamics (PPI-GaMD): Characterization of Protein Binding Thermodynamics and Kinetics. J. Chem. Theory Comput. 2022, 18, 1275–1285. [Google Scholar] [CrossRef]
- Chen, J.; Wang, W.; Pang, L.; Zhu, W. Unveiling conformational dynamics changes of H-Ras induced by mutations based on accelerated molecular dynamics. Phys. Chem. Chem. Phys. 2020, 22, 21238–21250. [Google Scholar] [CrossRef]
- Grant, B.J.; Gorfe, A.A.; McCammon, J.A. Ras Conformational Switching: Simulating Nucleotide-Dependent Conformational Transitions with Accelerated Molecular Dynamics. PLoS Comput. Biol. 2009, 5, e1000325. [Google Scholar] [CrossRef]
- Wang, J.; Miao, Y. Mechanistic Insights into Specific G Protein Interactions with Adenosine Receptors. J. Phys. Chem. B 2019, 123, 6462–6473. [Google Scholar] [CrossRef]
- Miao, Y.; McCammon, J.A. Mechanism of the G-protein mimetic nanobody binding to a muscarinic G-protein-coupled receptor. Proc. Natl. Acad. Sci. USA 2018, 115, 3036–3041. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, W.; Sun, H.; Pang, L.; Bao, H. Binding mechanism of inhibitors to p38α MAP kinase deciphered by using multiple replica Gaussian accelerated molecular dynamics and calculations of binding free energies. Comput. Biol. Med. 2021, 134, 104485. [Google Scholar] [CrossRef]
- Xiaoli, A.; Yuzhen, N.; Qiong, Y.; Yang, L.; Yao, X.; Bing, Z. Investigating the Dynamic Binding Behavior of PMX53 Cooperating with Allosteric Antagonist NDT9513727 to C5a Anaphylatoxin Chemotactic Receptor 1 through Gaussian Accelerated Molecular Dynamics and Free-Energy Perturbation Simulations. ACS Chem. Neurosci. 2022, 13, 3502–3511. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Liang, W.; Shi, X.; Fan, J.; Kong, R.; Liu, Y.; Zhang, J.; Chen, T.; Lu, S. Delineating the activation mechanism and conformational landscape of a class B G protein-coupled receptor glucagon receptor. Comput. Struct. Biotech. 2022, 20, 628–639. [Google Scholar] [CrossRef]
- Chen, J.; Zeng, Q.; Wang, W.; Sun, H.; Hu, G. Decoding the Identification Mechanism of an SAM-III Riboswitch on Ligands through Multiple Independent Gaussian-Accelerated Molecular Dynamics Simulations. J. Chem. Inf. Model. 2022, 62, 6118–6132. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Zeng, Q.; Wang, W.; Sun, H.; Wei, B. Exploring the deactivation mechanism of human β2 adrenergic receptor by accelerated molecular dynamic simulations. Front. Mol. Biosci. 2022, 9, 972463. [Google Scholar] [CrossRef]
- Amadei, A.; Linssen, A.B.M.; Berendsen, H.J.C. Essential dynamics of proteins. Proteins 1993, 17, 412–425. [Google Scholar] [CrossRef]
- Hayward, S.; Kitao, A.; Gō, N. Harmonicity and anharmonicity in protein dynamics: A normal mode analysis and principal component analysis. Proteins 1995, 23, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.; Liu, X.; Zhang, S.; Su, J.; Zhang, Q.; Chen, J. Molecular Dynamics Exploration of Selectivity of Dual Inhibitors 5M7, 65X, and 65Z toward Fatty Acid Binding Proteins 4 and 5. Int. J. Mol. Sci. 2018, 19, 2496. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, T.; Chen, J. Exploring drug-resistant mechanisms of I84 V mutation in HIV-1 protease toward different inhibitors by thermodynamics integration and solvated interaction energy method. Chem. Phys. Lett. 2018, 706, 400–408. [Google Scholar] [CrossRef]
- Ichiye, T.; Karplus, M. Collective motions in proteins: A covariance analysis of atomic fluctuations in molecular dynamics and normal mode simulations. Proteins 1991, 11, 205–217. [Google Scholar] [CrossRef]
- Liang, S.; Liu, X.; Zhang, S.; Li, M.; Zhang, Q.; Chen, J. Binding mechanism of inhibitors to SARS-CoV-2 main protease deciphered by multiple replica molecular dynamics simulations. Phys. Chem. Chem. Phys. 2022, 24, 1743–1759. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Liu, X.; Zhang, S.; Yan, F.; Zhang, Q.; Chen, J. Insight into selective mechanism of class of I-BRD9 inhibitors toward BRD9 based on molecular dynamics simulations. Chem. Biol. Drug Des. 2019, 93, 163–176. [Google Scholar] [CrossRef]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
- Bao, H.; Wang, W.; Sun, H.; Chen, J. Binding modes of GDP, GTP and GNP to NRAS deciphered by using Gaussian accelerated molecular dynamics simulations. SAR QSAR Environ. Res. 2023, 34, 65–89. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Zeng, J.; Xia, F.; Cui, Q.; Deng, X.; Xu, X. Conformations and binding pockets of HRas and its guanine nucleotide exchange factors complexes in the guanosine triphosphate exchange process. J. Comput. Chem. 2022, 43, 906–916. [Google Scholar] [CrossRef] [PubMed]
- Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
- Adasme, M.F.; Linnemann, K.L.; Bolz, S.N.; Kaiser, F.; Salentin, S.; Haupt, V.J.; Schroeder, M. PLIP 2021: Expanding the scope of the protein–ligand interaction profiler to DNA and RNA. Nucleic Acids Res. 2021, 49, W530–W534. [Google Scholar] [CrossRef]
- Salentin, S.; Schreiber, S.; Haupt, V.J.; Adasme, M.F.; Schroeder, M. PLIP: Fully automated protein–ligand interaction profiler. Nucleic Acids Res. 2015, 43, W443–W447. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Case, D.A.; Cheatham, T.E., III; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Meagher, K.L.; Redman, L.T.; Carlson, H.A. Development of polyphosphate parameters for use with the AMBER force field. J. Comput. Chem. 2003, 24, 1016–1025. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Joung, I.S.; Cheatham, T.E., III. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B 2008, 112, 9020–9041. [Google Scholar] [CrossRef] [PubMed]
- Joung, I.S.; Cheatham, T.E., III. Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters. J. Phys. Chem. B 2009, 113, 13279–13290. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Sinko, W.; Pierce, L.; Bucher, D.; Walker, R.C.; McCammon, J.A. Improved Reweighting of Accelerated Molecular Dynamics Simulations for Free Energy Calculation. J. Chem. Theory Comput. 2014, 10, 2677–2689. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of N-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Zaguirre, J.A.; Catarello, D.P.; Wozniak, J.M.; Skeel, R.D. Langevin stabilization of molecular dynamics. J. Chem. Phys. 2001, 114, 2090–2098. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef] [PubMed]
- Götz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef] [PubMed]
- McLachlan, A.D. Gene duplications in the structural evolution of chymotrypsin. J. Mol. Biol. 1979, 128, 49–79. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E., III. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]




| Hydrogen Bonds a | Occupancy (%) b | ||||
|---|---|---|---|---|---|
| Residue | GDP | WT | G12A | G12D | G12R |
| K16-N-H | O2B | 99.9 | 99.9 | 99.2 | 99.9 |
| A18-N-H | O2A | 99.4 | 98.5 | 83.4 | 99.2 |
| G15-N-H | O2B | 98.8 | 99.2 | 99.2 | 99.1 |
| S17-N-H | O3A | 98.1 | 99.8 | 85.6 | 99.6 |
| G13-N-H | O1B | 96.8 | 97.7 | 92.7 | 98.7 |
| V14-N-H | O2B | 41.2 | 30.6 | 32.3 | 30.1 |
| N116-ND2-HD21 | N7 | 89.4 | 93.1 | 85.9 | 92.8 |
| K117-NZ-HZ2 | O4’ | 20.3 | 16.9 | 11.8 | 23.7 |
| S145-OG-HG | N1 | 64.1 | 60.3 | 61.5 | 60.5 |
| K147-N-H | O6 | 86.8 | 85.2 | 83.9 | 87.1 |
| A146-N-H | O6 | 60.8 | 63.1 | 67.3 | 61.7 |
| D119-OD1 | N1-H1N | 97.6 | 80.1 | 88.5 | 95.1 |
| D119-OD2 | N2-H21 | 95.6 | 83.6 | 78.1 | 92.4 |
| V29-O | O2’-H2’ | 25.5 | 22.9 | 28.8 | 27.3 |
| D30-OD1 | O2’-H2’ | 19.6 | 10.3 | 25.4 | 10.9 |
| D30-OD2 | O3’-H3’ | 17.8 | 8.2 | 23.1 | 9.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, S.; Zheng, L.; Ren, Y.; Wang, Z. Impacts of Mutations in the P-Loop on Conformational Alterations of KRAS Investigated with Gaussian Accelerated Molecular Dynamics Simulations. Molecules 2023, 28, 2886. https://doi.org/10.3390/molecules28072886
Shi S, Zheng L, Ren Y, Wang Z. Impacts of Mutations in the P-Loop on Conformational Alterations of KRAS Investigated with Gaussian Accelerated Molecular Dynamics Simulations. Molecules. 2023; 28(7):2886. https://doi.org/10.3390/molecules28072886
Chicago/Turabian StyleShi, Shuhua, Linqi Zheng, Yonglian Ren, and Ziyu Wang. 2023. "Impacts of Mutations in the P-Loop on Conformational Alterations of KRAS Investigated with Gaussian Accelerated Molecular Dynamics Simulations" Molecules 28, no. 7: 2886. https://doi.org/10.3390/molecules28072886
APA StyleShi, S., Zheng, L., Ren, Y., & Wang, Z. (2023). Impacts of Mutations in the P-Loop on Conformational Alterations of KRAS Investigated with Gaussian Accelerated Molecular Dynamics Simulations. Molecules, 28(7), 2886. https://doi.org/10.3390/molecules28072886





